Neutral processes underlying the macro eco-evolutionary dynamics of mixed-ploidy systems

Abstract

Polyploidy, i.e. the occurrence of multiple sets of chromosomes, is regarded as an important phenomenon in plant ecology and evolution, with all flowering plants likely having a polyploid ancestry. Owing to genome shock, minority cytotype exclusion and reduced fertility, polyploids emerging in diploid populations are expected to face significant challenges to successful establishment. Their establishment and persistence are often explained by possible fitness or niche differences that would relieve the competitive pressure with diploid progenitors. Experimental evidence for such advantages is, however, not unambiguous, and considerable niche overlap exists among most polyploid species and their diploid counterparts. Here, we develop a neutral spatially explicit eco-evolutionary model to understand whether neutral processes can explain the eco-evolutionary patterns of polyploids. We present a general mechanism for polyploid establishment by showing that sexually reproducing organisms assemble in space in an iterative manner, reducing frequency-dependent mating disadvantages and overcoming potential reduced fertility issues. Moreover, we construct a mechanistic theoretical framework that allows us to understand the long-term evolution of mixed-ploidy populations and show that our model is remarkably consistent with recent phylogenomic estimates of species extinctions in the Brassicaceae family.

1. Introduction

Polyploidy, i.e. the outcome of whole-genome duplication, is an important source of speciation and species diversification, with extensive implications for plant ecology and evolution [1–5]. All flowering plants have a polyploid ancestry, while many well-known plant lineages (e.g. grasses, orchids and legumes) also show evidence for additional whole-genome duplications in their evolutionary history [3,6]. Despite their success, the establishment and evolution of polyploid taxa remain highly debated, as genome duplication also entails considerable costs. The minority cytotype exclusion (MCE) principle, for instance, postulates that the establishment of new cytotypes in a population may be hampered by a frequency-dependent mating disadvantage [7,8], while polyploids may also have significantly reduced fertility [9,10]. The formation of multi-valents during meiosis and subsequent mis-segregation of chromosomes lead to unbalanced gametes that compromise fertility, which has long been recognized as an important hurdle in polyploid establishment [11–14]. Reduced fertility in tetraploid maize progeny can range from 20 to 40% [15,16], and seed set rate can be less than 40% in polyploid rice [17]. It is thus reasonable to expect that not only MCE but also reduced fertility may have a strong impact on nascent polyploids, thereby imposing a great challenge for such organisms to emerge and persist among diploid relatives.

The emergence of polyploid populations has often been associated with their capacity to exploit new habitats owing to phenotypic differences, as well as enhanced resistance to environmental stress [4,18]. However, even though a few studies have been able to map niche divergence in allopolyploids [19,20], i.e. polyploids formed by hybridization of two or more species, there is scant evidence for niche differentiation in polyploids that emerge from a single species, or autopolyploids. Interestingly, recent research suggests that autopolyploids may be able to expand their niche, but niche shift alone cannot explain their coexistence with diploid relatives, since considerable niche and geographical overlap among cytotypes is often verified [14,21–24]. Moreover, the ability to explore and invade novel niches would be expected to make polyploids less prone to extinction, which contrasts with mounting evidence that extinction rates in polyploids exceed those of diploid species [25–29]. Levin [28] proposed that elevated extinction rates probably arise from the instability of neopolyploids, i.e. young and new polyploids, which are likely to have low persistence owing to their small geographical footprints. A comprehensive understanding of how polyploids might overcome genomic shock, MCE and reduced fertility, and enlarge their geographical footprints at the population and community level is nonetheless lacking.

Polyploid formation usually follows from the merging of unreduced gametes. Polyploids are formed at varying rates, with frequencies ranging from 0 to 90% across the plant kingdom and averaging around 2.52% across species in the Brassicaceae family [30,31]. Through analysis of unreduced gamete frequencies, and attempts to include fertility differences, mathematical and computational models built to study polyploid dynamics have been able to provide important insights into the conditions that may lead to polyploid establishment and persistence [8,32–37]. However, these models often provide strict analytical solutions that do not capture the variability found in real biological systems, rely on hypothetical fitness advantages or include niche differences that could potentially lead to coexistence. Also, the focus of such models has been primarily on the population level, and thus questions regarding community-level dynamics of mixed-ploidy populations remain largely unexplored.

Niche and fitness differences are not the only mechanisms leading to species coexistence and invasion. Neutral processes, which do not require trait or fitness differences between organisms, provide a different perspective on the spatial and temporal dynamics of biodiversity at local and regional scales [38,39]. Given the elusive effects of niche and positive fitness differences on polyploid dynamics, it becomes important to understand whether neutral dynamics can explain the establishment, speciation and extinction rates of higher ploidy taxa. The development of eco-evolutionary models following the onset of the neutral theory of biodiversity has allowed researchers to explain large patterns of biodiversity distribution and genetic evolution in natural systems [39–44]. In particular, speciation models of spatially explicit populations with finite genomes [39,45] provide an opportunity to understand the evolution of mixed-ploidy systems. A better understanding of why polyploids seem to experience higher extinction rates requires a theoretical framework that allows us to explore the evolution of populations in time and space.

Here, we present a new model of spatially structured populations of organisms with finite genomes aimed at understanding how mixed-ploidy populations evolve over time. Our model is neutral in the sense that different species emerging in the system display no fitness differences, and the environment does not impose any selection on particular genotypes. However, we test different levels of reduced fertility in polyploid organisms and aim to understand how it may affect the dynamics of the system, including the fully neutral scenario, i.e. 0% of polyploid reduced fertility. We examine the relationship between reduced fertility and unreduced gamete frequencies in populations interacting in space, and study the conditions that lead to polyploid establishment and coexistence. Moreover, by studying the evolution of our system, we can understand the mechanisms affecting speciation and extinction rates in mixed-ploidy systems. We then use a large phylogenomic dataset from the Brassicaceae family, as developed in recent work [29], to validate our results. With the model developed in this work, coupled with a real dataset on the Brassicaceae family, we can provide the most complete theoretical framework to date for the eco-evolutionary dynamics of mixed-ploidy systems.

2. Methods

(a) . General framework

Our model considers a homogeneous space represented by a square lattice of size 128 × 128 cells. A population of size S = 2500 is uniformly distributed in space and evolves as a result of mutation, recombination and dispersal. Initially, clonal individuals are diploids and represented by two identical vectors (chromosomes) of size |B| = 200, the elements of which can take any integer value from the set {0, 1, 2, 3}, corresponding to each of the four nucleotides found in genomes. Individuals are hermaphrodites, and reproduction is carried out between individuals whose gametes share a minimum genetic similarity GS_min = 95%. Generations are discrete, and at each time step, the population size is kept constant at its carrying capacity S. Each individual at every time step is a seeker, which has a set of potential partners defined by all individuals, including itself, inhabiting the region inside its mating radius R. There is a probability Q = 0.30 that a seeker will not reproduce at all, in which case a random individual inside its mating radius is chosen to reproduce instead. This is approximately the probability that an individual will not reproduce owing to drift when sampled from a population of size M with replacement in the limit M → ∞. Genetic constraints for mating, along with dispersal limitations, foster the clustering of genetically similar organisms which eventually become genetically isolated from their surroundings. For a deeper understanding of how GS_min and dispersal limitations induce sympatric speciation, we refer the reader to the seminal work of de Aguiar et al. [39], and for a more mathematical treatment of the framework, see de Aguiar [45].

(b) . Mating dynamics and meiosis

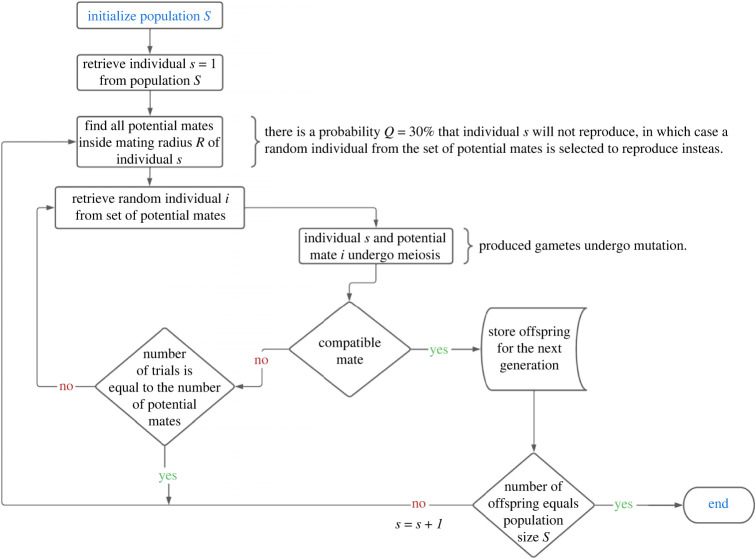
If there are N potential partners inside the seeker's mating radius R, then N trials with replacement are performed in search of a compatible mate (see §2c for a definition). This introduces sampling following a geometric distribution, which is a convenient way to describe successful mating probabilities in our system. If the seeker is not able to find a compatible mate, then the process is repeated until (i) it finds a mate, or (ii) it is replaced by a neighbour with probability Q (see figure 1 for a flowchart of the basic processes). Thus, individuals whose genetic structure differs strongly from their potential partners might be rapidly excluded from the system.

Figure 1.

Flowchart of the basic processes involved in the model. Arrows indicate the flux of processes. Conditional statements are represented by diamonds and closed actions by rectangles; curly braces indicate comments. The flowchart represents a run of the algorithm for a single generation, through the iterative update of the old population. The terminator at the lower right corner of the figure indicates the end of execution.

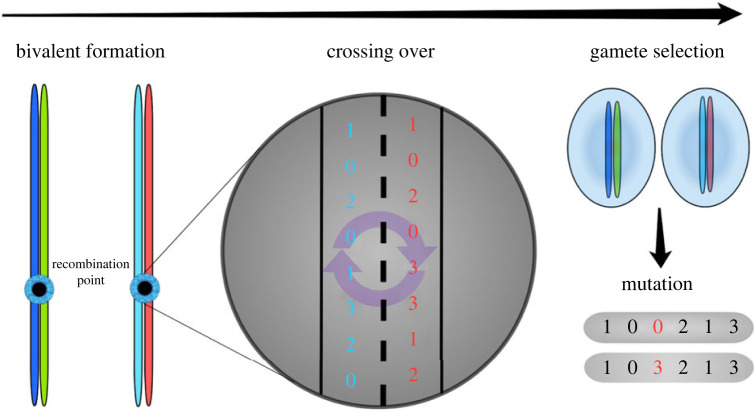
At each mating trial, both individuals undergo meiosis and produce gametes. This process is done by the pairing of chromosomes (bivalent formation): one in the case of diploids and two in the case of tetraploids. In the case of diploids, chromosomes break at a random location, signalling the point of meiotic recombination, and exchange nucleotides along a linear sequence of length l = 0.05|B| (see Results and electronic supplementary material, text S1 and figure S4 for different recombination rates). Then, a gamete is one of the chromosomes chosen with equal probability. There is a small chance, however, that gametes will be unreduced, i.e. a gamete is formed by selecting both chromosomes, and this is referred to as unreduced gamete frequency φ.

Meiosis in tetraploid individuals occurs in the same way as in diploid individuals. However, the number of possible bivalent pairs is ₄C₂ (tetraploids are represented by four copies of chromosomes, see below) and no preferential pairing of chromosomes is implemented, making all six possible combinations equally likely (see figure 2 for a schematic representation). This is a simplification of real autopolyploid systems, which exhibit multi-valent formation and complex molecular dynamics. Although we recognize the potential implications of meiotic dynamics for the genetic makeup of populations and their evolution, such considerations are outside the scope of the present work, as no genotype–phenotype maps are considered. To account for meiotic errors produced by multi-valent formation in polyploid meiosis, we introduce a parameter ε that corresponds to the probability of abnormal gamete formation and is referred to as reduced fertility. When an abnormal gamete is formed, the seeker must undergo meiosis once again and will keep searching for a compatible mate. In natural systems, the parameter ε is highly variable. Here we explore ε with values ranging from 0 (where the system assumes full neutrality) to 0.2.

Figure 2.

Schematic representation for the formation of new gametes in a tetraploid individual. Process flow is from left to right, represented by the black arrow on top of the image. First, chromosomes are paired, forming bivalents, after which the linear sequence for meiotic recombination is randomly placed along the chromosome length (recombination point). The nucleotides (represented by integer numbers in the zoomed region) are then swapped between sequences, which represents crossing over. A gamete is formed by randomly selecting one of the two available bivalents (chromosome colours are preserved in the figure), which is then submitted to a mutation rate per nucleotide μ (schematically drawn in the lower right corner of the figure). The paired gametes produced by two different organisms are then joined and form the genome of the offspring.

When gametes are formed, they are subject to a fixed mutation rate µ = 5 × 10⁻⁵ per nucleotide. We assume that the mutation rate on the genome is not influenced by ploidy changes and therefore remains constant among all individuals in the system. Then, an offspring is born by joining gametes from compatible mates and placing it at the position of the seeker for the next generation, or dispersed randomly, within a radius r cells from the seeker with probability α = 0.01 (see de Aguiar et al. [39]). Notice that because gametes can only be haploids or diploids, the system will only produce diploid and tetraploid organisms, where triploids are not possible because of the definition of what makes a compatible mate. Also, there are no restrictions on the number of individuals per lattice cell, with individuals having free movement over the lattice.

A newborn individual has a probability of n/N of finding a compatible mate inside its mating radius, where n is the number of compatible mates. This probability is 1 for all individuals at the start of the simulation because every individual has the same ploidy level and the same genome. A tetraploid seeker, in each of the N trials, will mate successfully with the following probability:

$$p={\displaystyle \frac{n}{N}{(1-\epsilon )}^2.}$$ 2.1

The term (1 − ε)² is a consequence of the independence of meiotic events at each mating trial. Also, as the mating dynamics implemented in our model follow a geometric distribution, the probability that a tetraploid successfully mates in at most x mating trials is given by the cumulative geometric distribution:

$$P(X\le x)=1-{(1-p)}^x.$$ 2.2

(c) . Mate compatibility and species identification

A compatible mate is an individual whose ploidy level (number of chromosomes) equals the seeker's ploidy level, i.e. no gene flow between different cytotypes is allowed, gametes from both parents have the same number of chromosomes, and gametes share a genetic similarity (GS) greater than or equal to GS_min. GS between two chromosomes is computed as the number of identical nucleotides between them relative to their length |B|. Let δ(x, y) denote a step function, where $x,y\in \mathbb{N}\cup 0$, defined as follows:

$$\delta (x,y)=\{\begin{array}{c}0\hspace{0.17em}\mathrm{if}\hspace{0.17em}x=y\\ 1\hspace{0.17em}\mathrm{if}\hspace{0.17em}x\ne y\end{array}.$$ 2.3

Then, the GS between chromosomes B_i and B_j is simply:

$$GS(B_i,B_j)={\displaystyle \frac{|B|-{\sum }_k\delta (B_{i,k},B_{j,k})}{|B|},}$$ 2.4

where $B_{i,k}$ is the kth element of the ith chromosome. To compute GS for two sets of more than one chromosome each, we simply seek the best alignment of chromosomes that maximizes genetic similarity (see electronic supplementary material, code S1). Individuals of different ploidies have GS = 0 by default. This condition constrains gene flow between ploidies and allows us to study polyploids as an independent system. Even though this is not necessarily the case in real biological systems, such an assumption further constrains polyploid mating opportunities, providing an important base scenario to understand how the relaxation of gene flow can foster polyploid emergence.

Finally, species are identified as clusters of reproductively compatible individuals, in which any member has at least one individual inside the cluster whose GS between chromosomes is greater than or equal to GS_min. This is the most inclusive GS-dependent definition of a species because it can consider incompatible individuals as the same species [39]. A species is then constructed by selecting a first individual and identifying all remaining individuals whose GS ≥ GS_min. With the first cluster formed, all remaining individuals outside the cluster are then compared with the second individual, the third, and so on. The process is repeated until the cluster is completely isolated from the remaining individuals in the system. Cluster sizes thus represent the population size of a species and can be used to compute species-abundance distributions, i.e. the number of individuals per species. Extinction rates of the identified species were quantified at time intervals of 500 simulation steps, or generations (see electronic supplementary material, code S1 for pseudo-codes).

(d) . Computational experiments and data analysis

We first tested the prediction that rates of unreduced gamete formation and the relative reduced fertility of tetraploids can explain the dynamics of mixed-ploidy systems in space. We therefore conducted experiments for different values of ε covering a range from 0 to 20%, in incremental steps of 0.25%, and φ covering a range from 0 to 5%, in incremental steps of 0.1%. These experiments allowed us to understand how such parameters influence the spatio-temporal dynamics of diploids and tetraploids. We not only quantified population sizes for both diploids and tetraploids over time, but also described the spatial dynamics of tetraploids. Rather than deriving any spatial statistics from the obtained distributions, we introduce a measure of MCE strength, defined as (1 − n/N), calculated for every tetraploid in the system, which serves as an elegant proxy for spatial clustering. When MCE strength is zero, all potential mating partners n* are compatible, i.e. all tetraploids have only genetically compatible tetraploids in their mating ranges. We further tested the qualitative robustness of our analyses by sensitivity analyses for different mating radius R and dispersal radius r (see Results and electronic supplementary material, figure S2).

In a subsequent step, we tested the hypothesis that emergent spatial patterns from the diploid–tetraploid system are critical to long-term eco-evolutionary dynamics of mixed-ploidy systems, determining patterns of speciation and extinction rates. We therefore quantified the number of species, their abundances, i.e. number of individuals per species, and extinctions at regular time intervals (500 generations) for both ploidies. We report results on the number of species as a function of time, i.e. how an initial single species evolves into a regional community of different (but functionally equal) species, and on the differences in species-abundance distributions and extinction rates between ploidy levels. Besides mixed-ploidy systems, we also studied the dynamics of systems displaying a single ploidy level, i.e. only diploids or only tetraploids, with and without a spatial structure (see Results and electronic supplementary material, text S1). To validate our results, we used data on speciation and extinction rates recently generated for 1333 species of the Brassicaceae family [29]. This validation is based on raw data provided by Román-Palacios et al. [29], reproduced with permission of the authors in electronic supplementary material, data S1.

All results presented in this work are based on 20 independent runs of the simulation for each of the analyses reported in the Results. In table 1, we summarize the parameters and their respective values, or ranges, used in this work. Also, the lattice size and number of individuals in the system do not have a qualitative influence on the results (see Results and electronic supplementary material, figure S1) and are therefore chosen based on computational tractability and visualization convenience. We further provide complete code documentation, with pseudo-codes and additional explanations for the logical structure of the simulation, which can also be found in electronic supplementary material, code S1.

Table 1.

Description of parameters and values used in the simulation. The table contains a brief description of each parameter, its values or ranges used in the simulations, and its symbol.

parameter description	range of values	parameter symbol
number of generations used for the evolution of the system	10 000	—
carrying capacity	2500	S
length of a single chromosome; diploids have 2 and polyploids 4	200	|B|
mating radius: defines the region around the seeker in which potential mates are retrieved	3 to 5 cells	R
dispersal radius: defines the potential region around the seeker in which offspring will be placed	2 to 5 cells	r
genetic similarity threshold used to define compatible mates	95%	GSmin
meiosis coefficient: determines how many nucleotides are exchanged between chromosomes during meiosis; given as a percentage of chromosome length	0 to 5%	l
probability that unreduced gametes will be formed following meiosis in diploids	0 to 5%	φ
probability that a nucleotide is mutated following meiosis	0.005%	µ
probability that offspring does not replace the seeker's position and is dispersed within a region defined by the dispersal radius	1%	α
probability that an individual is not selected for reproduction	30%	Q
probability that gametes are not correctly segregated during meiosis, i.e. reduced fertility.	0 to 20%	ε

3. Results

(a) . Population dynamics and polyploid establishment

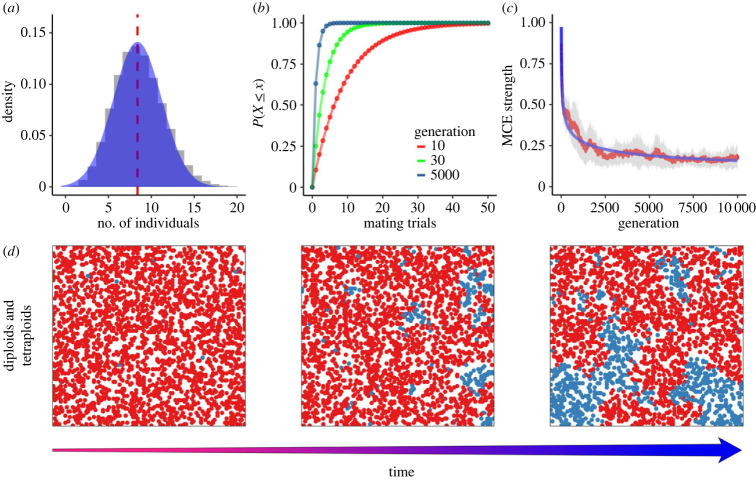
An important feature of the model is that the overall density of individuals along generations, measured as the set of potential mates for each individual, is well described by a normal distribution with a mean $\overline{n}=8.39$ and variance S² = 7.98 (figure 3a). The variance in the distribution of individuals in space is due only to dispersal upon the shift of generations and the initial configuration of the system. As time unfolds, tetraploids are born by the merging of unreduced gametes (produced with probability φ) between diploid parents. Consider a newborn tetraploid individual surrounded by diploids, (n = 1 in equation (2.1)). If we take N to be $\lfloor \overline{n}\rfloor$, i.e. the floor of $\overline{n}$, and ε = 0.2, then for N trials equation (2.2) gives a probability of 0.4868. A newborn tetraploid will then improve its chances of successfully reproducing either by having a lower ε or by being present in a region less densely occupied by diploids (see Methods).

Figure 3.

General dynamics of mixed-ploidy populations. Results are based on 20 independent runs with parameters φ = 0.05 and ε = 0.12. (a) Density distribution of the number of potential mates measured every 500 generations for a total of 10 000 generations; (b) number of mating trials for a successful mating event in three distinct generations, estimated by the averaging (1 − n⁄N). The solid line connecting points is for aesthetic purposes only; (c) temporal progression of MCE strength. A lower MCE strength represents a higher degree of spatial clustering. The solid blue line represents the best fit of a function of the form cx^(−1/4) as a guide for the eye, while the red line depicts the average, and shaded ribbons represent ±1 s.d.; (d) spatial patterns of diploids (red) and tetraploids (blue) as the simulation unfolds. Time increases from left to right, with the square lattices representing the state of the system at generations 10 (left), 500 (centre) and 5000 (right), respectively.

Diploids produce unreduced gametes continuously with probability φ, and thus, newborn tetraploids appear in every generation. The random emergence of tetraploids in space enables small clusters to emerge where the proportion of the higher ploidy cytotype is increased. If we assume n = 2 in the previous example, then equation (2.2) yields 0.7521. As a result, subpopulations, i.e. partitions of the original population, with higher proportions of tetraploids will tend to persist across generations because the number of offspring will reflect the proportions of the previous generations, resulting in persistent tetraploid clusters. Figure 3b depicts equation (2.2) as a function of mating trials, by averaging n/N at each generation for each tetraploid organism. As the simulation progresses, the number of mating trials required for tetraploids to have a successful mating is significantly reduced. These dynamics can also be seen by considering MCE strength over generations, as depicted in figure 3c. MCE strength decays rather quickly with time, driven by the iterative formation of contiguous tetraploid clusters (figure 3d). This process is unaltered with respect to the scale of the system (see electronic supplementary material, figure S1).

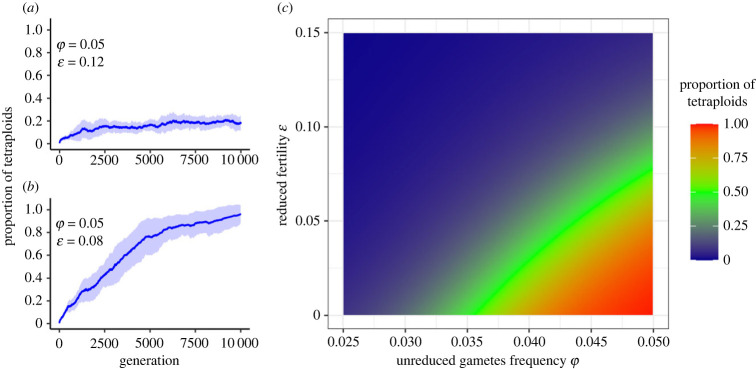
The stochastic and progressive spatial aggregation of tetraploids, culminating in persistent tetraploid spatial clusters, does not necessarily lead to a complete substitution of the parent cytotype. The frequency of unreduced gametes (φ) coupled with the reduced fertility of tetraploids (ε) determines whether different cytotypes can coexist throughout the simulation. For instance, for φ = 0.05 and ε = 0.12, stable coexistence, i.e. a constant proportion of both cytotypes in the system, can be verified for the entire run (figure 4a), while for φ = 0.05 and ε = 0.08, tetraploids will overtake the system, eventually erasing the parental cytotype from the population (figure 4b). The combined effects of φ and ε determine the degree to which polyploids invade the system (figure 4c). As long as the pair (φ,ε) generates a proportion of tetraploids below the 50% threshold, coexistence will be verified throughout the entire simulation, with small fluctuations in cytotype proportions due to range oscillations. Although the same patterns can be verified for different mating and dispersal radii, the probability of establishment and persistence of tetraploids decreases as these spatial constraints are relieved (i.e. when the dispersal and mating distances increase; see electronic supplementary material, figure S3).

Figure 4.

Dependence of the proportion of tetraploids on the frequency of unreduced gametes φ and reduced fertility ε. Temporal progression of the proportion of tetraploids in the system: (a) stable coexistence of tetraploids and diploids, and (b) substitution of the diploid population by tetraploids. (c) The proportion of tetraploids at generation 2500. As the pair (φ,ε) approaches the green arc (50% proportion of tetraploids), the diploid population is rapidly replaced by tetraploids. See electronic supplementary material, figure S2 for the evolution of tetraploid population sizes with more combinations of φ and ε.

(b) . Speciation, regional community dynamics and extinction events

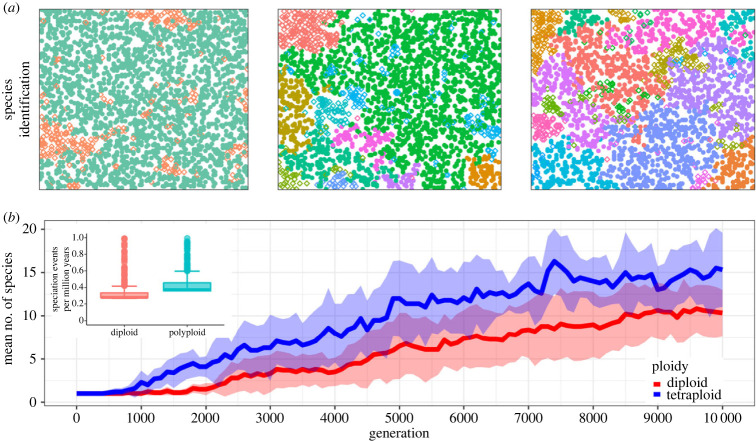
Thus far, we have analysed the dynamics of mixed-ploidy populations with respect to their spatial dynamics. However, a second level of organization operates in the genome space, i.e. the set of all genomes within the system. In general, the continuous accumulation of nucleotide polymorphisms among individuals, catalysed by mutations, recombination and limited dispersal, fractures the genome space into disjoint clusters, i.e. different species (figure 5a). The sampling of genomic configurations within different regions of space, driven by the mating radius R and GS_min, produces a continuum of genetic divergence in space, eventually leading to the interruption of gene flow among subpopulations (see electronic supplementary material, text S1 for the relationship between GS and Euclidean distance). In mixed-ploidy populations, with coexistence between cytotypes (φ = 0.05, and ε = 0.12), the first speciation event occurs at generation 500 for tetraploids, while for diploids, the first speciation event takes place on average 500 generations later (figure 5b). Notice that the number of tetraploid species is consistently higher than the number of diploid species. This is not the case for single-ploidy systems, where tetraploids display much lower speciation rates as compared with diploids (see electronic supplementary material, text S1).

Figure 5.

Speciation dynamics in mixed-ploidy populations. (a) Screenshots of an example simulation at generations 500 (left), 2500 (centre) and 10 000 (left). The different colours represent the different species identified in the system, open diamonds polyploids and filled circles diploids. In generation 500, the only two species present are the diploids (green) and tetraploids (orange), as no speciation event has taken place within the different cytotypes. (b) Diversification of tetraploids (blue) and diploids (red) along generations. The solid line represents the average number of species and shaded ribbons denote the respective s.d. Data were generated based on 20 independent runs. Inset corresponds to average speciation rates per million years from [29] for 1333 species from the Brassicaceae family. Notice that average speciation rates are higher for polyploid than for diploid species.

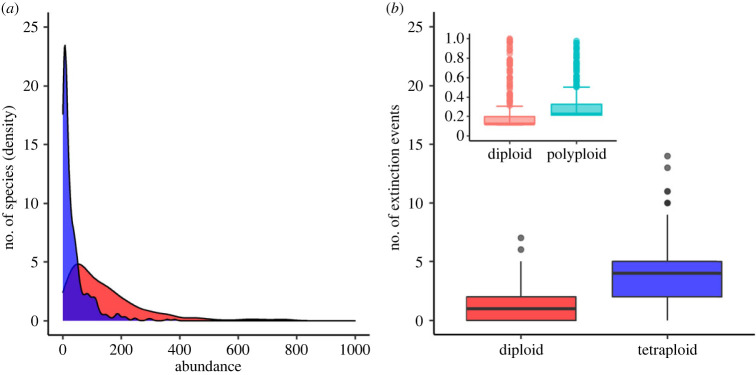
Tetraploid clusters are subject to pressure from surrounding diploids owing to fertility differences between cytotypes, and thus local extinctions occur frequently as a result of tetraploids' range oscillations in time (figure 6a). The vulnerability of tetraploid species was assessed by analysing the species-abundance distributions of both cytotypes. The frequency of low-abundance species is considerably higher for tetraploids than for diploids, and as no intercytotype or interspecies gene flow occurs, these low-abundance tetraploid species are sensitive to demographic stochastic fluctuations in the system, catalysing a higher rate of extinctions (figure 6b; see also electronic supplementary material, video S1 for a qualitative description). These patterns are consistent with data from the Brassicaceae family, as seen in the inset in figure 6b. The higher frequency of low-abundance tetraploid species in our model is due to recurrent tetraploid formation from already diverged diploid species. Such newly produced tetraploid species are then subject to competitive pressure from surrounding diploid organisms, which leads to the observed higher extinction rates in the evolution of the system.

Figure 6.

Species-abundance distribution of mixed-ploidy communities and their associated extinction rates. The distribution of diploid (red) and tetraploid (blue) species' abundances are depicted in (a), where the number of species has been transformed to density for better visualization (y-axis scale 10^–3). Extinction events were measured every 500 out of 10 000 generations in the model (b). Inset corresponds to average extinction events per million years for 1333 species of Brassicaceae family [29]. All results are based on 20 independent runs with φ = 0.05 and ε = 0.12.

4. Discussion

Here, we have built a new spatially explicit neutral model of speciation to examine tetraploid establishment and the eco-evolutionary dynamics of a diploid–tetraploid system. While technically our study focuses on diploid and tetraploid cytotypes, the patterns described can be extended to higher ploidy levels, owing to the absence of genotype–phenotype maps and a strict focus on spatial dynamics from a neutral perspective. In particular, we studied the influence of reduced fertility in tetraploids on the spatial dynamics of mixed-ploidy populations, and how such dynamics influence speciation and extinction rates. Fertility reduction is a significant phenomenon following increases in ploidy levels in the plant kingdom [9,14], and therefore our framework can be interpreted as the emergence of new cytotypes with reduced relative fertility in spatially structured populations. The simplifying assumption of only two cytotypes in an evolving population allowed us to perform analyses and draw conclusions with feasible computational power, and thus we choose to discuss our model within the context of diploid–polyploid systems.

We were able to show that even in the absence of niche differences between cytotypes, or among species, and with increased costs (reduced fertility), sexually reproducing polyploids can still establish and persist. Establishment and persistence are driven by the iterative and stochastic aggregation of polyploids in space, which mitigates frequency-dependent mating disadvantages and can circumvent reduced fertility. Depending on the rates of unreduced gametes produced by diploids and the probability of abnormal gamete formation in polyploid meiosis, higher-ploidy taxa can either coexist with the parental population, overtake it, or never establish. Most models studying dynamics in mixed-ploidy systems have neglected the importance of spatial interactions among organisms, even though space is potentially a crucial factor affecting the establishment of different cytotypes in a diploid population [34,36,37]. For example, recently, Spoelhof et al. [36], studying the dynamics of polyploids with their parental cytotypes at the population level, found that narrow ecological niches contribute to counteracting the effects of MCE to some degree by constraining dispersal and increasing the probability of successful reproduction. These findings are similar to those reported in the present study, albeit at different spatial and temporal scales.

The success of polyploid taxa need not necessarily be associated with fitness advantages or ecological niche shifts and can be solely explained by neutral processes, if local spatial interactions are explicitly considered. For example, Baack [34] parameterized a spatially explicit model based on the diploid–tetraploid system Ranunculus adoneus to show that local dispersal is positively associated with tetraploid establishment and hypothesized that plant families where seed dispersal is limited should have higher rates of polyploid emergence. Indeed, here we elucidate the mechanism by which polyploids can emerge given that dispersal and mating are constrained in space. In particular, the mechanism presented here adds a new perspective on polyploid dynamics. Polyploid organisms often coexist with their diploid relatives and progenitors, and in cases where niche divergence is detected, considerable overlap exists among ploidy levels [21,22,24,45]. In a recent review, Kolář et al. [46] showed that dominant cytotypes within a species are rarely spatially isolated, and autopolyploids and their diploid relatives have been documented to occur in sympatry in several systems [21,22,24,47,48]. Using niche suitability modelling, Gaynor et al. [23] found a decrease in range as the ploidy level increases in the system Galax urceolata, where autotetraploids and diploids display partial geographical overlap. The authors suggest that niche contraction might be the reason underlying such spatial configurations; however, this hypothesis is based on the study of the correlation between spatial occurrence and environmental variables and needs further support by measuring the physiological responses of the different cytotypes under different environmental conditions [23]. The factors leading to contiguous polyploid ranges among diploid relatives can also be explained based on the mechanics behind their establishment, namely, continuous aggregation in space, and may not necessarily be associated with niche contractions. Research to disentangle the mechanisms underlying current spatial patterns in polyploid systems is essential for our understanding of their establishment and stability.

To date, the hurdles associated with MCE and reduced fertility have not been considered together in spatial mixed-ploidy populations. In our model, the combination of these fundamental properties greatly undermines the stability of nascent polyploids, which enjoy greater persistence only when aggregated into contiguous subpopulations. In a recent study, Mráz et al. [49] showed that diploids and tetraploids of Centaurea stoebe can be temporarily stable on small spatial scales, which is likely due to the spatial segregation of the cytotypes. Such conjectures are endorsed by the present work but require further experimental work to precisely understand what factors drive the coexistence of multiple cytotypes in spatially structured populations. Our model extends these patterns into larger temporal scales to show that polyploid extinction rates can be explained by oscillations in their spatial ranges because of fertility differences between cytotypes, as well as neopolyploids that do not persist long enough to form large and stable contiguous populations. This finding supports Levin's [28] hypothesis that higher extinction rates in polyploid taxa are likely due to their high vulnerability upon emergence owing to smaller geographical ranges. The vulnerability of polyploid species is detected by the differential species-abundance distributions between ploidies in our model, where polyploid species have significantly lower abundances. Empirical data to confirm such expectations are needed, but as different cytotypes are often considered to be part of the same species complex, our ability to further understand mixed-ploidy systems is constrained [5,50].

The expected recurrent formation of polyploidy [51] has been explored by Servick et al. [52], where the authors show that the autotetraploid cytotype of Galax urceolata has emerged at least 46 times. As we have shown, the stochastic and recurrent formation of polyploids, associated with dispersal limitations, catalyses the assemblage of more stable and persistent polyploid populations in space. Such a phenomenon has been previously described for Senecio carniolicus, where restricted dispersal kernels have been identified as a plausible cause for the spatial clustering of the different cytotypes in the species [53], which may contribute to the persistence of these cytotypes. Although hybridization between species or introgression was not implemented in this work, we expect that interspecies and intercytotype gene flow can also aid the establishment and persistence of neopolyploid populations. The reduced post-zygotic barriers by means of hybridization or introgression, which may increase the number of compatible gametes, would allow individuals of emerging cytotypes to assemble in space more rapidly by enhancing maintenance of the edges in polyploid ranges. Thus, we argue that investigations on fertility differences, unreduced gametes frequency, and intercytotype gene flow, are of paramount importance to studying the stability of mixed-ploidy natural populations.

The analysis of speciation–extinction dynamics in mixed and single-ploidy populations shows that these systems behave quite differently from one another. We have shown that in mixed-ploidy systems, speciation events in both polyploids and diploids are much more frequent than in single-ploidy systems. Román-Palacios et al. [29] were able to demonstrate that polyploidy had a positive effect on net diversification rates within the Brassicaceae family, thereby significantly contributing to present-day species richness. As shown by our model, the recurrent formation of polyploids and the oscillations in their range sizes among diploid relatives can act as transient partial barriers to gene flow among diploids, contributing to faster divergence between disconnected clusters of diploids and thus increasing richness. Similarly, autopolyploids emerging in spatially distant populations of the same species enjoy faster divergence owing to decreased gene flow, increasing the net speciation rate of the system as a whole. Indeed, the same dynamics can be verified in natural systems. Two genetic clusters from Limonium narbonense, for example, have been found to be diverging owing to isolation by distance in the Iberian Peninsula [54]. The limited dispersal capability of the species contributes to genetic divergence that may eventually lead to speciation. We argue that such processes operating on large temporal scales can profoundly impact diversification rates in mixed-ploidy systems. This highlights the importance of considering the phylogeographic history of populations, which can greatly affect general conclusions drawn from different specific systems.

Data accessibility

All relevant data are within the manuscript and its electronic supplementary material. The code developed for running numerical simulations is available on a GitHub repository at https://github.com/KauaiFe/Polyploidy-V1.0. Readers will also find the code documentation within the electronic supplementary material [55].

Authors' contributions

F.K.: conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing—original draft; F.M.: conceptualization, formal analysis, methodology, project administration, supervision, validation, writing—review and editing; S.M.: conceptualization, investigation, methodology, validation, writing—review and editing; Y.V.d.P.: conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, writing—review and editing; D.B.: conceptualization, formal analysis, investigation, methodology, project administration, resources, supervision, validation; writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed herein.

Conflict of interest declaration

We declare we have no competing interests.

Funding

Y.V.d.P. acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (no. 833522) and from Ghent University (Methusalem funding, BOF.MET.2021.0005.01).