Brain Strain: Computational Model-Based Metrics for Head Impact Exposure and Injury Correlation

Abstract

Athletes participating in contact sports are exposed to repetitive subconcussive head impacts that may have long-term neurological consequences. To better understand these impacts and their effects, head impacts are often measured during football to characterize head impact exposure and estimate injury risk. Despite widespread use of kinematic-based metrics, it remains unclear whether any single metric derived from head kinematics is well-correlated with measurable changes in the brain. This shortcoming has motivated the increasing use of finite element (FE)-based metrics, which quantify local brain deformations. Additionally, quantifying cumulative exposure is of increased interest to examine the relationship to brain changes over time. The current study uses the atlas-based brain model (ABM) to predict the strain response to impacts sustained by 116 youth football athletes and proposes 36 new, or derivative, cumulative strain-based metrics that quantify the combined burden of head impacts over the course of a season. The strain-based metrics developed and evaluated for FE modeling and presented in the current study present potential for improved analytics over existing kinematically-based and cumulative metrics. Additionally, the findings highlight the importance of accounting for directional dependence and expand the techniques to explore spatial distribution of the strain response throughout the brain.

INTRODUCTION

Athletes participating in contact sports experience a wide range of impact scenarios and severities over the course of a season and their career. In addition to the risk of concussive injury, athletes are exposed to the effects of repetitive subconcussive impacts which occur during normal participation in the sport. Head injury in sport has been studied for many years to identify and describe the effects of concussive injury as well as repetitive subconcussive impacts which can occur at various levels of severity.¹⁴ Although football has a high rate of concussion, exposure to repetitive subconcussive head impacts, which occur during normal participation in the sport, are of increasing concern. A recent increase in public awareness of the long-term effects of repetitive head impacts has resulted in extensive research on head impact exposure in athletes. Recent studies have linked long-term brain changes and neurological deficits in athletes to exposure to these repetitive subconcussive head impacts.^3,59,71–73 Head impact exposure in football has been extensively studied, but the biomechanical effects of subconcussive head impacts is not well understood.^{13,20,25,40,77} To better understand how repetitive subconcussive impacts affect the brain, the relationship between impact characteristics (such as impact location and direction) and brain tissue response needs to be well-characterized. Understanding the underlying biomechanics of the full range of impacts experienced by athletes will aid in quantifying the cumulative burden of repetitive impacts.

Because they are thought to be indicative of the inertial response of the brain, head kinematic parameters are often used to evaluate injury risk. There are numerous injury metrics based on kinematic measures and although they are widely used in sports and automotive safety, it remains unclear whether any single kinematic measure is well-correlated with the occurrence of mild traumatic brain injury (mTBI).^{26,28,30,41,65,74,75,78} Many of these injury criteria consider only the peak values of kinematic response parameters and do not account for the effects of impact orientation or region of the head impacted. Directional dependence in brain response has been well-established throughout the literature using animal models as well as FE models.^{1,32,42,55,61,62,79,84} Additionally, impact location and direction of rotation has been shown to affect functional outcome.^4,6,10,11 While many brain injury metrics have been developed over the years, none fully characterize the influence of impact direction.

Human body finite element (FE) models allow detailed analysis of tissue response, and provide the opportunity for new metrics based on regional brain response. Furthermore, FE models are promising given the importance of injury location and the ability to quantify differences in brain response in specific regions of interest (ROIs). Numerous studies have used FE models to estimate strain response to impact with the goal of establishing model-based injury criteria and thresholds.^{16,43,51,52,70,74,83,85,88} The most widely used FE-based measures are the peak maximum principal strain (MPS) of the entire brain and the percentage of brain volume experiencing strains above a defined threshold, also known as cumulative strain damage measure (CSDM). Injury metrics have also been extended to ROIs, which as the brainstem, midbrain, corpus callosum, and thalamus, which has been proposed to better predict injury.^33,43,85 More recent studies have begun to look at strain along white matter fibers to characterize axonal elongation.^{15,18,19,33,39,45,66,80,81} Injury susceptibility measures have also been proposed for the white matter and in specific ROIs to quantify structural integrity and damage.^86,87

Quantifying the cumulative effects of head impacts is of increasing interest. The cumulative burden of head impacts has been quantified by summing the peak linear and rotational accelerations for each impact over a season.¹² An alternative method for quantifying cumulative exposure was proposed by Urban et al. (2013) which involved summing risk calculations for each individual impact using previously developed risk functions.⁷⁷ More recently, the Head Impact Exposure Estimate (HIEE) has been proposed, which estimates an athlete’s total hours of contact exposure using self-report interview. Another metric that incorporates self-report measures of exposure is the Cumulative Head Impact Index (CHII), which combines self-reported exposure with objective measures of exposure based on player position based on previously published studies.^44,59

The advent of wearable impact-sensing devices has allowed collection of head impacts to characterize on-field head impact exposure in athletes. In football specifically, on-field impacts have been collected in numerous studies at all levels of play using the Head Impact Telemetry (HIT) System (Simbex, Lebanon, NH).^{12,20,23,24,40,65,77} The HIT System uses linear accelerometers embedded in the existing padding of helmets to measure real-time head acceleration during normal football participation.⁸ For each registered impact, the following values are computed and saved: impact location, peak XYZ linear acceleration magnitudes, peak XYZ rotational acceleration magnitudes, a 40 ms resultant linear acceleration time history, Head Injury Criterion (HIC15), Gadd Severity Index (GSI) and the HIT-severity profile (HITsp) value.^22,34 The data processing algorithm and validation of the HIT System have been previously described in the literature.^21,49 Although there is some error associated with impact detection and acceleration measurement, these errors are within the acceptable range for other head impact measurement devices.^9,60,68 For the reasons and for its simplicity and availability, the HIT System has been to date the most widely used device for on-field head impact data collection in football.

There is currently no universal kinematic-based injury metric to decisively predict concussion or a corresponding injury tolerance threshold since kinematics are not directly related to the mechanical responses believed to initiate and contribute to injury.⁵³ Additionally, kinematic metrics do not account for region-specific properties and responses of the brain. Given the shortcoming of existing measures of exposure, the goal of the current study was to develop cumulative metrics that quantify response to head impacts using FE-based brain tissue deformation.

MATERIALS AND METHODS

In the current study, a high-resolution brain FE model, the atlas-based brain model (ABM), was used to develop new, or derivative, cumulative exposure metrics based on the strain response of the brain.^56,57 This model contains high anatomic accuracy – namely, detailed modeling of the folds on the surface of the brain, which are known to be important for modeling strain distributions throughout the brain.^17,48 These strain-based metrics quantify brain tissue deformation, which is believed to be a primary mechanism for concussion and diffuse axonal injury (DAI).^29,42,50,74 Additionally, these metrics are able to capture the difference in brain response due to direction of loading and are therefore thought to be a more accurate characterization of the impact burden than kinematic-based metrics, which do not account for impact direction.

Biomechanics Data

This study used a dataset of on-field head impact data collected from athletes participating in a local youth football organization over 6 years (2012–2017). Data collection methods, previously reported by Kelley et al. (2017), were conducted with the HIT System.⁴⁰ Quantitative data collected for each impact included peak X, Y, and Z linear and rotational acceleration, impact location (azimuth and elevation angles), and a 40 ms time history of resultant linear acceleration. Each time one of the six accelerometers in an instrumented helmet records an impact greater than 10 g, data acquisition is initiated, and a total of 40 ms of data with 8 ms of pre-trigger data is recorded at 1000 Hz. Impacts were collected using the standard HIT System processing with a peak resultant linear acceleration threshold of 10 g. All peak resultant rotational acceleration data were scaled by a factor of 0.648, as per Rowson and colleagues.⁶⁵

Head Impact Exposure

Cumulative head impact exposure was quantified for each athlete using various existing measures including number of impacts and kinematic-based metrics as well as new, strain-based metrics proposed in the current study. Summary statistics, including characteristics of distribution and spread, were calculated in SAS for all of the exposure metrics and compared. Additionally the cross-correlation matrix was computed, to identify which of the new strain metrics are correlated to each other on a whole-brain basis.

Cumulative exposure was quantified from impact kinematic data using the risk-weighted cumulative exposure (RWE), which is calculated for a given athlete using a non-linear weighted sum of all head impacts over the course of a season.⁷⁷ The risk of concussion for each impact was calculated using three different risk functions previously described in the literature: 1) linear acceleration, 2) rotational acceleration, and 3) the combined probability (CP) from linear and rotational acceleration (Table 1).^63–65 The risk for each head impact is then summed to generate the cumulative RWE values from each respective risk function referred to as RWE_L, RWE_R, and RWE_CP (Table 1). RWE is favorable to previously described exposure metrics because it is based on the player specific distribution of impacts and the associated risk of concussion for each impact during the season for each player.

TABLE 1.

Risk-weighted exposure (RWE), logistic regression equations, and regression coefficients for the injury risk functions.

	Risk function	RWE equation	Logistic regression equation	Regression coefficients
(1)	Linear	$RW{E}_L={\displaystyle {\displaystyle \sum _{i=1}^{n_{hits}}}R{\left(a\right)}_i}$	$R\left(a\right)=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_{1}a\right)}}$	${\beta }_0=-9.805,\hspace{0.17em}{\beta }_1=0.0510$
(2)	Rotational	$RW{E}_R={\displaystyle {\displaystyle \sum _{i=1}^{n_{hits}}}R{\left(\alpha \right)}_i}$	$R\left(\alpha \right)=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_1\alpha \right)}}$	${\beta }_0=-12.531,\hspace{0.17em}{\beta }_1=0.0020$
(3)	Combined Probability (CP)	$RW{E}_{CP}={\displaystyle {\displaystyle \sum _{i=1}^{n_{hits}}}CP{\left(a,\alpha \right)}_i}$	$CP=\frac{1}{1+e^{-\left({\beta }_0+{\beta }_{1}a+{\beta }_2\alpha +{\beta }_{3}a\alpha \right)}}$	${\beta }_0=-10.2,\hspace{0.17em}{\beta }_1=0.0433,\hspace{0.17em}{\beta }_2=0.00873,\hspace{0.17em}{\beta }_3=-9.2\text{E}-7$

n_hits is the total number of impacts in a season for a player; a is the measured linear acceleration; α is the measured rotational acceleration; β₀, β₁, β₂, and β₃ are regression coefficients.

Proposed Metrics

The ABM (Fig. 1) was used to predict the strain response for all impacts for each athlete collected for the current study and used to develop two sets of new cumulative exposure metrics. Additional details on the ABM, FE simulation technique, and strain estimation methods are included in Appendix A. The new sets of metrics proposed and examined in the current study are: (1) twelve metrics based on first principal strain (ε₁), (2) twelve metrics based on third principal strain (ε₃), and (3) twelve metrics based on shear strain (γ).

FIGURE 1.

Axial (a), sagittal (b), coronal (c) cross-sections, an isometric view showing the falx, tentorium, and ventricles (d), and isometric view of the outer surface of the brain (e) showing sulci and gyri of the ABM.

The first set of metrics was derived from the first principal strain (ε₁) in all brain elements over the course of an impact. The first two metrics measure the 95th percentile and maximum strain occurring during the impact by first determining the distribution of strain values in all the brain elements at each time point (Fig. 2a shows strain distributions at 22.5 and 27 ms, for example). From the distributions at each time point, the 95th and 100th percentile strain values are calculated to generate 95th and 100th percentile strain curves over time (Fig. 2b). The ε_1,95 and ε_1,100 metrics are defined as the peaks of the respective strain curves (ε_1,95 is the maximum of the red curve and ε_1,100 is the maximum of the blue curve in Fig. 2b).

FIGURE 2.

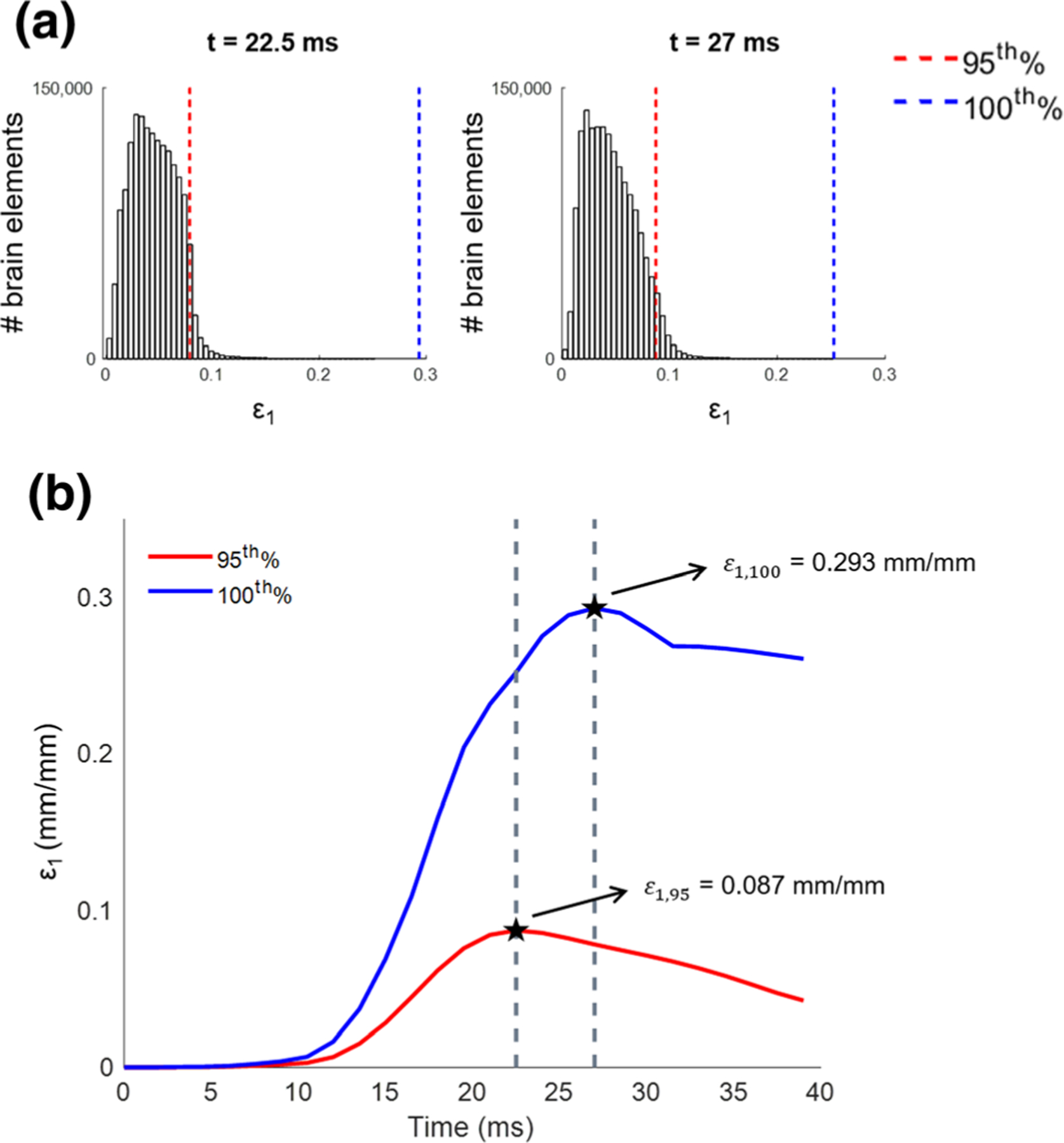
The strain distributions in all brain elements at 22.5 and 27 ms (a) and the 95th and 100th percentile strain response curves over time with Σε_1,95 and Σε_1,100 metrics identified as the curve peaks for an example impact (b).

The next two metrics, ${\dot{\epsilon }}_{1,95}$ and ${\dot{\epsilon }}_{1,100}$, were calculated from the first principal strain rate response of the brain. Strain rate was calculated numerically by differentiating strain using a five-point stencil.² Similar to the first two metrics, 95th and 100th percentile values were calculated at each time point and the corresponding metrics, ${\dot{\epsilon }}_{1,95}$ and ${\dot{\epsilon }}_{1,100}$, are defined as the peaks of the respective strain rate curves. Combinations of the strain and strain rate metrics were also calculated: ${\epsilon }_{1,95}\ast {\dot{\epsilon }}_{1,95}$ and ${\epsilon }_{1,100}\ast {\dot{\epsilon }}_{1,100}$.

The remaining first principal strain metrics were derived from the CSDM curve. The initial version of CSDM was developed by Bandak and Eppinger (1994) to account for large areas of deformation incurred in the creation of DAI and is based on the relationship between strain and the percentage of brain volume exceeding a given strain value.⁷ The CSDM curve for a given impact is generated from the maximum strain in each brain element and the percentage of brain volume experiencing each strain value (Fig. 3a). This curve was used to develop a new metric for the current study called the volumetric strain measure (VSM), which represents the area under the CSDM curve. An analogous metric derived from the relationship between strain rate and brain volume (Fig. 3b) was also developed, termed the volumetric strain rate measure (VSRM), which represents the area under the curve shown in Fig. 3b. Finally, the following combinations of the strain, strain rate, and volumetric metrics were also calculated and considered: VSM₁ * ε_1,95, VSM₁ * ε_1,100, $VS{M}_1\ast {\dot{\epsilon }}_{1,95}$, and $VS{M}_1\ast {\dot{\epsilon }}_{1,100}$. Unlike the strain and strain rate metrics which have 95th and 100th percentile versions, there is only one version of each volumetric metric. This means that the volumetric component of the two combination metrics VSM₁ * ε_1,95 and VSM₁ * ε_1,100 are the same.

FIGURE 3.

Relationship between strain and percent volume of brain (CSDM curve) highlighting the area under the curve, which corresponds to the new metric, VSM₁ (a) and relationship between strain rate and percent volume of brain highlighting new metric, VSRM₁ (b).

The second set of metrics was derived from the third principal strain (ε₃) and consists of twelve metrics analogous to the first twelve calculated from the first principal strain. For the impacts studied in the current analysis (youth football head impacts), the third principal strain is negative, so the metrics quantify the 5th percentile and minimum strain values, rather than the 95th and 100th percentiles discussed for the first set. The metric subscripts for this second set of metrics are therefore ‘5’ and ‘0’, instead of ‘95’ and ‘100’, as shown in Table 2.

TABLE 2.

Strain-based biomechanics exposure metrics

	Description	Metric	Cumulative metric	Units
First principal strain (ε1)	Strain (95th%)	ε 1,95	Σε 1,95	mm/mm
	Strain (100th%)	ε 1,100	Σε 1,100	mm/mm
	Strain rate (95th%)	${\dot{\epsilon }}_{1,95}$	$\Sigma {\dot{\epsilon }}_{1,95}$	s−1
	Strain rate (100th%)	${\dot{\epsilon }}_{1,100}$	$\Sigma {\dot{\epsilon }}_{1,100}$	s−1
	Strain*strain rate (95th%)	${\epsilon }_{1,95}\ast {\dot{\epsilon }}_{1,95}$	$\Sigma {\epsilon }_{1,95}\ast {\dot{\epsilon }}_{1,95}$	mm/mm*s−1
	Strain*strain rate (100th%)	${\epsilon }_{1,100}\ast {\dot{\epsilon }}_{1,100}$	$\Sigma {\epsilon }_{1,100}\ast {\dot{\epsilon }}_{1,100}$	mm/mm*s−1
	VSM	VSM 1	ΣVSM 1	mm/mm
	VSRM	VSRM 1	ΣVSRM 1	s−1
	VSM*strain (95th%)	VSM1 * ε1,95	ΣVSM1 * ε1,95	mm/mm
	VSM*strain (100th%)	VSM1 * ε1,100	ΣVSM1 * ε1,100	mm/mm
	VSM*strain rate (95th%)	$VS{M}_1\ast {\dot{\epsilon }}_{1,95}$	$\Sigma VS{M}_1\ast {\dot{\epsilon }}_{1,95}$	s−1
	VSM*strain rate (100th%)	$VS{M}_1\ast {\dot{\epsilon }}_{1,100}$	$\Sigma VS{M}_1\ast {\dot{\epsilon }}_{1,100}$	s−1
third principal strain (ε3)	strain (5th%)	ε 3,5	Σε 3,5	mm/mm
	strain (0%)	ε 3,0	Σε 3,0	mm/mm
	strain rate (5th%)	${\dot{\epsilon }}_{3,5}$	$\Sigma {\dot{\epsilon }}_{3,5}$	s−1
	strain rate (0%)	${\dot{\epsilon }}_{3,0}$	$\Sigma {\dot{\epsilon }}_{3,0}$	s−1
	strain*strain rate (5th%)	$\Sigma {\epsilon }_{3,5}\ast {\dot{\epsilon }}_{3,5}$	${\epsilon }_{3,5}\ast {\dot{\epsilon }}_{3,5}$	mm/mm*s−1
	strain*strain rate (0%)	$\Sigma {\epsilon }_{3,0}\ast {\dot{\epsilon }}_{3,0}$	${\epsilon }_{3,0}\ast {\dot{\epsilon }}_{3,0}$	mm/mm*s−1
	VSM	VSM 3	ΣVSM 3	mm/mm
	VSRM	VSRM 3	ΣVSRM 3	s−1
	VSM*strain (5th%)	VSM3 * ε3,5	ΣVSM3 * ε3,5	mm/mm
	VSM*strain (0%)	VSM3 * ε3,0	ΣVSM3 * ε3,0	mm/mm
	VSM*strain rate (5th%)	$VS{M}_3\ast {\dot{\epsilon }}_{3,5}$	$\Sigma VS{M}_3\ast {\dot{\epsilon }}_{3,5}$	s−1
	VSM*strain rate (0%)	$VS{M}_3\ast {\dot{\epsilon }}_{3,0}$	$\Sigma VS{M}_3\ast {\dot{\epsilon }}_{3,0}$	s−1
Shear strain (γ)	Shear strain (95th%)	γ 95	Σγ 95	mm/mm
	Strain (100th%)	γ 100	Σγ 100	mm/mm
	Strain rate (95th%)	${\dot{\gamma }}_{95}$	$\Sigma {\dot{\gamma }}_{95}$	s−1
	Strain rate (100th%)	${\dot{\gamma }}_{100}$	$\Sigma {\dot{\gamma }}_{100}$	s−1
	Strain*strain rate (95th%)	${\gamma }_{95}\ast {\dot{\gamma }}_{95}$	$\Sigma {\gamma }_{95}\ast {\dot{\gamma }}_{95}$	mm/mm*s−1
	Strain*strain rate (100th%)	${\gamma }_{100}\ast {\dot{\gamma }}_{100}$	$\Sigma {\gamma }_{100}\ast {\dot{\gamma }}_{100}$	mm/mm*s−1
	VSSM	VSSM	ΣVSSM	mm/mm
	VSSRM	VSSRM	ΣVSSRM	s−1
	VSSM*shear strain (95th%)	VSSM * γ95	ΣVSSM * γ95	mm/mm
	VSSM*shear strain (100th%)	VSSM * γ100	ΣVSSM * γ100	mm/mm
	VSSM*shear strain rate (95th%)	$VSSM\ast {\dot{\gamma }}_{95}$	$\Sigma VSSM\ast {\dot{\gamma }}_{95}$	s−1
	VSSM*shear strain rate (100th%)	$VSSM\ast {\dot{\gamma }}_{100}$	$\Sigma VSSM\ast {\dot{\gamma }}_{100}$	s−1

The third and final set of strain metrics was calculated from brain shear strain (γ). Similar to the first two metric groups, analogous strain, strain rate, volumetric, and combination metrics were calculated from the shear strain in each element. The volumetric metrics are calculated as the area under curves analogous to CSDM but calculated from shear strain and shear strain rate. The two shear volumetric metrics are termed the volumetric shear strain metric (VSSM) and the volumetric shear strain rate metric (VSSRM) (Table 2).

Cumulative strain metrics were then computed for each athlete by summing the values associated with the 36 metrics calculated for each impact measured over the course of a season. These cumulative metrics are identified by the addition of the summation symbol, Σ, to each metric name.

A cross-correlation analysis off all biomechanics metrics (RWE and strain metrics) was conducted to identify metrics that are highly correlated and those that are more independent and unique. It is expected that many of the metrics will be highly-correlated when compared on a whole-brain basis for these impacts, but it is believed that the strain-based metrics provide additional information and will allow a more nuanced exploration of brain response.

RESULTS

Complete biomechanics datasets were collected for 95 athletes over multiple seasons of youth football. Seventeen of the athletes participated for two seasons and two participated for three seasons, totaling 116 unique athlete-seasons. The participants ranged in age from 10 to 14 years. A total of 33,833 impacts were measured and the number of head impacts for a single athlete ranged from 22 to 1,016 over the course of a single season, with a mean of 292 and median of 223 impacts.

Head Impact Exposure

For each impact, the risk of injury was calculated using risk functions derived from linear acceleration, rotational acceleration, and the combined probability (CP) of each. The maximum injury risk for each athlete for a given impact ranged from 0.0393% to 30.1% for linear acceleration, from 0.0167 to 99.0% for rotational acceleration, and from 0.0771 to 93.2% for CP. Weighted sums were calculated using all three risk functions for each athlete and the distributions of associated RWE values (RWE_L, RWE_R, and RWE_CP) are displayed in Fig. 4a. The mean/median values were 0.1011/0.0615, 0.2880/0.0479, and 0.4431/0.1768 for RWE_L, RWE_R, and RWE_CP, respectively. The distributions of all three RWE metrics were right-skewed, with skewness measures ranging from 2.02 to 2.35 (skewness measures between −0.5 and 0.5 are considered normally distributed). The kurtosis measures ranged from 6.57 to 9.47 (a kurtosis value of 3 indicates normally distributed data) and the coefficients of variation (CV) ranged from 1.06 to 1.66 (distributions with CV values greater than 1 are considered to have high variance).

FIGURE 4.

Distributions of RWE_L, RWE_R, and RWE_CP (a), first principal strain metrics (b), third principal strain metrics (c), and shear strain metrics (d). S – skewness; K – kurtosis

Figures 4b and 4c show the distributions for the newly-derived cumulative strain metrics. Similar to the RWE metrics, most of the strain-based metrics are right-skewed, with the exception of the metrics based on third principal strain that do not involve multiplication (Σε_3,5, Σε_3,0, $\Sigma {\dot{\epsilon }}_{3,5}$, $\Sigma {\dot{\epsilon }}_{3,0}$, ΣVSM₃, and ΣVSRM₃) since the values are negative. The combination metrics with negative strain values ($\Sigma {\epsilon }_{3,5}\ast {\dot{\epsilon }}_{3,5}$, $\Sigma {\epsilon }_{3,0}\ast {\dot{\epsilon }}_{3,0}$, ΣVSM₃ * ε_3,5, ΣVSM₃ * ε_3,0, $\Sigma VS{M}_3\ast {\dot{\epsilon }}_{3,5}$, and $\Sigma VS{M}_3\ast {\dot{\epsilon }}_{3,0}$) result in positive metric values and are right-skewed since they involve two negative measures multiplied together. The strain metrics all exhibit similar degrees of skewness, with the absolute value of skew ranging from 1.09 to 1.50. Kurtosis values ranged from 3.75 to 5.10 and the absolute value of coefficients of variation ranged from 0.75 to 0.89.

To illustrate the potential value the new metrics offer for evaluating regional variation in strain response, we look more closely at the brain response to a single example impact. The impact examined was a frontal impact with peak linear and rotational accelerations of 58.7 g and 3,730 rad/s², respectively and peak rotational velocity of 15.4 rad/s. Selected first principal strain metrics for this impact were ε_1,95 = 0.1525, ε_1,100 = 0.4368, ${\dot{\epsilon }}_{1,95}=21.44\hspace{0.17em}{s}^{-1}$, ${\dot{\epsilon }}_{1,100}=66.17\hspace{0.17em}{s}^{-1}$, VSM₁ = 9.65 and VSSM₁ = 1430.8 s⁻¹, and the corresponding third principal strain metric values were ε_3,5 = −0.1546, ε_3,0 = −0.4369, ${\dot{\epsilon }}_{3,5}=-21.58\hspace{0.17em}{s}^{-1}$, ${\dot{\epsilon }}_{3,0}=-71.06\hspace{0.17em}{s}^{-1}$, VSM₃ = −9.604 and VSRM₃ = −1443.8 s⁻¹. The first and third principal strain responses for this impact both peak at 26 ms, and the strain state at the time of peak strain is visualized in Fig. 5 which shows the first principal strain (Fig. 5a) and third principal (Fig. 5b) strain contours throughout the whole brain as well as in an axial cross-section at the time of peak strain (Figs. 5c and 5d). Examining the strain response in the posterior portion of the cross-section, we see that there is more positive strain on the left side and in the anterior portion, there is higher strain on the right side. Another notable result observed in this impact is the high magnitude strain concentration at the anterior portion of the corpus callosum. It has been shown that the greatest strains commonly occur at this region of the corpus callosum, or the genu, and this region is frequently damaged in TBI.^{5,27,46,47,52,72,82} The strain response can also be visualized by identifying the elements experiencing the highest strain. Since ε_1,95, or the 95th percentile strain value, was 0.1595 at the time of peak strain, 5% of the total brain elements (n = 1,639,352), or 81,968 elements, experienced first principal strain greater than 0.1595. This set of elements was compared to the 5% of brain elements experiencing third principal strain less than the ε_3,5 value of −0.1546, since this metric quantifies the 5th percentile compressive strain. Approximately 61,000 elements (~ 74% of the top 5%) occurred in both element sets (Fig. 6a). In other words, ~ 61,000 elements experienced strain in the top 5% of positive strain as well as the top 5% of negative strain. The elements that only occurred in the top 5% for positive strain are shown in red in Fig. 6b and those only in the top 5% for negative strain are shown in blue. Figure 6 shows that the peak strain for this impact occurs on the superior surface of the left hemisphere and the inferior surface of the right hemisphere. We can also see that first principal strain dominates the response in the anterior portion of the brain, while there is more third principal strain response in the posterior portion and in the right parietal lobe.

FIGURE 5.

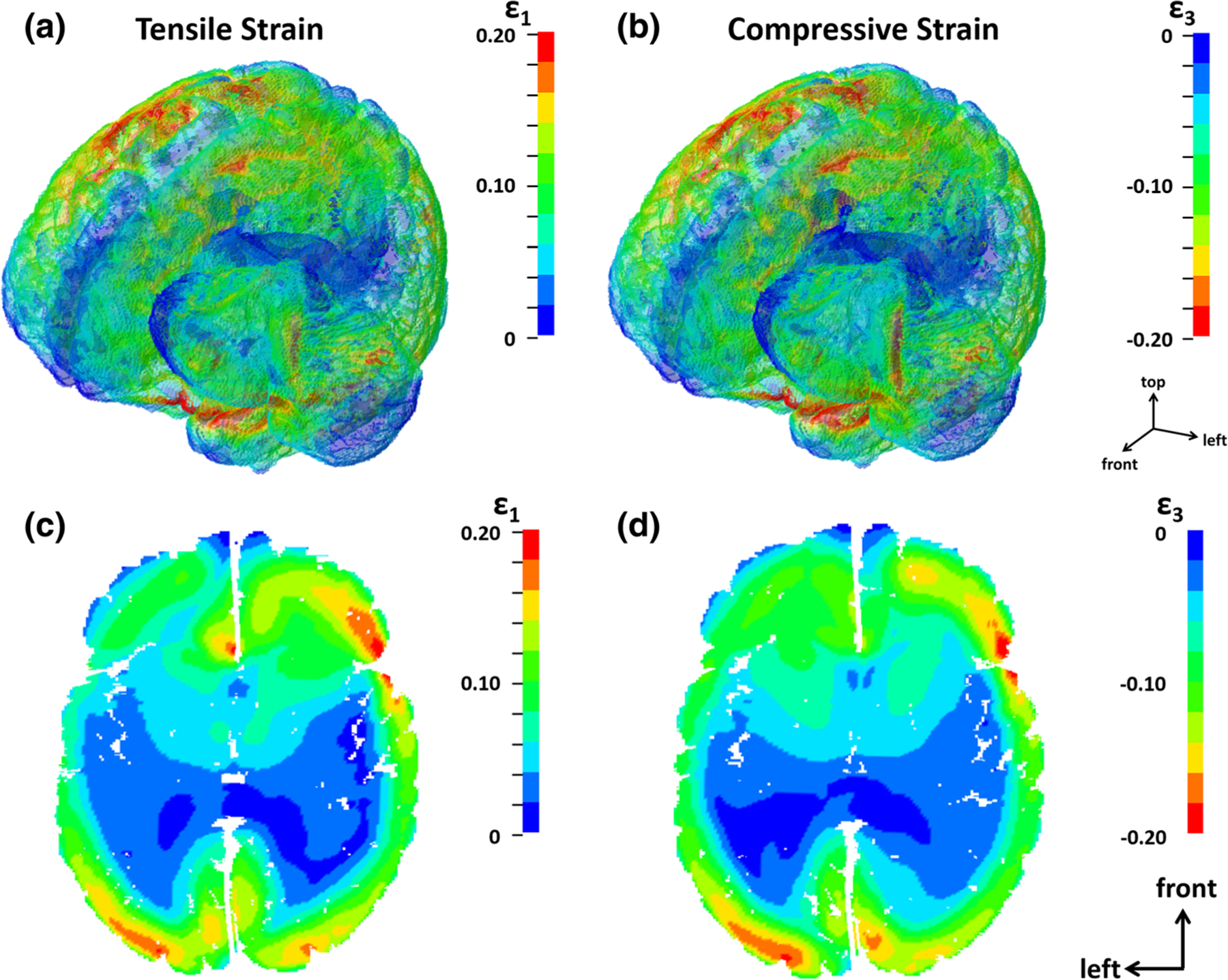
Strain contours for first principal strain (a) and third principal strain (b) in an isometric view as well as cross-sections sowing first principal strain (c) and third principal strain (d) distributions at time of maximum strain (26 ms).

FIGURE 6.

At the time of maximum strain, ~ 61,000 elements (highlighted in purple) experience strain values in the top 5% based on both positive and negative strain (a). The remaining elements experiencing the greatest positive and negative strain are highlighted in red and blue, respectively (b).

The relationships between biomechanical metrics on a whole-brain basis were investigated through cross-correlation analysis. Cross-correlation matrices show that many of the strain metrics are highly correlated to one another, which is to be expected. A majority of the strain-based metrics have strong relationships to all other strain metrics. In fact, 27 of the strain metrics (75%) are highly correlated (r² ≥ 0.95) to all 35 other strain metrics. The metric with the fewest number of significant relationships to other strain metrics was $\Sigma VSSM\ast {\dot{\gamma }}_{100}$, which displayed strong relationships (r² ≥ 0.95) with only 29 of the remaining strain metrics. The following five metrics had strong relationships (r² ≥ 0.95) with 32 of the 35 other strain metrics: Σε_1,100, Σε_3,0, $\Sigma VS{M}_1\ast {\dot{\epsilon }}_{1,100}$, $\Sigma VS{M}_3\ast {\dot{\epsilon }}_{3,0}$, and Σγ₁₀₀. In contrast to the strong linear relationships between all the strain metrics, the strain metrics exhibit comparatively much weaker relationships to the kinematic metrics. Average (± standard deviation) r² values for the 36 strain metrics describing the relationships to RWE_L, RWE_R, and RWE_CP were 0.70 (± 0.013), 0.26 (± 0.019), and 0.53 (± 0.031), respectively. An attribute of the proposed strain metrics, which is highlighted in the example shown in Figs. 5 and 6 is that these they are different for different regions of the brain for the same impact, a phenomenon which more region-based analyses might uncover in future studies which might further highlight their utility or uniqueness.

DISCUSSION

Cumulative head impact exposure was quantified for 116 athletes in the current study using multiple existing metrics as well as newly-proposed strain-based metrics. The average number of impacts per athlete, 292 impacts per season, is comparable to average numbers reported in the literature for youth football. Urban et al. (2013) reported an average of 240 impacts per season for 9 to 12 year olds and 341 impacts per season for 12 to 14 year olds.⁷⁷ In a study of cumulative head impact exposure in high school football, Urban et al. (2013) reports the average number of impacts per season to be 423 per athlete.⁷⁷ Also, the mean RWE values calculated in the current study are comparable to those calculated by Urban et al. (2013) for high school athletes. Mean RWE values of 0.19, 0.39, and 0.87 were reported for high school athletes compared to values of 0.10, 0.27, and 0.42 in the current study for RWE_L, RWE_R, and RWE_CP, respectively.⁷⁷ The values in the current study are slightly lower than those reported by Urban et al. (2013), but this increase in head impact exposure is expected with the increase in level of play from youth to high school football.

The newly derived metrics are not fully explored as they could be through correlation with medical imaging, neurocognition, or more regional anatomical analyses, but they provide great potential to describe the response to a single impact as well as to quantify long-term exposure. The distinction between positive (tensile), negative (compressive), and shear strain is important since these represent biomechanically different behaviors within the brain. Under positive strain the mechanism of injury is stretch deformation and damage of fibers and microvasculature throughout the brain.^37,69 Under compression, however, the mechanism of interest involves blood escaping capillaries that are temporarily under high pressure.^37,67,76 The rate at which pressure or stretch is applied to a local area of the brain is important and may affect the occurrence and severity of injury.^38,54 Shear strains, thought to be generated by angular acceleration of the head and more complex deformation patterns, can cause injury as the brain experiences regional deformation and can induce damaging effects such as DAI and injury at the junctions between gray and white matter.^35,37,76 The volumetric metrics in particular are a valuable contribution, as they capture the response throughout the brain volume of interest (in this case whole brain) on a continuous scale, compared to existing threshold-based metrics derived from CSDM (e.g., determining the percentage of elements exceeding 0.15 first principal strain). The FE-based metrics provide the opportunity to investigate location-based strain response, which can be also be extended to cumulative analyses.

Six of the new cumulative strain metrics were identified through cross-correlation analysis as the most independent based on having strong relationships (r² ≥ 0.95) with the fewest number of other strain metrics: Σε_1,100, Σε_3,0, $\Sigma VS{M}_1\ast {\dot{\epsilon }}_{1,100}$, $\Sigma VS{M}_{3,0}\ast {\dot{\epsilon }}_{3,0}$, Σγ₁₀₀, and $\Sigma VSSM\ast {\dot{\gamma }}_{100}$. These six metrics may be providing more independent information relative to the other strain metrics, as opposed to a metric like $\Sigma {\epsilon }_{1,100}\ast {\dot{\epsilon }}_{1,100}$, which is significantly correlated to all eleven other first principal strain metrics, all twelve third principal strain metrics, and all twelve shear strain metrics. However, such a conclusion is drawn only from whole-brain analyses conducted herein, and does not eliminate the utility of these metrics for brain region, or temporally-based analyses. Future analyses relating head impact exposure to imaging and cognitive changes will shed additional light on the importance of specific metrics.

While these metrics should be more fully explored, they provide an alternative to existing measures of exposure and provide a new method for quantifying the cumulative impact burden over a season of football. Figure 7 compares the number of impacts, an existing cumulative metric, RWE_CP, and one of the new strain metrics, Σε_1,95, for the 25 athletes with the largest number of impacts in the current study. This figure shows that the athletes with the largest RWE_CP do not necessarily have the greatest exposure based on Σε_1,95, which indicates that the strain metric provides information not captured by RWE_CP.

FIGURE 7.

Normalized number of impacts, RWE_CP, and Σε_1,95 exposure metrics sorted by number of impacts for 25 athletes with largest number of impacts.

Limitations

Limitations of the current study include error associated with experimental data collection methods as well as estimation of the boundary conditions used to drive the FE simulations. The HIT System used for the collection of biomechanical data is associated with some error in measurement for linear and rotational acceleration. In Beckwith et al. (2012), the HIT System overestimated linear acceleration by an average of 1% and underestimated rotational acceleration by an average of 6%, when compared to acceleration data measured from a 50th percentile Hybrid III anthropomorphic test device (ATD).⁹ However, the correlation between the HIT System and the Hybrid III ATD was significant for linear and rotational acceleration. There is also error associated with the estimation of 6 degree-of-freedom (6DOF) kinematic boundary conditions from the HIT System outputs. The authors have determined, however, that the previously developed algorithm estimates 6DOF motion to a sufficient degree necessary for use in FE simulation.⁵⁸

CONCLUSIONS

As an alternative to existing exposure metrics based on kinematic values, the current study developed and presented new approaches to quantify cumulative exposure using strain-based metrics. Thirty-six new or derivative cumulative exposure metrics based on local brain deformation were developed and presented. These metrics were derived from the strain, strain rate, and volumetric strain response in tension, compression and shear to provide an enhanced representation of exposure. These new metrics are volumetrically derived, meaning they are derived from or inclusive of the response of the complete volume of brain being considered, in this case whole brain, but the metrics could be used for regions or subvolumes of brain. They are also cumulative, referring to their use to sum individual impacts over the course of a time period of interest, however they could be used for individual impacts also. They should not necessarily be interpreted as an immediate improvement in injury predictive capability over existing kinematic-based methods; but rather they represent more complete information useful and necessary for further analyses. They may enhance metric sensitivity and may be a more complete and useful representation of response. This set of metrics presents a new way to quantify cumulative impact burden and offers potential for future analyses of brain response to head impacts experienced during a season of football. The new volumetric metrics are a novel approach to quantify strain response throughout the whole brain with a single value without the need to establish a threshold, such as is needed for CSDM (0.05), CSDM (0.10) and CSDM (0.15) measures. Future work will evaluate the relationship between these cumulative strain-based metrics and changes in medical imaging observed over the course of a season, since it has been suggested that subconcussive impacts play a part in later cognitive deficits and impairment.^31,36 Because the mechanism by which repetitive subconcussive impacts cause these neurological conditions is not yet understood, further study is needed, but the current study provides metrics that can be used to characterize the cumulative burden of these impacts. These findings will serve as the foundation for enhanced inquiry into the correlation between biomechanics and brain imaging changes, as well as between biomechanics and neurocognitive measures, which will further our understanding of the relationship between subconcussive impacts and adverse cerebral function or cognitive changes. The newly-derived metrics may also provide the basis for enhanced concussion prediction and improved discrimination of the varied clinical presentations of signs and symptoms related to concussion.

APPENDIX A

The atlas-based brain model (ABM) was used to predict the strain response for each real-world impact. The ABM has been validated against brain displacement measurements in five cadaver impact experiments originally conducted by Hardy et al.^1,3 The boundary conditions for each impact were derived using a previously developed transformation algorithm that estimates six-degree-of-freedom (6DOF) kinematics from corresponding HIT System outputs.⁴ Further information on the development and validation of this algorithm is reported by Miller et al.⁴ Estimated 6DOF kinematics were used as boundary conditions to drive ABM simulations and obtain brain strain for corresponding head impacts.

The current method of estimating strain response uses an approach similar to the pre-computed strain atlas presented by Ji and Zhao.^2,5 The approach used in the current study consists of previously run ABM simulations at 192 impact regions covering the head, defined in Miller et al.⁴ At each impact location, three sets of boundary conditions representing the most common pulse polarities for the given location were run at three different rotational velocities. For a given impact, strain response is estimated through interpolation after determining the impact region and polarity. If the polarity combination of a desired impact is not one of the three run at that location (and therefore does not have corresponding simulations for interpolating the strain response), that impact is excluded from the analysis. This was the case for only 198 of 33,833 impacts (0.59%) examined in the current study.

Impacts were sorted into 1 of the 192 regions (Fig. 8) based on the classifications defined in Miller et al. for the 5DOF-to-6DOF transformation algorithm.⁴ The number of impacts associated with a given impact region ranged from 23 to 1,430.

FIGURE 8.

Impact regions (a) and distribution of impacts by region (b).