Abstract
Solvent molecules alter the free energies of liquid phase species and adsorbed intermediates during catalytic reactions, thereby impacting rates and selectivities. Here, we examine these effects through the epoxidation of 1-hexene (C6H12) with hydrogen peroxide (H2O2) over hydrophilic and hydrophobic Ti-BEA zeolites immersed in aqueous solvent mixtures (acetonitrile, methanol, and γ-butyrolactone). Greater H2O mole fractions provide greater epoxidation rates, lower H2O2 decomposition rates, and hence improved H2O2 selectivities to the desired epoxide product in each combination of solvent and zeolite. The mechanisms for epoxidation and H2O2 decomposition remain constant across solvent compositions; however, H2O2 activates reversibly in protic solutions. Differences in rates and selectivities reflect the disproportionate stabilization of transition states within zeolite pores with respect to surface intermediates and fluid phase reactants, as evinced by turnover rates normalized by the activity coefficients of C6H12 and H2O2. Opposing trends in activation barriers suggest that the hydrophobic epoxidation transition state disrupts hydrogen bonds with solvent molecules, while the hydrophilic decomposition transition state forms hydrogen bonds with surrounding solvent molecules. Solvent compositions and adsorption volumes within pores, from 1H NMR spectroscopy and vapor adsorption, depend on the composition of the bulk solution and the density of silanol defects within pores. Strong correlations between epoxidation activation enthalpies and epoxide adsorption enthalpies from isothermal titration calorimetry indicate that the reorganization of solvent molecules (and associated entropy gains) required to accommodate transition states provides the most significant contribution to the stability of transition states that determine rates and selectivities. These results demonstrate that replacing a portion of organic solvents with H2O offers opportunities to increase rates and selectivities for zeolite-catalyzed reactions while reducing usage of organic solvents for chemical manufacturing.
A combination of kinetic, thermodynamic, and spectroscopic techniques demonstrates that increasing the water fraction within organic solvents accelerates alkene epoxidations while suppressing the undesired H2O2 decomposition pathway.
1. Introduction
Epoxides are used as intermediates to manufacture fragrances, plastics, and biologically active ingredients and are produced and consumed on a massive scale.1 The primary methods to produce epoxides industrially include the chlorohydrin process, organic-hydroperoxide (Halcon) process, and hydrogen peroxide (H2O2) to propylene oxide (HPPO) process.1 Industrial HPPO processes involve one of two combinations of a microporous titanosilicate catalyst and an aqueous organic solvent: Ti-MFI (i.e., titanosilicate-1) with aqueous methanol (CH3OH)2,3 or Ti-MWW with aqueous acetonitrile (CH3CN).3–7 The reactant streams for these processes often include aqueous H2O2, which introduces a mole fraction of water (xH2O) reported in the range of 0.05 to 0.3;2,3,5,6 however, patented processes add water (H2O) to the reaction mixture even when producing H2O2in situ from H2 and O2.3,4,7 These reports imply that H2O may improve epoxidation performance, but the reasons for these differences and the magnitude of the effects are not reported.2–7
The quantity of H2O combined with organic solvents in binary, ternary, or more complex solvents affects rates of catalytic reactions. For example, turnover rates for homogeneous Brønsted acid-catalyzed alcohol dehydrations increase by two to three orders of magnitude when changing the solvent from neat H2O to mixtures of H2O and organic solvents (i.e., >0.3 molar fraction of dimethyl sulfoxide, dioxane, tetrahydrofuran (THF), CH3CN, or gamma-valerolactone).8–10 A separate work revealed that furfuryl acid hydrolysis yields over Brønsted acidic zeolite H-MFI increased from less than 10% in neat H2O to nearly 70% in an equimolar THF–H2O mixture.11 Authors of these studies attribute rate changes to differences in the solvent environment around the reactant in the fluid phase or within the zeolite pores as the solvent composition varies. Solvent molecules interact with and alter the stability of reactive species, which can influence rates of homogeneous and heterogeneous catalytic reactions.12–16
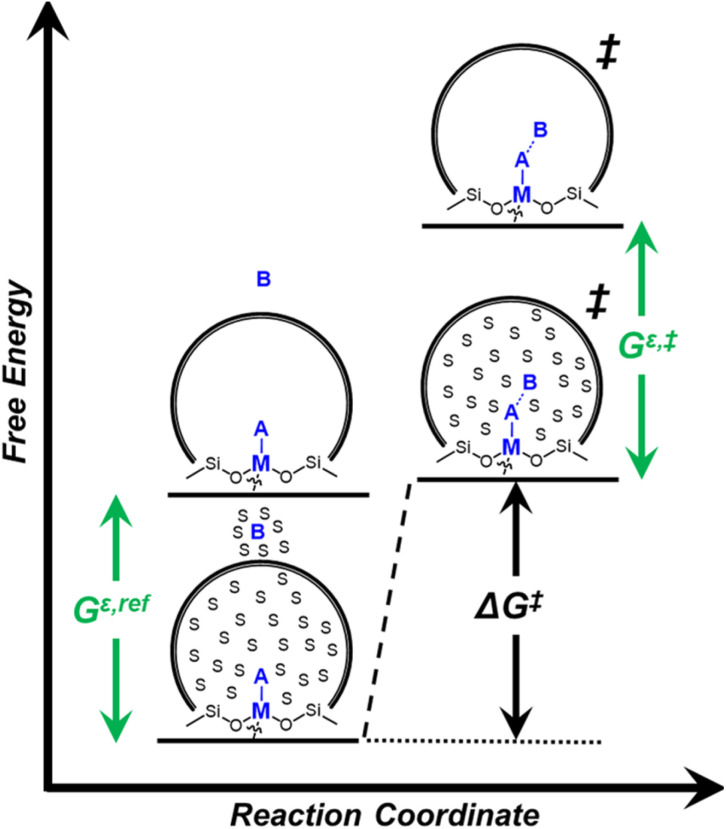
Within the field of organocatalysis, recent studies sought to manipulate the rates and selectivities achieved by catalytic complexes by tailoring outer-sphere interactions, also known as second coordination sphere effects.17,18 Outer-sphere interactions encompass hydrogen bonding, electrostatic, and hydrophobic interactions, among others. These interactions may be manipulated through alterations to the ligand structure and ion pairs but also by changes to the composition of the solvent.19 Researchers have long appreciated that solvents influence enzymatic20 and organocatalytic21 reactions, with publications dating to 1890 showing that the solvent choice altered rates for the quaternization of triethylamine with iodoethane by nearly 3 orders of magnitude.22 Classical theories (e.g., Kirkwood,23 Debye and Hückel,24 and Kamlet and Taft25) provide frameworks to understand the influence of solvents on reaction rates by correlating bulk solvent properties to the thermodynamic activity of reactive intermediates (i.e., solutes). These descriptions rely on mean-field descriptions and do not describe phenomena at a molecular level. For these reasons, they cannot account for outer-sphere or solvent-mediated interactions at solid–liquid interfaces. Recently, we described a conceptual framework14 for quantifying these effects within rate expressions for chemical reactions that captures the impact of solvent mediated interactions on the stability of reactive species through excess free energy contributions (Gε) (Scheme 1). These contributions arise from thermodynamic non-idealities that alter the activity coefficients of reactive species.26 The non-idealities brought about by solvent molecules are functionally identical to second coordination sphere effects considered for homogeneous, enzymatic, and electrochemical catalytic processes.
Scheme 1. Reaction coordinate depicting the influence of solvent molecules on a generic reaction over a metal (M)-incorporated zeolite between A and B through changes in the excess free energy of the reference state (Gε,ref) and transition state (Gε,‡).
Interactions between solvents and reactants at solid–liquid interfaces provide energetic contributions that strongly influence zeolite-catalyzed epoxidation reactions,27–34 among other chemistries. For example, the identity of the organic solvent affects alkene epoxidation turnover rates. Previous work from our group and others showed that CH3OH solvent gives greater epoxidation turnover rates for C6–C18 linear and cyclic alkenes than CH3CN over Ti-MFI,29,35–37 but lower rates than CH3CN over Ti-BEA29,37–39 and Ti-MWW.37,40,41 These differences reflect either direct effects of the zeolite topology or inadvertent or unrecognized effects that may include differences related to the densities of silanol defects ((SiOH)x, where x ranges from 1 to 4 and depends upon the mechanism of defect formation), variations in the crystal habit, particle dimensions, and associated intraparticle transport effects caused by variations in the synthesis protocol. Notably, the density of (SiOH)x impacts the hydrophilicity of the pores and the kinetics of liquid phase alkene epoxidations. Turnover rates for epoxidations of C6–C18 linear alkenes in CH3CN with aqueous H2O2 in hydrophilic Ti-BEA surpass rates in hydrophobic Ti-BEA by factors of 40 to 450.27,33,34 The most hydrophilic zeolites possess multiple (SiOH)x nests per unit cell that stabilize hydrogen bonded networks of H2O molecules within their pores, while the most hydrophobic zeolites contain far less than one (SiOH)x per unit cell and contain less H2O.42,43 During epoxidation turnovers, the formation of the alkene epoxidation transition state (or the adsorption of an epoxide) disrupts and displaces hydrogen bonded H2O and CH3CN molecules from pores and brings entropic gains that stabilize the transition state to increase rates.27,34 In general, solvent molecules alter rates and activation free energies for catalytic reactions through changes in Gε (Scheme 1).
Recent literature indicates that the presence of H2O influences rates of alkene epoxidation; however, discrepancies among reports regarding the magnitude of these effects, the values of xH2O needed, differences between organic solvents, and disagreement over the physical origins motivate closer examination of these phenomena across common aqueous organic solvent mixtures. A fraction of studies showed that increasing xH2O does not affect rates for alkene epoxidations. Ramachandran et al. reported that 1-hexene (C6H12) 35 epoxidation rates do not depend on xH2O (0.03 ≤ xH2O ≤ 0.3) and argued that H2O does not enter pores or reside near Ti active sites. Bregante et al. showed that 1-octene (C8H16) epoxidation rates did not change with xH2O (0.0002 ≤ xH2O ≤ 0.008) and reasoned that the intrapore H2O concentration remains constant in this dilute limit.27 Other reports found that adding H2O increases epoxidation rates of propylene (C3H6) 40 and C6H12.37,39 The rate increases for each C6H12 epoxidation study were attributed to the stabilization of titanium-hydroperoxo (Ti–OOH) reactive intermediates by the formation of a 5-membered ring with an H2O molecule.37,39 The ratio of the organic solvent (CH3CN) to H2O was proposed to affect rates by changing the hydrophilicity of the environment around Ti sites, which affected the access of C3H6 and H2O2 to Ti sites.40 Rates and barriers for H2O2 decomposition (an undesirable side reaction) also depend on the choice of organic solvent used in aqueous mixtures,39,44 however, the dependence upon xH2O has not been reported. Notably, these prior studies utilized different combinations of organic solvents (e.g., CH3OH, CH3CN, acetone), Ti-zeolites (i.e., *BEA, MFI, MWW frameworks), and reaction conditions (i.e., temperature, reactant, and H2O concentrations). Furthermore, reactant concentrations varied in ways that apparently yielded distinct kinetic regimes. Finally, speculative interpretations were rarely corroborated by complementary experimental methods to confirm the influence of xH2O on rates. Consequently, intentional pairing of solvents with surfaces for new systems of reactants, solvents, and catalysts relies on guesswork and experimentation. Solvent composition clearly influences the kinetics and possibly the mechanism for alkene epoxidation and H2O2 decomposition reactions at solid–liquid interfaces, underscoring the importance of understanding how xH2O influences epoxidation and H2O2 decomposition pathways.
Here, the interpretations of differences between the intrinsic kinetics for C6H12 epoxidation and H2O2 decomposition reactions in aqueous-organic solvent environments within Ti-BEA zeolites show that solvation effects primarily govern rates and barriers. These comparisons control for potential variations in zeolite framework and reaction conditions that differed among previous studies, strengthening conclusions that solvent structures interact with adsorbed and liquid phase reactive species to influence catalysis. Turnover rates for C6H12 epoxidation with aqueous H2O2 increase with xH2O (0.002 ≤ xH2O ≤ 0.8) while turnover rates for H2O2 decomposition decrease over hydrophilic (Ti-BEA-OH) and hydrophobic (Ti-BEA-F) zeolites in aqueous mixtures of three organic solvents (CH3CN, CH3OH, and γ-butyrolactone (GBL, C4H6O2)). These trends result in greater epoxide formation rates and H2O2 selectivities at higher xH2O, regardless of the identity of the organic component of the solvent. Comparisons among turnover rates normalized by the solvent-dependent activity coefficients of the fluid phase reactants demonstrate that the solvent composition strongly influences the stability of intermediates and transition states within the pores of Ti-BEA. The interpretation of measured activation enthalpies and entropies for epoxidation and H2O2 decomposition shows that epoxidation rates rise with higher xH2O due to a combination of increased thermodynamic activity of fluid phase C6H12 and increases in the entropy of the epoxidation transition state by the disruption of hydrogen bonds among intrapore H2O molecules. In contrast, H2O molecules likely enthalpically stabilize the hydrophilic transition state for H2O2 decomposition through hydrogen bonding but more significantly stabilize fluid phase H2O2 and Ti–OOH, leading to lower decomposition rates at higher xH2O. These interpretations agree with differences among 1,2-epoxyhexane adsorption enthalpies measured by isothermal titration calorimetry as functions of solvent composition. Analysis of the activation barriers for both reaction pathways and the trends in epoxide adsorption enthalpies show that multiple kinetic and thermodynamic parameters depend sensitively on the values of xH2O and vary more significantly with xH2O in Ti-BEA-OH than Ti-BEA-F. These comparisons agree with differences among intrapore solvent compositions between zeolites and organic solvents, which show that (SiOH)x nests facilitate preferential uptake of H2O within pores and lead to greater interaction among H2O molecules and surface intermediates at any given xH2O for the bulk fluid. Cumulatively, these findings show how the stability of reactive intermediates and transition states for epoxidation vary due to interactions with intrapore H2O molecules and demonstrate the ubiquity of these effects across solvent mixtures and zeolites with distinct hydrophilic or hydrophobic nature.
2. Materials and methods
2.1. Catalyst synthesis
Ti-BEA-OH was prepared by post-synthetic modification of commercial Al-BEA, following previously published procedures.45,46 Al-BEA (TOSOH, lot no. 94HA6X02Y; Si : Al = 20) was treated in refluxing HNO3 (Macron Chemicals, 68–70 wt%, 20 cm3 g−1) at 433 K for ∼24 h to remove Al atoms from the *BEA framework by forming soluble Al(NO3)3. The dealumination treatment was carried out 3 times to ensure thorough dealumination (Si : Al > 1200). Between dealumination, the *BEA sample was washed with deionized H2O (18.2 MΩ cm, Elga Purelab Flex 2, 50 cm3 gzeolite−1) and recovered by vacuum filtration. After the last dealumination, the dealuminated *BEA was heated to 823 K (5 K min−1) in flowing air (200 cm3 min−1; Airgas, Ultra Zero grade) and held at 823 K for 6 h to remove organic residues. The resulting material (Si-BEA-OH) was heated in a round-bottom flask under vacuum (<5 Pa, 473 K) to create a moisture-free environment, after which dichloromethane (CH2Cl2, Fisher Chemicals, 20 cm3 gzeolite−1) solvent was added to the flask. Titanium atoms were then incorporated into the framework by adding TiCl4 to the Si-BEA-OH and CH2Cl2 mixture under an inert atmosphere (328 K, refluxing CH2Cl2, ∼16 h, 50 cm3 min−1 Ar, Airgas, Ultra High Purity). The resulting Ti-BEA-OH was recovered by rotary evaporation and was heated to 823 K (5 K min−1) in flowing air (200 cm3 min−1) and held at 823 K for 6 h, resulting in a white powder sample.
Ti-BEA-F was synthesized by following a previous procedure.47,48 16.82 g of tetraethylammonium fluoride hydrate (TEAF, Sigma-Aldrich, 98%) was dissolved in 27 cm3 of deionized H2O (18.2 MΩ cm, Elga Purelab Flex 2) in a polypropylene container. 39.87 cm3 of tetraethylorthosilicate (TEOS, Sigma-Aldrich, >98 wt%) was added, and the mixture was stirred for 30 min at room temperature. 0.351 cm3 of titanium(iv) isopropoxide (TIPO, Sigma-Aldrich, 99.999%) was added, and the solution was covered and stirred for an additional 16 h to produce a white, opaque homogeneous solution. The cover was removed, and the mixture was stirred for 12 h to evaporate the alcohols formed from the hydrolysis of TIPO (isopropanol) and TEOS (ethanol). The mass of alcohols formed was estimated by assuming complete and stoichiometric hydrolysis of all TIPO and TEOS added. The solution was left uncovered to allow the alcohols to evaporate until the mass of the solution decreased by an amount equal to 115% of the calculated mass of the alcohols to increase the likelihood of complete evaporation of these alcohols. The alcohols are assumed to evaporate preferentially before water based on their greater volatility. A mass of deionized H2O equivalent to the difference between the total mass evaporated (36.8 g) and the calculated mass of alcohols formed (31.0 g) was added to account for the H2O lost during evaporation. The mixture was then transferred to a Teflon liner (Parr Instruments, 125 cm3, Model 4748). This yielded a gel with an approximate molar composition of 1Si : 0.006Ti : 0.56TEAF : 8.89H2O. A small amount of Si-BEA-OH seeds (3% by mass relative to SiO2 in the synthesis gel) from a previous synthesis was added to promote crystallization. The Teflon liner was loaded into a stainless-steel autoclave (Parr Instruments, 125 cm3, Model 4748) and heated to 413 K at dynamic conditions (60 rpm) in a convection oven (Yamato, DKN602C) for 20 days. The resulting material was recovered by centrifugation, washed with H2O, and dried in an oven for 12 h at 343 K. The dried solid was heated at 5 K min−1 to 823 K in flowing air (200 cm3 min−1) and held at 823 K for 6 h to produce a white powder Ti-BEA-F sample.
2.2. Catalyst characterization
The titanium (Ti), silicon (Si), and aluminum (Al) contents of the Ti-BEA catalysts were determined with energy-dispersive X-ray fluorescence (EDXRF). Finely ground samples of Ti-BEA (∼50 mg) were loaded into a polypropylene cup (1 cm diameter) sealed with ultralene film. The sample cups were loaded into the He-purged chamber of the spectrometer (Shimadzu, EDX-7000). The samples were scanned between 0 and 30 keV, and the intensities of the fluorescence features were used to calculate the mass of Ti, Si, and Al within the sample. The EDXRF measurements show that Ti-BEA-OH (Si : Al ∼ 1200) and Ti-BEA-F (Si : Al ∼ 1750) contain only trace quantities of Al. The trace amount of Al in Ti-BEA-F may result from Al impurities from the components used in the synthesis. Compositions of the Ti-BEA samples were also assessed by ICP-OES, which confirmed each sample contained negligible quantities of Al (Si : Al > 2800) and possessed Ti quantities consistent with the results from EDXRF. Ti loadings and Si : Al ratios for each zeolite are shown in Table 1.
Ti Content, Band Gap, and Relative Hydrophilicity of Synthesized Ti-BEA.
| Catalyst | Si : Al | Ti wt% | Band gapc (eV) | Φ IR d | BET surface areae (m2 g−1) | Micropore volumef (cm3 g−1) |
|---|---|---|---|---|---|---|
| Ti-BEA-OH | 1220a, 2800b | 0.36a, 0.34b | 4.3 | 2.25 | 628 | 0.172 |
| Ti-BEA-F | 1750a, 2880b | 0.26a, 0.25b | 4.3 | 0.27 | 543 | 0.173 |
Determined with EDXRF.
Measured with ICP.
Extracted from leading edge of Tauc plot from DRUV-vis.
Calculated from infrared transmission spectra of dehydrated Ti-BEA samples.
Measured by volumetric Ar physisorption.
Calculated using the t-plots from Ar physisorption.
The dispersity of the Ti atoms in the Ti-BEA catalysts was measured with diffuse reflectance UV-vis (DRUV-vis) spectroscopy. Magnesium oxide (MgO, Sigma-Aldrich, 99.9995%) was used as a background. Ti-BEA samples were mixed and ground into a fine powder with magnesium oxide at a MgO : Ti-BEA mass ratio of 10 : 1 to measure sample spectra on a UV-vis spectrophotometer (Varian, Cary 5G). The total reflectance spectra were measured under ambient conditions, and the band gap energies (Table 1) were determined by extrapolating the linear portion of the Tauc plots to the horizontal axis to determine the minimum energy of photons absorbed (eV) (Fig. S1†).
The crystallinities of the Ti-BEA samples were confirmed using an X-ray diffractometer (Bruker, D8 Advance) with Cu Kα radiation under ambient conditions. The Ti-BEA samples were ground into a fine powder and loaded into a polypropylene sample holder for the measurements. The diffractograms of the Ti-BEA samples match previously reported powder diffraction patterns for zeolite *BEA (Fig. S2†).49 These diffractograms confirm that all Ti-BEA samples possess the *BEA zeolite framework. Anatase TiO2 contains a strong feature at ∼25.5°,50 while the *BEA framework shows a weak feature in the same location. The patterns for each Ti-BEA and Si-BEA-OH in Fig. S2† possess a small feature in this region, suggesting that the feature either originates from a *BEA framework feature or minimal quantities of TiO2 present within the Ti-BEA materials.
Ex situ Raman spectra of the Ti-BEA catalysts were measured with a Raman spectrometer (Renishaw, InVia) equipped with a 532 nm laser. The measurements were performed at ambient conditions on pressed catalyst pellets. The accumulation time was 20 s per scan, and each Raman spectra was calculated by averaging 10 scans. The delivered power density was approximately 2 mW μm−2, as measured by a power meter (Gentec-EO, PRONTO-SI). The Raman spectra for each Ti-BEA (Fig. S3†) lack discernible features at 144 cm−1, which indicates the absence of Ti–O–Ti bonds present in anatase TiO2. In conjunction with the high band gaps (4.3 eV, Table 1) of these materials and the absence of strong TiO2 features on the XRD patterns, these spectra indicate that Ti atoms reside in tetrahedral positions within the *BEA framework.
The surface area and micropore volumes of each Ti-BEA were determined using gas-phase adsorption isotherms of N2 (77 K) and Ar (87 K). The effect of (SiOH)x density on gaseous solvent uptake was determined from adsorption isotherms of H2O and CH3OH (295 K). All adsorption isotherms were collected on a volumetric adsorption instrument (Micromeritics, 3Flex). The Ti-BEA samples were pelletized and sieved to retain particles from 100–250 μm in diameter. The samples were degassed under dynamic vacuum prior to adsorption (<7 × 10−4 Pa, 673 K, 3 h). The surface area was calculated using the Rouquerol-modified Brunauer–Emmett–Teller (BET) method,51 and the micropore volume was determined from the t-plot method.52 Fig. S4† shows the N2 and Ar isotherms, and Table S1† presents the total and external surface area, BET surface area and pore volume from N2 adsorption, and total pore volume for each Ti-BEA. The H2O and CH3OH isotherms are displayed in Fig. S5.†
The relative density of (SiOH)x groups within the Ti-BEA catalysts was measured using infrared spectroscopy. Catalyst pellets (∼50 mg) were loaded into a transmission cell configured with CaF2 windows. The transmission cell was connected to a temperature controller and gas manifold, then loaded into a Fourier-transform infrared spectrometer (Bruker, Vertex 70) equipped with a liquid N2-cooled HgCdTe detector, as described previously.53 The cell was first heated to 573 K at ∼5 K min−1 and held for 2 hours in flowing He (50 cm3 min−1, 99.997%, Airgas) to desorb any water and volatile compounds. Infrared spectra (128 scans, 1 cm−1) of the Ti-BEA samples were then taken at 573 K (Fig. S6†). Background spectra were obtained with the empty transmission cell at identical conditions. The vibrational modes on the dehydrated Ti-BEA spectra between 3300–3750 cm−1 and 1800–2100 cm−1 represent v(O–H) of (SiOH)x groups54,55 and Si–O–Si overtones56 of the *BEA framework, respectively. The sharp feature at 3740 cm−1 represents isolated SiOH groups that do not interact with other SiOH groups.54,55 The broader features from 3300 to 3700 cm−1 represent defects containing multiple interacting hydroxyl moieties present within (SiOH)x groups. The ratio of the areas for v(O–H) and v(Si–O–Si) at 1865 and 2000 cm−1 gives a relative measure of SiOH density in each Ti-BEA (ΦIR, eqn (1)). The area of the isolated SiOH feature is excluded from v(O–H) in ΦIR calculations. The v(O–H) region was deconvoluted into multiple peaks (see Section S1.5†), and the isolated SiOH peak area was subtracted from the combined area of the v(O–H) region.
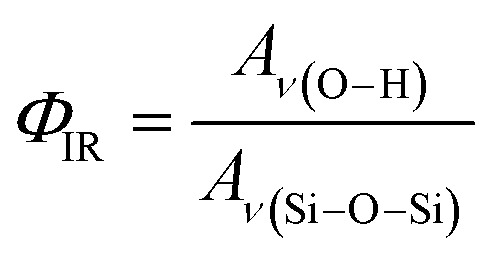 |
1 |
The ΦIR values (Table 1) suggest that Ti-BEA-OH contains a density of (SiOH)x groups nearly one order of magnitude greater than Ti-BEA-F.
Collectively, the characterization results provide strong evidence that Ti-BEA-OH and Ti-BEA-F materials contain atomically dispersed Ti atoms at framework positions within a crystalline *BEA framework. Moreover, these materials lack spectroscopically detectable quantities of TiO2 nanoparticles or crystallites. Each zeolite contains ∼1 Ti atom per 4 unit cells of *BEA, and Ti-BEA-OH contains 2.75 (SiOH)x nests per unit cell (calculation in ESI Section S1.6†). The synthesis method of Ti-BEA-F prohibits a direct calculation of (SiOH)x per unit cell, but previously established trends between ΦIR and (SiOH)x 28 indicate that the Ti-BEA-F sample synthesized for this work (ΦIR = 0.27, Table 1) contains < 0.1 (SiOH)x per unit cell.
2.3. Epoxidation turnover rate measurements
Turnover rates for 1-hexene (C6H12, Sigma-Aldrich, >99%) epoxidation with hydrogen peroxide (H2O2, Fisher Chemical, 30 mol% in H2O) in aqueous solutions of either acetonitrile (CH3CN, Fisher Chemical, HPLC Grade), methanol (CH3OH, Sigma-Aldrich, HPLC, ≥99.9%), or γ-butyrolactone (GBL, C4H6O2, Sigma-Aldrich, ≥99%) were measured in three-necked round-bottom flasks with magnetic stirring (700 rpm). The flasks were gently clamped to reflux condensers to avoid evaporative losses and submerged in a temperature-controlled H2O (308–318 K) or oil (323–338 K) bath on a hot plate (Corning, PC-420D). The reagents (C6H12 and H2O2) were combined with H2O (18.2 MΩ cm, Elga Purelab Flex 2) and CH3CN, CH3OH, or C4H6O2 along with benzene as an internal standard (Sigma-Aldrich, thiophene-free, >99%) and stirred for 0.5 h before an initial aliquot (∼0.5 cm3) was taken to determine the initial concentration of C6H12 and product, 1,2-epoxyhexane (C6H12O). Ti-BEA (∼20–50 mg) was then added to initiate the reaction, and aliquots were taken as a function of time using a syringe equipped with a polypropylene filter (Tisch Scientific, 0.22 μm) to separate the sample from the catalyst particles. The concentrations of alkene, benzene standard, and epoxide product were quantified with a gas chromatograph (Agilent, 6850) equipped with a polysiloxane column (HP-1, Agilent, 19091Z-115E), flame ionization detector, and liquid autosampler (CTC Analytics, GC Pal). Initial turnover rates were determined by fitting turnover numbers (moles of C6H12O per moles of Ti) as a function of time to a second-order polynomial with the y-intercept fixed at zero and determining the derivative at time equal to zero. All reported turnover rates were measured at differential conversion (<5%), with an uncertainty of ∼10% in reported rates, as shown with replicated measurements. The conditions used for rate measurements in this study avoid internal mass transfer constraints, as indicated by the linear dependence of turnover rates on alkene concentration (Section 3.1),57 which is consistent with expectations based on prior studies of reactions of H2O2 with alkenes in Ti substituted MFI, *BEA, and FAU at similar conditions.29,33,58 A mass-transfer limited material would show a sub-linear dependence on alkene concentration because the mean concentration of alkenes throughout the pores would not depend linearly on the fluid phase alkene concentration.
H2O2 consumption rates (−rH2O2) were measured with C6H12 present to calculate the selectivities for H2O2 consumption (SH2O2) as a co-reactant for epoxidation, as opposed to decomposition between two H2O2 molecules to form H2O and oxygen (−rdecomp). We note that solvent molecules may react with H2O2 to provide another contribution to −rdecomp, but rate changes with [H2O2] suggest that the bimolecular decomposition of H2O2 dominates contributions to −rdecomp (Fig. 2c). We define H2O2 selectivity as the ratio of the epoxidation rate (repox) to the overall H2O2 consumption rate (−rH2O2):
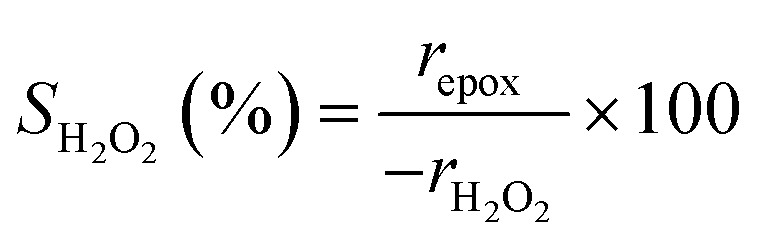 |
2 |
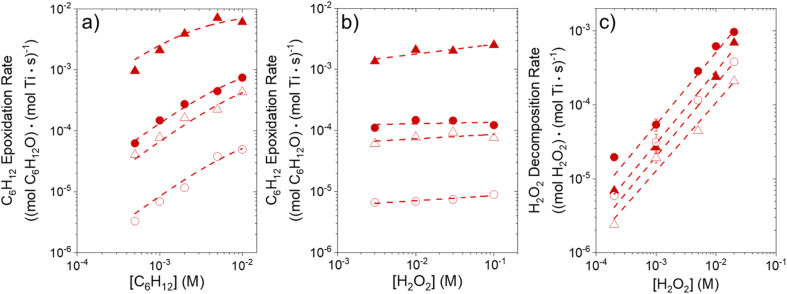
Fig. 2. Turnover rates for C6H12 epoxidation as a function of (a) C6H12 concentration (10 mM H2O2, 313 K), and (b) H2O2 concentration (1 mM C6H12, 313 K), and turnover rates for (c) H2O2 decomposition (313 K) as a function of H2O2 concentration for CH3OH mixtures with the minimum or maximum water contents examined (39 mM H2O, xH2O = 0.002 ( ); ∼31.6 M H2O, xH2O = 0.75 (
); ∼31.6 M H2O, xH2O = 0.75 ( )) over Ti-BEA-OH (solid points) and Ti-BEA-F (hollow points).
)) over Ti-BEA-OH (solid points) and Ti-BEA-F (hollow points).
Activation barriers for H2O2 decomposition were measured in the absence of C6H12. Solutions to measure H2O2 concentration were prepared using colorimetric titration with a titrant solution consisting of cupric sulfate (8.3 mM; VWR, 99%) and neocuproine hydrate (12 mM; SAGECHEM) in an aqueous solution of ethanol (4.3 M; Sigma-Aldrich, ≥99.5%). Aliquots from the reactions (0.15 cm3) were mixed with the titrant (1 cm3) and DI H2O (0.85 cm3). The absorbance of this solution at 454 nm was then measured using a UV-Vis spectrophotometer (Spectronic, 20 Genesys) to obtain the H2O2 concentration. A calibration curve was developed with solutions of known H2O2 concentration to convert absorbance to concentration. The concentrations were used to calculate H2O2 decomposition rates by subtracting the formation rate of 1,2-epoxyhexane from the total rate of H2O2 consumption.
2.4. In situ analysis of H2O2 activation
H2O2 activation over the Ti-BEA catalysts was examined using a UV-Vis spectrometer (Avantes, AvaSpec-2048) equipped with a pulsed xenon light source (Avantes, AvaLight-XE-Mini). Ti-BEA pellets (7 mm diameter) were loaded into a custom-built liquid flow cell attached to cartridge heaters and a temperature controller (Watlow, EZ-ZONE PM) to hold the cell at 313 K. The cell and spectrometer were connected to a 45-degree fiber optic diffuse reflection probe (Avantes, FC-UVIR600-2-BX-SR). Solvents and H2O2 were introduced continuously to the cell (1 cm3 min−1) using a high-performance liquid chromatography pump (Teledyne ISCO, ReaXus M1 Class). Background spectra were collected by flowing solvent without H2O2 (10–40 ms integration time, averaging 125–500 scans). Then solvent and H2O2 (0.1 M H2O2, 0.39 M H2O) flowed through the cell until spectra stopped changing (∼0.5 h), which indicated the coverage of H2O2-derived intermediates reached a steady state value. Finally, the cell was purged with flowing solvent without H2O2 for 1 h to examine the reversibility of H2O2 activation.
2.5. Liquid phase adsorption enthalpies for 1,2-epoxyhexane
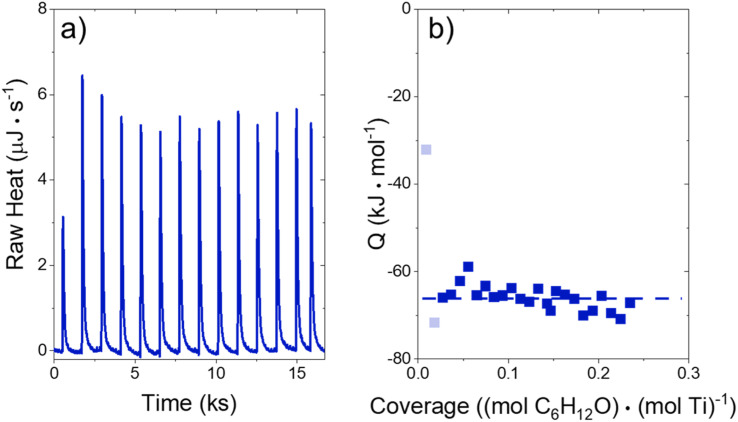
The heat released upon adsorption of C6H12O (TCI Chemicals, >96%) was measured with an isothermal titration calorimeter (ITC) (TA Instruments, NanoITC) equipped with sample and reference cells. A multi-step cleaning procedure was performed to prepare the sample and reference cells for each experiment. A cleaning solution (75 vol% of 1 M NaOH, 20 volume% CH3OH, 5 volume% dish soap) was first injected into the sample cell and left for 5 minutes at room temperature. The sample cell was then rinsed with 500 cm3 of DI H2O (18.2 MΩ cm, Elga Purelab Flex 2). Next, a 4 M NaOH (VWR, 10 N) solution was left in the cell for 2 hours at 353 K, followed by another rinse with 500 cm3 of DI H2O. Finally, the cell was treated with a solution of 4 M HNO3 (Macron Chemicals, 68–70 wt%) for 2 hours at 353 K, then a third rinse with 500 cm3 of DI H2O. The sample cell, reference cell, and 50 μL ITC syringe were then filled with H2O, and the syringe was loaded into the instrument. A subsequent electrical calibration used sequential pulses to determine the heat released from a calibrated Pt resistor. Finally, pure DI H2O was injected into DI H2O to ensure that the sample cell was clean enough to begin experiments. The cell was assumed to be clean when the H2O–H2O injection released negligible amounts of heat (±3 μJ for each injection of 1 μL). The cleaning procedure was repeated if the H2O–H2O injection did not give sufficiently low heat rates.
In a typical experiment, a slurry of Ti-BEA (15–30 mg) in organic solvent with H2O was titrated by a solution of epoxide (5–10 mM C6H12O) in the same solvent mixture. The mass of Ti-BEA in the sample cell was calculated by taking the difference between the mass added to the slurry and the mass remaining upon evaporation of the residual slurry after loading the cell. H2O concentrations were chosen to match conditions for kinetic turnover rate measurements (Section 3.1). The titrations were carried out at 313 K with a stirring rate of 250 rpm. The enthalpies of epoxide adsorption were calculated by averaging the integrated heats released upon adsorption of the epoxides to Ti-BEA sites from a 1 μL injection of titrant at low coverages (<0.25 mol epoxide (mol Ti)−1). The heats released in this low coverage regime remain approximately constant, suggesting that the calculated enthalpies represent the isosteric adsorption enthalpies for each epoxide.28
2.6. Liquid phase absorption of aqueous solvents
A nuclear magnetic resonance (NMR) spectrometer (Unity, INOVA 500 NB) was used to calculate the equilibrium compositions of aqueous solutions of organic solvents contacted to and equilibrated with Ti-BEA-OH and Ti-BEA-F samples by measuring 1H NMR peak areas. For each data point, an aliquot (∼0.25 cm3) of organic solvent and H2O was taken from a solvent solution (5 cm3) before and after 2 h contact with a Ti-BEA sample (∼500 mg) at a stirring rate of 700 rpm and temperature of 313 K to measure the change in the bulk liquid phase concentration. The catalyst and solvent mixture were in contact for 2 h to ensure solvent absorption had reached equilibrium. The sample of organic solvent and H2O was then mixed with deuterated methanol (CD3OD) as solvent and acetone or chloroform as an internal standard to prepare the NMR sample. The initial and final composition of the extrapore liquid was determined using areas of 1H-NMR features for H2O (4.5 ppm), acetone (2.2 ppm) or chloroform (7.8 ppm), and the organic solvent (CH3CN at 2.1 ppm, CH3OH at 3.3 ppm, C4H6O2 features at 2.3, 2.6 and 4.5 ppm). The intrapore solvent composition was estimated from the amount of solvent absorbed by the catalyst and the difference in extrapore liquid phase concentration before and after contacting the solvent with the catalyst (ESI Section S2†).
3. Results and discussion
3.1. Epoxidation and H2O2 decomposition rates depend on aqueous solvent composition
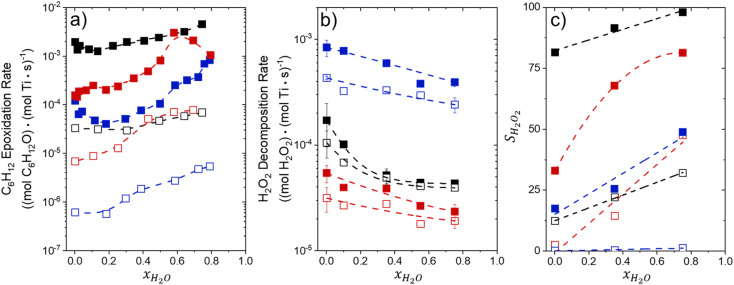
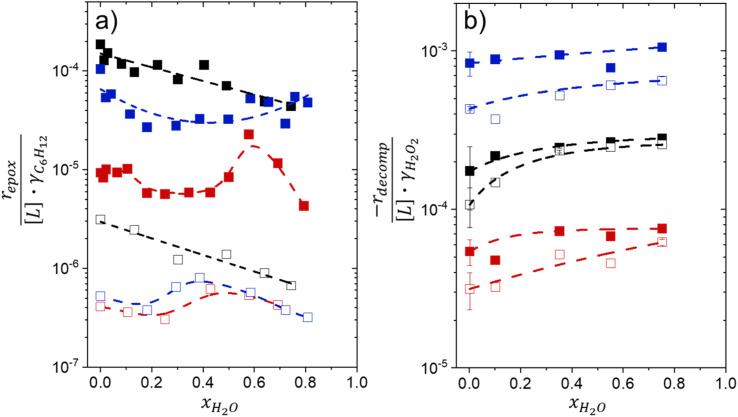
Fig. 1 shows that turnover rates for C6H12 epoxidation and H2O2 decomposition depend strongly on the identity of the organic component of the aqueous solvent and the value of xH2O. Turnover rates span four-orders of magnitude and, consequently, lead to H2O2 selectivities (SH2O2) that range from 0.1–98%. Fig. 1a shows that rates of C6H12 epoxidation increase as xH2O increases for all organic solvents over both Ti-BEA-OH and Ti-BEA-F. Ti-BEA-OH gives greater rates than Ti-BEA-F for each organic solvent at all xH2O. This systematic difference was previously attributed to entropy gains that reflect the disruption of greater quantities of hydrogen bonded H2O molecules in hydrophilic pores of Ti-BEA.27,33,34 Epoxidation turnover rates in C4H6O2 are consistently lowest among these organic solvents at all xH2O. CH3CN provides the greatest rates in all cases except when xH2O exceeds 0.4 over Ti-BEA-F, where rates in CH3OH surpass those in CH3CN.
Fig. 1. Turnover rates for (a) C6H12 epoxidation to form C6H12O (1 mM C6H12, 10 mM H2O2, 313 K), (b) H2O2 decomposition (1 mM H2O2, 313 K), and (c) H2O2 selectivities for epoxidation (1 mM C6H12, 10 mM H2O2, 313 K) as a function of H2O mole fraction in mixtures of CH3CN (■,□), CH3OH ( ), and C4H6O2 (
), and C4H6O2 ( ) with H2O over Ti-BEA-OH (solid points) and Ti-BEA-F (hollow points). The furthest left data points represent xH2O = 0.002, which comes from the aqueous H2O2 reagent solution (39 mM).
) with H2O over Ti-BEA-OH (solid points) and Ti-BEA-F (hollow points). The furthest left data points represent xH2O = 0.002, which comes from the aqueous H2O2 reagent solution (39 mM).
Fig. 1b shows that turnover rates for H2O2 decomposition (i.e., in the absence of C6H12) decrease with increasing xH2O for all combinations of organic solvent and zeolite, which opposes the trend for epoxidation turnover rates. Among organic solvents, C4H6O2 gives the greatest H2O2 decomposition rates and CH3OH gives the lowest rates at all xH2O. The lower H2O2 decomposition rates in CH3OH than in CH3CN mixtures agree with previous reports over Ti-incorporated zeolite materials,39,44 while turnover rates for C6H12 epoxidation in CH3CN that are greater than those in CH3OH mixtures concur with findings over Ti-BEA materials.29,37–39 Notably, H2O2 decomposition rates in Fig. 1b span less than two-orders of magnitude, which shows the decomposition pathway senses the identity of the solvent and zeolite less strongly than C6H12 epoxidation. The contrasting effects of organic solvent and xH2O on epoxidation and H2O2 decomposition rates evince that solvent molecules influence the stability of the fluid phase reactants and transition states within pores for the two pathways in different ways.
Fig. 1c reveals that all combinations of organic solvents and zeolites show significantly higher SH2O2 for C6H12 epoxidation at greater xH2O. Ti-BEA-OH gives greater values of SH2O2 than Ti-BEA-F in all cases, but SH2O2 increases more with xH2O over Ti-BEA-F relative to Ti-BEA-OH (see ESI Section S3†). The greatest SH2O2 (98%) occurs in Ti-BEA-OH with aqueous CH3CN (xH2O = 0.75) (Note: values of xH2O greater than 0.8 were not used due to miscibility issues with C6H12). Overall, CH3CN mixtures lead to the highest SH2O2 and C4H6O2 leads to the lowest SH2O2 at all xH2O in Ti-BEA-OH. This trend holds at lower xH2O values (≤0.35) in Ti-BEA-F, but CH3OH gives the highest SH2O2 at higher xH2O (≥0.75). Collectively, the data presented in Fig. 1 shows that increasing xH2O within each organic solvent provides greater epoxidation rates and more selective use of H2O2 for epoxidation over Ti-BEA zeolites with different (SiOH)x densities.
The differences in turnover rates for C6H12 epoxidation (Fig. 1a) and H2O2 decomposition (Fig. 1b) may result from changes in the coverage of reactive species, the reaction mechanism, or the kinetically relevant step; alternatively, these differences may reflect changes in the free energies of reagents, reactive intermediates, or key transition states due to direct interactions with solvent molecules. The coming sections distinguish these possibilities using the molecular interpretation of turnover rate expressions for the epoxidation and H2O2 decomposition reactions.
3.2. x H2O does not influence reaction mechanisms
Turnover rates for epoxidation and H2O2 decomposition reflect the stabilities of the associated transition states together with the coverages of reactive surface species formed during catalysis, which depend on the concentrations of the reactants and products present. Fig. 2a shows that C6H12 epoxidation rates depend linearly on C6H12 concentration ([C6H12], where brackets denote the concentration of a species or the number of surface intermediates) at low ratios of [C6H12] to [H2O2] (<0.5) in aqueous CH3OH mixtures over both Ti-BEA-OH and Ti-BEA-F. At these low ratios of [C6H12] to [H2O2], rates do not depend on values of [H2O2] (Fig. 2b). Rates show a sublinear dependence on [C6H12] at higher ratios of [C6H12] to [H2O2], which signifies a change in the most abundant reactive intermediate (MARI). In contrast, turnover rates for epoxidation depend weakly on [C6H12], linearly on [H2O2], and inversely on epoxide product concentration ([C6H12O]) at sufficiently high ratios of [C6H12] to [H2O2] ([C6H12] : [H2O2] > 50), consistent with previous work.58,59Fig. 2c demonstrates, however, that H2O2 decomposition turnover rates increase linearly with [H2O2] on both Ti-BEA materials for all xH2O examined. Measurements obtained from aqueous solutions of CH3CN and C4H6O2 (ESI Section S4†) exhibit effects of reactant concentrations on epoxidation and H2O2 decomposition turnover rates that match the behavior in aqueous CH3OH (Fig. 2). Collectively, these observations match the manner in which turnover rates for epoxidation of 1-alkenes (C6H12 to C18H36),27,29,33,34,58,60,61 cyclohexene,59 and styrene62–64 with H2O2 depend upon concentrations of reactants and products in CH3CN 27,29,33,58–64 and CH3OH 29,64 upon a range of titanosilicates (Ti-MFI,29,33 Ti-BEA,27,29,58,59,61–63 Ti-FAU,33,63 Ti–SiO2 60–63) and Fe- and Cr-incorporated metal–organic frameworks,64 which implies that conclusions for the effects of xH2O on epoxidation kinetics for C6H12 should extend broadly across alkenes.
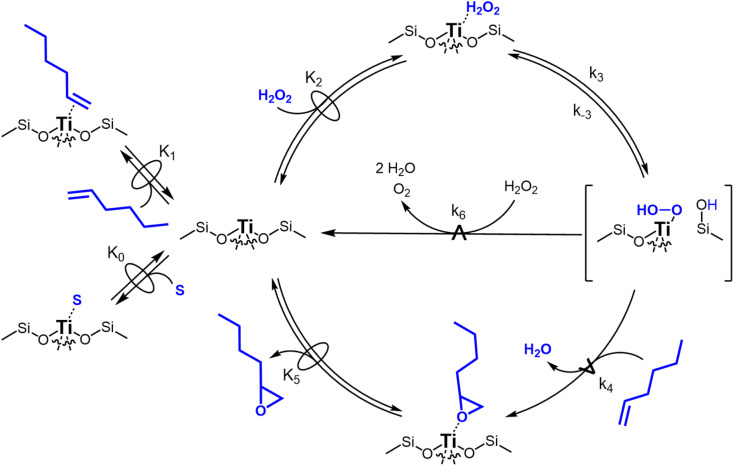
Scheme 2 depicts a plausible system of elementary steps that describe the epoxidation of C6H12 and the bimolecular decomposition of H2O2. The catalytic cycle begins with quasi-equilibrated adsorption of a solvent molecule (step 0), C6H12 (step 1), or H2O2 (step 2). Then, H2O2 activates to form a pool of Ti–OOH58,65–70 and titanium-peroxo (Ti-(η2-O2))58,62,69,70 intermediates (step 3). The H2O2-derived intermediates may protonate to reform H2O2 (reverse of step 3), react with C6H12 to form C6H12O (step 4), or react with a fluid phase H2O2 molecule to decompose to water and oxygen (step 6) in kinetically relevant processes. Radical clock experiments performed with cis-stilbene58 give evidence that Ti–OOH intermediates, commonly invoked as the reactive intermediate for epoxidations,58,62,69,71,72 primarily participate in the transfer of O-atoms to alkenes to form epoxides (rather than Ti-(η2-O2)). We, therefore, refer to the pool of H2O2-derived intermediates as Ti–OOH for simplicity. The formed epoxide then desorbs in a quasi-equilibrated manner to release the 1,2-epoxyhexane (C6H12O) product (step 5) and complete the catalytic cycle. This scheme accounts for differences in the apparent dependence of rates on reactant concentrations at low and high ratios of [C6H12] to [H2O2]. While O-atom transfer from Ti–OOH to C6H12 remains the kinetically relevant step for each kinetic regime,58 the MARI differs between the regimes. Ti–OOH intermediates saturate active sites at low ratios of [C6H12] to [H2O2], and the C6H12O product covers these sites at high ratios of [C6H12] to [H2O2]. Based upon Scheme 2 and the kinetic relevance of each step depicted, epoxidation rates (repox) follow a simple rate expression:
| repox = k4[Ti–OOH][C6H12] | 3 |
where k4 is the rate constant for step 4 (Scheme 2) and [Ti–OOH] represents the number of the H2O2-derived surface intermediates. Applying the pseudo-steady state hypothesis to Ti–OOH intermediates and a site balance yields a turnover rate expression (see Section S6† for full derivation) consistent with rate measurements:
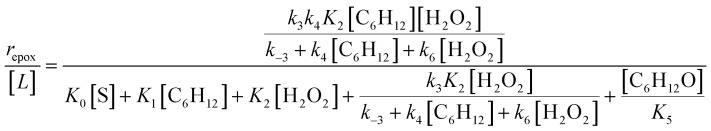 |
4 |
Scheme 2. Proposed mechanism for C6H12 epoxidation with H2O2 and H2O2 decomposition on Ti-BEA catalysts. 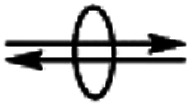 denotes a quasi-equilibrated step, while
denotes a quasi-equilibrated step, while 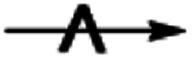 signifies kinetically relevant steps for formation of distinct products. The degree of reversibility of H2O2 activation (step 3) varies with the quantity of protic molecules in the solvent. The blue H atom in the Si–OH group adjacent to Ti–OOH originates from H2O2 during Ti–OOH formation. Solvent molecules have been omitted for clarity, except for the adsorption of a solvent molecule (S) to Ti sites in step 0.
signifies kinetically relevant steps for formation of distinct products. The degree of reversibility of H2O2 activation (step 3) varies with the quantity of protic molecules in the solvent. The blue H atom in the Si–OH group adjacent to Ti–OOH originates from H2O2 during Ti–OOH formation. Solvent molecules have been omitted for clarity, except for the adsorption of a solvent molecule (S) to Ti sites in step 0.
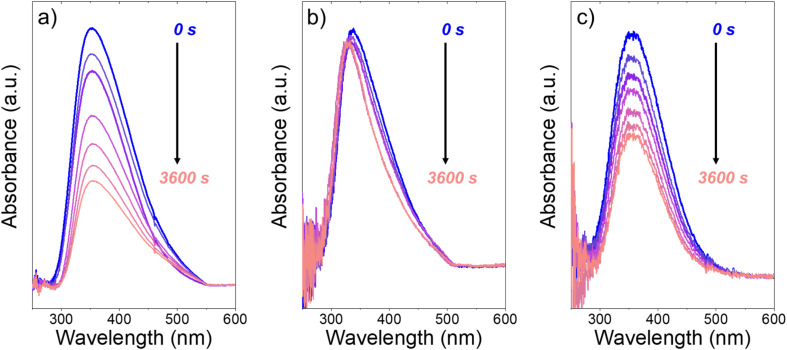
Fig. 3 presents evidence that the values of k−3 depend on the identity of the organic solvent and xH2O. In situ UV-Vis spectra give strong evidence that the H2O2-derived intermediates form reversibly in H2O (Fig. 3a) and irreversibly in C4H6O2 (Fig. 3b). Notably, the peak areas for Ti–OOH and Ti–(η2)–O2 attenuate by ∼60% in H2O (Fig. 3a) and by ∼6% in C4H6O2 (Fig. 3b) over a 1 h period after switching from an aqueous H2O2 solution to the neat solvent. Prior UV-Vis spectra suggest irreversible H2O2 activation in CH3CN29,59,62 and reversible activation in CH3OH.29,69 Therefore, these findings lead to the broader conclusion that protic solvents (i.e., H2O, CH3OH) protonate Ti–OOH and Ti–(η2–O2), which then desorb as H2O2, but these steps are much slower in aprotic solvents (i.e., CH3CN, C4H6O2). The H2O2 intermediate peak areas also attenuate by ∼40% in 1 h in an equimolar mixture of H2O and C4H6O2 (Fig. 3c), which indicates that including a sufficient quantity of a protic component within a solvent mixture allows for reversible H2O2 activation. These findings demonstrate that H2O2 may reform from Ti–OOH and Ti–(η2–O2) within all aqueous solvent combinations utilized here, where the rate of reformation depends on the concentration of protic solvent molecules present. Values of k−3 over Ti-BEA zeolites in CH3OH are up to 10-times greater than in neat H2O (Table S3†),29 which suggests that CH3OH facilitates the reformation of H2O2 more readily than H2O.
Fig. 3. In situ UV-Vis spectra of Ti-BEA-OH as a function of time within continuously flowing neat (a) H2O, (b) C4H6O2, and (c) equimolar H2O and C4H6O2 (313 K, 1 cm3 min−1) after H2O2 activation (100 mM H2O2, 390 mM H2O, 313 K, 1 cm3 min−1). Spectra were acquired every 600 s after H2O2 activation. Spectra for Ti-BEA-F and desorption rate constants are included in Section S5.†.
Despite the variations in the reversibility of H2O2 activation across solvent mixtures, the full rate expression (eqn (4)) simplifies to a common form when Ti–OOH intermediates saturate active sites (i.e., [Ti–OOH] ≈ [L]).
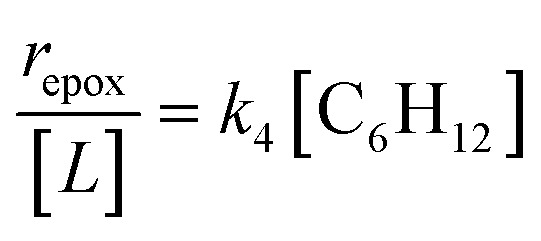 |
5 |
Eqn (5) predicts rates that match the data in Fig. 2a (at [C6H12] : [H2O2] < 0.5) and 2b, implicating Ti–OOH intermediates as the MARI for epoxidation. Notably, Fig. S9† and 2 together demonstrate that the regime of a Ti–OOH MARI and first-order kinetics with respect to [C6H12] holds for each combination of catalyst, organic solvent, and xH2O when molar ratios of H2O2 to C6H12 exceed two.
Rates for H2O2 decomposition depend on the coverage of Ti–OOH and [H2O2] because H2O2 decomposition involves a reaction between a Ti–OOH intermediate and a fluid phase H2O2 molecule. Therefore, H2O2 decomposition rates correspond to:
| −rdecomp = k6[Ti–OOH][H2O2] | 6 |
where k6 is the rate constant for step 6 in Scheme 2. Substituting terms for [Ti–OOH] and using the site balance for [L] gives a full rate expression:
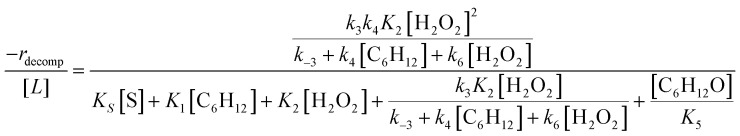 |
7 |
Once again, the rate expression simplifies when Ti–OOH intermediates saturate active sites, such that eqn (7) collapses to the form:
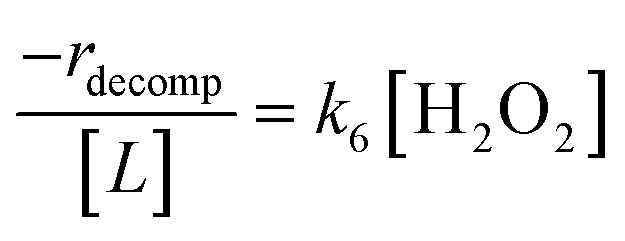 |
8 |
The rate expression in eqn (8) reproduces the turnover rate dependencies on [H2O2] shown in Fig. 2c. This interpretation also agrees with prior studies that invoked a mechanism in which fluid phase H2O2 reacts with an H2O2-derived intermediate over Ti-,65,73 Nb-,74 and Ta-incorporated75 microporous and mesoporous catalysts.
Notably, applying Ti–OOH as the MARI yields equations that match the data for C6H12 epoxidation (eqn (5)) and H2O2 decomposition (eqn (8)) in Fig. 2 simultaneously. The two pathways, therefore, proceed through the common reaction intermediate (Ti–OOH) that remains the MARI at all xH2O examined here in each zeolite. As shown for epoxidation rates, the simplified decomposition rate expression (eqn (8)) does not reflect the value of k−3, which implies that the reversibility of H2O2 activation does not impact rates of alkene epoxidation and H2O2 decomposition within the regime where Ti–OOH intermediates saturate active sites. This analysis indicates that kinetic measurements made under these conditions provide the requisite platform for direct and quantitative comparisons between solvent – catalyst pairs.
To summarize, similar rate dependences for both Ti-BEA-OH and Ti-BEA-F at high (0.002) and low (0.75) xH2O in each organic solvent suggest that epoxidation and H2O2 decomposition proceed through the same reaction mechanisms. Differences in epoxidation rates with different organic solvents, concentrations of water, and (SiOH)x defect densities within pores of *BEA (Fig. 1) do not result from changes in the reaction mechanisms or coverage of reactive species. These findings resemble the interpretation of prior investigations for homogeneous acid-catalyzed alcohol dehydration reactions that concluded solvent molecules influence the stability of fluid phase reactive species.10,76–78 Our group and others showed that solvent molecules within zeolite pores affect the stability of adsorbed reactive species for alkene epoxidation with H2O2,27,29,33 glucose isomerization,48,79–81 and alcohol dehydration.82–86 With mechanistic differences excluded, the rate differences for epoxidation and H2O2 decomposition in Fig. 1 and 2 must reflect interactions among solvent molecules and reactive species located both within pores and within the bulk solvent that drive changes in k4 (eqn (5)) and k6 (eqn (8)).
3.3. Activity coefficients show differences in intrapore and fluid phase species stability
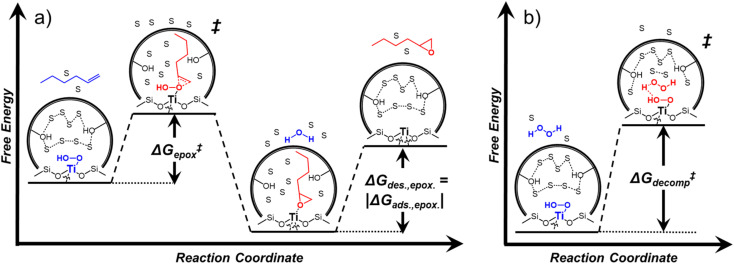
Activity coefficients (γ) of the fluid phase reactants (C6H12 and H2O2; γC6H12 and γH2O2) contribute to observed differences between turnover rates. Prior studies correlated values of fluid phase γ for 5-hydroxymethylfurfural87 and glucose48 to etherification and isomerization rates, respectively. Here, thermodynamic models were used to directly quantify γ values to determine how reagent stability changes with xH2O and organic solvent identity (ESI Section S7†). Fig. 4 shows turnover rates for C6H12 epoxidation and H2O2 decomposition normalized by γ values of the respective reactant at each xH2O, which accounts for the influence of intramolecular interactions (i.e., excess contributions) on the stability of the reactant in the fluid phase. When normalized by solvent-dependent values of γC6H12, the epoxidation turnover rates still span three-orders of magnitude and depend on both xH2O and the identity of the organic component of the solvent (Fig. 4a). In addition, the changes in activity-normalized turnover rates 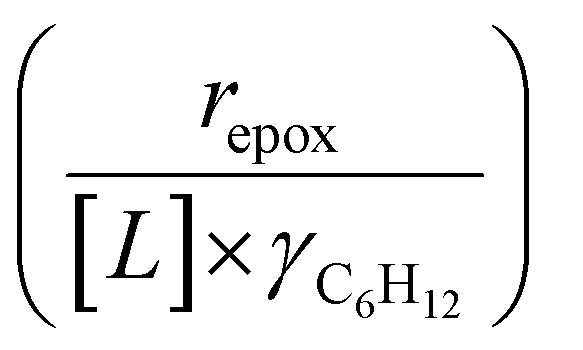 as functions of xH2O exhibit complex non-monotonic dependences, which may reflect the influence of pore confinement on the solvation shells of reactive species and transition states within *BEA pores. Indeed, these data indicate that the stabilities of reactive species in the pore (GTi–OOH,
as functions of xH2O exhibit complex non-monotonic dependences, which may reflect the influence of pore confinement on the solvation shells of reactive species and transition states within *BEA pores. Indeed, these data indicate that the stabilities of reactive species in the pore (GTi–OOH, 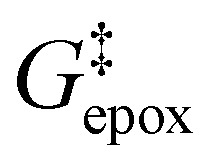 ) change with xH2O and affect rates significantly. Accounting for γC6H12 and γH2O2 values within turnover rate expressions for C6H12 epoxidation and H2O2 decomposition when Ti–OOH covers sites (eqn (5) and (8)) and defining alternate rate constants (
) change with xH2O and affect rates significantly. Accounting for γC6H12 and γH2O2 values within turnover rate expressions for C6H12 epoxidation and H2O2 decomposition when Ti–OOH covers sites (eqn (5) and (8)) and defining alternate rate constants (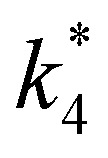 and
and 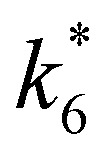 ) yields:
) yields:
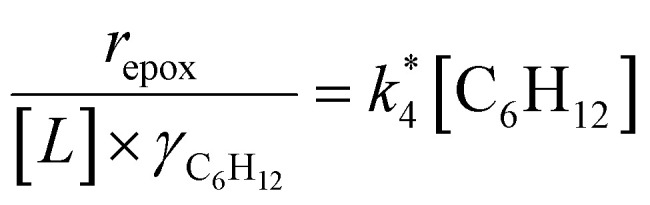 |
9 |
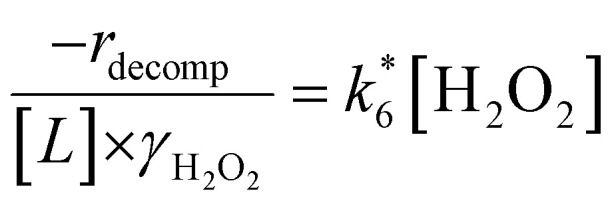 |
10 |
where 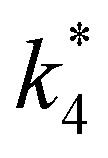 and
and 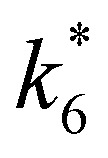 depend on corresponding alternate apparent activation free energies
depend on corresponding alternate apparent activation free energies 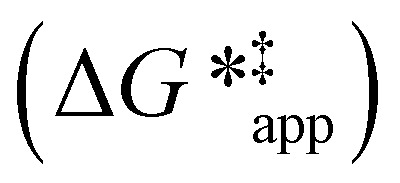 (see Section 3.4†). The non-monotonic trends in Fig. 4a must stem from differences in the structure and composition of the solvation shells for Ti-bound intermediates and transition states as a function of organic solvent, xH2O, and zeolite (SiOH)x density. The Ti–OOH intermediate and epoxidation transition state likely have different sizes and polarities (Scheme 3a), which promote different stoichiometries of water and co-solvent within their solvation shells.
(see Section 3.4†). The non-monotonic trends in Fig. 4a must stem from differences in the structure and composition of the solvation shells for Ti-bound intermediates and transition states as a function of organic solvent, xH2O, and zeolite (SiOH)x density. The Ti–OOH intermediate and epoxidation transition state likely have different sizes and polarities (Scheme 3a), which promote different stoichiometries of water and co-solvent within their solvation shells.
Fig. 4. Turnover rates for (a) C6H12O formation (1 mM C6H12, 10 mM H2O2, 313 K) normalized by γC6H12 and (b) H2O2 decomposition (1 mM H2O2, 313 K) normalized by γH2O2 as a function of xH2O in mixtures of CH3CN (■,□), CH3OH ( ), and C4H6O2 (
), and C4H6O2 ( ) with H2O over Ti-BEA-OH (solid points) and Ti-BEA-F (hollow points). Activity coefficients of C6H12 were calculated using the Volume-Translated Peng-Robinson (VTPR) method on ChemCAD, while activity coefficients of H2O2 were calculated with the nonrandom two-liquid (NRTL) method.
) with H2O over Ti-BEA-OH (solid points) and Ti-BEA-F (hollow points). Activity coefficients of C6H12 were calculated using the Volume-Translated Peng-Robinson (VTPR) method on ChemCAD, while activity coefficients of H2O2 were calculated with the nonrandom two-liquid (NRTL) method.
Scheme 3. Proposed reaction coordinate diagrams for (a) C6H12 epoxidation and (b) H2O2 decomposition over Ti-BEA zeolites, where solvent molecules are organic solvent or H2O and are denoted with an “S”. In (a), the alkene adsorbs into the pore and reacts with the Ti–OOH MARI to form the epoxide. The epoxide then desorbs to complete the reaction. In (b), the liquid phase H2O2 adsorbs and binds to the Ti–OOH MARI to form the transition state. The remainder of the reaction coordinate in which the products form (2H2O + O2) is not shown for brevity.
Fig. 4b reveals that rates for H2O2 decomposition normalized by γH2O2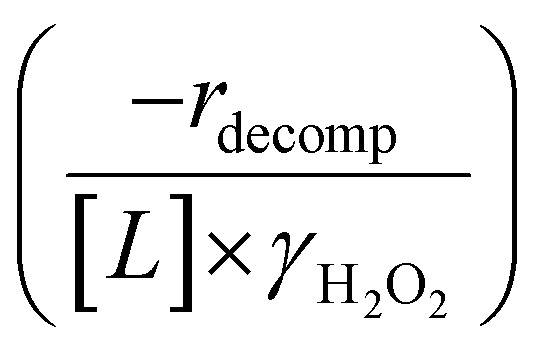 increase systematically with increasing xH2O in all combinations of zeolite and organic solvent. The decomposition transition state and Ti–OOH plausibly form hydrogen bonds with multiple H2O molecules (Scheme 3b), which stabilize these species at higher xH2O. Transition state stabilization through hydrogen bonds with H2O may outweigh the same effect for Ti–OOH because the transition state contains more hydrogen bonding functions. This disparity in hydrogen bond donating and accepting interactions generates the trends in activity-normalized turnover rates in Fig. 4b (eqn (10)). Overall,
increase systematically with increasing xH2O in all combinations of zeolite and organic solvent. The decomposition transition state and Ti–OOH plausibly form hydrogen bonds with multiple H2O molecules (Scheme 3b), which stabilize these species at higher xH2O. Transition state stabilization through hydrogen bonds with H2O may outweigh the same effect for Ti–OOH because the transition state contains more hydrogen bonding functions. This disparity in hydrogen bond donating and accepting interactions generates the trends in activity-normalized turnover rates in Fig. 4b (eqn (10)). Overall, 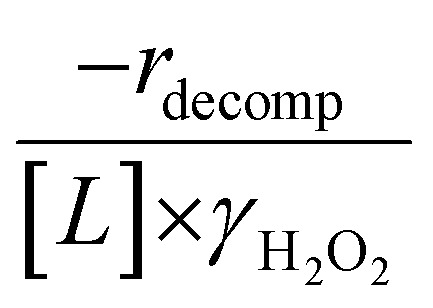 values change less significantly with xH2O than
values change less significantly with xH2O than 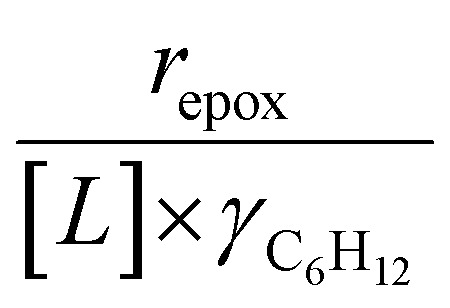 , indicating that differences in Ti–OOH stability largely cancel out with the decomposition transition state but differ more significantly from epoxidation transition state stability. The differences between the sensitivities of these reaction pathways to xH2O reflect the distinct size and structure of solvation shells surrounding the corresponding transition states within the pores of Ti-BEA catalysts and indicate that solvent molecules assist with the selective stabilization of certain transition states for these parallel pathways.
, indicating that differences in Ti–OOH stability largely cancel out with the decomposition transition state but differ more significantly from epoxidation transition state stability. The differences between the sensitivities of these reaction pathways to xH2O reflect the distinct size and structure of solvation shells surrounding the corresponding transition states within the pores of Ti-BEA catalysts and indicate that solvent molecules assist with the selective stabilization of certain transition states for these parallel pathways.
Variations between the trends for turnover rates in Fig. 1 and for 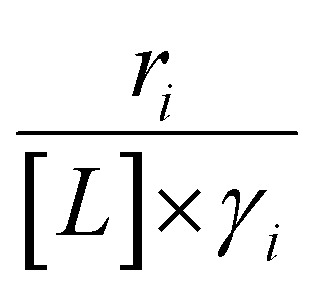 values in Fig. 4 and their dependence on xH2O directly reflect the stabilization of fluid phase C6H12 and H2O2 by interactions with fluid phase solvent molecules. As xH2O increases (0.002 ≤ xH2O ≤ 0.8), γC6H12 increases by factors of 12–15 while γH2O2 decreases by 3–6 fold (Fig. S13 and S14†). These opposing changes result from destabilizing interactions between hydrophobic C6H12 and H2O and stabilizing interactions between hydrophilic H2O2 and H2O. These γ trends correspond to the rate trends for C6H12 epoxidation and H2O2 decomposition in Fig. 1. The persistent dependence of
values in Fig. 4 and their dependence on xH2O directly reflect the stabilization of fluid phase C6H12 and H2O2 by interactions with fluid phase solvent molecules. As xH2O increases (0.002 ≤ xH2O ≤ 0.8), γC6H12 increases by factors of 12–15 while γH2O2 decreases by 3–6 fold (Fig. S13 and S14†). These opposing changes result from destabilizing interactions between hydrophobic C6H12 and H2O and stabilizing interactions between hydrophilic H2O2 and H2O. These γ trends correspond to the rate trends for C6H12 epoxidation and H2O2 decomposition in Fig. 1. The persistent dependence of 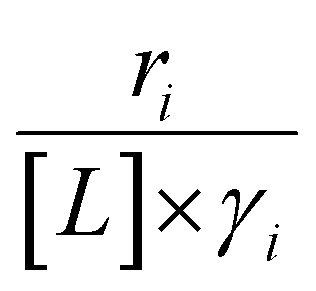 values in Fig. 4 on organic solvent identity, xH2O, and (SiOH)x density establishes that the stability of transition states and Ti–OOH intermediates in the pore respond to changes in fluid composition within the pores of *BEA. The following section provides further insight and quantitatively assesses the effect of xH2O on the stability of reactive species in the pores with activation barrier measurements.
values in Fig. 4 on organic solvent identity, xH2O, and (SiOH)x density establishes that the stability of transition states and Ti–OOH intermediates in the pore respond to changes in fluid composition within the pores of *BEA. The following section provides further insight and quantitatively assesses the effect of xH2O on the stability of reactive species in the pores with activation barrier measurements.
3.4. Stability of reactive species vary with organic solvent, xH2O, and (SiOH)x density
Turnover rate measurements (Fig. 1 and 2) show that C6H12 epoxidation and H2O2 decomposition turnover rates depend on the organic solvent, xH2O, and (SiOH)x density of Ti-BEA. The first two factors alter the solvent environment around reactive species in the bulk fluid phase, whereas all three factors influence the solvation of species at active sites within the pores of Ti-BEA. Consequently, these variables impact apparent activation enthalpies 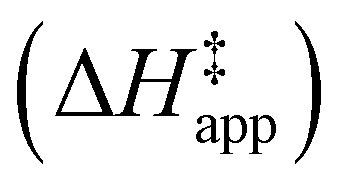 and entropies
and entropies  for epoxidation
for epoxidation 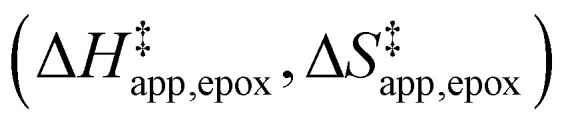 and H2O2 decomposition
and H2O2 decomposition 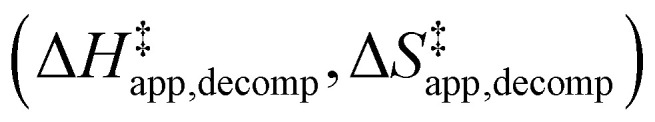 . Values of
. Values of 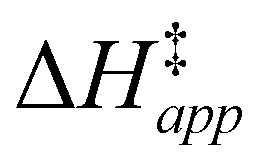 and
and 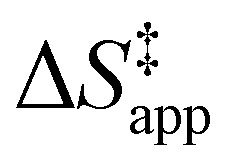 were measured in identical kinetic regimes, where C6H12 or H2O2 react with the Ti–OOH MARI to form the corresponding transition states (Scheme 3). The apparent activation free energy
were measured in identical kinetic regimes, where C6H12 or H2O2 react with the Ti–OOH MARI to form the corresponding transition states (Scheme 3). The apparent activation free energy 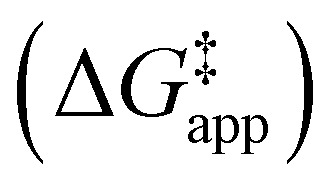 depends on
depends on 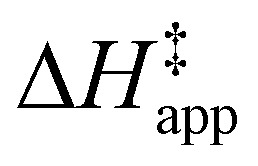 and
and 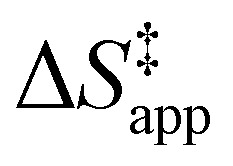 and can be defined as the difference between the free energy of the transition state and reference state components, shown here for C6H12 epoxidation:
and can be defined as the difference between the free energy of the transition state and reference state components, shown here for C6H12 epoxidation:
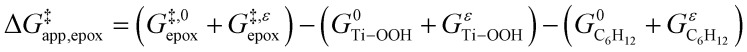 |
11 |
where free energies contain both standard state (G0) and excess (Gε) contributions. The excess free energy for a species i can be calculated from the activity coefficient for that species (γi), which depends on interactions with solvating molecules or nearby surfaces.
| Giε = RT × ln(γi) | 12 |
The excess free energies equal zero for ideal solutions (i.e., when the activity coefficient equals one) but are non-zero in non-ideal solutions and at solid–liquid interfaces.26 We can define apparent free energy terms 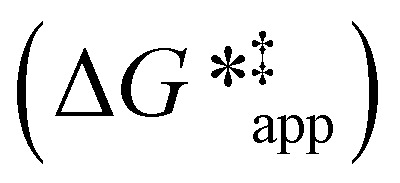 that exclude the activity coefficient of the reactant (i.e., C6H12), which correspond to the
that exclude the activity coefficient of the reactant (i.e., C6H12), which correspond to the 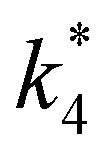 term represented in eqn (9):
term represented in eqn (9):
 |
13 |
To define 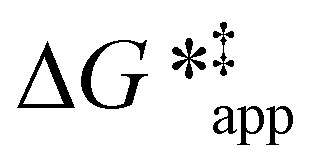 values, we must simply add GC6H12ε to each side of eqn (11):
values, we must simply add GC6H12ε to each side of eqn (11):
| 14 |
Note, an identical derivation of equations for H2O2 decomposition is included in the ESI (Section S6†). Values for γC6H12 were used to compute HC6H12ε (Section S7†). The HC6H12ε values allow for the derivation of an enthalpy term  analogous to
analogous to  :
:
| 15 |
Likewise, γH2O2 values yield values for HH2O2ε (ESI Section S7†), which allows for the calculation of a similar enthalpic term for H2O2 decomposition  :
:
| 16 |
ESI Section S9† includes the measured 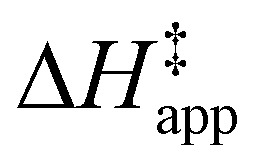 and
and  for each pathway and discusses the entropy trends, which align with the interpretation of the enthalpy trends that follow. Eqn (15) and (16) account for the dependence of enthalpy values on organic solvent identity, xH2O, and (SiOH)x density. The values of HC6H120 and HH2O20 do not depend on these variables, so differences in
for each pathway and discusses the entropy trends, which align with the interpretation of the enthalpy trends that follow. Eqn (15) and (16) account for the dependence of enthalpy values on organic solvent identity, xH2O, and (SiOH)x density. The values of HC6H120 and HH2O20 do not depend on these variables, so differences in  and
and  arise entirely from changes in Hε values for the Ti–OOH intermediate and respective transition states.
arise entirely from changes in Hε values for the Ti–OOH intermediate and respective transition states.
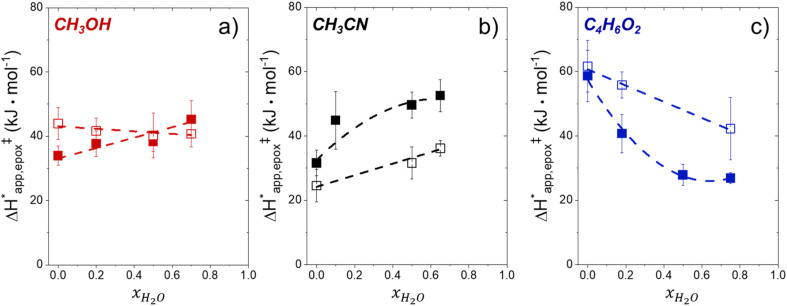
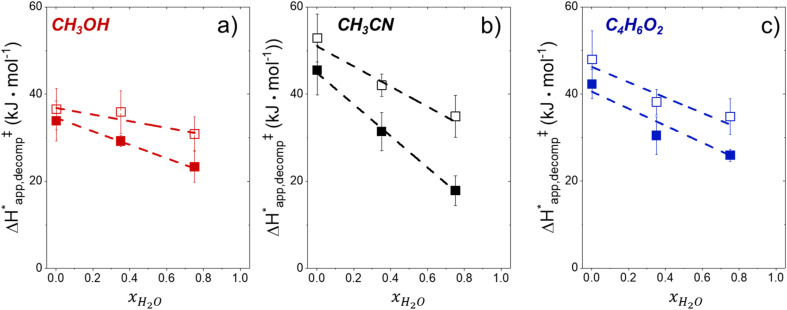
Fig. 5 shows that 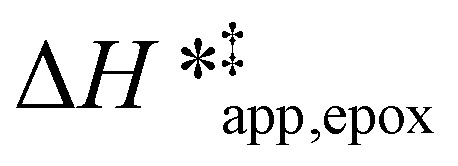 varies as a function of xH2O between Ti-BEA-OH and Ti-BEA-F, which indicates that the organization, density, and composition of solvent molecules within the pores of *BEA differ between these materials. Across organic solvents,
varies as a function of xH2O between Ti-BEA-OH and Ti-BEA-F, which indicates that the organization, density, and composition of solvent molecules within the pores of *BEA differ between these materials. Across organic solvents, 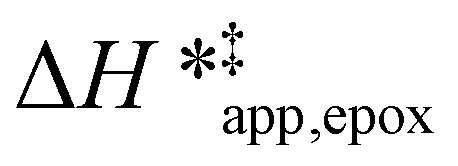 values span 4–19 kJ mol−1 between the lowest and highest xH2O for Ti-BEA-F and 12–32 kJ mol−1 over Ti-BEA-OH. These comparisons give evidence that the solvent structure in Ti-BEA-OH pores changes more significantly with increasing xH2O than in Ti-BEA-F.
values span 4–19 kJ mol−1 between the lowest and highest xH2O for Ti-BEA-F and 12–32 kJ mol−1 over Ti-BEA-OH. These comparisons give evidence that the solvent structure in Ti-BEA-OH pores changes more significantly with increasing xH2O than in Ti-BEA-F. 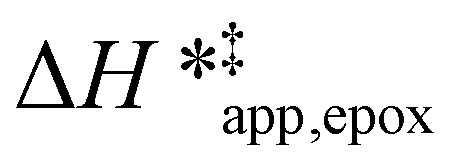 increases with increasing xH2O for CH3OH (Fig. 5a) and CH3CN (Fig. 5b) mixtures over Ti-BEA-OH, which may indicate the transition state disrupts a greater quantity of H2O within pores, which increases
increases with increasing xH2O for CH3OH (Fig. 5a) and CH3CN (Fig. 5b) mixtures over Ti-BEA-OH, which may indicate the transition state disrupts a greater quantity of H2O within pores, which increases 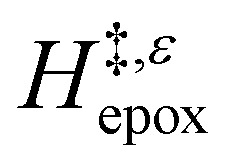 . For C4H6O2 mixtures (Fig. 5c),
. For C4H6O2 mixtures (Fig. 5c), 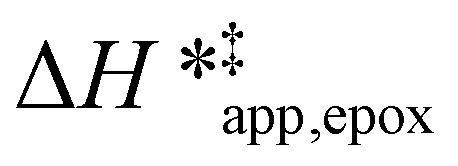 may decrease with increasing xH2O because the transition state needs to displace a smaller quantity of bulky C4H6O2 molecules, offsetting the enthalpic penalty of disrupting hydrogen bonded solvent molecules and reducing
may decrease with increasing xH2O because the transition state needs to displace a smaller quantity of bulky C4H6O2 molecules, offsetting the enthalpic penalty of disrupting hydrogen bonded solvent molecules and reducing 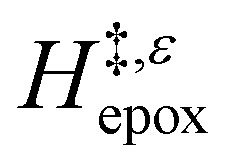 .
.
Fig. 5.
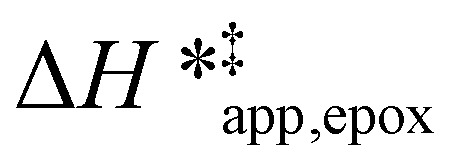 values for C6H12 epoxidation (1 mM C6H12, 10 mM H2O2, 308–333 K) as a function of xH2O in mixtures of (a) CH3OH (
values for C6H12 epoxidation (1 mM C6H12, 10 mM H2O2, 308–333 K) as a function of xH2O in mixtures of (a) CH3OH ( ), (b) CH3CN (■,□), and (c) C4H6O2 (
), (b) CH3CN (■,□), and (c) C4H6O2 ( ) with H2O over Ti-BEA-OH (solid) and Ti-BEA-F (hollow).
) with H2O over Ti-BEA-OH (solid) and Ti-BEA-F (hollow).
Fig. 6 demonstrates that values of  also depend strongly on xH2O in each organic solvent.
also depend strongly on xH2O in each organic solvent.  decreases with increasing xH2O in both Ti-BEA-OH and Ti-BEA-F because greater quantities of H2O near sites enthalpically stabilize the hydrophilic transition state for H2O2 decomposition more significantly than Ti–OOH (Scheme 3b). For a given organic solvent and xH2O, Ti-BEA-F gives greater
decreases with increasing xH2O in both Ti-BEA-OH and Ti-BEA-F because greater quantities of H2O near sites enthalpically stabilize the hydrophilic transition state for H2O2 decomposition more significantly than Ti–OOH (Scheme 3b). For a given organic solvent and xH2O, Ti-BEA-F gives greater  values than Ti-BEA-OH. More H2O molecules may adsorb and hydrogen bond with the transition state within Ti-BEA-OH, which yields lower
values than Ti-BEA-OH. More H2O molecules may adsorb and hydrogen bond with the transition state within Ti-BEA-OH, which yields lower 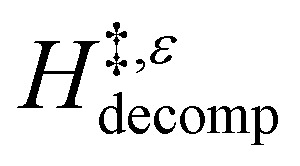 values.
values.  depends more strongly on xH2O for Ti-BEA-OH than Ti-BEA-F in each organic solvent, showing that xH2O affects the stability of adsorbed reactive species more significantly in Ti-BEA-OH than Ti-BEA-F. Between organic solvents,
depends more strongly on xH2O for Ti-BEA-OH than Ti-BEA-F in each organic solvent, showing that xH2O affects the stability of adsorbed reactive species more significantly in Ti-BEA-OH than Ti-BEA-F. Between organic solvents,  values differ by 4 kJ mol−1 over Ti-BEA-F and 8 kJ mol−1 over Ti-BEA-OH at the highest xH2O (0.75). The smaller changes observed in Ti-BEA-F imply that H2O molecules form similar first coordination solvation shells around the transition state and Ti–OOH intermediate at the highest xH2O. In contrast, the differences among Ti-BEA-OH may reflect contributions from extended hydrogen bonding networks of H2O and organic solvent molecules within Ti-BEA-OH that influence both the decomposition transition state and Ti–OOH intermediate.
values differ by 4 kJ mol−1 over Ti-BEA-F and 8 kJ mol−1 over Ti-BEA-OH at the highest xH2O (0.75). The smaller changes observed in Ti-BEA-F imply that H2O molecules form similar first coordination solvation shells around the transition state and Ti–OOH intermediate at the highest xH2O. In contrast, the differences among Ti-BEA-OH may reflect contributions from extended hydrogen bonding networks of H2O and organic solvent molecules within Ti-BEA-OH that influence both the decomposition transition state and Ti–OOH intermediate.  values differ by 6 kJ mol−1 for Ti-BEA-F and 26 kJ mol−1 over Ti-BEA-OH at the highest xH2O values, and the spans of values and differences between zeolites exceed that for
values differ by 6 kJ mol−1 for Ti-BEA-F and 26 kJ mol−1 over Ti-BEA-OH at the highest xH2O values, and the spans of values and differences between zeolites exceed that for  . This finding agrees with chemical intuition that the larger transition state for C6H12 epoxidation depends more sensitively on the secondary coordination sphere of solvent molecules within the pore than the smaller transition state for H2O2 decomposition (Scheme 3). Recent work demonstrated that solvent displacement dominates ΔHapp,epox differences as a function of alkene carbon number in aqueous CH3CN, suggesting that changes in (SiOH)x and intrapore solvent composition more significantly affect the stability of larger transition states that displace more solvent.34
. This finding agrees with chemical intuition that the larger transition state for C6H12 epoxidation depends more sensitively on the secondary coordination sphere of solvent molecules within the pore than the smaller transition state for H2O2 decomposition (Scheme 3). Recent work demonstrated that solvent displacement dominates ΔHapp,epox differences as a function of alkene carbon number in aqueous CH3CN, suggesting that changes in (SiOH)x and intrapore solvent composition more significantly affect the stability of larger transition states that displace more solvent.34
Fig. 6.
 values for H2O2 decomposition (1 mM H2O2, 313–343 K) as a function of xH2O in mixtures of (a) CH3OH (
values for H2O2 decomposition (1 mM H2O2, 313–343 K) as a function of xH2O in mixtures of (a) CH3OH ( ), (b) CH3CN (■,□), and (c) C4H6O2 (
), (b) CH3CN (■,□), and (c) C4H6O2 ( ) with H2O over Ti-BEA-OH (solid) and Ti-BEA-F (hollow).
) with H2O over Ti-BEA-OH (solid) and Ti-BEA-F (hollow).
The differences in the functional dependencies of  and
and  on xH2O must reflect differences in the hydrophilicity of the transition state complexes for these competing reaction pathways. Greater xH2O may increase Hε of the hydrophobic transition state for epoxidation from a combination of increased disruption of H2O molecules and unfavorable interactions between the transition state and intrapore H2O. In contrast, greater quantities of H2O molecules likely lower Hε for the transition state for H2O2 decomposition in all organic solvents. Among organic solvents, changing xH2O in CH3OH mixtures has the least significant effect on both
on xH2O must reflect differences in the hydrophilicity of the transition state complexes for these competing reaction pathways. Greater xH2O may increase Hε of the hydrophobic transition state for epoxidation from a combination of increased disruption of H2O molecules and unfavorable interactions between the transition state and intrapore H2O. In contrast, greater quantities of H2O molecules likely lower Hε for the transition state for H2O2 decomposition in all organic solvents. Among organic solvents, changing xH2O in CH3OH mixtures has the least significant effect on both  and
and  values. The weak effects of xH2O in CH3OH likely reflect the more similar hydrogen bonding ability of CH3OH to H2O than CH3CN or C4H6O2 (see Section S10† for solvent parameters). Therefore, CH3OH molecules may hydrogen bond with reactive species in the pore similarly to H2O, which lessens the differences in the solvent organization within pores brought about by replacing a fraction of CH3OH with H2O.
values. The weak effects of xH2O in CH3OH likely reflect the more similar hydrogen bonding ability of CH3OH to H2O than CH3CN or C4H6O2 (see Section S10† for solvent parameters). Therefore, CH3OH molecules may hydrogen bond with reactive species in the pore similarly to H2O, which lessens the differences in the solvent organization within pores brought about by replacing a fraction of CH3OH with H2O.
Overall, activation barrier measurements for epoxidation and H2O2 decomposition in Fig. 5 and 6 suggest that the organic solvent, xH2O, and (SiOH)x density in Ti-BEA affect the stability of the Ti–OOH intermediate and transition states for epoxidation and H2O2 decomposition. The differences in stability result from differences between the organization and composition of fluid-like molecules within Ti-BEA pores, as described next.
3.5. Intrapore solvent composition depends on bulk solvent composition and (SiOH)x density
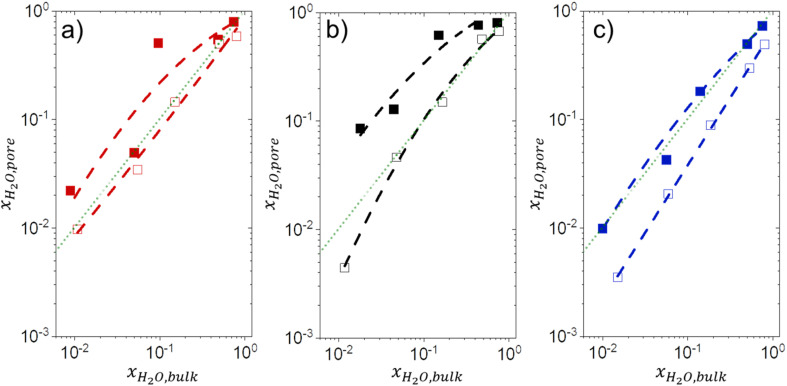
The bulk solvent composition79,88,89 and intrapore (SiOH)x density90–92 affect the intrapore composition of solvent molecules and other adsorbates in aqueous-organic solvent mixtures. Fig. 7 presents measured mole fractions of H2O within pores (xH2O,pore) (see Section S2†) in equilibrated mixtures of H2O with CH3CN, CH3OH, and C4H6O2 as a function of the bulk H2O fraction (xH2O,bulk). For each organic solvent and zeolite, increasing xH2O,bulk leads to greater xH2O,pore values across the full range of conditions examined. These observations agree with the interpretations of changes in turnover rates and activation parameters as functions of xH2O (Sections 3.1 and 3.4) and explains how altering xH2O,bulk influences the stabilities of reactive species both in the bulk (i.e., C6H12 and H2O2) and in pores (i.e., Ti–OOH and transition states). Ti-BEA-OH adsorbs a greater fraction of H2O than Ti-BEA-F for all combinations of organic solvents and xH2O,bulk, consistent with vapor adsorption results (Fig. S8a†) that show (SiOH)x groups promote H2O adsorption. The ratio of xH2O,pore between Ti-BEA-OH and Ti-BEA-F generally decreases as xH2O,bulk increases. This suggests that (SiOH)x functions carry a stronger influence on H2O adsorption at low xH2O,bulk, because the pores contain fewer H2O molecules. This interpretation agrees with previously published binary adsorption measurements that indicate values of xH2O,pore in hydrophilic zeolites depend more strongly on xH2O,bulk from mixtures with methanol,93 ethanol,94,95 and acetic acid96 at lower xH2O,bulk values. As xH2O,bulk increases, H2O molecules associate with H2O already within pores, which leads to a weaker influence of the (SiOH)x density and organic co-solvent on adsorption. This explanation agrees with CH3CN mixtures that give the greatest difference in xH2O,pore between zeolites at low xH2O,bulk. CH3CN contains a lower sum of hydrogen bond donors and acceptors (1) than CH3OH (3) or C4H6O2 (4) (Scheme S1†), as such, CH3CN molecules offer fewer sites for H2O molecules to associate than other organic solvents. Furthermore, CH3CN mixtures give greater uptakes of H2O within Ti-BEA-OH than the other organic solvents at similar xH2O,bulk. CH3OH and C4H6O2 may interact with (SiOH)x more strongly than CH3CN, which suggests those molecules may compete with H2O for (SiOH)x sites more effectively than CH3CN. The bulky nature of C4H6O2 may also lead to a lower available pore volume for H2O molecules to co-adsorb.
Fig. 7. Intrapore mole fraction of H2O (xH2O,pore) as a function of the equilibrium bulk H2O fraction (xH2O,bulk) at 313 K in mixtures of (a) CH3OH ( ), (b) CH3CN (■,□), and (c) C4H6O2 (
), (b) CH3CN (■,□), and (c) C4H6O2 ( ) with H2O over Ti-BEA-OH (solid points) and Ti-BEA-F (hollow points). The faint green lines signify the parity line.
) with H2O over Ti-BEA-OH (solid points) and Ti-BEA-F (hollow points). The faint green lines signify the parity line.
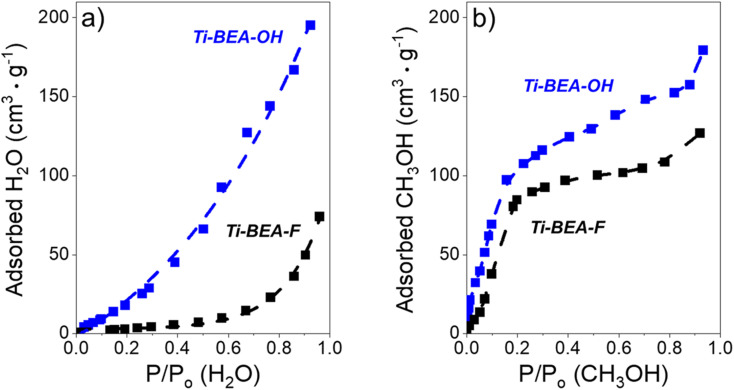
For all organic solvents, Ti-BEA-OH shows greater xH2O,pore values than Ti-BEA-F, and an increase in xH2O,bulk leads to a corresponding increase in xH2O,pore. These observations correspond to our interpretations of the effect of xH2O on C6H12 epoxidation and H2O2 decomposition, as outlined in the previous sections. While Fig. 7 demonstrates that Ti-BEA-OH promotes a more H2O-rich pore solvent environment (higher xH2O,pore), the vapor adsorption isotherms from Fig. 8a also suggest that Ti-BEA-OH likely adsorbs greater numbers of H2O molecules. Ti-BEA-OH adsorbs a greater volume of H2O than Ti-BEA-F at all P/P0 values, with the largest difference between the zeolites (∼10-fold) occurring at 0.5 PH2O/PH2O,0. The greater H2O uptake in Ti-BEA-OH agrees with previous vapor H2O adsorption measurements over MFI42,97,98 and *BEA27,43,48 zeolites that observed increasing H2O uptake with increasing (SiOH)x density. Furthermore, the isotherm in Fig. 8b signifies that Ti-BEA-OH preferentially adsorbs CH3OH molecules, with the maximum difference between Ti-BEA-OH and Ti-BEA-F (∼3.5-fold) at 0.03 PCH3OH/PCH3OH,0. The H2O and CH3OH uptake in Ti-BEA-OH exceeds Ti-BEA-F by more than 3 and 1.3 times, respectively, at all P/P0 values greater than 0.01, which cannot stem from the differences between BET surface areas and pore volumes in Table 1. The experimental capabilities of the vapor adsorption instrument prohibit measurements with CH3CN and C4H6O2. Nevertheless, these observations provide strong evidence that (SiOH)x defects promote the uptake of molecules with hydrogen bonding functions, an interpretation supported by prior infrared spectroscopy experiments and molecular dynamics simulations showing that Ti-BEA-OH adsorbs more CH3CN molecules than Ti-BEA-F.34 Therefore, Ti-BEA-OH likely contains greater quantities of both H2O and the organic co-solvent (i.e., CH3CN, CH3OH, C4H6O2) at all conditions, which leads to higher solvent densities within pores. These differences in intrapore solvent densities lead to greater C6H12 epoxidation turnover rates through displacement and reorganization of hydrogen bonded solvent molecules, as reported for CH3CN.34
Fig. 8. (a) H2O (295 K) and (b) CH3OH (295 K) adsorption isotherms over Ti-BEA-OH ( ) and Ti-BEA-F (black). The samples were degassed at 673 K under vacuum (<0.7 Pa) before adsorption.
) and Ti-BEA-F (black). The samples were degassed at 673 K under vacuum (<0.7 Pa) before adsorption.
More generally, the data in Fig. 7 and 8 demonstrate that the solvent composition and density within porous catalysts can be tuned by altering the bulk composition and catalyst (SiOH)x density. This knowledge allows for control of the intrapore and bulk solvent environment for any liquid phase chemistry, which can significantly influence rates and selectivities for catalysis and adsorption processes.
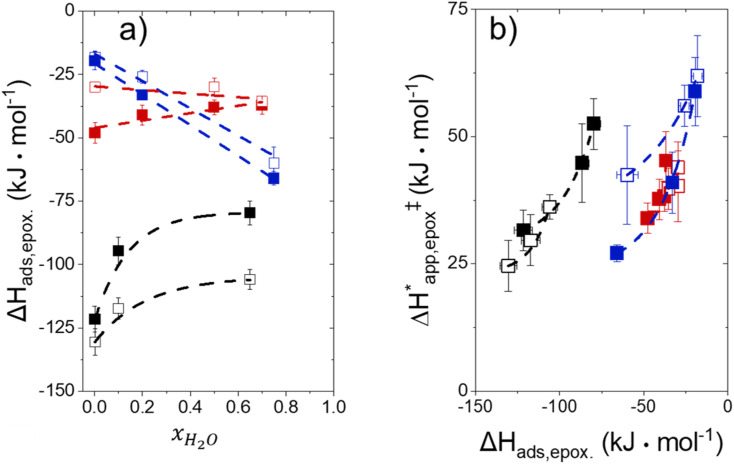
3.6. Measured enthalpies for adsorption and activation reveal influence of intrapore solvents on surface species
Brønsted–Evans–Polanyi relations propose that the intrinsic activation energy for an elementary step scales linearly with the enthalpy of reaction for the same process.99–101 Hammond postulated that the transition state structurally resembles the reaction state (i.e., reactant or product) most similar in energy, which leads to strong correlations between reaction kinetics and thermodynamics for adsorption of reactant or product molecules, as demonstrated frequently on metal surfaces and in computation.102,103 Recently, the validity of these concepts were demonstrated within solvent-filled pore of zeolite catalysts used for alkene epoxidations. Values of 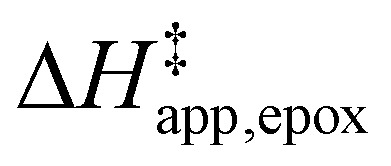 correlate with the liquid phase enthalpy of epoxide adsorption (ΔHads,epox) for C6H12 epoxidation and C6H12O adsorption over *BEA zeolites containing different active metals (i.e., Ti, Nb, W)58 and C6–C18 alkenes and epoxides over Ti-BEA with varying (SiOH)x densities.28,34 The positive correlations between the enthalpies in these previous studies indicate that the transition state for epoxidation structurally resembles the adsorbed epoxidation product (Scheme 3a), because excess enthalpy contributions from interactions with surrounding solvent molecules affect epoxide adsorption and epoxidation transition state formation similarly. Measuring differences in ΔHads,epox provides a complementary method to examine how the composition of the organic solvent, xH2O, and (SiOH)x density of Ti-BEA catalysts impact the structure of intrapore solvation structures and their influence on the stability of surface intermediates.
correlate with the liquid phase enthalpy of epoxide adsorption (ΔHads,epox) for C6H12 epoxidation and C6H12O adsorption over *BEA zeolites containing different active metals (i.e., Ti, Nb, W)58 and C6–C18 alkenes and epoxides over Ti-BEA with varying (SiOH)x densities.28,34 The positive correlations between the enthalpies in these previous studies indicate that the transition state for epoxidation structurally resembles the adsorbed epoxidation product (Scheme 3a), because excess enthalpy contributions from interactions with surrounding solvent molecules affect epoxide adsorption and epoxidation transition state formation similarly. Measuring differences in ΔHads,epox provides a complementary method to examine how the composition of the organic solvent, xH2O, and (SiOH)x density of Ti-BEA catalysts impact the structure of intrapore solvation structures and their influence on the stability of surface intermediates.
Isothermal titration calorimetry (ITC) experiments provided values of ΔHads,epox for C6H12O. The calorimeter releases heat upon each injection of C6H12O solution into a solution of Ti-BEA, as shown in a representative ITC thermogram in Fig. 9a. Fig. 9b shows the molar heats of adsorption from Fig. 9a at low C6H12O coverages (<0.25 mol C6H12O (mol Ti)−1), a regime in which all epoxide molecules are assumed to adsorb to Ti sites.28 Values of ΔHads,epox for 1,2-epoxyhexane within each combination of solvent and Ti-BEA zeolite were calculated from the average value of the heat released in this low coverage regime. The first injection (transparent) was omitted from the ΔHads,epox calculation, because these values exhibit much lower heat than other points due to well-known instrumental errors (e.g., evaporation of titrant from syringe needle, leading to smaller than expected injected volumes). The thermograms and integrated heat data for the remaining solvent combinations and zeolites are found in Section S11.†
Fig. 9. (a) Thermogram from the titration of Ti-BEA-OH with 1,2-epoxyhexane (10 mM C6H12O in xC4H6O2 = 0.25 (7.6 M) with H2O (22.8 M), 313 K, 1 μL per injection) during isothermal titration calorimetry (ITC), and (b) the corresponding heats released as a function of 1,2-epoxyhexane coverage. Transparent points are omitted due to common errors associated with early injections.
Fig. 10a displays ΔHads,epox values for C6H12O as a function of xH2O. Notably, aqueous CH3CN mixtures and neat CH3CN give significantly more exothermic ΔHads,epox values than either CH3OH or C4H6O2 solutions, which suggests that CH3CN mixtures provide the greatest stability to adsorbed C6H12O. These comparisons appear to explain why CH3CN mixtures show greater C6H12 epoxidation turnover rates (Fig. 1) than the other solvents examined. Fig. 10b shows that ΔHads,epox values correlate with  values across all combinations of solvent composition and zeolites, which signifies the strong structural similarities between the intrapore solvation environment of 1,2-epoxyhexane bound to Ti active sites and the transition states for epoxidation that form in these same environments. The dependence of
values across all combinations of solvent composition and zeolites, which signifies the strong structural similarities between the intrapore solvation environment of 1,2-epoxyhexane bound to Ti active sites and the transition states for epoxidation that form in these same environments. The dependence of  and ΔHads,epox on xH2O is weaker over Ti-BEA-F than Ti-BEA-OH (see Fig. 5 and 10a) for all solvents, which shows that increases in xH2O lead to less significant changes in the solvent structure within Ti-BEA-F (see Section 3.5). Based on insight gained from quantitative comparisons between GCMD simulations and ITC measurements of ΔHads,epox values,34 the more endothermic
and ΔHads,epox on xH2O is weaker over Ti-BEA-F than Ti-BEA-OH (see Fig. 5 and 10a) for all solvents, which shows that increases in xH2O lead to less significant changes in the solvent structure within Ti-BEA-F (see Section 3.5). Based on insight gained from quantitative comparisons between GCMD simulations and ITC measurements of ΔHads,epox values,34 the more endothermic 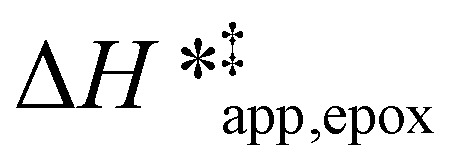 and ΔHads,epox values in CH3CN mixtures at higher xH2O reflect the disruptions of greater numbers of hydrogen bonds that involve H2O molecules upon adsorption of the epoxide. Presumably, the changes of
and ΔHads,epox values in CH3CN mixtures at higher xH2O reflect the disruptions of greater numbers of hydrogen bonds that involve H2O molecules upon adsorption of the epoxide. Presumably, the changes of 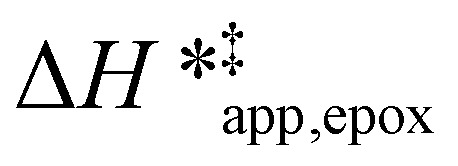 and ΔHads,epox with xH2O in CH3OH mixtures over Ti-BEA-OH reflect similar processes that displace solvent molecules, however, the lower magnitude of these changes in CH3OH likely stems from the greater hydrogen bonded character of neat CH3OH relative to neat CH3CN. Hence, the addition of small quantities of H2O leads to more significant changes in the organization of CH3CN molecules within pores than CH3OH. In contrast, the values of
and ΔHads,epox with xH2O in CH3OH mixtures over Ti-BEA-OH reflect similar processes that displace solvent molecules, however, the lower magnitude of these changes in CH3OH likely stems from the greater hydrogen bonded character of neat CH3OH relative to neat CH3CN. Hence, the addition of small quantities of H2O leads to more significant changes in the organization of CH3CN molecules within pores than CH3OH. In contrast, the values of 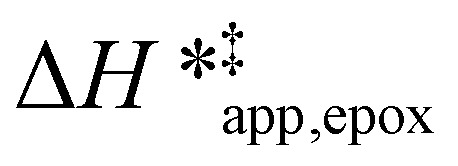 and ΔHads,epox become more exothermic with increasing xH2O in C4H6O2 mixtures. While the full reasons for this trend remain unclear presently, these results give evidence that the spatial positioning of C4H6O2 within pores responds to the presence of water.
and ΔHads,epox become more exothermic with increasing xH2O in C4H6O2 mixtures. While the full reasons for this trend remain unclear presently, these results give evidence that the spatial positioning of C4H6O2 within pores responds to the presence of water.
Fig. 10. (a) C6H12O enthalpies of adsorption (5–10 mM C6H12O, 313 K) as a function of xH2O and (b) difference between the enthalpy of the transition state for C6H12 epoxidation (1 mM C6H12, 308–333 K) and the Ti–OOH and standard state C6H12 enthalpies as a function of C6H12O enthalpies of adsorption (5–10 mM C6H12O, 313 K) in aqueous mixtures of (a) CH3OH ( ), (b) CH3CN (■,□), and (c) C4H6O2 (
), (b) CH3CN (■,□), and (c) C4H6O2 ( ) over Ti-BEA-OH (solid points) and Ti-BEA-F (hollow points).
) over Ti-BEA-OH (solid points) and Ti-BEA-F (hollow points).
Notably, 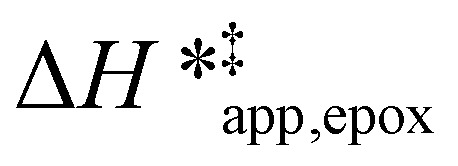 and ΔHads,epox show a positive and super-linear correlation for every combination of solvent and zeolite (Fig. 9b). The derivative of the correlation increases at more endothermic enthalpies, which indicates that the transition state for epoxidation resembles the epoxide product more closely at more endothermic
and ΔHads,epox show a positive and super-linear correlation for every combination of solvent and zeolite (Fig. 9b). The derivative of the correlation increases at more endothermic enthalpies, which indicates that the transition state for epoxidation resembles the epoxide product more closely at more endothermic 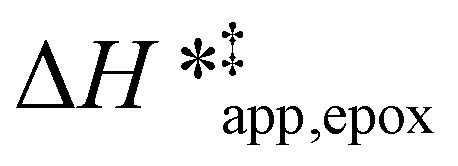 values, following Hammond's postulate.102 We cannot, however, exclude the possibility that HTi–OOHε varies systematically with xH2O and contributes to the non-linear trend. Nevertheless, the positive correlations between
values, following Hammond's postulate.102 We cannot, however, exclude the possibility that HTi–OOHε varies systematically with xH2O and contributes to the non-linear trend. Nevertheless, the positive correlations between 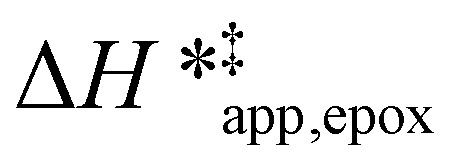 and ΔHads,epox suggests that interactions with solvent molecules affect the stability of the epoxidation transition state and the adsorbed epoxide in similar ways. These findings show that solvent molecules and solvent composition influence the stability of solutes in bulk solvents and at solid–liquid interfaces during catalysis. These concepts can guide the design of not only heterogeneously catalyzed reactions, but also liquid phase homogeneously catalyzed and organic reactions in which reactant γ values carry significance.
and ΔHads,epox suggests that interactions with solvent molecules affect the stability of the epoxidation transition state and the adsorbed epoxide in similar ways. These findings show that solvent molecules and solvent composition influence the stability of solutes in bulk solvents and at solid–liquid interfaces during catalysis. These concepts can guide the design of not only heterogeneously catalyzed reactions, but also liquid phase homogeneously catalyzed and organic reactions in which reactant γ values carry significance.
4. Conclusions
The organic solvent choice, xH2O, and zeolite (SiOH)x density influence rates and selectivities of liquid phase zeolite-catalyzed reactions by altering Gε values of reactants in the bulk fluid phase and at solid–liquid interfaces, as demonstrated with interpretations of alkene epoxidation kinetics. While the organic solvent identity and xH2O influence the reversibility of H2O2 activation, neither the solvent nor zeolite choice influences the mechanisms for alkene epoxidation or H2O2 decomposition. Instead, differences among turnover rates and selectivities stem from the distinct dependence of Gε values of reactive species for C6H12 epoxidation and H2O2 decomposition on xH2O. Greater rates of C6H12 epoxidation in each zeolite and organic solvent at greater xH2O appear to be primarily driven by incommensurate changes in the activity coefficients of C6H12 and for epoxidation transition states. However, H2O2 decomposition rates decrease at higher xH2O for both Ti-BEA-OH and Ti-BEA-F, likely because stabilization of the hydrophilic transition state by H2O is outweighed by the stabilization of fluid phase H2O2 and the Ti–OOH intermediate.
The findings reported here demonstrate the significance of interactions between solvent molecules and reactants in the liquid phase and at solid–liquid interfaces during catalytic reactions. Broadly, the findings suggest that introducing a more polar reaction environment promotes zeolite-catalyzed reaction pathways with predominantly hydrophobic reactants and transition states while suppressing pathways with hydrophilic reactive species. For industrial purposes, diluting organic solvents with H2O increases separation costs for epoxidation, may increase rates of ring-opening of the epoxide product40,104,105 (not observed under differential conversions in this study), and may influence the long-term stability of zeolite catalysts.106–108 Results presented here show that simply adding more H2O increases rates and H2O2 selectivities for C6H12 epoxidation in confined environments. Evidently, proper selection of organic solvent, xH2O, and catalyst polarity and topology can improve the performance of liquid phase reactions. The concepts outlined here can guide the design of adsorption and catalytic processes in the liquid phase and at solid–liquid interfaces.
Data availability
Characterization plots, supplemental kinetics and UV-Vis spectra, full rate derivations, activity coefficient values, activation barriers, tabulated solvent parameters, and all calorimetry thermograms have been included as part of the ESI.†
Author contributions
D. S. P. synthesized and characterized the zeolites, performed the NMR and UV-Vis spectroscopy experiments, and conducted measurements of rates and enthalpies of adsorption. C. T. performed the vapor H2O and CH3OH adsorption measurements. O. K. assisted with the kinetic measurements and synthesis of zeolites. D. W. F. conceptualized the manuscript. The manuscript was written by D. S. P. with input from all authors. All authors have given approval to the final version of the manuscript.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
The authors thank Dr E. Zeynep Ayla and Dr Claudia E. Berdugo-Díaz for helpful feedback on the manuscript. The authors also thank Professor Damien Guironnet for the use of laboratory equipment for the synthesis of Ti-BEA-OH and the preparation of 1H NMR sample solutions. EDXRF, XRD, and DRUV-vis measurements were carried out in the Frederick Seitz Materials Research Laboratory at the University of Illinois. Vapor adsorptions (N2, Ar, H2O, CH3OH) and ICP measurements were carried out in the Microanalysis Lab at the University of Illinois. This work was supported by the Department of Energy (DE-SC0020224). D. S. P. and C. T. acknowledge support from the National Science Foundation Graduate Research Fellowship Program (DGE-1746047, DGE-1144245).
Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sc06473a
Notes and references
- Oyama S. T., Rates, Kinetics, and Mechanisms of Epoxidation, in Mechanisms in Homogeneous and Heterogeneous Epoxidation Catalysis, Elsevier, 2008, pp. 3–99 [Google Scholar]
- Degussa AG and Uhde GmbH, Process for the epoxidation of propene, WO Pat., WO 2005/000827A1, 2005
- BASF SE and Dow Global Technologies LLC, Process for preparing propylene oxide, US Pat., US10435381B2, 2019
- Lyondell Chemical Technology LP, Process for the preparation of propylene oxide, EP Pat., EP1742928B1, 2011
- BASF SE, Process for the preparation of propylene oxide, US Pat., US10544115B2, 2020
- BASF SE and Dow Global Technologies LLC, Catalyst system for preparing propylene oxide, US Pat., US10053439B2, 2018
- Sumitomo Chemical Company, Limited, Method for producing propylene oxide, WO Pat., WO2009/008493A2, 2009
- Mellmer M. A. Sener C. Gallo J. M. Luterbacher J. S. Alonso D. M. Dumesic J. A. Solvent effects in acid-catalyzed biomass conversion reactions. Angew. Chem., Int. Ed. 2014;53(44):11872–11875. doi: 10.1002/anie.201408359. [DOI] [PubMed] [Google Scholar]
- Mellmer M. A. Sanppitsekree C. Demir B. Bai P. Ma K. Neurock M. Dumesic J. A. Solvent-Enabled Control of Reactivity for Liquid Phase Reactions of Biomass-Derived Compounds. Nat. Catal. 2018;1:199–207. doi: 10.1038/s41929-018-0027-3. [DOI] [Google Scholar]
- Walker T. W. Chew A. K. Li H. Demir B. Zhang Z. C. Huber G. W. Van Lehn R. C. Dumesic J. A. Universal kinetic solvent effects in acid-catalyzed reactions of biomass-derived oxygenates. Energy Environ. Sci. 2018;11(3):617–628. doi: 10.1039/C7EE03432F. [DOI] [Google Scholar]
- Mellmer M. A. Gallo J. M. R. Martin Alonso D. Dumesic J. A. Selective Production of Levulinic Acid from Furfuryl Alcohol in THF Solvent Systems over H-ZSM-5. ACS Catal. 2015;5(6):3354–3359. doi: 10.1021/acscatal.5b00274. [DOI] [Google Scholar]
- Sievers C. Noda Y. Qi L. Albuquerque E. M. Rioux R. M. Scott S. L. Phenomena Affecting Catalytic Reactions at Solid–Liquid Interfaces. ACS Catal. 2016;6(12):8286–8307. doi: 10.1021/acscatal.6b02532. [DOI] [Google Scholar]
- Li G. Wang B. Resasco D. E. Water-Mediated Heterogeneously Catalyzed Reactions. ACS Catal. 2020;10(2):1294–1309. doi: 10.1021/acscatal.9b04637. [DOI] [Google Scholar]
- Potts D. S. Bregante D. T. Adams J. S. Torres C. Flaherty D. W. Influence of solvent structure and hydrogen bonding on catalysis at solid–liquid interfaces. Chem. Soc. Rev. 2021;50(22):12308–12337. doi: 10.1039/D1CS00539A. [DOI] [PubMed] [Google Scholar]
- Bates J. S. Gounder R. Kinetic effects of molecular clustering and solvation by extended networks in zeolite acid catalysis. Chem. Sci. 2021;12(13):4699–4708. doi: 10.1039/D1SC00151E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G. Wang B. Resasco D. E. Solvent effects on catalytic reactions and related phenomena at liquid–solid interfaces. Surf. Sci. Rep. 2021;76(4):100541. doi: 10.1016/j.surfrep.2021.100541. [DOI] [Google Scholar]
- Trouvé J. Gramage-Doria R. Beyond hydrogen bonding: recent trends of outer sphere interactions in transition metal catalysis. Chem. Soc. Rev. 2021;50(5):3565–3584. doi: 10.1039/D0CS01339K. [DOI] [PubMed] [Google Scholar]
- Raynal M. Ballester P. Vidal-Ferran A. van Leeuwen P. W. Supramolecular catalysis. Part 1: non-covalent interactions as a tool for building and modifying homogeneous catalysts. Chem. Soc. Rev. 2014;43(5):1660–1733. doi: 10.1039/C3CS60027K. [DOI] [PubMed] [Google Scholar]
- Dyson P. J. Jessop P. G. Solvent effects in catalysis: rational improvements of catalysts via manipulation of solvent interactions. Catal. Sci. Technol. 2016;6(10):3302–3316. doi: 10.1039/C5CY02197A. [DOI] [Google Scholar]
- Silverman D. N. McKenna R. Solvent-mediated proton transfer in catalysis by carbonic anhydrase. Acc. Chem. Res. 2007;40(8):669–675. doi: 10.1021/ar7000588. [DOI] [PubMed] [Google Scholar]
- Reichardt C. and Welton T., Solvents and solvent effects in organic chemistry, John Wiley & Sons, 2011 [Google Scholar]
- Menschutkin N. Über die Affinitätskoeffizienten der Alkylhaloide und der Amine. Z. Phys. Chem. 1890;6(1):41. doi: 10.1515/zpch-1890-0607. [DOI] [Google Scholar]
- Kirkwood J. G. Theory of Solutions of Molecules Containing Widely Separated Charges with Special Application to Zwitterions. J. Chem. Phys. 1934;2(7):351–361. doi: 10.1063/1.1749489. [DOI] [Google Scholar]
- Debye P. Hückel E. Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen. Phys. Z. 1923;24(9):185–206. [Google Scholar]
- Kamlet M. J. Abboud J. L. M. Abraham M. H. Taft R. W. Linear solvation energy relationships. 23. A comprehensive collection of the solvatochromic parameters,.pi.*,.alpha., and.beta., and some methods for simplifying the generalized solvatochromic equation. J. Org. Chem. 1983;48(17):2877–2887. doi: 10.1021/jo00165a018. [DOI] [Google Scholar]
- Madon R. J. Iglesia E. Catalytic reaction rates in thermodynamically non-ideal systems. J. Mol. Catal. A: Chem. 2000;163(1–2):189–204. doi: 10.1016/S1381-1169(00)00386-1. [DOI] [Google Scholar]
- Bregante D. T. Johnson A. M. Patel A. Y. Ayla E. Z. Cordon M. J. Bukowski B. C. Greeley J. Gounder R. Flaherty D. W. Cooperative Effects between Hydrophilic Pores and Solvents: Catalytic Consequences of Hydrogen Bonding on Alkene Epoxidation in Zeolites. J. Am. Chem. Soc. 2019;141:7302–7319. doi: 10.1021/jacs.8b12861. [DOI] [PubMed] [Google Scholar]
- Bregante D. T. Flaherty D. W. Impact of Specific Interactions Among Reactive Surface Intermediates and Confined Water on Epoxidation Catalysis and Adsorption in Lewis Acid Zeolites. ACS Catal. 2019;9(12):10951–10962. doi: 10.1021/acscatal.9b03323. [DOI] [Google Scholar]
- Tan J. Z. Bregante D. T. Torres C. Flaherty D. W. Transition state stabilization depends on solvent identity, pore size, and hydrophilicity for epoxidations in zeolites. J. Catal. 2022;405:91–104. doi: 10.1016/j.jcat.2021.11.029. [DOI] [Google Scholar]
- Wu L. Tang Z. Yu Y. Yao X. Liu W. Li L. Yan B. Liu Y. He M. Facile synthesis of a high-performance titanosilicate catalyst with controllable defective Ti(OSi)3OH sites. Chem. Commun. 2018;54(49):6384–6387. doi: 10.1039/C8CC02794C. [DOI] [PubMed] [Google Scholar]
- Tang Z. Yu Y. Liu W. Chen Z. Wang R. Liu H. Wu H. Liu Y. He M. Deboronation-assisted construction of defective Ti(OSi)3OH species in MWW-type titanosilicate and their enhanced catalytic performance. Catal. Sci. Technol. 2020;10(9):2905–2915. doi: 10.1039/D0CY00126K. [DOI] [Google Scholar]
- Wang L. Sun J. Meng X. Zhang W. Zhang J. Pan S. Shen Z. Xiao F.-S. A significant enhancement of catalytic activities in oxidation with H2O2 over the TS-1 zeolite by adjusting the catalyst wettability. Chem. Commun. 2014;50(16):2012–2014. doi: 10.1039/C3CC48220K. [DOI] [PubMed] [Google Scholar]
- Bregante D. T. Chan M. C. Tan J. Z. Ayla E. Z. Nicholas C. P. Shukla D. Flaherty D. W. The shape of water in zeolites and its impact on epoxidation catalysis. Nat. Catal. 2021;4(9):797–808. doi: 10.1038/s41929-021-00672-4. [DOI] [Google Scholar]
- Potts D. S. Jeyaraj V. S. Kwon O. Ghosh R. Mironenko A. V. Flaherty D. W. Effect of Interactions between Alkyl Chains and Solvent Structures on Lewis Acid Catalyzed Epoxidations. ACS Catal. 2022;12(21):13372–13393. doi: 10.1021/acscatal.2c03493. [DOI] [Google Scholar]
- Ramachandran C. Du H. Kim Y. Kung M. Snurr R. Broadbelt L. Solvent effects in the epoxidation reaction of 1-hexene with titanium silicalite-1 catalyst. J. Catal. 2008;253(1):148–158. doi: 10.1016/j.jcat.2007.10.016. [DOI] [Google Scholar]
- Langhendries G. De Vos D. E. Baron G. V. Jacobs P. A. Quantitative Sorption Experiments on Ti-Zeolites and Relation with α-Olefin Oxidation by H2O2. J. Catal. 1999;187(2):453–463. doi: 10.1006/jcat.1999.2608. [DOI] [Google Scholar]
- Fan W. Wu P. Tatsumi T. Unique solvent effect of microporous crystalline titanosilicates in the oxidation of 1-hexene and cyclohexene. J. Catal. 2008;256(1):62–73. doi: 10.1016/j.jcat.2008.03.001. [DOI] [Google Scholar]
- Van Der Waal J. C. Van Bekkum H. Zeolite titanium beta: a versatile epoxidation catalyst. Solvent effects. J. Mol. Catal. A: Chem. 1997;124(2–3):137–146. doi: 10.1016/S1381-1169(97)00074-5. [DOI] [Google Scholar]
- Corma A. Esteve P. Martínez A. Solvent Effects during the Oxidation of Olefins and Alcohols with Hydrogen Peroxide on Ti-Beta Catalyst: The Influence of the Hydrophilicity-Hydrophobicity of the Zeolite. J. Catal. 1996;161:11–19. doi: 10.1006/jcat.1996.0157. [DOI] [Google Scholar]
- Song F. Liu Y. M. Wang L. L. Zhang H. J. He M. Y. Wu P. Highly efficient epoxidation of propylene over a novel Ti-MWW catalyst. Stud. Surf. Sci. Catal. 2007;170:1236–1243. doi: 10.1016/S0167-2991(07)80983-9. [DOI] [Google Scholar]
- Yin J. Xu H. Wang B. Tian W. Yin J. Jiang J. Wu P. Highly selective 1-pentene epoxidation over Ti-MWW with modified microenvironment of Ti active sites. Catal. Sci. Technol. 2020;10(17):6050–6064. doi: 10.1039/D0CY00478B. [DOI] [Google Scholar]
- Bregante D. T. Potts D. S. Kwon O. Ayla E. Z. Tan J. Z. Flaherty D. W. Effects of Hydrofluoric Acid Concentration on the Density of Silanol Groups and Water Adsorption in Hydrothermally Synthesized Transition-Metal-Substituted Silicalite-1. Chem. Mater. 2020;32(17):7425–7437. doi: 10.1021/acs.chemmater.0c02405. [DOI] [Google Scholar]
- Gounder R. Davis M. E. Beyond shape selective catalysis with zeolites: hydrophobic void spaces in zeolites enable catalysis in liquid water. AIChE J. 2013;59(9):3349–3358. doi: 10.1002/aic.14016. [DOI] [Google Scholar]
- Potekhin V. V. Kulikova V. A. Kochina E. G. Potekhin V. M. Decomposition of hydrogen peroxide in protic and polar aprotic solvents on TS-1 heterogeneous catalyst. Russ. J. Appl. Chem. 2011;84(7):1195–1200. doi: 10.1134/S1070427211070123. [DOI] [Google Scholar]
- Wolf P. Hammond C. Conrad S. Hermans I. Post-synthetic preparation of Sn-, Ti- and Zr-beta: a facile route to water tolerant, highly active Lewis acidic zeolites. Dalton Trans. 2014;43(11):4514–4519. doi: 10.1039/C3DT52972J. [DOI] [PubMed] [Google Scholar]
- Bregante D. T. Priyadarshini P. Flaherty D. W. Kinetic and spectroscopic evidence for reaction pathways and intermediates for olefin epoxidation on Nb in *BEA. J. Catal. 2017;348:75–89. doi: 10.1016/j.jcat.2017.02.008. [DOI] [Google Scholar]
- Blasco T. Camblor M. A. Corma A. Esteve P. Guil J. M. Martinez A. Perdigon-Melon J. A. Valencia S. Direct synthesis and characterization of hydrophobic aluminum-free Ti-beta zeolite. J. Phys. Chem. B. 1998;102:75–88. doi: 10.1021/jp973288w. [DOI] [Google Scholar]
- Cordon M. J. Harris J. W. Vega-Vila J. C. Bates J. S. Kaur S. Gupta M. Witzke M. E. Wegener E. C. Miller J. T. Flaherty D. W. Hibbitts D. D. Gounder R. Dominant Role of Entropy in Stabilizing Sugar Isomerization Transition States within Hydrophobic Zeolite Pores. J. Am. Chem. Soc. 2018;140(43):14244–14266. doi: 10.1021/jacs.8b08336. [DOI] [PubMed] [Google Scholar]
- Newsam J. M. Treacy M. M. J. Koetsier W. T. Gruyter C. B. D. Structural characterization of zeolite beta. Proc. R. Soc. London, Ser. A. 1988;420(1859):375–405. [Google Scholar]
- Shirke B. S. Korake P. V. Hankare P. P. Bamane S. R. Garadkar K. M. Synthesis and characterization of pure anatase TiO2 nanoparticles. J. Mater. Sci.: Mater. Electron. 2011;22(7):821–824. doi: 10.1007/s10854-010-0218-4. [DOI] [Google Scholar]
- Rouquerol J., Llewellyn P. and Rouquerol F., Is the BET equation applicable to microporous adsorbents?, in Studies in Surface Science and Catalysis, Elsevier, Amsterdam and Oxford, 2007, vol. 160, pp. 49–56 [Google Scholar]
- Galarneau A. Villemot F. Rodriguez J. Fajula F. Coasne B. Validity of the t-plot Method to Assess Microporosity in Hierarchical Micro/Mesoporous Materials. Langmuir. 2014;30(44):13266–13274. doi: 10.1021/la5026679. [DOI] [PubMed] [Google Scholar]
- Wang J. Kispersky V. F. Delgass W. N. Ribeiro F. H. Determination of the Au active site and surface active species via operando transmission FTIR and isotopic transient experiments on 2.3 wt% Au/TiO2 for the WGS reaction. J. Catal. 2012;289:171–178. doi: 10.1016/j.jcat.2012.02.008. [DOI] [Google Scholar]
- Zecchina A. Bordiga S. Spoto G. Marchese L. Petrini G. Leofanti G. Padovan M. Silicalite characterization. 2. IR spectroscopy of the interaction of carbon monoxide with internal and external hydroxyl groups. J. Phys. Chem. 1992;96(12):4991–4997. doi: 10.1021/j100191a048. [DOI] [Google Scholar]
- Dzwigaj S. Peltre M. J. Massiani P. Davidson A. Che M. Dzwigaj S. Massiani P. Sen T. Sivasanker S. Incorporation of vanadium species in a dealuminated β zeolite. Chem. Commun. 1998;(1):87–88. doi: 10.1039/A704556E. [DOI] [Google Scholar]
- Jentys A. and Lercher J., Techniques of zeolite characterization, in Studies in Surface Science and Catalysis, Elsevier, 2001, vol. 137, pp. 345–386 [Google Scholar]
- Chorkendorff I. and Niemantsverdriet J. W. H., Concepts of Modern Catalysis and Kinetics, Wiley-VCH Verlag Gmbh & Co., Weinheim, 2nd edn, 2007, pp. 203–214 [Google Scholar]
- Ayla E. Z. Potts D. S. Bregante D. T. Flaherty D. W. Alkene Epoxidations with H2O2 over Groups 4–6 Metal-Substituted BEA Zeolites: Reactive Intermediates, Reaction Pathways, and Linear Free-Energy Relationships. ACS Catal. 2021;11(1):139–154. doi: 10.1021/acscatal.0c03394. [DOI] [Google Scholar]
- Bregante D. T. Flaherty D. W. Periodic Trends in Olefin Epoxidation over Group IV and V Framework-Substituted Zeolite Catalysts: A Kinetic and Spectroscopic Study. J. Am. Chem. Soc. 2017;139(20):6888–6898. doi: 10.1021/jacs.7b01422. [DOI] [PubMed] [Google Scholar]
- Ayla E. Z. Patel D. Harris A. Flaherty D. W. Identity of the Metal Oxide Support Controls Outer Sphere Interactions that Change Rates and Barriers for Alkene Epoxidations at Isolated Ti Atoms. J. Catal. 2022;411:167–176. doi: 10.1016/j.jcat.2022.05.013. [DOI] [Google Scholar]
- Bregante D. T. Tan J. Z. Schultz R. L. Ayla E. Z. Potts D. S. Torres C. Flaherty D. W. Catalytic Consequences of Oxidant, Alkene, and Pore Structures on Alkene Epoxidations within Titanium Silicates. ACS Catal. 2020;10(17):10169–10184. doi: 10.1021/acscatal.0c02183. [DOI] [Google Scholar]
- Bregante D. T. Thornburg N. E. Notestein J. M. Flaherty D. W. Consequences of Confinement for Alkene Epoxidation with Hydrogen Peroxide on Highly Dispersed Group 4 and 5 Metal Oxide Catalysts. ACS Catal. 2018;8(4):2995–3010. doi: 10.1021/acscatal.7b03986. [DOI] [Google Scholar]
- Bregante D. T. Tan J. Z. Sutrisno A. Flaherty D. W. Heteroatom substituted zeolite FAU with ultralow Al contents for liquid-phase oxidation catalysis. Catal. Sci. Technol. 2020;10(3):635–647. doi: 10.1039/C9CY01886G. [DOI] [Google Scholar]
- Yang R. A. Sarazen M. L. Mechanistic Impacts of Metal Site and Solvent Identities for Alkene Oxidation over Carboxylate Fe and Cr Metal–Organic Frameworks. ACS Catal. 2022:14476–14491. doi: 10.1021/acscatal.2c04351. [DOI] [Google Scholar]
- Yoon C. W. Hirsekorn K. F. Neidig M. L. Yang X. Tilley T. D. Mechanism of the Decomposition of Aqueous Hydrogen Peroxide over Heterogeneous TiSBA15 and TS-1 Selective Oxidation Catalysts: Insights from Spectroscopic and Density Functional Theory Studies. ACS Catal. 2011;1(12):1665–1678. doi: 10.1021/cs2003774. [DOI] [Google Scholar]
- Brutchey R. L. Ruddy D. A. Andersen L. K. Tilley T. D. Influence of Surface Modification of Ti-SBA15 Catalysts on the Epoxidation Mechanism for Cyclohexene with Aqueous Hydrogen Peroxide. Langmuir. 2005;21(21):9576–9583. doi: 10.1021/la051182j. [DOI] [PubMed] [Google Scholar]
- Sever R. R. Root T. W. DFT Study of Solvent Coordination Effects on Titanium-Based Epoxidation Catalysts. Part One: Formation of the Titanium Hydroperoxo Intermediate. J. Phys. Chem. B. 2003;107(17):4080–4089. doi: 10.1021/jp026056s. [DOI] [Google Scholar]
- Neurock M. Manzer L. E. Theoretical insights on the mechanism of alkene epoxidation by H2O2 with titanium silicalite. Chem. Commun. 1996;10:1133–1134. doi: 10.1039/CC9960001133. [DOI] [Google Scholar]
- Bonino F. Damin A. Ricchiardi G. Ricci M. Spanò G. D'Aloisio R. Zecchina A. Lamberti C. Prestipino C. Bordiga S. Ti-Peroxo Species in the TS-1/H2O2/H2O System. J. Phys. Chem. B. 2004;108(11):3573–3583. doi: 10.1021/jp036166e. [DOI] [Google Scholar]
- Antonova N. S. Carbó J. J. Kortz U. Kholdeeva O. A. Poblet J. M. Mechanistic Insights into Alkene Epoxidation with H2O2 by Ti- and other TM-Containing Polyoxometalates: Role of the Metal Nature and Coordination Environment. J. Am. Chem. Soc. 2010;132(21):7488–7497. doi: 10.1021/ja1023157. [DOI] [PubMed] [Google Scholar]
- Clerici M. G. Ingallina P. Epoxidation of Lower Olefins with Hydrogen Peroxide and Titanium Silicalite. J. Catal. 1993;140:71–83. doi: 10.1006/jcat.1993.1069. [DOI] [Google Scholar]
- Bravo-Suárez J. J. Bando K. K. Lu J. Haruta M. Fujitani T. Oyama T. Transient Technique for Identification of True Reaction Intermediates: Hydroperoxide Species in Propylene Epoxidation on Gold/Titanosilicate Catalysts by X-ray Absorption Fine Structure Spectroscopy. J. Phys. Chem. C. 2008;112(4):1115–1123. doi: 10.1021/jp077501s. [DOI] [Google Scholar]
- Yu Y. Tang Z. Wang J. Wang R. Chen Z. Liu H. Shen K. Huang X. Liu Y. He M. Insights into the efficiency of hydrogen peroxide utilization over titanosilicate/H2O2 systems. J. Catal. 2020;381:96–107. doi: 10.1016/j.jcat.2019.09.045. [DOI] [Google Scholar]
- Morlanes N. Notestein J. M. Kinetic study of cyclooctene epoxidation with aqueous hydrogen peroxide over silica-supported calixarene–Ta (V) Appl. Catal., A. 2010;387(1–2):45–54. doi: 10.1016/j.apcata.2010.07.063. [DOI] [Google Scholar]
- Bregante D. T. Priyadarshini P. Flaherty D. W. Kinetic and spectroscopic evidence for reaction pathways and intermediates for olefin epoxidation on Nb in* BEA. J. Catal. 2017;348:75–89. doi: 10.1016/j.jcat.2017.02.008. [DOI] [Google Scholar]
- Mellmer M. A. Sanpitakseree C. Demir B. Bai P. Ma K. Neurock M. Dumesic J. A. Solvent-enabled control of reactivity for liquid-phase reactions of biomass-derived compounds. Nat. Catal. 2018;1(3):199–207. doi: 10.1038/s41929-018-0027-3. [DOI] [Google Scholar]
- Mellmer M. A. Sanpitakseree C. Demir B. Ma K. Elliott W. A. Bai P. Johnson R. L. Walker T. W. Shanks B. H. Rioux R. M. Neurock M. Dumesic J. A. Effects of chloride ions in acid-catalyzed biomass dehydration reactions in polar aprotic solvents. Nat. Commun. 2019;10(1):1132. doi: 10.1038/s41467-019-09090-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chew A. K. Walker T. W. Shen Z. Demir B. Witteman L. Euclide J. Huber G. W. Dumesic J. A. Van Lehn R. C. Effect of Mixed-Solvent Environments on the Selectivity of Acid-Catalyzed Dehydration Reactions. ACS Catal. 2019;10(3):1679–1691. doi: 10.1021/acscatal.9b03460. [DOI] [Google Scholar]
- Qi L. Alamillo R. Elliott W. A. Andersen A. Hoyt D. W. Walter E. D. Han K. S. Washton N. M. Rioux R. M. Dumesic J. A. Scott S. L. Operando Solid-State NMR Observation of Solvent-Mediated Adsorption-Reaction of Carbohydrates in Zeolites. ACS Catal. 2017:3489–3500. doi: 10.1021/acscatal.7b01045. [DOI] [Google Scholar]
- Cordon M. J. Hall J. N. Harris J. W. Bates J. S. Hwang S.-J. Gounder R. Deactivation of Sn-Beta zeolites caused by structural transformation of hydrophobic to hydrophilic micropores during aqueous-phase glucose isomerization. Catal. Sci. Technol. 2019;9(7):1654–1668. doi: 10.1039/C8CY02589D. [DOI] [Google Scholar]
- Vega-Vila J. C. Gounder R. Quantification of Intraporous Hydrophilic Binding Sites in Lewis Acid Zeolites and Consequences for Sugar Isomerization Catalysis. ACS Catal. 2020;10(20):12197–12211. doi: 10.1021/acscatal.0c02918. [DOI] [Google Scholar]
- Pfriem N. Hintermeier P. H. Eckstein S. Kim S. Liu Q. Shi H. Milakovic L. Liu Y. Haller G. L. Baráth E. Liu Y. Lercher J. A. Role of the ionic environment in enhancing the activity of reacting molecules in zeolite pores. Science. 2021;372:952–957. doi: 10.1126/science.abh3418. [DOI] [PubMed] [Google Scholar]
- Chen F. Shetty M. Wang M. Shi H. Liu Y. Camaioni D. M. Gutiérrez O. Y. Lercher J. A. Differences in Mechanism and Rate of Zeolite-Catalyzed Cyclohexanol Dehydration in Apolar and Aqueous Phase. ACS Catal. 2021;11(5):2879–2888. doi: 10.1021/acscatal.0c05674. [DOI] [Google Scholar]
- Shi H. Eckstein S. Vjunov A. Camaioni D. M. Lercher J. A. Tailoring nanoscopic confines to maximize catalytic activity of hydronium ions. Nat. Commun. 2017;8(1):15442. doi: 10.1038/ncomms15442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y. Vjunov A. Shi H. Eckstein S. Camaioni D. M. Mei D. Baráth E. Lercher J. A. Enhancing the catalytic activity of hydronium ions through constrained environments. Nat. Commun. 2017;8(1):14113. doi: 10.1038/ncomms14113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates J. S. Bukowski B. C. Greeley J. Gounder R. Structure and solvation of confined water and water–ethanol clusters within microporous Brønsted acids and their effects on ethanol dehydration catalysis. Chem. Sci. 2020;11(27):7102–7122. doi: 10.1039/D0SC02589E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen M. C. Hoffman A. J. Liu T.-W. Webber M. S. Hibbitts D. Schwartz T. J. Highly Selective Cross-Etherification of 5-Hydroxymethylfurfural with Ethanol. ACS Catal. 2020;10(12):6771–6785. doi: 10.1021/acscatal.0c01328. [DOI] [Google Scholar]
- Dejaco R. F. Bai P. Tsapatsis M. Siepmann J. I. Adsorptive Separation of 1-Butanol from Aqueous Solutions Using MFI- and FER-Type Zeolite Frameworks: A Monte Carlo Study. Langmuir. 2016;32(8):2093–2101. doi: 10.1021/acs.langmuir.5b04483. [DOI] [PubMed] [Google Scholar]
- Bai P. Tsapatsis M. Siepmann J. I. Multicomponent Adsorption of Alcohols onto Silicalite-1 from Aqueous Solution: Isotherms, Structural Analysis, and Assessment of Ideal Adsorbed Solution Theory. Langmuir. 2012;28(44):15566–15576. doi: 10.1021/la303247c. [DOI] [PubMed] [Google Scholar]
- Zhang K. Lively R. P. Noel J. D. Dose M. E. McCool B. A. Chance R. R. Koros W. J. Adsorption of Water and Ethanol in MFI-Type Zeolites. Langmuir. 2012;28(23):8664–8673. doi: 10.1021/la301122h. [DOI] [PubMed] [Google Scholar]
- Dejaco R. F. Dorneles De Mello M. Nguyen H. G. T. Jeon M. Y. Zee R. D. Tsapatsis M. Siepmann J. I. Vapor- and liquid-phase adsorption of alcohol and water in silicalite-1 synthesized in fluoride media. AIChE J. 2020;66(4):e16868. doi: 10.1002/aic.16868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pahari S. Dorneles De Mello M. Shah M. S. Josephson T. R. Ren L. Nguyen H. G. T. Van Zee R. D. Tsapatsis M. Siepmann J. I. Ethanol and Water Adsorption in Conventional and Hierarchical All-Silica MFI Zeolites. ACS Phys. Chem. Au. 2021;2(2):79–88. doi: 10.1021/acsphyschemau.1c00026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah D. Kissick K. Ghorpade A. Hannah R. Bhattacharyya D. Pervaporation of alcohol–water and dimethylformamide–water mixtures using hydrophilic zeolite NaA membranes: mechanisms and experimental results. J. Membr. Sci. 2000;179(1–2):185–205. doi: 10.1016/S0376-7388(00)00515-9. [DOI] [Google Scholar]
- Oumi Y., Miyajima A., Miyamoto J. and Sano T., Binary mixture adsorption of water and ethanol on silicalite, in Studies in Surface Science and Catalysis, Elsevier, 2002, vol. 142, pp. 1595–1602 [Google Scholar]
- Ahn H. Lee H. Lee S.-B. Lee Y. Pervaporation of an aqueous ethanol solution through hydrophilic zeolite membranes. Desalination. 2006;193(1–3):244–251. doi: 10.1016/j.desal.2005.06.062. [DOI] [Google Scholar]
- Sano T. Ejiri S. Yamada K. Kawakami Y. Yanagishita H. Separation of acetic acid-water mixtures by pervaporation through silicalite membrane. J. Membr. Sci. 1997;123(2):225–233. doi: 10.1016/S0376-7388(96)00224-4. [DOI] [Google Scholar]
- Ahunbay M. G. Monte Carlo Simulation of Water Adsorption in Hydrophobic MFI Zeolites with Hydrophilic Sites. Langmuir. 2011;27(8):4986–4993. doi: 10.1021/la200685c. [DOI] [PubMed] [Google Scholar]
- Humplik T. Raj R. Maroo S. C. Laoui T. Wang E. N. Effect of hydrophilic defects on water transport in MFI zeolites. Langmuir. 2014;30(22):6446–6453. doi: 10.1021/la500939t. [DOI] [PubMed] [Google Scholar]
- Bell R. P. The theory of reactions involving proton transfers. Proc. R. Soc. London, Ser. A. 1936;154(882):414–429. [Google Scholar]
- Evans M. Polanyi M. Further considerations on the thermodynamics of chemical equilibria and reaction rates. Trans. Faraday Soc. 1936;32:1333–1360. doi: 10.1039/TF9363201333. [DOI] [Google Scholar]
- Brønsted J. Pedersen K. Stöchiometrie und verwandtschaftslehre. Z. Phys. Chem. 1924;108:185–235. doi: 10.1515/zpch-1924-10814. [DOI] [Google Scholar]
- Hammond G. S. A Correlation of Reaction Rates. J. Am. Chem. Soc. 1955;77(2):334–338. doi: 10.1021/ja01607a027. [DOI] [Google Scholar]
- Anslyn E. V. and Dougherty D. A., Modern Physical Organic Chemistry, University Science, 2005, pp. 374–377 [Google Scholar]
- Alvear M. Eränen K. Murzin D. Y. Salmi T. Study of the Product Distribution in the Epoxidation of Propylene over TS-1 Catalyst in a Trickle-Bed Reactor. Ind. Eng. Chem. Res. 2021;60(6):2430–2438. doi: 10.1021/acs.iecr.0c06150. [DOI] [Google Scholar]
- Wu G. Wang Y. Wang L. Feng W. Shi H. Lin Y. Zhang T. Jin X. Wang S. Wu X. Epoxidation of propylene with H2O2 catalyzed by supported TS-1 catalyst in a fixed-bed reactor: experiments and kinetics. Chem. Eng. J. 2013;215:306–314. doi: 10.1016/j.cej.2012.11.055. [DOI] [Google Scholar]
- Zhang L. Chen K. Chen B. White J. L. Resasco D. E. Factors that Determine Zeolite Stability in Hot Liquid Water. J. Am. Chem. Soc. 2015;137(36):11810–11819. doi: 10.1021/jacs.5b07398. [DOI] [PubMed] [Google Scholar]
- Heard C. J. Grajciar L. Uhlík F. Shamzhy M. Opanasenko M. Čejka J. Nachtigall P. Zeolite (in) stability under aqueous or steaming conditions. Adv. Mater. 2020;32(44):2003264. doi: 10.1002/adma.202003264. [DOI] [PubMed] [Google Scholar]
- Resasco D. E. Crossley S. P. Wang B. White J. L. Interaction of water with zeolites: a review. Catal. Rev.: Sci. Eng. 2021;63(2):302–362. doi: 10.1080/01614940.2021.1948301. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Characterization plots, supplemental kinetics and UV-Vis spectra, full rate derivations, activity coefficient values, activation barriers, tabulated solvent parameters, and all calorimetry thermograms have been included as part of the ESI.†