Risk Tolerance Measured by Probability Discounting Among Individuals With Primary Mood and Psychotic Disorders

Abstract

Objective:

Change in risk tolerance is a feature of multiple psychiatric disorders and may contribute to adverse outcomes. We used a probability discounting (PD) task to measure risk-taking behavior among individuals with bipolar disorder (BPAD), major depressive disorder (MDD), schizoaffective disorder (SCAD), and schizophrenia (SCZ).

Method:

A PD task was administered to 117 patients and 88 healthy controls (HCs), along with a cognitive battery using the Cambridge Neuropsychological Test Automated Battery, and relevant symptomatology scales. We examined differences in PD rates between diagnostic groups, and compared with HCs, while controlling for potential confounding factors including measures of cognitive functioning.

Results:

Individuals with a diagnosis of BPAD or SCAD/SCZ prefer smaller, more guaranteed rewards rather than larger, less likely rewards as compared with healthy controls (p = .002 and p = .034, respectively). There was no effect of performance on cognitive tasks, antipsychotic treatment, or symptomatology on the rate of probability discounting.

Conclusion:

This study supports the transdiagnostic measurement of risk-taking behaviors, even when such behaviors are not the primary area of psychopathology. Quantifying risk-taking may enable targeted therapeutic strategies across disorders.

General Scientific Summary

Given that risk-taking behaviors contribute to medication nonadherence, substance abuse and aggression, performance on a probability discounting task may have important implications in understanding adverse outcomes in serious mental illness.

There has been continued interest in categorizing symptoms that cut across traditional psychiatric diagnostic groups(Cuthbert, 2015; Cuthbert & Insel, 2013; Grisanzio et al., 2018). Impulsivity, and in particular risk-taking behaviors, occurs across diagnostic categories, and can result from impairments in both information processing and regulating response output(Dalley & Robbins, 2017). We have previously examined impulsive behavior transdiagnostically in the context of the delay discounting (DD) task (Brown, Hart, Snapper, Roffman, & Perlis, 2018). Here, we sought to examine probability discounting (PD), a different measurement of risk-taking behavior on the basis of the extent to which the perceived value of a reward decreases as the probability of occurrence decreases. In the PD task, participants are posed a series of hypothetical questions from which they must choose between a guaranteed smaller amount of money and a less certain larger amount of money; the task measures their risk preference. A steeper rate of PD indicates a decreased value placed on the larger, but riskier and less probable reward. The PD task tests participants’ risk tolerance independent of time.

Performance on the PD task may have particular clinical relevance in a psychiatric population, as it represents a measure of riskier behaviors, which could include self-harm, medication nonadherence, or substance use(Bruce et al., 2016). However, there has been a paucity of studies examining performance on this task across psychiatric diagnoses such as bipolar disorder (BPAD), major depressive disorder (MDD), and schizophrenia or schizoaffective disorder (SCZ/SCAD). However, other tasks examining risk-taking behaviors demonstrate that individuals with SCZ are more risk averse compared with those with BPAD and healthy controls (HCs), and individuals with depressive symptoms are more risk averse compared with HCs, and make more decisions that avoid negative feedback (Cheng, Tang, Li, Lau, & Lee, 2012; Reddy et al., 2014; Smoski et al., 2008). These studies suggest that there are differences between psychiatric populations and healthy controls in their preferences for risk-taking versus risk averse behaviors. However, further studies comparing across diagnostic categories are still needed. We sought to conduct such analyses using the PD task.

Given the lack of literature examining the PD task across mood and psychotic disorders, we sought to examine performance on the PD task between groups with BPAD, MDD, and SCZ/SCAD, as well as in comparison to HCs. The availability of additional clinical and neurocognitive measures in this cohort further allowed us to investigate potentially confounding effects of these features.

Aims of the Study

On the basis of previous work examining risk-taking behavior, we hypothesized that individuals with BPAD would be more risk-prone compared with individuals with SCZ/SCAD and HCs, and thus have a lower rate of probability discounting. Conversely, we hypothesized that those with SCZ/SCAD would be less risk-prone and have a higher rate of probability discounting compared with both HCs and individuals with BPAD. We hypothesized that individuals with MDD would have a higher rate of probability discounting (more risk averse) compared with HCs due to increased anhedonia and a decreased interest in greater rewards.

Method

Participants

All participants were recruited from the outpatient setting, as part of a broader clinical assessment for a cellular biobanking study (Sellgren et al., 2017). The study protocol and informed consent procedure were approved by the Partners Institutional Review Board. Participants were between ages of 20 years and 65 years and were in the following diagnostic categories: 43 participants with MDD, 23 participants with BPAD, 51 participants with a primary psychotic disorder (SCZ [n = 33] or SCAD [n = 18]), as well as 88 healthy controls (HCs). Diagnosis (or lack of diagnosis for HCs) was confirmed by an expert clinician rater, using the Structured Clinical Interview for DSM–IV (SCID; First, Spitzer, & Gibbon, 1996) and the Mini-International Neuropsychiatric Interview (MINI; Sheehan et al., 1998). For patients with a diagnosis of SCZ or SCAD, a trained physician performed the Positive and Negative Syndrome Scale (PANSS) to evaluate psychotic symptoms(Kay, Fiszbein, & Opler, 1987). For all participants, the Inventory of Depressive Symptomatology-Self-Report (IDS-SR, Rush, Gullion, Basco, Jarrett, & Trivedi, 1996), a 30-item assessment of symptom severity, was administered. The study clinician recorded current and past medications using a questionnaire, confirming medication name, dose, and treatment duration. Smoking status was obtained by self-report and smokers were classified as individuals who reported smoking between several days and nearly every day in the last two weeks. Individuals were designated as HCs if they had no psychiatric diagnosis based on the SCID or MINI, and no intellectual disability (defined by IQ <70). We excluded participants with neurologic illnesses, including Parkinson’s disease, multiple sclerosis, and Alzheimer’s disease based on patient report and clinician review of electronic health records.

Neuropsychiatric Battery

All participants completed the Weschler Abbreviated Scale of Intelligence (2nd ed.; Wechsler, 1999) to determine full scale IQ, using the vocabulary and matrix reasoning subsections. Participants also completed a computerized neuropsychiatric cognitive battery, the Cambridge Neuropsychological Test Automated Battery, which tests participants’ abilities within a range of cognitive domains(Sahakian & Owen, 1992). For this assessment, we focused on spatial working memory (SWM), attention switching task (AST), paired-associates learning (PAL), and stop signal task (SST). For SWM, we examined the number of errors made between attempts, for PAL we focused on the total number of errors, for AST the percent correct trials, and for SST the proportion of successful stops.

Probability Discounting Task

In the PD task, participants chose between a guaranteed smaller reward and a larger, but less probable reward. For example, participants were asked, “Would you rather have five dollars for sure (100% chance) or ten dollars with a 75% chance?” Probabilities of obtaining the larger reward were 100%, 90%, 75%, 50%, and 25%. The monetary values shown in the task range from $0 to $10 in $0.50 increments. Participants were instructed to answer quickly and instinctively. The program begins with estimates of the ranges of possible minimum and maximum values for the indifference points. The point of indifference is the value at which the participant has no preference between the two choices (i.e., the participant puts equal value on the fixed guaranteed smaller reward and the less likely greater reward; Richards, Zhang, Mitchell, & de Wit, 1999). Depending on whether the participant chooses the varied monetary amount or the set monetary amount ($10), the program adjusts the ranges of minimum and maximum possible indifference points. When the difference between the upper limit of these two ranges is $0.50, the indifference point is set to be the corresponding varied (less likely) monetary amount. A point of indifference is calculated for each probability, including the 100% probability of obtaining the larger reward. A more in-depth explanation of this adjustment is available from the manufacturer (Millisecond Software, 2014).

Data Analysis

All analyses were done using R software (Version 3.2.1; R Core Team, 2016). Consistent with previously published methods, the indifference points for each of the five probabilities were calculated for each participant and fitted with a best-fit hyperbolic curve (Richards et al., 1999). We used a hyperbolic model as is standard analysis for discounting tasks. When fitting the model, the probabilities of obtaining the larger reward were converted to oddsagainst receiving the larger reward (0, .11, .33, 1, and 3, respectively). If the program could not confirm an indifference point, then that particular point was not used to fit the curve, consistent with prior work (Mazur, 1987). The hyperbolic discounting rate for probability, h, was determined using a nonlinear least squares approach to fit the model. A lower h value denotes a less steep rate of PD, and a preference for the riskier option. A higher h value denotes a steeper rate of PD, and a preference for a more conservative option.

Consistent with previous literature on PD, we used the natural log (ln) of h to normalize the distribution of h for all subsequent analyses, since h was positively skewed. Participants with inconsistent responses were identified as follows: (1) if a participant has an indifference point that increases by more than 20% of the larger but less probable reward (a $2 increase in this paradigm) or (2) if the first and last indifference points do not differ by at least 10% of the larger, less probable reward (i.e., the first and last indifference points must differ by at least $1 in this paradigm in order to be consistent; Johnson & Bickel, 2002, 2008). As is typical in discounting studies, participants with inconsistent discounting curves were excluded from the primary analyses because the data cannot be interpreted using a hyperbolic model(Johnson & Bickel, 2008). However, because inconsistent performance could be related to disease-state, we compared excluded individuals to included individuals. Multivariate logistic regression was used to compare individuals with inconsistent and consistent indifference points by diagnosis, age, sex, antipsychotic use, smoking status, and IQ in crude and adjusted models.

We focused the rest of the analyses on the consistent cohort. Initially we applied a one-way analysis of variance (ANOVA) to compare differences in PD rates across diagnoses and used pairwise post hoc comparisons of PD rate between diagnostic groups. To assess the impact of diagnosis on PD, unadjusted linear regression models and adjusted linear models controlling for age, sex, smoking status, and IQ were generated. We also examined unadjusted and adjusted models of antipsychotic use across diagnostic categories, since use was present in all three diagnostic groups. Next, we substituted more precise cognitive measures (SWM, PAL, AST, and SST) for IQ in the adjusted model, to explore the relationship between PD and more specific aspects of cognition. To examine the impact of symptom severity on PD, we designed linear models specific to each diagnostic category. These models included clinical assessments specific to the diagnostic category (PANSS scores for patients with SCZ/SCAD, and IDS-SR scores for patients with MDD and BPAD) and controlled for age, sex, IQ, and smoking status.

In light of the substantial number of inconsistent responders identified among our three clinical groups in primary analysis, in a secondary analysis we elected to apply an alternate method that relies on area-under-the-curve (AUC), a model-free estimate of probability discounting. This approach uses the summed area of a series of trapezoids constructed from the indifference points as the measure of discounting (Borges, Kuang, Milhorn, & Yi, 2016). These scores are standardized so that a score of 1 represents no discounting, and a score of 0 represents the steepest discounting. Unlike the hyperbolic discounting model, AUC does not presuppose a response pattern as it is a model-free measurement, and allows for the inclusion of inconsistent responders in our analysis; however, it is important to note that the hyperbolic model is the standard analytic method for discounting tasks. After generating an AUC for each participant, we repeated the primary analysis in all participants (i.e., with no exclusions) using a one-way ANOVA to compare differences in PD rates across diagnosis with pairwise post hoc comparisons of PD rate between diagnostic groups.

Results

Demographic and Clinical Phenotypes

Demographic and clinical characteristics across diagnostic groups are described in Table 1. The distribution of age, race, and sex did not differ significantly across diagnostic groups, except for the HC population, which was on average younger than those in the diagnostic categories (M = 35.6 years, SD = 10.4). Among the SCZ/SCAD population, the mean PANSS total score was 70.8 (SD = 14.7), indicating a moderate degree of severity of psychotic symptoms. There was no significant difference in depression severity based on IDS-SR score between the BPAD and MDD group (t = −.78, p = .44); both groups had mean scores in the “moderate depression” range, and HCs had few or no depressive symptoms. Using one way ANOVA and Tukey post hoc comparisons, there was a significant difference in IQ scores between diagnostic groups, F(3, 199) = 12.32, p < .001; the SCZ/SCAD group had significantly lower mean IQ scores compared with HCs (p < .001) and individuals with MDD (p < .001), and the BPAD group had significantly lower mean IQ scores as compared with HCs (p = .008).

Table 1.

Clinical and Demographic Characteristics

Characteristic	SCZ/SCAD (n = 51)	BPAD (n = 23)	MDD (n = 43)	HC (n = 88)
Age M (SD)	43.6 (12.7)	46.6 (12.4)	44.3 (13.6)	35.6 (10.4)
Sex (male) n (%)	33 (64.7)	12 (52.2)	22 (51.2)	40 (45.5)
Current substance abuse n (%)	1 (2.0)	1 (4.3)	5 (11.6)	0 (.0)
Current antipsychotic use n (%)	45 (88.2)	15 (65.2)	9 (20.9)	0 (.0)
Smoking status n (%)	13 (25.5)	7 (30.4)	10 (23.3)	3 (3.4)
Race
Caucasian n (%)	37 (72.5)	18 (78.3)	35 (81.4)	63 (71.6)
African American n (%)	6 (11.8)	4 (17.4)	4 (9.3)	10 (11.4)
Asian n (%)	5 (9.8)	1 (4.3)	3 (7.0)	10 (11.4)
American Indian/Alaskan n (%)	2 (3.9)	0 (.0)	1 (2.3)	1 (1.1)
Other n (%)	1 (2.0)	0 (.0)	0 (.0)	4 (4.5)
Clinical measure M (SD)
IQ	92 (14.1)	96 (18.7)	105.8 (18)	107.7 (15.5)
PANSS–Positive	16.04 (6.2)
PANSS–Negative	22.8 (5.2)
PANSS–General	31.9 (6.7)
PANSS–Total score	70.8 (14.7)
IDS-SR	16.5 (12.1)	30.2 (17.5)	26.9 (15.5)	4.0 (3.7)
Lnh	1.07 (2.19)	1.84 (2.33)	.84 (1.94)	.40 (1.28)

Note. SCZ/SCAD = schizophrenia/schizoaffective disorder; BPAD = bipolar affective disorder; MDD = major depressive disorder; HC = healthy control; IQ = intelligence quotient; PANSS = Positive and Negative Syndrome Scale; IDS-SR = Inventory of Depressive Symptomatology–Self-Report; Lnh = the natural log of the hyperbolic discounting rate for probability, h.

Twenty-nine participants (14%) with inconsistent indifference points were excluded from the primary analysis based on the a priori analytic criteria: 17 individuals with SCZ/SCAD, two individuals with BPAD, five individuals with MDD, and five HCs. In general, excluded individuals were younger in age and had a lower IQ in adjusted models (see Table 2).

Table 2.

Crude and Adjusted Odds Ratio for Inconsistency Within Demographic Categories and Clinical Measures

Outcome	Unadjusted odds ratio	Unadjusted 95% confidence interval		Adjusted odds ratio	Adjusted 95% confidence interval
Age	1.007	.975	1.038	.941a	.892	.986
Sex	1.354	.615	3.063	.662	.224	1.901
Antipsychotic treatment	4.011	1.794	9.341	1.892	.368	10.802
BPAD	1.581	.216	7.918	.529	.041	5.009
MDD	2.184	.576	8.290	2.848	.539	15.280
SCZ/SCAD	8.300	3.017	26.906	3.590	.500	26.390
Smoking status	2.459	.930	6.084	.854	.222	3.044
IQ	.914	.880	.944	.888a	.842	.928

Note. BPAD = bipolar affective disorder; MDD = major depressive disorder; SCZ/SCAD = schizophrenia/schizoaffective disorder; IQ = intelligence quotient.

^aIndicates variables for which the confidence interval excludes 1.

Among participants with consistent indifference points, there were significant between-group differences in rate of PD, F(3,172) = 5.712, p = .001; in post hoc comparisons, individuals with BPAD and SCAD/SCAD had steeper rates of PD as compared with HCs (p = .002 and p = .034, respectively; see Table 1 in the online supplemental material). Next, we analyzed the impact of diagnosis on rate of PD in both unadjusted and adjusted models incorporating age, sex, antipsychotic use, smoking status, and IQ (see Table 3). In the unadjusted model, there was a significantly steeper rate of PD in the SCZ/SCAD and BPAD diagnostic groups as compared with HCs. There was no significant difference in PD rates between the MDD group and HCs (see Figure 1). We observed a significant unadjusted effect of IQ, with an increase in IQ corresponding to a less-steep rate of discounting. Finally, in the unadjusted model, the use of antipsychotic medications was associated with a significantly steeper rate of discounting.

Table 3.

Unadjusted and Adjusted Models of Probability Discounting Rate Among Consistent Participants

Model variables	Unadjusted model			Adjusted model
	β	t	p	β	t	p
BPAD	1.275	3.650	<.001*	1.228	2.896	.004*
MDD	.286	1.021	.309	.266	.883	.379
SCZ/SCAD	.797	2.739	.007*	.911	2.035	.044*
Age	.014	1.576	.117	.008	.741	.460
Sex	−.078	−.347	.729	−.282	−1.251	.213
Smoking status	.207	.639	.524	−.538	−1.558	.121
Antipsychotic treatment	.796	3.312	.001*	−.182	−.475	.636
IQ	−.025	−3.835	<.001*	−.020	−2.580	.011*

Note. Diagnostic groups are in comparison to the healthy control group. A positive β indicates a steeper probability discounting rate. BPAD = bipolar affective disorder; MDD = major depressive disorder; SCZ/SCAD = schizophrenia/schizoaffective disorder; IQ = intelligence quotient.

^*p < .05.

Figure 1.

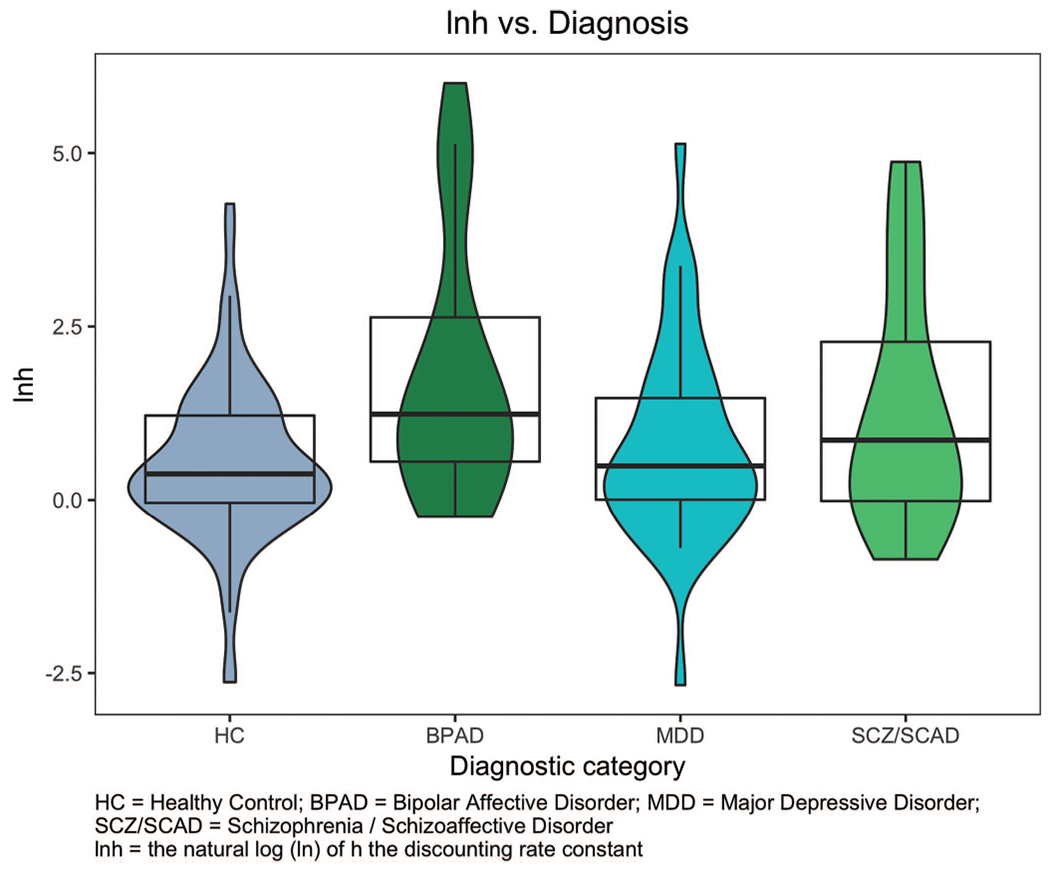
Distribution of rate of probability discounting across diagnostic category. See the online article for the color version of this figure.

In the adjusted model, as in the unadjusted model, a diagnosis of BPAD or SCZ/SCAD corresponded with a steeper rate of discounting compared with HCs. IQ remained a significant predictor of rate of discounting: a one-point increase in IQ corresponded with a .020 decrease in lnh (or for every one standard deviation increase in IQ (15 points), lnh decreases by 0.30). In other words, an increase in IQ corresponded to a decrease in rate of PD (indicating less risk aversion).

To better understand the specific impact of cognition on PD, we next examined the relationship between PD rate and four neuropsychological tasks (SWM, PAL, SST, and AST; see Table 2 in the online supplemental material). Within this model, there was a significant main effect of both BPAD and SCZ/SCAD diagnosis on rate of PD, again with both diagnostic categories having increased rates of discounting as compared with HCs. However, there was not a significant effect for any of the neuropsychological tasks included in the model.

We also sought to understand the relationship between symptom severity and probability discounting results (see Table 3 in the online supplemental material) and performed separate analyses within each diagnostic group, including diagnosis-specific clinical measures. There was no significant effect of symptom severity or IQ on PD within any of the diagnostic groups. Finally, we identified no significant difference in the rate of PD, F(3, 201) = 2.02, p = .112 between diagnostic groups using the AUC method of measuring discounting.

Discussion

In this study of 205 individuals undergoing neurocognitive and clinical assessment, we looked across major psychiatric diagnoses at a measure of risk-taking behavior (PD) and the relative effects of other symptom domains. These results demonstrate that participants with a diagnosis of BPAD and SCZ/SCAD display a steeper rate of PD compared with HCs: that is, individuals with BPAD and SCZ/SCAD prefer smaller, more guaranteed rewards rather than larger, less likely rewards. We did not find any effect of performance on cognitive tasks, antipsychotic treatment, or symptomatology on the rate of PD in adjusted models. These findings support our hypothesis that SCZ/SCAD participants are less risk prone, but are contrary to our hypothesized results that patients with BPAD (examined cross-sectionally) would be more risk prone. Our findings suggest that when compared with HCs, individuals with BPAD and SCZ/SCAD place a decreased value on uncertain outcomes, and thus are more risk averse. In contrast to the BPAD and SCZ/SCAD cohorts, we did not find any difference in the rate of PD between individuals with MDD and HCs.

We sought to understand why individuals with BPAD and SCZ/SCAD demonstrated this pattern of risk averse behavior. We first examined aspects of symptomatology. Patients with BPAD (in nonmanic states) and SCZ/SCAD frequently experience negative symptoms, including anhedonia and avolition, leading them to (incorrectly) conclude that the risk involved in acquiring a reward outweighs any perceived benefit. For example, individuals with SCZ who have higher levels of negative symptoms are less responsive to less probable rewards (i.e., display less effortful behavior to obtain the reward) compared with individuals with fewer negative symptoms(Gold et al., 2013). Yet in the present study, we did not find an effect of negative symptom severity among SCZ/SCAD patients on rate of PD. Interestingly, our BPAD cohort had a numerically greater average depression score (as measured by the IDS-SR) compared with our MDD cohort. As we initially hypothesized for our MDD cohort, depressive symptoms within the BPAD group may prevent individuals from taking more risks (i.e., making them more risk averse compared with HCs). If our BPAD cohort had been less depressed and shown more manic symptoms, the group may have been more risk prone. It is possible our MDD cohort did not experience severe enough depressive symptoms to observe a significant difference in rate of PD compared with HCs.

Individuals with positive psychotic symptoms (e.g., delusional beliefs, hallucinations) may prefer more guaranteed rewards, and avoid more risk-taking behaviors in the setting of suspiciousness, or guardedness. However, we did not find an effect of positive symptom severity on rate of PD, consistent with previous literature examining risk-taking tasks among individuals with SCZ (Reddy et al., 2014; Yu et al., 2017). Finally, we did not find an association between scores on the general psychopathology subscale of the PANSS and rate of PD among individuals with SCZ. However, we did not look at individual items from the general subscale in relation to rate of PD. For example, it is possible that individual items such as “poor impulse control” or “disturbance of volition” may correlate with a less steep rate of PD and risk proneness.

We did not find an effect of cognitive performance in any realm (SWM, PAL, SST, and AST) on rate of PD. These cognitive tasks may not be exact measures of skills used in the PD task. For example, the SWM task requires the ability to retain and use visuospatial information, as well as plan and strategize—skills that may not be relevant in a riskier decision-making paradigm such as PD. One may expect that SST, a measure of response inhibition and thus “impulse control,” to have an effect on rate of PD. Yet, SST measures more of a motor response inhibition, and thus likely not the same aspect of impulsivity as required in the PD task.

Our results that SCZ/SCAD individuals are less risk prone compared with HCs are consistent with other studies examining risk-taking behavior in this population. On the Balloon Analogue Risk Task, individuals with SCZ demonstrated more risk aversion compared with those with BPAD and HCs (Cheng et al., 2012; Reddy et al., 2014). In contrast, in the game of dice task (GDT), another measure of an individual’s preference for risky choices, individuals with SCZ revealed a preference for risky decisions. However, notably different from the PD task, in the GDT participants receive feedback regarding probability of winning and losing, and can adjust their strategies accordingly (Pedersen, Göder, Tomczyk, & Ohrmann, 2017). Even though SCZ patients used feedback much less than HCs in the GDT, in the PD task participants are not given any feedback and are instructed to answer instinctively, perhaps making them less likely to take risks.

Another task that measures risk and reward is the delay discounting (DD) task. Our previous results demonstrate individuals with SCZ/SCAD have a greater rate of delay discounting (DD), (i.e., are more likely to select the immediate smaller reward compared with the later larger reward), and are more impulsive compared with HCs, and there was no difference in rate of DD between individuals with BPAD and HCs (Brown et al., 2018). Among our consistent cohorts, performance on the PD and DD tasks are weakly correlated, r(126) = .33, p < .001. Our results suggest that DD and PD are not measures of a common construct (i.e., represent different aspects of impulsivity and risk-taking behavior). For example, DD may be more related to difficulty in delaying gratification, while PD is more related to risk averseness.

Performance on the PD task among individuals with addictive behaviors such as gambling and substance use disorders has been more widely examined than performance among individuals with primary mood or psychotic disorders. For example, individuals with a history of pathologic gambling behavior display less steep rates of PD, and thus put more value on a larger, but uncertain reward (i.e., take greater risks) compared with HCs(Green & Myerson, 2004; Holt, Green, & Myerson, 2003; Miedl, Peters, & Büchel, 2012). Other types of addictive behaviors have also been shown to affect the rate of PD: consumption of alcohol among nonalcohol dependent individuals leads to an increased value placed on uncertain outcomes (i.e., a lower rate of PD and thus more risk proneness; Bidwell et al., 2013). The relationship between smoking behavior and PD is less clear: one study demonstrates a steeper rate of PD among smokers compared with nonsmokers (i.e., smokers are more risk averse), whereas other studies do not show this relationship (Ohmura, Takahashi, & Kitamura, 2005; Reynolds, Richards, Horn, & Karraker, 2004).

One possible limitation to our study is the reward size offered in the PD task. It has previously been demonstrated that among HCs, the rate of probability discounting increases as the reward size increases (Myerson, Green, & Morris, 2011). The maximum hypothetical dollar amount participants in this study could obtain was $10; this amount may not be significantly large enough (or significantly different in amount compared with the more guaranteed reward) to risk obtaining. Another potential limitation is the PD task provides hypothetical rewards, and not actual monetary rewards. Previous research suggests hypothetical rewards are discounted similarly to real rewards in healthy populations (Johnson & Bickel, 2002; Locey, Jones, & Rachlin, 2011; Madden, Begotka, Raiff, & Kastern, 2003). However, individuals with SCZ may perform differently on a rewards task compared with HCs, depending on whether they receive real or hypothetical rewards (i.e., individuals with SCZ have higher rates of DD compared with HCs when receiving real, but not hypothetical rewards; Horan, Johnson, & Green, 2017). Further, as discussed above, in the PD paradigm, there is no negative consequence to choosing the larger, riskier reward (e.g., no punishment, no financial loss), and thus individuals with BPAD and SCZ/SCAD may be even more risk averse than we are measuring in this task. Taken together, some participants may not consider the PD task “risky” enough, and it may not be a true measure of their risk response. Another possible limitation in this study is the exclusion of inconsistent individuals (i.e., those whose responses do not fit a hyperbolic model). As previously discussed in our DD work, an individual’s pattern of inconsistent choice could be suggestive of a separate psychopathology and should be further characterized separately. Finally, it is important to note that employing an alternate means of analysis using AUC did not identify significant differences in the rate of PD between diagnostic groups. Results from both the hyperbolic model and the AUC method are non-normally distributed; however, a limitation of the AUC model is that there is no standard method to address such skew(Yoon et al., 2017). We emphasize that the hyperbolic model used in our primary analyses represents a more standard and well-validated approach to modeling PD (Bidwell et al., 2013; Holt et al., 2003; Yi, de la Piedad, & Bickel, 2006).

In sum, this work demonstrates differences in a measure of risk-proneness across psychiatric diagnoses, even when impairment in impulse control is not thought to be the primary psychopathology. The study suggests the utility of further investigation into the dimensional nature of risk proneness and averseness across major psychiatric illness, as a means of developing more targeted therapeutic approaches that take variation in risk-taking behaviors into account—for example, in interventions to prevent medication nonadherence, help with financial decision-making, long-term health care planning, and employment choices.