Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2023 Mar 9;8(11):10176–10184. doi: 10.1021/acsomega.2c07489

Role of Chalcogen Defect Introducing Metal-Induced Gap States and Its Implications for Metal–TMDs’ Interface Chemistry

Jeevesh Kumar 1, Mayank Shrivastava 1,*
PMCID: PMC10034985  PMID: 36969396

Abstract

graphic file with name ao2c07489_0014.jpg

The contact resistance of the transition metal dichalcogenide (TMD) devices is not comparable to that of their silicon counterparts, probably due to a lack of clarity in their interface chemistry. Looking beyond the conventional Schottky–Mott rule, the metal chalcogen orbital overlaps, tunnel barrier, and metal-induced gap states (MIGSs) are crucial factors determining different metals’ contact properties with TMDs. Exploring their properties helps TMDs’ contact resistance engineering, driven mainly by their orbital overlaps and perturbing parameters. This work presents the interface chemistry of TMDs (MoS2, MoSe2, WS2, and WSe2) with different metals (Au, Cr, Ni, and Pd) in detail using density functional theory computations. Additionally, the work discusses the role of the chalcogen vacancy and interstitial defects in the metal–TMD interactions and corresponding MIGS features. The investigations reveal that Au does not show any significant MIGS due to its weak interactions with all the TMDs. However, other investigated metals have a strong affinity with TMDs, making significant MIGS contributions. All the metals offer n-type doping characteristics to TMDs due to valence charge transfer from the metals toward TMDs. The chalcogen vacancy boosts the orbital overlaps of the TMDs with all the metals. The vacancy reduces metal–TMD interfacial distance, which can be a promising technique to reduce the tunnel barrier and contact resistance. The MIGS and defect-induced gap states (DIGSs) reflect the possibility of Fermi-level pinning in the TMDs’ contacts with Cr, Ni, and Pd. Besides, the work discloses that the chalcogen vacancy converts an n-type Pd–TMD interface into p-type due to reverse charge transfer after the vacancy. Chalcogen interstitial impurity also helps with contact resistance engineering for some metal–TMD systems by reducing the bond distance of the metal TMDs. Our study highlights the possibility of defect-assisted and MIGS-based contact engineering at the metal–TMD interfaces.

Introduction

Discovery of 2D materials, like graphene, transition metal dichalcogenides (TMDs), and phosphorene, makes the scientific land more fertile to harvest future generations of high-performance electronic devices.1−3 Among these materials, TMDs are most promising for switching applications, especially for sub-5 nm technology, due to their wide bandgap range, ambient stability, and relatively high effective mass.4 Despite these properties, the TMDs’ field-effect transistor (FET) performance is not up to the mark yet due to high contact resistance at the metal–TMD interfaces. Many research groups explored various contact resistance engineering approaches.5 However, the investigated methods are insufficient to make metal–TMD interface resistance compatible with silicon counterparts. Thus, further effort is required to achieve the desired milestone of contact resistance. Due to metal–TMD van der Waals (vdW) gap6 and lack of promising doping techniques,7 understanding the quantum chemistry of the metal–TMD interface is necessary to explore contact engineering opportunities beyond the conventional Schottky–Mott rule.8−13 Popov et al.14 explored Ti and Au interface properties with MoS2. Kang et al.15 discussed the interaction of different metals with MoS2 and WSe2, while Huang et al.16 studied the defect’s role in enhanced Fermi-level pinning at metal–TMD interfaces. However, a systematic study of metal–TMD interaction chemistry and its role in metal-induced gap states (MIGSs) has not been explored in detail yet. Besides, the scope of vacancy-assisted orbital overlap-based contact resistance engineering, like graphene,17−19 is yet to be explored for TMDs at the atomic level. Ansh et al.20,21 used MIGSs and defect-induced gap states (DIGSs) as engineering tools, drastically reducing contact resistance at the TMD–metal interfaces. They have investigated the role of MIGSs and DIGSs at the Pd–TMD bulk interfaces and implemented their findings in the TMD FETs. However, the authors have not given detailed atomic-level insights into the interface quantum chemistry of different metal–TMD combinations. Thus, it is worth investigating atomic-level orbital overlap interaction and the role of the chalcogen vacancy and interstitial impurity in the metal–TMD interaction and its consequences on interfacial distance, MIGSs, and contact resistances.

To explore the same, we systematically studied the interaction of different metals (Au, Cr, Ni, and Pd) with leading TMDs like MoS2, MoSe2, WS2, and WSe2 using the density functional theory (DFT) computational approach. Metal–TMD interface physics is mainly driven by the work function difference between the metal and TMDs. However, the electronegativity of the metal can also play a vital role in electron cloud sharing at the interfaces. Considering these two parameters and experimental uses of the metals, Au, Cr, Ni, and Pd are selected for further analysis, covering low and high work functions and electronegative metals. The article starts with a discussion about the interaction of different metals with intrinsic TMDs, followed by the n-type doping nature of metals. Consequently, the article talks about chalcogen vacancy-assisted metal–TMD bond distance reduction and the n-type to p-type conversion of Pd–TMD interfaces. Finally, the article highlights the role of chalcogen impurity in the metal–TMD interactions.

Results and Discussion

When the carrier (electron or hole) is transported through the metal–TMD contact, it encounters the tunnel barrier and the Schottky barrier at the interface. Although the Schottky barrier can be controlled by aligning the work function of the TMDs with that of a suitable metal,8 the tunnel barrier is a major challenge to be engineered because of the vdW gap between most of the metal and TMD surfaces.6 Thus, it is worth saying that understanding and engineering the tunnel barrier are the key factors that can open the contact resistance bottleneck at the interface. Besides, once the metal approaches TMDs, its wave function can overlap with the TMDs’ wave function and make a hybridized system.22,23 If the interaction is strong, many energy states are generated in the bandgap regions of the TMDs, known as MIGSs. Similar energy states are also generated due to chalcogen defects in the TMDs, called DIGSs. These MIGSs and DIGSs drive Fermi-level pinning that changes the overall Schottky barrier height at the interface.10 Therefore, atomic-level investigations are required across different TMD and metal combinations to reveal hidden mysteries behind metal–TMD interactions and explore corresponding contact resistance engineering techniques.

Usually, the work function difference between metals and TMDs drives their interface physics. However, the electronegativity of the metal can also play a vital role in electron cloud sharing at the interfaces. Thus, based on the previous experimental and theoretical investigation by Ansh et al.,20 gold (Au), chromium (Cr), nickel (Ni), and palladium (Pd) metals were picked for our atomic-level investigations using DFT. Cr/Au was picked as a low-/high-work function (∼4.5/∼5.4 eV) and low-/high-electronegativity (∼1.66/∼2.54) metal. On the other hand, Ni and Pd were picked as high-work function metals (∼5.2 eV) with relatively low (∼1.91) and high (∼2.20) electronegativity, respectively.5 Our studies span across MoS2, MoSe2, WS2, and WSe2, the most investigated TMDs for electronic device applications.

Intrinsic Metal–TMD Interfaces and MIGSs

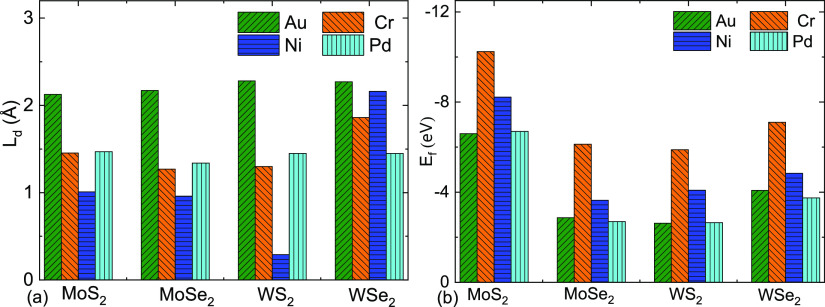
Metal atoms were kept over the TMD surfaces and were optimized using DFT to achieve their minimum energy. Energy-optimized structures (Figure 1), corresponding surface-metal distance, and their formation energies (Figure 2) of all the investigated combinations show that the metals have different bonding properties with TMDs. Ni has a strong binding affinity with least distance from MoS2, MoSe2, and WS2 among the investigated metals, while Pd has the same with WSe2 (Figure 2a,b). On the other hand, Au has weak interactions with all the TMDs. The metal stays more than 2 Å away from all the TMD surfaces, which resembles only vdW interactions of Au with TMDs. As observed in multiple experimental investigations, the weak vDW interaction is the reason for the weak adhesion of gold metal pads in the TMD devices.

Figure 1.

Figure 1

Open in a new tab

Energy-optimized interfaces of pristine TMDs with different metals: [a(1)] MoS2–Au, [a(2)] MoS2–Cr, [a(3)] MoS2–Ni, [a(4)] MoS2–Pd, [b(1)] MoSe2–Au, [b(2)] MoSe2–Cr, [b(3)] MoSe2–Ni, [b(4)] MoSe2–Pd, [c(1)] WS2–Au, [c(2)] WS2–Cr, [c(3)] WS2–Ni, [c(4)] WS2–Pd, [d(1)] WSe2–Au, [d(2)] WSe2–Cr, [d(3)] WSe2–Ni, and [d(4)] WSe2–Pd.

Figure 2.

Figure 2

Open in a new tab

(a) Optimized bond (interfacial) distances (Ld) of MoS2, MoSe2, WS2, and WSe2 from Au, Cr, Ni, and Pd. (b) Formation energy per metal atom (Ef) of the optimized metal–TMD systems. The formation energy (per metal atom) of the system is Ef = [Esys – (ETMD + 4 × Em)]/4, where Esys, ETMD, and Em are the optimized energies of the metal–TMD system, only the TMD, and only the single metal atom, respectively.

Due to weak interaction and long bond distance, Au–metal contact possibly offers wide tunnel barriers, which is a possible cause of their high contact resistance. Interestingly, Ni went very close (less than 1 Å) to MoS2, MoSe2, and WS2. The interaction reflects the strong affinity of Ni with all three TMDs. WSe2 has a relatively weak interaction with all the metals, whereas Au and Pd offer the lowest and strongest interactions, respectively. Optimized bond distances that eventually resemble interface tunnel barriers reflect that Ni should be the favorite choice as the contact metal for MoS2, MoSe2, and WS2, while Pd is favorable for WSe2. On the other hand, Au should be the least preferred metal as the contact for all the TMDs as far as the tunnel barrier bottleneck is concerned.

Once a metal approaches closer to the TMDs, its orbital overlaps strongly. The substantial orbital overlap rehybridizes the system and changes fundamental properties of the TMDs like the band structure, density of states (DOS), electron density (ED), and Fermi level. Additionally, the metal also induces mid-gap (trap) states (MIGS) in the materials, which primarily depends on the strength of the orbital overlaps. The trap states’ positions and densities determine the possibility of the MIGS-assisted Fermi-level pinning at corresponding bulk interfaces. The band structure of all the simulated combinations (Figure 3) shows that Au offers the least number of trap states (one or two) with all the TMDs [Figure 3a(1)–d(1)]. The few trap states are due to the weak interaction of Au with all the TMDs, as shown in Figures 1 and 2. Thus, Au cannot offer Fermi-level pinning at its contact due to weak orbital overlaps and, thus, very few trap states. On the other hand, other metals produce plenty of MIGSs with all the TMDs. The MIGS due to Pd is primarily near the valence band [Figure 3a(4)–d(4)], which can offer Fermi-level pinning near the valence band. Thus, Pd can give p-type contact by carefully engineering Fermi-level pinning in the TMDs. Fermi-level pinning by Cr cannot be predicted as the metal has MIGSs in the entire bandgap region [Figure 3a(2)–d(2)]. Ni has a different character from the TMDs in terms of MIGSs. The metal has MIGSs near the valence band for sulfur-based TMDs (MoS2 and WS2) [Figure 3a(3),c(3)]. However, it offers the MIGS in the entire bandgap for selenium-based TMDs (MoSe2 and WSe2) [Figure 3b(3),d(3)]. Thus, Ni can give p-type contact with MoS2 and WS2 under Fermi-level pinning. However, the metal can offer both types of contacts, depending on the Fermi-level pinning position, with MoSe2 and WSe2.

Figure 3.

Figure 3

Open in a new tab

Band structure of all the TMD–metal combinations along with pristine TMDs. (a–d) Pristine TMDs, [a(1)–d(1)] TMD–Au, [a(2)–d(2)] TMD–Cr, [a(3)–d(3)] TMD–Ni, and [a(4)–d(4)] TMD–Pd.

Metal-Assisted n-Type Doping

All the metals show n-type doping with all the TMDs. Metal generally offers electron-donating features during any chemical interaction. Thus, it dopes all the TMDs into n-type once it approaches the surface of the TMDs. Figure 3 shows that the Fermi level of all the pristine TMDs (Figure 3a–d) is in the middle of the bandgap. However, it shifts toward the conduction band once the metal approaches the TMDs’ surfaces (Figure 3). All the metals have similar doping strength with MoS2 (Figure 4a). However, they show different characteristics from other TMDs. Cr and Ni show more doping strength with MoSe2, Cr with WS2, and Ni with WSe2.

Figure 4.

Figure 4

Open in a new tab

Comparison of Fermi-level positions from valence maxima and conduction band minima for all the TMD–metal combinations. (a) MoS2, (b) MoSe2, (c) WS2, and (d) WSe2.

Chalcogen Vacancy-Assisted Orbital Overlap

TMDs have significant point defect density, especially the chalcogen vacancy, since their growth or synthesis.24 This chalcogen vacancy can perturb the chemistry of the materials with external agents.25 Interestingly, this vacancy can also be a contact engineering tool, as explored in other 2D materials like graphene.17 Thus, it is worth investigating the role of the chalcogen point vacancy in the interactions between metals and TMDs.

All the explored pristine combinations were optimized for minimum energy after one chalcogen vacancy in the TMDs (Figure 5). Due to the chalcogen vacancy, metal–TMD interfacial distance reduced significantly for all the interacting systems (Figure 6).

Figure 5.

Figure 5

Open in a new tab

Reduction in bond distance due to the S vacancy at the optimized MoS2–Au interface. (a) Intrinsic MoS2–Au system. (b) MoS2–Au system with one S vacancy at the central S position. Au atoms come closer to MoS2 due to the S vacancy. Other optimized metal–TMDs with chalcogen vacancy structures are available in the Supporting Information (Figure S1).

Figure 6.

Figure 6

Open in a new tab

(a) Average ED profile perpendicular to the basal plane of MoS2 (Z) in the MoS2/Au system. The minimum ED value in the metal and chalcogen bonding region increases (inset) with the chalcogen vacancy. ED profiles of other systems are available in the Supporting Information (Figure S2). (b) Reduction in the bond distance (ΔL) due to the chalcogen vacancy at the interfaces. ΔL is Lint – Lvac, where Lint and Lvac are the optimized distance of metals from the surface of the TMDs under pristine and chalcogen vacancy conditions, respectively. (c) Change in formation energy (ΔEf) due to the chalcogen vacancy at the interfaces. ΔEf is Ef-vac – Ef-pri, where Ef-pri and Ef-vac are the optimized formation energy of the metal–TMD systems under pristine (Figure 2b) and chalcogen vacancy conditions (Figure S3), respectively.

The pristine metal–TMD interface has the vdW gap due to the unavailability of overlapping free orbitals in the TMD. Once the chalcogen (S, Se) vacancy is created, the nearby atoms of the vacancy site have the unsaturated orbitals ready to bond with reacting elements. When the contact metal approaches the vacancy site, the unbound orbitals overlap with the metal, enhancing the metal–TMD bonding. The bonding enhancement reduces the metal–TMD interface gap at the interfaces. ED in the orbital overlap region of the metal and TMDs increases, as shown for the MoS2–Au combination in Figure 6a, in the presence of the chalcogen vacancy that eventually reduces the bonding distance (Figure 6b) and increases (more negative) the formation energy (Figure 6c). The increased minimum value of ED confirms chalcogen vacancy-assisted bonding between the metal and TMDs. The vacancy-assisted bond distance reduction, known as vacancy engineering hereafter, is effective for all the metal–TMD combinations (Figure 6b). Au, Cr, Pd, and Ni metal contacts are most sensitive to vacancy engineering for MoS2, MoSe2, WS2, and We2, respectively. Interestingly, the technique is very promising for all the metals for WSe2.

The reduction in metal distance from TMDs can be a promising tool for reducing contact resistance at the corresponding bulk interface. Metal–TMD bond distance is directly linked to the interface’s tunnel barrier width (d). The carrier transmission probability (T) at the interface is T ∝ e–2kd. Thus, chalcogen vacancy-assisted metal–TMD tunnel barrier reduction can reduce contact resistance at the interface.

Chalcogen vacancy-assisted orbital overlaps also enhance MIGSs in the TMDs. Figure 7 reflects that the band structure has more trap states once the metal interacts with TMDs in the presence of the chalcogen vacancy. Thus, the chalcogen vacancy at the metal–TMD interface can play a key role in MIGS-assisted contact resistance engineering at the interface as demonstrated by Ansh et al.20 for TMDs and by Kumar et al.17 for graphene.

Figure 7.

Figure 7

Open in a new tab

Band structure of WS2–Cr interfaces: (a) intrinsic and (b) S vacancy-engineered. (b) has more band densities near the Fermi level than (a), reflecting orbital overlap enhancement due to the chalcogen vacancy. Band structures of other metal–TMD systems are available in the Supporting Information (Figure S4).

Chalcogen Vacancy-Assisted n-Type to p-Type Transformation

As discussed previously, metal is generally an electron donor that offers n-type doping to a system. Interestingly, in the presence of a chalcogen vacancy, Pd makes all the TMDs into p-type. The p-type doping is due to charge transfer from TMDs to Pd in the presence of the chalcogen vacancy. In fact, in the presence of the chalcogen vacancy, the unsaturated orbitals make a strong bond with Pd, which does not allow a charge transfer mechanism from Pd to chalcogen, like pristine conditions. Due to the strong bond and chalcogen vacancy, extra energy states are created near the valence band which is occupied by the available free electron. The occupied and remaining free states drift the Fermi level near the valence band and make all the Pd–TMD systems p-type.

Pd shows different behavior than other metals, especially for the Ni element of the same group, probably due to its high electronegativity and delocalized f-orbitals. The electronegativity of Pd (2.20) is higher than that of Ni (1.91).5 Thus, the Pd metal has a better tendency to attract the overlapping electron. With pristine TMDs, the metals are in contact with chalcogen (non-metal) and thus act as usual electron donors. However, after the chalcogen vacancy, the guest metal (Ni/Pd) comes near exposed host metals (Mo/W) and is bonded with unsaturated orbitals. Thus, due to high electronegativity along with vacant delocalized f-orbitals, Pd acts as an electron acceptor and makes the system p-type in the presence of the chalcogen vacancy.

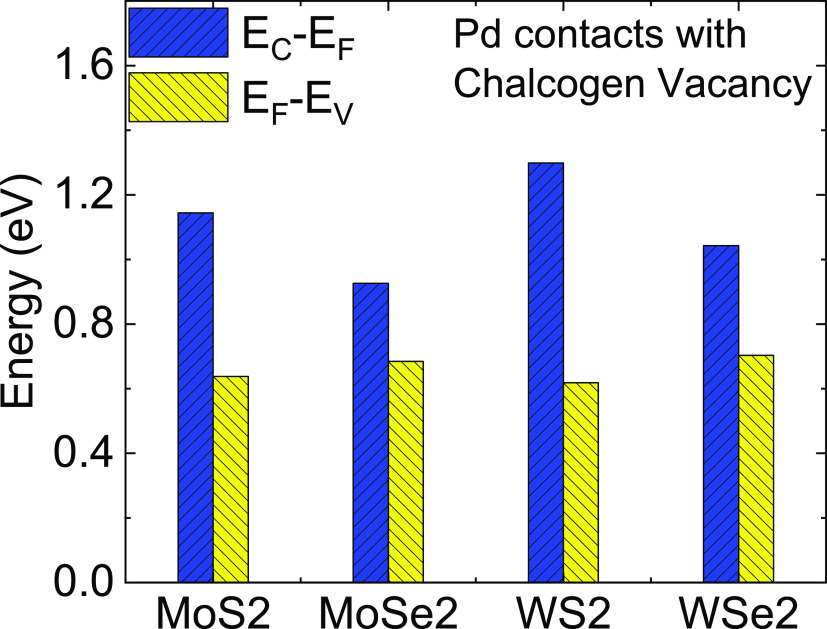
The DOS characteristics (Figure 8) clearly indicate that the Pd–TMD system’s Fermi level shifts from near the conduction band to near the valence band once the chalcogen vacancy is created at the interacting site. The doping effect is significant for all the TMDs, with the most impact on WS2 and the least on MoSe2 (Figure 9).

Figure 8.

Figure 8

Open in a new tab

DOS plot of (a) MoS2–Pd, (b) MoSe2–Pd, (c) WS2–Pd, and WSe2–Pd interfaces with and without vacancy engineering (chalcogen vacancy). The Fermi level is moved from near the CBM to near the VBM due to vacancy engineering in all the interfaces, indicating that vacancy engineering can be an effective technique for the n-type to p-type conversion of the TMD–Pd interface.

Figure 9.

Figure 9

Open in a new tab

Position of Fermi-level comparison of the Pd–TMD system under pristine and chalcogen vacancy conditions.

Role of Chalcogen Interstitial Doping

Like the chalcogen vacancy, chalcogen interstitial doping is also a promising tool to engineer metal–TMD interactions. In interstitial doping, the doped chalcogen atom mingles with metallic atoms (Figure 10). The interaction reduces the bonding distance of some metal–TMD interfaces, as shown in Figure 11.

Figure 10.

Figure 10

Open in a new tab

Reduction in bond distance due to Se interstitial doping at the optimized MoSe2–Au interface. (a) Intrinsic MoSe2–Au system. (b) MoSe2–Au system with one Se interstitial. Au atoms come closer to MoSe2 due to doping. Other optimized metal–TMDs with chalcogen interstitial structures are available in the Supporting Information (Figure S5).

Figure 11.

Figure 11

Open in a new tab

Change in bond distance due to chalcogen interstitial doping at the metal interface with (a) MoS2, (b) MoSe2, (c) WS2, and (d) WSe2.

The figure reflects that the interstitial doping-assisted bond distance reduction method is effective for MoS2 with Cr and Pd, MoSe2 with Au, WS2 with Au, and WSe2 with Cr and Ni. Thus, chalcogen interstitial doping can be a promising method to reduce the contact resistance of some metal–TMD interfaces. Like the chalcogen vacancy, interstitial doping also perturbs the band structure of the system. The doping introduces more mid-gap states near the valence band (Figure 12), which might be useful for MIGS-based contact engineering at the interfaces.

Figure 12.

Figure 12

Open in a new tab

Band structure of the WSe2/Ni system. (a) Pristine condition and (b) Se interstitial doping condition. Band structures of other metal–TMD systems are available in the Supporting Information (Figure S6).

Therefore, the chalcogen vacancy and interstitial doping give a contact resistance engineering technique to reduce the contact resistance. The method not only helps reduce the tunnel barrier by strengthening the contact metal and TMD bonding, but it also provides a knob to change the MIGS at the interface that offers the possibility of the Fermi-level pinning at the desired energy level. Ansh et al.20,21 have demonstrated contact resistance engineering of metal–TMD interfaces using MIGS and tunnel barrier engineering with the help of chalcogen interstitial doping. Their work confirms that the discussed atomic-level orbital overlap understanding and its implications, like tunnel barrier reduction and MIGSs, can be an effective tool to reduce the contact resistance of the metal–TMD interfaces.

Conclusions

In summary, we investigated the atomic-level interaction of metals like Au, Cr, Ni, and Pd with different TMDs like MoS2, MoSe2, WS2, and WSe2. Our study reveals that Au has a weak interaction with all the TMDs. Thus, it stays more than 2 Å away from the TMD surfaces. However, other metals show strong chemistry with TMDs. Due to weak interaction, Au offers very few MIGSs in all the TMDs. On the other hand, metals like Cr, Ni, and Pd are flooded the bandgap region of the TMDs with many MIGSs. During interactions, all the metals offer n-type doping to TMDs. The chalcogen vacancy enhances the interaction of the metals with all the TMDs. The vacancy leaves the unbound orbitals, which bond strongly with the approaching metals. The bonding enhancement reduces the metal–TMD distances that can be used in contact resistance engineering in their bulk counterparts. The chalcogen vacancy and chalcogen interstitial impurity further enhance the number of MIGSs in all the TMDs. Our investigations give a detailed picture of the atomic-level quantum chemistry of metal–TMD interactions, which can be used in the contact resistance reduction of the TMD–metal interfaces.

Computational Details

The DFT computational studies were done using the QuantumATK simulation package.26−28 A 5 × 5 × 1 supercell of all the monolayer TMDs (mTMDs) was taken (Figure 1), and ∼15 Å vacuum space was added on both sides of the mTMD plane to avoid interlayer wave function interaction. Four atoms of the corresponding metal were kept ∼2 Å above the chalcogen atoms of the TMDs before optimization to capture enough insights into the interface chemistry. A periodic boundary condition was applied in the further calculation to replicate bulk mTMD planes. The simulating modules were optimized with 0.01 eV/Å and 0.001 eV/Å3 force and energy cutoffs, respectively. The Perdew–Burke–Ernzerhof form of the generalized gradient approximation functional was used in DFT computation with a 5 × 5 × 1 k point sampling (7 × 7 × 1 for DOS).29 Grimme DFT-D2 vdW correction was taken into account to capture long-range metal–TMD vdW interaction.30

Acknowledgments

The authors would like to thank the NNetRA program of MeitY, DST, and MHRD, Govt. of India, and DRDO and CSIR, for supporting this work.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c07489.

  • Energy-optimized interfaces of TMDs, having one chalcogen vacancy, with different metals; average ED profile comparison perpendicular to the basal plane of TMDs with different metals under pristine and chalcogen vacancy conditions; formation energy per metal atom (Ef) of the optimized metal–vacTMD systems.; band structure of all the TMDs with one chalcogen vacancy (vac-TMDs) and metal combinations along with the vac-TMDs; energy-optimized interfaces of TMDs, having one chalcogen atom at the interstitial site, with different metals; and band structure of all the TMD, with one chalcogen at the interstitial site (int-TMDs), and metal combinations along with the int-TMDs (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao2c07489_si_001.pdf (7.5MB, pdf)

References

  1. Akinwande D.; Huyghebaert C.; Wang C. H.; Serna M. I.; Goossens S.; Li L. J.; Wong H. S. P.; Koppens F. H. L. Graphene and Two-Dimensional Materials for Silicon Technology. Nature 2019, 573, 507–518. Nature Publishing Group September 26 10.1038/s41586-019-1573-9. [DOI] [PubMed] [Google Scholar]
  2. Chhowalla M.; Jena D.; Zhang H. Two-Dimensional Semiconductors for Transistors. Nat. Rev. Mater. 2016, 1, 16052. 10.1038/natrevmats.2016.52. [DOI] [Google Scholar]
  3. Das S.; Sebastian A.; Pop E.; McClellan C. J.; Franklin A. D.; Grasser T.; Knobloch T.; Illarionov Y.; Penumatcha A. v.; Appenzeller J.; Chen Z.; Zhu W.; Asselberghs I.; Li L. J.; Avci U. E.; Bhat N.; Anthopoulos T. D.; Singh R. Transistors Based on Two-Dimensional Materials for Future Integrated Circuits. Nat. Electron. 2021, 4, 786–799. Nature Research November 1 10.1038/s41928-021-00670-1. [DOI] [Google Scholar]
  4. Shrivastava M.; Ramgopal Rao V. A Roadmap for Disruptive Applications and Heterogeneous Integration Using Two-Dimensional Materials: State-of-the-Art and Technological Challenges. Nano Lett. 2021, 21, 6359–6381. American Chemical Society August 11 10.1021/acs.nanolett.1c00729. [DOI] [PubMed] [Google Scholar]
  5. Schulman D. S.; Arnold A. J.; Das S. Contact Engineering for 2D Materials and Devices. Chem. Soc. Rev. 2018, 47, 3037–3058. Royal Society of Chemistry May 7 10.1039/c7cs00828g. [DOI] [PubMed] [Google Scholar]
  6. Liu Y.; Stradins P.; Wei S. H. Van Der Waals Metal-Semiconductor Junction: Weak Fermi Level Pinning Enables Effective Tuning of Schottky Barrier. Sci. Adv. 2016, 2, e1600069 10.1126/sciadv.1600069. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Wang Z.; Xia H.; Wang P.; Zhou X.; Liu C.; Zhang Q.; Wang F.; Huang M.; Chen S.; Wu P.; Chen Y.; Ye J.; Huang S.; Yan H.; Gu L.; Miao J.; Li T.; Chen X.; Lu W.; Zhou P.; Hu W. Controllable Doping in 2D Layered Materials. Adv. Mater. 2021, 33, e2104942 10.1002/adma.202104942. [DOI] [PubMed] [Google Scholar]
  8. Tung R. T. The Physics and Chemistry of the Schottky Barrier Height. Appl. Phys. Rev. 2014, 1, 011304. 10.1063/1.4858400. [DOI] [Google Scholar]
  9. Louie S. G.; Cohen M. L. Electronic Structure of a Metal-Semiconductor Interface*. Phys. Rev. B: Solid State 1976, 13, 2461. 10.1103/physrevb.13.2461. [DOI] [Google Scholar]
  10. Nishimura T.; Kita K.; Toriumi A. Evidence for Strong Fermi-Level Pinning Due to Metal-Induced Gap States at Metal/Germanium Interface. Appl. Phys. Lett. 2007, 91, 123123. 10.1063/1.2789701. [DOI] [Google Scholar]
  11. Kobayashi M.; Kinoshita A.; Saraswat K.; Wong H. S. P.; Nishi Y. Fermi Level Depinning in Metal/Ge Schottky Junction for Metal Source/Drain Ge Metal-Oxide-Semiconductor Field-Effect-Transistor Application. J. Appl. Phys. 2009, 105, 023702. 10.1063/1.3065990. [DOI] [Google Scholar]
  12. Allain A.; Kang J.; Banerjee K.; Kis A. Electrical Contacts to Two-Dimensional Semiconductors. Nat. Mater. 2015, 14, 1195–1205. Nature Publishing Group December 1 10.1038/nmat4452. [DOI] [PubMed] [Google Scholar]
  13. Sotthewes K.; van Bremen R.; Dollekamp E.; Boulogne T.; Nowakowski K.; Kas D.; Zandvliet H. J. W.; Bampoulis P. Universal Fermi-Level Pinning in Transition-Metal Dichalcogenides. J. Phys. Chem. C 2019, 123, 5411–5420. 10.1021/acs.jpcc.8b10971. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Popov I.; Seifert G.; Tománek D. Designing Electrical Contacts toMoS2Monolayers: A Computational Study. Phys. Rev. Lett. 2012, 108, 156802. 10.1103/PhysRevLett.108.156802. [DOI] [PubMed] [Google Scholar]
  15. Kang J.; Liu W.; Sarkar D.; Jena D.; Banerjee K. Computational Study of Metal Contacts to Monolayer Transition-Metal Dichalcogenide Semiconductors. Phys. Rev. X 2014, 4, 031005.American Physical Society 10.1103/PhysRevX.4.031005. [DOI] [Google Scholar]
  16. Huang L.; Tao L.; Gong K.; Li Y.; Dong H.; Wei Z.; Li J. Role of Defects in Enhanced Fermi Level Pinning at Interfaces between Metals and Transition Metal Dichalcogenides. Phys. Rev. B 2017, 96, 205303. 10.1103/PhysRevB.96.205303. [DOI] [Google Scholar]
  17. Kumar J.; Meersha A.; Variar H. B.; Mishra A.; Shrivastava M. Carbon Vacancy Assisted Contact Resistance Engineering in Graphene FETs. IEEE Trans. Electron Devices 2022, 69, 2066–2073. 10.1109/TED.2022.3151033. [DOI] [Google Scholar]
  18. Meersha A.; et al. Record Low Metal—(CVD) Graphene Contact Resistance Atomic Orbital Overlap Engineering. 2016 IEEE International Electron Devices Meeting (IEDM); IEEE, 2016; pp 3–5.
  19. Kumar J.; Meersha A.; Ansh; Shrivastava M.. A First Principle Insight into Defect Assisted Contact Engineering at the Metal-Graphene and Metal-Phosphorene Interfaces. 2019 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD); IEEE, 2019; pp 1–4.
  20. Ansh; Kumar M.; Sheoran J.; Variar G.; Mishra H. B.; Kuruva R.; Meersha H.; Mishra A.; Raghavan A.; Shrivastava S. Chalcogen-Assisted Enhanced Atomic Orbital Interaction at TMD-Metal Interface and Sulfur Passivation for Overall Performance Boost of 2-D TMD FETs. IEEE Trans. Electron Devices 2020, 67, 717–724. 10.1109/TED.2019.2958338. [DOI] [Google Scholar]
  21. Ansh; Kumar J.; Sheoran G.; Mishra R.; Raghavan S.; Shrivastava M. Selective Electron or Hole Conduction in Tungsten Diselenide (WSe2) Field-Effect Transistors by Sulfur-Assisted Metal-Induced Gap State Engineering. IEEE Trans. Electron Devices 2020, 67, 383–388. 10.1109/TED.2019.2956781. [DOI] [Google Scholar]
  22. Shen P. C.; Su C.; Lin Y.; Chou A. S.; Cheng C. C.; Park J. H.; Chiu M. H.; Lu A. Y.; Tang H. L.; Tavakoli M. M.; Pitner G.; Ji X.; Cai Z.; Mao N.; Wang J.; Tung V.; Li J.; Bokor J.; Zettl A.; Wu C. I.; Palacios T.; Li L. J.; Kong J. Ultralow Contact Resistance between Semimetal and Monolayer Semiconductors. Nature 2021, 593, 211–217. 10.1038/s41586-021-03472-9. [DOI] [PubMed] [Google Scholar]
  23. Lin Z.; Carvalho B. R.; Kahn E.; Lv R.; Rao R.; Terrones H.; Pimenta M. A.; Terrones M. Defect Engineering of Two-Dimensional Transition Metal Dichalcogenides. 2D Mater. 2016, 3, 022002.IOP Publishing Ltd April 13 10.1088/2053-1583/3/2/022002. [DOI] [Google Scholar]
  24. Addou R.; McDonnell S.; Barrera D.; Guo Z.; Azcatl A.; Wang J.; Zhu H.; Hinkle C. L.; Quevedo-Lopez M.; Alshareef H. N.; Colombo L.; Hsu J. W. P.; Wallace R. M. Impurities and Electronic Property Variations of Natural MoS2 Crystal Surfaces. ACS Nano 2015, 9, 9124–9133. 10.1021/acsnano.5b03309. [DOI] [PubMed] [Google Scholar]
  25. Kumar J.; Ansh; Kuruva H.; Shrivastava M.. Defect Assisted Metal-TMDs Interface Engineering: A First Principle Insight. 2020 Device Research Conference (DRC); IEEE, 2020; pp 1–2.
  26. Soler J. M.; Artacho E.; Gale J. D.; García A.; Junquera J.; Ordejón P.; Sánchez-Portal D. The Siesta Method for Ab Initio Order-N Materials Simulation. J. Phys.: Condens. Matter 2002, 14, 2745. 10.1088/0953-8984/14/11/302. [DOI] [PubMed] [Google Scholar]
  27. Synopsys . QuantumATK R-2020.09, 2020.
  28. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  29. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
  30. Grimme S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao2c07489_si_001.pdf (7.5MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES