Lyman-Kutcher-Burman normal tissue complication probability modeling for radiation-induced esophagitis in non–small cell lung cancer patients receiving proton radiotherapy

Abstract

Purpose:

To develop and test an Lyman-Kutcher-Burman (LKB) normal tissue complication probability (NTCP) model to predict radiation-induced esophagitis (RE) in non–small cell lung cancer (NSCLC) patients receiving passive-scattering proton therapy (PSPT).

Material and Methods:

We retrospectively reviewed 328 NSCLC patients receiving PSPT at our institution. Esophagitis severity was graded by physicians according to the Common Toxicity Criteria for Adverse Events version 3.0, and the primary endpoint was grade ≥2 RE within 6 months from the first treatment. LKB model parameters (n, m, and TD₅₀) were determined using maximum likelihood estimation. Overall performance of the model was quantified by Nagelkerke’s R² and the scaled Brier score. Discriminative ability was evaluated using the area under the receiver operating curve (AUC), and calibration was assessed with the Hosmer-Lemeshow goodness-of-fit test. Bootstrap internal validation was performed to assess the model uncertainty and generalizability.

Results:

Grade 2–3 RE was observed in 136 (41.5%) patients, and no grade 4–5 RE was reported. The optimal LKB parameters were: n = 0.24, m = 0.51, and TD₅₀ = 44.83 Gy (relative biological effectiveness). The optimism-corrected AUC was 0.783, and the Hosmer-Lemeshow test showed significant agreement between predicted and observed morbidity. Bootstrap validation verified that the model was robust to similar future populations.

Conclusion:

Our LKB NTCP model to predict grade ≥2 RE in NSCLC patients who received PSPT showed good predictive performance and robustness to similar future populations, and a smaller volume effect than the previously observed in photon-treated populations. External validation of the model is warranted.

Introduction

Radiation-induced esophagitis (RE) is a common side effect of definitive radiotherapy for patients with non–small cell lung cancer (NSCLC), potentially lowering quality of life and, in severe cases, resulting in a treatment break. To optimize tumor control and survival, it is crucial to prevent severe RE and thus avoid treatment interruption [1, 2] and enable safe dose escalation. Accurate prediction of RE based on a normal tissue complication probability (NTCP) model can help identify patients at risk, for whom precautions such as dietary guidance or tube feeding can be taken to reduce the complication risk. In addition, the NTCP model may be used by physicians to choose between proton radiotherapy and photon radiotherapy for patients according to the estimated clinical benefits of the different modalities [3, 4].

The Lyman-Kutcher-Burman (LKB) model [5–8] is the most well-known NTCP model and has been implemented in commercial treatment planning systems for plan evaluation [9]. The published parameterizations of the LKB model for RE complications are based on a photon-treated population receiving either three-dimensional conformal radiotherapy (3DCRT) [10, 11] or intensity-modulated radiotherapy (IMRT) [12, 13]. However, an LKB model for predicting RE in patients receiving proton radiotherapy has not been reported.

Compared with photon radiotherapy, proton radiotherapy has the potential to reduce complication risk [14, 15]. Proton beams, with their sharp dose fall-off around the Bragg peak, introduce no exit dose beyond their range, yielding a smaller low-to-intermediate dose region than conventional x-rays do. In recent years, the number of patients given proton radiotherapy has steadily increased [16]. Given the different dose distributions of protons and photons and proton’s potentially elevated relative biological effectiveness at the distal fall-off region, the esophagus dose-response model may differ between the modalities. Therefore, there is an urgent need for an effective NTCP model for plan evaluation and patient selection in proton radiotherapy.

In this study, we developed and evaluated the performance of an LKB NTCP model for predicting RE in NSCLC patients receiving passive-scattering proton therapy (PSPT).

Material and Methods

Patient selection

This retrospective study was approved by the institutional review board at The University of Texas MD Anderson Cancer Center (Houston, TX). We included 328 patients with NSCLC treated with PSPT, either alone or with concomitant chemotherapy, at MD Anderson during April 2006 to February 2012. The median total tumor dose was 74 Gy (relative biological effectiveness (RBE)), ranging from 50 to 82.5 Gy (RBE), and the fractional dose was 1.8–2.5 Gy (RBE).

Treatment

Each patient was immobilized using a T-bar handgrip, wing boards, and a personalized vacuum bag (Vac-Lok, CIVCO Radiotherapy). Before treatment, four-dimensional computed tomography (CT) images were acquired on a GE LightSpeed 16 Slice CT Scanner (GE Healthcare) with 2.5-mm slice spacing. Each four-dimensional CT dataset consisted of 10 three-dimensional CT sets corresponding to 10 equal respiratory phases, along with maximum intensity projection and average intensity projection images. The average intensity projection CT images were used for treatment planning.

The internal gross tumor volume was created using either the combination of gross tumor volume contours on all respiratory phases or the delineation on the maximum intensity projection CT images validated on each respiratory phase. The density of internal gross tumor volume was overridden by assigning the maximum Hounsfield units from the individual respiratory phases [17]. The internal target volume was created by isotropically expanding the internal gross tumor volume by 8 mm, and the planning target volume was defined as a 5-mm isotropic expansion of the internal target volume. All critical organs were delineated on the average intensity projection CT images. PSPT treatment plans were generated using the Eclipse treatment planning system (version 8.9, Varian Medical Systems). A constant RBE of 1.1 was assumed. The treatment plans were delivered by the synchrotron-based PROBEAT proton beam therapy system (Hitachi America, Ltd.).

Follow-up and esophagitis scoring

During the course of treatment, patients were followed up weekly. Patients were then followed up 1 month and then every 3 months for the rest of the first year after treatment completion, every 4–6 months in the following 2 years, and annually thereafter. Esophagitis severity was graded by a physician according to the Common Toxicity Criteria for Adverse Events version 3.0 (Table 1). In grade 1 RE, the patient has image changes, such as the thickening of the esophageal wall, but no clinical symptoms in terms of difficulty in swallowing or pain in swallowing. No medication was indicated. In grade 2, the patient has symptoms of RE, and pain medications are indicated. In grade 3, the patient needs intravenous hydration, feeding tube placement, or admission for the issue of dehydration or weight loss due to RE to maintain nutrition status. The endpoint of the study was grade 2 or higher esophagitis within 6 months from the start of treatment. Dose-volume histograms of the esophagus were extracted from the Eclipse treatment planning system for data analysis.

Table 1.

Common Toxicity Criteria for Adverse Events version 3.0 grading for radiation-induced esophagitis and the number of patients in each group

Grade	Symptoms	Incidence, no. (%)*
1	Asymptomatic, pathologic, radiographic, or endoscopic findings only	31 (9.5)
2	Symptomatic; altered eating/swallowing (e.g., altered dietary habits, oral supplements); intravenous fluids indicated <24 hours	121 (36.9)
3	Symptomatic and severely altered eating/swallowing (e.g., inadequate oral caloric or fluid intake); intravenous fluids, tube feedings, or total parenteral nutrition indicated ≥24 hours	15 (4.6)
4	Life-threatening consequences	0 (0)
5	Death	0 (0)

^*No RE was observed in 161 (49.1%) patients.

LKB NTCP modeling

In the LKB model [5–8], NTCP for an inhomogeneously irradiated critical organ is calculated as follows:

$$\text{NTCP}=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^t{e}^{-\frac{x^2}{2}}dx,$$

where

$$t=\frac{\text{EUD}-T{D}_{50}}{m*T{D}_{50}}$$

and

$$\text{EUD}={\left({\sum }_i{v}_i{D}_i^{\frac{1}{n}}\right)}^n,$$

in which EUD is the generalized equivalent uniform dose [18], ν_i is the relative volume that received a dose of D_i. TD₅₀ represents the dose tolerance of the whole organ and is associated with 50% complication risk; n indicates the volume effect [9]; and m describes the slope of the modeling curve at TD₅₀.

The optimal values of n, m, and TD₅₀ were determined by maximum likelihood estimation. The model that best fit to the complication data yields the maximum value of log likelihood (LL):

$$\text{LL}(\text{n},\text{m},\text{TD}50)={\sum }_{p=1}\text{ln}\left(\text{NTCP}\left(\text{n},\text{m},{\text{TD}}_{50}\right)\right)+{\sum }_{p=0}\text{ln}\left(1-\text{NTCP}\left(\text{n},\text{m},{\text{TD}}_{50}\right)\right)$$

The two terms on the right-hand side of the equation above are summed for patients with grade 2 or higher RE (p = 1) and for those without (p = 0), respectively. The search of the maximum LL over all possible combinations of n, m, and TD₅₀ was approached with the Nelder-Mead simplex algorithm [19] implemented in MATLAB (version R2016b, MathWorks, Inc.). Ninety-five percent confidence intervals (CI) of the optimal fit parameters were determined using the profile likelihood method [20, 21], where nuisance parameters were profiled out by maximum likelihood estimate, and uniform-integrated likelihood method, where nuisance parameters were eliminated by integration [22].

Model validation and performance

As recommended by Steyerberg et al. [23], we performed internal validation using bootstrap resampling to estimate the model performance in similar future populations. One thousand cohorts of 328 patients were drawn with replacement from the original patient data. The LKB model developed using each bootstrap sample was evaluated in both the bootstrap sample and the original sample. The optimism of the model was estimated by the difference between the performance of the bootstrap sample–based model on the bootstrap sample and that on the original sample. In addition, the variation of the optimal parameter fits was assessed using the above bootstrap validation. This non-parametric Monte Carlo simulation made no assumption of the underlying distribution of the parameters. The bias-corrected and accelerated method [24, 25] was used to obtained the non-parametric bootstrap CIs.

We evaluated the performance of the model using the metrics of overall performance, discriminative ability, and calibration [26]. Overall performance was measured by Nagelkerke’s R² and the scaled Brier score. Nagelkerke’s R² quantifies the amount of explained variation of the model, and Brier score calculates the differences between the observed and predicted outcomes. The discriminative ability was assessed using the area under the receiver operating curve (AUC) and the discrimination slope, defined as the absolute difference in the mean predicted NTCP values between patients with complications and those without. For the calibration of the model, Hosmer-Lemeshow test was performed to test the hypothesis that the predictions agree well with the observed outcomes, in which a p value of greater than 0.05 indicates good agreement.

All data analysis was done with self-written code in MATLAB (version R2016b, MathWorks, Inc.).

Results

Of the 328 patients studied, 136 (41.5%) patients experienced grade 2–3 RE (grade 2: 121 patients, grade 3: 15 patients), and 31 (9.5%) patients had grade 1 RE. No grade 4–5 RE was observed, and RE was not observed in 161 (49.1%) patients. Table 2 summarizes patient and treatment characteristics.

Table 2.

Patient and treatment characteristics

Characteristic	Value
Age, median (range)	70 years (33–95 years)
Sex, no. (%)
Male	185 (56.4)
Female	143 (43.6)
Stage, no. (%)
I	59 (18.0)
II	47 (14.3)
III	208 (63.4)
IV	14 (4.3)
Concomitant chemotherapy, no. (%)
Yes	198 (60.4)
No	130 (39.6)
Prescribed dose, median (range)	74 Gy (RBE) (50–82.5 Gy (RBE))

RBE = relative biological effectiveness.

The maximum likelihood estimates of the LKB parameters were: n = 0.24, m = 0.51, and TD₅₀ = 44.83 Gy (RBE). The NTCP curve and the 95% CI region of the model fit corresponding to the optimal parameters for the original sample are plotted in Figure 1 (a). The mean and standard deviation (SD) of the optimal parameter fits obtained for 1000 bootstrap samples were: n = 0.25 (SD = 0.09), m = 0.51 (SD = 0.08), and TD₅₀ = 44.83 Gy (RBE) (SD = 4.84), which are close to the optimal fit to the original sample. The 95% CIs for the parameters obtained using profile likelihood, uniform-integrated likelihood, and non-parametric bootstrap resampling were in good agreement (Table 3).

Figure 1.

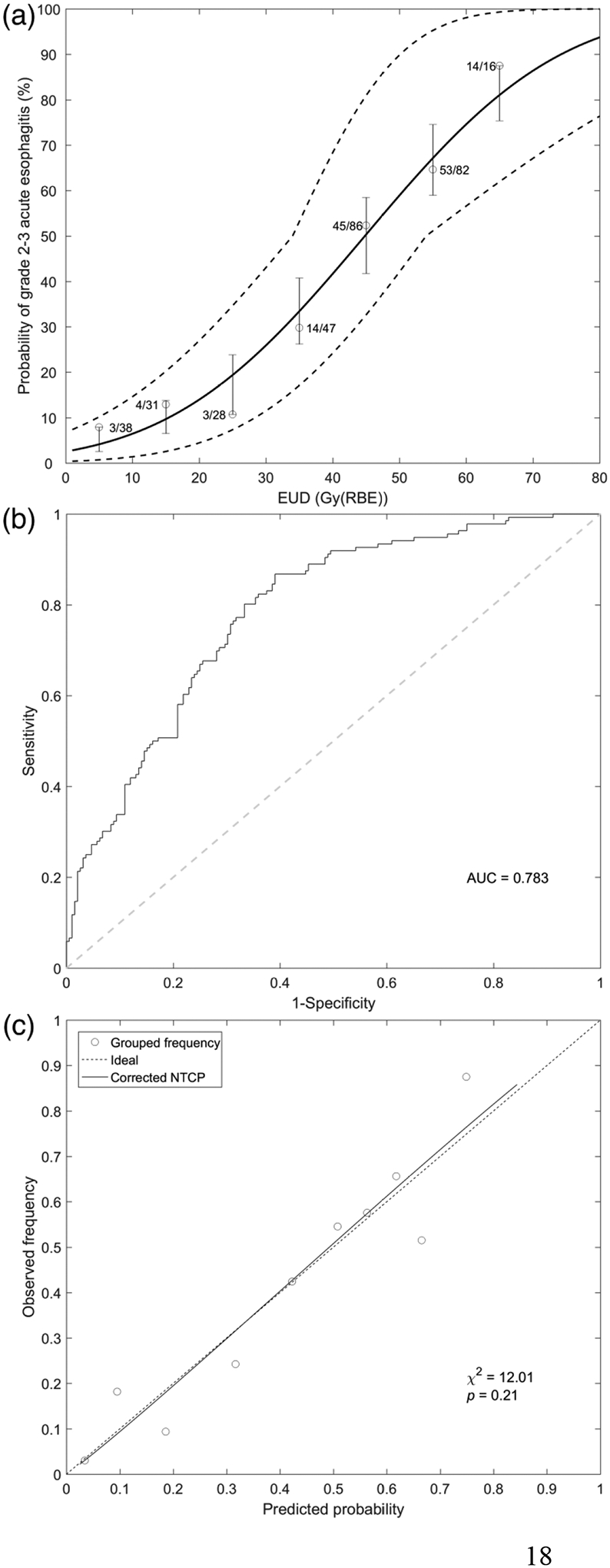
Lyman-Kutcher-Burman modeling results for predicting grade 2 or higher radiation-induced esophagitis (RE) in non–small cell lung cancer patients receiving proton radiotherapy. (a) Normal tissue complication probability (NTCP) curve versus equivalent uniform dose (EUD). Solid curve represents LKB NTCP model with optimal parameters: n = 0.24, m = 0.51, and TD₅₀ = 44.83 Gy (RBE). The dashed curves indicate the 95% confidence region of the NTCP model. Dose range was divided into eight equal parts with a EUD bin of 10 Gy (RBE). For each bin, the circle represents the actual incidence of grade 2 or higher RE. The lower and upper bounds of the bar are minimum and maximum values of the predicted NTCP within each bin. (b) Receiver operating characteristic curve. (c) Calibration plot with Hosmer-Lemeshow test results.

Table 3.

95% confidence intervals of parameters n, m, and TD₅₀ obtained using profile likelihood, uniform-integrated likelihood, and non-parametric bootstrap simulation.

Parameter	Profile likelihood CI	Integrated likelihood CI	Bootstrap CI
n	0.10–0.49	0.10–0.50	0.11–0.45
m	0.37–0.70	0.41–0.73	0.38–0.69
TD50	34.16–55.33	32.42–53.67	35.77–54.40

CI = confidence interval.

After optimism correction, Nagelkerke’s R² and the scaled Brier score of the model (Table 4) were 0.301 and 232, respectively. The optimism-corrected AUC was 0.783 (Figure 1 (b)), and the mean difference in NTCP values between patients with grade ≥2 RE (mean ± SD: 0.555 ± 0.182) and those without (0.318 ± 0.226) was 0.237 (Table 4). The Hosmer-Lemeshow test showed no significant difference (p = 0.21) between the observed outcomes and the predicted risk (Table 4). In the calibration plot (Figure 1 (c)), the trend line of the prediction versus the observation is close to the ideal line.

Table 4.

Bootstrap validation of model performance

Performance measure	Apparent	Bootstrap mean (95% CI)	Validated mean (95% CI)	Optimism mean (95% CI)	Optimism-corrected mean (95% CI)
Overall
Nagelkerke’s R2	0.315	0.318 (0.210–0.427)	0.304 (0.274–0.334)	0.014 (−0.096–0.124)	0.301 (0.191–0.411)
Scaled Brier score	0.242	0.245 (0.161–0.329)	0.235 (0.221–0.250)	0.010 (−0.071–0.091)	0.232 (0.150–0.313)
Discrimination
AUC	0.785	0.787 (0.737–0.836)	0.785 (0.777–0.792)	0.002 (−0.047–0.052)	0.783 (0.733–0.832)
Discrimination slope	0.237	0.242 (0.164–0.321)	0.238 (0.199–0.277)	0.004 (−0.040–0.048)	0.233 (0.189–0.277)
Calibration
Hosmer-Lemeshow test	χ2 = 12.01 (p = 0.21)

AUC = area under the receiver operator curve; CI = confidence interval.

Discussion

In this study, we developed and internally validated an LKB NTCP model to predict the incidence of grade 2 or higher RE in NSCLC patients who received PSPT. The model showed good discriminative ability and significant agreement between the predicted risk and observed outcomes. Bootstrap validation indicated the robustness of the model to similar future populations. This PSPT-based predictive model for RE provides additional guidelines for future treatment planning and plan evaluation in clinical practice. To the best of our knowledge, this is the first LKB NTCP model for RE after proton radiotherapy ever reported.

We found that the optimal n value of 0.24 indicates a relatively small volume effect [9] compared with previously reported n values in IMRT-treated populations, ranging from 0.69 to 1.04 [12, 13, 27]. A low value of n indicates the dependence of complication risk on a high dose exposure. This dependence was in part supported by the univariable logistic regression analysis for the dose-volume histogram parameters of the esophagus, which showed a significant increase in grade 2 or higher RE with all V10-V75 parameters, D_mean, and D_max (Table S1). However, in a study by Wijsman et al., the regression coefficients of V70 and D_max were not statistically significant [13]. Although PSPT significantly reduced the low-dose irradiated volume, PSPT was less conformal in the high-dose region than IMRT. In other words, PSPT may increase the high-dose volume in the normal tissues adjacent to the target, compared with IMRT. Therefore, the similarity between the incidence of RE in PSPT and that in IMRT may come from the decreased toxicity from low-dose irradiation and increased toxicity from high-dose irradiation for PSPT.

Previous studies suggested that photon-based NTCP models cannot be straightforwardly transferred to the proton cohort [28]. The LKB model parameter sets developed for 3DCRT [10] and IMRT [12] showed worse performance than our proton-based model (Figure S1). Although the two photon-based models yielded similar AUC values of 0.777 (3DCRT model) and 0.768 (IMRT model), they underestimated the clinically observed toxicity rate. The Hosmer-Lemeshow tests for these models both showed significant results (p < 0.001 for each), indicating poor agreement between the predicted risk and observed outcomes. Moreover, the differences in the Akaike information criterion values (ΔAIC) between the photon-based models and our proton-based model were greater than 10. According to Burnham and Anderson [29], a model with ΔAIC smaller than 2 has substantial support while a model with ΔAIC greater than 10 has essentially no support. Therefore, the photon-based LKB models could not be accepted as suboptimal models for the current data. Following the closed testing procedure suggested by Vergouwe et al. [30], we found that replacing only the TD₅₀ parameter with that in the IMRT-based model could yield a ΔAIC value smaller than 2 (Table S2). Potential explanations for the discrepancy between the photon-based model and the proton-treated patient data could be the differences in patient characteristics, planning and treatment techniques, or toxicity grading; inaccuracy of the models due to statistical limitations; or other uncertainties. Meanwhile, patient selection for proton therapy based on NTCP values is being investigated owing to the limited outcomes of clinical trials and treatment availability [3, 4]. The accuracy of such a model-based patient selection method is affected by the uncertainty of the NTCP model [31]. Our results strengthen the idea that the NTCP model should be independently validated before clinical implementation.

The benefits of the LKB model include the intuitive interpretation of the parameters, in which we could obtain information relating to an organ’s functional architecture, dose-response sensitivity, and dose tolerance level. However, the model did not take into account potentially significant clinical factors. Studies are proposed to generalize the LKB model to account for clinical factors by introducing a dose-modifying factor [32, 33]. For the current patient data, the LKB model showed a slightly lower AUC value than a multivariable logistic regression model (Table S3 and S4). With regard to clinical implementation, the LKB model would be preferred, as it has been configured in the clinical treatment planning system and has similar performance to that of the more complicated model. The lower optimism in the LKB model may indicate that with fewer parameters, model uncertainties would have less impact on selection accuracy for the LKB model than for the multivariable logistic regression model [31]. In addition to the model uncertainty, uncertainty of dosimetric data resulting from variations of planned dose from the treated dose may reduce the overall accuracy of the model.

A limitation of the study is that the model was developed within a relatively homogeneous patient population treated in a single institution. External validation of the findings in different treatment centers is necessary. Also, the enhanced biological effectiveness at the distal end of the proton beam may affect the complication risk, which should be explored in future studies.

In conclusion, we derived optimal parameters for the LKB NTCP model in predicting grade ≥2 RE in NSCLC patients who received PSPT, and the model shows a small volume effect along with good predictive performance and robustness to similar future populations. Investigation of the external validity of the parameters is warranted.

Highlights.

1. A cohort of 328 non–small cell lung cancer patients receiving passive-scattering proton therapy were investigated.

2. Optimal parameter fits of the Lyman-Kutcher-Burman normal tissue complication probability model for proton-treated cohort showed smaller volume effect than the previously observed in photon-treated populations.

3. The model showed good predictive performance and robustness to the similar future populations.

Abbreviations

LKB

Lyman-Kutcher-Burman

NTCP

normal tissue complication probability

RE

radiation-induced esophagitis

PSPT

passive-scattering proton therapy

EUD

equivalent uniform dose