Bayesian Design of Superiority Trials: Methods and Applications

Abstract

In this paper, we lay out the basic elements of Bayesian sample size determination (SSD) for the Bayesian design of a two-arm superiority clinical trial. We develop a flowchart of the Bayesian SSD that highlights the critical components of a Bayesian design and provides a practically useful roadmap for designing a Bayesian clinical trial in real world applications. We empirically examine the amount of borrowing, the choice of noninformative priors, and the impact of model misspecification on the Bayesian type I error and power. A formal and statistically rigorous formulation of conditional borrowing within the decision rule framework is developed. Moreover, by extending the partial borrowing power priors, a new borrowing-by-parts power prior for incorporating historical data is proposed. Computational algorithms are also developed to calculate the Bayesian type I error and power. Extensive simulation studies are carried out to explore the operating characteristics of the proposed Bayesian design of a superiority trial.

1. Introduction

Complex Innovative Trial Design (CID) Pilot Meeting Program was initiated by the U.S. Food and Drug Administration (FDA) in 2018 to support the goal of facilitating and advancing the use of complex adaptive, Bayesian, and other novel clinical trial designs (U.S. Food and Drug Administration, 2018). The first study ever selected by the FDA for the CID Pilot Meeting Program is the DYSTANCE 51 clinical trial sponsored by Wave Life Sciences, which is a global Phase 2/3, multicenter, randomized, double-blind, placebo-controlled clinical trial that evaluates the efficacy and safety of suvodirsen in ambulatory boys who are between 5 and 12 years of age (inclusive) with a genetically confirmed diagnosis of Duchenne muscular dystrophy (DMD) amenable to exon 51 skipping (Lake et al., 2021). DMD is a rapidly progressive form of muscular dystrophy that occurs primarily in males and manifests prior to the age of six years, affecting approximately 1 in 3,600 to 9,300 male births worldwide (Mah et al., 2014). From the experience with the CID Pilot Meeting Program shared by Wave Life Sciences, the DYSTANCE 51 clinical trial incorporates the capability to augment the placebo arm with historical data using Bayesian methods (Lake et al., 2021). Natural history studies can be used to support the development of safe and effective drugs and biological products for rare diseases. There has been a joint effort from the DMD communities and worldwide regulatory agencies to access the appropriateness of natural history data to supplement clinical development programs. The suitability in borrowing historical data of DMD has also been supported by studies (Goemans et al., 2020).

The literature on Bayesian sample size determination (SSD) has been growing recently due to recent advances in Bayesian computation and Markov chain Monte Carlo sampling. Joseph et al. (1995); Lindley (1997); Rubin and Stern (1998); Katsis and Toman (1999); and Inoue et al. (2005) are the Bayesian SSD articles cited in the FDA guidance for the use of Bayesian statistics in medical device clinical trials (U.S. Food and Drug Administration, 2010). The early literature on Bayesian SSD includes Rahme and Joseph (1998); Simon (1999); Wang and Gelfand (2002); Spiegelhalter et al. (2004); De Santis (2004, 2007); M’Lan et al. (2006); M’lan et al. (2008); Lee and Liu (2008); and Reyes and Ghosh (2013). Campbell (2011) and Berry et al. (2010) provided a list of Bayesian papers up to 2011. Gamalo-Siebers et al. (2016) gave an excellent review of Bayesian methods for the design and analysis of non-inferiority trials. Chen et al. (2011) developed a new Bayesian design methodology with a focus on controlling the type I error and power for non-inferiority trials. Chen et al. (2014) extended the methodology of Chen et al. (2011) to the Bayesian design of superiority clinical trials for recurrent events data. Li et al. (2015) developed the Bayesian design of non-inferiority clinical trials with co-primary endpoints and multiple dose comparison, and Li et al. (2018) proposed a Bayesian design via Bayes Factor. Bayesian methods for incorporating historical data include the power prior (Ibrahim and Chen, 2000; Ibrahim et al., 2015), the hierarchical prior (Chen et al., 2011), the commensurate prior (Hobbs et al., 2011, 2012), the meta-analytic-predictive (MAP) prior (Neuenschwander et al., 2010), the robust MAP prior (Schmidli et al., 2014), the covariate-adjusted hierarchical model-based prior (Han et al., 2017), and their respective variations. Recent review papers of these methods include Schmidli et al. (2020); Hall et al. (2021); Ghadessi et al. (2020); and van Rosmalen et al. (2018).

Motivated by the DYSTANCE 51 clinical trial, we explore different aspects in borrowing historical data within the Bayesian framework. Using the DMD natural history aggregate data, we develop a formal formulation of conditional borrowing of Allocco et al. (2010) via the decision rule. By extending the partial borrowing power priors (Ibrahim et al., 2012; Chen et al., 2014; Ibrahim et al., 2015), we propose a new borrowing-by-parts power prior for incorporating historical data. In this paper, we also address several critical issues in Bayesian SSD, namely, the amount of borrowing from the historical data, the choice of noninformative priors, and the impact of model misspecification on the Bayesian type I error and power.

The remaining part of the manuscript is organized as follows. In Section 2, we present the critical elements and necessary steps including the computational algorithm of a Bayesian design of a superiority trial and develop a flowchart of Bayesian SSD. In Section 3, we analytically examine the properties of the Bayesian type I error and the power when the variances are known and empirically investigate the choice of noninformative priors and the impact of model misspecification on the Bayesian type I error and power. Section 4 presents a comprehensive treatment of leveraging historical data in Bayesian SSD. In this section, we first introduce the DMD natural history aggregate data, then present two commonly used priors, namely, the power prior and the robust mixture prior, to leverage the historical data, and further investigate the impact of the amount of borrowing on the Bayesian type I error and power. In this very same section, the formal and statistically rigorous formulations of conditional borrowing and the borrowing-by-parts power prior are developed, and extensive simulation studies are conducted to examine the empirical performance of the proposed methodology. We conclude the paper with a brief discussion in Section 5.

2. Bayesian Design of a Superiority Trial

We consider designing a randomized, double-blind, placebo-controlled clinical trial to evaluate the superiority of a drug candidate over placebo with a continuous primary endpoint. Given the large amount of historical data available, we also consider borrowing the historical data to augment the placebo control in the clinical trial design. Let ${\mathit{y}}_t={\left(y_{t1},y_{t2},\dots ,y_{t{n}_t}\right)}^{\prime }$ and ${\mathit{y}}_c={\left(y_{c1},y_{c2},\dots ,y_{c{n}_c}\right)}^{\prime }$ be the primary endpoint data of test drug and placebo control, with sample sizes n_t and n_c, respectively. We assume ${\mathit{y}}_t$ and ${\mathit{y}}_c$ are independent, $y_{ti}\stackrel{i.i.d.}{\sim }N\left({\mu }_t,{\sigma }_t^2\right)$, and $y_{ci}\stackrel{i.i.d.}{\sim }N\left({\mu }_c,{\sigma }_c^2\right)$. The parameter of interest is the expectation of difference in the effects of the test drug and the placebo control, namely, $\delta ={\mu }_t-{\mu }_c$. The hypotheses of the superiority trial are $H_0:\delta \le 0$ versus $H_1:\delta >0$, equivalently, $H_0:{\mu }_t\le {\mu }_c$ versus $H_1:{\mu }_t>{\mu }_c$.

Let $\mathit{\theta }={\left({\mu }_c,{\mu }_t,{\sigma }_c^2,{\sigma }_t^2\right)}^{\prime }$. We also consider two special cases: (i) $\mathit{\theta }={\left({\mu }_c,{\mu }_t\right)}^{\prime }$ when the variances are known and (ii) $\mathit{\theta }={\left({\mu }_c,{\mu }_t,{\sigma }^2\right)}^{\prime }$ when the variances are equal but unknown, where ${\sigma }_t^2={\sigma }_c^2={\sigma }^2$. Let ${\mathit{y}}^{(n)}={\left({\mathit{y}}_t^{\prime },{\mathit{y}}_c^{\prime }\right)}^{\prime }$ and $n=n_t+n_c$. The joint distribution of ${\mathit{y}}^{(n)}$ and θ is written as

$$f\left({\mathit{y}}^{(n)}\mid \mathit{\theta }\right)\pi (\mathit{\theta }),$$

where $f\left({\mathit{y}}^{(n)}\mid \mathit{\theta }\right)$ is the conditional distribution of y⁽ⁿ⁾ given θ, which is the product of the normal densities corresponding to $N\left({\mu }_t,{\sigma }_t^2\right)$ and $N\left({\mu }_c,{\sigma }_c^2\right)$, respectively, and π (θ) denotes a prior distribution. Denote the fitting prior as ${\pi }^{(f)}(\mathit{\theta })$ and the sampling prior as ${\pi }^{(s)}(\mathit{\theta })$, where the fitting prior is used to fit the model and the sampling prior is used to generate the data (Wang and Gelfand, 2002). Then, the posterior is given by

$$\pi \left(\mathit{\theta }\mid {\mathit{y}}^{(n)},{\pi }^{(f)}\right)\propto f\left({\mathit{y}}^{(n)}\mid \mathit{\theta }\right){\pi }^{(f)}(\mathit{\theta }).$$ (2.1)

Let the null parameter space ${\Theta }_0=\left\{\mathit{\theta }:{\mu }_t\le {\mu }_c,{\sigma }_t^2>0,{\sigma }_c^2>0\right\}$ corresponding to the null hypothesis and the alternative parameter space ${\Theta }_1=\left\{\mathit{\theta }:{\mu }_t>{\mu }_c,{\sigma }_t^2>0,{\sigma }_c^2>0\right\}$ corresponding to the alternative hypothesis. The sampling priors ${\pi }_0^{\left(s\right)}(\mathit{\theta })$ and ${\pi }_1^{(s)}(\mathit{\theta })$, which are used to generate the data, are defined on ${\Theta }_0$ and ${\Theta }_1$ such that ${\int }_{{\Theta }_{\ell }}{\pi }_{\ell }^{\left(s\right)}\left(\mathit{\theta }\right)d\mathit{\theta }=1$ for $\ell =0,1$.

Let $T\left({\mathit{y}}^{(n)}\right)$ be a test statistic. We define a decision rule based on $T\left({\mathit{y}}^{(n)}\right)$ to reject H₀ as

$$\psi \left({\mathit{y}}^{(n)}\right)=\{\begin{array}{ccc}1,& \text{if}& T\left({\mathit{y}}^{(n)}\right)\ge T_0,\\ 0,& \text{if}& T\left({\mathit{y}}^{(n)}\right)<T_0,\end{array}$$ (2.2)

where T₀ is a critical value, which only depends on the study design, not on the data ${\mathit{y}}^{(n)}$. We define the Bayesian power function as

$${\beta }_s^{(n)}=E_s\left[\psi \left({\mathit{y}}^{(n)}\right)\mid {\pi }^{(s)}\right],$$ (2.3)

where the expectation is taken with respect to the marginal distribution of y⁽ⁿ⁾ under the sampling prior ${\pi }^{(s)}(\mathit{\theta })$. Based on the approach by (Chen et al., 2011), we take

$$T\left({\mathit{y}}^{(n)}\right)=P\left(\delta >0\mid {\mathit{y}}^{(n)},{\pi }^{(f)}\right),$$ (2.4)

where the probability is computed with respect to the posterior distribution given the data ${\mathit{y}}^{(n)}$ and the fitting prior ${\pi }^{(f)}(\mathit{\theta })$. Let $T_0=\gamma$ be a Bayesian credible level, where 0 < γ < 1. Then the Bayesian power function in (2.3) reduces to

$${\beta }_s^{(n)}=E_{{\pi }^{(s)}}\left[1\left\{P\left(\delta >0\mid {\mathit{y}}^{(n)},{\pi }^{(f)}\right)\ge \gamma \right\}\right],$$ (2.5)

where the indicator function $1\left\{A\right\}$ takes a value of “1” if A is true and “0” otherwise.

The analytical evaluation of (2.3) or (2.5) is often not available. The following computational algorithm can be used for ${\beta }_s^{(n)}$:

Step 0. Set n_t, n_c, γ, and N (the number of simulated datasets);

Step 1. Generate $\mathit{\theta }\sim {\pi }^{(s)}(\mathit{\theta })$;

Step 2. Generate ${\mathit{y}}^{(n)}\sim f\left({\mathit{y}}^{(n)}\mid \mathit{\theta }\right)$;

Step 3. Calculate $T\left({\mathit{y}}^{(n)}\right)=P\left(\delta >0\mid {\mathit{y}}^{(n)},{\pi }^{(f)}\right)$;

Step 4. Check whether $T\left({\mathit{y}}^{(n)}\right)\ge \gamma$ or not;

Step 5. Repeat Steps 1-4 N times;

Step 6. Compute the proportion of $\left\{T\left({\mathit{y}}^{(n)}\right)\ge \gamma \right\}$ in these N runs, which gives an estimate of ${\beta }_s^{(n)}$ in (2.3) or (2.5).

The Bayesian type I error ${\beta }_{s0}^{(n)}$ is ${\beta }_s^{(n)}$ with ${\pi }^{(s)}={\pi }_0^{(s)}(\mathit{\theta })$ in (2.5) while the Bayesian power ${\beta }_{s1}^{(n)}$ is ${\beta }_s^{(n)}$ with ${\pi }^{(s)}={\pi }_1^{(s)}(\mathit{\theta })$. The maximum Bayesian type I error is $\underset{{\pi }_0^{(s)}}{\sup }{\beta }_{s0}^{(n)}$. For given ${\alpha }_0>0$ and ${\alpha }_1>0$, we compute $n_{{\alpha }_0}=\min \left\{n:{\beta }_{s0}^{(n)}\le {\alpha }_0\right\}$ and $n_{{\alpha }_1}=\min \left\{n:{\beta }_{s1}^{(n)}\ge 1-{\alpha }_1\right\}$. The Bayesian sample size is then given by $n_B=\max \left\{n_{{\alpha }_0},n_{{\alpha }_1}\right\}$. Common choices of α₀ and α₁ are ${\alpha }_0=0.025$ and ${\alpha }_1=0.20$. With the Bayesian sample size of n_B, the type I error rate is intended to be less than or equal to 0.025 and the power is intended to be at least 0.80.

We summarize the above Bayesian SSD process in Figure 1. Every Bayesian SSD starts with the trial specification, which primarily consists of the type of trial (superiority, or non-inferiority, or equivalence) based on the objective of a study, the number of treatment arms, and the sample size allocation in each arm. The next step of Bayesian SSD shown in Figure 1 includes the specification of a statistical model for the current data, the derivation of the corresponding likelihood, and the mathematical formulation of scientific hypotheses according to the chosen model. According to (2.1), the next step in the flowchart is to specify a fitting prior and then to derive the posterior. One of the key components in Bayesian SSD is to construct a test statistic $T\left({\mathit{y}}^{(n)}\right)$ in (2.2), which leads to the formulation of a decision rule. The key design quantity, i.e., the Bayesian power function ${\beta }_s^{(n)}$ in (2.3), can be evaluated either analytically or numerically via a Monte Carlo method, under a given sampling prior ${\pi }_{\ell }^{(s)}(\mathit{\theta })$, which eventually leads to the final determination of Bayesian sample size. One additional component in Figure 1 is the historical data when available, which can be incorporated in the fitting priors via the decision rule. The inclusion of the historical data typically leads to a reduction of the Bayesian sample size while at the same time, it may increase the type I error. The technical details and potential issues in using a noninformative fitting prior or an informative prior by leveraging historical data are discussed in details in the next two sections.

Fig. 1.

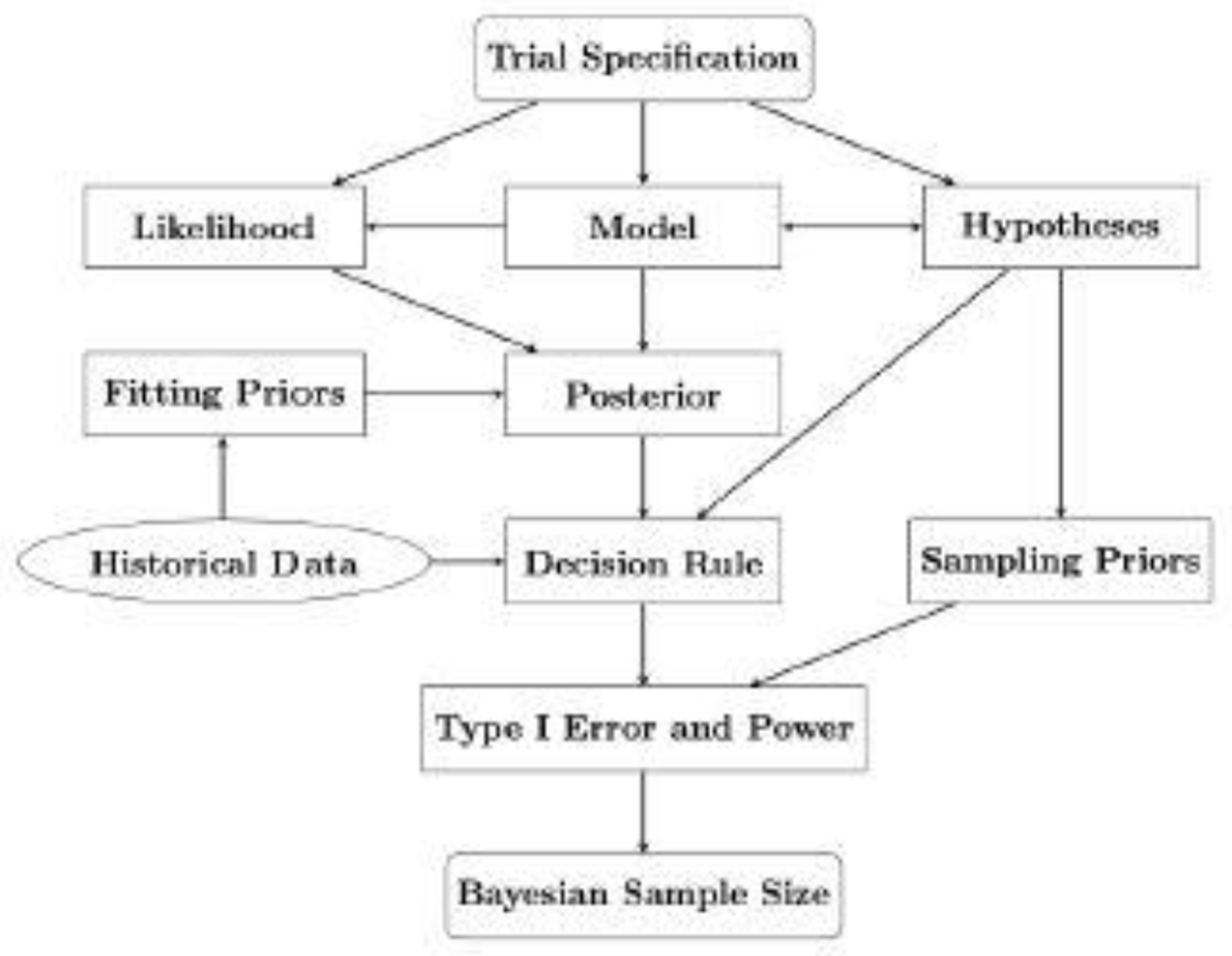
Flowchart of Bayesian SSD.

3. Bayesian SSD with Noninformative Priors

3.1. Theoretical Properties of the Bayesian Power Function with Known Variances

In this subsection, we assume the variances, i.e., ${\sigma }_t^2$ and ${\sigma }_c^2$ are known. Under this assumption, we have $\mathit{\theta }={\left({\mu }_c,{\mu }_t\right)}^{\prime }$. The null parameter space is ${\Theta }_0=\left\{\mathit{\theta }:{\mu }_t\le {\mu }_c\right\}$ and the alternative parameter space is ${\Theta }_1=\left\{\mathit{\theta }:{\mu }_t>{\mu }_c\right\}$. We assume a noninformative uniform prior for the fitting prior, namely, ${\pi }^{(f)}(\mathit{\theta })\propto 1$. Then, the joint distribution of ${\mathit{y}}^{(n)}$ is given by

$$f\left({\mathit{y}}^{(n)}\mid \mathit{\theta }\right)=\prod _{i=1}^{n_t}\frac{1}{\sqrt{2\pi }{\sigma }_t}\exp \{-\frac{{\left(y_{ti}-{\mu }_t\right)}^2}{2{\sigma }_t^2}\}\prod _{j=1}^{n_c}\frac{1}{\sqrt{2\pi }{\sigma }_c}\exp \{-\frac{{\left(y_{cj}-{\mu }_c\right)}^2}{2{\sigma }_c^2}\}.$$

From (2.1), the posterior distribution takes the form

$$\pi \left(\mathit{\theta }\mid {\mathit{y}}^{(n)},{\pi }^{(f)}\right)\propto f\left({\mathit{y}}^{(n)}\mid \mathit{\theta }\right){\pi }^{(f)}(\mathit{\theta })\propto \exp \{-\frac{{\left({\mu }_c-{\overline{y}}_c\right)}^2}{2{\sigma }_c^2/n_c}\}\exp \{-\frac{{\left({\mu }_t-{\overline{y}}_t\right)}^2}{2{\sigma }_t^2/n_t}\},$$

where ${\overline{y}}_c=\frac{1}{n_c}\sum _{i=1}^{n_c}{y}_{ci}$ and ${\overline{y}}_t=\frac{1}{n_t}\sum _{j=1}^{n_t}{y}_{tj}$. The test statistic $T\left({\mathit{y}}^{(n)}\right)$ in (2.4) is expressed as

$$T\left({\mathit{y}}^{(n)}\right)=P\left(\delta >0\mid {\mathit{y}}^{(n)},{\pi }^{(f)}\right)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{{\mu }_t}\pi \left(\mathit{\theta }\mid {\mathit{y}}^{(n)},{\pi }^{(f)}\right)d{\mu }_{c}d{\mu }_t=\Phi (\frac{{\overline{y}}_t-{\overline{y}}_c}{\sqrt{{\sigma }_c^2/n_c+{\sigma }_t^2/n_t}}),$$

where Φ is the standard normal N(0, 1) cumulative distribution function (cdf). The decision rule in (2.2) is to reject H₀ if

$$\Phi (\frac{{\overline{y}}_t-{\overline{y}}_c}{\sqrt{{\sigma }_c^2/n_c+{\sigma }_t^2/n_t}})\ge \gamma .$$ (3.1)

Taking ${\Phi }^{-1}$, which is the inverse function of Φ, from both sides of (3.1) gives

$${\overline{y}}_t-{\overline{y}}_c\ge Z_{\gamma }\sqrt{{\sigma }_c^2/n_c+{\sigma }_t^2/n_t},$$ (3.2)

where $Z_{\gamma }={\Phi }^{-1}(\gamma )$. Using (3.2), the critical function in (2.2) reduces to

$$\psi \left({\mathit{y}}^{(n)}\right)=\{\begin{array}{cc}1,& \text{if}{\overline{y}}_t-{\overline{y}}_c\ge Z_{\gamma }\sqrt{{\sigma }_c^2/n_c+{\sigma }_t^2/n_t},\\ 0,& \text{otherwise}.\hfill \end{array}$$ (3.3)

Assume the sampling prior ${\pi }^{(s)}(\mathit{\theta })={\pi }^{(s)}\left({\mu }_c\right){\pi }^{(s)}\left({\mu }_t\right)$ such that ${\int }_{-\infty }^{\infty }{\pi }^{(s)}\left({\mu }_c\right)d{\mu }_c=1$ and ${\int }_{-\infty }^{\infty }{\pi }^{(s)}\left({\mu }_t\right)d{\mu }_t=1$. Since ${\overline{y}}_t-{\overline{y}}_c\mid {\mu }_c,{\mu }_t\sim N\left({\mu }_t-{\mu }_c,{\sigma }_c^2/n_c+{\sigma }_t^2/n_t\right)$, using (3.3), the Bayesian power function (2.5) then becomes

$$\begin{gathered} {\beta }_s^{(n)}=E_{{\pi }^{(s)}}[\psi ({\mathit{y}}^{(n)})]=E_{{\pi }^{(s)}}[\Phi (\frac{{\mu }_t-{\mu }_c}{\sqrt{{\sigma }_c^2/n_c+{\sigma }_t^2/n_t}}-Z_{\gamma })] \\ ={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\pi }^{(s)}\left({\mu }_c\right){\pi }^{(s)}\left({\mu }_t\right)\times \Phi (\frac{{\mu }_t-{\mu }_c}{\sqrt{{\sigma }_c^2/n_c+{\sigma }_t^2/n_t}}-Z_{\gamma })d{\mu }_{c}d{\mu }_t. \end{gathered}$$ (3.4)

Taking ${\pi }^{(s)}(\mathit{\theta })={\pi }_0^{(s)}(\mathit{\theta })$ such that ${\int }_{-\infty }^{\infty }{\int }_{{\mu }_t}^{\infty }{\pi }^{(s)}\left({\mu }_c\right){\pi }^{(s)}\left({\mu }_t\right)d{\mu }_{c}d{\mu }_t=1$, using (3.4), the Bayesian type I error is given by

$${\beta }_{s0}^{(n)}={\int }_{-\infty }^{\infty }{\int }_{{\mu }_t}^{\infty }{\pi }^{(s)}\left({\mu }_c\right){\pi }^{(s)}\left({\mu }_t\right)\times \Phi (\frac{{\mu }_t-{\mu }_c}{\sqrt{{\sigma }_c^2/n_c+{\sigma }_t^2/n_t}}-Z_{\gamma })d{\mu }_{c}d{\mu }_t.$$

It is easy to show that

$${\beta }_{s0}^{(n)}\le \Phi \left(-Z_{\gamma }\right)=1-\Phi \left(Z_{\gamma }\right)=1-\gamma .$$ (3.5)

It is easy to see that the maximum type I error is attained at the boundary $\delta ={\mu }_t-{\mu }_c=0$ by specifying the sampling prior ${\pi }_0^{(s)}(\mathit{\theta })$ as a degenerate distribution at δ = 0, denoted by ${\Delta }_{\{\delta =0\}}$, i.e., $P(\delta =0)=1$. Furthermore, we take a point mass sampling prior

$${\pi }_1^{(s)}={\Delta }_{\left\{\delta ={\delta }_1\right\}},$$ (3.6)

which is a degenerate distribution at δ = δ₁, where δ₁ > 0. Using (3.4) and (3.6), the Bayesian power is given by

$${\beta }_{s1}^{(n)}=\Phi \left(\frac{{\delta }_1}{\sqrt{{\sigma }_c^2/n_c+{\sigma }_t^2/n_t}}-Z_{\gamma }\right).$$ (3.7)

We have the following results for the Bayesian type I error and power.

Result 1. The maximum Bayesian type I error is 1 − γ and is attained at the boundary of the parameter space corresponding to the null hypothesis.

Result 2. Using the point mass sampling prior in (3.6), for any choice of δ ∈ Θ₁ , the Bayesian power is equal to the frequentist power given by

$$\Phi (\frac{{\delta }_1}{\sqrt{{\sigma }_c^2/n_c+{\sigma }_t^2/n_t}}-Z_{1-{\alpha }_0}),$$ (3.8)

where 0 < α₀ < 1 is the type I error.

Suppose we specify the maximum type I error at α₀ = 0.025 , the power at 1 − α₁ = 0.8, and the randomization ratio with n_t : n_c = 2 : 1. Assume that ${\sigma }_t^2={\sigma }_c^2=25$, and δ₁ = 3.5. Solving

$${\beta }_{s1}^{(n)}=\Phi \left(\frac{{\delta }_1}{\sqrt{{\sigma }_c^2/n_c+{\sigma }_t^2/n_t}}-Z_{\gamma }\right)>1-{\alpha }_1$$

gives $n_c>3\times 5^2\times {\left(Z_{\gamma }+Z_{1-{\alpha }_1}\right)}^2/\left(2\times {\delta }_1^2\right)=24.03$. Thus, the required sample sizes are n_t = 50 and n_c = 25.

3.2. Choice of Noninformative Priors and Model Misspecification

Under the unequal variances assumption, $\mathit{\theta }={\left({\mu }_c,{\mu }_t,{\sigma }_c^2,{\sigma }_t^2\right)}^{\prime }$, while under the equal variances assumption, $\mathit{\theta }={\left({\mu }_c,{\mu }_t,{\sigma }^2\right)}^{\prime }$ with ${\sigma }^2={\sigma }_c^2={\sigma }_t^2$. For each case, the fitting prior is specified as ${\pi }^{(f)}(\mathit{\theta })\propto {\left({\sigma }_c^2{\sigma }_t^2\right)}^{-m}$ and ${\pi }^{(f)}(\mathit{\theta })\propto {\left({\sigma }^2\right)}^{-m}$, respectively, where m = 0 corresponds to a uniform prior, m = 1 corresponds to a reference prior, and m = 3/2 corresponds to a Jeffreys’s prior. The detailed derivation of the Bayesian power function in (2.5) under each of these priors is given in Appendix A. We set n_t = 50, n_c = 25, ${\mu }_c=0,\gamma =0.975$ and N = 10⁶ in the computational algorithm in Section 2 for calculating ${\beta }_s^{(n)}$ in the following calculations.

The Bayesian type I errors and powers with three noninformative fitting priors are given in Tables 1 and 2 under the models assuming unequal and equal variances, respectively. Several interesting observations are seen from these two tables. First, we see from the right block labeled with “Assuming Equal Variances” of Table 1 that (i) when ${\sigma }_c^2>{\sigma }_t^2$ (or ${\sigma }_c^2<{\sigma }_t^2$), the type I errors are 0.0281, 0.0325, and 0.0275 (or 0.0195, 0.0164, and 0.0199) under the uniform prior; (ii) when ${\sigma }_c^2={\sigma }_t^2$, the type I errors are 0.0236, 0.0235 and 0.0236, respectively, under the uniform prior; and (iii) the similar results are obtained under the reference prior and the Jeffreys’s prior, respectively. Thus, when the fitted model is misspecified, the type I errors are greater than 0.025 when one arm (“control”) has a smaller sample size coupled with a larger variance than another arm (“test”). On the contrary, the type I errors are less than 0.025 when one arm (“test”) has a larger sample size coupled with a larger variance than another arm (“control”). Second, we see from the left block labeled with “Assuming Unequal Variances” of Table 1 that the type I errors are smaller than, slightly smaller than, and almost at 0.025 under the uniform prior, the reference prior, and the Jeffreys’s prior, respectively, when we fit the model with unequal variances while the true model has equal variances. For example, the type I errors are 0.0195, 0.0235, and 0.0257 under these three priors, respectively, when we fit the model with unequal variances while the true model has ${\sigma }_c^2={\sigma }_t^2=20.25$.

Table 1.

Bayesian type I errors with noninformative fitting priors.

	Assuming Unequal Variances			Assuming Equal Variances
	${\sigma }_t^2$			${\sigma }_t^2$
	16	20.25	25	16	20.25	25
${\sigma }_c^2$	Uniform Prior (m = 0)
16	0.0196	0.0196	0.0195	0.0236	0.0195	0.0164
20.25	0.0196	0.0195	0.0197	0.0281	0.0235	0.0199
25	0.0196	0.0196	0.0196	0.0325	0.0275	0.0236
${\sigma }_c^2$	Reference Prior (m = 1)
16	0.0231	0.0233	0.0232	0.0247	0.0207	0.0176
20.25	0.0234	0.0235	0.0234	0.0299	0.0250	0.0213
25	0.0235	0.0237	0.0234	0.0340	0.0293	0.0249
${\sigma }_c^2$	Jeffreys’s Prior (m = 3/2)
16	0.0252	0.0253	0.0248	0.0257	0.0216	0.0180
20.25	0.0257	0.0257	0.0252	0.0307	0.0259	0.0220
25	0.0257	0.0257	0.0254	0.0349	0.0302	0.0259

Note that the sampling prior ${\pi }_0^{(s)}(\delta )={\Delta }_{\{\delta =0\}}$ is used in all calculations.

Table 2.

Bayesian powers with noninformative fitting priors.

	Assuming Unequal Variances			Assuming Equal Variances
	${\sigma }_t^2$			${\sigma }_t^2$
	16	20.25	25	16	20.25	25
${\sigma }_c^2$	Uniform Prior (m = 0)
16	92.31%	90.17%	87.59%	93.79%	90.48%	86.22%
20.25	87.42%	85.07%	82.37%	90.98%	87.38%	83.01%
25	81.62%	79.30%	76.63%	87.80%	84.05%	79.70%
${\sigma }_c^2$	Reference Prior (m = 1)
16	93.46%	91.51%	89.09%	94.13%	90.99%	86.92%
20.25	89.10%	86.90%	84.36%	91.40%	87.96%	83.71%
25	83.83%	81.58%	79.10%	88.25%	84.68%	80.50%
${\sigma }_c^2$	Jeffreys’s Prior (m = 3/2)
16	93.90%	92.01%	89.71%	94.27%	91.19%	87.18%
20.25	89.75%	87.65%	85.24%	91.58%	88.25%	84.14%
25	84.73%	82.62%	80.17%	88.50%	85.02%	80.87%

Note that the sampling prior ${\pi }_1^{(s)}(\delta )={\Delta }_{\{\delta =3.5\}}$ is used in all calculations.

With noninformative priors, a decreased type I error typically corresponds to a lower power, while an increased type I error is associated with a higher power. Tables 1 and 2 exactly show these patterns. For example, the powers are 87.80%, 88.25%, and 88.50% under the uniform prior, the reference prior, and the Jeffreys’s prior, respectively, when we fit the model with equal variances while the true model has ${\sigma }_c^2=25$ and ${\sigma }_t^2=16$. For ${\sigma }_c^2=25$ and ${\sigma }_t^2=16$, the powers are 81.62%, 83.83%, and 84.73%, respectively, under these three priors when we fit the model with unequal variances, which are lower than those when we fit the model with equal variances. Note that in this case, the model assuming equal variances lead to increased type I errors, as discussed earlier. Thus, when the true variances are unequal, the misspecified model assuming equal variances could lead to a substantial decrease or increase of the type I error and power, depending on whether ${\sigma }_c^2<{\sigma }_t^2$ or ${\sigma }_c^2>{\sigma }_t^2$. Moreover, the different noninformative priors lead to different type I errors and powers. From Tables 1 and 2, we see that the type I errors and powers under the uniform prior and the reference prior are lower than those under the Jeffreys’s prior, even when the fitted model is correctly specified. Furthermore, the type I errors and powers under the Jeffreys’s prior are very close to those under the frequentist method. Therefore, the Jeffreys’s prior is a more desirable noninformative prior than the other two noninformative priors we consider. Subsequently, the Jeffreys’s prior will be used as a default noninformative initial prior in constructing the informative priors.

Using the frequentist method, we use simulation to calculate type I error and power under the models with equal and unequal variances. We first introduce the following notation: let $S_c={\{\frac{1}{n_c-1}\underset{i=1}{\overset{n_c}{\Sigma }}{\left(y_{ci}-{\overline{y}}_c\right)}^2\}}^{1/2}$ and $S_t={\{\frac{1}{n_t-1}\underset{j=1}{\overset{n_t}{\Sigma }}{(y_{tj}-{\overline{y}}_t)}^2\}}^{1/2}$ denote the sample standard deviations, respectively, for the control and test arms. Also let $\mathrm{se}\left({\overline{y}}_t-{\overline{y}}_c\right)=\sqrt{\frac{\left(n_c-1\right)S_c^2+\left(n_t-1\right)S_t^2}{n_c+n_t-2}\left(1/n_c+1/n_t\right)}$ and $\mathrm{se}\left({\overline{y}}_t-{\overline{y}}_c\right)=\sqrt{S_c^2/n_c+S_t^2/n_t}$ denote the standard errors, respectively, under the models with equal and unequal variances, where ${\overline{y}}_c$ and ${\overline{y}}_t$ are defined in Section 3.1. Denote the critical value by $t_{1-{\alpha }_0}$ such that $F_{t_{\mathrm{df}}}\left(t_{1-{\alpha }_0}\right)=1-{\alpha }_0$, where $0<{\alpha }_0<1,F_{t_{\text{df}}}$ is the cdf of a central-t distribution with degrees of freedom df, which is taken as n_t + n_c − 2 or $\frac{{\left(S_c^2/n_c+S_t^2/n_t\right)}^2}{S_c^4/\left[n_c^2\left(n_c-1\right)\right]+S_t^4/\left[n_t^2\left(n_t-1\right)\right]}$ for the model with equal or unequal variances.

Using the corresponding df and $\mathrm{se}\left(\overline{y_t}-\overline{y_c}\right)$ for the model assuming equal variances or the model assuming unequal variances, the simulation algorithm is given as follows:

Step 1. Generate random samples y_c from $N\left({\mu }_c,{\sigma }_c^2\right)$ and y_t from $N\left({\mu }_c,{\sigma }_t^2\right)$ for the type I error or $N\left({\mu }_t,{\sigma }_t^2\right)$ for the power;

Step 2. Calculate ${\overline{y}}_c$, S_c, ${\overline{y}}_t$, S_t, and $\mathrm{se}\left({\overline{y}}_t-{\overline{y}}_c\right)$ for the corresponding model;

Step 3. Calculate test statistic $T^{\ast }=\frac{{\overline{y}}_t-{\overline{y}}_c}{\mathrm{se}\left({\overline{y}}_t-{\overline{y}}_c\right)}$ and its corresponding degrees of freedom df; Compare T* with $t_{1-{\alpha }_0}$ for the corresponding model;

Step 4. Repeat Steps 1-3 for 10⁷ times. The type I error or power is the proportion of $T^{\ast }\ge t_{1-{\alpha }_0}$.

For the case of ${\alpha }_0=0.025$, $n_t=50$, n_c = 25, μ_c = 0, ${\sigma }_c^2=25$, and δ = 3.5 , Figure 2 (a) shows the type I error under the model assuming equal variances. When the true ${\sigma }_t^2$ is different from ${\sigma }_c^2$, the type I error is increased in ${\sigma }_c^2-{\sigma }_t^2$ when ${\sigma }_t^2<{\sigma }_c^2=25$ and is decreased when ${\sigma }_t^2>{\sigma }_c^2=25$ under the wrong model. The type I errors under the model assuming unequal variances stay at 0.025 since the model is correctly specified. Figure 2 (b) shows the power under the model assuming equal variances and unequal variances. Compared with the powers under the model with unequal variances (cyan line), the powers under the model with equal variances (red line) are increased when ${\sigma }_t^2<{\sigma }_c^2=25$ and decreased when ${\sigma }_t^2>{\sigma }_c^2=25$. Thus, the misspecified model may increase or decrease the frequentist type I error and power, which is similar to the Bayesian framework.

Fig. 2.

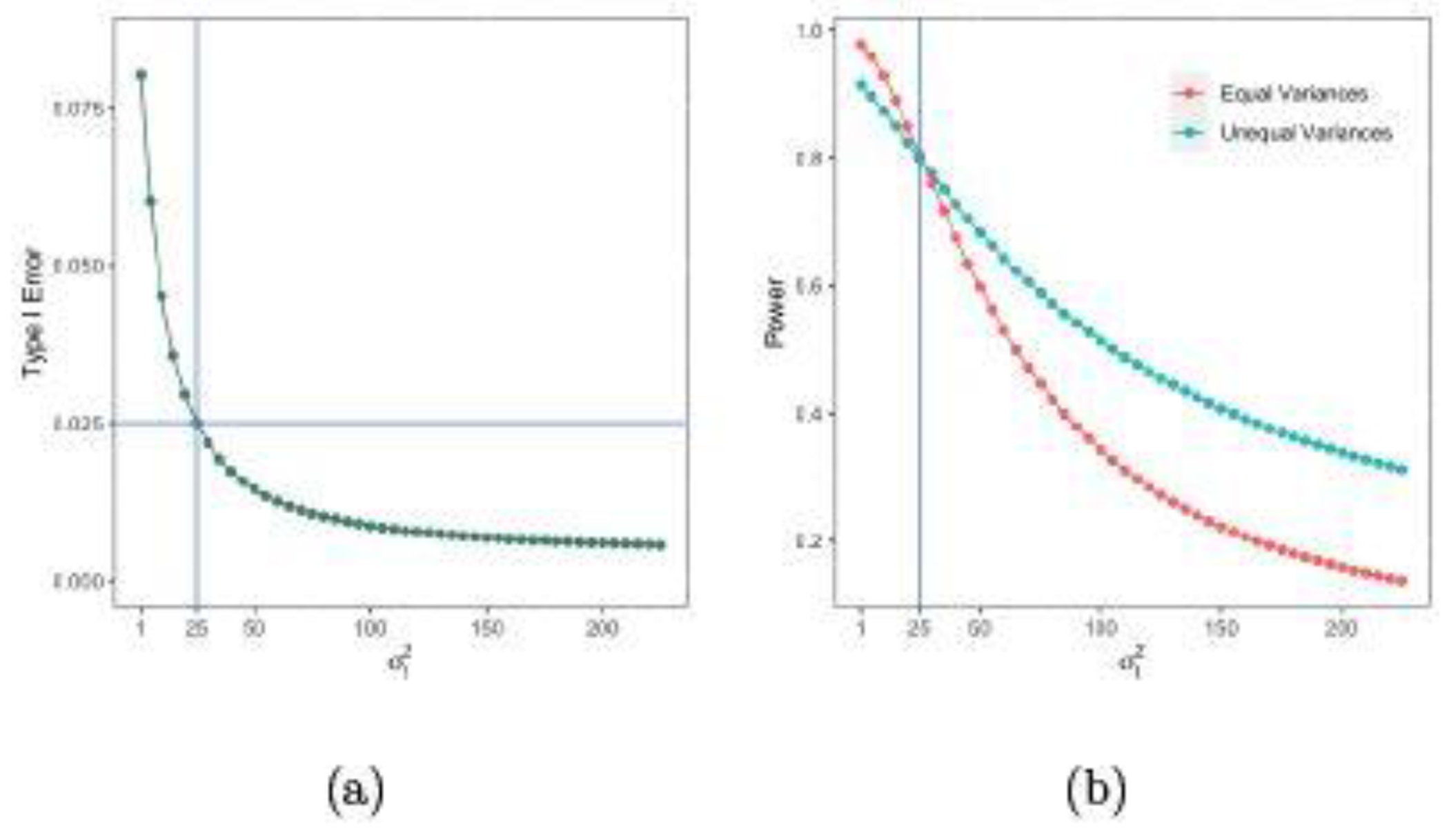
Plots of frequentist type I errors and powers versus σ_t.

4. Bayesian SSD with Informative Priors

4.1. Leveraging Historical Data

Historical data makes its impact on the fitting priors by various ways, including but not limited to full borrowing (Ibrahim and Chen, 2000), partial borrowing (Ibrahim et al., 2012; Chen et al., 2014; Ibrahim et al., 2015), dynamic borrowing (Viele et al., 2014; Pan et al., 2017; Lim et al., 2018), conditional borrowing (Allocco et al., 2010), and propensity score matching (Wang et al., 2019). Suppose that the historical data from a natural history study consists of the sample size of 44, the sample mean of −0.18, and the sample standard deviation of 3.38 for the primary endpoint. We next discuss how to leverage the historical data in Bayesian SSD via informative priors.

We first examine the effect of the amount of borrowing of the historical data on the gain in power within the frequentist SSD framework. For a randomized controlled trial, suppose the starting sample size ratio of the test arm versus the concurrent control arm is 2 : 1. When the concurrent control is augmented using historical data by 50% or 100% of the concurrent control sample size, the augmented sample size ratios of the test arm versus the concurrent control arm are then 2 : 1.5 or 2 : 2, respectively. Set δ = 3.5 and ${\sigma }_t^2=25$. Table 3 show the frequentist powers for ${\sigma }_c^2=11.42$, 16, 20.25 and 25; n_t = 32, 40, 44, and 52; and $n_t:n_c=2:1,n_t:n_c=2:1.5$, and n_t : n_c = 2 : 2. We notice that we assume (i) all random samples for the control arm in Table 3 are from the same normal distribution $N\left({\mu }_c,{\sigma }_c^2\right)$ and (ii) the model with unequal variances is used in all power calculations. From Table 3, we observe that (i) when ${\sigma }_c^2=11.42$, the powers are 79.8%, 86.5%, and 89.7% for n_t : n_c = 2 : 1, n_t : n_c, = 2 : 1.5, and n_t : n_c = 2 : 2, respectively, and the gains in power are 6.7% and 3.2% when the sample sizes on the control arm increase from 16 to 24 and 24 to 32, respectively; and (ii) the results remain similar for the other three values of ${\sigma }_c^2$. Thus, in all of these four cases, the most gain in power is achieved at the first 50% increase in sample size on the control arm, i.e., when n_t : n_c = 2 : 1 increases to n_t : n_c = 2 : 1.5.

Table 3.

Frequentist powers with different amounts of borrowing $\left(\delta =3.5,{\sigma }_t^2=25\right)$.

	nt : nc = 2 : 1		nt : nc = 2 : 1.5		nt : nc = 2 : 2
${\sigma }_c^2$	N	Power	N	Power	N	Power
11.42	32 + 16 = 48	79.8%	32 + 24 = 56	86.5%	32 + 32 = 64	89.7%
16	40 + 20 = 60	81.9%	40 + 30 = 70	89.4%	40 + 40 = 80	92.7%
20.25	44 + 22 = 66	80.2%	44 + 33 = 77	88.8%	44 + 44 = 88	92.7%
25	52 + 26 = 78	82.1%	52 + 39 = 91	90.5%	52 + 52 = 104	94.2%

We next explore the amount of borrowing within the Bayesian framework. The power prior and the robust mixture prior are considered to leverage the historical data. Let ${\mathit{y}}_0={\left(y_{01},y_{02},\dots ,y_{0n_0}\right)}^{\prime }$ be the historical data with sample size of n₀ from the control arm, and assume $y_{0i}\stackrel{i.i.d.}{\sim }N\left({\mu }_c,{\sigma }_c^2\right)$. Let ${\overline{y}}_0$ and $S_{0c}^2$ denote the sample mean and the sample variance of y₀. Write the historical data as $D_0=\left(n_0,{\overline{y}}_0,S_{0c}^2\right)$. Denote the likelihood of the historical data by $L\left({\mu }_c,{\sigma }_c^2\mid D_0\right)$. Under the unequal variances assumption, $\mathit{\theta }={\left({\mu }_c,{\mu }_t,{\sigma }_c^2,{\sigma }_t^2\right)}^{\prime }$. The power prior (Ibrahim and Chen, 2000) is given by

$${\pi }^{(f)}\left({\mu }_c,{\sigma }_c^2\mid D_0,a_0\right)\propto L{\left({\mu }_c,{\sigma }_c^2\mid D_0\right)}^{a_0}{\pi }_0^{(f)}\left({\mu }_c,{\sigma }_c^2\right),$$ (4.1)

where ${\pi }_0^{(f)}\left({\mu }_c,{\sigma }_c^2\right)$ is an initial prior and 0 ≤ a₀ ≤ 1 is the discounting parameter, which determines the amount of borrowing. The robust mixture prior (Greenhouse and Waserman, 1995; Ye et al., 2020) given p₀ is defined by

$${\pi }^{(f)}\left({\mu }_c,{\sigma }_c^2\mid D_0,p_0\right)=p_0{\pi }^{(f)}\left({\mu }_c,{\sigma }_c^2\mid D_0\right)+\left(1-p_0\right){\pi }_{\text{non }}^{(f)}\left({\mu }_c,{\sigma }_c^2\right),$$ (4.2)

where ${\pi }^{(f)}\left({\mu }_c,{\sigma }_c^2\mid D_0\right)={\pi }^{(f)}\left({\mu }_c,{\sigma }_c^2\mid D_0,a_0=1\right)$ with ${\pi }_0^{(f)}\left({\mu }_c,{\sigma }_c^2\right)\propto {\left({\sigma }_c^2\right)}^{-3/2}$ which is the power prior in (4.1) with a₀ = 1 and the weight $0\le p_0\le 1$ determines the amount of borrowing. In (4.2), the skeptical prior when p₀ = 0 is specified as ${\pi }_{\text{non}}^{(f)}\left({\mu }_c,{\sigma }_c^2\right)={\pi }_{\text{non}}^{(f)}\left({\mu }_c\mid {\sigma }_c^2\right){\pi }_{\text{non}}^{(f)}\left({\sigma }_c^2\right)$, where ${\pi }_{\text{non}}^{(f)}\left({\mu }_c\mid {\sigma }_c^2\right)\propto \frac{1}{{\sigma }_c}\exp \left\{-{\mu }_c^2/\left(2\times 1000{\sigma }_c^2\right)\right\}$ and ${\pi }_{\text{non }}^{(f)}\left({\sigma }_c^2\right)\propto \frac{1}{{\left({\sigma }_c^2\right)}^{1.001}}\times \exp \left(-0.001/{\sigma }_c^2\right)$, which correspond to the normal distribution $N\left(0,1000{\sigma }_c^2\right)$ and the inverse gamma distribution IG (0.001, 0.001). We further assume that $\left({\mu }_c,{\sigma }_c^2\right)$ and $\left({\mu }_t,{\sigma }_t^2\right)$ are independent a priori. Thus, we have ${\pi }^{(f)}\left({\mu }_c,{\sigma }_c^2,{\mu }_t,{\sigma }_t^2\right)={\pi }^{(f)}\left({\mu }_c,{\sigma }_c^2\right){\pi }^{(f)}\left({\mu }_t,{\sigma }_t^2\right)$. Since the historical data are available only for the control arm, ${\pi }^{(f)}\left({\mu }_c,{\sigma }_c^2\right)$ is taken as the robust mixture prior given in (4.2) and a non-informative prior, ${\pi }^{(f)}\left({\mu }_t,{\sigma }_t^2\right)\propto {\left({\sigma }_t^2\right)}^{-3/2}$, is specified for $\left({\mu }_t,{\sigma }_t^2\right)$.

Figure 3 (a) and (b) show the type I errors and the powers for different μ_c’s using the power prior given in (4.1) with a₀ = 0 (red lines), a₀ = 0.18 (green lines) and a₀ = 0.36 (blue lines) when n_t = 32, n_c = 16, $n_0=44,{\sigma }_t^2=25,{\sigma }_c^2=11.42,{\overline{y}}_0=-0.18,S_{0c}^2=11.42$, and δ = 3.5. Comparing the power gain from a₀ = 0 to a₀ = 8 / 44 = 0.18, and the power gain from a₀ = 8 / 44 = 0.18 to a₀ = 16 / 44 = 0.36, we see from Figure 3 (b) most gain in Bayesian power is achieved at the first 50% increase in sample size on the concurrent control arm, i.e., when a₀ = 0 increases to a₀ = 0.18. Specifically, the powers with a₀ = 0, 0.18, and 0.36 are 79.78%, 85.92%, and 88.73%, respectively, at μ_c = −0.51; 79.79%, 87.99%, and 91.51%, respectively, at μ_c = −0.18; and 79.76%, 91.59%, and 95.63%, respectively, at μ_c = 0.52. Thus, the power gains from a₀ = 0 to a₀ = 0.18 are 6.14%, 8.20%, and 11.83%, respectively, at μ_c = −0.51, −0.18, and 0.52 while the power gains from a₀ = 0.18 to a₀ = 0.36 are 2.81%, 3.52%, and 4.04%, respectively, at μ_c = −0.51, −0.18, and 0.52. Note that the type I errors with a₀ = 0, 0.18, and 0.36 are 0.025, 0.013, and 0.011, respectively, at μ_c = −0.51; 0.025, 0.018, and 0.017, respectively, at μ_c = −0.18; and 0.025, 0.030, and 0.038, respectively, at μ_c = 0.52. In the above discussion, we consider μ_c = −0.51, −0.18 and 0.52, since these values of μ_c lead to a negative bias, no bias, and a positive bias, respectively, compared with the historical mean. In Figure 3 (a), the maximum values of μ_c so that the type I error is less than 0.025 are 0.27 and 0.15, respectively, for a₀ = 0.18 and 0.36. These results indicate that (i) borrowing the historical data may lead to a gain in power and a reduction in type I error at the same time and an example for this scenario is that the power increases but the type I error decreases in a₀ when μ_c = −0.51; (ii) borrowing the historical data may lead to a gain in power and an increase in type I error and, for example, both the power and type I error increase in a₀ when μ_c = 0.52; (iii) the type I error can still be less than 0.025 (a prespecified significance level) even when the historical data and the data from the concurrent control arm are not similar, for example, the type I errors are less than 0.025 when μ_c < 0.27 when a₀ = 0.18; and (iv) when a₀ = 0 , the type I errors are around 0.025 and the powers are about 0.80, which may be due to the fact that a noninformative prior is specified as the initial prior.

Fig. 3.

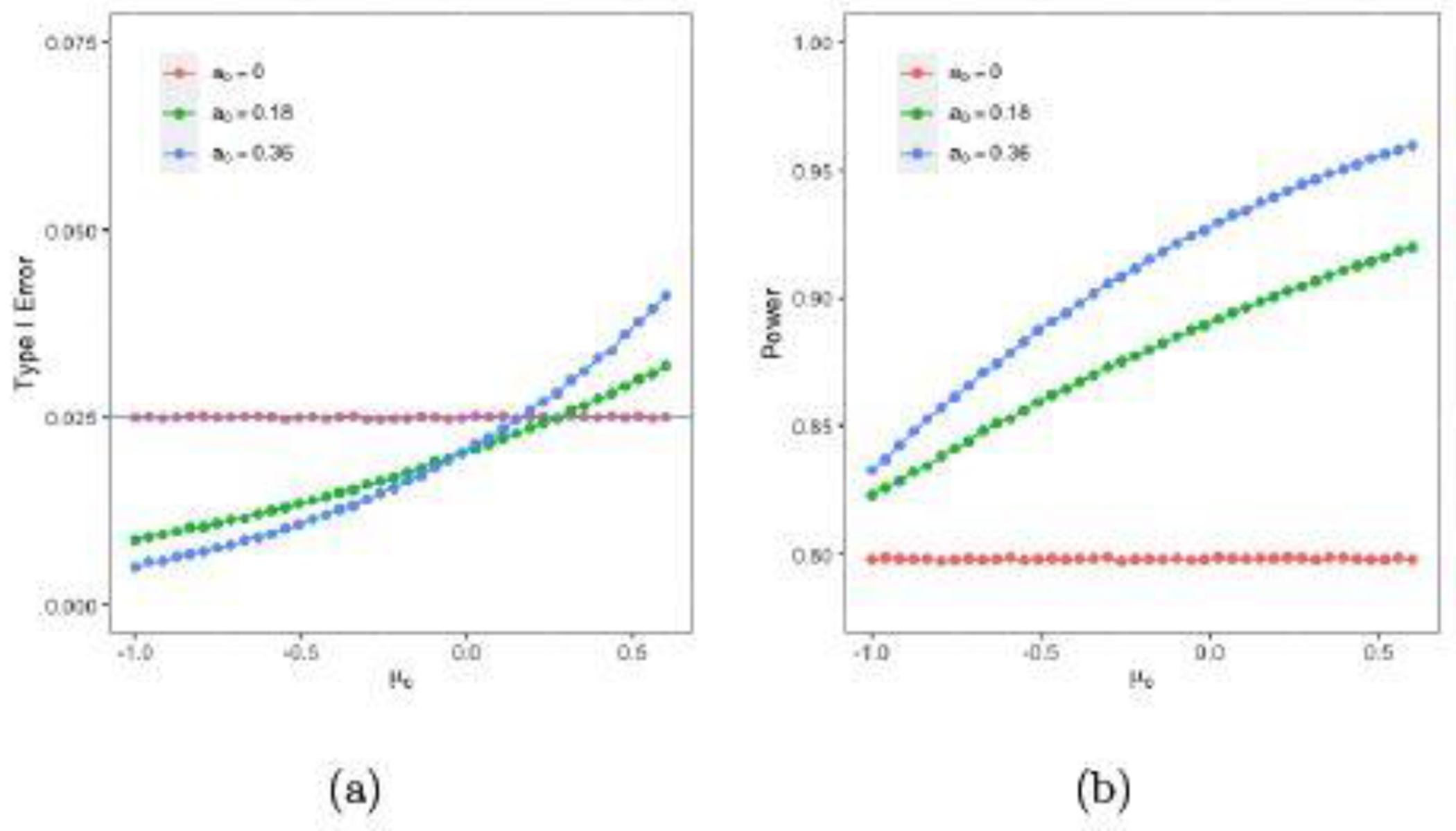
Plots of Bayesian type I errors and powers with the power prior versus μ_c.

Figure 4 (a) and (b) show the plots of the type I error and power using the robust mixture prior in (4.2) for p₀ = 0 , 0.18, 0.36, 0.5, and 1. The type I errors for p₀ = 0 , 0.18, 0.36, 0.5, and 1 are 0.025, 0.022, 0.019, 0.017, and 0.009, respectively, at μ_c = −0.51; 0.025, 0.024, 0.022, 0.022, and 0.018, respectively, at μ_c = −0.18; and 0.025, 0.031, 0.038, 0.043, and 0.060, respectively, at μ_c = 0.52. The powers for p₀ = 0 , 0.18, 0.36, 0.5, and 1 are 79.82%, 81.92%, 84.13%, 85.83%, and 91.82%, respectively, at μ = −0.51; 79.79%, 82.56%, 85.29%, 87.39%, and 95.08%, respectively, at μ = −0.18; and 79.79%, 83.13%, 86.52%, 89.14% and 98.59%, respectively, at μ_c = 0.52. Compared to those using the power prior, (i) the robust mixture prior leads to less gain in power when p₀ = a₀ <= 0.36; (ii) the powers using the robust mixture prior with p₀ = 0.5 are lower than those using the power prior with a₀ = 0.36 ; (iii) the type I errors are closer to 0.025 using the robust mixture prior than the power prior when p₀ = a₀ <= 0.36 ; and (iv) the skeptical prior given in (4.2) is quite noninformative in the sense that the type I errors are around 0.025 and the powers remain around 80% for all μ_c.

Fig. 4.

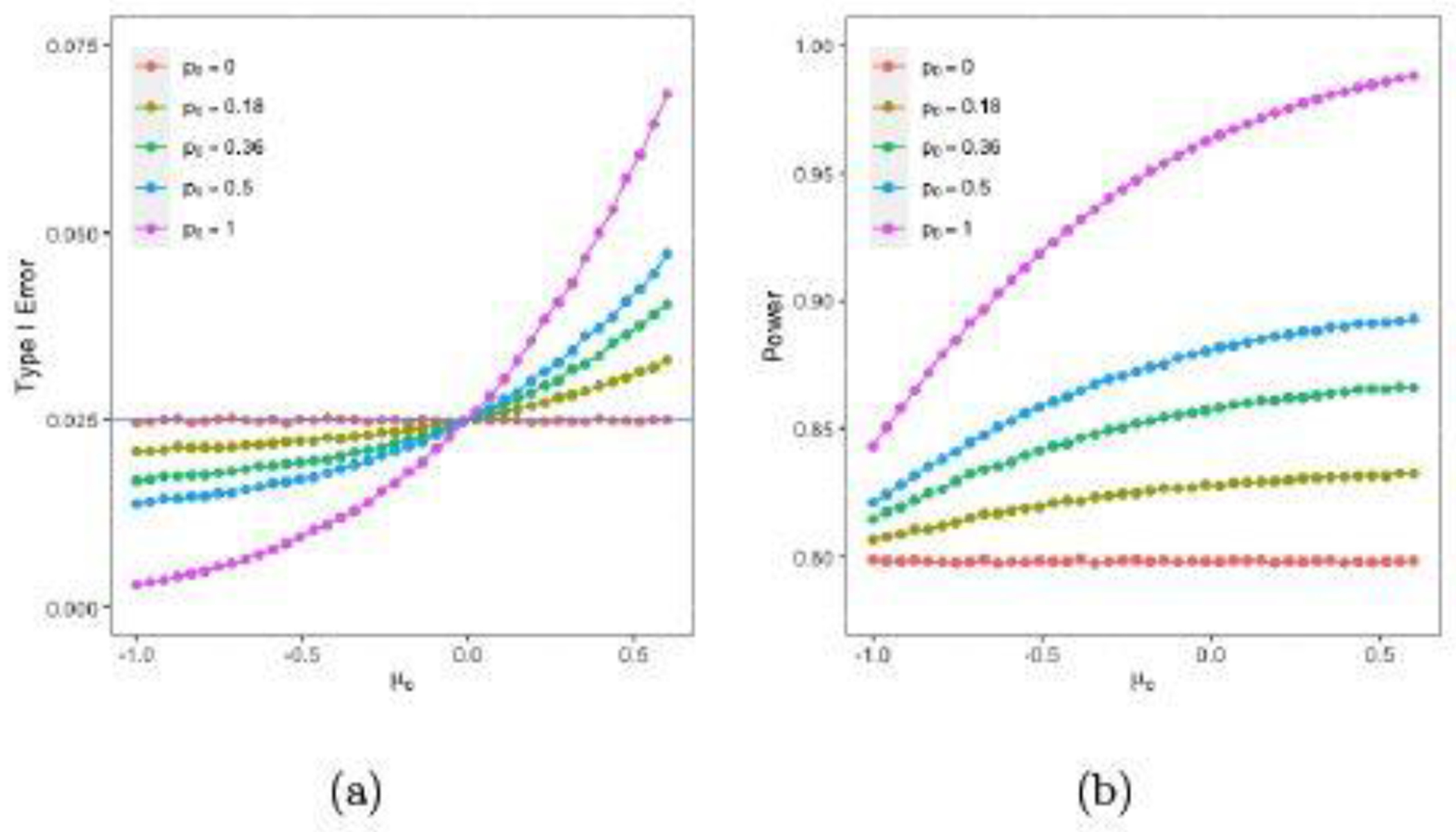
Plots of Bayesian type I errors and powers with the robust mixture prior versus μ_c.

4.2. Conditional Borrowing

Under the assumption of compatibility between the natural history data and the concurrent control data, the conditions on the primary end point can be further imposed in borrowing the historical data. We take

$$T\left({\mathit{y}}^{(n)}\right)=P\left(\delta >0\mid {\mathit{y}}^{(n)},{\pi }^{\left(f_1\right)}\right)1\left\{{\mathit{y}}^{(n)}\in A\right\}+P\left(\delta >0\mid {\mathit{y}}^{(n)},{\pi }^{\left(f_2\right)}\right)1\left\{{\mathit{y}}^{(n)}\in A^C\right\},$$ (4.3)

where ${\pi }^{\left(f_1\right)}$ and ${\pi }^{\left(f_2\right)}$ are two fitting priors, A denotes a subset of the sample space induced by y⁽ⁿ⁾ , and A^C is the complement of A. We let T₀ = γ , where 0 < γ < 1 is a Bayesian credible level. Thus the Bayesian power function is

$$\begin{gathered} {\beta }_s^{(n)}=E_{{\pi }^{(s)}}\left[1\left\{T\left({\mathit{y}}^{(n)}\right)\ge \gamma \right\}\right] \\ =E_{{\pi }^{(s)}}\left[1\left\{P\left(\delta >0\mid {\mathit{y}}^{(n)},{\pi }^{\left(f_1\right)}\right)\ge \gamma \right\}1\left\{{\mathit{y}}^{(n)}\in A\right\}+1\left\{P\left(\delta >0\mid {\mathit{y}}^{(n)},{\pi }^{\left(f_2\right)}\right)\ge \gamma \right\}1\left\{{\mathit{y}}^{(n)}\in A^C\right\}\right]. \end{gathered}$$

Suppose we impose a conditional borrowing region of $\pm S_{0c}/\left(2\sqrt{n_0}\right)$ for the mean and $\pm S_{0c}^2/\sqrt{2\left(n_0-1\right)}$ for the standard deviation of the concurrent control. Thus, $A=\{{\mathit{y}}^{(n)}:{\overline{y}}_0-S_{0c}/\left(2\sqrt{n_0}\right)<{\overline{y}}_c<\overline{y_0}+S_{0c}/\text{(}2\sqrt{n_0)},S_{0c}^2-S_{0c}^2/\sqrt{2\left(n_0-1\right)}<S_c^2<S_{0c}^2+S_{0c}^2/\sqrt{2\left(n_0-1\right)}\}$. Using the historical data $D_0=\left\{n_0=44,{\overline{y}}_0=-0.18,S_{0c}^2=11.42\right\}$ in Section 4.1, $A=\left\{{\mathit{y}}^{(n)}:-0.43<{\overline{y}}_c<0.07,10.19<S_c^2<12.66\right\}$. In (4.3), we specify the power prior in (4.1) for ${\pi }^{\left(f_1\right)}$ and the Jeffreys’s prior ${\left({\sigma }_t^2{\sigma }_c^2\right)}^{-3/2}$ for ${\pi }^{\left(f_2\right)}$. Figure 5 plots the type I errors and powers versus μ_c for a₀ = 0, 0.18, and 0.36 with conditional borrowing when n_t = 32, n_c = 16, $n_0=44$, ${\sigma }_t^2=25$, ${\sigma }_c^2=11.42$, ${\overline{y}}_0=-0.18$, $S_{0c}^2=11.42$, and δ = 3.5.

Fig. 5.

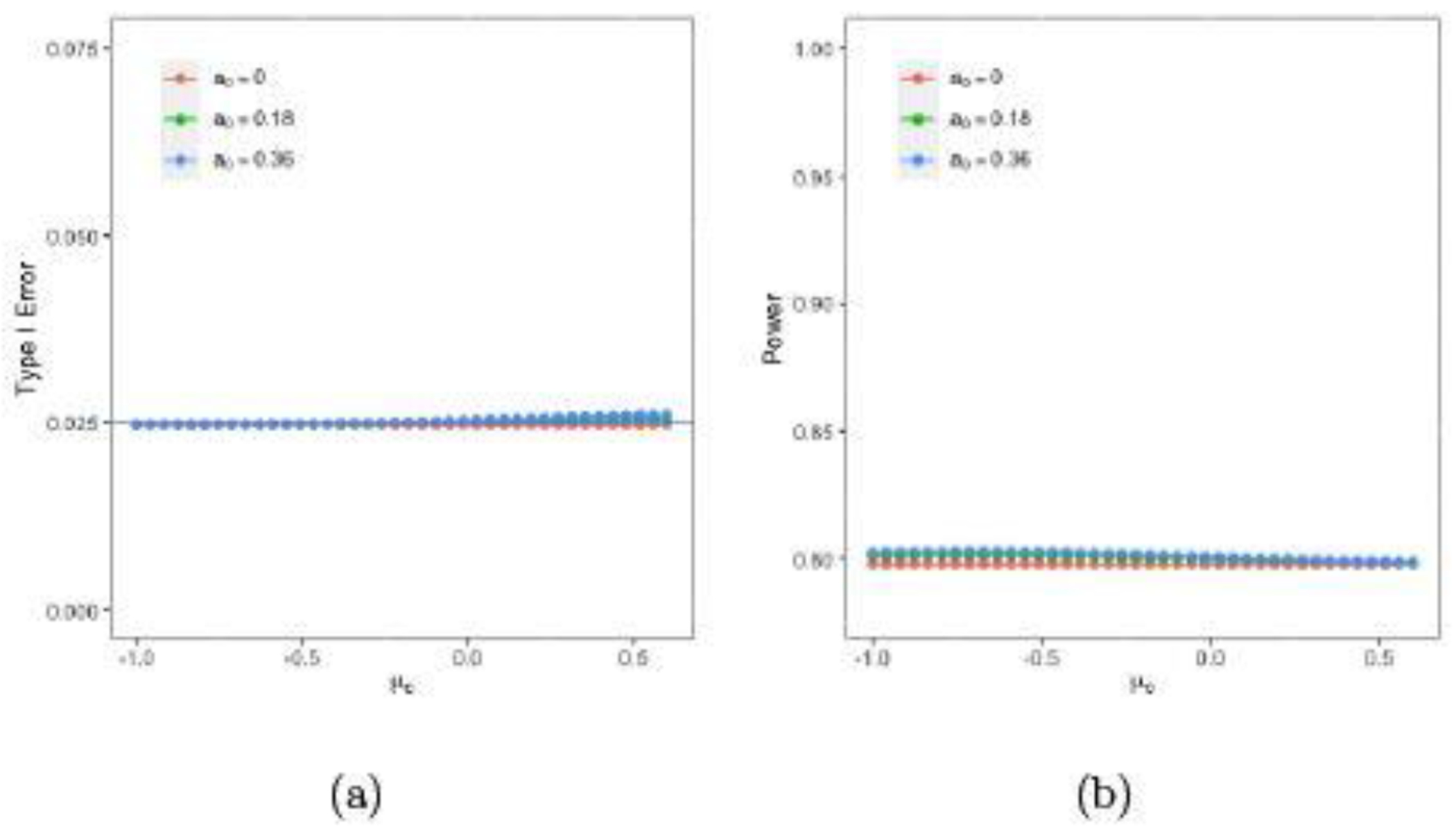
Plots of Bayesian type I errors and powers with conditional borrowing versus μ_c.

Note that the powers with a₀ = 0, 0.18, and 0.36 are 79.79%, 80.11%, and 80.25%, respectively, at μ_c = −0.51; 79.79%, 80.04%, and 80.13%, respectively, at μ_c = −0.18; and 79.79%, 79.84%, and 79.86%, respectively, at μ_c = 0.52. Thus, the power gains from a₀ = 0 to a₀ = 0.18 are 0.32%, 0.25%, and 0.05%, respectively, at μ_c = −0.51, −0.18, and 0.52 while the power gains from a₀ = 0.18 to a₀ = 0.36 are close to 0 at μ_c = −0.51, −0.18, and 0.52. Also note that the type I errors with a₀ = 0 , 0.18, and 0.36 are 0.025, 0.025, and 0.025, respectively, at μ_c = −0.51; 0.025, 0.025, and 0.025, respectively, at μ_c = −0.18; and 0.025, 0.025, and 0.026, respectively, at μ_c = 0.52. Compared with those obtained using the power prior and the robust mixture prior shown in Figures 3 and 4, (i) the type I errors shown in Figure 5 are better controlled with a small increase toward larger μ_c; and (ii) the powers shown in Figure 5 are lower than those under unconditional borrowing.

4.3. Borrowing-by-Parts Power Priors

Let $D=\left(n_t,{\overline{y}}_t,S_t^2,n_c,{\overline{y}}_c,S_c^2\right)$ denote the current data, where ${\overline{y}}_c$ and ${\overline{y}}_t$ are the sample means and $S_c^2$ and $S_t^2$ are the sample variances, respectively, for the concurrent control and the test arm. In (4.1), the historical data is borrowed all together via the power prior. A new variation of the power prior is the borrowing-by-parts power prior via distinct discounting parameters a₀₁ and a₀₂, given by

$${\pi }^{(f)}\left({\mu }_c,{\sigma }_c^2\mid D_0,{\mathit{a}}_0\right)\propto {[{({\sigma }_c^2)}^{-1/2}\exp \{-\frac{n_0{\left({\overline{y}}_0-{\mu }_c\right)}^2}{2{\sigma }_c^2}\}]}^{a_{01}}\times {[{(S_{0c}^2)}^{\left(n_0-3\right)/2}{({\sigma }_c^2)}^{-\left(n_0-1\right)/2}\exp \{-\frac{\left(n_0-1\right)S_{0c}^2}{2{\sigma }_c^2}\}]}^{a_{02}}{\pi }_0^{(f)}\left({\mu }_c,{\sigma }_c^2\right),$$ (4.4)

where $0\le a_{01},a_{02}\le 1$. In (4.4), the distinct discounting parameters a₀₁ and a₀₂ are used in borrowing the mean and the variance, respectively. In the case when the mean of the concurrent control is consistent with that of the historical data, however the variance of the concurrent control is not consistent with that of the historical data, a₀₁ > 0 and a₀₂ = 0 can be specified for borrowing the mean part but not borrowing the variance part. Compared with full borrowing, where a₀₁ = a₀₂ > 0 , borrowing only the mean part where a₀₁ > 0 and a₀₂ = 0 allows for achieving a desirable power while controlling the type I error at the same time.

Table 4 reports the type I errors and powers using the borrowing-by-parts power prior with consistent and inconsistent variances of the concurrent control compared with that of the historical control for n_t = 32, n_c = 16, $n_0=44,{\overline{y}}_0=-0.18,S_{0c}^2=11.42,{\mu }_c=0$, and Jeffreys’s prior. When ${\sigma }_t^2={\sigma }_c^2=25$, we see from Table 4 that (i) the type I error decreases and the power increases in a₀₁ when a₀₂ = 0; (ii) both the type I error and the power increase in a₀₂ when a₀₁ = 0; and (iii) the type I errors are less than 0.025 but the power increases considerably when a₀₁ = a₀₂ gets larger. When ${\sigma }_t^2=25$ and ${\sigma }_c^2=11.42$, we also see from Table 4 that (i) the type I errors are controlled at 0.025 and the powers under various values of a₀₁ and a₀₂ such that a₀₁ + a₀₂ > 0 (borrowing) are greater than those under a₀₁ = a₀₂ = 0 (no borrowing); (ii) the gain in the power is incremental when a₀₂ > 0 and a₀₁ = 0. These results indicate that borrowing the mean part of the historical data only or the whole historical data is more effective in increasing the power than borrowing the variance part of the historical data only. The results with μ_c = −1 and μ_c = 1 are given in Appendix C. Figure 6(a) plots the type I error against a₀₁ and a₀₂ and Figure 6(b) plots the type I error against $a_{01}=a_{02}=a_0$ for ${\sigma }_t^2={\sigma }_c^2=25$. When $a_{01}=a_{02}=a_0$, the type I error stays at or below 0.025 as a₀ increases. When a₀₂ = 0 , the type I error first decreases and then increases slightly as a₀₁ increases. When a₀₁ = 0 , the type I error increases as a₀₂ increases.

Table 4.

Bayesian type I errors and powers using the borrowing-by-parts power prior.

${\mu }_c=0,{\sigma }_t^2=25,{\sigma }_c^2=25$
a 01	a 02	Type I Error	Power
			δ = 3.5	δ = 4	δ = 4.5
0.00	0.00	0.0255	60.44%	71.93%	81.50%
0.18	0.00	0.0162	74.71%	85.46%	92.60%
0.36	0.00	0.0143	83.01%	91.82%	96.62%
0.00	0.18	0.0329	65.78%	76.67%	85.27%
0.00	0.36	0.0376	68.42%	78.88%	86.99%
0.18	0.18	0.0213	78.97%	88.55%	94.50%
0.36	0.36	0.0212	87.43%	94.44%	97.93%
${\mu }_c=0,{\sigma }_t^2=25,{\sigma }_c^2=11.42$
a 01	a 02	Type I Error	Power
			δ = 3.5	δ = 4	δ = 4.5
0.00	0.00	0.0247	79.79%	89.11%	94.84%
0.18	0.00	0.0202	88.68%	95.25%	98.33%
0.36	0.00	0.0205	92.40%	97.30%	99.21%
0.00	0.18	0.0243	80.24%	89.49%	95.09%
0.00	0.36	0.0242	80.45%	89.64%	95.18%
0.18	0.18	0.0202	89.03%	95.47%	98.45%
0.36	0.36	0.0206	92.72%	97.47%	99.29%

Fig. 6.

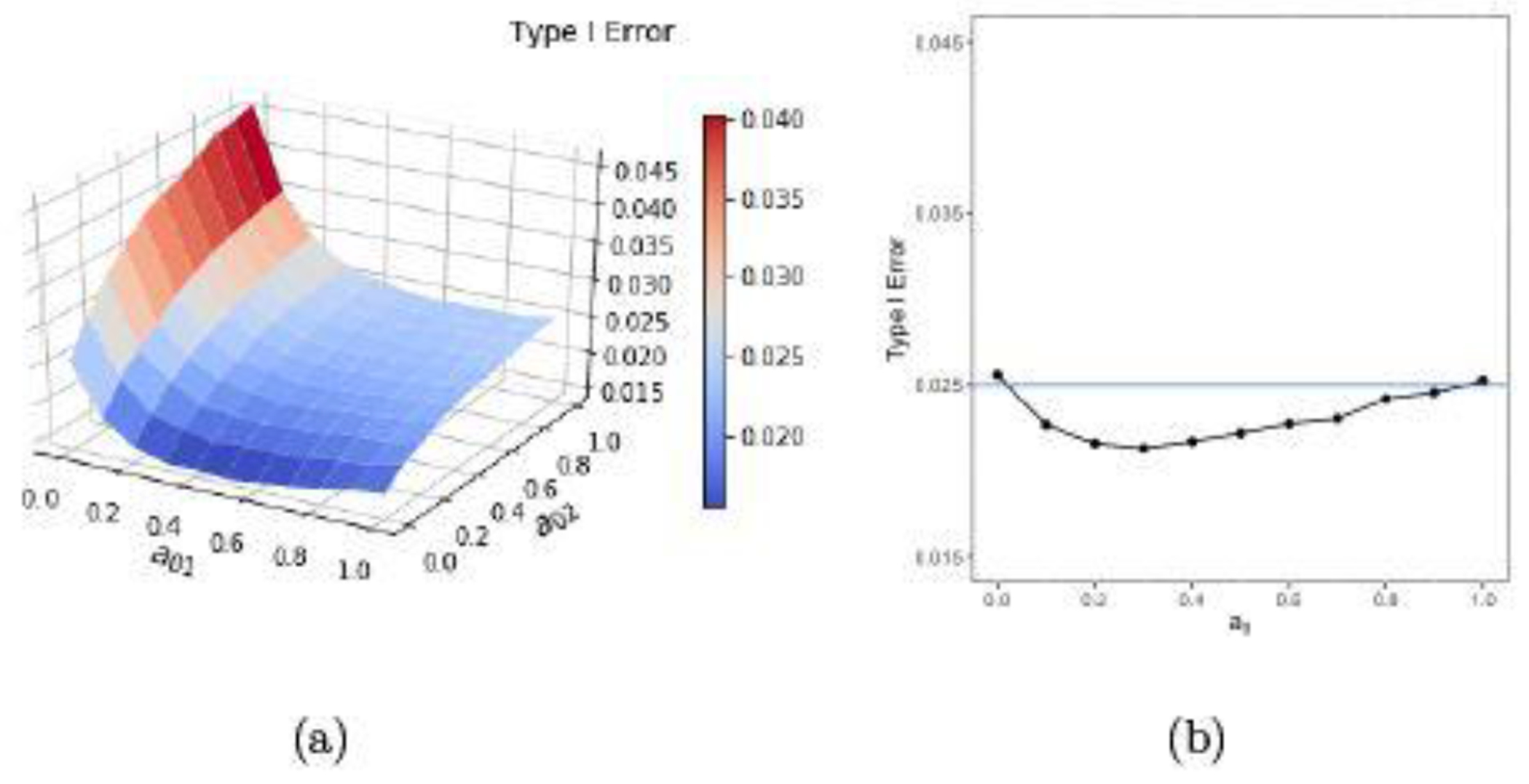
Bayesian type I errors with borrowing mean and/or variance as a function of $\left(a_{01},a_{02}\right)$ (a) and $a_0=a_{01}=a_{02}$ (b).

5. Discussion

In this paper, we develop a roadmap of Bayesian SSD as shown in Figure 1. We analytically explore the properties of the Bayesian type I error and power with noninformative priors when the variances are known. We also examine the impact of model misspecification and the choice of noninformative priors on the Bayesian type I error and power. For misspecified models, although it is a common practice that the variances for the test group and the control group are assumed to be equal under the normal distributions for a superiority trial, we empirically show that the type I error and power can be increased or decreased depending on the relationship of ${\sigma }_c^2$ and ${\sigma }_t^2$. The consequences of model misspecification are consistent for both frequentist and Bayesian methods. Also the choice of the priors matters even with noninformative priors.

For a 2 : 1 randomized controlled trial, we show that the first half in the amount of borrowing leads to more power gain than the second half in the amount of borrowing for both frequentist and Bayesian methods. This would be worth of consideration for both economical and practical point of view. We further demonstrate the risks and benefits of conditional borrowing. The type I error can be protected by the conditional borrowing, however, the power is lowered at the same time. We note that the conditional borrowing approach can be extended to the case in which multiple historical data sets are available (see the detailed elaboration in Appendix D of the Supplementary Materials).

We develop borrowing-by-parts power priors for incorporating the historical data in Bayesian SSD. The likelihood function is partitioned into the part of the parameter of primary interest and the part of the nuisance parameter, which are the mean and the variance, respectively, in the normal distribution case. By using separate discounting parameters a₀₁ and a₀₂, the historical data can be borrowed by either the mean part, or the variance part, or both. Although the borrowing-by-parts power priors are developed under the normal models, these priors can also be constructed under more general normal regression models or even more complex joint longitudinal and survival models such as those considered in Zhang et al. (2014, 2017); and Sheikh et al. (2021). As shown in Figure 3 and Table 4, borrowing the historical data can lead to inflation of type I errors when the concurrent control mean is greater than the sample mean of the historical data in certain magnitude or the variance of the future outcomes in the concurrent control arm quite differs from the sample variance of the historical data. The conditional borrowing approach discussed in Section 4.2 is quite effective in preventing inflation of type I errors, however, this approach also leads to much smaller gain in the power. Embedding the robust mixture prior and the borrowing-by-parts power priors into the conditional borrowing framework may yield a more promising approach which has a better control of the type I error and at the same time results in more gain in the power.

Although we assume that the historical data are available from the control arm, the proposed methodology can be extended to a more general case, in which the historical data are available for both the investigated product and control arms as considered in Chen et al. (2014). In this case, the borrowing-by-parts power priors may be even more attractive, which allows us to leverage different parts of the historical data within and between the investigated product arm and the control arm. When the historical effect such as the mean of the historical control is different from the mean of the concurrent control, the proposed conditional borrowing approach automatically takes this into consideration by essentially leveraging less amount of the historical data. Recently, the empirical profile approach (Wu et al., 2020) and the scale transformed power prior (Nifong et al., 2021) may be potentially more effective in dealing with different effects for the history control comparing with the concurrent control. These approaches can be integrated into our proposed borrowing-by-parts power priors and the conditional borrowing framework, which is another useful extension for the future research.