Abstract
High-resolution diffusion tensor imaging (DTI) can noninvasively probe the microstructure of cortical gray matter in vivo. In this study, 0.9-mm isotropic whole-brain DTI data were acquired in healthy subjects with an efficient multi-band multi-shot echo-planar imaging sequence. A column-based analysis that samples the fractional anisotropy (FA) and radiality index (RI) along radially oriented cortical columns was then performed to quantitatively analyze the FA and RI dependence on the cortical depth, cortical region, cortical curvature, and cortical thickness across the whole brain, which has not been simultaneously and systematically investigated in previous studies. The results showed characteristic FA and RI vs. cortical depth profiles, with an FA local maximum and minimum (or two inflection points) and a single RI maximum at intermediate cortical depths in most cortical regions, except for the postcentral gyrus where no FA peaks and a lower RI were observed. These results were consistent between repeated scans from the same subjects and across different subjects. They were also dependent on the cortical curvature and cortical thickness in that the characteristic FA and RI peaks were more pronounced i) at the banks than at the crown of gyri or at the fundus of sulci and ii) as the cortical thickness increases. This methodology can help characterize variations in microstructure along the cortical depth and across the whole brain in vivo, potentially providing quantitative biomarkers for neurological disorders.
Keywords: Cortical gray matter, Fractional anisotropy, Radiality index, Cortical depth, Cortical curvature, Cortical thickness
1. Introduction
Diffusion tensor imaging (DTI) has been extensively used over the past two decades to study white matter (WM) tracts and structural connectivity in the brain. More recently, it has also been used to noninvasively assess the microstructure of cortical gray matter (GM) (see Assaf et al., 2019 for a review), for example to study brain development (Eaton-Rosen et al., 2017; Neil and Smyser, 2018) or to detect changes in neurological disorders such as Alzheimer’s disease (Lee et al., 2020), Parkinson’s disease (Sampedro et al., 2019a), Huntington’s disease (Sampedro et al., 2019b), multiple sclerosis (Stock et al., 2020), and schizophrenia (Kim et al., 2019). However, in vivo DTI studies generally lack the spatial resolution and specificity to distinguish different cortical layers, which have a varying cytoarchitecture and myeloarchitecture along the cortical depth (Aggarwal et al., 2015; Waehnert et al., 2016; Sengupta et al., 2018). Histological studies have shown that neurodegeneration is not uniformly distributed across different cortical layers or cortical regions, which have distinct neuronal populations. For example, neuronal loss was found to be significantly higher in layers II and IV of the entorhinal cortex of patients with Alzheimer’s disease as compared to control subjects (Gómez-Isla et al., 1996). However, current imaging biomarkers of neurodegeneration, such as the cortical thickness or GM volume measured from structural MRI (Schwartz et al., 2016), lack the sensitivity to detect subtle neurodegeneration within such regions at the early stages of the disease. Thus, the development of a technique that can probe the microstructure of these selectively vulnerable neuronal populations within different cortical layers and across the whole brain in vivo is needed to enable more accurate and earlier diagnoses.
To probe variations in microstructure along the cortical depth and across a cortical thickness only ranging from approximately 1 mm to 4.5 mm, with an overall average of 2.5 mm (Fischl and Dale, 2000), a submillimeter spatial resolution is critical. High-resolution DTI studies of the cortex have shown that DTI metrics such as the fractional anisotropy (FA) (Basser and Pierpaoli, 1996) and radiality index (RI) (McNab et al., 2013) vary with the cortical depth, region-of-interest (ROI), and cortical curvature. For example, characteristic FA vs. cortical depth profiles, with local maxima and minima at specific cortical depths, were observed in both ex vivo (Kleinnijenhuis et al., 2013) and in vivo (Truong et al., 2014) studies. Furthermore, the primary somatosensory cortex in the postcentral gyrus was shown to have a primarily tangential diffusion orientation, in contrast to the primary motor cortex in the precentral gyrus and most other cortical regions, which have a primarily radial diffusion orientation (McNab et al., 2013; Gulban et al., 2018; Balasubramanian et al., 2021; Liao et al., 2021). Lastly, at the crown of gyri, the radial diffusion orientation in the deep cortical layers (close to the WM/GM interface) was shown to continue into the middle cortical layers, whereas at the banks or the fundus of sulci, the tangential diffusion orientation in the deep cortical layers transitions into a radial diffusion orientation in the middle cortical layers (Kleinnijenhuis et al., 2015; Cottaar et al., 2018; Schilling et al., 2018). However, none of these studies has simultaneously analyzed the FA and RI dependence on the cortical depth, ROI, cortical curvature, and cortical thickness across the whole brain, which would provide a more specific, systematic, and comprehensive assessment of the cortical microstructure.
Given the challenge to achieve a high spatial resolution, whole-brain coverage, and short scan time, most prior in vivo DTI studies used either a highly anisotropic voxel size or an isotropic voxel size of 1 mm or higher, and either covered only part of the brain or required a scan time ranging from 40 to 65 min to cover the whole brain. More recent studies using cutting-edge DTI acquisition and reconstruction techniques (Dai et al., 2021; Liao et al., 2021; Wang et al., 2021; Ramos-Llordén et al., 2021) have been able to achieve a shorter scan time and/or higher isotropic resolution (e.g., 600–860 μm) in the whole brain with a high signal-to-noise ratio (SNR) and high spatial fidelity. In some cases, however, the scan time was still long (e.g., 117 min or even 14.5 h across multiple sessions).
Here, we propose a column-based analysis that samples the FA and RI along radially oriented cortical “columns” using 0.9-mm isotropic whole-brain DTI data acquired in healthy subjects, thereby enabling a quantitative analysis of the FA and RI dependence on the cortical depth, ROI location, ROI size, cortical curvature, and cortical thickness across the whole brain. In this initial study, we develop the data acquisition and analysis pipeline and investigate the consistency of the results in healthy subjects, both between repeated scans from the same subjects and across different subjects, to better understand how the FA and RI vary as a function of the cortical depth, ROI, cortical curvature, and cortical thickness. Our long-term goal is to use this methodology to identify differences in the FA and RI vs. cortical depth profiles between patients and healthy controls to provide quantitative biomarkers for neurological disorders.
2. Methods
2.1. Data acquisition
Six healthy subjects (3 males, 3 females, age = 29 ± 7 years) were scanned on a 3T Premier Ultra-High Performance (UHP) MRI scanner (GE Healthcare, Milwaukee, WI) equipped with a 48-channel phasedarray head coil and a 60-cm gradient system with 100 mT/m amplitude and 250 T/m/s maximum slew rate. All subjects provided written informed consent to participate in this study under a protocol approved by the Duke University Health System Institutional Review Board. Foam paddings were inserted between the subject’s head and the head coil to minimize subject motion.
Whole-brain DTI data were acquired with a spin-echo multi-band multi-shot echo-planar imaging (EPI) sequence and the following parameters: acquisition plane = axial, number of bands = 2, number of shots = 4, repetition time = 8530 ms, echo time = 63.2 ms, field-of-view (FOV) = 154.8 mm × 309.6 mm (right/left × anterior/posterior), matrix size = 172 × 344 (frequency-encoding × phase-encoding), voxel size = 0.9 mm isotropic, number of slices = 134, partial Fourier ratio = 69%, b-value = 800 s/mm2, number of uniformly sampled diffusion-weighting directions = 38 (see Supplementary Material), number of baseline (b = 0) images = 4, scan time = 23:53 min. A blipped-CAIPI (Setsompop et al., 2012) shift by FOV/2 in the phase-encoding direction was applied to one of the two bands and a rectangular FOV was used to remove the overlap between the unshifted and shifted brain slices from the two bands, and hence the corresponding g-factor penalty. One additional set of b = 0 images was acquired with a reverse phase-encoding polarity to perform distortion correction.
Whole-brain T1-weighted anatomical images were also acquired with a 3D magnetization-prepared rapid acquisition gradient echo (MPRAGE) sequence and the following parameters: acquisition plane = axial, repetition time = 2180 ms, inversion time = 900 ms, echo time = 3.3 ms, flip angle = 8°, FOV = 230.4 mm × 230.4 mm, matrix size = 256 × 256, voxel size = 0.9 mm isotropic, number of slices = 134, acceleration factor = 2, scan time = 5 min. The total scan time for the entire protocol, which also included a short localizer and calibration scan, was about 30 min. Three out of the six subjects (subjects 1–3) were scanned twice on different days to assess the reproducibility of the results.
2.2. Data reconstruction
The DWI images were reconstructed with a multi-band multiplexed sensitivity-encoding (MB-MUSE) algorithm (Chen et al., 2013; Bruce et al., 2017) implemented in MATLAB (The MathWorks, Natick, MA) to correct for the shot-to-shot motion-induced phase errors (Fig. 1). The k-space data were first corrected for Nyquist ghosting artifacts by estimating the phase differences between even and odd ky lines from a reference scan. The corrected k-space data from each of the 4 shots were then reconstructed with a multi-band sensitivity-encoding (MB-SENSE) algorithm (Fig. 1A). In contrast to previous MUSE reconstruction algorithms (Chen et al., 2013; Bruce et al., 2017), the reconstructed complex images were then denoised slice-by-slice by using the Marchenko-Pastur principal component analysis (MPPCA) method, as implemented in the MRtrix3 command dwidenoise (Veraart et al., 2016; Cordero-Grande et al., 2019), which models the noise distribution within patches in the 2D images along both the shot and diffusion-weighting direction dimensions. This method ensures that the phase maps from the denoised images (Fig. 1C) are smoother than the original phase maps (Fig. 1B), but without becoming blurry at the anatomical boundaries. (Supplementary Fig. S1 shows that it results in less noisy FA maps than a conventional smoothing of the phase maps with a Hanning filter.) The inputs of this MPPCA denoising were the complex images reconstructed with MB-SENSE for each slice, all shots, and all diffusion-weighting directions. Thus, the input for each slice had a size of 172 × 344 × 1 × 168, since there were 4 shots × (4 b = 0 images + 38 diffusion-weighting directions) = 4 × 42 = 168, and a patch size of 13 × 13 × 1 ≈ 168 was chosen, as suggested by MRtrix3. Motion-induced phase errors from shot to shot were then corrected by modulating the coil sensitivity maps for individual shots with the corresponding denoised phase maps. Finally, the aliased images from all 4 shots were combined to reconstruct the final unaliased images (Fig. 1D).
Fig. 1.
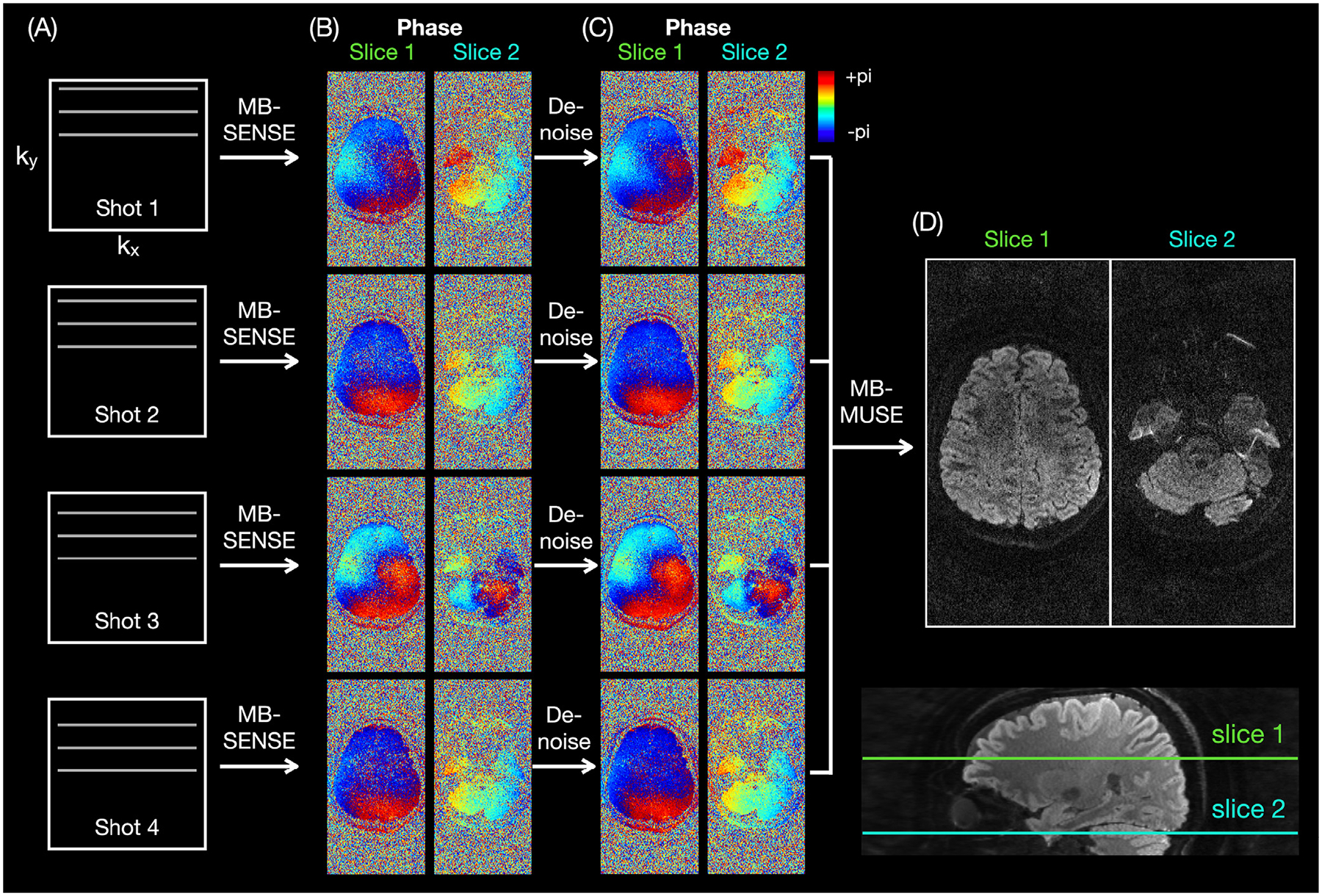
MB-MUSE reconstruction. The k-space data from each shot (A) are first reconstructed with MB-SENSE, resulting in noisy phase maps (B). The complex images are then denoised, resulting in phase maps that are smoother, but without blurring at the brain boundaries (C). Finally, the denoised phase maps are used to correct for the shot-to-shot motion-induced phase errors and to reconstruct the final images (D).
2.3. Data processing
Each DWI image volume reconstructed with MB-MUSE was preprocessed by applying MPPCA denoising (Veraart et al., 2016; Cordero-Grande et al., 2019) with the MRtrix3 command dwidenoise and a default patch size of 5 × 5 × 5 for our number of diffusion-weighting directions. This method was previously shown to improve the precision in the estimation of diffusion parameters, including the principal eigenvector V1, without compromising the accuracy and spatial resolution (Veraart et al., 2016). The denoised DWI images were then further preprocessed by applying Gibbs artifact removal (Kellner et al., 2016), susceptibility-induced distortion correction using the pairs of b = 0 images with opposite phase-encoding polarities (Andersson et al., 2003), eddy current-induced distortion correction (Andersson and Sotiropoulos, 2016), and bias field correction with MRtrix3 (Tournier et al., 2019) and FSL (Smith et al., 2004) (Fig. 2A).
Fig. 2.
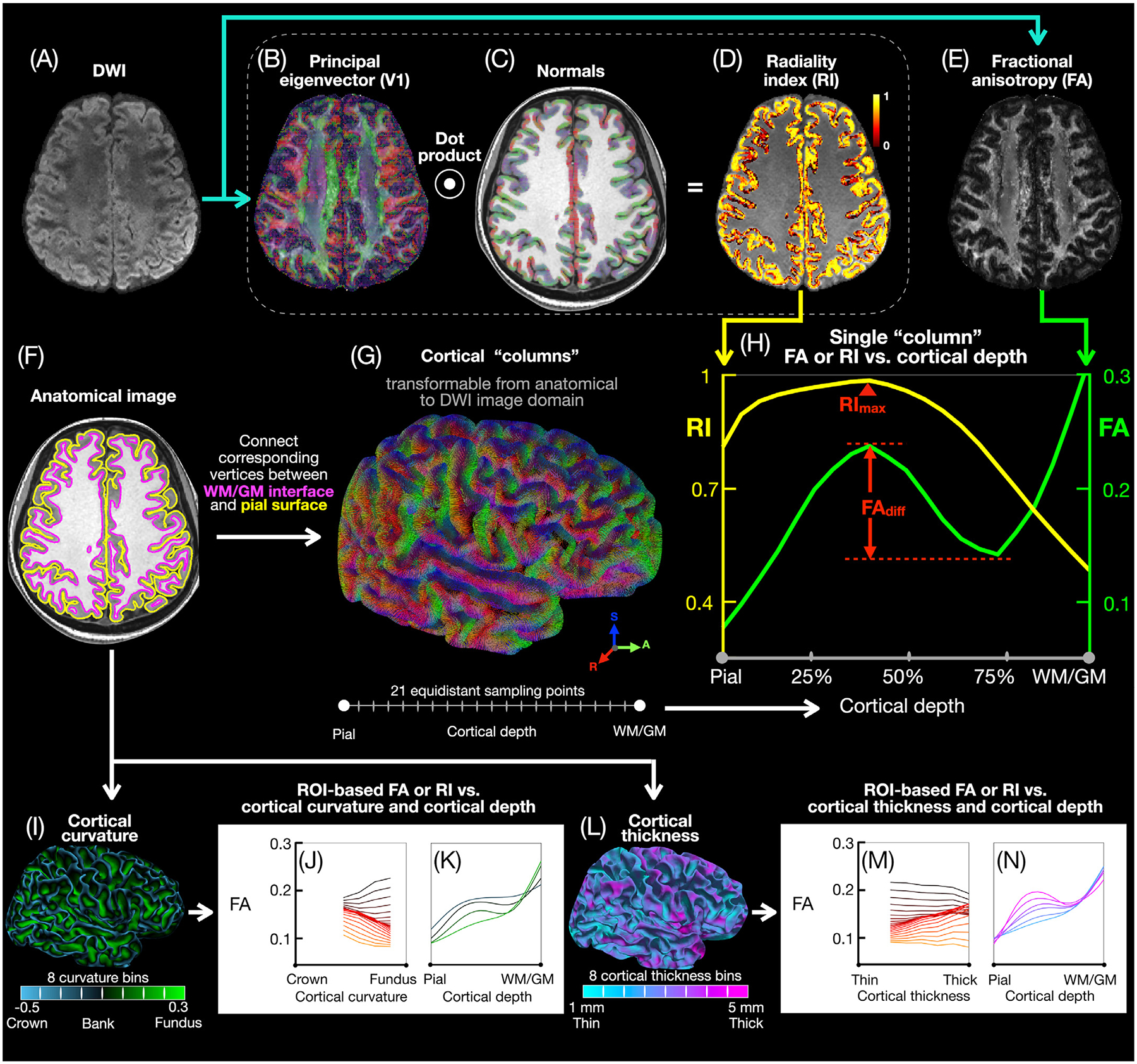
Cortical column-based and ROI-based analysis pipeline. After preprocessing, the DWI images (A) are used to derive V1 (B), RI (D), and FA (E) maps. The T1-weighted anatomical images are used to generate pial (yellow) and WM/GM (magenta) surface meshes (F) and normal vectors (C) to the WM/GM surface. Cortical “columns” (G) are generated by connecting corresponding vertices from the pial and WM/GM surface meshes, with 21 equidistant sampling points along each column, then transformed from the anatomical image domain to the DWI image domain to generate single-column FA and RI vs. cortical depth profiles (H), typically showing an FA local maximum and minimum (separated by FAdiff) and a single RI maximum (RImax). The cortical columns across all subjects are equally binned into 8 cortical curvature bins from the gyral crown to the sulcal fundus (I) or into 8 cortical thickness bins (L) to generate, in each ROI, FA and RI vs. cortical depth profiles for different curvature (K) or cortical thickness (N) bins as well as FA and RI vs. curvature (J) or cortical thickness (M) profiles for different cortical depths.
As recommended by MRtrix3, the DWI images were upsampled by a factor 2 with a cubic interpolation before calculating the diffusion tensor because doing so can reveal anatomical details not seen without upsampling (Dyrby et al., 2014). The diffusion tensor was then estimated by using the MRtrix3 command dwi2tensor with the default setting, which consisted of two steps: (1) weighted least-squares fit with weights based on the empirical signal intensities (Basser et al., 1994); (2) two iterations of weighted least-squares fit with weights determined by the signal predictions from the previous iteration (Veraart et al., 2013). V1 maps (Fig. 2B) and FA maps (Fig. 2E) were then generated in the DWI image domain.
The anatomical images were used with FreeSurfer (Fischl et al., 1999) to generate a pial surface mesh and a WM/GM surface mesh (Fig. 2F), along with the normal vector (Viessmann et al., 2019) to the WM/GM surface (Fig. 2C), the cortical curvature (Fig. 2I), and the cortical thickness (Fig. 2L) at each vertex in the anatomical image domain. The total area of the WM/GM surface mesh divided by the total number of vertices was 0.55 ± 0.01 mm2 (mean ± standard deviation across all subjects). The T2-weighted b = 0 images were registered to the anatomical images by using the FreeSurfer command bbregister with an affine transformation, resulting in a transformation matrix M. The registered b = 0 images were also included in the FreeSurfer reconstruction to improve the accuracy of the pial surface.
2.4. Column-based cortical depth analysis
Cortical “columns” (Fig. 2G) were generated by connecting corresponding pairs of vertices from the pial and WM/GM surface meshes, which were essentially the same surface mesh with the same vertices at different cortical depths. Generating FA and RI vs. cortical depth profiles requires FA and RI maps derived from the DWI images to be sampled along cortical columns derived from the anatomical images. However, registering the DWI images to the anatomical images to derive FA and RI maps in the anatomical image domain would cause blurring in the DWI images and inaccuracies in the FA and RI maps. Conversely, registering the anatomical images to the DWI images to derive cortical columns in the DWI image domain would cause blurring in the anatomical images and inaccuracies in the cortical columns (as well as the cortical curvature and cortical thickness values). To avoid any interpolation of the DWI or anatomical images, the cortical columns derived in the anatomical image domain were transformed to the DWI image domain by applying the inverse of the transformation matrix M to all vertices from the pial and WM/GM surface meshes. This method allowed the FA maps derived in the DWI image domain to be directly sampled along each transformed column at 21 equidistant cortical depths from the pial surface to the WM/GM surface (i.e., with a step size of 5% of the cortical thickness) to generate FA vs. cortical depth profiles (Fig. 2H, green), with FAdiff denoting the difference between the local maximum and minimum in the FA profile of each column, if any. The FA local maximum and minimum were determined by using the Matlab functions islocalmax and islocalmin to find all local maxima and minima within cortical depths ranging from 10% to 90% (if any) and then choosing those resulting in the largest FAdiff (if more than one local maximum or minimum).
Similarly, the normals to the WM/GM surface derived in the anatomical image domain were transformed to the DWI image domain by applying the inverse of the transformation matrix M. The dot product between these transformed normals and the V1 vectors derived in the DWI image domain were calculated to generate RI maps (Fig. 2D) (McNab et al., 2013), which were then sampled along each transformed column at 21 equidistant cortical depths to generate RI vs. cortical depth profiles (Fig. 2H, yellow), with RImax denoting the global maximum in the RI profile of each column. Even though the average cortical thickness only spans about 3 voxels, the pial and WM/GM surface meshes, and hence the cortical columns, are arbitrarily oriented with respect to the voxels, so that using 21 sampling points enables a more uniform sampling of the FA and RI values when averaging columns within an ROI, as opposed to using only 4 sampling points (see Koopmans et al. (2011) for a discussion of the effective resolution of cortical sampling). In addition, the FA and RI at the pial, middle (50% cortical depth), and WM/GM surfaces as well as the FAdiff and RImax of each column were displayed on the inflated cortical surface of each subject.
2.5. ROI-based cortical depth analysis
The easy_lausanne version (https://github.com/mattcieslak/easy_lausanne) of the Connectome Mapper (Daducci et al., 2012) was used to parcellate each subject’s brain according to the Lausanne multi-scale cortical parcellation (Cammoun et al., 2012), resulting in 5 atlases per subject containing 1000, 448, 219, 114, or 68 ROIs, with the larger ROIs encapsulating the smaller ROIs sequentially and with the latter atlas (containing 68 ROIs) corresponding to the Desikan-Killiany atlas (Desikan et al., 2006). The FA and RI vs. cortical depth profiles of single cortical columns were then averaged in each of these ROIs. For each ROI, correlation coefficients of these averaged profiles were calculated, either between both DTI scans from subjects 1–3 or across one DTI scan from each of the 6 subjects, to assess the consistency of the results between repeated scans from the same subjects or across different subjects, respectively. More specifically, Pearson’s correlation coefficients of these profiles (i.e., their covariance divided by the product of their standard deviations) were calculated to measure the linear correlation between them. The correlation coefficients across the 6 subjects were calculated as the average of the correlation coefficients from all 15 possible pairs of subjects. In addition, GM partial volume maps were also generated from the anatomical images with FreeSurfer, sampled along each cortical column in the anatomical image domain by using the MRtrix3 command mesh2voxel, and then averaged in each ROI to generate GM fraction vs. cortical depth profiles.
2.6. ROI-based cortical curvature and cortical thickness analyses
All cortical columns across the 6 subjects were binned into cortical curvature bins from the gyral crown to the sulcal fundus according to the FreeSurfer curvature value (Fig. 2I). This curvature was calculated at each vertex of the WM/GM surface mesh as the average of the two principal curvatures, which are the maximal and minimal curvatures of the two orthogonal tangent directions for which the curvatures are extremal (Pienaar et al., 2008). Similarly, all of the cortical columns were also binned into cortical thickness bins from 1 to 5 mm according to the FreeSurfer cortical thickness value (Fig. 2L), which was derived from the pial and WM/GM surface meshes and which could be any value rather than integer multiples of the voxel size. For both the curvature and cortical thickness, 8 bins were used to obtain relatively smooth FA and RI vs. curvature or cortical thickness profiles, while also ensuring that each bin contained a sufficiently high number of columns, which was further enforced by excluding bins containing less than 2000 columns from further analyses. For each ROI of the atlas with 68 ROIs, the FA and RI were averaged across one DTI scan from each of the 6 subjects, at each cortical depth and within each curvature bin or each cortical thickness bin, to generate FA and RI vs. cortical depth profiles for different curvature bins (Fig. 2K) or different cortical thickness bins (Fig. 2N) as well as FA and RI vs. curvature profiles (Fig. 2J) or vs. cortical thickness profiles (Fig. 2M) for different cortical depths. The FAdiff and RImax of each column were also averaged within each curvature bin or each cortical thickness bin to generate FAdiff and RImax vs. curvature or cortical thickness profiles.
3. Results
3.1. V1, RI, and FA maps
Fig. 3 shows representative high-resolution DWI images and DTI metrics revealing fine details of the cortical microstructure. For example, the V1 maps (Fig. 3B,F) show a primarily radial diffusion orientation in most cortical regions, as exemplified by the zoomed-in V1 maps of the precentral gyrus and the inferior and superior parietal cortices. This radial diffusion orientation, for which the angle between the V1 vector and the normal vector to the WM/GM surface is close to 0°, corresponds to a high RI in the RI maps (Fig. 3C,G). A different diffusion orientation observed in some voxels near the pial surface or WM/GM interface could be due to partial volume effects or misregistration between the DWI and anatomical images. The FA maps (Fig. 3D,H) show a band of low FA near the WM/GM interface in most cortical regions, as pointed to by the arrowheads in the FA maps. These bands of low FA can be observed along any direction rather than only along the frequency-encoding (right/left) direction, which suggests that they are not caused by residual Gibbs ringing artifacts. In the postcentral gyrus of both hemispheres, however, there is a primarily tangential diffusion orientation, lower RI values, and no band of low FA, which has also been observed in other studies (McNab et al., 2013; Gulban et al., 2018; Balasubramanian et al., 2021; Liao et al., 2021; Cottaar et al., 2018). While the two largest eigenvalues λ1 and λ2 are more different in the WM than in the GM, as expected, they are nevertheless generally still significantly different in the cortical GM, whether the diffusion orientation is primarily radial or tangential (Supplementary Fig. S2). The variations in FA and RI along the cortical depth and their characteristic features can be better visualized and quantified by using the proposed cortical column-based analysis, as shown below.
Fig. 3.
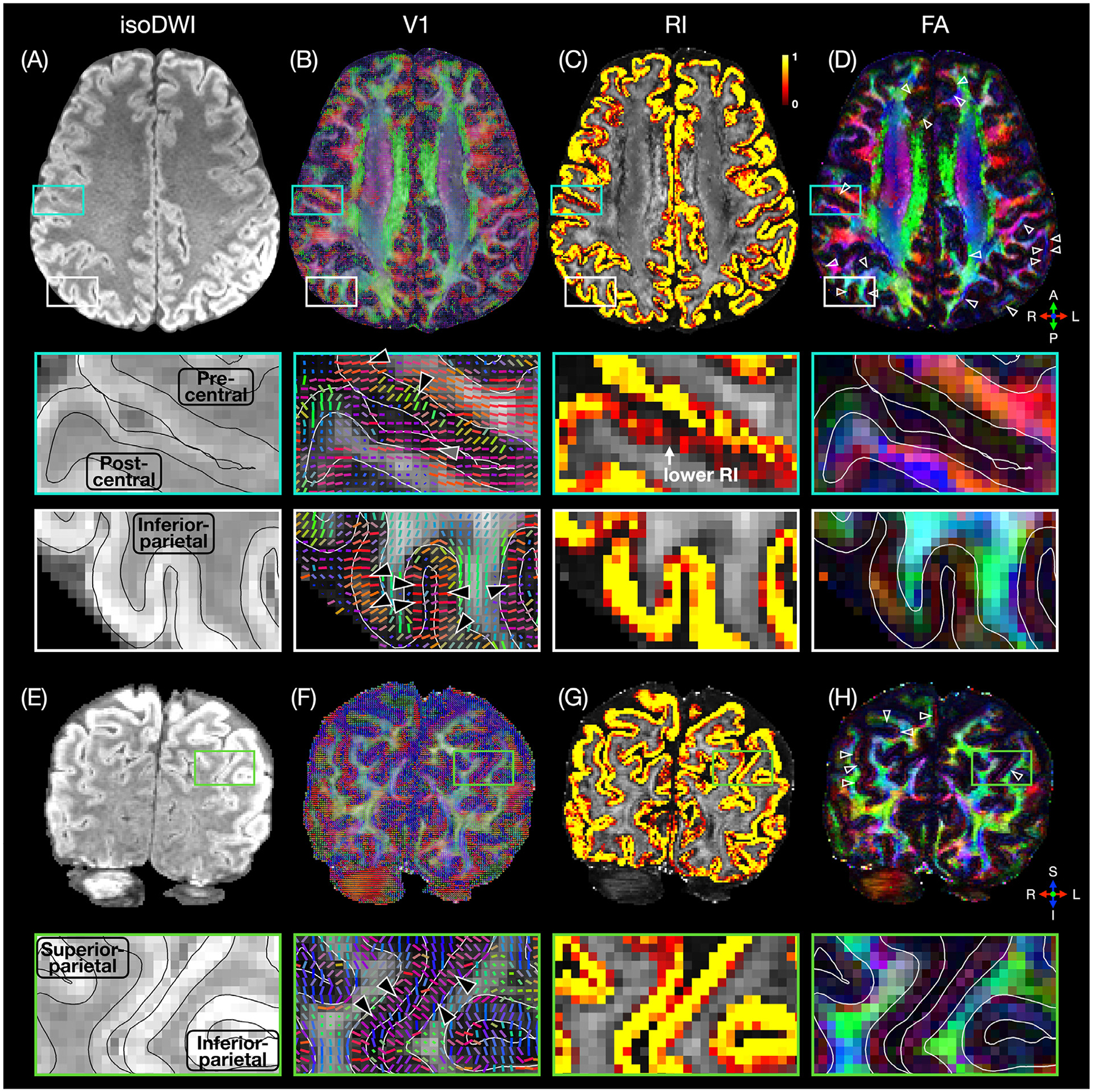
Axial and coronal isoDWI images (mean of all diffusion-weighted images; A,E), V1 maps (B,F), RI maps (C,G), and color-coded FA maps (D,H) from subject 3, showing a primarily radial diffusion orientation (black arrowheads in B,F), high RI values, and a band of low FA (open arrowheads in D,H) in most cortical regions, but a primarily tangential diffusion orientation (gray arrowhead in B), lower RI values, and no band of low FA in the postcentral gyrus. The black and white lines denote the pial surface and WM/GM interface derived from the registered T1-weighted anatomical images.
3.2. ROI-based FA and RI vs. cortical depth
Fig. 4 shows the ROI-based FA and RI vs. cortical depth profiles across the 6 subjects in 8 representative ROIs from each of the 5 at-lases. The profiles in most ROIs show characteristic shapes, with the FA profiles having a local maximum and a local minimum (or at least two inflection points) and the RI profiles having a single maximum at intermediate cortical depths. However, the postcentral ROI does not show any FA peaks and has much lower RI values compared to other ROIs (Fig. 4I, arrowheads). Overall, FAdiff decreases as the ROI size increases (black arrows) because more cortical columns are averaged in larger ROIs and because their FA profiles may vary within the ROIs. The RI profiles tend to be more similar for different ROI sizes, although in some cases (e.g., inferior and superior parietal ROIs) they become broader and flatter as the ROI size increases, again because more cortical columns are averaged in larger ROIs and because their RI profiles may vary within the ROIs.
Fig. 4.
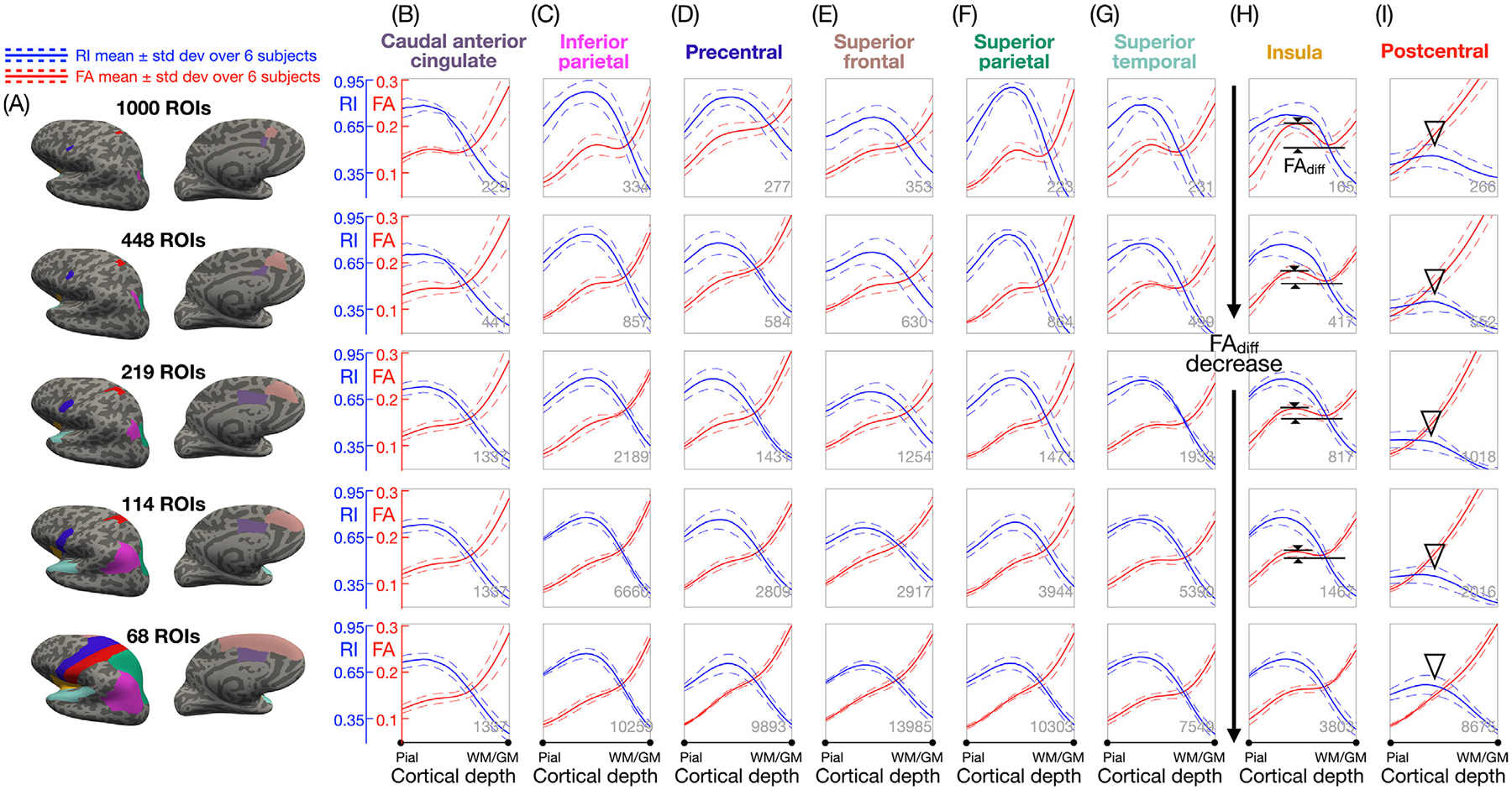
(A) 8 representative ROIs from each of the 5 atlases shown on inflated cortical surfaces, with the larger ROIs encapsulating the smaller ROIs sequentially. Note that the left and right hemispheres of the first four atlases are not symmetrical and that only results from the left hemisphere are displayed here. (B-I) Mean (solid lines) ± standard deviation (dashed lines) across the 6 subjects of the FA (red) and RI (blue) vs. cortical depth profiles in each of these ROIs, showing that FAdiff decreases as the ROI size increases (black arrows) and that there are no FA peaks and a lower RImax in the postcentral ROI (arrowheads). The number of cortical columns in each ROI (averaged over all 6 subjects) is shown at the bottom right corner of each plot.
Supplementary Figs. S3 and S4 show the ROI-based FA and RI vs. cortical depth profiles for each of the two DTI scans from subjects 1–3 and for the single DTI scan from subjects 4–6 to better visualize the consistency of the profiles within and across subjects. Profiles of the same color, representing pairs of repeated scans from the same subjects, generally align very well across all ROIs. The consistency across profiles of different colors, representing different subjects, is also high, although there is a higher consistency within subjects than across subjects, as expected.
Supplementary Figs. S5–S7 show DWI images, FA maps, and ROI-based FA and RI vs. cortical depth profiles without vs. with MPPCA denoising of the DWI images. The denoising substantially reduced the noise in the DWI images and FA maps, resulting in somewhat lower FA values in the FA profiles. However, the shape of these profiles and the corresponding local maximum and minimum (or inflection points) remain very similar. With denoising, the RI profiles are also very similar, with slightly higher RI values in most ROIs and slightly lower RI values in the postcentral ROI. Supplementary Figs. S8 and S9 show that up-sampling the DWI images by a factor 2 before calculating the diffusion tensor results in very similar FA and RI vs. cortical depth profiles, but with more prominent FA and RI peaks.
Supplementary Figs. S10 and S11 show that using a somewhat smaller or larger number of sampling points (i.e., 11 or 31 instead of 21) results in virtually identical FA and RI vs. cortical depth profiles. Supplementary Figs. S12 and S13 show that using a slightly higher or lower spatial resolution for both the DTI and anatomical scans (i.e., 0.8 or 1.0 mm instead of 0.9 mm isotropic and with 30 or 46 instead of 38 diffusion-weighting directions, respectively, to maintain a similar DTI scan time) results in very similar FA and RI vs. cortical depth profiles in most ROIs, with a few exceptions likely due to the trade-off between spatial resolution and SNR. All of these results show that the denoising and upsampling of the DWI images were beneficial, whereas the number of sampling points and spatial resolution (in the 0.8–1.0 mm range) did not significantly change the findings.
To provide more quantitative results, Fig. 5 shows the correlation coefficients of the FA and RI vs. cortical depth profiles, either between both DTI scans of subject 1 (Fig. 5B,D) or across one DTI scan from each of the 6 subjects (Fig. 5C,E), in each ROI of the 5 atlases. Additionally, Supplementary Fig. S14 shows the correlation coefficients between both DTI scans of subjects 2 and 3. The mean correlation coefficients between both scans of subjects 1–3 averaged over all ROIs of each atlas range from 0.959 to 0.994 for the FA profiles and from 0.897 to 0.993 for the RI profiles. The mean correlation coefficients across the 6 subjects averaged over all ROIs of each atlas are slightly lower, as expected, and range from 0.923 to 0.972 for the FA profiles and from 0.835 to 0.970 for the RI profiles. As the ROI size increases, the correlation coefficients increase for the RI profiles, whereas they increase and then decrease for the FA profiles. Yet, all of these correlation coefficients are very high, in agreement with the results from Supplementary Figs. S3 and S4, and show that the image acquisition, reconstruction, post-processing, and column-based cortical depth analysis can generate consistent FA and RI profiles, both between repeated scans from the same subjects and across different subjects.
Fig. 5.
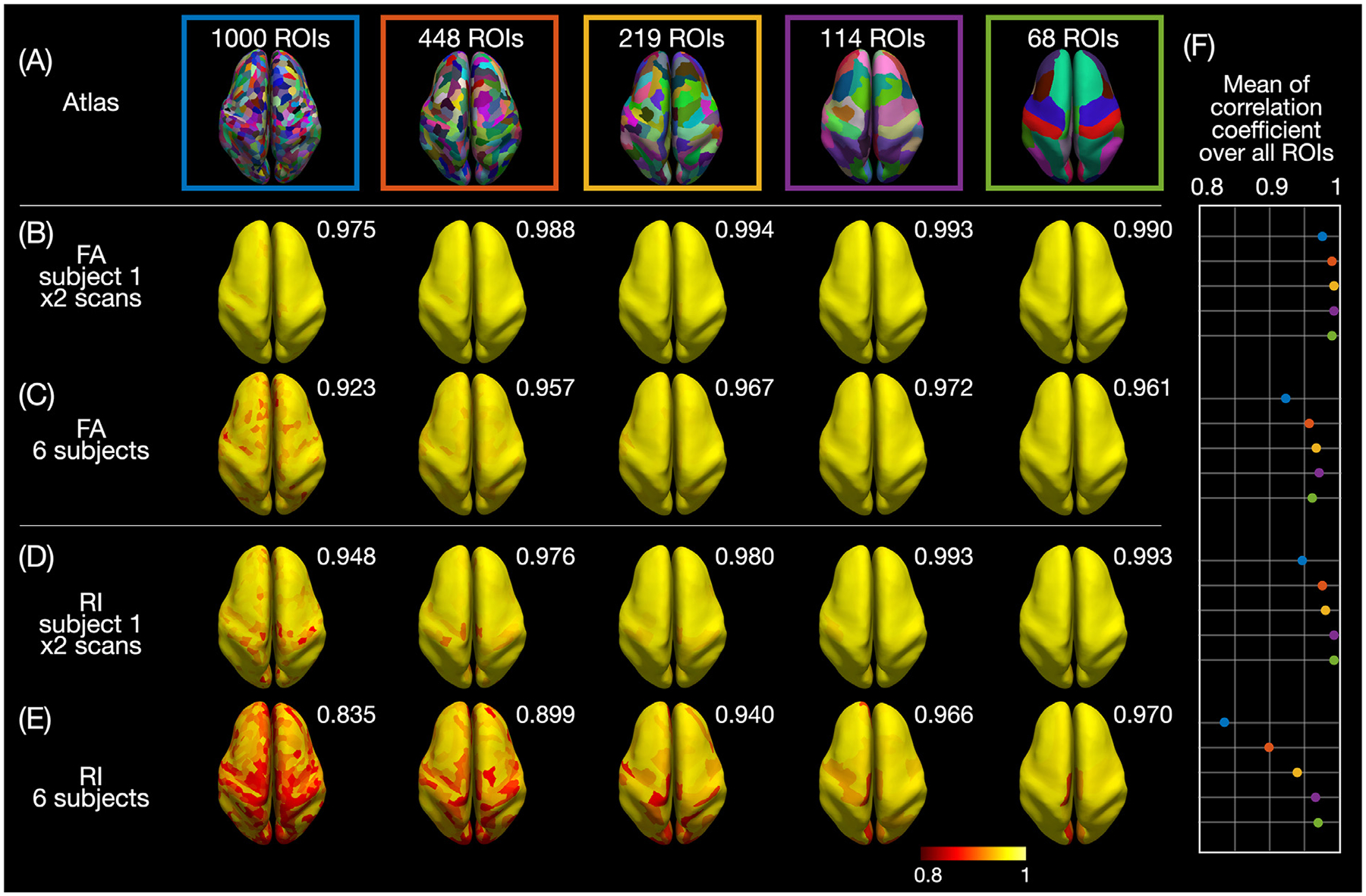
(A) ROIs from the 5 atlases displayed on the inflated cortical surface of subject 1. Correlation coefficient of the FA (B,C) or RI (D,E) vs. cortical depth profiles between both DTI scans of subject 1 (B,D) or across one DTI scan from each of the 6 subjects (C,E) calculated in each ROI and displayed on inflated cortical surfaces. (F) Plot of the mean correlation coefficients averaged over all ROIs (also shown at the top right corner of each brain).
Supplementary Fig. S15 shows the ROI-based GM fraction vs. cortical depth profiles. This fraction is about 0.5 near the pial surface and the WM/GM interface. Partial volume contaminations from cerebrospinal fluid (CSF), in which diffusion is isotropic, could decrease the FA and increase the noise in the RI measurement near the pial surface, whereas partial volume contaminations from WM could either increase or decrease the FA or RI near the WM/GM interface, depending on whether the diffusion orientation in the neighboring WM and GM regions is predominantly radial or tangential. In most ROIs, however, the GM fraction is close to 1 at intermediate cortical depths where the FA and RI peaks are located, showing that the FA and RI profiles are minimally affected by partial volume contaminations from CSF or WM at these cortical depths. The postcentral ROI, which has a smaller cortical thickness, has a narrower profile compared to other ROIs and may thus be more affected by partial volume effects.
3.3. Column-based FA and RI vs. cortical depth
Fig. 6 shows the column-based cortical curvature, cortical thickness, FA and RI at three cortical depths, as well as FAdiff and RImax on the inflated cortical surface of each subject. The DTI metrics show some patterns that are similar between the repeated scans from subjects 1–3 and across the 6 subjects and that are also correlated with the cortical curvature and cortical thickness. For example, blue arrowheads point to a thin band of high FA and RI (yellow bands in Fig. 6D,G) at the crown of the postcentral gyrus (blue band in Fig. 6A), while cyan arrowheads point to an adjacent wide band of high FA (yellow band in Fig. 6E), low FAdiff (gray band in Fig. 6F), and low RI and RImax (red bands in Fig. 6H,J) where the cortical thickness is the smallest (cyan band in Fig. 6B). As another example, red arrowheads in Fig. 6F point to a wide band of high FAdiff at the bank lateral to the intraparietal sulcus in the inferior parietal lobule, while yellow and white arrowheads point to two surrounding thin bands of low FAdiff at the crown and at the fundus, respectively, which will be shown more quantitatively in the FAdiff vs. curvature profiles in Fig. 7E.
Fig. 6.
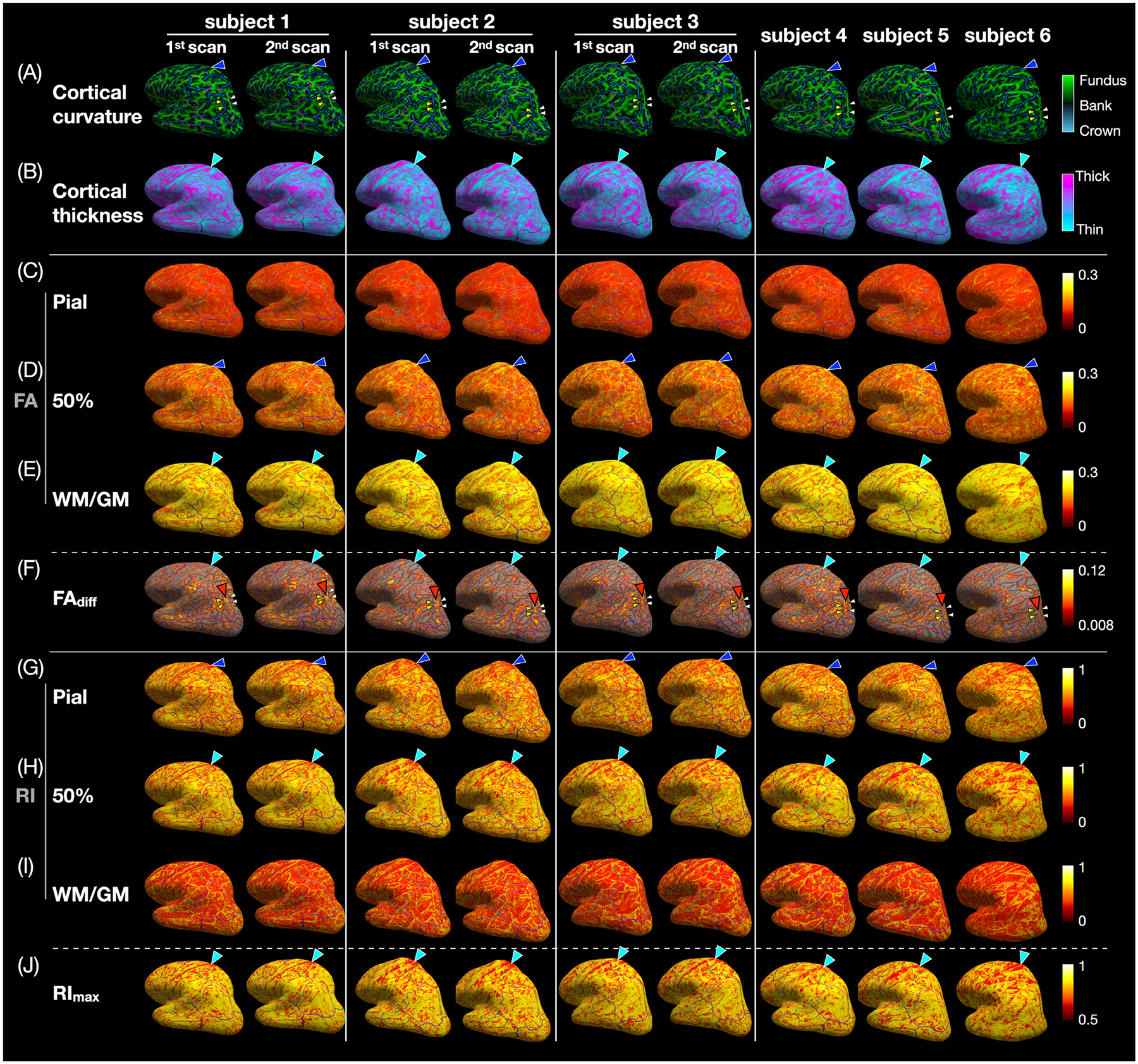
(A) Cortical curvature, (B) cortical thickness, (C-E) FA at the pial, middle, and WM/GM surfaces, (F) FAdiff, (G-I) RI at the pial, middle, and WM/GM surfaces, and (J) RImax displayed on each subject’s inflated cortical surface. In the postcentral gyrus, there is a thin band of high FA and RI at the crown (blue arrowheads) next to a wide band of high FA, low FAdiff, low RI, and low RImax where the cortical thickness is the smallest (cyan arrowheads). At the bank lateral to the intraparietal sulcus, there is a wide band of high FAdiff (red arrowheads) between two thin bands of low FAdiff at the crown (yellow arrowheads) and at the fundus (white arrowheads). In (D), the regions with FAdiff < 0.008 (i.e., with no significant FA local maximum and minimum in the FA vs. cortical depth profiles) are not color-coded and instead show the underlying inflated cortical surface, which is light gray in regions with a curvature between ± 0.15 (banks) and dark gray in regions with a curvature smaller than −0.15 (crown) or larger than 0.15 (fundus).
Fig. 7.
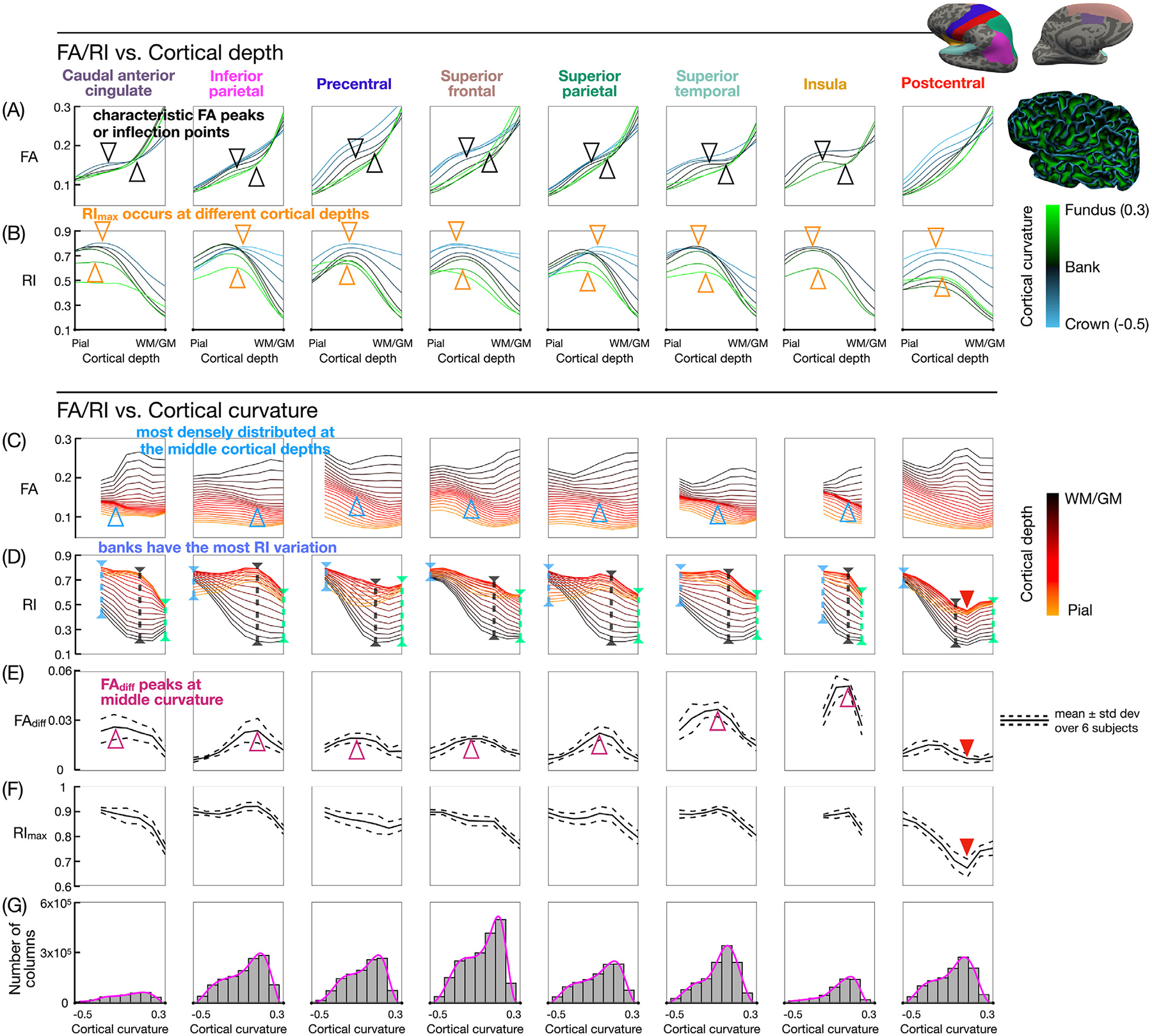
(A,B) FA and RI vs. cortical depth profiles at different curvature bins, color-coded from blue (crown) to black (banks) to green (fundus). (C,D) FA and RI vs. curvature profiles at different cortical depths, color-coded from orange (pial surface) to black (WM/GM interface). (E,F) FAdiff and RImax vs. curvature profiles. The FA local maximum and minimum (or inflection points) at the middle cortical depths and middle curvature bins (black arrowheads) correspond to the more densely distributed FA vs. curvature profiles (blue arrowheads) and to the peak in the FAdiff vs. curvature profiles (magenta arrowheads). RImax occurs at a different cortical depth and is lower in value towards the fundus (downward orange arrowheads) than towards the crown (upward orange arrowheads). The largest variation in RI along the cortical depth occurs at the banks (black dashed lines). The postcentral ROI shows lower RI, FAdiff, and RImax values (red arrowheads). (G) Histograms of the cortical curvature, with pink lines denoting the probability density function. Bins containing less than 2000 columns are excluded from the curvature-based analysis.
3.4. ROI-based FA and RI vs. cortical depth, cortical curvature, and cortical thickness
Fig. 7 shows how the cortical curvature affects the shape of the FA and RI vs. cortical depth profiles. Fig. 7A shows that the FA profiles have a more pronounced local maximum and minimum (or inflection points) at the middle curvature bins (black arrowheads) than at the fundus or the crown. Fig. 7B shows that the RI profiles towards the fundus have a peak that occurs at a different cortical depth and with a lower RImax value compared to the RI profiles towards the crown (orange arrowheads). These profiles also show that the RI tends to be lower at the WM/GM interface (i.e., more tangential diffusion orientation), higher at the middle cortical depth (i.e., more radial diffusion orientation), and somewhat lower again at the pial surface. This trend is more pronounced at the banks (black lines) than at the crown (blue lines) or the fundus (green lines). At the WM/GM interface, the RI is higher at the crown than at the banks or the fundus.
Fig. 7C shows that the FA vs. curvature profiles are more densely distributed and/or overlapped at the middle cortical depths than at the pial surface or the WM/GM interface and at the middle curvature bins than near the fundus or the crown (blue arrowheads). This denser distribution corresponds to the FA local maximum and minimum (or inflection points) in the FA vs. cortical depth profiles (Fig. 7A, black arrowheads) and to the peak in the FAdiff vs. curvature profiles (Fig. 7E, magenta arrowheads), both of which occur at the middle curvature bins. Specifically, since Fig. 7A and C both show the same FA data as a function of the cortical depth and curvature, but plotted in two different ways, moving along one of the lines in Fig. 7A, which represents a given curvature bin, is equivalent to moving vertically through different lines in Fig. 7C, which represent different cortical depths. Thus, if a line in Fig. 7A has a local maximum and minimum (or two inflection points), the lines in Fig. 7C at the corresponding curvature bin are more widely distributed near the pial surface and WM/GM interface and more densely distributed and/or overlapped at the middle cortical depths. Fig. 7D shows that there is a larger variation in RI along the cortical depth at the banks (black dashed lines) than near the crown (blue dashed lines) or the fundus (green dashed lines), which is consistent with Fig. 7B. Fig. 7E shows that FAdiff is larger at the banks than near the crown or fundus, which is also observed in Fig. 6F (red, yellow, and white arrowheads, respectively) and which is consistent with Fig. 7A. Finally, the postcentral ROI shows unique profiles with lower RI, FAdiff, and RImax values compared to other ROIs (red arrowheads).
Fig. 8 shows how the cortical thickness affects the shape of the FA and RI vs. cortical depth profiles. Fig. 8A shows that the FA profiles have a more pronounced local maximum and minimum (or inflection points) typically at the largest cortical thickness bin (black arrowheads). In contrast, no FA peaks were observed at the smallest cortical thickness bins, which only had one or two voxels across the cortex (cyan lines). Fig. 8B shows that the RI profiles with a larger cortical thickness have a peak that typically occurs closer to the WM/GM interface and with a higher RImax value compared to the RI profiles with a smaller cortical thickness (orange arrowheads). As in Fig. 7B, these profiles also show that the RI tends to be lower at the WM/GM interface, higher at the middle cortical depth, and typically somewhat lower again at the pial surface. This trend is more pronounced for larger cortical thickness bins (pink lines) than for smaller cortical thickness bins (cyan lines).
Fig. 8.
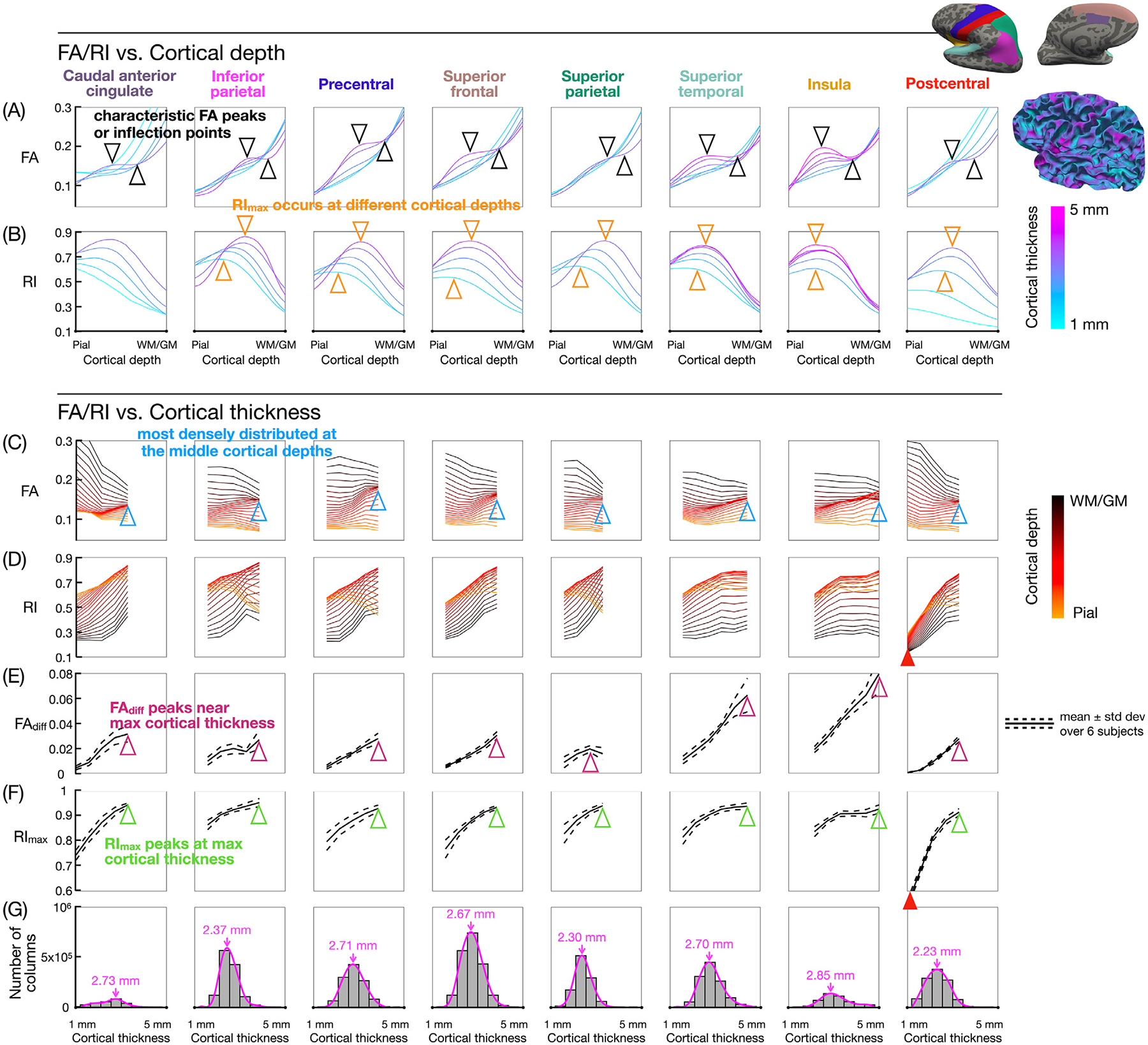
(A,B) FA and RI vs. cortical depth profiles at different cortical thickness bins, color-coded from cyan (minimum) to pink (maximum). (C,D) FA and RI vs. cortical thickness profiles at different cortical depths, color-coded from orange (pial surface) to black (WM/GM interface). (E,F) FAdiff and RImax vs. cortical thickness profiles. The FA local maximum and minimum (or inflection points) at the middle cortical depths and typically at the largest cortical thickness bin (black arrowheads) correspond to the more densely distributed FA vs. cortical thickness profiles (blue arrowheads) and to the peak in the FAdiff vs. cortical thickness profiles (magenta arrowheads). RImax typically occurs at larger cortical depths and is higher in value as the cortical thickness increases (orange and green arrowheads). The postcentral ROI shows lower RI and RImax values at the smallest cortical thickness bins (red arrowheads). (G) Histograms of the cortical thickness, with pink lines denoting the probability density function and pink arrows denoting its peak in each ROI. Bins containing less than 2000 columns are excluded from the cortical thickness-based analysis.
Fig. 8C shows that the FA vs. cortical thickness profiles are more densely distributed and/or overlapped at the middle cortical depths and at the largest cortical thickness bin (blue arrowheads). This denser distribution corresponds to the FA local maximum and minimum (or inflection points) in the FA vs. cortical depth profiles (Fig. 8A, black arrowheads) and to the peak in the FAdiff vs. cortical thickness profiles (Fig. 8E, magenta arrowheads), both of which typically occur at the largest cortical thickness bin. Fig. 8D shows that in most ROIs, the RI tends to increase with the cortical thickness at larger cortical depths, whereas it tends to decrease with the cortical depth at smaller cortical depths. Since Fig. 8B and D both show the same RI data as a function of the cortical depth and cortical thickness, but plotted in two different ways, moving along one of the lines in Fig. 8B, which represents a given cortical thickness bin, is equivalent to moving vertically through different lines in Fig. 8D, which represent different cortical depths. Thus, since the RI peak in Fig. 8B is more pronounced for larger cortical thickness bins as noted above, the lines in Fig. 8D are also more widely distributed for larger cortical thickness bins, with RI values increasing from the WM/GM interface to the middle cortical depths and then decreasing from the middle cortical depths to the pial surface.
Fig. 8F shows that the peak in the RImax vs. cortical thickness profiles also occurs at the largest cortical thickness bin (green arrowheads). These RImax values were first calculated along each cortical column (since this is how RImax is defined), then averaged in each cortical thickness bin, whereas the RI values at each cortical depth in Fig. 8D were just averaged in each bin. Thus, if RImax occurs at different cortical depths for different cortical columns within a bin, the average RImax value in Fig. 8F would be higher than the largest average RI value in Fig. 8D. However, the RImax profiles and the largest RI profiles follow the same trend (and similarly for Fig. 7). Finally, the postcentral ROI, which has a distribution of cortical thickness that is more skewed towards the thinner bins compared to other ROIs (Fig. 8G), has much lower RI and RImax values at the smallest cortical thickness bins (red arrowheads).
4. Discussion
The results of this study are consistent with those from previous high-resolution DTI studies of the cortex (Kleinnijenhuis et al., 2013; Truong et al., 2014; McNab et al., 2013; Gulban et al., 2018; Balasubramanian et al., 2021; Liao et al., 2021; Kleinnijenhuis et al., 2015; Cottaar et al., 2018; Schilling et al., 2018; Dai et al., 2021; Wang et al., 2021; Ramos-Llordén et al., 2021) in that for most cortical regions except for the postcentral gyrus, the FA, V1, and RI maps (Fig. 3) show a band of low FA near the WM/GM interface and a primarily radial diffusion orientation, while the ROI-based FA and RI vs. cortical depth profiles (Fig. 4, Supplementary Figs. S3 and S4) show an FA local maximum and minimum (or two inflection points) and an RI maximum at intermediate cortical depths.
In contrast to previous studies, however, we were able to perform a more specific and comprehensive analysis of the FA and RI dependence on the cortical depth, ROI location, ROI size, cortical curvature, and cortical thickness across the whole brain by using an efficient multi-band multi-shot EPI sequence to acquire 0.9-mm isotropic whole-brain DTI data in vivo and by using a column-based analysis to sample the FA and RI along radially oriented cortical columns. This method enables both column-based (Fig. 6) and ROI-based (Fig. 4, Supplementary Figs. S3 and S4) analyses. Averaging the FA and RI profiles from single cortical columns within ROIs provides a more robust way to measure their characteristic features and enables any similarities or differences across ROIs or across subjects to be identified. The ROI-based FA and RI vs. cortical depth profiles in 5 different atlases with increasing ROI sizes show that the FA (and to a lesser extent RI) peaks tend to become less prominent as the ROI size increases. Thus, using excessively large ROIs may reduce the specificity because of the higher spatial heterogeneity within the ROIs and the ROI size should be optimized for different applications.
While Gulban et al. (2018) also investigated the dependence of the diffusion anisotropy and radiality on the cortical depth and curvature (but not thickness) across the whole brain, the results were displayed on fiber orientation maps, along fiber tracts, as well as on cortical surfaces and as histograms at only three cortical depths (superficial, middle, deep), which did not allow the characteristic shapes of FA and RI profiles (e.g., local maximum and minimum) to be quantified. Cottaar et al. (2018) proposed a 3D coordinate system based on the gyral geometry for each voxel, but did not investigate the dependence of the diffusion anisotropy or radiality on the cortical depth, curvature, or thickness. They also tried to model the transition from mostly tangential orientations in the superficial WM to mostly radial orientations in the cortical GM with a sigmoidal function, but found that this model could only provide a qualitative measure. In contrast to these two previous studies, the proposed column-based cortical depth analysis of the FA and RI enables a systematic and quantitative assessment of their dependence on the cortical depth, ROI, cortical curvature, and cortical thickness across the whole brain, which is needed to provide quantitative biomarkers for neurological disorders.
In addition to averaging profiles from single cortical columns within ROIs, the cortical columns can also be sorted based on the cortical curvature (Fig. 7) or cortical thickness (Fig. 8) values to take into account the underlying variations in the layering of individual cortical layers along the cortical depth. Sorting cortical columns based on the cortical curvature can reduce any bias caused by averaging the FA or RI from cortical regions with different cortical curvatures because, according to the equivolume principle (Waehnert et al., 2014; Huber et al., 2021), deeper layers are thicker and superficial layers are thinner around gyri, while deeper layers are thinner and superficial layers are thicker around sulci. Thus, by only averaging the FA or RI across cortical columns with a similar curvature, the FA or RI values at a given cortical depth (e.g., 50%) are more likely to reflect the microstructure of the same cortical layers rather than potentially different cortical layers. Similarly, sorting cortical columns based on the cortical thickness can reduce any bias caused by averaging the FA or RI from cortical regions with different cortical thicknesses because the thickness of individual cortical layers does not vary proportionally with the total cortical thickness (Wagstyl et al., 2020). The cortical curvature and cortical thickness are not strongly correlated (Supplementary Fig. S16), so it is useful to investigate the dependence of the results on these two variables separately.
The cortical curvature-based analysis shows that the FA local maximum and minimum (or inflection points) do not necessarily appear at the crown or the fundus, but are more prominent at the banks in most ROIs (Fig. 7A,E). This result is consistent with the band of low FA near the WM/GM interface, seen in Fig. 3 and in previous studies at the banks but not at the crown, which has been attributed to: (1) crossing tangential and radial fibers in the deep cortical layers, and (2) a sharp transition of the fiber orientations at the banks as the fibers enter the cortex at an angle before becoming radial, but not at the crown where they enter radially (Gulban et al., 2018; Cottaar et al., 2018). In a similar DTI study performed in a sagittal slab centered on the inter-hemispheric fissure, such FA peaks were not as prominent (see Fig. 1b in Kleinnijenhuis et al., 2015), possibly because the FA profiles were averaged, and hence smoothed out, across the entire medial wall of the hemispheres, including regions such as the postcentral gyrus that show no FA peaks. However, both studies show that the FA tends to increase from the pial surface to the WM/GM interface for all cortical curvature bins (Fig. 7A) and that it tends to decrease from the crown to the fundus at intermediate cortical depths (Fig. 7C). In this work, we focused on analyzing the FA vs. cortical depth profiles that showed a local maximum and minimum, and we quantified the difference in FA values between them (i.e., FAdiff). In future work, this analysis could be extended to include the FA profiles that only show inflection points rather than peaks, and the difference in FA values between them could be quantified by calculating the derivative of the profiles.
The cortical curvature-based analysis also shows that the largest variation in RI along the cortical depth occurs at the banks rather than at the crown or the fundus (Fig. 7D), with the RI increasing from a more tangential to a more radial diffusion orientation when going from the WM/GM interface to intermediate cortical depths (Fig. 7B) and when going from the banks to the crown at larger cortical depths (Fig. 7D), which was also observed in the previous study (see Fig. 1c in Kleinnijenhuis et al., 2015). Both studies further show that the RI peak occurs at different cortical depths for different cortical curvature bins. The previous study found that the RI peak occurs closer to the WM/GM interface at the crown than at the fundus. The current study shows that this was also the case in some ROIs, but that in other ROIs, the RI peak occurs closer to the pial surface at the crown than at the fundus (Fig. 7B). This difference may be due to the two different cortical depth sampling methods used: the previous study used an equivolume sampling, which defines the cortical depth as a function of the cortical curvature (see Eq. (1) in Kleinnijenhuis et al., 2015), whereas we used an equidistant sampling to ensure that the cortical depth is an independent variable that does not depend on the cortical curvature, since we also investigated the FA and RI dependence on the cortical curvature. Such an equidistant sampling can affect the location of the RI peak, since at the crown, deeper layers are compressed and become thicker, whereas superficial layers are stretched and become thinner, which tends to shift all cortical layers, including the location of the RI peak, closer to the pial surface. Conversely, at the fundus, deeper layers are stretched and become thinner, whereas superficial layers and compressed and become thicker, which tends to shift all cortical layers, including the location of the RI peak, closer to the WM/GM interface. Since the equivolume sampling should already take into account the dependence of the cortical depth on the cortical curvature, the shift in the cortical depth of the RI peak observed in the previous study was thought more likely to be caused by partial volume effects (Kleinnijenhuis et al., 2015), which could also be a confound in our study.
The cortical thickness-based analysis shows that FAdiff and RImax, which reflect the underlying microstructure of different cortical layers, typically increase with the cortical thickness (Fig. 8E,F), which can be due to several reasons. First, as the cortical thickness increases, partial volume averaging across different cortical layers are reduced, thereby improving the ability to resolve layers with different FA and RI values, which would tend to increase FAdiff but also RImax since most cortical regions have a predominantly radial diffusion orientation. Second, the thickness of individual cortical layers does not increase proportionally with the total cortical thickness, which was shown to be primarily driven by layers III, V, and VI (Wagstyl et al., 2020), and this factor can further contribute to variations in the FA and RI vs. cortical depth profiles, and hence FAdiff and RImax.
Thus, establishing an accurate correspondence between specific cortical depths and cortical layers I-VI would require a sampling method that defines the cortical depth as a function of both the cortical curvature and cortical thickness, which would require additional information about the relative thickness of individual cortical layers in different cortical regions (e.g., from histological studies) and which may not be easily implemented across the whole brain. Nevertheless, the proposed cortical curvature- and cortical thickness-based analyses can still provide valuable information and do not necessarily require the cortical depths of individual cortical layers to be accurately known in order to identify any differences in FA and RI profiles between, for example, healthy subjects and patients with neurological disorders.
In this study, such analyses were performed by combining the cortical columns from all six subjects before sorting these columns by cortical curvature or cortical thickness to ensure a sufficiently high number of columns in each cortical curvature or cortical thickness bin. In addition, we used the atlas with 68 ROIs, which has the largest average number of cortical columns per ROI among the 5 atlases and which is the only one with a symmetrical cortical parcellation between the left and right hemispheres, so that the columns could be averaged across both hemispheres. Since the FA and RI profiles were already shown to be consistent across the six subjects, the cortical columns from all subjects were combined to increase the robustness of the cortical curvature- and cortical thickness-based analyses. In the future, however, further improvements in SNR could potentially enable such analyses to be performed on individual subjects or in smaller ROIs.
The goal of this study was not to use the highest possible spatial resolution or b-value, since doing so would inevitably come at the expense of a lower SNR, smaller number of diffusion-weighting directions, reduced spatial coverage, or longer scan time. Instead, we chose a pulse sequence and scan parameters that could simultaneously achieve a submillimeter isotropic resolution, sufficiently high SNR, whole-brain coverage, and reasonable scan time. Similarly, we chose to investigate DTI metrics such as FA and RI rather than use more advanced diffusion models (e.g., Tuch et al., 2002; Jensen et al., 2005; Assaf and Basser, 2005; Behrens et al., 2007; Tournier et al., 2007; Wedeen et al., 2008; Zhang et al., 2012; Kaden et al., 2016), which could potentially provide additional benefits such as the ability to resolve crossing fibers, but many of which require a higher angular resolution, higher b-value, and/or multi-shell acquisition, again at the expense of the spatial resolution, SNR, spatial coverage, or scan time. Thus, the pros and cons of different acquisition protocols and diffusion models need to be investigated in future studies.
This study was performed on a scanner with a maximum gradient strength of 100 mT/m. For a more conventional gradient strength of 40–50 mT/m, the TE is expected to be about 15–20 ms longer, resulting in a modest reduction in SNR of 13–17% (assuming a T2 value of 110 ms in GM at 3T (Wansapura et al., 1999)). Signal dropout due to subject motion was not observed in this study, but may affect future studies, in which case DWI image volumes with dropout artifacts should be discarded, reacquired, or corrected for with prospective motion correction methods, which have been developed for DWI with a multi-shot EPI acquisition and MUSE reconstruction (Herbst et al., 2015).
Finally, this initial study was performed in relatively young healthy subjects to develop the data acquisition and analysis pipeline and to assess the consistency of the results between repeated scans from the same subjects and across different subjects, which is a prerequisite before considering any potential clinical application of the proposed methodology. Importantly, such results are still valuable to better understand how the FA and RI vary as a function of the cortical depth, ROI, cortical curvature, and cortical thickness across the whole brain of healthy subjects. However, additional studies are needed in older healthy subjects and in patients with neurological disorders to investigate whether any differences in the FA and RI profiles due to normal aging or to pathology can be detected and to demonstrate the clinical utility of this methodology.
5. Conclusion
In this study, we performed a quantitative cortical column-based analysis of the FA and RI dependence on the cortical depth, ROI location, ROI size, cortical curvature, and cortical thickness using 0.9-mm isotropic whole-brain DTI data acquired in healthy subjects. The results showed characteristic FA and RI vs. cortical depth profiles, with an FA local maximum and minimum (or two inflection points) and a single RI maximum at intermediate cortical depths in most cortical regions, except for the postcentral ROI where no FA peaks and a lower RI were observed. These results were consistent between repeated scans from the same subjects and across different subjects. They were also dependent on the cortical curvature and cortical thickness in that the characteristic FA and RI peaks were more prominent at the middle curvature bins (i.e., at the banks rather than at the crown or the fundus) and at the largest cortical thickness bins. This high-resolution DTI methodology can help characterize variations in microstructure across the cortex and over the whole brain in vivo, which can potentially be used to provide quantitative biomarkers for neurological disorders.
Supplementary Material
Acknowledgments
This work was in part supported by a Wrenn Fellowship in Alzheimer’s Disease Research from the Duke Institute for Brain Sciences, the National Institutes of Health (grants R01 EB028644, R01 NS075017, and S10 OD021480), the Foundation of the American Society of Neuroradiology, and the Taiwan Ministry of Science and Technology (109-2222-E-182-001-MY3). We thank Yuxin Hu, Fuyixue Wang, and Xucheng Zhu for helpful discussions about the image reconstruction.
Abbreviations:
- CSF
cerebrospinal fluid
- DTI
diffusion tensor imaging
- DWI
diffusion-weighted imaging
- EPI
echo-planar imaging
- FA
fractional anisotropy
- FOV
field-of-view
- GM
gray matter
- MB-MUSE
multi-band multiplexed sensitivity-encoding
- MB-SENSE
multi-band sensitivity-encoding
- MPPCA
Marchenko-Pastur principal component analysis
- RI
radiality index
- ROI
region-of-interest
- SNR
signal-to-noise ratio
- WM
white matter
Footnotes
Declaration of Competing Interest
None
Credit authorship contribution statement
Yixin Ma: Conceptualization, Methodology, Software, Investigation, Formal analysis, Writing – original draft. Iain P. Bruce: Methodology, Software, Writing – review & editing. Chun-Hung Yeh: Methodology, Writing – review & editing. Jeffrey R. Petrella: Conceptualization, Writing – review & editing, Funding acquisition. Allen W. Song: Conceptualization, Methodology, Writing – review & editing, Funding acquisition. Trong-Kha Truong: Conceptualization, Methodology, Investigation, Writing – original draft, Supervision, Funding acquisition.
Supplementary materials
Supplementary material associated with this article can be found, in the online version, at doi: 10.1016/j.neuroimage.2023.119993.
Data and code availability statement
The data used in this study are not available because the study participants did not consent to sharing their data. The code used for the data analysis is available upon request to the corresponding authors.
References
- Aggarwal M, Nauen DW, Troncoso JC, Mori S, 2015. Probing region-specific microstructure of human cortical areas using high angular and spatial resolution diffusion MRI. Neuroimage 105, 198–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson JLR, Skare S, Ashburner J, 2003. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 20 (2), 870–888. [DOI] [PubMed] [Google Scholar]
- Andersson JLR, Sotiropoulos SN, 2016. An integrated approach to correction for o!-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaf Y, 2019. Imaging laminar structures in the gray matter with diffusion MRI. Neuroimage 197, 677–688. [DOI] [PubMed] [Google Scholar]
- Assaf Y, Basser PJ, 2005. Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. Neuroimage 27, 48–58. [DOI] [PubMed] [Google Scholar]
- Balasubramanian M, Mulkern RV, Neil JJ, Maier SE, Polimeni JR, 2021. Probing in vivo cortical myeloarchitecture in humans via line-scan diffusion acquisitions at 7 T with 250–500 μm radial resolution. Magn. Reson. Med 85 (1), 390–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D, 1994. Estimation of the effective self-diffusion tensor from the NMR spin echo. J. Magn. Reson. B 103, 247–254. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C, 1996. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J. Magn. Reson. B 111 (3), 209–219. [DOI] [PubMed] [Google Scholar]
- Behrens TE, Berg HJ, Jbabdi S, Rushworth MF, Woolrich MW, 2007. Probabilistic diffusion tractography with multiple fibre orientations: what can we gain? Neuroimage 34, 144–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruce IP, Chang HC, Petty C, Chen NK, Song AW, 2017. 3D-MB-MUSE: a robust 3D multi-slab, multi-band and multi-shot reconstruction approach for ultrahigh resolution diffusion MRI. Neuroimage 159, 46–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cammoun L, Gigandet X, Meskaldji D, Thiran JP, Sporns O, Do KQ, Maeder P, Meuli R, Hagmann P, 2012. Mapping the human connectome at multiple scales with diffusion spectrum MRI. J. Neurosci. Methods 203 (2), 386–397. [DOI] [PubMed] [Google Scholar]
- Chen NK, Guidon A, Chang HC, Song AW, 2013. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage 72, 41–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordero-Grande L, Christiaens D, Hutter J, Price AN, Hajnal JV, 2019. Complex diffusion-weighted image estimation via matrix recovery under general noise models. Neuroimage 200, 391–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cottaar M, Bastiani M, Chen C, Dikranian K, Van Essen D, Behrens TE, Sotiropoulos SN, Jbabdi S, 2018. A gyral coordinate system predictive of fibre orientations. Neuroimage 176, 417–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daducci A, Gerhard S, Griffa A, Lemkaddem A, Cammoun L, Gigandet X, Meuli R, Hagmann P, Thiran JP, 2012. The connectome mapper: an open-source processing pipeline to map connectomes with MRI. PLoS ONE 7 (12), e48121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai E, Liu S, Guo H, 2021. High-resolution whole-brain diffusion MRI at 3T using simultaneous multi-slab (SMSlab) acquisition. Neuroimage 237, 118099. [DOI] [PubMed] [Google Scholar]
- Desikan RS, Segonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ, 2006. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 31, 968–980. [DOI] [PubMed] [Google Scholar]
- Dyrby TB, Lundell H, Burke MW, Reislev NL, Paulson OB, Ptito M, Siebner HR, 2014. Interpolation of diffusion weighted imaging datasets. Neuroimage 103, 202–213. [DOI] [PubMed] [Google Scholar]
- Eaton-Rosen Z, Scherrer B, Melbourne A, Ourselin S, Neil JJ, Warfield SK, 2017. Investigating the maturation of microstructure and radial orientation in the preterm human cortex with diffusion MRI. Neuroimage 162, 65–72. [DOI] [PubMed] [Google Scholar]
- Fischl B, Dale AM, 2000. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc. Natl. Acad. Sci. U. S. A 97 (20), 11050–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Sereno MI, Tootell RB, Dale AM, 1999. High-resolution intersubject averaging and a coordinate system for the cortical surface. Hum. Brain Mapp 8 (4), 272–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gómez-Isla T, Price JL, McKeel DW Jr, Morris JC, Growdon JH, Hyman BT, 1996. Profound loss of layer II entorhinal cortex neurons occurs in very mild Alzheimer’s disease. J. Neurosci 16 (14), 4491–4500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulban OF, De Martino F, Vu AT, Yacoub E, U ğurbil K, Lenglet C, 2018. Cortical fibers orientation mapping using in-vivo whole brain 7 T diffusion MRI. Neuroimage 178, 104–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herbst M, Zahneisen B, Knowles B, Zaitsev M, Ernst T, 2015. Prospective motion correction of segmented diffusion weighted EPI. Magn. Reson. Med 74 (6), 1675–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber LR, Poser BA, Bandettini PA, Arora K, Wagstyl K, Cho S, Goense J, Nothnagel N, Morgan AT, van den Hurk J, Müller AK, 2021. LAYNII: a software suite for layer-fMRI. Neuroimage 237, 118091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K, 2005. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med 53, 1432–1440. [DOI] [PubMed] [Google Scholar]
- Kaden E, Kelm ND, Carson RP, Does MD, Alexander DC, 2016. Multi-compartment microscopic diffusion imaging. Neuroimage 139, 346–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellner E, Dhital B, Kiselev VG, Reisert M, 2016. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn. Reson. Med 76 (5), 1574–1581. [DOI] [PubMed] [Google Scholar]
- Kim H, Shon SH, Joo SW, Yoon W, Lee JH, Hur JW, Lee J, 2019. Gray matter microstructural abnormalities and working memory deficits in individuals with schizophrenia. Psychiatry Investig. 16 (3), 234–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinnijenhuis M, van Mourik T, Norris DG, Ruiter DJ, van Cappellen van Walsum AM, Barth M, 2015. Diffusion tensor characteristics of gyrencephaly using high resolution diffusion MRI in vivo at 7T. Neuroimage 109, 378–387. [DOI] [PubMed] [Google Scholar]
- Kleinnijenhuis M, Zerbi V, Küsters B, Slump CH, Barth M, van Cappellen van Walsum AM, 2013. Layer-specific diffusion weighted imaging in human primary visual cortex in vitro. Cortex 49 (9), 2569–2582. [DOI] [PubMed] [Google Scholar]
- Koopmans PJ, Barth M, Orzada S, Norris DG, 2011. Multi-echo fMRI of the cortical laminae in humans at 7 T. Neuroimage 56, 1276–1285. [DOI] [PubMed] [Google Scholar]
- Lee P, Kim HR, Jeong Y, 2020. Detection of gray matter microstructural changes in Alzheimer’s disease continuum using fiber orientation. BMC Neurol. 20 (1), 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao C, Bilgic B, Tian Q, Stockmann JP, Cao X, Fan Q, Iyer SS, Wang F, Ngamsombat C, Lo WC, Manhard MK, 2021. Distortion-free, high-isotropic-resolution diffusion MRI with gSlider BUDA-EPI and multicoil dynamic B0 shimming. Magn. Reson. Med 86 (2), 791–803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNab JA, Polimeni JR, Wang R, Augustinack JC, Fujimoto K, Stevens A, Janssens T, Farivar R, Folkerth RD, Vanduffel W, Wald LL, 2013. Surface based analysis of diffusion orientation for identifying architectonic domains in the in vivo human cortex. Neuroimage 69, 87–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neil JJ, Smyser CD, 2018. Recent advances in the use of MRI to assess early human cortical development. J. Magn. Reson 293, 56–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pienaar P, Fischl B, Caviness V, Makris N, Grant PE, 2008. A methodology for analyzing curvature in the developing brain from preterm to adult. Int. J. Imaging Syst. Technol 18, 42–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramos-Llordén G, Vegas-Sánchez-Ferrero G, Liao C, Westin CF, Setsompop K, Rathi Y, 2021. SNR-enhanced diffusion MRI with structure-preserving low-rank denoising in reproducing kernel Hilbert spaces. Magn. Reson. Med 86 (3), 1614–1632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sampedro F, Martínez-Horta S, Marín-Lahoz J, Pagonabarraga J, Kulisevsky J, 2019a. Longitudinal intracortical diffusivity changes in de-novo Parkinson’s disease: a promising imaging biomarker. Parkinsonism Relat. Disord 68, 22–25. [DOI] [PubMed] [Google Scholar]
- Sampedro F, Martínez-Horta S, Perez-Perez J, Horta-Barba A, Martin-Lahoz J, Alonso-Solís A, Corripio I, Gomez-Anson B, Kulisevsky J, 2019b. Widespread increased diffusivity reveals early cortical degeneration in Huntington disease. AJNR Am. J. Neuroradiol 40 (9), 1464–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schilling K, Gao Y, Janve V, Stepniewska I, Landman BA, Anderson AW, 2018. Confirmation of a gyral bias in diffusion MRI fiber tractography. Hum. Brain Mapp 39 (3), 1449–1466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz CG, et al. , 2016. A large-scale comparison of cortical thickness and volume methods for measuring Alzheimer’s disease severity. NeuroImage Clin. 11, 802–812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengupta S, Fritz FJ, Harms RL, Hildebrand S, Tse DHY, Poser BA, Goebel R, Roebroeck A, 2018. High resolution anatomical and quantitative MRI of the entire human occipital lobe ex vivo at 9.4 T. Neuroimage 168, 162–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL, 2012. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn. Reson. Med 67 (5), 1210–1224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, et al. , 2004. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 23, S208–S219. [DOI] [PubMed] [Google Scholar]
- Stock B, Shrestha M, Seiler A, Foerch C, Hattingen E, Steinmetz H, Deichmann R, Wagner M, Gracien RM, 2020. Distribution of cortical diffusion tensor imaging changes in multiple sclerosis. Front. Physiol 11, 116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, Connelly A, 2007. Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution. Neuroimage 35, 1459–1472. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Smith R, Raffelt D, Tabbara R, Dhollander T, Pietsch M, Christiaens D, Jeurissen B, Yeh CH, Connelly A, 2019. MRtrix3: a fast, flexible and open software framework for medical image processing and visualisation. Neuroimage 202, 116137. [DOI] [PubMed] [Google Scholar]
- Truong TK, Guidon A, Song AW, 2014. Cortical depth dependence of the diffusion anisotropy in the human cortical gray matter in vivo. PLoS ONE 9 (3), e91424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuch DS, Reese TG, Wiegell MR, Makris N, Belliveau JW, Wedeen VJ, 2002. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn. Reson. Med 48 (4), 577–582 29(6), 1310–1320. [DOI] [PubMed] [Google Scholar]
- Veraart J, Sijbers J, Sunaert S, Leemans A, Jeurissen B, 2013. Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls. Neuroimage 81, 335–346. [DOI] [PubMed] [Google Scholar]
- Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E, 2016. Denoising of diffusion MRI using random matrix theory. Neuroimage 142, 394–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viessmann O, Scheffler K, Bianciardi M, Wald LL, Polimeni JR, 2019. Dependence of resting-state fMRI fluctuation amplitudes on cerebral cortical orientation relative to the direction of B0 and anatomical axes. Neuroimage 196, 337–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waehnert MD, Dinse J, Schäfer A, Geyer S, Bazin PL, Turner R, Tardif CL, 2016. A subject-specific framework for in vivo myeloarchitectonic analysis using high resolution quantitative MRI. Neuroimage 125, 94–107. [DOI] [PubMed] [Google Scholar]
- Waehnert MD, Dinse J, Weiss M, Streicher MN, Waehnert P, Geyer S, Turner R, Bazin PL, 2014. Anatomically motivated modeling of cortical laminae. Neuroimage 93, 210–220. [DOI] [PubMed] [Google Scholar]
- Wagstyl K, Larocque S, Cucurull G, Lepage C, Cohen JP, Bludau S, Palomero–Gallagher N, Lewis LB, Funck T, Spitzer H, Dickscheid T, 2020. BigBrain 3D atlas of cortical layers: cortical and laminar thickness gradients diverge in sensory and motor cortices. PLoS Biol. 18 (4), e3000678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F, Dong Z, Tian Q, Liao C, Fan Q, Hoge WS, Keil B, Polimeni JR, Wald LL, Huang SY, Setsompop K, 2021. In vivo human whole-brain Connectom diffusion MRI dataset at 760μm isotropic resolution. Sci. Data 8 (1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wansapura JP, Holland SK, Dunn RS, Ball WS Jr., 1999. NMR relaxation times in the human brain at 3.0 tesla. J. Magn. Reson. Imaging 9, 531–538. [DOI] [PubMed] [Google Scholar]
- Wedeen VJ, Wang RP, Schmahmann JD, Benner T, Tseng WYI, Dai G, Pandya DN, Hagmann P, D’Arceuil H, de Crespigny AJ, 2008. Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers. Neuroimage 41 (4), 1267–1277. [DOI] [PubMed] [Google Scholar]
- Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC, 2012. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage 61 (4), 1000–1016. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data used in this study are not available because the study participants did not consent to sharing their data. The code used for the data analysis is available upon request to the corresponding authors.


