Mutually beneficial confluence of structure-based modeling of protein dynamics and machine learning methods

Abstract

Proteins sample an ensemble of conformers under physiological conditions, having access to a spectrum of modes of motions, also called intrinsic dynamics. These motions ensure the adaptation to various interactions in the cell, and largely assist in, if not determine, viable mechanisms of biological function. In recent years, machine learning frameworks have proven uniquely useful in structural biology, and recent studies further provide evidence to the utility and/or necessity of considering intrinsic dynamics for increasing their predictive ability. Efficient quantification of dynamics-based attributes by recently developed physics-based theories and models such as elastic network models provides a unique opportunity to generate data on dynamics for training ML models towards inferring mechanisms of protein function, assessing pathogenicity, or estimating binding affinities.

Introduction

Recent years have seen a growing number of machine learning (ML)-based approaches that assist in advancing structural biology research, especially in structure prediction [1]. A prime example is the development of a neural network (NN)-based tool, AlphaFold, by DeepMind [2,3]. This artificial intelligence (AI) system has now predicted the structures of 200 million proteins listed in UniProt, a breakthrough compared to the deposition of <200,000 structures in the Protein Data Bank since its inception in 1976 [4].

ML applications in biology were originally made in the realm of sequence comparisons; this is how the field of bioinformatics emerged [5]. The extension to 3D structures naturally arose with ML’s powerful pattern recognition and computer vision algorithms that apply equally well to 3D shapes, not only a string of letters. Further development of sequence-based deep learning (DL) methods, especially those based on sequence co-evolution [6,7] or genome-scale genetic data demonstrated remarkable success in structure prediction [8]. The purpose of this opinion is to discuss how the progress made in physics-based computational evaluation of structural dynamics, not only structure, can be leveraged if used in conjunction with ML or DL methods.

It is now established that knowledge of a single structure provides useful but incomplete insights into the mechanisms of function. A 3D structure only provides a single snapshot from amongst a multitude of conformations that the protein can sample during its function. The bridge between structure and function is structural dynamics [9,10], in accord with the sequence → structure → dynamics → function paradigm. Structural dynamics refers to fluctuations between (microscopic) conformations accessible near the folded (macro)state. These motions range from cooperative domain movements typical of allosteric machines to highly localized fluctuations at densely packed regions. They collectively form the intrinsically accessible ‘spectrum of modes of motions’ that enable adaptation to different environments and interactions and are often recruited to accomplish function while retaining the 3D fold [10,11].

Analyses based on elastic network models (ENMs) provide an effective description of the anisotropic fluctuations of proteins in agreement with experimental data [12], and robust evidence on the functional significance of structural dynamics [10,11,13,14]. Several examples of functional motions, e.g., opening and closure for binding and stabilizing a substrate, transition between outward-facing and inward-facing states of the transporters, allosteric structural changes in response to ligand binding, or simply breathing motions enabling the channeling of ions or small molecules through pores or cavities, are predictable by ENMs as highly probable modes of motions uniquely defined by the inter-residue contact topology. Such structure-encoded intrinsic dynamics pre-exists, independent of substrate/ligand binding. Ligand binding simply exploits these pre-existing mechanisms of reconfiguration to enable function.

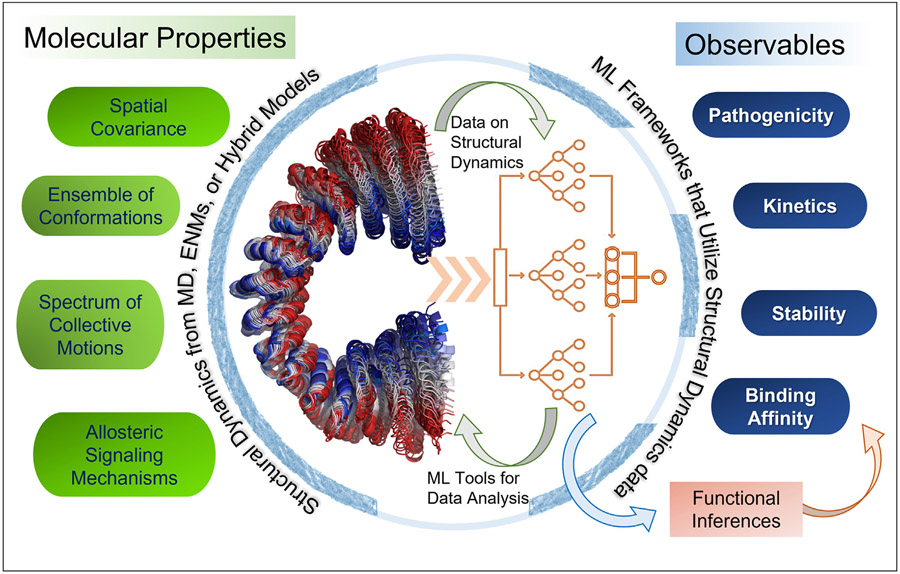
Given the importance of protein dynamics, it is not surprising that ML studies that leverage structural dynamics data increasingly gain traction. The merger of ML and structural dynamics theory and methods is expected to be mutually beneficial (Fig. 1): dynamics data incorporated into ML algorithms can increase the accuracy of functional inferences, as exemplified by a recent pathogenicity predictor [15]; conversely, DL methods put to use for analyzing full-atomic simulations can help extract information on proteins’ kinetics [16]. In both cases, the confluence of ML/DL and structural dynamics data is expected to generate knowledge that will help close the gap between experimental and computed quantities. We point below to such recent developments and their prospective utilities.

Figure 1. Utility of combining microscopic time-dependent features predicted by structure-based models, methods, and simulations with ML frameworks for making functional inferences.

The confluence of the structural dynamics (molecular) data (left part of the circle) with ML methods (right part of the circle) enables us to evaluate macroscopic properties (observables) from molecular properties.

Structural dynamics is a determinant of mutation pathogenicity

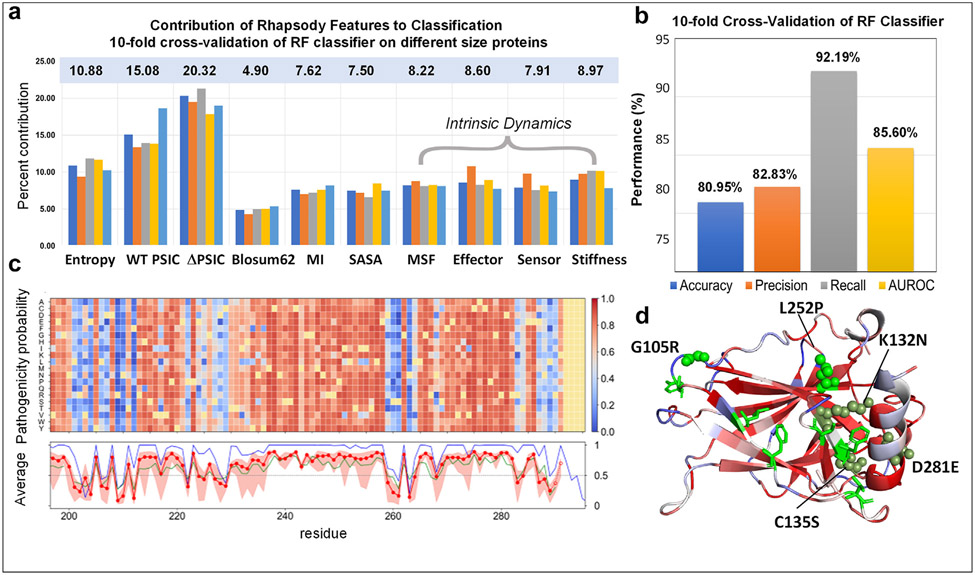
Single amino acid variants (SAVs) or point mutations are associated with more than half of human inherited diseases. They may directly compromise the active sites or have allosteric effects, and act as ‘latent drivers’ associated with cancer development and drug resistance [17]. The growing SAV data has led to the development of databases and ML frameworks for predicting pathogenicity [18-23]. We recently explored whether considering the intrinsic dynamics of the protein might improve the accuracy of SAV pathogenicity prediction [15]. A simple random forest (RF)-based ML tool benchmarked against >20,000 SAVs indeed confirmed that this is the case [15] (Fig. 2b). The tool, implemented in Rhapsody [20], shows that while sequence-based features make the largest contributions to predictions, dynamic features also make important contributions (e.g., larger than solvent-accessible surface area, SASA) (Fig. 2a). Among dynamics features, allosteric signaling effectiveness emerged as an important factor. More recently, the Rhapsody feature set has been expanded to incorporate sixteen additional features from Rosetta (excluding SASA) [24]; and dynamics-based attributes in Rhapsody have been used along with sequence- and structure-based attributes to construct an XGBoost classifier within the LYRUS tool to predict pathogenicity [25].

Figure 2. ML-based pathogenicity predictor Rhapsody takes account of structural dynamics, yields highly accurate predictions, and can be used to generate in silico saturation mutagenesis heatmaps.

(a) Descriptors used in Rhapsody: sequence (conservation (entropy), position specific independent counts (PSIC) and change in PSIC (ΔPSIC), amino acid substitution (Blosum62), mutual information (MI)), structure (SASA) and structural dynamics (mean-square fluctuations (MSF) of mutated residue, propensity to serve as effector or sensor of allosteric signals (see previous work [26]), and mechanical stiffness). The bars display the percent contribution of these descriptors to the trained classifier. A set of five bars is displayed for each descriptor, corresponding to subsets of proteins of different sizes, with numbers of residues lying in the ranges [150–249] (orange), [250–361] (gray), [362–520] (yellow), and [521 –3636] (light blue). The first bar (dark blue) in each group refers to the entire set. The corresponding percent contributions of different features are listed in the light blue box. (b) Prediction performance based on different metrics. (c) In silico saturation mutagenesis heatmap. These are pathogenicity probabilities (see the scale bar on the right) evaluated for all 19 substitutions (ordinate) at each residue position (abscissa), shown here for a 100-residue segment of p53. Structural and dynamic features are based on the tetrameric structure (PDB id: 3KMD) [27]. The curves underneath are the averages over all 19 substitutions for each residue, predicted by Rhapsody (red dots), PolyPhen-2 (dark blue) [28] and EVMutation (green) [19]. The Pearson correlation coefficient (PCC) between each pair of results is around 0.74; whereas that between PolyPhen-2 and EVMutation is 0.58. (d) Color-coded pathogenicity results for p53 monomer. Mutations at sites colored red are highly susceptible to be pathogenic. A few such residues are labeled. These are reported in ClinVar to be pathogenic (green spheres), likely pathogenic (olive spheres), or unknown (green sticks).

Fig. 2c-d illustrates the application of Rhapsody to p53. The heatmap in c displays the in silico saturation mutagenesis results for a 100-residue portion (see the complete map at Rhapsody interface; and detailed description in the figure caption). Several SAVs are ‘newly’ evaluated here, in the sense that they were not included in the training set. Panel d displays some of them (residues in green spheres) that are confirmed to be pathogenic according to the data reported in the literature; residues shown in green sticks are variants of unknown significance that are predicted to be pathogenic, waiting for validation.

ENMs such as the anisotropic network model (ANM) [12,29] and the Gaussian network model (GNM) [30] that are most broadly used in the literature (and in Rhapsody) provide residue-level information on structural dynamics and lack amino acid specificity. Atomic-level residue-specific information on the role of conformational dynamics in disease-causing missense mutations, on the other hand, can be inferred from MD trajectories, as illustrated in a recent study [31]. A recent ML- and MD-based study showed how the pathogenicity of mutations at sites that are neither evolutionarily conserved nor directly involved in biochemical activity could be explained by dynamic couplings [32]. Therein, the data from MD were used to train a feedforward NN for pathogenicity prediction. In another study, attributes extracted from MD were used in a rule-based classifier to predict the pathogenicity of unclassified variants of BRCA1 BRCT repeats [33]. Similarly, a K-nearest neighbor predictor of disease specificity was built for calmodulin variants, as well as Aβ peptide variants, using the distributions of (φ, ψ) angles and the root-mean-square deviations (RMSDs) and fluctuations (RMSFs) in atomic positions observed in MD simulations conducted for the two wild type proteins and the corresponding sets of variants [34]. The DL tool DiffNets, on the other hand, predicts the biochemical differences between variants using self-supervised autoencoders that learn the associated latent space from MD-sampled structural ensembles [35].

Note that residue-specificity can also be incorporated within the ENMs. DynaSig-ML is a package that utilizes elastic network contact model (ENCoM)-predicted modes and ML to predict biomolecular function and proved useful in a recent prediction of the evolutionary fitness of a bacterial enzyme [36]. ENCoM differs from the elastic network models ANM and GNM by the inclusion of residue-specificity through contact surface evaluation for interacting pairs [37]. It is worth noting that there are also other ENMs that are residue-specific, such as the ANM with inter-residue spring constants proportional to the number of atom—atom contacts, introduced in modeling the Markovian diffusion of allosteric signals [38], and even the original ENM of Tirion where uniform harmonic potentials were used between all atom pairs [39].

Overall, recent studies highlight the utility of using structural dynamics data, at either low or high resolution (e.g., ENMs or MD), in ML platforms, to accurately predict the effect of SAVs on (dys)function.

Neural networks help learn molecular properties from MD trajectories

Recent studies point to the utility of NNs for learning from MD trajectories [16]. The NNs take as input the coordinates of all atoms (or α-carbons in coarse-grained MD), and output properties such as potential energy surface or operating force fields. ML models trained on MD trajectories can learn the “latent space” accessible to the protein, and predict new trajectories or conformations not observed in the original MD runs [40,41], allowing for rapid and more complete sampling of conformational space.

Methods of unsupervised learning applied to MD data further assist in transition kinetics modeling [42]. The last decade has seen a broad use of Markov state models (MSMs) for analyzing MD trajectories [43]. While the underlying stochastic theory and Master equation formalism go back to early 1900s, its use for characterizing ensembles of protein conformations to define states (or substates) and their transition kinetics took center stage in the last two decades. We demonstrated the utility of this formalism for mapping conformational space and kinetics in the early 2000s using toy models for proteins [44,45]. MSMs are now broadly used for extracting functional information from multiple or long MD runs. While their use originally required significant human input, DL algorithms can now automatically determine the significant features for defining representative states, e.g., VAMPNets [46] provides a fully automated framework to evaluate collective variables and MSM transition matrices [47,48]. Recently, Zhu and coworkers used GNNs to predict allosteric communication pathways from MD simulations [49].

Confluence of structural dynamics and DL methods in drug discovery

Binding affinity at constant temperature and pressure, quantified as the Gibbs free energy change ΔG associated with binding, depends on the accompanying changes in enthalpy (H) and entropy (S) as ΔG = DH - TΔS. An important source of ΔS is the conformational entropy change upon binding. ΔS scales with ln [det(σ_b)/det(σ_u)] [50] where det(σ_b) is the determinant of the positional covariance matrix of the protein in ligand-bound form, and det(σ_u) is that in the unbound form. Thus, the equilibrium dynamics of the protein, manifested by covariance in the fluctuations of residues/atoms, is an inseparable part of any binding event. In fact, entropic effects are so salient that many proteins evolved to co-localize their ligand-binding sites with global hinge centers [14], associated rotation axes [51] or domain interfaces [52] where entropy loss upon ligand binding is minimal.

ML-aided drug screening approaches have shown success in recent years. For example, a generative tensorial reinforcement learning model [53] outperformed adversarial models and identified novel potent inhibitors of DDR1 kinase, which were experimentally validated. In a later version, generating 3D structures of drug-like compounds were conditioned on a receptor binding site and validated on receptors with mutations [54]. However, these and most of ML approaches for drug screening do not adequately consider the protein intrinsic dynamics (while the translational and rotational motions of the small molecule are thoroughly sampled). One of the exceptions is AtomNet [55], a structure-based deep-convolutional NN, trained on multiple poses of active compounds bound to a single target site as well as experimentally verified inactive compounds, which proved to outperform established scoring functions. In another study, inclusion of MD descriptors was shown to improve the discrimination of good caspase-8 inhibitors from poor ones [56].

In contrast, recent ML algorithms for predicting drug-resistant mutations do utilize structural dynamics data from MD [57,58] to generate dynamics-based features that are trained, often by RF and feedforward multilayer perceptron, using labels of ~1000 drug-sensitive or -resistant mutants extracted from the Platinum database [59]. Similarly, SUSPECT-RIF uses a residue-specific version of ENM (ENCoM) [60] to take account of dynamics in predicting drug resistance [61]. ENMs provide an efficient platform to uniformly generate data on equilibrium dynamics by virtue of their applicability at omics scale without bias [62], as validated by comparisons with NMR-sampled equilibrium dynamics [63] and X-ray crystallographically solved ensembles of structures for the same protein in different states [13].

ML-based methods are not necessarily more accurate than MM/GBSA evaluation of binding free energy [64]. The value of ML-based methods in drug screening lies in their efficiency. ML methods may also be subject to challenges including applicability to new cases as well as uncertainties in experimental data (e.g., affinity data reported for the same protein-ligand complex may differ by orders of magnitude). Yet, ML-based docking [65] or re-ranking scheme [55] could be efficiently adopted together with a conformational sampling scheme for a first screening (also called ensemble docking) before performing (for selected cases) MD-based free energy evaluations. The latter could be even used for screening purposes [66], empowered by the accelerations enabled by GPUs. Finally, data-driven ML efforts could be advantageously redirected to areas where first principles of physical sciences fall short, such as predictions of cell toxicity and PK/PD in animals, which are important elements of drug development.

Ensemble analyses based on equilibrium dynamics are yet to be routinely used in ML-based stability predictions

Despite advances in computational methods, in silico predictions for changes in Gibbs free energy (ΔΔG) of folding associated with SAVs still suffer from limitations and challenges [67]. As mentioned above, the entropic contribution to ΔΔG, which directly relates to the distribution of residue fluctuations, or the curvature of the energy minimum near equilibrium is often overlooked. Among ML studies for predicting the effect of mutations on stability, DynaMut [68] is distinguished, as it utilizes the changes in vibrational entropy predicted by ENCoM [60].

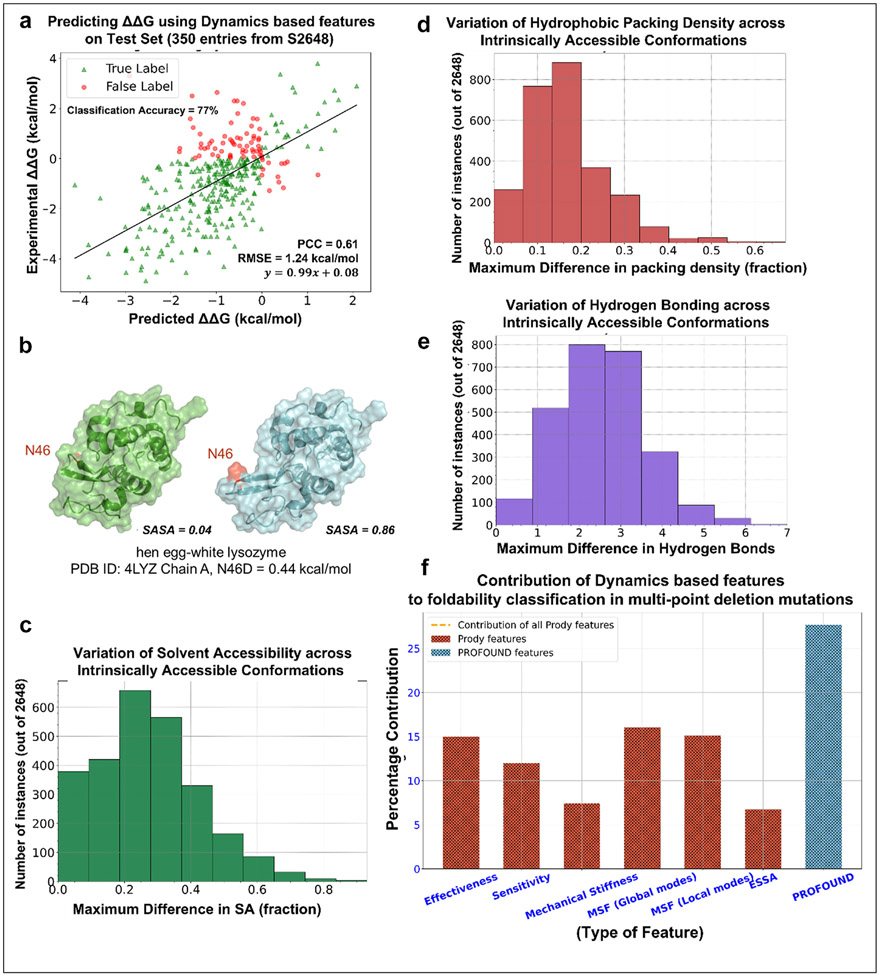
For illustrative purposes, we examined how well a simple gradient boosting regressor exclusively trained on equilibrium dynamics data predicts the changes in stability (ΔΔG values) associated with point mutations (Fig. 3a). The regressor uses ESSA scores as a measure of the impact of mutation on the global modes’ frequency dispersion or on the energy minimum curvature in the subspace of essential motions [69], in addition to residue MSFs, and perturbation response scanning [70] and mechanical stiffness data trained on 2,298 mutations in the S2648 database [71]. The predictions tested on 350 mutations yield a PCC of 0.61 with experimental data together with an RMSE of 1.24 kcal/mol. Around 77% of tested cases are correctly identified to be destabilizing (ΔΔG <0). The fact that this much can be achieved by equilibrium dynamics-based attributes exclusively points to the unexploited potential of equilibrium dynamics in improving the predictions of ΔΔG (or ΔΔS).

Figure 3. Significance of equilibrium dynamics and variation of physicochemical attributes across ensembles of conformers in developing ML-predictors of stability.

(a) A gradient boosting regressor (scikit-learn package with n_estimators = 1500, subsample = 0.7, max_depth = 5, max_features = 7) trained on dynamics-based attributes (ESSA score (for wt and substituted residues and their difference); MSFs in the softest 2% of modes, MSFs in the stiffest 5% modes, allosteric signaling sensitivity and effectiveness; mechanical stiffness) The regressor yielded a PCC of 0.61 and a RMSE of 1.24 kcal/mol on a widely benchmarked test set consisting of 350 SAVs. (b) Hen egg-white lysozyme N46 corresponding to two intrinsically accessible conformations show a widely varying SASA, from 0.04 to 0.86. (c) The distribution of the maximum difference in solvent accessibility, (d) distribution of hydrophobic packing density (the ratio of hydrophobic residues within 5 Å sphere radius of the mutated residue to the total number of residues within the same radius), (e) distribution of the changes in the number of hydrogen bonds near the investigated residue, (f) Contribution of indicated (abscissa labels) dynamics-based attributes and the 39 additional attributes from PROFOUND) to foldability prediction.

We further posit ML models may be improved upon considering properties based on ensemble of conformers accessible under equilibrium conditions, as opposed to a single structure. For example, in Fig. 3b, show that the SASA of hen egg-white lysozyme Asn46 varies from 0.04 to 0.86 across two intrinsically accessible states (the full range is 0 ≤ SASA ≤1, from completely buried and completely exposed). A regressor trained on a fixed SASA score in this case would thus be misleading. Fig. 3c displays the distribution of the difference in SASAs for all residues in all proteins in the S2648 database, obtained by generating 40 conformers for each case using ClustENMD. Similarly, Fig. 3 panels d and e show that the hydrophobic packing density and the number of hydrogen bonds near mutating residues may vary considerably across intrinsically accessible states. The availability of hybrid simulation methods [72] enables a high-throughput generation of such ensembles of conformers. Using such ensembles, the variance of different physicochemical attributes, not only their means, may be used in ML algorithms to help design better ΔΔG predictors.

The prediction of the change in stability due to insertions/deletions (InDels) of amino acids in proteins is another important but neglected area. The ML tool PROFOUND [73] was recently introduced to predict the change in stability associated with multiple (contiguous) amino acids deletions. As the dependence on residue specificity is lower for deletions than substitutions, we explored the change in stability predicted by PROFOUND using ENM-based attributes. We found that the dynamics-based attributes could adequately predict the change in stability (recall = 78.0% on 10-fold cross-validation on positive-unlabeled-learning). Upon combining dynamics-based features with the PROFOUND features, we could achieve a recall of 84.3%. Fig. 3f shows that equilibrium dynamics/ensemble-based attributes contribute 72.3% to classification. This further highlights the importance of considering equilibrium dynamics for in silico prediction of change in stability.

Conclusion

ML methods have been taking advantage of the rapid growth in structural data in the PDB, and soon they may take advantage of the accumulation of ensembles of structures for a given protein. With the increased generation of alternative conformers for a given protein, using either full atomic simulations such as MD, coarse-grained approaches such as those based on elastic network models, or hybrid models, it is conceivable that NNs will be trained for each protein or homologous proteins on their ensemble of conformers. Such models would predict the changes in distances, potentially at multiple scales, not only between amino acid pairs, but also entire domains or subunits, and enable a more comprehensive mapping of the space of conformational dynamics, thus providing new tools for bridging structure and function. Integration of ML techniques with data on structural dynamics are likely to uncover disease mechanisms that are otherwise intractable by experiments alone, as demonstrated in a recent study [74].

Notably, ENM-predicted structural dynamics depend on inter-residue contact topology. The latter has been pointed out to be a major a descriptor that discriminates pathogenic human variants [22]. The significance of contact topology is also borne out by the predictive performance of Rhapsody that incorporates ENM-derived descriptors (Fig. 2b). ENMs further reveal the pre-existing paths of collective reconfiguration of proteins.

It is important to note, however, that ENMs such as the ANM and the GNM are agnostic to the chemical nature of amino acids and cannot predict the effect of specific substitutions/mutations in amino acids. Despite its lack of amino acid specificity, the GNM proved useful when used within pathogenicity predictors such as Rhapsody. One way to explain this dichotomy is that ENMs identify critical sites or specific positions in the 3D structure, which could play an important mechanical role, or a critical site for allosteric communication, and thus would not tolerate mutations irrespective of the specific substitution. We previously demonstrated for example that the location of enzyme active sites can be inferred from GNM-predicted mechanical hinges even in the absence of the coordinates of amino acid side chains [14,62]; and such hinge sites tend to be evolutionarily conserved [62]. Mutations at those sites, either enhancing or reducing local flexibility, may impair the enzyme activity [75]. Dynamics-based features thus provide information on the adaptability of specific positions to substitutions purely based on 3D topology (a collective structural property). Sequence conservation, substitution, or co-evolution properties further shed light on the likelihood of (or tolerance to) specific substitutions at those positions along the sequence (or on the 3D structure). In other words, structural dynamics provides an overall estimate for the specific position (as can be seen by the vertical red or blue slabs that show little dependence on specific amino acid type in Fig. 2C), and sequence information further discriminates between different types of substitutions.

It is conceivable that if a structure is available for the mutant, and if this structure is sufficiently different from the native fold, ENMs could be applied to both structures to deduce the effect of mutation. However, some amino acid substitutions may have minimal effect on the protein backbone while altering the protein specificity or functionality. For example, at a solvent-exposed substrate-recognition site, the change in amino acid may not affect the overall fold/topology but may impair the substrate recognition and cause a loss of function. While sequence-specific ENMs (such as ENCoM) may help in discriminating between amino acid types, an assessment of gain or loss of function may further require knowledge of substrate-binding sites, or protein-substrate interaction interfaces. Existing databases permit us to learn about protein—protein interaction interfaces using ML methods. Thus, inclusion of such knowledge of interaction interfaces between pairs of proteins, learned by ML methods, may be a future direction for further improving our evaluation of missense variants.

In summary, ENMs may indirectly contain the effects of sequences and structure following the sequence-encodes-structure-encodes-dynamics paradigm, and this may partially explain their success in predicting the pathogenicity of SAVs or the effect of indels on stability. However, a direct consideration of sequence properties, including both conservation and co-evolution behavior, which is best achieved by ML methods, is essential to the success of existing predictors. Comprehensive mapping of the conformational dynamics space, potentially at multiple scales, will help build increasingly powerful ML tools for bridging structure and function.

Data availability

Data will be made available on request.