Odour motion sensing enhances navigation of complex plumes

Abstract

Odor plumes in the wild are spatially complex and rapidly fluctuating structures carried by turbulent airflows^1–4. To successfully navigate plumes in search of food and mates, insects must extract and integrate multiple features of the odor signal, including odor identity⁵, intensity⁶, and timing^6–12. Effective navigation requires balancing these multiple streams of olfactory information and integrating them with other sensory inputs, including mechanosensory and visual cues^9,12,13. Studies dating back a century have indicated that, of these many sensory inputs, the wind provides the main directional cue in turbulent plumes, leading to the longstanding model of insect odor navigation as odor-elicited upwind motion^{6,8–12,14,15}. Here, we show that Drosophila shape their navigational decisions using an additional directional cue – the direction of motion of odors – which they detect using temporal correlations in the odor signal between their two antennae. Using a high-resolution virtual reality paradigm to deliver spatiotemporally complex fictive odors to freely-walking flies, we demonstrate that such odor direction sensing employs algorithms analogous to those in visual direction sensing¹⁶. Combining simulations, theory, and experiments, we show that odor motion contains valuable directional information absent from the airflow alone, and that both Drosophila and virtual agents are aided by that information in navigating naturalistic plumes. The generality of our findings suggests that odor direction sensing may exist throughout the animal kingdom and could improve olfactory robot navigation in uncertain environments.

Odor motion sensing without wind

Like many animals, insects sense odors using two spatially separated sensors – their antennae. This pair of sensors can detect local concentration differences, which encode odor concentration gradients and allow flies to navigate simple plumes such as steady ribbons, where gradients are resolvable and informative^17,18. But the relevance of bilateral sensing for natural plume navigation is less clear, since in turbulent flows odor gradients fluctuate rapidly and do not reliably point toward the source³.

Here, we propose a distinct role for bilateral sensing: inferring the direction of motion of odor signals. To intuit the “motion” of an odor signal, picture smoke emanating from a chimney on a windy day. The dispersing smoke plume quickly breaks into disconnected filaments, and while these filaments move in seemingly random directions, their direction of motion at some instant is obvious by eye. We can think of the motion of odors (which are invisible) as analogous to the motion of these smoke filaments. Importantly, due to the dispersive effects of turbulence and molecular diffusion, the filaments’ direction can differ from the wind¹⁹, thereby providing a directional cue distinct from the local airflow.

To investigate whether flies sense and respond to odor motion, we first re-analyzed a dataset of walking Drosophila navigating a complex, visualizable odor plume whose odor statistics resemble those in turbulent flows¹⁰ (Fig. 1a). In this plume, gradients can be randomly oriented relative to the source, and often differ substantially from the direction of odor motion (Fig. 1a; green and magenta vectors). Since the odor is visible, we can quantify the odor signal encountered during navigation, as well as infer the projections across the antennae of the odor gradient and of the odor velocity (which encodes the direction of odor motion) (Fig. 1b and Extended Data Fig. 1), while simultaneously measuring fly behavior (Fig. 1b). Odor velocity was estimated by cross-correlating the odor concentration in the left and right antenna regions across subsequent frames (Methods), similar to methods that compute velocity using tracer particles in fluids.

Figure 1. Drosophila turning behaviors are correlated with the direction of odor motion in a spatiotemporally complex odor plume.

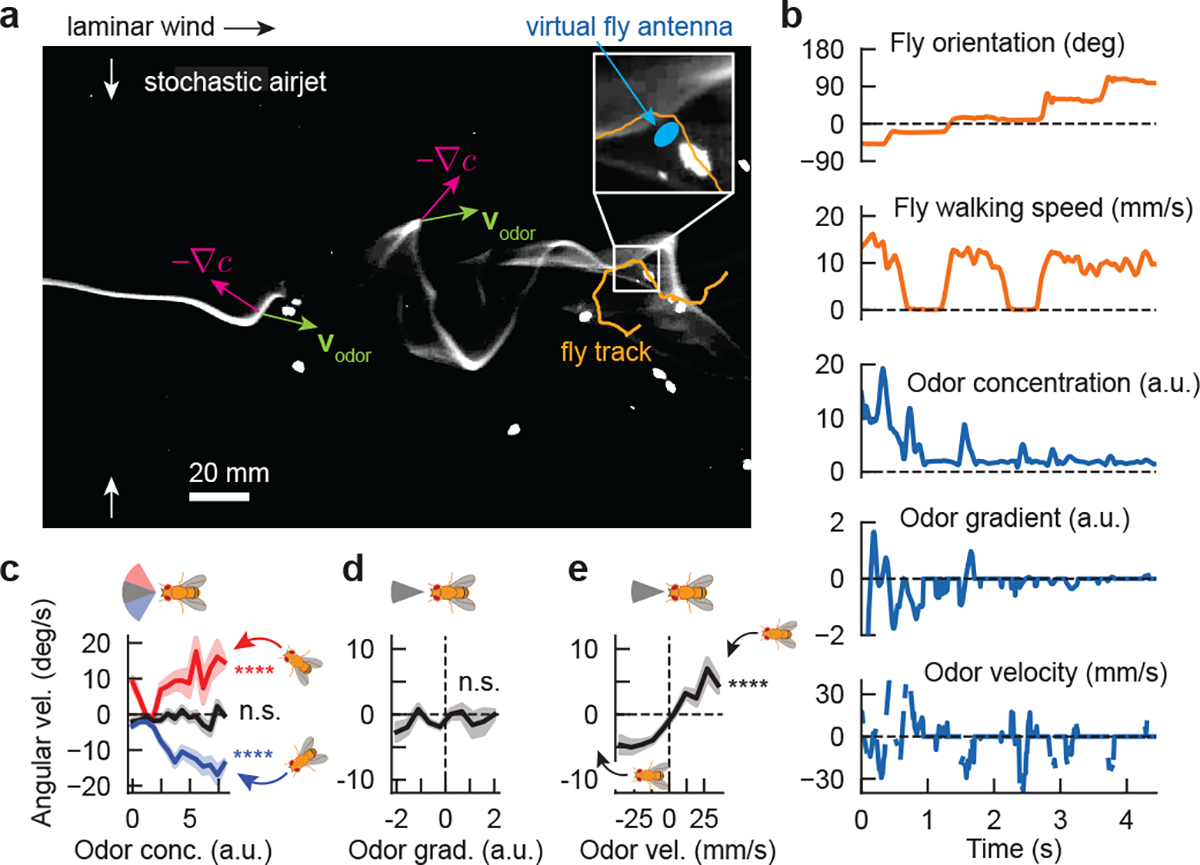
a, Snapshot of walking flies navigating a spatiotemporally complex odor plume generated by stochastically perturbing an odor ribbon in laminar flow with lateral airjets, as described previously¹⁰. Odor gradients (magenta arrows) and odor velocity (green arrows) do not necessarily align and can point in random directions relative to the odor source. Blue oval: virtual fly antennae region used to estimate signal quantities during navigation. b, Example time traces of fly behaviors (orange) and signal-derived quantities (blue) for track shown in a. Odor velocity was computed by cross-correlating the signal in the virtual antenna over successive frames and determining the spatial shift with maximal correlation. Odor gradient was computed as the slope of the odor concentration along the major axis of the virtual antenna. c, Fly angular velocity as a function of odor concentration, for flies oriented in a 40° upwind sector (black), or in a 40° sector centered 40° clockwise (red) or counterclockwise (blue) from the upwind direction. Positive values: counterclockwise turn. Curve shades: SEM. Correlations are significant for flies in the off-axis sectors (slopes = 0.037 ± 0.005, n = 174 tracks and −0.039 ± 0.003, n = 312 tracks for clockwise and counterclockwise sectors, respectively. p < 1e-6 (two-tailed t-test) for both sectors), but not those oriented directly upwind (slope = 0.005 ± 0.003, p = 0.09, n = 285 tracks). d-e, Fly angular velocity versus odor gradient and odor velocity for flies oriented in a 40° sector upwind. Angular velocity is uncorrelated with odor gradient (mean slope = −0.005 ± 0.003, p = 0.072, two-tailed t-test, n = 284 tracks) but significantly correlated with odor velocity (mean slope = 0.040 ± 0.003, p < 1e-6, two-tailed t-test, n = 282 tracks) across the virtual antenna.

Insects turn upwind when encountering odor signals^6,9,10,15, which we verified for flies oriented slightly away from the upwind direction (blue and red curves in Fig. 1c). For flies already oriented upwind, there was no turning bias relative to the intensity or gradient of the odor (Fig. 1c–d). Strikingly, their turn bias did correlate significantly with odor velocity (Fig. 1e), suggesting that flies respond to the direction of odor motion in the absence of directional information from the wind.

Still, since odors are transported by the airflow, odor motion and wind motion are inherently correlated. To break this correlation, we turned to optogenetic stimulation of olfactory receptor neurons (ORNs) using the channelrhodopsin Chrimson^20,21. We generated spatially complex, dynamic fictive odor stimuli by using a DMD projector to display light patterns²² onto blind, freely-walking flies in the 27×17 cm² arena used in Fig 1 (Fig. 2a). This setup enabled optogenetic stimulation with sufficient spatial (< 300 um) and temporal (< 6 ms) precision to hit fly antennae independently. We verified with electrophysiology and behavioral controls that optogenetic stimulation of Orco-expressing ORNs acts as an attractive fictive odor²¹ (Methods, Extended Data Figs. 2a–c), and that flies walking either on the bottom or upside down on the top glass responded similarly to the signal (Extended Data Fig. 2d). Using this setup, we first presented a simple stimulus consisting of traveling fictive odors bars in the absence of wind. Flies oriented perpendicular to the bar motion receive differential stimulation across their antennae when the edges of each bar pass across them. If flies responded selectively to the direction of fictive odor motion, we would expect opposing behaviors for bars traveling rightward versus leftward. We thus presented 5mm-wide bars traveling 15 mm/s either left or right, in 5s-long blocks followed by a 5s-long block of no stimulus (Fig. 2b). Indeed, right-moving bars elicited a net displacement of fly position to the left, and vice versa (Fig. 2c). Further, flies oriented against the direction of motion during the 5s stimulus block, but exhibited no asymmetry during the 5s blank (Fig. 2d). Notably, both of these behaviors were absent in Orco>Chrimson flies with one antenna ablated (Extended Data Fig. 3a–b), but were preserved when Chrimson was expressed only in ORNs expressing the receptor Or42b (Extended Data Fig. 3c–d), which is known to drive olfactory attraction to vinegar²³ and represents a small fraction of all ORNs. These experiments suggested that flies’ olfactory responses were direction selective, and that direction selectivity is enabled by bilateral sensing from the two antennae. The key indicator of direction selectivity was counterturning against bar motion – a reasonable response for locating an odor source emitting propagating odor signals.

Figure 2. Turning responses are consistent with direction sensing, not gradient sensing.

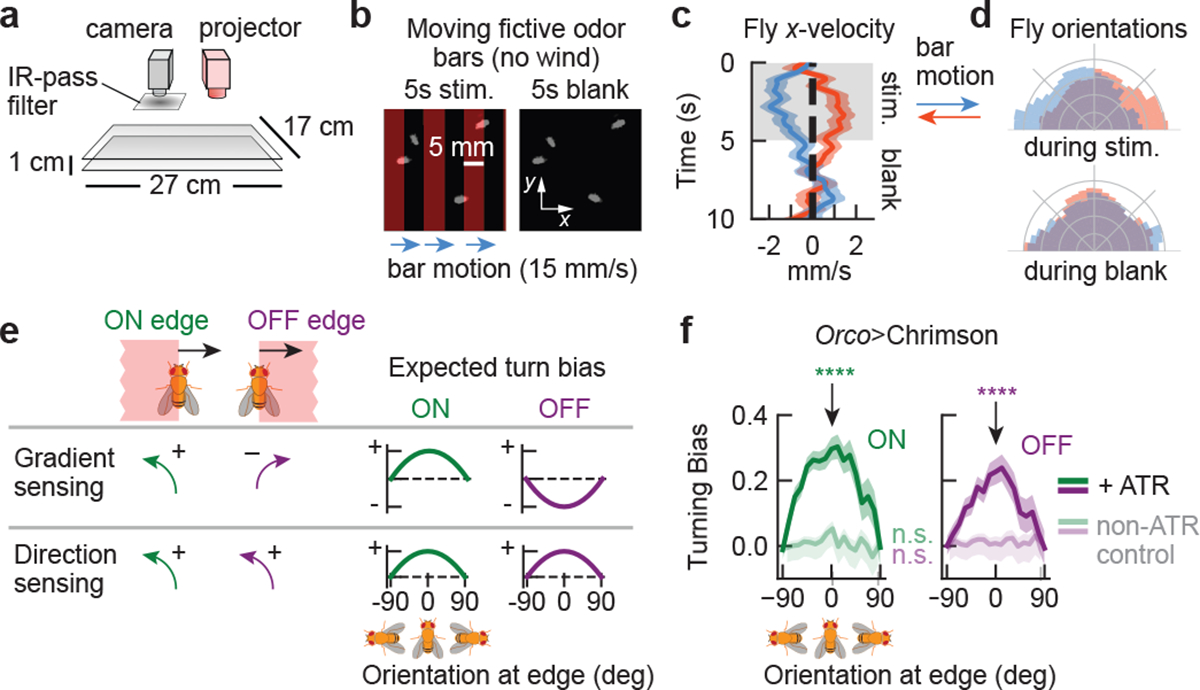
a, Schematic of optogenetic fly walking assay. Flies with Chrimson expressed in ORNs receive optical stimulation from a video projector mounted above the arena. b, Fictive odor bars moving at 15 mm/s are presented in 5s blocks, interleaved with a 5s blank period. c, Component of fly walking velocity along +x direction during the stimulus (shaded grey) and blank periods, for bars moving in +x (blue; n=178 tracks) or -x (orange, n=192 tracks). Shaded error bars: SEM. Only flies facing in the 90° sector perpendicular to bar motion at odor onset (t = 0) are included; d, Distribution of fly orientations during stimulus (top) and blank periods (bottom); colors same as c. Orientations are symmetrized over the x-axis. e, Direction sensing can be differentiated from gradient sensing by measuring turning responses versus fly orientation at both edges of wide, moving fictive odor bars: the ON edge (when the fictive odor first passes onto the fly) and the OFF edge (when it leaves the fly). f, Fly turning bias versus orientation for ON (green) and OFF (purple) edges moving at 10–15 mm/s. Darker curves: flies fed ATR; lighter curves: not fed ATR. Turning bias is quantified as the sign of orientation change following edge onset, where (−1) +1 is (counter)clockwise. Each point covers ±45°; thus, distinct points contain overlapping data. Error bars: SEM. Turning bias for ATR-fed flies, when oriented perpendicular to the bar motion (θ = 0), are significantly different from zero for both ON and OFF edges (p < 1e-6 for both edges, chi-squared test; n=1673, 1509 ON and OFF edge encounters, respectively). Turning biases are not statistically distinct from zero for non-ATR fed flies (p=0.09 and p=0.77 (chi-squared test) and n=1397 and 1484, for ON and OFF edges, respectively).

Direction sensing at ON and OFF edges

Since insects and vertebrates both detect spatial gradients of odor concentration and use them to navigate^18,24, we wondered whether gradient sensing could explain the directional biases we observed. We repeated the experiments above with wider (30–45 mm) bars, which allowed us to quantify responses to each edge individually — the ON edge, when the fictive odor first passes over the fly, and the OFF edge, when fictive odor leaves the fly (Fig. 2e). Responses to these stimuli would clearly distinguish direction selectivity from gradient sensing, since gradient sensing would result in opposing behaviors at the ON and OFF edges while direction sensing responses would be the same (Fig. 2e). We calculated fly turning bias, defined as the sign of the cumulative change in orientation between 150 and 300 ms after the edge hit, as a function of the fly’s orientation relative to the moving edge. For both ON and OFF edges moving at 10–15 mm/s, these plots had strong positive peaks for fly’s oriented parallel to the edge (i.e. when the two antennae were stimulated differentially), indicating that flies are responding to the odor motion, not the spatial gradient (Fig. 2f). Meanwhile, the responses were flat for control flies (Fig. 2f and Extended Data Fig. 3e). Repeating this for various bar speeds, we found strong direction selectivity for bars moving at 10 and 15 mm/s, while for higher speeds (20–30 mm/s), the ON response was significant but reduced and the OFF response was abolished (Extended Data Fig. 3e). At slower speeds 1–5 mm/s, the ON response was still present, but the OFF response was now slightly negative, though not statistically significant (Extended Data Fig. 3e). We attributed this to gradient sensing in the slow edges, which are nearly static odor environments: odor direction and gradients are parallel for ON edges but antiparallel for OFF edges (Fig. 2e), so the behavioral responses to motion and gradients compound for the former but cancel for the latter. Finally, similar directional turning responses for both ON and OFF edges were present in Or42b>Chrimson flies (Extended Data Fig. 3f), indicating direction selectivity at the level of a single ORN type. These observations were robust to changes in the behavioral integration window (Extended Data Fig. 3g), consistent with previously reported reaction times for ON responses^9,25.

Motion sensing sums with wind sensing

Insects bias their heading upwind in the presence of attractive odors^{6–8,10,12,15}, but the role of odor motion in this upwind response is unknown. Our patterned optogenetic setup allowed us to investigate this by independently controlling the wind and odor motion, which is otherwise prohibitive in natural environments. In our earlier experiments, we quantified turning bias in response to odor motion, but without wind (Fig. 2). In the presence of both wind and odor motion, we reasoned that fly responses would reflect some sort of summation of the responses to the isolated stimuli. We therefore presented fictive odors in the presence of wind, but without any motion of the odor. To remove odor motion, we flowed laminar wind and flashed the entire arena with light for 2.5 seconds, followed by 2.5 seconds of no stimulus (Fig. 3a). This stimulates both antennae simultaneously, removing bilateral information — an artificial stimulus that is difficult to deliver with natural odors. In this situation, flies bias their heading upwind (against the wind) at the onset of the flash (Fig. 3b), reminiscent of their tendency to turn “against” the odor motion in the absence of wind (Fig. 2f and reproduced in Fig. 3c). The similarity of turning responses to wind and odor motion separately is illustrated by fitting the turning bias versus orientation plots to a sinusoid (Fig. 3b–c; dashed lines). In both cases, the plots are well fit by Acosθ, where A_wind = −0.40 and A_odor = −0.30.

Figure 3. Turning responses to odor and wind direction are summed.

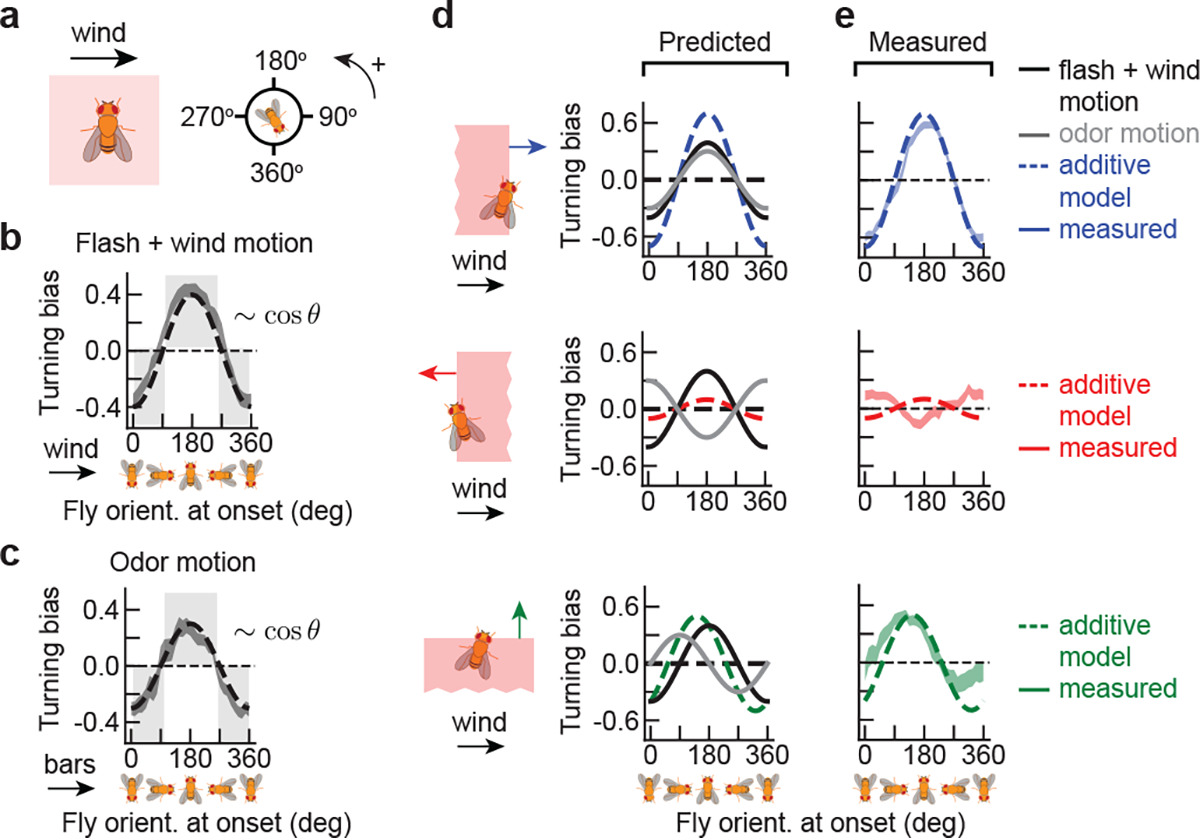
a, Flashing the whole arena stimulates both antennae simultaneously, removing any directional odor cues. Laminar wind is introduced at 150 mm/s. b, Turning bias versus fly orientation, defined as in Fig. 2, for fictive bilateral odor flashes in the presence of wind (top; n = 1240 odor hits); error shades: SEM. Grey shaded boxed regions: values for which fly turns counter to the wind direction; all measured values lie in this range. Dotted line: fit to −0.4cos θ. c, Turning bias versus fly orientation for moving fictive odor bars without wind, at the ON edge (same data as the darker green curve in Fig. 2f, but without symmetrizing orientations). Grey shades: values for which flies turn counter to bar direction. Dashed line: fit to −0.3cos θ. d, By row: expected turning bias versus orientation (dashed curve) for bars moving parallel, antiparallel, or perpendicular to the wind, assuming that turning bias is the sum of the fitted cosines from b (black curve) and c (grey curve). In the 2^nd and 3^rd row, the grey curve has a phase shift depending on the bar direction relative to the wind. e, Solid curves: mean of measured data. Bars move at 15 mm/s. Dashed curves: expected responses from d. Shaded regions: SEM. n = 1361, 1679, and 696 ON edge hits for bars parallel, antiparallel, and perpendicular to the wind, respectively. The additive model is also consistent with faster bar speeds, which have reduced responses (Extended Data Figs. 4e–f).

These simple functional forms encouraged us to consider a simple hypothesis for how flies respond to fictive odor edges moving at a given angle relative to the wind. We hypothesized that the response to the combined signal is a sum of the bar motion and odor motion responses. This hypothesis predicts that when the odor motion direction and wind direction are aligned, the peak response should increase in magnitude and remain centered at 0° and 180° (Fig. 3d; first row). If odor and wind motion oppose each other, these peaks should nearly cancel (Fig. 3d; middle row). Finally, in the interesting case of wind and odor velocity perpendicular to each other, the peaks should shift leftward to ~145° and ~325° (Fig. 3d; bottom row). To test these predictions, we presented fictive odor bars either parallel, antiparallel, or perpendicular to 150 mm/s laminar wind. When the wind and odor were aligned, the turning bias at ON edges was nearly perfectly fit by the additive prediction (Fig. 3e). The antiparallel motion of bars and odors was also fit well – extrema remained at 0° and 180°, though the cancellation overshot slightly. Notably, the response to perpendicularly oriented wind and odor reproduced the shift of the response curve peak from ~180° to 145°, and nearly reproduced the shift of the minimum from ~360° to ~325°. These results suggest that odor direction selective responses integrate with directional information from the wind in a largely, but not entirely, additive fashion. Moreover, universally observed upwind turning responses are more than naive mechanosensory reactions triggered by the presence of odor – they can be enhanced and even cancelled by directional information from the odor itself. Interestingly, responses to OFF edges in the presence of laminar wind were very weak, suggesting other nonlinear interactions between the loss of odor and wind (Extended Data Fig. 4).

Odor motion sensing is correlation-based

We next tested the extent to which our observations were consistent with elementary motion detection algorithms. We began by analyzing our data for moving bars in the absence of wind (Fig. 2). Odor motion creates a difference in latency ΔT between the stimulation of the two spatially separated antennae, the sign and magnitude of which determines the output of direction-selective models such as the classical Hassenstein-Reichardt correlator (HRC)¹⁶. In our assay, ΔT can be inferred from the velocity of the bars relative to the flies using simple geometric considerations (Extended Data Fig. 5a; Methods). This allows us to express turning bias as a function of ΔT, thereby directly testing the predictions of an HRC model. In a simple rightward-selective HRC with two antennal inputs (Fig. 4a), a signal from the left antenna is multiplied with the delayed signal from the right antenna, where the delay is implemented as an exponential filter e^−t/τ. Subtracting this product from a mirror-symmetric computation gives the detector output r(t). We modeled the turning bias as the time integral of r(t), for which the HRC predicts a turning bias proportional to 1 − e^−ΔT/τ for rightward moving edges. Thus, plotting the turning bias against ΔT would allow us to extract the filter time constant τ for this model, revealing the timescale of olfactory motion detection. Pooling the data from both ON and OFF edges at 10–15 mm/s in the absence of wind (i.e., data in Fig. 2f), we found that the prediction was fit well, with filter timescales in the range τ = 25 ± 12 ms (Fig. 4b). Though this estimate is approximate and limited by the temporal and spatial resolution of the projector, it is notable that the timescale is comparable to those of visual motion detection in Drosophila²⁶ and humans²⁷.

Figure 4. Odor motion sensing employs an algorithm sensitive to correlations.

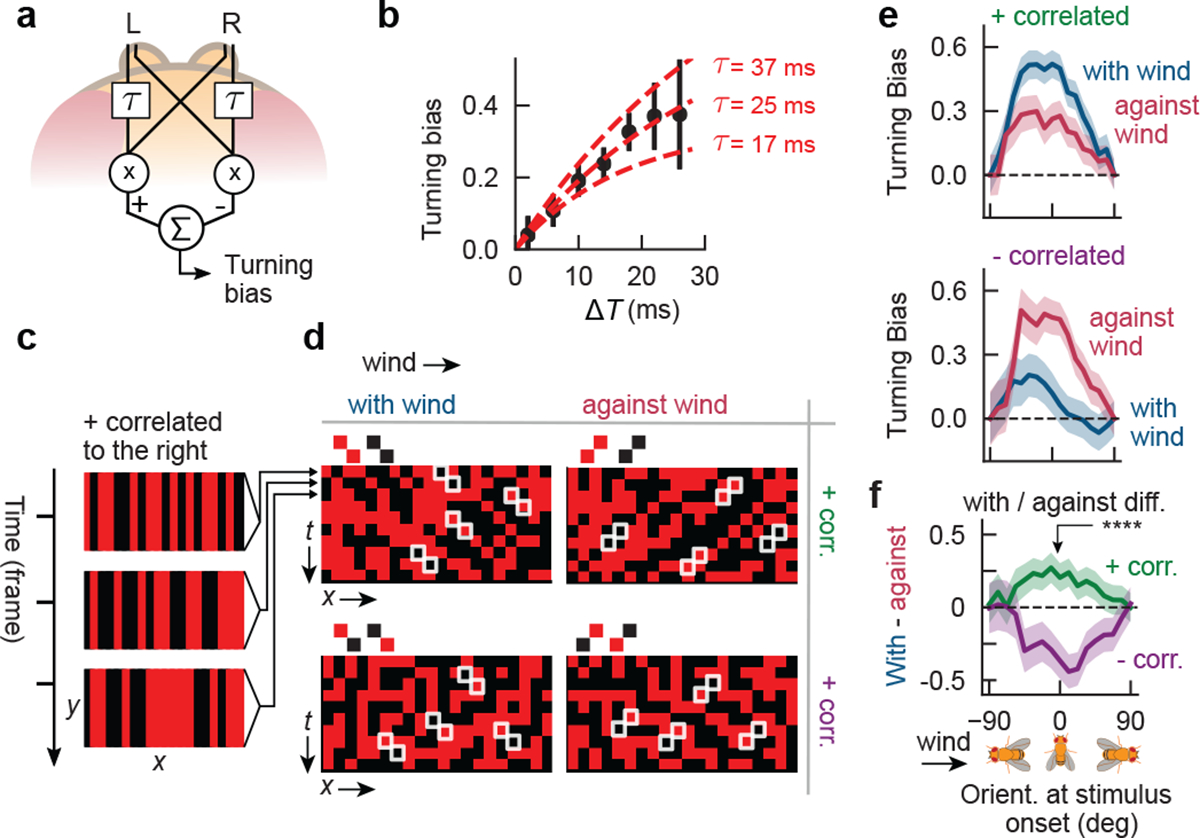
a, Schematic of hypothesized HRC model in the olfactory circuit. b, Black dots: turning bias versus ΔT, using the moving bar data from Fig. 2f. Each datapoint spans ±4 ms. Middle (outer) red lines: fit of HRC model to the mean (± 1 SEM) of turning bias. n = 1475 hits. c, Correlated noise stimuli consist of 1-pixel-wide fictive odor bars. In one frame (3 frames shown), each bar is independently light or dark. Here, bars are positively correlated along +x, so a light bar at a given x in one frame is likely to be proceeded by a light bar one x-pixel to its right in the next frame. Visually, this appears as a rightward moving pattern. d, Illustration of patterns over time, for the 4 different types of correlated noise stimuli. Each pixel denotes the luminance of a bar at a given x-position, at a given time. The 4 stimulus types are defined by correlation displacement (along +x, i.e. with-wind, or along −x, i.e. against-wind) and correlation parity (+ or -). For example, for “with-wind” positively correlated stimuli, bars are correlated with their righthand neighbors in the subsequent frame – this produces red-red or black-black diagonal patterns throughout the x-t plot. e, Turning bias versus fly orientation for positively correlated (top) and negatively correlated (bottom) stimuli. Stimuli presented in 4s blocks; turning bias defined as sign of orientation change over 300 ms after stimulus onset. n = 337, 327 onset events for positively correlated with- and against-wind; n = 219, 227 for negatively correlated with- and against-wind, respectively. Shaded errors: SEM. f, Difference between with-wind and against-wind responses from e, for positive (green) and negative (purple) correlations. Curves differed significantly for θ = 0 (p <1e-6, chi-squared test).

Elementary motion detection algorithms respond fundamentally to correlations in the signal over space and time. To better compare behavior to the predictions of the HRC, we moved beyond ON and OFF odor edges and turned to correlated noise stimuli, which have been used to characterize direction selective computations in fly vision²⁶. A snapshot of a correlated noise stimuli is a pattern of 1-pixel wide bars, each of which is either light or dark (Fig. 4c). The pattern updates in time in such a way that it contains well-defined positive or negative correlations between adjacent pixels. Intuitively, a positive correlation in the +x direction means that light bar at a given x is likely – but not guaranteed -- to be proceeded in the subsequent frame by a light bar 1 pixel to its right; visually, this would appear to be a rightward moving pattern. To enhance the strength of the odor motion behavior, we simultaneously flowed laminar wind as in the experiments in Fig. 3. Thus, there were four types of correlated noise stimuli, corresponding to the possible combinations of correlation displacement (with or against the wind) and parity (negative or positive) (Fig. 4d), each of which is uniquely defined by its correlation function C(Δx,Δt) (Extended Data Fig. 5b).

In this experiment, turning responses to positively-correlated noise stimuli mimicked those to moving bars: upwind turning was suppressed when the correlation displacement opposed the wind direction (Fig. 4e; first plot). Importantly, spatial gradients in these stimuli quickly average to zero, so only a computation sensitive to spatiotemporal correlations — and not gradients — could account for behavioral suppression when the correlation displacement and wind were misaligned. Repeating for negative correlations, we found that upwind turning was suppressed when the correlation and wind were aligned (Fig. 4e; second plot). Notably, this response is also consistent with a correlation-based algorithm, which predicts a reversal in the perceived direction of motion when the correlation changes sign²⁶. In fact, this “reverse phi” phenomenon is a common visual illusion – a feature of correlation-based algorithms – that has been observed and investigated across several species^26,28–30, including humans³¹. Subtracting the with-wind and against-wind responses for each polarity indicated clearly that the reverse phi prediction was satisfied (Fig. 4f).

We corroborated our results using gliders, another class of correlated stimuli^32,33. Visually, a glider is a random pattern of light and dark bars moving in one direction (Extended Data Fig. 5c). Unlike correlated noise, the bars are correlated not only with a neighboring bar in the subsequent frame, but also with more distant bars at later times. However, unlike the weaker magnitude correlations for correlated noise, the correlations in glider stimuli are perfect (Extended Data Fig. 5d, see Methods), so we expected similar trends as before, but with larger effect sizes. For positively correlated gliders, we found similar trends as with correlated noise, but much larger separations between the with-wind and against-wind responses (Extended Data Fig. 5e). We were also able to explore a range of correlation times by adjusting the frame update times. For update times in the range of 17–30 ms, we find direction selective responses, while for shorter update times (11 ms), direction selectivity disappeared (Extended Data Fig. 5f). Interestingly, the maximum separation of with-wind and against-wind responses was with a frame update of 17–22 ms, consistent with the estimate of the HRC filter time constant using moving bars (Fig. 4b).

For flies to sense these correlations in our assay, their antennae must be optogenetically stimulated by distinct pixels. We satisfied this requirement by mounting the projector such that the x-pixel width (~290 μm) approximated the D. melanogaster antennal separation (Extended Data Fig. 5g). We predicted that effects would also reduce for bars wider than the antennal separation, since antennae were less likely to be stimulated independently. Indeed, when we repeated the experiments with the bar width doubled, we found no significant differences between with-wind and against-wind responses (Extended Data Fig. 5h). Together, these data suggest that Drosophila odor direction sensing employs a correlation-sensitive algorithm.

ORN timing enables motion sensing

Our results so far have supported a correlation-sensitive model of direction sensing, tuned to inter-antennal odor latencies as short as ~15 ms (Extended Data Fig. 5f). This raises the question of how temporal precision in the olfactory periphery enables the detection of such latencies. To address this, we turned to electrophysiological measurements of odor-elicited ORN responses, using these to predict HRC model outputs for naturalistic stimuli. We recorded responses of 14 ab3A ORNs from one antenna in 2 flies to 20 short (50 ms) puffs of ethyl acetate (Fig. 5a). Across all 280 presentations, we found a jitter of 5.1 ms in the timing of the first odor-elicited spike, significantly smaller than in prior studies³⁴, but not insignificant compared to the 15 ms timescale of odor motion detection. To quantify how a correlator could extract directional information from noisy ORN responses, we chose at random a pair of spike trains measured in two different ORNs, shifted them in time by −ΔT/2 and ΔT/2, respectively, and then passed this pair through the two arms of the HRC model (Fig. 5b). This procedure mimics how ORNs in each antenna would respond to a rightward traveling odor filament: i.e. the shifted “right” ORN would receive the same signal as the unshifted “left” ORN, but ΔT later. Odor speed and direction are set by scaling or flipping the sign of ΔT, respectively. We found that for |ΔT| above ~10 ms, HRC output was positive for rightward moving signals (ΔT > 0) and negative for leftward moving signals (−ΔT < 0) (Fig. 5b), indicating direction selectivity. Moreover, HRC responses were very similar across odor presentation trials (Fig. 5c), meaning that odor direction could be extracted reliably without averaging over multiple encounters. Finally, extending this to all 19,600 possible pairings of 140 “left” and 140 “right” ORNs, we found that the simple HRC model could reliably resolve odor direction over a broad range of inter-antennal latencies 11 < ΔT < 153 ms (Fig. 5d), corresponding to odor speeds as high as 25 mm/s. Altogether, this indicated that, at least at the level of single, noisy ORN pairs, sufficient information was present to encode odor direction. Moreover, the HRC timescale of τ = 15 ms does not set a hard lower bound on the resolvable latency ΔT. This is because the filters in the HRC model smear the signals in time, so that HRC outputs are non-zero over a range of ΔT, not just when ΔT = τ. Thus, the HRC is strongly direction-selective even at latencies far from τ.

Figure 5. The temporal precision of ORN responses is sufficient to encode odor directionality.

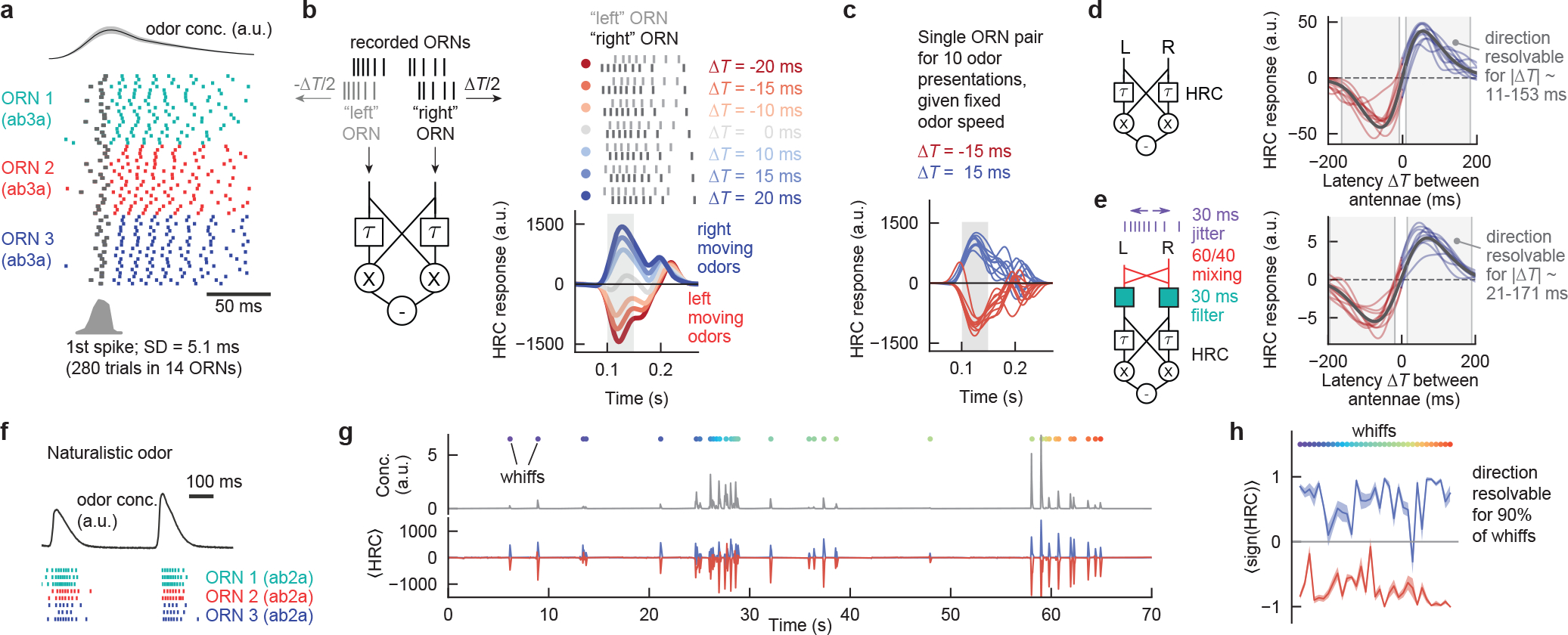
a, Spike rasters for ab3A ORNs responding to 50 ms puffs of ethyl acetate. Odors were presented 20 times each (rows) to different ORNs (colors) with 3s intervals. Top trace: odor concentration measured by PID. Histogram: distribution of timing of first spike after odor presentation. b, Left: HRC schematic. To calculate HRC responses to moving odor signals, ORN spike trains from a (taken from different ORNs in a single antenna) were designated as “left” or “right” antennal ORNs by adding appropriate delays. Right: HRC responses over time for various ΔT. c, Same as b, for the same pair of ORNs, over 10 different odor presentations and |ΔT| = 15 ms. d, Time-averaged HRC response versus ΔT. Black: mean over all pairings of “left” and “right” ORNs. Light curves: 10 representative pairings. Odor direction is deemed resolvable if the mean is outside 1 SD of zero. Since SD rather than SEM is used, this corresponds to resolving odor direction with one odor presentation. e, Same as d, but now including circuit transformations and noise. f, Representative ORN rasters to a few whiffs of a naturalistic odor signal (full trace in g). g, Odor signal (top) and calculated mean HRC response ⟨HRC⟩ (bottom) for odor latencies of ΔT = ±15 ms for a naturalistic odor signal. 4 “Left” and 4 “right” ORN spike trains were generated from 8 single antenna recordings as described in b, and the mean is taken over the 16 left/right pairs. Colored dots: individual whiffs, defined by times at which the firing rate exceeded 30 Hz. h, Sign of HRC response, averaged over 16 ORN pairs, for all whiffs in g. Shaded regions: SEM over all 16 ORN pairs.

Next, to see how some known downstream transformations might affect direction sensitivity, we added two processing steps upstream of the HRC computation: bilateral mixing of ORN signals with a 60/40 ratio¹⁷ and a 30 ms lowpass filter representing projection neuron (PN) responses³⁴. Additionally, we jittered each ORN spike up to 30 ms³⁴ to represent variability across the ORN population. The aggregate effect of these 3 transformations was to shift the resolvable response range to 21 < ΔT < 171 ms (Fig. 5e) – a remarkably small reduction in sensitivity. In fact, we show mathematically that temporal filtering should not degrade the resolution to a level naively suggested by the filtering timescales. For instance, an HRC receiving inputs that have been filtered over τ_filt = 100 ms can still respond direction selectively to latencies much lower than τ_filt (Methods and Extended Data Fig. 6). Intuitively, while the PN filter smears the two inputs, it acts on each input equally, thereby retaining the relative signal delay between them.

We next repeated the same calculations using the responses of ab2A ORNs to a naturalistic odor stimulus from our prior study³⁵, which is composed of brief bursts of odor, or “whiffs,” interspersed with periods of clean air (Fig. 5f). In this signal, the whiffs concentrations and durations spanned an order of magnitude, typical of odor statistics in turbulent flows³. We estimated the HRC response to left- and right-traveling odors as above, by pairing different recorded ab2A ORNs and shifting them appropriately (Fig. 5g). Averaging over all “left” and ”right” pairs, we found that odor direction for latencies |ΔT| = ± 15 ms was resolvable in more than 90% of the individual whiff encounters (Fig. 5h). Altogether, these findings reveal that the temporal precision of ORN responses, together with putative circuit transformations in the Drosophila olfactory periphery, can robustly encode the direction of natural odor signals.

Finally, we note that despite the robustness of the direction selective odor computations shown above, our estimates here remain a worst-case-scenario. We have simulated HRC responses using individual ORNs on each antenna, but Drosophila antenna contain populations of ORNs of each type, which are pooled in PN responses. This convergence increases detection accuracy by averaging over noise^34,36, and a similar denoising upstream of direction sensing computations should enhance robustness beyond what we have demonstrated here.

Odor motion sensing in natural plumes

In principle, animals could use measurements of odor motion to help them navigate complex plumes, provided this information complements other directional cues such as gradients or wind. To quantify the distribution of odor signal directions in a naturalistic plume, we ran numerical simulations of an environment replicating the plume from Fig. 1. These simulations provide not only a more finely resolved concentration field, but also the airflow velocity field (Fig. 6a), which is experimentally inaccessible. We first compared, for a few fixed points in the plume, the odor velocity v_odor and the airflow v_wind at a single time. Both v_odor and v_wind had x-components comparable to the mean flow speed 150 mm/s. However, v_odor also had large crosswind components v_y,odor pointing outward from the plume centerline, which were noticeably absent from v_wind (Fig. 6b; left). Averaging over all detectable odor filaments in the 120s simulation revealed a similar trend: away from the plume centerline, the distribution of v_odor spanned a tight angular range, pointing consistently outward in the crosswind direction (Fig. 6b; middle column). Meanwhile, v_wind was distributed largely downwind, with much smaller outward angles (Fig. 6b; right column). To visualize the “flow” of odor motion, we calculated the time-average of 〈v_odor〉 at all locations in the plume. We compared this to the time-average of the wind vector conditional on the presence of odor, 〈v_wind|odor〉. We used the latter rather than the unconditional wind velocity, 〈v_wind〉, since for an ideal point source of odor within homogeneous turbulence, the latter does not encode the lateral location of the source. Throughout the plume, 〈v_odor〉 flowed strongly outward from the plume center, while 〈v_wind|odor〉 was directed essentially downwind (Fig. 6c).

Figure 6. Odor direction sensing enhances naturalistic plume navigation.

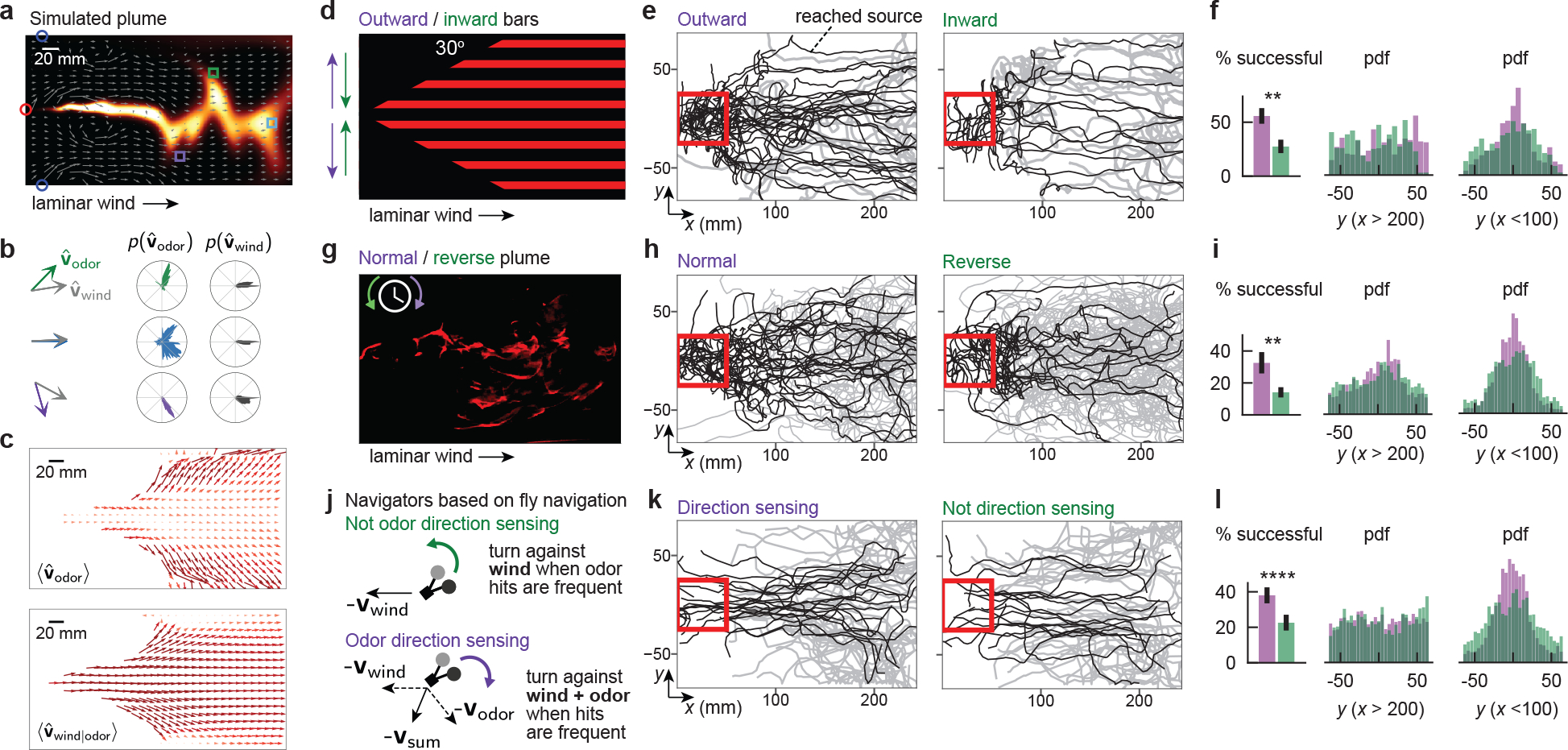
a, Snapshot of simulation of plume from Fig. 1. Grey arrows: wind direction at snapshot instant. b, left column: Odor velocity (colors) and wind (grey) vectors at snapshot instant, at boxed locations in a. Middle and right column: Distributions of same over whole simulation. c, Top: Mean odor velocity field. Bottom: Mean wind field for detectable odor concentrations. d, Illustration of fictive odor “plume” in which 2 mm-wide bars move outward or inward from arena centerline at 15 mm/s. Laminar wind flows at 150 mm/s. e, Measured fly tracks for flies beginning in the downwind 50 mm end of the arena, for outward (left) or inward (right) bars. Black tracks: flies that reached a 50 mm box around the fictive plume source. f, Left: Flies in outward bar plume were more likely to reach the source: 56% (28/50 tracks) vs. 28% (12/43 tracks) (p=1.13e-3, one-tailed t-test). Middle and right: Distributions of flies’ lateral (y) position, in the downwind (left) or upwind (right) end of the arena, respectively. g, Projected complex plume, played either normally or in reverse. h-i Analog of e-f. Flies in normal playback were more likely to reach the source: 32% (22/69 tracks) vs. 14% (13/91 tracks) (p=6.39e-3, one-tailed t-test). j, Simulated agent model based on Drosophila odor navigation¹⁰. Non-direction-selective (DS-) agents increase the upwind bias of stochastic left/right turns with odor hit frequency (top; green). Direction-selective (DS+) agents turn against the vector sum of the wind and odor directions as hit frequency increases (bottom; purple). k, Tracks of DS+ (left) and DS- (right) agents navigating complex plume in g. l, Analogue of f and i. DS+ agents were more likely to reach source (34% vs. 25%, p = 9.98e-5; 1-tailed t-test).

This analysis suggests that in naturalistic plumes emanating from a point source, the direction of odor motion is a strong indicator of the direction towards the centerline of the plume. This directional cue is not reflected in the local wind, nor in the local gradients, though we did find that odor gradients have a similar crosswind structure closer to the source, where the plume is less intermittent (Extended Data Fig. 7a). Of course, to be useful for navigation, odor motion must be resolvable on realistic timescales. By calculating the running average of the odor direction at a fixed location, we found that in most of the plume extent, only several hundred milliseconds were necessary to resolve the lateral components (Extended Data Fig. 7b–c). Since odor bursts occurred at ~1–5 Hz in this particular plume¹⁰, a navigator could estimate the direction of odor motion orthogonal to the mean flow after only a few odor hits.

To investigate how Drosophila use odor motion during navigation, we designed a fictive odor plume whose boundaries were subtended by a cone — as if emanating from a source — and within which thin bars moved laterally outward from or inward toward the centerline, while laminar wind flowed along the cone axis (Fig. 6d). The bars moved at 15 mm/s and were spaced by 5, 10, or 15 mm (data is pooled), giving fictive odor hits with short durations and frequencies ~1–3 Hz, similar to the complex plume considered above (Fig. 1a). We reasoned that inward moving bars, which are reversed from their natural flow, would degrade the ability of the fly to move towards the plume axis, and therefore to localize the odor “source,” i.e. the tip of the cone. We found that for both bar directions, flies stayed within the conical fictive odor region, but were significantly more likely to reach the upwind source region when the bars moved outward (56% versus 28% for outward versus inward bars, respectively, p < 0.01, one-tailed t-test) (Fig. 6e–f). Moreover, performance gains were attributed to increased lateral navigation toward the plume centerline (Fig. 6f and Extended Data Fig. 8a), as predicted. Notably, the fictive odor signals in these two paradigms at each location do not differ by frequency, duration, or spatial gradients — differences in performance (Fig. 6f) can be explained by odor direction sensing alone.

Next, we tried the more realistic case of projecting a video of a recorded complex smoke plume, playing the video not only normally, but also reversed in time (Fig. 6g). As in the previous conical bar stimulus, reverse playback reverses odor motion without perturbing the steady state distribution of spatial gradients or the frequency or duration of odor hits measured at each point. Remarkably, the likelihood to reach the odor source significantly degraded when the plume was played in reverse (32% versus 14%; p < 0.01, one-tailed t-test) (Fig. 6h), again driven by enhanced navigation toward the plume axis (Fig. 6i and Extended Data Fig. 8b). Together, these results indicate that the odor motion provides a directional cue complementary to odor gradients and wind motion, and strongly enhances navigation in complex odor plumes, even when other aspects of the odor signal remain unchanged.

Finally, with an eye toward practical applications, we used in silico experiments to explore the value of odor motion sensing for olfactory robots. Virtual navigators were modeled as in our previous study¹⁰: low-curvature walking bouts were interrupted with stochastic left/right turns at a fixed Poisson rate, and turns were more likely to be directed upwind as the frequency of odor hits increased (Fig. 6j). These virtual agents are not direction-sensing (DS- agents); meanwhile, direction sensing (DS+) agents obeyed the same strategy, but with turns biased against the vector sum of the odor motion direction and the wind direction (Fig. 6j). We simulated both DS+ and DS- agents in the imaged complex plume (Fig. 6g), finding that DS+ agents were better localized within the plume extent than DS- agents (Fig. 6k) and significantly more likely to find the odor source (n=100 agents; 34% vs. 25%, p < 1e-4; 1-tailed t-test) (Fig. 6l). As above, performance was aided by increased drift toward the plume centerline (Fig. 6l). These results were not a byproduct of the model’s behavioral repertoire: we found similar performance gains for direction-sensing virtual robots navigating a grid with a much simpler strategy (Extended Data Fig. 9). Together, these in silico experiments show that odor motion sensing can enhance the robustness of complex plume navigation in both simplistic and bioinspired navigational algorithms. The simplicity of the direction sensing mechanism, together with computational methods to detect fast odor transients using metal oxide sensors^37,38, suggests that odor motion detection could be incorporated into olfactory robots in a variety of existing schemes^39,40 (see Methods and Extended Data Fig. 10 for a discussion of the relationship between odor motion detection, the distance between the two sensors, and the statistics of the turbulent air flow).

Discussion

Olfactory navigation relies on integrating various sensory signals that contain information about the odor source. Which features exist, and how much information they carry, can vary considerably between plume structures^41–43. Gradient sensing can provide reliable directional information when navigating laboratory-controlled plumes, such as static ribbons¹⁸, or very close to the source of natural plumes before odor patches have dispersed (Extended Data Fig. 7). Further away from the source, however, turbulent air motion stretches and fragments odor patches as they are carried downstream, producing odor signals that are patchy and intermittent^1–3, and which span many spatial scales – the so-called inertial convective range – from macroscopic eddies to molecular diffusion⁴⁴. In these regions, concentration gradients tend to orient randomly, and so have limited value. Even in turbulent boundary layers, where concentrations are more regular⁴, gradients could aid navigation, but would require amplifying the gradient to an extreme degree not consistent with data⁶.

In contrast, our work suggests an entirely new role for bilateral sensing: measuring the direction of odor motion by comparing concentrations in both space and time. This information stream is especially relevant within the inertial convective range of turbulent plumes. Parallel to the plume axis, odor motion is redundant with the average wind direction. But perpendicular to the plume axis odor packets spread via random continuous motions, with an effective diffusivity much larger than molecular diffusion¹⁹. What results is a strong flux of odor packets outward from the plume centerline, providing a directional cue orthogonal – and thus complementary – to the mean wind. We corroborated this with theoretical analysis of a simple turbulent plume model (Methods), finding that the outward flow of odor motion we observed in simulations (Fig. 6c) exists in turbulent plumes more generally (Extended Data Fig. 10a–b), Moreover, these lateral odor velocity components can be detected by computing temporal correlations between two nearby points (Extended Data Fig. 10c). Thus, odor motion sensing is not just relevant to walking fruit flies; this directional cue could in principle enhance natural plume navigation across the animal kingdom, across distinct olfactory anatomies, and in distinct locomotive regimes (see Supplementary Text).

Our setup allows us to test the predictions of the HRC model using artificial correlation-type stimuli which would be prohibitive to produce with natural odors. In particular, we generated a reverse phi illusory percept for negative correlations, a signature of correlation-based algorithms observed in visual motion detection in flies^26,28 and other species^16,29,30, including humans³¹. While the HRC model replicates several features of odor direction sensing, it is an incomplete description of the odor motion sensing algorithm, neglecting asymmetries between ON/OFF responses and higher-order correlations in odor scenes (see Supplementary Discussion).

Where could direction selectivity occur in the olfactory circuit? Most ORNs project to both antennal lobes, but ipsilateral and contralateral signals differ in magnitude and timing¹⁷, which could be amplified further downstream to enact bilateral computations. One potential region of interest is the third-order olfactory center, the lateral horn (LH), which mediates innate odor responses and projects bilaterally^23,45.

The lack of smooth concentration fields in naturalistic plumes has inspired a number of navigation studies focusing on how animals use the temporal features of the odor signal, such as the frequency or duration of encounters with odorized air packets. This reliance on timing is enabled by the remarkable degree of temporal precision in olfactory circuits^35,46–50. Here, we show that odor timing can be combined with bilateral sensing to measure odor motion, a directional cue distinct from the only other reliable directional cue in turbulent plumes – the wind. Our findings reveal a valuable role for bilateral sensing in the complex, dynamic odor environments that animals navigate in the wild.

METHODS

Fly strains and handling

Flies were reared at 25°C and 50% humidity on a 12 hour/12 hour light-dark cycle in plastic vials containing 10 mL standard glucose-cornmeal medium (i.e. 81.8% water, 0.6% agar, 5.3% cornmeal, 3.8% yeast, 7.6% glucose, 0.5% propionic acid, 0.1% methylparaben, and 0.3% ethanol. Media was supplied by Archon Scientific, Durham, NC, USA). All flies used in behavioral experiments were female. Between 10 and 30 females were collected for starvation and placed in empty vials containing water-soaked cotton plugs at the bottom and top. All flies were 3–10 days old and 3 days starved when experiments were performed. Flies in optogenetic experiments were fed 1 mM all trans-Retinal (ATR) (MilliporeSigma, Burlington, MA, USA; previously Sigma Aldrich) dissolved in water. ATR was fed to flies 1 day prior to recording, and all flies were housed in the dark from the time of ATR feeding until the time of the recording.

All flies used throughout the study included a GMR-hid transgene, which causes photoreceptors to die, making these flies blind. Optogenetic activation was achieved by expressing Chrimson (20X-UAS-CsChrimson) in Orco-expressing olfactory receptor neurons (Orco-GAL4) in almost all experiments⁵¹. The one exception was the single-Or experiments (Extended Data Fig. 3c–d), which expressed Chrimson in only neurons expressing the olfactory receptor Or42b.

The genotypes used are listed in the following table:

1	w;gmr-hid;+		Gift from Mala Murthy
2	w;+;20XUAS-Chrimson		Bloomington ID: 55136
3	w;+;Orco-Gal4		Gift from John Carlson
4	w;+;Or42b-Gal4		Gift from John Carlson
5	w;gmr-hid/+;20XUAS-Chrimson/Orco-Gal4	Figs. 2–6	Constructed from 1,2,3
6	w;gmr-hid/+;20XUAS-Chrimson/Or42b-Gal4	Fig. 2	Constructed from 1,2,4

Behavioral assay and optogenetic stimulation

The fly walking arena is identical to the one used in a previous study¹⁰. All experiments were performed in a behavioral room held at 21–23°C and 50% humidity. The walking arena is 270×170×10mm (see Fig. 2a) and consists of top and bottom glass surfaces and acrylic sidewalls. The upwind end is an array of plastic coffee straws, which laminarize the airflow (when wind is turned on); the downwind end is a plastic mesh. For experiments with wind, dry air is passed through the straws at a flow rate giving a laminar flow at 150 mm/s within the arena. The only exception was the forward and reverse playback complex virtual plumes (Fig. 7g), for which the laminar flow speed was reduced to 100 mm/s to match the flow speed used to generate the recorded smoke plume (see Recorded Smoke Plume below). Flies are introduced by aspirating through a hole near the downwind plastic mesh. Flies were illuminated using 850 nm IR LED strips (Waveform Lighting) placed parallel to the acrylic sidewalls.

Experiments were recorded at 60 Hz with a FLIR (Wilsonville, OR, USA) Grasshopper USB 3.0 camera with IR-pass filter. Optogenetic stimuli were delivered using a LightCrafter 4500 digital light projector (Texas Instruments, Dallas, TX, USA) mounted 310 mm above the arena, illuminating an area larger than in the original method²². Only the red LED (central wavelength 627 nm) was used throughout this study. We used the native resolution of the projector (912 ×1140 pixels), which illuminated the entire walking arena with pixels of size 292 μm (along wind axis) x 146 μm (perpendicular to wind axis). The majority of our experiments used a 60 Hz stimulus update rate; the exceptions were the faster 20–30 mm/s bar stimuli (Extended Data Fig. 3e; Extended Data Figs. 4e–f), the glider experiments (Extended Data Figs. 5e–f), and the complex virtual plume playback (Fig. 7g), for which we used a 180 Hz update of projected images. The average intensity of the red light within the walking arena was 4.25 μW/mm². Though all data presented in this article used blind flies, initial exploratory experiments used flies that were not blind. To remove visual effects from the stimulating red light, we shone green light using an LED (Luxeon Rebel LED 530 nm) throughout the arena to flood the visual response. Though this was not necessary for blind flies, we retained the green light throughout the experiments presented here to compare to past data.

The projector and camera have distinct coordinate axes – camera and projector pixels are different sizes and their native coordinates systems are not the same handedness. To infer the virtual encountered stimuli for navigating flies, one must transform between a 2D camera coordinate x_cam and a 2D stimulus coordinate x_stim. We assume that the two are related by a combination of linear transformations and translations:

$${\mathbf{x}}_{\text{cam}}=\mathbf{A}{\mathbf{x}}_{\text{stim}}+\mathbf{B}.$$

To estimate the matrix A and vector B, 3 mm diameter dots were projected at random locations ${\mathbf{x}}_{\text{stim}}^i$ in the arena while recording with the camera; camera coordinates ${\mathbf{x}}_{\text{cam}}^i$ were determined in the imaged frame using the SimpleBlobDetector function in OpenCV. The 6 elements of A and B were then determined by minimized the least squares difference:

$$C=\sum _i{\left({\mathbf{x}}_{\text{cam}}^i-\mathbf{A}{\mathbf{x}}_{\text{stim}}^i-\mathbf{B}\right)}^2$$

We verified manually that this procedure generated accurate transformations. We generated all stimuli using custom-written scripts in Python 3.7.4, and delivered these stimuli to the projector using the Python package PyschoPy, version 2020.2.4.post1.

Recorded smoke plume

The complex odor plume presented virtually with light (Fig. 6g) was derived from an imaged smoke plume in the same arena. The smoke plume was obtained using an identical protocol as in our previous work¹⁰, but with slightly modified airflow conditions. There, the laminar flow speed was 150 mm/s, while here it was reduced to 100 mm/s. The speed of the two lateral perturbing upwind airjets was also reduced from ~1500 mm/s to ~1000 mm/s. The airjets were stochastically switched at a Poisson rate of 10 s⁻¹ as in the original study. To convert the smoke plume to the virtual optogenetic plume, the images in the video were scaled with an affine transformation and presented with 8-bit resolution.

Electrophysiology

Single sensillum recordings from Drosophila antennae were performed as described previously^35,47,52. The recording electrode was inserted into a sensillum on the antenna of an immobilized fly and a reference electrode was placed in the eye. Electrical signals were amplified using an Ext-02F extracellular amplifier (NPI electronic instruments, Tamm, Germany). The ab2 sensillum was identified by i) its size and location on the antenna, and ii) test pulses of Ethyl 3-HyrdoxyButyrate, to which the B neuron is very sensitive. Spikes from the A and B neurons in this sensillum were identified and sorted as described previously³⁵, using a spike-sorting software package written in MATLAB (Mathworks, Inc., Natick, MA, USA) (https://github.com/emonetlab/spikesort). For responses to real odor stimuli (Fig. 5), odors were delivered as in our previous work^35,53. Briefly, an odorized stream was fed into a main airstream and delivered through a glass tube positioned within 10 mm of the fly antenna, while mass flow controllers (Aalborg instruments and Controls, Inc. (Orangeburg, NY, USA) and Alicat Scientific (Tuscon, AZ, USA)) were used to regulate airflows.

Experimental protocol

Experiments were carried out between 9 AM and 12 PM. This corresponds to between 0 and 3 hours after lights-on in our incubators, in which lights were on from 9 AM to 9 PM. Between 10 and 30 flies were aspirated into the arena and allowed to acclimate for 2 minutes before experiments began. Before all experiments, optogenetic activation was verified by presenting static fictive odor ribbons (as in Extended Data Fig. 2c) with laminar wind for 120 seconds, and ensuring that flies followed the ribbons upwind as a positive control. In our assay, flies could walk on the top glass surface or bottom glass surface, and since the spacing between the surfaces was appreciable (1 cm), flies could flip to the top surface during a trial without climbing the sidewalls. In our videos, we could not reliably distinguish which surface the fly walked on, so we pooled flies for all analyses throughout. We verified that optogenetic activation of ORNs for flies on either surface was similar, by manually annotating 300 tracks of flies navigating fictive odor ribbons, and demonstrating that both similarly followed fictive odor ribbons upwind (Extended Data Fig. 2d). Unless otherwise noted, each experiment ran for 60–120 seconds, with 60 seconds in between experiments.

No statistical tests were used to determine sample size. More than 50 flies were used for each experimental condition. Since flies were reared in vials containing 10–15 individuals, this gave 5–10 vials per experimental condition, sufficient to mitigate outlier effects from any single vial. All experiments were replicated more than three times on the same flies, and the same conditions were replicated at least 10 times with different flies over several days. Investigators were not blind to fly genotype. Throughout, experiments were interleaved such that the directions of the moving stimuli were randomized. No more than 30 videos were recorded on a single set of flies.

Quantification of fly behavior and encountered fictive odor stimulus

Extraction of fly position, speed, and orientation from videos

All scripts were written in Python 3.7.4. Fly centroids were determined using SimpleBlobDetector in OpenCV, assuming a minimum area of 5 mm². Given the centroids, fly identities were determined using custom tracking scripts. Briefly, centroids in subsequent frames were matched to the nearest centroid, and if the centroids could not be matched, they were marked as disappeared. Flies marked as disappeared for more than 30 frames (0.5 seconds) were then deregistered. Subsequent detected centroids were then marked as new fly tracks. Fly orientations θ were determined by first using the canny function in the Python module scikit-image to determine the points defining the fly edges around the centroid, then fitting these to an ellipse using custom-written Python scripts. Fly orientations are defined on the interval [0, 360°], but ellipse-fitting does not distinguish head (0°) from rear (180°). We properly resolved this using the fly velocity (below).

The above data defines the fly positions (x, y) and orientations θ. To remove measurement noise, we filtered each of these quantities with a Savitsky-Golay filter using a 4^th-order polynomial and window size of 21 points (to avoid branch cuts in θ, it was first converted to an un-modded quantity). Velocities $\dot{x}$ and $\dot{y}$ and angular velocity $\dot{\theta }$ were defined by taking the analytical derivative of the fitted Savitsty-Golay polynomials for x, y, and θ. To resolve the two-fold symmetry in the fitted ellipses, and therefore distinguish the fly head from the rear, we used the fly velocity. For fly speeds greater than a given speed threshold, we matched the orientation to the fly velocity vector since flies predominantly walked forward. For other times, we matched the fly heading at the beginning and end of bouts when fly speed was below the speed threshold. The result was an estimate that may still have errors which occur as unnatural jumps in orientation. We repeated this process for various speed thresholds from 1 to 4 mm/s, and chose the orientation trace with the least number of jumps. We verified manually with several tracks that this procedure was highly reliable.

We noticed that during the experiments, particularly those with long fictive odor encounters such as the wide bars in Figs. 2 and 3, there was a slow, gradual bias toward one side of the arena (along the shorter axis of the arena). This only occurred for flies with optogenetic constructs that were fed ATR, and we reasoned it might be due to a shadowing effect of the projector light from the fly body onto the antenna, or from one antenna onto the other, since the projector lens is nearer to the bottom of its projected image. This shadowing effect appears to create a fictive odor gradient across the arena. To account for this bias, we repeated all experiments that had an asymmetry in the perpendicular direction, such as bars perpendicular to the wind (Fig. 3d; 3^rd row), in both directions. We then averaged the turning biases from these two directions, after flipping the orientations appropriately. This would retain the effects due to direction sensing but remove the bias, under the assumption that this bias was an additive effect.

Estimation of encountered fictive odor stimulus in antennae

Given these smoothed and corrected x, y, θ measurements, we then estimated the encountered fictive odor signal in the antenna region by defining a virtual antenna at a location 1.5 mm from its centroid along the ellipse major axis toward the fly head. To generate stable estimates – i.e. not relying on a single pixel value – we use the stimulus value averaged over a box of 0.25 mm² around this location. Stimulus values in the antennal region are not measured by imaging, since the images are IR-pass filtered. Rather, they are obtained from knowledge of the stimulus pattern and the stimulus-to-camera coordinate transformation defined above. In PsychoPy, stimulus values are defined as 8-bit integers, from 0 to 255, but in practice we only deliver stimuli as max intensity (255) or 0. Accordingly, we treat the signal in the virtual antenna as binary, equal to 1 when the average stimulus value in the 0.25 mm² region is above 200, and 0 otherwise.

Quantification of behavior for moving bar stimuli

For all wide bar stimuli, only flies walking between 2 and 20 mm/s at the time of the edge hit are included. For fast moving bars (Fig. 2b–d and Extended Data Fig. 3), only tracks lasting longer than 10 seconds and whose mean speed is between 3 and 10 mm/s are included. For the bar stimuli in Figs. 2–3, we identified ON and OFF edge hits as the times that the antennal signal switched from 0 to 1 or 1 to 0, respectively, where this binarization was calculated as described above. To calculated turning biases, we followed prior work¹⁰ and considered saccadic turning events, identified as points at which the absolute value of the angular velocity exceeded 100°/s, and ignored small jitters. Turn biases at a given time t_i (e.g. at an ON or OFF edge hit (Fig. 2–3)), were defined as the sign of the change in fly orientation from t_i + 150 ms to t_i + 300 ms, provided the absolute value of angular velocity in that window exceeded 100°/s at some point in that window. We used this 150 ms latency after t_i to account for uncertainties in t_i due to uncertainties in exact position of the antenna, which we estimated as being upper bounded by 2 mm. For all plots, to remove tracks in which flies may have been turning before the hit, we ignored points for which the absolute angular velocity exceeded 100°/s between 300 ms and 150 ms before the hit. The dependence of the results on this window is shown in Extended Data Fig. 3g; though the effects are largest in this regime, they are not strongly sensitive to the choice of window following t_i.

Quantification of behavior for correlated noise and glider stimuli

Turn biases for correlated noise and glider stimuli (Fig. 4) were calculated similarly to those for moving bars. Correlated noise and glider stimuli (Fig. 4) were presented in blocks of 4s stimulus interleaved with 4s of no stimulus; thus the stimulus turned on at times 0, 8, 16 seconds, etc. For correlated noise stimuli, we considered orientation changes from t_i to t_i + 300 ms, where t_i was time of the stimulus initiation (i.e. 0s, 8s, 16s, etc…); the 150 ms latency used for bar stimuli was not needed in this case since the signal was independent of fly behavior, so the hit time was known to the precision of the inverse frame rate (6 ms). For glider stimuli, we considered orientation changes from t_i + 200 to t_i + 500 ms stimuli as this gave the largest response. We also only included flies with speeds < 12 mm/s for glider responses, since long-range correlations can interfere with the intended correlation if fly walking speed is near the glider speed.

Plume simulations

Direct numerical simulations were generated using the CFX^® hydrodynamic simulation software package of ANSYS 2019 (Ansys, Inc., Canonsburg, PA, USA). Parameters were chosen to emulate the flow and intermittent odor structure of the plume analyzed in Fig. 1¹⁰. The mean flow speed was 150 mm/s, with an air viscosity of 1.5e-5 m²/s. An odorant with molecular diffusivity D_m = 7.3e-6 m²/s was injected mid-stream (vertically and horizontally). The odorant was modeled as a conservative, neutrally buoyant tracer. The dimensions of the computational model domain were 30×18×1 cm, approximately matching those of the walking arena¹⁰. The computational air inlet boundary was modeled as a uniform velocity condition, representing an idealized collimated flow. The outlet boundary condition was modeled as a zero-pressure gradient opening allowing for bidirectional flow across the boundary. Walls were modeled using hydraulically smooth, no-slip boundary conditions. To reproduce the stochastic airjets creating the complex flow and plume, alternating jet pulses of air were applied from two orifices on opposite sides of the flume. The time series of pulses were identical to the experiments¹⁰. The model domain was broken up into 4.7e6 tetrahedral elements where velocity and concentration were computed, with the largest element’s length at 5 mm with an inflation layer along the domain boundaries and a refined mesh around the inlet orifices.

The flow was simulated at a 2.5 ms time step using a k-ϵ eddy viscosity model⁵⁴, which solves the Reynold-averaged Navier Stokes equations, where the momentum equation is defined as:

$$\frac{\partial \rho U_i}{\partial t}+\frac{\partial }{\partial x_j}\left(\rho U_i{U}_j\right)=-\frac{\partial p}{\partial x_i}+\frac{\partial }{\partial x_i}\left({\mu }_{\text{eff}}\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)\right)$$

and the continuity equation as:

$$\frac{\partial p}{\partial t}+\frac{\partial }{\partial x_j}\left(\rho U_j\right)=0,$$

where ρ is the fluid density, p is pressure and μ_eff is the effective fluid viscosity. The turbulent eddy viscosity is treated analogously to viscosity in laminar flow such that μ_eff = μ_t + μ where μ_t is the turbulent viscosity and μ the fluid viscosity. The k-ϵ model assumes the local turbulent viscosity is related to the local turbulent kinetic energy (k) and the eddy dissipation rate (ε) as follows:

$${\mu }_t\propto \rho \frac{k^2}{\epsilon }$$

The advection-diffusion equation for conservative tracers was used to model the transport of the odorant:

$${\partial }_t{C}_x+\mathit{u}\cdot \mathit{\nabla }C=(D_m+\epsilon ){\mathit{\nabla }}^2{C}_x$$

where C_x is the tracer concentration, u is the velocity field, D_m is the molecular diffusivity and ε is the local eddy diffusivity solved from the turbulence model. For all further analysis, we used the concentration and velocity in a plane 1 mm above the bottom of the domain, in the approximate z-plane of the fly antennae.

Mathematical modeling and data analysis

Inter-antennal latency of edge hit ΔT

The inter-antennal latency ΔT as a function of fly walking speed |v_fly| and bar speed |v_bar| can be calculated with basic geometric considerations. Here, we assume that the fly speed along the bar direction is sufficiently slow such that the bar passes over the fly. Consider a coordinate system in the frame of the moving bar, where the bar direction is +y (i.e. the bar’s edge is in x). The fly velocity in this frame is

$${\mathbf{v}}_r=[-|{\mathbf{v}}_{\text{fly}}|\sin \varphi ,|{\mathbf{v}}_{\text{fly}}|\cos \varphi -|{\mathbf{v}}_{\text{bar}}\left|\right]$$

where ϕ is the angle of rotation from v_bar to v_fly in the experimenter frame. The inter-antennal latency ΔT is then the projection of the antennal spacing L along v_bar divided by the projection of v_r along v_bar. The former is L sin ϕ and the latter is the y-component of v_r; the sign of L sin ϕ is treated as meaningful, so that a positive/negative value means the left/right antenna is hit first. Thus:

$$\mathrm{\Delta }T=\frac{L\sin \varphi }{\left|{\mathbf{v}}_{\text{bar}}\right|-\left|{\mathbf{v}}_{\text{fly}}\right|\cos \varphi }$$

where the sign is given by the numerator since the denominator is always positive for bars passing over the fly.

This expression ignores the fly’s angular velocity while walking. Assuming that the fly is walking forward while also turning at a rate ω, then the total accumulation of orientation over the ΔT interval is ωΔT, which for typical values of the maximum rotation rate during normal turns (ω ~ 300°/s) and typical inter-antennal latencies without turning (ΔT~15 ms) is ~5°. This would be if the fly were turning at a maximum angular velocity. More typically, rotation rates are approximately 20°/s ¹⁰, giving an accumulated angle during of less than 1°. If we incorporate this error as an uncertainty on ϕ, δϕ, then ΔT acquires an error of

$$\delta \mathrm{\Delta }T=\delta \varphi [\frac{L\cos \varphi }{\left|{\mathbf{v}}_{\text{bar}}\right|-\left|{\mathbf{v}}_{\text{fly}}\right|\cos \varphi }+\frac{\left|{\mathbf{v}}_{\text{fly}}\right|L{\sin }^2\varphi }{(\left|{\mathbf{v}}_{\text{bar}}\right|-\left|{\mathbf{v}}_{\text{fly}}\right|{\text{cos}\varphi )}^2}]$$

With the values assumed throughout, |δΔT| < 1 ms, so ω is safely ignored to the resolution of our experiments.

HRC output versus ΔT for traveling edges

Our prediction for the turning bias as a function of the latency ΔT at which an edge of odor hits the right antenna after hitting the left, is based on the output r(t) of a mirror-symmetrized Hassenstein-Reichardt correlator¹⁶. To calculate r(t), we model the correlator architecture as depicted in Fig. 4a. Specifically, the time-varying signals from the 2 sensors are s_L(t) and s_R(t). In one arm of the computation, s_L(t) is linearly filtered with an exponential ${\frac{1}{\tau }e}^{-\frac{t}{\tau }}$, while s_R(t) is transmitted unchanged; these are then multiplied. For a traveling ON edge moving left to right, we have s_L(t) = H(t) and s_R(t) = H(t − ΔT), where H(⋅) is the Heaviside function. Then the product of the filtered values is:

$$s_{LR}\left(t\right)=H\left(t-\mathrm{\Delta }T\right)\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^t{e}^{-\frac{t-t^{\prime }}{\tau }}H\left(t^{\prime }\right)d{t}^{\prime }$$

$$s_{LR}\left(t\right)=H\left(t-\mathrm{\Delta }T\right)\frac{1}{\tau }{\int }_0^t{e}^{-\frac{t-t^{\prime }}{\tau }}d{t}^{\prime }$$

$$s_{12}\left(t\right)=H\left(t-\mathrm{\Delta }T\right)\left(1-e^{-\frac{t}{\tau }}\right)$$

The other arm is similar, except that s₂(t) is filtered and s₁(t) is transmitted unchanged. Then the product of the filtered inputs is:

$$s_{RL}=H\left(t\right)\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^t{e}^{-\frac{t-t^{\prime }}{\tau }}H\left(t^{\prime }-\mathrm{\Delta }T\right)d{t}^{\prime }$$

$$=H\left(t-\mathrm{\Delta }T\right)\left(1-e^{-\frac{t-\mathrm{\Delta }T}{\tau }}\right)$$

The correlator output is therefore:

$$r\left(t\right)=s_{LR}\left(t\right)-s_{RL}\left(t\right)=H\left(t-\mathrm{\Delta }T\right)\left(e^{-\frac{t-\mathrm{\Delta }T}{\tau }}-e^{-t/\tau }\right)$$

Assuming that flies sense odor motion using this computation, the output of the correlator, r(t), must be converted to a behavior; here, we model this behavior as the turning bias being proportional to ∫ r(t)dt:

$$\begin{gathered} \text{Turning}\text{bias}\propto {\int }_{-T_{-}}^{T_{+}}r\left(t\right)dt={\int }_{\mathrm{\Delta }T}^{T_{+}}\left(e^{-\frac{t-\mathrm{\Delta }T}{\tau }}-e^{-t/\tau }\right)dt \\ {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}r\left(t\right)dt\propto \left(1-e^{-\frac{\mathrm{\Delta }T}{\tau }}\right) \end{gathered}$$

provided that behavioral timescales T₋ and T₊, over which the correlator response is integrated to produce the turning response, are large compared to both τ and ΔT. Long after the edge hit, t ≫ T₋, the signals are both s_L = s_R = 1, giving an HRC output of 0, as expected for the anti-symmetric architecture.

To estimate the filtering constant τ, we minimize:

$${C\left(A,\tau \right)=\left[\text{Turning}\text{bias}\left(\mathrm{\Delta }T\right)-A\left(1-e^{-\frac{\mathrm{\Delta }T}{\tau }}\right)\right]}^2$$

over A, τ. The turning bias is plotted in increments of ΔT = 4 ms, where the value at a given ΔT includes values from ± 4 ms. Neighboring points therefore contain overlapping data; this has the effect of smoothing – but not biasing – the turning bias vs. ΔT curve.

Responses to rightward moving OFF edges are analogous. The signal switches from 1 to 0 at the OFF edge (set it to t = 0), so the signal on the left sensor is s_L(t) = 1 − H(t) and for the right sensor is s_R = 1 − H(t − ΔT). Then one arm of the HRC is:

$$s_{LR}\left(t\right)=(1-H\left(t-\mathrm{\Delta }T\right))\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^t{e}^{-\frac{t-t^{\prime }}{\tau }}(1-H\left(t^{\prime }\right))d{t}^{\prime }$$

$$s_{LR}\left(t\right)=\left(1-H\left(t-\mathrm{\Delta }T\right)\right)\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^0{e}^{-\frac{t-t^{\prime }}{\tau }}d{t}^{\prime }t>0$$

$$s_{LR}\left(t\right)=e^{-\frac{t}{\tau }},0<t<\mathrm{\Delta }T$$

and s_LR(t) = 0 for t > ΔT and s_LR(t) = 1 for t < 0. The other arm output is simply s_RL = 1 for t < 0 and s_RL = 0 for t > 0, since the non-delayed arm drops to zero as soon as the edge passes it at t = 0. Thus the output is:

$$r\left(t\right)=s_{LR}\left(t\right)-s_{RL}\left(t\right)=e^{-\frac{t}{\tau }}H(t)(1-H\left(t-\mathrm{\Delta }T\right))$$

Integrating this quantity over time gives the same turning bias as the ON edge.

Generation of correlated noise stimuli and C(Δx, Δt)

Correlated noise stimuli were generated as previously described²⁶. We used optogenetic bars that were parallel to the short axis (y) of the arena (e.g. perpendicular to the wind direction, which runs along x). Each bar has a width of one x-pixel – thus, we refer to an x-pixel as a “pixel,” since correlations are defined just in the x-direction. The stimulus value (where −1 and 1 are for dark and light bars, respectively) of a bar at pixel location x and time t is given by $c\left(x,t\right)=\text{sgn}(\eta \left(x,t\right)+\alpha \eta (x+\beta \mathrm{\Delta }x,t+\mathrm{\Delta }t)$), where each values of the random field η(x, t) is independently chosen from a standard normal distribution. Δx is the pixel spacing; Δt is the inter-frame interval. The constant β governs the direction of the correlations: +1 for stimuli correlated in the +x direction (“with-wind” in the main text) and −1 for stimuli correlated in the −x direction (“against-wind”). The constant α governs the polarity of the correlations; +1 or −1 for positive or negative correlations, respectively.

The spatiotemporal correlations in pixel intensity can be computed straightforwardly, as previously described²⁶. Assume that α = β = 1; the other cases are analogous. The correlation between two pixels separated by spacing x′ and timing t′ is denoted by the correlation function $C(x\prime ,t\prime )=⟨c\left(x,t\right)c\left(x+x^{\prime },t+t\prime \right)⟩$. In general,

$$C(x\prime ,t\prime )=⟨\text{sgn}{\left(\right(\eta }_1+{\eta }_2\left)\right({\eta }_3+{\eta }_4\left)\right)⟩$$

where η_i is one sample of η. For most choices of t′, x′, all η_i are distinct, so the correlation reduces to 0 since the sums are independent. For x′ = t′ = 0, the correlation reduces to the variance of c(x, t), which is 1. However, for t′ = Δt and x′ = Δx, η₂ = η₃. Then,

$$C(x\prime ,t\prime )=⟨\text{sgn}{\left(\right(\eta }_1+{\eta }_2\left)\right({\eta }_2+{\eta }_4\left)\right)⟩$$

$$C(x,t)=⟨\text{sgn}{\left(\right(\eta }_1-{\eta }_2\left)\right({\eta }_2-{\eta }_4\left)\right)⟩$$

since the random variables are symmetric about 0. The sign depends only on the ordering of the η_i, which are 3 independent samples from a standard normal distribution. There are 6 ways to uniquely order the η_i, only two of which give a positive sign (η₁ > η₂ > η₄ and η₁ < η₂ < η₄); thus the expected value is 1/3²⁶. An analogous property holds for t′ = −Δt, x′ = −Δx. Finally, the α and β factors are incorporated straightforwardly as scale factors, giving:

$$C\left(x\prime ,t\prime \right)={\delta }_{x^{\prime },0}{\delta }_{t^{\prime },0}+\alpha \frac{1}{3}({\delta }_{x^{\prime },\beta \mathrm{\Delta }x}{\delta }_{t^{\prime },\mathrm{\Delta }t}+{\delta }_{x^{\prime },-\beta \mathrm{\Delta }x}{\delta }_{t^{\prime },-\mathrm{\Delta }t})$$

where the δ denotes the Kronecker delta function. Note that the correlation can be calculated by averaging over all of spacetime, or just in space for a fixed set of times, or just in time for a fixed set of points. The latter is our interpretation for the HRC output from fixed antennae, assuming the correlation direction is perpendicular to the fly body.

Generation of glider stimuli

Here, the stimulus value of a bar at pixel location x and time t is given by c(x, t) = B(x − βtΔx/Δt), where B = 2X − 1 with X ~ Bernoulli(p = 0.5), Δx is the pixel spacing, and Δt is the inter-frame interval. The correlation between two pixels separated by spacing x′ and timing t′ is

$$C(x\prime ,t\prime )=⟨[B\left(x-\frac{\beta t\mathrm{\Delta }x}{\mathrm{\Delta }t}\right)B\left(x+x^{\prime }-\frac{\beta t\mathrm{\Delta }x}{\mathrm{\Delta }t}-\frac{\beta t^{\prime }\mathrm{\Delta }x}{\mathrm{\Delta }t}\right)]⟩.$$

Then, C(x′, t′) = 1 when $\frac{x^{\prime }}{t^{\prime }}=\frac{\beta \mathrm{\Delta }x}{\mathrm{\Delta }t}$ – i.e., the correlation matrix has a diagonal or antidiagonal structure for β = 1 and β = −1, respectively. These stimuli are a class of glider stimuli with a two-point correlation structure^32,33. Visually, these gliders are a frozen pattern of random light and dark bars moving statically at constant speed in the βx direction.

HRC output for correlated noise stimuli

Here we calculate the HRC output for correlated noise stimuli, which has been computed before for any pair of filters on the two arms of the HRC^26,55. Assume that the antennae are held at approximately the spacing of the correlation shift Δx (see Generation of correlated noise stimuli and C(Δx, Δt) section), and that the correlation direction is +x (rightward over the fly body), so β = 1 from the last section. Then one arm of the HRC gives:

$$s_{LR}\left(t\right)=s_R(t)\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^t{e}^{-\frac{t-t^{\prime }}{\tau }}{s}_L(t^{\prime })d{t}^{\prime }$$

Averaging over time gives:

$${⟨s}_{LR}\left(t\right)⟩=⟨c\left(x,t\right)\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^t{e}^{-\frac{t-t^{\prime }}{\tau }}c\left(x-\mathrm{\Delta }x,t^{\prime }\right)d{t}^{\prime }\rangle$$

Since β = 1, then only the last term in the correlation equation applies:

$${⟨s}_{LR}\left(t\right)⟩=⟨c\left(x,t\right)\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^0{e}^{t^{″}/\tau }c\left(x-\mathrm{\Delta }x,t+t″\right)d{t}^{″}\rangle$$

$${⟨s}_{LR}\left(t\right)⟩=\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^0{e}^{t^{″}/\tau }\alpha \frac{1}{3}{\delta }_{t^{″},-\mathrm{\Delta }t}d{t}^{″}$$

$${⟨s}_{LR}\left(t\right)⟩=\alpha \frac{1}{3\tau }{e}^{-\mathrm{\Delta }t/\tau },\mathrm{\Delta }t>0$$

This equation holds for Δt being positive. The other arm is analogous, for Δt < 0.

$$s_{RL}\left(t\right)=s_L(t)\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^t{e}^{-\frac{t-t^{\prime }}{\tau }}{s}_R(t^{\prime })d{t}^{\prime }$$

$${⟨s}_{RL}\left(t\right)⟩=⟨c\left(x,t\right)\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^t{e}^{-\frac{t-t^{\prime }}{\tau }}c\left(x+\mathrm{\Delta }x,t^{\prime }\right)d{t}^{\prime }\rangle$$

$${⟨s}_{RL}\left(t\right)⟩=⟨c\left(x,t\right)\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^0{e}^{\frac{t^{″}}{\tau }}c\left(x+\mathrm{\Delta }x,{t+t}^{″}\right)d{t}^{″}\rangle$$

$${⟨s}_{RL}\left(t\right)⟩=\frac{1}{\tau }{\int }_{-\mathrm{\infty }}^0{e}^{\frac{t^{″}}{\tau }}\alpha \frac{1}{3}{\delta }_{t^{″},\mathrm{\Delta }t}d{t}^{″}$$

$${⟨s}_{RL}\left(t\right)⟩=\alpha \frac{1}{3\tau }{e}^{\mathrm{\Delta }t/\tau },\mathrm{\Delta }t<0$$

Thus, the full correlator output is

$${\int }_{t}r\left(t\right)dt=⟨s_{LR}\left(t\right)⟩-⟨s_{RL}\left(t\right)⟩=\alpha \cdot \text{sgn}(\mathrm{\Delta }t)\frac{1}{3\tau }{e}^{-\frac{\left|\mathrm{\Delta }t\right|}{\tau }}$$

Note that the correlator output response switches sign if the correlation polarity α flips – this is the reverse phi response. There is a slight artificiality in this expression, in that the response is discontinuous at Δt = 0. We have assumed an exponential filter, which technically has an immediate response time, violating causality. In addition, the optimal response occurs for an inter-frame interval Δt that is arbitrarily small. As a more realistic filter, one can use $\frac{t}{{\tau }^2}{e}^{-t/\tau }$, which has zero response at time zero and maximal response at t = τ. Then:

$${\int }_{t}r\left(t\right)dt=⟨s_{LR}\left(t\right)⟩-⟨s_{RL}\left(t\right)⟩=\alpha \cdot \text{sgn}(\mathrm{\Delta }t)\frac{1}{3{\tau }^2}\left|\mathrm{\Delta }t\right|e^{-\left|\mathrm{\Delta }t\right|/\tau }$$

This filter is continuous at Δt = 0, and the maximum correlator output occurs when the filter timescale τ matches the interframe interval Δt. In either case, the salient point is that the response is antisymmetric in both the temporal shift Δt and the correlation polarity α, as expected.

HRC response for pre-filtered inputs

Here, we motivate how filtering of inputs affects the response curve of the HRC – i.e. HRC output as a function of stimulus latency ΔT. We assume delta-correlated stimuli (as in the Generation of correlated noise stimuli and C(Δx, Δt) section), for which the response functions are expressed in simple, interpretable forms. Thus, we set cross-correlation between the left antennal stimulus and right antennal stimulus at $c\left(t^{\prime }\right)=⟨s_L\left(t\right)s_R\left(t-t^{\prime }\right)⟩=\delta (t^{\prime }-\mathrm{\Delta }T)$, where the average is taken over instantiations of the stimulus – which is equivalent in this case to taking an average over time. Defining as f₁ and f₂ the delay filters for the two arms (e.g. 1 fast and 1 slow filter) and in the absence of any other filters, the averaged HRC output from 1 side of the detector is:

$$s_{LR}\left(\mathrm{\Delta }T\right)=⟨\int {d{t}^{\prime }f}_1\left(t^{\prime }\right)s_L\left(t-t^{\prime }\right)\int {d{t}^{″}f}_2\left(t^{″}\right)s_R\left(t-t^{″}\right)⟩$$

$$=\int d{t}^{\prime }d{t}^{″}{f}_1\left(t^{\prime }\right)f_2\left(t^{″}\right)\delta (t^{\prime }-t^{″}-\mathrm{\Delta }T)$$

$$=\int d{t}^{\prime }{f}_1\left(t^{\prime }\right)f_2(t^{\prime }-\mathrm{\Delta }T)$$

$$=\left(f_1\otimes f_2\right)\left(\mathrm{\Delta }T\right).$$

In other words, the response is the convolution of the two filters. Further assuming that f₂(t) is fast (i.e. a delta function response), this reduces to the slow filter evaluated at the inter-antennal latency:

$$s_{LR}\left(\mathrm{\Delta }T\right)=f_1\left(\mathrm{\Delta }T\right)$$

Note that this and related derivations (and interpretations) have been given in prior studies^26,55.

Now, assuming that the signals are each pre-filtered with a smoothing filter f₃(t), we get:

$$s_{LR}\left(\mathrm{\Delta }T\right)={⟨\int {d{t}^{\prime }dt″f}_1\left({t\prime -t}^{″}\right)f_3\left(t″\right)s_L\left(t-t\prime \right)\int {d{t″}^{\prime }dt″″f}_2\left({t‴-t}^{″″}\right)f_3\left(t″″\right)s_R\left(t-t‴\right)⟩}_t$$

$$=\int d{t}^{\prime }d{t}^{″}d{t}^{‴}d{t}^{″″}{f}_1\left(t^{\prime }-t^{″}\right)f_3\left(t^{″}\right)f_2\left({t‴-t}^{″″}\right)f_3\left(t^{″″}\right)\delta (t‴-t^{\prime }-\mathrm{\Delta }T)$$

$$=\int d{t}^{\prime }d{t}^{″}d{t}^{″″}{f}_1\left(t\prime -t^{″}\right)f_3\left(t″\right)f_2\left({t^{\prime }+\mathrm{\Delta }T-t}^{″″}\right)f_3\left(t″″\right)$$

$$=\int d{t}^{″}d{t}^{″″}{f}_1\left(t^{\prime }-t^{″}\right)f_2\left({t^{\prime }+\mathrm{\Delta }T-t}^{″″}\right)(f_3\otimes f_3)(t^{″}-t^{″″})$$

$$=\int dt″dt″″(f_1\otimes f_2)(\mathrm{\Delta }T-t^{″″}+t^{″})(f_3\otimes f_3)(t^{″}-t^{″″})$$

$$=\left(f_1\otimes f_2\right)\otimes (f_3\otimes f_3)\left(\mathrm{\Delta }T\right)$$

Again, if f₂ is a delta function response, this gives:

$$s_{LR}\left(\mathrm{\Delta }T\right)=f_1\otimes (f_3\otimes f_3)\left(\mathrm{\Delta }T\right)$$

The full HRC response is this quantity, anti-symmetrized:

$$HRC\left(\mathrm{\Delta }T\right)=s_{LR}\left(\mathrm{\Delta }T\right)-s_{LR}\left(-\mathrm{\Delta }T\right)=f_1\otimes \left(f_3\otimes f_3\right)\left(\mathrm{\Delta }T\right)-f_1\otimes (f_3\otimes f_3)(-\mathrm{\Delta }T)$$

Thus, the HRC response is essentially the slow filter convolved with the autocorrelation of the pre-filter. Indeed, the effect of the pre-filter, a linear operation, is to “smear out” the HRC response – though it acts twice, once for the right sensor and once for the left sensor.

What effect does pre-filtering have on the HRC response? Since the HRC is defined anti-symmetrically in ΔT, it is direction selective by construction, so the pre-filtering will not affect direction selectivity. However, filtering can affect the signal-to-noise ratio, and thus the regime for which direction selectivity is resolvable given the noise. For concreteness, let us calculate the closed-form HRC response, assuming that the slow filter and pre-filter are each exponential filters with timescales τ_HRC and τ_smear, respectively, and assuming that there is noise in the external signal. We are considering binary valued correlated signals, so we imbue the noise as a random variable that adds external variability to the timing of the signals. Since we are looking at antenna-to-antenna correlations, we add the noise to just one antenna for simplicity.

In the prior derivation, noise changes the integrated time t‴ to t‴ + X, where we take X ~ N(0,δt) as the noise. Then the noisy HRC response is:

$$HRC\left(\mathrm{\Delta }T|\delta T\right)=s_{LR}\left(\mathrm{\Delta }T-X\right)-s_{LR}\left(-\mathrm{\Delta }T+X\right)=f_1\otimes \left(f_3\otimes f_3\right)\left(\mathrm{\Delta }T-X\right)-f_1\otimes (f_3\otimes f_3)(-\mathrm{\Delta }T-X)$$

In other words, the noise simply manifests as ΔT → ΔT − X in the HRC response. We thus just designate ΔT_δT = ΔT + X as a normal random variable with mean ΔT and standard deviation δT.

Now, the autocorrelation of an exponential pre-filter is:

$$\left(f_3\otimes f_3\right)\left(t\right)=\frac{1}{{\tau }_{\text{smear}}^2}t{e}^{-\frac{t}{{\tau }_{\text{smear}}}}H\left(t\right)$$

and thus the response of 1 arm of the noisy HRC gives:

$$s_{LR}\left(\mathrm{\Delta }{T}_{\delta t}\right)=\frac{1}{{{\tau }_{\text{HRC}}\tau }_{\text{smear}}^2}\left(-\frac{\mathrm{\Delta }{T}_{\delta t}}{{\lambda }^{\mathrm{*}}}{e}^{-\frac{\mathrm{\Delta }{T}_{\delta t}}{{\tau }_{\text{smear}}}}+\frac{1}{{\lambda }^{{\mathrm{*}}^2}}\left(e^{-\frac{\mathrm{\Delta }{T}_{\delta t}}{{\tau }_{\mathrm{H}\mathrm{R}\mathrm{C}}}}-e^{-\frac{\mathrm{\Delta }{T}_{\delta t}}{{\tau }_{\text{smear}}}}\right)\right)H\left(\mathrm{\Delta }{T}_{\delta t}\right),{\tau }_{\text{HRC}}\ne {\tau }_{\text{smear}}$$

$$s_{LR}\left(\mathrm{\Delta }{T}_{\delta t}\right)=\frac{1}{{2\tau }_{\mathrm{H}\mathrm{R}\mathrm{C}}^3}{\left(\mathrm{\Delta }{T}_{\delta t}\right)}^2{e}^{-\left(\mathrm{\Delta }{T}_{\delta t}\right)/{\tau }_{\mathrm{H}\mathrm{R}\mathrm{C}}}H\left(\mathrm{\Delta }{T}_{\delta t}\right),{\tau }_{\text{HRC}}={\tau }_{\text{smear}}.$$

where ${\lambda }^{*}=\frac{1}{{\tau }_{\text{smear}}}-\frac{1}{\tau }$. Again, the full response is $HRC\left(\mathrm{\Delta }{T}_{\delta t}\right)=s_{LR}\left(\mathrm{\Delta }{T}_{\delta t}\right)-s_{LR}\left(-\mathrm{\Delta }{T}_{\delta t}\right)$. We then define the minimum “resolvable” ΔT as:

$$\mathrm{\Delta }{T}_{\text{resolvable}}\left(\delta t\right)=\min \left|\mathrm{\Delta }T\right|\mathrm{s}.\mathrm{t}.{⟨HRC\left(\mathrm{\Delta }{T}_{\delta t}\right)⟩}_X>\sqrt{{⟨HRC{\left(\mathrm{\Delta }{T}_{\delta t}\right)}^2⟩}_X-{{⟨HRC\left(\mathrm{\Delta }{T}_{\delta t}\right)⟩}_X}^2}$$

In words, it is, for a given noise level δt, the minimum inter-antennal latency ΔT for which the mean of the response is larger than the standard deviation of the responses. In realistic scenarios, the negative responses for ΔT_δt < 0 can mix with the positive responses for ΔT_δt > 0, confounding responses for ΔT near 0, and our interest here is the magnitude of this effect. We calculate ΔT_resolvable(δt) numerically for the two-exponential response given the above expressions (Extended Data Fig. 6) for various values of τ_smear. We find that the minimum resolvable ΔT is limited entirely the noise level δt, regardless of whether τ_smear is much larger or much smaller than of τ_HRC. This indicates that the pre-filter certainly affects the values of the HRC output, but it does not affect the direction sensing capabilities of the HRC.

Calculated HRC responses from electrophysiological measurements

To estimate HRC outputs from a pair of recorded ORN spike trains, we first manually shifted one recording from the pair by −ΔT/2 and the other by ΔT/2, which mimics an odor edge traveling from left to right, hitting the two antennae sequentially at a latency of ΔT. The magnitude of ΔT is inversely proportional to the odor speed; assuming an interantennal distance of 300 μm, the corresponding odor speed is 300/ΔT mm/s. Leftward traveling odors are simulated by choosing ΔT < 0. We first produce ORN firing rates from these spike trains by convolving the binary spike trains with a Gaussian filter (σ = 15 ms). HRC outputs were generated from these firing rates using the procedure described in the above sections, choosing a τ = 15 ms exponential filter for the delay arm.

For the scenario in which we added multiple sources of noise (Fig. 5e), we first took the recorded spike trains and shifted each spike by τ_jitter, where τ_jitter was chosen uniformly from −30 to 30 ms. Next, these spikes were shifted by ±ΔT/2 as above, to assign “left” and “right” ORNs, and then filtered in time as above to get ORN firing rates r_ORN,L(t) and r_ORN,R(t). Left and right PNs receive input from both ORNs, but with differing weights¹⁷, which we mimicked by taking the input to the left PN $r_{\mathrm{P}\mathrm{N}\mathrm{i}\mathrm{n},\mathrm{L}}\left(t\right)=0.6r_{\mathrm{O}\mathrm{R}\mathrm{N},\mathrm{L}}\left(t\right)+0.4r_{\mathrm{O}\mathrm{R}\mathrm{N},\mathrm{R}}\left(t\right)$, and $r_{\mathrm{P}\mathrm{N}\mathrm{i}\mathrm{n},\mathrm{R}}\left(t\right)=0.6r_{\mathrm{O}\mathrm{R}\mathrm{N},\mathrm{R}}\left(t\right)+0.4r_{\mathrm{O}\mathrm{R}\mathrm{N},\mathrm{L}}\left(t\right)$. PNs average over many ORN inputs by filtering over 30 ms³⁴, which we mimicked by designating the PN response as $r_{\mathrm{P}\mathrm{N},\mathrm{L}}=f_{\mathrm{P}\mathrm{N}}\otimes r_{\mathrm{P}\mathrm{N}\mathrm{i}\mathrm{n},\mathrm{L}}$, where f_PN(t) is a 30 ms exponential filter. Finally, r_PN,L and r_PN,R were fed used as inputs the HRC described above.

Analysis of imaged plume

We re-analyzed behavioral data previously extracted from Drosophila navigating an imaged complex plume of smoke¹⁰ in the same walking assay used throughout this study. The signal in the virtual antenna was quantified as described previously; briefly, the virtual antenna is defined as an ellipse perpendicular to the body axis with the long axis given by the width of the fly (1.72 ± 0.24 mm) and the small axis equal to one-fifth the minor axis of the fly (0.46 ± 0.24 mm). We re-analyzed the imaged fly and signal data to resolve the virtual antenna signal into 14 pixels along its long axis (averaged along its short axis). Thus, the signal is a vector ${\mathit{s}}_{\text{ant}}\left(t\right)=[s\left(x_1,t\right),s\left(x_2,t\right),\dots ,s(x_{14},t\left)\right]$ defined at locations along the antenna’s long axis x_ant = [x₁, …, x₁₄] for a given time t.

The overall concentration in the antenna was calculated as the average signal over the center of the virtual antenna – at the locations [x₅,x₆,x₇,x₈]. The gradient ∇c_ant in the virtual antenna at a given t was calculated by regressing s_ant against x_ant and extracting the slope. The odor velocity in the virtual antenna was estimated by calculating correlations of the virtual antenna signal over space and time. For a given t, we calculated $\widehat{\mathrm{\Delta }x}={\text{argmax}}_{\mathrm{\Delta }x}{⟨s\left(x_i,t\right)s\left(x_i+\mathrm{\Delta }x,t+\mathrm{\Delta }t\right)⟩}_{x_i}$, where Δx spanned integers from −7 to 7, and Δt is the interframe interval (11 ms), and s(⋅) were mean subtracted. This gives the signed number of pixels for which the correlation between two successive frames is maximized, up to the length of the antenna. The odor velocity was then defined as $\widehat{\mathrm{\Delta }x}\cdot \text{frame}\text{rate}\cdot \text{resolution}$, where the imaging frame rate was 90 frames per second and the spatial resolution is 0.153 mm per pixel. We disregarded points for which $\widehat{\mathrm{\Delta }x}$ was ±7, since those may not represent local maxima but were instead limited by the size of the antenna. All three quantities – total concentration, gradient, and odor velocity – were smoothed in time using a Savitsky-Golay filter of order 2 and smoothing window of 25 timepoints ~ 270 μs.

To remove boundary effects from the arena extent, we only used for Fig. 1c–e points for which the fly was in the central region of the arena, 100 < x < 250 mm, |y − y₀| < 40 mm, where y₀ is the plume’s central axis, and only points for which fly speed was greater than 0.1 mm/s. Angular velocity was calculated as the average orientation change over 200 ms.

Analysis of simulated plume

The simulation generated concentration fields c(x_i, y_i, t) and flow velocity fields v_wind(x_i, y_i, t) defined on grid points (x_i, y_i) of a non-uniform mesh. We first generated values on a 0.5 mm square lattice, by triangulating the data and performing barycentric linear interpolation over each triangle (scipy.interpolate.griddata in Python, with method ‘linear’). Fields in Fig. 6 and Extended Data Fig. 7 were plotted every 1 cm, (i.e. every 20 pixels on the original 0.5 mm lattice). Wind speed vectors at each point on this 1 cm lattice were generated by averaging v_wind over the 20 × 20 values in a 1 cm² box. The plotted v_wind|odor field was generated by only considering wind vectors for which the odor concentration was above 1e-3. Odor gradients were generated by calculating local differences ∇c_x and ∇c_y in the x- and y- directions, respectively. Specifically, for ∇c_x, we calculated (x₊ − x₋)/(x₊ + x₋), where x₊ and x₋ were the averages in the right and left half of a 1 cm² box centered at each lattice point, respectively. ∇c_y was calculated analogously, using the top and bottom half of the same box. Odor velocities were calculated similarly to those in the imaged plume used in Fig. 1, by correlating the values in a given spatial region between two frames. Specifically, to get v_{x, odor} at a given time t, we calculated ${\text{argmax}}_{\mathrm{\Delta }x}{⟨s\left(x_j,t\right)s\left(x_j+\mathrm{\Delta }x,t+\mathrm{\Delta }t\right)⟩}_{x_j}$, where s(x_j, t) was the odor concentration in a 1 cm² box averaged over the y-direction for each x_j pixel spaced by 0.5 mm. The shifts Δx ran from −20 to 20 pixels (±1 cm). This quantity was multiplied by the frame rate of 100 frames per second and by the spatial resolution 0.5 mm per pixel to get v_{x, odor} in mm/s. An analogous operation was done for v_{y, odor} using the same 1 cm² box. All odor gradient and odor velocity values for very low odor concentrations were set to Nan, as were any odor velocity values that produced a maximum shift |Δx| = 20. The resulting wind speed, gradient, and odor velocity were all smoothed in time using a Savitsky-Golay filter of order 1 and window length 11 (110 ms).

Analysis of fly navigation in complex virtual plumes

For the plume navigation experiments (Fig. 7), we considered tracks that began in the downwind 50 mm of the arena (x > 230 mm) and had an average walking speed of at least 0.5 mm/s. For the histograms (middle and right plots in Fig. 7f, 7i), we only plotted instances at which the fly’s instantaneous walking speed was greater than 5 mm/s. For the success ratios (lefthand plots in Fig. 7f, 7i), we considered tracks which lasted 30 seconds or longer, or which reached the upwind end of the arena (x < 50 mm) before then.

In silico virtual agent model and simulation

We use two different navigation algorithms for the agent-based simulations.

The bio-inspired algorithm (Fig. 7j-l) was modeled on our previous work¹⁰, which quantified the navigational behavior of walking Drosophila in spatiotemporally complex odor plumes. We ran the agents in the imaged complex plume used in the plume navigation experiments (Fig. 6g). We recapitulate the algorithm briefly here, but refer the reader to the original study for all details.

We generated two types of agents: DS- agents, which obeyed the original navigational model and could not sense odor direction, and DS+ agents, which combined the original model with odor direction sensing. Both DS+ and DS- agents navigated using the timing of odor “hits” – times at which c(t) exceeded a threshold, here chosen to be 3 (the digitized signal ranges from 0 to 255). At each frame, agents underwent stochastic transitions between walking, turning, and stopped states. Agents walked at a constant speed of 10 mm/s. During walking, their heading underwent rotational diffusion, with a standard deviation of 0.22° every frame (each frame is 1/60s). Transitions from a stopped to walking were inhomogeneous Poisson processes, in which the transition rate increased monotonically with the frequency of odor hits. Transitions from walking to a stopped state were also an inhomogeneous Poisson processes, where the rate dipped at each odor hit, before decaying back to a baseline – thus, flies keep walking when the frequency of odor hits is high. Turns only occurred while walking, and were Poisson events with a rate of 0.5 Hz. Each turn magnitude was a random sample from N(30°,8°).

The key navigational aspect of the bio-inspired algorithm was the turn direction. For DS- agents, the turn direction was a binary random variable, either upwind or downwind, where p(upwind) = min(1,0.5 + αw(t)), where α = 1 and w(t) is a running average of the frequency of odor hits. As in the original study, the running average is computed by convolving the binary vector of odor hit onsets (‘1’ at the onset of each odor hits; ‘0’ elsewhere) with an exponential filter of timescale 2s. Thus, for frequent odor hits, the turns are more likely to be directed upwind. For DS+ agents, the turn direction was a binary variable, either against or toward v_sum, where v_sum is the vector sum of the odor motion direction and wind direction: p(against) = min(1,0.5 + αw(t)), where α = 1. Thus, as the frequency of the odor hits increases, the agent is more likely to direct its turns against the summed direction v_sum.

To compute the odor hit times (for both DS- and DS+ agents) and odor direction (for only DS+ agents), the agents had two antennae separated by 1.5 mm, and each antennae received an odor signal, c_L(t) and c_R(t), respectively, that was the average signal value in a 0.5×0.5 mm² region. The total odor signal c(t) was $\frac{c_L\left(t\right)+c_R\left(t\right)}{2}$. For DS+ agents, the odor motion direction was computed by taking the sign of $c_{\mathrm{o}\mathrm{d}\mathrm{o}\mathrm{r}}\left(t\right)=c_L\left(t\right)c_R\left(t+\mathrm{\Delta }T\right)-c_L\left(t+\mathrm{\Delta }T\right)c_R\left(t\right)$, where the delay ΔT was chosen as 1 time frame. For c_odor(t) > 0, odor direction vector pointed θ + 90°, and for c_odor(t) < 0, odor direction vector pointed θ − 90°, where θ is the agent heading. In other words, the agent can resolve only the direction, left or right, of the odor motion. If the correlation magnitude is too low (|c_odor| < 5), then DS+ agents ignore c_odor and turn against the wind direction like DS- agents.

All 100 agents in the bio-inspired algorithm were initialized in the back 50 mm of the arena and uniformly in the lateral direction, and their headings were initialized randomly in the upwind 180 sector. Agents were simulated for 2500 frames, or 41.7 seconds. If agents reached the rectangular boundary of the arena, they were reflected ballistically from the wall.

In the simple algorithm (Extended Data Fig. 9), virtual agents with 2 spatially separated sensors navigated the simulated plume (Fig. 6a) using a simple algorithm. All agents were initialized at the back of the arena, facing upwind. At each frame (10 ms), agents turned either left or right 90° (except for upwind oriented DS- flies when within the odor signal – these flies maintained upwind), depending on the navigation strategy as described in the main text, and stepped forward 0.75 mm. The sensors were placed 0.5 mm to the left or right of the agent centroid. The measured odor signal concentration was defined as $c=\frac{\left(c_L+c_R\right)}{2}$, where the concentration in each sensor was c_L and c_R, respectively. We set the detection threshold at c₀ = 1e-3. The odor correlation between the two sensors was defined as $c_{\mathrm{o}\mathrm{d}\mathrm{o}\mathrm{r}}\left(t\right)=c_L\left(t\right)c_R\left(t+\mathrm{\Delta }T\right)-c_L\left(t+\mathrm{\Delta }T\right)c_R\left(t\right)$, where the delay timescale ΔT was chosen as 1 frame (1/100 s). From c_odor, the direction of odor motion v_odor was defined +1 if $\mathrm{a}\mathrm{b}\mathrm{s}\left(c_{\mathrm{o}\mathrm{d}\mathrm{o}\mathrm{r}}\left(t\right)\right)>$1e-8 and $\mathrm{s}\mathrm{g}\mathrm{n}\left(c_{\mathrm{o}\mathrm{d}\mathrm{o}\mathrm{r}}\left(t\right)\right)>0$, as −1 if $\mathrm{a}\mathrm{b}\mathrm{s}\left(c_{\mathrm{o}\mathrm{d}\mathrm{o}\mathrm{r}}\left(t\right)\right)>$ 1e-8 and $\mathrm{s}\mathrm{g}\mathrm{n}\left(c_{\mathrm{o}\mathrm{d}\mathrm{o}\mathrm{r}}\left(t\right)\right)<0$, and as 0 otherwise. In general, odor signals with a leftward component over the virtual agent in its body frame had v_odor = 1 and, while those with a rightward component had v_odor = −1. Simulations were carried out separately for agents that could sense (DS+) and could not sense (DS-) odor motion. Agents followed the strategy as described in the main text. For DS+ flies, whenever c_odor was below threshold ($\mathrm{a}\mathrm{b}\mathrm{s}\left(c_{\mathrm{o}\mathrm{d}\mathrm{o}\mathrm{r}}\left(t\right)\right)>$1e-8), but the odor was still detectable (c > c₀), the decisions obeyed the DS- strategy. All agents were initialized in the back 50 mm of the arena and uniformly in the crosswind direction, and simulated for 2500 timesteps, or 25 s.

Theoretical analysis of odor motion in turbulent odor plumes

Here we investigate the motion of odor signals perpendicular to the mean flow using a toy model of turbulent plume similar in spirit to those used in^19,56,57. Odor packets are released from a point source at a given rate. The concentration around the center of each packet is given by a local diffusive process that spreads the concentration via molecular diffusion of the odor. Meanwhile, the packets themselves are advected downwind by the mean flow, while being dispersed by the fluctuating velocity u¹⁹. We consider the simple case of an isolated packet and calculate its expected velocity crosswind to the flow, at different locations throughout the plume. For analytical simplicity, we assume stationary homogeneous and isotropic turbulence and model the turbulent velocity u as a telegraph process that switches between left motion and right motion at speed v, where the switching rates from left to right and vice versa are both λ = 1/T. Thus, 2T is equivalent to the Lagrangian integral time scale and the packet speed v to the r.m.s. of the turbulent velocity field. While the velocity u switches discontinuously between +v and −v, its time correlation function is the same as that of the Ornstein-Uhlenbeck (O-U) process often used to model homogeneous isotropic turbulence^19,54:

$$⟨u\left(t\right)u\left(t^{\prime }\right)⟩\propto e^{-\frac{\left|t-t^{\prime }\right|}{2T}}$$

Our goal is an estimate of the average odor motion velocity at a given lateral distance from the plume, at a given time $t,{⟨v⟩}_{y,t}$. Since packets are advected downwind at some speed U ≫ v, we have t ≈ x/U, so that this is equivalent to finding the average lateral velocity at some x, y position in the plume⁵⁴. Run times are distributed as $\frac{1}{T}{e}^{-t/T}$, so packets reaching a given y will have been traveling for some distance $\tilde{y}$, where $\tilde{y}$ is distributed as $p\left(\tilde{y}\right)=\frac{1}{Tv}{e}^{-\tilde{y}/Tv}$. If the packets were originally uniformly distributed, then the average velocity at y would be 0. However, an asymmetry arises due to the non-uniform packet distribution, which is dispersing laterally from a delta function at y = 0. For times t ≫ T, the distribution of packets is approximately the diffusion kernel with effective turbulent diffusivity D_T = Tv²:

$$p\left(y,t\right)=\frac{1}{\sqrt{2\pi T{v}^2}t}{e}^{-y^2/2T{v}^{2}t}$$

Under these assumptions, the average velocity at the fixed point 〈v〉_y,t is:

$${⟨v⟩}_{y,t}=\frac{v{\int }_{-\mathrm{\infty }}^{y}p\left(y^{\prime },t-y^{\prime }/v\right)e^{-\frac{y-y^{\prime }}{vT}}d{y}^{\prime }-v{\int }_y^{\mathrm{\infty }}p\left(y^{\prime },t-y^{\prime }/v\right)e^{-\frac{y\prime -y}{vT}}d{y}^{\prime }}{{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}p\left(y^{\prime },t-y^{\prime }/v\right)e^{-\frac{|y-y^{\prime }|}{vT}}d{y}^{\prime }}$$

The first term in the numerator is for packets reaching y that have come from its left (these are traveling in the +y direction), while the second is for those reaching y that have come from the right, which are traveling in the −y direction. The denominator is a normalization factor given by the total number of packets reaching y at time t. This equation can be integrated numerically. To obtain an analytical approximation, we neglect the change in the packet distribution over the time of traveling one correlation time, approximating $p(y^{\prime },t-y^{\prime }/v)$ by p(y′,t), since the packet distribution does not change appreciably over that time (the validity of this assumption was verified by simulations). Integrating:

$${⟨v⟩}_{y,t}=v\frac{(R_{+}-R_{-})}{(R_{+}+R_{-})},$$

where

$$R_{+}=e^{\frac{y}{Tv}}(1-\mathrm{erf}\frac{vt+y}{\sqrt{2T{v}^{2}t}})$$

$$R_{-}=e^{-\frac{y}{Tv}}(1-\mathrm{erf}\frac{vt-y}{\sqrt{2T{v}^{2}t}})$$

for |y| < vt, and 0 otherwise. We are interested in i) whether the average lateral velocity of the packets is directed outward from the plume, which would be indicated by an asymmetrical dependence in y, and ii) how this asymmetry depends on the correlation time T. The profile of 〈v〉_y,t is odd for all T (Extended Data Fig. 10a), indicating that for any T, the velocity of odor packets in the crosswind direction points away from the plume’s central axis. Moreover, for higher T, the velocity component points more strongly outward through a larger portion of the plume, indicating that correlations in the packet motion underlie this directional cue (Extended Data Fig. 10a).

We next investigate how the combination of packet diffusion and packet centroid motion together can influence a spacetime correlation of the odor concentration, as would be computed by time-resolved bilateral measurements. For simplicity, we do this computation in one dimension, considering diffusion of packets and dispersion of their centroids in the y direction only, along with ballistic transport in the x direction. We start with a single packet. Assuming y_i(t) is the trajectory of the centroid of the packet and $\varphi \left(y,t|y_i\left(t\right)\right)=\frac{1}{\sqrt{4\pi D_{p}t}}{e}^{-{\left(y-y_i\right)}^2/4D_{p}t}$ is the local concentration at a given location y and time t around the packet. We define the correlator as:

$$C(\mathrm{\Delta }y,\mathrm{\Delta }t|y,t,y_i\left(t\right))={\varphi }_{++}{\varphi }_{--}-{\varphi }_{+-}{\varphi }_{-+},$$

where

$${\varphi }_{++}=\varphi (y+\mathrm{\Delta }y/2,t+\mathrm{\Delta }t/2|y_i\left(t\right))$$

$${\varphi }_{--}=\varphi (y-\mathrm{\Delta }y/2,t-\mathrm{\Delta }t/2|y_i\left(t\right))$$

$${\varphi }_{+-}=\varphi (y+\mathrm{\Delta }y/2,t-\mathrm{\Delta }t/2|y_i\left(t\right))$$

$${\varphi }_{-+}=\varphi (y-\mathrm{\Delta }y/2,t+\mathrm{\Delta }t/2|y_i\left(t\right))$$

Thus, the correlator C(Δy, Δt|y, t, y_i(t)) is a time-antisymmetrized quantity, which at time t and position y computes the correlation of the odor concentration between two points in the direction perpendicular to the mean wind, separated by Δy at times separated by Δt, given a packet whose center is at (x_i,y_i) and which was released at t = 0. We stress that we do not imply that this correlator is being enacted by any circuitry, nor is it a unique definition. However, it has key features – namely comparisons across space and time, and time anti-symmetry – which we will show to be sufficient to detect the lateral odor velocity. Expanding this correlator gives

$$C\left(\mathrm{\Delta }y,\mathrm{\Delta }t|y,t,y_i\left(t\right)\right)=\mathrm{\Delta }y\mathrm{\Delta }t\left({\varphi {\partial }_t{\partial }_y\varphi -\partial }_y\varphi {\partial }_t\varphi \right)$$

to lowest order. For the packet model, at appreciable times t ≫ T, this gives:

$$C\left(\mathrm{\Delta }y,\mathrm{\Delta }t|{y,t,y}_i\left(t\right)\right)=\mathrm{\Delta }y\mathrm{\Delta }t\frac{t{\dot{y}}_i+y-y_i}{8\pi D_p^2{t}^3}{e}^{-{\left(y-y_i\right)}^2/2D_{p}t}$$

Now we take the average of the correlator over the packet distribution p(y_i, t) to get the expectation at a fixed y, t:

$$⟨\mathrm{C}\left(\mathrm{\Delta }y,\mathrm{\Delta }t|y,t\right)⟩=\int d{y}_{i}C\left(\mathrm{\Delta }y,\mathrm{\Delta }t|{y,t,y}_i\left(t\right)\right)p(y_i,t)$$

where $p\left(y_i,t\right)=\frac{1}{\sqrt{2\pi T{v}^2}t}{e}^{-y_i^2/2T{v}^{2}t}$ for t ≫ T, as above. We can approximate $\dot{y_i}$ by ${⟨v⟩}_{y_i,t}$ – the average velocity for a packet at position y_i as derived above. The expression for 〈C(Δy, Δt|y, t)〉 does not lend itself to a closed-form expression due to the complexity of ${⟨v⟩}_{y_i,t}$; we integrate it numerically.

In nature, the strength of the turbulence will vary in space and time, so it is informative to examine how the average correlator output 〈C(Δy, Δt|y, t)〉 depends on the Lagrangian integral time scale T and the r.m.s. of the turbulent velocity field v, which controls the packet speed in the direction perpendicular to mean wind direction. We find that for D_p ≪ D_T = v²T, the correlator 〈C(Δy, Δt|y, t)〉 has a clear asymmetry about y = 0 as expected, and that the peaks are stronger with increasing correlation time T (Extended Data Fig. 10b). Moreover, 〈C(Δy, Δt|y, t)〉 increases on average with v, while decreasing with D_p (Extended Data Fig. 10c), indicating that the response essentially derives from correlated motion over the detector rather than molecular diffusion alone.

Statistical quantification

All error bars, when shown, represent standard error of the mean. Statistical tests used and significance levels (p value) for given comparisons are indicated in the main text. Throughout, *, **, ***, and **** refer to p-values of < 5e-2, <1e-2, <1e-3, and <1e-4. In some instances, **** may refer to p < 1e-6, if indicated in the text. For the plume navigation data, SEMs are taken over distinct fly trajectories.

Extended Data

Extended Data Fig. 1. Verification of odor velocity calculation and distributions of signal-derived quantities in measured plume.

a, Mean odor velocity measured in the virtual antenna at all times for navigating flies in measured smoke plume, plotted as a function of fly orientation. The –cos(θ) trend reflects the fact that the main component of odor velocity is parallel to the mean wind direction 90°, as expected – a consistency check on the odor velocity calculation. b-d, Histograms of signal-derived quantities measured in the fly virtual antenna; the x-axis limits in Fig. 1c–e are determined by the extent of these histograms.

Extended Data Fig. 2. Electrophysiological and behavioral verification of optogenetic activation of Drosophila ORNs.

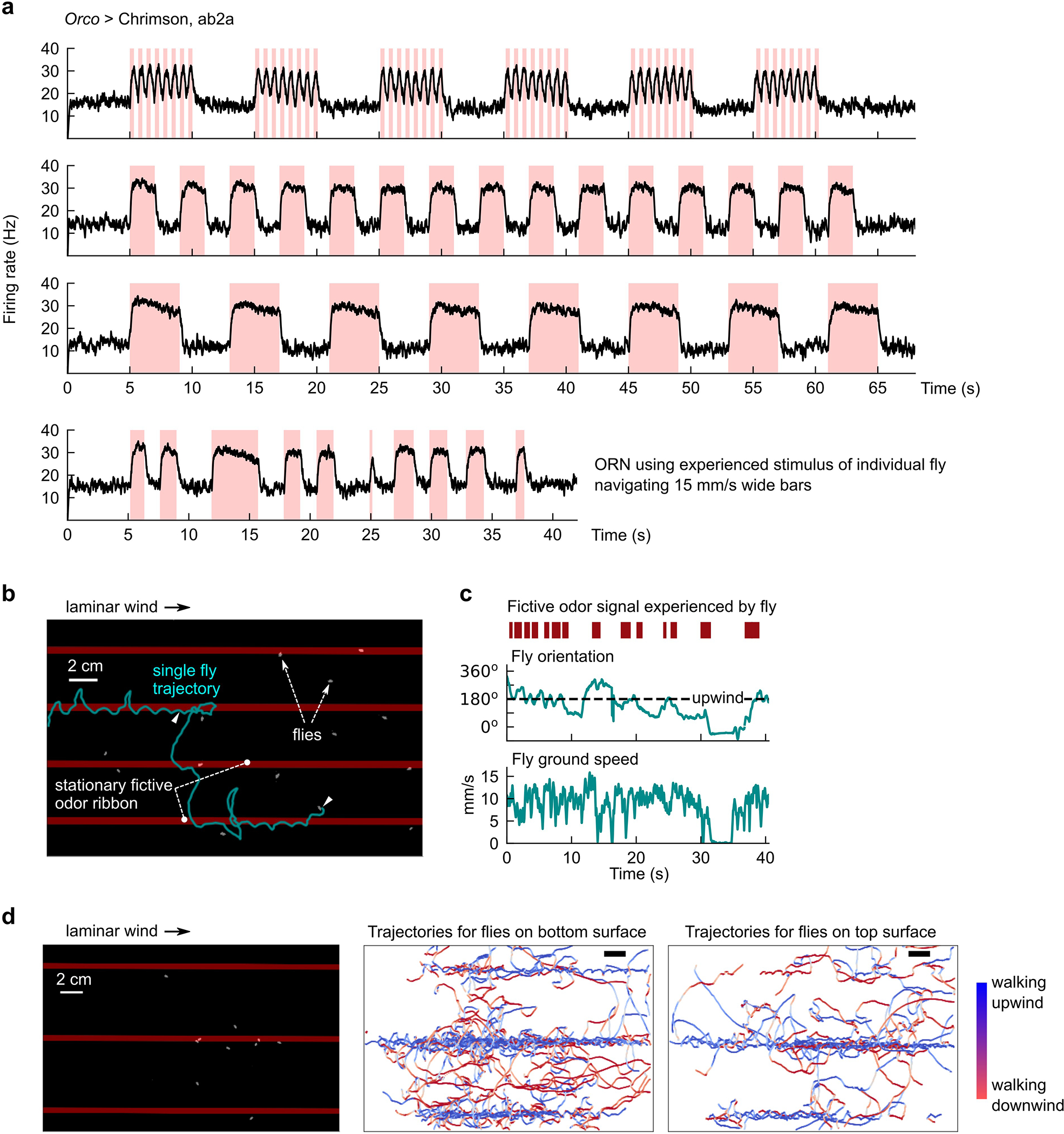
a, Extracellular measurements of ab2A firing rates for various odor signals mimicking those we use throughout our study. Stimuli (red shades) are delivered using a Luxeon Rebel 627 nm red LED (Lumileds Holding B.V., Amsterdam, Netherlands) at 10 uW/mm². The frequency and duty cycle for the stimuli in the first plot are 1.5 Hz and 50% respectively, which mimics what a stationary fly in the 5 cm wide, 15 mm/s fast moving bars (Fig. 2b) would encounter. Longer stimuli approximate the experienced stimuli in the wide moving bars (Fig. 2e–f). Last plot shows the experienced stimulus and corresponding firing rate for one representative measured fly navigating 15 mm/s moving wide bars. All recordings were taken from 5 ab2a ORNs in 2 different flies. b, Illustrative track of fly following stationary fictive odor ribbons upwind. Red bars: optogenetic stimulus location – bars are overlaid on the figure, but not actually imaged since the image is IR-pass filtered. c, Fictive odor signal for fly (red bars) can be simultaneously quantified with fly behavior (teal) by aligning camera and projector coordinate systems (Methods). Plotted are the encountered fictive odor signal and behaviors for the track shown in b. d, Verification that flies on both top and bottom glass surface of assay respond similarly to fictive odor signals (here, 3 odor ribbons in laminar wind; left). Flies were manually annotated as being on the top or bottom surface. In both cases (middle and right), flies followed the fictive odor ribbons upwind, similar to behavioral responses with real odors¹⁰.

Extended Data Fig. 3. Odor direction selectivity in single antenna and single Or flies and ON/OFF edge responses across speeds and for negative controls.

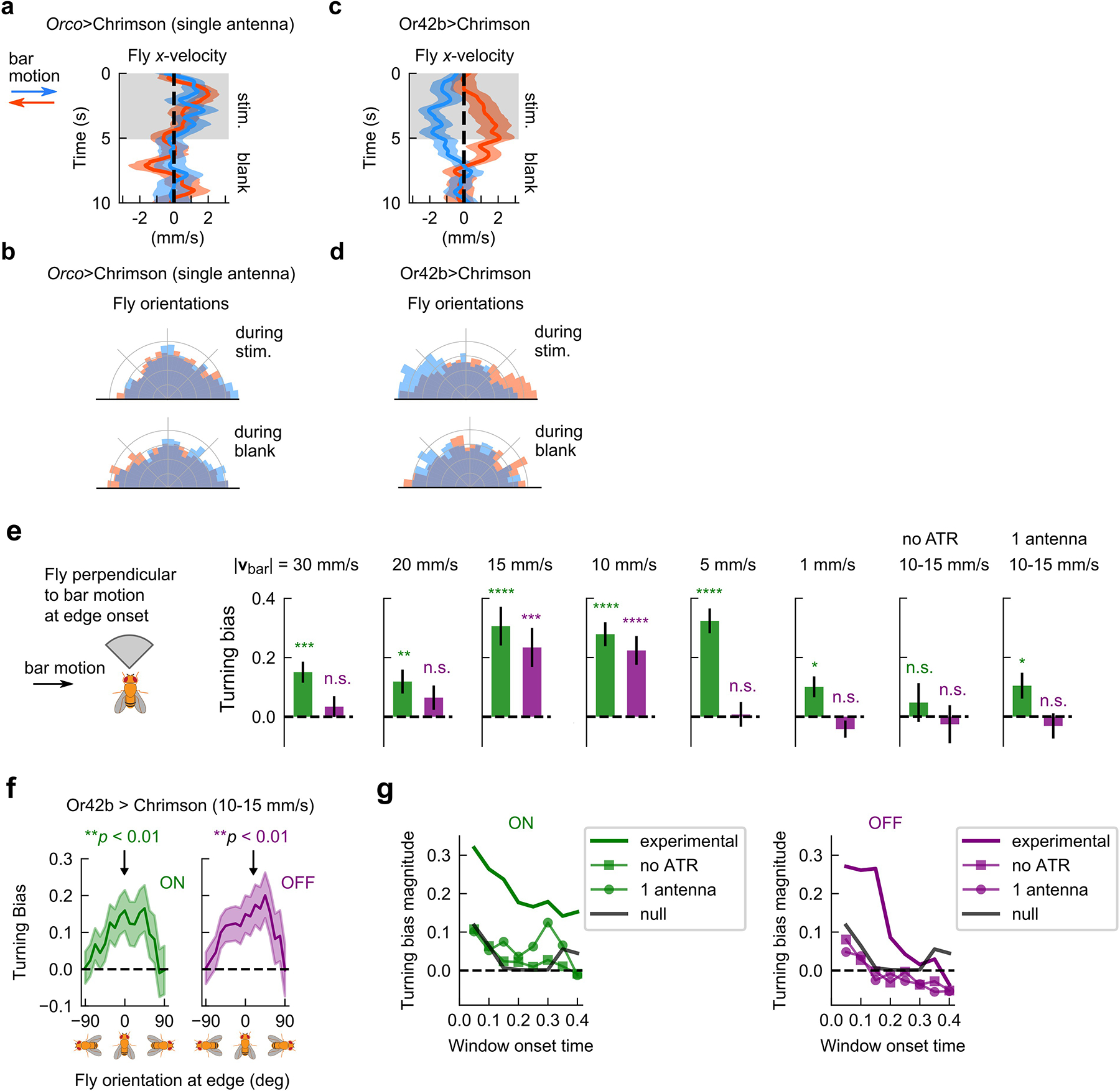
a, Component of fly walking velocity along +x direction during the 5s stimulus (shaded grey) and blank periods (illustrated in Fig. 2b), in Orco>Chrimson flies that have one antenna ablated (compare to Fig. 2d). Shaded errors: SEM. Blue and orange denote rightward and leftward moving bars, respectively. Since it is difficult to distinguish flies walking on the top and bottom surface of the assay, right- and left-antenna ablated flies are pooled. n = 100, 89 tracks for rightward and leftward bar motion, respectively. Only flies oriented in the 90° sector perpendicular to the bar motion are included. b, Distribution of fly orientations during the 5s stimulus (top) and 5s blank periods (bottom), for rightward (blue) and leftward (orange) bar motion, Orco>Chrimson flies with one antenna ablated (compare Fig. 2d). Orientations are symmetrized over the x-axis. c-d, Same as a-b, for Or42b>Chrimson flies with both antennae intact. n = 37, 50 tracks for rightward and leftward bar motion, respectively. e, Turning bias for all instances that flies encounter the fictive odor ON (green) or OFF (purple) edge, for flies oriented within a 90° sector of the direction perpendicular to bar motion. Turning bias calculated as sign of fly orientation change from 150 ms to 300 ms after the edge hit. All flies are Orco>Chrimson and fed ATR (i.e. optogenetically active) except in the 7^th plot, which are not fed ATR. Data are shown for bars that move at various speeds (left 6 plots), as well as for negative controls (7^th and 8^th plot). Error bars: SEM. P values calculated using the chi-squared test (****p < 1e4, ***p < 1e-3, **p < 1e-2, *p < 0.05). Specifically, p=9.60e-5 for n=1472 ON edge hits and p=0.23 for n=1661 OFF edge hits for 30 mm/s bars; p=3.49e-3 for n = 1167 ON edge hits and p=0.132 for n=1306 OFF edge hits for 20 mm/s; p=1.03e-6 for n = 548 ON edge hits and p=1.18e-3 for n=470 OFF edge hits for 15 mm/s; p<1e-6 for n = 1125 ON edge hits and p=1.78e-5 for n=1039 OFF edge hits for 10 mm/s; p<1e-6 for n = 1000 ON edge hits and p=0.816 for N=987 OFF edge hits for 5 mm/s; p=0.012 for n = 1284 ON edge hits and p=0.2106 for n=1633 edge hits for 1 mm/s; p=0.423 for n = 1387 ON edge hits and p=0.701 for n=1484 OFF edge hits for no ATR 10–15 mm/s; and p=0.0295 for n = 988 ON edge hits and p=0.454 for n=1153 OFF edg hits for 1 antenna 10–15 mm/s. Direction selectivity is satisfied if both ON and OFF edge responses have the same sign; gradient sensing would require opposite signs for the two edges. Data indicate that flies counterturn against the direction of fictive odor bars at both edges, within a range of bar speeds. Large ON responses for slow bar speeds are likely attributed to gradient sensing: since the direction of odor motion and gradients are the same for ON edges but opposite for OFF edges, this would give appreciable ON edge responses at slower speeds, but diminished OFF edge responses. f, Turning responses for Or42b > Chrimson flies, in which light activates only one ORN type, in response to bars moving at 10–15 mm/s. Error shades: SEM. Turning responses are consistent with direction selectivity (compare Fig. 2f). p=4.82e-3 for n = 706 ON edge hits and p=5.51e-3 for n=763 OFF edge hits. g, Dependence of results on choice of window over which turning bias is calculated. The x-axis shows the onset time of the window; the offset time was 150 ms later. The y-axis plots turning bias for flies oriented within a 90° sector of the direction perpendicular to bar motion (as in e). “Experimental” flies refer to Orco > Chrimson in response to bars moving at 10–15 mm/s (same as in Fig. 2); “no-ATR” and “1 antenna” are the same flies not fed ATR or with only 1 antenna, respectively. The “null” condition is calculated using random chosen trajectories and calculating angle changes following fictitious moving bars at random angles not actually presented to the flies. Over window onsets of 0–200 ms, the no ATR, 1 antenna and null responses are all within the same regime (< ~0.1), while the experimental responses are significantly higher. These results are consistent with previous findings. OFF response reaction times of ~500 ms have been observed⁹, but those were for flies counterturning back into static ribbons – the differing locomotive repertoire (flying vs. walking) and plume dynamics (static vs. dynamic) would account for this discrepancy. Reaction times of 400 ms have been observed for walking flies, but this may reflect imprecision in odor delivery⁶; indeed, reaction times are as low as 100 ms for tethered flies whose ORNs are stimulated optogenetically¹⁷ and as low as 85ms when ORNs are stimulated with real odors ²⁵.

Extended Data Fig. 4. OFF edge responses with laminar and ON edge responses for fast 30 mm/s bars.

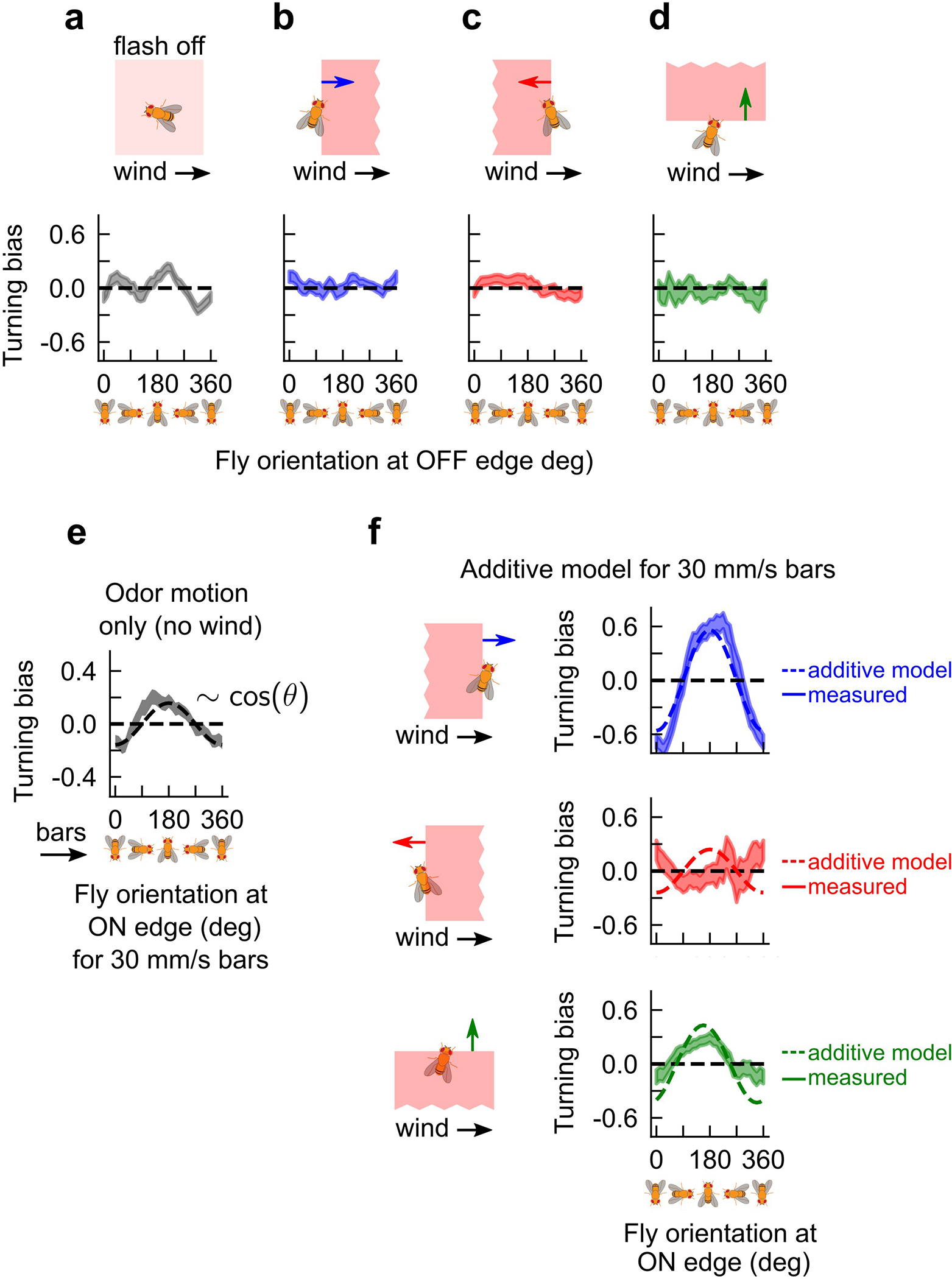
a, Turning bias versus fly orientation when bilateral optogenetic stimulus is turned off (compare first plot in Fig. 3B for flash onset). n = 1490 OFF flash hits. b-d, Fly turning bias for 15 mm/s bars moving parallel, antiparallel, and perpendicular to 150 mm/s laminar wind (compare Fig. 3d). Shaded errors: SEM. n = 1493, 1588, and 671 OFF edge encounters for bars parallel, antiparallel, and perpendicular to the wind, respectively. e, Fly turning bias vs. fly orientation at ON edge for faster 30 mm/s fictive odor bars without wind (analogous to 15 mm/s bar responses in second plot of Fig. 3b). Dotted line: fit of response to −0.16 cosθ. N = 1472 ON edge encounters. f, Additive model for ON edges of 30 mm/s bars; analogous to Fig. 3d. Solid shaded region: mean ± 1 SEM; dotted lines: additive model prediction. N = 323, 319, and 1013 ON edge encounters for odor bars with parallel, antiparallel, and perpendicular to the wind, respectively.

Extended Data Fig. 5. Supplementary figures and additional evidence that direction sensing is enacted using a correlation-based algorithm.

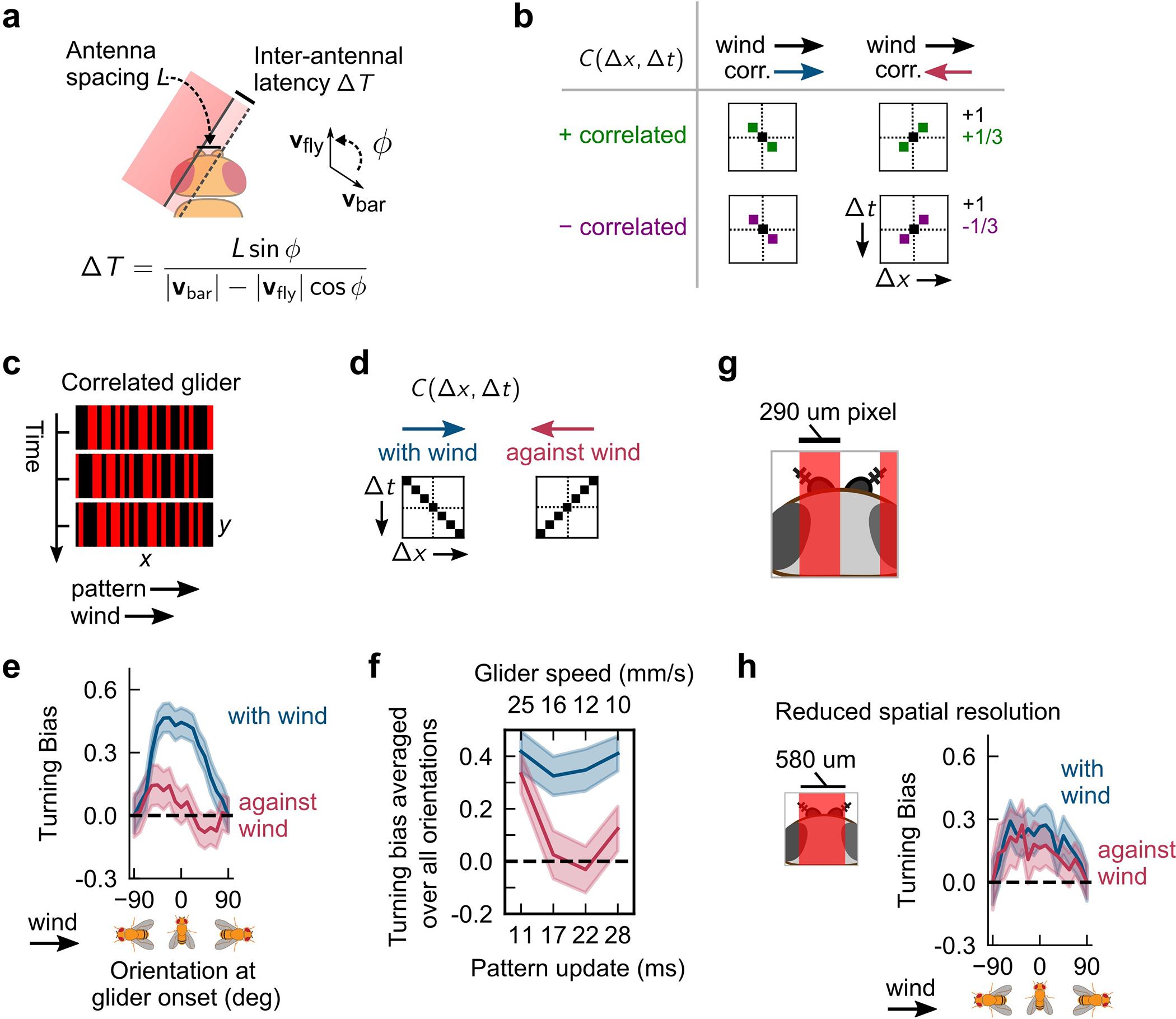
a, Schematic illustrating calculation of latency ΔT between antennae hits for moving edges. Correlation-based models for direction selectivity depend on the latency ΔT of the time the edge hits the two sensors – in this case, the fly’s two antennae. Measuring ΔT does not require resolving the image or stimulus at antennal resolution (~300 μm), rather ΔT can be inferred with knowledge of the fly’s orientation relative to the bar direction ϕ, as well as the speeds of the fly and bar – all of which are known. See Methods for details of the calculation and an estimate of the uncertainty. b, Spatiotemporal correlation functions for correlated noise stimuli (Fig. 4c–f). Each type of correlated noise stimulus is characterized by the correlation function C(Δx,Δt) computed between all pairs of bars separated spatiotemporally by Δx pixels and Δt frames. Since our stimuli are generated by summing and binarizing Gaussian variables, nonzero correlations off of the origin have magnitude 1/3²⁶. For example, for positively correlated with-wind stimuli (top left plot), C(1,1) = C(−1,−1) = 1/3, and the remaining correlations are zero, while for negatively correlated with-wind stimuli (bottom left plot), C(1,1) = C(−1,−1) = −1/3. c, Snapshots of glider stimulus with correlations along +x axis, for 3 consecutive frames. In one instance of time, stimulus is a random pattern of light and dark 1-pixel-wide bars perpendicular to 150 mm/s laminar wind. Each x-pixel is perfectly correlated with the pixel to its right in the next frame; thus the pattern in the next frame is the same as the pattern in the current frame, but shifted by one pixel. Visually, this would be perceived as a fixed pattern moving coherently to the right in discrete steps. d, Like correlated noise stimuli, gliders are defined by their correlation matrix C(Δx,Δt). Unlike correlated noise, the correlations i) have magnitude 1, and ii) exist for many spacetime points. That is, for rightward correlated gliders, a given pixel in a given frame is perfectly correlated with the pixel to its right one frame later, but also with the second pixel to its right 2 frames later, etc. Thus C(Δx,Δt) has values +1 along the diagonal. Similarly, C(Δx,Δt) has values 1 along the anti-diagonal. Since +x points downwind, we call gliders with correlations to the right “with-wind”, and gliders with correlations to the left “against-wind,” in analogy to the correlated noise stimuli (Fig. 4d). e, Turning bias versus fly orientation for with-wind (blue) and against-wind (red) gliders. Data using pattern update rates of 45 or 60 Hz are pooled. Shaded errors: SEM. Gliders are presented in 4s blocks, interleaved with 4s of no stimulus. Turning bias is defined as the sign of the change in orientation from 200 to 500 ms after the block onset. We only used flies with speeds < 12 mm/s for gliders, since long-range correlations can interfere with the intended correlation if fly walking speed is near the glider speed. n = 301, 247, for with-wind and against-wind, respectively. f, Turning bias averaged over all orientations for different glider speeds. Glider speed is calculated as (pixel width)⋅(pattern update rate) where the pixel width is 290 μm and the pattern rate is some multiple of the inverse frame rate, 1/(180 Hz). n = 141, 163, 138, 190 onset events for with-wind stimuli at glider speeds 25, 16, 12, and 10 mm/s, respectively; n = 159, 119, 128, 137 onset events for against-wind stimuli at same glider speeds, respectively. g, For correlated stimuli to be sensed in our assay, the bar width (size of x-pixel, 290 μm), must be on the order of the fly antennal separation (~300 μm⁵⁸). h, Glider stimuli experiments repeated for bars that were double the width, 580 μm. Differences now disappear for with and against-wind correlations, consistent with bilaterally-enabled direction sensing, since these bars are too wide to consistently stimulate antennae differentially. Shaded errors: SEM. n = 195, 169 for with-wind and against-wind, respectively.

Extended Data Fig. 6. HRC response is robust to signal pre-filtering.

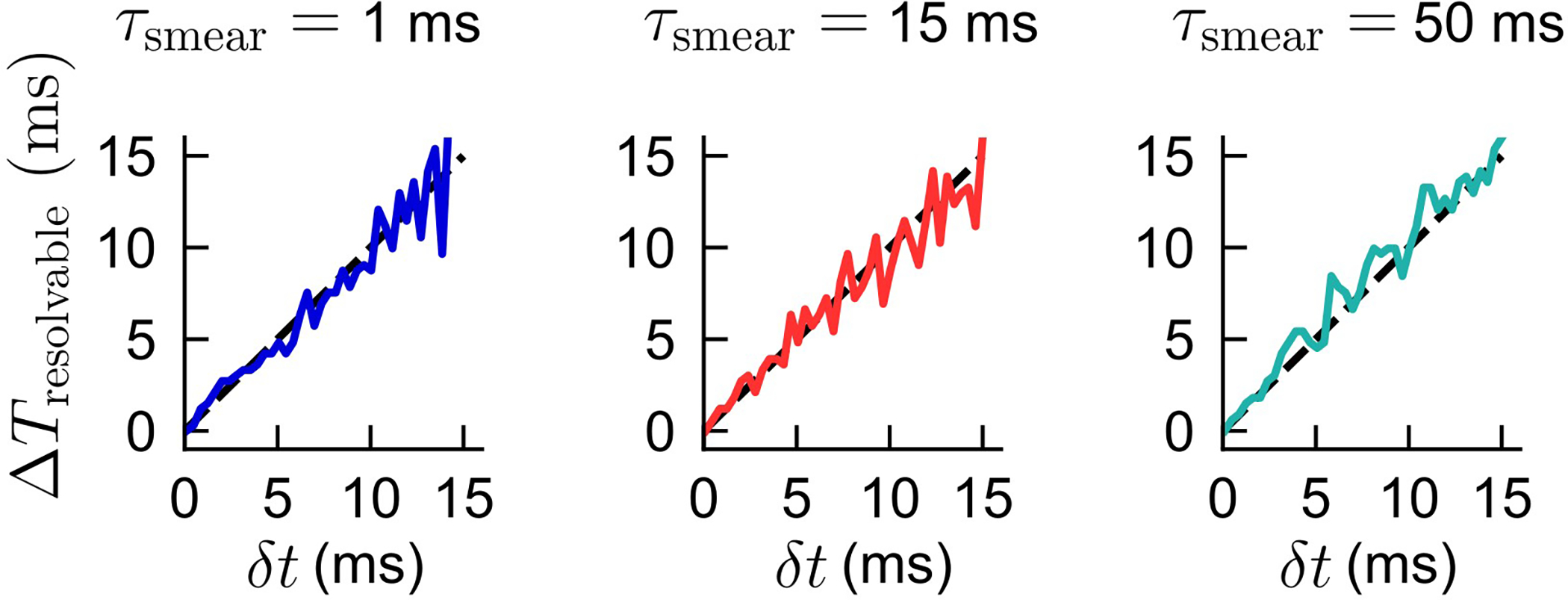
Minimum resolvable inter-antennal latency ΔT as a function of the noise level, for exponential pre-filters of varying timescale, τ_smear = 1, 15, 50 ms, respectively, for the 3 plots. Noise level is quantified as a random shift of ΔT, where each shift is chosen from a normal distribution with mean zero and standard deviation δt. The HRC’s delayed arm has an exponential filter of timescale τ_HRC = 15 ms. Dotted line: identity. A particular value of ΔT is deemed resolvable if the SD over HRC responses is greater than the mean over HRC responses (see Methods for details). The mean and SD are calculated over 100 samples (i.e. 100 random shifts of ΔT) for a given noise level δt.

Extended Data Fig. 7. Odor velocity and concentration gradients provide complementary directional information in complex plumes.

a, Vector field of the negative gradient of odor concentration −∇c, averaged over the full simulation (compare to Fig. 6c in the main text). Gradients contain strong lateral components near the odor source. b, Time course of an estimate of the direction of odor motion ${\theta }_{\text{odor}}={\tan }^{-1}{(\mathbf{v}}_{\text{y}\text{,odor}},{\mathbf{v}}_{\mathbf{x}\text{,odor}})$ at the center of the boxed regions in Fig. 6a, determined by averaging all detectable θ in the past t seconds. Error bars are found by repeating this for 16 different 10 s time windows throughout the simulation, and taking the average and standard deviation over these 16 samples – these correspond to the mean and standard error of the mean. Dots indicate the time needed to distinguish the direction of odor motion from 0° (downwind) with a 68% confidence level for the 3 regions. c, Heatmap of time taken to distinguish the direction of odor motion from 0° to within 68% confidence for fixed locations throughout plume. Black values include the possibility that the odor motion direction is not distinguishable from downwind no matter how long one samples.

Extended Data Fig. 8. Odor motion sensing aids plume navigation by increasing lateral motion toward the plume centerline.

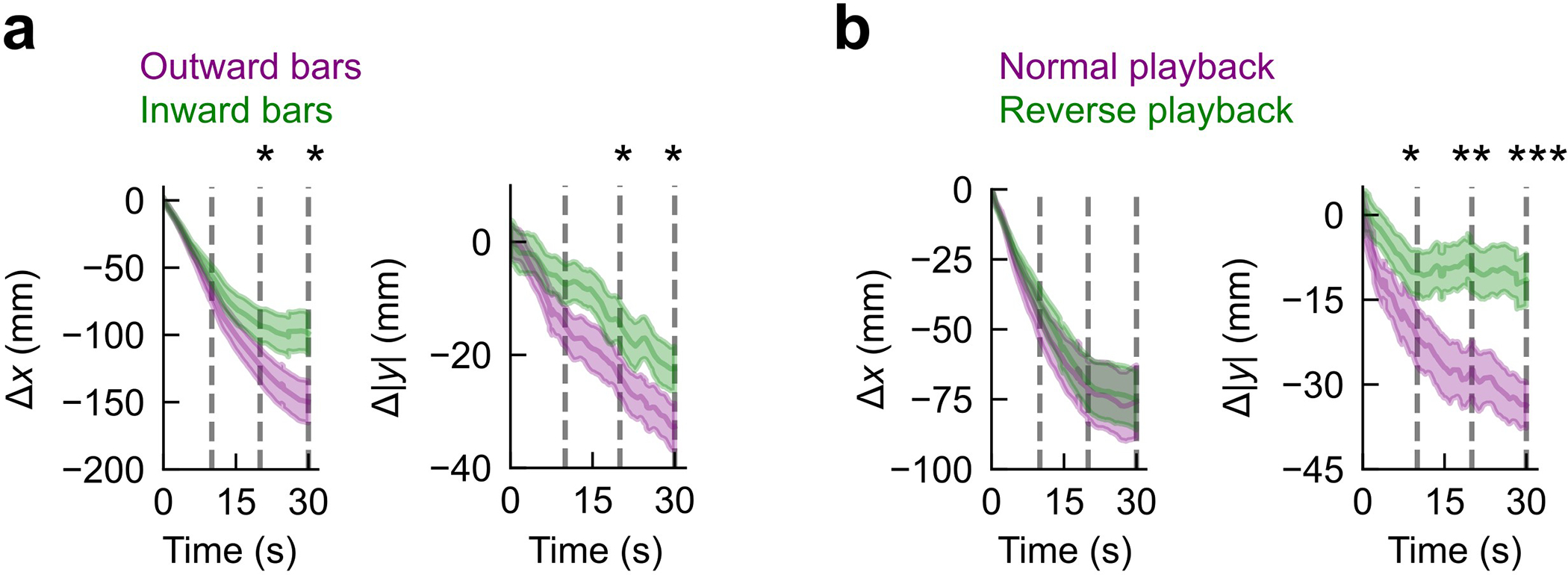
a, Average change in position parallel to wind, x (left), and away from the plume centerline, |y| (right), in outward (purple) and inward (green) moving bars plume (Fig. 6d), as a function of time. Note that x = 0, y = 0 is the fictive plume’s odor source location. The initial values at t = 0 of x (y) were subtracted, so the change Δx (Δy) is plotted – this is negative because flies progress toward to the centerline (decreasing y) and upwind (decreasing x). Only flies beginning in the rear 50 mm of the arena and which navigated for at least 30s were considered. Shades: SEM over distinct fly trajectories. Dotted lines: times t = 10, 20, 30s. By t = 20s, flies in the outward bar plume have made more progress both in the upwind direction (p = 0.025; 1-tailed t-test) and toward the plume centerline (p = 0.032; 1-tailed t-test). b, same for fictive odor plume shown in Fig. 6g, played normally (purple) or in reverse (green). Here, flies make equal progress upwind by 30s (left plot), but significantly faster progress toward the plume centerline in the forward played plume than the reverse one (right plot) (p=0.035 at t = 10s, p=3.0e=3 at t = 20s, at p=1.6e-4 at t = 30s; 1-tailed t-test). Shades: SEM over distinct fly trajectories.

Extended Data Fig. 9. Odor motion sensing enhances performance of virtual robots obeying a simple navigation strategy on a grid.

a, Model of 2-sensor virtual agents navigating the simulated odor plume (Fig. 6a). Agents are always oriented at 0°, 90°, 180° or 270°, and at each timestep turn 90° either left or right and move forward one step. Agents are either odor direction sensing (DS+) or not odor direction sensing (DS-). When odor concentration c exceeds some threshold c₀, DS- agents turn upwind. DS+ agents, for c > c₀, turn against the direction of odor motion when oriented upwind or downwind; crosswind agents always turn upwind. DS+ agents infer the direction of odor signals using an HRC-like computation between their 2 sensors (Methods). b, Example trajectories of robots navigating plume in a, when they are initialized in the back 50 mm of the arena, for DS- (top) and DS+ (bottom) agents. c, Percentage of 100 agents reaching the 50×50 mm red source region; more DS+ agents reach the source than DS- agents (38% vs. 19%; p < 1e-6; 1-tailed t-test) d, Lateral distance from plume axis |y| over time, for agents initialized near the plume edges (>60 mm from plume axis, indicated by the solid boxes in b; top plot) or near the plume axis (<60 mm from axis, indicated by the dashed boxes in b; bottom plot). Odor direction sensing enhances lateral drift toward the plume centerline, particularly for robots initialized at the plume edges.

Extended Data Fig. 10. Odor velocity in model of turbulent plumes points outward from plume centerline and is computed by local space-time correlators.

A packet model of turbulent plumes. Packets are released from a source and disperse in the lateral direction while being advected downwind (see Methods for model and calculation details). a, Packet velocity 〈v〉_y,t in the plume model, as a function of $\overline{y}=y/\sqrt{T}$, for two correlation times, T = 0.2 (purple) and T = 1 (green), at a fixed time t = 4. Here, v is set to 1. To directly compare velocity for plumes with different T, (and therefore different diffusivities) we plot the velocity versus the normalized length $\overline{y}$. Specifically, since 〈y²〉 = 2Tv²t for t ≫ T then at a given t, the packet distribution in terms of $\overline{y}$ is the same for plumes with distinct T. The distribution of packets for either T is a function of $\overline{y}$ is shown in grey. The velocity is an odd function of y, i.e. it points outward from the plume axis. In addition, the asymmetry is steeper for higher correlation times. b, The value of the correlator 〈C(Δy,Δt|y,t)〉 as a function of lateral distance y, for various times t for T = 0.1 (left) and T = 0.3 (right). Here, D_p = 0.005. Since the packets are advected downwind with a velocity U ≫ v, the time axis is proportional to the downwind distance. The packet distribution is shown on the bottom; the limits of the y-axis are chosen such that the plume extents are the same in both plots. c, The total y-integral of the absolute value of 〈C(Δy,Δt|y,t)〉 at a fixed t = 4, as a function of odor packet speed (y-axis) and molecular diffusivity (D_p), with T = 1, v = 1. This integral indicates the degree of directional sensing on average. The integral is highest for greater packet speeds and lower molecular diffusivities (top left corner).

DATA AVAILABILITY STATEMENT

All experimental data are available on Dryad at https://doi.org/10.5061/dryad.1ns1rn8xd.