Unsupervised contrastive learning based transformer for lung nodule detection

Abstract

Objective.

Early detection of lung nodules with computed tomography (CT) is critical for the longer survival of lung cancer patients and better quality of life. Computer-aided detection/diagnosis (CAD) is proven valuable as a second or concurrent reader in this context. However, accurate detection of lung nodules remains a challenge for such CAD systems and even radiologists due to not only the variability in size, location, and appearance of lung nodules but also the complexity of lung structures. This leads to a high false-positive rate with CAD, compromising its clinical efficacy.

Approach.

Motivated by recent computer vision techniques, here we present a self-supervised region-based 3D transformer model to identify lung nodules among a set of candidate regions. Specifically, a 3D vision transformer is developed that divides a CT volume into a sequence of non-overlap cubes, extracts embedding features from each cube with an embedding layer, and analyzes all embedding features with a self-attention mechanism for the prediction. To effectively train the transformer model on a relatively small dataset, the region-based contrastive learning method is used to boost the performance by pre-training the 3D transformer with public CT images.

Results.

Our experiments show that the proposed method can significantly improve the performance of lung nodule screening in comparison with the commonly used 3D convolutional neural networks.

Significance.

This study demonstrates a promising direction to improve the performance of current CAD systems for lung nodule detection.

1. Introduction

Global cancer statistics in 2018 indicate that Lung cancer is the most popular, i.e. 11.6% of the total cases, and the leading cause of cancer death, up to 18.4% of the total cancer deaths (Bray et al 2018). Various studies have shown that early detection and timely treatment of lung nodules can improve the 5 year survival rate (Blandin Knight et al 2017). Therefore, major efforts have been made on early and accurate detection of lung nodules in different aspects, such as imaging technologies (NLST 2017, Niu et al 2022), diagnosis workflows (MacMahon et al 2005), and computer aided detection and computer aided diagnostic systems (Messay et al 2010). Particularly, recent results indicate that computer aided detection/diagnosis (CAD) systems empowered by artificial intelligence (AI) algorithms as the second or concurrent reader can improve the performance of lung nodule detection on chest radiographs (Yoo et al 2021) and computed tomography (CT) images (Roos et al 2010, Prakashini et al 2016).

Lung cancer CAD systems usually involve lung region segmentation, nodule candidate generation, nodule detection, benign and malignant nodule recognition, and different types of lung cancer classification. In recent years, deep learning methods were developed for CAD systems, continuously improving the performance of some or all the key components in a CAD system. For example, Harrison et al (2017), Hofmanninger et al (2020) showed that deep learning methods for CT lung segmentation significantly improved the performance through training the models with a variety of datasets. Motivated by the progress in deep learning based objection detection (Ren et al 2015, Lin et al 2017) in various domains (Jiang and Learned-Miller 2017, Niu et al 2018), the performance of lung nodule candidate generation and detection was significantly improved by adapting advanced object detection algorithms (Jaeger et al 2020, Baumgartner et al 2021). Nevertheless, a high false positive rate is still a main challenge for accurate lung nodule detection (Pinsky et al 2018). Clearly, a key step for accurate nodule detection is to effectively reduce the false positive rate for nodule candidates. Recent studies addressed this issue using various techniques, such as 3D convolutional neural network (Dou et al 2017), multi-scale prediction (Gu et al 2018, Cheng et al 2019), relation learning (Yang et al 2020), multi-checkpoint ensemble (Jung et al 2018), multi-scale attention (Zhang et al 2022), etc. After identifying lung nodules, various methods were proposed to further analyze them, i.e. predicting the malignancy (Shen et al 2017, Al-Shabi et al 2022) and sub-types (Liu et al 2018, Yuan et al 2018) of lung nodules. It is exciting that adapting emerging techniques in machine learning and computer vision based on domain knowledge leads to great progress in CAD systems with great potential for clinical translation.

Recently, transformers (Vaswani et al 2017), originally developed for natural language processing (NLP), have achieved great success in various tasks of computer vision. The key component of the transformer is the attention mechanism that utilizes global dependencies between input and output. For the first time, vision transformer (ViT) divides an image into a sequence of non-overlap patches, analyzes them as a sequence of elements similar to words, and produces state-of-the-art results demonstrating the effectiveness and superiority in image classification (Dosovitskiy et al 2020). Since then, ViT has been successfully applied to various other vision tasks including medical imaging (Pan et al 2021) and medical image analysis (Lyu et al 2021). However, the performance of the original ViT relies on a large labeled image dataset including 300 million images, and the conventional wisdom is that the transformers do not generalize well if they are trained on insufficient amounts of data. Therefore, directly adopting the transformers for CAD systems is not trivial when labeled data are scarce.

The lack of labeled data is a common problem in medical imaging and many other fields. A most promising direction of deep learning is the so-called unsupervised or self-supervised learning (Niu et al 2020, 2020, 2021) that recently achieved remarkable results which even approach the performance of supervised counterparts. Particularly, unsupervised learning works by pre-training a neural network on a large scale unlabeled dataset to benefit downstream supervised tasks that only offer a limited number of training samples (He et al 2019). For unsupervised or self-supervised learning (Niu and Wang 2022a, 2022b), the pretext task is the core to learn meaningful representation features. Recent progress suggests that instance contrastive learning (Chen et al 2020) and masked autoencoding (He et al 2021) are the two most effective and scalable pretext tasks for unsupervised representation learning. Specifically, instance contrastive learning maximizes the mutual information between two random transformations of the same instance (e.g. an object in a natural image or a patient represented by a CT volume). This can be achieved by forcing the representation features from different transformations of the same instance to be similar while the features from different instances to be dissimilar. On the other hand, masked autoencoding recovers masked parts from the rest visible data, which has been used for pre-training in various tasks and recently produced encouraging results (He et al 2021), using an asymmetric encoder-decoder architecture and a high proportion masking strategy.

Based on the above progress, here we study how to effectively adapt ViT and unsupervised pretraining for lung nodule detection, so that the false positive rate can be reduced for lung nodules to be effectively singled out of a set of candidates, in comparison with the commonly used 3D CNNs. In our work, we adapt the original transformer to a CT volume with the fewest possible modifications. Advantages of keeping the original transformer configuration as much as possible include the scalability in the modeling capacity and the applicability across multiple modality datasets. With this preference in mind, we simply divide a 3D CT volume into non-overlap cubes and extract their linear embeddings as the input to the transformer. These cubes are equivalent to the tokens or words in NLP. However, without pretraining on large-scale datasets, the superiority of the transformer cannot be realized, especially for lung nodule analysis where labeled data are usually expensive and scarce, e.g. there are only over one thousand labels in public datasets. To overcome this difficulty, we perform unsupervised region-based contrastive learning on public CT images from the LIDC-IDRI dataset to effectively train the adapted transformer. Our experimental results show that while the adapted 3D transformer trained with a relatively small number of labeled lung nodule data from scratch achieved worse results than the 3D CNN model, the pretraining techniques enabled the adapted transformer to outperform the commonly used 3D CNN. Interestingly, we found that unsupervised pretraining is more effective than supervised pretraining with natural images in a transfer learning manner to boost the performance of the adapted transformer.

The rest of this paper is organized as follows. In the next section, we describe our transformer architecture and implementation details. In the third section, we report our experimental design and representative results in comparison to competing CNN networks. In the last section, we discuss relevant issues and conclude the paper.

2. Methodology

2.1. Vision transformer for lung nodule detection

In this section, we describe the architecture of our adapted Transformer for lung nodule detection in a CT volume. The whole architecture is depicted in figure 1, where there are four parts. The details on each part are given as follows.

Figure 1.

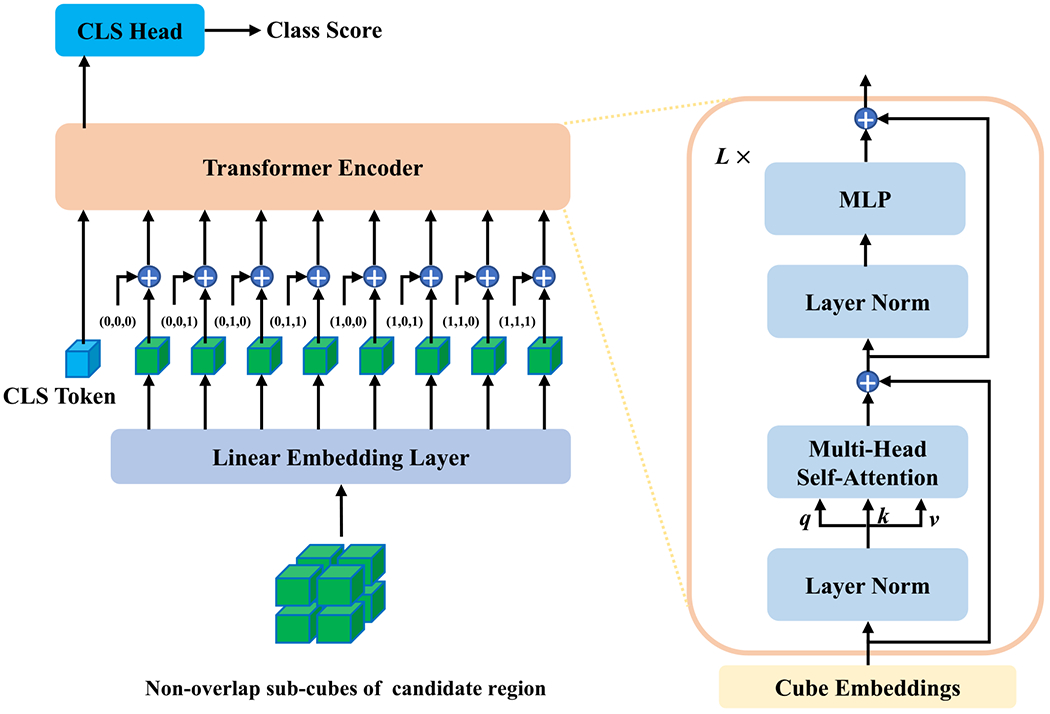
Transformer architecture for lung nodule detection.

Input and linear embedding:

The input is a 3D tensor, $\mathit{x}\in {\mathbb{R}}^{H\times W\times D}$, which is a local candidate volumetric region of interest in a whole CT volume. Similar to what ViT does, the image volume is divided into a sequence of non-overlap cubes, ${\mathit{x}}_c\in {\mathbb{R}}^{S\times S\times S}$, similar to words in NLP, where H, W, D are the input volume size, S is the cube size, and c is the index for cubes. Then, the linear embedding layer maps these cubes to embedding features independently. In practice, the linear embedding layer is implemented as a 3D convolutional layer, where both the kernel size and convolutional stride are S × S × S. Therefore, this embedding layer can directly take the original 3D volume as input and outputs the embedding features of non-overlapped cubes, i.e. ${\mathit{z}}_{\mathit{c}}=\mathit{E}\left({\mathit{x}}_c\right)\in {\mathbb{R}}^d$, where c = 1, 2, …, S × S × S, and d is the dimension of embedding. As in ViT, the [class] token of a learnable embedding is prepended to the sequence of embedded cubes, and the final sequence of linear embedding features are denoted as [z₀; z₁; ⋯; z_N], where z₀ denotes the learnable class embedding, and N = S × S × S + 1 this the total number of input embeddings.

Position embedding:

For the model to be aware of the relative position of each cube, position embeddings are coupled with the feature embeddings. In this study, we extend the sin-cosine position encoding (Dosovitskiy et al 2020) into the 3D space. Specifically, sine and cosine functions of different frequencies are used to encode 3D position information as

$$\begin{gathered} PE\left(x,y,z\right)=\left[P{E}_{\sin }\left(x\right),P{E}_{\cos }\left(x\right),P{E}_{\sin }\left(y\right),P{E}_{\cos }\left(y\right),P{E}_{\sin }\left(z\right),P{E}_{\cos }\left(z\right)\right], \\ P{E}_{\sin }\left(p\right)=\sin \left(p/{10000}^{i/d_{pos}}\right),i=0,1,\cdots ,d_{pos}-1, \\ P{E}_{\text{cos}}\left(p\right)=\cos \left(p/{10000}^{i/d_{pos}}\right),i=0,1,\cdots ,d_{pos}-1, \end{gathered}$$ (1)

where (x, y, z) is the relative position of a cube and $PE\left(x,y,z\right)\in {\mathbb{R}}^d$ is the corresponding position embedding, here the position embedding of the class token is a zero vector. The position embedding consists of six parts and the dimension of each part is d/6. To be consistent with the notations of feature embeddings, we use PE_c to denote the position embedding of a specific cube. Finally, the point-wise summations of position and feature embeddings are input to the transformer encoder.

Transformer encoder:

The transformer encoder consists of L stacked identical blocks, where each block has two layers, i.e. a multi-head self-attention layer and a simple position wise fully-connected layer. As shown in figure 1, the residual connection and layer normalization are applied in these two sub-layers. More specifically, given a sequence of input embeddings, ${\mathit{z}}^0=\left[{\mathit{z}}_0^0+P{E}_0;{\mathit{z}}_1^0+P{E}_1;\cdots ,{\mathit{z}}_{S^3}^0+P{E}_{S^3}\right]\in {\mathbb{R}}^{N\times d}$, the output of the lth multi-head self-attention layer is computed as

$$\begin{gathered} \left[{\mathit{q}}^{lm},{\mathit{k}}^{lm},{\mathit{v}}^{lm}\right]=LN\left({\mathit{z}}^{l-1}\right){\mathit{U}}_{qkv}^{lm}, \\ {\mathit{A}}^{lm}=softmax\left({\mathit{q}}^{lm}{\mathit{k}}^{l{m}^T}\right), \\ {\mathit{z}}^{lm}={\mathit{A}}^{lm}{\mathit{v}}^{lm},m=1,2,\cdots ,M, \\ {\mathit{z}}_{att}^l=\left[{\mathit{z}}^{l1},{\mathit{z}}^{l2},\cdots ,{\mathit{z}}^{lM}\right]{\mathit{U}}_{msa}^l+{\mathit{z}}^{l-1},l=1,2,\cdots ,L, \end{gathered}$$ (2)

where the first three equations describe the operation of a specific self-attention head and the last equation represents the integration of multiple heads. Specifically, LN(·) denotes the layer norm function, ${\mathit{U}}_{qkv}^{lm}\in {\mathbb{R}}^{d\times 3d_m}$ represents a linear layer that maps each input embedding vector z^l−1 into three vectors, ${\mathit{q}}^{lm},{\mathit{k}}^{lm},{\mathit{v}}^{lm}\in {\mathbb{R}}^{N\times d_m}$, which are known as the query, key, and value vectors respectively, ${\mathit{A}}^{lm}\in {\mathbb{R}}^{N\times N}$ is the self-attention weight matrix computed as the inner product between query and key vectors followed by a softmax function. Then, the output, ${\mathit{z}}^{lm}\in {\mathbb{R}}^{N\times d_m}$, of each self-attention head is the weighted sum over all input embeddings to realize global attention. There are M self-attention heads running in parallel, with m being the head index, which jointly attend to information from different representation subspaces at different positions (Vaswani et al 2017). To avoid increasing the number of parameters, the vector dimension in each self-attention head is split to $d_m=d/M$. The output ${\mathit{z}}_{att}^l$ of the multi-head self-attention layer is the concatenation of all self-attention outputs transformed by a linear layer ${\mathit{U}}_{msa}^l\in {\mathbb{R}}^{d\times D}$ and increased by the signal from the residual connection. Then, this output is forwarded to the MLP layer for the final output of the lth block:

$${\mathit{z}}^l=MLP\left(LN\left({\mathit{z}}_{att}^l\right)\right)+{\mathit{z}}_{att}^l.$$ (3)

Thus, the final output of the transformer encoder is ${\mathit{z}}^L\in {\mathbb{R}}^{N\times d}$, which has the same dimension as the input embeddings.

Classification head:

The classification head is a linear layer that projects extracted features by the transformer encoder to classification scores. The classification head only takes the feature vector at the position of the [class] token and outputs a classification score as

$$\mathit{y}={\mathit{z}}_0^L{\mathit{U}}_{cls},$$ (4)

where ${\mathit{z}}_0^L\in {\mathbb{R}}^{1\times d},{\mathit{U}}_{cls}\in {\mathbb{R}}^{d\times C}$, and C is the number of classes.

2.2. Region-based contrastive learning

It is well known that the transformer is extremely data-hungry but labeled lung nodule data is relatively scarce. Hence, we propose a region-based contrastive learning method to pretrain the adapted transformer model by leveraging more unlabeled CT volumes. The popular constrastive learning framework is adopted in figure 2. It consists of two branches that take many pairs of similar samples and outputs the their features. Generally, this framework enforces similar samples to be closer to each other while dissimilar samples to be more distinct in the representation feature space as measured by the InfoNCE (Oord 1807) loss.

Figure 2.

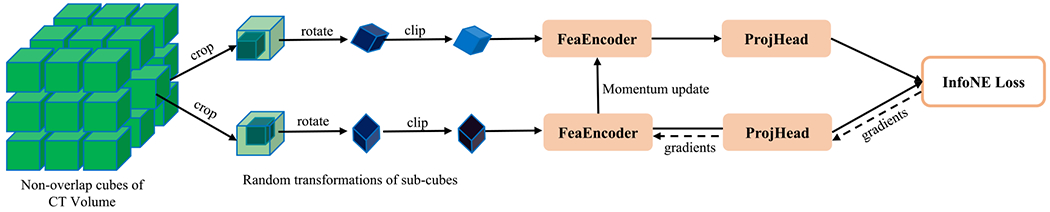
Region-based contrastive learning framework for lung nodule detection.

In the unsupervised context, how to properly define similar and dissimilar samples is the key component (Tian et al 2020). Although great progress was reported by introducing various random transformation techniques, it is still an open problem on how to keep useful information and compress noise and artifacts in representation features for downstream tasks. Actually, knowledge of specific downstream tasks plays an important role in defining appropriate similar samples (Tian et al 2020).

In our application, similar and dissimilar samples can be defined as follows. First, as we focus on classifying sub-volumes of a CT volume as lung nodule or not, we divide the whole CT volume into a set of non-overlap cubes and regard each as a unique instance. This assumes that every 3D sub-region in a patient is different from the others. Second, two sub-regions with a large intersection should be similar to each other. Third, although different organs/tissues are usually inspected under different HU windows, the same region under slightly different HU windows should be similar to each other. Fourth, two sub-regions different by a random rotation should be similar to each other as the angular information is not critical in detecting lung nodules.

Based on the above assumptions, we first divide a CT volume into a set of non-overlap S₁ × S₁ × S₁ cubes from all patient CT scans to build the whole training dataset, ${\left\{{\mathit{x}}_i\right\}}_{i=1}^I$, where I is the total number of cubes. During training, two sub-cubes of S₂ × S₂ × S₂ (S₂ < S₁) voxels are randomly cropped from a given cube and randomly rotated, and their HU values are randomly clipped, as shown in figure 2. In each training iteration, a set of B cubes are randomly selected, and then each cube is randomly transformed into two sub-cubes ${\mathit{x}}_i^{\text{'}},{\mathit{x}}_i^{"}$. Finally, the network parameters are optimized with the InfoNCE (Oord 1807) loss as follows:

$$ℒ=\frac{1}{2B}{\sum }_{i=1}^B\left(ℒ\left({\mathit{x}}_i^{\prime },{\mathit{x}}_i^{″}\right)+ℒ\left({\mathit{x}}_i^{″},{\mathit{x}}_i^{\prime }\right)\right),ℒ\left({\mathit{x}}_i^{\prime },{\mathit{x}}_i^{″}\right)=-\log \left(\frac{\exp \left(𝒫{\left(ℱ\left({\mathit{x}}_i^{\prime };{\mathit{\theta }}_{ℱ}\right);{\mathit{\theta }}_{𝒫}\right)}^T𝒫\left(ℱ\left({\mathit{x}}_i^{″};{\mathit{\theta }}_{ℱ}^m\right);{\mathit{\theta }}_{𝒫}^m\right)/\tau \right)}{{\sum }_{j=1,j\ne i}^I\exp \left(𝒫{\left(ℱ\left({\mathit{x}}_i^{\prime };{\mathit{\theta }}_{ℱ}\right);{\mathit{\theta }}_{𝒫}\right)}^T𝒫\left(ℱ\left({\mathit{x}}_j^{\prime \prime };{\mathit{\theta }}_{ℱ}^m\right);{\mathit{\theta }}_{𝒫}^m\right)/\tau \right)}\right),$$ (5)

where ℱ and 𝒫 represent the feature encoder and projection head functions with parameters θ_ℱ and θ_𝒫 to be optimized, ${\mathit{\theta }}_{ℱ}^m$ and ${\mathit{\theta }}_{𝒫}^m$ are the moving averaging versions of θ_ℱ and θ_𝒫 respectively, i.e. ${\mathit{\theta }}_{ℱ}^m\leftarrow \mu {\mathit{\theta }}_{ℱ}^m+(1-\mu ){\mathit{\theta }}_{ℱ}$ and ${\mathit{\theta }}_{𝒫}^m\leftarrow \mu {\mathit{\theta }}_{𝒫}^m+(1-\mu ){\mathit{\theta }}_{𝒫}$, which are updated in each iteration, here μ ∈ [0, 1) is a momentum coefficient, μ was to 0.99 the same as that in Chen et al (2021), and τ is a temperature parameter and was set to 1. Note that the feature encoder is exactly the transformer model without the classification head, and the projection head is the same as in MoCo v3 (Chen et al 2021). As defined in equation (5), the InfoNCE loss term $ℒ\left({\mathit{x}}_i^{\prime },{\mathit{x}}_i^{″}\right)$ maximizes the cosine similarity between features from two random transformations of the same cube (i.e. the ith cube) in the numerator while minimizing the cosine similarity between the ith cube and other cubes (i.e. ∀j≠i) in the denominator. Although the InfoNCE loss has a similar formulation to the commonly used softmax-based cross-entropy loss function in the supervised classification task, the difference is that it directly compares the features between different transformations of the same cube and the features between different cubes without using any annotations. The final loss ℒ is the average over a batch of B samples.

2.3. Implementation details

In our adapted transformer, the size of a candidate region was set to H = W = D = 72, the size of each non-overlap cube S = 8, the embedding dimension d = 384, the number of blocks L = 11, and the number of attention heads M = 12. In our region-based contrastive learning, the size of non-overlap sub-regions was set to S₁ = 96, and the size of each input cube S₂ = 72, the low and high HU values of the clip window were randomly sampled from [ −1200, −1000] and [600, 800] respectively. During unsupervised pre-training, the batch size was set to B = 1024, Adamw was used to optimize the model, the learning rate was 0.0001 with cosine annealing. At the fine-tuning stage, only the pretrained linear embedding layer and transformer encoder were kept, the projection head was removed, a randomly initialized classification head was added, the batch size was set to 64, and all other hyperparameters for training were kept the same as those in MoCo v3 (Chen et al 2021). To address the imbalance issue, we randomly sampled each training batch according to the predefined positive sampling ratio meaning that each batch approximately had a fixed ratio of positive to negative samples. By default, the positive sampling ratio was set to 0.2, and the effects of different sampling ratios on the performance were empirically evaluated in section 3.5.

3. Experimental design and results

3.1. Dataset and preprocessing

In this study, two evaluation settings were created to evaluate the effectiveness of the presented method. In the first evaluation setting, the lung nodules larger than 6 mm were selected from the LUNA16 (Setio et al 2017) dataset (a subset of the LIDC-IDRI (Armato et al 2011) dataset) as the Fleischner Society guidelines suggest that the nodule size threshold (diameter) for determining the need for follow-up has been increased to 6 mm (Sumikawa et al 2008, Callister et al 2015). Then, 436 patients containing 684 nodules were obtained, which were further randomly divided into a training set containing 349 patients and a testing set containing 87 patients. Here we assume that the candidate regions have been obtained. Specifically, the preprocessing process is as follows: (1) each CT volume was first bi-linearly interpolated along the longitudinal direction so that the longitudinal resolution is the same as the axial resolution; (2) the annotated nodules were center-cropped into the 96 × 96 × 96 positive regions; (3) 100 × 436 (100 from each patient) negative regions of 96 × 96 × 96 (not overlapping with any positive regions) were randomly cropped based on the candidate points provided in LUNA16 (Setio et al 2017). To test the generalizability of different methods, the testing set from another dataset LUNGx (Kirby et al 2016) was used to evaluate the performance of different models trained on the LIDC-IDRI dataset. The LUNGx testing set consists of 73 CT scans, each of them contains 1 or 2 positive nodules and 200 negative regions per scan, where the negative regions were randomly selected and other prepossessing steps are the same as those for LIDC-IDRI dataset. Some positive and negative samples are shown in figure 3, where it can be seen that the appearance of positive nodules maybe very different, and similar structures in the negative regions present strong interference. Also, these datasets are extremely unbalanced (#positive:#negative «1:100 and 1:200), making this task challenging. This evaluation setting was used in sections 3.3, 3.4, and 3.5.

Figure 3.

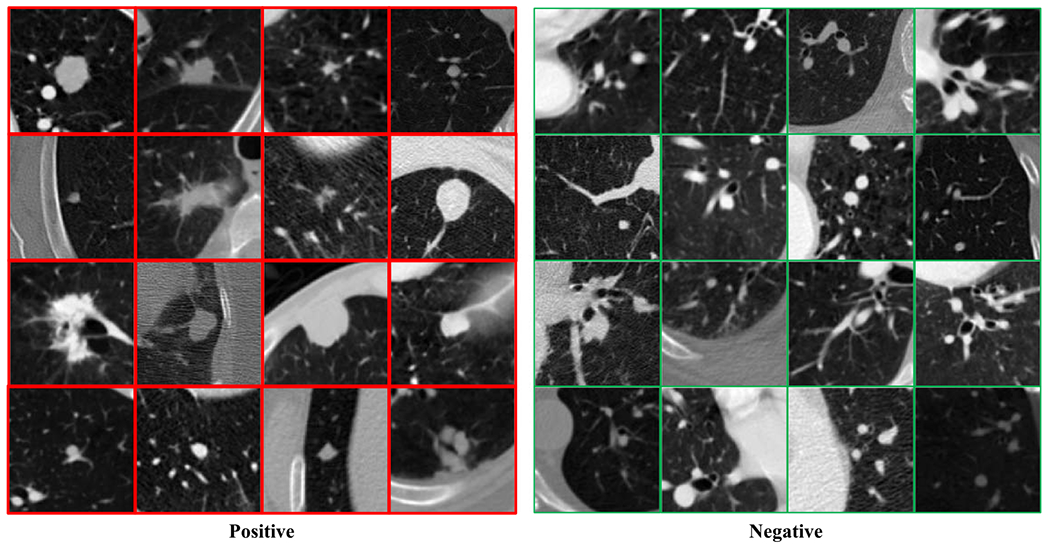
Samples in the lung nodule dataset. The red and green boxes are positive and negative samples respectively.

In the second evaluation setting, the full LUNA16 dataset was used to evaluate the presented method, where the testing set is the same as that in the first evaluation setting and the rest 801 CT volumes were used as the training set, and all nodules larger than 3 mm were selected as the positive nodules. In this setting, we implemented the popular Faster R-CNN Ren et al (2015) object detection method for detecting candidate nodule regions, and more details are described in section 3.6.

For region-based unsupervised contrastive learning, 84 875 non-overlap regions were collected from 801 CT volumes (excluding the testing set of 87 CT volumes in the above two settings) in the LUNA16 dataset. Specifically, each volume was first bi-linearly interpolated along the longitudinal direction so that the longitudinal resolution is the same as the axial resolution, and then split into a set of 96 × 96 × 96 cubes in a non-overlap manner, as illustrated in figure 2. For each dimension, if the size cannot be exactly divided by 96, the margins will be removed evenly.

Also, the nodule distributions are shown in figure 4 in terms of physical size and the number of pixels for the training and testing datasets in different settings. As the LUNGx dataset only provides the locations of nodules without information, the corresponding distribution is not known.

Figure 4.

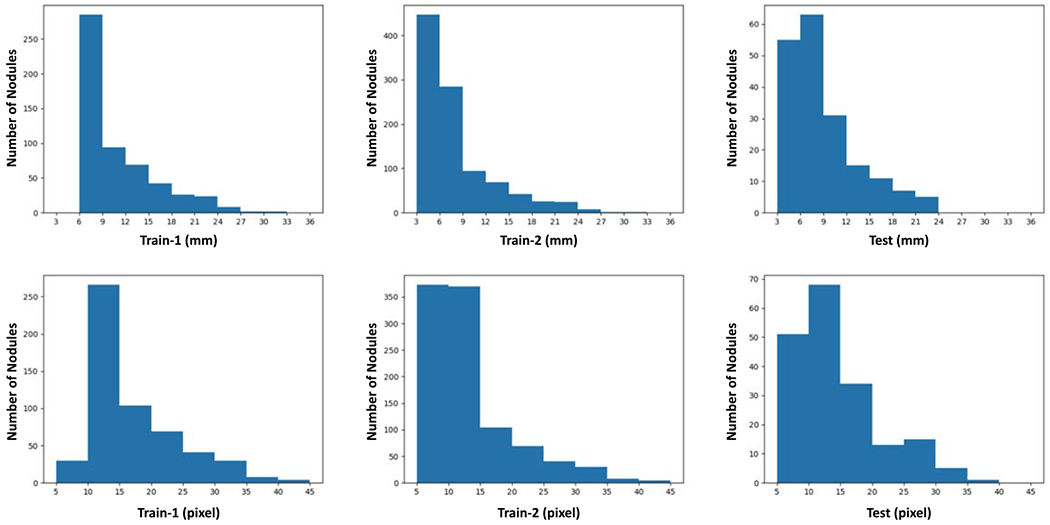
Long nodule distributions on different datasets. ‘Train-1’ and ‘Train-2’ show the nodule size distribution for the training datasets in the fist and second settings respectively, and ‘Test’ denotes the distributions on the test dataset in the fist and second settings. ‘mm’ and ‘pix’ represent the physical size and the number of pixels of nodule diameter respectively.

3.2. Evaluation metric

Due to imbalance of positive and negative samples in the evaluation dataset, the common free response receiver operating characteristic (FROC) curve and competition performance metric (CPM) were used to evaluate the model performance. Specifically, the true positive rate (TPR) and false positive rate (FPR) are defined as

$$\begin{gathered} \text{TPR =}\frac{\text{TP}}{\text{TP+FN}}, \\ \text{FPR =}\frac{\text{FP}}{\text{TN+FP}}, \end{gathered}$$ (6)

where TP, FN, TN, FP are the number of true positive, false negative, true negative, and false positive, respectively. Then, the average number of false positives per scan, FPS, is defined as

$$\text{FPS =}\frac{\text{FPR}\times \text{TN}}{\text{NS}},$$ (7)

where NS is the number of CT scans. The FROC curve is plotted as TPR v.s. FPS, which is a variant of the ROC curve, i.e. TPR v.s. FPR. The CPM score is defined as the average TPR (also called sensitivity) at the predefined FPS points: 0.125, 0.25, 0.5, 1, 2, 4, and 8 respectively.

3.3. Comparative analysis

In this sub-section, we evaluated the effectiveness of the proposed method relative to the following three baselines. First, we modified ResNet (He et al 2016) to the 3D version, named ResNet3D, as a strong baseline method. Second, the transformer model was trained from scratch, named ScratchTrans. To make sure that ScratchTrans be sufficiently trained, we doubled the number of training epochs and observed the essentially same results. Third, we initialized the transformer model with the weights of the pretrained DeiT on the labeled ImageNet dataset in a transfer learning manner, named the resultant network DeiTTrans. Finally, our proposed transformer model pretrained via unsupervised region-based contrastive learning is referred to as URCTrans.

The comparison results in terms of the sensitivity and CPM scores are summarized in table 1, and the FROC curves are plotted in Figure 5. These results show that the ResNet3D model is a very strong baseline with a 0.920 CPM score. The ScratchTrans achieved the worst results among these methods, which is consistent to the results in other domains showing that the transformer is extremely data-hungry and cannot perform well without a large-scale dataset. Through transfer learning, DeiTTrans significantly improved the performance of the transformer model and produced results similar to that obtained with ResNet3D. In contrast, our pretraining method without leveraging any labeled data offered the best performance among all comparison methods (0.950 CPM score, 3% higher than DeiTTrans and the commonly used ResNet3D). Further inspecting the sensitivities at different FPS points, it can be seen that the URCTrans model performed significantly better than the others when the average number of false positive nodules per scan is small (⩽1). That is the most desired result to effectively avoid falsely reported nodules. Clearly, our experimental results demonstrate that the transformer pretrained with more CT data through contrastive learning promises a performance superior to the commonly used 3D CNN models.

Table 1.

Quantitative results. The sensitivities at different FPS points and CPM scores were computed, with the best result highlighted in bold.

Methods	0.125	0.25	0.5	1	2	4	8	CPM
ResNet3D	0.773	0.879	0.924	0.947	0.955	0.977	0.985	0.920
ScratchTrans	0.561	0.659	0.712	0.765	0.788	0.841	0.909	0.748
DeiTTrans	0.803	0.879	0.902	0.932	0.962	0.977	0.985	0.920
URCTrans	0.902	0.917	0.955	0.962	0.962	0.977	0.977	0.950

Figure 5.

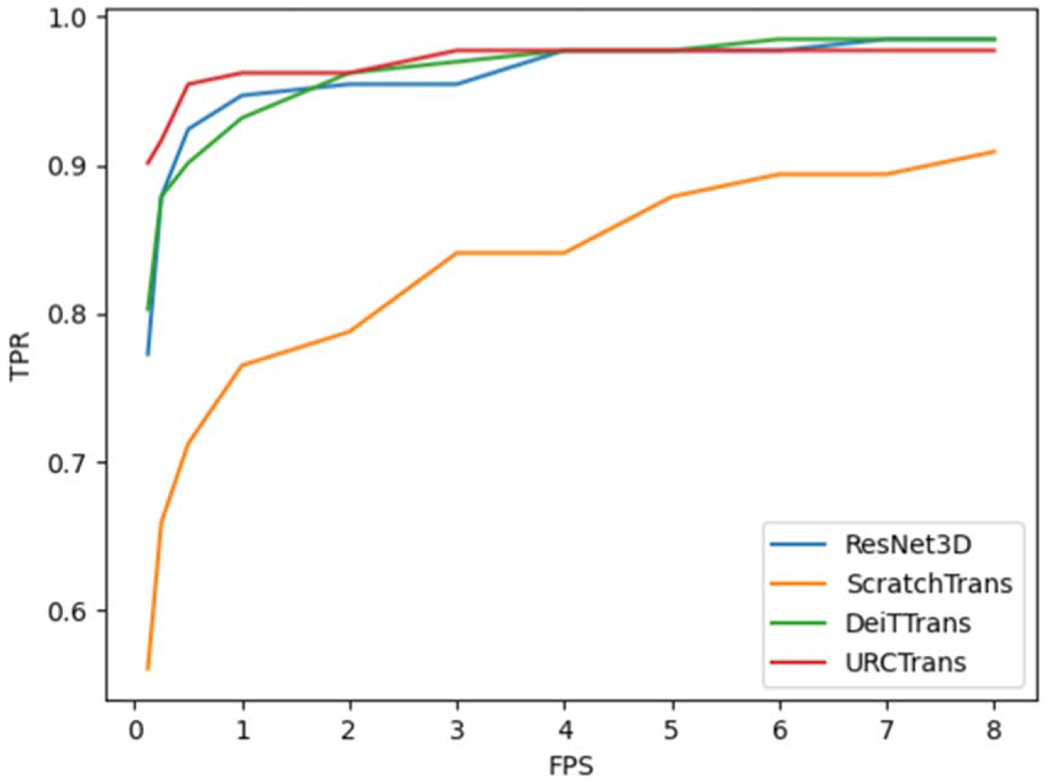
FROC curves for different methods.

The generalizability performance results on LUNGx are reported in table 2, where the models trained on LIDC-IDRI were directly evaluated. Although the relative performance of different methods is the same as above, the performance improvement of URCTrans is significantly increased in ccomparison with ResNet3D and DeiTTrans counterparts especially for the lower false positive number (⩽1). These results further demonstrated the superiority of the presented method in terms of the generalizability.

Table 2.

Generalizability performance results on LUNGx. The sensitivities at different FPS points and CPM scores were computed, with the best result highlighted in abold.

Methods	0.125	0.25	0.5	1	2	4	8	CPM
ResNet3D	0.712	0.767	0.808	0.890	0.918	0.959	0.973	0.861
ScratchTrans	0.630	0.685	0.740	0.863	0.863	0.904	0.932	0.802
DeiTTrans	0.781	0.822	0.877	0.890	0.904	0.904	0.904	0.869
URCTrans	0.822	0.849	0.918	0.945	0.959	0.959	0.959	0.916

3.4. Effects of the input size

As mentioned in Gu et al (2018), Cheng et al (2019), different sizes of an input tensor allow various levels of contextual information, leading to different performance metrics. Combining the results from multi-scale inputs would boost the performance further. In this sub-section, we investigate the effect of the input size on the performance of the transformer model for lung nodule detection. The results are in table 3, showing that the medium input size of 72 achieved the best result. It seems heuristic that there is a trade-off between the input size and the model performance, since a too large input may bring more interfering structures while a too small input may not contain enough contextual information to identify lung nodules. Nevertheless, these relatively similar results indicate that the transformer model is robust to the input size.

Table 3.

Quantitative results obtained by URCTrans with different input sizes. The best result is highlighted in bold.

Input size	0.125	0.25	0.5	1	2	4	8	CPM
64	0.826	0.879	0.917	0.947	0.962	0.977	0.985	0.926
72	0.902	0.917	0.955	0.962	0.962	0.977	0.977	0.950
80	0.916	0.916	0.932	0.939	0.962	0.977	0.977	0.946

3.5. Effects of the positive sampling ratio

In section 2.3, we applied a strategy that each batch of training samples was randomly sampled according to a predefined positive sampling ratio. Here we evaluated the effects of positive sampling ratios on the lung nodule detection performance of the transformer model. The results in table 4 show that when the positive sampling ratio was set to 0.2, the result is the best. Actually, the larger positive sampling ratio the more positive nodules the model tends to predict, as demonstrated in table 4. Nevertheless, it can be seen that the model is quite robust to this hyper-parameter as there is no big difference in performance.

Table 4.

Quantitative results obtained by URCTrans using different positive sampling ratios. The best result is highlighted in bold. The numbers of positive nodules predicted by the transformer model trained with different positive sampling ratios, where the input region is regarded as positive if the prediction score ≥ 0.5.

Positive ratio	0.125	0.25	0.5	1	2	4	8	CPM	#Predicted
0.1	0.795	0.841	0.894	0.924	0.933	0.947	0.969	0.900	158
0.2	0.826	0.879	0.917	0.947	0.962	0.977	0.985	0.926	217
0.3	0.765	0.856	0.917	0.932	0.969	0.977	0.985	0.915	247
0.4	0.788	0.841	0.879	0.917	0.962	0.962	0.962	0.902	369
0.5	0.795	0.841	0.909	0.947	0.947	0.970	0.970	0.911	409

3.6. Effectiveness on faster R-CNN candidates

In this section, we evaluated the effectiveness of the presented method on processing the nodule candidates detected by the Faster R-CNN model. Specifically, we adapted the plain Faster R-CNN model for the lung nodule detection task based on the Detetron2¹ platform. In our implementation, the fourth CNN layer of the ResNet-50 backbone was used as the detection features, the anchor sizes were set to 8, 18, 32, 64, 128, the input size is 3 × 512 × 512, here 512 × 512 is the original dimension of CT slices and 3 means three adjacent slices were used as the input, and the HU window was set to [−1200, 600]. During training, the total number of training iterations was set to 90 000, and all other hyper-parameters were the default values in Detectron2. In the inference stage, each and every slice (along with its two adjacent slices) of a patient CT volume is forwarded to the trained Faster R-CNN model to output 2D candidate regions on slices. Then, all candidate 2D regions were merged to the 3D candidates according to the principle that if two 2D candidates are on two adjacent slices and their intersection-over-union (IoU) is larger than 0.5, then these two candidates belong to the same 3D candidate, and the score of the merged 3D candidate is the mean score of its 2D candidates. Next, top 100 candidates (including both the merged 3D and isolated 2D candidates) were preserved according to the predicted score. Finally, the center of each selected region is regarded as the location of a nodule candidate, and a 72 × 72 × 72 candidate region was center-cropped at the predicted location.

Given the candidate regions detected by the Faster R-CNN model, the true positive and false positive regions can be identified by comparing with the annotations, where the IoU between the predicted and annotated regions is larger than 0.1 is regarded as the true positive and otherwise as the negative. Then, the same process introduced in section 3.1 was used to train and evaluate the presented and the competing models. The results of different methods on Faster R-CNN candidates are shown in figure 6. It can be seen that the presented URCTrans can effectively improve the detection performance of the Faster R-CNN detection results and consistently outperforms the 3D CNN baseline. Also, if the ViT model is not appropriately pretrained, its performance is even worse than that of the 3D CNN.

Figure 6.

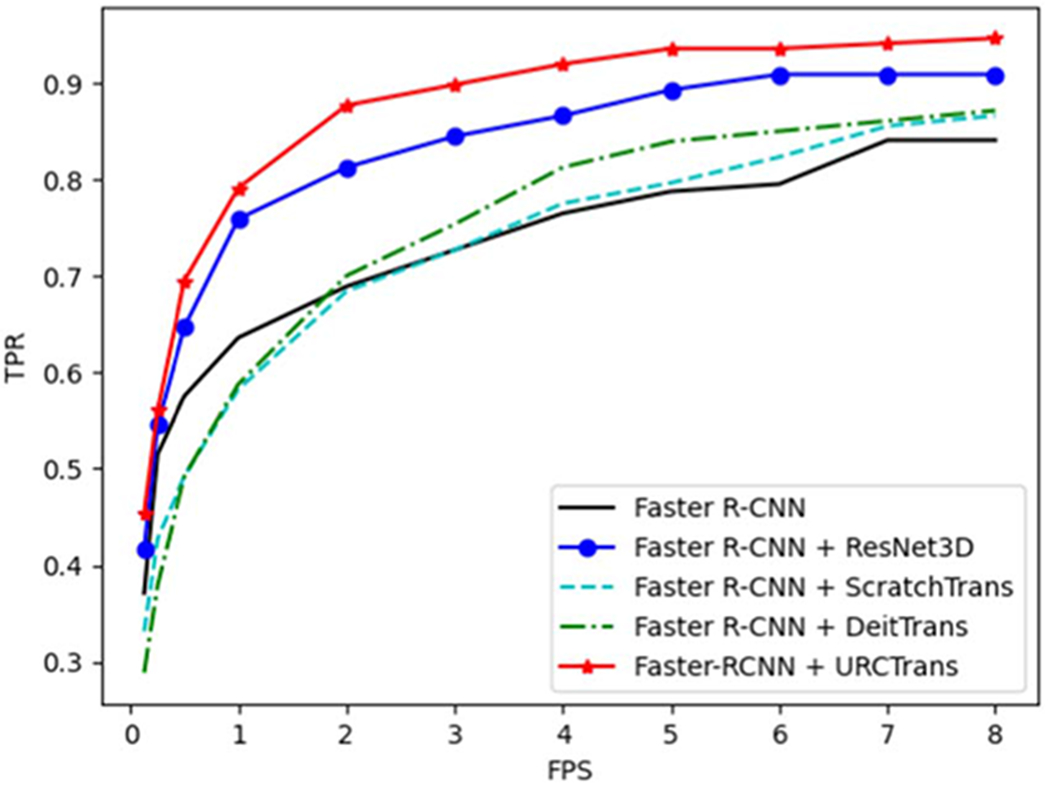
FROC curves for different methods on Faster R-CNN candidates.

4. Discussions and conclusion

In this study, we have adapted the ViT model and unsupervised contrastive learning for lung nodule detection from a CT volume. Using neither multi-scale inputs nor assembling techniques, our presented transformer model pretrained in an unsupervised manner has outperformed the state-of-the-art 3D CNN models. Importantly, we have found that unsupervised representation learning or pretraining on a large-scale dataset can significantly benefit the transformer model, which is scalable, and highly desirable especially when labeled data are scarce.

However, it is worth mentioning the limitations of this study. First, we only applied ViT with unsupervised pretraining to the false positive reduction stage for lung nodule detection, and its effectiveness could be further studied in the nodule candidate detection stage. Second, the number of CT volumes used for pretraining can be scaled up, and the performance with respect to different numbers of pretraining volumes could be studied in the future.

Nevertheless, our pilot results suggest that for the medical analysis tasks where labeled data are expensive and limited, it is very promising to build a large-scale model, pre-trains it on a related big dataset via domain-knowledge driven self-supervised, and transfers the learned large-scale prior to benefit down-stream tasks. Although this study was only focused on CT image representation learning, combining specific imaging modality data with other modalities, such as diagnostic text reports, clinical data, other imaging approaches, etc, has the potential to unleash strong power of AI for diagnosis and treatment.

In conclusion, we have presented an adapted 3D ViT model pretrained via region-based contrastive learning for lung nodule detection. Specifically, we have introduced how to adapt the generic transformer model for lung nodule detection. To make the transformer model work well on a relatively small labeled dataset, we have introduced a self-learning method leveraging public CT data. The comparative results have demonstrated the superiority of the presented approach over the state of the art 3D CNN baselines. These findings suggest a promising direction to improve CAD systems via deep learning.