Multiple Conductance States of Lipid Pores during Voltage-Clamp Electroporation

Abstract

We used voltage-clamp electroporation to obtain single-channel recordings of lipid pores and analyzed the idealized dwell-time sequences using Maximum-Likelihood Fitting. We observed traces with multiple current levels and determined whether they were a result of the presence of multiple pores or a single pore with multiple conductance states. We found that, within the same recording, the bilayer can have a single pore with multiple conductance states or multiple independent pores. Using high sampling rates (100 kHz) we were able to observe pores with 40 μs lifetimes, and in experiments using high-voltage pulses we observed the existence of long-lived fluctuations minutes after the removal of the electric field. These results come closer to reconciling the nanosecond lifetime pores in molecular dynamics simulations and the long-lived permeability of cells after electroporation.

1. Introduction

In this work, we investigate single channel recordings of planar lipid bilayers obtained during voltage-clamp electroporation. Electroporation refers to the creation of pores in lipid membranes in response to an applied electric field. These pores have been referred to as electropores, but since they can be induced by other variables such as temperature, pressure, and pH (1), we will refer to them by the more general term, lipid pores.

Previously, we showed that current-clamp conditions do not necessarily result in the creation of a single pore (2). It has been suggested that the presence of individual pores can be inferred during voltage-clamp conditions due to the abrupt transitions between conductance levels (3). Imaging of electropores during voltage-clamp electroporation confirmed the presence of a single pore at low voltages (4). At higher voltages, multiple conductance levels are usually observed, and it is typically assumed that the presence of multiple conductance levels in a recording must be due to the presence of multiple pores (3, 5–7). Laub suggested that some recordings clearly indicate the presence of subconductance states of the same pore (8). However, in many cases, it becomes difficult to discriminate between multiple pores and multiple conductance states, and it is necessary to use statistical methods. This problem has previously been addressed by counting the number of transitions between different conductance levels and using a corresponding Chi-Squared test (9). Here, we use a Maximum-Likelihood method to determine if our recordings reflect the presence of multiple pores or a single pore adopting multiple conductance states.

In addition, by using high sampling rates (100 kHz), we identified pores with lifetimes < 50 μs. We also report the existence of long-lived current fluctuations induced by short, high voltage pulses. These observations bring planar lipid bilayer experiments closer to the 100 ns timescale pores observed in molecular dynamics simulations, and the long-lived permeability of cells following electroporation.

2. Materials and Methods

2.1. Experimental Methods

A Nanopore Reader and BLMchip Flowcells were obtained from Elements SRL (Cesena, Italy). DPhPC lipids (1,2-diphytanyol-sn-glycero-3-phosphocoline) were purchased from Avanti Polar Lipids (Birmingham, AL). Chloroform was evaporated from the lipid stock solutions with a steady stream of nitrogen gas. Lipids were resuspended in n-decane for a final concentration of 10 mg/mL. Unless specifically mentioned, the electrolyte solution used consisted of 1 M KCl, 5mM HEPES, buffered at pH 7.0.

Bilayers were painted using the lipid-covered air bubble method (10). Briefly, using a p20 pipette, a micropipette tip is dipped in the lipid solution. Excess lipids are removed by dabbing the tip on a Kimwipe. The pipette tip is immersed in the electrolyte solution and brought in the vicinity of the BLMchip hole. By pressing down on the pipette plunger, air is pushed out of the pipette tip to form a lipid-covered air bubble, which is used to paint the bilayer. Bilayer thinning is monitored by the increase in capacitance. A schematic of the experimental setup is shown in Figure 1.

Figure 1:

Horizontal planar lipid bilayer schematic diagram with hypothetical pore strucutre

2.2. Analytical Methods

The data was exported from the Elements Data Analyzer software (version 1.4.6) into MATLAB (version R2021B) for analysis. A current recording was idealized by first manually determining the number and amplitudes of conductance levels by inspecting the all-points amplitude histogram. Next, abrupt changes in the signal, known as changepoints, were detected using the findchangepts() function in MATLAB. The average conductance value for each interval between two adjacent changepoints was computed, and intervals were assigned to conductance levels closest to their respective averages. The idealized record was then reorganized into a dwell time sequence. A fixed dead time of 150 μs was imposed on the dwell time sequence by combining each dwell time which was shorter than the dead time with the preceding dwell time.

3. Results

The Markov models considered in this work are shown in Figure 2. In all models shown, C₁, O₁, and O₂ correspond to the three different conductance levels, and O₁ + O₁ = O₂. The general two pore model consists of two independent pores with different rate constants. The combined two-pore model is equivalent to the general two-pore model, but simply combined into one Markov chain instead of two. The lumped two-pore model is a special case where the two pores have identical rate constants. The multi-conductance model consists of a single pore which can adopt multiple conductance states. The rate constants (k₁, k₂, k₃, k₄) refer to the same numerical values within the set of two-pore models, but correspond to different values in the multi-conductance model. The corresponding Q-matrix for each model is determined by the rate constants, and likelihood functions are computed as described elsewhere (11). A first-order approximation was used to correct for missed events (12). Maximum-Likelihood fitting of the dwell time sequences was accomplished by maximizing the likelihood function and was implemented using the fmincon() function in MATLAB.

Figure 2:

Markov Models. The Two-Pore Model is equivalent to the Combined Two-Pore Model. The Lumped Two-Pore Model is a special case where k₁ = k₃ and k₂ = k₄.

Notice that the lumped two-pore model is nested in the multi-conductance model. In particular, the multi-conductance model reduces to the lumped two-pore model when k₁ = 2k₃ and k₄ = 2k₂. As a result, the likelihood-ratio test was used for model selection (13). Meanwhile, the combined two-pore model is not nested in the multi-conductance model, so an alternative Monte-Carlo approach was used for model selection (14). Functions simCTMC.m and simCTMC_t.m from the MATLAB file exchange were used for simulations (15).

For the Maximum-Likelihood analysis, we used two excerpts from the same recording sampled at 20 kHz. We will refer to these excerpts as excerpt ‘A’ and excerpt ‘B’. Excerpt A was 48 s in length and consisted of 937 dwell times while excerpt B was 27 s in length and consisted of 573 dwell times. Both excerpts were recorded at 350 mV. The BLM chip hole was 200 μm in diameter. The Capacitance and Resistance were approximately 200 pF and 0.1 GΩ respectively. In excerpt A, we had to omit a brief 307 ms fragment because it was too difficult to idealize, and a brief 81 ms fragment because of an external disturbance or noise.

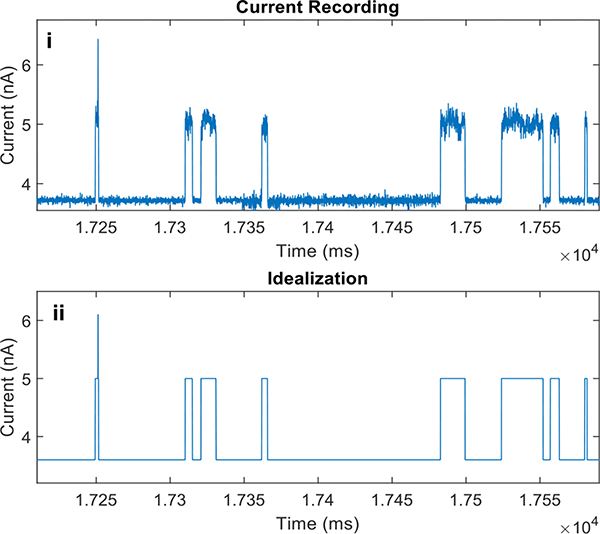
Portions of the current recordings and their respective idealizations are shown in Figures 3 and 4. Excerpt A was characterized by “bursting” behavior between level O₁ and level O₂ while Excerpt B was characterized by rare double openings, but almost double the density of single openings. The existence of bursts was previously used to justify the existence of more than one closed state (3). In the case of excerpt A, the bursts suggest the existence of more than one open state. To confirm our suspicion, we proceeded with the Maximum-Likelihood analysis.

Figure 3:

Representative trace from excerpt A. (i) Original recording. (ii) Idealization. (iii) Zoomed in version. (D) Idealization.

Figure 4:

Representative trace from excerpt B. (i) Original recording. (ii) Idealization.

The Maximum-Likelihood parameter values and corresponding log-likelihood values for the two-pore model and the multi-conductance model are shown in Table I. The log-likelihood ratio is ΔLL = LL₂ − LL₁ = 703.8. Notice that the maximum likelihood parameter values for the two-pore model converged to the case k₁ = k₃ and k₂ = k₄. This corresponds to the lumped two-pore model. Taking advantage of the fact that the lumped two-pore model is nested in the multi-conductance model, we were able to use the likelihood-ratio test for model selection. The likelihood-ratio test states that 2ΔLL is ${\chi }_k^2$ distributed with degrees of freedom k equal to the difference in number of free parameters between the two models (14, 16, 17).

Table I:

(Excerpt A) Maximum Likelihood parameter estimates and corresponding Log-Likelihood Values for the Two-Pore Model and the Multi-Conductance Model

	Two-Pore	Multi-Conductance
k1	5.4744 s−1	6.1173 s−1
k2	158.0670 s−1	245.1418 s−1
k3	5.4744 s−1	210.6290 s−1
k4	158.0670 s−1	232.0310 s−1
LL	2193.3	2897.1

We confirmed that 2ΔLL follows a ${\chi }_2^2$ by doing extensive simulations under the lumped model and computing the corresponding log-likelihood ratios (Supplementary Figure 1). We conclude that the multi-conductance model is the correct model (2ΔLL = 1407.6, P < 3 × 10⁻³⁰⁶). The Dwell-Time histograms and corresponding maximum-likelihood probability density functions are shown in Figure 5.

Figure 5:

Dwell-Time Histograms and maximum-likelihood probability density functions (pdf) for excerpt A.

Next, we investigated excerpt B. After idealization and imposing the dead time, there were only 13 dwell times in level O₂. It should be emphasized that the start of excerpt B is only 13 seconds after the end of excerpt A and under identical recording conditions. The Maximum-Likelihood parameter values and corresponding log-likelihood values for the two-pore model and the multi-conductance model are shown in Table II. The log-likelihood ratio is ΔLL = LL₂ − LL₁ = −12.8385. This time the general two-pore model did not reduce to the lumped two-pore model, and since the models are not nested, we were unable to use the likelihood-ratio test. Instead, we calculated the empirical distributions of ΔLL under each model by doing extensive simulations. This approach is similar to ones described previously (14, 16).

Table II:

(Excerpt B) Maximum Likelihood parameter estimates and corresponding Log-Likelihood Values for the Two-Pore Model and the Multi-Conductance Model

	Two-Pore	Multi-Conductance
k1	4.5388 s−1	11.4195 s−1
k2	603.4175 s−1	189.2130 s−1
k3	7.1779 s−1	5.9177 s−1
k4	135.9515 s−1	1819.1 s−1
L	1584.3	1571.4

As shown in Figure 6, the ΔLL of the data is not compatible with the multi-conductance model (P < 0.001), but is compatible with the two-pore model. The Dwell-Time histograms and corresponding maximum-likelihood probability density functions are shown in Figure 7.

Figure 6:

Distributions of ΔLL under the two-pore model and multi-conductance model using parameter values from Table II. Solid line indicates the value of ΔLL calculated from the experimental data. 1000 simulations were performed for each model.

Figure 7:

Dwell-Time Histograms and maximum-likelihood probability density functions (pdf) for excerpt

Lastly, we demonstrate the existence of short-lived pores (< 50 μs), and the existence of a long-lived current fluctuations minutes after the removal of the electric field in Figures 8 and 9 respectively. For the experiments in Figures 8 and 9, 3M KCl was used. The long-lived current fluctuations were observed in experiments with short (2 ms) high-voltage pulses (500–600 mV), after which the bilayer entered a state of high conductance (<1 GΩ). A low voltage (50 mV) test pulse was used to measure the current fluctuations to rule out the possibility of creating new pores with the test pulse.

Figure 8:

(Top) Fragment from recording at 100 kHz. (Bottom) zoomed in version

Figure 9:

(i) Current Fluctuations induced by high voltage pulses (ii) Fluctuations persist after over 3 minutes after last pulse (iii) Voltage protocol corresponding to panel i (600 mV, 2 ms pulses) (iv) Voltage protocol corresponding to panel ii (50 mV test pulse)

4. Discussion

It is typically assumed that the presence of multiple conductance levels in a current recording must be due to the presence of multiple pores (3, 5–7).This interpretation follows from the theoretical pore-energy landscape which has only one metastable conducting state (2). Here, we show that within the same current recording, it can appear as though a single pore has multiple conductance states (excerpt A), or the current recording may reflect the presence of multiple independent pores (excerpt B). It should be noted that a single pore with multiple conductance states will be kinetically indistinguishable from multiple pores which are strongly coupled (18). One feature of electroporation is that pores can exist anywhere on the membrane and are able to diffuse in different directions (4). One can imagine if two pores are close to each other on the membrane, their kinetics may be coupled. On the other hand, if the pores diffuse in different directions along the membrane, they will become uncoupled and behave independently.

In the past, it has been suggested that lipid pores obey fractal kinetics instead of Markov kinetics, but it was noted that for lifetimes up to 100 ms, the single pore dwell-time histograms can be well fit with double-exponential functions (5). Interestingly, the probability distribution function (pdf) of a two-pore Markov model is a double-exponential function. For the current recordings analyzed here, we were able to achieve a good fit of the dwell-time histograms with the appropriate Markov models. However, we only observed lifetimes < 50 ms. It is possible that the fractal kinetics only become obvious at longer lifetimes.

The average conductance of the pores in Figure 3 and 4 was about G = 4 nS. Taking the conductivity of 1M KCl to be 10.9 S/m (19), and using a cylindrical pore model, we find that the average pore radius is around 0.86 nm. The toroidal pore model gives a pore radius of 0.99 nm. These estimates are close to values previously reported (3, 6, 20).

Finally, we showed the existence of short-lived pores (< 50 μs) using higher sampling rates (100 kHz). This brings planar lipid bilayer experiments closer to results from molecular dynamics simulations, which report lifetimes on the order of 100 ns after the electric field is removed (21). The 40 μs lifetime in Figure 8 is measured without removing the electric field. Due to the membrane’s capacitive response, we cannot measure pore lifetimes immediately after removing the electric field. In addition, we report the existence of long-lived fluctuations minutes after the removal of the electric field. This typically occurred when we exposed the membrane to short, high-voltage pulses similar to the ones used in electroporation protocols. This observation indicates the presence of long-lived conductive pores and brings planar lipid bilayer experiments closer to the long-lived permeability observed in cells (21). It was previously suggested that hydrophobic pores may be responsible for the background current of membranes (22). The fact that the long-lived conductance fluctuations we observed were also associated with a state of high conductance suggests a connection between the background conductance and electroporation. However, in other experiments, bilayers with high conductance (<1 GΩ) did not exhibit current fluctuations.

Discrete conduction events similar to the ones we have observed here have reported in rubber membranes, and it was suggested that the conduction pathway was through the seal region rather than through the membrane (23). However, simultaneous electrical and optical single channel recordings have shown that the conduction pathway for voltage-clamp electroporation of lipid bilayers is through the membrane (4). Current recordings have the advantage of high temporal resolution but suffer from a lack of spatial resolution. Future work combining current recordings and optical single channel recordings (4) is needed to better understand the spatiotemporal dynamics of electroporation.

Key Points:

• Individual pores are observed in voltage-clamp electroporation

• Lipid pores can be coupled or adopt multiple conductance states

• Long-lived conductive pores are observed in planar lipid bilayers