Abstract
Statistical shape modelling (SSM) is an emerging tool for risk assessment of thoracic aortic aneurysm. However, the head branches of the aortic arch are often excluded in SSM. We introduced an SSM strategy based on principal component analysis that accounts for aortic branches and applied it to a set of patient scans. Computational fluid dynamics were performed on the reconstructed geometries to identify the extent to which branch model accuracy affects the calculated wall shear stress (WSS) and pressure. Surface-averaged and location-specific values of pressure did not change significantly, but local WSS error was high near branches when inaccurately modelled.
Keywords: Thoracic Aorta, Statistical Shape Modelling, Computational Fluid Dynamics
Introduction
Aneurysms are characterized by dilation of a segment of an artery, leading to risk of further inflation, delamination, or rupture. They can develop in various locations, including the thoracic aorta, abdominal aorta, and cerebral vessels. The focus of this study is thoracic aortic aneurysm (TAA) with particular attention to the aortic arch. Though the expansion of the vessel in itself is largely asymptomatic, a rupture or dissection of the affected region is a highly lethal cardiothoracic emergency with a post-operative mortality rate of up to 25% (Harky et al. 2019). The diagnosis and treatment of TAAs remains challenging. It is estimated that only 5% of TAAs are symptomatic prior to rupture or dissection, and even within symptomatic cases, more than half of them are not diagnosed until a post-mortem examination is performed (Elefteriades et al. 2015).
Of particular interest are methods that use computational fluid-structure interaction models to assess the mechanical state of the aneurysm and aorta and predict rupture or dissection. Such approaches have been applied to human data (Leo et al. 2019) and mouse models (Bazzi et al. 2022, Trachet et al. 2015), and inverse methods based on biofluid and solid mechanics have been used to assess aortic wall stiffness (Bertoglio et al. 2012, Farzaneh et al. 2019). There is also potential for combining patient-specific geometry with fluid-structure interaction simulations to gain mechanical insight from pulse wave velocity measurements (Shahmirzadi and Konofagou 2014). However, the computational demand of such simulations is high, and there is a relative lack of large datasets that could be used to fitting/training and testing a correlative model, these challenges have led to considerable interest for reduced-simulation representation of the aorta and the potential to generate synthetic aortic geometry (Romero et al. 2019). For such problems, statistical shape models (SSMs) are particularly attractive.
SSMs capture and describe the geometry of semantically similar objects and have become increasingly popular in biomedical research by virtue of their ability to recover intuitive variations in morphological features. TAAs have been studied under the SSM framework (Bruse et al. 2017, Catalano et al. 2021, Liang et al. 2017), demonstrating its potential to correlate geometric features with clinically relevant metrics such as rupture risk (Cosentino et al. 2020). These SSMs, however, considered only the ascending and descending portion of the thoracic aorta and removed the branching head vessels of the aortic arch: the brachiocephalic artery (BCA), left subclavian artery (LSA), and left common coronary artery (LCCA).
The presence of these branches could affect the blood flow profile close to the branches, introducing regions of recirculation, and skewing the peak velocity towards the branch junction (Chen and Lu 2004). These recirculation regions could generate low wall shear stress and create a propensity to develop atherosclerotic lesions in the ascending aorta (Endo et al. 2014). Subjects with abnormal branching variants of the aortic arch were also found to have increased risk of developing thoracic aortic disease (McMurry et al. 2015), including type B aortic dissection (Shalhub et al. 2018). Moreover, total removal of head branches in a flow study on aortic dissection subjects could significantly reduce the downstream wall shear stress values (Jiang et al. 2019).Given the possibility that these branches play a significant role in the mechanics experienced by the aorta, the inclusion of the branches into the SSM is highly desirable.
In this work, we developed an SSM scheme that allows inclusion of the branch vessel locations in the shape function, and we tested the approach on a set of patient scans. The geometrical accuracy of the reconstructed SSM was quantified, and changes in the flow dynamics within the reconstructed aorta were examined using computational fluid dynamic (CFD) simulations. Of particular interest is the extent to which these branches have to be modelled accurately and the effect of misrepresentation of the branches on the flow dynamics in the aorta. The capability of the proposed model to generate synthetic data from the shape basis were also demonstrated.
Methods
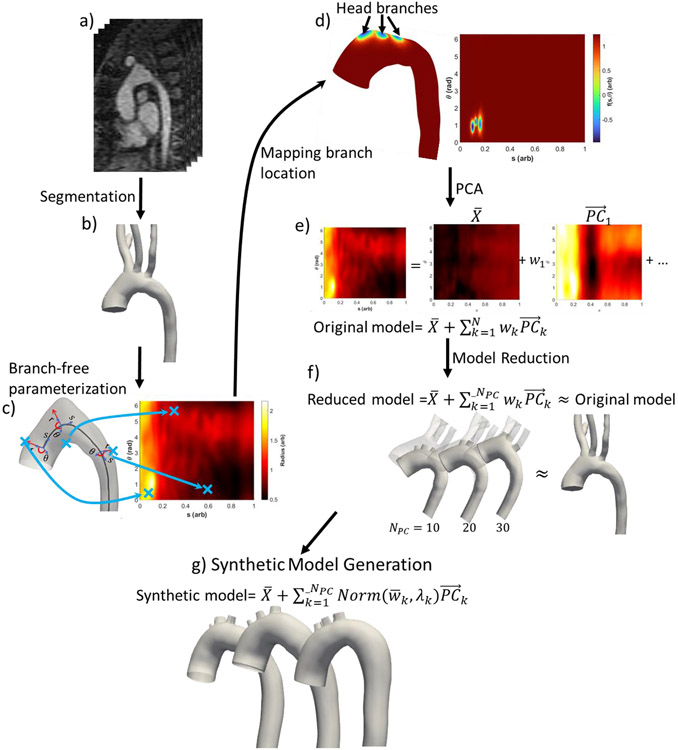
We extended the standard SSM framework (Liang, Liu, Martin, Elefteriades and Sun 2017) to permit incorporation of the location of the head vessels into the shape descriptor. A general SSM framework is described as follows, with the new branch modelling step marked in italics (Figure 1):
Figure 1.
Methodology for Branch-Including Statistical Shape Model of the Aorta. (a) CT scan of the aorta. (b) Segmented geometric model. (c) Centerline/cylindrical parameterization of branch-free model. Points near the proximal end of the aorta (small s) have larger r(s, θ) values because of vessel taper. (d) Branch boundary signed distance function f(θ,s). (e) Principal component analysis decomposition of the shape function. (f) Reduced-dimension shape representation. (g) Synthetic aortic models generated by random combinations of the principal components.
Geometry extraction: 3D, patient-specific geometry is extracted from segmented medical image data.
Aorta parameterization: The aorta is parameterized onto a periodic rectangular parametric domain defined by the longitudinal and circumferential axes.
Branch modelling: The location of branches on the aorta is described using a levelset of geodesic distance of branch boundary, as defined over the parameterization space.
Principal component analysis: Principal component analysis (PCA) is used to extract the dominant shape modes from the remeshed geometries.
Artificial geometry generation: New geometries can be artificially generated using the SSM.
Each of these steps is detailed below, followed by a description of computational fluid dynamics (CFD) studies done to evaluate the SSM performance.
Geometry Extraction
A total of 33 patient datasets were obtained. Aortic models of 24 patient models were obtained from the the publicly available Vascular Model Repository (Wilson et al. 2013). The rest were obtained from MRI of subjects with Marfan syndrome, provided from Washington University in St. Louis. Detailed patient descriptions are available from the repository, and a summary is given in supplementary material 1. Five additional aortas, obtained from (Radl et al. 2022), were not used for principal component generation but were reconstructed to benchmark the fit of reconstructed geometry on general population.
The aortic geometries were segmented and extracted from 3D medical images (Figure 1a-b), using Simvascular (Updegrove et al. 2017) to generate meshes of the thoracic aorta, including the aortic root, the head branches, and descending thoracic aorta. The head branches were truncated with a plane tangent to the surface of the aortic arch in MeshMixer (Autodesk 2018), offset by a few centimeters in the downstream direction of the branch. This truncation created branchless aortas to be used for parameterization.
Aorta Parameterization
Once the branchless aortic geometry had been defined, its centerline was extracted using VMTK (Izzo et al. 2018). This centerline did not span the full aorta and was slightly truncated at the two ends. The parametric domain was defined by a cylindrical coordinate system, as described by the vessel radius (r), polar angle (θ ∈ [0,2π)), and normalized length along the centerline (s ∈ [0,1]) from the aortic root (s = 0) to the distal end of the model (s = 1). The longitudinal axis of the cylinder was defined as the tangent to the centerline, while the polar axes are found on the plane perpendicular to the longitudinal axis. Injectivity of the parameterization is ensured by checking the maximum radius of the cylinder, which must be less than the radius of the osculating sphere of the centerline . When this condition was not met, the centerline was smoothed by moving average on its curvature. The surface of aorta was then described by the distribution of vessel radius on the (θ, s) plane (Figure 1c). Likewise, any surface-quantifiable values can be described in the shared parametric space of (θ, s).
Before geometrical comparison could be made, the geometry had to be scaled and aligned. The meshes were scaled isotropically by the same scale as was used to normalize the centerline length to [0,1]. Once scaled, the meshes were rigidly transformed to be aligned based on generalized Procrustes analysis (Goodall 1991).
Branch Modelling
The presence of a branch in generates additional holes on the geometry. However, the presence of additional holes violates the cylinder homeomorphicity constraint of the vessel. Instead, we define the presence of a branch by an area on the aorta that is bounded by a closed curve in (θ, s) space. This curve marks the location of these holes, which would be excised at the end of the branch modelling step. First, the intersection of original geometry with a truncating plane for each branch was used to generate the coordinates of the bounding curve, which was mapped onto the aortic surface by parameterization onto the (θ, s) space. Once the coordinates on the bounding curve had been obtained in (θ, s) space, the curve that passed through these points was defined implicitly as the level set of a function in the (θ, s) domain.
The function chosen is based on logistic mapping of a signed geodesic distance function (SGDF) in (θ, s) domain. The SGDF returns the minimum geodesic distance (G) from a given point x to the closed boundary (∂Ω), where the sign is determined by whether the point lies on the interior (ΩI) or exterior (ΩE) of the boundary. If the point is inside the boundary, the distance is assigned as negative, otherwise it is assigned as positive. The SGDF (Gsigned) in the (θ, s) is thus:
| (1) |
For a point with physical coordinate x, the function G(x, ∂Ω) returns the shortest geodesic distance from x to a point on the boundary ∂Ω. G(x, ∂Ω) was computed on the triangular STL mesh using an extension of Dijkstra's algorithm (Dijkstra 1959) as implemented in Matlab (Kirsanof 2021).
The Gsigned distribution is not evenly weighted between interior (ΩI) and exterior (ΩE) points, since the vast majority of the aortic surface is outside of the branch boundaries (i.e. in the positive Gsigned space), resulting in a much larger range of positive Gsigned values than of negative ones. The resulting PCA bases would inevitably skew towards accommodating the high positive Gsigned, but they would not carry much information: any points far enough distance from the boundary would decidedly lie in ΩE. Therefore, the magnitude of the Gsigned values was capped via a logistic function (f(θ, s)), given as:
| (2) |
where k = ∣min(Gsigned)∣ is the magnitude of the largest negative SGDF across all cases. f(θ, s) symmetrically caps the magnitude of positive and negative SGDF, with the −3dB cutoff at 0.6k. The boundary of the branches can then be described as the curve that is implicitly defined on (θ, s) at f(θ, s) = L, where L is the level set. A plot of f vs. s and θ is given in Figure 1d.
In the original geometry, the value of L is trivial as the branch boundary is at geodesic distance of zero (∴ L = 0). However, when reconstructing the aorta via PCA, some information is lost, particularly the steep gradient that delineates the branch boundary. With fewer principal components (small NPC), the reconstructed f(θ, s) may not cross L = 0, but the minima in f(θ, s) that should define δΩ is still present. Therefore, the value of L is dynamically changed by an auto-thresholding algorithm (Ridler and Calvard 1978) on points with f(θ, s) < (0.5 × ∣min(Gsigned)∣). Once the location of a branch was determined, the branch was extruded in the direction of the mean surface normal of the points found in the branch lumen (ΩI). Fourier smoothing was performed on δΩ to obtain a more circular outlet area and simplify the meshing.
Principal Component Analysis (PCA)
PCA (Pearson 1901) is a fundamental dimension reduction technique. Specifically, it builds a hierarchical coordinate system that captures the most dominant statistical variations seen in a data set. The steps involved in PCA are described below within the context of SSM for TAAs.
First a shape descriptor matrix M of size N × (3Ns + 2NθNs) was constructed, where N is number of aortas being studied, while Ns and Nθ are number of discretized sample points along s and θ direction, taken to be 200 points in each direction for the current study. Each row vector of M (i.e. ) acts as a shape descriptor of the aorta in a patient (n), following equation:
| (3) |
is a concatenated list of centerline coordinates along the s dimension of a patient (n). is a concatenated list of surface distributed properties of the sample point, which includes the radius of each sample points (rp) and its logistic/sigmoidal SGDF (fp). Each concatenated parameter set (e.g. ) was centered and normalized by the case mean and standard deviation (σx). Normalized parameters are labelled with a “hat” symbol (^).
The covariance matrix was calculated from M and underwent singular value decomposition into its eigenvalue and eigenvectors. These eigenvectors, the principal components , were indexed in descending order based on the corresponding eigenvalues. These s served as basis vectors for a new coordinate system, such that the normalised shape descriptor can be reconstructed as:
| (4) |
where is the weight of each principal component vector , and NPC is the number of principal components used for the reconstruction (Figure 1e). was then deparameterized to obtain an approximate reconstructed geometry. A reduced-dimension description of a shape can be generated from equation (4), with NPC less than number of aorta geometries used to generate s (Figure 1f).
Artificial Geometry Generation and Normality Testing
The Kogolmorov-Smirnov test was used to test the normality of the distribution of the weights among subjects (n). As will be seen in the Results section, the distributions of were found to be normal, allowing their means and standard deviations to be used to define each distribution. The probability distribution for each weight was randomly sampled within 1 standard deviation about the mean to generate synthetic aorta models (Figure 1g). Out of these artificial geometries, two were chosen to run in CFD.
Computational Fluid Dynamics (CFD)
Once the statistical shape model had been generated, the extent to which the model could sufficiently represent the original branched geometry was assessed. Aside from a geometrical comparison by distance and curvature, CFD simulations were also performed to investigate how the flow profiles were affected due to the geometric simplifications.
The computed geometries were then meshed with ~1 million tetrahedral elements. A mesh convergence study is considered converged when the asymptotic rate of convergence approaches unity (Roache 1994). We estimated the asymptotic rate of convergence of the WSS to be approximately 1.06 for ~1 million elements, a refinement ratio of 1.7, and a safety factor of 1.25x. The detailed calculation of the asymptotic rate of convergence and mesh convergence study plot is available as supplementary material 3. A finer mesh layer was used near the boundary to model the near-wall velocity distribution accurately. A total of 231 simulations were performed: simulations across NPC = 5, 10, 15, 20, 25, 30 and the original geometries of the 33 subjects.
CFD was performed with the Simvascular biofluids software (Updegrove, Wilson, Merkow, Lan, Marsden and Shadden 2017). The Simvascular code solves the incompressible, laminar, unsteady, 3D Navier-Stokes equations for balance of momentum (eqn (5)) and continuity (eqn (6)):
| (5) |
| (6) |
where ρ and μ are the density and viscosity of blood, is the blood velocity, P is the pressure, and t is time.
Equation (5) and (6) were solved in Simvascular using a modified Newton-Raphson method, stabilized by Petrov-Galerkin weighting functions to reduce the convective instability associated with solving equation (5) in its weak form (Brooks and Hughes 1982). Spatial discretization were done linearly on tetrahedral meshes, with a second order generalized-α method for temporal integration (Jansen et al. 2000). The detailed methodology used by Simvascular is available in (Esmaily-Moghadam et al. 2015) and (Esmaily-Moghadam et al. 2013).
Boundary conditions were specified as parabolic inflow (obtained from PC-MRI), no slip at the vessel wall, and a three element windkessel model at each outlets, with two resistors (distal and proximal) and one capacitor. All of the branches were described as windkessels, whose parameters were calibrated using differential evolution (Storn and Price 1997), with L2 norm error of the flow distribution and mean pressures as the objective function, if the flowrate and pressure values are known. Some of the subjects did not have their flowrates measured (including artificial cases). For these cases, boundary parameters were interpolated and scaled based on the aortic arch volume of the known cases. Furthermore, when branches were merged to form a single outlet due to its under-representation in low NPC, the windkessels boundaries would be merged and parallelized. Blood was modelled as a Newtonian fluid flow with viscosity of 4cP and density of 1.06g/cm3 (Kim et al. 2009), and the flow was treated as laminar. Blood is known to be a non-Newtonian fluid, but the non-Newtonian effect diminishes in large vessels such as the aorta (Apostolidis et al. 2016, Caballero and Laín 2015, Perktold et al. 1989). The flowrates obtained across different branches were compared against 4D MRI flow dataset at the branches, when available in some cases as validation. These data are available in supplementary material 1. The flowrates found in these cases vary greatly (min:130.95, max: 506.68cm3/s) since the dataset is from both adult and pediatric subjects (age 3-81), resulting in wide range of not just geometry, but boundary conditions tested.
Simulations were run up to the fifth cardiac cycle, at which point the model stabilized. Each cycle was divided into 500 timesteps with approximately 0.002s. Time step convergence was deemed achieved when the residual value was less than 1E-4 in all momentum and continuity equations.
Definition of Calculated Parameter
The Dean number (De) is defined as
| (7) |
where d is the approximated diameter of the ascending aorta, Rc is the centerline radius of curvature, vpeak is the velocity magnitude at peak systole, and ρ and μ are the blood’s density and viscosity respectively.
Results
Statistical shape modelling
Figure 2a shows cumulative sum of explained variation in the data based on the number of principal components (NPC), and Figure 2b and c displays the errors in the geometric parameters for reconstructed geometries that were used to generate the principal components (PC) and external dataset. Radius errors were normalized by the original geometry’s radius, branch location area errors were normalized with the area of the branch holes, and centerline distance errors were normalized by the length of the centerline. In both data sets, the fitting errors decrease as NPC increases, with more variation in the geometry being accounted for by a larger basis. The effect of additional bases on the geometry can be broken down as contribution of , , and carried across different . The first few are dominated by radius information, with radius error decreasing pronouncedly at NPC = 1 (Figure 2b,c). Geodesic distance (i.e., branch location) error decreased more at moderate to high NPC values. Meanwhile the centerline contained the least amount of information; its error started small and only decreased moderately even for large NPC. In the external dataset, the errors did not reach 0% at maximum number of principal components but plateaued at NPC ≈ 20, resulting in the averaged baseline error of 5.8%, 6.1%, and 3.1% for radius, branch, and centerline location at maximum PC, respectively. Therefore, the population used to generate the shape descriptors is general enough to suitably represent external population’s aortic geometry variation, or at least the population described in (Radl, Jin, Pepe, Li, Gsaxner, Zhao and Egger 2022).
Figure 2.
a) Cumulative sum of the explained variance across NPC for radius, centerline and branch location. (b) &( c) The normalized errors obtained from the dataset used to generate the principal components (b) and an external dataset (c). Error bars are standard errors. d) Geometry for reconstructed aorta for geometry used for generation of principal components (left) and external dataset (right). Full-opacity image is reconstructed aorta, and semi-transparent image is the original geometry.
The result is consistent in the reconstructed geometry (Figure 2d). Radius changes greatly at low NPC and stabilizes at high NPC but, both branch location and centerline curvature continue changing dynamically at high NPC. A video demonstrating the evolution of all studied geometry across NPC is available as (Video 1). Radius information crossed the −3dB explained variance threshold at NPC = 1, but NPC = 9 was required for branch location and NPC = 14 for the centerline.
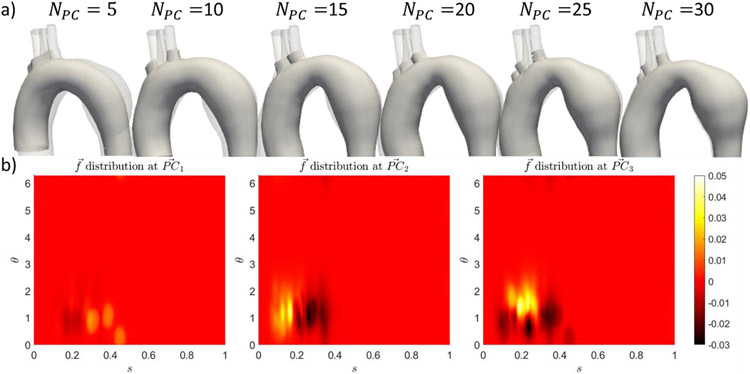
The distribution of aorta geometries over the first three s is shown in Figure 3a. As previously mentioned, the first few s are dominated by radius information, so the distribution of weights in the first few s mainly describes the radius distributions. In general, the first describes the average radius, while the other s describe the variation of radius along the centerline. This effect is illustrated by a spider plot of select cases (Figure 3b). Case 12, with a small vessel radius and long centerline, resulted in the highest weight of . describes the extent of radial dilation in the ascending thoracic aortas, found in cases such as case 3. , in contrast, describes dilation/constriction distal to the aortic arch, towards the descending thoracic aorta, such as seen in case 15. Cases with relatively uniform radius along the centerline, such as case 12, shows comparable values for w2 and w3.
Figure 3.
a) Distribution of geometry over the first three . (b) Spider plot of first three weights of sample cases. (c) Distribution of r(θ,s) for the first three PCs.
The contribution of different s to different regions of the aorta is further illustrated in the relative magnitude of the radius found in the first few s (Figure 3c). has a negative contribution to radius with little variation across s and θ. and , in contrast, show radius contributions centered around zero, with positive and negative contributions in different sections of the aorta. All three s showed little θ dependence.
The effect of on the branching pattern is observable in the sample geometry shown in Figure 4a, and the distribution of sigmoid geodesic distance in Figure 4b. Most of the cases have three head vessel branches, found at s = 0.1 − 0.5, which were captured in . However, the head branches were often found to be merged at the low PCs. The later s generate vertical streaks of large gradient (Figure 4b), thus providing the necessary refinement to separate the merged branches. It is noted that NPC = 20 was often required for the aorta to display three distinct branch holes.
Figure 4.
a) Evolution of branches across NPC for case 19. (b) Distribution of sigmoidal signed geodesic distance for first three PCs.
Artificial aorta models were generated from a random set of principal component weights (wnPC). The weights were assumed to be independent of each other since the diagonal terms of the covariance matrix of the weights are about 4 orders of magnitude higher in absolute value than the off-diagonal terms. The weights were also tested for normality using the Kolmogorov-Smirnov test, with minimum p-values of 0.17 across each wnPC. The fit of these functions for several wnPCs and sample artificial geometry shown in Figure 5a. Based on the normality test, the weights followed independent Gaussian distributions, with mean μwn and standard deviation σwn. Artificial geometries were then generated from uniform random sampling within μwn ± 1σwn. The main issue with the generated artificial cases came from the modelling of the branches. Despite having reasonably located branches, only 3 out of 20 cases had the 3 distinct branch holes at NPC = 20, while others had them merged (Figure 5b). Meanwhile, the curvature of the centerline and the variation of radius along the centerline appear to be reasonable for all the artificial cases generated. CFD was performed on two of the artificial geometries, one of which is shown in Figure 5c. The artificial geometries generated similar flow patterns as the ones obtained from clinical dataset: systolic flow was dominated by Dean flow, backflow at the branches were observed during end systole, and regions of high wall shear stresses were found near the location of the branches.
Figure 5.
a) Cumulative distribution function for selected wnpc nPC and the corresponding Gaussian model. The weight w1 has the lowest Kolmogorov-Smirnov test p-value of 0.17. (b) Sample synthetic geometries. (c) CFD results forf an geometry in (b).
CFD comparison
Wall Shear Stress (WSS) and pressure fields were examined for all CFD simulations, and comparisons between the reconstructed and original geometries were made. Additionally, transverse WSS values were examined, with similar pattern observed as the WSS. The transverse WSS comparison is available in supplementary material 3. Any claim of significant difference in this study is calculated based on the paired t-test, with P-value<0.05 showing significant difference across NPC. The full table of comparisons for this statistical analysis is available as supplementary material 2. First, the time and surface-averaged wall pressure across NPC are shown in Figure 6a. The time- and surface- averaged pressures across NPC did not vary significantly from the original geometry for most of the cases (paired, two-tailed t-test’s P-values > 0.05) as flow impedances were mainly determined by the outflow windkessel parameters. Furthermore, resistance of the aorta, as a function of radius and centerline length, was already well represented in the lower NPC. While the lower NPC cases often had merged branches of the head vessels, if the windkessel parameters were also merged in parallel, the aberrant branching pattern hardly affected the surface averaged pressures.
Figure 6.
Time and surface averaged error in pressure and WSS across NPC. (a) Averaged over the whole wall. (b) Location specific error; Error bars in (a) and (b) are standard errors. (c) Distribution of the location specific errors. Pressure and WSS errors are normalized to the original geometry’s value. Euclidean distance and Gaussian curvature errors were normalized by the centerline length. Errors were correlated at branch locations (dashed line), aortic inlet (solid line), and the descending thoracic aorta (dotted line).
Similar to the pressure, the surface and time-averaged wall shear stress (SA-TAWSS) did not differ significantly from the original geometry at NPC ≥ 10 (paired, two-tailed t-test’s P-values > 0.05), and its error decreased with increasing NPC (Figure 6a). For NPC = 5, the geometrical differences were sufficient to cause WSS differences from the original geometry with p-value of 0.02. Moreover, the distribution of the WSS error on the surface is more sensitive to the local geometry of the aorta (Figure 6b). While the surface-averaged values at NPC ≥ 10 are similar, the wall shear stress pattern can differ (see Video 2, Figure 6c, and Figure 7).
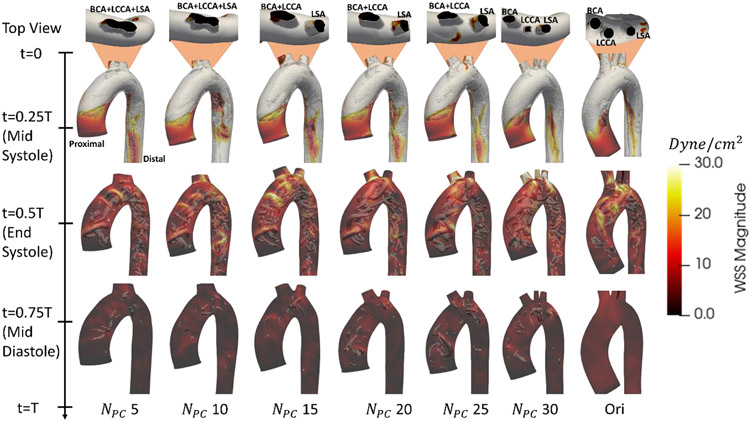
Figure 7.
Wall shear stress contours overlayed on vortices, visualized based on Q-criterion, for reconstructed geometries. The top view displays variation in branching pattern across NPC: BCA- brachiocephalic artery, LSA- left subclavian artery, LCCA- left common carotid artery. Video representation is available as Video 2.
Surface distributions of Euclidean distance, Gaussian curvature, and WSS errors are shown in Figure 6c. There were localized regions that appear to show correlation between these errors. The inlet region has the highest correlation between TAWSS and distance/curvature error. The branched regions also have some correlation: the highest WSS error occurred where the branches were found (Figure 6c) and is also the location of highest WSS (Figure 7). This error was due to misrepresentation of the branches, resulting in high curvature and distance error, particularly at low NPC. Another region of note is at the bend into the descending aorta, distal to the head branches. There is a band of high wall shear stress and curvature error, which corresponds to the location of aneurysm or stenosis after the aortic arch, towards the descending thoracic aorta. Aside from these regions, there is little correlation between local wall shear stress errors and local geometric based errors (Pearson’s Correlation coefficient, r2, <0.5).
Figure 7 describes the distribution of the wall shear stress for different NPC values for a case in which the branching pattern varied with NPC. The systolic flow did not differ significantly over NPC. The systolic flow is dominated by the presence of two counter-rotating vortices, forming at a Dean number (eqn (7)) in the range of 200-1400. As the vortices travelled down the descending aorta, they left a trail of low WSS at the descending aorta, appearing as reddish-brown streak in Figure 7 (t=0.25T). The flow behavior is primarily described by the Dean number, which did not differ significantly across NPC. The averaged error in Dean number at NPC = 5 is about 12% and decreases with increasing NPC. Therefore, the systolic flow profile and wall shear stress pattern remained consistent across NPC.
The dominance of Dean flow and curvature changes are observable in the flow profile at the cross sections along the tube (Figure 8). During mid-systole, the flow pattern mainly follows the expected Dean flow along the cross sections. As NPC increases, the Dean vortices’ symmetry axis was rotated to match the original geometry’s result in planes upstream of the branch (Figure 8, plane 1). The axial symmetry of the Dean vortices follows the inner to outer curvature of the geometry (Tallapragada et al. 2015), and therefore its effects was mainly caused by changes in curvature across NPC. At the branch location (Figure 8, plane 2), the same axial rotation was observed. However, the branch caused the vortices to break their symmetry: the vortex closer to the branch shrunk as it fed flow into the branch, allowing the other to expand. This phnenomenon is just as importantly affected by the curvature, as the rotation of the symmetry axis allows only one of the vortices have access to the outflow. The effect of branches quickly dissipates downstream (Figure 8, plane 3), as the vortices regained their symmetry. The Dean flow symmetry is recovered within 10% of the centerline length away from the branch.
Figure 8.
Flow field for cross sections along the aorta. Color contour shows magnitude of the out of plane velocity, with positive out of plane velocity indicating proximal-to-distal flow. Black dotted line at mid-systole marks the axes of symmetry of Dean vortices. Black star in Plane 2, mid-systole, marks the location of vortex core that shifts towards outflow branch, breaking vortex symmetry.
The largest difference in flow was seen at end systole, when backflow may occur at the branches and descending aorta. This backflow effect, however, is not a product of the branch shape, but the windkessel boundary conditions used. At this time, the bulk flow through the aortic valve was low, which allowed flow to fluctuate (Figure 7, t=0.5T). The flow also varied downstream or upstream of the branch, with remnant effects of the Dean vortices symmetry axis rotation present.
The WSS variation observed was mainly due to the decrease in hydraulic diameter, as the branches split flow into smaller lumen areas, resulted in higher WSS in the daughter than in the parent vessel. This effect is less pronounced at lower NPC, where the three branches were merged. Merged branches have higher lumen area to the wetted perimeter ratio. Therefore, at consistent flow split, the merged branches’ larger hydraulic diameter would result in lower WSS than separate individual branches (up to 70% difference). However, WSS during the end-systole to diastole period have lower magnitude than during mid-systole, and therefore WSS variation during end-systole, and diastole, did not affect the temporal average value much. Yet, the combined effect of branch misrepresentation and minor deviation in the Dean flow caused the flow at NPC = 5 to be sigificantly different from the original (p<0.05).
Discussion
We have demonstrated a method to include branching in the statistical shape representation of the aorta, which raises an obvious question of whether accurately describing these branches is important. The branching pattern did not significantly affect the global averaged measures: SAWSS did not change significantly for NPC ≥ 10, and surface-averaged pressure did not change significantly across NPC. Both surface-averaged and location-specific pressure errors were low across NPC (Figure 6b), as the shape of the aorta only contributes a small portion of the overall flow impedances. While variation in branches, such as branching angle, can cause pressure drops across vessels to vary, the resulting changes in pressure are generally small (Cho et al. 1985). This effect only becomes significant when applied repeatedly to a fractal model of arterial branches (Gabryś et al. 2005), which affect the downstream windkessel parameters.
To be clear, the relatively small changes in global averaged pressure and WSS do not suggest that modelling of the branches is unnecessary. These branches are responsible for diverting 30-40% of aortic flow to the head. Failure to model this flow split would surely affect downstream fluid forces. In a study of flow simulation in aortic dissection subjects with and without total removal of the head branches, the WSS in the true lumen were observed to decrease by 40% in one patient and 70% in another (Jiang, Qiu, Li, Yuan, Zheng and Peng 2019). In contrast, our study did not fully remove the branches, thus, the effect is much less drastic, with WSS decreases at low NPC, by 6% and 2% for NPC = 5 & 10 respectively. It also is necessary to model the branches accurately if a more detailed flow profile near or surrounding the branches are required. Accuracy in the local flow profile is particularly important in studies of atherosclerosis, in which plaque formation often occurs near the location of these branches (Khoury et al. 1997). When such detail is not needed, however, a crude representation of the branches is sufficient. In our case, sufficient accuracy might be obtained at NPC = 10.
WSS was affected by more localized variation in wall structure, but its surface averaged values were sufficiently captured at NPC ≥ 10. At NPC ≥ 10. However, high WSS error was still observed locally at the branch locations, the main arch, and near the aortic root. The region near branches was also the location with high WSS and its associated error. In cylindrical tubes, the presence of branches skews the peak velocity closer to where the branch is found (He and Ku 1996), resulting in greater shear local rates near branches. High WSS near branched region was also found in other computational model (Lantz et al. 2012) and clinical data (Huo et al. 2008, Lantz, Gårdhagen and Karlsson 2012). Thus, if one is concerned about the flow field near the branches, then accurate representation of their location is - unsurprisingly - important.
Just as important is the dependence of the flow in the aorta on its curvature. The curvature of the aorta introduces secondary flow patterns that spiral downstream, depending on its curvature (Dean 1928). There are also reports associating the risk of aneurysm with the tortuosity of the vessel (Kliś et al. 2020, Pappu et al. 2008). Systolic WSS is dominated with this type of flow, with high errors found near the aortic root, where the curvature affects the angle of inflow boundary condition and therefore the inlet WSS error. Therefore, low NPC maybe sufficient to describe the average WSS distribution, but a high NPC is required to obtain more accurate surface distribution.
We emphasize that this work focused on shape representation, not on producing a realistic model of aortic flow. We simplified the flow in the aorta so to allow the multiple simulation runs needed for comparison across cases. Here, blood was modelled as Newtonian, whereas non-Newtonian flow could produce more skewed peak velocity to the branch location (Chen and Lu 2004) and possibly an increase in the WSS found near branches. However, the non-Newtonian effect of blood is scale dependent; in the aorta, the size of the blood cells and its clusters gets much smaller relative to the vessel diameter and its behaviour would tend toward Newtonian (Pialot et al. 2021). a comparison of CFD model of the aorta showed close prediction at systole and slight differences in diastolic WSS in Newtonian models as compared to the non-Newtonian ones (Caballero and Laín 2015, Karimi et al. 2014). Moreover, the aorta deforms considerably in response to flow pressures (Campobasso et al. 2018, Goergen et al. 2011), which were not modelled in this study. Still, the comparative nature of this study would alleviate some of the modelling errors.
Conclusion
We performed PCA of the aorta with models accounting for the presence of head branches. Our method proved successful in capturing aortic geometry, branch geometry, within ~ 20 principal components. This result is promising but also demonstrates the need for a high number of principal components to capture geometric details. CFD was then performed on the geometries reconstructed using various NPC to investigate the effect of various branching patterns on the flow profiles. Time- and wall-surface-averaged values and location-specific values of pressures did not change significantly over NPC. In contrast, local WSS values were more sensitive to the changes in the geometry. Averaged WSS value did not deviate significantly for NPC ≥ 10, but the location specific errors could be particularly high in regions where the branches are found, since the branches could be mis-represented under low NPC.
Supplementary Material
Acknowledgement
Funding provided by NIH grant U01-HL139471 (VHB) and the Faculty Grant Program from the Marfan Foundation (JEW), computational resources were provided by Minnesota Supercomputing Institute.
Footnotes
Conflict of Interest Statement
Authors have no conflict of interest to declare.
References
- Apostolidis AJ, Moyer AP, Beris AN. 2016. Non-Newtonian effects in simulations of coronary arterial blood flow. Journal of Non-Newtonian Fluid Mechanics.233:155–165. [Google Scholar]
- Meshmixer [2018. Version 3.5: Autodesk Inc., San Rafael, CA, USA. [Google Scholar]
- Bazzi MS, Balouchzadeh R, Pavey SN, Quirk JD, Yanagisawa H, Vedula V, Wagenseil JE, Barocas VH. 2022. Experimental and Mouse-Specific Computational Models of the Fbln4SMKO Mouse to Identify Potential Biomarkers for Ascending Thoracic Aortic Aneurysm. Cardiovascular Engineering and Technology.1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertoglio C, Moireau P, Gerbeau JF. 2012. Sequential parameter estimation for fluid–structure problems: Application to hemodynamics. International Journal for Numerical Methods in Biomedical Engineering.28:434–455. [DOI] [PubMed] [Google Scholar]
- Brooks AN, Hughes TJ. 1982. Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations. Computer methods in applied mechanics and engineering.32:199–259. [Google Scholar]
- Bruse JL, Zuluaga MA, Khushnood A, McLeod K, Ntsinjana HN, Hsia T-Y, Sermesant M, Pennec X, Taylor AM, Schievano S. 2017. Detecting clinically meaningful shape clusters in medical image data: metrics analysis for hierarchical clustering applied to healthy and pathological aortic arches. IEEE Transactions on Biomedical Engineering.64:2373–2383. [DOI] [PubMed] [Google Scholar]
- Caballero A, Laín S. 2015. Numerical simulation of non-Newtonian blood flow dynamics in human thoracic aorta. Computer methods in biomechanics and biomedical engineering.18:1200–1216. [DOI] [PubMed] [Google Scholar]
- Campobasso R, Condemi F, Viallon M, Croisille P, Campisi S, Avril S. 2018. Evaluation of peak wall stress in an ascending thoracic aortic aneurysm using FSI simulations: effects of aortic stiffness and peripheral resistance. Cardiovascular engineering and technology.9:707–722. [DOI] [PubMed] [Google Scholar]
- Catalano C, Agnese V, Gentile G, Raffa GM, Pilato M, Pasta S. 2021. Atlas-Based Evaluation of Hemodynamic in Ascending Thoracic Aortic Aneurysms. Applied Sciences.12:394. [Google Scholar]
- Chen J, Lu X-Y. 2004. Numerical investigation of the non-Newtonian blood flow in a bifurcation model with a non-planar branch. Journal of biomechanics.37:1899–1911. [DOI] [PubMed] [Google Scholar]
- Cho Y, Back L, Crawford D. 1985. Experimental investigation of branch flow ratio, angle, and Reynolds number effects on the pressure and flow fields in arterial branch models. [DOI] [PubMed] [Google Scholar]
- Cosentino F, Raffa GM, Gentile G, Agnese V, Bellavia D, Pilato M, Pasta S. 2020. Statistical shape analysis of ascending thoracic aortic aneurysm: correlation between shape and biomechanical descriptors. Journal of Personalized Medicine.10:28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dean W 1928. LXXII. The stream-line motion of fluid in a curved pipe (Second paper). The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science.5:673–695. [Google Scholar]
- Dijkstra EW. 1959. A note on two problems in connexion with graphs. Numerische mathematik.1:269–271. [Google Scholar]
- Elefteriades JA, Sang A, Kuzmik G, Hornick M. 2015. Guilt by association: paradigm for detecting a silent killer (thoracic aortic aneurysm). Open Heart.2:e000169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endo S, Goldsmith HL, Karino T. 2014. Flow patterns and preferred sites of atherosclerotic lesions in the human aorta–I. Aortic arch. Biorheology.51:239–255. [DOI] [PubMed] [Google Scholar]
- Esmaily-Moghadam M, Bazilevs Y, Marsden AL. 2013. A new preconditioning technique for implicitly coupled multidomain simulations with applications to hemodynamics. Computational Mechanics.52:1141–1152. [Google Scholar]
- Esmaily-Moghadam M, Bazilevs Y, Marsden AL. 2015. A bi-partitioned iterative algorithm for solving linear systems arising from incompressible flow problems. Computer Methods in Applied Mechanics and Engineering.286:40–62. [Google Scholar]
- Farzaneh S, Trabelsi O, Chavent B, Avril S. 2019. Identifying local arterial stiffness to assess the risk of rupture of ascending thoracic aortic aneurysms. Annals of Biomedical Engineering.47:1038–1050. [DOI] [PubMed] [Google Scholar]
- Gabryś E, Rybaczuk M, Kędzia A. 2005. Fractal models of circulatory system. Symmetrical and asymmetrical approach comparison. Chaos, Solitons & Fractals.24:707–715. [Google Scholar]
- Goergen CJ, Azuma J, Barr KN, Magdefessel L, Kallop DY, Gogineni A, Grewall A, Weimer RM, Connolly AJ, Dalman RL. 2011. Influences of aortic motion and curvature on vessel expansion in murine experimental aneurysms. Arteriosclerosis, thrombosis, and vascular biology.31:270–279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodall C 1991. Procrustes methods in the statistical analysis of shape. Journal of the Royal Statistical Society: Series B (Methodological).53:285–321. [Google Scholar]
- Harky A, Fan KS, Fan KH. 2019. The genetics and biomechanics of thoracic aortic diseases. Vascular Biology.1:R13–R25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X, Ku DN. 1996. Pulsatile Flow in the Human Left Coronary Artery Bifurcation: Average Conditions. Journal of Biomechanical Engineering.118:74–82. [DOI] [PubMed] [Google Scholar]
- Huo Y, Guo X, Kassab GS. 2008. The flow field along the entire length of mouse aorta and primary branches. Annals of biomedical engineering.36:685–699. [DOI] [PubMed] [Google Scholar]
- Izzo R, Steinman D, Manini S, Antiga L. 2018. The vascular modeling toolkit: a Python library for the analysis of tubular structures in medical images. Journal of Open Source Software.3:745. [Google Scholar]
- Jansen KE, Whiting CH, Hulbert GM. 2000. A generalized-α method for integrating the filtered Navier–Stokes equations with a stabilized finite element method. Computer methods in applied mechanics and engineering.190:305–319. [Google Scholar]
- Jiang Y, Qiu Y, Li D, Yuan D, Zheng T, Peng L. 2019. Influence of aortic branch arteries on the hemodynamics of patient-specific type B aortic dissection following TEVAR. Medicine in Novel Technology and Devices.4:100028. [Google Scholar]
- Karimi S, Dabagh M, Vasava P, Dadvar M, Dabir B, Jalali P. 2014. Effect of rheological models on the hemodynamics within human aorta: CFD study on CT image-based geometry. Journal of Non-Newtonian Fluid Mechanics.207:42–52. [Google Scholar]
- Khoury Z, Gottlieb S, Stern S, Keren A. 1997. Frequency and distribution of atherosclerotic plaques in the thoracic aorta as determined by transesophageal echocardiography in patients with coronary artery disease. The American journal of cardiology.79:23–27. [DOI] [PubMed] [Google Scholar]
- Kim HJ, Vignon-Clementel IE, Figueroa CA, LaDisa JF, Jansen KE, Feinstein JA, Taylor CA. 2009. On coupling a lumped parameter heart model and a three-dimensional finite element aorta model. Annals of biomedical engineering.37:2153–2169. [DOI] [PubMed] [Google Scholar]
- Exact Geodesic for Triangular Meshes [2021. Version 1.0.0.0: The MathWorks Inc., Natick Massachusetts. [Google Scholar]
- Kliś KM, Krzyżewski RM, Kwinta BM, Łasocha B, Brzegowy P, Stachura K, Popiela TJ, Borek R, Gąsowski J. 2020. Increased tortuosity of basilar artery might be associated with higher risk of aneurysm development. European radiology.30:5625–5632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lantz J, Gårdhagen R, Karlsson M. 2012. Quantifying turbulent wall shear stress in a subject specific human aorta using large eddy simulation. Medical engineering & physics.34:1139–1148. [DOI] [PubMed] [Google Scholar]
- Leo H, Ong C, Kabinejadian F, Xiong F, Wong Y, Toma M, Nguyen Y, Cui F, Ho P, Chua K. 2019. Pulsatile flow investigation in development of thoracic aortic aneurysm: an in-vitro validated fluid structure interaction analysis. Journal of Applied Fluid Mechanics.12:1855–1872. [Google Scholar]
- Liang L, Liu M, Martin C, Elefteriades JA, Sun W. 2017. A machine learning approach to investigate the relationship between shape features and numerically predicted risk of ascending aortic aneurysm. Biomechanics and modeling in mechanobiology.16:1519–1533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMurry TL, Hu Y, Blackstone EH, Kozower BD. 2015. Propensity scores: methods, considerations, and applications in the Journal of Thoracic and Cardiovascular Surgery. The Journal of thoracic and cardiovascular surgery.150:14–19. [DOI] [PubMed] [Google Scholar]
- Pappu S, Dardik A, Tagare H, Gusberg RJ. 2008. Beyond fusiform and saccular: a novel quantitative tortuosity index may help classify aneurysm shape and predict aneurysm rupture potential. Annals of vascular surgery.22:88–97. [DOI] [PubMed] [Google Scholar]
- Pearson K 1901. LIII. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin philosophical magazine and journal of science.2:559–572. [Google Scholar]
- Perktold K, Peter R, Resch M. 1989. Pulsatile non-Newtonian blood flow simulation through a bifurcation with an aneurysm. Biorheology.26:1011–1030. [DOI] [PubMed] [Google Scholar]
- Pialot B, Gachelin J, Provost J, Couture O. 2021. Exploitation of blood non-Newtonian properties for ultrasonic measurement of hematocrit. Scientific Reports.11:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radl L, Jin Y, Pepe A, Li J, Gsaxner C, Zhao F-h, Egger J. 2022. AVT: Multicenter aortic vessel tree CTA dataset collection with ground truth segmentation masks. Data in Brief.40:107801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridler T, Calvard S. 1978. Picture thresholding using an iterative selection method. IEEE trans syst Man Cybern.8:630–632. [Google Scholar]
- Roache PJ. 1994. Perspective: a method for uniform reporting of grid refinement studies. [Google Scholar]
- Romero P, Santos S, Sebastian R, Martıne-Gil F, Serra D, Calvillo P, Rodrıguez A, Puig RM, Martı-Bonmatı L, Alberich-Bayarri A. Reconstruction of the aorta geometry using canal surfaces. Proceedings of the International Conference on Computational and Mathematical Biomedical Engineering; 2019. [Google Scholar]
- Shahmirzadi D, Konofagou EE. 2014. Quantification of arterial wall inhomogeneity size, distribution, and modulus contrast using FSI numerical pulse wave propagation. Artery research.8:57–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shalhub S, Schäfer M, Hatsukami TS, Sweet MP, Reynolds JJ, Bolster FA, Shin SH, Reece TB, Singh N, Starnes BW. 2018. Association of variant arch anatomy with type B aortic dissection and hemodynamic mechanisms. Journal of Vascular Surgery.68:1640–1648. [DOI] [PubMed] [Google Scholar]
- Storn R, Price K. 1997. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. Journal of global optimization.11:341–359. [Google Scholar]
- Tallapragada P, Hasabnis N, Katuri K, Sudarsanam S, Joshi K, Ramasubramanian M. 2015. Scale invariant hydrodynamic focusing and sorting of inertial particles by size in spiral micro channels. Journal of Micromechanics and Microengineering.25:084013. [Google Scholar]
- Trachet B, Bols J, Degroote J, Verhegghe B, Stergiopulos N, Vierendeels J, Segers P. 2015. An animal-specific FSI model of the abdominal aorta in anesthetized mice. Annals of biomedical engineering.43:1298–1309. [DOI] [PubMed] [Google Scholar]
- Updegrove A, Wilson NM, Merkow J, Lan H, Marsden AL, Shadden SC. 2017. SimVascular: an open source pipeline for cardiovascular simulation. Annals of biomedical engineering.45:525–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson NM, Ortiz AK, Johnson AB. 2013. The vascular model repository: a public resource of medical imaging data and blood flow simulation results. Journal of medical devices.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.