Abstract
Infancy is a critical period for the human brain development, and brain age is one of the indices for the brain development status associated with neuroimaging data. The difference between the predicted age based on neuroimaging and the chronological age can provide an important early indicator of deviation from the normal developmental trajectory. In this study, we utilize the Graph Convolutional Network (GCN) to predict the infant brain age based on resting-state fMRI data. The brain connectivity obtained from rs-fMRI can be represented as a graph with brain regions as nodes and functional connections as edges. However, since the brain connectivity is a fully connected graph with features on edges, current GCN cannot be directly used for it is a node-based method for sparse graphs. Hence, we propose an edge-based Graph Path Convolution (GPC) method, which aggregates the information from different paths and can be naturally applied on dense graphs. We refer the whole model as Brain Connectivity Graph Convolutional Networks (BC-GCN). Further, two upgraded network structures are proposed by including the residual and attention modules, referred as BC-GCN-Res and BC-GCN-SE to emphasize the information of the original data and enhance influential channels. Moreover, we design a two-stage coarse-to-fine framework, which determines the age group first and then predicts the age using group-specific BC-GCN-SE models. To avoid accumulated errors from the first stage, a cross-group training strategy is adopted for the second stage regression models. We conduct experiments on infant fMRI scans from 6 to 811 days of age. The coarse-to-fine framework shows significant improvements when being applied to several models (reducing error over 10 days). Comparing with state-of-the-art methods, our proposed model BC-GCN-SE with coarse-to-fine framework reduces the mean absolute error of the prediction from >70 days to 49.9 days. The code is now available at https://github.com/SCUT-Xinlab/BC-GCN.
Index Terms—: Age prediction, deep learning, Graph Convolutional Networks, infant brain, rs-fMRI
I. Introduction
Neuroimaging-based age prediction is important for brain development and aging analysis and brain disease diagnosis [1], [2], [3], [4], [5], [6]. In pediatric brains, the difference or gap between the “predicted age” and the “chronological age” can provide an important early indicator of deviation from the normal developmental trajectory, which may suggest neurodevelopmental delays or disorders, such as autism, attention-deficit/hyperactivity disorder (ADHD), etc. Meanwhile, the identified most contributive regions and features for age prediction can serve as important biomarkers of brain ages, thus helping us better understand the early brain development. In clinical applications, age prediction would be beneficial when the prediction errors in healthy subjects achieved by the trained model are significantly smaller than the “brain age difference” between the abnormal subjects and healthy subjects [1], [2], [3], [4], [5], [6].
According to recent researches, brain resting-state functional magnetic resonances imaging (rs-fMRI) [7] data could be used to predict brain age [1]. The rs-fMRI is an in vivo brain functional imaging technique, which measures blood oxygen level-dependent (BOLD) signals [8], [9] when scanning subjects in natural rest without any explicit task engagement [10]. Based on fMRI time series, brain functional connectivity is defined as the temporal correlation of neuronal activities among anatomically determined brain regions [11], [12], [13]. It has advanced our understanding of the human brain and its development [14], [13]. Dynamic functional connectivity (DFC) is related to a variety of different neurological disorders, and has been suggested to be a more accurate representation of functional brain networks.
In the past few years, several statistical methods and machine learning methods have been used to predict brain age using rs-fMRI and brain functional connectivity. For instance, Monti et al. [15] proposed a method that used the Principal Component Analysis (PCA) to extract features from the brain connectivity. In [16], researchers adopted the Support Vector Machine (SVM) or Support Vector Regression (SVR) directly on the functional connectivity matrix. In [17], a Gaussian Processes Regression (GPR) machine was trained to recognize patterns of data that matched a given age label. Liem et al. [18] combined SVR with Random Forest (RF) through an ensemble learning method to improve the performance of age prediction. Although encouraging, there are still major limitations in these methods, especially under complicated scenarios like large age span, dynamic early brain development and limited datasets.
With the emergence and development of deep learning, effective tools have been developed to identify embedded and high-level features from data, such as multi-layer perceptron (MLP) for vector quantity, Convolutional Neural Networks (CNN) [19], [20] for images and Recurrent Neural Networks (RNN) [21], [22] for sequences. They demonstrate more powerful feature extraction capabilities than traditional machine learning methods. Among these deep learning methods, CNN and its extensions have superior capabilities to extract features from data with regular structures, and have achieved great success in the image-based classification and regression problems. They have been applied to predict the age given different types and modalities of image data, such as face images [23] and brain MR images [1]. Unfortunately, the brain connectivity is a graph-like data, which is essentially different from regular grid-like image data. It is thus difficult to utilize CNN directly on rs-fMRI data. Forcibly applying CNN on the connectivity matrix cannot extract meaningful features, resulting in task failure [24].
Besides CNN, there were several studies analyzing brain connectivity through other deep learning frameworks. In [25], the similarities of connectivity between different people were analyzed, and some regions of high correlation were chosen to predict fluid intelligence by MLP. He et al. [26] constructed a model in the order of encoder-decoder, MLP and SVM to predict cognitive deficits in infants. Takagi et al. [27] extracted feature of each region from connectivity and multiplied them with a learnable matrix to predict intelligence and cognitive outcomes. In [28], a deep encoder-decoder model was trained and then the encoded time series of regions were used to diagnose Mild Cognitive Impairment. All these methods regard brain connectivity as a general matrix or independent vector, without taking the specific spatial structure of brain network prior into account, thus limiting their abilities of extracting features and classification and regression tasks.
Mathematically, brain functional connectivity can be represented as a fully connected graph, in which the brain regions are defined as nodes and the correlation between regional signals is regarded as the weight of the edge [29]. There are two noteworthy characteristics of the graph formed by brain functional connectivity. First, all pairs of nodes are connected by edges, that is, it is a fully connected dense graph. Second, information is contained in all the edges, while the nodes carry nothing. These characteristics of brain connectivity graph make it different from other general sparse graphs, and require us to design a special deep learning method. BrainNetCNN [30] was a promising attempt to migrate CNN to the brain connectivity graph. It treated the graph connection as a pixel in the image, and adopted the CNN-like kernel to calculate the convolution of the connections. It was an effective method for fMRI data. However, its CNN-based operations cannot capture and characterize graph topology information, which limits its feature extraction ability and increases its computational complexity.
Recently, there are lots of work focusing on the Graph Convolutional Networks (GCN), which combines the deep neural networks and graph models [31], [32], [33]. GCN extracts features considering both raw input and topology, making it efficient for analyzing graph data. By computing the eigen-decomposition of the graph Laplacian, the graph convolution operation can be defined in the spectral domain. Defferr et al. [33] used Chebyshev polynomial to approximate the eigenvalue matrix of graph Laplacian. Kipf et al. [31] further simplified calculation and developd layer-wise convolution structure, which makes GCN easy to be implemented by matrix multiplication. Parisot et al. [34] proposed a population graph and adopted GCN for the prediction of Autism and Alzheimer. In this method, individuals were considered as nodes with rs-fMRI data and personal data as features, and the social relationship was the edge connecting people. The population graph was a social relationship defined sparse node-based graph, which is different from rs-fMRI data defined dense edge-based brain connectivity graph. Current GCN-based algorithms mostly focus on node-based graphs, which learn message passing from nodes to nodes [24]. It is more suitable for the sparse graph with representative features on nodes, because too many edges would bring noise and hurt neighborhood aggregation as well as the performance of GCN [35]. However, the rs-fMRI based brain connectivity graph is a fully connected graph with edge-based features. Although we can make the brain connectivity sparse by using a threshold-based method, it will inevitably lose information. Hence, GCN and its variations are not very suitable to our graphs.
Therefore, it is imperative to develop edge-based graph learning algorithms to analyze large fully-connected graph data. Edges of brain connectivity graph represent the strength of functional connections between brain regions, which have great practical significance in communication between brain regions. Besides directly connected edges, the indirect connections between brain regions (through other brain regions) also play an import role in brain communication [36]. All these directly and indirectly connected edges are defined as paths in graph theory, and we develop a novel Graph Path Convolution (GPC) method to extract features from different graph paths. After GPC, Edge Pooling (E-P) and Node Pooling (N-P) are adopted to downsample the data from edges and nodes. Thus, the GPC, E-P and N-P are basic components of our proposed model, i.e., Brain Connectivity Graph Convolutional Network (BC-GCN). Inspired by ResNet [37] and Squeeze-and-Excitation Network (SE Net) [38], we further propose to combine Res block and SE block with GPC layer to emphasize the characteristics of data and enhance influential channels. The model with GPC-Res layers or GPC-SE layers is called BC-GCN-Res or BC-GCN-SE, respectively. While applying a single model to predict infant age, we also found a noteworthy phenomenon: the prediction error is generally lower in the middle age group than the ones in young and old groups. This indicates that during infancy, the brain develops so rapidly that a single pattern is hard to describe the feature in different age periods [39]. So we design a two-stage coarse-to-fine framework to first coarsely divide subjects into three age groups and then finely predict an accurate age through the group-specific model.
By employing BC-GCN-SE as the basic model for the classification and prediction tasks in the coarse-to-fine framework, we can greatly improve the performance. Furthermore, we propose a specific backtracking method for our proposed graph deep learning model. It employs gradients to automatically calculate the importance of features, so that the relationship between brain functional connection and infant development can be revealed.
In general, our contributions are in three aspects. First, to aggregate the information of direct and indirect connections between brain regions, we design a new Graph Path Convolution (GPC) method and develop a Brain Connectivity Graph Convolutional Networks (BC-GCN) as a base model. Second, we propose two extended models BC-GCN-Res and BC-GCN-SE, including Res block and SE block, which further improve the performance of the base model. Third, to solve the unbalanced error distributions among different age groups, we design a two-stage coarse-to-fine framework that determines age group and predicts age in sequence. By testing on infant rs-fMRI scans from 6 to 811 days of age, our proposed model significantly outperforms the state-of-the-art by a mean average error (MAE) of 49.9 days. Furthermore, predictive functional connections can be discovered by a specifically-designed backtracking method, which contributes to better understand infant brain development. It is worth noting that, our proposed BC-GCN series models can be applied to many rs-fMRI based tasks, as they are very generic.
II. Data and Pre-processing
We use a public dataset including 612 (256 males and 356 females) rs-fMRI scans from 248 typically-developing infant subjects with age ranged from 6 to 811 days [40]. The subject demographics is shown in Table I. Images were acquired on 3T Siemens Prisma MRI scanners using a 32-channel head coil. T1-weighted MR images were obtained with TR/TE/TI = 2400/2.24/1600 ms, flip angle = 8, acquisition matrix = 320×320, and resolution = 0.8×0.8×0.8 mm3. T2-weighted MR images with TR/TE = 3200/564 ms, acquisition matrix = 320×320, and resolution = 0.8×0.8×0.8 mm3. For the same cohort, rs-fMRI scans were acquired with TR = 800 ms, TE = 37 ms, flip angle = 80°, FOV = 208 mm, resolution = 2×2×2 mm3, total volume = 420 (5 min 47 sec).
TABLE I.
Subject demographics (D: day; the distribution of age is represented by mean±standard deviation.)
| <100D | 100–200D | 200–300D | 300–400D | 400–600D | >600D | |
|---|---|---|---|---|---|---|
| Subjects (Male) | 23 (7) | 45 (22) | 50 (20) | 50 (26) | 47 (17) | 33 (14) |
| Age (days) | 69±23 | 157±28 | 260±30 | 349±30 | 482±54 | 724±53 |
All functional MRI scans were preprocessed following an infant specific procedure [41], [42], including the following major steps: (1) head motion and spatial distortion correction; (2) alignment of fMRI scans onto their structural MRI scans based on tissue boundary maps [43]; (3) one-time resampling of fMRI data in each subject’s native space by concatenation of the above transformations to avoid interpolation and smoothing of functional signals for multiple times; (4) removing linear trends in fMRI data using a conservative high-pass filtering; (5) decomposing each fMRI into 150 components using individual independent component analysis; and (6) removing noisy components based on a deep-learning model [44]. Scans with large head motion were excluded for further analysis. After preprocessing, the fMRI time series were aligned into the individual’s physical space (T1w) to establish the correspondence between the structure image and the functional image. We partitioned the brain volume into 112 regions of interest (ROIs) by wrapping a brain atlas [45] onto each scan based on tissue maps. For each ROI, the average time series was used as the representative time series of this ROI for network construction.
III. Proposed Method
The flowchart of our proposed coarse-to-fine framework is illustrated in Fig. 1, including (Step A) the computation of slice-based dynamic functional connectivity matrices, (Step B) the age group classification, and (Step C) the group-specific age prediction. Specifically, in Step A, the input is brain region-based sequential rs-fMRI data, the blood oxygen level-dependent (BOLD) signal, and we utilize a sliding window with a constant stride to cut the sequence into several small slices along the time axis. For each slice, we adopt the FSLNets1 to compute the Pearson’s correlation matrix, which characterizes the connectivity properties between brain regions. These matrices, also referred as dynamic functional connectivity (DFC) matrices, define the short-time functional graph of brain regions, and are also the inputs of the following Steps B and C. Steps B and C are the coarse stage and the fine stage, respectively. Within these two stages, the core model is our proposed novel Graph Path Convolution (GPC) method, which aggregates the information of direct and indirect connections between brain regions, and Brain Connectivity Graph Convolutional Networks (BC-GCN) are designed accordingly. Then, we incorporate Res block and SE block for two extended models, i.e., BC-GCN-Res and BC-GCN-SE, to emphasize the characteristics of data and enhance influential channels. We use BC-GCN-SE in Steps B and C. Step B is the coarse stage, where subjects are divided into three age groups: young, middle and old. The BC-GCN-SE based classification model returns the classification result of every slice. Then, by averaging the classification scores of all belonging matrices, each subject can be classified into a specific age group. It determines the model selected in Step C, which is the fine stage. Given the age group, we choose the group-specific model to predict the age of every slice-wise correlation matrix, and obtain the final prediction of subjects by averaging.
Fig. 1.
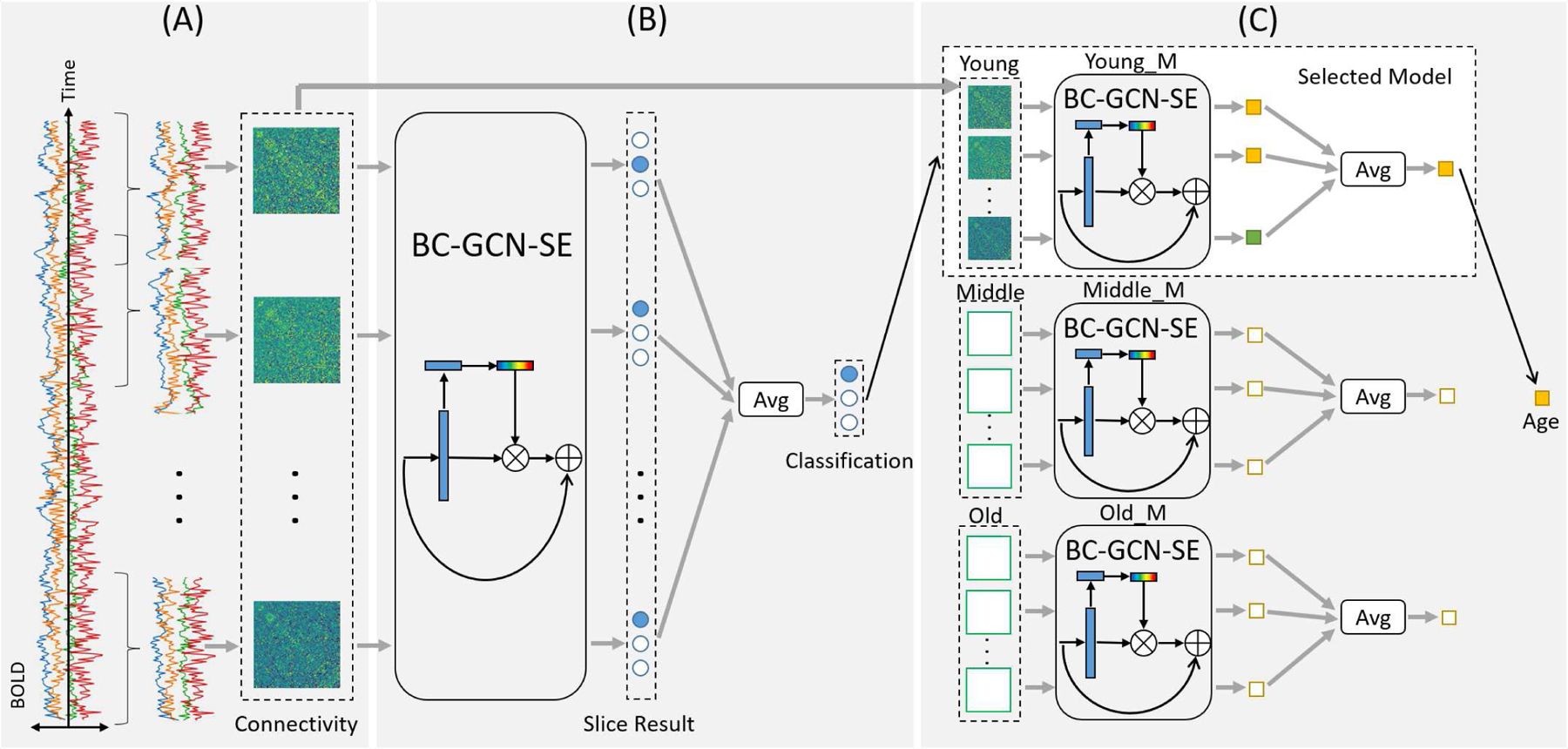
The general flowchart of our proposed framework. Input is the blood oxygen level-dependent (BOLD) signals of infants in natural rest without any explicit task engagement, and output is the predicted age of each infant. The whole process consists of three steps. Step A (data processing) calculates the dynamic brain connectivity matrices from each subject using FSLNets tool and sliding window with overlap, Step B (coarse stage) utilizes a classification model to determines the age group (young, middle or old) of subjects, and Step C (fine stage) predicts the age through the regression model (Young_M, Middle_M or Old_M) selected based on the classified age group in Step B. All the models in Step B and Step C use the connectivity matrices from Step A as input.
In the following section, we will first introduce the proposed Brain Connectivity Graph Convolutional Networks (BC-GCN) and its extended versions BC-GCN-Res and BC-GCN-SE, then expound the strategy of our two-stage coarse-to-fine framework, and finally derive a backtracking formula for the proposed algorithm.
A. Brain Connectivity Graph Convolutional Networks (BC-GCN)
1). Graph Structure of Brain Connectivity:
A graph can be represented as G = (N, E), where N is the set of nodes and E is the set of edges. By considering brain regions as nodes and their connections as edges, the brain connectivity can be regarded as a graph. In general, for the sparse graph, only few nodes are connected by edges. But in brain connectivity, nodes are fully connected. If we set n as the number of nodes, then the number of edges is n2, that is, and . As mentioned above, Graph Convolutional Networks (GCN) is a node-based deep learning method that learns the message passing from nodes to nodes. GCN pays more attention on nodes and their features, and is mainly used for sparse graph [24], while the brain connectivity is essentially a fully connected graph with edge-related features. Therefore, GCN is unsuitable for the brain connectivity.
Hence, we design an edge-based graph network algorithm dedicated for the fully connected brain connectivity, called Brain Connectivity Graph Convolutional Networks (BC-GCN). BC-GCN model is consist of three basic layers, i.e., Graph Path Convolution (GPC), Edge Pooling (E-P) and Node Pooling (N-P). GPC is adopted to extract features from edges. After GPC, E-P and N-P are used to downsample data from edges and nodes to get the output feature. Besides these three basic layers, two structures Res block and SE block are proposed, which can extend GPC layer to GPC-Res or GPC-SE and will be detailed in section III-B. Fig. 2 shows the illustration of BC-GCN-SE, an advanced version of BC-GCN, in which GPC layers are replaced by GPC-SE layers.
Fig. 2.
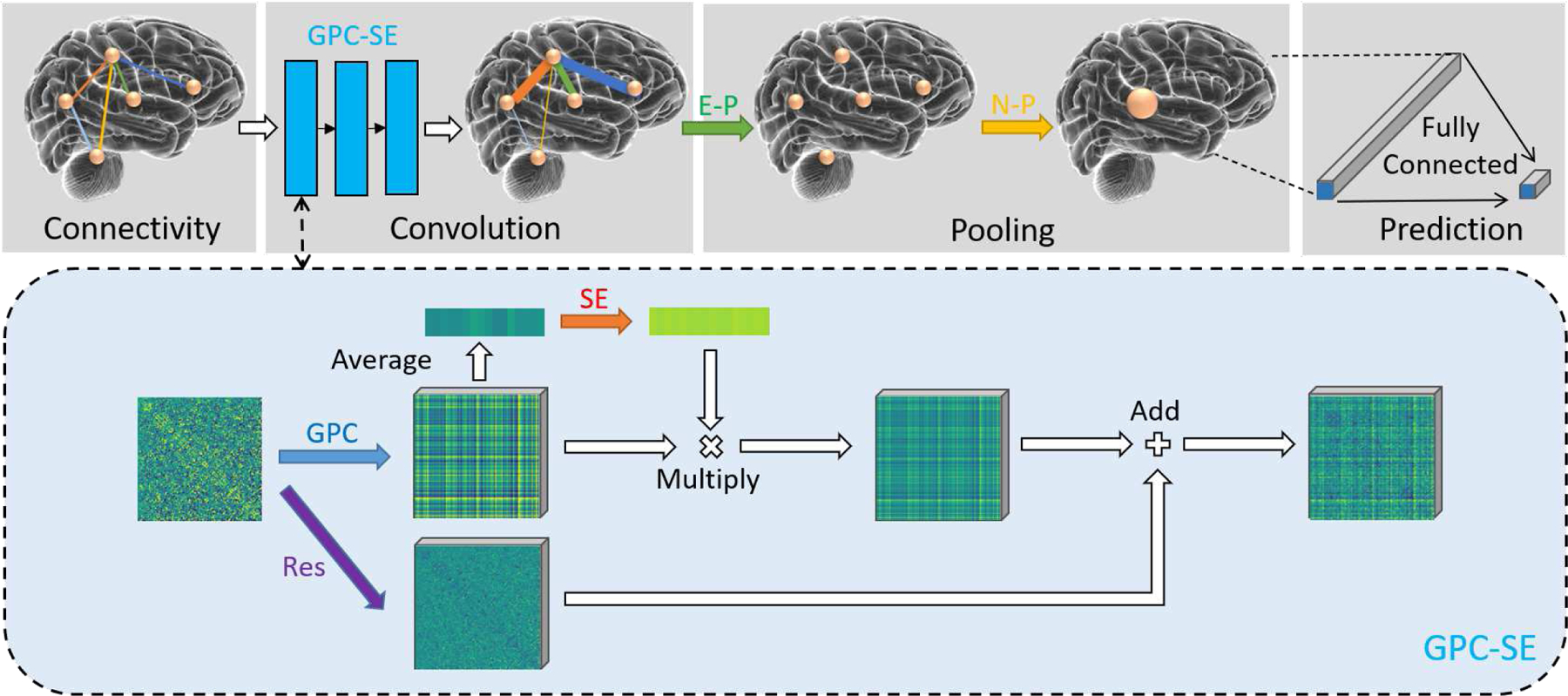
Illustration of the proposed BC-GCN-SE model. The input is a graph-like brain connectivity data, where nodes represent brain regions and edges represent function connections. Firstly three GPC-SE layers extract the features on edges, and real data changes are visualized in the dashed box. Then E-P pools data from edges to node, leaving only the node structure, and N-P pools data on edges to get a single output. Note this single output is actually a channel-number-dimensionality vector, and a fully connected layer is needed to make a final prediction.
2). Graph Path Convolution (GPC):
In the human brain, the relationships between brain regions are complex and multilevel. The direct contact and indirect contact between brain regions both play important roles in brain communication. For example, the communication between brain region i and brain region j not only has connection i – j, but also has the indirect connection, e.g., the connection i – k – j through another brain region k. Although the direct connection between brain regions i and j might be weak, they can still relate to each other through the route i – k – j. All these direct and indirect connections are basics of communication between brain regions [36].
The route i – j or i – k – j is defined as a “path” in graph theory, which represents the direct or indirect connection between two nodes. As shown in Fig. 3(a), we define the direct connection as a 0-order path, the indirect connection through only one other node as 1-order path, and so on for 2-order path and 3-order path. The abbreviation for these paths are , , and . Actually, is a scalar equal to the sum of its compositional edges, for example, is the edge Ei,j, and is the sum of Ei,k and Ek,j. As analyzed before, these paths may include important information about the relation between brain regions. To aggregate multi-order information from these paths, we propose Graph Path Convolution (GPC):
| (1) |
where represents the kth s-order path between node i and node j, and GPi,j is the aggregation of all the paths between i and j. S limits the highest order of paths, and is the number of s-order paths. ws,k and θs are learnable parameters, i.e., ws,k is the weight for kth s-order path and θs is for order s. GPC can aggregates data form 0-order paths to S-order paths and extracts meaningful features from these paths.
Fig. 3.
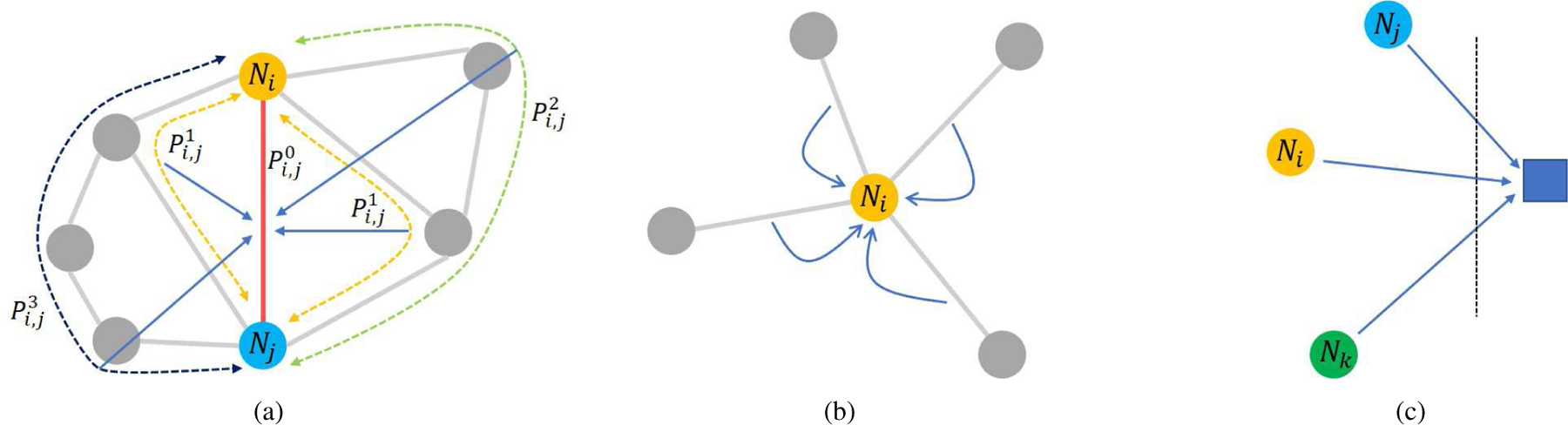
Schematic diagram of three basic layers in BC-GCN. (a) Aggregating information from paths with different orders by Graph Path Convolution (GPC). (b) Data pooling from edges to node (Edge Pooling, E-P for short). (c) Data pooling from isolated nodes to a single output (Node Pooling, N-P for short).
Eq. 1 is the basic formula of GPC, and it plays a role of extracting features in the BC-GCN model. Deep learning methods usually stack the basic layers to enlarge receptive field and improve their performance. By setting the GPi,j as the 0-order path for next layer, we can also make a layer-wise GPC and it can be repeated like basic layers. Using superscript l to represent the lth layer of data, the layer-wise GPC can be represented as follow:
| (2) |
where means the kth s-order path between node i and node j of lth layer data, and is the 0-order path between node i and node j of (l + 1)th layer specifically. However, the computational complexity of the base GPC is too high with too many parameters. Hence, referring to the simplification ideas in [31], we set S = 1 and only consider the 0-order paths and 1-order paths. Although the single GPC layer’s receptive field become smaller, by stacking layers, we can still calculate higher-other paths and obtain larger receptive field. 0-order paths and 1-order paths can be easily represented by Ei,j and Ei,k + Ek,j, and is the (l + 1)th layer of edge data. To be specific:
| (3) |
Note that, the 1-order paths Ei,k + Ek,j have a limitation that k ≠ i, j. However, if we let k = i (or k = j), then Ei,k + Ek,j = Ei,i + Ei,j = 0 + Ei,j = Ei,j, that is, 0-order paths can be represented by the same formula as 1-order paths, and they can be merged into one formula. Inspired by [31], setting some parameters to be consistent can reduce model complexity and enhance its robustness. By setting and , we get the simplest expression:
| (4) |
where n is the number of nodes, and wk is the learnable parameters for 0-order and 1-order paths. Although we only consider 0-order and 1-order paths in this simplified process, by stacking several GPC layers, meaningful features from high-order paths can be learnt from the brain connectivity.
3). Edge Pooling (E-P) and Node Pooling (N-P):
GPC can effectively extract features without changing the graph structure of data. Pooling is an important layer to reduce data size while retaining useful information. Therefore, after GPC, Edge Pooling (E-P) and Node Pooling (N-P) are employed to aggregate the data from edges and nodes. By taking the same approach as the E2N layer and N2G layer in BrainNetCNN [30], E-P aggregates data from edges to their central nodes (N ), as shown in Fig. 3(b), and N-P brings all node data together (Fig. 3(c)), generating a final single output to represent the whole graph (G). Both of two layers require learnable parameters in the aggregating process. Mathematically, they are defined as follows:
| (5) |
| (6) |
Note that although we utilize the same letter wk to represent the learnable parameters in GPC, E-P, and N-P, they are independent of each other without sharing weights. GPC, E-P and N-P are sequentially spliced together, as shown in Fig. 2, among them GPC can be repeated several times (3 times in this work). Fully connected layer is used to get the final output from a channel-wise dimensional vector. By changing the output dimensionality and activation function of the last fully connected layer, the proposed model can be either a classifier or a predictor.
B. Extended Structure
Inspired by CNN extend module, we propose two extended structures to emphasize the characteristics of data and enhance influential channels by including Res block and SE (Squeeze-and-Excitation) block.
1). Res Block:
ResNet[37] emphasizes the characteristics of data itself by adding residual structure between the convolution layers and achieves good results. In our GPC, because each edge can collect information from 2 × n edges (Eq. 4) of the previous layer, the influence of edge itself is neglected to some extent. So inspired by ResNet, we define our Res block:
| (7) |
where u is a learnable parameter to adaptively transform the edge itself, R represents the result of Res block, and its data size is the same as the edge E. The Res block is used in conjunction with GPC, called GPC-Res:
| (8) |
where fGPC and fRes are abbreviated representations of GPC layer and Res block, and O is the output of GPC-Res. The addition of Res block can make GPC layer more flexible, and the basic model BC-GCN with Res block called BC-GCN-Res.
2). SE Block:
Inspired by another CNN model Squeeze-and-Excitation Network (SE Net) [38], we propose to extend the BC-GCN model by including a channel attention layer learnt by SE block, referred as BC-GCN-SE.
The SE block is designed similar with the original SE network but the convolution is changed as above discussed GPC. After GPC, we can get a vector of channel-number-dimensionality by global average pooling. Then, three fully connected layers with activation function are used to learn an attention vector to impact the channel of data by multiplication. The whole channel-wise attention process is as follows:
| (9) |
where fAvg means global average pooling and we can get a vector V through fAvg. Vse means the attention score learned by SE block fSE, and Ese is the output of this channel-wise attention process.
SE block focuses on feature extraction, while Res block aims to emphasize the data itself, and they can work together:
| (10) |
As in our BC-GCN-SE model, both SE block and Res block are combined with GPC layer, referred as GPC-SE and shown in Fig. 2.
C. Two-stage Coarse-to-fine Framework
In the infant age prediction, there is a noticeable phenomenon, that is, the prediction error is generally low in the middle age group while high in young and old age group. We plot the prediction error curves along the age of several different methods in Fig. 6(a), and all these curves follow a “high-low-high” distribution. This “high-low-high” phenomenon is because the infant brain develops heterogeneously and a single regression method cannot well represent their temporal differences and longitudinal inter-subject variations. Hence, inspired by [39], we propose a two-stage coarse-to-fine framework as shown in Fig. 1. By partitioning the age range into three age groups (i.e., young, middle, and old), the model first classifies the age group and then predicts the age using the prediction model of the corresponding group. In this way, different prediction models can capture characteristics of different age groups and avoid performance degradation. In our experiment, we set the data size of these three groups similar to balance three corresponding prediction models, i.e. the number of subjects in three age groups are similar.
Fig. 6.
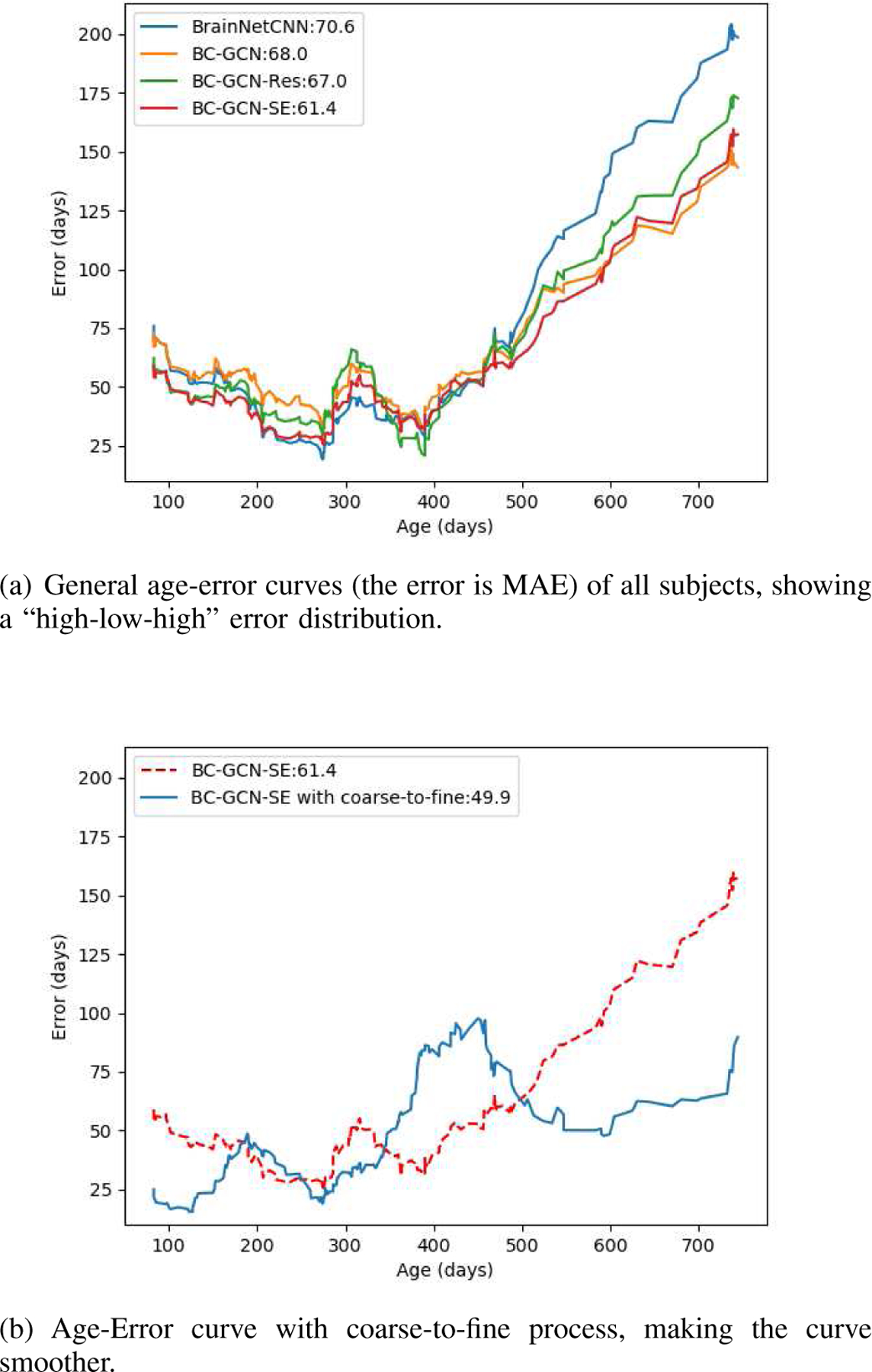
Age-Error curves of different methods and with proposed coarse-to-fine process.
However, age is a continuous variable, not discrete categories. The first stage classification error could affect the final result to some extent. Based on our experiments and observation, for the first stage, the subject has high probability of being mis-classfied to its neighboring age groups (i.e. the subjects of young age group can only be mis-classified to middle group, details shown in Table IV). In view of this, we adjust the training data of the three group-specific prediction models and make sure some data from neighboring groups can also be included. Hence, even if the error occurs in the first stage, the prediction model can still make a reasonable estimation for it has seen similar samples in its training set. For example, for the prediction model of the old age group, the training data includes both second half of the middle age group and the whole old age group subjects. The regrouping training strategy is illustrated in Fig. 4.
TABLE IV.
Classification results of BC-GCN-SE classifier, including the accuracy of validation set and test set and the error rate for different situations.
| Classification Situation | Rate |
|---|---|
| correct (validation set) correct (test set) |
85% 75% |
| mis-classify young to middle mis-classify young to old |
7% 0% |
| mis-classify middle to young mis-classify middle to old |
2% 6% |
| mis-classify old to young mis-classify old to middle |
0% 9% |
Fig. 4.
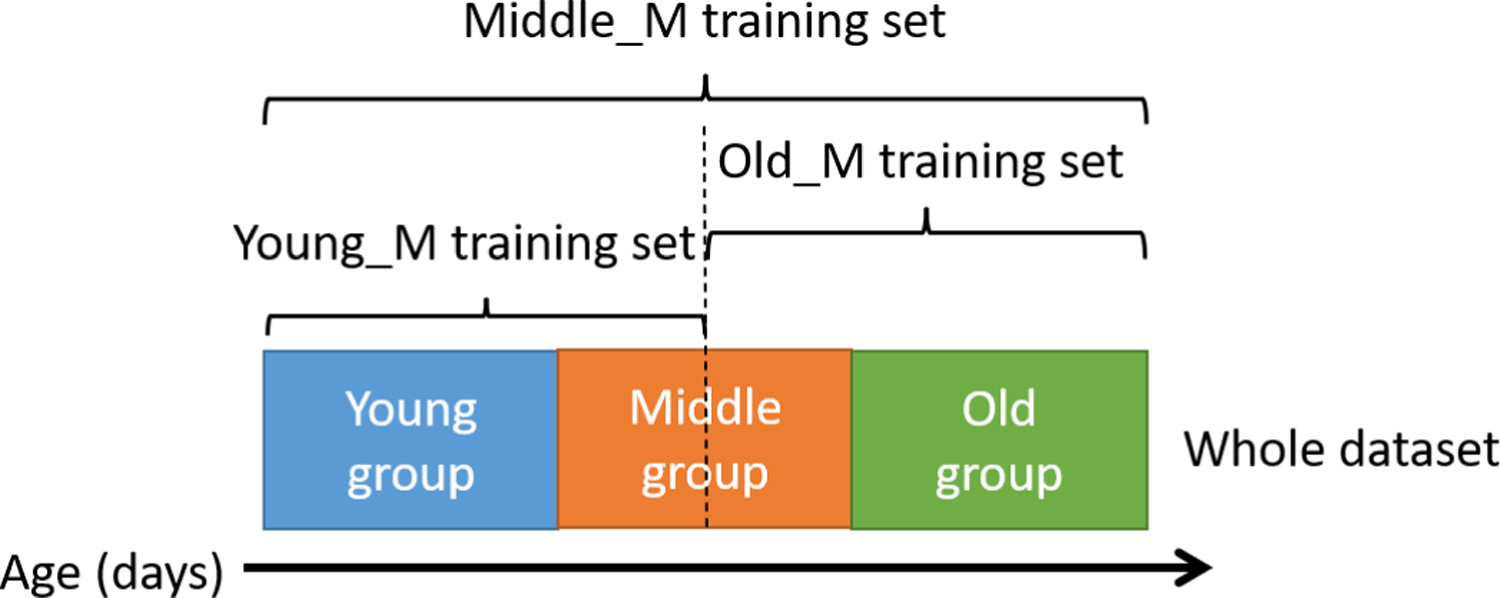
Cross-group training strategy of three prediction networks. The training set covering part of adjacent data sets can reduce the impact of classification errors from the coarse stage on the prediction in the fine stage.
D. Backtracking
Besides accurately predicting age, it is also very important to explore the relationship between the age and brain regions, i.e., the output and input of the prediction model, because it can reveal physiological changes in the developing brain. Previous methods for analyzing features importance can only be applied to traditional machine learning method (like counting the information divergence of the Decision Tree) or CNN (like CAM [46] or Grad-CAM [47]) but not GCN, because they would lead to the asymmetric connective matrix, which violates the definition of the graph model. In other words, those backtracking methods cannot correctly learn the feature importance for GCN models. Hence, based on the proposed model, we design a new backtracking algorithm that allows us to identify the impact of every brain functional connection for the final result.
In the deep learning model, we have the predicted output y and the loss L (we adopt MAE as our loss in experiments) comparing with its ground-truth label. Then through the chain rule, the gradient can be computed as:
| (11) |
where xi is the ith feature of input x. can be calculated through the automatic back propagation (BP) algorithm of deep learning framework like PyTorch. It’s worth to notice that is the gradient to make L larger, and the inverse gradient is the significance of xi to y. Therefore, we have:
| (12) |
where ∆xi indicates the significance of the ith feature of input x to output y.
The process is as follows. First, save a well-trained model and make prediction for each subject. Then, instead of using ground-truth age, the label of target age is set to a value larger than the predicted age and used to compute the loss with predicted age. To be specific, we set the label to the predicted age plus one day, so actually the computed loss of each output is one. Finally, we can calculate ∆x by Eq. 11 and Eq. 12, and it actually means how the brain connectivity would change if the subject becomes one day older.
However, the ∆x obtained from the input is asymmetric, which contradicts the symmetric input connectivity matrix. This is because the data in the symmetric position of the connectivity matrix, which means the same edge actually, have different flow directions when passing through GPC, E-P and N-P. For illustration, we show a simple example in Fig. 5, where the input graph has only three nodes i, j and k. The top box shows GPC, E-P and N-P layer in graph form and their specific formula representations. According to these formulas, we draw this process in matrix form and focus on the path that Eij and Eji through. Specifically, Eij enters output G by multiplying parameters , while Eji multiplies different parameters , which makes their gradient different.
Fig. 5.
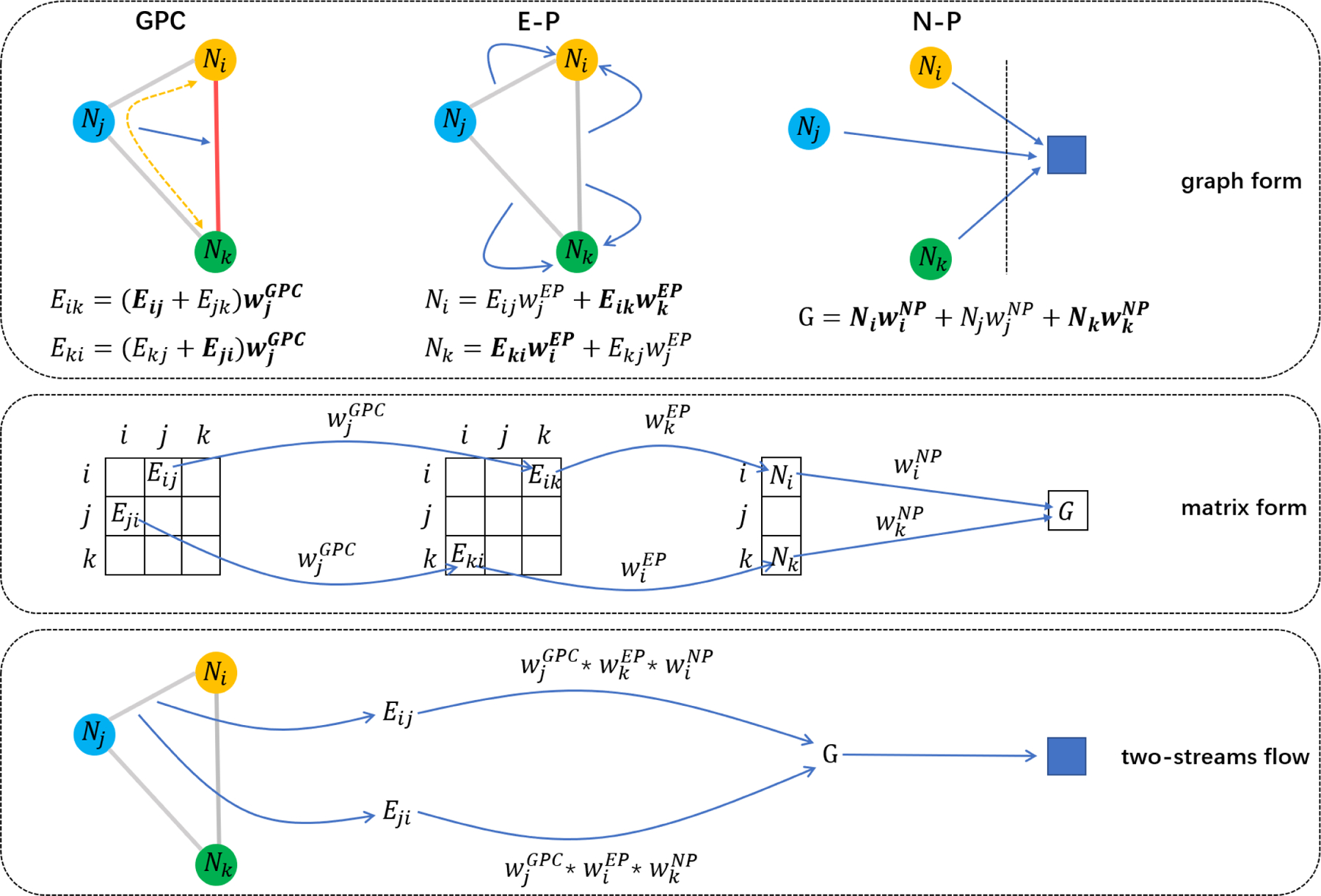
Illustration of GPC, E-P and N-P in graph form and matrix form. They show that even though they represent the same edge, Eij and Eji get through different path in model, which make their gradient different. So we should regard Eij and Eji as two streams of the edge and use multi-stream BP algorithm to calculate its real gradient.
Hence, we should regard Eij and Eji as two streams of the same edge, and these two streams are both meaningful and effective in the forward prediction and back propagation (BP). According to the multi-stream BP algorithm, the gradient accumulation of different path calculations can get the input gradient, which means that the sum of ∆Eij and ∆Eji is the real gradient of the edge, so we transpose the calculated ∆x and add to itself to get the real gradient:
| (13) |
There are four networks in our coarse-to-fine framework, one classification network in coarse stage and three prediction models (Young_M, Middle_M and Old_M) in fine stage (shown in Fig. 1). The classification network is not considered in backtracking for it is only a simple guide to the network behind. As for the three prediction networks, we divide the subjects into three groups according to the classification network, and utilize these subjects to calculate gradient through their corresponding networks. By averaging the gradient of slice matrices of same subjects, we can get each subject’s gradient, and the gradients of subjects in the same group are averaged to get three final gradients to represent the three age groups.
IV. Experimental Results
In our functional MRI scan with 420 time points, we adopted a sliding window of 50 points and a stride of 37 points, cutting it into 11 slices and calculating their connectivity matrices respectively. These correlation matrices of all the slices were taken as input samples for all comparison models. In the testing, we averaged the classification or prediction result of each slice to get the result of this MRI scan, and a subject’s final age prediction result was the average of all his scans (PA, AP, or retest) at the same age. We employed the 10-fold cross validation strategy for model evaluation. To prevent information leakage, subjects in the testing set were totally different from the ones in training set. Moreover, with stratified cross validation, the age distributions of the training set and testing set were kept similar to ensure the model reliability. There are four models in our coarse-to-fine framework, including one coarse stage classification model and three fine stage prediction models. In each fold of training, we first trained the classification model with the training set. Then, by fixing the well-trained classification model, we further trained three prediction models separately according to the subject’s age group. All models were trained with the same settings, including SGD optimizer with momentum of 0.9, batch size of 64 and learning rate as 0.001. The classification model was trained 20 times with 30 epochs each time, while the prediction models were trained 20 times with 20 epochs each time. We used L1 as the loss function, and calculated mean absolute error (MAE) and Pearson’s Correlation Coefficient to evaluate the performance of each method.
A. BC-GCN Model Ablation Study
We first test the regression performance of our proposed BC-GCN and compare it with other related methods. In this experiment, the input is the connectivity matrices of sliced rs-fMRI data, and the output is the predicted age of each subject. BC-GCN, BC-GCN-Res and BC-GCN-SE have the structure as described in Section III-A1. To conduct the fair comparison with BrainNetCNN [30], we adopted their proposed neural network structure and extended it into BrainNetCNN-Res and BrainNetCNN-SE by adding Res and SE block.
Methods in this experiment include BrainNetCNN [30] series and BC-GCN series. Both BC-GCN, BC-GCN-Res and BC-GCN-SE have the same structure of three 16-channel GPC layers, one 64-channel E-P layer and one 256-channel N-P layer. Note that the GPC layers in BC-GCN-Res and BC-GCN-SE are GPC-Res and GPC-SE separated. BrainNetCNN is set to a similar structure of three 16-channel E2E layers, one 64-channel E2N layer and one 256-channel N2G layer, and the Res blocks or SE blocks are added to the E2E layers to form BrainNetCNN-Res or BrainNetCNN-SE. For the fair comparison, we have carefully fined-tuned the BrainNetCNN and reported its results based on its best setting on our data set. ReLU activation function is used between any adjacent layers. The result of each method is shown in Table II.
TABLE II.
Prediction model performance by different methods.
| Method | MAE (days) | Method | MAE (days) |
|---|---|---|---|
| BrainNetCNN [30] | 70.57 | BC-GCN | 68.03 |
| BrainNetCNN-Res | 69.90 | BC-GCN-Res | 66.99 |
| BrainNetCNN-SE | 67.67 | BC-GCN-SE | 61.40 |
Beside experiments on the whole dataset, we further implemented the comparison with infants from birth to one year of age, because the the first year is the most important developmental stage in the lifespan. The experimental setting is the same as above. The corresponding MAE of age prediction is shown in Table III.
TABLE III.
Prediction model performance of subjects in year one.
| Method | MAE (days) | Method | MAE (days) |
|---|---|---|---|
| BrainNetCNN [30] | 36.54 | BC-GCN | 34.95 |
| BrainNetCNN-Res | 36.71 | BC-GCN-Res | 32.88 |
| BrainNetCNN-SE | 35.81 | BC-GCN-SE | 31.62 |
According to Table II and Table III, Res block and SE block can clearly improve the accuracy, especially in BC-GCN. Also BC-GCN series have better performance than BrainNetCNN series. In general, regardless of the age range of subjects, BC-GCN-SE performs the best. Therefore, we use BC-GCN-SE model for the following experiments.
B. Coarse-to-fine Prediction Framework
Based on experiments in the previous sub-section, we illustrate the prediction error curves along the age of several models, as shown in Fig. 6(a). All the models work well in the middle age group but badly in the young and old age group, showing a “high-low-high” age-error curve. It verified our assumption that brain connectivity developmental patterns are different in different age ranges and a single prediction model cannot model the heterogeneity well. As discussed in Section III-C, we set that age < 200 days as young, 200 – 400 days as middle and age > 400 days as old, and test the coarse-to-fine framework for its ability to improve the prediction accuracy.
In order to verify the feasibility of classification, we utilized BC-GCN-SE, the best model in the prediction task, and transformed it into a classifier. To be specific, the classifier output is 1 × 3 as the age group after a softmax function. To make the experiment more reasonable, we took 10% data from the training set as the validation data. The classification result is shown in Table IV.
As shown in Table IV, the accuracy in validation set is 85%. However, due to the lack of data, the model is not very robust and only reaches an accuracy of 75% in test set. But we can also see that all errors are between the adjacent categories, that is, the subject can only be mis-classified as its neighboring age groups. Therefore, as discussed in Section III-C, we adjust the training data of the three group-specific prediction models to make sure that some data from neighboring groups can also be included, as shown in Fig. 4.
Now we have one model as classifier to identify the age range and three age group specific models to predict infant age. In the following experiments, we adopted the same structure BC-GCN-SE for all four models but different parameters. These four models were trained respectively with different training sets. The experimental results are shown in Table V and Fig. 6(b). In Fig. 6(b), we show the comparison plot of prediction error. With the two-stage coarse-to-fine prediction framework, errors of the young and old age are significantly reduced. The error of middle age group has increased slightly, this is because even if our middle predicted model is trained by the whole dataset (as shown in Fig. 4), which make it equivalent to the original model, but some middle age subjects may be mis-classify to young age or old age and be predicted by wrong model, making it worse than being predicted by middle model (equal to original model). However, the improvement of young and old is so huge that the total performance of coarse-to-fine framework is still excellent.
TABLE V.
Experimental results (MAE) of three age ranges and overall results. CF: coarse-to-fine framework.
| Method | Age (days) | Overall | ||
|---|---|---|---|---|
| <200 | 200–400 | >400 | ||
| BC-GCN-SE | 49.99 | 37.71 | 100.73 | 61.40 |
| BC-GCN-SE-Deep | 51.47 | 40.54 | 104.66 | 64.22 |
| BC-GCN-SE with CF | 29.38 | 40.33 | 79.35 | 49.92 |
In Table V, prediction errors of different age ranges and overall results are shown. Obviously, a single BC-GCN-SE model can not work well in all age ranges while BC-GCN-SE with the coarse-to-fine framework strikes a balance between different age groups and has greatly improved the result in young group (< 200) and old group (> 400). To further verify the effectiveness of the coarse-to-fine model, we implemented a deeper model, BC-GCN-SE-Deep, which has one more GPC layer. However, its results are the worst among all three models, indicating the deeper model cannot help.
Besides, to evaluate the effect of data imbalance among age groups, we have designed an additional experiment, where the data is divided equally into three groups: < 248 days (83 subjects), 200 – 400 days (83 subjects) and > 394 days (82 subjects). We compare the age prediction error of these two different training data division methods and show them in Table VI. There is only subtle difference between their results. This indicates that slight data imbalance of training subject groups have very limited effects on the final result. As long as we employ separate models for different age groups, with the proper coarse-to-fine framework, the results can be clearly improved. Since the imbalanced data division strategy has better performance, we will use this setting in the following experiments.
TABLE VI.
Experimental results of three equal and unequal age groups in terms of MAE. CF: coarse-to-fine framework.
| Method | Overall MAE (days) | |||
|---|---|---|---|---|
| Equally divided groups (days) | <248 | 248–394 | >394 | |
| Subject number | 83 | 83 | 82 | |
| BC-GCN-SE | 46.89 | 38.52 | 99.26 | 61.40 |
| BC-GCN-SE with CF | 31.37 | 38.90 | 88.09 | 53.33 |
| Unequally divided groups (days) | <200 | 200–400 | >400 | |
| Subject number | 68 | 100 | 80 | |
| BC-GCN-SE | 49.99 | 37.71 | 100.73 | 61.40 |
| BC-GCN-SE with CF | 29.37 | 40.33 | 79.35 | 49.92 |
Moreover, we tested the performance of the coarse-to-fine framework on BrainNetCNN series models and BC-GCN series model, as shown in Table VII. In all experiments, the coarse-to-fine framework shows significant improvements compared with the origin models (more than 10 days improvement for each model), which further proves its effectiveness and universality. We think it is a powerful method and could be used more broadly in other applications.
TABLE VII.
Experiments of the coarse-to-fine framework on different models in terms of MAE. CF: coarse-to-fine framework.
| Method | Age (days) | Overall | ||
|---|---|---|---|---|
| <200 | 200–400 | >400 | ||
| BrainNetCNN –with CF |
61.27 36.96 |
34.29 42.68 |
123.82 99.07 |
70.57 59.30 |
| BrainNetCNN-Res –with CF |
60.50 34.21 |
37.09 38.27 |
118.89 97.69 |
69.90 56.32 |
| BrainNetCNN-SE –with CF |
57.41 27.69 |
36.32 35.99 |
115.59 89.33 |
67.67 50.92 |
| BC-GCN –with CF |
62.03 30.23 |
44.97 45.53 |
101.94 88.52 |
68.03 55.20 |
| BC-GCN-Res –with CF |
53.77 37.61 |
40.65 43.37 |
111.16 85.50 |
66.99 55.38 |
| BC-GCN-SE –with CF |
49.99 29.38 |
37.71 40.33 |
100.73 79.35 |
61.40 49.92 |
C. Comparison with State-of-the-art Methods
Several popular machine learning methods have been applied in the brain rs-fMRI, e.g., Multi-layer Perceptron (MLP), Convolutional Neural Networks (CNN) and Graph convolutional Networks (GCN) [31]. Recently, BrainNetCNN [30], PR-GNN [48] and BrainGNN [49] have been specifically proposed for fMRI data and performed well on various tasks. These methods can also be used for the task of infant age prediction. In this section, we will test and compare the performance of all these methods. These models’ setting are as follows. 1) The MLP model has two fully connected layers with channels of 64, 16. 2) CNN model has four convolution layers with channels of 16, 16, 64, 256. 3) GCN model consists of two graph convolution layers with channels of 32 and 8. 4) PR-GNN has two GATConv layers with channels of 64, 32, two TopK pooling layers with ratio 0.5 and a fully connected layer with channels of 16. 5) BrainGNN has two Ra-GConv layers with cluster of 8 and channels of 64, 32, two TopK pooling layers with ratio 0.5 and a fully connected layer with channels of 16. All comparing methods have been carefully adjusted and fine-tuned to reach their best performance on our dataset, including the number of layers, the channels of each layer and some regularization methods. Table VIII shows the MAE, Pearson’s correlation and numbers of parameters of these models and Fig. 7 shows the error bar of these models. Note that the mean MAE and std are calculated by 20 times of 10-fold results.
TABLE VIII.
Comparison with state-of-the-art methods. CF: coarse-to-fine framework. M = 106.
| Method | MAE (days) | Pearson | Parameters |
|---|---|---|---|
| MLP | 82.16±0.46 | 0.8619 | 0.804M |
| CNN | 89.90±1.72 | 0.8440 | 0.162M |
| GCN [31] | 95.10±1.74 | 0.8390 | 0.004M |
|
| |||
| BrainNetCNN [30] | 70.57±1.25 | 0.8965 | 2.011M |
| PR-GNN [48] | 79.02±2.51 | 0.8791 | 0.010M |
| BrainGNN [49] | 75.55±1.94 | 0.8869 | 0.076M |
|
| |||
| BC-GCN | 68.03±1.33 | 0.8979 | 2.009M |
| BC-GCN-Res | 66.99±1.15 | 0.9035 | 2.010M |
| BC-GCN-SE | 61.40±1.02 | 0.9032 | 2.010M |
|
| |||
| BC-GCN with CF | 55.20±1.80 | 0.9395 | 8.036M |
| BC-GCN-Res with CF | 55.38±1.94 | 0.9490 | 8.040M |
| BC-GCN-SE with CF | 49.92±1.00 | 0.9512 | 8.040M |
Fig. 7.
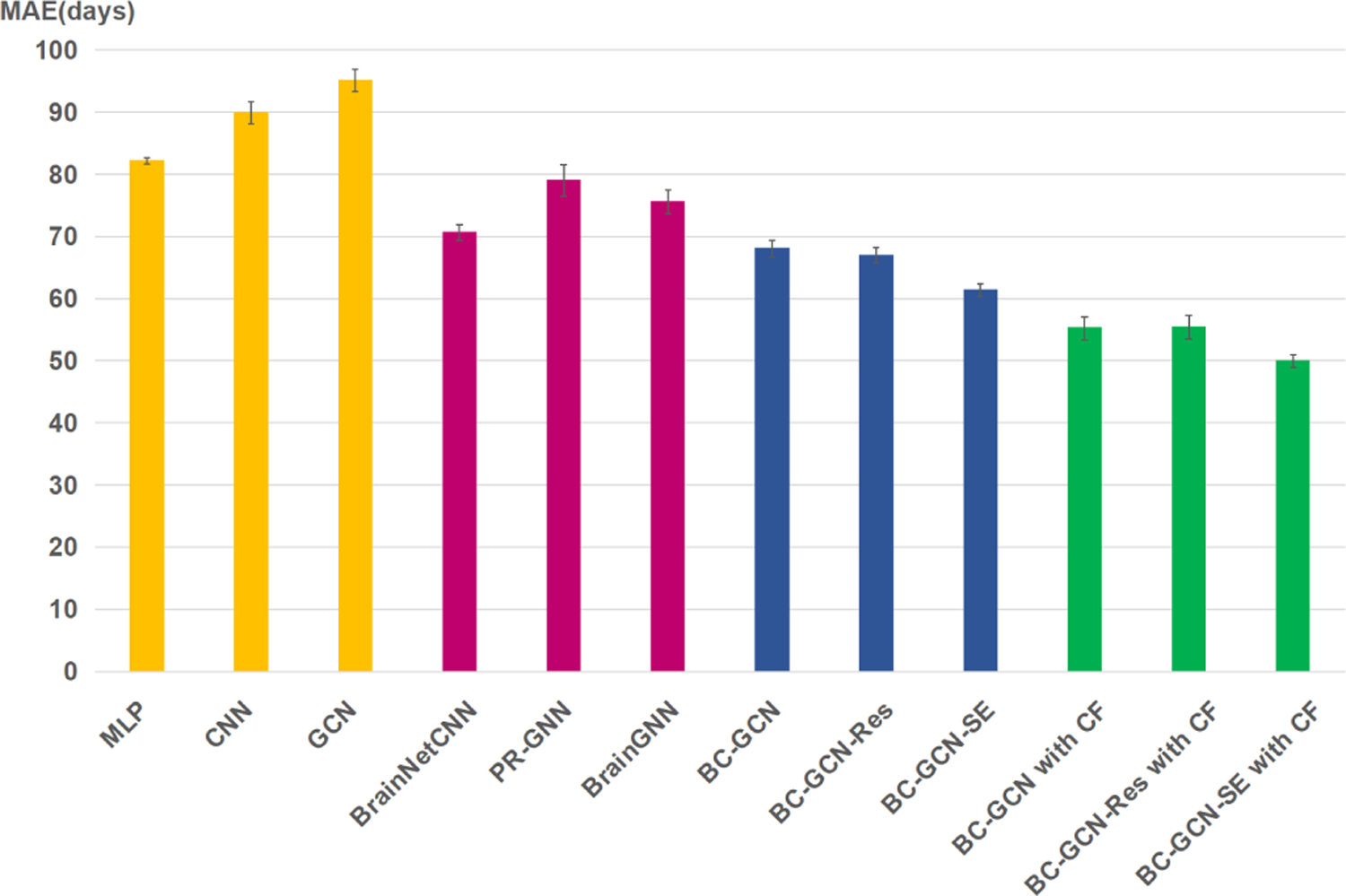
Error bars of state-of-the-art methods in terms of MAE with 20 times 10-fold cross validation experiments.
In Fig. 7, the yellow, pink, blue and green bars represent baseline methods, recent methods, proposed methods and proposed methods with the coarse-to-fine framework, respectively. Obviously, our proposed methods perform better than baseline methods and recent methods, and the coarse-to-fine framework can further improve the performance. As can be seen in Table VIII, our proposed method BC-GCN-SE with the coarse-to-fine framework reached the minimum MAE of 49.92 days and the maximum Pearson’s correlation 0.9512. From the view of parameters, MLP, CNN, GCN, PR-GNN and BrainGNN use very few parameters, but their results are poor. In fact, even if we increase the number of parameters in these models, their performance only degrades, showing their ineffectiveness. BC-GCN series, especially BC-GCN-SE, has the same number of parameters, but better performance compared with Brain-NetCNN. By combining with the coarse-to-fine framework, results of every BC-GCN method are significantly improved, even though it has more parameters. In general, our proposed BC-GCN-SE model and coarse-to-fine framework reach the state-of-the-art result of infant age prediction using the rs-fMRI data.
D. Maps of Predictive Connections
In order to find which connections are learned by BC-GCN to be predictive for age, we utilized the gradient backtracking method in III-D to calculate the importance of every functional connection. Since we have three prediction models (Young_M, Middle_M and Old_M) to represent three age groups, they should be calculated independently. According to the results of classification network in coarse stage, all subjects were classified in one of the three groups. Then, the gradient of each prediction network can be calculated through specific subject groups. The results are shown in Fig. 8, where a thicker line means a gradient with a larger absolute value and indicates greater impacts on brain development.
Fig. 8.
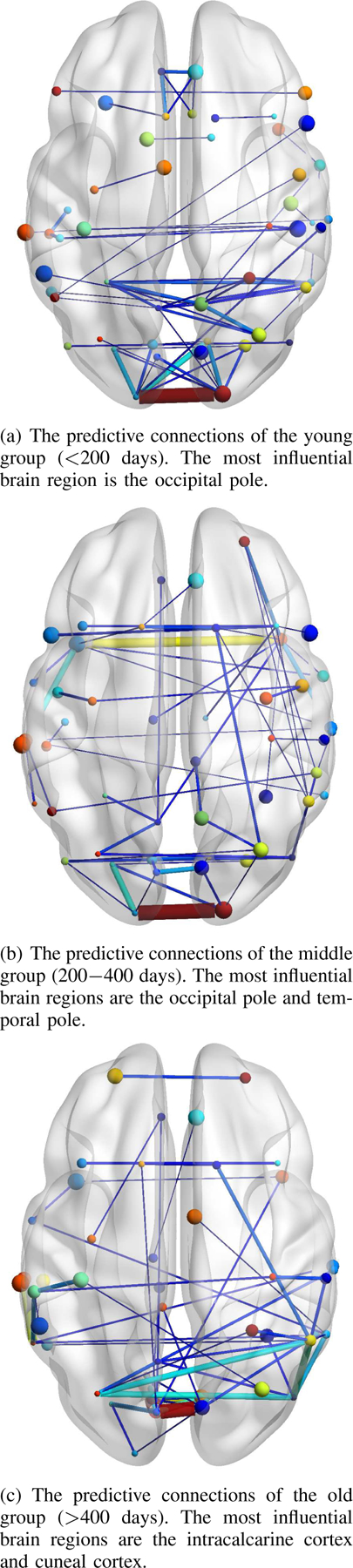
The predictive connections calculated from three prediction models (Young_M, Middle_M and Old_M), representing three age groups, respectively. The thicker edges indicate greater impacts on infant brain development.
As shown in Fig. 8, taking all three age groups into account, the left hemisphere and right hemisphere develop largely symmetrically during infancy, and the rapid development is concentrated in the brain regions associated with the primary senses like vision and hearing. To be specific, in the young age group (<200 days), the occipital pole shows great influence, and in the middle age group (200–400 days), beside the occipital pole, the temporal pole also develops rapidly. The occipital pole is mainly responsible for vision, while the temporal pole is involved in audiovisual and language functions, revealing the tendency of infant brain development. In the old age group (>400 days), the brain development focuses on the intra-calcarine cortex and cuneal cortex. Although not the primary responsible area of vision, the visual center of the brain is located near the intra-calcarine cortex and the area which controls peripheral vision located at the front of the region, making the entire area fairly important, as well as the cuneal cortex, which is most known for its involvement in basic visual processing. In general, the human brain develops so rapidly during infancy that the main influential brain regions are largely different among three age periods, while all these brain regions are closely related to vision or hearing.
V. Conclusions and Future Work
In this paper, we proposed Brain Connectivity Graph Convolutional Networks (BC-GCN) and its extended versions, BC-GCN-Res and BC-GCN-SE, to analyze rs-fMRI based functional connectivity network and applied them to predict the infant brain age. Further, we proposed a two-stage coarse-to-fine framework with one classification model and three group-specific prediction models (BC-GCN-SE with coarse-to-fine). Of note, these four models share the same network structure but different parameters. BC-GCN and its extended models show clear advantages over the competing methods. The coarse-to-fine framework further improved the performance, reducing the prediction error to as low as 49.9 days. In the future, we will apply the proposed BC-GCN and its extended models to other brain connectivity related problems.
Acknowledgments
X. Zhang and X. Xu are supported in part by the National Natural Science Foundation of China under grant U1801262; Guangdong Provincial Key Laboratory of Human Digital Twin Technology under grant 2022B1212010004; Science and Technology Program of Guangzhou under grant 2018-1002-SF-0561; Natural Science Foundation of Guangdong Province under grant 2018A030313295 and 2019A1515012146; Guangdong Basic and Applied Basic Research Foundation under grant No. 2021A1515011870.
The work of Gang Li was supported in part by NIH under Grant MH116225, Grant MH117943, and Grant MH123202. The work of Li Wang was supported in part by NIH under Grant MH117943.
Footnotes
Contributor Information
Yu Li, School of Electronic and Information Engineering, South China University of Technology, Guangzhou, CN 510640 China.
Xin Zhang, School of Electronic and Information Engineering, South China University of Technology, Guangzhou, CN 510640 China.
Jingxin Nie, School of Psychology, South China Normal University, Guangzhou, CN 510631 China.
Guowei Zhang, School of Electronic and Information Engineering, South China University of Technology, Guangzhou, CN 510640 China.
Ruiyan Fang, School of Electronic and Information Engineering, South China University of Technology, Guangzhou, CN 510640 China.
Xiangmin Xu, School of Electronic and Information Engineering, South China University of Technology, Guangzhou, CN 510640 China.
Zhengwang Wu, Department of Radilogy and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA.
Dan Hu, Department of Radilogy and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA.
Li Wang, Department of Radilogy and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA.
Han Zhang, Department of Radilogy and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA.
Weili Lin, Department of Radilogy and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA.
Gang Li, Department of Radilogy and Biomedical Research Imaging Center, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599 USA.
References
- [1].Cole JH and Franke K, “Predicting age using neuroimaging: innovative brain ageing biomarkers,” Trends in Neurosciences, vol. 40, no. 12, pp. 681–690, 2017. [DOI] [PubMed] [Google Scholar]
- [2].Bashyam VM et al. , “MRI signatures of brain age and disease over the lifespan based on a deep brain network and 14 468 individuals worldwide,” Brain, vol. 143, no. 7, pp. 2312–2324, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Armanious K and Yang B, “Age-Net: An MRI-based iterative framework for brain biological age estimation,” IEEE Transactions on Medical Imaging, 2021. [DOI] [PubMed]
- [4].Hu D et al. , “Disentangled-Multimodal Adversarial Autoencoder: Application to Infant Age Prediction With Incomplete Multimodal Neuroimages,” IEEE Transactions on Medical Imaging, vol. 39, no. 12, pp. 4137–4149, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Feng X et al. , “Estimating brain age based on a uniform healthy population with deep learning and structural magnetic resonance imaging,” Neurobiology of Aging, vol. 91, pp. 15–25, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Cheng J et al. , “Brain Age Estimation From MRI Using Cascade Networks with Ranking Loss,” IEEE Transactions on Medical Imaging, 2021. [DOI] [PubMed]
- [7].Craddock RC et al. , “Imaging human connectomes at the macroscale,” Nature Methods, vol. 10, no. 6, p. 524, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Smith SM et al. , “Functional connectomics from resting-state fMRI,” Trends in Cognitive Sciences, vol. 17, no. 12, pp. 666–682, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Griffanti L et al. , “Challenges in the reproducibility of clinical studies with resting state fMRI: An example in early Parkinson’s disease,” NeuroImage, vol. 124, pp. 704–713, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Farràs-Permanyer L, Guàrdia-Olmos J, and Peró-Cebollero M, “Mild cognitive impairment and fMRI studies of brain functional connectivity: the state of the art,” Frontiers in Psychology, vol. 6, p. 1095, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Biswal BB et al. , “Toward discovery science of human brain function,” National Academy of Sciences, vol. 107, no. 10, pp. 4734–4739, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Solo V et al. , “Connectivity in fMRI: Blind spots and breakthroughs,” IEEE Transactions on Medical Imaging, vol. 37, no. 7, pp. 1537–1550, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Van Den Heuvel MP and Pol HEH, “Exploring the brain network: A review on resting-state fmri functional connectivity,” European Neuropsychopharmacology, vol. 20, pp. 519–534, 2010. [DOI] [PubMed] [Google Scholar]
- [14].Dosenbach NU et al. , “Prediction of individual brain maturity using fMRI,” Science, vol. 329, no. 5997, pp. 1358–1361, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Monti RP et al. , “Interpretable brain age prediction using linear latent variable models of functional connectivity,” PloS One, vol. 15, no. 6, p. e0232296, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Vergun S et al. , “Characterizing functional connectivity differences in aging adults using machine learning on resting state fMRI data,” Frontiers in Computational Neuroscience, vol. 7, p. 38, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Smyser CD et al. , “Prediction of brain maturity in infants using machine-learning algorithms,” NeuroImage, vol. 136, pp. 1–9, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Liem F et al. , “Predicting brain-age from multimodal imaging data captures cognitive impairment,” NeuroImage, vol. 148, pp. 179–188, 2017. [DOI] [PubMed] [Google Scholar]
- [19].Kam T-E, Zhang H, Jiao Z, and Shen D, “Deep learning of static and dynamic brain functional networks for early MCI detection,” IEEE Transactions on Medical Imaging, vol. 39, no. 2, pp. 478–487, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Lawrence S, Giles CL, Tsoi AC, and Back AD, “Face recognition: A convolutional neural-network approach,” IEEE Transactions on Neural Networks, vol. 8, no. 1, pp. 98–113, 1997. [DOI] [PubMed] [Google Scholar]
- [21].Wang H et al. , “Recognizing brain states using deep sparse recurrent neural network,” IEEE Transactions on Medical Imaging, vol. 38, no. 4, pp. 1058–1068, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Wang Y, Wang Y, and Lui YW, “Generalized recurrent neural network accommodating dynamic causal modeling for functional MRI analysis,” NeuroImage, vol. 178, pp. 385–402, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Antipov G, Baccouche M, Berrani S-A, and Dugelay J-L, “Effective training of convolutional neural networks for face-based gender and age prediction,” Pattern Recognition, vol. 72, pp. 15–26, 2017. [Google Scholar]
- [24].Zhou J et al. , “Graph neural networks: A review of methods and applications,” AI Open, vol. 1, pp. 57–81, 2020. [Google Scholar]
- [25].Finn ES et al. , “Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity,” Nature Neuroscience, vol. 18, no. 11, p. 1664, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].He L, Li H, Holland SK, Yuan W, Altaye M, and Parikh NA, “Early prediction of cognitive deficits in very preterm infants using functional connectome data in an artificial neural network framework,” NeuroImage: Clinical, vol. 18, pp. 290–297, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Takagi Y, Hirayama J.-i., and Tanaka SC, “State-unspecific modes of whole-brain functional connectivity predict intelligence and life outcomes,” BioRxiv, p. 283846, 2018. [Google Scholar]
- [28].Suk H-I, Wee C-Y, Lee S-W, and Shen D, “State-space model with deep learning for functional dynamics estimation in resting-state fMRI,” NeuroImage, vol. 129, pp. 292–307, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Bullmore E and Sporns O, “Complex brain networks: graph theoretical analysis of structural and functional systems,” Nature Reviews Neuroscience, vol. 10, no. 3, pp. 186–198, 2009. [DOI] [PubMed] [Google Scholar]
- [30].Kawahara J et al. , “BrainNetCNN: Convolutional neural networks for brain networks; towards predicting neurodevelopment,” NeuroImage, vol. 146, pp. 1038–1049, 2017. [DOI] [PubMed] [Google Scholar]
- [31].Kipf TN and Welling M, “Semi-supervised classification with graph convolutional networks,” in Proceedings of International Conference on Learning Representations, 2017. [Google Scholar]
- [32].Niepert M, Ahmed M, and Kutzkov K, “Learning convolutional neural networks for graphs,” in Proceedings of International Conference on Machine Learning, 2016. [Google Scholar]
- [33].Defferrard M, Bresson X, and Vandergheynst P, “Convolutional neural networks on graphs with fast localized spectral filtering,” in Proceedings of International Conference on Neural Information Processing, 2016. [Google Scholar]
- [34].Parisot S et al. , “Disease prediction using graph convolutional networks: application to autism spectrum disorder and Alzheimer’s disease,” Medical image analysis, vol. 48, pp. 117–130, 2018. [DOI] [PubMed] [Google Scholar]
- [35].Zheng C et al. , “Robust graph representation learning via neural sparsification,” in Proceedings of International Conference on Machine Learning, 2020. [Google Scholar]
- [36].Stam C et al. , “The relation between structural and functional connectivity patterns in complex brain networks,” International Journal of Psychophysiology, vol. 103, pp. 149–160, 2016. [DOI] [PubMed] [Google Scholar]
- [37].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016. [Google Scholar]
- [38].Hu J, Shen L, and Sun G, “Squeeze-and-excitation networks,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2018. [Google Scholar]
- [39].Hu D, Wu Z, Lin W, Li G, and Shen D, “Hierarchical rough-to-fine model for infant age prediction based on cortical features,” Biomedical and Health Informatics, vol. 24, no. 1, pp. 214–225, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Howell BR et al. , “The UNC/UMN Baby Connectome Project (BCP): An overview of the study design and protocol development,” NeuroImage, vol. 185, pp. 891–905, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Zhang H, Shen D, and Lin W, “Resting-state functional MRI studies on infant brains: a decade of gap-filling efforts,” NeuroImage, vol. 185, pp. 664–684, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Hu D et al. , “Existence of Functional Connectome Fingerprint During Infancy and Its Stability Over Months,” Journal of Neuroscience, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Wang L et al. , “Volume-based analysis of 6-month-old infant brain MRI for autism biomarker identification and early diagnosis,” in Proceedings of International Conference on Medical Image Computing and Computer-assisted Intervention, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Kam T-E et al. , “A deep learning framework for noise component detection from resting-state functional MRI,” in Proceedings of International Conference on Medical Image Computing and Computer-Assisted Intervention, 2019. [Google Scholar]
- [45].Smith SM et al. , “Advances in functional and structural MR image analysis and implementation as FSL,” NeuroImage, vol. 23, no. Suppl 1, pp. S208–S219, 2004. [DOI] [PubMed] [Google Scholar]
- [46].Zhou B, Khosla A, Lapedriza A, Oliva A, and Torralba A, “Learning deep features for discriminative localization,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016. [Google Scholar]
- [47].Selvaraju RR, Cogswell M, Das A, Vedantam R, Parikh D, and Batra D, “Grad-cam: Visual explanations from deep networks via gradient-based localization,” in Proceedings of the IEEE International Conference on Computer Vision, 2017. [Google Scholar]
- [48].Li X et al. , “Pooling regularized graph neural network for fMRI biomarker analysis,” in Proceedings of International Conference on Medical Image Computing and Computer-Assisted Intervention, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].——, “Braingnn: Interpretable brain graph neural network for fMRI analysis,” bioRxiv, pp. 2020–05, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]


