A Framework for a Health Economic Evaluation Model for Patients with Sickle Cell Disease to Estimate the Value of New Treatments in the United States of America

Abstract

Background

Sickle cell disease (SCD) is an inherited blood disorder associated with lifelong morbidity and increased risk of mortality that affects approximately 100,000 individuals in the United States (US), primarily of African–American descent. Due to these complications, individuals with SCD typically incur high healthcare costs. With a number of costly but potentially curative SCD therapies on the horizon, understanding the progression of SCD and economic burden to insurers and patients is vital.

Objective

The aim is to develop a framework to understand the progression and costs of SCD that could be used to estimate how new treatments can impact the progression and costs of the disease.

Methods

We detail how we will create a simulation model that represents the natural history of a population and allows for the characterization of the impact of novel therapies on the disease, associated costs, and outcomes in comparison to current management.

Conclusion

In this report, we describe a conceptual approach to modeling SCD to determine the relative clinical and economic impact of new gene therapies compared to conventional therapies with a goal of providing a flexible approach that could inform the clinical management of SCD for patients, payers, and policy makers.

Key Points for Decision Makers

Long-term simulation models are often necessary to estimate the benefits and costs of new treatments for sickle cell disease.

The Hutchinson Institute Sickle Cell Disease Outcomes Research and Economics (HISCORE) model is designed to capture patient disease progression and be able to take short- or medium-term effects and extrapolate them across a patient’s lifetime.

Introduction

Sickle cell disease (SCD) is an inherited blood disorder caused by a mutation in the β-globin gene that affects approximately 100,000 individuals in the United States (US), primarily of African–American descent, and is associated with lifelong morbidity and increased risk of mortality [1]. Individuals with SCD experience numerous debilitating and life-threatening complications throughout their lifetimes, including vaso-occlusive pain episodes, which occur when vascular obstruction leads to ischemic tissue damage, and are the most common reason for hospital admission [2–4].

Due to these complications, individuals with SCD typically incur high healthcare costs, with inpatient care contributing the greatest share [5]. Understanding the progression of SCD and economic burden to health insurers and patients is particularly important at this time. A number of very costly but potentially curative therapies for SCD are on the horizon [6], with ten gene therapies currently in the clinical testing stage [7]. These therapies have the potential to revolutionize care for SCD; however, with expected prices of nearly $2 million in US dollars per treatment [8], issues of economic burden, affordability and access will be points of concern among patients, payers, and policy makers [9, 10].

Worldwide, economic evaluation is a tool that provides quantitative synthesis of expected benefits and costs of new therapies, such that their value can be compared to existing treatments for the disease and across many diseases [11]. A core aspect of most economic evaluations is creating a simulation model that can clearly and accurately represent the natural history for populations. Such models enable health technology assessors to characterize the impact of novel therapies on the disease, associated costs, and outcomes in comparison to current management. Research on economic evaluation within SCD has found that the majority of prior studies used modeling and the most common modeling approach was cohort-based Markov models, which have benefits—they are easier to understand and computationally less demanding than other approaches—but also limitations [12]. Specifically, cohort-based Markov models follow the cohort as it moves across health states, and have a memoryless “Markovian” assumption (i.e., that transition probabilities only depend on the current health state, not one’s health history). It is possible to create additional states that can capture a cohort’s history; but this can quickly result in “state explosion” [13]. This is particularly concerning for SCD as it is associated with dozens of conditions that are interrelated. For SDC, there is rarely a “standard” patient experience, rather there is a large amount of heterogeneity in experiencing different related acute and chronic conditions. Therefore, to fully capture the complex, dynamic nature of disease progression, we outline the creation of an individual-based microsimulation model that allows for patients to have unique health experiences. Accordingly, in this report, we outline a conceptual approach to creating a patient-level epidemiological model for patients with SCD, the Hutchinson Institute Sickle Cell disease Outcomes Research and Economics (HISCORE) model, to determine the relative clinical and economic impact of new gene therapies against current therapy.

Methods

Approach to Economic Evaluations

Modeling

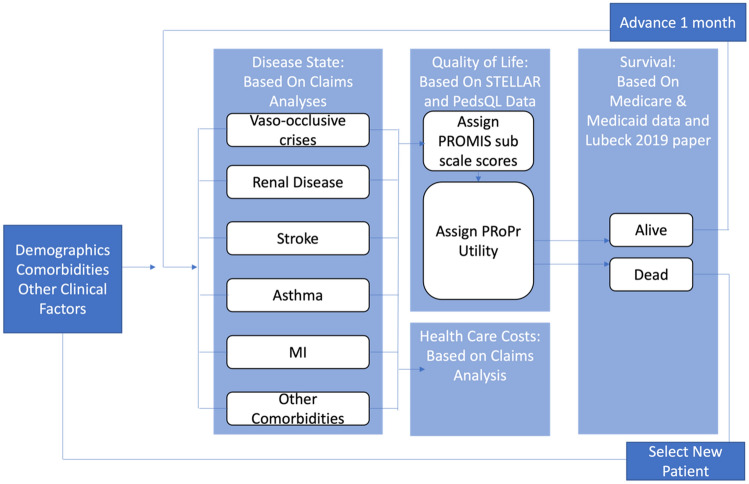
We will develop a patient-level epidemiological model (microsimulation) informed with data from insurance claims datasets (Truven MarketScan, Medicare, and Medicaid), previously published research, and clinical trial data (see Table 1) for SCD patients called the Hutchinson Institute Sickle Cell disease Outcomes Research and Economics (HISCORE). The model will be a patient-level life-course epidemiological model for the SCD population for any duration from the health care payer perspective (Fig. 1). The basic assumptions of this SCD simulation model are that SCD is a progressive chronic disease and that the risk of chronic and acute complications for a period of time are dependent on sociodemographic data (e.g., age and gender) and acute and chronic disease history (see Fig. 1 for the model structure and selected variables). To build this model, we follow established model development guidelines from the International Society for Pharmacoeconomics and Outcomes Research (ISPOR)-Society of Medical Decision Making [14, 15].

Table 1.

Source of data for model components

Model component	Source of data
Acute and chronic disease states	Medicare, Medicaid, and MarketScan claims data
Utility weights	PROMIS29 data for adults PedsQL for children
Survival	Medicare and Medicaid claims Lubeck et al. 2019 [1]
Cost	Medicare, Medicaid, and MarketScan claims data

PedsQL Pediatric Quality of Life, PROMIS Patient-Reported Outcomes Measurement Information System

Fig. 1.

The Hutchinson Institute Sickle Cell disease Outcomes Research and Economics (HISCORE) model structure. MI myocardial infarction, PedsQL Pediatric Quality of Life, PROMIS Patient-Reported Outcomes Measurement Information System, PROPr PROMIS-Preference score, STELLAR Sickle cell Transplantation Evaluation of Long-term and Late Effects Registry

The model is based on a stochastic, discrete-time, illness-death model with monthly cycles that integrates separate risk equations for acute and chronic health states and mortality, each derived from empirical research (described in the next section).

During each monthly cycle, the probability of every outcome is calculated for each patient according to the suite of risk equations. Using Monte Carlo modeling principles, each probability is compared to a random number drawn from a uniform distribution (range 0–1) to determine whether each patient develops the given outcome. Patients are allowed to have multiple outcomes in any given year. Probability of death is calculated based on complication histories from the previous years and current year. When the model predicts death, the total years lived are calculated and the individual exits the model; otherwise, the individual survives that cycle, and the patient characteristics and disease histories update for the next monthly cycle. For model development and simulation, we will use Stata MP 17.

Databases

For this study, we plan to create a longitudinal cohort of patients with SCD using health insurance claims data. We will create a prevalence cohort of all patients diagnosed with SCD in claims data between 2007 and 2018. These dates were chosen due to data availability; specifically, prescription drug data for the Medicare population were reliably available starting in 2007, and newer data were not available when the project was started. We will use Medicare claims to construct a model for patients over 65 and Truven Health Analytics MarketScan data for patients with SCD under age 65. The Truven database contains claims data for over 115 million individuals and their dependents from all 50 states with employer-sponsored private health insurance. For those over 65, we used Medicare fee-for-service claims. Both data sources include outpatient and inpatient medical claims, prescription drug claims, health utilization records, payer and individual costs, and demographic characteristics of individuals, including their age at enrollment, sex, geographic region, and insurance plan type. We are not able to track patients as they move between insurers, as patient identifiers are not consistent between data sources.

We will identify patients who have SCD as having at least one inpatient claim or two outpatient or emergency department (ED) claims for SCD in any position using International Classification of Disease 9th and 10th edition codes (ICD-9 282.6, 282.41, 282.42, ICD-10 D57, D57.8, excluding 282.5 and D57.3; sickle cell trait). In prior work, this criterion was found to have over 90% sensitivity and specificity in identifying individuals with SCD [16]. Individuals will be followed from the start of when they enrolled in their health insurance plan and claims are observable (irrespective of when SCD was diagnosed). Patients will be followed from identification in claims until death, disenrollment, or the study completion date of December 31, 2018. The study period was divided into monthly periods. We required patients to be continuously enrolled for at least 1 year.

Characterizing Illness History and SCD-Related Complications from Health Insurance Claims

SCD is characterized by acute disease-related events that can be self-limited and long-term comorbidities that can progress in severity over time. Acute and chronic conditions are referred to as health states in the health economic evaluation literature. The included acute and chronic conditions are shown in Tables 2 and 3.

Table 2.

Event rates for chronic conditions for patients with sickle cell disease who received health insurance from Medicare or Medicaid

Health state	Individuals	Months	Events	Incidence rate per 10,000 person-month	95% confidence interval
Chronic mental health condition	41,295	2,559,825	7392	28.8	(28.23–29.54)
Myocardial infarction	42,845	2,897,195	1404	4.8	(4.6–5.11)
Chronic pain	41,077	2,494,750	8108	32.5	(31.8–33.22)
Leg ulcers	85,675	5,814,647	1230	2.1	(2–2.24)
Fatigue	82,347	4,980,404	16,496	33.1	(32.63–33.63)
Chronic renal disease	79,992	4,897,729	17,881	36.4	(35.84–36.9)
Liver disease	85,798	5,822,314	2000	3.4	(3.29–3.59)
Asthma	77,664	4,563,446	16,689	36.6	(36.02–37.13)
Pulmonary hypertension	83,890	5,480,684	7107	13	(12.67–13.27)
Avascular necrosis	82,858	5,295,591	8429	15.9	(15.58–16.26)
Chronic lung disease	81,337	4,985,315	14,223	28.4	(27.73–29.05)
Cognitive impairment	84,408	5,559,580	5592	10.1	(9.8–10.33)
Sleep breathing	81,422	4,815,332	18,563	38.5	(38–39.11)
Other cardiovascular disease	74,808	4,077,692	42,301	59.6	(58.85–60.35)
Ocular disease	85,803	5,822,016	1164	2	(1.89–2.12)

Table 3.

Event rates for acute conditions for patients with sickle cell disease who received health insurance from Medicare or Medicaid

Health state	Events	Events per 10,000 person-month	95% confidence interval	Intraclass coefficient*
Vaso-Occlusive Crisis	760,411	1211.1	(1197.93–1224.2)	0.3764
Fever	157,125	264.3	(261.11–267.52)	0.0808
Cholecystitis	31,675	56.4	(54.75–58.05)	0.1041
Splenic	9281	15.9	(15.21–16.53)	0.0518
Priapism	11,102	17.9	(16.63–19.23)	0.2086
Dactylitis	2387	4	(3.73–4.29)	0.0324
Acute Chest Syndrome	66,690	108.2	(106.47–109.96)	0.0512
Infection	273,628	455.4	(450.59–460.28)	0.1137
Sepsis	59,044	107.7	(105.1–110.24)	0.1405
Acute Renal Disease	53,587	103	(100.2–105.85)	0.1882
Multiple Organ Failure	7292	15.6	(14.68–16.58)	0.1458
Acute Anemia	15,362	25.3	(24.3–26.35)	0.0814

*Proportion of total variance estimated using linear random-effects model with constant term only

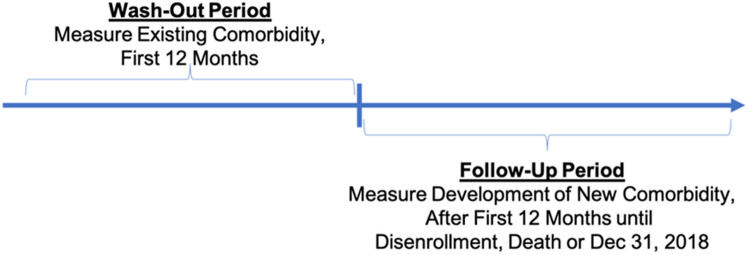
Patients enter and exit the database at various times in their disease history, making it difficult to distinguish between new and pre-existing comorbidities that a patient had when they were first observed in the database. Consistent with other research in pharmacoepidemiology and modeling, we break time into “wash-out” and “follow-up” observation periods (Fig. 2). In the “wash-out” period, patient records are scanned for claims associated with a specific comorbidity. If present, the comorbidity is considered pre-existing (i.e., a prevalent case). However, if the patient has claims associated with a comorbidity in the “follow-up” period but not in the “wash-out” period, it is considered to be new (an incident case). For acute events that are transitory, it is not necessary to identify a new versus a previously experienced acute event.

Fig. 2.

Identification of SCD-related comorbid conditions. Time is broken into “wash-out” and “follow-up” observation periods to help distinguish between new and pre-existing comorbidities. SCD sickle cell disease

Using these data sources, we will break the data into two samples, a model development sample (70% of the data) and a hold-out sample (30% of the sample). The hold-out sample will be used to test how well the model predicts outcomes.

Creating Risk Equations for the SCD-Related Comorbidities and Survival

Risk equations (referred to as disease modules in the health economic evaluation literature) quantify the relationship between a patient’s demographics and other comorbidities and developing a new disease of interest. Specifically, for comorbidities, multivariate Cox time-to-event models, using age to estimate the time until incidence of a new chronic disease, will be developed [17]. We include all demographics and indicators of other health states as candidate covariates in the model but only include covariates that are statistically significant. We test that the Cox model does not violate the proportional hazards assumptions based on Schoenfeld residuals and adjust the model to overcome any violations. The final model transitions from a non-parametric Cox model to a parametric survival model, which is standard in health economic models as they can easily estimate transition probabilities and are able to extrapolate outside the study period window. We determine the appropriate functional form (Weibull, Gompertz, or exponential) based on the models’ Akaike information criterion (AIC) and Bayesian information criterion (BIC). For acute conditions, we utilize logistic equations, adjusting for patients’ demographics and health status, and account for repeated observations by clustering standard errors at the patient level.

We estimate mortality for patients using multiple approaches depending on a patients age and insurance status. For individuals who receive Medicare benefits either due to age or disability and low-income (i.e., dual eligibles), the data measures mortality. For these individuals, we will develop equations that quantify the relationship between demographics and comorbidities and mortality. We use the same approach detailed above when developing disease modules. Briefly, we estimate a multivariate Cox time-to-event model that includes statistically significant covariates and convert this model into a parametric time-to-event model based on the fit of the model. For younger, privately insured patients (i.e., patients under age 65), claims data have limited and unreliable information on mortality. For this population, we create age- and sex-specific survival probabilities based on previously published survival estimates of the sickle cell population (1) and then digitize the survival curves using GraphGrabber. We then compare the survival rates between the two approaches for younger populations, and if similar (predictions with 95% confidence intervals overlapping), we use the equations based on the Medicare and Medicaid populations.

Accounting for Quality of Life

For this study, we will use measurements of patient’s quality of life from representative studies of SCD patients. One potential source is the Sickle cell Transplantation Evaluation of Long-Term and Late Effects Registry (STELLAR) study [18]. STELLAR collects information on multiple outcomes over time, including quality of life, for individuals that receive a transplant and matched controls. STELLAR collected demographic, health states/status, and quality-of-life data using Patient-Reported Outcomes Measurement Information System (PROMIS) 29 at multiple time points. PROMIS29 is a validated and widely used computer adaptive measure of quality of life. For children, quality of life has been measured using the Pediatric Quality of Life (PedsQL) from the Sickle Cell Clinical Research and Intervention Program (SCCRIP) [19]. The PedsQL consists of four domains: physical, emotional, social, and school functioning. Notably for this study, it does not have a pain-specific domain. For the PedsQL, we will directly transform the PedsQL scores to a quality-adjusted life year (QALY) value using published algorithms based on a UK sample of children [20].

Using the rich data source for adults, the PROMIS29 collects quality-of-life data for the following seven domains: (1) physical function, (2) fatigue, (3) pain interference, (4) depressive symptoms, (5) anxiety, (6) ability to participate in social roles and activities, and (7) sleep disturbance.

We estimate a patient’s domain-specific quality of life as a function of demographics and health states using a generalized linear model with an appropriate link and family. The regression-based approach will allow us to do the following: (1) incorporate any change in quality of life as people age, (2) estimate the effect of having multiple health states and if there are interactions between health states, and (3) estimate the temporary impact of having an acute condition as well as the continued impact of having a chronic condition. We will do this for each of the seven PROMIS29 domains.

By modeling quality of life at the domain level, we will be able to directly model and understand how different acute and chronic conditions impact patients’ experiences of any of the seven domains. We believe this domain-specific modeling approach is essential in being able to incorporate the influence of pain. However, this study is unlikely to be able to measure the impact of vaso-occulusive crises (VOCs) on patients’ quality of life as they are transitory. Therefore, we will rely on previous published research to directly change the pain domain score [21]. This approach ensures that we incorporate both VOCs and other sources of pain when estimating patients’ overall quality of life.

We then aggregate across domains and transform the PROMIS scores into a QALY value using the PROMIS-Preference score (PROPr) algorithm [22]. This transforms a multi-dimensional measurement of quality of life into a one-dimensional QALY measure. If there are any health states/events that patients did not experience in this dataset, we rely on other previously published research [23] to either adjust their PROMIS overall or domain-specific score or the QALY value that was estimated. This approach is extremely flexible and ensures that we can incorporate relevant research into our model seamlessly. For our model (Fig. 1), we take the quality-of-life equations and use them to assign a patient their QALY values at the end of each cycle based on their demographics, existing health states, and any newly entered health states.

Measuring Costs

For this model, we use the health care claims used to characterize disease progression to assign monthly health care spending. The analysis employs a two-part model where the first part of the model predicts if a patient had any spending and the second part of the model estimates the spending among patients who have spending that month. We use logistic regression adjusting for demographics and health states for part one of the two-part cost model, clustering standard errors at the patient level to account for repeated observations. For the second part of the two-part cost model, we use a generalized linear model adjusted for demographics and health states with a log link and identify the appropriate family determined using a modified Park test. Similar to estimating a patients QALY value, we take the spending equations and use them to assign a patient their spending at the end of each cycle based on their demographics, existing health states, and any newly identified health events.

Results

Generating Outcomes from the Model

In the prior sections we detailed the various components that will be used in the model and provided some detail on how the pieces would be related to each other. In this section, we will build on the prior section and detail how the simulation model that we intend to use will estimate SCD progression and costs and how we would be able to estimate the potential cost-effectiveness of treatments and programs.

Using the equations that we previously detailed, we create a patient-level life course epidemiological model, a microsimulation model, for patients with SCD. The model integrates separate risk equations for health states and the relationships between experienced health states and risks for related health states (e.g., myocardial infarction and stroke). For each cycle, we first estimate if a patient has one or more health events. Then we assign a patient’s costs and QALYs based on the events a patient experienced as well as a patient’s overall health states and demographics. When a patient dies in the model, their experiences (years lived, time in health states, QALYs, and health care costs) are recorded and the individual exits the model.

Model users are able to take short-term clinical trial results to estimate the long-term impact of new treatments and their impact on many aspects of patient well-being. One unique aspect is how the model characterizes pain, a prominent and debilitating feature of SCD with multiple etiologies. If a treatment impacts a patient’s experience of pain, we directly incorporate that into the model given the flexible approach we have used in incorporating pain in quality of life and health care utilization. Second, we quantify the long-term impact of reducing the risk of some events, such as asthma, MI, or renal disease. For example, if we reduce or at least delay patient’s asthma, we can demonstrate how this slows the cascade of additional events. Third, we can directly estimate how both of these factors impact health care spending on patients over time and the relative value of treatments.

Validation and Calibration

To assess internal validity, consistent with recommendations from the ISPOR Good Research Practices Task Force, the models are subjected to extensive internal testing and debugging, with evidence provided as to the process [14, 15]. Additionally, we test null and extreme input values to determine whether the model produces expected outputs.

Following this step, we assess the calibration of the model by visual inspection comparing the observed and predicted outcome for the hold-out sample, as well as conduct a formal statistical test (e.g., Hosmer–Lemeshow test). We compare the forecasted cumulative incidence of complications and death to the expected cumulative incidence in the hold-out sample using non-parametric (lifetable) methods. If at any stage, we find that the predicted and actual outcomes are not similar, then we re-estimate the equations to examine if different functional forms or specification of covariates improves prediction. However, if not, we calibrate the model by modifying intercepts and covariate coefficients until we match trends observed in the hold-out sample.

We externally validate our model by comparing age-adjusted rates of comorbidities and acute events generated from the model to those observed in prior research. We expect that the model may under-report VOCs, as many patients manage these events without having to go to the hospital or see their physician. If this is found, we will examine the literature to identify what proportion of VOC events we are not observing and amend the VOC event model to include an additional event of “VOC without medical intervention.” It is important to distinguish VOCs that require medical intervention and those that do not as they have different spending and quality-of-life implications.

Uncertainty Analysis

Once the optimal model is chosen, bootstrapping, which involves resampling the original data, will be used to estimate uncertainty around all health state and cost model parameters. All equations will be re-estimated simultaneously to capture the confidence intervals of all models as well as the correlation/covariance of model parameters. We will report not only the confidence intervals for all model parameters, but also the correlation and covariance matrix for all regression-based models. This allows us and others to easily conduct probabilistic sensitivity analyses in order to address higher order uncertainty.

Discussion

Using the Model for Decision Making and Policy

Several gene therapy and pain management trials exist for improving SCD outcomes [24, 25]. While all of these trials have had, or are expected to have, success in improving SCD outcomes, it remains unclear which of these new therapies are most cost-effective [9]. In addition, none of these strategies exists in isolation and different combinations of the individual strategies may be considered.

The approach outlined for model development is applicable and transferrable to many other progressive chronic conditions that result in the development of other acute and chronic conditions. However, SCD is unique since patients are born with this disease. Therefore, when we observe a 30-year-old in the data, we assume that the person has had SCD for their entire life. This is rarely true with other conditions and limits the generalizability of the approach.

The HISCORE model has limitations. First, disease progression is based on claims data and, therefore, biomarkers are not measured or incorporated into disease progression. Second, we are not able to directly link patients across datasets, which limits our ability to track the disease progression overtime for patients. However, we require a year wash-out period in hopes of capturing chronic disease burden even if a patient has switched insurers. Third, since we are relying on insurance records, we will not include patients who are uninsured, and therefore, results may not be generalizable to this population. Fourth, the study uses costs from the US, which are not valid in other settings; however, future research could amend the cost assumptions to be suited for their environment. However, the natural history of the disease should be transferable to wealthy countries.

Using the HISCORE model, we will compare the forecasted clinical, economic, and health disparity implications of new SCD treatments. We hope that the results from this model directly inform payers decision making when trying to understand the value of new treatments. We plan to quantify the incremental benefit of improving SCD outcomes and reducing mortality. For example, we can estimate the increase in life expectancy and QALYs of gene therapy for populations of SCD patients or the impact of better pain management. In each of these proposed studies, the HISCORE model will be used to evaluate the cost and incremental cost-effectiveness of alternative new strategies for the management of SCD overall and across different health care payers (in the US, Medicaid, private insurers, and Medicare, and public insurers in other countries) over a patient’s lifetime. This analysis is essential for policy makers to understand whether a new treatment with high upfront costs will yield economic and health benefits for decades and could not be estimated without using a simulation model. This essential knowledge helps payers when developing coverage and reimbursement policies for the innovative treatments that balance the needs of SCD patients and budget realities payers face.

Declarations

Funding

This research was, in part, funded by the National Institutes of Health (NIH) Agreements OT3HL152448 and OT3HL151434. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the NIH.

Conflict of interest/competing interest

Dr. Aaron Winn reports consulting for Takeda Pharmaceuticals. Dr. Scott D. Ramsey reports consulting or advisory roles with Bayer Corporation, Bristol-Myers Squibb, AstraZeneca, Merck & Company Inc., Pfizer, Seattle Genetics, Biovica, GRAIL, and Genentech (institution); research funding from Bayer Corporation and Bristol-Myers Squibb; and travel accommodations or expenses from Bayer Schering Pharma, Bristol-Myers Squibb, GRAIL, and Bayer. The reported relationships may not relate to the subject matter of the article. The authors have no other disclosures to report.

Ethics approval

This study received ethics approval from the University of Washington.

Author contributions

All authors contributed to the development of the model framework and to the writing and editing of the manuscript. AW provided Fig. 2 and Tables 1, 2, 3. All authors have read and approved of the final manuscript.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of data and material

We will publish the results of this study in a peer reviewed journal, which will include publishing the equations of the simulation model to ensure others are able to use them.

Code availability

Code is available upon request.