Abstract
Purpose
In this study, we propose a deep learning (DL)–based voxel-based dosimetry method in which dose maps acquired using the multiple voxel S-value (VSV) approach were used for residual learning.
Methods
Twenty-two SPECT/CT datasets from seven patients who underwent 177Lu-DOTATATE treatment were used in this study. The dose maps generated from Monte Carlo (MC) simulations were used as the reference approach and target images for network training. The multiple VSV approach was used for residual learning and compared with dose maps generated from deep learning. The conventional 3D U-Net network was modified for residual learning. The absorbed doses in the organs were calculated as the mass-weighted average of the volume of interest (VOI).
Results
The DL approach provided a slightly more accurate estimation than the multiple-VSV approach, but the results were not statistically significant. The single-VSV approach yielded a relatively inaccurate estimation. No significant difference was noted between the multiple VSV and DL approach on the dose maps. However, this difference was prominent in the error maps. The multiple VSV and DL approach showed a similar correlation. In contrast, the multiple VSV approach underestimated doses in the low-dose range, but it accounted for the underestimation when the DL approach was applied.
Conclusion
Dose estimation using the deep learning–based approach was approximately equal to that in the MC simulation. Accordingly, the proposed deep learning network is useful for accurate and fast dosimetry after radiation therapy using 177Lu-labeled radiopharmaceuticals.
Keywords: Radiation dosimetry, Deep learning, 3D U-net, Dose kernel, Radionuclide therapy, Monte Carlo simulation
Introduction
177Lu-octreotate (177Lu-DOTATATE) peptide receptor radionuclide therapy is used to treat patients with metastatic neuroendocrine tumors (NETs) [1]. Since the peptide receptor has high efficacy for tumor targeting and since 177Lu emits beta particles with sufficient energy for killing tumor cells, the therapy has low side effects and good therapeutic efficacy [2]. However, retrospective dosimetry is needed to ensure efficient and accurate treatment. Maximization of tumor doses and minimization of organs at risk for further treatment can be realized through dosimetry.
There are two main types of dosimetry: (1) organ-based dosimetry and (2) voxel-based dosimetry [3, 4]. Organ-based dosimetry uses organ-specific S-values derived from sex- and age-specific digital phantoms. It has been used because it is easy to perform, but it is not appropriate for patient-specific dosimetry, since the anatomical characteristics of each patient are different from those of the digital phantoms. Consequently, voxel-based dosimetry has been proposed for patient-specific application. It uses anatomical information acquired from CT images and spatial information of radioactivity distribution from radioisotope imaging techniques, such as SPECT and PET. Voxel-based dosimetry using Monte Carlo (MC) simulations can yield accurate dose estimates, but is not practical because it requires very long computational times [5–8]. The multiple voxel S-value (VSV) approach has been suggested as an alternative [9, 10], which provides accurate and fast dose estimates not only for diagnostic 68 Ga PET data, but also for 177Lu-DOTATATE treatment cases.
In previous studies, various deep learning (DL) approaches have been applied for medical image correction, segmentation, and denoising [11–19]. Several approaches for voxel-based dosimetry using DL have also been reported. Lee et al. attempted DL-based dosimetry for the first time using a 3D U-net structure [20]. Gotz et al. proposed a 3D U-net structure and improved the accuracy using the hybrid deep neural network and empirical mode decomposition method [21]. Azadeh et al. performed a study to predict patient-specific dose kernels rather than generating direct dose maps [22]. The predicted patient-specific dose kernels were then convolved with the activity map to yield a dose map. Zongyu et al. proposed a network that used PET images in addition to SPECT images to improve image resolution [23].
In this study, a U-net-based network for voxel-based dosimetry was proposed. In particular, dose maps acquired using the multiple VSV approach were used for residual learning. The multiple VSV approach provides an accurate voxel-wise dose map in most regions, but an error occurs at the boundary regions (i.e., between the lung and adjacent region or bone and adjacent region). The proposed network was validated by comparison with MC simulations and the multiple VSV approach.
Materials and Methods
Data Acquisition
177Lu-DOTATATE SPECT/CT images acquired from seven patients who underwent 177Lu-DOTATATE treatment for up to four cycles were used in this study (total 22 datasets). A GE NM 670 SPECT/CT system was used for imaging. SPECT/CT images were acquired 4, 24, 48, and 120 h after intravenous injection of 177Lu-DOTATATE. The total time taken for single-bed scan covering the chest and abdomen was approximately 30 min. The reconstructed CT image contained 161 CT slices of 512 × 512 pixels. The corresponding SPECT images had 128 slices of 128 × 128 pixels. The voxel size was 0.98 × 0.98 × 2.5 mm3 and 3.87 × 3.87 × 3.87 mm3 for CT and SPECT, respectively. The attenuation correction and resolution recovery were applied when performing SPECT reconstruction using an ordered subset expectation maximization algorithm. A medium-energy high-resolution and sensitivity collimator was used for shielding, and activity calibration was performed using a cylindrical phantom filled with a known activity concentration. Linearity was confirmed using various activity concentrations.
MC Simulation
The dose maps generated from the MC simulation were used as the reference approach and target images for network training. Geant4 Application for Emission Tomography (GATE) v.8.2 was used for the MC simulation, as in previous studies [9, 10, 24]. Before the simulation, the CT images were resampled to have same voxel sizes as that of the SPECT image. Furthermore, co-registration of sequential SPECT/CT images was performed to generate time-integrated activity (TIA) maps. The TIA maps were acquired using a voxel-wise trapezoidal sum according to Eq. 1 [25]:
| 1 |
where is the activity in each voxel of the ith SPECT image acquired at (-, , and is the physical decay factor of 177Lu.
In GATE, “DoseActor” was used for voxel-based dosimetry. Patient-specific phantom images derived from the CT image and TIA map for the voxelized source were used as input files for the simulation. To generate patient-specific phantoms, CT images in the Hounsfield unit were converted into a density map (g/cm3) based on a published database [26]. The simulation was conducted for 1% of the time-integrated activity considering the computation time, as in previous studies [9, 10]. A dose map (Gy) was generated from the simulation, which was performed using an in-house computing cluster with 60 CPU cores and 128 GB of RAM.
Multiple VSV Approach
The multiple VSV approach was used for residual learning and compared with dose maps generated from DL [9, 10]. In this study, the multiple VSV approach with 20 kernels was used for dosimetry, because it provides accurate dose maps compatible with the MC simulation in the case of 177Lu-DOTATATE dosimetry [10]. The single-VSV approach has also been used for dosimetry. By contrast, the multiple-VSV approach comprises four steps: (1) generation of VSV kernels using MC simulation, (2) convolution of the TIA map with each VSV kernel, (3) masking each medium-specific dose map with the corresponding medium mask map, and (4) summation of all masked dose maps to generate the final dose map. Further details can be found in a previous study [9].
DL Approach
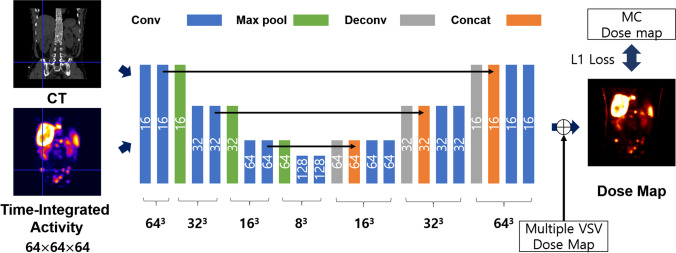
The residual learning strategy was applied for DL approach. The conventional 3D U-net network was modified for residual learning, as illustrated in Fig. 1 [27]. 3D patch-based learning was performed by considering the size of the network, which took CT and TIA patch images with a size of 64 64 64 as inputs, and was trained to yield a dose map. Supervised learning was achieved by using an MC dose map as the target image. Each encoding layer comprised two 3 3 3 convolution layers and a 2 2 2 max-pooling layer. Each convolution layer was followed by batch normalization and rectified linear unit (ReLU) activation function. The decoding layer comprised one 3 3 3 convolution layer, a concatenating path, and two 3 3 3 convolution layers. Each convolution layer involved the ReLU activation function. The number of feature maps in the first layer was set to 16 via empirical fine-tuning. It was then doubled as it passed through the encoding layer, and reduced by half as it passed through the decoding layer. After passing through all the layers, the feature maps were contracted to one image by a 1 1 1 convolution. The residual learning was applied for network training in contrast to the previous study as described above [20]. The image generated after the 1 1 1 convolution was summated with a multiple VSV dose map for the residual learning. The multiple VSV dose map using 20 VSV kernels was used. Therefore, the network was trained to compensate the difference between multiple VSV approach and reference image (i.e., MC approach).
Fig. 1.
Modified 3D U-net structure for residual learning
The network was trained and tested using a cross-validation strategy with sevenfold, the same as the number of patients. In other words, for each fold, datasets from one patient were used as test sets, and datasets from other patients were used for training to avoid network overfitting. Therefore, all 22 SPECT/CT dataset were used for the training and validation of the network. Each SPECT and CT dataset was split into 125 patches of size 64 64 64, forming one dataset for training and testing. The L1 loss between the dose map from the MC simulation and the network was estimated for training. An adaptive moment optimizer was used to minimize loss. Network training was implemented using a computer system with 32 GB of RAM and an NVIDIA GeForce RTX 3090 graphics card.
Dose Estimation
The absorbed dose at the organ level was calculated as the mass-weighted average of the volume of interest (VOI) as below:
| 2 |
where and are the mass and dose of the ith voxel, respectively, and is the total mass of the VOI. The kidneys, liver, spleen, bone marrow in the lumbar spine, and tumor region were considered for dose estimation. The VOIs for these organs and tumor region were manually drawn on a CT image as in the previous study [10]. The 3D Slicer software was used for organ delineation [28]. For tumor regions, the PET-edge technique provided by MIM software was applied to SPECT/CT images for the delineation (MIM Software Inc., Cleveland, OH). The mean absolute error (MAE) of each method (i.e., the multiple VSV, single VSV, and DL approaches) compared to MC was calculated as follows:
| 3 |
where n denotes the number of dataset (i.e., n = 22). Furthermore, error maps in the voxel-level and dose-line profiles were generated to observe discrepancies in the voxel levels.
Results
Absorbed Doses
The absorbed doses of the organs estimated using different approaches are summarized in Table 1. The mean absorbed doses for the kidneys, bone marrow, liver, spleen, and tumors estimated through MC, regarded as a reference approach in this study, were 6.41, 1.76, 10.00, 6.25, and 15.28 Gy, respectively. The multiple VSV approach yielded relatively accurate dose estimates. The MAEs of multiple VSV were 1.56, 1.21, 2.79, 2.28, and 4.66% for kidneys, bone marrow, liver, spleen, and tumors, respectively. The DL approach provided a slightly more accurate estimation than the multiple-VSV approach, but the results were not statistically significant (P > 0.05). The MAEs of the DL approach were 1.04, 0.81, 0.54, 1.34, and 3.18, respectively. The single-VSV approach yielded a relatively inaccurate estimation. The MAEs of the single-VSV approach were 5.45, 11.84, 6.82, 9.30, and 13.62 in the same order. The single VSV approach yielded high errors for the bone marrow and tumor regions, where the medium properties of the regions were different from those of water.
Table 1.
Absorbed Dose (Gy) estimated using 4 different approaches (mean ± standard deviation) and mean absolute error (MAE, %) compared to Monte Carlo simulation
| Absorbed dose (Gy) & MAE (%) |
Kidneys | Bone marrow | Liver | Spleen | Tumors | |
|---|---|---|---|---|---|---|
| MC | Dose | 6.41 ± 1.34 | 1.76 ± 1.61 | 10.00 ± 7.29 | 6.25 ± 3.04 | 15.28 ± 12.63 |
| Single VSV | Dose | 6.75 ± 1.40 | 1.99 ± 1.82 | 10.69 ± 7.80 | 6.62 ± 3.32 | 16.81 ± 13.36 |
| MAE | 5.45 | 11.84 | 6.82 | 9.30 | 13.62 | |
| Multiple VSV | Dose | 6.36 ± 1.32 | 1.78 ± 1.64 | 9.76 ± 7.05 | 6.18 ± 2.96 | 15.15 ± 12.10 |
| MAE | 1.56 | 1.21 | 2.79 | 2.28 | 4.66 | |
| DL | Dose | 6.46 ± 1.36 | 1.77 ± 1.62 | 10.02 ± 7.28 | 6.26 ± 3.05 | 15.54 ± 12.64 |
| MAE | 1.04 | 0.81 | 0.54 | 1.34 | 3.18 | |
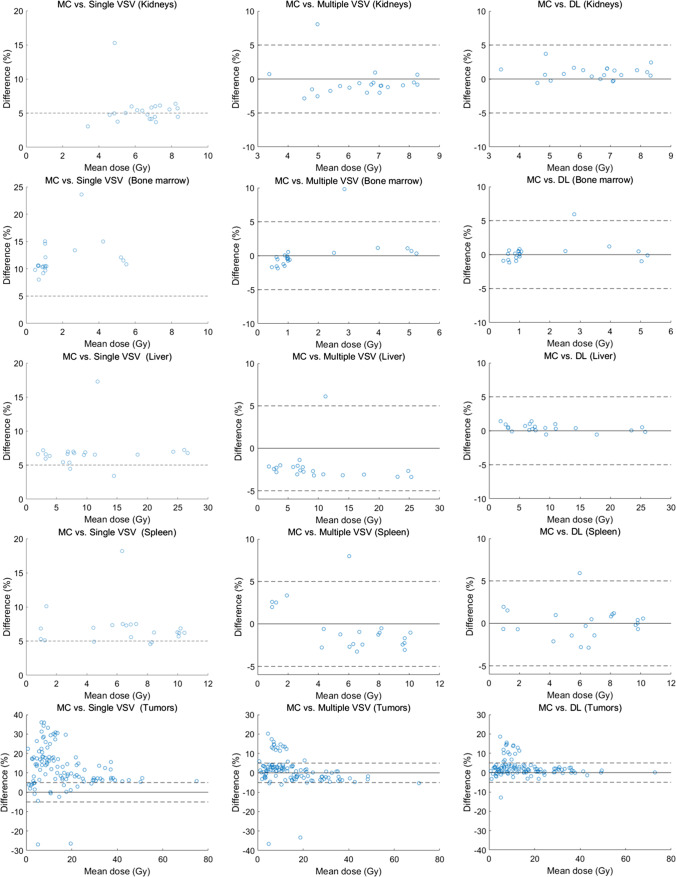
The Bland–Altman plots for the relative difference of each approach compared with the MC are presented in Fig. 2. As described above, the single-VSV approach showed a relatively high error in bone marrow and tumor dose estimations. The relative differences were approximately 5% for kidneys, liver, and spleen in most cases. Furthermore, the multiple VSV and DL approach showed lower errors, regardless of the organs. The relative differences between MC and these two approaches were less than 5% in most cases. The DL approach was marginally more accurate than the multiple-VSV approach, particularly for the liver.
Fig. 2.
The Bland–Altman plots for comparison of dose estimation for each organ between the MC simulation approach and three different approaches. The first column is for the single VSV approach, the second for the multiple VSV approach, and the third for the DL-based approach. The dashed lines represent the baseline at − 5 and 5%
Dose Maps and Error Maps
Figure 3 shows the dose maps generated using each approach and the corresponding relative and absolute error maps from SPECT/CT images of a 74-year-old male patient diagnosed with rectal NET who received 177Lu-DOTATATE of 7.62 GBq. Figure 4 shows dose maps and error maps of a 69-year-old male patient diagnosed with rectal NET who received 177Lu-DOTATATE of 7.51 GBq.
Fig. 3.
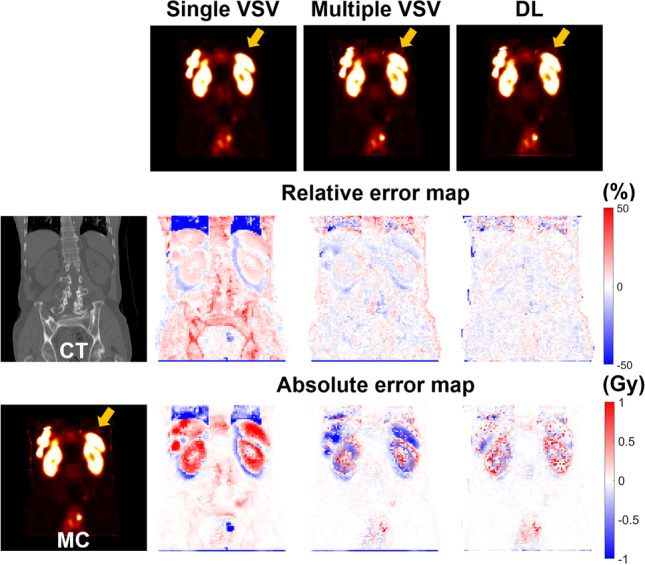
Relative and absolute error maps of single VSV, multiple VSV, and DL-based approaches compared to MC simulation with corresponding CT and dose maps for a 74-year-old male patient diagnosed with rectal NET
Fig. 4.
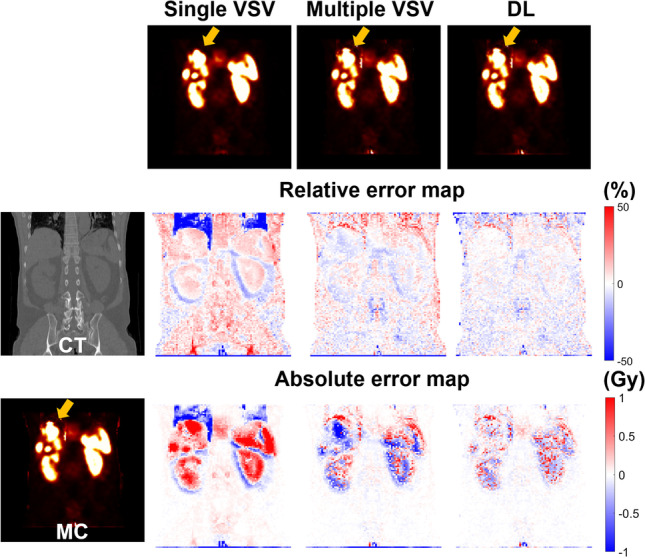
Relative and absolute error maps of single VSV, multiple VSV, and DL-based approaches compared to MC simulation with corresponding CT and dose maps for a 69-year-old male patient diagnosed with rectal NET
The orange arrows in the figures indicate the lung-liver interface regions. The dose maps generated by the single VSV approach showed large errors in the regions, regardless of the patient. These discrepancies were identified not only in the dose maps, but also in the difference maps. However, the multiple VSV and DL approach provided similar dose maps compared to the MC simulation, as shown in the difference maps. No significant difference was noted between the multiple VSV and DL approach on the dose maps. However, this difference is prominent in the error maps. The errors at the voxel level were minimum at the lung-liver interface regions, kidneys, spleen, and tumors in the liver when the DL approach was used.
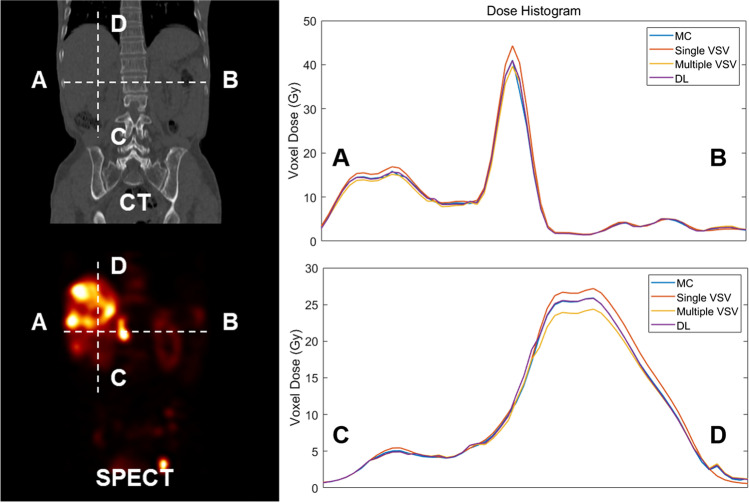
Figure 5 shows the dose-line profiles of each approach acquired using SPECT/CT images of a 63-year-old male patient diagnosed with rectal NET who received 177Lu-DOTATATE of 6.11 GBq. A bone metastatic tumor is observed on the horizontal line (A–B) in the figure. A vertical line (C–D) was drawn to pass through the cancer in the liver and region of the lung-liver interface. As shown in the dose-line profile along the horizontal direction, the DL approach was approximately identical to the MC simulation, particularly in the bone metastasis region. Furthermore, the superiority of the DL approach was highlighted for metastases in the liver region, as shown in the vertical dose-line profile. In the lung-liver interface region, the multiple VSV approach was as accurate as the DL approach.
Fig. 5.
The dose-line profile of MC, single VSV, multiple VSV, and DL-based approaches
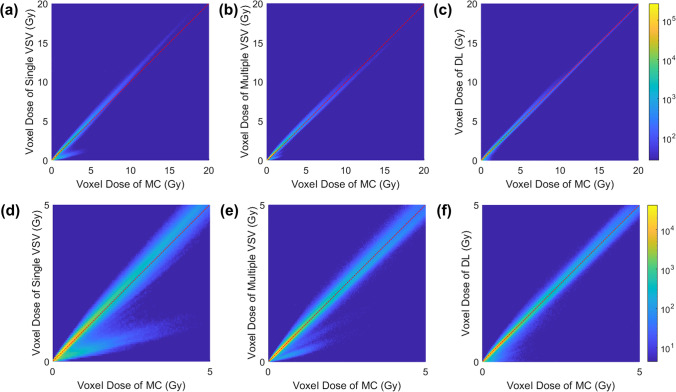
Voxel-Wise Correlation
The voxel-wise correlations between MC simulation and the three different approaches were analyzed to observe the accuracy of each model at the voxel level. As shown in Fig. 6-a and d, the single VSV approach overestimated the doses in the high-dose range (> 5 Gy) and underestimated the doses in the low-dose range (< 5 Gy). The multiple VSV and DL approach showed a similar correlation. However, the multiple VSV approach underestimated doses in the low-dose range, as shown in Fig. 6-b and e but it accounted for the underestimation when the DL approach was applied, as shown in Fig. 6-c and f. Furthermore, the DL-based approach had a slightly narrower plotting shape than that in the multiple VSV approach. The voxel-wise correlations were 0.9809, 0.9939, and 0.9954 over the entire dose range for the single VSV, multiple VSV, and DL approach, respectively, and 0.9641, 0.9891, and 0.9911 over the low-dose range, respectively.
Fig. 6.
The voxel-wise correlation between MC and (a, d) the single VSV approach, (b, e) the multiple VSV approach, and (c, f) the DL-based approach. The figures in the upper row and lower row are the same but the ranges of axes are different
Calculation Time
The computation time for the MC simulation was longer than 48 h, although the simulation was executed for 1% of time-integrated activity. Furthermore, the simulation time increased with the total time-integrated activity. The time for the single VSV, multiple VSV, and DL approach was approximately 1, 2, and 3 s, respectively, including image file input/output and dose map generation. The time taken by these three approaches were not affected by the total time-integrated activity.
Discussion
A DL network with residual learning for accurate voxel-based dosimetry was proposed and validated in this study. Validation was performed at the organ and voxel levels. The single VSV approach showed the highest error among the three approaches for organ-specific dose estimation, as presented in Table 1, and as discussed in previous studies [9, 10, 29]. As the single VSV approach assumes that the medium properties of the human body are the same as that of water, an error occurs in the medium where the density is different from that of water. In contrast, the multiple VSV and DL approach considered the characteristics of the medium property at the voxel level through the CT images. Therefore, these two approaches provided accurate voxel-based dose estimations for most voxels. The errors of organ-specific dose estimation obtained using the two approaches were less than 5%, regardless of the organ regions, as presented in Table 1. Although the multiple-VSV approach was sufficiently accurate at the organ level, it would be a result of cancelation of positive and negative errors at the voxel level occurring in the process of summing the values of voxels. Therefore, it can be inferred that the multiple VSV approach has room for improvement compared to MC when viewed in units of voxels.
In this study, the DL network was trained using a residual learning strategy. The network could predict a relatively accurate initial dose map at an early time, because a multiple VSV dose map was used for the residual map. As the learning progresses, the network recognizes the discrepancy between the label map (i.e., the MC dose map) and the predicted dose map. Finally, a network was constructed to compensate for the error between the residual map and label map. The effect of this compensation is reflected at the voxel level by an error map, dose-line profile, and voxel-wise correlation. The DL approach compensated for underestimation and overestimation, especially in the tumor and organ interface regions, as shown in Figs. 3 and 4. This effect was more prominent in the dose-line profile as shown in Fig. 5. The multiple VSV approach underestimated doses in high-dose regions, but it was alleviated when the DL approach was applied. Furthermore, the compensation resulted in narrower voxel-wise correlation plots, as depicted in Fig. 6. Although the DL approach takes 3 s in addition to the time cost for residual map generation using the multiple VSV approach, it could be inferred that the additional time is worth considering in terms of accuracy.
One of the limitations of this study is the small number of 177Lu-DOTATATE SPECT/CT datasets. Although patch-based learning and cross-validation have been applied to prevent network overfitting, validation of the network with datasets from a large population is required. The second limitation is that scatter correction was not applied for the reconstruction of the 177Lu-DOTATATE SPECT/CT dataset. Validation of the network using SPECT/CT images reconstructed with scatter correction is required. However, this does not affect the intrinsic performance of the network.
The network used in this study was similar to that suggested in a previous study, but it involved residual learning to improve the reliability of the network [20]. Furthermore, 68 Ga-NOTA-RGD PET/CT diagnostic images were used in a previous study. Moreover, the SPECT/CT of 177Lu-DOTATATE was used in this study, which is a therapeutic radiopharmaceutical method. Therefore, the robustness of the U-net-based DL network on different types of radioisotopes was validated, although there are differences from previous studies. This fast and accurate voxel-based dosimetry tool can be used for practical patient-specific dosimetry after targeted radionuclide therapy to optimize the injection dose for safety and efficacy of the therapy. In particular, it would be helpful for the development of a new 177Lu-based radiopharmaceutical, such as PSMA, because dosimetry is required in clinical trials.
Conclusions
The proposed DL approach was used for voxel-based dosimetry of 177Lu-DOTATATE treatment cases, which involved residual learning for precise dose estimation. The network was validated by comparison with MC simulation at the organ and voxel levels. In addition, the single VSV and multiple VSV approaches were used for parallel comparison. The single-VSV approach showed the highest error at the organ and voxel levels compared to the MC simulation. The multiple-VSV approach yielded sufficiently accurate dose estimation, but mild errors were observed at the voxel level. In contrast, the DL approach was superior not only at the organ level but also at the voxel level. Dose estimation through the deep learning–based approach was approximately the same as that in the MC simulation.
It is expected that the network could yield reliable result to the external dataset as residual learning strategy was applied although the network was trained using a small dataset. In other words, the network is stable because the residual map was used for the network provided initial information for prediction. Accordingly, the proposed deep learning network is useful for accurate and fast dosimetry after radiation therapy using general 177Lu-labeled radiopharmaceuticals. As a result, safe and optimized therapy can be achieved by efficiently managing the administration of radiopharmaceuticals through the accurate dosimetry.
Author Contribution
The study was designed by Keon Min Kim, Min Sun Lee, and Jae Sung Lee. Material preparation and data collection were conducted by Min Seok Suh and Gi Jeong Cheon. Data analysis was performed by Keon Min Kim. The results were interpreted by Keon Min Kim, Min Sun Lee, and Jae Sung Lee. The first draft of the manuscript was written by Keon Min Kim, and all the authors commented on the previous versions of the manuscript. All authors have read and approved the final manuscript. The study was supervised by Jae Sung Lee.
Funding
This work was supported by grants from the National Research Foundation of Korea (NRF), funded by the Korean Ministry of Science and ICT (Grant No. 2020M2D9A1093989). This funding source was not involved in the study design, collection, analysis, or interpretation.
Data Availability
Data are available upon request owing to privacy/ethical restrictions.
Declarations
Ethics Approval and Consent to Participate
The retrospective use of the scan data and waiver of consent were approved by the institutional review board of Seoul National University Hospital.
Consent for Publication
Participants signed a consent form to publish their data.
Competing Interests
Keon Min Kim, Min Sun Lee, Min Seok Suh, Gi Jeong Cheon, and Jae Sung Lee declare no conflict of interest.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Kwekkeboom DJ, de Herder WW, Kam BL, van Eijck CH, van Essen M, Kooij PP, et al. Treatment with the radiolabeled somatostatin analog [177 Lu-DOTA 0, Tyr3]octreotate: toxicity, efficacy, and survival. J Clin Oncol. 2008;26(13):2124–2130. doi: 10.1200/JCO.2007.15.2553. [DOI] [PubMed] [Google Scholar]
- 2.Hosono M, Ikebuchi H, Nakamura Y, et al. Manual on the proper use of lutetium-177-labeled somatostatin analogue (Lu-177-DOTA-TATE) injectable in radionuclide therapy (2nd ed.) Ann Nucl Med. 2018;32(3):217–35. doi: 10.1007/s12149-018-1230-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Siegel JA, Thomas SR, Stubbs JB, Stabin MG, Hays MT, Koral KF, et al. MIRD pamphlet no. 16: Techniques for quantitative radiopharmaceutical biodistribution data acquisition and analysis for use in human radiation dose estimates. J Nucl Med. 1999;40(2):37S–61S. [PubMed] [Google Scholar]
- 4.Dewaraja YK, Frey EC, Sgouros G, Brill AB, Roberson P, Zanzonico PB, et al. MIRD pamphlet No. 23: quantitative SPECT for patient-specific 3-dimensional dosimetry in internal radionuclide therapy. J Nucl Med. 2012;53(8):1310–25. doi: 10.2967/jnumed.111.100123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Furhang EE, Chui CS, Sgouros G. A Monte Carlo approach to patient-specific dosimetry. Med Phys. 1996;23(9):1523–1529. doi: 10.1118/1.597882. [DOI] [PubMed] [Google Scholar]
- 6.Gosewisch A, Ilhan H, Tattenberg S, et al. 3D Monte Carlo bone marrow dosimetry for Lu-177-PSMA therapy with guidance of non-invasive 3D localization of active bone marrow via Tc-99m-anti-granulocyte antibody SPECT/CT. EJNMMI Res. 2019;9(1):76. doi: 10.1186/s13550-019-0548-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Goetz TI, Lang EW, Prante O, et al. Three-dimensional Monte Carlo-based voxel-wise tumor dosimetry in patients with neuroendocrine tumors who underwent 177Lu-DOTATOC therapy. Ann Nucl Med. 2020;34(4):244–253. doi: 10.1007/s12149-020-01440-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pacilio M, Lanconelli N, Lo Meo S, et al. Differences among Monte Carlo codes in the calculations of voxel S values for radionuclide targeted therapy and analysis of their impact on absorbed dose evaluations. Med Phys. 2009;36(5):1543–1552. doi: 10.1118/1.3103401. [DOI] [PubMed] [Google Scholar]
- 9.Lee MS, Kim JH, Paeng JC, Kang KW, Jeong JM, Lee DS, et al. Whole-body voxel-based personalized dosimetry: the multiple voxel S-value approach for heterogeneous media with nonuniform activity distributions. J Nucl Med. 2018;59(7):1133–1139. doi: 10.2967/jnumed.117.201095. [DOI] [PubMed] [Google Scholar]
- 10.Kim KM, Lee MS, Suh MS, Selvam H, Tan TH, Cheon GJ, et al. Comparison of voxel S-value methods for personalized voxel-based dosimetry of (177) Lu-DOTATATE. Med Phys. 2022;49:1888–1901. doi: 10.1002/mp.15444. [DOI] [PubMed] [Google Scholar]
- 11.Hwang D, Kang SK, Kim KY, Choi H, Seo S, Lee JS. Data-driven respiratory phase-matched PET attenuation correction without CT. Phys Med Biol. 2021 doi: 10.1088/1361-6560/abfc8f. [DOI] [PubMed] [Google Scholar]
- 12.Kang SK, Yie SY, Lee JS. Noise2Noise improved by trainable wavelet coefficients for PET denoising. Electronics. 2021;10:1529. doi: 10.3390/electronics10131529. [DOI] [Google Scholar]
- 13.Park J, Bae S, Seo S, Park S, Bang JI, Han JH, et al. Measurement of glomerular filtration rate using quantitative SPECT/CT and deep-learning-based kidney segmentation. Sci Rep. 2019;9:4223. doi: 10.1038/s41598-019-40710-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kang SK, Shin SA, Seo S, Byun MS, Lee DY, Kim YK, et al. Deep learning-Based 3D inpainting of brain MR images. Sci Rep. 2021;11(1):1673. doi: 10.1038/s41598-020-80930-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hwang D, Kang SK, Kim KY, Seo S, Paeng JC, Lee DS, et al. Generation of PET attenuation map for whole-body time-of-flight (18)F-FDG PET/MRI using a deep neural network trained with simultaneously reconstructed activity and attenuation maps. J Nucl Med. 2019;60(8):1183–1189. doi: 10.2967/jnumed.118.219493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kang SK, An HJ, Jin H, Kim JI, Chie EK, Park JM, et al. Synthetic CT generation from weakly paired MR images using cycle-consistent GAN for MR-guided radiotherapy. Biomed Eng Lett. 2021;11(3):263–271. doi: 10.1007/s13534-021-00195-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Murthy MYB, Koteswararao A, Babu MS. Adaptive fuzzy deformable fusion and optimized CNN with ensemble classification for automated brain tumor diagnosis. Biomed Eng Lett. 2022;12(1):37–58. doi: 10.1007/s13534-021-00209-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kim JY, Suh HY, Ryoo HG, Oh D, Choi H, Paeng JC, et al. Amyloid PET quantification via end-to-end training of a deep learning. Nucl Med Mol Imaging. 2019;53(5):340–348. doi: 10.1007/s13139-019-00610-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yie SY, Kang SK, Hwang D, Lee JS. Self-supervised PET Denoising. Nucl Med Mol Imaging. 2020;54(6):299–304. doi: 10.1007/s13139-020-00667-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lee MS, Hwang D, Kim JH, Lee JS. Deep-dose: a voxel dose estimation method using deep convolutional neural network for personalized internal dosimetry. Sci Rep. 2019;9(1):10308. doi: 10.1038/s41598-019-46620-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gotz TI, Schmidkonz C, Chen S, Al-Baddai S, Kuwert T, Lang EW. A deep learning approach to radiation dose estimation. Phys Med Biol. 2020;65(3):035007. doi: 10.1088/1361-6560/ab65dc. [DOI] [PubMed] [Google Scholar]
- 22.Akhavanallaf A, Shiri I, Arabi H, Zaidi H. Whole-body voxel-based internal dosimetry using deep learning. Eur J Nucl Med Mol Imaging. 2021;48(3):670–682. doi: 10.1007/s00259-020-05013-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Li Z, Fessler JA, Mikell JK, Wilderman SJ, Dewaraja YK. DblurDoseNet: a deep residual learning network for voxel radionuclide dosimetry compensating for single-photon emission computerized tomography imaging resolution. Med Phys. 2022;49(2):1216–1230. doi: 10.1002/mp.15397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jan S, Santin G, Strul D, Staelens S, Assie K, Autret D, et al. GATE: a simulation toolkit for PET and SPECT. Phys Med Biol. 2004;49(19):4543–4561. doi: 10.1088/0031-9155/49/19/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Guerriero F, Ferrari ME, Botta F, Fioroni F, Grassi E, Versari A, et al. Kidney dosimetry in Lu-177 and Y-90 peptide receptor radionuclide therapy: influence of image timing, time-activity integration method, and risk factors. Biomed Res Int. 2013;2013:935351. doi: 10.1155/2013/935351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schneider W, Bortfeld T, Schlegel W. Correlation between CT numbers and tissue parameters needed for Monte Carlo simulations of clinical dose distributions. Phys Med Biol. 2000;45(2):459–478. doi: 10.1088/0031-9155/45/2/314. [DOI] [PubMed] [Google Scholar]
- 27.Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. 3D U-Net: learning dense volumetric segmentation from sparse annotation. arXiv preprint. 2016; 10.48550/arXiv.1606.06650.
- 28.Fedorov A, Beichel R, Kalpathy-Cramer J, et al. 3D slicer as an image computing platform for the quantitative imaging network. Magn Reson Imaging. 2012;30(9):1323–1341. doi: 10.1016/j.mri.2012.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Brosch-Lenz J, Uribe C, Gosewisch A, Kaiser L, Todica A, Ilhan H, et al. Influence of dosimetry method on bone lesion absorbed dose estimates in PSMA therapy: application to mCRPC patients receiving Lu-177-PSMA-I&T. EJNMMI Phys. 2021;8(1):26. doi: 10.1186/s40658-021-00369-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data are available upon request owing to privacy/ethical restrictions.