Abstract
In healthcare domain, complication risk profiling which can be seen as multiple clinical risk prediction tasks is challenging due to the complex interaction between heterogeneous clinical entities. With the availability of real-world data, many deep learning methods are proposed for complication risk profiling. However, the existing methods face three open challenges. First, they leverage clinical data from a single view and then lead to suboptimal models. Second, most existing methods lack an effective mechanism to interpret predictions. Third, models learned from clinical data may have inherent pre-existing biases and exhibit discrimination against certain social groups. We then propose a multi-view multi-task network (MuViTaNet) to tackle these issues. MuViTaNet complements patient representation by using a multi-view encoder to exploit more information. Moreover, it uses a multi-task learning to generate more generalized representations using both labeled and unlabeled datasets. Last, a fairness variant (F-MuViTaNet) is proposed to mitigate the unfairness issues and promote healthcare equity. The experiments show that MuViTaNet outperforms existing methods for cardiac complication profiling. Its architecture also provides an effective mechanism for interpreting the predictions, which helps clinicians discover the underlying mechanism triggering the complication onsets. F-MuViTaNet can also effectively mitigate the unfairness with only negligible impact on accuracy.
Keywords: Fairness, Equal opportunity, Regularization, Multi-view, Multi-task, Complication risk profiling, Attention, Contrastive learning
1. Introduction
Cardiovascular diseases are widely known as the leading causes of mortality in breast cancer survivors [1–4]. With the recent substantial improvement of breast cancer survival rates, predicting the onset of multiple cardiac complications has become a critical task for enhancing patients’ life quality. It is also a key to cost-effective disease management and prevention. However, this task is highly challenging because of the complex interactions between heterogeneous clinical entities. Effectively capturing these interactions may lead to more precise prediction and treatment for cancer survivors.
Over the past few decades, the rapid growth of real-world clinical data such as electronic health record (EHR) and insurance claims makes them valuable data sources used in data-driven (e.g., deep learning) systems for clinical risk prediction, especially complication risk profiling [5–7]. As shown in Fig. 1, this data includes heterogeneous clinical entities (e.g., visit, disease, medication) and can be considered from multiple views (i.e., sequence of visits, set of features). However, the existing methods for complication risk profiling have some limitations: (C1) these models cannot capture complex relationships between heterogeneous clinical entities and may result in the less optimal treatments for cancer survivors; (C2) most of them lack an efficient mechanism to interpret the predictions, thereby cannot help clinicians discover the underlying mechanism triggering the onset and make better clinical decisions; (C3) these models may be biased and violate fairness with respect to different patient groups in their predictions.
Fig. 1.
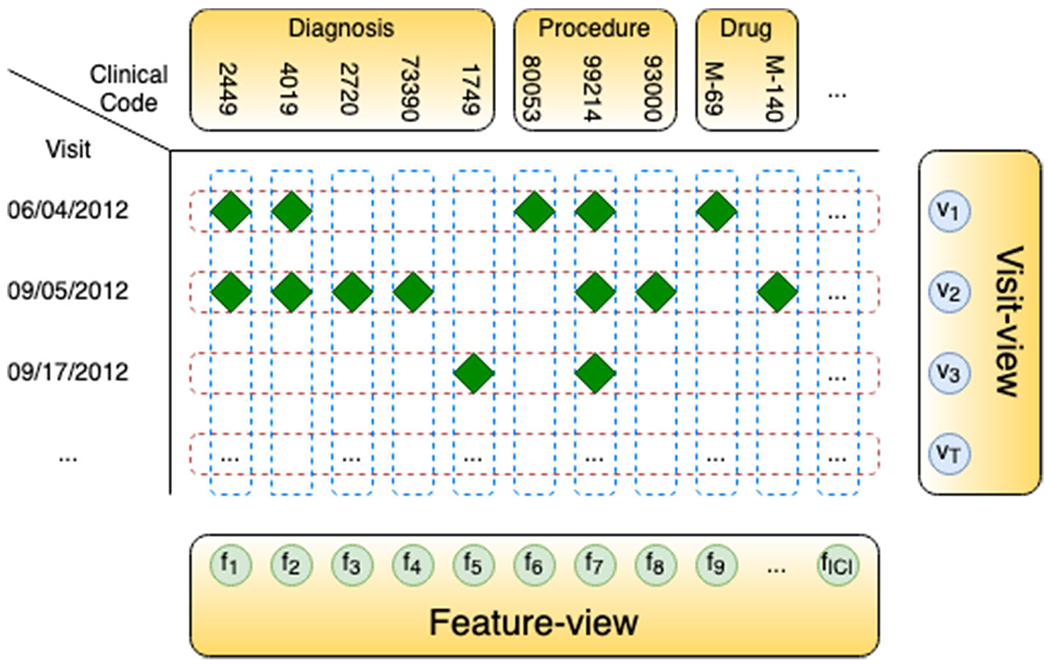
Visit-view (sequence of clinical visits (rows)) and feature-view (set of clinical codes (columns)) of clinical data
The potential reasons for these limitations are as follows. First, due to the heterogeneous and hierarchical structure of clinical data, there are multiple views to consider patient records: treating them as sequences of visits or as sets of clinical features. Encoding patient records from either view cannot provide comprehensive representations of patients, and may fail to capture dynamic patterns of clinical features or dependencies among clinical visits. Second, treating each complication onset prediction independently can lead to suboptimal models, because the dependencies among complications that are manifestations caused by their common underlying condition cannot be captured. This is particularly the case when data are limited. Third, interpretable predictions help clinicians better interact with models and make optimal treatment decisions. However, it is challenging to establish a simple and effective interpretation mechanism for complex models. Fourth, models built with heterogeneous, unbalanced clinical data may easily exhibit discrimination against certain patient groups. As shown in Sect. 4 (i.e., Table 10), the existing approach for optimizing clinical risk prediction models (i.e., minimizing binary cross-entropy objective function) exhibits disparities in model predictions across different social groups and prediction tasks. This phenomenon is more critical for minority groups and rare diseases. Then, how to ensure the fairness and health equity while preserving a sufficient level of model accuracy is another challenge [8].
Table 10.
Comparison between single-task (MuViTaNet-task-specific) and multi-task (MuViTaNet) learning in terms of accuracy (AU-ROC) and fairness (FPRG) for cardiac complication risk profiling
| Metric | Model | AF | CAD | HF | Hypertension | PAD | Stroke |
|---|---|---|---|---|---|---|---|
| AU-ROC | MuViTaNet | 0.8120 ± 0.0457 | 0.8070 ± 0.0147 | 0.8408 ± 0.0177 | 0.8462 ± 0.0089 | 0.7986 ± 0.0199 | 0.7914 ± 0.0174 |
| MuViTaNet-task-specific | 0.6864 ± 0.0631 | 0.7336 ± 0.0322 | 0.7641 ± 0.0072 | 0.8316 ± 0.0099 | 0.6949 ± 0.0252 | 0.7222 ± 0.0204 | |
| FPRG | MuViTaNet | 0.0940 ± 0.0552 | 0.1004 ± 0.0211 | 0.0259 ± 0.0183 | 0.0491 ± 0.0036 | 0.1094 ± 0.0552 | 0.1772 ± 0.0174 |
| MuViTaNet-task-specific | 0.1361 ± 0.0690 | 0.1174 ± 0.0346 | 0.0356 ± 0.0100 | 0.0672 ± 0.0114 | 0.1407 ± 0.0528 | 0.2047 ± 0.0295 |
To tackle the aforementioned challenges, we propose a new neural network-based framework named Multi-View Multi-Task Network (MuViTaNet) and its fairness variant (F-MuViTaNet) for cardiac complication risk profiling. These proposed models consist of a multi-view encoder and a novel multi-task learning (MTL) scheme (deal with C1 and C2), and a fairness-informed objective function (deal with C3). In particular, the multi-view encoder includes visit-view and feature-view encoders that simultaneously capture information from clinical visits and features: visit-view encoder considers a patient record as the sequence of clinical visits and captures their temporal relation by Gated Recurrent Unit (GRU) network; feature-view encoder considers the patient record as the set of temporal medical features whose temporal patterns are extracted separately using convolutional neural networks (CNN), following which are max-pooling operations that extract the most significant signals from temporal sequences. The MTL scheme utilizes an attention mechanism to learn complication-specific representation from shared information generated by the multi-view encoder. This scheme allows MuViTaNet to exploit additional information from related complications and unlabeled data to generate more generalized representations for patients, which enables more accurate predictions. By leveraging the attention mechanism associated multi-view encoder, the proposed model provides an efficient way to interpret its predictions from multiple perspectives, thereby helping clinicians discover the underlying mechanism triggering the onset and making better clinical treatments. Figure 2 distinguishes our multi-view multi-task learning approach from the existing works for clinical risk prediction. To mitigate unfairness in clinical prediction across different patient groups, we incorporate fairness constraint by adding regularization to the model objective function (F-MuViTaNet) during training.
Fig. 2.
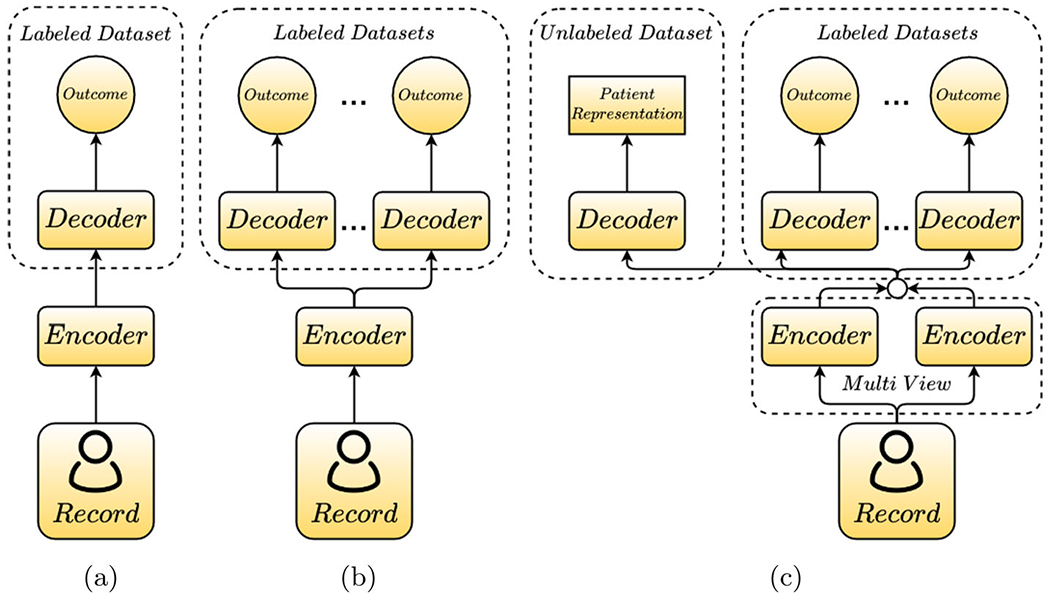
General schemes for learning from clinical data. a Single-view single-task learning, b single-view multi-task learning, c multi-view multi-task learning. Our proposed model belongs to multi-view multi-task learning with the multi-view encoder (i.e., visit-view and feature-view) and the task-specific attention mechanisms and decoders for both labeled and unlabeled datasets
By conducting experiments on multiple datasets derived from real-world data (i.e., insurance claim database) under the real clinical scenario (i.e., predicting chances of developing cardiac complications in the future for breast cancer patients), we demonstrate that the proposed model MuViTaNet is interpretable (i.e., Tables 8 and 9, and Fig. 5) and significantly outperforms the state-of-the-art approaches (i.e., Tables 5 and 6) for complication risk profiling. We show that compared to task-specific models, MTL scheme can affect fairness property by mitigating group disparity in predictions (i.e., Table 10). Further, when enforcing fairness constraint to MuViTaNet, the fairness can be improved significantly with only negligible impacts on model accuracy (i.e., Figs. 6, 7, 8). These results indicate that our proposed model can be applied to achieve both fair and accurate predictions for cardiac complication risk profiling in clinical practice. Our contributions can be summarized as follows:
We design a multi-view multi-task neural network architecture1 (MuViTaNet) that accurately predicts multiple complication onsets and efficiently interprets its predictions. It includes (1) a multi-view encoder to explicitly capture dependencies among clinical visits and clinical features from clinical data; (2) a MTL scheme that utilizes a complication-specific attention mechanism on top of the multi-view encoder to capture additional clinical information from related complications and unlabeled datasets.
We design a fairness variant (F-MuViTaNet) that mitigates unfairness across different patient groups while maintaining accurate predictions.
Finally, we conduct comprehensive experiments to demonstrate the effectiveness of MuViTaNet in terms of both accuracy, interpretability, and fairness for cardiac complication risk profiling.
Table 8.
Top 10 most important clinical features (i.e., with the highest attention weights) for each cardiac complication as identified by MuViTaNet
| Atrial fibrillation | Coronary artery disease | Heart failure |
|---|---|---|
| Nonrheumatic mitral valve disorders (I34) | Other cardiac arrhythmias (I49) | Other cardiac arrhythmias (I49) |
| Other cardiac arrhythmias (I49) | Nonrheumatic mitral valve disorders (I34) | Varicose veins of lower extremities (I83) |
| Complications and ill-defined heart disease (I51) | Varicose veins of lower extremities (I83) | Diseases of capillaries (I78) |
| Paroxysmal tachycardia (I47) | Diseases of capillaries (I78) | Other disorders of veins (I87) |
| Diseases of capillaries (I78) | Type 2 diabetes mellitus (E11) | Embolism and thrombosis (I82) |
| Embolism and thrombosis (I82) | Other peripheral vascular diseases (I73) | Type 2 diabetes mellitus (E11) |
| Other conduction disorders (I45) | Embolism and thrombosis (I82) | Complications and ill-defined heart disease (I51) |
| Varicose veins of lower extremities (I83) | Hypotension (I95) | Nonrheumatic mitral valve disorders (I34) |
| Nonrheumatic aortic valve disorders (I35) | Other disorders of veins (I87) | Other peripheral vascular diseases (I73) |
| Other disorders of veins (I87) | Angina pectoris (I20) | Overweight and obesity (E66) |
| Hypertension | Peripheral arterial disease | Stroke |
|
| ||
| Other cardiac arrhythmias (I49) | Other cardiac arrhythmias (I49) | Other cardiac arrhythmias (I49) |
| Abnormal blood-pressure reading, without diagnosis (R03) | Varicose veins of lower extremities (I83) | Nonrheumatic mitral valve disorders (I34) |
| Type 2 diabetes mellitus (E11) | Diseases of capillaries (I78) | Varicose veins of lower extremities (I83) |
| Nonrheumatic mitral valve disorders (I34) | Nonrheumatic mitral valve disorders (I34) | Other peripheral vascular diseases (I73) |
| Varicose veins of lower extremities (I83) | Other disorders of veins (I87) | Embolism and thrombosis (I82) |
| Overweight and obesity (E66) | Non-specific lymphadenitis (I88) | Type 2 diabetes mellitus (E11) |
| Diseases of capillaries (I78) | Other peripheral vascular diseases (I73) | Other disorders of veins (I87) |
| Other peripheral vascular diseases (I73) | Embolism and thrombosis (I82) | Hypotension (I95) |
| Other disorders of veins (I87) | Other non-infective disorders of lymphatic vessels (I89) | Pain in throat and chest (R07) |
| Pain in throat and chest (R07) | Type 2 diabetes mellitus (E11) | Complications and ill-defined heart disease (I51) |
Table 9.
Top 5 most important clinical visits and features (i.e., with the highest attention weights) for the 2 patients illustrated in Fig. 5
| Positive patient from heart failure dataset | |||||
| Visits | Visit 9 (0.11) | Visit 3 (0.11) | Visit 11 (0.10) | Visit 8 (0.09) | Visit 6 (0.09) |
| Features | 796.2 (0.26) | 250.00 (0.25) | 278.00 (0.12) | 882.0 (0.05) | 19083 (0.04) |
| Negative patient from hypertension dataset | |||||
| Visits | Visit 9 (0.11) | Visit 11 (0.11) | Visit 7 (0.10) | Visit 4 (0.10) | Visit 3 (0.09) |
| Features | M-174 (0.56) | 250.00 (0.22) | S0612 (0.13) | J3010 (0.02) | 82043 (0.02) |
Fig. 5.
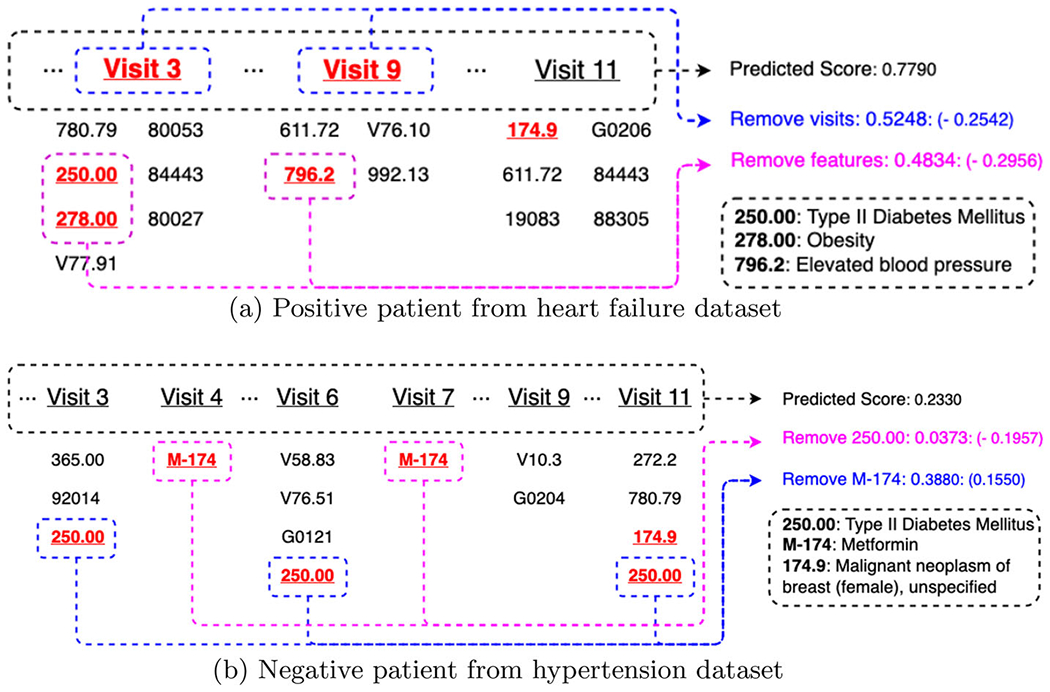
Visualization of 2 patient records (i.e., positive patient from heart failure dataset and negative patient from hypertension dataset) from breast cancer cohort. We only show important visits in clinical records due to limited space
Table 5.
Comparison of prediction performance measured by AU-ROC scores on six complication risk profiling tasks
| Method | AF | CAD | HF | Hypertension | PAD | Stroke | Average | ||
|---|---|---|---|---|---|---|---|---|---|
| Single-task | Classical | LR | 0.6133 ± 0.0437 | 0.6402 ± 0.0165 | 0.6982 ± 0.0088 | 0.7901 ± 0.0088 | 0.5700 ± 0.0341 | 0.6150 ± 0.0128 | 0.6545 ± 0.0208 |
| RF | 0.7159 ± 0.0434 | 0.7187 ± 0.0260 | 0.7863 ± 0.0147 | 0.8066 ± 0.0090 | 0.6880 ± 0.0525 | 0.7172 ± 0.0262 | 0.7388 ± 0.0286 | ||
| Recurrent-based | GRU | 0.6701 ± 0.0425 | 0.7218 ± 0.0116 | 0.7805 ± 0.0033 | 0.8122 ± 0.0084 | 0.6884 ± 0.0368 | 0.7213 ± 0.0103 | 0.7324 ± 0.0188 | |
| Bi-GRU | 0.6620 ± 0.0533 | 0.7295 ± 0.0079 | 0.7845 ± 0.0058 | 0.8155 ± 0.0098 | 0.6967 ± 0.0172 | 0.7291 ± 0.0088 | 0.7362 ± 0.0171 | ||
| Time-aware | T-LSTM | 0.6739 ± 0.0518 | 0.7052 ± 0.0133 | 0.7651 ± 0.0156 | 0.8024 ± 0.0118 | 0.6802 ± 0.0239 | 0.6994 ± 0.0203 | 0.7210 ± 0.0228 | |
| Attention-based | Dipole | 0.6804 ± 0.0661 | 0.7287 ± 0.0120 | 0.7791 ± 0.0026 | 0.8157 ± 0.0081 | 0.6839 ± 0.0320 | 0.7247 ± 0.0040 | 0.7354 ± 0.0209 | |
| RETAIN | 0.6493 ± 0.0465 | 0.6780 ± 0.0196 | 0.7360 ± 0.0139 | 0.8078 ± 0.0086 | 0.6731 ± 0.0224 | 0.6770 ± 0.0112 | 0.7035 ± 0.0126 | ||
| Transformer | 0.6516 ± 0.0563 | 0.7021 ± 0.0155 | 0.7502 ± 0.0069 | 0.8107 ± 0.0076 | 0.6721 ± 0.0392 | 0.6981 ± 0.0135 | 0.7141 ± 0.0183 | ||
| LSAN | 0.6069 ± 0.0556 | 0.6910 ± 0.0135 | 0.7567 ± 0.0180 | 0.8163 ± 0.0085 | 0.6464 ± 0.0464 | 0.6897 ± 0.0206 | 0.7012 ± 0.0271 | ||
| Multi-task | Recurrent-based | GRU | 0.7915 ± 0.0475 | 0.7759 ± 0.0144 | 0.8186 ± 0.0136 | 0.8143 ± 0.0096 | 0.7524 ± 0.0253 | 0.7458 ± 0.0222 | 0.7831 ± 0.0221 |
| Bi-GRU | 0.7984 ± 0.0524 | 0.7824 ± 0.0121 | 0.8279 ± 0.0125 | 0.8189 ± 0.0100 | 0.7503 ± 0.0189 | 0.7462 ± 0.0237 | 0.7873 ± 0.0216 | ||
| Time-aware | T-LSTM | 0.7944 ± 0.0466 | 0.7591 ± 0.0093 | 0.8134 ± 0.0124 | 0.8106 ± 0.0087 | 0.7382 ± 0.0285 | 0.7419 ± 0.0232 | 0.7763 ± 0.0214 | |
| Attention-based | Dipole | 0.7823 ± 0.0620 | 0.7814 ± 0.0213 | 0.8239 ± 0.0095 | 0.8210 ± 0.0092 | 0.7554 ± 0.0350 | 0.7611 ± 0.0194 | 0.7875 ± 0.0261 | |
| RETAIN | 0.7686 ± 0.0485 | 0.7554 ± 0.0083 | 0.8024 ± 0.0165 | 0.8029 ± 0.0066 | 0.7312 ± 0.0263 | 0.7376 ± 0.0254 | 0.7661 ± 0.0219 | ||
| Transformer | 0.7697 ± 0.0649 | 0.7738 ± 0.0110 | 0.8049 ± 0.0164 | 0.8092 ± 0.0106 | 0.7484 ± 0.0423 | 0.7643 ± 0.0083 | 0.7784 ± 0.0256 | ||
| LSAN | 0.7775 ± 0.0576 | 0.7788 ± 0.0225 | 0.8082 ± 0.0150 | 0.8226 ± 0.0061 | 0.7599 ± 0.0319 | 0.7533 ± 0.0147 | 0.7834 ± 0.0246 | ||
| Ours | MuViTaNet | 0.8120 ± 0.0457 | 0.8070 ± 0.0147 | 0.8408 ± 0.0177 | 0.8462 ± 0.0089 | 0.7986 ± 0.0199 | 0.7914 ± 0.0174 | 0.8160 ± 0.0117 |
We report the average AU-ROC scores and their corresponding standard deviation. AF Atrial fibrillation, CAD Coronary artery disease, HF Heart failure, PAD Peripheral arterial disease
Table 6.
Adjusted p-values for model performance’s pairwise comparisons computed by Quade’s post hoc test
| GRU | Bi-GRU | T-LSTM | Dipole | RETAIN | Transformer | LSAN | MuViTaNet | |
|---|---|---|---|---|---|---|---|---|
| GRU | 1.0 | 0.3667 | 0.1856 | 0.1856 | 0.0055 | 0.6045 | 0.3031 | 0.0015 |
| Bi-GRU | 0.3667 | 1.0 | 0.0298 | 0.6659 | 0.0004 | 0.1595 | 0.8968 | 0.0162 |
| T-LSTM | 0.1856 | 0.0298 | 1.0 | 0.0106 | 0.1161 | 0.4136 | 0.0221 | 3 × 10−5 |
| Dipole | 0.1856 | 0.6659 | 0.0106 | 1.0 | 0.0001 | 0.0695 | 0.7623 | 0.0439 |
| RETAIN | 0.0055 | 0.0004 | 0.1161 | 0.0001 | 1.0 | 0.0199 | 0.0003 | 2 × 10−7 |
| Transformer | 0.6045 | 0.1595 | 0.4136 | 0.0695 | 0.0199 | 1.0 | 0.1259 | 0.0003 |
| LSAN | 0.3031 | 0.8968 | 0.0221 | 0.7623 | 0.0003 | 0.1259 | 1.0 | 0.0221 |
| MuViTaNet | 0.0015 | 0.0162 | 3 × 10−5 | 0.0439 | 2 × 10−7 | 0.0003 | 0.0221 | 1.0 |
Fig. 6.
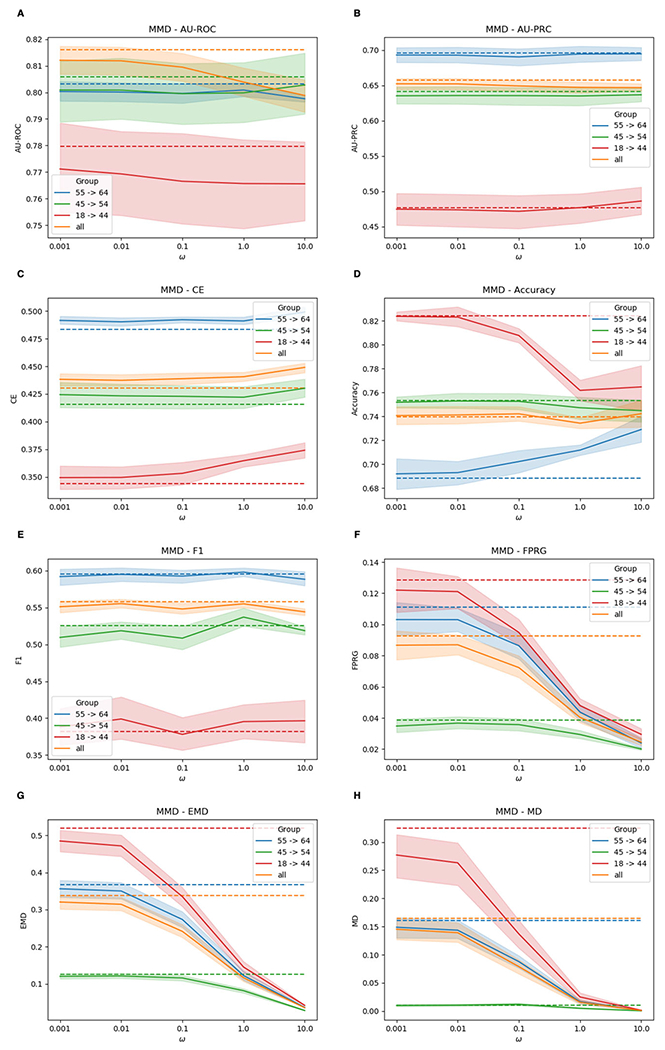
Performances of F-MuViTaNet (using MMD to enforce fairness) for cardiac complication risk profiling with respect to accuracy (i.e., AUROC (↑), AU-PRC (↑), CE (↓), Accuracy (↑), F1 (↑)) and fairness (FPRG (↓), EMD (↓), MD (↓)) metrics. The arrows show the direction to optimum scores for these metrics. Performances of baseline method (MuViTaNet) are shown by dash lines. The shade areas represents standard deviation ranges of scores calculated from cross-validation setting
Fig. 7.
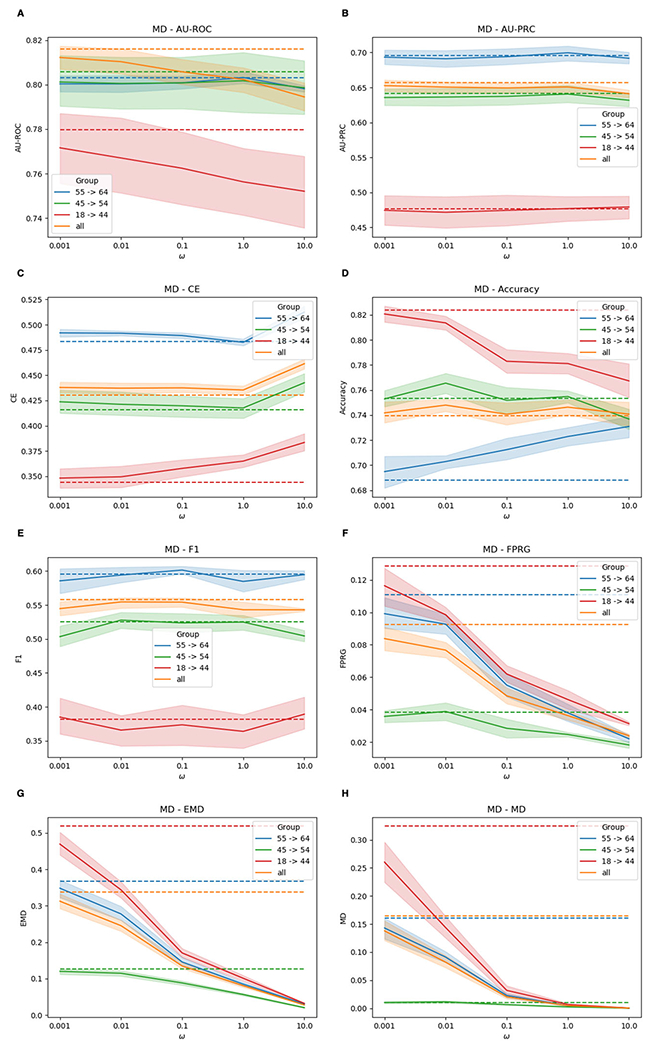
Performances of F-MuViTaNet (using MD to enforce fairness) for cardiac complication risk profiling with respect to accuracy (i.e., AUROC (↑), AU-PRC (↑), CE (↓), Accuracy (↑), F1 (↑)) and fairness (FPRG (↓), EMD (↓), MD (↓)) metrics. The arrows show the direction to optimum scores for these metrics. Performances of baseline method (MuViTaNet) are shown by dash lines. The shade areas represents standard deviation ranges of scores calculated from cross-validation setting
Fig. 8.
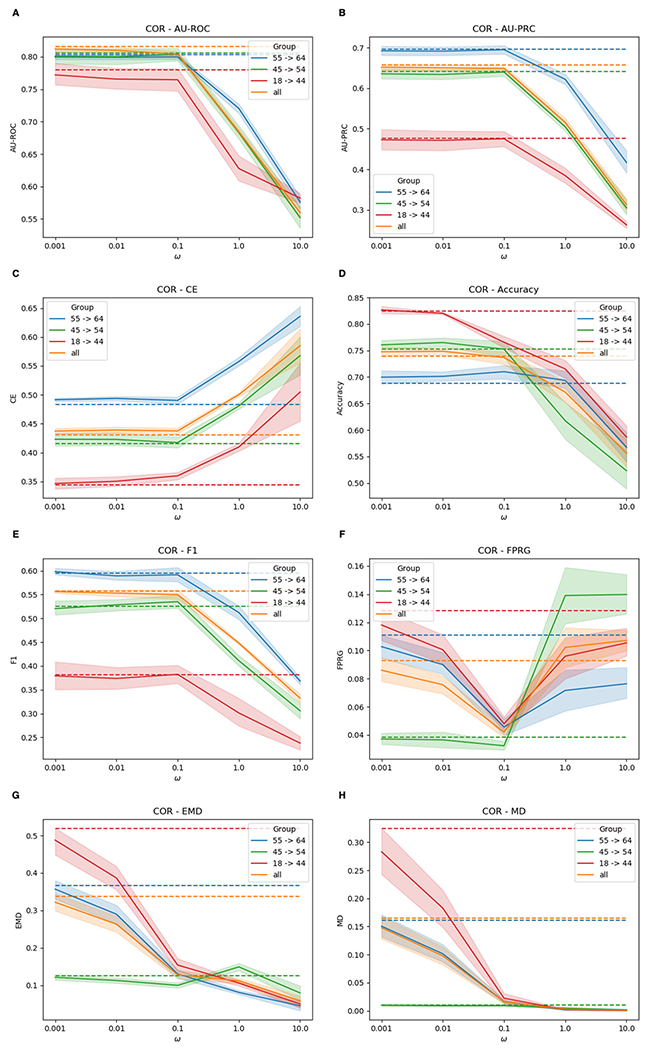
Performances of F-MuViTaNet (using MMD to enforce fairness) for cardiac complication risk profiling with respect to accuracy (i.e., AUROC (↑), AU-PRC (↑), CE (↓), Accuracy (↑), F1 (↑)) and fairness (FPRG (↓), EMD (↓), MD (↓)) metrics. The arrows show the direction to optimum scores for these metrics. Performances of baseline method (MuViTaNet) are shown by dash lines. The shade areas represents standard deviation ranges of scores calculated from cross-validation setting
Note that the present work is an extension of our conference paper [9], in which MuViTaNet was first introduced. The key differences are the followings:
We focus on the unfairness issues in this work. To mitigate group disparity and promote health equity, we propose a fairness mechanism by incorporating the fairness objective function as regularization into MuViTaNet. The resulting model (F-MuViTaNet) achieves both accurate and fair predictions for cardiac complication risk profiling tasks.
We conduct comprehensive empirical studies to investigate the impact of MTL on unfairness and examine the impact of enforcing fairness constraint on prediction performances under MTL setting.
The remainder of the paper is organized as follows. Section 2 summarizes related works on clinical risk prediction as well as complication risk profiling, and fairness in machine learning and healthcare applications. Section 3 describes the technical details of the proposed models (MuViTaNet and F-MuViTaNet). Section 4 presents experimental results and discussions. Finally, Sect. 5 concludes the paper.
2. Related works
In this section, we briefly review existing works related to our study, including patient representation learning and MTL for clinical risk prediction and complication risk profiling. We also review the fair machine learning literature by presenting the common fairness criteria and approaches to satisfying these criteria, and the recent advances in domain of healthcare.
Patient representation learning.
The abundance of real-world data in recent years creates an unprecedented opportunity to apply machine learning and data mining methods for clinical risk predictions [10–12]. With the advancement of deep learning theory and the acceleration in computational technologies, neural network-based architectures can significantly improve prediction performance due to their ability to extract rich representations from data. Because of the temporal nature of clinical data, most existing methods rely on recurrent neural network architectures to learn patient representations, which are then used to make predictions for future clinical events (e.g., diagnosis, mortality, readmission, etc.) [5–7, 13, 14]. These works focused on designing attention mechanisms to capture dependencies among clinical visits [5, 13, 14] and time-aware mechanisms to incorporate temporal information [6, 15, 16] into patient representation for making better predictions. Nonetheless, these models cannot explicitly capture the relationships among clinical features. Instead of considering EHR data as sequences of clinical visits, Concare [17] treats the record as the set of clinical features and extracts dynamic patterns of these features separately. Then, the predictions are made by aggregating representations of all clinical features. However, all the existing methods only extract information from a single view of clinical data which makes the learned patient representations suboptimal. In contrast, we propose a multi-view model for capturing information from multiple views of clinical data simultaneously.
Multi-task learning.
Multi-task learning (MTL) has been used widely across many applications of machine learning and data mining. By sharing information among related tasks, the prediction model can generalize better. In healthcare domain, some existing works applied MTL techniques to leverage information from related tasks to improve model performance in clinical risk prediction. In particular, both classical machine learning [18–20] and deep learning models [21–23] are formulated as MTL frameworks and are applied on a wide range of healthcare applications including disease progression modeling [18], mortality prediction [21], disease onset prediction [22], and diagnosis classification [23].
Complication risk profiling.
Mitigating the risk of complications is crucial for many disease management programs. Despite its importance, there have not been many existing methods designed for this task. Unlike a single clinical risk prediction task, complication risk profiling requires multiple predictions for onset of complications. Thus, capturing relationships among related complications is crucial to achieving good prediction performances. Some methods have been proposed to predict the onset of complications of some diseases and clinical procedures. For example, multi-task logistic regression has been used to predict complication risks for diabetes care [19, 24]. Besides linear models, the deep learning method is also used to predict complications of this chronic disease [25] but this work considers each complication independently. For breast cancer survivors, relationships between cardiac complications and cancer were also investigated [3, 4, 26] to show the correlation between these two diseases.
Fairness in machine learning.
Machine learning has been increasingly used in domains with intensive impacts on society such as healthcare, policy and hiring. While the hope is to improve the societal benefits, they may exhibit biases against certain demographic groups [8, 27–29]. To measure and remedy the unfairness, various fairness notions have been proposed in the literature and they can be roughly classified into two classes: group fairness and individual fairness. For group fairness notions (e.g., demographic parity [30], equalized odds [31], equal opportunity [31]), the entire population is categorized into different groups based on some sensitive attributes (e.g., age, gender, race, etc.), and certain statistical measures are (approximately) equalized across these groups. For example, demographic parity [31, 32] requires the similar ratio of positive outcomes for every sensitive groups; equalized odds [31] states that the protected and unprotected groups should have equal rates for true positives and false positives; equal opportunity [31] only requires equal true positive rates for different groups. In contrast, individual fairness notions (e.g., counterfactual fairness, fairness through awareness) target the individual, rather than group level. It requires the similar individuals to be treated similarly [30]. For example, counterfactual fairness implies that a prediction for an individual is fair if it is unchanged when individual belonged to a different group [33].
To satisfy certain fairness notions, many methods haven been proposed and they can be roughly classified into three categories: (1) Pre-processing approach that modifies training data to eliminate confounding bias from data [34–36]. For example, variational autoencoder and generative adversarial network have been proposed to obfuscate sensitive information in the learned representations, thereby allowing machine learning models to learn fair predictions [37–39]. (2) In-processing approach that introduces fairness during training by modifying the learning algorithms such as imposing fairness constraints or changing objective functions. For example, [40–42] learn fair models by solving constrained optimization with fairness criteria serving as constraints; [43–45] achieve fairness by imposing fairness-specific regularization term in optimization. (3) Post-processing approach that calibrates model predictions across sensitive groups to remove bias [31, 46].
Fairness in healthcare applications.
Unfairness issues arisen from using machine learning models have also been well-documented in many healthcare applications. For example, the accuracy of predictive systems for intensive care unit monitoring differs across different racial groups [8, 27]; medical resources may be disproportionately allocated among patients with different socioeconomic status [8]; skin-cancer detection models may fail to detect early-stage disease in patients with dark skin [29]; atherosclerotic cardiovascular disease risk prediction models may have racial bias [28]. Fairness notions and approaches introduced above have also been used in clinical applications. For example, [27] uses the disparity in false-positive/false-negative/accuracy as a measure of unfairness and mitigates the unfairness via data collection; [47] considers the disparity in conditional prediction/calibration/AUROC as unfairness measures and reduces disparity by adjusting models through regularization; [28] adopts equalized odds fairness notion [31] and uses adversarial learning approach to satisfying fairness constraint; [48] extends counterfactual fairness [33] and trains a fair model via counterfactual inference using a variational autoencoder.
3. Methodology
In this section, we first give brief introduction about patient records, complication risk profiling task and the corresponding notations. Then, we present our proposed model MuViTaNet as well as its fairness variant F-MuViTaNet.
3.1. Definitions and basic notations
Definitions and notations used in this study are shown in the following paragraphs and are summarized in Table 1.
Table 1.
Notation definition
| Notation | Description |
|---|---|
| C | Set of clinical codes/features |
| P | A patient record |
| ci | ith clinical codes in set C |
| xi ∈ {0, 1}|C| | Vector representation of code ci |
| v j | jth clinical visit in P |
| c j | Set of clinical codes in visit vj |
| tj | Timestamp of visit vj |
| Vj ∈ {0, 1}|C| | Vector representation of visit vj |
| Xj ∈ {0, 1}|ci|×|C| | Matrix representation of visit vj |
| Xvisit ∈ {0, 1}T×|C| | Visit-level representation of P |
| Xfeature ∈ T × ({0, 1}|ci|×|C|) | Feature-level representation of P |
| d demo | Vector representation of demographics |
| Attention weights of codes in visit vj | |
| Task-specific attention weights for features | |
| Task-specific attention weights for visits | |
| Temporal encoding vector of visit vj | |
| Representation learned by visit-view encoder | |
| Patient representation | |
| Representation learned by feature-view encoder | |
| Visit-view task-specific representation for kth task | |
| Feature-view task-specific representation for kth task | |
| Task-specific representation for kth task | |
| yk | Ground-truth output for kth task |
| Predicted output for kth task |
Patient record.
The heterogeneous and hierarchical structure of a patient record is defined as follows.
Definition 1 (Clinical code). C = {c1, c2, …, c|C|} is the set of unique clinical codes including diagnosis, procedure, and medication codes with |C| is the number of these unique codes. Each code ci can be represented by binary vector xi ∈ {0, 1}|C| where ith element of this vector is 1 and other elements are 0.
Definition 2 (Clinical visit). A visit is a hospital stay from admission to discharge. Each visit vj is a tuple of (cj, tj) where cj = {cj1, cj2, ⋯, cj|cj|} ∈ C|cj| with set of indexes {j1, ⋯, j|cj|} ∈ {1, 2, ⋯, |C|} and tj is the timestamp of the visit. cj can be represented by binary vector Vj ∈ {0, 1}|C| where the ith element is 1 if cj contains the code ci. Besides vector representation, cj can also be expressed as matrix Xj ∈ {0, 1}|cj|×|C| where ith row of this matrix is the binary vector xji ∈ {0, 1}|C| of code cji.
Definition 3: (Patient record). The patient record P is a sequence of visits [v1, v2, ⋯, vT] where T is the number of visits. Like clinical visit representation, P can be represented at the two different granularities. At visit-level, P can be represented as a binary matrix Xvisit ∈ {0, 1}T×|C| where jth row of this matrix is binary vector Vj of visit vj. At feature-level, P can be represented as the sequence of matrices Xfeature = [X1, X2, ⋯, XT].
Definition 4: (Demographic information). Besides clinical information, a patient record can have demographic information about the patient such as age, gender, and region. It can be represented by binary vector ddemo ∈ {0, 1}ddemo, where ddemo is the number of demographic attributes.
Clinical risk profiling.
The aim of this task is to find a set of functions F = (F1, F2, ⋯, FN} that predicts the onset of complications from patient record P, where N is the number of complications. In MTL setting, F1, F2, …, FN generally have some shared parameters to learn shared information from related tasks for better predictions.
3.2. MuViTaNet
Overview architecture.
This section presents our proposed multi-view multi-task network (MuViTaNet) for predicting onset of multiple complications from patient records. MuViTaNet is designed to explicitly capture the dependencies among clinical visits and clinical features from patient records. It also leverages additional information from both related labeled and unlabeled data to achieve accurate predictions and efficient interpretation. In particular, MuViTaNet consists of four main components as follows. (1) Feature-view Encoder. This component considers a patient record as a set of temporal clinical features and then encodes information of each feature separately. (2) Visit-view Encoder. This component formulates a patient record as a sequence of visits and then learns a representation for each visit in the sequential context. Specifically, this component is designed as a hierarchical model that exploits patient records in the two levels, including feature-level and visit-level. (3) Task-specific Attention. After learning the shared representation from feature-view and visit-view encoders, an attention mechanism is employed to extract task-specific representation for each task from the shared representation. (4) Task-specific Decoder. The task-specific representations are fed into the corresponding task-specific decoders to predict clinical outcomes for patients in complication datasets and to project representations to unit hypersphere for patients in unlabeled dataset. Figure 3 shows the overview architecture of MuViTaNet and technical details of its components are presented as follows.
Fig. 3.
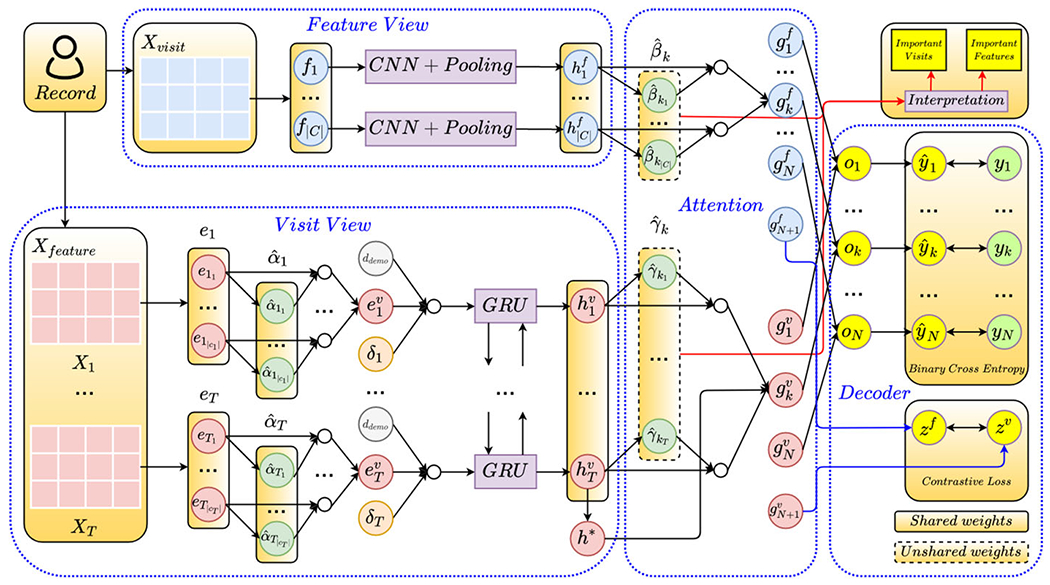
The overall architecture of MuViTaNet. The proposed framework consists of four main components: feature-view encoder, visit-view encoder, task-specific attention, and task-specific decoder. Given a patient record, MuViTaNet first extracts information from clinical visits and features by looking at the record in two different ways: sequence of clinical visits and set of clinical features. Then, the shared representation learned by these two encoders is put into the task-specific attention to learn the task-specific representation. Finally, the clinical predictions are generated by the task-specific decoders. Note that the figure only shows the task-specific attention for one prediction task for simplicity
Feature-view encoder.
This component treats patient data as a set C of clinical codes which are represented by the set of temporal sequences (i.e., columns of matrix Xvisit ∈ {0, 1}T×|C|). In particular, given clinical code ci, its temporal data can be represented by a binary vector fi ∈ {0, 1}T which is ith column of Xvisit. Then, one-dimensional convolutional neural networks (Conv1d) and max-pooling (MaxPool) operation are employed to extract temporal patterns from each clinical code separately. In particular, Conv1d with kernel size k (i.e., k = 3 in our setting) takes as inputs the sub-sequences of length k from vector fi to learn the representation of code ci as follows.
| (1) |
where are the output of Conv1d and 4d is the number of filters used in convolution operations. Next, the row-wise max-pooling is applied to to generate vector representation for clinical code ci.
| (2) |
Note that the weights of Conv1d are not shared between clinical codes. The output of feature-view encoder is matrix .
Visit-view encoder.
This component formulates patient data as a sequence of visits in which each visit can be seen as a set of clinical codes. Due to the hierarchical characteristic of this data structure, the visit-view encoder is also designed hierarchically to capture information at different levels. Given visit vj, we represent this visit by matrix Xj ∈ {0, 1}|cj|×|C| which is jth element of the sequence Xfeature. Because different clinical codes associated with the same visit can have disparate impacts, instead of treating these clinical codes uniformly when aggregating them to represent the visit, the location attention mechanism is employed to learn the contributions of these clinical codes to their visit representation. In particular, given a binary representation xji ∈ Xj of code cji, 1-layer feed-forward neural network is applied to learn the dense representation from sparse vector of this clinical code as follows.
| (3) |
where is the learned weight matrix of clinical codes, is the bias vector, and ReLU is rectified linear unit activation function. Then, the 2-layer feed-forward neural network FFNN2 with Tanh activation function is used to generate the attention score αji for this clinical code as follows.
| (4) |
The attention vector which represents the contributions of clinical codes in visit vj is fed into the softmax layer to get the normalized vector .
| (5) |
Then, the representation of visit vj are computed as the weighted average of its clinical codes.
| (6) |
where denotes the jth visit’s representation. To generate personalized representation for each visit, demographic information including age and region is incorporated into every clinical visit as follows.
| (7) |
where Concat is the concatenation operation and is the weight matrix mapping concatenated vectors to the original embedding space. Besides clinical codes, each visit is also associated with its timestamp. In order to capture the elapsed time between visits, we add the temporal encoding vector to each visit as follows.
| (8) |
where is the temporal encoding vector whose design is inspired by the positional encoding used in Transformer architecture [49]. In particular, it is computed by trigonometric functions as follows.
| (9) |
where 0 ≤ 2t < d − 1. From Equation (9), we can see that temporal embedding encodes similar time intervals into similar vectors in embedding space.
To generate the sequential representations for visits in the sequential context, we put the independent representations for visits learned from previous steps into the bidirectional GRU layer. Specifically, the sequential representation for these visits is computed as follows.
| (10) |
where . Then, the patient representation is computed based on the last visit in the visit sequence.
| (11) |
In summary, the outputs of the visit-view encoder include the sequential representations of clinical visits and the patient representation .
Task-specific attention.
Given the shared representations generated by feature-view and visit-view encoders, attention mechanisms are employed to generate the task-specific representations for the patient. Specifically, the attention weights of clinical features and visits for kth task are computed as follows.
| (12) |
where , are 2-layer feed-forward neural networks with Tanh activation function that compute the weights of clinical features and visits from their representations. Then, we obtain the task-specific representation for kth task as follows.
| (13) |
Task-specific decoder.
For a patient in labeled dataset (i.e., complication dataset), the 2-layer feed forward neural network with Sigmoid activation function at the last layer is employed to predict the probability of complication onset for this patient.
| (14) |
For a patient in unlabeled dataset, the 2-layer feed forward neural network with normalization operation (Norm) is used to project the feature-view and visit-view representations of this patient on the unit hypersphere.
| (15) |
Optimization.
To train MuViTaNet in MTL setting, we follow the alternating training strategy [50] in which each task is selected randomly and then is optimized for a fixed number of parameter updates before switching to other tasks (Algorithm 1). In our setting, different tasks have datasets of different sizes, so we select a task to optimize with probability , where Dk and nk are the dataset and batch size for kth task, and N is the number of complication datasets.
For labeled datasets, the binary cross-entropy (BCE) loss function is used to optimize the prediction based on ground-truth labels. Specifically, for kth task with dataset Dk, the loss function for this task is computed as follows.
| (16) |
where yk and are the ground-truth and predicted outputs for kth task, respectively. For unlabeled dataset, we leverage the contrastive (CL) loss function [51] to pull together the normalized representations of feature-view and visit-view of the same patient and to push apart these representations from representations of other patients.
| (17) |
where A(zi) ≡ Z \ zi in which .
3.3. F-MuViTaNet with fairness constraint
Measures of unfairness.
Many group fairness criteria have been proposed in the literature to mitigate the unfairness issues in machine learning systems. Under these criteria, the population is partitioned into different groups based on some sensitive attributes (e.g., age, gender, race, etc.), and certain statistical measures are (approximately) equalized across these groups. In this work, we focus on one of the most widely used criterion named equal opportunity [31]. Formally, denote Y, , S as ground-truth label, prediction, and sensitive attribute, respectively, then equal opportunity requires that given Y, and S are conditional independent, i.e., . In the case of binary classification, it means the equality of true/false positive rates (TPR/FPR) across groups.
In our medical context, we will focus on FPR. The goal is to avoid the patients from certain groups being mistakenly diagnosed as positive at a rate that is higher than other groups. That is,
| (18) |
where S is the set of all possible values of sensitive attribute S. Above formulation can be extended to non-binary settings where there exist scores that predict the likelihoods of samples being positive. Specifically, we will study the following two cases:
1). Threshold-based case:
Predictions are binary and are attained by thresholding prediction scores , i.e., if , otherwise . We can quantify the violation of equal opportunity using FPR gap (FPRG) defined below:
| (19) |
2). Threshold-free case:
In the presence of prediction scores , we can use the earth mover’s distance (EMD) [52] and mean distance (MD) to quantify violation of equal opportunity , i.e.,
| (20) |
| (21) |
Above metrics can be empirically computed from sampled data as follows.
| (22) |
| (23) |
| (24) |
Fairness as regularization.
As introduced in Sect. 2 , there are roughly three types of approaches to achieving fairness: pre-processing, in-processing, and post-processing. In our study, we adopt in-processing approach by achieving fairness via regularization. Specifically, for kth task, we penalize the fairness violation by adding an additional regularization term to prediction loss, i.e.,
| (25) |
where is the prediction loss measured by binary cross-entropy mentioned in the previous section, is the regularization term (fairness loss), and ω is the hyper-parameter that controls the ratio between prediction loss and fairness loss. In particular, we use maximum mean discrepancy (MMD) [53], mean distance (MD) and correlation (COR) to quantify fairness loss.
| (26) |
| (27) |
| (28) |
where are LF calculated by MMD, MD, and COR, respectively, and task index k is omitted for simplicity.
4. Experiments
In this section, we evaluate the performances of MuViTaNet on six real-world insurance claim datasets and compare its results with state-of-the-art clinical risk prediction models to demonstrate the effectiveness of our method. Besides achieving accurate prediction, we also show the robustness of MuViTaNet in terms of interpretability. Finally, we examine the fairness properties of MuViTaNet and study the impact of imposing fairness constraint by investigating the trade-off between accuracy and fairness. Note that although we conduct experiments on insurance claim data which includes clinical codes only, our proposed method is not limited to this setting. Specifically, it can be easily extended to work with heterogeneous clinical data [54] (e.g., clinical notes, lab tests, vital signs) by incorporating more encoders designed to handle these data types [55, 56].
4.1. Datasets
Breast cancer cohort construction.
We extract clinical records of female breast cancer patients from the MarketScan Commercial Claims and Encounter (CCAE) database provided by Truven Health2 to construct cardiac complication risk profiling datasets. According to the previous work [24], the records from 2012 to 2017 of de-identified patients are selected based on the following criteria.
Ages of the selected patients are from 18 to 65 at the initial diagnosis of breast cancer.
The selected patients have at least six months of records and ten clinical visits before being diagnosed with breast cancer.
There is no cardiac complication diagnosis until the initial diagnosis of breast cancer of the selected patients.
Cardiac complication datasets construction.
After construing the breast cancer cohort, we create a distinct dataset for each cardiac complication onset prediction task. In our setting, we focus on profiling the risk of developing cardiac complications in a six-month window after the initial diagnosis of breast cancer (i.e., prediction window), and the positive instances are defined as patients who have cardiac complications in this window. Following previous clinical research [3,4], we identify six cardiac complications including atrial fibrillation (AF), coronary artery disease (CAD), heart failure (HF), hypertension, peripheral arterial disease (PAD), and stroke. Patients with cardiac complication onsets during prediction windows are considered positive instances. Patients without any cardiac complication onsets during prediction windows are considered negative instances. The negative instances are randomly selected from the breast cancer cohort with a ratio of 3:1 compared to positive instances. To mimic the real clinical scenario, information until the initial diagnosis of breast cancer (i.e., index date) is used to predict whether patients develop cardiac complication onsets during the prediction window. Descriptions, ICD codes, and the corresponding numbers of positive/negative instances of these complications are shown in Tables 2 and 3. The data construction process is visualized in Fig. 4.
Table 2.
Cardiac complications in female breast cancer cohort and their corresponding ICD codes, numbers of positive instances, and average record length (number of clinical visits)
| Complication | Description | ICD-10 Codes | #subjects | Record length |
|---|---|---|---|---|
| Atrial fibrillation | An irregular, often rapid heart rate that commonly causes poor blood flow | I48 | 322 | 33.6716 ± 20.7659 |
| Coronary artery disease | Damage or disease in the heart’s major blood vessels | I20–I25 | 769 | 34.0257 ± 21.7465 |
| Heart failure | A chronic condition in which the heart doesn’t pump blood as well as it should | I11, I13 I42, I50 | 1124 | 33.0436 ± 20.8930 |
| Hypertension | A condition in which the force of the blood against the artery walls is too high | I10, I16 | 6787 | 32.8804 ± 20.8836 |
| Peripheral arterial disease | A circulatory condition in which narrowed blood vessels reduce blood flow to the limbs | I70 | 340 | 33.6860 ± 21.3025 |
| Stroke | Damage to the brain from interruption of its blood supply | I60–I69 | 592 | 34.0908 ± 21.3674 |
Table 3.
Cardiac complication onset statistic in female breast cancer cohort
| Dataset | Outcome statistic |
|||||
|---|---|---|---|---|---|---|
| 18–44 |
45–54 |
55–64 |
||||
| #subjects | %positive | #subjects | %positive | #subjects | %positive | |
| Atrial fibrillation | 272 | 0.1434 | 456 | 0.2171 | 560 | 0.3286 |
| Coronary artery disease | 697 | 0.1506 | 1067 | 0.2455 | 1312 | 0.3064 |
| Heart failure | 1149 | 0.2663 | 1632 | 0.2408 | 1715 | 0.2478 |
| Hypertension | 5900 | 0.1358 | 9690 | 0.2269 | 11558 | 0.3277 |
| Peripheral arterial disease | 273 | 0.0952 | 472 | 0.2331 | 615 | 0.3317 |
| Stroke | 503 | 0.1372 | 832 | 0.2091 | 1033 | 0.3379 |
Data are grouped on the basis of age and cardiac complications. %positive is the proportion of breast cancer patients that developed cardiac complication onsets in 6-month window
Fig. 4.
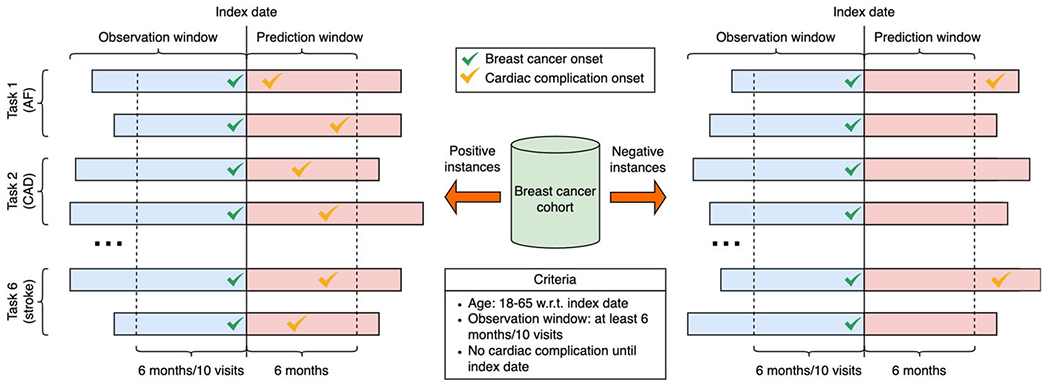
Cardiac complication datasets construction. Data for six cardiac complication prediction tasks (i.e., atrial fibrillation (AF), coronary artery disease (CAD), heart failure (HF), hypertension, peripheral arterial disease (PAD), and stroke) are extracted from the breast cancer cohort. Index dates are dates when patients are initially diagnosed to have breast cancer. Patients with cardiac complication onsets during prediction windows are considered positive instances. Patients without any cardiac complication onsets during prediction windows are considered negative instances. The ratio between positive and negative instances is 1:3 for all six datasets. Information until the index dates is used to predict whether patients develop cardiac complication onsets during the prediction window
Unlabeled dataset construction.
The negative patients that are not selected for complication datasets are used to construct a dataset for contrastive learning. MuViTaNet leverages this dataset as additional information to improve the prediction performances of complication onset prediction tasks.
Feature selection.
We use the following information to profile cardiac complications for breast cancer patients.
Demographics including age and region information. We cluster patients into three age groups (i.e., 18 – 44, – 45 — 54, 55 – 65) and five region groups.
Clinical codes including diagnosis, procedure, and medication codes. For diagnosis codes, all ICD-9 codes are converted to ICD-10 codes. To alleviate data sparsity, we group all diagnosis and procedure codes based on their first three characters and remove codes that appear in less than 200 patients. For medication codes, we group them by their therapeutic classes. This preprocessing step results in 1188 features.
4.2. Experimental setup
Baseline models.
To validate the performance of the proposed model for cardiac complication risk profiling task, we compare it with several state-of-the-art models. Based on their architectures, these models are categorized into four main groups including classical model, recurrent-based model, attention-based model, and time-aware model. The details of these models are presented as follows.
Logistic Regression (LR). A classical model used in binary classification. To deal with insurance claim data, a patient record is converted to the whose ith element is the frequency of ith clinical code in that record, and is then fed into LR.
Random Forest (RF) [57]. A classical ensemble model whose prediction is the average computed from predictions of a number of decision tree classifiers. Inputs for RF are similar to LR.
Gated Recurrent Unit (GRU) [58]. A variant of recurrent neural network (RNN) that uses gating mechanism.
Bidirectional GRU (Bi-GRU) [25]. An improved version of GRU by employing an additional GRU model to learn the sequence data in reverse order.
Dipole [5]. An attention-based model that utilizes attention mechanism over the sequence generated by Bi-GRU to learn the dependencies between visits.
RETAIN [13]. An attention-based model that first employs a reverse RNN to process clinical records in reverse order to mimic physicians’ decisions. Then two attention modules are used to identify significant visits and variables.
T-LSTM [6]. A time-aware model designed for handling irregularity visits in clinical records. The memory cell of LSTM is modified to capture time intervals between two consecutive visits.
Transformer [49]. A fully attention-based model that uses multi-head attention mechanisms to learn the dependencies among elements in sequential data.
LSAN [59]. An attention-based model that uses Transformer to capture global information and CNN to capture local information.
MTL Models: We develop the MTL version for each of the aforementioned neural network-based models by employing task-specific attention and decoder over the output generated by these models.
MuViTaNet-visit-view: A variant of MuViTaNet by removing the visit-view encoder.
MuViTaNet-feature-view: A variant of MuViTaNet by removing the feature-view encoder.
MuViTaNet-task-speciflc: A variant of MuViTaNet by removing the task-specific attention and decoder for single-task learning (STL) setting.
MuViTaNet-unlabeled: A variant of MuViTaNet trained with labeled datasets only.
F-MuViTaNet: A fairness variant of MuViTaNet by incorporating fairness loss as regularization.
Implementation details.
All neural network-based architectures are implemented by PyTorch.3 For classical models including LR and RF, we use their Python implementations from Scikit-Learn [60]. We use ADAM algorithm [61] to optimize the prediction performances for neural network-based models. The batch size is set as 16 for labeled datasets and 256 for unlabeled dataset, and the initial learning rate is 0.0001. All experiments are conducted on a single server with 8-core CPU, 16 GB memory of RAM, and 16 GB memory of GPU V100.
Evaluation metrics.
We conduct experiments under 5-fold cross-validation setting. 10% instances from the training set are used to construct the validation set, and the results on the testing set are determined based on the best results on the validation set. The area under the receiver operating characteristic (AU-ROC) is used to measure the performances of prediction models for cardiac complication risk profiling. To understand the impact of imposing fairness constraint, we examine the fairness-accuracy trade-off for each task by varying hyper-parameter ω. We consider both threshold-based and threshold-free cases, and metrics for accuracy and fairness of both cases are summarized in Table 4. To binarize prediction scores (i.e., changing from threshold-free to threshold-based settings), we use J-statistic [62] to select optimum thresholds from the validation sets. Age (i.e., 18-44, 45-54, 55-64) is treated as the sensitive attribute in the experiments.
Table 4.
Accuracy/fairness metrics for threshold-based/free cases
| Accuracy metric | Fairness metric | |
|---|---|---|
| Threshold-based | F 1 | FPR gap (FPRG) |
| Accuracy | ||
| Threshold-free | Area under the receiver operating characteristic (AU-ROC) | Earth mover’s distance (EMD) |
| Area under the precision-recall curve (AU-PRC) | Mean distance (MD) | |
| Cross-entropy (CE) |
4.3. Results
We conduct experiments to answer the following questions.
Q1. How accurate is MuViTaNet for cardiac complication risk profiling task comparing to previous works?
Q2. How each component of MuViTaNet contributes to its prediction performance?
Q3. How to effectively interpret the predictions made by MuViTaNet?
Q4. How is MuViTaNet’s fairness property can be affected by MTL scheme?
Q5. How F-MuViTaNet performs in terms of fairness-accuracy trade-off for cardiac complication risk profiling?
Cardiac complication risk profiling.
As shown in Table 5, MuViTaNet achieves the best performances compared to other baselines for cardiac complication risk profiling task measured by AU-ROC score. Generally, it achieves an average (i.e., over six datasets) AU-ROC score of 0.8102, which is 11% better than the best previous method. Looking into each complication dataset, we also observe that MuViTaNet consistently outperforms other methods in terms of AU-ROC score. Such improvements indicate the advantage of MuViTaNet by using (1) multi-view encoder to extract comprehensive information and (2) MTL scheme to leverage information from both related labeled and unlabeled datasets to improve its prediction performance.
To further support our conclusion, we conduct statistical tests for all models under a multitask learning setting. According to the guidelines in [63], we first conduct Friedman test [64, 65] to determine if there are any differences between the prediction performances of models. This test returns a test statistic of 31.06 and the corresponding P-value of 7 × 10−5 (< 0.05) resulting in the rejection of the null hypothesis (i.e., no difference). In other words, we have sufficient evidence to conclude that there are differences between the performances of models. However, this test does not tell us which models are different from each other. To find out exactly whether our proposed model is significantly different from the baseline models, we further conduct Quade’s post hoc test [66]. The adjusted p-value from the statistical test of each pair of classifiers is shown in Table 6. All p-values between our proposed model and baseline models (i.e., in the last row/column) are significantly less than 0.05, then indicating that our model achieves significantly better prediction performances for cardiac complication risk profiling.
For baseline methods, we can observe that formulating complication risk profiling as MTL significantly improves the prediction performances of these methods. The improvements are more noteworthy for small datasets, including AF (31%), CAD (19%), PAD (22%), and stroke (13%). These results demonstrate the importance of leveraging task-related information for predicting the onset of complications. We also see that GRU-based models achieve slightly improved performances compared to other neural network models. For STL setting, the averaged prediction performances of deep learning models are on par with RF and are much better than LR. To investigate more, we zoom into the prediction performance for each dataset and observe that RF outperforms deep learning models for AF, CAD, PAD, and stroke datasets whose sizes are relatively small compared to HF and hypertension datasets. This result is reasonable because deep learning methods generally require large training data to achieve good prediction performance.
Ablation study.
To investigate the contribution of each component in MuViTaNet, we conduct an ablation study by comparing MuViTaNet with its simpler variants including MuViTaNet-visit-view, MuViTaNet-feature-view, MuViTaNet-task-specific, and MuViTaNet-unlabeled on the six aforementioned datasets. The AU-ROC scores of these models are shown in Table 7. We can observe that encoding clinical data solely by a single-view encoder is not as good as a multi-view encoder. AU-ROC score of MuViTaNet decreases to 0.7906 (resp. 0.7942) when only using visit-view (resp. feature-view) encoder. This result demonstrates the necessity of aggregating information from multiple views. The performance of MuViTaNet also drops significantly when we remove the task-specific attention mechanism and decoder, which further confirms the importance of formulating complication risk profiling task as MTL with both labeled and unlabeled datasets.
Table 7.
Average performances of MuViTaNet variants over 6 complication datasets (F Feature-view, V Visit-view, L Labeled, U Unlabeled)
| Models | Multi-view |
Multi-task |
AU-ROC | ||
|---|---|---|---|---|---|
| F | V | L | U | ||
| MuViTaNet-task-specific | ✓ | ✓ | ✗ | ✗ | 0.7385 ± 0.0239 |
| MuViTaNet-feature-view | ✗ | ✓ | ✓ | ✗ | 0.7906 ± 0.0286 |
| MuViTaNet-visit-view | ✓ | ✗ | ✓ | ✗ | 0.7942 ± 0.0248 |
| MuViTaNet-unlabeled | ✓ | ✓ | ✓ | ✗ | 0.8102 ± 0.0136 |
| MuViTaNet | ✓ | ✓ | ✓ | ✓ | 0.8160 ± 0.0117 |
Model interpretability.
The deployment of data-driven systems to healthcare applicants in real-world requires not only models with good prediction performance but also efficient mechanisms to interpret the automated decision to clinicians. By leveraging the multi-view multi-task architecture, our proposed model can interpret the prediction for each complication in multiple perspectives, thereby helping clinicians understand which clinical entities contribute most to the prediction.
To characterize cardiac complications, we find the most important features for each of these cardiac complications by averaging the feature-view attention weights over all positive patients for clinical features in each complication dataset. Due to the varied number of features across patients, we rescale attention weights by multiplying them with the number of features appeared in the corresponding records before averaging. Then, top-10 clinical features for 6 cardiac complications are shown in Table 8. We observe that these complications share many common features such as I34 (nonrheumatic mitral valve disorders) and I49 (other cardiac arrhythmias). This result is reasonable because all of these complications belong to cardiovascular disease class. Moreover, many important features determined by our model are known to be clinically associated with the corresponding complications. For example, patients with type II diabetes are two to four times more likely to develop heart diseases than someone without diabetes [67]. Obesity is another major known risk factor for heart failure and hypertension patients [68, 69]. Angina pectoris is the type of chest pain caused by reduced blood flow to the heart and is considered as a symptom of coronary artery disease [70].
Case study for model interpretability.
To further investigate the interpretability of MuViTaNet, we look at two case studies to visualize the learned attention weights for finding risk factors of each complication. The case studies include a positive patient from heart failure dataset and a negative patient from hypertension dataset. Their clinical records are illustrated in Fig. 5. The most important visits and features determined by their associated attention weights from visit-view and feature-view task-specific attention components are shown in Table 9. For the positive patient (Fig. 5a), the predicted probability for heart failure onset is 0.7790. As shown in Table 9, the visit-view attention focuses more on visits 3 and 9, which include clinical codes 250.00 (Type II diabetes mellitus) and 278.00 (Obesity) and these codes are also determined as the most important features by the feature-view attention. This result is also consistent with clinical research in which type II diabetes mellitus and obesity have been shown as the common risk factors for heart failure disease [67, 69], thereby demonstrating the effectiveness of MuViTaNet in capturing the correlation between risk factors and corresponding diseases. To further investigate the robustness of our model, we remove important visits and features indicating heart failure’s risk factors from the patient record and predict the probability of heart failure onset based on the modified records for capturing the changes in model output. Figure 5a shows that the predicted score decreases to 0.5284 and 0.4834 when removing visits (3 and 9) and codes (250.00, 278.00, and 796.2), respectively. Thus, MuViTaNet is capable to focus on clinical-related visits and features when predicting onset of complications.
Figure 5b shows a clinical record of the negative patient who has type II diabetes mellitus but is also treated by M-174 (Metformin). Table 9 indicates that MuViTaNet pays more attention on M-174 and 250.00 when predicting onset of hypertension. To verify whether our model can capture the relationship between disease and treatment, we remove these codes from the patient record as we did for the positive patient. Figure 5b shows that the predicted probability increases from 0.2330 to 0.3380 when removing Metformin (diabetes medication) and decreases to 0.0373 when removing code 250.00 (diabetes). This result indicates that MuViTaNet considers the impact of both disease and treatment on complication development when making predictions.
Impact of multi-task learning on unfairness.
In this task, we do not impose any fairness constraint and empirically study the fairness property of MuViTaNet. We consider three groups distinguished by age (i.e., 18-44, 45-54, 55-64). The statistic of each age group corresponding to each complication onset dataset is shown in Table 3. We aim to examine that without fairness intervention, whether MuViTaNet exhibits the disparate performance across different groups, and how the disparity is affected under multi-task learning. To this end, we compute AU-ROC and FPRG scores of MuViTaNet (MTL) and MuViTaNet-task-specific (STL). The results are shown in Table 10.
The results show that MuViTaNet achieves superior performances compared to MuViTaNet-task-specific in terms of both accuracy and fairness. The improvements are more significant for prediction tasks with limited data (i.e., AF, CAD, PAD, stroke). It further illustrates that MTL can capture additional information from related datasets and is effective in developing accurate and fair clinical prediction systems. Moreover, we recognize that fairness property is also affected by the data quantity and groups’ similarity of incident rates: the fairness violation is milder in the prediction tasks with abundant data (i.e., hypertension) and similar incident rates (i.e., HF) than the tasks with limited data and different incident rates across groups (i.e., AF, CAD, PAD, stroke).
Impact of imposing fairness constraints.
Although MTL can help mitigate unfairness, there are still gaps in predictions generated by MuViTaNet across sensitive groups. We further incorporate fairness constraint by adding regularization to the model objective function (F-MuViTaNet) and then train the model on 6 cardiac complication onset datasets. We empirically investigate the trade-off between fairness and accuracy by varying the hyper-parameter ω from 10−3 (weak fairness violation penalty) to 10 (strong fairness violation penalty). For each setting, we observe the accuracy and fairness violation, and measure the performances of F-MuViTaNet by averaging over 6 prediction tasks. The results are shown in Figs. 6, 7, and 8.
In the following, we focus on the experiments using MMD as the regularization method and report the results of F-MuViTaNet in Fig. 6 by multiple metrics including AU-ROC, AU-PRC, CE, accuracy, F1 (accuracy metrics), and FPRG, EMD, MD (fairness metrics). Analogous patterns are also observed when using MD and COR to enforce fairness and are shown in Figs. 7 and 8, respectively. The first observation is the effect of hyper-parameter ω on unfairness. In most settings, the larger ω (i.e., more penalty on fairness violation) during training leads to better fairness on the testing sets. When ω approaches 10 (the largest value in the experimental setting), the disparity across sensitive groups is almost eliminated that FPR scores are similar across different groups. The only exception is the case of using COR with large ω (ω > 0.1), where both accuracy and FPRG get worse under COR constraint.
In general, we observe the trade-off between accuracy and fairness in the testing when varying ω but this trade-off is negligible in most cases. In particular, when increasing ω from 0.001 to 0.1, the prediction performance remains almost the same with respect to all accuracy metrics including AU-ROC, AU-PRC, CE, accuracy, and F1 while the fairness violation is reduced significantly (i.e., from 0.0867 to 0.0723 for FPRG, from 0.3203 to 0.2414 for EMD, and from 0.1453 to 0.0789 for MD). When we continue increasing ω to 10, fairness violations are almost eliminated (i.e., 0.0245 for FPRG, 0.0356 for EMD, and 0.0010 for MD) while most of the accuracy metrics remain almost the same, except for AU-ROC which decreases from 0.8160 to 0.7989 (Fig. 6A). However, this trade-off is acceptable as the predictions are almost perfectly fair. The only exception, as we mentioned previously, is when using large ω and COR as the regularization method. In that case, large ω significantly hurts both accuracy and fairness. However, we can still achieve a good fairness-accuracy trade-off with COR as we have for MMD and MD when selecting the suitable value for ω (i.e., ω = 0.1 as shown in Fig. 8).
We also compare different groups by looking into per-group results. Without imposing fairness constraint, age group 18-44 experiences the worse performance in both fairness and accuracy compared to the other two age groups (45-54 and 55-64). This is because age groups 45-54 and 55-64 have the higher breast cancer and cardiac complication rates than age group 18-44, leading to more data instances in training dataset. Consequently, the trained model can be more in favor of majority group (e.g., age groups 45-54 and 55-64) but less favorable to the minority group (18-44). However, as shown in the results, the disparity across different age groups can be mitigated significantly by adding fairness constraint during training.
5. Conclusions
In this paper, we propose a novel multi-view multi-task network (MuViTaNet) that leverages clinical data to profile multiple complications for patients. To tackle the issues of existing methods, MuViTaNet considers patient record as both the sequence of clinical visits (visit-view) and the set of clinical features (feature-view) and then employs the multi-view encoder to effectively exploit patient information. Due to the correlation among different complications, we utilize MTL architecture to learn task-specific representations of patients from both labeled and unlabeled datasets. Finally, the predictions for each complication onset are generated from the task-specific representation by the corresponding decoder. To prevent MuViTaNet unfairly treating certain patient groups, we further propose a fairness mechanism (F-MuViTaNet) by incorporating the fairness constraint into the optimization objective. We evaluate the prediction performances of MuViTaNet and F-MuViTaNet on the insurance claim database. The experiments demonstrate that our proposed model outperforms other state-of-the-art models for the complication risk profiling task. More importantly, MuViTaNet provides an efficient mechanism to interpret their prediction from multiple perspectives, and F-MuViTaNet can significantly mitigate unfairness in predictions across different groups with only an negligible impact on accuracy.
Acknowledgements
This work was funded in part by the National Science Foundation under award number CBET-2037398, by the National Institutes of Health under award number UL1TR002733, and by The Ohio State University President’s Research Excellence Accelerator Grant.
Biographies

Thai-Hoang Pham is currently a Ph.D. student at Department of Computer Science and Engineering, The Ohio State University (OSU). Before coming to OSU, he received bachelor’s degree from FPT University in 2015. His research interests are trustworthy machine learning (i.e., fairness, robustness, interpretability, causal inference, uncertainty quantification) and its application to biomedical domains (i.e., predictive modeling, drug discovery).

Changchang Yin is a Ph.D. student at the Department of Computer Science and Engineering, The Ohio State University (OSU). His research interests lie in data mining, machine learning and their application to trustworthy AI (e.g., fairness and causal inference), computational medicine (e.g., predictive modeling, patient subtyping and medical imaging).

Laxmi Mehta is a cardiologist, Professor in the Division of Cardiovascular Medicine, director of the Lipid Clinics and section director of Preventative Cardiology and Women’s Cardiovascular Health at The Ohio State University Wexner Medical Center (OSUWMC). She specializes in women’s cardiovascular health, prevention and cardiac imaging.

Xueru Zhang is an Assistant Professor in the Department of Computer Science and Engineering at The Ohio State University. Before joining OSU, she received her Ph.D. degree from the University of Michigan in 2021. Her recent works focus on understanding societal impacts of machine learning, and developing algorithms that are aligned with social norms (e.g., privacy, fairness) and reliable to dynamic environments. She was a recipient of Predoctoral Fellowship at the University of Michigan in 2020, a Rising Stars in EECS in 2020, and a Caltech’s Young Investigators lecturer in 2021.

Ping Zhang is an Assistant Professor at The Ohio State University (OSU), with joint appointments at the Department of Computer Science and Engineering (CSE), and the Department of Biomedical Informatics (BMI). He leads the AIMed (Artificial Intelligence in Medicine) Lab at OSU. His research focuses on machine learning, data mining, and their applications to trustworthy AI (e.g., explainability, fairness, robustness, causal inference, uncertainty quantification), computational medicine (e.g., predictive modeling, medical imaging, clinical NLP, real-world evidence, drug discovery & development).
Footnotes
References
- 1.Schairer C, Mink PJ, Carroll L, Devesa SS (2004) Probabilities of death from breast cancer and other causes among female breast cancer patients. J Natl Cancer Inst 96(17) [DOI] [PubMed] [Google Scholar]
- 2.Patnaik JL, Byers T, DiGuiseppi C, Dabelea D, Denberg TD (2011) Cardiovascular disease competes with breast cancer as the leading cause of death for older females diagnosed with breast cancer: a retrospective cohort study. Breast Cancer Res 13(3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Abdel-Qadir H, Thavendiranathan P, Fung K, Amir E, Austin PC, Anderson GS, Lee DS (2019) Association of early-stage breast cancer and subsequent chemotherapy with risk of atrial fibrillation. JAMA Netw Open 2(9) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Strongman H, Gadd S, Matthews A, Mansfield KE, Stanway S, Lyon AR, dos-Santos-Silva I, Smeeth L, Bhaskaran K (2019) Medium and long-term risks of specific cardiovascular diseases in survivors of 20 adult cancers: a population-based cohort study using multiple linked uk electronic health records databases. Lancet 394(10203) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ma F, Chitta R, Zhou J, You Q, Sun T, Gao J (2017) Dipole: diagnosis prediction in healthcare via attention-based bidirectional recurrent neural networks. In: KDD’17 [Google Scholar]
- 6.Baytas IM, Xiao C, Zhang X, Wang F, Jain AK, Zhou J (2017) Patient subtyping via time-aware LSTM networks. In: KDD’17 [Google Scholar]
- 7.Gao J, Xiao C, Wang Y, Tang W, Glass LM, Sun J (2020) Stagenet: stage-aware neural networks for health risk prediction. In: WWW’20 [Google Scholar]
- 8.Rajkomar A, Hardt M, Howell MD, Corrado G, Chin MH (2018) Ensuring fairness in machine learning to advance health equity. Ann Intern Med 169(12):866–872 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pham T-H, Yin C, Mehta L, Zhang X, Zhang P (2021) Cardiac complication risk profiling for cancer survivors via multi-view multi-task learning. In: IEEE international conference on data mining [Google Scholar]
- 10.Cheng Y, Wang F, Zhang P, Hu J (2016) Risk prediction with electronic health records: a deep learning approach. In: Proceedings of the 2016 SIAM international conference on data mining, SIAM, pp 432–440 [Google Scholar]
- 11.Ghassemi M, Pimentel M, Naumann T, Brennan T, Clifton D, Szolovits P, Feng M (2015) A multivariate timeseries modeling approach to severity of illness assessment and forecasting in ICU with sparse, heterogeneous clinical data. In: Proceedings of the AAAI conference on artificial intelligence, vol 29 [PMC free article] [PubMed] [Google Scholar]
- 12.Caballero Barajas KL, Akella R (2015) Dynamically modeling patient’s health state from electronic medical records: a time series approach. In: Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining, pp 69–78 [Google Scholar]
- 13.Choi E, Bahadori MT, Kulas JA, Schuetz A, Stewart WF, Sun J (2016) Retain: an interpretable predictive model for healthcare using reverse time attention mechanism. In: NIPS’16 [Google Scholar]
- 14.Song H, Rajan D, Thiagarajan J, Spanias A (2018) Attend and diagnose: clinical time series analysis using attention models. In: AAAI’18, vol 32 [Google Scholar]
- 15.Bai T, Zhang S, Egleston BL, Vucetic S (2018) Interpretable representation learning for healthcare via capturing disease progression through time. In: KDD’18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kwon BC, Choi M-J, Kim JT, Choi E, Kim YB, Kwon S, Sun J, Choo J (2018) Retainvis: visual analytics with interpretable and interactive recurrent neural networks on electronic medical records. IEEE Trans Vis Comput Gr 25(1) [DOI] [PubMed] [Google Scholar]
- 17.Ma L, Zhang C, Wang Y, Ruan W, Wang J, Tang W, Ma X, Gao X, Gao J (2020) Concare: personalized clinical feature embedding via capturing the healthcare context. In: AAAI’20, vol 34 [Google Scholar]
- 18.Zhou J, Yuan L, Liu J, Ye J (2011) A multi-task learning formulation for predicting disease progression. In: KDD’11 [Google Scholar]
- 19.Liu B, Li Y, Sun Z, Ghosh S, Ng K (2018) Early prediction of diabetes complications from electronic health records: a multi-task survival analysis approach. In: AAAI’18, vol 32 [Google Scholar]
- 20.Wiens J, Guttag J, Horvitz E (2016) Patient risk stratification with time-varying parameters: a multitask learning approach. J Mach Learn Res 17(1) [Google Scholar]
- 21.Nori N, Kashima H, Yamashita K, Ikai H, Imanaka Y (2015) Simultaneous modeling of multiple diseases for mortality prediction in acute hospital care. In: KDD’15 [Google Scholar]
- 22.Razavian N, Marcus J, Sontag D (2016) Multi-task prediction of disease onsets from longitudinal laboratory tests. In: MLHC’16. PMLR [Google Scholar]
- 23.Lipton ZC, Kale DC, Elkan C, Wetzel R (2016) Learning to diagnose with LSTM recurrent neural networks. In: ICLR’16 [Google Scholar]
- 24.Liu B, Li Y, Ghosh S, Sun Z, Ng K, Hu J (2019) Complication risk profiling in diabetes care: a bayesian multi-task and feature relationship learning approach. IEEE Trans Knowl Data Eng 32(7) [Google Scholar]
- 25.Ljubic B, Hai AA, Stanojevic M, Diaz W, Polimac D, Pavlovski M, Obradovic Z (2020) Predicting complications of diabetes mellitus using advanced machine learning algorithms. J Am Med Inf Assoc 27(9) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Guo A, Zhang KW, Reynolds K, Foraker RE (2020) Coronary heart disease and mortality following a breast cancer diagnosis. BMC Med Inf Decis Mak 20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen IY, Johansson FD, Sontag D (2018) Why is my classifier discriminatory? In: Proceedings of the 32nd international conference on neural information processing systems. NIPS’18. Curran Associates Inc., Red Hook, NY, USA, pp 3543–3554 [Google Scholar]
- 28.Pfohl S, Marafino B, Coulet A, Rodriguez F, Palaniappan L, Shah NH (2019) Creating fair models of atherosclerotic cardiovascular disease risk. In: Proceedings of the 2019 AAAI/ACM conference on AI, ethics, and society, pp 271–278 [Google Scholar]
- 29.Adamson AS, Smith A (2018) Machine learning and health care disparities in dermatology. JAMA Dermatol 154(11):1247–1248 [DOI] [PubMed] [Google Scholar]
- 30.Dwork C, Hardt M, Pitassi T, Reingold O, Zemel R (2012) Fairness through awareness. In: Proceedings of the 3rd innovations in theoretical computer science conference, pp 214–226 [Google Scholar]
- 31.Hardt M, Price E, Srebro N (2016) Equality of opportunity in supervised learning 29:3315–3323 [Google Scholar]
- 32.Zliobaite I (2015) On the relation between accuracy and fairness in binary classification. In: The 2nd workshop on fairness, accountability, and transparency in machine learning (FATML) at ICML’ 15 [Google Scholar]
- 33.Kusner M, Loftus J, Russell C, Silva R (2017) Counterfactual fairness. In: Proceedings of the 31st international conference on neural information processing systems, pp 4069–4079 [Google Scholar]
- 34.Mehrabi N, Morstatter F, Peng N, Galstyan A (2019) Debiasing community detection: the importance of lowly connected nodes. In: 2019 IEEE/ACM international conference on advances in social networks analysis and mining (ASONAM), IEEE, pp 509–512 [Google Scholar]
- 35.Brunet M-E, Alkalay-Houlihan C, Anderson A, Zemel R (2019) Understanding the origins of bias in word embeddings. In: International conference on machine learning, PMLR, pp 803–811 [Google Scholar]
- 36.Kamiran F, Calders T (2012) Data preprocessing techniques for classification without discrimination. Knowl Inf Syst 33(1):1–33 [Google Scholar]
- 37.Beutel A, Chen J, Zhao Z, Chi EH (2017) Data decisions and theoretical implications when adversarially learning fair representations. arXiv preprint arXiv:1707.00075 [Google Scholar]
- 38.Madras D, Creager E, Pitassi T, Zemel R (2018) Learning adversarially fair and transferable representations. In: International conference on machine learning, PMLR, pp 3384–3393 [Google Scholar]
- 39.Zemel R, Wu Y, Swersky K, Pitassi T, Dwork C (2013) Learning fair representations. In: International conference on machine learning, PMLR, pp 325–333 [Google Scholar]
- 40.Agarwal A, Beygelzimer A, Dudik M, Langford J, Wallach H (2018) A reductions approach to fair classification. In: International conference on machine learning, PMLR, pp 60–69 [Google Scholar]
- 41.Goh G, Cotter A, Gupta M, Friedlander MP (2016) Satisfying real-world goals with dataset constraints. In: Advances in neural information processing systems, pp 2415–2423 [Google Scholar]
- 42.Cotter A, Gupta M, Jiang H, Srebro N, Sridharan K, Wang S, Woodworth B, You S (2019) Training well-generalizing classifiers for fairness metrics and other data-dependent constraints. In: International conference on machine learning, PMLR, pp 1397–1405 [Google Scholar]
- 43.Beutel A, Chen J, Doshi T, Qian H, Woodruff A, Luu C, Kreitmann P, Bischof J, Chi EH (2019) Putting fairness principles into practice: Challenges, metrics, and improvements. In: Proceedings of the 2019 AAAI/ACM conference on AI, ethics, and society, pp 453–459 [Google Scholar]
- 44.Zafar MB, Valera I, Rogriguez MG, Gummadi KP (2017) Fairness constraints: mechanisms for fair classification. In: Artificial intelligence and statistics, PMLR, pp 962–970 [Google Scholar]
- 45.Zafar MB, Valera I, Gomez-Rodriguez M, Gummadi KP (2019) Fairness constraints: a flexible approach for fair classification. J Mach Learn Res 20(1):2737–2778 [Google Scholar]
- 46.Pleiss G, Raghavan M, Wu F, Kleinberg J, Weinberger KQ (2017) On fairness and calibration. NIPS’17, Curran Associates Inc., Red Hook, NY, USA, pp 5684–5693 [Google Scholar]
- 47.Pfohl SR, Foryciarz A, Shah NH (2021)An empirical characterization of fairmachine learning for clinical risk prediction. J Biomed Inform 113:103621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Pfohl SR, Duan T, Ding DY, Shah NH (2019) Counterfactual reasoning for fair clinical risk prediction. In: Machine learning for healthcare conference, PMLR, pp 325–358 [Google Scholar]
- 49.Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser L, Polosukhin I (2017) Attention is all you need. In: NIPS’17 [Google Scholar]
- 50.Dong D, Wu H, He W, Yu D, Wang H (2015) Multi-task learning for multiple language translation. In: ACL’15 [Google Scholar]
- 51.Chen T, Kornblith S, Norouzi M, Hinton G (2020) A simple framework for contrastive learning of visual representations. In: ICML’20. PMLR [Google Scholar]
- 52.Ramdas A, Trillos NG, Cuturi M (2017) On wasserstein two-sample testing and related families of nonparametric tests. Entropy 19(2):47 [Google Scholar]
- 53.Gretton A, Borgwardt KM, Rasch MJ, Schölkopf B, Smola A (2012) A kernel two-sample test. J Mach Learn Res 13(1):723–773 [Google Scholar]
- 54.Moody GB, Mark RG (1996) A database to support development and evaluation of intelligent intensive care monitoring. In: Computers in cardiology 1996, IEEE, pp 657–660 [Google Scholar]
- 55.Yin C, Liu R, Zhang D, Zhang P (2020) Identifying sepsis subphenotypes via time-aware multi-modal auto-encoder. In: Proceedings of the 26th ACM SIGKDD international conference on knowledge discovery & data mining, pp 862–872 [Google Scholar]
- 56.Zhang D, Yin C, Zeng J, Yuan X, Zhang P (2020) Combining structured and unstructured data for predictive models: a deep learning approach. BMC Med Inform Decis Mak 20(1):1–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Breiman L (2001) Random forests. Mach Learn 45(1) [Google Scholar]
- 58.Cho K, Van Merriënboer B, Gulcehre C, Bahdanau D, Bougares F, Schwenk H, Bengio Y (2014) Learning phrase representations using RNN encoder-decoder for statistical machine translation. In: EMNLP’14 [Google Scholar]
- 59.Ye M, Luo J, Xiao C, Ma F (2020) LSAN: modeling long-term dependencies and short-term correlations with hierarchical attention for risk prediction. In: CIKM’20 [Google Scholar]
- 60.Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E (2011) Scikit-learn: machine learning in python. J Mach Learn Res 12 [Google Scholar]
- 61.Kingma DP, Ba J (2015) Adam: a method for stochastic optimization. In: ICLR’15 [Google Scholar]
- 62.Youden WJ (1950) Index for rating diagnostic tests. Cancer 3(1):32–35 [DOI] [PubMed] [Google Scholar]
- 63.Demšar J (2006) Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res 7:1–30 [Google Scholar]
- 64.Friedman M (1937) The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J Am Stat Assoc 32(200):675–701 [Google Scholar]
- 65.Friedman M (1940) A comparison of alternative tests of significance for the problem of m rankings. Ann Math Stat 11(1):86–92 [Google Scholar]
- 66.Quade D (1979) Using weighted rankings in the analysis of complete blocks with additive block effects. J Am Stat Assoc 74(367):680–683 [Google Scholar]
- 67.Kenny HC, Abel ED (2019) Heart failure in type 2 diabetes mellitus: impact of glucose-lowering agents, heart failure therapies, and novel therapeutic strategies. Circ Res 124(1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Mikhail N, Golub MS, Tuck ML (1999) Obesity and hypertension. Prog Cardiovasc Dis 42(1) [DOI] [PubMed] [Google Scholar]
- 69.Ebong IA, Goff DC Jr, Rodriguez CJ, Chen H, Bertoni AG (2014) Mechanisms of heart failure in obesity. Obes Res Clin Pract 8(6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Mosseri M, Yarom R, Gotsman M, Hasin Y (1986) Histologic evidence for small-vessel coronary artery disease in patients with angina pectoris and patent large coronary arteries. Circulation 74(5) [DOI] [PubMed] [Google Scholar]


