Abstract
Purpose
To develop a weakly supervised 3D perivascular spaces (PVS) segmentation model that combines the filter-based image processing algorithm and the convolutional neural network.
Methods
We present a weakly supervised learning method for PVS segmentation by combing a rule-based image processing approach Frangi filter with a canonical deep learning algorithm Unet using conditional random field theory. The weighted cross entropy loss function and the training patch selection were implemented for the optimization and to alleviate the class imbalance issue. The performance of the model was evaluated on the Human Connectome Project data.
Results
The proposed method increases the true positive rate compared to the rule-based method and reduces the false positive rate by 36% in the weakly supervised training experiment and 39.4% in the supervised training experiment compared to Unet, which results in superior overall performance. In addition, by training the model on manually quality controlled and annotated data which includes the subjects with the presence of white matter hyperintensities, the proposed method differentiates between PVS and white matter hyperintensities, which reduces the false positive rate by 78.5% compared to weakly supervised trained model.
Conclusions
Combing filter-based image processing algorithm and convolutional neural network algorithm could improve the model’s segmentation accuracy, while reducing the training dependence on the large scale annotated PVS mask data by the trained physician. Compared to the filter-based image processing algorithm, data driven PVS segmentation model using quality-controlled data as the training target could differentiate the white matter hyperintensity from PVS resulting low false positive rate.
Keywords: Perivascular spaces, Convolutional Neural Network, Conditional Random Field, Structural MRI, Image processing
Introduction
Perivascular spaces (PVS) have attracted research attention recently due to their role in brain homeostasis 1. Because of the extensive PVS distribution in the brain and tubular structure it presents, manual segmentation of PVS from Magnetic Resonance Image (MRI) modalities is a time-consuming process and requires trained physicians to ensure accurate segmentation. Effective and reliable automatic PVS segmentation methods are of high clinical and research values. Methods have been developed to delineate PVS via in-vivo structural MRI data using either algorithmic filter-based image processing algorithms 2,3 or deep supervised learning algorithms 4–7. Both methods have their own advantages and disadvantages. Normally, supervised learning methods can automatically learn the segmentation process with short inference time, but long training time. However, these methods are dependent on the availability of manually annotated ground truth models, which are costly to acquire. The algorithmic filter-based methods use pre-defined rules, which is time consuming and results in segmentation accuracy that is affected by the accuracy of the regional parcellation. Another factor which contributes to false positive results generated by algorithmic filter-based methods is the presence of white matter hyperintensities (WMH) 8. WMH have similar intensity contrast to PVS in T1-Weighted and T2-Weighted modalities. Without using additional image modalities (such as Fluid-attenuated inversion recovery (FLAIR)), algorithmic filter-based methods cannot differentiate WMH from PVS, resulting in false positive segmentation results.
Since annotating PVS maps is time and labor intensive, we used automatically generated filter based PVS maps as the training target. The Frangi filter 9 generated PVS maps usually contain false positives caused by the image noise and false negatives caused by imperfect anatomical mask, which is the reason we defined those training targets as the weak labels. To effectively utilize those weak labels to teach the model the PVS distribution, we proposed a hybrid algorithm named weakly supervised perivascular spaces segmentation (WPSS). WPSS is a weakly supervised deep learning algorithm trained with brain patches and benefits from PVS saliency guided post-processing. Training the model with brain patches would teach the model to learn PVS distribution based on the PVS contrast and geometrical shape regardless of the anatomical locations, which could be helpful to reduce the false negatives caused by the imperfect anatomical mask. The incorporated post-processing could help the model to refine the segmentation results and reduce the false positives. WPSS shows superior segmentation over algorithmic filter-based and deep learning methods. We trained and tested our model using the HCP lifespan dataset 10–12 which covers a broad age range and provides a diverse cohort to test our model accuracy across a continuum of PVS morphological complexity.
Related work
Algorithmic filter-based Image processing that use Frangi filtration is one popular approach to detect the tubular structure of anatomical shapes, such as PVS and other vasculature, in 2D and 3D image data 2,3. The MRI modality used for these techniques is either structural T1w MRI modality 3, or the PVS visibility enhanced modality. A recent technique developed by our group combines T1w and T2w modalities to enhance PVS visibility and improve tissue specific sensitivity 2. With the increased availability of large population and high-resolution neuroimaging datasets, data-driven methods such as machine learning algorithms have also been utilized for PVS segmentation tasks 4–7. Boutinaud P. et al. proposed a method to segment PVS using the 3D convolutional autoencoder and the U-net algorithm with T1 weighted MRI modality 4. The algorithm involves two stages. At the first stage, it uses the autoencoder to reconstruct T1 weighted MRI modality. At the second stage, weights from the trained autoencoder are used for the weight initialization for the U-net model and U-net segments PVS using T1 weighted MRI as input modality. In another research Zhang.j, et al utilized three types of vascular filters with structured random forest algorithm to achieve the binary classification of PVS and background 5. Even though these techniques can already generate fairly good PVS segmentation results, there are still some limitations in these techniques. Supervised learning methods require large amount of manually annotated ground truth labels which are expensive to acquire, and Frangi filter-based methods majorly rely on the accurate regional parcellation. Therefore, in this current study we propose a hybrid model which can overcome the two limitations.
PVS has tubular shape in the structural MRI modalities. Therefore, Frangi filter is commonly used for PVS segmentation. Frangi filter 9 is an algorithmic image processing technique which analyses the second order partial derivatives on the scalar field to measure vesselness probability in the medical image. Frangi filter transfers the MRI modality from the image domain to the probability domain embedded with PVS information, in which voxels with probability equal to 1 have the highest chance of containing a PVS voxels while voxels with probability 0 are the least probable PVS voxels. Because PVS probability maps contain information related to the relative probabilities of PVS presence, they are better candidates for the PVS segmentation post-processing compared to the MRI image itself.
Convolutional neural network (CNN) is one of the commonly used neural network methods for image processing tasks, and has been utilized for PVS segmentation 4,6,7. LianC. et al. designed a multi-channel multi-scale CNN by recursively incorporating PVS segmentation maps as additional input channels to provide enriched contextual information for PVS segmentation 6. In another study by Sudre C. H. et al., they extended region based convolutional neural network (RCNN) from 2D to 3D to achieve both the segmentation of extremely small objects while simultaneously classifying both lacunes and enlarged PVS 7.
While CNN could generate pretty good segmentation of natural images, the boundary between each pair of two classes generated by CNN sometimes is not sharp enough 13. In the semantic segmentation task, the post-processing step is commonly adopted after the segmentation step to refine the coarse segmentation boundaries resulted from CNN, and to improve the segmentation accuracy. Conditional random field (CRF) 14 is a commonly used probabilistic model for the post-processing step of the semantic segmentation 13. Incorporating both CNN segmentation and CRF post-processing steps into the same architecture can fully harness the strength of CRF so that CNN can adapt training weights to the CRF behavior during the training phase 15. For the semantic segmentation task, CRF transforms the task to a probabilistic inference problem by building on top of the images a graph in which adjacent or similar location pixels have strong connections so that they can be classified into the same group. Because of the nature of CRF, it is a suitable candidate to refine the coarse boundaries of the segmentation result from CNN by regrouping the boundary pixels based on the pixels’ locations and similarity. Conditional random field as recurrent neuronal network (CRF-RNN) 15 utilizes fully connected CRF inference achieved by reformulated message passing 16 to incorporate both CNN and CRF into the same trainable model architecture.
There was a previous attempt to implement the CRF-RNN algorithm for 3D medical image segmentation directly, but the segmentation accuracy was not improved compared to the CNN algorithm 17. By using the Frangi filter generated PVS probability maps as the post-processing guidance for CRF-RNN, our segmentation result accuracy has improved compared to the CNN. Our strategy outperformed the original CRF-RNN algorithm, where CRF-RNN used the whole input image as the post-processing guidance. PVS probability maps generated by Frangi filter capture the likeliness of the PVS structure which we call PVS saliency. PVS probability maps help CRF-RNN to refine the segmentation boundaries more effectively. Since most of the voxels that are not part of PVS have already been assigned a score close to 0 by the PVS probability maps, they are eliminated prior to CRF post-processing of the segmentation map. In the following sections we will explain the mechanism of the proposed method WPSS and how salient guidance of the Frangi filter can enhance CRF-RNN to segment PVS with higher performance compared to classic CNN algorithms.
Methods
In this section, the proposed weakly supervised PVS segmentation method WPSS is elaborated in details. We start from the network architecture followed by the mechanism of each individual steps. Then we describe operations which improve segmentation performance and relieve the class imbalance issue of PVS segmentation training. The detailed implementations are described in the Èxperiments` subsection.
Network architecture
As shown in Figure 1, WPSS is composed of three parts: Frangi filter as CNN, CNN, and CRF as RNN. Frangi filter 9 extracts the tubular structure probability (vesselness) map from an enhanced PVS contrast image 2 which provides salient post-processing guidance for the CNN 18 to reduce false positive and false negative segmentation predictions. Frangi filter is also integrated to CNN with fixed gaussian kernels. According to 9, the vesselness probability function is defined as Equation (1):
| (1) |
where νo is the probability of a given voxel belonging to tubular structure (PVS in this study), while α, β and c are three pre-defined parameters which control the sensitivity of the filter to the tubular structure measures RA, RB and S. λ1, λ2 and λ3 are three eigenvalues of hessian matrix of each voxel and they were sorted in the incremental order |λ1| < |λ2| < |λ3|, thus, they are not trainable. Perfect tubular structure voxels have the property of |λ1| ≈ 0, |λ1| ≪ |λ2| and λ2 ≈ λ39. In the EPC modality, PVS is visible in the darker contrast compared to the adjacent brain tissue, thus, we set condition λ2 ≤ 0 and λ3 ≤ 0 as the vesselness condition 9 in Equation. (1). RA, RB and S are three tubular structure measure parameters derived from the EPC modality. , and . RB deviates the blob-like structures from plate-like and line-like structures. RA distinguishes between the plate-like structures and line-like structures. S measures the high vesselness contrast and low vesselness contrast 9. The output of Frangi filter CNN is the 3-channel PVS probability map which is derived by using three gaussian kernels with fixed standard deviations to convolve input images to generate three sets of RA, RB and S and to compute the probability maps based on Equation (1). By integrating Frangi filter into CNN, parameters α, β and c can be trained automatically during the WPSS training step. Therefore, PVS segmentation results by the CNN-Frangi filter relies only on PVS morphologic and contextual information from the data distribution instead of user knowledge.
Figure 1. The architecture of the proposed weakly supervised learning segmentation method (WPSS).
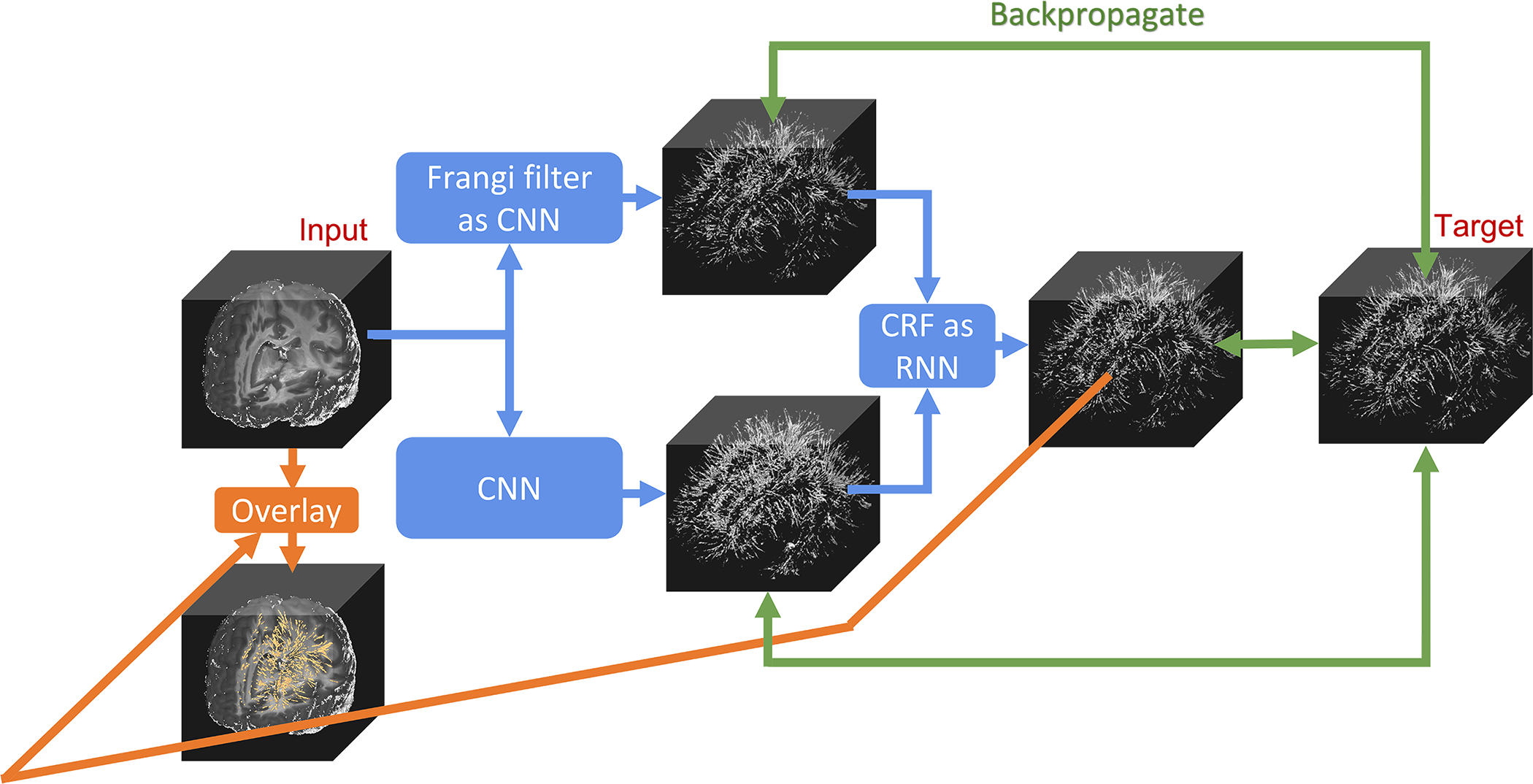
WPSS is composed of mainly two parts: a Frangi filter as convolution neural network (CNN) with fixed Gaussian kernels, and a simple convolutional neural network Unet. The results from these two parts are used as inputs of a conditional random field (CRF) as the recurrent neural network (RNN) to perform segmentation post-processing. The three parallel backpropagations (denoted by green lines) are conducted during each training step to effectively train all the weights and parameters of WPSS.
CRF as RNN 15 efficiently extend the post-processing method into a one pass training instead of applying CRF inference as a post-processing step disconnected from the neural network training process. We followed the CRF as RNN algorithm implementation as proposed in the original paper, except at the pairwise energy components computation step. There are two components for fully connected pairwise CRF model energy function E(x) as indicated in Equation (2):
| (2) |
where Ψu is the unary energy component, which is the output from CNN of WPSS, and Ψp as indicated in Equation (3) is the pairwise energy component that is computed via guidance from the Frangi filter output of WPSS; xi is the segmented output voxel and fi is the representation vector belong to the 3-channel Frangi filter generated PVS probability maps.
| (3) |
Unary energy component in Equation (2) was initialized with the output X of CNN module. For each recurrent unit, pairwise energy component in Equation (3) was computed using the 3-channel PVS saliency map F and unary energy component was updated by adding the pairwise energy component. After 8 recurrent units, the original unary energy component which was initialized with the output of CNN module was refined.
We introduced self-attention (SA) 19,20 to compute Km(fi,fj), which is used to measure the pairwise similarity, in Equation (4) to improve the network’s training efficiency and accuracy:
| (4) |
where fi is the representation vector that belongs to the 3-channel PVS probability map and contains the appearance feature vector ai and the spatial vector pi. ω1 and ω2 are two trainable weight parameters. For each pair of fi, fj, feature vectors ai, aj and spatial vectors pi, pj were used to compute the pairwise similarity. As SA implementation is shown in Figure S1, ai is the feature vector with 3-channel probability vector generated by Frangi filter CNN and pi is the three-dimension spatial vector; C is the number of channels and h, w, d represent the size of each dimension in the three-dimension space; f(x) and g(x) represent the convolution process. Two pairwise similarity maps S were calculated for pairwise feature vectors ai, aj and spatial vectors pi, pj respectively to be used to measure kernel function Km(fi,fj).
As for the CNN of WPSS, we utilized the encoder-decoder network Unet 21. We implemented Unet with 4 – layer encoder, 4 – layer decoder and one output layer. For the encoder, the number of output channels for each layer are 64, 128, 256, and 256 respectively. For the decoder, the number of output channels for each layer are 256, 128, 64, and 64 respectively.
The Forward-backward process is conducted during the network training. At the forward stage, one channel EPC image used as input image goes through Frangi filter CNN and CNN in parallel as shown in Figure 1. The 3-channel PVS probability map that was generated by Frangi filter CNN, and the 2-channel PVS segmentation map generated by CNN gather into CRF with 8 recurrent units to generate the final segmentation output. The 3-channel PVS probability map was used to compute the pairwise energy component by CRF, and 2-channel PVS segmentation map was used as the initial unary energy component in CRF. Final output of CRF has two channels which represent binary one-hot-encoding for PVS voxels and background voxels. The target used in training is the one-hot encoded 2-channel binary PVS map resulting from thresholding PVS probability map generated by Frangi filter 2. Then, the weighted cross entropy loss will be calculated to get three losses, which are between target and final output, between target and Frangi filter CNN results, and between target and CNN results. For the loss between target and Frangi filter CNN results, 3-channel PVS probability map goes through one 1 × 1 × 1 convolution layer to transform to 2-channel probability map, so that the loss could be computed. At the backward stage, these three losses will backpropagate through the whole network, and gradients will be calculated for training parameters in the network to update the parameters accordingly. The backpropagations of three modules were independent from each other, which means the backpropagations were stopped for both Frangi filter CNN and CNN modules when the CRF module’s weights gets updated by calculating the loss function between the final output and target as shown in Figure 1.
We used patches extracted from EPC modality with voxel size 16 × 16 × 16 as the input for the model training and testing. We formulated the PVS segmentation task as the binary classification problem and realized the segmentation by minimizing the binary cross entropy loss between real PVS distribution and model generated PVS distribution.
Patch selection
Patch selection is the method to select the training data to ensure that the data used for the model training consists of sufficient amount of PVS for the model to learn the PVS distribution. Considering the PVS distribution in the brain, and different amount of PVS across subjects that can vary by age, sex, BMI and more 22, we conducted patch selection at the pre-processing stage. We selected brain patches with a sufficient amount of PVS to support a better learning process and the selection criteria will be elaborated in the following experiments section. Note that patch selection was only used during the training phase to feed the model as much PVS information as possible, while patch selection was not conducted in the testing phase. The threshold used for patch selection was 0.01, so that patches with PVS volume ratio less then 0.01 will be discarded, PVS volume ratios is calculated with Equation (5) as following:
| (5) |
Weighted cross entropy
For the PVS segmentation task, the boundary between PVS and background voxels need to be properly classified. Because PVS volume only occupies a small portion of the brain volume, we adopted weighted cross entropy loss to alleviate the class imbalance issue. Cross entropy loss function is a commonly used loss function to train the CNN model for the segmentation task. Weighted cross entropy loss takes the class imbalance issue into consideration of the model training by assigning the minority class a bigger weight, so that cross entropy loss is not dominated by the errors of the majority class 23. The weighted binary cross entropy (WCE) loss is formulated with Equation (6) as following:
| (6) |
where q is the one-hot-encoded 2-channel PVS training target in our experiment, p is the result generated by WPSS and beta is the weight assigned to the majority class. In our experiment, the majority class was the background label which was assigned with weight beta = 0.1 in the loss function, while minority class was the PVS label which was assigned with weight (1 − beta) = 0.9 in the loss function. WCE loss was calculated at the beginning of the backpropagation stages as shown in Figure 1.
Experiments
Data preparation
Human connectome project data
In this paper we used structural MRI data derived from 1396 (784 females) healthy, cognitively normal volunteers between 8 and 90 years of age (M±SD=34.17±20.07 years) from the Lifespan Human connectome project (HCP) 24 (HCP Development 10, HCP Young adult 11 and HCP aging 12,25). More details of HCP cohorts and acquisition parameters can be found in Supporting Information Table S1 and Supporting Information Table S2. 400 subjects were randomly selected from HCP lifespan cohorts in the present study, in which 200 randomly sampled subjects were used for the quality control. The NIMH Data Archive Data Use Certification was approved by the National Institute of Mental Health and Restricted Data generated by HCP access was approved by the WU-Minn HCP Consortium.
Preprocessing
T1w and T2w images were preprocessed in parallel through LONI pipeline 26 using the HCP minimal processing pipeline version 4.0.1 27 and FreeSurfer 28 version 6. The preprocessing steps started with gradient nonlinearity corrections. Structural images were registered together, then brought into native space via anterior commissure-posterior commissure alignment, and then registered to MNI space using FSL’s FNIRT 29. The native space images were used to generate individual regional subcortical PVS features for white and pial surfaces using FreeSurfer. Extensive descriptions of the minimal preprocessing applied can be found in prior publications 27.
Enhanced PVS Contrast
For automatic segmentation and quantification of PVS, we used Enhanced PVS Contrast (EPC) that increases PVS visibility on MRI and was optimized and tested on HCP structural data 2. Briefly, the EPC was achieved by combining T1-weighted and T2-weighted images that were adaptively filtered to remove non-structural high frequency spatial noise using an adaptive non-local mean filtering technique. This was followed by an automated quantification of PVS based on Hessian Frangi vesselness filtering of the input image, and then an application of a threshold that was optimized to achieve the highest concordance with expert neuroradiology scoring 2. Using HCP scan-rescan data, we found excellent reliability using this technique [interclass correlation of 0.97, CI: 0.95–0.97, F=38.49, p<1e-20] 2.
Quality assurance and manual segmentation protocol
Originally, 200 subjects from the HCP Lifespan cohorts were selected (100 HCP-A, 50 HCP-YA and 50 HCP-D) for quality assurance procedures. Quality control (QC) efforts and PVS segmentation correction were carried out by 4 individuals trained by an experienced physician to discriminate PVS from other hyperintense white matter lesions. Prior to the manual corrections, raters practiced on the same 5 test cases to ensure consistency among PVS segmentations. Additionally, 33% of subjects randomly selected from the sample were manually corrected by 2 raters to enable inter-rater reliability assessments. Raters overlaid the automated PVS segmentation on the EPC image with ITK-SNAP software 30 and removed false positive PVS labels, including WMH, microbleeds, and ventricle borders. PVS labels were also removed if labels were not continuous across at least 3 consecutive axial slices. Scans were also rated on a scale from 1 to 3 on scan quality and subject motion (1=good scan quality/no perceptible motion, 3=poor tissue contrast/excess motion and ringing), where subjects with a score of 3 on the scan quality and motion scales were excluded from analyses. In total, 11 subjects were excluded from analyses due to excess motion, resulting in 189 participants for the current study. Raters also ranked the severity of WMH from 1 to 3 based on the size and number of WMH, where 1 denoted no observable WMH, 2 denoted 3–4 small or medium-sized WMH and/or 1 large WMH, and 3 reflected more than 8 small or medium-sized WMH and/or greater than 3 large WMH.
Implementation
For the Frangi filter CNN, we used three Gaussian kernels to process the input image to optimize the number of segmented PVS voxels. The three standard deviations in the Gaussian kernels were not trainable and they were uniformly picked from the range of 0.01 to 5 and fixed during the training 2. We also defined the parameters α, β and c as variables, so that they would be automatically assigned during the learning process.
We implemented CNN as a simple Unet with a 4 layers encoder and 4 layers decoder structure and skipped connection between encoder and decoder. To preserve PVS details, there was no down-sampling in the encoder or up-sampling in the decoder, which means each CNN layer has stride 1 with kernel size 3 and no pooling layer. Batch normalization 31, dropout 32 and Leaky ReLU activation function 33 follow each CNN layer except the final output layer of the CNN, which uses the softmax activation function 34.
The CRF module was implemented following 15, except we redesigned the Gaussian filtering part by adopting a self-attention module. A Self-attention module calculates the similarity of each pair of feature vectors by considering the appearance feature and spatial information. This means feature vectors with similar appearance and closer distance are more likely to have higher similarity scores. Additionally, CRF as RNN has 8 iterations message passing 16 to refine the segmentation map result from CNN with the guidance of Frangi Filter CNN’s 3-channel probability map.
All models were implemented with TensorFlow 35 (version 1.12.2) and deployed training on NVIDIA GPU cluster equipped with eight V100 GPUs.
Training and testing
For each of the 189 QC subjects and 200 non-QC subjects which were randomly selected and motion corruption controlled from across HCP-A, HCP-YA and HCP-D for WPSS training, 36864 patches with voxel size 16×16×16 were extracted with overlapping for model training. Each pair of adjacent patches have either 16 × 16 × 4, 16 × 4 × 16 or 4 × 16 × 16 overlapping regions. Subjects from QC subjects are also age matched with non-QC subjects. Since patch selection was used for the training phase, the actual number of training patches for each subject varies and is around 5000. Each training target is a 2-channel one-hot-encoded PVS binary map for the corresponding EPC patch. We set learning rate as 0.001, batch size as 5 and used Adam optimizer 36 for the optimization process. For the first experiment, we used 200 non-QC subjects to train the model and 189 QC subjects to evaluate the trained WPSS and Unet models with weak supervision. In this case, QC data was only used to test the model performance but not used for model training. For the second experiment, to fully utilize the QC dataset, we performed the supervised training by utilizing the QC PVS map as the training target. In this case, 95 subjects out of 189 QC subjects were used for training and validation and the remaining 94 subjects were used for testing. Considering the large number of patches extracted from the training data, we didn’t implement data augmentation. In order to combat the model overfitting issue, regularization techniques including L1 regularization, dropout layer and early stopping were implemented. The total number of trainable parameters of Unet we implemented in the experiment is 2515908. The total number of trainable parameters of the WPSS is 2517760.
Evaluation and saliency analysis
False positive rate, precision, recall (sensitivity), and Fβ score were used as evaluation metrics, which are defined as Equations (7), (8), (9), and (10) respectively:
| (7) |
| (8) |
| (9) |
| (10) |
where β in Equation (10) is a positive real factor which indicates that recall is considered β times as important as precision. Higher precision indicates less relative false positive prediction, whereas higher recall indicates less relative false negative prediction. Since QC work focused mainly on correcting false positives based on Frangi filter results, we chose β in Equation (10) as 0.5 by default to assign more emphasis to precision than recall.
Through our QC effort, we experienced that superior region of the white matter like centrum semiovale region tend to have clearer PVS presence. We chose these anatomical regions to do the additional model analysis since these regions typically have less image noise and better white matter segmentation by FreeSurfer, therefore reducing the possibility of potential incorrect segmentation by Frangi filter. The detailed list of centrum semiovale region parcellation by FreeSurfer can be found in Supporting Information Table S3.
Because WPSS utilized both advantages of Frangi filter and CNN, it can be trained using either weakly supervised or supervised learning methods. To fully evaluate the WPSS performance, we did a second set of experiments using the QC data as the training target. Gradient based class activation mapping (Grad-CAM) 37 is a commonly used CNN visualization technique to investigate the semantic features of the input image which contribute to final model prediction. Grad-CAM uses the gradients of any target class flow towards the final convolutional layer to produce a coarse localization map that highlights the important regions in the image for the class prediction. We adopted Grad-CAM for both weakly supervised and supervised trained WPSS models to produce the semantic feature visualization of PVS segmentation.
Results
WPSS follows a weakly supervised learning manner since the target we used in the experiment resulted from the Frangi filter, which did not involve manual intervention.
As shown in Figure 2, the PVS at the most superficial part of the white matter were not segmented by the Frangi filter but segmented by both WPSS and Unet. This improved sensitivity (true positive rate) highlights the superiority of the data driven deep learning methods over the rule-based approach. Even though both WPSS and Unet increased sensitivity of segmentation results, there is a noteworthy number of false positives present in the results generated by Unet which are not present in the results generated by WPSS. This suggests that while Unet increased the sensitivity it also increased the false positive rate and shows the advantages of the hybrid technique over the simple deep learning method.
Figure 2. Qualitative assessment of segmentation results of Unet and WPSS.
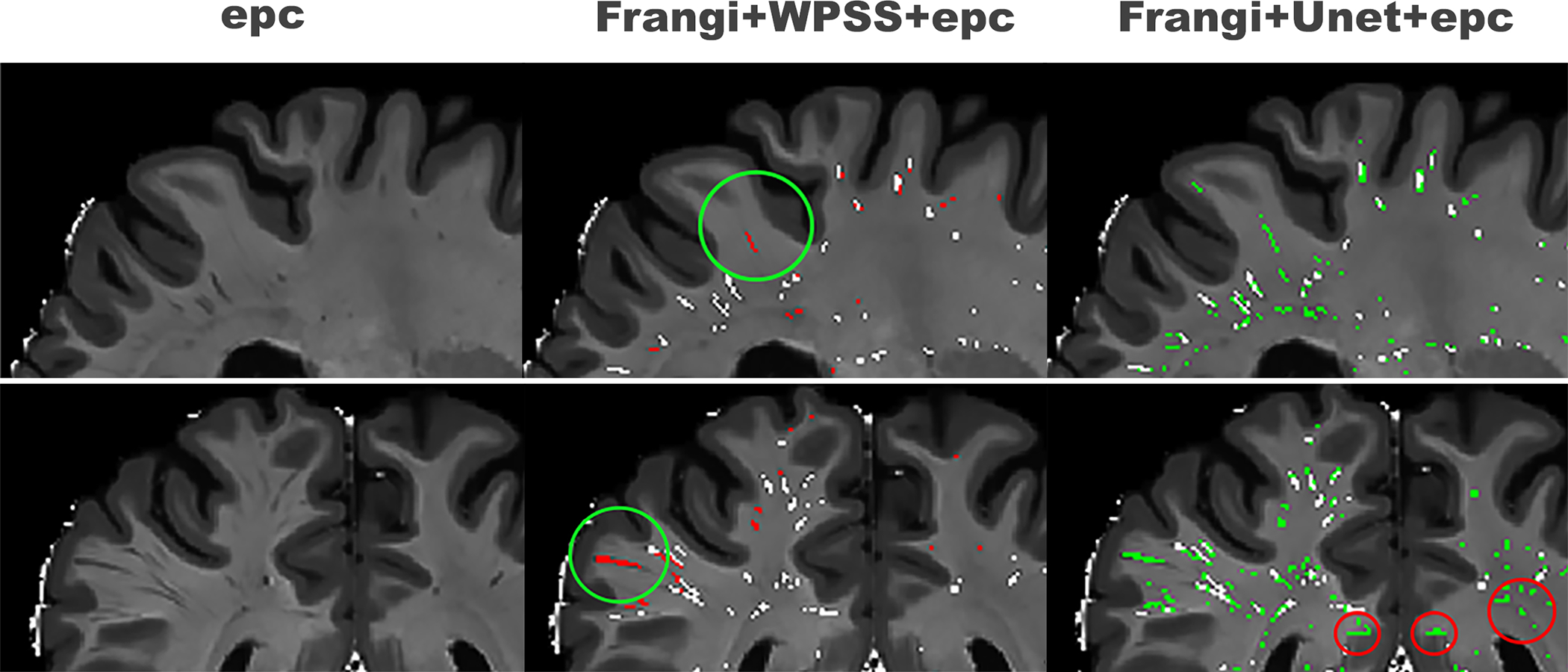
First column shows the input data using EPC; second column shows the results of segmentation using WPSS (red) overlaid by Frangi filter results (white); Third column shows segmentation results using Unet (green) overlaid by Frangi filter results (white).
We quantitatively evaluated the WPSS and Unet results using 189 QC data including 97 participants in the aging group, 42 participants in the development group, and 50 participants in the young adult group. Since the QC process was done by correcting false positive voxels in the results generated by Frangi filter, we only evaluated the False positive rate of the PVS segmentation map. As shown in Table 1, False positive rate (FP) was calculated between segmented results and QC data. Frangi filter generated results have FP=0.0067±0.0063, WPSS generated results have FP=0.0093±0.0069 and Unet generated results have FP=0.0146±0.0096, which means WPSS reduces the FP rate 36% compared to results generated by Unet. Also, the participants from the young adult group have the lowest FP rate and participants from the aging group have the highest FP rate, which is consistent across all three models.
Table 1.
False positive result analysis using QC data for the models trained using weakly supervised technique.
| HCA (97) | HCD (42) | HCPY (50) | Total (189) | |
|---|---|---|---|---|
|
| ||||
| Frangi | 0.0096±0.0075 | 0.0041±0.0016 | 0.0033±0.0020 | 0.0067±0.0063 |
| WPSS | 0.0131±0.0078 | 0.0064±0.0019 | 0.0044±0.0016 | 0.0093±0.0069 |
| Unet | 0.0207±0.0095 | 0.0103±0.0031 | 0.0062±0.0017 | 0.0146±0.0096 |
First column shows the results across the HCP-aging cohort, second column shows the results across the HCP-development cohort, third column shows the results across HCP-young adult cohort, and the final column shows the results across three cohorts. Note that the WPSS and Unet models were trained in the weakly supervised manner.
To further investigate the effectiveness of WPSS, we trained both WPSS and Unet using the QC data. We randomly split the QC data into two sets, with 95 participants for training and validation and 94 participants for testing. As shown in Table 2, Frangi filter results have FP=0.0068±0.0060, WPSS results have FP=0.0020±0.0026 and Unet results have FP=0.0033±0.0035. By training the models in the supervised manner, both false positive rates for WPSS and Unet have been reduced
Table 2.
False positive result analysis for the models trained with supervision by QC data.
| HCA (48) | HCD (21) | HCPY (25) | Total (94) | |
|---|---|---|---|---|
|
| ||||
| WPSS (qc) | 0.0030±0.0030 | 0.0006±0.0004 | 0.0007±0.0005 | 0.0020±0.0026 |
| Unet (qc) | 0.0048±0.0039 | 0.0012±0.0007 | 0.0013±0.0007 | 0.0033±0.0035 |
| Frangi | 0.0100±0.0066 | 0.0037±0.0010 | 0.0033±0.0022 | 0.0068±0.0060 |
Notice that for the supervised training purpose, we only used half of the 189 subjects for training and the other half for testing.
78.5%, and 77.4% respectively. WPSS reduces the FP rate by 39.4% compared to Unet, and 70.6% compared to Frangi filter. Unet reduces FP rate by 51.5% compared to results generated by Frangi filter. As shown in Figure 3, by training the model using QC data, both WPSS and Unet were able to correct the false positive predictions caused by imperfect white matter masks, illustrating the benefit of supervised learning.
Figure 3. Comparison between results generated by weakly supervised trained models and supervised trained models.
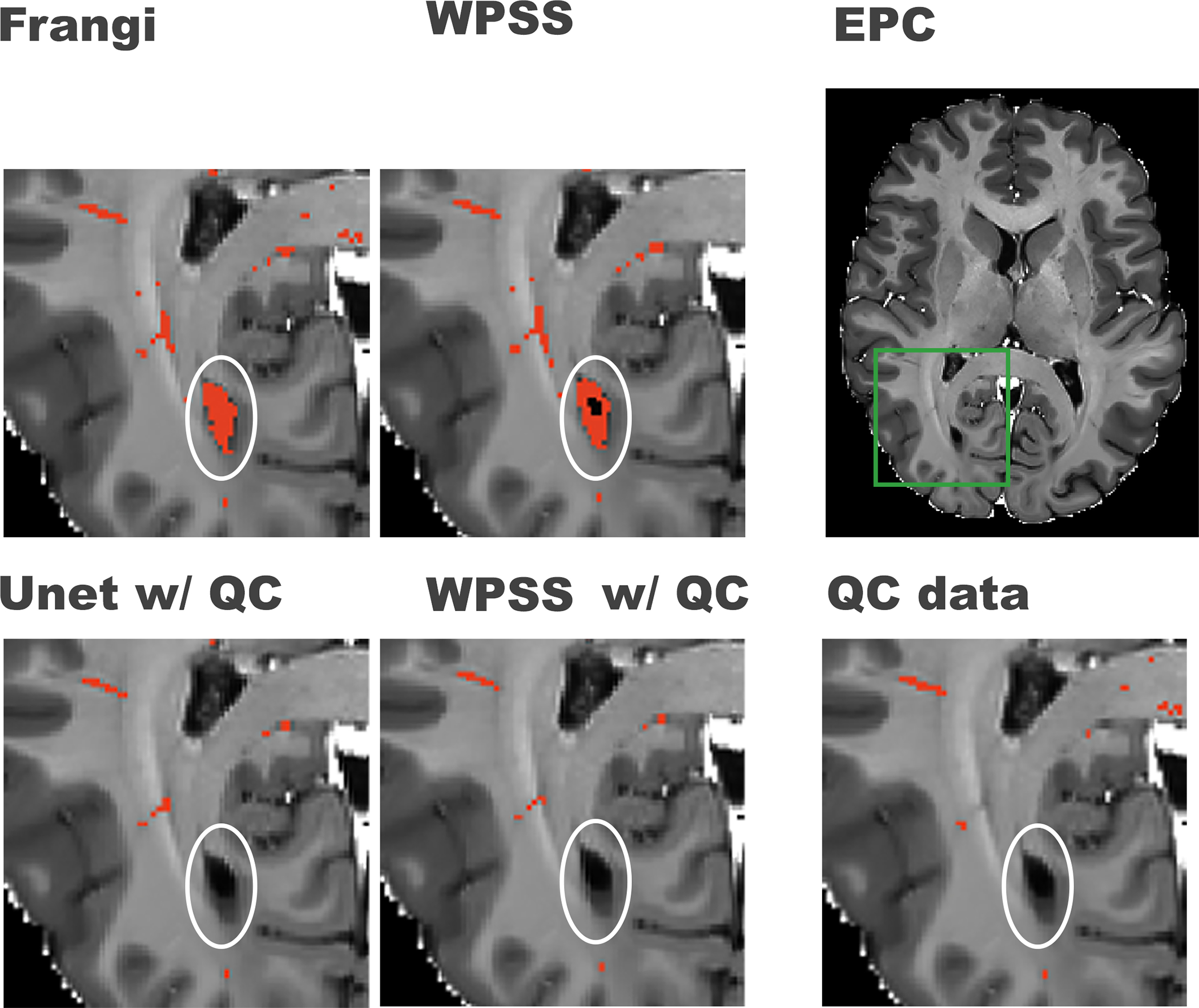
First row from right to left shows the original EPC image, green box notating the region that was zoomed-in for better visualization in the rest of the subplots in this figure, PVS mask (in red) generated by WPSS, and the PVS mask (in red) generated by the Frangi filter. The second row from left to right shows the PVS mask generated by Unet trained with QC data, PVS mask generated by WPSS trained with QC data, and the QC data overlaid on top of the EPC image. White circles denote regions that could present false positive PVS prediction.
For the regional analysis, we chose centrum semiovale, the superior region of the white matter as our Region-Of-Interest (ROI) which tends to have clear PVS presence and are more resistant to high false positive or false negative segmentation by Frangi filter, and then calculated Fβ score. As shown in Table 3 (first column), for ROI WPSS analysis, the Fβ score=0.8188±0.0958, whereas the Frangi filter Fβ score=0.7976±0.1136. This was followed by Unet with Fβ score= 0.7768±0.0959. Table 3 (second column) shows the analysis in the whole white matter, in which WPSS has Fβ score=0.7583±0.0977, Frangi filter has Fβ score=0.7358±0.0994, and Unet has Fβ score=0.7257±0.0944. For the ROI analysis, WPSS results improved Fβ score 2.7% compared to Frangi filter. Furthermore, WPSS improved the Fβ score by 3.1% compared to Frangi filter when the analysis was performed for the whole white matter.
Table 3.
Fβ score (β=0.5) analysis for the models trained with supervision by QC data in selected anatomical regions.
| Total (94) w/ ROI | Total (94) w/o ROI | |
|---|---|---|
|
| ||
| WPSS (qc) | 0.8188±0.0958 | 0.7583±0.0977 |
| Unet (qc) | 0.7768±0.0959 | 0.7257±0.0944 |
| Frangi | 0.7976±0.1136 | 0.7358±0.0994 |
First column shows the Fβ score in the superior regions of white matter. Second column shows the Fβ in the whole white matter.
Grad-CAM was used to generate the saliency map to demonstrate the likelihood of the PVS structure captured by weakly supervised and supervised trained models. In the saliency map Figure 4 column 1, bright red indicates the most PVS relevant voxels, whereas dark blue indicates the least PVS relevant voxels. Figure 4(A.) presents the PVS segmentation result generated by a weakly supervised trained model and Figure 4(B.) presents the PVS segmentation result generated by a supervised trained model using QC data. As observed in the saliency map, PVS has a salience score above 60. The red circles in Figure 4(A.) indicate the WMH 8 which have similar intensity as PVS, but with different shape morphology, and should not be segmented as PVS. However, in Figure 4(A.), WMH have a salience score around 60 and are segmented as PVS by the weakly supervised trained model. In Figure 4(B.), WMH have a salience score around 45 and are excluded from PVS generated by the supervised trained model.
Figure 4. Saliency maps of WPSS models trained without supervision and with supervision using QC data.
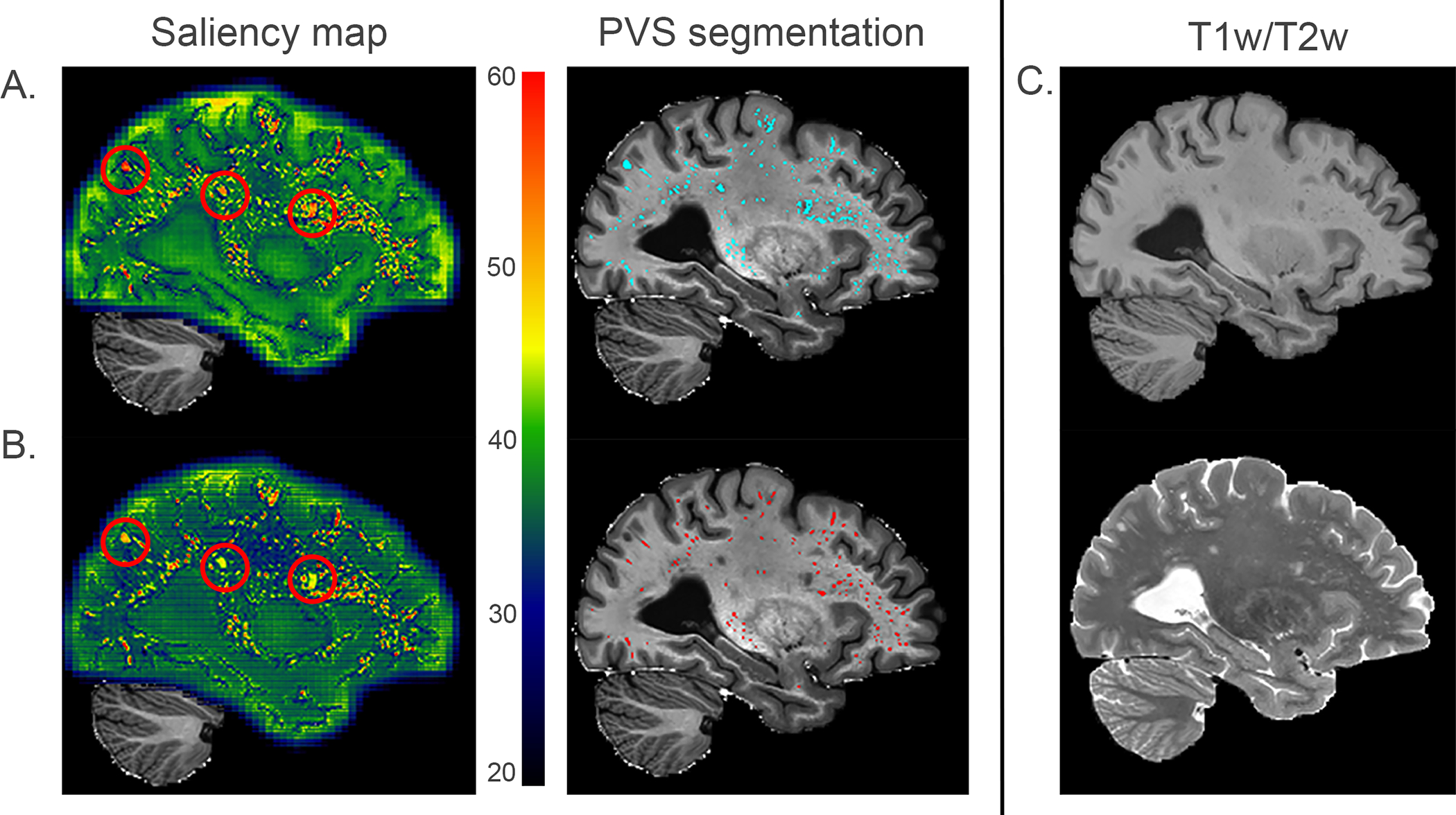
A. presents the saliency map of results generated by WPSS trained in weak supervision and PVS segmentation results (cyan color) overlayed on EPC. Segmented PVS map has false positive rate = 0.0129, precision = 0.665, *recall = 0.97, Fβ score (β=0.5) = 0.666. B. presents the saliency map of results generated by WPSS trained with QC data supervision and PVS segmentation results (red color) overlayed on EPC. Segmented PVS map has false positive rate = 0.0032, precision = 0.818, *recall = 0.684, Fβ score (β=0.5) = 0.787. C. from top to bottom corresponding T1w and T2w modalities are presented. Because the QC effort was performed by only focusing on correcting false positive segmentations for Frangi filter results, recall is not a valid evaluation metric to use for the model performance, which is why it is marked as *recall.
Discussion
We have proposed a data driven PVS segmentation method by combining both Frangi filter and convolutional neural networks. With CRF as RNN technique, we were able to incorporate the PVS probability map to further refine the PVS segmentation. The probability map involves scoring the voxels’ tubular structure likelihood generated by the Frangi filter, which serves as the salient guidance for the convolutional neural networks.
Our experiment showed the advantages of using the WPSS model over the Frangi filter and Unet methods to segment PVS within the HCP dataset using the enhanced perivascular spaces contrast. Weakly supervised trained WPSS reduced the false positive rate by 36% compared to the weakly supervised trained Unet. Supervised trained WPSS with QC data reduced false positive rate by 39.4% compared to the supervised trained Unet with QC data, and by 70.6% compared to Frangi filter methods. The higher false positive rate in the aging group compared to the young adult group and development group could be due to more observed motion corruption in the aging group subjects.
Previous work 17 concluded that the incorporation of conditional random fields in the 3D model did not improve the segmentation result because MRI images do not possess the high contrast and sharp edges observed in natural images. We agree that using CRF directly on the 3D model would be challenging. To enhance the contrast of the boundary of PVS, we first use the EPC as the input image of the segmentation network. Frangi filter was then added as a salient guiding network into the model to enable the CNN to focus on PVS structure, and thus improve the segmentation accuracy on both weakly supervised and supervised learning. We also replaced the CNN kernel with a fixed Gaussian kernel to enable tuning of Frangi filter function parameters by the model training. the usage of CRF as RNN technique also facilitates model training efficiency, since it reforms CRF using message passing 16 into RNN structure 15. Therefore, CRF parameters can be trained with CNN parameters simultaneously during the model training.
Brain regions with WMH are hypointense in T2w MRI scans 8. WMH have the similar intensity level as PVS in T1 weighted or T2 weighted MRI images, which cannot be differentiated by Frangi filter and requires additional efforts of physicians to annotate or use additional MRI modality uniquely sensitized to WMH tissue properties, such as T2 FLAIR. The QC effort focused on correcting false positive voxels of the PVS map generated by Frangi filter. We utilized QC data as the PVS target to train the WPSS and the model was able to capture the difference between WMH and PVS voxels on EPC data. According to the saliency map of the QC data trained WPSS model, we did visual inspections of PVS segmentation results for 43 subjects, based on WMH severity reported above `2` during our QC process. the model was able to differentiate WMH from PVS by giving WMH voxels much lower confidence scores compared to PVS voxels, which both the Frangi filter and weakly supervised trained WPSS methods were not able to accomplish. Since the FLAIR modality was not available for the dataset we used, we can’t systematically quantify the performance of WPSS regarding the WMH identification. But, since we have the visual inspected QC data for the presence of WMH, we were able to differentiate PVS from WMH.
The QC data trained model shows the advantages of lower false positive rate and ability to differentiate WMH from PVS. According to our experiments, the WPSS method was able to capture more PVS that were missing in the Frangi filter-based PVS map due to white matter mask boundary errors, which benefits from training the model using patches. Because our quality control effort focused mainly on correcting false positives based on traditional filter-based methods, there are still false negatives presented in the quality controlled PVS masks and it is also the reason we didn’t use the false negative rate as an evaluation metric. WPSS model could capture the PVS voxels which were missed by filter-based methods (false negatives) by utilizing the weak labels information. But we couldn’t directly evaluate this outperformance using false negative rate and those captured PVS voxels contributed to the higher false positive rate of WPSS model in Table 1 when false positive rate was evaluated using quality-controlled masks. This is the main reason WPSS generated PVS masks have higher false positive rate compared to Frangi filter generated masks. We plan to address this limitation in our future work. Even though supervised trained Unet results have half the false positive rates compared to Frangi filter results as shown in Table 3, Frangi filter results have higher Fβ scores compared to Unet results. Our assumption is that since QC did not correct false negatives based on Frangi filter results, the total number of positive volumes are not the best representative and may affect the accuracy of recall and Fβ score.
Excess motion corruption could highly impair the segmentation accuracy, which is the reason we removed all the motion corrupted subjects out from the training, validation, and testing datasets. 200 non-QC data which were used for the weakly supervised training were controlled for motion corruption. To ensure that non-QC dataset do not contain motion corrupted subjects, we performed visual inspection and ensured that no subject data were corrupted by motion among non-QC subjects. For the QC dataset, we removed the subjects with the presence of excess motion and only kept the 189 subjects for the model evaluation and supervised training purpose. As shown in Figure S3 from a motion corrupted subject outside of our studied sample, excess motion could mislead Frangi filter to generate weak labels with large number of false positives, which also causes the quality control process to be very challenging. We believe motion corruption is a challenging issue in the data acquisition phase. The strategy to alleviate the motion corruption to further increase the PVS contrast such as motion simulation would be one of our future works. Furthermore, the current WPSS model uses patches as the training data, which do not include whole brain geometric information. In future work, we plan to use the large size patches which contain more anatomical contrast or complete brain imaging data as the training data which could be helpful in finding the connection between PVS and their distribution within the brain.
Conclusion
Here we proposed WPSS, which is an end-to-end segmentation model that jointly learns the parameters of the Frangi filter, CNN, and CRF in one unified deep neural network. Additionally, what makes WPSS training more efficient is a unified framework including a modified CNN Frangi filter with fixed Gaussian kernels, an incorporated CRF as RNN model, and a novel three-path parallel backpropagation.
WPSS is a weakly supervised learning method that benefits from both CNN and algorithmic filter-based segmentation methods. Using a Frangi filter generated probability map as a salient map for CRF, WPSS can alleviate the high false positive rate results generated by CNN. Training the model with automatic Frangi filter segmented PVS map enables weakly supervised training process, so that the time and cost for manual PVS annotation by the trained physicians could be reduced. Weakly supervised trained WPSS reduces the FP rate 36% compared to weakly supervised trained Unet. Supervised trained WPSS reduces the FP rate by 39.4% compared to supervised trained Unet, 70.6% compared to Frangi filter, and 78.5% compared to the weakly supervised trained WPSS. Supervised trained WPSS increases Fβ score 3.1% compared to Frangi filter in the whole white matter region and 2.7% in the centrum semiovale region. We also demonstrated the value of using QC data to train the WPSS model in a supervised manner. In this way, WPSS can differentiate between PVS and WMH.
Supplementary Material
Acknowledgements
The research reported in this publication was supported by the National Institute of Mental Health of the NIH under Award Number RF1MH123223, and National Institute on Aging of NIH under Award Number R01AG070825 and R41AG073024. Author KML is supported by the National Institute on Aging (NIA) of the NIH Institutional Training Grant T32AG058507.
Footnotes
Source code will be made available on the github page https://github.com/Haoyulance.
Data availability statement
Data were provided [in part] by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
References
- 1.Wardlaw JM, Benveniste H, Nedergaard M, et al. Perivascular spaces in the brain: anatomy, physiology and pathology. Nat Rev Neurol. 2020;16(3):137–153. doi: 10.1038/s41582-020-0312-z [DOI] [PubMed] [Google Scholar]
- 2.Sepehrband F, Barisano G, Sheikh-Bahaei N, et al. Image processing approaches to enhance perivascular space visibility and quantification using MRI. Sci Rep. 2019;9(1):1–12. doi: 10.1038/s41598-019-48910-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ballerini L, Lovreglio R, Valdés Hernández MDC, et al. Perivascular Spaces Segmentation in Brain MRI Using Optimal 3D Filtering. Sci Rep. 2018;8(1):1–11. doi: 10.1038/s41598-018-19781-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Boutinaud P, Tsuchida A, Laurent A, et al. 3D segmentation of perivascular spaces on T1-weighted 3 Tesla MR images with a convolutional autoencoder and a U-shaped neural network * Corresponding author : Marc Joliot. bioRxiv. Published online 2020:1–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhang Jun, Gao Y Sang Hyun Park, Zong Xiaopeng, Lin W, Shen D. Structured Learning for 3D Perivascular Spaces Segmentation Using Vascular Features. IEEE Trans Biomed Eng. 2017;64(12):2803–2812. doi: 10.1109/TBME.2016.2638918.Structured [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lian C, Zhang J, Liu M, et al. Multi-channel multi-scale fully convolutional network for 3D perivascular spaces segmentation in 7T MR images. Med Image Anal. 2018;46:106–117. doi: 10.1016/j.media.2018.02.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sudre CH, Gomez Anson B, Lane CD, et al. 3D Multirater RCNN for Multimodal Multiclass Detection and Characterisation of Extremely Small Objects.; 2019. [Google Scholar]
- 8.Lee S, Viqar F, Zimmerman ME, et al. White matter hyperintensities are a core feature of Alzheimer’s disease: evidence from the dominantly inherited Alzheimer network. Ann Neurol. 2016;79.6:929–939. doi: 10.1002/ana.24647.White [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Frangi AF, Niessen WJ, Vincken KL, Viergever MA. Multiscale vessel enhancement filtering. International conference on medical image computing and computer-assisted intervention Springer, Berlin, Heidelberg,. 1998;1496:130–137. doi:10.1007/bfb0056195 [Google Scholar]
- 10.Somerville LH, Bookheimer SY, Buckner RL, et al. The Lifespan Human Connectome Project in Development: A large-scale study of brain connectivity development in 5–21 year olds. Neuroimage. 2018;183(July):456–468. doi: 10.1016/j.neuroimage.2018.08.050 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Van Essen DC, Smith SM, Barch DM, Behrens TEJ, Yacoub E, Ugurbil K. The WU-Minn Human Connectome Project: An overview. Neuroimage. 2013;80:62–79. doi: 10.1016/j.neuroimage.2013.05.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bookheimer SY, Salat DH, Terpstra M, et al. The Lifespan Human Connectome Project in Aging: An overview. Neuroimage. 2019;185(October 2018):335–348. doi: 10.1016/j.neuroimage.2018.10.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen LC, Papandreou G, Kokkinos I, Murphy K, Yuille AL. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans Pattern Anal Mach Intell. 2018;40(4):834–848. doi: 10.1109/TPAMI.2017.2699184 [DOI] [PubMed] [Google Scholar]
- 14.Lafferty J, McCallum A, Fernando C.Pereira N. Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data. Published online 2001. doi: 10.1007/978-3-030-63416-2_300238 [DOI] [Google Scholar]
- 15.Zheng S, Jayasumana S, Romera-Paredes B, et al. Conditional random fields as recurrent neural networks. Proceedings of the IEEE International Conference on Computer Vision. 2015;2015 Inter:1529–1537. doi: 10.1109/ICCV.2015.179 [DOI] [Google Scholar]
- 16.Krähenbühl P, Koltun V. Efficient inference in fully connected crfs with Gaussian edge potentials. Advances in Neural Information Processing Systems 24: 25th Annual Conference on Neural Information Processing Systems 2011, NIPS 2011. Published online 2011:1–9. [Google Scholar]
- 17.Monteiro M, Figueiredo MAT, Oliveira AL. Conditional Random Fields as Recurrent Neural Networks for 3D Medical Imaging Segmentation. Published online 2018:1–11. [Google Scholar]
- 18.LeCun Y, Haffner P, Bottou L, Bengio Y. Object recognition with gradient-based learning. Shape, contour and grouping in computer vision Springer, Berlin, Heidelberg. 1999;1681:319–345. doi: 10.1007/3-540-46805-6_19 [DOI] [Google Scholar]
- 19.Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Adv Neural Inf Process Syst. 2017;2017-Decem(Nips):5999–6009. [Google Scholar]
- 20.Lan H, Toga AW, Sepehrband F. Three-dimensional self-attention conditional GAN with spectral normalization for multimodal neuroimaging synthesis. Magn Reson Med. 2021;86(3):1718–1733. doi: 10.1002/mrm.28819 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. In: Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). Vol 9351. Springer; 2015:234–241. doi: 10.1007/978-3-319-24574-4_28 [DOI] [Google Scholar]
- 22.Barisano G, Lynch KM, Sibilia F, et al. Imaging perivascular space structure and function using brain MRI. Neuroimage. 2022;257(May):119329. doi: 10.1016/j.neuroimage.2022.119329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ben naceur M, Akil M, Saouli R, Kachouri R. Fully automatic brain tumor segmentation with deep learning-based selective attention using overlapping patches and multi-class weighted cross-entropy. Med Image Anal. 2020;63. doi: 10.1016/j.media.2020.101692 [DOI] [PubMed] [Google Scholar]
- 24.Van Essen DC, Ugurbil K, Auerbach E, et al. The Human Connectome Project: A data acquisition perspective. Neuroimage. 2012;62(4):2222–2231. doi: 10.1016/j.neuroimage.2012.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Harms MP, Somerville LH, Ances BM, et al. Extending the Human Connectome Project across ages: Imaging protocols for the Lifespan Development and Aging projects. Neuroimage. 2018;183(July):972–984. doi: 10.1016/j.neuroimage.2018.09.060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dinov ID, Van Horn JD, Lozev KM, et al. Efficient, distributed and interactive neuroimaging data analysis using the LONI pipeline. Front Neuroinform. 2009;3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Glasser MF, Sotiropoulos SN, Wilson JA, et al. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage. 2013;80:105–124. doi: 10.1016/j.neuroimage.2013.04.127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Fischl B FreeSurfer. Neuroimage. 2012;62(2):774–781. doi: 10.1016/j.neuroimage.2012.01.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM. FSL. 2012;62:782–790. doi: 10.1016/j.neuroimage.2011.09.015 [DOI] [PubMed] [Google Scholar]
- 30.Yushkevich PA, Piven J, Hazlett HC, et al. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. Neuroimage. 2006;31(3):1116–1128. doi: 10.1016/j.neuroimage.2006.01.015 [DOI] [PubMed] [Google Scholar]
- 31.Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. 32nd International Conference on Machine Learning, ICML 2015. 2015;1:448–456. [Google Scholar]
- 32.Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. The journal of machine learning research. 2014;15.1:1929–1958. doi: 10.1016/0370-2693(93)90272-J [DOI] [Google Scholar]
- 33.Agarap AF. Deep Learning using Rectified Linear Units (ReLU). 2018;(1):2–8. [Google Scholar]
- 34.Nwankpa C, Ijomah W, Gachagan A, Marshall S. Activation Functions: Comparison of trends in Practice and Research for Deep Learning. Published online 2018:1–20. [Google Scholar]
- 35.Abadi M´ın, Barham P, Chen, et al. TensorFlow: A system for large-scale machine learning. 12th USENIX symposium on operating systems design and implementation (OSDI 16). Published online 2016:265–283. doi: 10.1016/0076-6879(83)01039-3 [DOI] [Google Scholar]
- 36.Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. Published online December 22, 2014. http://arxiv.org/abs/1412.6980
- 37.Selvaraju RR, Cogswell M, Das A, Vedantam R, Parikh D, Batra D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. Int J Comput Vis. 2020;128(2):336–359. doi: 10.1007/s11263-019-01228-7 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data were provided [in part] by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.


