Abstract
Synchronization plays a key role in learning and memory by facilitating the communication between neurons promoted by synaptic plasticity. Spike-timing-dependent plasticity (STDP) is a form of synaptic plasticity that modifies the strength of synaptic connections between neurons based on the coincidence of pre- and postsynaptic spikes. In this way, STDP simultaneously shapes the neuronal activity and synaptic connectivity in a feedback loop. However, transmission delays due to the physical distance between neurons affect neuronal synchronization and the symmetry of synaptic coupling. To address the question that how transmission delays and STDP can jointly determine the emergent pairwise activity-connectivity patterns, we studied phase synchronization properties and coupling symmetry between two bidirectionally coupled neurons using both phase oscillator and conductance-based neuron models. We show that depending on the range of transmission delays, the activity of the two-neuron motif can achieve an in-phase/anti-phase synchronized state and its connectivity can attain a symmetric/asymmetric coupling regime. The coevolutionary dynamics of the neuronal system and the synaptic weights due to STDP stabilizes the motif in either one of these states by transitions between in-phase/anti-phase synchronization states and symmetric/asymmetric coupling regimes at particular transmission delays. These transitions crucially depend on the phase response curve (PRC) of the neurons, but they are relatively robust to the heterogeneity of transmission delays and potentiation-depression imbalance of the STDP profile.
Keywords: Transmission delay, Synchronization, Spike-timing-dependent plasticity, Synaptic plasticity, Coupling symmetry
Introduction
Synchronization between neuronal assemblies is crucial for information transfer across different brain regions (Buzsáki and Draguhn 2004; Wang et al. 2011; Li et al. 2021), cognition (Wang 2010), learning mechanisms and memory formation (Axmacher et al. 2006; Fell and Axmacher 2011). In plastic networks, synchronized neuronal activity can promote synaptic connectivity by coordinating the firing dynamics of neurons in a feedback loop (Gilson et al. 2009; Popovych et al. 2013; Madadi Asl et al. 2018c). Particularly, spike-timing-dependent plasticity (STDP) is a form of synaptic plasticity that modifies the synaptic strengths according to the coincidence of pre- and postsynaptic spikes between neuron pairs (Gerstner et al. 1996; Markram et al. 1997; Bi and Poo 1998). When the presynaptic spike precedes the postsynaptic spike (i.e., pre-post pairing), the corresponding synapse undergoes long-term potentiation (LTP), whereas long-term depression (LTD) is induced in the opposite direction (i.e., post-pre pairing) (Markram et al. 1997). In this way, neuronal activity reshapes patterns of synaptic connectivity between neurons through STDP which, in turn, determines the spiking events of neurons (Aoki and Aoyagi 2009; Madadi Asl et al. 2018c).
The question that how STDP influences the synchronization properties of neurons has been previously addressed in numerous studies (Zhigulin et al. 2003; Lubenov and Siapas 2008; Kozloski and Cecchi 2010; Knoblauch et al. 2012; Matias et al. 2015; Madadi Asl et al. 2017, 2018a; Kim and Lim 2018). When STDP is equilibrated, synapses between those correlated neurons that causally fire together (with small time lags) are stronger than the synapses between uncorrelated neurons that fire with large time lags due to the competitive nature of STDP (Song et al. 2000). On the other hand, strong connections between neurons supposedly further synchronize their activity, while the activity of loosely connected neurons remains relatively desynchronized (Kozloski and Cecchi 2010). Yet, functional implications of STDP, particularly its relation to the synchronization in neuronal networks may depend on several variables. In fact, transitions between coherent and incoherent firing modes are critically determined by the relation between transmission delays and the oscillatory period (Ermentrout and Kopell 1998; Woodman and Canavier 2011). More specifically, transmission delay between neurons determines their synchronization tendency (Ernst et al. 1995; Madadi Asl et al. 2018b), which is predicted by their dynamical properties (i.e., type-I vs. type-II excitability) given by the phase response curve (PRC) of the neurons (Ermentrout 1996; Câteau et al. 2008; Achuthan and Canavier 2009). In the case of two reciprocally coupled neurons, for example, when the range of transmission delay lies in the region where the gradient of PRC is negative, an in-phase firing mode is achieved (Woodman and Canavier 2011; Madadi Asl et al. 2017). On the contrary, transmission delays associated with a positive gradient of PRC can lead to an anti-phase firing mode (Woodman and Canavier 2011; Madadi Asl et al. 2017).
When large plastic networks with massively interconnected neurons are subjected to STDP, the emerging dynamics and structure are determined as a result of the interactions between neuronal activity and synaptic connectivity (Aoki and Aoyagi 2009; Madadi Asl et al. 2018b). The synchronizing/desynchronizing nature of neuronal activity is determined by the interplay between transmission delays and the PRC of neurons (Woodman and Canavier 2011). This leads to a rewiring of the synaptic connections mediated by STDP (Câteau et al. 2008) which, in turn, adjusts the neuronal activity in a feedback cycle (Kozloski and Cecchi 2010; Knoblauch et al. 2012; Madadi Asl et al. 2018c). Short-range transmission delays in local neuronal circuits or long-range transmission delays between distant neuronal populations embedded in different brain regions can strongly impact on these reciprocal interactions (Knoblauch and Sommer 2003). For instance, axonal delays can decouple neurons firing in synchrony by imposing a strong decoupling force on the synaptic dynamics through STDP (Lubenov and Siapas 2008). However, when the neurons fire in a desynchronized state, the same force promotes coupling strengths (Lubenov and Siapas 2008).
More specifically, STDP-driven neuronal networks with (dendritic and/or axonal) transmission delays may show multistable dynamics (Madadi Asl et al. 2018a), i.e., coexistence of qualitatively different stable attractor states such that either symmetric coupling (i.e., strong bidirectional loops or loosely connected states) or asymmetric coupling (i.e., unidirectional connections) can emerge between pairs of neurons (Madadi Asl et al. 2017, 2018a). These network properties can be explained by inspecting the effect of STDP on pairwise interactions of neurons (Babadi and Abbott 2013; Madadi Asl et al. 2017), i.e., two-neuron motifs, providing an analytically tractable way to relate the emergent connectivity pattern of networks to the properties of the STDP rule that modifies the synapses (Babadi and Abbott 2013). The transitions between symmetric and asymmetric coupling regimes is determined by the range of transmission delays (Barardi et al. 2014) and its interplay with STDP (Madadi Asl et al. 2018a). Since neuronal activity and synaptic connectivity are simultaneously shaped by STDP, changes in the coupling symmetry can be accompanied by transitions between phase synchronization states (Xie et al. 2016; Saa 2018; Khoshkhou and Montakhab 2019; Berner et al. 2021), so that symmetry/asymmetry in the coupling of neurons determines the synchronization/desynchronization properties of neurons (Saa 2018; Mikkelsen et al. 2013).
Computationally, phase difference between cortical areas can modulate information transfer by modifying the synchronization properties and connectivity patterns of networks (Ter Wal and Tiesinga 2017), likely regulated by inter-areal transmission delays (Barardi et al. 2014) and STDP (Matias et al. 2015). However, the joint action of transmission delays and STDP on the emergent dynamics and structure of networks is still not well known. Although STDP is a local rule that modifies the strength of synapses between pairs of neurons, it can determine the global connectivity pattern in large networks (Izhikevich et al. 2004; Morrison et al. 2007; Gilson et al. 2009). Hence, study of the STDP-induced pairwise interactions of neurons at the level of simple two-neuron motifs may enable an understanding of the dynamics and structure arising in large networks. To shed light on this complex interaction, we studied the dynamics and structure between two reciprocally delayed-coupled neurons with plastic synapses using both neuronal phase oscillator model and conductance-based spiking neuron model.
We theoretically analyzed the two-neuron motif using both type-I and type-II phase oscillator models and examined how the range of transmission delays can lead to in-phase/anti-phase transitions of synchronization or symmetric/asymmetric transitions of coupling structure in the motif, depending on the PRC of neurons. For analytical tractability, the dynamics of the systems was first theoretically analyzed from the perspective of no plasticity and then from the perspective of no neuronal dynamics. The theoretical results were able to predict the emergent phase synchronization state and the corresponding coupling regime in the simulations where the full coevolutionary dynamics was present, i.e., simultaneous evolution of the neuronal system and synaptic weights. Computer simulation results for both the phase oscillator model and conductance-based model qualitatively verified the theoretical predictions.
Furthermore, we showed that these transitions between in-phase/anti-phase synchronization states or symmetric/asymmetric coupling regimes are relatively robust to the heterogeneity of transmission delays between the two neurons and the dominance of potentiation/depression regime in the STDP profile. Our results demonstrate that the coevolution of neuronal activity and synaptic connectivity in plastic delayed-coupled two-neuron motifs determines the future state of the system. This notion can be translated to the network level and, in this way, affect the emergent structure and dynamics in large, plastic neuronal networks.
Methods
Spike-timing-dependent plasticity (STDP)
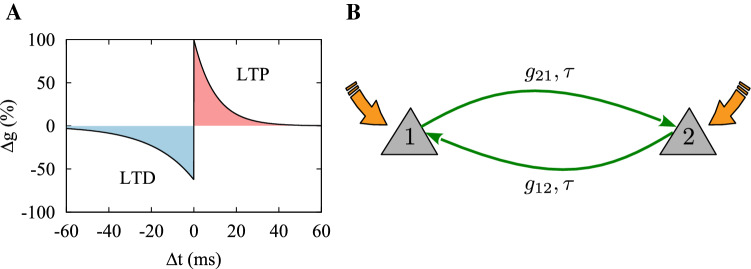
The synaptic strengths between neurons were modified according to the classical STDP rule characterized by an asymmetric learning window shown in Fig.1A (Bi and Poo 1998):
| 1 |
where and are the learning rate and the effective time window for synaptic potentiation (depression), and is a sign function where is 1 if and otherwise. The time lag between pre- and postsynaptic spike pairs is represented by , and denotes the effective delay perceived at the synapse, i.e., the difference between dendritic () and axonal () transmission delays (Madadi Asl et al. 2017).
Fig. 1.
Delayed-coupled two-neuron motif mediated by STDP. A The classic STDP profile characterized by an asymmetric learning window. STDP parameters were , , and . The change in the synaptic strengths is represented relative to the baseline where no synaptic change was induced, i.e., . B Two schematic neurons (1,2) reciprocally coupled via plastic excitatory synapses characterized by the strengths , and the transmission delay , supposedly isolated from a network. (Color figure online)
The instantaneous synaptic change over the period of spiking (T) can be approximated by separating the potentiation and depression terms in Eq. (1) which compete to determine the net synaptic change as follows (Madadi Asl et al. 2017):
| 2 |
where is the time lag used by STDP for potentiation of the synapse and represents the depression time lag.
The coupling strengths were updated by an additive rule at each step, i.e., . The value of the coupling strengths was confined in the range , so that they were set to () via hard bound saturation constraint once they crossed the lower (upper) bound of their allowed range.
Neuronal phase oscillator model
The general form of weakly pulse-coupled neuronal oscillators characterized by intrinsic frequency and infinitesimal phase sensitivity can be approximated by the phase-reduced model when the rate of the synaptic change is negligible on the fast timescale of the neuronal interactions (Izhikevich 1999). The evolution of the phases () of the two neurons (schematically shown in Fig.1B) is given by:
| 3 |
where () is the coupling strength of the synapse (). is the rescaled delay, where is the total transmission delay between the two neurons in the motif, i.e., the sum of dendritic and axonal delays. We assumed that the transmission delays are identical in both directions (i.e., identical feedforward and feedback delays). The neuronal phase oscillators spike once their phase crosses multiples of .
Coupling asymmetry index
In order to measure that to what extent the coupling between the two neurons is symmetric we defined the quantity as follows:
| 4 |
In a fully asymmetric two-neuron motif characterized by unidirectional connection between neurons (potentiation of one synapse and depression of the reverse synapse), the asymmetry index approaches unity, i.e., . On the contrary, symmetric changes of the synaptic strengths (either symmetric potentiation or symmetric depression of both synapses) lead to the emergence of a fully symmetric two-neuron motif (i.e., either strong bidirectional loops or loosely connected neurons) with .
Dynamical analysis of the pairwise interactions
By introducing the phase lag between the spike events of two bidirectionally coupled neurons as , the evolution of the phase difference can be written as follows (Madadi Asl et al. 2017):
| 5 |
For simplicity and analytical tractability, we assumed that the frequency mismatch between the two neurons is negligible (i.e., ) (Madadi Asl et al. 2017). For an analysis of the situation that the frequency mismatch is not neglected see Madadi Asl et al. (2018a). The PRC function for a type-I neuron is mainly positive where its shape can be approximated by , whereas the PRC function for a type-II neuron exhibits both positive and negative regions which can be approximated by (Achuthan and Canavier 2009; Sadeghi and Valizadeh 2014). The fixed point of the phase lag () can then be calculated as follows (Madadi Asl et al. 2017, 2018a):
| 6 |
| 7 |
where is the coupling asymmetry index defined in Eq. (4).
Conductance-based neuronal and synaptic model
Wang-Buzsáki (WB) (Wang and Buzsáki 1996) and Hodgkin-Huxley (HH) (Hodgkin and Huxley 1952) models were considered to simulate conductance-based neurons in which their dynamics resembles the dynamics of the type-I and type-II oscillators, respectively. The dynamics of the membrane potential of neuron i () obeys the following differential equation in both WB and HH models:
| 8 |
where C is the membrane capacitance. , , and are maximal conductances of sodium, potassium and leak currents. , and are the corresponding Nernst equilibrium potentials. The numerical values of the parameters used in the simulations are listed in Table 1. The parameters n, m and h are gating variables that satisfy the following differential equations in the case of WB (Wang and Buzsáki 1996) and HH (Hodgkin and Huxley 1952) models, respectively:
| 9 |
| 10 |
where , and the functions and describe the transition rates between open and closed states of the channels according to the following differential equations in the case of WB (Wang and Buzsáki 1996) and HH (Hodgkin and Huxley 1952) models, respectively:
| 11 |
| 12 |
Table 1.
Parameters of conductance-based models used in the simulations
| Parameter | Symbol | WB | HH | Unit |
|---|---|---|---|---|
| Membrane capacitance | C | 1 | 1 | |
| Spiking threshold | −40 | −40 | ||
| Resting membrane potential | −65 | −65 | ||
| Sodium equilibrium potential | 55 | 50 | ||
| Potassium equilibrium potential | −90 | −77 | ||
| Leak equilibrium potential | −65 | −54.4 | ||
| Sodium maximal conductance | 35 | 120 | ||
| Potassium maximal conductance | 9 | 36 | ||
| Leak maximal conductance | 0.1 | 0.3 | ||
| Applied current | 1 | 10 |
In Eq. (8), is the applied current to the neuron i. In the case of conductance-based models, we assumed that neurons are connected to each other by excitatory chemical synapses where represents the synaptic current from the presynaptic neuron (j) to the postsynaptic neuron (i):
| 13 |
where is the synaptic strength, is the total transmission delay between pre- and postsynaptic neurons, is the voltage of the postsynaptic neuron, and is the synaptic reversal potential that characterizes excitatory or inhibitory nature of the synapse. The function s(t) denotes the fraction of open channels and obeys the following differential equation (Wang and Buzsáki 1996):
| 14 |
where and are channel opening and closing rates, respectively. The function guarantees the activation of the synapse whenever the presynaptic voltage crosses and the parameter is a constant.
Results
Theoretical predictions
Transitions of phase synchronization
To inspect how transmission delays and STDP jointly shape the dynamics and structure between neurons we considered a two-neuron motif schematically shown in Fig. 1B, assumed to be isolated from a network. The two neurons were reciprocally delayed-coupled to each other via plastic synapses subjected to the STDP rule given by Eq. (1). For analytical tractability we used neuronal phase oscillator model to provide theoretical predictions. In order to present a more general overview, we considered both dynamical type-I and type-II phase oscillators characterized by their approximated analytical PRCs (see Methods).
For simplicity, we first assumed that STDP is OFF. As shown in Fig. 2A1,B1, we systematically varied the transmission delay () and the coupling asymmetry index (), and theoretically calculated the fixed point of phase lag () between the spiking events of neurons according to Eqs. (6) and (7) for the type-I (A1) and type-II (B1) phase oscillators, respectively. The transmission delay is reasonably varied up to the spiking period of the phase oscillators (i.e., ). Fig. 2A1,B1 shows that depending on the excitability nature of the phase oscillators, the transitions between in-phase (zero phase lag) and anti-phase ( phase lag) synchronization occur at particular coupling asymmetry and transmission delay.
Fig. 2.
Theoretical prediction of in-phase/anti-phase synchronization transitions in the two-neuron motif. Colors show the fixed point of phase lag theoretically calculated by Eq. (6) in (A1) and Eq. (7) in (B1) for the type-I and type-II phase oscillators, respectively, when STDP was OFF. Points a2-b3 denote the examplary set of parameters used to depict the panels A2-B3 representing the phase dynamics (arrows) of the two-neuron motif calculated by Eq. (3) and the asymptotic phase lag (colors) for different values of the transmission delay and asymmetry index denoted above each panel in the case of the type-I (A2,A3) and type-II (B2,B3) phase oscillator. (Color figure online)
As shown in Fig. 2A1,B1, in the fully symmetric coupling regime (i.e., ) characterized by either strong bidirectional loops or loosely connected states, the fixed point of phase lag can merely attain in-phase (blue) or anti-phase (red) synchronization state, depending on the delay. This can be traced back to Eqs. (6) and (7) where substituting yields . In this case, in the type-I phase oscillator (Fig. 2A1) in-phase/anti-phase synchronization transition occurs when , whereas in the type-II phase oscillator in Fig. 2B1 such a transition occurs when and . As the value of the coupling asymmetry index is gradually increased toward the fully asymmetric coupling regime (i.e., ) characterized by unidirectional coupling between neurons, the phase lag experiences a mixture of states between in-phase and anti-phase synchronization limits represented by different colors.
In Fig. 2A2-B3, the phase dynamics of the oscillators and the corresponding phase lag is shown for examplary combination of the transmission delay and coupling asymmetry index. Fig. 2A2-B3 shows how changing the transmission delay at a given coupling asymmetry index can determine the phase lag between neurons and lead to the in-phase/anti-phase synchronization transitions. For instance, in Fig. 2A3,B2 the two-neuron motif tends to achieve an in-phase synchronization state, whereas an anti-phase synchronization state is more likely to occur in Fig. 2A2,B3. The difference between the synchronization properties of the type-I and type-II phase oscillators arises due to their PRC which determines the fixed point of phase lag and delay-dependent transitions between in-phase and anti-phase states.
Transitions of coupling symmetry between neurons
When the synapses between the two neurons are modified according to the STDP rule, the coupling asymmetry index is determined by the interplay between neuronal and synaptic dynamics in a self-organized manner (Madadi Asl et al. 2017). In fact, the neuronal activity and synaptic connectivity compete to shape the ultimately emerging phase lag and coupling asymmetry index. In this way, STDP stabilizes the dynamics and structure of the two-neuron motif in desired basins of attraction determined by the transmission delay.
To theoretically explore the role of STDP in the stabilization of neuronal and synaptic dynamics, in Fig. 3A we assumed the transmission delay and phase lag as free parameters (a fixed neuronal dynamics) and estimated the emergent coupling symmetry between the two neurons based on the synaptic change. Note that is the difference between dendritic and axonal delays that enters Eq. (1) and modifies the synaptic dynamics, whereas is the sum of dendritic and axonal delays that enters Eq. (3) and modifies the neuronal dynamics (Madadi Asl et al. 2017). Fig. 3A shows that different combinations of the transmission delay and phase lag give rise to a variety of coupling scenarios ranging from a fully symmetric coupling regime (light color) to a fully asymmetric coupling regime (dark color). Given a fixed neuronal dynamics, STDP shapes the reciprocal synaptic connectivity to determine the coupling symmetry between the two neurons.
Fig. 3.
Theoretical prediction of coupling symmetry/asymmetry transitions in the two-neuron motif. A Colors show the emergent two-neuron synaptic coupling calculated based on the synaptic change in Eq. (2) over the spiking period when STDP parameters were , , and . Points b1-b3 denote the set of parameters used to depict panels B1-B3. B1-B3 Examplary synaptic dynamics (arrows) of the system calculated by Eq. (1) and the coupling asymmetry index (colors) for different values of the transmission delay and phase lag denoted above each panel. (Color figure online)
Fig. 3B1-B3 shows the synaptic dynamics of the two-neuron motif subjected to STDP. The arrows show the flow of the synaptic change calculated from Eq. (1) and colors show the coupling asymmetry index between neurons. Based on the range of the transmission delay and phase lag, the two-neuron motif can attain a strong bidirectionally coupled (symmetric) regime characterized by both of the synaptic strengths saturated to unity (, ; B1), a loosely connected (symmetric) state where both of the synaptic strengths approach zero (, ; B2), and a unidirectional connectivity (asymmetric) state characterized by the synaptic strengths saturated in the opposite directions (, or , ; B3).
A notable observation is that the emergent coupling regime in the two-neuron motif is bistable such that depending on the initial synaptic strengths qualitatively different coupling regimes can emerge. For instance, in Fig. 3B1 the bistability is between the bidirectional and unidirectional coupling regimes. The system favors the bidirectional regime when the initial values of the synaptic strengths are close to each other. However, in Fig. 3B2 the bistability is between the loosely connected state and unidirectional coupling regime, whereas changing the initial synaptic strengths in Fig. 3B3 can only change the neuron with stronger outgoing synapse (always unidirectional). The emergence of these bistable states due to STDP was attributed to the frequency-dependent effects in the two-neuron motif, i.e., the presence of a frequency mismatch between the neurons (Madadi Asl et al. 2018a).
Simulation results
Transitions are jointly shaped by transmission delays and STDP
To inspect the validity of the theoretical predictions, we simulated the emergent phase synchronization and coupling structure in the two-neuron motif with full coevolutionary dynamics, i.e., in the presence of neuronal dynamics and plasticity. To demonstrate that the results obtained for the type-I and type-II neuronal phase oscillators can be translated to conductance-based spiking neuron models, we also simulated WB and HH neuron models. The dynamics and the PRC of WB and HH neurons resemble the type-I and type-II phase oscillators, respectively. This suggests that the theoretical predictions should be qualitatively valid for conductance-based neuron models.
To extract the effect of coupling symmetry on neuronal dynamics, we first assumed that STDP is OFF . The results are shown in Fig. 4 where the phase synchronization state of the type-I and type-II phase oscillators (blue color) as well as the WB and HH neurons (cyan color) are simulated for different values of transmission delay and coupling asymmetry index between neurons (STDP OFF state). In accordance with the theoretical predictions presented in Fig. 2A1,B1, in the fully symmetric coupling regime (i.e., ), the phase lag between the type-I (Fig. 4A1, blue) and type-II (Fig. 4B1, blue) phase oscillators can merely attain well-defined in-phase and anti-phase states where the in-phase/anti-phase transitions occur at the same theoretically-predicted delays. For a relatively symmetric coupling, the distribution of steady-state phase lags between neurons fairly follows the slope of the analytical PRC (orange curves) of the type-I and type-II neuronal phase oscillators (see Fig. 4A1,A2 and B1,B2). The spiking period of the WB and HH neurons were mapped into the period of the phase oscillators to better illustrate their resemblance. Fig. 4A1,B1 (cyan) shows that the phase synchronization transitions of the WB and HH neurons are consistent with the type-I and type-II phase oscillators, respectively.
Fig. 4.
Delay-induced phase synchronization in the two-neuron motif due to coupling asymmetry when STDP was OFF. A1-A3 Reciprocally coupled type-I phase oscillators and WB neurons. B1-B3 Reciprocally coupled type-II phase oscillators and HH neurons. The coupling asymmetry index is increased from fully symmetric (; top) to fully asymmetric (; bottom) regime. Orange curves show the slope of the analytical PRC in the case of type-I () and type-II () phase oscillators. The spiking period of phase oscillators is . The spiking period of WB and HH neurons is and when injected by and currents, respectively. (Color figure online)
STDP was OFF in Fig. 4, hence, we manually varied the coupling symmetry to explore its effect on the distribution of phase lags. As the coupling asymmetry index is increased from top to bottom in Fig. 4A1-A3 and B1-B3, the distribution of phase lags is smoothed such that in the fully asymmetric coupling regime (i.e., ) in Fig. 4A3,B3 the phase lags are linearly proportional to the transmission delay between neurons (i.e., ) and achieve a mixture of in-phase and anti-phase synchronization states. Such a relationship between the phase lag and transmission delay is the characteristic of unidirectional connections between neurons (Sadeghi and Valizadeh 2014; Madadi Asl et al. 2017). It is notable that in this case the linear dependence of steady-state distribution of phase lags on the transmission delay takes a universal form irrespective of the PRC nature of the neurons (type-I vs. type-II) or the neuron model (phase oscillator vs. conductance-based). In either case, the simulation results are in good agreement with the theoretical predictions.
We then turned ON the STDP rule to study the full coevolutionary dynamics in Fig. 5. In this case, the coupling symmetry in the two-neuron motif is continuously adjusted due the competition between neuronal activity and synaptic connectivity. In other words, STDP modifies the synaptic strengths based on the spike timing of neurons and, in return, the strength of synapses modifies the coincidence of neuronal spikes in a feedback loop. The change in the synaptic weights occurs on a slower time scale in comparison to the fast phase dynamics (Ratas et al. 2021). This allows the fixed point of phase lag given by Eq. (5) to modify the synaptic strengths in Eq. (2) over a spiking cycle, leading to a full coevolutionary dynamics. As shown in Fig. 5A1,B1, both the type-I and type-II phase oscillators favor nearly in-phase or anti-phase synchronization and symmetric connections in most transmission delays. However, near the extremum points of the PRC function of each phase oscillator the coupling has a tendency to avoid symmetric states. These behaviors can be jointly explained by Figs. 2 and 3 where the emergent two-neuron structure was theoretically predicted based on the range of transmission delay and phase lag. Note that the symmetric loosely connected states may not be stable since fluctuations of the phase lag between neurons in this case can self-organize the motif toward the emergence of unidirectional connections (Madadi Asl et al. 2017).
Fig. 5.
STDP determines the level of synchronization by shaping coupling symmetry. A1,A2 Reciprocally coupled type-I phase oscillators (A1) and WB neurons (A2). B1,B2 Reciprocally coupled type-II phase oscillators (B1) and HH neurons (B2). The spiking period of phase oscillators is . The spiking period of WB and HH neurons is and when injected by and currents, respectively. C1,C2 Examplary time course of the phase lag and coupling asymmetry index is shown for the HH neurons at delays marked in panel B2 by arrows: (c1) and (c2) . (Color figure online)
The simulation results for the conductance-based WB and HH spiking neuron models (shown in Fig. 5A2,B2) qualitatively follow the results obtained for the type-I and type-II phase oscillators (shown in Fig. 5A1,B1), respectively. In this case, relatively small transmission delays can lead to the emergence of out-of-phase synchronization (cyan color) followed by fully asymmetric coupling between neurons (magenta color). However, in greater delays either in-phase or anti-phase synchronization results in the emergence of a fully symmetric connection between neurons. Fig. 5C1,C2 shows the time course of the steady-state phase lag and the emergent coupling asymmetry index for two examplary points marked by c1 and c2 in Fig. 5B2. The two-neuron motif achieved a nearly in-phase synchronization state (cyan color) characterized by a fully asymmetric coupling regime (magenta color) in Fig. 5C1 when . On the contrary, when the transmission delay was , nearly anti-phase synchronization state emerged with a fully symmetric connection between neurons in Fig. 5C2.
Heterogeneity of the transmission delays
So far, we assumed that the transmission delays between neurons are identical for both directions. To inspect how the heterogeneity of the transmission delays can impact on the neuronal activity and synaptic connectivity, we systematically varied the transmission delays in both directions ( and ) and observed the phase lag and coupling asymmetry index in computer simulations for both the type-I and type-II phase oscillators subjected to STDP. Due to the dynamical correspondence between the conductance-based model and phase oscillator model, one can assume that similar behavior would appear in the conductance-based neurons.
The results are shown in Fig. 6A1-A4 which fairly follow the theoretical predictions presented in Fig. 2A1,B1 for the identical transmission delays. In fact, the symmetry of the two-neuron motif leads to the emergence of a phase lag (Fig. 6A1,A2) and coupling asymmetry index (Fig. 6B1,B2) so that there is no preferred direction for the transmission delay. The notable observation is that the previously obtained theoretical and simulation results are robust to the heterogeneity of the transmission delays such that keeping fixed and changing yields the same result as when is fixed and is changed.
Fig. 6.
Heterogeneity of the transmission delays. A1,A2 The color-coded steady-state phase lag between neurons is shown for two reciprocally coupled type-I (A1) and type-II phase oscillators (A2) for non-identical transmission delays. B1,B2 The color-coded coupling asymmetry index is shown for two reciprocally coupled type-I (B1) and type-II phase oscillators (B2). C1,C2 Examplary time course of the phase lag and coupling asymmetry index is shown for delays marked by points (c1) and (c2) denoted above each panel. (Color figure online)
In the type-I phase oscillator model, the asymmetric coupling (Fig. 6B1, dark color) can only emerge when one of the transmission delays is small (in comparison to the spiking period of the oscillators). In this case, the phase lag fluctuates between in-phase and anti-phase synchronization states (Fig. 6A1, green). When the transmission delays are increased, the phase lag saturates to an anti-phase state (Fig. 6A1, red) and then to an in-phase state (Fig. 6A1, blue), but the coupling structure favors a symmetric connection in either case (Fig. 6B1, light color).
However, in the type-II phase oscillator model, for transmission delays smaller than half of the spiking period, the phase lag attains a nearly in-phase synchronization state (Fig. 6A2, blue), whereas for greater delays the phase lag is saturated to a nearly anti-phase synchronization state (Fig. 6A2, red). For either of these cases, the two-neuron motif favors the emergence of symmetric connections (Fig. 6B2, light color), except at those transmission delays where the gradient of the PRC of the neurons changes its sign (Fig. 6B2, dark color).
The time course of the phase lag and coupling asymmetry index is examplary shown for two sets of transmission delays in Fig. 6C1,C2 marked by points c1 and c2 in Fig. 6A1-B2. When and , the type-I phase oscillator model achieves an out-of-phase state characterized by a nearly asymmetric coupling regime (Fig. 6C1). However, the type-II phase oscillator model attains a nearly in-phase synchronization state accompanied with a fully symmetric coupling regime at the same delay setting. This observation suggests that the range of the transmission delays does not solely determine the emergent neuronal activity and synaptic connectivity between neurons, and the dynamical nature of the neuron (i.e., type-I vs. type-II excitability) is crucial.
Potentiation-depression imbalance of the STDP profile
In this study, we assumed a generic STDP profile characterized by a greater amplitude and smaller time window for potentiation regime in comparison to the depression regime, i.e., and (also see Fig. 1A, red regime vs. blue regime), so that the stability condition is ensured, i.e., . Such a STDP profile is typically observed in stimulus pairing experiments in hippocampal (Bi and Poo 1998) and cortical (Froemke and Dan 2002) slices. However, to explore the effect of STDP potentiation-depression imbalance on the emergent neuronal activity and synaptic connectivity in the two-neuron motif we systematically varied the ratio of potentiation-depression amplitude (i.e., ) and time constant (i.e., ) by keeping the depression parameters fixed.
The results are shown in Fig. 7A1-A4 for the type-I phase oscillator model and in Fig. 7B1-B4 for the type-II phase oscillator model. Each column is plotted at a particular transmission delay denoted above the corresponding panel. Overall, the emergent phase lag and coupling asymmetry index is fairly robust to the imbalance of STDP potentiation and depression regimes. In the two-neuron motif modeled by the type-I phase oscillators, the phase lag achieved a nearly anti-phase synchronization state characterized by nearly symmetric coupling regime both at (Fig. 7A1,A3) and (Fig. 7A2,A4).
Fig. 7.
Potentiation-depression imbalance of the STDP profile. A1-A4 The color-coded steady-state phase lag (A1,A2) and coupling asymmetry index (A3,A4) are shown for two reciprocally coupled type-I phase oscillators subjected to STDP with imbalanced potentiation and depression regimes. Each column was depicted at a specific transmission delay (denoted above panel). STDP depression parameters were and , whereas STDP potentiation parameters were varied. B1-B4 Same as panels A1-A4, but for two reciprocally coupled type-II phase oscillators. (Color figure online)
The threshold (marked by arrow in Fig. 7A1) qualitatively divides the phase synchronization states shown in Fig. 7A1,A2. For instance, in the type-I oscillator, the fully anti-phase synchronization state is destabilized (Fig. 7A1, orange) when . In the type-II oscillator at , shifting from the regime to the regime leads to a transition of the phase synchronization from the in-phase state to the nearly anti-phase state (Fig. 7B1, blue to red). This is accompanied with a fair transition of coupling structure from a fully symmetric regime (Fig. 7B3, light color) toward more asymmetric regimes (Fig. 7B3, dark color). The separation of time scales of phase dynamics and synaptic change allows the fixed point of phase lag from Eq. (5) to enter Eq. (2) and modify the slowly-varying synaptic weights (Ratas et al. 2021). This leads to a full coevolutionary dynamics that determines the future state of the system. On the other hand, both the phase synchronization and coupling asymmetry index were robust to these changes when (see Fig. 7B2,B4).
Discussion
In this study, we employed theoretical approximations and computer simulations to demonstrate that transmission delays and STDP jointly determine the phase synchronization properties and coupling structure between neurons. We tested our hypothesis by using both the phase oscillator models and conductance-based spiking neuron models in a two-neuron motif. As shown previously, with a reasonable assumption that the neurons remain nearly phase-locked, the two-neuron results can be translated to large neuronal networks where pairwise interactions between neurons build up to shape the future state of the network (Babadi and Abbott 2013; Madadi Asl et al. 2017). Our results showed that the excitability nature of the neurons determines the tendency of the motif to achieve an in-phase/anti-phase synchronization state at a given delay. Depending on the phase synchronization state and the range of delays, STDP stabilizes the coupling structure of the motif in a symmetric/asymmetric regime.
Our findings indicated that when the coupling between neurons is symmetric, the spiking events of the neurons remain in a perfectly in-phase or anti-phase synchronized state. On the contrary, asymmetric coupling between neurons leads to a mixture of phase synchronization states. For instance, in-phase firing can remain stable between several neurons, e.g. in a three-neuron motif, but anti-phase state ( phase lag) gives rise to multiple competing metastable states leading to frustrated dynamics in three-neuron loops (Madadi Asl et al. 2017). By changing the delay, the dynamics of the system undergoes a transition between in-phase/anti-phase synchronization states and symmetric/asymmetric coupling regimes. When STDP comes to play, the coupling symmetry is interactively modulated by the phase synchronization properties and symmetric/asymmetric coupling transitions may occur. The response of the motif to changing the range of delay crucially depends on the PRC of the system. However, these behaviors are relatively robust to the heterogeneity of transmission delays and the potentiation-depression imbalance of the STDP profile. In addition, transmission delays have dual effects on the dynamics of the motif: The sum of dendritic and axonal delays modify the neuronal dynamics, whereas their difference adjusts the synaptic dynamics.
Inter-areal connections between different brain regions may assume transmission delays as large as tens of milliseconds (Stoelzel et al. 2017). Dendritic delays are typically smaller than axonal delays (Lubenov and Siapas 2008), ranging from sub-millisecond to a few milliseconds (Agmon-Snir and Segev 1993; Schierwagen and Claus 2001). Axons, however, can exhibit significant transmission delays, e.g., about 10-20 in cortico-cortical loops (Swadlow 1990), and even more up to 40-50 in cortico-thalamic pathways (Stoelzel et al. 2017). Transmission delays can crucially impact on the neuronal dynamics required for reliable generation and transmission of synchronized neuronal activity (Rezaei et al. 2020; Ziaeemehr and Valizadeh 2021). For instance, long-range delays between two bidirectionally coupled cortical populations can self-organize the two-module system to either in-phase or anti-phase synchronized states and affect information transfer between the two populations (Barardi et al. 2014). When the synaptic strengths are adjusted by STDP, continuous feedback between the synaptic modifications and the coherence in the neuronal firing leads to the simultaneous regulation of neuronal activity and synaptic connectivity (Aoki and Aoyagi 2009; Madadi Asl et al. 2018b). In this way, STDP can enhance in-phase or anti-phase synchronization by promoting the coupling dynamics between neurons (Ren and Zhao 2007; Xie et al. 2016). Transmission delays determine the transitions between in-phase and anti-phase synchronization states, or symmetric and asymmetric coupling dynamics (Xie et al. 2016). The interplay between different phase synchronization states and synaptic coupling regimes shaped by STDP plays a key role in cognitive tasks related to learning and memory in cortical areas (Matias et al. 2015).
Ultimately, maladaptive synaptic plasticity is implicated in a number of neuropsychiatric disorders (Madadi Asl et al. 2019, 2022b; Asadi et al. 2022). STDP provides a temporally precise mechanistic model for synaptic plasticity that may help the brain to preserve collective neuronal oscillations in their healthy range despite long-range transmission delays emerging from the physical distance between neurons embedded in different brain regions (Knoblauch and Sommer 2004; Buzsáki et al. 2013). This may be realized by shaping qualitatively different stable attractor states, i.e., physiological states (strong synchronization, strong connectivity) as opposed to pathological states (weak synchronization, weak connectivity) (Madadi Asl et al. 2022a, b). Taking into account the interplay between transmission delays and STDP in simple modeling studies may shed light on the complex role of their interaction in shaping the structure-function relationships in brain networks. This can contribute to the development of brain-inspired cognitive computing devices designed to emulate the essential properties of biological neurons and synapses (Madadi Asl and Ramezani Akbarabadi 2021).
Author contributions
Mojtaba Madadi Asl: Conceptualization, Methodology, Investigation, Visualization, Writing - original draft, Writing - review & editing, Supervision, Project administration. Saeideh Ramezani Akbarabadi: Methodology, Investigation, Visualization, Writing - original draft, Writing - review & editing.
Funding
No specific funding was received for conducting this study.
Data availability
All data generated or analysed during this study are included in this published article.
Code availability
Not applicable.
Declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
Not applicable.
Consent to participate
Not applicable.
Consent for publication
Not applicable.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Achuthan S, Canavier CC. Phase-resetting curves determine synchronization, phase locking, and clustering in networks of neural oscillators. J Neurosci. 2009;29(16):5218–5233. doi: 10.1523/JNEUROSCI.0426-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agmon-Snir H, Segev I. Signal delay and input synchronization in passive dendritic structures. J Neurophysiol. 1993;70(5):2066–2085. doi: 10.1152/jn.1993.70.5.2066. [DOI] [PubMed] [Google Scholar]
- Aoki T, Aoyagi T. Co-evolution of phases and connection strengths in a network of phase oscillators. Phys Rev Lett. 2009;102(3):034101. doi: 10.1103/PhysRevLett.102.034101. [DOI] [PubMed] [Google Scholar]
- Asadi A, Madadi Asl M, Vahabie AH, Valizadeh A. The origin of abnormal beta oscillations in the parkinsonian corticobasal ganglia circuits. Parkinson’s Disease. 2022;2022(7524066):1–13. doi: 10.1155/2022/7524066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axmacher N, Mormann F, Fernández G, Elger CE, Fell J. Memory formation by neuronal synchronization. Brain Res Rev. 2006;52(1):170–182. doi: 10.1016/j.brainresrev.2006.01.007. [DOI] [PubMed] [Google Scholar]
- Babadi B, Abbott LF. Pairwise analysis can account for network structures arising from spike-timing dependent plasticity. PLoS Comput Biol. 2013;9(2):e1002906. doi: 10.1371/journal.pcbi.1002906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barardi A, Sancristóbal B, Garcia-Ojalvo J. Phase-coherence transitions and communication in the gamma range between delay-coupled neuronal populations. PLoS Comput Biol. 2014;10(7):e1003723. doi: 10.1371/journal.pcbi.1003723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berner R, Vock S, Schöll E, Yanchuk S. Desynchronization transitions in adaptive networks. Phys Rev Lett. 2021;126(2):028301. doi: 10.1103/PhysRevLett.126.028301. [DOI] [PubMed] [Google Scholar]
- Bi GQ, Poo MM. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci. 1998;18(24):10464–10472. doi: 10.1523/JNEUROSCI.18-24-10464.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304(5679):1926–1929. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- Buzsáki G, Logothetis N, Singer W. Scaling brain size, keeping timing: evolutionary preservation of brain rhythms. Neuron. 2013;80(3):751–764. doi: 10.1016/j.neuron.2013.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Câteau H, Kitano K, Fukai T. Interplay between a phase response curve and spike-timing-dependent plasticity leading to wireless clustering. Phys Rev E. 2008;77(5):051909. doi: 10.1103/PhysRevE.77.051909. [DOI] [PubMed] [Google Scholar]
- Ermentrout B. Type i membranes, phase resetting curves, and synchrony. Neural Comput. 1996;8(5):979–1001. doi: 10.1162/neco.1996.8.5.979. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB, Kopell N. Fine structure of neural spiking and synchronization in the presence of conduction delays. Proc Natl Acad Sci. 1998;95(3):1259–1264. doi: 10.1073/pnas.95.3.1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ernst U, Pawelzik K, Geisel T. Synchronization induced by temporal delays in pulse-coupled oscillators. Phys Rev Lett. 1995;74(9):1570. doi: 10.1103/PhysRevLett.74.1570. [DOI] [PubMed] [Google Scholar]
- Fell J, Axmacher N. The role of phase synchronization in memory processes. Nat Rev Neurosci. 2011;12(2):105–118. doi: 10.1038/nrn2979. [DOI] [PubMed] [Google Scholar]
- Froemke RC, Dan Y. Spike-timing-dependent synaptic modification induced by natural spike trains. Nature. 2002;416(6879):433–438. doi: 10.1038/416433a. [DOI] [PubMed] [Google Scholar]
- Gerstner W, Kempter R, van Hemmen JL, Wagner H. A neuronal learning rule for sub-millisecond temporal coding. Nature. 1996;383(6595):76. doi: 10.1038/383076a0. [DOI] [PubMed] [Google Scholar]
- Gilson M, Burkitt AN, Grayden DB, Thomas DA, van Hemmen JL. Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks iv. Biol Cybern. 2009;101(5–6):427. doi: 10.1007/s00422-009-0346-1. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117(4):500. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich EM. Weakly pulse-coupled oscillators, fm interactions, synchronization, and oscillatory associative memory. IEEE Trans Neural Networks. 1999;10(3):508–526. doi: 10.1109/72.761708. [DOI] [PubMed] [Google Scholar]
- Izhikevich EM, Gally JA, Edelman GM. Spike-timing dynamics of neuronal groups. Cereb Cortex. 2004;14(8):933–944. doi: 10.1093/cercor/bhh053. [DOI] [PubMed] [Google Scholar]
- Khoshkhou M, Montakhab A. Spike-timing-dependent plasticity with axonal delay tunes networks of izhikevich neurons to the edge of synchronization transition with scale-free avalanches. Front Syst Neurosci. 2019;13:73. doi: 10.3389/fnsys.2019.00073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SY, Lim W. Effect of spike-timing-dependent plasticity on stochastic burst synchronization in a scale-free neuronal network. Cogn Neurodyn. 2018;12(3):315–342. doi: 10.1007/s11571-017-9470-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knoblauch A, Hauser F, Gewaltig M-O, Körner E, Palm G. Does spike-timing-dependent synaptic plasticity couple or decouple neurons firing in synchrony? Front Comput Neurosci. 2012;6(55):55. doi: 10.3389/fncom.2012.00055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knoblauch A, Sommer FT. Synaptic plasticity, conduction delays, and inter-areal phase relations of spike activity in a model of reciprocally connected areas. Neurocomputing. 2003;52:301–306. doi: 10.1016/S0925-2312(02)00792-0. [DOI] [Google Scholar]
- Knoblauch A, Sommer FT. Spike-timing-dependent synaptic plasticity can form zero lag links for cortical oscillations. Neurocomputing. 2004;58:185–190. doi: 10.1016/j.neucom.2004.01.041. [DOI] [Google Scholar]
- Kozloski J, Cecchi GA. A theory of loop formation and elimination by spike timing-dependent plasticity. Front Neural Circuits. 2010;4:7. doi: 10.3389/fncir.2010.00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X, Wu Y, Wei M, Guo Y, Yu Z, Wang H, Li Z, Fan H. A novel index of functional connectivity: phase lag based on wilcoxon signed rank test. Cogn Neurodyn. 2021;15(4):621–636. doi: 10.1007/s11571-020-09646-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lubenov EV, Siapas AG. Decoupling through synchrony in neuronal circuits with propagation delays. Neuron. 2008;58(1):118–131. doi: 10.1016/j.neuron.2008.01.036. [DOI] [PubMed] [Google Scholar]
- Madadi Asl M, Asadi A, Enayati J, Valizadeh A. Inhibitory spike-timing-dependent plasticity can account for pathological strengthening of pallido-subthalamic synapses in parkinson’s disease. Front Physiol. 2022;13(915626):1–13. doi: 10.3389/fphys.2022.915626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madadi Asl M, Ramezani Akbarabadi S. Voltage-dependent plasticity of spin-polarized conductance in phenyl-based single-molecule magnetic tunnel junctions. PLoS ONE. 2021;16(9):e0257228. doi: 10.1371/journal.pone.0257228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madadi Asl M, Vahabie AH, Valizadeh A. Dopaminergic modulation of synaptic plasticity, its role in neuropsychiatric disorders, and its computational modeling. Basic Clinical Neurosci. 2019;10(1):1. doi: 10.32598/bcn.9.10.125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madadi Asl M, Vahabie AH, Valizadeh A, Tass PA. Spike-timing-dependent plasticity mediated by dopamine and its role in parkinson’s disease pathophysiology. Front Netw Physiol. 2022;2(817524):1–18. doi: 10.3389/fnetp.2022.817524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madadi Asl M, Valizadeh A, Tass PA. Dendritic and axonal propagation delays determine emergent structures of neuronal networks with plastic synapses. Sci Rep. 2017;7(1):39682. doi: 10.1038/srep39682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madadi Asl M, Valizadeh A, Tass PA. Delay-induced multistability and loop formation in neuronal networks with spike-timing-dependent plasticity. Sci Rep. 2018;8(1):12068. doi: 10.1038/s41598-018-30565-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madadi Asl M, Valizadeh A, Tass PA. Dendritic and axonal propagation delays may shape neuronal networks with plastic synapses. Front Physiol. 2018;9:1849. doi: 10.3389/fphys.2018.01849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madadi Asl M, Valizadeh A, Tass PA. Propagation delays determine neuronal activity and synaptic connectivity patterns emerging in plastic neuronal networks. Chaos. 2018;28(10):106308. doi: 10.1063/1.5037309. [DOI] [PubMed] [Google Scholar]
- Markram H, Lübke J, Frotscher M, Sakmann B. Regulation of synaptic efficacy by coincidence of postsynaptic aps and epsps. Science. 1997;275(5297):213–215. doi: 10.1126/science.275.5297.213. [DOI] [PubMed] [Google Scholar]
- Matias FS, Carelli PV, Mirasso CR, Copelli M. Self-organized near-zero-lag synchronization induced by spike-timing dependent plasticity in cortical populations. PLoS ONE. 2015;10(10):e0140504. doi: 10.1371/journal.pone.0140504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikkelsen K, Imparato A, Torcini A. Emergence of slow collective oscillations in neural networks with spike-timing dependent plasticity. Phys Rev Lett. 2013;110(20):208101. doi: 10.1103/PhysRevLett.110.208101. [DOI] [PubMed] [Google Scholar]
- Morrison A, Aertsen A, Diesmann M. Spike-timing-dependent plasticity in balanced random networks. Neural Comput. 2007;19(6):1437–1467. doi: 10.1162/neco.2007.19.6.1437. [DOI] [PubMed] [Google Scholar]
- Popovych OV, Yanchuk S, Tass PA. Self-organized noise resistance of oscillatory neural networks with spike timing-dependent plasticity. Sci Rep. 2013;3(1):1–6. doi: 10.1038/srep02926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratas I, Pyragas K, Tass PA. Multistability in a star network of kuramoto-type oscillators with synaptic plasticity. Sci Rep. 2021;11(1):1–15. doi: 10.1038/s41598-021-89198-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren Q, Zhao J. Adaptive coupling and enhanced synchronization in coupled phase oscillators. Phys Rev E. 2007;76(1):016207. doi: 10.1103/PhysRevE.76.016207. [DOI] [PubMed] [Google Scholar]
- Rezaei H, Aertsen A, Kumar A, Valizadeh A. Facilitating the propagation of spiking activity in feedforward networks by including feedback. PLoS Comput Biol. 2020;16(8):e1008033. doi: 10.1371/journal.pcbi.1008033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saa A. Symmetries and synchronization in multilayer random networks. Phys Rev E. 2018;97(4):042304. doi: 10.1103/PhysRevE.97.042304. [DOI] [PubMed] [Google Scholar]
- Sadeghi S, Valizadeh A. Synchronization of delayed coupled neurons in presence of inhomogeneity. J Comput Neurosci. 2014;36(1):55–66. doi: 10.1007/s10827-013-0461-9. [DOI] [PubMed] [Google Scholar]
- Schierwagen A, Claus C. Dendritic morphology and signal delay in superior colliculus neurons. Neurocomputing. 2001;38:343–350. doi: 10.1016/S0925-2312(01)00417-9. [DOI] [Google Scholar]
- Song S, Miller KD, Abbott LF. Competitive hebbian learning through spike-timing-dependent synaptic plasticity. Nat Neurosci. 2000;3(9):919–926. doi: 10.1038/78829. [DOI] [PubMed] [Google Scholar]
- Stoelzel CR, Bereshpolova Y, Alonso J-M, Swadlow HA. Axonal conduction delays, brain state, and corticogeniculate communication. J Neurosci. 2017;37(26):6342–6358. doi: 10.1523/JNEUROSCI.0444-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swadlow HA. Efferent neurons and suspected interneurons in s-1 forelimb representation of the awake rabbit: receptive fields and axonal properties. J Neurophysiol. 1990;63(6):1477–1498. doi: 10.1152/jn.1990.63.6.1477. [DOI] [PubMed] [Google Scholar]
- Ter Wal M, Tiesinga PH. Phase difference between model cortical areas determines level of information transfer. Front Comput Neurosci. 2017;11:6. doi: 10.3389/fncom.2017.00006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang R, Zhang Z, Qu J, Cao J. Phase synchronization motion and neural coding in dynamic transmission of neural information. IEEE Trans Neural Networks. 2011;22(7):1097–1106. doi: 10.1109/TNN.2011.2119377. [DOI] [PubMed] [Google Scholar]
- Wang XJ. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol Rev. 2010;90(3):1195–1268. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang XJ, Buzsáki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J Neurosci. 1996;16(20):6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodman MM, Canavier CC. Effects of conduction delays on the existence and stability of one to one phase locking between two pulse-coupled oscillators. J Comput Neurosci. 2011;31(2):401–418. doi: 10.1007/s10827-011-0315-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie H, Gong Y, Wang Q. Effect of spike-timing-dependent plasticity on coherence resonance and synchronization transitions by time delay in adaptive neuronal networks. Eur Phys J B. 2016;89(7):1–7. doi: 10.1140/epjb/e2016-70282-4. [DOI] [Google Scholar]
- Zhigulin VP, Rabinovich MI, Huerta R, Abarbanel HD. Robustness and enhancement of neural synchronization by activity-dependent coupling. Phys Rev E. 2003;67(2):021901. doi: 10.1103/PhysRevE.67.021901. [DOI] [PubMed] [Google Scholar]
- Ziaeemehr A, Valizadeh A. Frequency-resolved functional connectivity: role of delay and the strength of connections. Front Neural Circuits. 2021;15:608655. doi: 10.3389/fncir.2021.608655. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data generated or analysed during this study are included in this published article.
Not applicable.