Kinetic Understanding of Catalytic Selectivity and Product Distribution of Electrochemical Carbon Dioxide Reduction Reaction

Abstract

CO₂ can be electrochemically reduced to different products depending on the nature of catalysts. In this work, we report comprehensive kinetic studies on catalytic selectivity and product distribution of the CO₂ reduction reaction on various metal surfaces. The influences on reaction kinetics can be clearly analyzed from the variation of reaction driving force (binding energy difference) and reaction resistance (reorganization energy). Moreover, the CO₂RR product distributions are further affected by external factors such as electrode potential and solution pH. A potential-mediated mechanism is found to determine the competing two-electron reduction products of CO₂ that shifts from thermodynamics-controlled product formic acid at less negative electrode potentials to kinetic-controlled product CO at more negative electrode potentials. Based on detailed kinetic simulations, a three-parameter descriptor is applied to identify the catalytic selectivity of CO, formate, hydrocarbons/alcohols, as well as side product H₂. The present kinetic study not only well explains the catalytic selectivity and product distribution of experimental results but also provides a fast way for catalyst screening.

Introduction

Excessive CO₂ emission has brought a series of climate changes and environmental issues, which seriously threaten the ecological balance and human safety, and have attracted great concerns from researchers around the world.¹ The electrochemical or photochemical CO₂ reduction reaction (CO₂RR) enables the conversion of renewable electric energy and solar energy into storable chemical energy. It is one of the most important carbon-negative technologies to meet global environmental requirements and achieve “carbon neutrality”.²⁻⁵ Although great advances in catalytic performance have been achieved, electrocatalytic CO₂RR still faces challenges from catalytic activity and product selectivity that restrict its practical application and technological commercialization.⁶⁻⁸

Since pioneering studies in 1980s,^9,10 massive efforts have been devoted to promote the catalytic performance of electrochemical CO₂RR especially within the past decade.¹¹⁻¹⁷ There has been increasing mechanistic understanding as well as many encouraging experimental progresses on this complicated reaction system. CO₂ can be electrochemically reduced to different products depending on the nature of catalysts. CO, formic acid (FA), hydrocarbons, and side product H₂ are the four main types of CO₂RR products detected. Bagger et al. proposed that the binding energies of COOH* and H* can explain the H₂, CO, or FA products in CO₂ reduction while the binding energies of CO* and H* can be used to predict products beyond CO*.¹⁸ DFT calculations by Feaster et al. demonstrated that COOH* and HCOO* binding energies emerged as descriptors for the volcano trend of CO₂RR to CO and formate among selected metals.¹⁹ Kuhl et al. quantified reaction rates for the electrocatalytic conversion of CO₂ to methane and methanol and described catalyst activity and selectivity in the framework of CO binding energies for different transition metal surfaces.²⁰ Qiao and co-workers classified copper-based bimetallic materials into four groups based on O and H affinities to determine their CO₂RR selectivity trends.²¹

In these studies, simple descriptor systems based mainly on thermodynamic computations are related to catalytic performance in the theoretical framework of linear scaling relations and the volcano model (Sabatier’s principle).^22,23 However, the reaction mechanism estimated by pure thermodynamic computations may be inconsistent with kinetic simulations. Because reaction barriers of competing parallel reactions may exhibit significantly different scaling relations with the corresponding reaction free energies, as shown in Scheme S1. For the initial two-electron CO₂ reduction process, CO and FA share the same reactants but entirely different reaction pathways (intermediates). Seifitokaldani et al. demonstrated that the dominant reduction product on the silver electrode could be altered from CO to formate by modulating transition state kinetics in highly concentrated alkaline solution.²⁴ In addition, the Faradaic efficiencies of CO and FA are found intensively affected by applied potentials.^25,26 The pH and potential-mediated CO/FA selectivity of CO₂RR can be hardly understood by pure thermodynamic computations because the external experimental factors should impose the same influence on the electrochemical potential of electron-proton pairs for competing CO₂ conversion to either CO or FA.

Current density, overpotential, and Faradaic efficiency (FE) are the three most important performance indexes of electrocatalysts. They are intrinsically related to the kinetic properties of catalytic processes since current density (overpotential) reflects the polarization relation and Faradaic efficiency embodies the distribution relation of reaction rates. In order to predict the catalytic activity and selectivity toward a specific product, calculations of the activation energy in various elementary steps are needed to evaluate the potential-dependent reaction rates for direct comparison with electrochemical measurements.²⁷⁻³⁰

The commonly used approach to determine the reaction barrier of the electrode reaction is based on transition state theory (TST) such as the climbing-image nudged elastic band (CI-NEB) method, in which the transition states were obtained by searching the minimum energy path along the single-state potential energy curve of the hydrogen atom transfer reaction.²⁸⁻³³ In order to obtain the potential-dependent electrochemical kinetics, transition state searching at different electrode potentials is required. However, DFT calculations at constant electrode potential are still challenging and computationally expensive.³⁴⁻³⁶ Alternatively, the potential-dependent kinetic behavior can be deduced by combining with the phenomenological Butler–Volmer equation,³¹ in which the symmetry factor β (slope of activation barrier E_a with applied potential U, also known as charge transfer coefficient) is determined from the charge analysis.²⁷⁻²⁹

A new microkinetic model^37,38 based on Marcus charge transfer theory was recently developed to compute the reaction barriers by a “four-point method”,³⁹ in which the transition state was confirmed from the “intersection point” of two potential energy curves with different electronic states, as shown in Scheme S2. It allows the computed reaction barriers to change continuously with the applied potential, leading directly to the current-potential polarization relation. This kinetic model has been successfully applied to study the facet-dependent catalytic activity and product selectivity of CO reduction on copper electrodes.⁴⁰ The predicted potential-mediated behavior of competing COH* and CHO* formations is in well agreement with constant-potential model simulations.³⁰ Under the framework of Marcus charge transfer theory, the influences on reaction barriers can be clearly analyzed from the variation of reaction free energies and reaction reorganization energies.^37,38 Unlike constant charge transfer coefficient assumed in Butler-Volmer kinetics, the symmetry factor obtained under Marcus kinetics is potential-dependent.

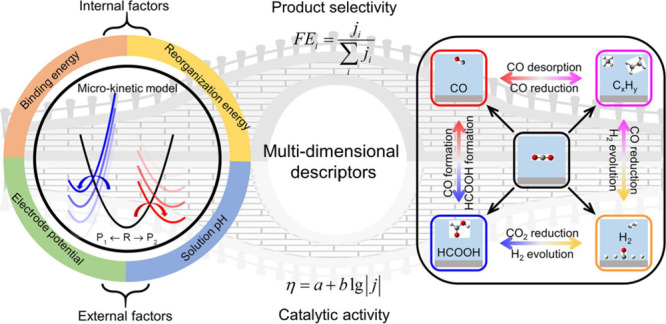
In this work, we report theoretical studies on catalytic selectivity and product distribution of CO₂RR over various metal surfaces by using a combination of density functional theory and electrochemical micro-kinetic model, as shown in Scheme 1. Specifically, the influence of both internal factors (binding energy and reorganization energy) and external factors (electrode potential and solution pH) on the competing CO and FA production is discussed. The competitions of CO₂RR with hydrogen evolution reaction (HER) side reactions are discussed under a unified kinetic model. Finally, a three-parameter descriptor consisting of binding energies of HCOO*, COOH*, and CO* are applied for fast CO₂RR catalyst screening aiming to specific products such as FA, CO, and hydrocarbons/alcohols.

Scheme 1. Schematic Illustration of Micro-Kinetic Model as a Bridge Connecting Electrocatalytic Performance of CO₂ Reduction and Micro Reaction Mechanism.

Computational Details

Electronic structure calculations were performed with the framework of density functional theory (DFT), as implemented by the Vienna ab initio simulation package (VASP).^41,42 The exchange–correlation energies were calculated using the PBE functional⁴³ within the generalized gradient approximation (GGA).⁴⁴ A plane wave basis set with a cutoff energy of 400 eV was used in the representation of the valence electrons and projector augmented wave (PAW)⁴⁵ was used to represent core electrons. The convergence criteria for electronic self-consistent iteration were set to 1.0 × 10^–5 eV, and the ionic relaxation loop was limited for all forces smaller than 0.02 eV/Å for free atoms.

An implicit solvation model with the combined linear Poisson–Boltzmann and polarizable continuum model⁴⁶ was used to describe the solvation effect of adsorbate with VASPsol, which provides systematic corrections of 0.15 eV.^47,48 The relative dielectric constant of water is set to be 78.4. It is found that adding water molecules as the explicit solvent has a slight influence on the computed reaction free energies and reorganization energies (see Tables S1 and S2).

The electrodes are represented by periodically repeated slabs with four layers (3 × 3) surface cells with the bottom two layers fixed combined (4 × 4 × 1) k-point sampling, respectively. For all models, a vacuum layer of 15 Å was used to separate the periodic repeated slabs in the direction perpendicular to the slabs. Adsorption configurations and binding energies of key reaction species are listed in Table S3. In this work, the binding energy is defined as follows:¹⁸

1

where E(A), E(*), and E(A*) represent the electronic energy of the free adsorbate, metal substrate, and adsorbed A on the metal surface. Thus, more negative values of binding energies mean stronger adsorption interactions.

Gibbs free energies were calculated from DFT total energy corrected by zero–point energy (ZPE), heat capacity (C_p), and entropy (TS). The standard ideal gas method was employed to compute E_ZPE, ∫C_pdT, and TS from temperature (298.15 K) and pressure (1 atm), and vibrational energies by using the VASPKIT code.⁴⁹

2

The reaction barriers of electrochemical proton–electron transfer reactions are calculated by a “four-point method”,³⁹ in which the shape of quadradic function potential energy curves of the reactant and product is determined by the reorganization energy (λ_R and λ_P) and the energy difference between two potential energy curve minimums is determined by the reaction free energy (ΔG). The transition state was confirmed from the “intersection point” of two potential energy curves with different electronic and protonic states.^37,38 A comparison of reaction barriers calculated by Marcus kinetics and transition state theory method can be found in Tables S4 and S5.

3

As presented in eq 3, the computed reaction barriers generally decrease with the negative movement of ΔG and increase with the increase of λ_R and λ_P. Thus, ΔG is viewed as the “reaction driving force” and λ_R and λ_P are viewed as the “reaction resistance”. Heterogenous charge transfer rate constants under adiabatic transition state assumption^33,35 are calculated by Marcus-Gerischer theory,^50,51 which accounts for the sum of the partial electron transition probabilities between the redox level at energy ε_r and the electron states with energy ε_k in the electrode. The energy difference between ε_r and the electron states with energy ε_k at the Fermi level is assumed to be the reaction free energy ΔG. The integration over all energy states ε in the electrode provides the total rate constant,

4

where f(ε) is the Fermi–Dirac distribution and ρ(ε) is the density of states in the electrode that can be obtained from electronic structure computations. More details of the microkinetic model can be found in the Supporting Information.

Results and Discussion

Influence of Internal Factors on the Electrochemical Performance of CO₂RR

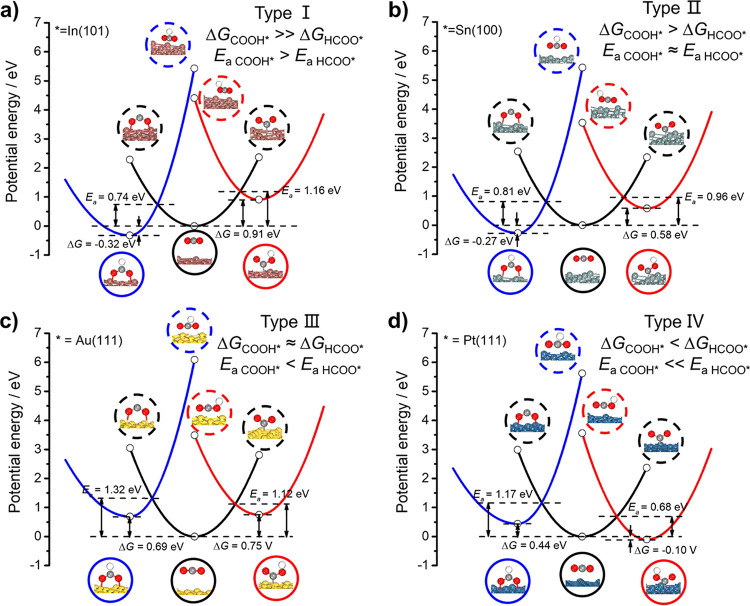
CO and FA are competing products of the two-electron process of CO₂RR. The widely accepted reaction mechanism includes the production of CO through a unidentate COOH* intermediate with C-end adsorption and FA through a bidentate HCOO* intermediate with O-end adsorption. As shown in Figure 1, CO₂ is physisorbed on metal surfaces with a distance of about 3.5 Å. The C–H (O–H) hydrogenation of CO₂* via a proton-coupled electron transfer process leads to HCOO* (COOH*). The calculated reaction barriers of competing COOH* and HCOO* formations are strongly influenced by both the reaction driving force (−ΔG, listed in Table S6) and the reaction resistance (λ_R and λ_P, listed in Table S7). In general, the reorganization energies of COOH* productions are smaller than those of HCOO* formations due to smaller nuclear configuration changes. The reaction free energies of ΔG_COOH* and ΔG_HCOO*, however, are quite sensitive to the nature of metal catalysts.

Figure 1.

Influence of binding energies and reorganization energies on the reaction activation barriers of competing COOH* and HCOO* formations on (a) In(101), (b) Sn(100), (c) Au(111), and (d) Pt(111) surfaces at U = 0 V vs SHE. The structures in the lower solid circles show stable configurations located at the potential energy curve minimum. The structures in the upper dashed circles show the adjusted configurations the same as lower solid circles after solvent reorganization.

The investigated model metal catalysts can be categorized into four types according to the formation free energies and activation free energies for the production of COOH* and HCOO* intermediates. For type I catalysts including In, Tl, and Pb, the binding energy of bidentate HCOO* with O-end adsorption is much larger than that of unidentate COOH* with C-end adsorption, resulting in ΔG_COOH* much higher than ΔG_HCOO*. The driving force to produce HCOO* is great enough to overcome the larger reaction resistance of C–H hydrogenation. As shown in Figure 1a, the reaction free energy of HCOO* formation on the In(101) surface is 1.23 eV more negative than that of COOH* formation and the activation energy of HCOO* pathway is 0.42 eV lower than that of the COOH* pathway. It is in agreement with FA as the main product on In,^52,53 Tl,^9,10 and Pb.^54,55

For type II catalysts such as Sn, Zn, and Cd, the thermodynamics-controlled (larger −ΔG) HCOO* pathway competes with the kinetics-controlled (smaller λ) COOH* pathway, leading to quite similar reaction activation barriers. As shown in Figure 1b, ΔG_HCOO* on the Sn(100) surface is 0.85 eV lower than ΔG_COOH*. However, the activation energy of the HCOO* pathway is only 0.15 eV lower than that of the COOH* pathway. The calculated results satisfactorily account for both CO and FA being produced on Zn, Cd, and Sn in experiments.^9,10,26

As for type III catalysts Au and Cu, the driving forces to produce HCOO* and COOH* intermediates are quite close. Thus, the reorganization energy becomes the key factor in determining reaction kinetics and therefore reaction pathways. As shown in Figure 1c, ΔG_HCOO* on the Au(111) surface is 0.06 eV slightly smaller than ΔG_COOH*. Nevertheless, the activation energy of the COOH* pathway is 0.20 eV lower than that of the HCOO* pathway on the contrary. Under such circumstances, the reaction pathway predicted from the activation free energy is just opposite to the reaction pathway predicted from reaction free energy.

D-block transition metals Ni, Pd, and Pt can be classified into type IV catalysts, on which the binding energy of C-end bonded COOH* strongly enhances, approaching or even surpassing O-end bonded HCOO*. As a result, ΔG_COOH* is smaller than ΔG_HCOO* and the activation energy to produce COOH* is much lower than HCOO*. As shown in Figure 1d, the activation energy of the COOH* pathway on the Pt(111) surface is 0.65 eV lower than that of the HCOO* pathway. It is illustrated in Figure 1 that thermodynamic calculations of reaction free energies are not adequate to estimate the competing COOH* and HCOO* formation pathways because the activation barriers of these two reactions show significantly different BEP relations with the corresponding ΔG, as shown in Figure S1. The reaction barriers of both COOH* and HCOO* formations decrease with the increase of reaction driving force (−ΔG) with similar scaling relations between E_a and ΔG. However, the reaction barriers of COOH* formations are about 0.3 eV lower than that of HCOO* formations for the same ΔG value. The uncertainty of calculated reaction barriers caused by a simple approximation of the present kinetic model should not change the basic judgment that HCOO* formation is thermodynamics-controlled while COOH* formation is kinetics-controlled.

Figure 2 shows the potential energy curves of two-electron reduction of CO₂ to CO or FA on four representative metal surfaces at U = 0 V vs SHE, which includes the initial adsorption of CO₂ on the metal surface, two successive proton-coupled electron transfer steps, and desorption of CO or FA. The potential energy curves of CO₂RR on the other metal surfaces are presented in Figure S2.

R1a

R1b

R2a

R2b

Figure 2.

Potential energy curves of two-electron reduction of CO₂ on (a) In(101), (b) Sn(100), (c) Au(111), and (d) Pt(111) surfaces at U = 0 V vs SHE.

Here, the reaction pathway of FA production through the COOH* intermediate reported elsewhere^56,57 is not considered since the C–H hydrogenation of COOH* to produce FA requires much larger reorganization energy than O–H hydrogenation to produce CO and water. In view of reaction activation barriers, the most possible reaction pathway evolves as the change of relative binding energies of critical intermediates COOH* and HCOO*. On type I catalysts such as In (Figure 2a),^52,53 Tl,^9,10 and Pb,^54,55 CO₂ reduction occurs via the thermodynamic-controlled HCOO* to produce FA, which is weakly adsorbed on metal surfaces. Thus, ultrahigh conversion efficiency of FA could be achieved on these main group metal-based materials.⁵⁸

Conversely, CO generation through COOH* is kinetically more favorable on the type III Au surface, as shown in Figure 2c. In addition, the desorption of CO from Au surfaces is thermodynamically spontaneous, which makes Au one of the most widely studied noble metal catalysts for CO production with high selectivity.^11,59,60Figure 2b shows the patterns of CO₂RR potential energy curves on type II catalysts such as Sn lie somewhere between type I and type III catalysts, where FA and CO are competing products through the thermodynamics-controlled HCOO* pathway and the kinetics-controlled COOH* pathway, respectively.²⁶

As for type IV catalysts, the dominant reaction pathway for CO₂RR on Pt (Figure 2d), Ni, Pd, Rh, and Ir is CO* formation. Although CO can be produced at relatively low onset potentials on transition metals,²⁰ desorption of CO from these metal surfaces is quite difficult, resulting catalyst poisoning by adsorbed CO*. These metals favor the competing process of H₂ generation due to their low overpotentials for H⁺ reduction.^9,10 It is noticed that the Faradaic efficiency of CO catalyzed by Pd electrode can reach up to 28.3%,¹⁰ which appears to be conflicted with the strong binding energy of CO* on Pd(111) surface (−2.14 eV). In situ X-ray absorption spectroscopy studies confirmed the phase transition from Pd to Pd–H under electrochemical reduction conditions.⁶¹ DFT calculations showed that the reduced binding energies of CO and COOH intermediates on Pd–H surface are key parameters to the high current density and Faradaic efficiency for CO₂ to CO conversion.^61,62

Influence of External Factors on the Electrocatalytic Performance of CO₂RR

According to the above discussions, the binding energies and reorganization energies of HCOO* and COOH* intermediates play important role in product selectivity. The difference in binding energies and reorganization energies of HCOO* and COOH* on various metal surfaces are mainly determined by the inherent nature of catalysts. They are defined as internal factors that influence the reaction kinetics. On top of that, the electrochemical reaction kinetics can be effectively regulated by external factors such as electrode potential and solution pH by adjusting the electrochemical potential of electrons and chemical potential of protons.

A significant difference between electrocatalysis and classical heterogeneous catalysis is that both the reaction thermodynamics (reaction free energy) and reaction kinetics (activation free energy) of an electrochemical reaction can be easily regulated by the applied potentials. Figure 3 shows how the reaction pathways of electrochemical CO₂RR are mediated by the applied electrode potentials. In general, the formation free energies of HCOO* are lower than those of COOH* except for type IV transition metals. At lower potentials (more positive potentials such as U₁ and U₂), CO₂ reduction favors HCOO* pathway due to larger −ΔG. However, the reorganization energies for COOH* formation are normally smaller than those for HCOO* formation. Therefore, the activation barrier of COOH* formation decreases more quickly with the negative movement of electrode potential than HCOO* formation. At higher potentials (more negative potentials such as U₃ and U₄), CO₂ reduction inclines to the COOH* pathway due to smaller λ. It is illustrated in Figure 3 that increasing reaction driving force is beneficial for improving the selectivity of kinetics-controlled product CO.³⁸

Figure 3.

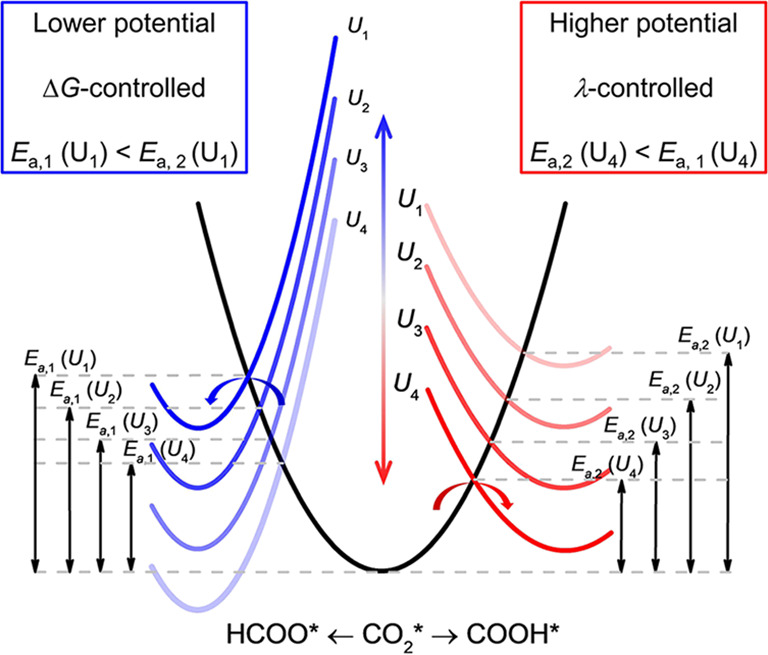
Electrode potential-mediated reaction pathways of electrochemical CO₂RR. At lower potential, FA is the main product through a ΔG-controlled HCOO* pathway (blue lines). At higher potential, CO is the main product through a λ–controlled COOH* (red lines) pathway.

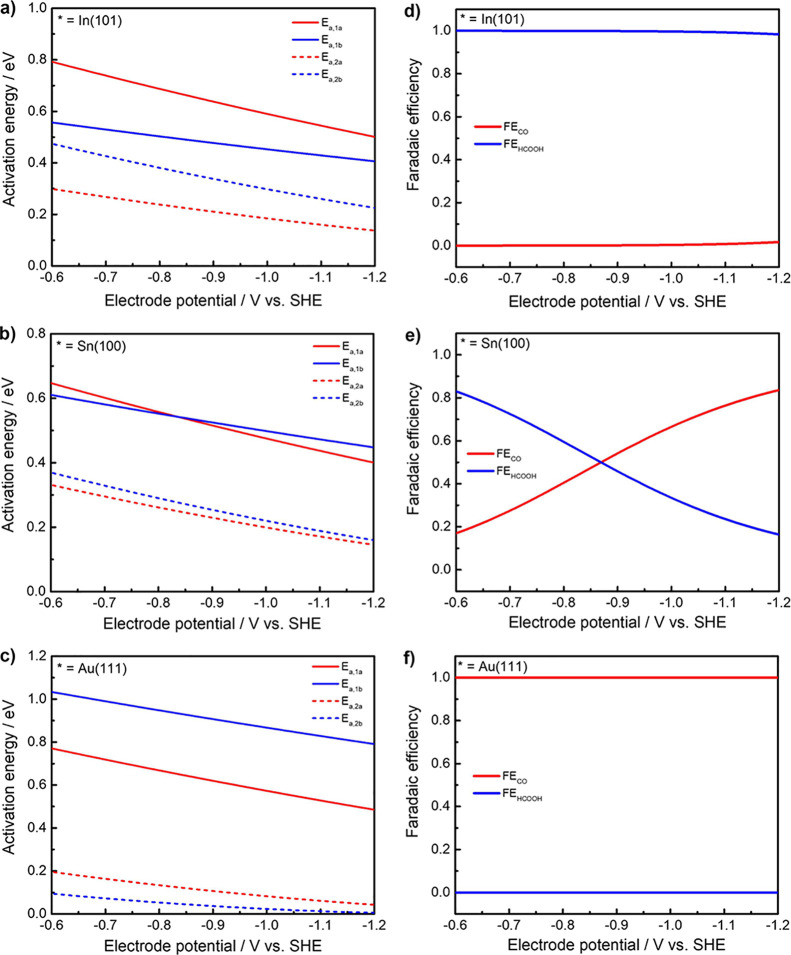
Specifically, Figure 4 presents the potential-dependent reaction activation barriers and Faradaic efficiencies of CO₂RR on In(001), Sn(100), and Au(111) surfaces within the potential range from −0.6 to −1.2 V vs SHE. See Figure S3 for the other metal surfaces.

Figure 4.

Potential-dependent reaction activation barriers of elementary steps of CO₂RR on (a) In(101), (b) Sn(100), and (c) Au(111) surfaces. Potential-dependent Faradaic efficiencies of CO and FA formations on (d) In(101), (e) Sn(100), and (f) Au(111) surfaces.

As seen from the calculated potential-dependent rate constants presented in Figure S4, the rate-determining step (RDS) for CO and FA formation is the first electron transfer step reactions R1a or R1a. The Faradaic efficiencies of CO and FA are defined as follows:

5

6

For type I catalysts such as In, the computed activation energies of reaction R1b (the RDS for FA production) are consistently lower than those of reaction R1a (the RDS for CO production) within the chosen potential range, as shown in Figure 4a. Although the energy difference between E_a,R1a and E_a,R1b gradually decreases from 0.22 eV at U = −0.6 V to 0.09 eV at U = −1.2 V, the product distribution is still dominated by FA, as shown in Figure 4d.

The situation for type III catalysts such as Au is just opposite to type I catalysts. As shown in Figure 4c,f, the computed activation energy of reaction R1a is consistently lower than that of reaction R1b and the Faradaic efficiency of CO remains nearly 100% from U = −0.6 V to U = −1.2 V. The predicted Faradaic efficiencies of CO₂RR on Tl and Au surfaces are in good agreement with experimental results by Hori et al.^9,10

It is found that the symmetry factor β of reaction R1a is always larger than that of reaction R1b. Thus, the ratio of k_R1a to k_R1b increases with the decrease of the electrode potential. The fitted activation barriers and symmetry factors as a function of electrode potential U are listed in Table S8. Under the displaced harmonic oscillator model of Marcus theory, the symmetry factor β varies around 0.5 as a function of ΔG and λ.

7

8

By using the RDS approximation, the apparent charge transfer coefficient and Tafel slope can be derived from the symmetry factor of RDS. The fitted β for FA and CO formation on the Sn(100) surface are 0.30 and 0.47, respectively. After converting the symmetry factors to the Tafel slopes, they are about 196 mV dec^–1 for FA formation and 126 mV dec^–1 for CO formation. Experimentally, the measured Tafel slope is 176 mV dec^–1 for FA production on bulk Sn and Sn nanoparticles.^63,64 The reported Tafel slopes for CO₂ to CO conversion on three Sn-modified N-doped porous carbon nanofiber electrodes fall in a range from 79 to 134 mV dec^–1.⁶⁵ Lee et al. illustrated the Tafel slope of CO formation (99 mV dec^–1) was smaller than that of FA formation (163 mV dec^–1) on the same carbon-supported Sn catalyst.²⁵

It seems that the product selectivity is not seriously affected by the applied potential for type I and type III catalysts. However, the product distribution can be effectively mediated by electrode potential for type II catalysts, as shown in Figure 4e. As the negative movement of electrode potential, the main product of CO₂RR on the Sn(100) surface changes from FA to CO. At a lower potential of U = −0.6 V, the activation energy for HCOO* formation is 0.04 eV smaller than that for COOH* formation. Instead, the activation energy for HCOO* formation is 0.05 eV larger than that for COOH* formation at a higher potential of U = −1.2 V. The proposed potential-mediated catalytic selectivity of CO₂RR on the Sn(100) surface is supported by competing the parallel reduction of CO₂ to both CO and FA in experiments.⁶⁶ The decrease of FE_FA/FE_CO from −0.82 to −1.02 V vs NHE was observed by Ito and coworkers in the study of CO₂RR performance on the reduced-graphene-oxide-supported Sn catalyst.²⁶ Similarly, Lee et al. observed FE_CO (from 14.23 to 48.36) increases much faster than FE_FA (from 1.72 to 6.90) for CO₂RR on carbon-supported Sn catalysts in the potential range from −0.46 to −0.84 V vs RHE.²⁵ Dai and coworkers reported that the formate FEs at a small current density (low overpotential) were higher than those at large current density (high overpotential) for CO₂RR on a Cu-based catalyst.⁶⁷

The potential-mediated catalytic selectivity mechanism is also found for Ag, Zn, Cd, and Cu (Figure S5). Specially, the potential-dependent product distribution on the Cu electrode in the experiment can be understood by our kinetic model.^68,69 It was found that the current efficiency of formate decreases from 0.25 to nearly 0 while the selectivity of CO-beyond products (mainly CH₄) increase from 0.01 to 0.51 as the electrode potential shifts from −0.89 V to −1.17 V vs RHE. Since FA cannot be further reduced to other products as a result of its weak binding strength on catalysts, the mechanistic pathway to produce various hydrocarbons must go through CO*. The potential-dependent experimental results match well with the proposed transformation of CO₂RR selectivity from thermodynamics-controlled FA to kinetics-controlled CO* with the increase of overpotential.

Table 1 compares the simulated FEs of CO and FA on various metal surfaces (U = −0.8 to −1.2 V vs SHE) with experimental results from Hori et al.^9,10 The computational results well explain the large gap between lower-limit and upper-limit FE measured on the Zn electrode. Although FA is believed to be the main product of CO₂RR on the Sn electrode,⁶⁶ the increase of CO selectivity with the negative movement of the electrode potential was also reported elsewhere.^25,26 It is worth noting that the calculated FE_CO on Ag single crystal facets, particularly under low reduction potential, are obviously lower than the experimental value measured on the Ag electrode or nanostructures, which were considered as one of the best catalysts to reduce CO₂ to CO.^11,70,71 Borha et al. attributed the discrepancy between the theoretical simulation and experimental performance of Ag catalysts to the lateral adsorbate interactions that inhibit FA production and promote CO selectivity.⁷² Zhang et al. explained the unfavorable FA formation on Ag electrodes as the low barrier of the reverse reaction of HCOO* dehydrogenation and the high barrier of the forward reaction of HCOO* hydrogenation.⁷³ Seifitokaldani et al. proposed that the favored CO₂RR pathway on Ag surfaces can be manipulated by the reaction environment. The product selectivity switched from entirely CO under neutral conditions to over 50% formate in the alkaline environment.²⁴ It is noticed that the calculated product distribution on the Sn(100) surface at lower overpotentials such as U = −0.6 V (FE_CO = 23.5%, FE_FA = 76.5%) and product distribution on Ag(111) surface at higher overpotentials such as U = −1.4 V (FE_CO = 85.5%, FE_FA = 14.5%) match quite well with experimental values.^9,10 The discrepancy between the theoretical simulation and experimental results for Sn and Ag electrodes may arise from a gap between the applied potential in the experiment and the potential used in calculations.

Table 1. Comparison of Computed Faradaic Efficiency of CO and FA on Various Metal Surfaces at the U = −0.8 to −1.2 V vs SHE with Experimental Results.

surfaces	COcal.	COexp.	FAcal.	FAexp.
Au(111)	100	81.2–93.0a	0	0.4–1.0a
Ag(111)	4.6–48.2	61.4–89.9a	51.8–95.4	1.6–4.6a
Zn(001)	2.6–29.8	3.3–63.3a	70.2–97.4	17.6–85.0a
Cd(001)	0.6–9.1	6.2–11.1a	90.9–99.4	65.3–67.2a
Sn(100)	40.5–83.6	7.1b	16.4–59.5	88.4b
Pb(111)	0.5–11.3	0.3–0.6a	88.7–99.5	72.5–88.8a
In(101)	0.1–1.7	0.9–2.2a	98.3–99.9	92.7–97.6a
Tl(111)	0–0.3	0b	99.7–100	95.1b

^aData from ref (9).

^bData from ref (10).

As discussed above, the selectivities of CO₂ reduction to CO or FA are influenced by various factors, both internal and external. Thus, multi-dimensional descriptors are needed to estimate whether CO₂ is reduced to CO or FA or both on different metal surfaces and with different electrode potentials. Figure 5 compares CO/FA selectivity predicted by traditional thermodynamic calculations and our kinetic simulations. Figure 5a shows the calculated limiting potential (defined as the most negative potential required to drive all the elementary reactions being spontaneous) difference of CO and FA formations on various metal surfaces. Obviously, pure thermodynamic calculations cannot match well with experimental results,^9,10 especially for Au and Cu.

Figure 5.

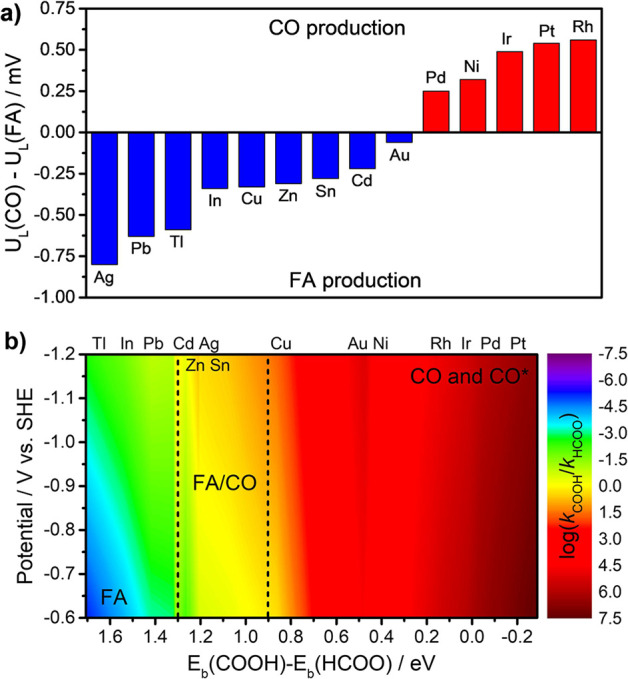
Comparison of product selectivity for two-electron reduction of CO₂ by thermodynamic calculations and kinetic simulations. (a) Limiting potential differences for CO and FA formations on different metal surfaces. (b) Contour graphs of log(k_COOH/k_HCOO) as a function of binding energies difference of intermediates and applied electrode potentials.

Figure 5b shows that the relative activity of log(k_RDS(CO)/k_RDS(FA)) varies as a function of binding energies difference ΔE_b of HCOO* and COOH* (internal factors) and applied potentials U (external factors). The catalytic selectivities of competing CO and FA formations are illustrated with rainbow gradient color (violet for FA and red for CO). In general, type III and IV catalysts with ΔE_b smaller than 0.9 eV exhibit high selectivity to produce CO or CO*. On the contrary, type I catalysts such as In, Tl, and Pb with ΔE_b larger than 1.3 eV perform high selectivity to produce FA.⁷⁴ While type II catalysts Sn,^66,75 Zn,⁹ Cd,¹⁰ and Ag^24,72 can reduce CO₂ to both CO and FA. It is demonstrated in Figure 5b that the electrocatalytic selectivity and activity of CO₂ conversion to CO and FA on arbitrary catalysts can be predicted theoretically by using multi-dimensional descriptors including E_b(COOH*), E_b(HCOO*), and electrode potential.

Competition between CO₂RR and HER

Figure 6 presents an overview of mechanistic proposals and product selectivity of CO₂RR on different metal catalysts. There are two critical T-junction branches involved in the CO₂ reduction, leading to different reaction pathways and products.^2,3,76 The first T-junction branches include the competing CO₂ reduction to FA through the ΔG-controlled HCOO* pathway and CO* through the λ-controlled COOH* pathway, as well as the hydrogen evolution side reaction. The adsorbed CO* is the key species for the second T-junction branches: (1) CO* desorption; (2) CO* activation (reduction); and (3) CO poisoning depending on the binding strength of CO* on catalyst surfaces.⁷⁷

Figure 6.

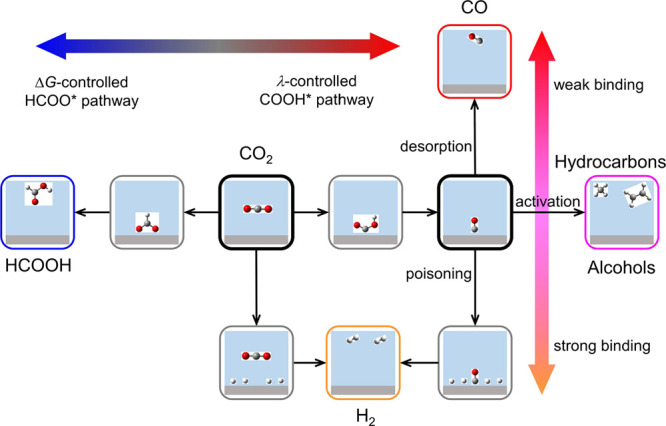
General reaction mechanism and pathways of electrochemical CO₂ reduction.

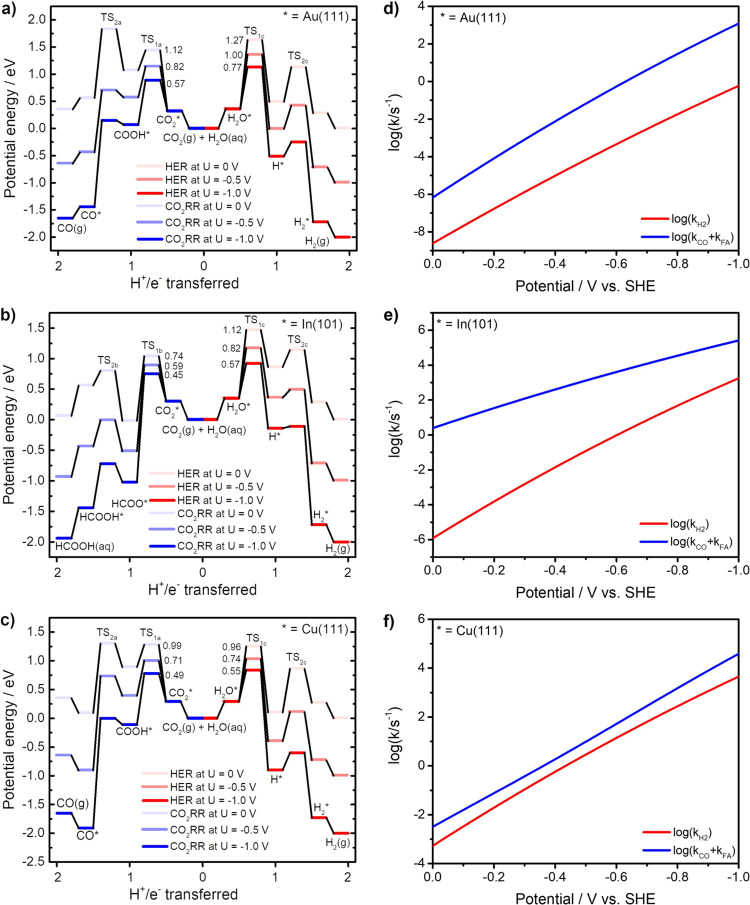
Experimental results indicate the selective reduction of CO₂ to CO on the Au electrode or FA on In electrode almost unaffected by HER. However, it becomes a serious side reaction during CO₂RR on Cu electrodes.^9,10Figure 7 compares the reaction kinetics of two-electron transfer CO₂RR and HER (the left T-junction shown in Figure 6) on representative Au(111), In(101), and Cu(111) surfaces. The competition between hydrogen evolution and CO₂ reduction was studied by a unified kinetic model, in which the electron and proton acceptors are adsorbed H₂O and CO₂, respectively. It was illustrated by Koper and co-workers that the HER proceeds primarily via water reduction under CO₂ reduction conditions, even in a relatively acidic electrolyte.⁷⁸ The potential-dependent reaction barriers of the Volmer reaction (R1c) and the Heyrovsky reaction (R2c) are presented in Figure S6. As seen in Figure 7a,b, the computed reaction barriers of CO production on Au and FA generation on In are always lower than those of the competing HER. In addition, the activation energy difference between reactions R1a and reactions R1c on the Au(111) surface increases from 0.15 eV at U = 0 V to 0.20 eV at U = −1 V. Conversely, the reaction barrier difference between reactions R1b and reactions R2c on the In(101) surface decreases from 0.38 eV at U = 0 V to 0.12 eV at U = −1 V. The main reason to cause their different potential-dependent kinetic behaviors is that the reorganization energy of H* formation falls between COOH* formation and HCOO* formation, as listed in Table S10. The potential-dependent kinetic simulations presented in Figure 7d,e suggest that more negative electrode potential is beneficial to CO production⁶⁰ while more positive electrode potential will help improve FA selectivity⁵³ by suppressing HER.

Figure 7.

Potential-dependent potential energy curves of competing two-electron reduction of CO₂RR and HER on (a) Au(111), (b) In(101), and (c) Cu(111) surfaces. Reaction rates of CO₂RR and HER as a function of applied potential on (d) Au(111), (e) In(101), and (f) Cu(111) surfaces.

R1c

R2c

The intensive influence of HER on CO₂RR on Cu electrodes can be understood from kinetics studies shown in Figure 7c,f. As seen, the formation free energy of COOH* is 0.67 eV more positive than H* formation. The computed reaction barrier of reaction R1a (0.99 eV) is slightly larger than that of reaction R1c (0.92 eV) at U = 0 V. As the electrode potential moves to U = −1.0 V, the reaction barrier of reaction R1c (0.53 eV) exceeds reaction R1a (0.49 eV) due to larger reorganization energies. Figure 7f demonstrates that the rate constants of HER and CO₂RR are quite close, which explains that the HER side reaction is unavoidable on Cu electrodes.^11,14 Similar to the situation on Au, the HER on the Cu electrode is expected to be suppressed at a more negative electrode potential, which is supported by the decrease of the hydrogen production efficiency with the increase of overpotential during CO₂RR in experiments.^68,69

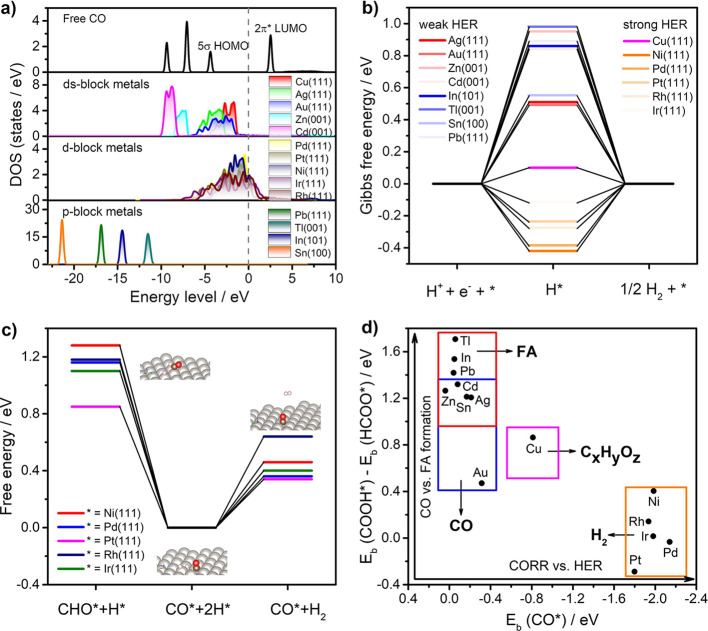
Figure 8 further illustrates competitions between HER and CO₂RR beyond CO (the right T-junction shown in Figure 6). To figure out the binding energy difference of CO on various metal surfaces, the density of states (DOS) analysis of adsorbed and free CO is shown in Figure 8a. The interaction of the CO adsorbate with the metal substrate can be understood as σ-donating of the carbon lone pair (5σ ΗΟΜΟ) to the empty orbital of metal atoms and π-feedback of the metal d orbital to the CO antibonding orbital (2π* LUMO).⁷⁹ Because the LUMO level of CO is closer to the Fermi level than the HOMO level, the d−π interaction should make major contribution to the M-CO interaction.⁸⁰ As seen from Figure 8a, the distributions of the d-orbital above the Fermi level are very slight for most ds-block and p-block metals. In contrast, the apparent overlap of the d-orbital of transition metals with the LUMO of CO molecules can be observed above the Fermi level, resulting in strong CO binding energy.

Figure 8.

(a) Density of states of the analysis of CO adsorption on various metal surfaces. (b) Free energy diagram of HER occurred on various metal surfaces calculated by the RPBE functional. (c) Free energy diagrams of competing CO hydrogenation in the Langmuir–Hinshelwood mechanism and HER in the Tafel mechanism on various transition metal surfaces. The insets are adsorption configures of reaction species on the Pt(111) surface. (d) Product distribution of CO₂RR characterized by three-parameter descriptors including the binding energies of CO*, COOH*, and HCOO*.

The Gibbs free energies for the HER on various metal surfaces are presented in Figure 8b. For p-block metals and ds-block metals except for Cu, the formation energies of H* are quite large (>0.5 eV), leading to low HER activity on these surfaces.⁸¹ Detailed kinetic simulations shown in Figure 7 demonstrate that the influence of HER on CO₂RR on typical Au and In surfaces is very weak. On the other hand, d-block transition metals and Cu exhibit nearly thermoneutral (|Δ_adG_H| smaller than 0.4 eV) hydrogen adsorption energy, indicating that strong HER activity can be achieved. Copper was considered as the only pure element metal to catalyze CO₂ reduction to various hydrocarbons and alcohols.⁶⁸ However, the catalytic selectivity of Cu-based catalysts is suppressed by the strong HER side reaction.

Figure 8c further compares the energy diagrams for the competing CO hydrogenation reaction (CO* + H* → CHO*) via the Langmuir–Hinshelwood mechanism and the associated desorption of adsorbed hydrogen (2H* → H₂) via the Tafel mechanism on five transition metal surfaces. The adsorption configurations of the reaction species on Pt(111) are shown as insets. It is shown that CO hydrogenation takes place in a much more difficult manner than hydrogen evolution. The computed free energy changes of CO hydrogenations are 0.5–0.8 eV higher than that of hydrogen evolutions. This is in line with the fact that CO poisoning occurs on these metal surfaces and H₂ becomes the main product during CO₂RR.^9,10 The excessively high binding energy of CO hinders its further reduction to hydrocarbons and alcohols unless ultrahigh overpotential is applied.²⁰

Figure 8d demonstrates that the product distribution of CO₂RR on different catalysts can be characterized by a three-parameter descriptor including E_b(COOH*), E_b(HCOO*), and E_b(CO*). It should be noticed that the kinetic factors such as reorganization energies have already been included. As discussed in Figure 5, the binding energy difference ΔE_b between COOH* and HCOO* as the vertical coordinate can be used to estimate the catalytic selectivity of CO/FA production. The dominated two-electron reduction product of CO₂RR gradually varies from FA to CO with the decrease of ΔE_b between COOH* and HCOO*. Specifically, type III catalysts including Cd, Zn, Sn, and Ag with moderate ΔE_b fall into the overlapping region, where both CO and FA can be produced during CO₂RR and their selectivity is sensitive to the applied potential.

The binding energy of CO* as the horizontal coordinate can be applied to evaluate reaction pathways beyond adsorbed CO. It is found that the binding energies of CO* show an almost linear relation with the binding energies of H*. As seen in Figure S7, the studied metal catalysts are divided into three regions. P-block metals and Ds-block metals except Cu fall into the CO desorption region, where the HER activity is also very weak due to weak H* binding energy. Transition metals fall into the CO poisoning region, where CO hydrogenations take place extremely nonspontaneously while HER shows high activity. Remarkably, Cu is located at a unique region, which is separated from all the other metals due to simultaneously advanced CO selection over FA and appropriate CO binding strength for further reduction. Only if CO rather than FA is selectively produced during the initial two-electron reduction process and the binding strength of CO is neither too weak nor too strong could it be further reduced to hydrocarbons and alcohols. However, the catalytic selectivity toward hydrocarbons on Cu electrodes is seriously suffered by the HER side reaction.^68,69 Such an inherent drawback of Cu as CO₂RR catalysts can be addressed by electronic structure tuning strategies such as facet engineering,⁸² interface modulation,⁸³ as well as alloying with HER inert guest metals.⁸⁴

Conclusions

In summary, the catalytic selectivity and product distribution of CO₂RR over various model metal single crystal surfaces are investigated by our newly developed micro-kinetic model, which gives a clear illustration of how the electrocatalytic kinetics is influenced by intrinsic binding energy and reorganization energy as well as external applied potentials. This approach acts as a bridge to connect the calculated potential-dependent reaction rates with experimental measured current density, Tafel slope, and Faradaic efficiency. For the competing two-electron reduction of CO₂ to CO and FA, the metal catalysts are classified into four groups according to the reaction free energy and the activation free energy of COOH* and HCOO* formations. The product distribution gradually varies from FA dominated on type I catalysts, then to mixed FA and CO on type II catalysts, and finally to CO dominated on type III and type IV catalysts with the change of the binding energy difference of COOH* and HCOO*. The product distribution can be further affected by the applied electrode potentials. Higher (more negative) electrode potentials are beneficial to produce kinetics-controlled product CO* while lower (more positive) electrode potentials favor the generation of thermodynamics-controlled product FA. Among all the metal catalysts, Cu exhibits unique catalytic selectivity to produce a deeply reduced product due to simultaneously advanced CO selection over FA and moderate CO binding strength for further reduction. It is found that only if CO instead of FA is selectively produced on catalysts and the binding strength of CO is neither too weak nor too strong could it be further reduced to hydrocarbons and alcohols. This work provides a research paradigm for predicting the product selectivity and catalytic activity of electrochemical CO₂RR based on microkinetic computations. The proposed multi-dimensional descriptors could be applied for fast screening catalysts aiming at specific products such as FA, CO, and hydrocarbons/alcohols.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.3c00002.

• Details of the microkinetic model used in this work; adsorption configurations of key intermediates; reaction thermodynamics versus kinetics; simulated potential energy curves, activation barriers, and Faradaic efficiencies; and kinetic data of the HER (PDF)

Author Contributions

D.-J.S. and S.-Q.X. contributed equally to this work. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.