Abstract
Modern semiempirical electronic structure methods have considerable promise in drug discovery as universal “force fields” that can reliably model biological and drug-like molecules, including alternative tautomers and protonation states. Herein, we compare the performance of several neglect of diatomic differential overlap-based semiempirical (MNDO/d, AM1, PM6, PM6-D3H4X, PM7, and ODM2), density-functional tight-binding based (DFTB3, DFTB/ChIMES, GFN1-xTB, and GFN2-xTB) models with pure machine learning potentials (ANI-1x and ANI-2x) and hybrid quantum mechanical/machine learning potentials (AIQM1 and QDπ) for a wide range of data computed at a consistent ωB97X/6-31G* level of theory (as in the ANI-1x database). This data includes conformational energies, intermolecular interactions, tautomers, and protonation states. Additional comparisons are made to a set of natural and synthetic nucleic acids from the artificially expanded genetic information system that has important implications for the design of new biotechnology and therapeutics. Finally, we examine the acid/base chemistry relevant for RNA cleavage reactions catalyzed by small nucleolytic ribozymes, DNAzymes, and ribonucleases. Overall, the hybrid quantum mechanical/machine learning potentials appear to be the most robust for these datasets, and the recently developed QDπ model performs exceptionally well, having especially high accuracy for tautomers and protonation states relevant to drug discovery.
I. INTRODUCTION
Alchemical free energy (AFE) simulations1 are widely used for the prediction of ligand–protein binding energies in drug discovery. These predictions are used to prioritize compounds for costly synthesis and testing in the lead optimization cycle.2 The predictive capability of these methods relies critically on the accuracy of the force fields that are used.3 For well-studied biological systems such as proteins4–6 and common solvents such as water7–11 and monovalent ions,12–15 several molecular mechanical (MM) force fields16,17 have been developed and have undergone extensive validation and revision based on comparison with a wide range of experiments. These force fields have evolved to become increasingly robust and reliable in long-time molecular dynamics simulations, despite the simplicity of their functional forms. On the other hand, the “general” molecular mechanical force fields needed to model drug-like molecules that may not have ever been synthesized before are generally much less reliable. Moreover, conventional MM force fields are not “universal” in the sense that they use a pre-defined covalent bonding topology and are thus limited in their ability to model alternative tautomers and protonation states. This is important as 30% of the compounds in vendor databases and 21% of the compounds in drug databases have potential tautomers;18,19 furthermore, it has been estimated that up to 95% of drug molecules contain ionizable groups18 (∼75% weak bases and ∼20% weak acids20,21).
Modern semiempirical quantum mechanical (QM) electronic structure methods22,23 provide an attractive alternative to the general MM force fields for drug discovery. The reason is that, unlike a typical protein that may contain several thousands of atoms, ∼79% of drugs are between 10 and 40 non-hydrogen atoms, and the vast majority are less than 100 non-hydrogen atoms.24 This is of the size range where semiempirical QM methods are able to be used in combined quantum mechanical/molecular mechanical (QM/MM) simulations that include explicit MM representations of the entire protein and surrounding solvent bath under periodic boundary conditions.25–28 Highly efficient [including parallel and graphics processing unit (GPU)-accelerated] implementations of semiempirical molecular orbital29 and density-functional tight-binding30 have been made and are available for molecular dynamics simulations. More importantly, in the context of AFE simulations, these QM/MM potentials can be efficiently integrated into thermodynamic cycles using indirect (or sometimes referred to as “book-ending” or “reference potential”) approaches31–35 that apply an end-state MM → QM free energy correction to a high-precision MM AFE simulation.
One potential caveat is the high level of accuracy required by drug discovery applications that seek to distinguish binding free energies at a resolution below kBT (0.59 kcal/mol at 300 K).36–38 This is extremely challenging for even the most advanced modern semiempirical QM methods. One path forward that appears promising is to use machine-learning potentials (MLPs) either as stand-alone alternative models,39–44 or else to augment existing semiempirical QM methods.45–51 We will refer to the former class as “pure MLPs” and the latter class as “QM/Δ-MLPs”. MLPs have emerged as powerful tools to enable fast and accurate chemical models within the scope of their training.39,41–44 Many such models have emerged for different applications,52–67 although few, if any, have been used to their full potential in rigorous AFE simulations. Application of these models in drug discovery AFE simulations is challenging because they must: (1) make robust predictions for molecules within the relevant medicinal chemistry space that may have never been synthesized or characterized;68 (2) model a wide range of intra- and intermolecular interactions, including relative conformational energies, hydrogen bonding,69 π stacking,70,71 London dispersion,72 and mixed interactions; (3) quantitatively handle different tautomers,18,19,73 and protonation states.21 Currently, the ANI63,74–76 class of models, and particularly the second generation ANI-2x,76 have received widespread attention. A limitation of these models is that they were built for neutral molecules, and their functional forms do not explicitly account for total molecular charge or spin state. Consequently, they are not able to reliably predict the energetics of changing protonation states. This is a serious limitation, as it has been estimated that up to 95% of drug molecules contain ionizable groups.18 Related to this, some of the pure MLPs did not initially treat long-ranged electrostatic interactions, although there have been efforts to remedy this.66 Alternatively, there have been several recent efforts to develop new QM/Δ-MLPs,45–51,77 the most relevant in the current context being AIQM1,46 which is based on the novel ODMx class of semiempirical models78 and has recently been demonstrated to be robust for transition state optimizations.79
Very recently, we introduced a first-generation QM/Δ-MLP for drug discovery.77 The Quantum Deep-learning Potential Interaction (QDπ) model uses a fast, robust third-order self-consistent density-functional tight binding (DFTB3/3OB) model80,81 that is corrected to high-level accuracy through an MLP correction (Δ-MLP) based on our range-corrected deep-learning potential (DPRc)47,48 as part of the DeePMD-kit82 interfaced with AMBER.83 The underlying DFTB3 model is able to capture long-range electrostatic interactions as well as changes in charge, protonation, and spin state. The intramolecular and short- to mid-range intermolecular interactions are made quantitatively accurate by training the DPRc model to correct the total energy and forces to match those of high-level ab initio methods.
In the present work, we compare the performance of several modern semiempirical QM, QM/Δ-MLP, and pure MLP models against consistent reference data derived from databases relevant for drug discovery. Of particular focus in the present work is characterizing the ability of different potentials to accurately model intermolecular interactions, tautomers, and protonation states. Toward that end, we consider the dataset of natural and synthetic nucleic acids from the artificially expanded genetic information system (AEGIS)84–87 that is being used for a wide range of biotechnology applications.88 The system uses 12 different nucleobases in its genetic code, including the four canonical nucleobases found in DNA (adenine, cytosine, guanine, and thymine), in addition to eight synthetic nucleobases. These serve as good test systems as they contain complex covalent bonding and exhibit a rich set of tautomer forms, hydrogen bonded complexes, and alternative protonation states. The remainder of the article is organized as follows: Sec. II describes the computational details pertaining to the various semiempirical QM (MNDO/d,89 AM1,90 PM6,91 PM6-D3H4X,92,93 PM7,94 ODM2,78 DFTB3,95 GFN1-xTB,96 GFN2-xTB,97 and DFTB/ChIMES98), MLP (ANI-1x74 and ANI-2x76), and QM/Δ-MLP (AIQM146 and most recently QDπ77) models, as well as the key modified databases (DBs) used as reference data at the ωB97X/6-31G*77,99 level. Section III presents and analyzes data for a set of ten broad-spectrum databases for intermolecular interactions, tautomers, protonation states, and 2D conformational energy profiles. Further application is made to examine the performance of modern semiempirical QM, MLP, and QM/Δ-MLPs against the AEGIS dataset.85,86 Finally, the paper provides contextual examples of acid/base chemistry relevant for RNA cleavage reactions catalyzed by small nucleolytic ribozymes and ribonucleases.100
II. METHODS
A. Models compared in the current work
1. Density-functional reference data
ωB97X/6-31G*99 was performed using Gaussian 16.101 Reference energy and forces (including geometry optimizations, where needed) were performed at a consistent ωB97X/6-31G*99 level of theory.
2. NDDO-based semiempirical models
Semiempirical quantum mechanical (QM) models based on the neglect of diatomic differential overlap (NDDO) approximation enable the number of electron repulsion integrals to be drastically reduced and the single-particle density matrix to be decomposed into effective atom-centered atomic orbital products (and their resulting electrostatics represented as multipoles).102 The NDDO approximation also eliminates the need to explicitly enforce orthogonalization of the molecular orbitals that normally would be achieved by having an overlap matrix in the generalized eigenvalue equation. Consequently, this may lead to poor modeling of conformational energies and their barriers if left uncorrected. Much work has been performed to introduce orthogonalization corrections into the theoretical framework, which has resulted in the OMX class of methods.103–106 In the current work, the following NDDO-based methods are considered: MNDO/d,89 AM1,90 and PM691 that were evaluated with the AMBER 20107 SQM module;108 the ODM278 method that was evaluated using the MNDO program109 kindly provided by Dr. Axel Koslowski; and PM6-D3H4X92,93 and PM794 that were performed using the MOPAC software.110 PM6-D3H4X and PM7 correct PM6 using classical potentials and are often claimed to be the most suitable methodology for drug design among NDDO-based semiempirical models.111,112
3. DFTB-based semiempirical models
Density-functional tight binding methods offer an intriguing alternative to the NDDO-based semiempirical models. DFTB methods use an expansion of the energy113 about a sum of neutral atom densities together with a two-center integral approximation to enable a framework for highly efficient calculations (speed is very comparable with NDDO-based methods). Unlike the NDDO-based methods, DFTB methods keep the overlap matrix in the generalized eigenvalue equation and thus explicitly deal with orbital orthogonalization. However, this complicates the decomposition of the density matrix, which now contains two-center products. Various density-matrix partition schemes can be used to map the density onto atomic centers such that an atom-centered (typically monopolar) representation can be made for the second-order electrostatic term in the expansion. The DFTB-based methods considered here include DFTB395 (3OB parameters114) that was performed using the AMBER 20107 SQM module;108,115 and GFN1-xTB,96 GFN2-xTB,97 and DFTB/ChIMES98 (3OB parameters114 and ChIMES parameters116 kindly provided by Dr. Cong Huy Pham) models evaluated with the DFTB+ software.30
Compared to DFTB3 and GFN1-xTB, GFN2-xTB represents the first broadly parameterized tight-binding method, primarily designed for the fast calculation of structures and noncovalent interaction energies, to include electrostatic and exchange-correlation Hamiltonian terms up to second order in the multipole expansion.97 In this way, the model takes into account anisotropic second order density fluctuation effects via short-range damped interactions of cumulative atomic multipole moments. DFTB/ChIMES,116 on the other hand, leverages the relative simplicity of linear regression machine learning in the recently developed Chebyshev Interaction Model for Efficient Simulation (ChIMES) method.117 Validation tests of DFTB/ChIMES demonstrate the model exhibits both transferability and extensibility and enables physical and chemical predictions with up to coupled-cluster accuracy.116
It should be noted that the use of machine learning methods to enhance DFTB models in one form or another is not new. Notable works along these lines, in addition to DFTB/ChIMES, include but are not limited to the ML-Hamiltonian approach of Yaron and co-workers,118 the development of many-body potentials from deep tensor neural networks,119,120 Gaussian process regression,121 and unsupervised machine learning.122
4. Machine learning potentials (MLPs)
The pure machine learning potentials considered in this work produce energies and atomic forces of a molecule given the positions and elements. These potentials are quite fast compared with semiempirical QM models, and they have more favorable scaling properties. However, some initial pure MLPs were built for neutral molecules in singlet ground states, so they do not reliably model changes in charge state that occur with the addition or loss of electrons and/or protons. The latter of which is important for drug molecules that contain ionizable sites. The pure MLPs considered here include ANI-1x74 and ANI-2x76 models performed using the TorchANI software.123 Both the ANI-1x and ANI-2x models use the ANI descriptor63 with a cutoff radius of 6 Å and were trained against ωB97X/6-31G* with active learning cycles. The training data of ANI-1x only include energies, and the training data of ANI-2x include both energies and forces.
5. Combined semiempirical quantum mechanical and machine-learning potentials (QM/Δ-MLPs)
An attractive alternative to either semiempirical QM or pure MLPs is to combine the strengths of both into a combined QM/Δ-MLP. In this way, it builds off of a fast and robust semiempirical QM that inherently can accommodate changes in electronic charge and spin states while using MLPs to greatly enhance the accuracy across a broad spectrum of chemical environments. The QM/Δ-MLPs considered here include the QDπ77 model, which is based on DFTB3/3OB95,107,108,114,115 and the deep-learning potential available in DeePMD-kit,82,83 and the AIQM1@DFT*46 model, which is based on an ODM278,109 model (which includes the D4 dispersion correction124) and a trained neural network correction using TorchANI.123 The MLP component of QDπ uses the DeepPot-SE descriptor61 with a cutoff radius of 6 Å and was trained against ωB97X/6-31G* energies and forces for 241 M steps; the MLP part of AIQM1@DFT* uses the ANI descriptor63 with a cutoff radius of 6 Å and was trained against ωB97X/def2-TZVPP energies and forces for 1000 epochs.46
All geometry optimizations using semiempirical QM, MLP, or QM/Δ-MLP models were performed using the Limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) algorithm125 in the ASE126 package. Relaxed 2D torsion profiles were made using the same method described in Ref. 77.
B. Databases and reference data used in the current work
The reference data used in the current work includes the modified ANI-1x,74,77,127 the modified COMP5,74,77,128–130 S66x8,74,131,132 HB375x10,77,133 TautoBase (TB),77,134,135 amino acids (AAs) and nucleic acids (NAs),77,136 PA26 and TAUT15,77,137 RegioSQM20,77,138 and the artificially expanded genetic information system (AEGIS).77,84–86 All reference data were computed (or re-computed77) at the ωB97X/6-31G* level of theory (consistent with the most extensive ANI-1x and COMP5 databases).
Among all reference data, the ANI-1x (or modified version) dataset was used to parameterize DFTB/ChIMES, ANI-1x, ANI-2x, QDπ, and AIQM1; S66x8 was used to parameterize PM6-D3H4X, ANI-2x, and QDπ; and TB, AA, NA, PA, and AEGIS were used for the training of QDπ.
III. RESULTS AND DISCUSSION
The focus of the current article is on comparing modern semiempirical electronic structure methods and machine learning potentials with respect to their ability to accurately model conformers, tautomers, and protonation states of biological and drug-like molecules. These methods have potential impact for drug discovery owing to their efficiency and robustness.
A. Comparison of broad-spectrum databases
Important properties for consideration include relative conformational energies, a wide range of intermolecular interactions, as well as tautomeric and protonation state relative energies. The QDπ model was trained with the same reference theory level as ANI-2x76 (ωB97X/6-31G*) and considered a number of DBs that encompass conformational energies (ANI-1x, COMP5), intermolecular interactions (S66x8, HB375x10), tautomers (TautoBase, Taut15), and protonation state relative energies (AA, NA, PA26, and RegioSQM20) that are described in detail elsewhere.77 A comparison of 11 semiempirical quantum and machine learning models is compared against ten databases in Table I.
TABLE I.
Mean absolute errors for different datasets used for training and testing of the QDπ model.a Boldface denotes a vector.
| ANI-1x | S66 | TB | AA | NA | PA | COMP5 | HB | T15 | SQM | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | F | ΔE | ΔE | ΔE | ΔE | ΔE | E | F | ΔE | ΔE | ΔE | |
| QDπ | 0.83 | 1.16 | 0.13 | 0.82 | 0.09 | 0.17 | 0.39 | 1.48 | 1.14 | 0.44 | 0.70 | 2.53 |
| AIQM1 | ⋯ | 3.10 | 0.57 | 2.07 | 7.30 | 4.71 | 5.06 | ⋯ | 2.59 | 0.71 | 1.37 | 2.75 |
| ANI-1x | 1.48 | 4.48 | 1.41 | 1.73 | 86.95 | 52.68 | 43.02 | 1.96 | 3.72 | 1.25 | 1.63 | 16.85 |
| ANI-2x | 1.07 | 2.11 | 0.37 | 1.76 | 70.52 | 52.48 | 23.80 | 1.67 | 1.86 | 1.40 | 1.00 | 13.64 |
| GFN2-xTB | ⋯ | 5.81 | 0.74 | 5.68 | 5.77 | 8.45 | 7.35 | ⋯ | 4.33 | 0.85 | 2.84 | 4.12 |
| GFN1-xTB | ⋯ | 4.69 | 0.77 | 5.23 | 5.00 | 11.73 | 4.43 | ⋯ | 3.68 | 0.87 | 5.32 | 4.10 |
| DFTB3 | ⋯ | 7.58 | 1.14 | 5.45 | 8.63 | 10.85 | 12.54 | ⋯ | 5.46 | 1.17 | 3.65 | 4.59 |
| DFTB/ChIMES | ⋯ | 4.82 | 1.72 | 5.04 | 9.47 | 9.70 | 12.87 | ⋯ | 4.14 | 1.36 | 3.00 | 6.70 |
| ODM2 | ⋯ | 12.80 | 1.24 | 3.37 | 9.13 | 5.26 | 6.04 | ⋯ | 9.97 | 1.29 | 3.64 | 3.99 |
| PM6 | ⋯ | 12.96 | 1.19 | 4.90 | 11.23 | 11.03 | 17.84 | ⋯ | 9.33 | 1.24 | 5.60 | 5.30 |
| PM6-D3H4X | ⋯ | 13.60 | 0.63 | 5.44 | 9.67 | 11.72 | 7.78 | ⋯ | 10.27 | 0.84 | 6.16 | 6.61 |
| PM7 | ⋯ | 11.98 | 0.84 | 4.34 | 7.24 | 10.72 | 10.11 | ⋯ | 8.54 | 1.00 | 3.74 | 5.93 |
| AM1 | ⋯ | 14.95 | 2.17 | 5.01 | 4.43 | 7.32 | 13.51 | ⋯ | 12.13 | 2.57 | 3.99 | 4.13 |
| MNDO/d | ⋯ | 15.14 | 6.67 | 9.69 | 11.71 | 11.29 | 13.07 | ⋯ | 11.52 | 9.36 | 7.78 | 5.18 |
Mean absolute errors in the energy (E, kcal/mol), forces (F, kcal/mol/Å), and ΔE for ANI-1x,74,127 S66x8 (S66),74,131,132 TautoBase (TB),134,135 amino acid and nucleic acid proton affinities (AA and NA),136 PA26 (PA),137 COMP5,74,128–130 HB375x10 (HB),133 Taut15 (T15),137 and RegioSQM20 (SQM)138 databases. The datasets on the right were not part of the QDπ training.
1. Conformational energy datasets
With respect to the diverse conformational energy datasets (ANI-1x74,127 and COMP574,77,128–130), the mean absolute errors (maEs) in the forces are smallest for the MLP and Δ-MLP potentials (QDπ, ANI-2x, AIQM1, and ANI-1x), and the QDπ model performs the overall best (maE values of 1.16 and 1.14 kcal/mol/Å for the ANI-1x and COMP5 datasets, respectively). This is likely due to the fact that the ANI-1x dataset was an integral part of the training of these models. In general, the DFTB models (GFN1-xTB, GFN2-xTB, and DFTB3/3OB) have lower force errors with respect to the reference ωB97X/6-31G* values (maE values range from 4.69 to 7.58 and 3.68 to 5.46 kcal/mol/Å for ANI-1x and COMP5, respectively), whereas the NDDO-based methods have considerably larger errors (maE values range from 11.98 to 15.14 and 8.54 to 12.13 kcal/mol/Å for ANI-1x and COMP5, respectively), with PM7 performing the best of the NDDO methods.
2. Intermolecular interaction datasets
With respect to intermolecular interaction DBs (S66x874,131,132 and HB375x10133), several models have ΔE values below 1 kcal/mol on average (QDπ, AIQM1, GFN1-xTB, GFN2-xTB, PM6-D3H4X, and PM7), with QDπ and AIQM1 having exceptional agreement with the reference data: QDπ has maE values of 0.13 and 0.44 kcal/mol, and AIQM1 has maE values of 0.57 and 0.71 kcal/mol for S66x8 and HB375x10, respectively. The ANI-2x model has excellent maE values for S66x8 (maE 0.37 kcal/mol) but does not perform quite as well for the HB375x10 DB (maE 1.40 kcal/mol). The DFTB3, DFTB/ChIMES, ODM2, and PM6 methods perform similarly with ΔE maE values that range from 1.14 to 1.72 (S66x8) and 1.17 to 1.36 (HB375x10) kcal/mol for these DBs. The MNDO/d method has the largest ΔE errors (6.67–9.36 kcal/mol), stemming from known limitations in the core–core interactions that particularly affect hydrogen bonding, which the empirical modified core–core repulsions in AM1 were designed in part to partially alleviate (AM1 maE values range from 2.17 to 2.57 kcal/mol).
3. Tautomer datasets
With respect to the tautomer databases, TautoBase134,135 (TB) and Taut15137 (T15), only the QDπ model achieves ΔE errors less than 1 kcal/mol (maE values of 0.82 and 0.70 kcal/mol for TB and T15, respectively). The AIQM1 and ANI models perform admirably with errors generally below 2 kcal/mol (maE values range from 1.73 to 2.07 and 1.00 to 1.37 kcal/mol for TB and T15, respectively). The remainder of the DFTB-based methods have maE values in excess of 5 kcal/mol for TB and similar values for the AM1, PM6, and PM6-D3H4X methods. The ODM2 method makes a notable improvement with reduced errors relative to the other NDDO-based methods (maE values of 3.37 and 3.64 kcal/mol for TB and T15, respectively). The MNDO/d method overall performs the worst with maE values for TB and T15 exceeding 9 kcal/mol.
4. Relative protonation datasets
The relative protonation datasets include amino and nucleic acid model compounds136 (AA and NA) as well as more general proton affinity (PA26137) datasets and a subset of the RegioSQM20138 (SQM) database containing C, H, O, and N elements. The latter involves many relative protonation energies not related to ionizable sites in biological or drug-like molecules, and hence may be of less relevance for drug discovery. For the AA, NA, and PA26 datasets, the QDπ model stands alone with respect to having very high accuracy in relative deprotonation energies (maE values range from 0.09 to 0.39 kcal/mol). The next best models are AIQM1 (maE 4.71–7.30 kcal/mol). The other semiempirical QM models exhibit much larger ranges: GFN2-xTB (5.77–8.45 kcal/mol), GFN1-xTB (5.00–11.73 kcal/mol), DFTB3 (8.63–12.54 kcal/mol), DFTB/ChIMES (9.47–12.87), ODM2 (5.26–9.13 kcal/mol), PM6 (11.03–17.84 kcal/mol), PM6-D3H4X (7.78–11.72), PM7 (7.24–10.72), AM1 (4.43–13.51 kcal/mol), and MNDO/d (11.29–13.07 kcal/mol). With respect to the SQM dataset, again the QDπ and AIQM1 models perform best (maE values of 2.53 and 2.75 kcal/mol, respectively), and the remaining semiempirical QM models perform similarly with maE values that range from 3.99 to 6.70 kcal/mol. The pure MLP models (ANI-1x and ANI-2x) break down with respect to their ability to predict relative protonation/deprotonation energies, as these potentials were designed for neutral molecules.
Overall, the QDπ model performs exceptionally well across all datasets. The AIQM1 model is also impressive in this regard, with the exception of the protonation/deprotonation energies, where AIQM1 has larger errors for the AA, NA, and PA datasets. Clearly, the QM/Δ-MLP form, using DFTB3 or ODM2 as a QM base model, considerably enhances the accuracy across all datasets listed in Table I. The pure MLP models, and particularly ANI-2x, generally perform better than the semiempirical QM models, with the exception of protonation/deprotonation energies, where the model gives very large errors. Of the semiempirical QM models, the DFTB-based methods have smaller force errors than the NDDO-based models. The GFN1-xTB, GFN2-xTB, PM6-D3H4X, and PM7 models perform well for intermolecular interactions, slightly better than the DFTB3, DFTB/ChIMES, and ODM2 models. All of the semiempirical QM models are fairly comparable in modeling tautomer energy differences (with the exception of MNDO/d, which is less accurate), with ODM2 performing best over a broad range of data. For protonation/deprotonation energies, however, there is no clear trend with the semiempirical QM potentials—they all deviate from the reference data with ΔE maE values exceeding 8 kcal/mol for at least one of the datasets (AA, NA, PA, or SQM).
In the remainder of the article, we focus on comparisons to the most recent modern semiempirical QM (DFTB3, DFTB/ChIMES, GFN2-xTB, ODM2, PM6-D3H4X, PM7), MLP (ANI-2x), and QM/Δ-MLP (QDπ and AIQM1) models.
B. Comparison of 2D conformation energy profiles
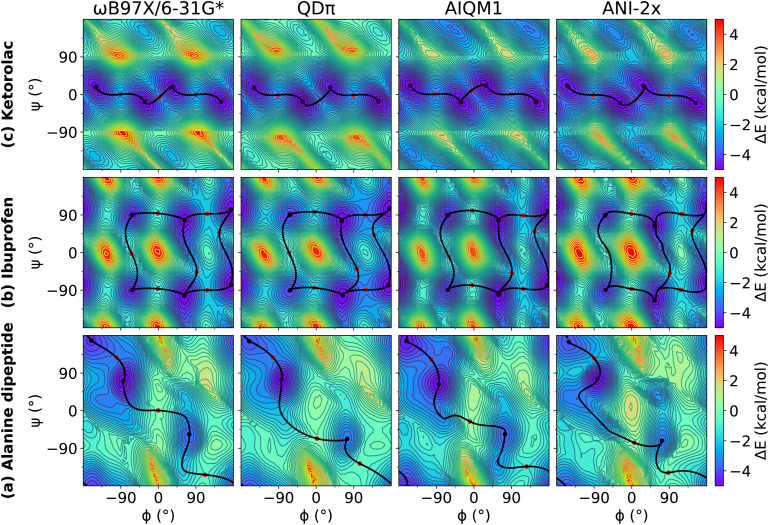
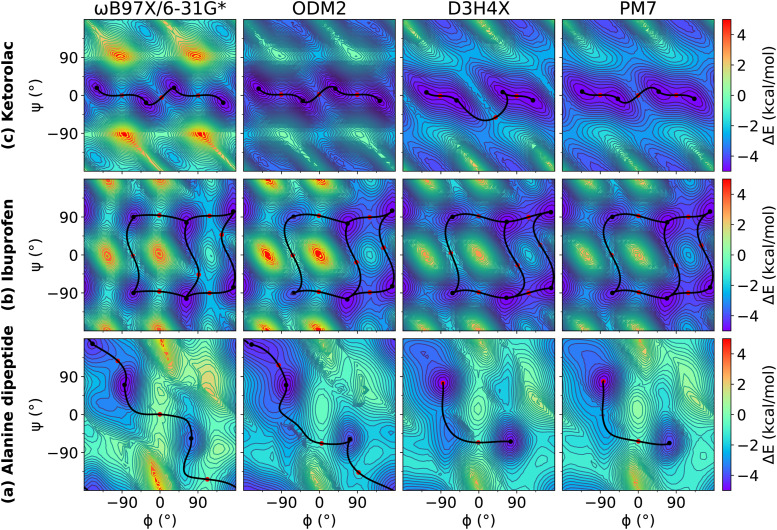
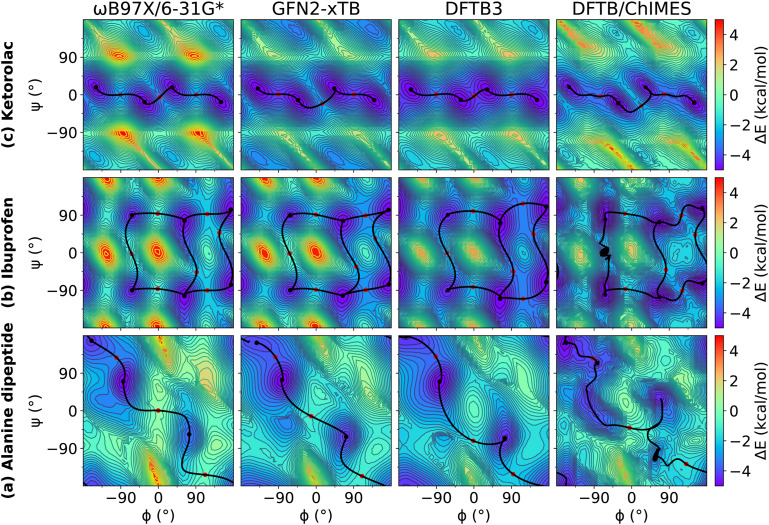
We examined relaxed 2D torsion profiles for three systems: the alanine dipeptide and the drug molecules ibuprofen and ketorolac, as illustrated in Figs. 1–3. These figures compare 2D torsion profiles at the ωB97X/6-31G* reference level with the QM/Δ-MLP/pure MLP models QDπ, AIQM1, and ANI-2x (Fig. 1), DFTB-based GFN2-xTB, DFTB3 and DFTB/ChIMES (Fig. 2), and NDDO-based ODM2, PM3-D3H4X, and PM7 (Fig. 3) models. The relative energy values for the stationary points are provided in Table S1 of the supplementary material. All of the models qualitatively predict the correct trends. A modest exception occurs with PM6-D3H4X and PM7, which do not predict a pronounced minimum in the β region (∼180/180) of the ϕ/ψ map (Fig. 3). Overall, the QDπ and AIQM1 models have the closest agreement with ωB97X/6-31G*, with the ANI-2x model only slightly worse. The GFN2-xTB, DFTB3, and ODM2 semiempirical QM models tend to systematically under-estimate the conformational barriers between minima (Table S1 in the supplementary material). The largest errors that occur for the QDπ model are for the transition states in the ibuprofen example, which like the semiempirical QM models, are systematically underestimated.
FIG. 1.
Relaxed 2D torsion profiles for (a) alanine dipeptide; (b) ibuprofen; and (c) ketorolac. Each molecule was computed using ωB97X/6-31G*, QDπ, AIQM1, and ANI-2x, respectively. The reference level of theory is ωB97X/6-31G*. The color bars represent the potential energy (with respect to the minimum energy) in kcal/mol.
FIG. 3.
Relaxed 2D torsion profiles for (a) alanine dipeptide; (b) ibuprofen; and (c) ketorolac. Each molecule was computed using ωB97X/6-31G*, ODM2, PM6-D3H4X, and PM7, respectively. The reference level of theory is ωB97X/6-31G*. The color bars represent the potential energy (with respect to the minimum energy) in kcal/mol.
FIG. 2.
Relaxed 2D torsion profiles for (a) alanine dipeptide; (b) ibuprofen; and (c) ketorolac. Each molecule was computed using ωB97X/6-31G*, GFN2-xTB, DFTB3, and DFTB/ChIMES, respectively. The reference level of theory is ωB97X/6-31G*. The color bars represent the potential energy (with respect to the minimum energy) in kcal/mol.
C. Comparison of hydrogen bond complex energies for natural and artificial nucleic acids
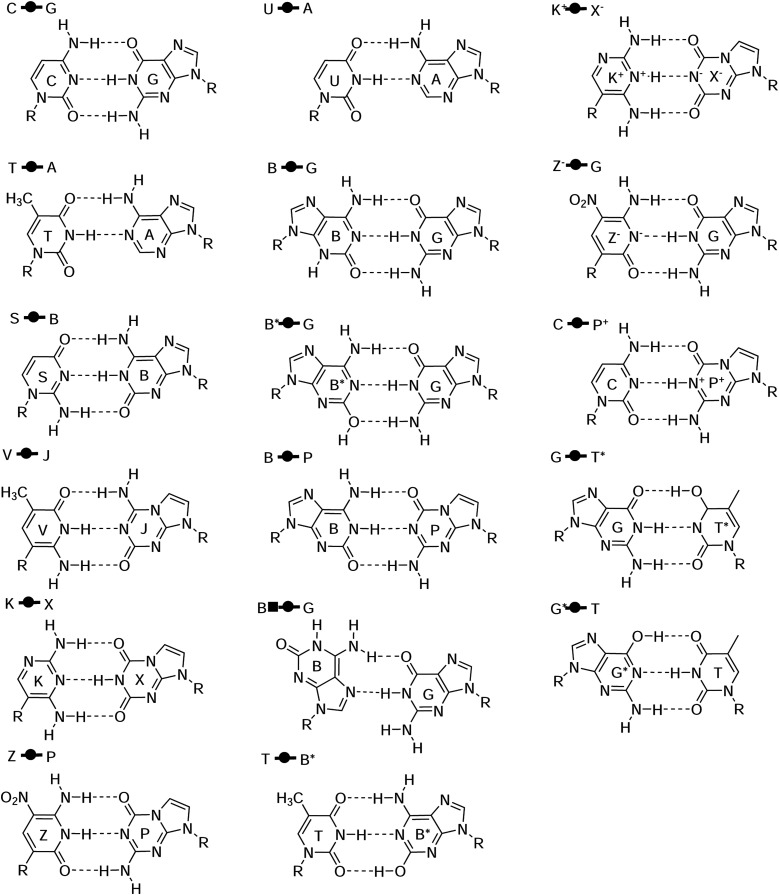
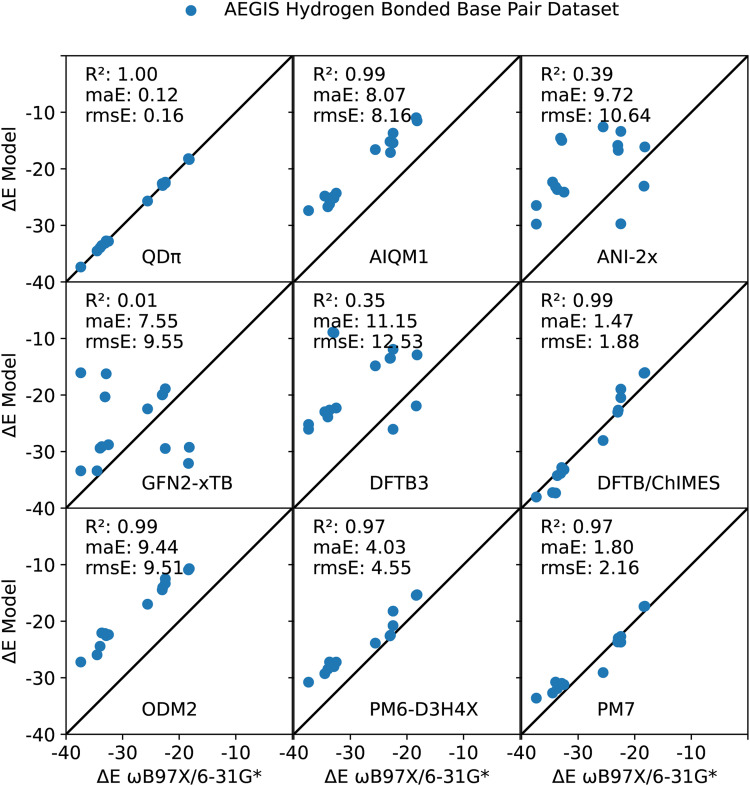
The natural and modified nucleic acids exhibit a wide range of canonical and non-canonical hydrogen bonded base pairs, including some that involve non-standard tautomer forms and protonation states. The base pairs considered in the AEGIS dataset77,85,86 are illustrated in Fig. 4. This dataset represents a rich set of hydrogen bonding interactions between endocyclic and exocyclic amines and carbonyl and hydroxyl functional groups. The results are listed in Table II, and the neutral base pairs are illustrated in Fig. 5. Overall, the QDπ model gives excellent agreement with the ωB97X/6-31G* reference level over the entire set with ΔE maE of 0.11 kcal/mol and a maximum error of 0.39 kcal/mol for G*  T. The DFTB/ChIMES model has the next lowest error (maE 1.99 kcal/mol), followed by PM7 (maE 2.77 kcal/mol), GFN2-xTB (maE 4.25 kcal/mol), and PM6-D3H4X (maE 4.87 kcal/mol). The remainder of the models have maE values in excess of 8 kcal/mol. The ANI-2x model has a large maE value (14.17 kcal/mol), but the errors are dominated by base pairs involving ionized nucleobases that range from 11.58 to 79.73 kcal/mol, whereas the range of errors for neutral base pairs is much smaller (3.39–13.00 kcal/mol; maE of the neutral subset is 9.72 kcal/mol).
T. The DFTB/ChIMES model has the next lowest error (maE 1.99 kcal/mol), followed by PM7 (maE 2.77 kcal/mol), GFN2-xTB (maE 4.25 kcal/mol), and PM6-D3H4X (maE 4.87 kcal/mol). The remainder of the models have maE values in excess of 8 kcal/mol. The ANI-2x model has a large maE value (14.17 kcal/mol), but the errors are dominated by base pairs involving ionized nucleobases that range from 11.58 to 79.73 kcal/mol, whereas the range of errors for neutral base pairs is much smaller (3.39–13.00 kcal/mol; maE of the neutral subset is 9.72 kcal/mol).
FIG. 4.
Structures for the artificially expanded genetic information system (AEGIS) base pair dataset77,85,86 with Leontis and Westhof symbols used for the classification of nucleic acid base pairs.139–141
Table II.
Hydrogen bond complex energies from ωB97X/6-31G* and model errors (kcal/mol) for the artificially expanded genetic information system (AEGIS) base pair dataset77,85,86 with Leontis and Westhof symbols used for the classification of nucleic acid base pairs,139–141 including complexes that involve alternative tautomers and protonation states.a
| QM/Δ-MLP or MLP | DFTB | NDDO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ωB97X | QDπ | AIQM1 | ANI-2x | GFN2 | DFTB3 | ChIMES | ODM2 | D3H4X | PM7 | |
| Complex | ΔE | Err | Err | Err | Err | Err | Err | Err | Err | Err |

|
‒32.90 | 0.16 | 7.75 | 9.84 | 3.66 | 10.98 | 0.08 | 10.35 | 4.87 | 1.92 |

|
‒18.22 | ‒0.14 | 6.71 | 3.65 | 2.15 | 9.33 | 2.19 | 7.51 | 2.90 | 0.88 |

|
‒18.36 | 0.17 | 7.39 | 3.39 | 2.12 | 9.35 | 2.22 | 7.45 | 2.94 | 0.96 |

|
‒37.40 | 0.03 | 10.01 | 7.67 | 3.99 | 11.34 | ‒0.64 | 10.18 | 6.62 | 3.80 |

|
‒34.52 | ‒0.00 | 9.70 | 8.04 | 2.43 | 9.32 | ‒2.73 | 8.57 | 5.25 | 1.83 |

|
‒22.46 | ‒0.08 | 7.06 | 6.34 | 2.13 | 9.56 | 1.99 | 9.14 | 1.69 | ‒1.24 |

|
‒33.11 | ‒0.05 | 8.13 | 10.77 | 3.65 | 10.14 | ‒0.76 | 10.93 | 5.50 | 1.83 |

|
‒32.50 | ‒0.31 | 8.20 | 8.38 | 3.72 | 10.21 | ‒0.69 | 10.13 | 5.28 | 1.28 |

|
‒33.68 | 0.13 | 7.45 | 10.02 | 4.56 | 11.02 | ‒0.56 | 11.61 | 6.47 | 1.77 |

|
‒22.46 | 0.09 | 8.76 | 9.08 | 3.56 | 10.54 | 3.50 | 9.95 | 4.24 | ‒0.24 |

|
‒33.99 | 0.03 | 7.28 | 10.79 | 4.59 | 10.11 | ‒3.34 | 9.56 | 5.51 | 3.22 |

|
‒23.00 | 0.39 | 7.82 | 7.14 | 3.03 | 9.49 | ‒0.04 | 8.55 | 0.41 | ‒0.67 |

|
‒25.59 | ‒0.11 | 8.99 | 13.00 | 3.14 | 10.75 | ‒2.45 | 8.60 | 1.71 | ‒3.49 |

|
‒22.92 | ‒0.03 | 5.80 | 6.18 | 3.04 | 9.44 | 0.24 | 8.88 | 0.43 | ‒0.08 |

|
‒144.48 | 0.10 | 12.53 | 79.73 | 14.30 | 18.59 | 8.26 | 15.79 | 15.52 | 15.29 |

|
‒43.33 | ‒0.07 | 12.36 | 11.58 | 6.69 | 15.35 | 3.42 | 12.16 | 4.25 | 1.90 |

|
‒47.17 | 0.04 | 6.77 | 24.45 | 3.38 | 13.41 | 0.87 | 9.41 | 7.35 | 4.82 |
| maE | … | 0.11 | 8.46 | 14.17 | 4.25 | 11.22 | 1.99 | 10.08 | 4.87 | 2.77 |
| rmsE | … | 0.15 | 8.66 | 22.51 | 5.09 | 11.49 | 2.83 | 10.26 | 5.97 | 4.44 |
Models and datasets are described in Sec. II. An illustration of each of the complexes is provided in Fig. 4. Complexes include adenine (A), cytosine (C), guanine (G), thymine (T), uracil (U), isoguanine (B), isocytosine (S), 6-amino-5-nitropyridin-2-one (Z), 2-aminoimidazo[1,2a][1,3,5]triazin-4(1H)-one (P), imidazo[1,2-a]-1,3,5-triazine-2(8H)-4(3H)-dione (X), 2,4-diaminopyrimidine (K), 4-aminoimidazo[1,2-a][1,3,5]triazin-2(8H)-one (J), and 6-amino-3-methylpyridin-2(1H)-one (V).86,142 The “*” symbol refers to tautomeric form, and the “+” and “−” symbols refer to the positive and negative charge.
FIG. 5.
Relation between hydrogen bond complex energies calculated by ωB97X/6-31G* and QDπ, AIQM1, ANI-2x, GFN2-xTB, DFTB3, DFTB/ChIMES, ODM2, PM6-D3H4X, and PM7 for the artificially expanded genetic information system (AEGIS) base pair dataset,86 including complexes that involve alternative tautomers and protonation states. Illustrations of each of the complexes are provided in Fig. 4. The three base pairs that involve ionized nucleobases are excluded from the regression as they have much larger binding energy values that would artificially skew the correlation.
Examination of the correlation of hydrogen complex energies for neutral nucleobases reveals that QDπ has the highest correlation (R2 value of 0.999), followed by DFTB/ChIMES, AIQM1, and ODM2 with R2 values of 0.99. Whereas DFTB/ChIMES is well aligned with the reference data, the ODM2 and related AIQM1 models have values that have been systematically shifted to lower ΔE values. Both PM7 and PM6-D3H4X models show impressive correlation (R2 values of 0.97) and low maE values (1.80 and 4.03 kcal/mol, respectively) for complexes of these neutral nucleobases.
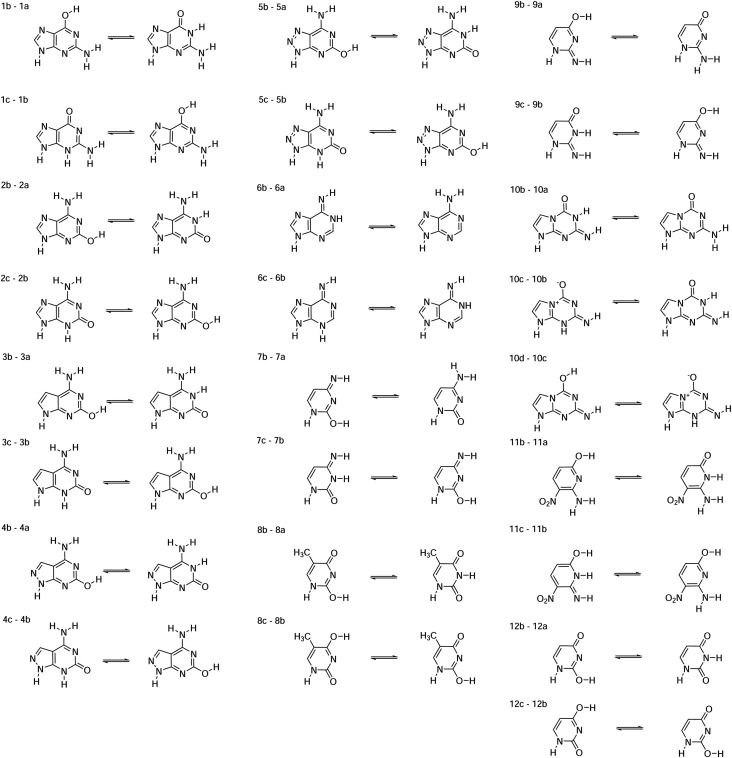
D. Comparison of tautomer energies for natural and artificial nucleic acids
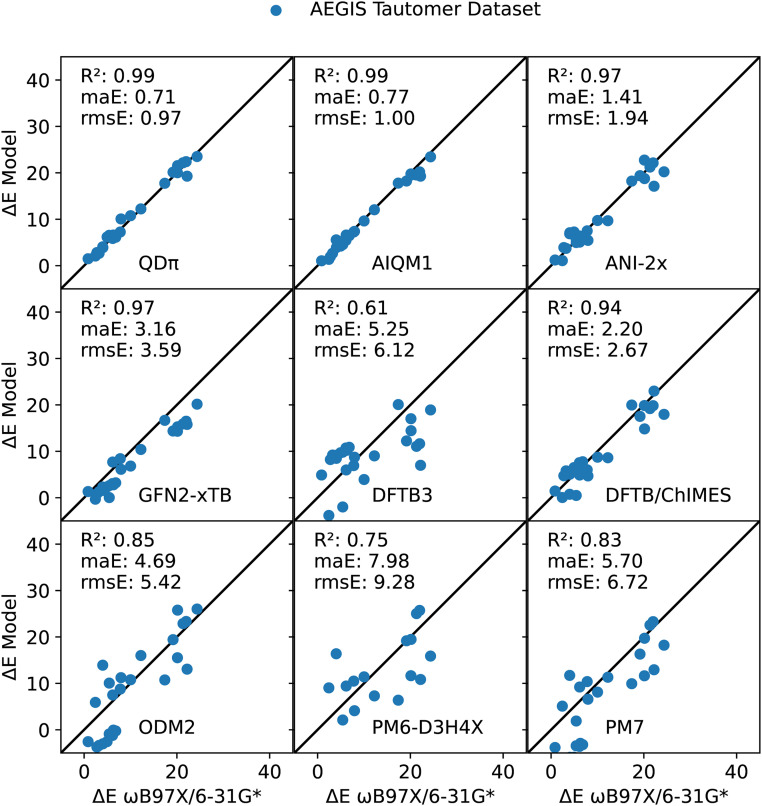
The artificially expanded genetic information system (AEGIS) dataset also exhibits a rich set of tautomeric forms that have been extensively studied with computational methods.77,85–87 These tautomeric pairs are illustrated in Fig. 6, and their ΔE values are listed in Table III and illustrated in Fig. 7. Overall, both QDπ and AIQM1 give excellent agreement with the ωB97X/6-31G* reference values, with ΔE maE values of 0.71 and 0.77 kcal/mol, respectively, and high correlation (R2 value of 0.99). The ANI-2x is the next most accurate, but with errors roughly twice as large (maE 1.41 kcal/mol) and (R2 value of 0.97). The DFTB/ChIMES and GFN2-xTB models have considerably higher errors (maE values of 2.20 and 3.16 kcal/mol, respectively), but maintain high correlation with the reference values (R2 value of 0.97), whereas DFTB3 and ODM2 have larger errors (maE values of 5.25 and 4.69 kcal/mol, respectively), and lower correlation (R2 values of 0.61 and 0.85, respectively). The largest errors occur for PM7 and PM6-D3H4X (maE values of 5.70 and 7.98 kcal/mol, respectively).
FIG. 6.
Structures for the artificially expanded genetic information system (AEGIS) tautomer dataset.77,85 Guanine derivatives (1–5, 2: nucleobase code B), codes 6: A, 7: C, 8: T, 9: S, 10: P, and 11: Z.
TABLE III.
Tautomerization energies from ωB97X/6-31G* and model errors (kcal/mol) for the artificially expanded genetic information system (AEGIS) tautomer dataset.a
| QM/Δ-MLP or MLP | DFTB | NDDO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ωB97X | QDπ | AIQM1 | ANI-2x | GFN2 | DFTB3 | ChIMES | ODM2 | D3H4X | PM7 | |
| Tautomer pair | ΔE | Err | Err | Err | Err | Err | Err | Err | Err | Err |
| 1b–1a | 2.43 | ‒0.36 | ‒1.07 | ‒1.35 | ‒2.75* | ‒6.25* | ‒2.38 | 3.48 | 6.60 | 2.67 |
| 1c–1b | 17.39 | 0.36 | 0.40 | 0.83 | ‒0.72 | 2.68 | 2.58 | ‒6.65 | ‒11.01 | ‒7.46 |
| 2b–2a | ‒5.41 | ‒1.12 | 0.13 | ‒0.29 | 2.81 | ‒4.39 | ‒1.02 | 6.31* | 12.62* | 8.85* |
| 2c–2b | 4.95 | 1.22 | ‒0.74 | 2.30 | ‒2.61 | 4.74 | 1.54 | ‒7.50* | ‒14.46* | ‒10.85* |
| 3b–3a | ‒6.32 | ‒0.28 | ‒0.16 | 0.89 | 3.53 | ‒3.90 | ‒0.77 | 6.39* | 12.95* | 9.24* |
| 3c–3b | 4.05 | ‒0.15 | ‒0.15 | 3.05 | ‒2.48 | 4.44 | 1.02 | ‒7.07* | ‒13.56* | ‒9.97* |
| 4b–4a | ‒6.81 | 0.69 | 0.37 | 0.58 | 3.60 | ‒4.06 | ‒0.94 | 7.06* | 13.49* | 10.01* |
| 4c–4b | 2.76 | 0.06 | ‒0.82 | 1.14 | ‒1.90 | 5.47 | 1.98 | ‒6.48* | ‒12.55* | ‒8.93* |
| 5b–5a | ‒6.12 | ‒0.41 | 0.66 | ‒0.28 | 3.07 | ‒4.60 | ‒1.43 | 7.34* | 13.36* | 9.71* |
| 5c–5b | 3.23 | ‒0.57 | ‒0.57 | 0.49 | ‒1.92 | 5.97 | 2.56 | ‒6.59* | ‒13.03* | ‒9.41* |
| 6b–6a | 12.24 | ‒0.01 | ‒0.20 | ‒2.56 | ‒1.85 | ‒3.22 | ‒3.63 | 3.76 | ‒4.94 | ‒0.92 |
| 6c–6b | 20.12 | ‒0.10 | ‒0.35 | 2.63 | ‒5.80 | ‒3.10 | ‒0.26 | ‒4.60 | ‒8.47 | ‒8.48 |
| 7b–7a | 20.15 | 1.40 | ‒0.63 | ‒1.39 | ‒4.87 | ‒5.71 | ‒5.32 | 5.63 | ‒0.67 | ‒0.43 |
| 7c–7b | ‒19.17 | ‒0.96 | 0.94 | ‒0.22 | 4.79 | 6.93 | 1.64 | ‒0.25 | ‒0.01 | 2.86 |
| 8b–8a | 21.32 | 0.84 | ‒1.79 | ‒0.08 | ‒5.43 | ‒10.25 | ‒2.12 | 1.57 | 3.71 | 1.24 |
| 8c–8b | ‒6.16 | 0.31 | ‒0.43 | 1.10 | ‒1.52 | 0.18 | 1.28 | ‒1.34 | ‒3.27 | ‒3.05 |
| 9b–9a | 5.42 | 0.77 | ‒0.89 | ‒0.45 | ‒5.39 | ‒7.41* | ‒4.94 | 4.64 | ‒3.31 | ‒3.53 |
| 9c–9b | ‒10.02 | ‒0.74 | 0.40 | 0.29 | 3.20 | 6.10 | 1.29 | ‒0.76 | ‒1.38 | 1.91 |
| 10b–10a | 7.95 | 2.11 | ‒0.57 | ‒2.50 | ‒1.83 | 0.77 | ‒3.26 | 3.28 | ‒3.84 | ‒1.36 |
| 10c–10b | 22.20 | ‒2.92 | ‒2.92 | ‒5.08 | ‒6.40 | ‒15.21 | 0.78 | ‒9.14 | ‒11.36 | ‒9.26 |
| 10d–10c | 4.01 | 0.04 | 1.54 | 2.86 | ‒1.71 | 5.13 | ‒3.27 | 9.90 | 12.36 | 7.71 |
| 11b–11a | ‒0.86 | ‒0.63 | ‒0.19 | ‒0.36 | ‒0.47 | ‒4.04 | ‒0.58 | 3.42* | 7.69* | 4.68* |
| 11c–11b | 24.35 | ‒0.84 | ‒0.90 | ‒4.13 | ‒4.19 | ‒5.43 | ‒6.39 | 1.67 | ‒8.47 | ‒6.13 |
| 12b–12a | 22.00 | 0.41 | ‒1.80 | 0.14 | ‒5.51 | ‒10.37 | ‒2.16 | 1.34 | 3.73 | 1.31 |
| 12c–12b | ‒7.79 | 0.54 | 0.54 | 0.29 | ‒0.62 | 0.87 | 1.78 | ‒0.98 | ‒2.70 | ‒2.59 |
| maE | … | 0.71 | 0.77 | 1.41 | 3.16 | 5.25 | 2.20 | 4.69 | 7.98 | 5.70 |
| rmsE | … | 0.97 | 1.00 | 1.94 | 3.59 | 6.12 | 2.67 | 5.42 | 9.28 | 6.72 |
FIG. 7.
Relation between tautomerization energies calculated by ωB97X/6-31G* and QDπ, AIQM1, ANI-2x, GFN2-xTB, DFTB3, DFTB/ChIMES, ODM2, PM6-D3H4X, and PM7 for the artificially expanded genetic information system (AEGIS) tautomer dataset. An illustration of each of the complexes is provided in Fig. 6. In the regression plot shown, the sign convention (direction of the tautomer reaction) is chosen such that the reference ΔE value is positive (this is performed to circumvent “spreading out” of the data and artificially inflating the correlation).
It has been estimated that 30% of the compounds in vendor databases and 21% of the compounds in drug databases have potential tautomers.18,19 For drug discovery applications, it is thus vitally important to be able to model alternative tautomer forms, discern which forms are relevant for ligand–protein binding, and if binding induces a change in tautomer state, to quantitatively determine the tautomerization energy contribution to binding with sub-kcal/mol accuracy. In some cases, the semiempirical QM models incorrectly predict the lowest energy tautomer (one case for GFN2-xTB, two cases for DFTB3, and nine cases each for ODM2, PM6-D3H4X, and PM7). For the models compared here, only QDπ and AIQM1 are able to achieve the requisite accuracy for quantitative prediction of ligand–protein binding applications.
E. Comparison of protonation energies for common general acids and bases
Modeling protonation states is important for drug discovery applications as it has been estimated that up to 95% of drug molecules contain ionizable groups18 (∼75% weak bases and ∼20% weak acids20,21), and protonation states can sometimes change upon ligand binding. Hence, quantitatively accurate modeling of protonation/deprotonation events at these ionizable sites is critical to obtain high predictive capability. As an illustrative set of examples, we examine simple model systems that mimic the acid/base chemistry associated with RNA cleavage reactions catalyzed by small nucleolytic RNA enzymes (ribozymes) and protein enzymes (ribonucleases).100 In these reactions, the 2′OH of an RNA nucleotide, modeled by the secondary alcohol isopropanol (iPrOH), becomes activated (deprotonated) by a general base that in ribozymes is often an ionized (deprotonated) guanine residue (), and in RNase A143–145 is generally believed to be a histidine (His:Nϵ) although it has been speculated that a neutral lysine (Lys:NH2) might also be capable. The activated nucleophile then attacks the scissile phosphate, passing through a pentavalent transition state, followed by the departure of the 5′O leaving group (modeled by the primary alkoxide ethoxide (EtO−) with the assistance of a general acid that in ribozymes can be either a protonated adenine at the N1 or N3 positions (A:N1H+ and A:N3H+, respectively) or an ionized (protonated) cytosine (C:N3H+), and in RNase A is a protonated histidine (His:NϵH+).
Table IV lists relative protonation/deprotonation reactions that model general acid/base events in RNA cleavage reactions.100 Overall, QDπ performs extremely well, with ΔE maE of 0.50 kcal/mol. Of the semiempirical QM methods, GFN2-xTB is the least inaccurate (maE value of 5.94 kcal/mol), followed by PM7 (6.97 kcal/mol), with other models notably higher (maE values ranging from 9.12 to 14.67 kcal/mol). As mentioned earlier, the ANI-2x model was not designed to handle ions; it produces errors on the order of 100 kcal/mol. The AIQM1 model is greatly improved with respect to ANI-2x and ODM2 (the base QM model). The QDπ ΔE maE value is dominated by large positive errors involving the ethoxide and protonated nucleobases (0.89–1.25 kcal/mol). The ethoxide anion is a primary alkoxide that is only marginally stable in the gas phase, and thus especially challenging. The QDπ model is by far the most accurate for protonation/deprotonation energies. It is a promising candidate for use in drug discovery applications.
TABLE IV.
Selected relative protonation/deprotonation energies from ωB97X/6-31G* and model error (kcal/mol) relevant to acid/base catalysis in RNA cleavage reactions.a
| QM/Δ-MLP or MLP | DFTB | NDDO | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ωB97X | QDπ | AIQM1 | ANI-2x | GFN2 | DFTB3 | ChIMES | ODM2 | D3H4X | PM7 | |
| Protonation pair | ΔE | Err | Err | Err | Err | Err | Err | Err | Err | Err |
| [Lys:NH2,iPrOH] | 167.76 | 0.00 | ‒0.64 | ‒115.04 | 0.04 | 6.11 | ‒6.87 | ‒15.24 | ‒13.15 | ‒10.15 |
| [His:Nϵ,iPrOH] | 158.33 | 0.08 | ‒9.22 | ‒126.62 | ‒7.02 | ‒11.33 | ‒17.47 | ‒18.74 | ‒12.96 | −6.19 |
| [EtO−,His:NϵH+] | ‒160.25 | ‒0.02 | 12.82 | 137.70 | 9.66 | 11.71 | 18.09 | 21.92 | 12.24 | 5.36 |
| [,iPrOH] | 43.06 | ‒1.11 | ‒1.15 | ‒28.62 | −2.69 | ‒8.63 | ‒11.17 | ‒10.84 | 0.89 | 5.45 |
| [EtO−,A:N1H+] | ‒165.06 | 1.25 | 12.94 | 137.24 | 10.02 | 15.21 | 23.15 | 20.74 | 8.07 | 1.25 |
| [EtO−,A:N3H+] | ‒190.89 | 1.21 | 12.88 | 143.42 | 11.40 | 16.00 | 24.17 | 19.43 | 17.97 | 8.39 |
| [EtO−,C:N3H+] | ‒160.33 | 0.89 | 12.78 | 145.20 | 6.58 | 4.66 | 16.93 | 20.19 | 7.03 | 2.22 |
| [,A:N1H+] | ‒120.07 | 0.08 | 8.19 | 97.55 | 4.69 | 6.20 | 11.36 | 6.73 | 9.69 | 7.53 |
| [,A:N3H+] | ‒145.91 | 0.04 | 8.12 | 103.73 | 6.07 | 6.99 | 12.38 | 5.41 | 19.58 | 14.67 |
| [,C:N3H+] | ‒115.34 | ‒0.27 | 8.03 | 105.50 | 1.25 | ‒4.35 | 5.14 | 6.17 | 8.64 | 8.51 |
| maE | … | 0.50 | 8.68 | 114.06 | 5.94 | 9.12 | 14.67 | 14.54 | 11.02 | 6.97 |
| rmsE | … | 0.72 | 9.72 | 118.72 | 6.96 | 9.96 | 15.87 | 15.84 | 12.17 | 7.88 |
Models and datasets are described in Sec. II. Protonation pairs are written in the general form as follows: [B, A]: B + A → BH+ + A−, or [B−, AH+]: B− + AH+ → BH + A. Here, B/BH+ and B−/BH are the base/conjugate acid pairs and A/A− and AH+/A are the acid/conjugate base pairs. These are model systems for general acid and base catalysis in RNA cleavage reactions by small nucleolytic ribozymes and ribonucleases.100 The molecules indicated are isopropanol (iPrOH), ethoxide (EtO−), neutral lysine (Lys:NH2), neutral histidine (His:Nϵ), protonated histidine (His:NϵH+), deprotonated guanine at the N1 position (), protonated adenine at the N1 and N3 positions (A:N1H+ and A:N3H+), and protonated cytosine at the N3 position (C:N3H+).
IV. CONCLUSION
We have compared the performance of several NDDO-based (MNDO/d, AM1, PM6, PM6-D3H4X, PM7, and ODM2) and density-functional tight-binding based (DFTB3, DFTB/ChIMES, GFN1-xTB, and GFN2-xTB) semiempirical models with pure machine learning potentials (ANI-1x and ANI-2x) and hybrid quantum mechanical/machine learning potentials (AIQM1 and QDπ). We examine broad datasets computed at a consistent ωB97X/6-31G* level of theory that includes conformational energies, intermolecular interactions, tautomers, and protonation states. The methods were further compared against the AEGIS dataset and acid/base chemistry relevant for RNA cleavage reactions catalyzed by small nucleolytic ribozymes and ribonucleases. Overall, the recently developed QDπ model performs exceptionally well across all datasets, with especially high accuracy for tautomers and protonation states relevant to drug discovery. The AIQM1 model also has impressive performance in many cases, including tautomerization energies. All other methods examined have various strengths and weaknesses, but none have the broad range of quantitative accuracy of the QDπ model for the data examined. Taken together, this suggests that QM/Δ-MLPs such as QDπ and AIQM1 have considerable promise as universal force fields for drug discovery applications.
SUPPLEMENTARY MATERIAL
See the supplementary material for relative energies for the minima and transition states of the alanine dipeptide, ibuprofen, and ketorolac.
ACKNOWLEDGMENTS
The authors are grateful for the financial support provided by the National Institutes of Health (Grant No. GM107485 to D.M.Y.) and the National Science Foundation (Grant No. 2209718 to D.M.Y.). Computational resources were provided by the Office of Advanced Research Computing (OARC) at Rutgers, The State University of New Jersey, the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation under Grant No. ACI-1548562 (supercomputer Expanse at SDSC through allocation under Grant No. CHE190067), and by the Texas Advanced Computing Center (TACC) at the University of Texas at Austin (supercomputer Longhorn through allocation under Grant No. CHE20002).
Note: This paper is part of the JCP Special Topic on Modern Semiempirical Electronic Structure Methods.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
Author Contributions
Jinzhe Zeng (曾晋哲): Data curation (equal); Software (equal); Visualization (equal); Writing – original draft (equal); Writing – review & editing (equal). Yujun Tao (陶玉君): Data curation (equal); Visualization (equal); Writing – review & editing (equal). Timothy J. Giese: Writing – review & editing (equal). Darrin M. York: Formal analysis (equal); Funding acquisition (equal); Project administration (equal); Resources (equal); Supervision (equal); Writing – original draft (equal); Writing – review & editing (equal).
DATA AVAILABILITY
QDπ-v1.0 is openly available in our GitLab repository at https://gitlab.com/RutgersLBSR/qdpi, which was previously released.77 The data that support the findings of this study are available from the corresponding author upon reasonable request.
REFERENCES
- 1.Lee T.-S., Allen B. K., Giese T. J., Guo Z., Li P., Lin C., T. D. McGee, Jr., Pearlman D. A., Radak B. K., Tao Y., Tsai H.-C., Xu H., Sherman W., and York D. M., “Alchemical binding free energy calculations in AMBER20: Advances and best practices for drug discovery,” J. Chem. Inf. Model. 60, 5595–5623 (2020). 10.1021/acs.jcim.0c00613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jorgensen W. L., “Efficient drug lead discovery and optimization,” Acc. Chem. Res. 42, 724–733 (2009). 10.1021/ar800236t [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cole D. J., Horton J. T., Nelson L., and Kurdekar V., “The future of force fields in computer-aided drug design,” Future Med. Chem. 11, 2359–2363 (2019). 10.4155/fmc-2019-0196 [DOI] [PubMed] [Google Scholar]
- 4.A. D. MacKerell, Jr., “Empirical force fields for biological macromolecules: Overview and issues,” J. Comput. Chem. 25, 1584–1604 (2004). 10.1002/jcc.20082 [DOI] [PubMed] [Google Scholar]
- 5.Lindorff-Larsen K., Maragakis P., Piana S., Eastwood M. P., Dror R. O., and Shaw D. E., “Systematic validation of protein force fields against experimental data,” PLoS One 7, e32131 (2012). 10.1371/journal.pone.0032131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Piana S., Klepeis J. L., and Shaw D. E., “Assessing the accuracy of physical models used in protein-folding simulations: Quantitative evidence from long molecular dynamics simulations,” Curr. Opin. Struct. Biol. 24, 98–105 (2014). 10.1016/j.sbi.2013.12.006 [DOI] [PubMed] [Google Scholar]
- 7.Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., “Comparison of simple potential functions for simulating liquid water,” J. Chem. Phys. 79, 926–935 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- 8.Horn H. W., Swope W. C., Pitera J. W., Madura J. D., Dick T. J., Hura G. L., and Head-Gordon T., “Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew,” J. Chem. Phys. 120, 9665–9678 (2004). 10.1063/1.1683075 [DOI] [PubMed] [Google Scholar]
- 9.Wu Y., Tepper H. L., and Voth G. A., “Flexible simple point-charge water model with improved liquid-state properties,” J. Chem. Phys. 124, 024503 (2006). 10.1063/1.2136877 [DOI] [PubMed] [Google Scholar]
- 10.Izadi S., Anandakrishnan R., and Onufriev A. V., “Building water models: A different approach,” J. Phys. Chem. Lett. 5, 3863–3871 (2014). 10.1021/jz501780a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Izadi S. and Onufriev A. V., “Accuracy limit of rigid 3-point water models,” J. Chem. Phys. 145, 074501–074510 (2016). 10.1063/1.4960175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Joung I. S. and Cheatham T. E. III, “Molecular dynamics simulations of the dynamic and energetic properties of alkali and halide ions using water-model-specific ion parameters,” J. Phys. Chem. B 113, 13279–13290 (2009). 10.1021/jp902584c [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li P., Roberts B. P., Chakravorty D. K., and K. M. Merz, Jr., “Rational design of particle mesh Ewald compatible Lennard-Jones parameters for +2 metal cations in explicit solvent,” J. Chem. Theory Comput. 9, 2733–2748 (2013). 10.1021/ct400146w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li P. and K. M. Merz, Jr., “Taking into account the ion-induced dipole interaction in the nonbonded model of ions,” J. Chem. Theory Comput. 10, 289–297 (2014). 10.1021/ct400751u [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Li P. and Merz K. M., “Metal ion modeling using classical mechanics,” Chem. Rev. 117, 1564–1686 (2017). 10.1021/acs.chemrev.6b00440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lopes P. E. M., Guvench O., and A. D. MacKerell, Jr., “Current status of protein force fields for molecular dynamics simulations,” Methods Mol. Biol. 1215, 47–71 (2015). 10.1007/978-1-4939-1465-4_3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tian C., Kasavajhala K., Belfon K. A. A., Raguette L., Huang H., Migues A. N., Bickel J., Wang Y., Pincay J., Wu Q., and Simmerling C., “ff19SB: Amino-acid-specific protein backbone parameters trained against quantum mechanics energy surfaces in solution,” J. Chem. Theory Comput. 16, 528–552 (2020). 10.1021/acs.jctc.9b00591 [DOI] [PubMed] [Google Scholar]
- 18.Martin Y. C., “Experimental and pKa prediction aspects of tautomerism of drug-like molecules,” Drug Discovery Today: Technol. 27, 59–64 (2018). 10.1016/j.ddtec.2018.06.006 [DOI] [PubMed] [Google Scholar]
- 19.Milletti F. and Vulpetti A., “Tautomer preference in PDB complexes and its impact on structure-based drug discovery,” J. Chem. Inf. Model. 50, 1062–1074 (2010). 10.1021/ci900501c [DOI] [PubMed] [Google Scholar]
- 20.Wells J. I., Pharmaceutical Preformulation: The Physicochemical Properties of Drug Substances (E. Horwood, Chichester, UK, 1988). [Google Scholar]
- 21.Navo C. D. and Jiménez-Osés G., “Computer prediction of pKa values in small molecules and proteins,” ACS Med. Chem. Lett. 12, 1624–1628 (2021). 10.1021/acsmedchemlett.1c00435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Thiel W., “Semiempirical quantum–chemical methods,” Wiley Interdiscip. Rev.: Comput. Mol. Sci. 4, 145–157 (2014). 10.1002/wcms.1161 [DOI] [Google Scholar]
- 23.Kříž K. and Řezáč J., “Benchmarking of semiempirical quantum-mechanical methods on systems relevant to computer-aided drug design,” J. Chem. Inf. Model. 60, 1453–1460 (2020). 10.1021/acs.jcim.9b01171 [DOI] [PubMed] [Google Scholar]
- 24.Khanna V. and Ranganathan S., “Physicochemical property space distribution among human metabolites, drugs and toxins,” BMC Bioinf. 10, S10 (2009). 10.1186/1471-2105-10-s15-s10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Darden T., York D., and Pedersen L., “Particle mesh Ewald: An N log(N) method for Ewald sums in large systems,” J. Chem. Phys. 98, 10089–10092 (1993). 10.1063/1.464397 [DOI] [Google Scholar]
- 26.Nam K., Gao J., and York D. M., “An efficient linear-scaling Ewald method for long-range electrostatic interactions in combined QM/MM calculations,” J. Chem. Theory Comput. 1, 2–13 (2005). 10.1021/ct049941i [DOI] [PubMed] [Google Scholar]
- 27.Giese T. J., Panteva M. T., Chen H., and York D. M., “Multipolar Ewald methods, 2: Applications using a quantum mechanical force field,” J. Chem. Theory Comput. 11, 451–461 (2015). 10.1021/ct500799g [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Giese T. J. and York D. M., “Ambient-potential composite Ewald method for ab initio quantum mechanical/molecular mechanical molecular dynamics simulation,” J. Chem. Theory Comput. 12, 2611–2632 (2016). 10.1021/acs.jctc.6b00198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Margraf J. T., Hennemann M., and Clark T., “EMPIRE: A highly parallel semiempirical molecular orbital program: 3: Born-Oppenheimer molecular dynamics,” J. Mol. Model. 26, 43 (2020). 10.1007/s00894-020-4293-z [DOI] [PubMed] [Google Scholar]
- 30.Hourahine B., Aradi B., Blum V., Bonafé F., Buccheri A., Camacho C., Cevallos C., Deshaye M. Y., Dumitrică T., Dominguez A., Ehlert S., Elstner M., van der Heide T., Hermann J., Irle S., Kranz J. J., Köhler C., Kowalczyk T., Kubař T., Lee I. S., Lutsker V., Maurer R. J., Min S. K., Mitchell I., Negre C., Niehaus T. A., Niklasson A. M. N., Page A. J., Pecchia A., Penazzi G., Persson M. P., Řezáč J., Sánchez C. G., Sternberg M., Stöhr M., Stuckenberg F., Tkatchenko A., Yu V. W.-z., and Frauenheim T., “DFTB+, a software package for efficient approximate density functional theory based atomistic simulations,” J. Chem. Phys. 152, 124101 (2020). 10.1063/1.5143190 [DOI] [PubMed] [Google Scholar]
- 31.Giese T. J. and York D. M., “Development of a robust indirect approach for MM → QM free energy calculations that combines force-matched reference potential and Bennett’s acceptance ratio methods,” J. Chem. Theory Comput. 15, 5543–5562 (2019). 10.1021/acs.jctc.9b00401 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kearns F. L., Hudson P. S., Woodcock H. L., and Boresch S., “Computing converged free energy differences between levels of theory via nonequilibrium work methods: Challenges and opportunities,” J. Comput. Chem. 38, 1376–1388 (2017). 10.1002/jcc.24706 [DOI] [PubMed] [Google Scholar]
- 33.Boresch S. and Woodcock H. L., “Convergence of single-step free energy perturbation,” Mol. Phys. 115, 1200–1213 (2017). 10.1080/00268976.2016.1269960 [DOI] [Google Scholar]
- 34.Hudson P. S., Aviat F., Meana-Pañeda R., Warrensford L., Pollard B. C., Prasad S., Jones M. R., Woodcock H. L., and Brooks B. R., “Obtaining QM/MM binding free energies in the SAMPL8 drugs of abuse challenge: Indirect approaches,” J. Comput.-Aided Mol. Des. 36, 263–277 (2022). 10.1007/s10822-022-00443-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Schöller A., Kearns F., Woodcock H. L., and Boresch S., “Optimizing the calculation of free energy differences in nonequilibrium work SQM/MM switching simulations,” J. Phys. Chem. B 126, 2798–2811 (2022). 10.1021/acs.jpcb.2c00696 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Arya G., “Models for recovering the energy landscape of conformational transitions from single-molecule pulling experiments,” Mol. Simul. 42, 1102–1115 (2016). 10.1080/08927022.2015.1123257 [DOI] [Google Scholar]
- 37.Naganathan A. N., Doshi U., and Muñoz V., “Protein folding kinetics: Barrier effects in chemical and thermal denaturation experiments,” J. Am. Chem. Soc. 129, 5673–5682 (2007). 10.1021/ja0689740 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Basran J., Patel S., Sutcliffe M. J., and Scrutton N. S., “Importance of barrier shape in enzyme-catalyzed reactions,” J. Biol. Chem. 276, 6234–6242 (2001). 10.1074/jbc.m008141200 [DOI] [PubMed] [Google Scholar]
- 39.Behler J., “Perspective: Machine learning potentials for atomistic simulations,” J. Chem. Phys. 145, 170901 (2016). 10.1063/1.4966192 [DOI] [PubMed] [Google Scholar]
- 40.Butler K. T., Davies D. W., Cartwright H., Isayev O., and Walsh A., “Machine learning for molecular and materials science,” Nature 559, 547–555 (2018). 10.1038/s41586-018-0337-2 [DOI] [PubMed] [Google Scholar]
- 41.Noé F., Tkatchenko A., Müller K.-R., and Clementi C., “Machine learning for molecular simulation,” Annu. Rev. Phys. Chem. 71, 361–390 (2020). 10.1146/annurev-physchem-042018-052331 [DOI] [PubMed] [Google Scholar]
- 42.M. Pinheiro, Jr., Ge F., Ferré N., Dral P. O., and Barbatti M., “Choosing the right molecular machine learning potential,” Chem. Sci. 12, 14396–14413 (2021). 10.1039/d1sc03564a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Manzhos S. and T. Carrington, Jr., “Neural network potential energy surfaces for small molecules and reactions,” Chem. Rev. 121, 10187–10217 (2021). 10.1021/acs.chemrev.0c00665 [DOI] [PubMed] [Google Scholar]
- 44.Zeng J., Cao L., and Zhu T., “Neural network potentials,” in Quantum Chemistry in the Age of Machine Learning, edited by Dral P. O. (Elsevier, 2022) Chap. 12, pp. 279–294. [Google Scholar]
- 45.Pan X., Yang J., Van R., Epifanovsky E., Ho J., Huang J., Pu J., Mei Y., Nam K., and Shao Y., “Machine-learning-assisted free energy simulation of solution-phase and enzyme reactions,” J. Chem. Theory Comput. 17, 5745–5758 (2021). 10.1021/acs.jctc.1c00565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zheng P., Zubatyuk R., Wu W., Isayev O., and Dral P. O., “Artificial intelligence-enhanced quantum chemical method with broad applicability,” Nat. Commun. 12, 7022 (2021). 10.1038/s41467-021-27340-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Zeng J., Giese T. J., Ekesan Ş., and York D. M., “Development of range-corrected deep learning potentials for fast, accurate quantum mechanical/molecular mechanical simulations of chemical reactions in solution,” J. Chem. Theory Comput. 17, 6993–7009 (2021). 10.1021/acs.jctc.1c00201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Giese T. J., Zeng J., Ekesan Ş., and York D. M., “Combined QM/MM, machine learning path integral approach to compute free energy profiles and kinetic isotope effects in RNA cleavage reactions,” J. Chem. Theory Comput. 18, 4304–4317 (2022). 10.1021/acs.jctc.2c00151 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gómez-Flores C. L., Maag D., Kansari M., Vuong V.-Q., Irle S., Gräter F., Kubař T., and Elstner M., “Accurate free energies for complex condensed-phase reactions using an artificial neural network corrected DFTB/MM methodology,” J. Chem. Theory Comput. 18, 1213–1226 (2022). 10.1021/acs.jctc.1c00811 [DOI] [PubMed] [Google Scholar]
- 50.Böser J., Kubař T., Elstner M., and Maag D., “Reduction pathway of glutaredoxin 1 investigated with QM/MM molecular dynamics using a neural network correction,” J. Chem. Phys. 157, 154104 (2022). 10.1063/5.0123089 [DOI] [PubMed] [Google Scholar]
- 51.Dral P. O., Zubatiuk T., and Xue B.-X., “Learning from multiple quantum chemical methods: Δ-learning, transfer learning, co-kriging, and beyond,” in Quantum Chemistry in the Age of Machine Learning, edited by Dral P. O. (Elsevier, 2022) Chap. 21, pp. 491–507. [Google Scholar]
- 52.Behler J. and Parrinello M., “Generalized neural-network representation of high-dimensional potential-energy surfaces,” Phys. Rev. Lett. 98, 146401–146404 (2007). 10.1103/physrevlett.98.146401 [DOI] [PubMed] [Google Scholar]
- 53.Bartók A. P., Payne M. C., Kondor R., and Csányi G., “Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons,” Phys. Rev. Lett. 104, 136403 (2010). 10.1103/physrevlett.104.136403 [DOI] [PubMed] [Google Scholar]
- 54.Behler J., “Atom-centered symmetry functions for constructing high-dimensional neural network potentials,” J. Chem. Phys. 134, 074106 (2011). 10.1063/1.3553717 [DOI] [PubMed] [Google Scholar]
- 55.Gastegger M., Schwiedrzik L., Bittermann M., Berzsenyi F., and Marquetand P., “wACSF—Weighted atom-centered symmetry functions as descriptors in machine learning potentials,” J. Chem. Phys. 148, 241709 (2018). 10.1063/1.5019667 [DOI] [PubMed] [Google Scholar]
- 56.Chmiela S., Tkatchenko A., Sauceda H. E., Poltavsky I., Schütt K. T., and Müller K.-R., “Machine learning of accurate energy-conserving molecular force fields,” Sci. Adv. 3, 1603015 (2017). 10.1126/sciadv.1603015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Schütt K. T., Arbabzadah F., Chmiela S., Müller K. R., and Tkatchenko A., “Quantum-chemical insights from deep tensor neural networks,” Nat. Commun. 8, 13890 (2017). 10.1038/ncomms13890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Schütt K. T., Sauceda H. E., Kindermans P.-J., Tkatchenko A., and Müller K.-R., “SchNet – A deep learning architecture for molecules and materials,” J. Chem. Phys. 148, 241722 (2018). 10.1063/1.5019779 [DOI] [PubMed] [Google Scholar]
- 59.Chen X., Jørgensen M. S., Li J., and Hammer B., “Atomic energies from a convolutional neural network,” J. Chem. Theory Comput. 14, 3933–3942 (2018). 10.1021/acs.jctc.8b00149 [DOI] [PubMed] [Google Scholar]
- 60.Zhang L., Han J., Wang H., Car R., and E W., “Deep potential molecular dynamics: A scalable model with the accuracy of quantum mechanics,” Phys. Rev. Lett. 120, 143001 (2018). 10.1103/physrevlett.120.143001 [DOI] [PubMed] [Google Scholar]
- 61.Zhang L., Han J., Wang H., Saidi W., Car R., and E W., “End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems,” in Advances in Neural Information Processing Systems 31, edited by Bengio S., Wallach H., Larochelle H., Grauman K., Cesa-Bianchi N., and Garnett R. (Curran Associates, Inc., 2018), pp. 4436–4446. [Google Scholar]
- 62.Zhang Y., Hu C., and Jiang B., “Embedded atom neural network potentials: Efficient and accurate machine learning with a physically inspired representation,” J. Phys. Chem. Lett. 10, 4962–4967 (2019). 10.1021/acs.jpclett.9b02037 [DOI] [PubMed] [Google Scholar]
- 63.Smith J. S., Isayev O., and Roitberg A. E., “ANI-1: An extensible neural network potential with DFT accuracy at force field computational cost,” Chem. Sci. 8, 3192–3203 (2017). 10.1039/c6sc05720a [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Unke O. and Meuwly M., “PhysNet: A neural network for predicting energies, forces, dipole moments, and partial charges,” J. Chem. Theory Comput. 15, 3678–3693 (2019). 10.1021/acs.jctc.9b00181 [DOI] [PubMed] [Google Scholar]
- 65.Glick Z. L., Metcalf D. P., Koutsoukas A., Spronk S. A., Cheney D. L., and Sherrill C. D., “AP-Net: An atomic-pairwise neural network for smooth and transferable interaction potentials,” J. Chem. Phys. 153, 044112 (2020). 10.1063/5.0011521 [DOI] [PubMed] [Google Scholar]
- 66.Zubatiuk T. and Isayev O., “Development of multimodal machine learning potentials: Toward a physics-aware artificial intelligence,” Acc. Chem. Res. 54, 1575–1585 (2021). 10.1021/acs.accounts.0c00868 [DOI] [PubMed] [Google Scholar]
- 67.Khajehpasha E. R., Finkler J. A., Kühne T. D., and Ghasemi S. A., “CENT2: Improved charge equilibration via neural network technique,” Phys. Rev. B 105, 144106 (2022). 10.1103/physrevb.105.144106 [DOI] [Google Scholar]
- 68.Hirano Y., Okimoto N., Fujita S., and Taiji M., “Molecular dynamics study of conformational changes of tankyrase 2 binding subsites upon ligand binding,” ACS Omega 6, 17609–17620 (2021). 10.1021/acsomega.1c02159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kenny P. W., “Hydrogen-bond donors in drug design,” J. Med. Chem. 65, 14261–14275 (2022). 10.1021/acs.jmedchem.2c01147 [DOI] [PubMed] [Google Scholar]
- 70.Yuki H., Tanaka Y., Hata M., Ishikawa H., Neya S., and Hoshino T., “Implementation of π–π interactions in molecular dynamics simulation,” J. Comput. Chem. 28, 1091–1099 (2007). 10.1002/jcc.20557 [DOI] [PubMed] [Google Scholar]
- 71.Chen T., Li M., and Liu J., “π–π Stacking interaction: A nondestructive and facile means in material engineering for bioapplications,” Cryst. Growth Des. 18, 2765–2783 (2018). 10.1021/acs.cgd.7b01503 [DOI] [Google Scholar]
- 72.Mohebifar M., Johnson E. R., and Rowley C. N., “Evaluating force-field London dispersion coefficients using the exchange-hole dipole moment model,” J. Chem. Theory Comput. 13, 6146–6157 (2017). 10.1021/acs.jctc.7b00522 [DOI] [PubMed] [Google Scholar]
- 73.Vazquez-Salazar L. I., Boittier E. D., Unke O. T., and Meuwly M., “Impact of the characteristics of quantum chemical databases on machine learning prediction of tautomerization energies,” J. Chem. Theory Comput. 17, 4769–4785 (2021). 10.1021/acs.jctc.1c00363 [DOI] [PubMed] [Google Scholar]
- 74.Smith J. S., Nebgen B., Lubbers N., Isayev O., and Roitberg A. E., “Less is more: Sampling chemical space with active learning,” J. Chem. Phys. 148, 241733–241743 (2018). 10.1063/1.5023802 [DOI] [PubMed] [Google Scholar]
- 75.Smith J., Nebgen B., Zubatyuk R., Lubbers N., Devereux C., Barros K., Tretiak S., Isayev O., and Roitberg A., “Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning,” Nat. Commun. 10, 2903 (2019). 10.1038/s41467-019-10827-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Devereux C., Smith J. S., Huddleston K. K., Barros K., Zubatyuk R., Isayev O., and Roitberg A. E., “Extending the applicability of the ANI deep learning molecular potential to sulfur and halogens,” J. Chem. Theory Comput. 16, 4192–4202 (2020). 10.1021/acs.jctc.0c00121 [DOI] [PubMed] [Google Scholar]
- 77.amd Yujun Tao J. Z., Giese T. J., and York D. M., “QDπ: A quantum deep potential interaction model for drug discovery,” J. Chem. Theory Comput. 19, 1261–1275 (2023). 10.1021/acs.jctc.2c01172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Dral P. O., Wu X., and Thiel W., “Semiempirical quantum-chemical methods with orthogonalization and dispersion corrections,” J. Chem. Theory Comput. 15, 1743–1760 (2019). 10.1021/acs.jctc.8b01265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Chen Y., Ou Y., Zheng P., Huang Y., Ge F., and Dral P. O., “Benchmark of general-purpose machine learning-based quantum mechanical method AIQM1 on reaction barrier heights,” J. Chem. Phys. 158, 074103 (2023). 10.1063/5.0137101 [DOI] [PubMed] [Google Scholar]
- 80.Yang Y., Yu H., York D. M., Cui Q., and Elstner M., “Extension of the self-consistent-charge density-functional tight-binding method: Third-order expansion of the density functional theory total energy and introduction of a modified effective coulomb interaction,” J. Phys. Chem. A 111, 10861–10873 (2007). 10.1021/jp074167r [DOI] [PubMed] [Google Scholar]
- 81.Gaus M., Lu X., Elstner M., and Cui Q., “Parameterization of DFTB3/3OB for sulfur and phosphorus for chemical and biological applications,” J. Chem. Theory Comput. 10, 1518–1537 (2014). 10.1021/ct401002w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Wang H., Zhang L., Han J., and E W., “DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics,” Comput. Phys. Commun. 228, 178–184 (2018). 10.1016/j.cpc.2018.03.016 [DOI] [Google Scholar]
- 83.Liang W., Zeng J., York D. M., Zhang L., and Wang H., “Learning DeePMD-kit: A guide to building deep potential models,” in A Practical Guide to Recent Advances in Multiscale Modeling and Simulation of Biomolecules, edited by Wang Y. and Zhou R. (AIP Publishing, 2023), Chap. 6, pp. 6–1–6–20. [Google Scholar]
- 84.Yang Z., Hutter D., Sheng P., Sismour A. M., and Benner S. A., “Artificially expanded genetic information system: A new base pair with an alternative hydrogen bonding pattern,” Nucleic Acids Res. 34, 6095–6101 (2006). 10.1093/nar/gkl633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Eberlein L., Beierlein F. R., van Eikema Hommes N. J. R., Radadiya A., Heil J., Benner S. A., Clark T., Kast S. M., and Richards N. G. J., “Tautomeric equilibria of nucleobases in the hachimoji expanded genetic alphabet,” J. Chem. Theory Comput. 16, 2766–2777 (2020). 10.1021/acs.jctc.9b01079 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Biondi E. and Benner S. A., “Artificially expanded genetic information systems for new aptamer technologies,” Biomedicines 6, 53 (2018). 10.3390/biomedicines6020053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Behera B., Das P., and Jena N. R., “Accurate base pair energies of artificially expanded genetic information systems (AEGIS): Clues for their mutagenic characteristics,” J. Phys. Chem. B 123, 6728–6739 (2019). 10.1021/acs.jpcb.9b04653 [DOI] [PubMed] [Google Scholar]
- 88.Jerome C. A., Hoshika S., Bradley K. M., Benner S. A., and Biondi E., “In vitro evolution of ribonucleases from expanded genetic alphabets,” Proc. Natl. Acad. Sci. U. S. A. 119, e2208261119 (2022). 10.1073/pnas.2208261119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Dewar M. J. S. and Thiel W., “A semiempirical model for the two-Center repulsion integrals in the NDDO approximation,” Theor. Chim. Acta 46, 89–104 (1977). 10.1007/bf00548085 [DOI] [Google Scholar]
- 90.Dewar M. J. S., Zoebisch E., Healy E. F., and Stewart J. J. P., “Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model.” J. Am. Chem. Soc. 107, 3902–3909 (1985). 10.1021/ja00299a024 [DOI] [Google Scholar]
- 91.Stewart J. J. P., “Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements,” J. Mol. Model. 13, 1173–1213 (2007). 10.1007/s00894-007-0233-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.R̆ezác̆ J. and Hobza P., “Advanced corrections of hydrogen bonding and dispersion for semiempirical quantum mechanical methods,” J. Chem. Theory Comput. 8, 141–151 (2012). 10.1021/ct200751e [DOI] [PubMed] [Google Scholar]
- 93.Řezáč J. and Hobza P., “A halogen-bonding correction for the semiempirical PM6 method,” Chem. Phys. Lett. 506, 286–289 (2011). 10.1016/j.cplett.2011.03.009 [DOI] [Google Scholar]
- 94.Stewart J. J. P., “Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters,” J. Mol. Model. 19, 1–32 (2013). 10.1007/s00894-012-1667-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Gaus M., Cui Q., and Elstner M., “DFTB3: Extension of the self-consistent-charge density-functional tight-binding method (SCC-DFTB),” J. Chem. Theory Comput. 7, 931–948 (2011). 10.1021/ct100684s [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Grimme S., Bannwarth C., and Shushkov P., “A robust and accurate tight-binding quantum chemical method for structures, vibrational frequencies, and noncovalent interactions of large molecular systems parametrized for all spd-block elements (Z = 1–86),” J. Chem. Theory Comput. 13, 1989–2009 (2017). 10.1021/acs.jctc.7b00118 [DOI] [PubMed] [Google Scholar]
- 97.Bannwarth C., Ehlert S., and Grimme S., “GFN2-xTB—An accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions,” J. Chem. Theory Comput. 15, 1652–1671 (2019). 10.1021/acs.jctc.8b01176 [DOI] [PubMed] [Google Scholar]
- 98.Goldman N., Kweon K. E., Sadigh B., Heo T. W., Lindsey R. K., Pham C. H., Fried L. E., Aradi B., Holliday K., Jeffries J. R., and Wood B. C., “Semi-automated creation of density functional tight binding models through leveraging Chebyshev polynomial-based force fields,” J. Chem. Theory Comput. 17, 4435–4448 (2021). 10.1021/acs.jctc.1c00172 [DOI] [PubMed] [Google Scholar]
- 99.Chai J.-D. and Head-Gordon M., “Systematic optimization of long-range corrected hybrid density functionals,” J. Chem. Phys. 128, 084106 (2008). 10.1063/1.2834918 [DOI] [PubMed] [Google Scholar]
- 100.Bevilacqua P. C., Harris M. E., Piccirilli J. A., Gaines C., Ganguly A., Kostenbader K., Ekesan Ş., and York D. M., “An ontology for facilitating discussion of catalytic strategies of RNA-cleaving enzymes,” ACS Chem. Biol. 14, 1068–1076 (2019). 10.1021/acschembio.9b00202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Petersson G. A., Nakatsuji H., Li X., Caricato M., Marenich A. V., Bloino J., Janesko B. G., Gomperts R., Mennucci B., Hratchian H. P., Ortiz J. V., Izmaylov A. F., Sonnenberg J. L., Williams-Young D., Ding F., Lipparini F., Egidi F., Goings J., Peng B., Petrone A., Henderson T., Ranasinghe D., Zakrzewski V. G., Gao J., Rega N., Zheng G., Liang W., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Throssell K., J. A. Montgomery, Jr., Peralta J. E., Ogliaro F., Bearpark M. J., Heyd J. J., Brothers E. N., Kudin K. N., Staroverov V. N., Keith T. A., Kobayashi R., Normand J., Raghavachari K., Rendell A. P., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Millam J. M., Klene M., Adamo C., Cammi R., Ochterski J. W., Martin R. L., Morokuma K., Farkas O., Foresman J. B., and Fox D. J., Gaussian 16 Revision A.03, Gaussian, Inc., Wallingford CT, 2016. [Google Scholar]
- 102.Beveridge D. L., Approximate Molecular Orbital Theory of Nuclear and Electron Magnetic Resonance Parameters (Springer, Boston, 1977). [Google Scholar]
- 103.Tuttle T. and Thiel W., “OMx-D: Semiempirical methods with orthogonalization and dispersion corrections. Implementation and biochemical application,” Phys. Chem. Chem. Phys. 10, 2159–2166 (2008). 10.1039/b718795e [DOI] [PubMed] [Google Scholar]
- 104.Tuna D., Lu Y., Koslowski A., and Thiel W., “Semiempirical quantum-chemical orthogonalization-corrected methods: Benchmarks of electronically excited states,” J. Chem. Theory Comput. 12, 4400–4422 (2016). 10.1021/acs.jctc.6b00403 [DOI] [PubMed] [Google Scholar]
- 105.Dral P. O., Wu X., Spörkel L., Koslowski A., Weber W., Steiger R., Scholten M., and Thiel W., “Semiempirical quantum-chemical orthogonalization-corrected methods: Theory, implementation, and parameters,” J. Chem. Theory Comput. 12, 1082–1096 (2016). 10.1021/acs.jctc.5b01046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Dral P. O., Wu X., Spörkel L., Koslowski A., and Thiel W., “Semiempirical quantum-chemical orthogonalization-corrected methods: Benchmarks for ground-state properties,” J. Chem. Theory Comput. 12, 1097–1120 (2016). 10.1021/acs.jctc.5b01047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Case D. A., Belfon K., Ben-Shalom I. Y., Brozell S. R., Cerutti D. S., Cheatham T. E. III, Cruzeiro V. W. D., Darden T. A., Duke R. E., Giambasu G., , Gilson M. K., Gohlke H., Goetz A. W., Harris R., Izadi S., Izmailov S. A., Kasavajhala K., Kovalenko K., Krasny R., Kurtzman T., Lee T., Le-Grand S., Li P., Lin C., Liu J., Luchko T., Luo R., Man V., Merz K., Miao Y., Mikhailovskii O., Monard G., , Nguyen H., Onufriev A., Pan F., Pantano S., Qi R., Roe D. R., Roitberg A., Sagui C., Schott-Verdugo S., Shen J., Simmerling C. L., Skrynnikov N., Smith J., Swails J., Walker R. C., Wang J., Wilson R. M., Wolf R. M., Wu X., Xiong Y., Xue Y., York D. M., and Kollman P. A., AMBER 20, University of California, San Francisco, CA, 2020. [Google Scholar]
- 108.Walker R. C., Crowley M. F., and Case D. A., “The implementation of a fast and accurate QM/MM potential method in Amber,” J. Comput. Chem. 29, 1019–1031 (2008). 10.1002/jcc.20857 [DOI] [PubMed] [Google Scholar]
- 109.Thiel M., MNDO, Max-Planck-Institut für Kohlenforschung, Mülheim an der Ruhr, 2022.
- 110.Stewart J. J. P., “MOPAC: A semiempirical molecular orbital program,” J. Comput.-Aided Mol. Des. 4, 1–105 (1990). 10.1007/bf00128336 [DOI] [PubMed] [Google Scholar]
- 111.Hostaš J., Řezáč J., and Hobza P., “On the performance of the semiempirical quantum mechanical PM6 and PM7 methods for noncovalent interactions,” Chem. Phys. Lett. 568, 161–166 (2013). 10.1016/j.cplett.2013.02.069 [DOI] [Google Scholar]
- 112.Sulimov A. V., Kutov D. C., Katkova E. V., Ilin I. S., and Sulimov V. B., “New generation of docking programs: Supercomputer validation of force fields and quantum-chemical methods for docking,” J. Mol. Graphics Modell. 78, 139–147 (2017). 10.1016/j.jmgm.2017.10.007 [DOI] [PubMed] [Google Scholar]
- 113.Giese T. J. and York D. M., “Density-functional expansion methods: Grand challenges,” Theor. Chem. Acc. 131, 1145 (2012). 10.1007/s00214-012-1145-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Gaus M., Goez A., and Elstner M., “Parametrization and benchmark of DFTB3 for organic molecules,” J. Chem. Theory Comput. 9, 338–354 (2013). 10.1021/ct300849w [DOI] [PubMed] [Google Scholar]
- 115.Seabra G., Walker R. C., Elstner M., Case D. A., and Roitberg A. E., “Implementation of the SCC-DFTB method for hybrid QM/MM simulations within the amber molecular dynamics package,” J. Phys. Chem. A 111, 5655–5664 (2007). 10.1021/jp070071l [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Pham C. H., Lindsey R. K., Fried L. E., and Goldman N., “High-accuracy semiempirical quantum models based on a minimal training set,” J. Phys. Chem. Lett. 13, 2934–2942 (2022). 10.1021/acs.jpclett.2c00453 [DOI] [PubMed] [Google Scholar]
- 117.Lindsey R. K., Fried L. E., and Goldman N., “ChIMES: A force matched potential with explicit three-body interactions for molten carbon,” J. Chem. Theory Comput. 13, 6222–6229 (2017). 10.1021/acs.jctc.7b00867 [DOI] [PubMed] [Google Scholar]
- 118.Li H., Collins C., Tanha M., Gordon G. J., and Yaron D. J., “A density functional tight binding layer for deep learning of chemical Hamiltonians,” J. Chem. Theory Comput. 14, 5764–5776 (2018). 10.1021/acs.jctc.8b00873 [DOI] [PubMed] [Google Scholar]
- 119.Zhu J., Vuong V. Q., Sumpter B. G., and Irle S., “Artificial neural network correction for density-functional tight-binding molecular dynamics simulations,” MRS Commun. 9, 867–873 (2019). 10.1557/mrc.2019.80 [DOI] [Google Scholar]
- 120.Stöhr M., Medrano Sandonas L., and Tkatchenko A., “Accurate many-body repulsive potentials for density-functional tight binding from deep tensor neural networks,” J. Phys. Chem. Lett. 11, 6835–6843 (2020). 10.1021/acs.jpclett.0c01307 [DOI] [PubMed] [Google Scholar]
- 121.Panosetti C., Engelmann A., Nemec L., Reuter K., and Margraf J. T., “Learning to use the force: Fitting repulsive potentials in density-functional tight-binding with Gaussian process regression,” J. Chem. Theory Comput. 16, 2181–2191 (2020). 10.1021/acs.jctc.9b00975 [DOI] [PubMed] [Google Scholar]
- 122.Kranz J. J., Kubillus M., Ramakrishnan R., von Lilienfeld O. A., and Elstner M., “Generalized density-functional tight-binding repulsive potentials from unsupervised machine learning,” J. Chem. Theory Comput. 14, 2341–2352 (2018). 10.1021/acs.jctc.7b00933 [DOI] [PubMed] [Google Scholar]
- 123.Gao X., Ramezanghorbani F., Isayev O., Smith J. S., and Roitberg A. E., “TorchANI: A free and open source PyTorch-based deep learning implementation of the ANI neural network potentials,” J. Chem. Inf. Model. 60, 3408–3415 (2020). 10.1021/acs.jcim.0c00451 [DOI] [PubMed] [Google Scholar]
- 124.Caldeweyher E., Bannwarth C., and Grimme S., “Extension of the D3 dispersion coefficient model,” J. Chem. Phys. 147, 034112 (2017). 10.1063/1.4993215 [DOI] [PubMed] [Google Scholar]
- 125.Liu D. C. and Nocedal J., “On the limited memory BFGS method for large scale optimization,” Math. Program. 45, 503–528 (1989). 10.1007/bf01589116 [DOI] [Google Scholar]
- 126.Hjorth Larsen A., Jørgen Mortensen J., Blomqvist J., Castelli I. E., Christensen R., Dułak M., Friis J., Groves M. N., Hammer B., Hargus C., Hermes E. D., Jennings P. C., Bjerre Jensen P., Kermode J., Kitchin J. R., Leonhard Kolsbjerg E., Kubal J., Kaasbjerg K., Lysgaard S., Bergmann Maronsson J., Maxson T., Olsen T., Pastewka L., Peterson A., Rostgaard C., Schiøtz J., Schütt O., Strange M., Thygesen K. S., Vegge T., Vilhelmsen L., Walter M., Zeng Z., and Jacobsen K. W., “The atomic simulation environment—A Python library for working with atoms,” J. Phys.: Condens. Matter 29, 273002 (2017). 10.1088/1361-648x/aa680e [DOI] [PubMed] [Google Scholar]
- 127.Smith J. S., Zubatyuk R., Nebgen B., Lubbers N., Barros K., Roitberg A. E., Isayev O., and Tretiak S., “The ANI-1ccx and ANI-1x data sets, coupled-cluster and density functional theory properties for molecules,” Sci. Data 7, 134 (2020). 10.1038/s41597-020-0473-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Fink T., Bruggesser H., and Reymond J.-L., “Virtual exploration of the small-molecule chemical universe below 160 daltons,” Angew. Chem., Int. Ed. 44, 1504–1508 (2005). 10.1002/anie.200462457 [DOI] [PubMed] [Google Scholar]
- 129.Blum L. C. and Reymond J.-L., “970 million druglike small molecules for virtual screening in the chemical universe database GDB-13,” J. Am. Chem. Soc. 131, 8732–8733 (2009). 10.1021/ja902302h [DOI] [PubMed] [Google Scholar]
- 130.Law V., Knox C., Djoumbou Y., Jewison T., Guo A. C., Liu Y., Maciejewski A., Arndt D., Wilson M., Neveu V., Tang A., Gabriel G., Ly C., Adamjee S., Dame Z. T., Han B., Zhou Y., and Wishart D. S., “DrugBank 4.0: Shedding new light on drug metabolism,” Nucleic Acids Res. 42, 1091–1097 (2014). 10.1093/nar/gkt1068 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Goerigk L., Kruse H., and Grimme S., “Benchmarking density functional methods against the S66 and S66x8 datasets for non-covalent interactions,” ChemPhysChem. 12, 3421–3433 (2011). 10.1002/cphc.201100826 [DOI] [PubMed] [Google Scholar]
- 132.Brauer B., Kesharwani M. K., Kozuch S., and Martin J. M. L., “The S66x8 benchmark for noncovalent interactions revisited: Explicitly correlated ab initio methods and density functional theory,” Phys. Chem. Chem. Phys. 18, 20905–20925 (2016). 10.1039/c6cp00688d [DOI] [PubMed] [Google Scholar]
- 133.Řezáč J., “Non-covalent interactions atlas benchmark data sets: Hydrogen bonding,” J. Chem. Theory Comput. 16, 2355–2368 (2020). 10.1021/acs.jctc.9b01265 [DOI] [PubMed] [Google Scholar]
- 134.Wahl O. and Sander T., “Tautobase: An open tautomer database,” J. Chem. Inf. Model. 60, 1085–1089 (2020). 10.1021/acs.jcim.0c00035 [DOI] [PubMed] [Google Scholar]
- 135.Wieder M., Fass J., and Chodera J. D., “Fitting quantum machine learning potentials to experimental free energy data: Predicting tautomer ratios in solution,” Chem. Sci. 12, 11364–11381 (2021). 10.1039/d1sc01185e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Moser A., Range K., and York D. M., “Accurate proton affinity and gas-phase basicity values for molecules important in biocatalysis,” J. Phys. Chem. B 114, 13911–13921 (2010). 10.1021/jp107450n [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Goerigk L., Hansen A., Bauer C., Ehrlich S., Najibi A., and Grimme S., “A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions,” Phys. Chem. Chem. Phys. 19, 32184–32215 (2017). 10.1039/c7cp04913g [DOI] [PubMed] [Google Scholar]
- 138.Ree N., Göller A. H., and Jensen J. H., “RegioSQM20: Improved prediction of the regioselectivity of electrophilic aromatic substitutions,” J. Cheminf. 13, 10 (2021). 10.1186/s13321-021-00490-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Leontis N. B. and Westhof E., “Geometric nomenclature and classification of RNA base pairs,” RNA 7, 499–512 (2001). 10.1017/s1355838201002515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Leontis N. B., Stombaugh J., and Westhof E., “The non-Watson–Crick base pairs and their associated isostericity matrices,” Nucleic Acids Res. 30, 3497–3531 (2002). 10.1093/nar/gkf481 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Leontis N. B. and Westhof E., “Analysis of RNA motifs,” Curr. Opin. Struct. Biol. 13, 300–308 (2003). 10.1016/s0959-440x(03)00076-9 [DOI] [PubMed] [Google Scholar]
- 142.Singh I., Kim M.-J., Molt R. W., Hoshika S., Benner S. A., and Georgiadis M. M., “Structure and biophysics for a six letter DNA alphabet that includes imidazo[1,2-a]-1,3,5-triazine-2(8H)-4(3H)-dione (X) and 2,4-diaminopyrimidine (K),” ACS Synth. Biol. 6, 2118–2129 (2017). 10.1021/acssynbio.7b00150 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Raines R. T., “Ribonuclease A,” Chem. Rev. 98, 1045–1066 (1998). 10.1021/cr960427h [DOI] [PubMed] [Google Scholar]
- 144.Gu H., Zhang S., Wong K.-Y., Radak B. K., Dissanayake T., Kellerman D. L., Dai Q., Miyagi M., Anderson V. E., York D. M., Piccirilli J. A., and Harris M. E., “Experimental and computational analysis of the transition state for ribonuclease A-catalyzed RNA 2′-O-transphosphorylation,” Proc. Natl. Acad. Sci. U. S. A. 110, 13002–13007 (2013). 10.1073/pnas.1215086110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Harris M. E., Piccirilli J. A., and York D. M., “Integration of kinetic isotope effect analyses to elucidate ribonuclease mechanism,” Biochim. Biophys. Acta, Proteins Proteomics 1854, 1801–1808 (2015). 10.1016/j.bbapap.2015.04.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for relative energies for the minima and transition states of the alanine dipeptide, ibuprofen, and ketorolac.
Data Availability Statement
QDπ-v1.0 is openly available in our GitLab repository at https://gitlab.com/RutgersLBSR/qdpi, which was previously released.77 The data that support the findings of this study are available from the corresponding author upon reasonable request.