Modern semiempirical electronic structure methods and machine learning potentials for drug discovery: Conformers, tautomers, and protonation states

Abstract

Modern semiempirical electronic structure methods have considerable promise in drug discovery as universal “force fields” that can reliably model biological and drug-like molecules, including alternative tautomers and protonation states. Herein, we compare the performance of several neglect of diatomic differential overlap-based semiempirical (MNDO/d, AM1, PM6, PM6-D3H4X, PM7, and ODM2), density-functional tight-binding based (DFTB3, DFTB/ChIMES, GFN1-xTB, and GFN2-xTB) models with pure machine learning potentials (ANI-1x and ANI-2x) and hybrid quantum mechanical/machine learning potentials (AIQM1 and QDπ) for a wide range of data computed at a consistent ωB97X/6-31G* level of theory (as in the ANI-1x database). This data includes conformational energies, intermolecular interactions, tautomers, and protonation states. Additional comparisons are made to a set of natural and synthetic nucleic acids from the artificially expanded genetic information system that has important implications for the design of new biotechnology and therapeutics. Finally, we examine the acid/base chemistry relevant for RNA cleavage reactions catalyzed by small nucleolytic ribozymes, DNAzymes, and ribonucleases. Overall, the hybrid quantum mechanical/machine learning potentials appear to be the most robust for these datasets, and the recently developed QDπ model performs exceptionally well, having especially high accuracy for tautomers and protonation states relevant to drug discovery.

I. INTRODUCTION

Alchemical free energy (AFE) simulations¹ are widely used for the prediction of ligand–protein binding energies in drug discovery. These predictions are used to prioritize compounds for costly synthesis and testing in the lead optimization cycle.² The predictive capability of these methods relies critically on the accuracy of the force fields that are used.³ For well-studied biological systems such as proteins^4–6 and common solvents such as water^7–11 and monovalent ions,^12–15 several molecular mechanical (MM) force fields^16,17 have been developed and have undergone extensive validation and revision based on comparison with a wide range of experiments. These force fields have evolved to become increasingly robust and reliable in long-time molecular dynamics simulations, despite the simplicity of their functional forms. On the other hand, the “general” molecular mechanical force fields needed to model drug-like molecules that may not have ever been synthesized before are generally much less reliable. Moreover, conventional MM force fields are not “universal” in the sense that they use a pre-defined covalent bonding topology and are thus limited in their ability to model alternative tautomers and protonation states. This is important as 30% of the compounds in vendor databases and 21% of the compounds in drug databases have potential tautomers;^18,19 furthermore, it has been estimated that up to 95% of drug molecules contain ionizable groups¹⁸ (∼75% weak bases and ∼20% weak acids^20,21).

Modern semiempirical quantum mechanical (QM) electronic structure methods^22,23 provide an attractive alternative to the general MM force fields for drug discovery. The reason is that, unlike a typical protein that may contain several thousands of atoms, ∼79% of drugs are between 10 and 40 non-hydrogen atoms, and the vast majority are less than 100 non-hydrogen atoms.²⁴ This is of the size range where semiempirical QM methods are able to be used in combined quantum mechanical/molecular mechanical (QM/MM) simulations that include explicit MM representations of the entire protein and surrounding solvent bath under periodic boundary conditions.^25–28 Highly efficient [including parallel and graphics processing unit (GPU)-accelerated] implementations of semiempirical molecular orbital²⁹ and density-functional tight-binding³⁰ have been made and are available for molecular dynamics simulations. More importantly, in the context of AFE simulations, these QM/MM potentials can be efficiently integrated into thermodynamic cycles using indirect (or sometimes referred to as “book-ending” or “reference potential”) approaches^31–35 that apply an end-state MM → QM free energy correction to a high-precision MM AFE simulation.

One potential caveat is the high level of accuracy required by drug discovery applications that seek to distinguish binding free energies at a resolution below k_BT (0.59 kcal/mol at 300 K).^36–38 This is extremely challenging for even the most advanced modern semiempirical QM methods. One path forward that appears promising is to use machine-learning potentials (MLPs) either as stand-alone alternative models,^39–44 or else to augment existing semiempirical QM methods.^45–51 We will refer to the former class as “pure MLPs” and the latter class as “QM/Δ-MLPs”. MLPs have emerged as powerful tools to enable fast and accurate chemical models within the scope of their training.^39,41–44 Many such models have emerged for different applications,^52–67 although few, if any, have been used to their full potential in rigorous AFE simulations. Application of these models in drug discovery AFE simulations is challenging because they must: (1) make robust predictions for molecules within the relevant medicinal chemistry space that may have never been synthesized or characterized;⁶⁸ (2) model a wide range of intra- and intermolecular interactions, including relative conformational energies, hydrogen bonding,⁶⁹ π stacking,^70,71 London dispersion,⁷² and mixed interactions; (3) quantitatively handle different tautomers,^18,19,73 and protonation states.²¹ Currently, the ANI^63,74–76 class of models, and particularly the second generation ANI-2x,⁷⁶ have received widespread attention. A limitation of these models is that they were built for neutral molecules, and their functional forms do not explicitly account for total molecular charge or spin state. Consequently, they are not able to reliably predict the energetics of changing protonation states. This is a serious limitation, as it has been estimated that up to 95% of drug molecules contain ionizable groups.¹⁸ Related to this, some of the pure MLPs did not initially treat long-ranged electrostatic interactions, although there have been efforts to remedy this.⁶⁶ Alternatively, there have been several recent efforts to develop new QM/Δ-MLPs,^45–51,77 the most relevant in the current context being AIQM1,⁴⁶ which is based on the novel ODMx class of semiempirical models⁷⁸ and has recently been demonstrated to be robust for transition state optimizations.⁷⁹

Very recently, we introduced a first-generation QM/Δ-MLP for drug discovery.⁷⁷ The Quantum Deep-learning Potential Interaction (QDπ) model uses a fast, robust third-order self-consistent density-functional tight binding (DFTB3/3OB) model^80,81 that is corrected to high-level accuracy through an MLP correction (Δ-MLP) based on our range-corrected deep-learning potential (DPRc)^47,48 as part of the DeePMD-kit⁸² interfaced with AMBER.⁸³ The underlying DFTB3 model is able to capture long-range electrostatic interactions as well as changes in charge, protonation, and spin state. The intramolecular and short- to mid-range intermolecular interactions are made quantitatively accurate by training the DPRc model to correct the total energy and forces to match those of high-level ab initio methods.

In the present work, we compare the performance of several modern semiempirical QM, QM/Δ-MLP, and pure MLP models against consistent reference data derived from databases relevant for drug discovery. Of particular focus in the present work is characterizing the ability of different potentials to accurately model intermolecular interactions, tautomers, and protonation states. Toward that end, we consider the dataset of natural and synthetic nucleic acids from the artificially expanded genetic information system (AEGIS)^84–87 that is being used for a wide range of biotechnology applications.⁸⁸ The system uses 12 different nucleobases in its genetic code, including the four canonical nucleobases found in DNA (adenine, cytosine, guanine, and thymine), in addition to eight synthetic nucleobases. These serve as good test systems as they contain complex covalent bonding and exhibit a rich set of tautomer forms, hydrogen bonded complexes, and alternative protonation states. The remainder of the article is organized as follows: Sec. II describes the computational details pertaining to the various semiempirical QM (MNDO/d,⁸⁹ AM1,⁹⁰ PM6,⁹¹ PM6-D3H4X,^92,93 PM7,⁹⁴ ODM2,⁷⁸ DFTB3,⁹⁵ GFN1-xTB,⁹⁶ GFN2-xTB,⁹⁷ and DFTB/ChIMES⁹⁸), MLP (ANI-1x⁷⁴ and ANI-2x⁷⁶), and QM/Δ-MLP (AIQM1⁴⁶ and most recently QDπ⁷⁷) models, as well as the key modified databases (DBs) used as reference data at the ωB97X/6-31G*^77,99 level. Section III presents and analyzes data for a set of ten broad-spectrum databases for intermolecular interactions, tautomers, protonation states, and 2D conformational energy profiles. Further application is made to examine the performance of modern semiempirical QM, MLP, and QM/Δ-MLPs against the AEGIS dataset.^85,86 Finally, the paper provides contextual examples of acid/base chemistry relevant for RNA cleavage reactions catalyzed by small nucleolytic ribozymes and ribonucleases.¹⁰⁰

II. METHODS

A. Models compared in the current work

1. Density-functional reference data

ωB97X/6-31G*⁹⁹ was performed using Gaussian 16.¹⁰¹ Reference energy and forces (including geometry optimizations, where needed) were performed at a consistent ωB97X/6-31G*⁹⁹ level of theory.

2. NDDO-based semiempirical models

Semiempirical quantum mechanical (QM) models based on the neglect of diatomic differential overlap (NDDO) approximation enable the number of electron repulsion integrals to be drastically reduced and the single-particle density matrix to be decomposed into effective atom-centered atomic orbital products (and their resulting electrostatics represented as multipoles).¹⁰² The NDDO approximation also eliminates the need to explicitly enforce orthogonalization of the molecular orbitals that normally would be achieved by having an overlap matrix in the generalized eigenvalue equation. Consequently, this may lead to poor modeling of conformational energies and their barriers if left uncorrected. Much work has been performed to introduce orthogonalization corrections into the theoretical framework, which has resulted in the OMX class of methods.^103–106 In the current work, the following NDDO-based methods are considered: MNDO/d,⁸⁹ AM1,⁹⁰ and PM6⁹¹ that were evaluated with the AMBER 20¹⁰⁷ SQM module;¹⁰⁸ the ODM2⁷⁸ method that was evaluated using the MNDO program¹⁰⁹ kindly provided by Dr. Axel Koslowski; and PM6-D3H4X^92,93 and PM7⁹⁴ that were performed using the MOPAC software.¹¹⁰ PM6-D3H4X and PM7 correct PM6 using classical potentials and are often claimed to be the most suitable methodology for drug design among NDDO-based semiempirical models.^111,112

3. DFTB-based semiempirical models

Density-functional tight binding methods offer an intriguing alternative to the NDDO-based semiempirical models. DFTB methods use an expansion of the energy¹¹³ about a sum of neutral atom densities together with a two-center integral approximation to enable a framework for highly efficient calculations (speed is very comparable with NDDO-based methods). Unlike the NDDO-based methods, DFTB methods keep the overlap matrix in the generalized eigenvalue equation and thus explicitly deal with orbital orthogonalization. However, this complicates the decomposition of the density matrix, which now contains two-center products. Various density-matrix partition schemes can be used to map the density onto atomic centers such that an atom-centered (typically monopolar) representation can be made for the second-order electrostatic term in the expansion. The DFTB-based methods considered here include DFTB3⁹⁵ (3OB parameters¹¹⁴) that was performed using the AMBER 20¹⁰⁷ SQM module;^108,115 and GFN1-xTB,⁹⁶ GFN2-xTB,⁹⁷ and DFTB/ChIMES⁹⁸ (3OB parameters¹¹⁴ and ChIMES parameters¹¹⁶ kindly provided by Dr. Cong Huy Pham) models evaluated with the DFTB+ software.³⁰

Compared to DFTB3 and GFN1-xTB, GFN2-xTB represents the first broadly parameterized tight-binding method, primarily designed for the fast calculation of structures and noncovalent interaction energies, to include electrostatic and exchange-correlation Hamiltonian terms up to second order in the multipole expansion.⁹⁷ In this way, the model takes into account anisotropic second order density fluctuation effects via short-range damped interactions of cumulative atomic multipole moments. DFTB/ChIMES,¹¹⁶ on the other hand, leverages the relative simplicity of linear regression machine learning in the recently developed Chebyshev Interaction Model for Efficient Simulation (ChIMES) method.¹¹⁷ Validation tests of DFTB/ChIMES demonstrate the model exhibits both transferability and extensibility and enables physical and chemical predictions with up to coupled-cluster accuracy.¹¹⁶

It should be noted that the use of machine learning methods to enhance DFTB models in one form or another is not new. Notable works along these lines, in addition to DFTB/ChIMES, include but are not limited to the ML-Hamiltonian approach of Yaron and co-workers,¹¹⁸ the development of many-body potentials from deep tensor neural networks,^119,120 Gaussian process regression,¹²¹ and unsupervised machine learning.¹²²

4. Machine learning potentials (MLPs)

The pure machine learning potentials considered in this work produce energies and atomic forces of a molecule given the positions and elements. These potentials are quite fast compared with semiempirical QM models, and they have more favorable scaling properties. However, some initial pure MLPs were built for neutral molecules in singlet ground states, so they do not reliably model changes in charge state that occur with the addition or loss of electrons and/or protons. The latter of which is important for drug molecules that contain ionizable sites. The pure MLPs considered here include ANI-1x⁷⁴ and ANI-2x⁷⁶ models performed using the TorchANI software.¹²³ Both the ANI-1x and ANI-2x models use the ANI descriptor⁶³ with a cutoff radius of 6 Å and were trained against ωB97X/6-31G* with active learning cycles. The training data of ANI-1x only include energies, and the training data of ANI-2x include both energies and forces.

5. Combined semiempirical quantum mechanical and machine-learning potentials (QM/Δ-MLPs)

An attractive alternative to either semiempirical QM or pure MLPs is to combine the strengths of both into a combined QM/Δ-MLP. In this way, it builds off of a fast and robust semiempirical QM that inherently can accommodate changes in electronic charge and spin states while using MLPs to greatly enhance the accuracy across a broad spectrum of chemical environments. The QM/Δ-MLPs considered here include the QDπ⁷⁷ model, which is based on DFTB3/3OB^{95,107,108,114,115} and the deep-learning potential available in DeePMD-kit,^82,83 and the AIQM1@DFT*⁴⁶ model, which is based on an ODM2^78,109 model (which includes the D4 dispersion correction¹²⁴) and a trained neural network correction using TorchANI.¹²³ The MLP component of QDπ uses the DeepPot-SE descriptor⁶¹ with a cutoff radius of 6 Å and was trained against ωB97X/6-31G* energies and forces for 241 M steps; the MLP part of AIQM1@DFT* uses the ANI descriptor⁶³ with a cutoff radius of 6 Å and was trained against ωB97X/def2-TZVPP energies and forces for 1000 epochs.⁴⁶

All geometry optimizations using semiempirical QM, MLP, or QM/Δ-MLP models were performed using the Limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) algorithm¹²⁵ in the ASE¹²⁶ package. Relaxed 2D torsion profiles were made using the same method described in Ref. 77.

B. Databases and reference data used in the current work

The reference data used in the current work includes the modified ANI-1x,^74,77,127 the modified COMP5,^{74,77,128–130} S66x8,^74,131,132 HB375x10,^77,133 TautoBase (TB),^77,134,135 amino acids (AAs) and nucleic acids (NAs),^77,136 PA26 and TAUT15,^77,137 RegioSQM20,^77,138 and the artificially expanded genetic information system (AEGIS).^77,84–86 All reference data were computed (or re-computed⁷⁷) at the ωB97X/6-31G* level of theory (consistent with the most extensive ANI-1x and COMP5 databases).

Among all reference data, the ANI-1x (or modified version) dataset was used to parameterize DFTB/ChIMES, ANI-1x, ANI-2x, QDπ, and AIQM1; S66x8 was used to parameterize PM6-D3H4X, ANI-2x, and QDπ; and TB, AA, NA, PA, and AEGIS were used for the training of QDπ.

III. RESULTS AND DISCUSSION

The focus of the current article is on comparing modern semiempirical electronic structure methods and machine learning potentials with respect to their ability to accurately model conformers, tautomers, and protonation states of biological and drug-like molecules. These methods have potential impact for drug discovery owing to their efficiency and robustness.

A. Comparison of broad-spectrum databases

Important properties for consideration include relative conformational energies, a wide range of intermolecular interactions, as well as tautomeric and protonation state relative energies. The QDπ model was trained with the same reference theory level as ANI-2x⁷⁶ (ωB97X/6-31G*) and considered a number of DBs that encompass conformational energies (ANI-1x, COMP5), intermolecular interactions (S66x8, HB375x10), tautomers (TautoBase, Taut15), and protonation state relative energies (AA, NA, PA26, and RegioSQM20) that are described in detail elsewhere.⁷⁷ A comparison of 11 semiempirical quantum and machine learning models is compared against ten databases in Table I.

TABLE I.

Mean absolute errors for different datasets used for training and testing of the QDπ model.^a Boldface denotes a vector.

	ANI-1x		S66	TB	AA	NA	PA	COMP5		HB	T15	SQM
	E	F	ΔE	ΔE	ΔE	ΔE	ΔE	E	F	ΔE	ΔE	ΔE
QDπ	0.83	1.16	0.13	0.82	0.09	0.17	0.39	1.48	1.14	0.44	0.70	2.53
AIQM1	⋯	3.10	0.57	2.07	7.30	4.71	5.06	⋯	2.59	0.71	1.37	2.75
ANI-1x	1.48	4.48	1.41	1.73	86.95	52.68	43.02	1.96	3.72	1.25	1.63	16.85
ANI-2x	1.07	2.11	0.37	1.76	70.52	52.48	23.80	1.67	1.86	1.40	1.00	13.64
GFN2-xTB	⋯	5.81	0.74	5.68	5.77	8.45	7.35	⋯	4.33	0.85	2.84	4.12
GFN1-xTB	⋯	4.69	0.77	5.23	5.00	11.73	4.43	⋯	3.68	0.87	5.32	4.10
DFTB3	⋯	7.58	1.14	5.45	8.63	10.85	12.54	⋯	5.46	1.17	3.65	4.59
DFTB/ChIMES	⋯	4.82	1.72	5.04	9.47	9.70	12.87	⋯	4.14	1.36	3.00	6.70
ODM2	⋯	12.80	1.24	3.37	9.13	5.26	6.04	⋯	9.97	1.29	3.64	3.99
PM6	⋯	12.96	1.19	4.90	11.23	11.03	17.84	⋯	9.33	1.24	5.60	5.30
PM6-D3H4X	⋯	13.60	0.63	5.44	9.67	11.72	7.78	⋯	10.27	0.84	6.16	6.61
PM7	⋯	11.98	0.84	4.34	7.24	10.72	10.11	⋯	8.54	1.00	3.74	5.93
AM1	⋯	14.95	2.17	5.01	4.43	7.32	13.51	⋯	12.13	2.57	3.99	4.13
MNDO/d	⋯	15.14	6.67	9.69	11.71	11.29	13.07	⋯	11.52	9.36	7.78	5.18

^a Mean absolute errors in the energy (E, kcal/mol), forces (F, kcal/mol/Å), and ΔE for ANI-1x,^74,127 S66x8 (S66),^74,131,132 TautoBase (TB),^134,135 amino acid and nucleic acid proton affinities (AA and NA),¹³⁶ PA26 (PA),¹³⁷ COMP5,^74,128–130 HB375x10 (HB),¹³³ Taut15 (T15),¹³⁷ and RegioSQM20 (SQM)¹³⁸ databases. The datasets on the right were not part of the QDπ training.

1. Conformational energy datasets

With respect to the diverse conformational energy datasets (ANI-1x^74,127 and COMP5^{74,77,128–130}), the mean absolute errors (maEs) in the forces are smallest for the MLP and Δ-MLP potentials (QDπ, ANI-2x, AIQM1, and ANI-1x), and the QDπ model performs the overall best (maE values of 1.16 and 1.14 kcal/mol/Å for the ANI-1x and COMP5 datasets, respectively). This is likely due to the fact that the ANI-1x dataset was an integral part of the training of these models. In general, the DFTB models (GFN1-xTB, GFN2-xTB, and DFTB3/3OB) have lower force errors with respect to the reference ωB97X/6-31G* values (maE values range from 4.69 to 7.58 and 3.68 to 5.46 kcal/mol/Å for ANI-1x and COMP5, respectively), whereas the NDDO-based methods have considerably larger errors (maE values range from 11.98 to 15.14 and 8.54 to 12.13 kcal/mol/Å for ANI-1x and COMP5, respectively), with PM7 performing the best of the NDDO methods.

2. Intermolecular interaction datasets

With respect to intermolecular interaction DBs (S66x8^74,131,132 and HB375x10¹³³), several models have ΔE values below 1 kcal/mol on average (QDπ, AIQM1, GFN1-xTB, GFN2-xTB, PM6-D3H4X, and PM7), with QDπ and AIQM1 having exceptional agreement with the reference data: QDπ has maE values of 0.13 and 0.44 kcal/mol, and AIQM1 has maE values of 0.57 and 0.71 kcal/mol for S66x8 and HB375x10, respectively. The ANI-2x model has excellent maE values for S66x8 (maE 0.37 kcal/mol) but does not perform quite as well for the HB375x10 DB (maE 1.40 kcal/mol). The DFTB3, DFTB/ChIMES, ODM2, and PM6 methods perform similarly with ΔE maE values that range from 1.14 to 1.72 (S66x8) and 1.17 to 1.36 (HB375x10) kcal/mol for these DBs. The MNDO/d method has the largest ΔE errors (6.67–9.36 kcal/mol), stemming from known limitations in the core–core interactions that particularly affect hydrogen bonding, which the empirical modified core–core repulsions in AM1 were designed in part to partially alleviate (AM1 maE values range from 2.17 to 2.57 kcal/mol).

3. Tautomer datasets

With respect to the tautomer databases, TautoBase^134,135 (TB) and Taut15¹³⁷ (T15), only the QDπ model achieves ΔE errors less than 1 kcal/mol (maE values of 0.82 and 0.70 kcal/mol for TB and T15, respectively). The AIQM1 and ANI models perform admirably with errors generally below 2 kcal/mol (maE values range from 1.73 to 2.07 and 1.00 to 1.37 kcal/mol for TB and T15, respectively). The remainder of the DFTB-based methods have maE values in excess of 5 kcal/mol for TB and similar values for the AM1, PM6, and PM6-D3H4X methods. The ODM2 method makes a notable improvement with reduced errors relative to the other NDDO-based methods (maE values of 3.37 and 3.64 kcal/mol for TB and T15, respectively). The MNDO/d method overall performs the worst with maE values for TB and T15 exceeding 9 kcal/mol.

4. Relative protonation datasets

The relative protonation datasets include amino and nucleic acid model compounds¹³⁶ (AA and NA) as well as more general proton affinity (PA26¹³⁷) datasets and a subset of the RegioSQM20¹³⁸ (SQM) database containing C, H, O, and N elements. The latter involves many relative protonation energies not related to ionizable sites in biological or drug-like molecules, and hence may be of less relevance for drug discovery. For the AA, NA, and PA26 datasets, the QDπ model stands alone with respect to having very high accuracy in relative deprotonation energies (maE values range from 0.09 to 0.39 kcal/mol). The next best models are AIQM1 (maE 4.71–7.30 kcal/mol). The other semiempirical QM models exhibit much larger ranges: GFN2-xTB (5.77–8.45 kcal/mol), GFN1-xTB (5.00–11.73 kcal/mol), DFTB3 (8.63–12.54 kcal/mol), DFTB/ChIMES (9.47–12.87), ODM2 (5.26–9.13 kcal/mol), PM6 (11.03–17.84 kcal/mol), PM6-D3H4X (7.78–11.72), PM7 (7.24–10.72), AM1 (4.43–13.51 kcal/mol), and MNDO/d (11.29–13.07 kcal/mol). With respect to the SQM dataset, again the QDπ and AIQM1 models perform best (maE values of 2.53 and 2.75 kcal/mol, respectively), and the remaining semiempirical QM models perform similarly with maE values that range from 3.99 to 6.70 kcal/mol. The pure MLP models (ANI-1x and ANI-2x) break down with respect to their ability to predict relative protonation/deprotonation energies, as these potentials were designed for neutral molecules.

Overall, the QDπ model performs exceptionally well across all datasets. The AIQM1 model is also impressive in this regard, with the exception of the protonation/deprotonation energies, where AIQM1 has larger errors for the AA, NA, and PA datasets. Clearly, the QM/Δ-MLP form, using DFTB3 or ODM2 as a QM base model, considerably enhances the accuracy across all datasets listed in Table I. The pure MLP models, and particularly ANI-2x, generally perform better than the semiempirical QM models, with the exception of protonation/deprotonation energies, where the model gives very large errors. Of the semiempirical QM models, the DFTB-based methods have smaller force errors than the NDDO-based models. The GFN1-xTB, GFN2-xTB, PM6-D3H4X, and PM7 models perform well for intermolecular interactions, slightly better than the DFTB3, DFTB/ChIMES, and ODM2 models. All of the semiempirical QM models are fairly comparable in modeling tautomer energy differences (with the exception of MNDO/d, which is less accurate), with ODM2 performing best over a broad range of data. For protonation/deprotonation energies, however, there is no clear trend with the semiempirical QM potentials—they all deviate from the reference data with ΔE maE values exceeding 8 kcal/mol for at least one of the datasets (AA, NA, PA, or SQM).

In the remainder of the article, we focus on comparisons to the most recent modern semiempirical QM (DFTB3, DFTB/ChIMES, GFN2-xTB, ODM2, PM6-D3H4X, PM7), MLP (ANI-2x), and QM/Δ-MLP (QDπ and AIQM1) models.

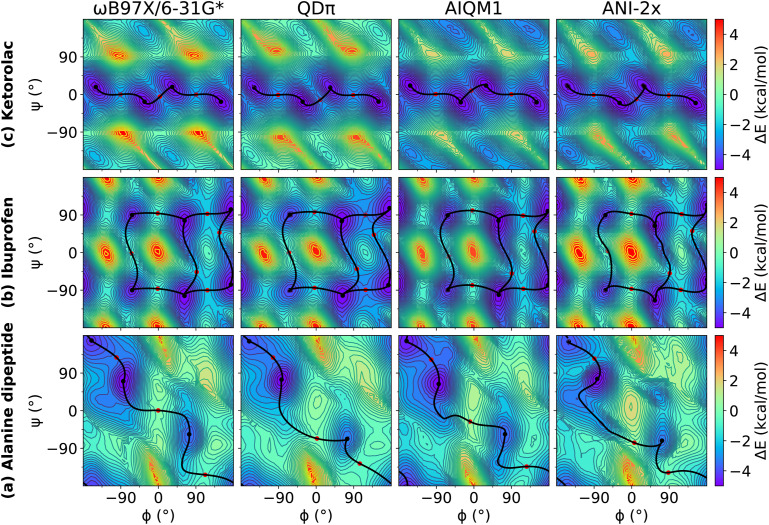
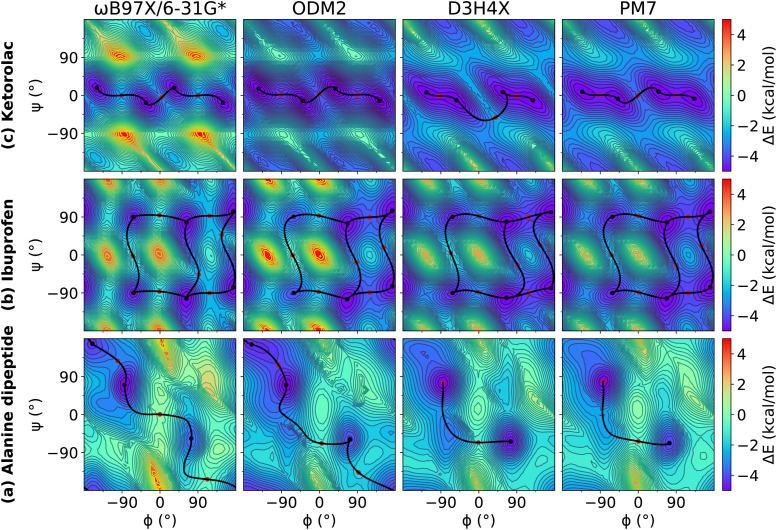
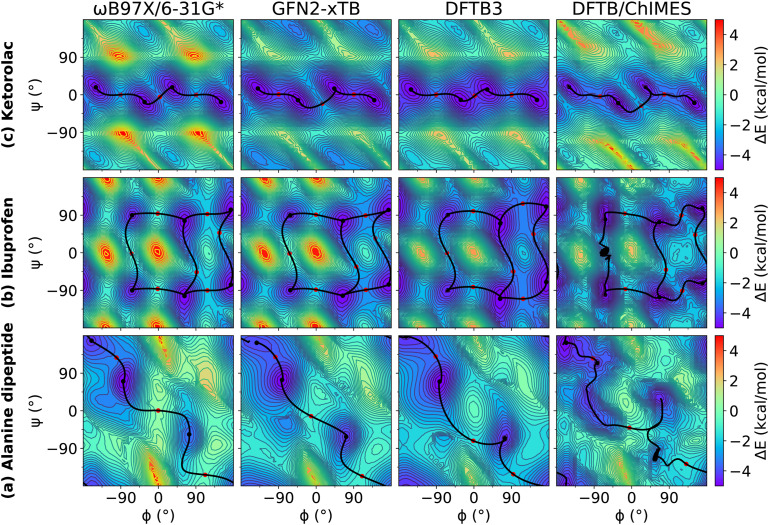
B. Comparison of 2D conformation energy profiles

We examined relaxed 2D torsion profiles for three systems: the alanine dipeptide and the drug molecules ibuprofen and ketorolac, as illustrated in Figs. 1–3. These figures compare 2D torsion profiles at the ωB97X/6-31G* reference level with the QM/Δ-MLP/pure MLP models QDπ, AIQM1, and ANI-2x (Fig. 1), DFTB-based GFN2-xTB, DFTB3 and DFTB/ChIMES (Fig. 2), and NDDO-based ODM2, PM3-D3H4X, and PM7 (Fig. 3) models. The relative energy values for the stationary points are provided in Table S1 of the supplementary material. All of the models qualitatively predict the correct trends. A modest exception occurs with PM6-D3H4X and PM7, which do not predict a pronounced minimum in the β region (∼180/180) of the ϕ/ψ map (Fig. 3). Overall, the QDπ and AIQM1 models have the closest agreement with ωB97X/6-31G*, with the ANI-2x model only slightly worse. The GFN2-xTB, DFTB3, and ODM2 semiempirical QM models tend to systematically under-estimate the conformational barriers between minima (Table S1 in the supplementary material). The largest errors that occur for the QDπ model are for the transition states in the ibuprofen example, which like the semiempirical QM models, are systematically underestimated.

FIG. 1.

Relaxed 2D torsion profiles for (a) alanine dipeptide; (b) ibuprofen; and (c) ketorolac. Each molecule was computed using ωB97X/6-31G*, QDπ, AIQM1, and ANI-2x, respectively. The reference level of theory is ωB97X/6-31G*. The color bars represent the potential energy (with respect to the minimum energy) in kcal/mol.

FIG. 3.

Relaxed 2D torsion profiles for (a) alanine dipeptide; (b) ibuprofen; and (c) ketorolac. Each molecule was computed using ωB97X/6-31G*, ODM2, PM6-D3H4X, and PM7, respectively. The reference level of theory is ωB97X/6-31G*. The color bars represent the potential energy (with respect to the minimum energy) in kcal/mol.

FIG. 2.

Relaxed 2D torsion profiles for (a) alanine dipeptide; (b) ibuprofen; and (c) ketorolac. Each molecule was computed using ωB97X/6-31G*, GFN2-xTB, DFTB3, and DFTB/ChIMES, respectively. The reference level of theory is ωB97X/6-31G*. The color bars represent the potential energy (with respect to the minimum energy) in kcal/mol.

C. Comparison of hydrogen bond complex energies for natural and artificial nucleic acids

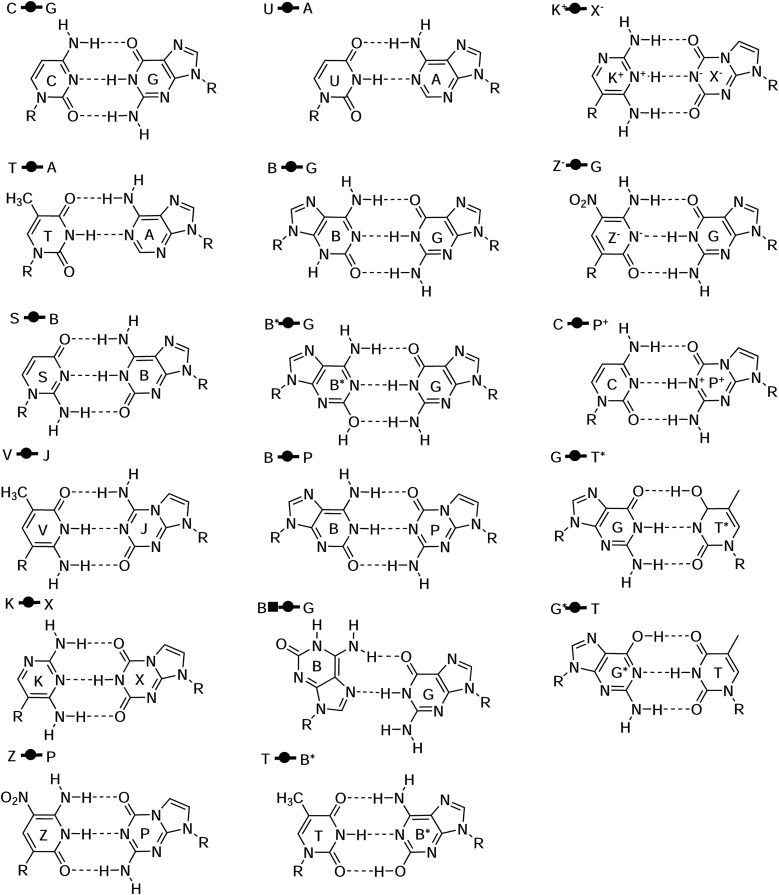
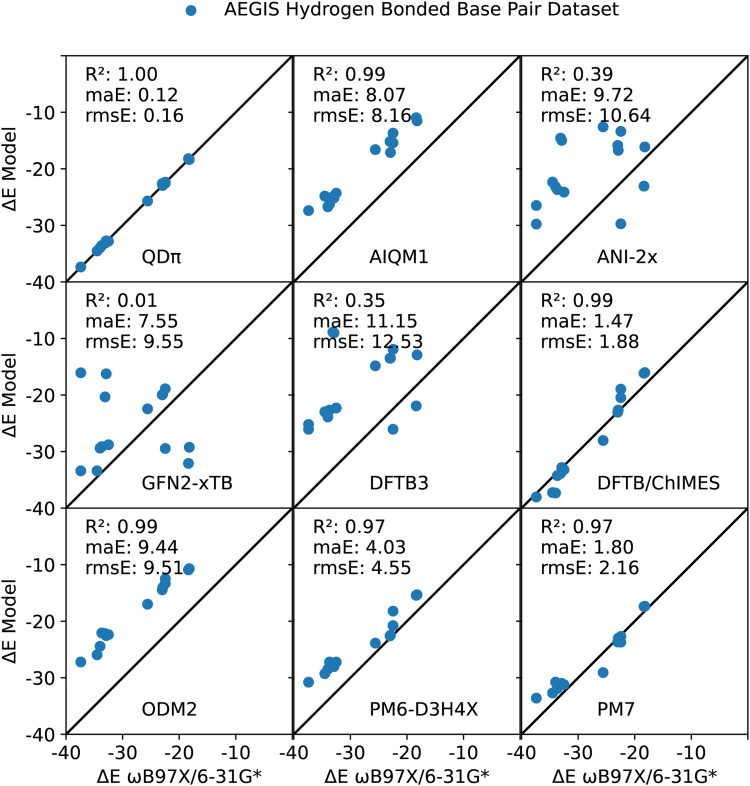
The natural and modified nucleic acids exhibit a wide range of canonical and non-canonical hydrogen bonded base pairs, including some that involve non-standard tautomer forms and protonation states. The base pairs considered in the AEGIS dataset^77,85,86 are illustrated in Fig. 4. This dataset represents a rich set of hydrogen bonding interactions between endocyclic and exocyclic amines and carbonyl and hydroxyl functional groups. The results are listed in Table II, and the neutral base pairs are illustrated in Fig. 5. Overall, the QDπ model gives excellent agreement with the ωB97X/6-31G* reference level over the entire set with ΔE maE of 0.11 kcal/mol and a maximum error of 0.39 kcal/mol for G* T. The DFTB/ChIMES model has the next lowest error (maE 1.99 kcal/mol), followed by PM7 (maE 2.77 kcal/mol), GFN2-xTB (maE 4.25 kcal/mol), and PM6-D3H4X (maE 4.87 kcal/mol). The remainder of the models have maE values in excess of 8 kcal/mol. The ANI-2x model has a large maE value (14.17 kcal/mol), but the errors are dominated by base pairs involving ionized nucleobases that range from 11.58 to 79.73 kcal/mol, whereas the range of errors for neutral base pairs is much smaller (3.39–13.00 kcal/mol; maE of the neutral subset is 9.72 kcal/mol).

FIG. 4.

Structures for the artificially expanded genetic information system (AEGIS) base pair dataset^77,85,86 with Leontis and Westhof symbols used for the classification of nucleic acid base pairs.^139–141

Table II.

Hydrogen bond complex energies from ωB97X/6-31G* and model errors (kcal/mol) for the artificially expanded genetic information system (AEGIS) base pair dataset^77,85,86 with Leontis and Westhof symbols used for the classification of nucleic acid base pairs,^139–141 including complexes that involve alternative tautomers and protonation states.^a

		QM/Δ-MLP or MLP			DFTB			NDDO
	ωB97X	QDπ	AIQM1	ANI-2x	GFN2	DFTB3	ChIMES	ODM2	D3H4X	PM7
Complex	ΔE	Err	Err	Err	Err	Err	Err	Err	Err	Err
	‒32.90	0.16	7.75	9.84	3.66	10.98	0.08	10.35	4.87	1.92
	‒18.22	‒0.14	6.71	3.65	2.15	9.33	2.19	7.51	2.90	0.88
	‒18.36	0.17	7.39	3.39	2.12	9.35	2.22	7.45	2.94	0.96
	‒37.40	0.03	10.01	7.67	3.99	11.34	‒0.64	10.18	6.62	3.80
	‒34.52	‒0.00	9.70	8.04	2.43	9.32	‒2.73	8.57	5.25	1.83
	‒22.46	‒0.08	7.06	6.34	2.13	9.56	1.99	9.14	1.69	‒1.24
	‒33.11	‒0.05	8.13	10.77	3.65	10.14	‒0.76	10.93	5.50	1.83
	‒32.50	‒0.31	8.20	8.38	3.72	10.21	‒0.69	10.13	5.28	1.28
	‒33.68	0.13	7.45	10.02	4.56	11.02	‒0.56	11.61	6.47	1.77
	‒22.46	0.09	8.76	9.08	3.56	10.54	3.50	9.95	4.24	‒0.24
	‒33.99	0.03	7.28	10.79	4.59	10.11	‒3.34	9.56	5.51	3.22
	‒23.00	0.39	7.82	7.14	3.03	9.49	‒0.04	8.55	0.41	‒0.67
	‒25.59	‒0.11	8.99	13.00	3.14	10.75	‒2.45	8.60	1.71	‒3.49
	‒22.92	‒0.03	5.80	6.18	3.04	9.44	0.24	8.88	0.43	‒0.08
	‒144.48	0.10	12.53	79.73	14.30	18.59	8.26	15.79	15.52	15.29
	‒43.33	‒0.07	12.36	11.58	6.69	15.35	3.42	12.16	4.25	1.90
	‒47.17	0.04	6.77	24.45	3.38	13.41	0.87	9.41	7.35	4.82
maE	…	0.11	8.46	14.17	4.25	11.22	1.99	10.08	4.87	2.77
rmsE	…	0.15	8.66	22.51	5.09	11.49	2.83	10.26	5.97	4.44

^a Models and datasets are described in Sec. II. An illustration of each of the complexes is provided in Fig. 4. Complexes include adenine (A), cytosine (C), guanine (G), thymine (T), uracil (U), isoguanine (B), isocytosine (S), 6-amino-5-nitropyridin-2-one (Z), 2-aminoimidazo[1,2a][1,3,5]triazin-4(1H)-one (P), imidazo[1,2-a]-1,3,5-triazine-2(8H)-4(3H)-dione (X), 2,4-diaminopyrimidine (K), 4-aminoimidazo[1,2-a][1,3,5]triazin-2(8H)-one (J), and 6-amino-3-methylpyridin-2(1H)-one (V).^86,142 The “*” symbol refers to tautomeric form, and the “+” and “−” symbols refer to the positive and negative charge.

FIG. 5.

Relation between hydrogen bond complex energies calculated by ωB97X/6-31G* and QDπ, AIQM1, ANI-2x, GFN2-xTB, DFTB3, DFTB/ChIMES, ODM2, PM6-D3H4X, and PM7 for the artificially expanded genetic information system (AEGIS) base pair dataset,⁸⁶ including complexes that involve alternative tautomers and protonation states. Illustrations of each of the complexes are provided in Fig. 4. The three base pairs that involve ionized nucleobases are excluded from the regression as they have much larger binding energy values that would artificially skew the correlation.

Examination of the correlation of hydrogen complex energies for neutral nucleobases reveals that QDπ has the highest correlation (R² value of 0.999), followed by DFTB/ChIMES, AIQM1, and ODM2 with R² values of 0.99. Whereas DFTB/ChIMES is well aligned with the reference data, the ODM2 and related AIQM1 models have values that have been systematically shifted to lower ΔE values. Both PM7 and PM6-D3H4X models show impressive correlation (R² values of 0.97) and low maE values (1.80 and 4.03 kcal/mol, respectively) for complexes of these neutral nucleobases.

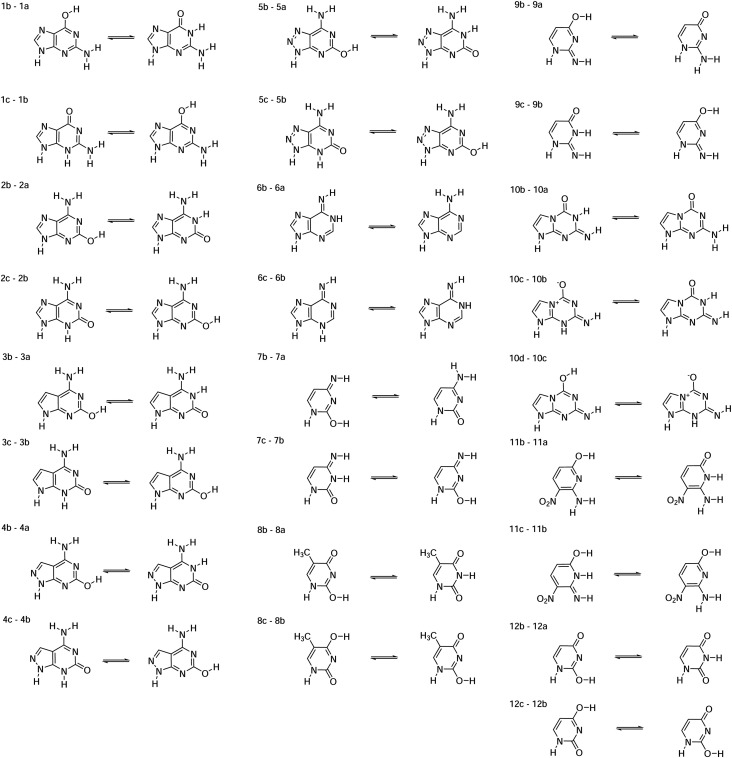
D. Comparison of tautomer energies for natural and artificial nucleic acids

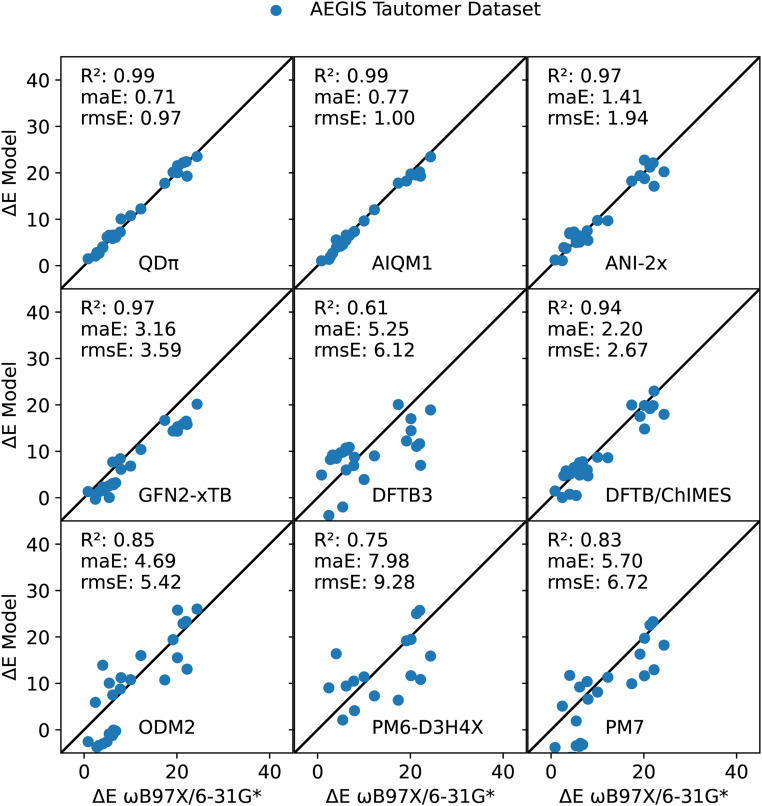
The artificially expanded genetic information system (AEGIS) dataset also exhibits a rich set of tautomeric forms that have been extensively studied with computational methods.^77,85–87 These tautomeric pairs are illustrated in Fig. 6, and their ΔE values are listed in Table III and illustrated in Fig. 7. Overall, both QDπ and AIQM1 give excellent agreement with the ωB97X/6-31G* reference values, with ΔE maE values of 0.71 and 0.77 kcal/mol, respectively, and high correlation (R² value of 0.99). The ANI-2x is the next most accurate, but with errors roughly twice as large (maE 1.41 kcal/mol) and (R² value of 0.97). The DFTB/ChIMES and GFN2-xTB models have considerably higher errors (maE values of 2.20 and 3.16 kcal/mol, respectively), but maintain high correlation with the reference values (R² value of 0.97), whereas DFTB3 and ODM2 have larger errors (maE values of 5.25 and 4.69 kcal/mol, respectively), and lower correlation (R² values of 0.61 and 0.85, respectively). The largest errors occur for PM7 and PM6-D3H4X (maE values of 5.70 and 7.98 kcal/mol, respectively).

FIG. 6.

Structures for the artificially expanded genetic information system (AEGIS) tautomer dataset.^77,85 Guanine derivatives (1–5, 2: nucleobase code B), codes 6: A, 7: C, 8: T, 9: S, 10: P, and 11: Z.

TABLE III.

Tautomerization energies from ωB97X/6-31G* and model errors (kcal/mol) for the artificially expanded genetic information system (AEGIS) tautomer dataset.^a

		QM/Δ-MLP or MLP			DFTB			NDDO
	ωB97X	QDπ	AIQM1	ANI-2x	GFN2	DFTB3	ChIMES	ODM2	D3H4X	PM7
Tautomer pair	ΔE	Err	Err	Err	Err	Err	Err	Err	Err	Err
1b–1a	2.43	‒0.36	‒1.07	‒1.35	‒2.75*	‒6.25*	‒2.38	3.48	6.60	2.67
1c–1b	17.39	0.36	0.40	0.83	‒0.72	2.68	2.58	‒6.65	‒11.01	‒7.46
2b–2a	‒5.41	‒1.12	0.13	‒0.29	2.81	‒4.39	‒1.02	6.31*	12.62*	8.85*
2c–2b	4.95	1.22	‒0.74	2.30	‒2.61	4.74	1.54	‒7.50*	‒14.46*	‒10.85*
3b–3a	‒6.32	‒0.28	‒0.16	0.89	3.53	‒3.90	‒0.77	6.39*	12.95*	9.24*
3c–3b	4.05	‒0.15	‒0.15	3.05	‒2.48	4.44	1.02	‒7.07*	‒13.56*	‒9.97*
4b–4a	‒6.81	0.69	0.37	0.58	3.60	‒4.06	‒0.94	7.06*	13.49*	10.01*
4c–4b	2.76	0.06	‒0.82	1.14	‒1.90	5.47	1.98	‒6.48*	‒12.55*	‒8.93*
5b–5a	‒6.12	‒0.41	0.66	‒0.28	3.07	‒4.60	‒1.43	7.34*	13.36*	9.71*
5c–5b	3.23	‒0.57	‒0.57	0.49	‒1.92	5.97	2.56	‒6.59*	‒13.03*	‒9.41*
6b–6a	12.24	‒0.01	‒0.20	‒2.56	‒1.85	‒3.22	‒3.63	3.76	‒4.94	‒0.92
6c–6b	20.12	‒0.10	‒0.35	2.63	‒5.80	‒3.10	‒0.26	‒4.60	‒8.47	‒8.48
7b–7a	20.15	1.40	‒0.63	‒1.39	‒4.87	‒5.71	‒5.32	5.63	‒0.67	‒0.43
7c–7b	‒19.17	‒0.96	0.94	‒0.22	4.79	6.93	1.64	‒0.25	‒0.01	2.86
8b–8a	21.32	0.84	‒1.79	‒0.08	‒5.43	‒10.25	‒2.12	1.57	3.71	1.24
8c–8b	‒6.16	0.31	‒0.43	1.10	‒1.52	0.18	1.28	‒1.34	‒3.27	‒3.05
9b–9a	5.42	0.77	‒0.89	‒0.45	‒5.39	‒7.41*	‒4.94	4.64	‒3.31	‒3.53
9c–9b	‒10.02	‒0.74	0.40	0.29	3.20	6.10	1.29	‒0.76	‒1.38	1.91
10b–10a	7.95	2.11	‒0.57	‒2.50	‒1.83	0.77	‒3.26	3.28	‒3.84	‒1.36
10c–10b	22.20	‒2.92	‒2.92	‒5.08	‒6.40	‒15.21	0.78	‒9.14	‒11.36	‒9.26
10d–10c	4.01	0.04	1.54	2.86	‒1.71	5.13	‒3.27	9.90	12.36	7.71
11b–11a	‒0.86	‒0.63	‒0.19	‒0.36	‒0.47	‒4.04	‒0.58	3.42*	7.69*	4.68*
11c–11b	24.35	‒0.84	‒0.90	‒4.13	‒4.19	‒5.43	‒6.39	1.67	‒8.47	‒6.13
12b–12a	22.00	0.41	‒1.80	0.14	‒5.51	‒10.37	‒2.16	1.34	3.73	1.31
12c–12b	‒7.79	0.54	0.54	0.29	‒0.62	0.87	1.78	‒0.98	‒2.70	‒2.59
maE	…	0.71	0.77	1.41	3.16	5.25	2.20	4.69	7.98	5.70
rmsE	…	0.97	1.00	1.94	3.59	6.12	2.67	5.42	9.28	6.72

^a Models and datasets are described in Sec. II. Illustrations of each of the tautomerization reactions are provided in Fig. 7. Errors corresponding to wrong prediction of more stable tautomer are indicated by an asterisk (*).

FIG. 7.

Relation between tautomerization energies calculated by ωB97X/6-31G* and QDπ, AIQM1, ANI-2x, GFN2-xTB, DFTB3, DFTB/ChIMES, ODM2, PM6-D3H4X, and PM7 for the artificially expanded genetic information system (AEGIS) tautomer dataset. An illustration of each of the complexes is provided in Fig. 6. In the regression plot shown, the sign convention (direction of the tautomer reaction) is chosen such that the reference ΔE value is positive (this is performed to circumvent “spreading out” of the data and artificially inflating the correlation).

It has been estimated that 30% of the compounds in vendor databases and 21% of the compounds in drug databases have potential tautomers.^18,19 For drug discovery applications, it is thus vitally important to be able to model alternative tautomer forms, discern which forms are relevant for ligand–protein binding, and if binding induces a change in tautomer state, to quantitatively determine the tautomerization energy contribution to binding with sub-kcal/mol accuracy. In some cases, the semiempirical QM models incorrectly predict the lowest energy tautomer (one case for GFN2-xTB, two cases for DFTB3, and nine cases each for ODM2, PM6-D3H4X, and PM7). For the models compared here, only QDπ and AIQM1 are able to achieve the requisite accuracy for quantitative prediction of ligand–protein binding applications.

E. Comparison of protonation energies for common general acids and bases

Modeling protonation states is important for drug discovery applications as it has been estimated that up to 95% of drug molecules contain ionizable groups¹⁸ (∼75% weak bases and ∼20% weak acids^20,21), and protonation states can sometimes change upon ligand binding. Hence, quantitatively accurate modeling of protonation/deprotonation events at these ionizable sites is critical to obtain high predictive capability. As an illustrative set of examples, we examine simple model systems that mimic the acid/base chemistry associated with RNA cleavage reactions catalyzed by small nucleolytic RNA enzymes (ribozymes) and protein enzymes (ribonucleases).¹⁰⁰ In these reactions, the 2′OH of an RNA nucleotide, modeled by the secondary alcohol isopropanol (iPrOH), becomes activated (deprotonated) by a general base that in ribozymes is often an ionized (deprotonated) guanine residue (${\text{G:N}}_1^{-}$), and in RNase A^143–145 is generally believed to be a histidine (His:N_ϵ) although it has been speculated that a neutral lysine (Lys:NH₂) might also be capable. The activated nucleophile then attacks the scissile phosphate, passing through a pentavalent transition state, followed by the departure of the 5′O leaving group (modeled by the primary alkoxide ethoxide (EtO⁻) with the assistance of a general acid that in ribozymes can be either a protonated adenine at the N1 or N3 positions (A:N₁H⁺ and A:N₃H⁺, respectively) or an ionized (protonated) cytosine (C:N₃H⁺), and in RNase A is a protonated histidine (His:N_ϵH⁺).

Table IV lists relative protonation/deprotonation reactions that model general acid/base events in RNA cleavage reactions.¹⁰⁰ Overall, QDπ performs extremely well, with ΔE maE of 0.50 kcal/mol. Of the semiempirical QM methods, GFN2-xTB is the least inaccurate (maE value of 5.94 kcal/mol), followed by PM7 (6.97 kcal/mol), with other models notably higher (maE values ranging from 9.12 to 14.67 kcal/mol). As mentioned earlier, the ANI-2x model was not designed to handle ions; it produces errors on the order of 100 kcal/mol. The AIQM1 model is greatly improved with respect to ANI-2x and ODM2 (the base QM model). The QDπ ΔE maE value is dominated by large positive errors involving the ethoxide and protonated nucleobases (0.89–1.25 kcal/mol). The ethoxide anion is a primary alkoxide that is only marginally stable in the gas phase, and thus especially challenging. The QDπ model is by far the most accurate for protonation/deprotonation energies. It is a promising candidate for use in drug discovery applications.

TABLE IV.

Selected relative protonation/deprotonation energies from ωB97X/6-31G* and model error (kcal/mol) relevant to acid/base catalysis in RNA cleavage reactions.^a

		QM/Δ-MLP or MLP			DFTB			NDDO
	ωB97X	QDπ	AIQM1	ANI-2x	GFN2	DFTB3	ChIMES	ODM2	D3H4X	PM7
Protonation pair	ΔE	Err	Err	Err	Err	Err	Err	Err	Err	Err
[Lys:NH2,iPrOH]	167.76	0.00	‒0.64	‒115.04	0.04	6.11	‒6.87	‒15.24	‒13.15	‒10.15
[His:Nϵ,iPrOH]	158.33	0.08	‒9.22	‒126.62	‒7.02	‒11.33	‒17.47	‒18.74	‒12.96	−6.19
[EtO−,His:NϵH+]	‒160.25	‒0.02	12.82	137.70	9.66	11.71	18.09	21.92	12.24	5.36
[${\text{G:N}}_1^{-}$,iPrOH]	43.06	‒1.11	‒1.15	‒28.62	−2.69	‒8.63	‒11.17	‒10.84	0.89	5.45
[EtO−,A:N1H+]	‒165.06	1.25	12.94	137.24	10.02	15.21	23.15	20.74	8.07	1.25
[EtO−,A:N3H+]	‒190.89	1.21	12.88	143.42	11.40	16.00	24.17	19.43	17.97	8.39
[EtO−,C:N3H+]	‒160.33	0.89	12.78	145.20	6.58	4.66	16.93	20.19	7.03	2.22
[${\text{G:N}}_1^{-}$,A:N1H+]	‒120.07	0.08	8.19	97.55	4.69	6.20	11.36	6.73	9.69	7.53
[${\text{G:N}}_1^{-}$,A:N3H+]	‒145.91	0.04	8.12	103.73	6.07	6.99	12.38	5.41	19.58	14.67
[${\text{G:N}}_1^{-}$,C:N3H+]	‒115.34	‒0.27	8.03	105.50	1.25	‒4.35	5.14	6.17	8.64	8.51
maE	…	0.50	8.68	114.06	5.94	9.12	14.67	14.54	11.02	6.97
rmsE	…	0.72	9.72	118.72	6.96	9.96	15.87	15.84	12.17	7.88

^a Models and datasets are described in Sec. II. Protonation pairs are written in the general form as follows: [B, A]: B + A → BH⁺ + A⁻, or [B⁻, AH⁺]: B⁻ + AH⁺ → BH + A. Here, B/BH⁺ and B⁻/BH are the base/conjugate acid pairs and A/A⁻ and AH⁺/A are the acid/conjugate base pairs. These are model systems for general acid and base catalysis in RNA cleavage reactions by small nucleolytic ribozymes and ribonucleases.¹⁰⁰ The molecules indicated are isopropanol (iPrOH), ethoxide (EtO⁻), neutral lysine (Lys:NH₂), neutral histidine (His:N_ϵ), protonated histidine (His:N_ϵH⁺), deprotonated guanine at the N1 position (${\text{G:N}}_1^{-}$), protonated adenine at the N1 and N3 positions (A:N₁H⁺ and A:N₃H⁺), and protonated cytosine at the N3 position (C:N₃H⁺).

IV. CONCLUSION

We have compared the performance of several NDDO-based (MNDO/d, AM1, PM6, PM6-D3H4X, PM7, and ODM2) and density-functional tight-binding based (DFTB3, DFTB/ChIMES, GFN1-xTB, and GFN2-xTB) semiempirical models with pure machine learning potentials (ANI-1x and ANI-2x) and hybrid quantum mechanical/machine learning potentials (AIQM1 and QDπ). We examine broad datasets computed at a consistent ωB97X/6-31G* level of theory that includes conformational energies, intermolecular interactions, tautomers, and protonation states. The methods were further compared against the AEGIS dataset and acid/base chemistry relevant for RNA cleavage reactions catalyzed by small nucleolytic ribozymes and ribonucleases. Overall, the recently developed QDπ model performs exceptionally well across all datasets, with especially high accuracy for tautomers and protonation states relevant to drug discovery. The AIQM1 model also has impressive performance in many cases, including tautomerization energies. All other methods examined have various strengths and weaknesses, but none have the broad range of quantitative accuracy of the QDπ model for the data examined. Taken together, this suggests that QM/Δ-MLPs such as QDπ and AIQM1 have considerable promise as universal force fields for drug discovery applications.

SUPPLEMENTARY MATERIAL

See the supplementary material for relative energies for the minima and transition states of the alanine dipeptide, ibuprofen, and ketorolac.

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

Author Contributions

Jinzhe Zeng (曾晋哲): Data curation (equal); Software (equal); Visualization (equal); Writing – original draft (equal); Writing – review & editing (equal). Yujun Tao (陶玉君): Data curation (equal); Visualization (equal); Writing – review & editing (equal). Timothy J. Giese: Writing – review & editing (equal). Darrin M. York: Formal analysis (equal); Funding acquisition (equal); Project administration (equal); Resources (equal); Supervision (equal); Writing – original draft (equal); Writing – review & editing (equal).

DATA AVAILABILITY

QDπ-v1.0 is openly available in our GitLab repository at https://gitlab.com/RutgersLBSR/qdpi, which was previously released.⁷⁷ The data that support the findings of this study are available from the corresponding author upon reasonable request.