Pattern completion and disruption characterize contextual modulation in mouse visual cortex

Abstract

A key role of sensory processing is integrating information across space. Neuronal responses in the visual system are influenced by both local features in the receptive field center and contextual information from the surround. While center-surround interactions have been extensively studied using simple stimuli like gratings, investigating these interactions with more complex, ecologically-relevant stimuli is challenging due to the high dimensionality of the stimulus space. We used large-scale neuronal recordings in mouse primary visual cortex to train convolutional neural network (CNN) models that accurately predicted center-surround interactions for natural stimuli. These models enabled us to synthesize surround stimuli that strongly suppressed or enhanced neuronal responses to the optimal center stimulus, as confirmed by in vivo experiments. In contrast to the common notion that congruent center and surround stimuli are suppressive, we found that excitatory surrounds appeared to complete spatial patterns in the center, while inhibitory surrounds disrupted them. We quantified this effect by demonstrating that CNN-optimized excitatory surround images have strong similarity in neuronal response space with surround images generated by extrapolating the statistical properties of the center, and with patches of natural scenes, which are known to exhibit high spatial correlations. Our findings cannot be explained by theories like redundancy reduction or predictive coding previously linked to contextual modulation in visual cortex. Instead, we demonstrated that a hierarchical probabilistic model incorporating Bayesian inference, and modulating neuronal responses based on prior knowledge of natural scene statistics, can explain our empirical results. We replicated these center-surround effects in the multi-area functional connectomics MICrONS dataset using natural movies as visual stimuli, which opens the way towards understanding circuit level mechanism, such as the contributions of lateral and feedback recurrent connections. Our data-driven modeling approach provides a new understanding of the role of contextual interactions in sensory processing and can be adapted across brain areas, sensory modalities, and species.

Introduction

Across animal species, sensory information is processed in a context-dependent manner and, therefore, the perception of a specific stimulus varies with context. This mechanism allows to flexibly adjust sensory processing to changing environments and tasks. In vision, context is provided by global aspects of the visual scene. For example, reliable object detection not only depends on integrating local object features like contours or textures, but also on the visual scene surrounding the object (Biederman et al., 1982; Hock et al., 1974). Physiologically, this is reflected by the fact that responses of visual neurons to stimuli presented in their receptive field (RF) center (i.e. classical RF) — the region of space in which visual stimuli evoke responses — are modulated by stimuli presented in their RF surround (i.e. extra-classical RF). This center-surround contextual modulation has been described across several processing levels of the visual system, from the retina to visual cortex (Chiao and Masland, 2003; Goldin et al., 2022; Alitto and Usrey, 2008; Knierim and Van Essen, 1992; Keller et al., 2020b; Jones et al., 2012; Rossi et al., 2001; Vinje and Gallant, 2000), and is mediated by both lateral interactions and feedback from higher visual areas (Nassi et al., 2013; Nurminen et al., 2018; Keller et al., 2020a; Shen et al., 2022; Adesnik et al., 2012).

How context modulates visual activity has so far largely been studied in non-ecological settings with well-interpretable parametric stimuli, like oriented gratings. Studies in nonhuman primates, and more recently mice (Keller et al., 2020a; Self et al., 2014; Samonds et al., 2017; Keller et al., 2020b), have provided important insights into center-surround modulations in the primary visual cortex (V1). The most commonly observed center-surround modulation is suppression, where neuronal responses to stimuli presented in the center RF decrease in the presence of certain surrounding stimuli (Knierim and Van Essen, 1992; Levitt and Lund, 1997; Kapadia et al., 1999; Sceniak et al., 1999; Cavanaugh et al., 2002b,c; Nassi et al., 2013; Nurminen et al., 2018). The strength of the suppression tends to be the highest when the surrounding elements have the same orientation as the stimulus within the center RF (Knierim and Van Essen, 1992; Cavanaugh et al., 2002c; Self et al., 2014). Surround excitation is less commonly observed and has largely been reported in cases where the stimulus in the center RF is not salient, such as low contrast (Levitt and Lund, 1997; Polat et al., 1998; Keller et al., 2020b).

In general, contextual modulation of visual responses depends on a variety of stimulus features such as contrast and size of the grating presented in the RF center (Levitt and Lund, 1997; Kapadia et al., 1999; Sceniak et al., 1999; Polat et al., 1998; Cavanaugh et al., 2002b), the difference in orientation between center and surround stimuli (Knierim and Van Essen, 1992; Cavanaugh et al., 2002c), and the spatial resolution of the surround pattern (Li et al., 2006). Although these stimulus features interact with each other (Kapadia et al., 1999), they are usually studied independently due to limited experimental time. Moreover, parametric stimuli such as gratings likely drive visual neurons sub-optimally. This is because many visual neurons — like in mouse V1 (Walker et al., 2019; Franke et al., 2022; Ustyuzhaninov et al., 2022) and primate higher visual areas (Pasupathy and Connor, 2001; Bashivan et al., 2019) — exhibit strong selectivity to complex stimuli like corners, checkerboards or textures.

The dependence of contextual modulation on different stimulus features and the strong neuronal preference for complex visual stimuli calls for a more systematic and data-driven way to characterize center-surround interactions using stimuli with ecologically relevant statistics. So far, this has been challenging due to the high dimensionality of natural stimuli and the difficulty in interpreting neuronal responses to a natural input. Here, we overcome these challenges and systematically study center-surround modulations in mouse V1 using naturalistic stimuli by performing inception loops, a closed-loop paradigm circling between large-scale neuronal recordings, convolutional neural network (CNN) models that accurately predict neuronal responses to arbitrary natural stimuli, in silico optimization of non-parametric center and surround images and in vivo verification (Walker et al., 2019; Franke et al., 2022; Bashivan et al., 2019).

Using our data-driven CNN model, we synthesized non-parametric surround images that maximally excite and inhibit the activity of mouse V1 neurons to their optimal visual stimulus in the RF center and subsequently verified their accuracy in vivo. Synthesized surround images contained complex features also present in natural scenes, but were more effective in modulating neuronal activity than natural surround images. Interestingly, we found that the excitatory surround stimuli appeared congruent, completing the spatial pattern of the center stimulus, whereas the inhibiting surround stimuli appeared incongruent. We confirmed this qualitative effect by showing that when we extrapolated the natural image statistics of the center into the surround, the resulting surround images resembled model-derived optimized excitatory surrounds. In addition, excitatory surround images, compared to inhibitory ones, exhibited a larger similarity in neuronal response space to natural scenes, which are known to be spatially correlated and congruent (Geisler et al., 2001; Sigman et al., 2001). Finally, we showed that excitation and inhibition of visual activity by congruent and incongruent surround stimuli, respectively, emerge within a simple hierarchical generative model that encodes an important aspect of natural scene statistics, which is long-range spatial correlations, thereby supporting a new functional role of contextual modulation in sensory processing. Our results regarding contextual modulation are reproduced in a large-scale functional connetomics dataset spanning multiple areas of mouse visual cortex (MICrONS Consortium et al., 2021), which opens the way to dissect its circuit mechanism, including delineating the role of lateral and feedback recurrent connections.

Our work is the first data-driven approach to study contextual interactions in the mouse visual system. It can be easily adapted to other visual areas, animal species and sensory systems, providing the unique possibility to systematically study how context shapes neuronal tuning.

Results

Deep neural network model accurately predicts center-surround modulation of visual responses in mouse primary visual cortex

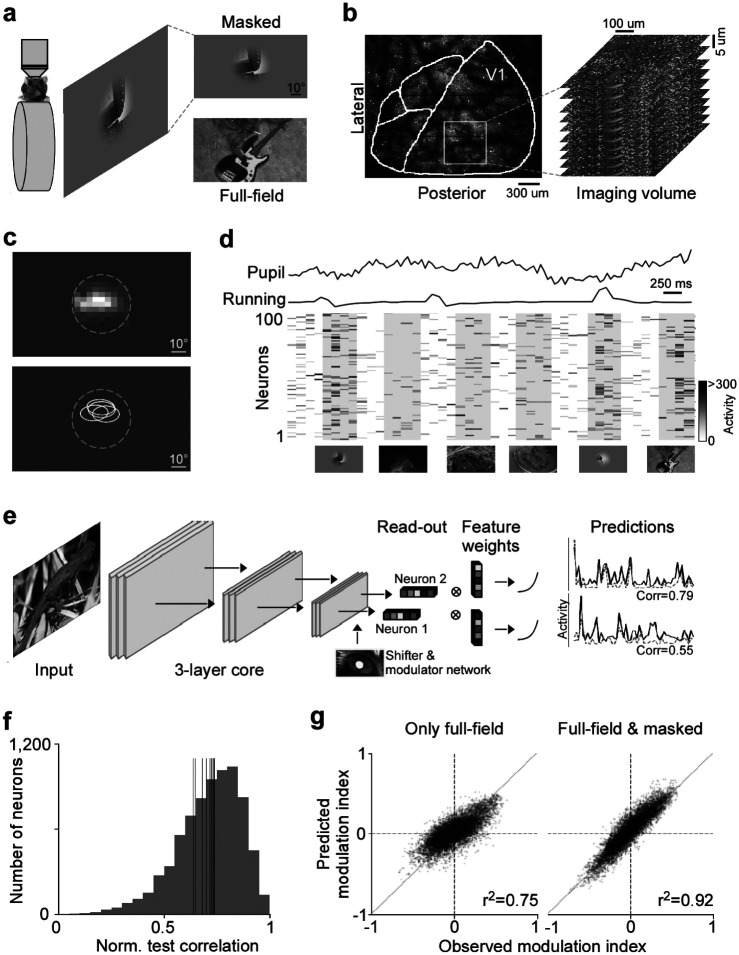
We combined large-scale population imaging and neural predictive modeling to systematically characterize contextual modulation in mouse primary visual cortex (V1). The experimental and modeling setup was adapted based on (Walker et al., 2019). Specifically, we used two-photon imaging to record the population calcium activity in L2/3 of V1 (630×630 μm, 10 planes, 7.97 volumes/s) in awake, head-fixed mice positioned on a treadmill, while presenting the animal with natural images (Fig. 1a,b). To capture center-surround interactions, we presented full-field natural images, which activate both center (classical RF) and surround (extra-classical RF) of V1 neurons, and local masked images that predominantly drive the center of the recorded neurons. Natural images were masked by applying an aperture of 48° visual angle in diameter in the center of the image. For each functional recording, the center RF across all recorded neurons – estimated as minimal response field (MRF) using a sparse noise stimulus (Jones and Palmer, 1987) – was centered on the monitor (Fig. 1c). This ensured that the RF center of the majority of neurons was within the area of the presented masked images. Then, we used the recorded neuronal activity in response to full-field and masked natural images to train a convolutional neural network (CNN) model to predict neuronal responses as a function of visual input. The model also considered eye movements and the modulatory gain effect of the animal’s behavior on neuronal responses (Niell and Stryker, 2010), by using the recorded pupil and running speed traces as input to a shifter and modulator network (Fig. 1d; Walker et al., 2019). An example model (architecture shown in Fig. 1e) that was trained on 7,741 neurons and 4,182 trials (i.e. images) yielded a normalized correlation between model predictions and mean observed responses of 0.73±0.20 (mean ± standard deviation; Fig. 1f). This is comparable to state-of-the-art models of mouse V1 (Franke et al., 2022; Willeke et al., 2022; Lurz et al., 2021). Importantly, masking half of the training images improved the model’s prediction of contextual modulation (Fig. 1g): The prediction of how neuronal responses differ between a masked image and its full-field counterpart significantly increased when using masked natural images during model training (for statistics, see figure legend). Together, this shows that our deep neural network approach accurately captures center-surround modulation of visual responses in mouse primary visual cortex, allowing us to study contextual modulation in the setting of complex and naturalistic visual stimuli.

Fig. 1. Deep neural network approach captures center-surround modulation of visual responses in mouse primary visual cortex.

a, Schematic of experimental setup: Awake, head-fixed mice on a treadmill were presented with full-field and masked natural images from the ImageNet database, while recording the population calcium activity in V1 using two-photon imaging. b, Example recording field. GCaMP6s expression through cranial window, with the borders of different visual areas indicated in white. Area borders were identified based on the gradient in the retinotopy (Garrett et al., 2014). The recording site was chosen to be in the center of V1, mostly activated by the center region of the monitor. The right depicts a stack of imaging fields across V1 depths (10 fields, 5μstep in z, 630×630μ, 7.97 volumes/s). c, Top shows heat map of aggregated population RF of one experiment, obtained using a sparse noise stimulus. The dotted line indicates the aperture of masked natural images. The bottom shows RF contour plots of n=4 experiments and mice. d, Raster plot of neuronal responses of 100 example cells to natural images across 6 trials. Trial condition (full-field vs. masked) indicated below each trial. Each image was presented for 0.5s, indicated by the shaded blocks. e, Schematic of model architecture. The network consists of a convolutional core, a readout, a shifter network accounting for eye movements by predicting a gaze shift, and a modulator predicting a gain attributed to behavior state of the animal. Model performance was evaluated by comparing predicted responses to a held-out test set to observed responses. f, Distribution of normalized correlation between predicted and observed responses averaged over repeats (maximal predictable variability) for an example model trained on data from n=7,741 neurons and n=4,182 trials. Vertical lines indicate mean performance of other animals. g, Accuracy of model predictions of surround modulation for only full-field versus full-field and masked natural images. Each test image was presented in both full-field and masked, allowing us to compute a surround modulation index per image per neuron. The modulation indices across images were averaged per neuron. Left and right shows predicted vs. observed surround modulation indices for a model trained on only full-field images and full-field and masked images, respectively. The model trained on both full-field and cropped images predicted surround modulation significantly better than the model trained on only full-field images (p-value<0.001). The total number of training images was the same, and the data was collected from the same animal in the same session.

CNN model identifies non-parametric excitatory and inhibitory surround images of mouse V1 neurons

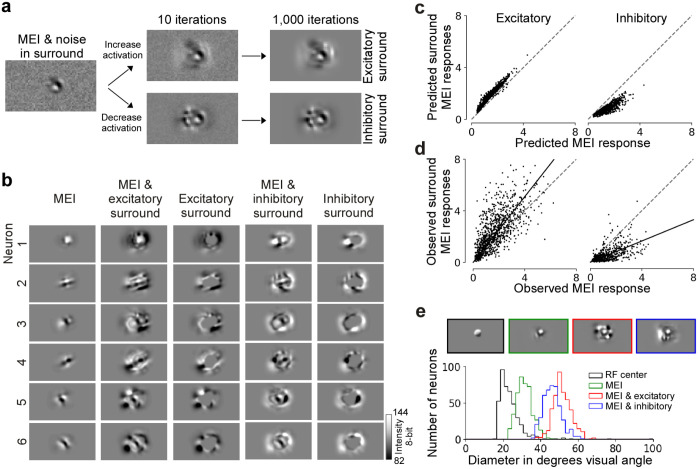
We used the trained CNN model as a “digital twin” of the mouse visual cortex to identify non-parametric surround images that greatly modulate neuronal activity. For that, we focused on the most exciting and most inhibiting surround image, which enhances and reduces the response of a single neuron to its optimal stimulus in the center, respectively. The rationale behind this approach was to identify surround images that maximally modulate the encoding of the neuron’s preferred visual feature. To identify the optimal center stimulus per neuron, we first optimized the most exciting input (MEI) using gradient ascent as previously described (Walker et al., 2019; Franke et al., 2022). In the following, we use the MEI as approximation for the RF center and consider all visual space beyond the MEI as RF surround. To generate excitatory and inhibitory surround images, we used a second optimization step that started with the MEI and initial Gaussian noise in the surround and during optimization, only pixels in the surrounding area of the MEI were updated (Fig. 2a). Thereby, the center (i.e. MEI) of the surround images remained unchanged while redistributing the contrast in the surround (Suppl. Fig. 1a and b). This yielded complex surround images of V1 neurons (Fig. 2b), which were predicted by the model to either enhance or reduce visual responses to optimal stimuli in the center (Fig. 2c). Interestingly, the excitatory surround images were predicted to be less effective in modulating the neurons’ activity than the inhibitory ones (Fig. 2c)..

Fig. 2. Modeling approach accurately predicts non-parametric excitatory and inhibitory surround images of single neurons in mouse V1.

a, Schematic of the optimization of surround images. The initial image is Gaussian noise with the center replaced by the MEI. During optimization, the gradient only flows in the region where the inverse MEI mask is non-zero, leaving the center unchanged. We optimized for the most exciting or the most inhibiting image in the surround. After 1,000 iterations, we reached the final image of the excitatory or the inhibitory surround. b, Panel shows MEI, excitatory surround with MEI, the difference between the two, inhibitory surround with MEI, and the difference between the two for 5 example neurons. Since the gradient was set to zero during optimization for the area within the MEI mask, the center remained the same as the MEI. c, Model predicted responses to the excitatory (left) and inhibitory (right) surround images (y-axis), compared to the predicted responses to the MEIs (x-axis). Responses are depicted in arbitrary units, corresponding to the output of the model. d, Observed responses to the excitatory (left) and inhibitory (right) surround (y-axis), compared to the observed responses to the MEIs (x-axis). For each neuron, responses are normalized by the standard deviation of responses to all images. Across the population, the modulation was significant for both excitatory (p-value=1.15×10⁻⁷⁵, Wilcoxon signed rank test) and inhibitory surround images (p-value=8.79×10⁻⁷¹). Across stimulus repetitions, 28.4% neurons responded significantly stronger to the excitatory surround image than to the MEI (n=6 animals, 960 cells, two-sided t-test, p-value<0.05) while 2.6% responded weaker. 55.1% neurons responded significantly weaker to the inhibitory surround image than to the MEI while 0.4% responded stronger (n=3 animals, 510 cells). Solid line indicates the regression line across the population, and dotted gray line indicates the diagonal. e, Diameters of RFs estimated using sparse noise, the MEIs, and the MEIs with excitatory and inhibitory surround. The mean of center RF (gray distribution) sizes across all neurons (n=4, 419 cells) is 23.4 degrees ± 0.34 (mean ± s.e.m.). The mean of the MEI (green distribution) size across all neurons (n=4, 434 cells) is 31.3 degrees ± 0.20. The size of the MEI is larger than the center RF. The sizes of both the excitatory (red distribution) and inhibitory (blue distribution) surround are much larger than the center RF, measuring 51.4 ± 0.23 and 46.1 ± 0.23 (mean ± s.e.m.) respectively (n=4, 434 cells).

To verify the efficacy of the synthesized surround images in vivo, we performed inception loop experiments (Walker et al., 2019; Bashivan et al., 2019): After model training and stimulus optimization, we presented MEIs and the respective surrounds back to the same mouse on the next day while recording from the same neurons, thereby testing whether they effectively modulate neuronal responses as predicted by the model. We found that the in silico predictions (Fig. 2c) matched the in vivo results (Fig. 2d, Suppl. Fig. 2): The responses of the neuronal population significantly increased and decreased by the synthesized excitatory and inhibitory surround images, respectively, compared to presenting the MEI alone. While 55.1% of the neurons verified in vivo during inception loop experiments were significantly inhibited by their inhibitory surround images across stimulus repetitions, only 28.4% were significantly facilitated by their excitatory surround images, in line with the lower modulation strength of excitatory compared to inhibitory surround images predicted by the model. Critically, less than 3% were significantly modulated in the direction opposite to what the model predicted. These results from the inception loop experiments demonstrate the accuracy of our CNN model in predicting non-parametric modulatory surround images of mouse V1 neurons. Notably, we also reproduced the described center-surround effects in the large-scale multi-area functional connectomics MICrONS dataset (MICrONS Consortium et al., 2021) that used natural movies instead of static images as visual stimuli (Suppl. Fig. 3). This opens the way to dissect circuit mechanisms underlying contextual modulation in mouse visual cortex, including delineating the role of lateral and feedback recurrent connections.

We verified that the observed response modulations indeed originated from activating the surround (i.e. extra-classical RF) of the neurons. First, we demonstrated that the synthesized surround images extend beyond the center (i.e. classical RF) of the neurons (Fig. 2e). Specifically, we estimated each neuron’s center RF as the minimal response field (MRF) using a sparse noise stimulus (Jones and Palmer, 1987) and compared its size to the size of the MEI and the excitatory and inhibitory surround, respectively. The MRF was, on average, smaller than the MEI, suggesting that the MEI itself corresponds to an overestimation of the RF center. Importantly, both the excitatory and inhibitory surround were much larger than the MRF, indicating that the modulatory effect on neuronal activity we observed by the surround images was indeed elicited by activating the surround component of V1 RFs. In line with this, in additional control experiments we show that the response modulation persisted in silico and in vivo in a “far” surround region not directly adjacent to the MEI (Suppl. Fig. 4). In addition, we showed that increasing the contrast in the center was more effective in driving the neurons than adding the same amount of contrast in the surround of the image (Suppl. Fig. 5), consistent with the idea that the enhancement in neuronal response from the surround is modulatory (Allman et al., 1985; Cavanaugh et al., 2002a; Jones et al., 2001; Knierim and Van Essen, 1992). Together, these results demonstrate that the observed response modulation by model-derived surround images originates from activating the surround RF of V1 neurons.

Surround images are ecologically relevant and correspond to the optimal modulating stimulus

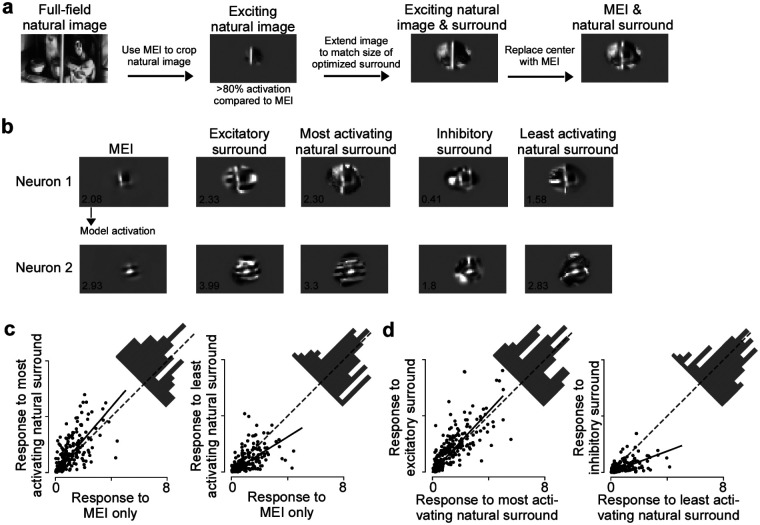
We next asked the question whether the center-surround modulation we observed with our non-parametric images exhibits ecological relevance, meaning that a similar contextual modulation of V1 neuronal activity can be observed with surround images present in ecological images. To address this, we compared the modulation elicited by model-derived surround images to the modulation by natural images. We focused this analysis on natural image surrounds that contain the neuron’s preferred center feature, similar to the optimized surround images that have the MEI in the center. To obtain surrounds of natural images, we therefore screened a new set of 5,000 masked natural images and identified the most exciting natural images per neuron (>80 % activation compared to the MEI activation), matching the size, location and contrast of its MEI (Fig. 3a). We then replaced the center of these images by the MEI, and masked the images to match the average size and contrast of excitatory and inhibitory surround images. For each neuron, this yielded a set of images with the same optimal stimulus in the center (i.e. the MEI), but diverse natural surrounds. To obtain the modulation strength of these natural surrounds, we presented the natural surround images to the model and compared the predicted activations to the activation of the MEI alone.

Fig. 3. Surround images correspond to the optimal modulating stimulus and are ecologically relevant.

a, Schematic illustrating how we obtained natural surround images for one example neuron. b, Optimized excitatory and inhibitory surround images, most exciting and inhibiting natural surrounds and MEI of two example neurons. The predicted activation score is indicated in the bottom left of the images. c, Observed responses to the MEI with natural surround images compared to the MEI alone. Across the population, the least activating natural surround images suppressed neuronal response (p-value=1.84×10⁻⁸, Wilcoxon signed rank test), and the most activating natural surround images enhanced neuronal response (p-value=2.44×10⁻⁹, Wilcoxon signed rank test). Across stimulus repetitions, 23% responded significantly stronger to the most activating natural images than to the MEI (n=3 animals, 226 cells, two-sided t-test, p-value<0.05) and 25% of the neurons responded significantly weaker to the least activating natural surround images than to the MEI. Solid line indicates the regression line across the population, and dotted gray line indicates the diagonal. d, Observed responses to the MEI with natural surround images compared to the MEI with excitatory/inhibitory surround. Across the population, the MEI with inhibitory surround suppressed neuronal response more than the MEI with the least activating natural surround (p-value=1.98×10⁻²⁰, Wilcoxon signed rank test). The MEI with excitatory surround enhanced neuronal response more than the MEI with most activating natural surround (p-value=1.05×10⁻⁶, Wilcoxon signed rank test). Across stimulus repetitions, 37% of neurons responded significantly weaker to the MEI with inhibitory surround compared to the MEI with the least activating natural surround and 19% of the neurons responded significantly stronger to the MEI with excitatory surround compared to the MEI with the most activating natural surround (n=3 animals, 226 cells, two-sided t-test, p-value<0.05). Solid line indicates the regression line across the population, and dotted gray line indicates the diagonal.

We found that there are indeed natural surrounds that enhance and reduce V1 model responses to the preferred visual feature, similar to our synthesized surround images (Fig. 3b). We tested this in silico prediction by performing inception loop experiments with the synthesized surround images and the most and least activating natural surrounds per neuron, as predicted by the model. Across the neuronal population, the most activating natural surrounds significantly enhanced V1 responses to their optimal center stimulus, while the least activating natural surround resulted in reduced activity (Fig. 3c). In addition, across the population, the synthesized inhibitory surround images were more effective in modulating V1 neuronal activity than the least activating natural surrounds (Fig. 3d). In contrast, the modulation strength of the most activating natural surround images was comparable to the synthesized excitatory surrounds (Fig. 3d). Together, these findings strongly suggest that the model-derived surround images exhibit ecological relevance, as they modulate V1 responses to their preferred center feature in a similar way as surround patches of natural images.

Completion and disruption of center features characterize excitatory and inhibitory surround images

Center-surround modulation of visual activity corresponds to a neuronal implementation for integrating visual information across space, thereby providing context for visual processing. So far, little is known about the natural image statistics that drive contextual modulation in vision, due to the lack of tools that allow unbiased and systematic testing of such highdimensional visual inputs. Here, we used our data-driven model and the optimized surround images to systematically investigate the rules that determine contextual excitation versus inhibition in a naturalistic setting.

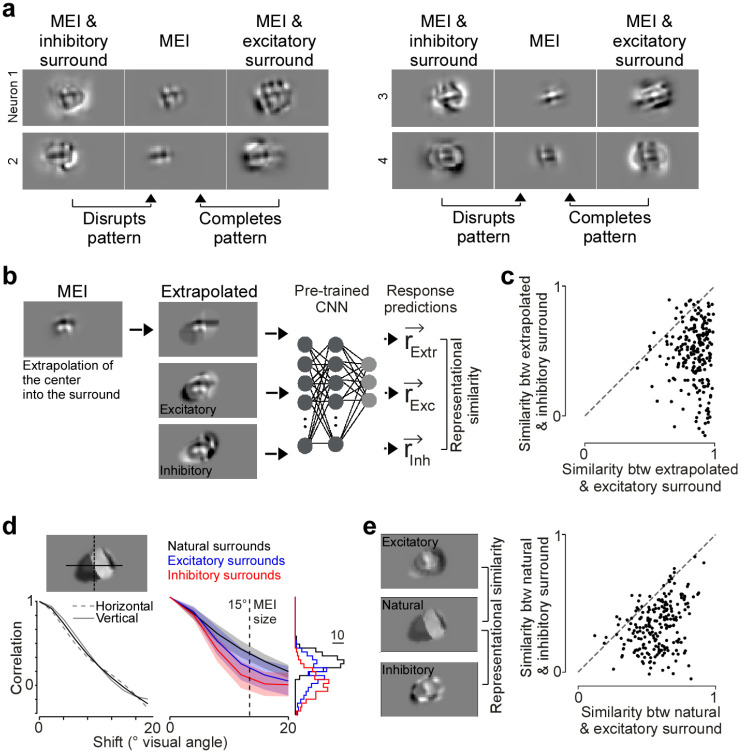
We observed that the excitatory surround images appeared more congruent with respect to the MEI in the center compared to the inhibitory surround images (Fig. 4a). Spatial patterns in the MEI, such as orientation, were mostly maintained and completed by the excitatory surround but often disrupted and opposed by the inhibitory surround. Therefore, we hypothesized that the excitatory and inhibitory surround can be characterized by pattern completion and disruption, respectively, with respect to the preferred feature in the center. We tested these predictions by performing a set of in silico experiments. First, we used the MEI in the RF center to extrapolate its spatial patterns into the surround based on a bivariate spline approximation, thereby creating a congruent surround that completes patterns present in the center (Fig. 4b). For most neurons, the extrapolated surround perceptually looked more similar to the excitatory than the inhibitory surround (Suppl. Fig. 6). To quantify the perceptual similarity of optimized and extrapolated surrounds, we computed the “representational similarity” for a given pair of images in the neuronal response space. We chose to use representational similarity instead of pixel-wise correlation to quantify similarity between images because (i) the representational space more closely mimics perceptual similarity (Kriegeskorte et al., 2008) and (ii) this process gets rid of irrelevant image features, such as high spatial frequency noise. Specifically, we presented the optimized and extrapolated surround images to the trained CNN model, obtained a vector of neuronal responses per image and estimated the cosine similarity between the response vectors of an image pair (i.e. extrapolated and excitatory surround; Fig. 4b). We found that the extrapolated surround images that complete the spatial structure of the MEI exhibit a high representational similarity to the MEI with excitatory surround images, while the similarity to the MEI with inhibitory surrounds was much weaker (Fig. 4c). This suggests that excitatory surround images of V1 neurons are characterized by pattern completion of the optimal center stimulus.

Fig. 4. Pattern completion and disruption characterize excitatory and inhibitory surround images.

a, MEI with excitatory and inhibitory surround of four example neurons, illustrating that excitatory and inhibitory surround images complete and disrupt, respectively, spatial patterns of the MEI. b, MEI of example neuron, with extrapolated and excitatory and inhibitory surround images. Right shows a schematic illustrating how we compared the similarity of surround images using representational similarity. In brief, each surround image was presented to the trained CNN model to obtain a response vector. The response vectors for different images were than compared using Pearson’s correlation coefficient. c, Representational similarity (as Pearson’s correlation coefficient) of extrapolated surround images to excitatory and inhibitory surround (p-value=2.26×10⁻³⁶, two-sided Wilcoxon signed rank test, n=3 animals, 219 neurons). d, Left shows auto-correlation function of an example natural surround image, for a vertical (dotted line) and horizontal (solid line) projection through the center of mass of the image (mean in black). Right shows the mean auto-correlation functions of natural (black), excitatory (blue) and inhibitory (red) surround images (n=3 animals, 219 neurons; shading: s.d.), with the histograms of correlation coefficients for a spatial shift of 15° visual angle indicated on the right. For a shift of 15° visual angle, corresponding to the mean radius of MEIs, inhibitory surround images exhibited significantly weaker spatial correlations than excitatory surround images (p-value=1.8×10⁻¹⁵, two-sided Wilcoxon signed rank test). e, Excitatory and inhibitory surround of an example neuron, with one exciting natural image and surround (left) and representational similarity (as Pearson’s correlation coefficient, right; p-value=5.28×10⁻³⁵, two-sided Wilcoxon signed rank test, n=3 animals, 219 neurons) of natural surround images with excitatory and inhibitory surround. Each dot represents the mean across natural surrounds per neuron.

We further tested this hypothesis by quantifying the statistics of our model-derived surround images. Specifically, we took advantage of the well-described fact that natural images are correlated across space and often contain congruent structures that form object contours and continuous patterns (Geisler et al., 2001; Sigman et al., 2001). Therefore, excitatory surround images should share statistical properties with and be perceptually similar to the surrounds of natural image patches, more so than inhibitory surround images. We compared the spatial correlation structure of optimized MEI with surround images to the one of natural surrounds that contain the neuron’s preferred image feature in the center (>80% activation compared to the MEI activation). Spatial correlations were quantified using the auto-correlation function of intensity profiles through the center of the surround images (Fig. 4d). We found that, like natural image patches, the MEI with excitatory surround displayed significantly higher spatial correlations than the MEI with the inhibitory surround image (Fig. 4d), at least for spatial shifts of the mean MEI size across neurons. Next, we used the representational similarity metric introduced above to quantify the similarity between optimized and natural center-surround images. This revealed that natural surround images with the neuron’s preferred center feature exhibit a larger similarity with excitatory than inhibitory surround images (Fig. 4e). Taken together, our results demonstrate that surround excitation and inhibition in mouse primary visual cortex can be characterized by pattern completion and disruption, respectively, thereby identifying a clear relationship between natural image statistics and modulation of neuronal activity.

Probabilistic perception via Bayesian inference can explain observed center-surround effects

Finally, we linked our observed center-surround effects to normative, first-principle theories of perceptual inference. In general, the goal of perception is to infer useful features from the world, but given that ambiguous, noisy sensory stimuli often conceal these features, it is beneficial to combine information from the incoming sensory stimulus with prior knowledge of the environment (Von Helmholtz, 1867). One principled way how the brain could accomplish this is to perform Bayesian inference over relevant latent variables (features) underlying the stimulus using a statistical generative model of the world (Knill and Richards, 1996; Kersten et al., 2004; Lochmann and Deneve, 2011; Fiser et al., 2010). Here, we demonstrate that surround excitation and inhibition by congruent and incongruent surround patterns, respectively, is consistent with this theory by using a simple hierarchical generative model of the stimulus that encodes long-range spatial correlations of natural image statistics in its prior.

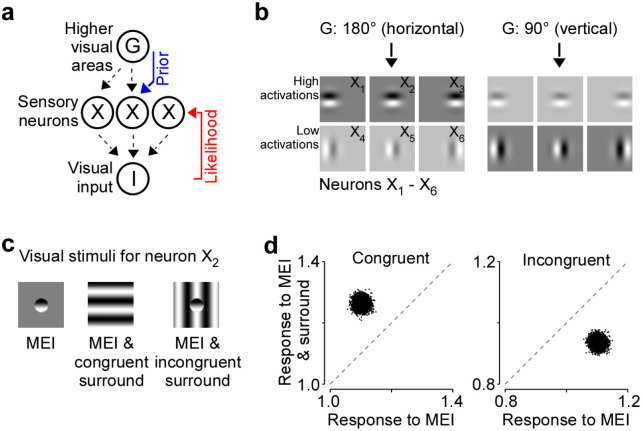
Our hierarchical generative model is similar to ones previously proposed (Haefner et al., 2016; Bányai et al., 2019). Specifically, in our model we assume that a set of oriented Gabor-shaped filters located in the center and surround of visual space are linearly combined to generate the observed image I (Fig. 5a). We further assume that the activation of each of these filters depends on a global orientation variable, G, which boosts the activity of compatible filters, and suppresses those of incompatible filters (Fig. 5b). Upon observing a stimulus, i.e. during perception, the brain inverts the generative model to compute the posterior distribution p(G,X|I). Specifically, the brain combines the latent global orientation G which is provided by feedback from higher areas and the feedforward sensory information given the image I. As a result of this inference process, the neuronal responses X to a given stimulus are influenced by both the stimulus I and the global orientation G.

Fig. 5. Explaining observed center-surround effects via Bayesian inference and neural sampling.

a, Assumed hierarchical generative model of the stimulus as maintained by the brain. G represents a higher visual area, encoding a global orientation variable, X represents sensory neuronal responses, which are activations of local Gabor filters, and I represents the visual input. The idea is that when visual input I is presented, the (simplified model of the) brain probabilistically infers a global orientation and the activations of the Gabor filters from the visual input via posterior inference, i.e., computes p(G,X|I) and samples from it. Posterior samples of X, i.e., of sensory neurons depend on the visual input I (likelihood, feedforward) as well as on G (prior, feedback). b, Gabor filters corresponding to the 6 model neurons as activated only by the prior, i.e., by G. In our model, we have 3 neurons with vertical Gabor filters and 3 others with horizontal Gabor filters. Gabor filters that have orientations similar to the global orientations have higher activations, as opposed to those that have orientations dissimilar to the global orientation. These activations are interpreted as sensory neuronal responses. We consider the neuron with a horizontal Gabor at the center as the “center neuron”. c, Collection of visual stimuli we present to the model. All stimuli, i.e., MEI, MEI & congruent surround, and MEI & incongruent surround are defined w.r.t the center neuron. d-f, Scatterplot of posterior samples from the center neuron under various stimulus presentations, reproducing the key experimental observations of surround-based excitation and inhibition.

To quantify the center-surround interactions in this model, we presented three stimuli tailored to an example sensory neuron whose RF is located in the center of visual space (Fig. 5c): (1) the MEI of the example neuron, (2) the MEI with a spatially congruent stimulus in the surround, (3) the MEI with a spatially incongruent stimulus in the surround. These three conditions match the pattern completion and disruption that characterize the contextual modulations we found in mouse V1. For each stimulus condition, we computed the posterior p(G,X|I) in our hierarchical model to obtain a distribution of global orientations and responses given the stimulus condition. The model responses reproduced our key experimental results (Fig. 5d): (1) the example neuron is driven strongly by the MEI alone, (2) the spatially congruent stimulus drives the example neuron in the center stronger than its MEI, (3) the spatially incongruent stimulus inhibits the responses of the neuron, despite the MEI being present in the center.

In summary, our probabilistic inference model reproduced the main experimental findings of our study, with congruent surround stimuli being excitatory and incongruent surround stimuli being inhibitory with respect to the neuron’s preferred feature. The key driver of this behavior in our model is the higher certainty about the global orientation induced by congruency of center and surround and, as a result, a stronger prior on the lower level features of similar orientation. As a result, even neurons with RFs in the center are more strongly activated.

Discussion

Our study discovered a novel rule of surround modulation in mouse V1: Completion (or extension) of visual features in the RF center governed surround excitation, whereas disruption (or termination) of RF center features produced inhibition. Non-linearity and high dimensionality in the neuronal responses to natural images have so far made it challenging to accurately define the RF center properties and to model the interactions with the RF surround. Our accurate digital twin models allowed us to model the non-linearity both within and beyond the RF center, and to predict the best modulating stimuli in the surround without any parametric assumptions about their underlying statistical structure. We verified the predictions from the model experimentally in a closed-loop manner, and found that combining an optimal stimulus in the RF center with an excitatory surround yielded images that were more similar to natural scenes than images consisting of optimal center stimulus and inhibitory surround. This type of surround facilitation by congruent structures emerged within a simple hierarchical model that modulates neuronal responses based on prior knowledge of natural scene statistics, and may potentially enhance the encoding of prominent features in the visual scene, such as contours and edges, especially when the sensory input is noisy and ambiguous.

Relationship between surround modulation and stimulus statistics

Classical studies in monkeys have investigated the spatial patterns driving contextual modulation in primary visual cortex using oriented stimuli such as gratings and bars (Knierim and Van Essen, 1992; Levitt and Lund, 1997; Kapadia et al., 1999; Sceniak et al., 1999; Cavanaugh et al., 2002b,c; Nassi et al., 2013; Nurminen et al., 2018). This revealed that suppression is the dominant form of surround modulation and that surround stimuli congruent with the center stimulus tend to be the most suppressive (Knierim and Van Essen, 1992; Levitt and Lund, 1997; Kapadia et al., 1999; Sceniak et al., 1999; Cavanaugh et al., 2002b,c; Nassi et al., 2013; Nurminen et al., 2018). The suppression strength decreased as the surrounding stimulus becomes less congruent (Knierim and Van Essen, 1992; Kapadia et al., 1999). In contrast, surround facilitation has been much more rarely observed, and it requires more specific configurations of the center stimulus such as low contrast or even absence of stimulation (Polat et al., 1998; Lee and Nguyen, 2001). This is in line with our finding that excitatory surround images are less effective in modulating visual responses than inhibitory surround images.

However, our results based on naturalistic stimuli and a data-driven approach, which does not make any assumptions about stimulus selectivity, reveal a different principle of surround modulation in mouse primary visual cortex. We find that the most excitatory surround stimulus is congruent with respect to the center stimulus, while the most inhibiting surround stimulus is incongruent. So far, the spatial patterns driving surround excitation versus inhibition in mouse V1 are less conclusive compared to primates. Some previous studies have reported suppression and facilitation of mouse V1 neurons by congruent and incongruent parametric surround stimuli (Keller et al., 2020a; Self et al., 2014), respectively, consistent with the results in primates. However, there seems to be a large variability across neurons, where surround stimuli that have the same orientation as the center stimulus can be either excitatory or inhibitory (Samonds et al., 2017) and different orientations of the surround relative to the center can be excitatory (Keller et al., 2020b). In part, this variability across neurons might be related to the fact that parametric stimuli like gratings and bars drive mouse V1 neurons sub-optimally, due to the neurons’ selectivity for more complex visual features (Walker et al., 2019). It is well established that contextual modulation depends on the center stimulus (Knierim and Van Essen, 1992; Kapadia et al., 1999) and, therefore, it might be critical to condition surround stimuli on the optimal stimulus in the RF center, corresponding to the MEI (Walker et al., 2019).

The inconsistencies in surround patterns eliciting excitation and inhibition reported in studies on mouse and primate V1 might partially be due to differences in stimulus design. For example, the complex naturalistic stimuli we used vary from parametric stimuli with respect to image statistics and likely result in different neuronal responses (Froudarakis et al., 2014; David et al., 2004), which may influence the modulatory effect of the surround on the RF center. Other critical stimulus parameters that impact neuronal responses are stimulus contrast and luminance. It has been previously shown that at lower contrast, congruent surround stimuli facilitate responses in monkey V1 neurons to the preferred center stimulus (Polat et al., 1998), similar to the pattern of surround excitation we describe here. In monkeys, surround facilitation turned into suppression as the contrast of the center stimulus increased (Polat et al., 1998). We optimized the MEIs and surround images to minimize clipping of pixel values outside the 8-bit range, even for the contrast-matched MEIs that had higher contrast in the center (cf. Suppl Fig. 4), and presented them at mesopic light levels. Without further experiments, it is challenging to compare our non-parametric MEIs and surround stimuli to previous results using parametric grating stimuli presented at varying contrasts and light levels (Polat et al., 1998; Adesnik et al., 2012; Keller et al., 2020b,a). Importantly, it is worth noting that, in addition to the experimental and technical differences described above, there likely exist species-specific differences in the stimulus statistics that drive surround modulation. Primates and mice may have distinct strategies in visual processing due to ethological differences, and, therefore, surround modulation of visual responses might serve a different computational goal. Future experiments are required to further understand possible species-specific roles of contextual modulation in vision.

Circuit-level mechanism of contextual modulation in visual cortex

Mechanistically, surround suppression in V1 can be partially accounted for by feedback projections from higher visual areas. In monkeys, inactivation of feedback from V2 and V3 reduces surround suppression induced by large grating stimuli (Nassi et al., 2013; Nurminen et al., 2018) and also results in an increase in RF size (Sceniak et al., 1999; Nurminen et al., 2018). In mice, feedback from higher visual areas also strongly modulates V1 responses to center stimuli and even elicits strong responses without any stimulation of the center RF, thereby creating a feedback RF (Keller et al., 2020b; Shen et al., 2022). The cellular substrate of surround modulation has been predominantly studied in mice, due to available genetic tools for cell-type specific circuit manipulations. Different types of inhibitory neurons have been identified as key players of surround modulation, including somatostatin (SOM)- and vasoactive intestinal peptide (VIP)-expressing cells, which inhibit each other as well as excitatory V1 neurons and are further modulated by feedback (Adesnik et al., 2012; Keller et al., 2020a; Shen et al., 2022). Based on these results, surround suppression in mouse V1, and likely primate V1, is dependent on the exact balance between the excitatory input from feedforward and feedback projections and the inhibitory inputs from locally present inhibitory neuron types.

To further explain surround modulation of individual visual neurons as a function of local and long-range network connectivity, one can take advantage of recent advances in functional connectomics, combining large-scale neuronal recordings with detailed anatomical information at the scale of single synapses. Here, we demonstrated that the observed center-surround effects of mouse V1 neurons were reproduced in a recently published functional connectomics dataset (MICrons dataset) spanning V1 and multiple higher areas of mouse visual cortex (MICrONS Consortium et al., 2021). Specifically, this dataset includes responses of >75k neurons to natural movies and the reconstructed sub-cellular connectivity of the same cells from electron microscopy data. A dynamic recurrent neural network (RNN) model of this mouse’s visual cortex exhibits not only a high predictive performance for natural movies, but also accurate out-of-domain performance on other stimulus classes such as drifting Gabor filters, directional pink noise, and random dot kinematograms (Wang et al., 2023). We took advantage of the model’s ability to generalize to other visual stimulus domains and showed that MEIs and surround images optimized using the RNN model trained on the same natural movies used in the MICrons dataset closely resemble those obtained from our model. The MICrons dataset provides ample resources to link connectivity among neurons within V1 and across areas to the functional properties observed with regard to contextual modulation, thereby further delineating the role of local and feedback recurrent connections.

Theoretical implications of surround facilitation

We discovered that surround facilitation is a prominent feature of contextual modulation in mouse primary visual cortex, thereby highlighting that center-surround interactions cannot simply be explained by suppression of sensory responses. Importantly, excitatory surround images with the optimal center stimulus exhibited a high representational similarity with natural images, indicating that congruent patterns frequently present in natural scenes (Geisler et al., 2001; Sigman et al., 2001) are associated with high neuronal activations. Excitation by congruent surround structures relative to the center may be explained by preferential long-range connections between neurons with co-linearly aligned RFs described in mice (Iacaruso et al., 2017) and higher mammals (Bosking et al., 1997; Schmidt et al., 1997; Sincich and Blasdel, 2001) and might serve perceptual phenomena like edge detection, contour integration and object grouping observed in humans and primates (Kapadia et al., 1995; Geisler et al., 2001).

Our empirical results of surround facilitation are surprising in the light of a long line of theoretical work that explains sensory responses using principles like redundancy reduction (Barlow et al., 1967) or predictive coding (Rao and Ballard, 1999). The idea that neurons should minimize redundancy has given rise to contrast normalization models (Schwartz and Simoncelli, 2001) that were recently expanded to a flexibly-gated center-surround normalization model (Coen-Cagli et al., 2015) most relevant to our data. The key idea behind the latter model is to only normalize (typically reduce) center activation when the surround is similar, and otherwise ignore the surround. This proposal cannot explain our empirical findings. Analogously, predictive coding proposes that neuronal activity reflects prediction errors, and that therefore the center activation should be lower when it can be well predicted from the surround (Rao and Ballard, 1999; Keller and Mrsic-Flogel, 2018) – again in contradiction to our finding that excitatory surrounds appear to ‘complete’ the center stimulus, and frequently occuring in natural scenes.

In contrast, our results are expected within an alternative framework for understanding sensory neurons: perceptual (Bayesian) inference (Von Helmholtz, 1867; Knill and Richards, 1996). Here, sensory responses compute beliefs about latents in a hierarchical model with higher level latents both representing larger, more complex features of the image and acting as priors on lower level latents that represent localized parts of the image via feedback signals (Lee and Mumford, 2003). In such a model, global image structure can increase or decrease responses of neurons with localized RFs, depending on whether the global structure increases or decreases the probability of the local feature being present in the image (Haefner et al., 2016; Bányai et al., 2019). In fact, our toy-model which qualitatively reproduces our empirical findings is an example of such a model. Our approach of characterizing contextual modulation in a data-driven way for arbitrary stimuli, without any assumptions about neuronal selectivity, have revealed a novel relationship between surround modulation and natural image statistics, providing evidence for a role of contextual modulation in hierarchical inference, rather than only minimizing redundancy or prediction errors.

Materials and Methods

Animals and surgical preparation

All experimental procedures complied with guidelines of the NIH and were approved by the Baylor College of Medicine Institutional Animal Care and Use Committee (permit number: AN-4703), expressing GCaMP6s in cortical excitatory neurons. Mice used in this study (n=7, 3 males and 4 female, aged 2.5 to 3.5 month) were heterozygous crosses between Ai162 and Slc7a7-Cre transgenic lines (JAX #031562 and #023527, respectively). To expose V1 for optical imaging, we performed a craniotomy and installed a window that was 4mm in diameter and centered at 3mm lateral to midline and 2mm anterior to lambda (Reimer et al., 2014; Froudarakis et al., 2014). Mice were housed in a facility with reverse light/dark cycle to ensure optimal alertness during the day when experiments were performed.

Neurophysiological experiments and data processing

We recorded calcium signals using 2-photon imaging with a mesoscope (Sofroniew et al., 2016) which was equipped with a custom objective (0.6 numerical aperture, 21 mm focal length). The imaging fields of each recording were 630×630 μm² per frame at 0.4 pixels μm⁻¹ xy resolution and were positioned in the center of V1 according to the retinotopic map (Fig. 1b). Z resolution was 5 μm with a total of ten planes from −200μm to −245μm relative to cortical surface. The laser power increased exponentially as imaging plane moved farther from the surface according to:

$$P=P_0{e}^{z/L_z}$$

Here P is the laser power used at target depth z, P₀ is the power used at the surface (19.71 mW ± 4.68, mean ± standard deviation), and L_z is the depth constant (220 μm). The highest laser output was of 54.79 mW ± 13.67 and was used at approximately 240 μm from the surface. Most scans did not require more than 50 mW at maximal depth, except for one mouse where the average laser power at the deepest scanning field was 82.03 mW.

For each animal, we first performed retinotopic mapping across the whole cranial window to identify the border of V1 (Fig. 1b and c; Schuett et al., 2002). At the beginning of each imaging session, we measured the aggregated population RF to ensure precise placement of the monitor with regard to the imaging site. We used stimuli consisting of dark (pixel value=0) square dots of size 6 degrees in visual angle on a white background (pixel value=255). The dots were randomly displayed at locations on a 10 by 10 grid covering the central region of the monitor and at each location the dot was shown for 200 ms and repeated 10 times over the whole duration of dot mapping. The mean calcium signal was deconvolved and averaged across repeated trials to produce the population RF. The monitor was placed such that the population RF was centered on the monitor.

The full two-photon imaging processing pipeline is available at (https://github.com/cajal/pipeline). Briefly, raster correction for bidirectional scanning phase row misalignment was performed by iterative greedy search at increasing resolution for the raster phase resulting in the maximum cross-correlation between odd and even rows. Motion correction for global tissue movement was performed by shifting each frame in x and y to maximize the correlation between the cross-power spectra of a single scan frame and a template image, generated from the Gaussian-smoothed average of the Anscombe transform from the middle 2000 frames of the scan. Neurons were automatically segmented using constrained non-negative matrix factorization, then traces were deconvolved to extract estimates of spiking activity, within the CalmAn pipeline (Giovannucci et al., 2019). Cells were further selected by a classifier trained to separate somata versus artifacts based on segmented cell masks, resulting in exclusion of 8.1% of the masks.

A 3D stack of the volume imaged was collected at the end of each day to allow registration of the imaging plane and identification of unique neurons. The stack was composed of two volumes of 150 planes spanning from 50 μm above the most superficial scanning field to 50 μm below the deepest scanning field. Each plane was 500 × 800 μm, together tiling a 800 × 800 μm field of view (300 μm total overlap), and repeated 100 times per plane.

Visual stimulation

Visual stimuli were displayed on a 31.8 × 56.5 cm (height × width) HD widescreen LCD monitor with a refresh rate of 60 Hz at a resolution of 1080 × 1920 pixels. When the monitor was centered on and perpendicular to the surface of the eye at the closest point, this corresponded to a visual angle of 2.2°/cm on the monitor. We recorded the voltage of a photodiode (TAOS TSL253) taped to the top left corner of the monitor to measure the gamma curve and luminance of the monitor before each experimental session. The voltage of the photodiode is linearly correlated with the luminance of the monitor. To convert from photodiode voltage to monitor luminance, we used a luminance meter (LS-100 Konica Minolta) to measure monitor luminance for 16 equidistant pixel values from 0–255 while recording the photodiode voltage. The gamma value for experiments in this paper ranged from 1.751 to 1.768 (mean = 1.759, standard deviation = 0.005). The minimum luminance ranged from 0.23 cd/m² to 0.97 cd/m² (0.49 ± 0.25, mean ± standard deviation), and the maximum ranged from 84.11 cd/m² to 86.04 cd/m² (85.07 ± 0.72, mean ± standard deviation).

ImageNet stimulus.

Natural images were randomly selected from the ImageNet database (Deng et al., 2009), converted to gray scale, and cropped to the monitor aspect ratio of 16:9. To probe center-surround interactions, we modified the images using a circular mask that was approx. 48 degrees in visual angle in diameter with smoothed edges. The mask radius was defined as fraction of monitor width, i.e. r_aperture = 1 means a full-field mask. We used r_aperture = 0.2

$$r=\frac{r_{\text{pixel}}-r_{\text{aperture}}}{\alpha }+1$$

$$M=\{\begin{array}{ll}\frac{1+\text{cos}(\pi r)}{2}\hfill & 0<r<1\hfill \\ 1\hfill & r\le 0\hfill \\ 0\hfill & \mathit{\text{otherwise}}\hfill \end{array}$$

where M is the mask, r is the radius, and α is the width of the transition. We presented 5,000 unique natural images without repetition during each scan, half of which were masked. We also presented the same 100 images repeated 10 times as full-field and 10 times as masked. The 100 images that were repeated were conserved across experiments, while the unique images varied across scans. Each trial consisted of one image presented for 500 ms with a preceding blanking period of 300 – 500 ms (randomly determined per trial).

Eye tracking

A movie of the animal’s eye and face was captured throughout the experiment. A hot mirror (Thorlabs FM02) positioned between the animal’s left eye and the stimulus monitor was used to reflect an IR image onto a camera (Genie Nano C1920M, Teledyne Dalsa) without obscuring the visual stimulus. The position of the mirror relative to the camera was manually adjusted if necessary per session to ensure that the camera focuses on the pupil. The field of view was manually cropped for each session. The field of view contained the left eye in its entirety, 282–300 pixels height × 378–444 pixels width at 20 Hz. Frame times were time stamped in the behavioral clock for alignment to the stimulus and scan frame times.

Light diffusing from the laser during scanning through the pupil was used to capture pupil diameter and eye movements. A DeepLabCut model (Mathis et al., 2018) was trained on 17 manually labeled samples from 11 animals to label each frame of the compressed eye video with 8 eyelid points and 8 pupil points at cardinal and intercardinal positions. Pupil points with likelihood >0.9 (all 8 in 93% ± 8% of frames) were fit with the smallest enclosing circle, and the radius and center of this circle was extracted. Frames with <3 pupil points with likelihood >0.9 (0.7% ± 3% frames per scan), or producing a circle fit with outlier >5.5 standard deviations from the mean in any of the three parameters (center x, center y, radius, <1.3% frames per scan) were discarded (total <3% frames per scan). Trials affected by gaps in the frames were discarded (<2% trials for all animals except one, where the animal’s eye appeared irritated).

Registrations of neurons in 3D stack

We densely sampled the imaging volume to avoid losing cells due to tissue deformation from day to day. Therefore, some cells were recorded in more than one plane. To select unique cells, we sub-sampled our recorded cells based on proximity in 3D space. Each functional scan plane was independently registered to the same 3D structural stack. Specifically, we used an affine transformation matrix with 9 parameters estimated via gradient ascent on the correlation between the sharpened average scanning plane and the extracted plane from the sharpened stack. Using the 3D centroids of all segmented cells, we iteratively grouped the closest two cells from different scans until all pairs of cells are at least 10 μm apart or a further join produces an unrealistically tall mask (20 μm in z). Sequential registration of sections of each functional scan into the structural stack was performed to assess the level of drift in the z dimension. The drift over the 2 to 2.5 hour recording was 4.70 ± 2.64, and for most of them the drift was limited to <5 μm.

Model architecture and training

The convolutional neural network used in this study consisted of two parts: a core and a readout. The core captured the nonlinear image representations and was shared among all neurons. The readout mapped the features of the core into neuronal responses and contained all neuron specific parameters.

Core.

To get a rich set of nonlinear features, we used a deep CNN as our core. We used a CNN with 3 layers and 32 feature channels per layer as previously described in (Walker et al., 2019). These architectures were chosen with a hyper-parameter search, with the objective of maximizing a validation score (see Training and evaluation). Each of the 2D convolutional layers was followed by a batch normalization layer and an ELU non-linearity.

Readouts.

The goal of the readout was to find a linear-nonlinear mapping from the output of the last core layer Φ(x) to a single scalar firing rate for every neuron. We used a pyramid readout, as described in Sinz et al. (2018). We computed a linear combination of the feature activations at a spatial position, parameterized as (x,y) relative coordinates (the middle of the feature map being (0,0)). Training this readout poses the challenge of maintaining gradient flow when optimizing the objective function. We tackled this challenge by recreating multiple sub-sampled versions of the feature maps and learning a common relative location for all of them. We then passed these features through a linear regression and a non-linearity to obtain the final neuronal responses.

Training and evaluation.

Natural images in the training, validation and test sets were all Z-scored using the mean and standard deviation of the training set. The mean and standard deviation for the cropped natural images were weighted by the mask used to crop the images to avoid artificially lowering the mean and standard deviation due to large gray areas in the cropped images.

The networks were trained to minimize Poisson loss $\frac{1}{m}{\sum }_{i=1}^m\left({\widehat{r}}^{(i)}-r^{(i)}\text{\hspace{0.17em}log\hspace{0.17em}}{\widehat{r}}^{(i)}\right)$ where m denotes the number of neurons, $\widehat{r}$ the predicted neuronal response and r the observed response. We implemented early stopping on the correlation between predicted and measured neuronal responses on the validation set: if the correlation failed to increase during 10 consecutive epochs through the entire training set, we stopped the training and restored the best performing model over the course of training. After each stopping, we either decreased the learning rate or stopped training altogether if the number of learning-rate decay steps was reached. Network parameters were optimized via stochastic gradient descent using the Adam optimizer. Once training completed, the trained network was evaluated on the validation set to yield the score used for hyper-parameter selection.

MEI and surround image generation

Because our neuronal recordings were performed with dense sampling (Z spacing = 5μm), we first needed to select unique neurons. We registered the planes of the functional experiments to the stack of the volume (see Registration of neurons in 3D stack) and identified unique neurons.

Then, we optimized the MEIs and the surround images in two steps.

MEI generation.

We used regularized gradient ascent by solving the optimization problem defined as

$$x^{*}=\text{arg\hspace{0.17em}}\underset{x}{\text{max}}{f}_i(x)$$

on our trained deep neural network models to obtain a maximally exciting input image for each neuron, given by x

$$x\in {ℝ}^{n\times m}$$

(Walker et al., 2019). We initialized with a Gaussian white noise image. In each iteration of gradient ascent, we showed the image to the model and calculated the gradients of the image w.r.t. the model activation of a single neuron. We then blurred the obtained gradient with Gaussian blurring, with a Gaussian sigma of 1 pixel. Following this, we stepped our optimizer to change the image as given by the gradients. Finally, we calculated the standard deviation of the resulting image and compared it to a fixed budget of 0.05 for the MEI. The standard deviation budget can be effectively thought of as a contrast constraint. The contrast budget was chosen to minimize the number of pixels with values exceeding those corresponding to 0 and 255, which are the lower and upper bound for pixel values displayed on the monitor. We used the Stochastic Gradient Descent (SGD) optimizer with step size=0.1 and ran each optimization for 1,000 iterations.

Surround image generation.

A tight mask (ranging between 0 and 1) around the MEI was computed by thresholding (see below) which we used to define the ‘center’ and set it apart from the ‘surround’ during the next step of optimization. By applying the inverse MEI mask to the target image x, we optimized the surrounding area in the image by allowing more contrast (RMS contrast = 0.1) outside of the MEI mask. To define the center stimuli, we computed a mask around the MEI for each neuron by thresholding at 1.5 standard deviations above the mean. We then blurred the mask with Gaussian sigma = 1 pixel. We initialized an image with Gaussian noise and cropped out the center of this image using the MEI mask and added the MEI at a fixed contrast = 0.05. At the same time, we used the inverse of the MEI mask to set the contrast for the area outside of the mask to 0.1. A gradient was computed on the modified image and we blurred the gradient with a Gaussian sigma = 1. We used the same SGD optimizer to update the image at each iteration, and due to the inverse of the mask being applied to the image, only pixels outside of the MEI mask could be changed (illustrated in Fig. 2a). We set the full-field image contrast to an arbitrary value within the training image regime (0.1) to prevent the pixel values from getting out of range and this step was not differentiable. At the end of each iteration, we normalized the contrast in the center and the surround again to reach the optimal stimulus with correct contrast (MEI=0.05, surround=0.1). We repeated these steps for 1,000 iterations. To generated the extend mask for the MEI used in Suppl. Fig. 4, we set the value between 1 and 0.001, i.e. in the blurred area, in the original mask to 1 and blurred the new mask with the same Gaussian filter that was applied to the MEI mask. We applied the extended mask to the surround images to produced a new set of masked surround images that were slightly smaller than the original ones, and tested surround modulation restricted only to the ‘near’ surround region.

Probabilistic model

Hierarchical generative model.

We simulated inference using a simple probabilistic generative model of the stimulus as would be learned by the brain as an attempt to explain our center-surround results. In our model, G is represented in a higher visual area, encoding a global orientation variable, X represents our model sensory neurons, each with an oriented Gabor filter as its projective field (PF), and I represents the visual input. We assume the existence of a single G ~ 𝒰 (0,π). We model sensory neurons as $X={\left\{x_i\right\}}_i^{n_x}$, where n_x is the number of sensory neurons (n_x = 6 in our case), conditioned on G as $x_i\mid G~\frac{1}{\lambda (i)}\text{exp}\left(-\frac{x_i}{\lambda (i)}\right)H\left(x_i\right)$ where λ(i) is the firing rate function of the ith neuron defined by a von Mises function around the global orientation G as $\lambda (i)=\text{exp}\left(\kappa \frac{\text{cos}\left({\theta }_i-G\right)}{2\pi I_0(\kappa )}\right)$, where θ_i is the preferred orientation of the ith neuron. In other words, the closer the preferred orientation of a neuron to the global orientation, the higher is its firing rate. This way, we induce a positive (prior) correlation among neurons that prefer similar orientations, i.e. neurons with vertical PFs have high correlation with each other, as do neurons with horizontal PFs. Finally, the visual input in our model is assumed to be a noisy, linear combination of the Gabor PFs of neurons with neuronal activations, i.e. $I~𝒩\left(I\mid {\sum }_i^{n_x}{\text{PF}}_i{x}_i,{\sigma }^2\right)$, where PF_i is the PF and x_i is the activation (spike count) of the ith neuron.

Inference.

Our assumption is that when presented with a visual input, the brain computes the posterior over variables X and G using the (learned) generative model, i.e. computes p(G,X|I). We sampled from this posterior for various stimuli via No-U-Turn-Sampler (NUTS) using python’s PyMC package. For each stimulus, we sampled 4,000 samples of G and each neuron x_i after a burn-in period of 1,000 samples. We then visualized the samples of the center neuron across different stimuli in Fig. 5d. We computed the mean of the samples of the center neuron for a given stimulus in order to quantify the effect that the particular stimulus had. The mean of the center neuron for the different stimuli reproduced our key experimental results: (1) the example neuron’s mean was driven strongly by the MEI alone, (2) the spatially congruent stimulus drove the example neuron’s mean in the center stronger than its MEI, (3) the spatially incongruent stimulus inhibited the mean of the samples of the neuron, despite the MEI being present in the center.

Closed-loop experiments

Selection of neurons for closed-loop.

We ranked the neurons recorded in one experiment based on the reliability and model performance (test correlation). Specifically, we correlated the leave-one-out mean response with the remaining single-trial response across repeated images in the test set to obtain a measurement of neuronal response reliability. We then computed an averaged rank score of each neuron from its reliability rank and model test correlation rank. After removing duplicate neurons following the procedure described above, we selected the top 150 neurons according to the averaged rank of the correlation between predicted response and observed response averaged over repeats and the correlation between the leave-one-out mean response of repeated test trials to the left-out test trial response for closed-loop experiments.

Stimulus presentation.

We converted the images generated by the model back to pixel space by reversing the Z-score step with the stats of the training set. Each image was repeated 40 times. We shuffled all the images with repeats across different classes (MEI, excitatory and inhibitory surrounds and contrast-matched MEI, masked surround controls) and presented them at random orders. Each trial consisted of one image presented for 500 ms with a preceding blanking period of 300 – 500 ms (randomly determined per trial).

Matching neurons across experiments.

We matched neurons from different experiments according to the spatial proximity in the volume of the same anatomical 3D stack. Each functional scan plane was registered to the 3D stacks collected after each day’s experiment. We chose the neurons that had the highest matching frequency across all stacks, and included them as a valid neuron in the closed-loop analysis.

Estimation of center RF size

To measure to size of the minimum response field (MRF) for each neuron, we presented stimuli consisting of circular bright (pixel value=255) and dark (pixel value=0) dots of size 7 degrees in visual angle on a gray background (pixel value=128) in conjunction with natural image stimuli. The dots were randomly shown at locations on a 9 by 9 grid covering 40% of the monitor in the center along the horizontal edge, and at each location, the dot was shown for 250 ms and repeated 16 times. The responses were averaged across repeats, and a 2D Gaussian was fitted to the On and Off response maps, respectively. The size of the MRF was measured as the largest distance between points on the border of the 2D Gaussian at 1.5 standard deviations away for both On and Off responses.

To estimate the size of the MEIs and the excitatory and inhibitory surround, we first computed the mask for each image as described in section MEI and surround image generation. The size was computed in pixels as the longest distance between points on the border of the mask. The size was converted to degrees in visual angle according to the ratio between pixel and degrees in visual angle.

Exciting natural image patches and natural surrounds

All natural images in the ImageNet dataset were first Z-scored with the mean and standard deviation of the training dataset. We then cropped the images with the MEI masks and normalized to match the contrast of the MEI within the mask. The images were presented to the model to get the predicted response. Images that elicited activations above 80% of MEI activation were chosen as the maximally exciting natural image patches. Images used to train the specific model were removed from this collection. For neurons with more than 10 maximally exciting natural image patches, we replaced the center of the natural image with the MEI and included the surround region of the natural image to the same extend as the average size of the excitatory and the inhibitory surround.

Representational similarity

The maximally exciting natural image patches of a neuron plus the surround of the same image were normalized to the same contrast as the excitatory and the inhibitory surround images and were presented to the model. The excitatory and the inhibitory surround images were cropped with the average mask of the two to match the size, contrast-adjusted and presented to the model. The activation of all neurons in the model were taken as an approximation of the given image in ‘representational space’. We computed Pearson correlation between a natural image patch with surround and an image of the MEI with either excitatory or inhibitory surround. The Pearson correlation is an estimation of ‘representational similarity’.

Auto-correlation function

To quantify correlations across space of optimized and natural center-surround images, we computed the auto-correlation function of each image (Rikhye and Sur, 2014). For each neuron, we first identified exciting natural images (>80 % activation relative to the MEI) with the preferred feature in the center as described above. We then cropped the optimized and exciting natural images based on the average mask of the excitatory and inhibitory surrounds, extracted horizontal and vertical intensity profiles through the center of mass of each image and computed the mean auto-correlation function of these intensity projections for excitatory and inhibitory center-surround images, as well as for all exciting natural images per cell. We shifted the intensity projections in steps of 2 degrees visual angle and for maximally 20 degrees visual angle, thereby extending beyond the MEI (radius approx. 15 degrees visual angle) into the surround.

Extrapolated surround images

We generated extrapolated surround images based on the spatial pattern of the MEI using a bivariate spline interpolation method on a rectangular grid (RectBivariateSpline function of scipy package). Specifically, we first cropped out the MEI using a 95% threshold of the MEI mask and fit the cropped MEI with the RectBivariateSpline function. Then, we used the fit to extrapolate from the MEI into the surround and cropped the extrapolated surround based on the mask of optimized surround images.

Replication of center-surround modulation in functional connectomics dataset

Recently, we and others released a large-scale functional connectomics dataset of mouse visual cortex (“MICrONS dataset”), including responses of >75k neurons to full-field natural movies and the reconstructed sub-cellular connectivity of the same cells from electron microscopy data (MICrONS Consortium et al., 2021). A dynamic recurrent neural network (RNN) model of this mouse’s visual cortex—digital twin—exhibits not only a high predictive performance for natural movies, but also accurate out-of-domain performance on other stimulus classes such as drifting Gabor filters, directional pink noise, and random dot kinematograms (Wang et al., 2023). Here, we took advantage of the model’s ability to generalize to other visual stimulus domains and presented our full-field and masked images to this digital twin model in order to relate specific functional properties to the neurons’ connectivity and anatomical properties. Specifically, we recorded the visual activity of the same neuronal population to static natural images as well as to the identical natural movies that were used in the MICrONS dataset. Neurons were matched anatomically as described for the closed loop experiments. Based on the responses to static natural images we trained a static model as described above, and from the responses to natural movies we trained a dynamic model using a RNN architecture described in (Wang et al., 2023). We then presented the same static natural image set that we showed to the mice also to their dynamic model counterparts and trained a second static model using these predicted in silico responses. This enabled us to compare the MEIs and surround images for the same neurons generated from two different static models: one trained directly on responses from real neurons, and another trained on synthetic responses to static images from dynamic models (D-MEI and D-surround). To quantify similarity, we presented both versions of MEIs and surround images to an independent static model trained on the same natural images and responses but initialized with a different random seed, thereby avoiding model-specific biases.

Code and data availability

The analysis code and all data will be publicly available in an online repository latest upon journal publication. Please contact us if you would like access before that time.