Abstract
A defining characteristic of intelligent systems, whether natural or artificial, is the ability to generalize and infer behaviorally relevant latent causes from high-dimensional sensory input, despite significant variations in the environment. To understand how brains achieve generalization, it is crucial to identify the features to which neurons respond selectively and invariantly. However, the high-dimensional nature of visual inputs, the non-linearity of information processing in the brain, and limited experimental time make it challenging to systematically characterize neuronal tuning and invariances, especially for natural stimuli. Here, we extended “inception loops” — a paradigm that iterates between large-scale recordings, neural predictive models, and in silico experiments followed by in vivo verification — to systematically characterize single neuron invariances in the mouse primary visual cortex. Using the predictive model we synthesized Diverse Exciting Inputs (DEIs), a set of inputs that differ substantially from each other while each driving a target neuron strongly, and verified these DEIs’ efficacy in vivo. We discovered a novel bipartite invariance: one portion of the receptive field encoded phase-invariant texture-like patterns, while the other portion encoded a fixed spatial pattern. Our analysis revealed that the division between the fixed and invariant portions of the receptive fields aligns with object boundaries defined by spatial frequency differences present in highly activating natural images. These findings suggest that bipartite invariance might play a role in segmentation by detecting texture-defined object boundaries, independent of the phase of the texture. We also replicated these bipartite DEIs in the functional connectomics MICrONs data set, which opens the way towards a circuit-level mechanistic understanding of this novel type of invariance. Our study demonstrates the power of using a data-driven deep learning approach to systematically characterize neuronal invariances. By applying this method across the visual hierarchy, cell types, and sensory modalities, we can decipher how latent variables are robustly extracted from natural scenes, leading to a deeper understanding of generalization.
Introduction
The key challenge of visual perception is inferring behaviorally relevant latent features in the world despite drastic variations in the environment. For example, to recognize food in a cluttered environment, the brain must extract relevant features from light patterns in a way that is robust and generalizable to variations such as viewing distance, 3D pose, scale, and illumination, while still consistently identifying the food. Contrary to often being labeled as “nuisance”, these variations in the input must also be represented by the brain since they play a crucial role in other tasks such as navigating the environment.
To understand how brains effectively disentangle high-dimensional sensory inputs and robustly extract latent variables, it is essential to identify the features that neurons exhibit selectivity and invariance toward. Invariance refers to the property of neurons to maintain consistent responses despite changes in the input.
However, characterizing neuronal tuning is difficult because identifying invariances in the enormous search space of visual stimuli is challenging, experimental time is limited, and information processing in the brain is non-linear. Because of this, it is infeasible to present all images at all possible variations to systematically map invariances. As a result, most previous studies have been limited to using parametric stimuli (e.g., gratings) or semantic categories (e.g., objects and faces) (1–6) with strong assumptions about the types of invariances encoded. The classic example of this approach is Hubel and Wiesel’s complex cells in the primary visual cortex (V1) (7), which are tuned to oriented gratings of a preferred orientation but are invariant to spatial phases. In contrast, simple cells, are selective to spatial phase. However, we know little about other types of invariances along the visual hierarchy beyond these classes of parametric stimuli. This is critical for understanding how the brain robustly disentangles latent variables from a variable visual input (8).
To systematically study invariances, we combined in-vivo large-scale calcium imaging of the primary visual cortex in mice with deep convolutional neural networks (CNNs) to learn accurate neural predictive models. Using the CNN models as a “digital twin” of the visual cortex, we synthesized a set of stimuli that highly activated neurons while being distinct from each other — “Diverse Exciting Inputs” (DEIs). We subsequently presented these stimuli back to the animal while recording the activity of the same neurons and verified in vivo that these neurons responded invariantly to the stimulus set. Our experiments discovered a novel type of invariance where one part of the receptive field (RF) was highly activated by specific textures like checkerboards translated over a wide range of phases, creating a local phase invariance. In contrast, the other part of the RF was selective for a fixed spatial pattern. We found that this bipartite structure of the RF often matched with object boundaries defined by a frequency difference in highly activating natural stimuli. Taken together, these findings suggest that bipartite invariance may play a role in supporting object boundary detection based on texture cues. In addition, we adapted our methodology to compute invariances using natural movies, which we then applied to the functional connectomics MICrONs data set (9). Our analysis successfully replicated bipartite DEIs in the MICrONS data set, providing a pathway toward understanding the circuit-level mechanisms underlying this novel form of invariance.
Results
Diverse Exciting Inputs (DEIs) identify invariant stimulus manifold
In this study, we used inception loops (10, 11), a closed-loop experimental paradigm, to investigate the invariances of single neurons in mouse V1 (Fig. 1b). An inception loop encompasses the following steps:
Neuronal recordings: Large-scale recordings with high-entropy natural stimuli.
Fit digital twin: Train a deep CNN (10, 12, 13) to predict the activity of neurons to arbitrary natural images. The CNN uses a non-linear core composed of convolutional layers shared among all recorded neurons, followed by a neuron-specific linear readout (Fig. 1d).
In silico experiments: Use the CNN predictive model as a functional “digital twin” of the brain to perform in silico experiments to systematically study the computations of the modeled neurons and derive experimentally testable predictions.
In vivo verification: Verify the predictions of the digital twin in the brain.
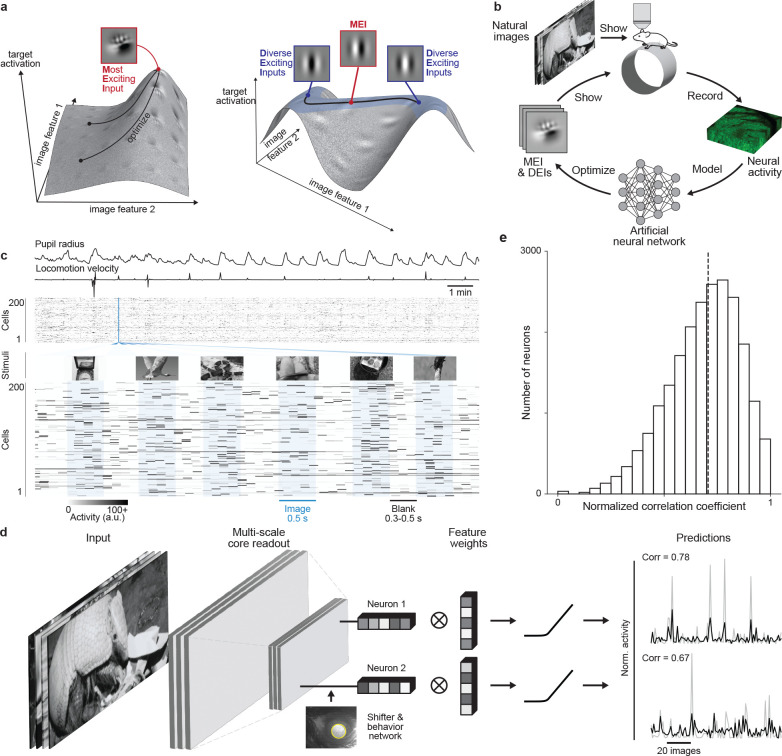
Fig. 1. Deep neural network well captures mouse V1 responses to natural scenes.
a, Illustration of the optimization of Most Exciting Inputs (MEI) and Diverse Exciting Inputs (DEIs).The vertical axes represent the activation of a model neuron with no obvious invariance (left) and another model neuron with phase invariance to its optimal stimulus (right) as a function of two example image dimensions. The black curves depict optimization trajectories of the same MEI (left) starting from different initializations and of the DEIs (right) as different perturbations starting from the MEI along the invariance ridge. b, Schematic of the inception loop paradigm. On day 1, we presented sequences of natural images and recorded in vivo neuronal activity using two-photon calcium imaging. Overnight, we trained an ensemble of CNNs to reproduce the measured neuronal responses and synthesized artificial stimuli for each target neuron in silico . On day 2, we showed these stimuli back to the same neurons in vivo to compare the measured and the predicted responses. c, We presented 5,100 unique natural images to an awake mouse for 500 ms, interleaved with gray screen gaps of random length between 300 and 500 ms. A subset of 100 images was repeated 10 times each to estimate the reliability of neuronal responses. Neuronal activity was recorded at 8 Hz in V1 L2/3 using a wide-field two-photon microscope. Behavioral traces including pupil dilation and locomotion velocity were also recorded. d, Schematic of the CNN model architecture. Our network consists of a 3-layer convolutional core followed by a single-point readout predicting neuronal responses, a shifter network accounting for eye movements, and a behavior modulator predicting an adaptive gain for each neuron (10, 12). Traces on the right show average responses (gray) to test images of two example neurons and corresponding model predictions (black). e, Normalized correlation coefficient (CCnorm, see Methods) (14) between measured and predicted responses to test images for all 22,083 unique neurons across 10 mice selected for MEI and DEIs generation, a metric measuring the fraction of variation in neuronal responses to identical stimuli accounted for by the model prediction(median = 0.71 as indicated by the dashed line). Neurons with CCmax smaller than 0.1 (0.31%) were excluded and CCnorm larger than 1 (1.19%) were clipped to 1 in the histogram.
We presented 5,100 unique natural images to awake, head-fixed mice while recording the activity of thousands of V1 layer 2/3 (L2/3) excitatory neurons using two-photon calcium imaging (Fig. 1c). We used the recorded neuronal activity to train CNNs to predict the responses of these neurons to arbitrary images. The predictive model included a shifter network to compensate for eye movements and a modulator network for predicting an adaptive gain based on behavioral variables like running velocity and pupil size (10, 12) (Fig. 1d). When tested on a held-out set of novel natural images, the model achieved a median normalized correlation coefficient of 0.71 (14) (Fig. 1e), comparable to state-of-the-art models of mouse V1 (13, 15, 16).
We adapted a previously introduced method (17) to map the invariances of individual neurons in silico. The method extends optimal stimulus synthesis described recently (10, 11): instead of finding the Most Exciting Input (MEI) for each neuron, it generates a set of optimal images — Diverse Exciting Inputs (DEIs). The DEIs are generated such that each of them highly excites the target neuron while being maximally different from all other DEIs in the set. For every model neuron, we initialized the DEI optimization with its MEI perturbed with different seeds of white noise and then re-optimized the image so that each of them drives the target neuron strongly while at the same time achieving the greatest pixel-wise Euclidean distance to the other DEIs of that neuron (see Methods for optimization loss). Our DEI synthesis method correctly characterized the invariances of simulated Hubel & Wiesel simple and complex cells. Specifically, all the DEIs of a simulated simple cell exhibited the same orientation, spatial frequency and phase of a Gabor patch (Fig. 2a simulated), as expected from linear-nonlinear (LN) models (18–20). For a simulated complex cell, the DEIs exhibited different phases, as expected from the phase invariance of complex cells (Fig. 2a simulated).
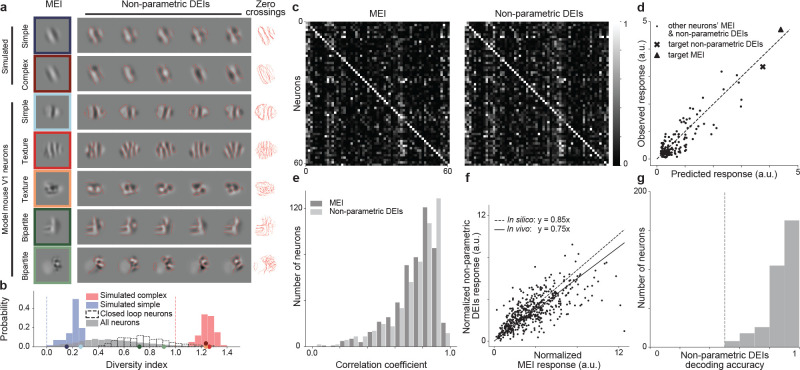
Fig. 2. Non-parametric DEIs evoked strong and selective responses in target neurons while containing perceivable differences.
a, Examples of MEI and non-parametric DEIs for simulated simple and complex cells and model mouse V1 neurons. Zero crossing contours from individual DEIs are overlaid for easier comparison of the spatial pattern across the images. While DEIs strongly resemble the MEI, they exhibit complex features different from the MEI and also among themselves. We observed 2 types of novel invariances: global phase invariance (texture) and local phase invariance (bipartite). b, Diversity indexes for 60 simulated complex cells (red), 60 simulated simple cells (blue), and 6464 model V1 neurons (gray), 617 among which we tested in closed-loop experiments (unfilled). The expected diversity index of a noiseless simple cell (blue dashed line) and a noiseless complex cell (red dashed line) are shown for reference. Example neurons from a were indicated on the x axis with the corresponding colors. c, Both MEI and DEIs activated neurons with high specificity. The confusion matrices show the responses of each neuron to MEI (left) and DEIs (right) of 61 neurons in mouse 3. MEI response was averaged across 20 repeats of the same image while DEIs response was averaged across 20 different images with single repeat each. The responses of each neuron were normalized, and each row was scaled so the maximum response across all images equals 1. Responses of neurons to their own MEI and DEIs (along the diagonal) were larger than those to other MEIs and DEIs respectively (one-sided permutation test, P < 10−9 for both cases). d, Predicted versus observed responses of one example neuron (from mouse 2) to its own MEI and DEIs and 79 other neurons’ MEI and DEIs. e, Pearson correlation coefficients between predicted and observed responses to all the presented MEI and DEIs for all 500 neurons pooled across 8 mice (median = 0.74 for MEI and 0.75 for DEIs). f, Each point corresponds to the normalized response of a single neuron to its MEI and DEIs. The linear relationship between DEIs and MEI responses was estimated by averaging over 1000 repeats of robust linear regression using the RANSAC algorithm (21). DEIs stimulated in vivo closely to the level predicted in silico with respect to MEI (75% versus 85%) (two-sided Wilcoxon signed-rank test, W = 51360, P =4.92 × 10−4), with only 12.8% of all neurons showing different responses between DEIs and 85% of MEI (P < 0.05, two-tailed Welch’s t-test with 34.4 average d.f.). g, Differences between the most different pair of DEIs in pixel space are distinguishable by the mouse V1 population. Logistic regression classifiers were used to decode DEI identity of individual trials from V1 population responses. Decoding accuracies across neurons (median=0.9) were higher than chance level (0.5 as indicated by the dashed line) (one sample t-test, t = 70.1,P < 10−9). Data were pooled over 320 neurons from 4 mice.
The DEIs of the modeled mouse V1 neurons strongly resembled their corresponding MEIs but with specific image variations that defined different types of invariances (Fig. 2a model mouse V1 neurons, more examples in Fig. S1). Some neurons had DEIs that were almost identical, indicating that the cells were not invariant, like the simulated simple cells. Among the neurons that were strongly activated by stimuli deviating from Gabor-shaped RFs (10, 13), some appeared to be stimulated strongly by random crops from an underlying texture pattern, demonstrating global phase invariance. We refer to these neurons as texture cells, similar to those found in the hidden layers of Artificial Neural Networks (ANNs) trained on object recognition (17). Many neurons exhibited a novel type of invariance: a bipartite RF invariance. For these neurons, one portion of their RF responded to a fixed spatial pattern while the rest was invariant to phase shifts of the stimuli, similar to texture cells. We denote these neurons as bipartite cells. We verified that this bipartite RF structure is unlikely the result of signal contamination from neighboring neurons since the MEI and DEIs optimized for different imaging slices in depth from the same neurons are highly consistent (Fig. S2). To quantify the prevalence of this phenomenon, we computed a diversity index for each neuron using its DEIs. This index was defined as the normalized average pairwise Euclidean distance in pixel space across the DEIs (see Methods). In particular, an index of 0 and 1 corresponds to classical simple and complex cells, respectively, while bipartite cells will have an index in between. We observed that the diversity indexes of mouse V1 neurons spanned a continuous spectrum, with those of simulated simple and complex cells on the two extremes (Fig. 2b).
We validated the model’s predictions by confirming the responses of the synthesized DEIs in vivo. Note that the mean luminance and root mean square (RMS) contrast of all the DEIs and MEIs of all neurons were matched (see Methods). When presented back to the animal, both MEIs and DEIs were highly selective, consistently eliciting higher activity in their target neurons than in most other neurons (Fig. 2c, S3). Moreover, the closed-loop experiments also confirmed that our CNN model accurately predicted the responses to all synthesized MEIs and DEIs (Fig. 2d, e). Importantly, DEIs strongly activated their target neurons in vivo, achieving 75% of their corresponding MEI activation (Fig. 2f), close to the model prediction of 85%. One potential concern is that the difference across DEIs may be due to features that are indistinguishable to the mouse visual system. Therefore, we tested if the mouse visual system can detect the changes across DEIs by presenting pairs of the most dissimilar DEIs in pixel space to V1 neurons. Using a logistic regression classifier, we decoded the DEI class using the V1 population responses on a trial-by-trial basis and found a median classification accuracy of 0.9, significantly higher than the chance level (Fig. 2g). This result confirmed that the mouse visual system is able to accurately detect the differences between DEIs.
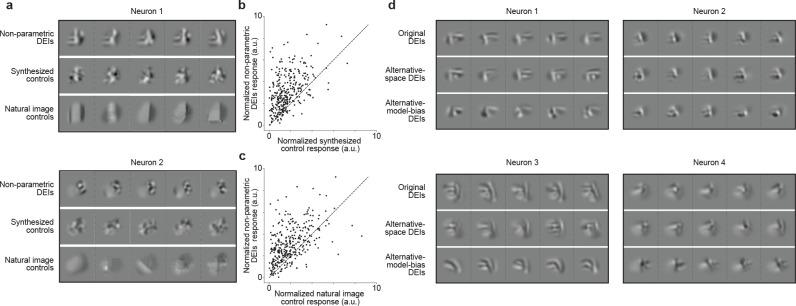
Next, we wanted to test whether DEIs follow specific invariant trajectories from the MEI that preserve high activity whereas random directions are sharply tuned. Similar to the DEI generation, we perturbed the MEI with different additive Gaussian white noise to generate a set of 20 control images with maximal diversity (Fig. 3a synthesized controls). In contrast to the DEI generation, in this case, the loss function did not require the images to be highly activating, yet enforced all the synthesized control images to be closer to the MEI than DEIs as measured by Euclidean distance in pixel space (see Methods). When shown back to the animal during inception loop experiments, these control images elicited significantly lower responses to their target neurons compared to the DEIs (Fig. 3b). In a separate set of experiments, we examined the neuronal activation patterns elicited by natural images in the vicinity of the MEIs (Fig. 3a natural image controls). For each neuron, we searched through more than 41 million natural patches to identify 20 images that were strictly closer to the MEI than all the DEIs as measured by Euclidean distance in pixel space. Again, these natural image patches elicited significantly weaker activations than DEIs (Fig. 3c). These findings suggested that DEIs reflect invariances along specific directions away from the MEIs in the image manifold, and that proximity to the MEIs alone does not guarantee strong neuronal activation.
Fig. 3. DEIs evoked stronger responses than synthesized and natural control stimuli in target neurons and generalized across different synthesis conditions.
a, Examples of non-parametric DEIs (top), synthesized controls (middle), and natural controls (bottom) for 2 neurons. Synthesized controls were generated by perturbing the MEI in random directions while natural controls were found by searching through random natural patches. Both natural and synthesized controls were restricted to be strictly closer to the MEI in pixel space than all DEIs. b-c, Each point corresponds to the normalized activity of a single neuron in response to its DEIs versus its synthesized controls (b) or natural (c) controls. Response to each stimulus type was averaged over 20 different images with single-repeat. DEIs activated their target neurons stronger than their corresponding synthesized (one-sided Wilcoxon signed-rank test, W = 3258, P < 10−9) and natural image controls (one-sided Wilcoxon signed-rank test, W = 6442, P < 10−9) with 47.2% and 41.0% of all neurons showing greater response to DEIs respectively (P < 0.05, one-tailed Welch’s t-test with 30.4 and 31.1 average d.f., respectively). Data were pooled over 318 neurons from 5 mice. d, Examples of non-parametric DEIs synthesized with diversity evaluated as Euclidean distance in pixel space (top), or as Pearson correlation in in silico population responses (middle), or using a predictive model of different architecture and trained on different stimulus domain (bottom).
We next demonstrated that the DEIs generalize across different diversity metrics, stimulus data sets, and predictive model architectures. First, we examined if DEIs could be robustly produced based on diversity evaluated in a different representational space. Thus far, we used the Euclidean distance in pixel space as a measure of diversity to generate DEIs. As an alternative, we now used a loss function that measured diversity in the predicted population neuronal response space (see Methods). The DEIs resulting from this new optimization were similar to those generated with the pixel-space diversity and were similarly effective at activating target neurons in vivo (Fig. 3d, S4). Second, we wanted to determine if DEIs are robust across predictive models with distinct architecture trained on different stimulus domains. To do this, we developed a method to synthesize DEIs from the dynamic digital twin trained on natural movies in the MICrONS functional connectomics data set (9, 22). Specifically, we presented to the same neuronal population a static set of natural images as well as the identical set of natural movies used in the MICrONs data set. We then trained two different static image models: one directly on in vivo static responses, and another on in silico predicted responses to the identical static images from a recurrent neural network trained on movie stimuli (22). We found that the MEIs and DEIs generated from these two models were perceptually similar (Fig. 3d) and both strongly activated their corresponding neurons as evaluated on another independent model (Fig. S5b, c). The ability to reproduce these invariances in the MICrONS data set provides an avenue for exploring the synaptic-level mechanisms underlying bipartite invariances.
Bipartite parametrization of DEIs
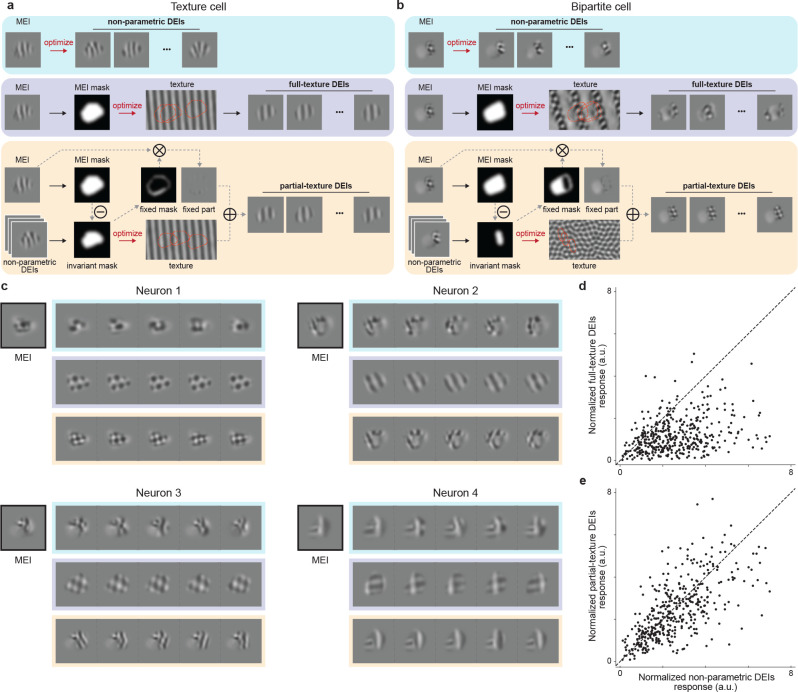
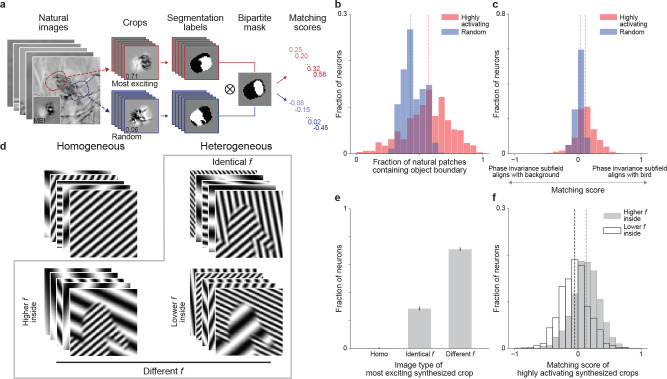
Up until this point, we only discussed the types of invariances we observed for the texture and bipartite invariant cells in qualitative terms. Here we provide a more interpretable and quantitative model to account for the invariances we observed. We first used a texture synthesis model that could characterize the invariances of neurons similar to classical complex cells which maintain high activation when presented with phase-shifted versions of their preferred texture. To do this, we followed a previous method (17) to synthesize a full-field texture for each neuron by maximizing the in silico average activation of uniformly sampled crops from the texture (Fig. 4a, b middle rows). We then sampled random crops from the optimized texture which we denote as full-texture DEIs (DEIsfull). However, for many neurons this method failed to produce DEIs that resembled the original non-parametric DEIs (Fig. 4b middle vs. top rows, 4c middle vs. top rows). Indeed, when shown back to the animal, the responses of many neurons (52.9%) were significantly lower when presented with DEIsfull compared to the non-parametric DEIs (Fig. 4d). We hypothesized that the difference in responses was due to the fact that texture phase invariance alone could not account for the bipartite cells that have heterogeneous subfields in the RF (Fig. 2a) and are thus not well characterized by a homogeneous full-field texture model.
Fig. 4. Partial-texture DEIs activated target neurons similarly as non-parametric DEIs.
a-b, Schematic of non-parametric (DEIs), full-texture (DEIsfull), and partial-texture (DEIs partial) DEIs synthesis for an example texture cell (left) and an example bipartite cell (right). DEIsfull were synthesized by optimizing an underlying texture canvas from which uniformly sampled cropped by the MEI mask maximally activate the target neuron. In contrast, DEIspartial are composed of two non-overlapping subfields: a fixed one masked directly from the MEI, and a phase invariant one synthesized similarly to DEIsfull except that the mask used for texture optimization is only part of MEI mask. c, MEI, DEIs, DEIsfull, and DEIspartial of 4 example neurons, with each type of DEIs indicated by the corresponding color in a. DEIspartial visually resembles non-parametric DEIs for most neurons while DEIsfull captures non-parametric DEIs only for texture-like neurons. d-e, Normalized responses to DEIsfull (d) and DEIspartial (e) responses versus non-parametric DEIs. Each point corresponds to the normalized activity of a single neuron, averaged over 20 different images with single repeat. d, DEIsfull failed to stimulate their target neurons compared to non-parametric DEIs (one-sided Wilcoxon signed-rank test, W = 4389, P < 10−9) with 52.9% of all neurons showing lower responses to DEIsfull (P < 0.05, one-tailed Welch’s t-test with 29.4 average d.f.). e, DEIspartial activated their target neurons similarly to non-parametric DEIs (two-sided Wilcoxon signed-rank test, W = 32429, P = 7.01 × 10−4) with only 8.7% of all neurons showing different responses (P < 0.05, two-tailed Welch’s t-test with 33.5 average d.f.). Data were pooled over 8 mice, displaying a total of 401 neurons.
Thus, we introduced a new model to explain bipartite DEIs. We parameterized DEIs as the summation of two non-overlapping subfields within the RF: (1) a phase invariant subfield, which is cropped from a synthesized full-field texture and (2) a fixed subfield, which is masked from the original MEI and shared across all DEIs (Fig. 4a,b bottom rows). The invariant subfield was determined by finding the region of the RF with high pixel-wise variance across the non-parametric DEIs (see Methods). We then optimized a full-field texture, using a similar approach as the DEIsfull method, but with a key difference: we used crops masked with the invariant subfield instead of the whole RF. Finally, we combined randomly sampled crops from the optimized texture and the fixed subfield to achieve partial-texture DEIs (DEIspartial) (for more details see Methods). This model has the flexibility to represent a spectrum of phase invariance properties ranging from simple cells (or other non-invariant neurons) to complex cells (or other texture phase invariant neurons), as well as the bipartite cells we observed. Under this model, for simple cells, the fixed subfield occupies the entire RF, while for complex cells, the phase invariant subfield is the predominant component. Remarkably, DEIspartial not only captured the visual complexity of non-parametric DEIs (Fig. 4a, b, c bottom vs. top rows) but when shown back to the animal, highly activated neurons comparable to the non-parametric DEIs (Fig. 4e), with only a small proportion of neurons (8.7%) showing significantly different responses. Critically, the diversity of DEIspartial was comparable to that of the non-parametric DEIs (Fig. S6 b).
We next tested the necessity and specificity of the two subfields in DEIspartial (Fig. S7 a). Both subfields were necessary — the removal of either the phase invariant or the fixed subfield resulted in lower activation (Fig. S7 b, c). When we swapped the phase invariant subfields with texture crops optimized for other random neurons or swapped the fixed subfields with random natural patches, these control stimuli also failed to strongly activate the neurons (Fig. S7 d, e). This demonstrates the specificity of the combination of the fixed and phase invariant subfields.
All of the closed-loop verification results shown up until now came from neurons with high invariance levels (see Methods). We also verified that all results presented in this section generalized to randomly selected neuronal populations (Fig. S8). Together, these findings suggest that most mouse V1 neurons, regardless of their level of invariance, were better explained by a model that parameterizes heterogeneous properties by partitioning the RF into two non-overlapping subfields, one of which contains phase invariance.
Invariant and fixed subfields detect boundaries in natural images with spatial frequency differences
It has been shown that the complex spatial features exhibited by MEIs are frequently present in natural scenes (10). Here, we wondered what visual tasks in the real world would benefit from this particular RF property of subfield division with phase invariance. Intuitively, these neurons may be involved in segmentation, such as detecting boundaries based on luminance changes (“first-order” cues) or texture variations (“second-order” cues) (23–25). Since our partial-texture model partitions the DEIs into two subfields, often with distinct patterns, we hypothesized that these neurons may be preferentially activated by object boundaries defined by texture discontinuities.
To test this hypothesis, we selected a natural image data set with manual segmentation labels, namely Caltech-UCSD Birds-200–2011 (CUB) (26), that enables us to locate the corresponding boundary between the object (a bird) and the background in each image. We screened more than one million crops with standardized RMS contrast from the CUB data set to identify highly activating crops for each V1 neuron in silico (Fig. 5a). We found that across the population, highly activating crops were significantly more likely to contain object boundaries than a random set of crops (Fig. 5b). To assess how well the segmentation masks defined by the object boundary in these highly activating natural images were aligned with the RF subfields extracted from DEIspartial, we computed a matching score (Fig. 5a). For each image, the matching score would equal to 1 or −1 if the object perfectly matched with the phase invariant or the fixed subfield, respectively. Across the population, the phase invariant subfield was significantly aligned with the object rather than the background of the image (Fig. 5c, for more examples see Fig. S9a). In contrast, random image crops were not significantly aligned to the bipartite masks of the DEIs showing that the effect we observed was not due to biases in the images. Next, we asked what low-level visual statistics could contribute to such matching results. We noticed that the DEIs appeared to exhibit differences in the spatial frequency preference between the fixed and phase invariant subfields. To investigate this, we replaced the DEI content within the two subfields with synthesized textures of different spatial frequency content. The textures were generated using Perlin noise (27)—a pseudo-random procedural texture synthesis method with naturalistic properties (Fig. S10a). Our findings revealed that a significantly larger proportion of neurons (41.08%) were most activated when the phase invariant subfield contained higher frequency content than the fixed part while very few neurons (8.67%) preferred the opposite (Fig. S10b). Therefore, we hypothesized that object boundaries defined by differences in spatial frequency would strongly activate V1 neurons. To explicitly address this, we replaced the original contents in the CUB data set with grating stimuli of varying spatial frequencies while still keeping the naturalistic boundaries (CUB-grating images) and presented them to our modeled neurons (Fig. 5d). Our results confirmed that neurons preferred images with object boundaries defined by the different spatial frequencies of the gratings (71.08%) significantly more than boundaries defined by grating orientation alone (28.58%) and homogeneous gratings with no boundaries (0.34%) (Fig. 5e). Just like in the natural image patches that strongly activated neurons (Fig. 5c), segmentation masks based on object boundaries in highly activating CUB-grating images also aligned significantly with the bipartite mask extracted from DEIspartial (Fig. 5f). Notably, the phase invariant and fixed portions aligned with high and low spatial frequency, respectively, rather than with the object or background of the CUB-grating images (Fig. 5f). Overall, we found that mouse V1 neurons preferred object boundaries constructed by frequency changes, with phase invariances biased toward the higher frequency subfields.
Fig. 5. Invariant and fixed subfields detect object boundaries defined by spatial frequency differences.
a, We standardized and passed 1 million crops from the Caltech-UCSD Birds-200–2011 (CUB) data set through our predictive model to find the 100 most highly activating (red) and 100 random (blue) crops with their corresponding manual segmentation labels for each neuron. Then for each crop, we computed a matching score based on the segmentation label and the target neuron’s bipartite mask identified by DEIspartial. A score of 1 indicates perfect matching between the phase invariant subfield and bird content (white to white) within the RF while a score of −1 indicates the opposite. b, Highly activating natural crops were more likely to contain object boundaries compared to randomly crops (one-sided Wilcoxon signed-rank test, W = 472123, P < 10−9, for more details see Methods). c, Highly activating CUB crops yielded median matching scores that were positive (one-tailed one sample t-test, t = 21.4, P < 10−9) and higher than those for random natural crops (one-sided Wilcoxon signed-rank test, W = 597254, P < 10−9) with 59.25% of all neurons showing greater matching to highly activating crops than to random crops (P < 0.05, one-tailed Welch’s t-test with 186.4 average d.f.). d, We constructed a parametric data set termed “CUB-grating” using four different image types: (1) homogeneous stimuli containing single gratings (2 millions), (2) heterogeneous stimuli with boundaries borrowed from the CUB data set, but the bird and the background were replaced with either identical frequency (2 millions), (3) higher frequencies within inside the bird (1 million), or (4) higher frequencies outside of the bird (1 million). All images in the data set were synthesized with independent uniformly sampled orientations and phases, with identical mean and contrast. Additionally, we used a Gaussian filter to blur the boundaries between birds and backgrounds to avoid edge artifacts. e, In the CUB-grating data set, neurons preferred heterogeneous crops with frequency differences (71.08%) more than crops with identical frequency (28.58%) or crops with homogeneous signals (0.34%) (one-way chi-squared test, χ2 = 913.2, P < 10−9; one-sided test using bootstrapping, P < 10−9 for both comparisons). Error bars were bootstrapped STD. f, Highly activating CUB-grating crops with higher frequency inside the bird yielded positive median matching scores (one-tailed one sample t-test, t = 18.5, P < 10−9) while those with lower frequency inside the bird yield negative median matching scores (one-tailed one sample t-test, t = −8.7, P < 10−9). Remarkably, the matching scores between highly activating CUB-grating crops with higher frequency inside the bird and highly activating CUB crops were not significantly different (two-sided Wilcoxon signed-rank test, W = 347557, P = 0.82). Responses were normalized by the corresponding MEI activation. Data were pooled over 6 mice, displaying a total of 1200 neurons.
Discussion
Invariant object recognition, the ability to discriminate objects from each other despite tremendous variation in their appearances, is a hallmark of visual perception. From the perspective of the object manifold disentanglement theory, visual input is gradually transformed and re-represented by visual neurons along the ventral visual pathway and ultimately achieves linear decoding of object identity from the population representation at the top of the hierarchy (8). Experimental and theoretical evidence suggested that single neurons in higher visual areas extract and integrate information from simple feature detectors in lower areas to represent more complex features and also build up response invariance to feature transformations (28–31). Discovering neuronal invariances is critical to understand how the brain generalizes to novel stimuli, and helps define the latent variables that animals use to guide actions. However, single-cell invariance properties have not been characterized systematically despite a few classical examples discovered using parametric or semantically meaningful stimuli that are largely human-biased (6, 7, 32). A few recent studies have developed non-parametric image synthesis approaches to find preferred stimuli of visual neurons (10, 11, 33). Yet most efforts along this direction characterized purely neuronal selectivity instead of invariance, and also mostly focused on feature visualization without further interpreting the functional roles of neurons. In this study, we extended the previous work of combining large-scale neuronal recording and deep neural networks to study neuronal selectivity (10) to the invariance problem. Particularly, we modified a diverse feature visualization approach previously developed in ANNs (17) to synthesize DEIs for individual neurons in mouse V1 layer 2/3 and verified these model-predicted near-optimal diverse images in vivo. Given that the changes across DEIs were decodable at the V1 population level and that DEIs preserved target neuron activation better than other diverse image sets that were strictly more similar to the MEI in pixel space, our DEIs successfully captured non-trivial and highly specific invariant tuning directions. Note that revealing such specific activation-preserving image perturbations is nearly impossible without the inception loop paradigm because of the extremely high-dimensional stimulus search space and the high sparsity of mouse visual neurons’ responses (10, 34). Importantly, we demonstrated that our DEI methodology yielded similar results across variations in diversity metric, stimulus domain, and model bias, so this paradigm should be adaptable to characterize neuronal invariances systematically across different cortical regions of interest, sensory modalities, and even animal species.
While the current study focused on invariances around the optimal stimulus, one could easily generalize our method to study the entire tuning landscape by varying the desired neuronal response. Ultimately, our work is a first attempt to characterize single-neuron invariances in biological systems in a systematic and unbiased fashion, paving the way for more holistic approaches that combine invariance and selectivity to understand the neuronal tuning landscape in the future. Mouse V1 DEIs revealed a novel type of bipartite phase invariance that could be parsimoniously parameterized by a partial-texture generative model: one part prefers a fixed spatial pattern while the other prefers a random windowed crop from an underlying texture. These parametric DEIspartial are not only strikingly indistinguishable from the non-parametric version but also excited their target neurons similarly when shown back to the mice. In contrast, when homogeneous phase change throughout the entire RF was assumed, the optimized DEIsfull failed to stimulate target neurons in vivo. Overall, the essence of such partial-texture parameterization is the introduction of heterogeneity in both selectivity and invariance between two subfields of the RF. This is a property that fundamentally deviates from the homogeneous representation assumed in traditional simple and complex cells.
While we have focused primarily on phase invariance, we do not attempt to claim it is the only type of invariance existing in mouse V1. As an initial effort to parameterize novel empirical invariances, it is also worth acknowledging that our partial-texture model proposes a simple hypothesis of a binary division of the presence and absence of phase invariance in the RF without considering more complicated scenarios of multi-region invariances or nonlinear cross-subfield interactions. Nonetheless, we believe the novel bipartite phase invariance can be of great use as a computational principle for future designs of biologically-plausible or brain-inspired computer vision systems (35). On the other hand, it can also serve as an empirical test for theoretically-driven (36–38) or data-driven models (39) that aim to explain and predict neural responses in the visual system.
The observed heterogeneity between the two RF subfields corresponded not only in phase invariance but also in preferred spatial frequency. This property is remarkably similar to that observed in “high-low frequency detectors”, a term introduced previously to describe single units in ANNs that look for low-frequency patterns on one side of their RF and high-frequency ones on the other side (40). As these ANN units were speculated to encode natural boundaries defined by frequency variation, we indeed found supporting evidence that V1 layer 2/3 neurons preferred natural image patches containing object boundaries. This bipartite phase invariance with frequency bias might be common in both biological and artificial vision systems for boundary detection. Importantly, our results are consistent with previous findings showing that mice are behaviorally capable of utilizing texture-based cues to solve segmentation (25, 41). While these studies particularly focused on object boundaries constructed mostly by orientation or phase difference (41), our evidence suggests spatial frequency bias as yet another type of second-order (texture variation-based) visual cue (23) important for detecting object boundaries.
To investigate the neuronal wiring that allows the formation of bipartite invariance, one can take advantage of recent advances in functional connectomics, combining large-scale neuronal recordings with detailed anatomical information at the scale of single synapses. Here, we demonstrated that the DEIs of mouse V1 neurons were reproduced (Fig. S5e) in a recently published MICrONS functional connectomics data set spanning V1 and multiple higher areas of mouse visual cortex (9). This data set includes responses of >75k neurons to natural movies and the reconstructed sub-cellular connectivity of the same cells from electron microscopy data. The MICrONs data set provides unprecedentedly ample resources to link morphology and connectivity among neurons to examine the circuit-level mechanisms that give rise to bipartite phase invariance.
Methods
Neurophysiological experiments
The following procedures were approved by the Institutional Animal Care and Use Committee of Baylor College of Medicine. Ten mice (Mus musculus: 6 male, 4 female) aged from 6 to 17 weeks, expressing GCaMP6s in excitatory neurons via Slc17a7-Cre and Ai162 transgenic lines (stock nos. 023527 and 031562, respectively; The Jackson Laboratory) were selected for experiments. The mice were anesthetized and a 4 mm craniotomy was made over the visual cortex of the right hemisphere as described previously (34, 42). For functional imaging, mice were head-mounted above a cylindrical treadmill and calcium imaging was performed using a Chameleon Ti-Sapphire laser (Coherent) tuned to 920 nm and a large field-of-view mesoscope equipped with a custom objective (0.6 numerical aperture, 21 mm focal length) (43). Laser power at the cortical surface was kept below 58 mW and maximum laser output of 61 mW was used at 245 μm from the surface.
We also recorded the rostro-caudal treadmill movement as well as the pupil dilation and movement. The treadmill movement was measured via a rotary optical encoder with a resolution of 8,000 pulses per revolution and was recorded at approximately 100 Hz in order to extract locomotion velocity. The images of the left eye were reflected through a hot mirror and captured with a GigE CMOS camera (Genie Nano C1920M; Teledyne Dalsa) at 20 fps with a resolution of 246–384 pixels × 299–488 pixels.
A DeepLabCut model (44) was trained on 17 manually labeled samples from 11 animals to label each frame of the compressed eye video with 8 eyelid points and 8 pupil points at cardinal and intercardinal positions. Pupil points with likelihood >0.9 (all 8 in 93% ± 8% of frames) were fit with the smallest enclosing circle, and the radius and center of this circle was extracted. Frames with <3 pupil points with likelihood >0.9 (0.7% ± 3% frames per scan), or producing a circle fit with outlier >5.5 standard deviations from the mean in any of the three parameters (center x, center y, radius, <1.3% frames per scan) were discarded (total <3% frames per scan).
We delineated visual areas by manually annotating the retinotopic map generated by pixel-wise response to a drifting bar stimulus across a 4,000 × 3,600μm2 region of interest (0.2pxμm−1) at 200 μm depth from the cortical surface. The imaging site in V1 was chosen to minimize blood vessel occlusion and maximize stability. Imaging was performed using a remote objective to sequentially collect ten 630 × 630μm2 fields per frame at 0.4 pxμm−1 xy resolution at approximately 8 Hz for all scans. We allowed only 5μm spacing across depths to achieve dense imaging coverage of a 630 × 630 × 45μm3 xyz volume. The most superficial plane positioned in L2/3 was around 200μm from the surface of the cortex. Thanks to our dense sampling, cells in the imaged volume were heavily over-sampled, often appearing in at least 2 or more imaging planes. This allowed matching across days with 2.5 ± 2.6μm vertical distance between masks (see details below). We performed raster and motion correction on the imaging data and then deployed CNMF algorithm (45) implemented by the CaImAn pipeline (46) to segment and deconvolve the raw fluorescence traces . Additionally, cells were selected by a classifier (46) trained to detect somata based on the segmented cell masks to result in 6,014–7,987 soma masks per scan. The full two-photon imaging processing pipeline is available at (https://github.com/cajal/pipeline). We did not employ any statistical methods to predetermine sample sizes but our sample sizes are similar to those reported in previous publications. Data collection and analysis were not performed blind to the conditions of the experiments but no animal or collected data point was excluded for any analysis performed.
Visual stimuli presentation
Visual stimuli were presented 15 cm away from the left eye with a 25” LCD monitor (31.8 × 56.5 cm, ASUS PB258Q) at a resolution 1080 × 1920 pixels and refresh rate of 60 Hz. We positioned the monitor so that it was centered on and perpendicular to the surface of the eye at the closest point, corresponding to a visual angle of 2.2°/cm on the monitor. In order to estimate the monitor luminance, we taped a photodiote at the top left corner of the monitor and recorded its voltage during stimulus presentation, which is approximated linearly correlated with the monitor luminance. The conversion between photodiode voltage and luminance was estimated from luminance measurements from a luminance meter (LS-100 Konica Minolta) for 16 equidistant pixel values ranging from 0 to 255 while simultaneously recording photodiode voltage. Since the relationship between photodiode voltage and luminance is usually stable, we only perform such measurement every a few months. In the beginning of every experimental session, we computed the gamma between pixel intensity and photodiode voltage by measuring photodiode voltage at 52 equidistant pixel values ranging from 0 to 255; then we further interpolated the corresponding luminance at each pixel intensity. For closed loop experiments, the pixel-luminance interpolation computed on day 1 was used throughout the loop. All stimuli used in the current study were presented at gamma value ranging from 1.60 to 1.74 and monitor luminance ranging from 0.07 ± 0.16 to 9.58 ± 0.65.
Monitor positioning across days
In order to optimize the monitor position for centered visual cortex stimulation, we mapped the aggregate receptive field of the scan field region of interest (ROI) using a dot stimulus with a bright background (maximum pixel intensity) and a single dark dot (minimum pixel intensity). We tiled the center of the screen in a 10×10 grid with single dots in random locations, with 10 repetitions of 200 ms presentaion at each location. The RF was then estimated by averaging the calcium trace of an approximately 150 × 150μm2 window in the ROI from 0.5–1.5 s after stimulus onset across all repetitions of the stimulus for each location. The resulted two-dimensional map was fitted with an elliptic two-dimensional Gaussian to find a center. To keep a consistent monitor placement across all imaging sessions, we positioned the monitor such that the aggregate RF of ROI in the first session was placed at the center of the monitor and then fixed the monitor position across the subsequent sessions within a closed loop experiment. An L-bracket on a six dimensional arm was fitted to the corner of the monitor at its location in the first session and locked in position such that the monitor could be returned to the same position between scans and across imaging sessions.
Cell matching across days
In order to return to the same image site, the craniotomy window was leveled with regard to the objective with six d.f., five of which were locked between days. A structural 3D stack encompassing the volume was imaged at 0.8 × 0.8 × 1 px3 μm−3 xyz resolution with 100 repeats. The stack contained two volumes each with 150 fields spanning from 50 μm above the most superficial scanning field to 50 μm below the deepest scanning field; each field was 500 × 800μm2, together tiling a 800 × 800μm2 field of view (300μm overlapped). This was used to register the scan average image into a shared xyz frame of reference between scans across days. To match cells across imaging scans, each two-dimensional scanning plane was registered to the three-dimensional stack through an affine transformation (with nine d.f.) to maximize the correlation between the average recorded plane and the extracted plan from the stack. Based on its estimated coordinates in the stack, each cell was matched to its closest cell across scans. To further evaluate the functional stability of neurons across scans, we included in every visual stimulus an identical set of 100 natural images with each repeated 10 times (referred as oracle images). For each pair of matched neurons from two different scans, we compute the correlation between their average-trial responses to the 100 oracle images. In order to be included for downstream analyses, the matched cell pair had to (1) have an inter-cellular distance smaller than 10μm; (2) achieve a functional correlation equal to or greater than the top 1 percentile of correlation distribution between all unmatched cell pairs (0.42); (3) survive manual curation of the matched pair’s physical appearance in the processed two-photon imaging average frame. On average, 58 ± 13% of closed-loop neurons survived all three criteria.
Presentation of natural stimuli
To fit neurons’ responses, 5,100 natural images from ImageNet (ILSVRC2012) were cropped to fit a 16:9 monitor aspect ratio and converted to gray scale. To collect data for training a predictive model of the brain, we showed 5,000 unique images as well as 100 additional images repeated 10 times each. This set of 100 images were shown in every scan for evaluating cell response reliability within and between scans. Each image was presented on the monitor for 500 ms followed by a blank screen lasting between 300 and 500 ms, sampled uniformly.
Preprocessing of neural responses and behavioral data
Neuronal responses were deconvolved using constrained nonnegative calcium deconvolution and then accumulated between 50 and 550ms after stimulus onset of each trial using a Hamming window. The corresponding pupil movement and treadmill velocity for each trial were also extracted and integrated using the same Hamming window. Each data set consists of 4500 and 500 unique images for training and validation, respectively; an additional set of 100 images presented with 10 repeats were used for model testing. The original stimuli presented to the animals were isotropically downsampled to 64×36 px for model training. Input images, neuronal responses, and behavioral traces were normalized (z-scored for input images and divided by standard deviation for the rest) across either the training set or all data during model training.
Predictive model architecture and training
We followed the same network architecture and training procedure as described previously (10, 12). The network is composed of four components: a common nonlinear core for all neurons, a linear readout dedicated for each neuron, a modulator network that scales the responses based on the animal’s pupil dilation and running velocity, and a shifter network predicting RF shifts from pupil position changes. The common core is a 3-layer CNN with full skip connections. Each layer contains a convolutional layer with no bias, followed by batch normalization, and an exponential linear unit (ELU) nonlinearity. The readout models the neural response as an affine function of the core outputs followed by ELU nonlinearity and an offset of 1 to guarantee positiveness. Additionally, we model the location of a neuron’s RF with a spatial transformer layer reading from a single grid point that extracts the feature vector from the same location at different scales of the downsampled feature outputs. The modulator computes a gain factor for each neuron that simply scales the output of the readout layer using a two-layer fully connected multiplayer perceptron with rectified linear unit (RELU) nonlinearity and a shifted exponential nonlinearity to ensure positive outputs. Finally, because training mice to fixate their gaze is impractical, we estimated the trial-by-trial RF displacement shared across all neurons using a shifter network composed of a three-layer MLP with a tanh nonlinearity. For model training, we followed the procedure detailed in (10). Four instances of the same network with different initialization were trained by minimizing the Poisson loss where denotes the number of neurons, the predicted neuronal response and the observed response. We used all segmented neuronal masks for training, including the duplicate ones due to dense imaging. Predictions from these four models are then averaged at inference.
Evaluation of neuronal reliability and model performance
To study how neurons encode visual stimuli using the predictive model, we restricted all analyses to neurons that exhibit reasonable level of response reliability as well as model predictive accuracy. We evaluated reliability using an oracle score for each neuron by correlating its leave-one-out mean response with that to the remaining trial across 100 images with each repeated 10 times in the test set. The model performance for each neuron was computed on the test set as the correlation between the model predicted response and the recorded responses averaged across 10 repetitions:
We hard thresholded on both of the evaluation metrics to select neurons for synthetic stimuli generation and downstream analyses (see further on).
We also measured the fraction of variation in neuronal responses to identical stimuli accounted for by the model prediction as the normalized correlation coefficient (14) estimated as
serves as the upper bound of the correlation coefficient and is computed as
where is the in vivo responses, and is the number of trials. We threshold neurons on to be larger than 0.1 (0.31% of neurons) to avoid unreliable estimate of . Then we clipped values outside of 0 and 1 (1.19% of neurons).
Neuron selection for synthetic stimuli generation
We first excluded neuronal masks within 10 μm from the edge of the imaging volume, and then rank the remaining masks based on descending model predictive accuracy. To avoid duplicated neurons, we started from the lowest-ranked neuron and iteratively added neurons such that they that are at least 25 μm apart and have functional correlation <0.4 with all neurons selected. Such filtering left us with 2,081–2,676 unique neurons for each of the ten mice. We then hard thresholded on oracle score and model test correlation to include approximately the top 22% of the population for mouse 1–2 for synthesis stimuli generation; we relaxed the thresholding to include approximately 79% of the population for mouse 3–10 and randomly sampled one-thirds of all unique neurons for synthetic stimuli generation.
Generation of Most Exciting Input (MEI)
For each individual neuron, we adapted the activation maximization procedure described earlier (10) to find the stimulus that optimally drive each individual neuron. We started from a Gaussian white noise and iteratively added the gradient of the target neuron’s predicted response to the image. At every optimization step, we smoothened the gradient using a Gaussian filter with s.d = 1.0 to avoid high frequency artifact; after each gradient ascent step, we standardized the resultant image such that the mean and root mean square (RMS) contrast within the receptive field (estimated as the MEI mask, see details below) approximately match the corresponding values of the training set.
Generation of MEI mask
We computed a weighted mask for each MEI to capture the region containing most of the variance in the image so that the resulting masked MEI activates the in silico neuron slightly less than the original unmasked MEI.
We computed a pixel-wise z-score on the MEI and thresholded at z-score above 1.5 to identify the highly contributing pixels. Then we closed small holes/gaps using binary closing, searched for the largest connected region to create a binary mask M where M = 1 if the pixel is in the largest region identified. Then, a convex hull was calculated using the identified pixels. Lastly, to avoid edge artifacts, we smoothed out the mask using a Gaussian filter with σ = 1.5 to avoid potential edge effects.
In silico image presentation
In order to obtain the most trustworthy prediction from the predictive model, we would like to present all images in silico at statistics comparable to the training set images. On average, the training set images have approximately mean 0 and standard deviation 0.8 in the z-score space inside the MEI masks. To match the training set statistics, we synthesized MEIs with a range of full-field constraints and found the best match at approximately full-field mean 0 and RMS contrast 0.25. With this, we standardized all images before presenting them in silico to the predictive model following the same procedure: masking the image with the corresponding MEI mask and then normalizing the entire image to mean 0 and RMS contrast 0.25.
Generation of Diverse Exciting Inputs (DEIs) and diversity evaluation
We modified procedures described previously (17) to optimize DEIs. For each individual neuron, we synthesized a set of images initiating from MEI that preserve high activation while differ as much as possible from each other. To optimize this set, we initiated from 20 instances of the target neuron’s MEI with different additive Gaussian white noises where and iteratively minimize the loss:
| (1) |
where and are the model predicted response to and MEI, is the minimum activation relative to that we target each DEIs for, is the distance between and measured either in pixel Euclidean space or population representation space (see further on). The first term encourages all DEIs to achieve high activation, while the second term maximizes the minimum pair-wise distance among DEIs. Note that the minimum, instead of average distance, is used in the second term to avoid solutions that form the set of DEIs into clusters by pushing apart the most similar pair of DEIs at every iteration. Additionally, we employed two strategies to attenuate the prevalence of high-frequency artifact during CNN image synthesis - (1) we blurred the gradient for every image in the set at every step using a Gaussian filter; (2) we decayed the gradient for all images as a function of number of iterations. We performed the optimization for every target neuron with a series of diversity regularization hyper-parameter , densely sampled from 1×10−4 to 5×10−2. For each neuron, the set optimized using the largest that preserved a minimal response greater than 85% of the MEI response was selected as the DEIs and used for downstream analyses.
Selection of natural control and generation of synthesized control
To show that our predictive model indeed did a good job finding stimuli with both high activation and high diversity, we demonstrated that DEIs preserve activation better than control stimuli resulted from perturbation from the MEI in random directions. These stimuli need to be at comparable distance away from the MEI as the DEIs; to be extra conservative, we required each control stimulus to be strictly closer the MEI than all of the DEIs. We designed two types of such control stimuli through either natural image search or direct image synthesis. For each target neuron, we first computed the mininum distance from the DEIs to the MEI within the MEI mask as and use it as the distance budget for searching for or synthesizing control images. For natural control, we augmented a pool of 124,647 ImageNet images of 256×144 px to 41,881,392 image patches of 64×36 px and searched for patches that have distance from the MEI within the MEI mask smaller than . Since it would be pointless to include controls too close to the MEI (i.e. no perturbation), we additionally excluded images that have distance to MEI smaller 80% of . For the synthesized controls, we synthesized a diverse set of random perturbations from MEI following our DEIs synthesis objective except that the first term is changed to match a targeted distance from the MEI rather than a desired in-silico activation as follows:
| (2) |
For both types of controls, we created 20 different images for each neuron and presented them in vivo with single repetition each.
Diversity index
To calculate neurons’ diversity indexes on a meaningful spectrum with interpretable reference points, we estimated theoretical references for diversity indexes of idealized simple and complex cells. Particularly, we estimated the lower/upper bounds ( and ) as the median average pairwise Euclidean distance of DEIs from a population of noiseless simple/complex cells, respectively. To get a precise estimation, we identified DEIs via performing an exhaustive search through the Gabor filter parameter spaces. Since DEIs are standardized with a fixed mean and standard deviation, idealized simple cells have the same average pairwise Euclidean distance regardless of the underlying Gabor parameters. Similarly, idealized complex cells with different Gabor parameters have identical but higher average pairwise Euclidean distance among themselves. Then for each real neuron, a diversity index is calculated for each mouse V1 neuron based on the average Euclidean pairwise distance of its DEIs as
| (3) |
Neuron selection for closed-loop verification
For 9 out of 10 mice, we randomly selected neurons with relatively high level of invariance (detailed below); for 1 mouse, we randomly selected neurons from all candidates that survived our oracle score and model performance criteria (see above). To remove the confounding effect of RF size on neurons’ invariance level, we fit a least squares regression from the MEI mask size to the diversity index computed from DEIs (see above) using 1000 random neurons compiled across 8 pilot data sets. For each neuron, the residual between the actual average DEIs pair-wise Euclidean distance and the predicted distance from the MEI mask size was calculated as its diversity residual. This diversity residual served as an size-independent evaluation of neuron’s invariance level. For each of the 9 mice, we randomly selected 80 neurons from the top 50 percentile among all neurons with positive diversity residuals.
Presentation of synthetic stimuli
For all MEIs, DEIs, DEIs controls, and texture DEIs (see further on), we masked the stimuli with the MEI mask and standardized all masked stimuli such that they have fixed value of mean and RMS contrast in the luminance space within the MEI mask with very small amount of variation due to clipping within the 8-bit range. The fixed mean and contrast valued were chosen to be close to the corresponding values of the training set while minimizing the amount of clipping. All pixels outside of the MEI mask are at 128, the same intensity as the blank screen in between consecutive trials. For each neuron, its MEI was presented for 20 repeats and each of its 20 DEIs or 20 DEIs controls were presented once.
Decoding DEIs from population responses
To confirm whether there exists perceivable difference across DEIs, for each target neuron, we selected the most different pair of DEIs (based on the corresponding diversity measurement space) from 20 synthesized DEIs. We presented each DEI (DEI1 and DEI2) for 20 repeats per neuron for the whole V1 population. We performed a 5-fold cross-validation logistic classification with L2 regularization on the population responses to classify whether each single trial response originated from DEI1 or DEI2. The regularization strength was optimized empirically from fitting logistic regression to decode DEIs across 1 pilot data set.
Simple and complex cell models
The response of an idealized simple cell was modeled as convolution with a 2D Gabor filter followed by a rectified linear activation function (ReLU). An idealized complex cell was formulated by the classical energy model, where the response was modeled as the square root of the summation of squared outputs to a quadrature pair of 2D Gabor filters. In order to obtain a noisy predictive model for these idealized simulated neurons, we followed the same protocol of data presentation and model training for these idealized neurons as that for the real brain neurons. Specifically, we collected the idealized responses to 5000 random ImageNet images and used each response as the mean of a Poisson distribution from which a noisy response was sampled. Then we used the noisy input-response data set to train a predictive model with an identical architecture to that of the real neurons. The same MEI and DEIs optimization procedure described above was then performed on the resultant simple and complex cell predictive models.
Generation of DEIs in population representational space
To test whether DEIs could generalize across diversity representational spaces, we optimized DEIs using the same loss function as in 5 but now measuring pair-wise DEI diversity as the negative Pearson correlation between model predicted population neuronal response vectors and to and :
| (4) |
where are the mean population responses. We obtained the population responses by shifting all neurons’ RF center to that of the target neuron that the DEIs were optimized for. Therefore, each population response vector served as a proxy of the “perceptual representation” of the corresponding image. We denote these DEIs as population-based DEIs.
Replication of DEIs in functional connectomics data set
Recently, a large-scale functional connectomics data set of mouse visual cortex (“MICrONS data set”), including responses of >75k neurons to full-field natural movies and the reconstructed sub-cellular connectivity of the same cells from electron microscopy data (9). A dynamic recurrent neural network (RNN) model cite eric) of this mouse visual cortex—digital twin—exhibits not only a high predictive performance for natural movies, but also accurate out-of-domain performance on other stimulus classes such as drifting Gabor filters, directional pink noise, and random dot kinematograms. Here, we took advantage of the model’s ability to generalize to other visual stimulus domains and presented MEIs and DEIs to this digital twin model in order to relate specific functional properties to the neurons’ connectivity and anatomical properties. Specifically, we recorded the visual activity of the same neuronal population to static natural images as well as to the identical natural movies that were used in the MICrONS data set. Neurons were matched anatomically as described for the closed loop experiments. Based on the responses to static natural images we trained a static model as described above, and from the responses to natural movies we trained a dynamic model using a RNN architecture described in REF. We then presented the same static natural image set that we showed to the mice also to their dynamic model counterparts and trained a second static model using these predicted in silico responses. This enabled us to compare the MEIs and DEIs for the same neurons generated from two different static models: one trained directly on responses from real neurons, and another trained on synthetic responses to static images from dynamic models (D-MEI and D-DEIs). To quantify similarity, we presented both versions of MEIs and DEIs to an independent static model trained on the same natural images and responses but initialized with a different random seed, thereby avoiding model-specific biases.
Generation of full-texture and partial-texture DEIs
A neuron with perfect partial phase invariance should maintain high activation to phase-shifted version of its preferred texture pattern within the spatial region that tolerates phase changes. Thus, we proposed a texture generative model to produce texture-based DEIs composed of two complementary subfields as follows:
| (5) |
where the first term is the phase invariant subfield randomly cropped from an optimized texture canvas using a mask . The second term is a fixed subfield masked directly from the original MEI. This model could be simplified to a full-texture model to describe global phase invariance if the entire receptive field (i.e. the MEI mask ) was used as . We generated the texture following (17) by maximizing the average activation of randomly sampled crops from using . We followed the same loss as in non-parametric DEIs generation 1 to jointly maximize the activation and diversity of DEIs with the same regularizations (i.e. Gaussian blurring on the gradient and learning rate decay) but in this case, DEIs were parameterized as in 5. The parametric DEIs were standardized to the same mean and RMS contrast as the MEI after each gradient step.
To ensure that captures the region of the non-parametric DEIs from which we observed the most diversity, we precomputed a series of s with increasing sizes by varying the threshold on the pixel-wise variance across the DEIs. Specifically, starting from the pixels with the largest variance across DEIs, we kept expanding the by requesting increasing fraction of the total variance from 0.2 to 0.6 within the phase invariant subfield. In general, the average predicted activation of the texture-based DEIs decreased as the size of increased. While an ideal complex cell should exhibit an almost flat line, an ideal simple cell should exhibit rapid activation decay. Most V1 neurons behaved as if in between the classical cell types, demonstrating an initial slow decrease in activation before steeper decay when the proposed phase invariant region expanded beyond the desirable target (Fig. S6a).
For each set of texture-based DEIs resultant from a phase invariant mask , we computed the harmonic mean between normalized activation and diversity index.
| (6) |
where is the average normalized activation, and is the average pair-wise Euclidean distance normalized by the maximal value across all different sets of stimulus corresponding to the series of . We denoted the set of texture-based DEIs resultant with the maximum score as the partial-texture DEIs.. On the other hand, the set of texture DEIs resultant from the full-texture model were denoted as full-texture DEIs.
Necessity and specificity of the two subfields in partial-texture DEIs
To test whether both the phase invariant and the fixed subfields are necessary for the high activation of the partial texture DEIs, we presented the content within each subfield alone and see if the neuronal activation decreased compared to the MEI activation. To ensure pixels within each subfield stay at their entirety, we computed a binary mask for each subfield and smoothed the edge of the mask only outside of the binary mask. To test the specificity of the content within each subfield, we swapped the subfield content to random patterns and see if the activation is lower than that of the original partial-texture DEIs. Particularly, we swapped each neuron’s phase invariant content to samples cropped from textures optimized for different random neurons and each neuron’s fixed content to random natural image crops. When presented to the animals, these content-swapped stimuli were standardized to match the mean and RMS contrast in the luminance space as the original partial texture DEIs.
The CUB and CUB-grating data sets
To study the relationship between invariance and natural stimuli, we created a data set from the Caltech-UCSD Birds-200–2011 (CUB) image data set (26). The original data set contains 11,788 natural images belonging to 200 bird categories. Each image contains a single bird appearing in its natural habitat resulting in ideal and ethnologically relevant stimuli for mice. Each original image is then resized to 64 × 64 pixels and then sampled using a window of size 36 × 36 pixels with a stride of size 2. In addition, each image has a semantic segmentation label identifying the region of the image containing the bird by hand. This segmentation label is then thresholded at 0.5 to get the final binarized segmentation. To test if object boundaries defined by differences in spatial frequency would strongly activate V1 neurons, we replaced textures in the CUB data set with grating stimuli (CUB-grating images) with the frequency of 5.83°/cycle to 15.55°/cycle (high-frequency range) and 15.55°/cycle to 58.3°/cycle (lowfrequency range). These frequency bounds were derived empirically from fitting gratings to 1000 random neurons compiled across 8 pilot data sets.
Analyses on highly activating crops in the CUB and CUB–grating data set
To test whether the division of subfields identified from neurons’ bipartite parameterization corresponds to object boundary in natural images, we searched for highly activating natural crops in silico for each target neuron. We masked these crops with the MEI mask and standardized all masked stimuli such that they have the same mean and RMS contrast within the MEI mask as the target neuron’s MEI. We screened through 1 million of these standardized crops for each target neuron and identified 100 most highly activating natural crops as well as 100 random ones. A natural crop was classified as containing both object and background if it contained at least 20% of both object and background within the RF of the target neuron. For the CUB-grating images, we followed the same protocol but reported on the most exciting crop for simplicity (Fig. 5e). Note that our reported results were stable regardless of the specific choice of the number of stimuli searched and the definition of natural crops containing both object and background.
To measure the alignment of the image crop segmentation label and neurons’ bipartite mask in both the CUB and the CUB-grating data sets, we devised a matching score as follows. For each neuron, we first defined a bipartite mask from the bipartite parameterization of DEIs as , where and denotes the binarized version of the MEI mask and the phase invariant subfield mask , respectively, when we hard-thresholded on the masks at 0.3. In , a value of 1 and −1 denotes pixels within the phase invariant subfield and within the fixed subfield, respectively, and 0 elsewhere. On the other hand, for each crop from the CUB and the CUB-grating data sets, we first assigned pixels within the bird to 1 and pixels belonging to the background to −1 and then masked it with to achieve the segmentation mask of the crop. For each target neuron and each of its highly activating crops , a matching score is calculated as follow:
| (7) |
A highly activating crop would yield a matching score of 1 if the phase invariant subfield perfectly matched with the bird and the fixed subfield perfectly matched with the background and a score of −1 if the reverse was true. For random crops, however, a score of 0 is expected.
Perlin noise stimuli
To quantify if the phase invariant and fixed subfields extracted from DEIpartial systematically preferred different frequencies, we replaced the DEI content in each subfield with synthesized textures of Perlin noise (27) with different spatial frequency biases. Specifically, the texture images with size of 64 × 64 pixels were generated by combining 8 octaves of Perlin noises with lacunarity factor of 2 and a persistence of either 1.0 (high frequency texture images) or 0.1 (low frequency texture images).
In vivo response comparisons and statistical analysis
Recorded responses were normalized across all presented images per scan. The normalized responses of the matched neurons were then averaged across either 20 repetitions of a single image for MEI or single repetitions of 20 different images for all other image types including non-parametric DEIs (both pixel-based and population-based), synthesized & natural image controls, partial- & full-texture DEIs, fixed & phase invariant subfields alone, partial-texture DEIs with swapped subfields. For single neurons, the statistical significance of the difference in responses was assessed using either one-tailed or two-tailed Welch’s t-tests. The overall difference in average responses pooled across all neurons was assessed using either one-tailed or two-sided Wilcoxon signed-rank tests.
Statistics
All statistical tests performed with the corresponding sample sizes, statistical values, and p-values are reported in the figure caption. All permutation testings and bootstrappings were performed with 10,000 permutations/resamplings. Normality was assumed for Welch’s t-test and one-sample t-test, although this was not explicitly tested. When p-values were less than 10−9, they were reported as P < 10−9; otherwise the exact p-values were reported.
Supplementary Material
ACKNOWLEDGEMENTS
The authors thank David Markowitz, the IARPA MICrONS Program Manager, who coordinated this work during all three phases of the MICrONS program. We thank IARPA program managers Jacob Vogelstein and David Markowitz for co-developing the MICrONS program. We thank Jennifer Wang, IARPA SETA for her assistance. The work was supported by the Intelligence Advanced Research Projects Activity (IARPA) via Department of Interior/Interior Business Center (DoI/IBC) contract numbers D16PC00003, D16PC00004, and D16PC0005. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon. XP acknowledges support from NSF CAREER grant IOS-1552868. XP and AST acknowledge support from NSF NeuroNex grant 1707400. AST also acknowledges support from National Institute of Mental Health and National Institute of Neurological Disorders And Stroke under Award Number U19MH114830 and National Eye Institute/National Institutes of Health Core Grant for Vision Research (no. T32-EY-002520-37). Disclaimer: The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of IARPA, DoI/IBC, or the U.S. Government.
This work was also supported by the European Research Council (ERC) under the European Union’s Horizon Europe research and innovation programme (Grant agreement No. 101041669) as well as the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), project ID 432680300 (SFB 1456, project B05).
Footnotes
Data and code availability.
All data and the analysis code will be made publicly available in an online repository latest upon journal publication. Please contact us if you would like to get access before that time.
References
- 1.Gross Charles G, de Rocha-Miranda CE, and Bender DB. Visual properties of neurons in inferotemporal cortex of the macaque. Journal of neurophysiology, 35(1):96–111, 1972. [DOI] [PubMed] [Google Scholar]
- 2.Tsao Doris Y, Freiwald Winrich A, Tootell Roger BH, and Livingstone Margaret S. A cortical region consisting entirely of face-selective cells. Science, 311(5761):670–674, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yamins Daniel LK and DiCarlo James J. Using goal-driven deep learning models to understand sensory cortex. Nature neuroscience, 19(3):356–365, 2016. [DOI] [PubMed] [Google Scholar]
- 4.Cadieu Charles, Kouh Minjoon, Pasupathy Anitha, Connor Charles E, Riesenhuber Maximilian, and Poggio Tomaso. A model of v4 shape selectivity and invariance. Journal of neurophysiology, 98(3):1733–1750, 2007. [DOI] [PubMed] [Google Scholar]
- 5.Sharpee Tatyana O, Kouh Minjoon, and Reynolds John H. Trade-off between curvature tuning and position invariance in visual area v4. Proceedings of the National Academy of Sciences, 110(28):11618–11623, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.El-Shamayleh Yasmine and Pasupathy Anitha. Contour curvature as an invariant code for objects in visual area v4. Journal of Neuroscience, 36(20):5532–5543, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hubel David H and Wiesel Torsten N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. The Journal of physiology, 160(1):106, 1962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.DiCarlo James J and Cox David D. Untangling invariant object recognition. Trends in cognitive sciences, 11(8):333–341, 2007. [DOI] [PubMed] [Google Scholar]
- 9.MICrONS Consortium, Bae J Alexander, Baptiste Mahaly, Bodor Agnes L, Brittain Derrick, Buchanan Joann, Bumbarger Daniel J, Castro Manuel A, Celii Brendan, Cobos Erick, Collman Forrest, da Costa Nuno Maçarico, Dorkenwald Sven, Elabbady Leila, Fahey Paul G, Fliss Tim, Froudarakis Emmanouil, Gager Jay, Gamlin Clare, Halageri Akhilesh, Hebditch James, Jia Zhen, Jordan Chris, Kapner Daniel, Kemnitz Nico, Kinn Sam, Koolman Selden, Kuehner Kai, Lee Kisuk, Li Kai, Lu Ran, Macrina Thomas, Mahalingam Gayathri, McReynolds Sarah, Miranda Elanine, Mitchell Eric, Mondal Shanka Subhra, Moore Merlin, Mu Shang, Muhammad Taliah, Nehoran Barak, Ogedengbe Oluwaseun, Papadopoulos Christos, Papadopoulos Stelios, Patel Saumil, Pitkow Xaq, Popovych Sergiy, Ramos Anthony, Reid R Clay, Reimer Jacob, Schneider-Mizell Casey M, Seung H Sebastian, Silverman Ben, Silversmith William, Sterling Amy, Sinz Fabian H, Smith Cameron L, Suckow Shelby, Takeno Marc, Tan Zheng H, Tolias Andreas S, Torres Russel, Turner Nicholas L, Walker Edgar Y, Wang Tianyu, Williams Grace, Williams Sarah, Willie Kyle, Willie Ryan, Wong William, Wu Jingpeng, Xu Chris, Yang Runzhe, Yatsenko Dimitri, Ye Fei, Yin Wenjing, and Yu Szi-Chieh. Functional connectomics spanning multiple areas of mouse visual cortex. August 2021. [Google Scholar]
- 10.Walker Edgar Y, Sinz Fabian H, Cobos Erick, Muhammad Taliah, Froudarakis Emmanouil, Fahey Paul G, Ecker Alexander S, Reimer Jacob, Pitkow Xaq, and Tolias Andreas S. Inception loops discover what excites neurons most using deep predictive models. Nature neuroscience, 22(12):2060–2065, 2019. [DOI] [PubMed] [Google Scholar]
- 11.Bashivan Pouya, Kar Kohitij, and DiCarlo James J. Neural population control via deep image synthesis. Science, 364(6439):eaav9436, 2019. [DOI] [PubMed] [Google Scholar]
- 12.Sinz Fabian, Ecker Alexander S, Fahey Paul, Walker Edgar, Cobos Erick, Froudarakis Emmanouil, Yatsenko Dimitri, Pitkow Zachary, Reimer Jacob, and Tolias Andreas. Stimulus domain transfer in recurrent models for large scale cortical population prediction on video. Advances in neural information processing systems, 31, 2018. [Google Scholar]
- 13.Franke Katrin, Konstantin F Willeke Kayla Ponder, Galdamez Mario, Zhou Na, Muhammad Taliah, Patel Saumil, Froudarakis Emmanouil, Reimer Jacob, Sinz Fabian H, et al. State-dependent pupil dilation rapidly shifts visual feature selectivity. Nature, 610(7930):128–134, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schoppe Oliver, Harper Nicol S, Willmore Ben DB, King Andrew J, and Schnupp Jan WH. Measuring the performance of neural models. Frontiers in computational neuroscience, 10:10, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Willeke Konstantin F, Fahey Paul G, Bashiri Mohammad, Pede Laura, Burg Max F, Blessing Christoph, Cadena Santiago A, Ding Zhiwei, Lurz Konstantin-Klemens, Ponder Kayla, Muhammad Taliah, Patel Saumil S, Ecker Alexander S, Tolias Andreas S, and Sinz Fabian H. The sensorium competition on predicting large-scale mouse primary visual cortex activity. June 2022. [Google Scholar]
- 16.Lurz Konstantin-Klemens, Bashiri Mohammad, Willeke Konstantin, Jagadish Akshay K, Wang Eric, Walker Edgar Y, Cadena Santiago A, Muhammad Taliah, Cobos Erick, Tolias Andreas S, Ecker Alexander S, and Sinz Fabian H. Generalization in data-driven models of primary visual cortex. In Proceedings of the International Conference for Learning Representations (ICLR), page 2020.10.05.326256, October 2020. [Google Scholar]
- 17.Cadena Santiago A, Weis Marissa A, Gatys Leon A, Bethge Matthias, and Ecker Alexander S. Diverse feature visualizations reveal invariances in early layers of deep neural networks. In Proceedings of the European Conference on Computer Vision (ECCV), pages 217–232, 2018. [Google Scholar]
- 18.Bussgang Julian Jakob. Crosscorrelation functions of amplitude-distorted gaussian signals. Technical Report 216, 1952. [Google Scholar]
- 19.Jones Judson P and Palmer Larry A. An evaluation of the two-dimensional gabor filter model of simple receptive fields in cat striate cortex. Journal of neurophysiology, 58(6):1233–1258, 1987. [DOI] [PubMed] [Google Scholar]
- 20.Heeger David J. Half-squaring in responses of cat striate cells. Visual neuroscience, 9(5):427–443, 1992. [DOI] [PubMed] [Google Scholar]
- 21.Fischler Martin A and Bolles Robert C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM, 24(6):381–395, 1981. [Google Scholar]
- 22.Wang Eric Y., Fahey Paul G., Ponder Kayla, Ding Zhuokun, Muhammad Taliah, Patel Saumil, Franke Katrin, Ecker Alexander S., Reimer Jacob, Pitkow Xaq, Sinz Fabian H., and Tolias Andreas S.. Towards a foundation model of the mouse visual cortex. In preparation, 2023. [Google Scholar]
- 23.Zhan Chang’an A and Baker Curtis L Jr. Boundary cue invariance in cortical orientation maps. Cerebral Cortex, 16(6):896–906, 2006. [DOI] [PubMed] [Google Scholar]
- 24.Karklin Yan and Lewicki Michael S. Emergence of complex cell properties by learning to generalize in natural scenes. Nature, 457(7225):83–86, 2009. [DOI] [PubMed] [Google Scholar]
- 25.Kirchberger Lisa, Mukherjee Sreedeep, Schnabel Ulf H, van Beest Enny H, Barsegyan Areg, Levelt Christiaan N, Heimel J Alexander, Lorteije Jeannette AM, van der Togt Chris, Self Matthew W, et al. The essential role of recurrent processing for figure-ground perception in mice. Science advances, 7(27):eabe1833, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wah Catherine, Branson Steve, Welinder Peter, Perona Pietro, and Belongie Serge. The caltech-ucsd birds-200–2011 dataset. 2011.
- 27.Perlin Ken. An image synthesizer. ACM Siggraph Computer Graphics, 19(3):287–296, 1985. [Google Scholar]
- 28.Fukushima Kunihiko. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological cybernetics, 36(4):193–202, 1980. [DOI] [PubMed] [Google Scholar]
- 29.Tanaka Keiji. Inferotemporal cortex and object vision. Annual review of neuroscience, 19(1):109–139, 1996. [DOI] [PubMed] [Google Scholar]
- 30.Poggio Tomaso and Bizzi Emilio. Generalization in vision and motor control. Nature, 431(7010):768–774, 2004. [DOI] [PubMed] [Google Scholar]
- 31.Yamins Daniel LK, Hong Ha, Cadieu Charles F, Solomon Ethan A, Seibert Darren, and DiCarlo James J. Performance-optimized hierarchical models predict neural responses in higher visual cortex. Proceedings of the national academy of sciences, 111(23):8619–8624, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Quiroga R Quian, Reddy Leila, Kreiman Gabriel, Koch Christof, and Fried Itzhak. Invariant visual representation by single neurons in the human brain. Nature, 435(7045):1102–1107, 2005. [DOI] [PubMed] [Google Scholar]
- 33.Ponce Carlos R, Xiao Will, Schade Peter F, Hartmann Till S, Kreiman Gabriel, and Livingstone Margaret S. Evolving images for visual neurons using a deep generative network reveals coding principles and neuronal preferences. Cell, 177(4):999–1009, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Froudarakis Emmanouil, Berens Philipp, Ecker Alexander S, Cotton R James, Sinz Fabian H, Yatsenko Dimitri, Saggau Peter, Bethge Matthias, and Tolias Andreas S. Population code in mouse v1 facilitates readout of natural scenes through increased sparseness. Nature neuroscience, 17(6):851–857, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dapello Joel, Marques Tiago, Schrimpf Martin, Geiger Franziska, Cox David, and DiCarlo James J. Simulating a primary visual cortex at the front of cnns improves robustness to image perturbations. Advances in Neural Information Processing Systems, 33:13073–13087, 2020. [Google Scholar]
- 36.Maruyama Minoru, Girosi Federico, and Poggio Tomaso. A connection between grbf and mlp. 1992.
- 37.Poggio Tomaso and Girosi Federico. Networks for approximation and learning. Proceedings of the IEEE, 78(9):1481–1497, 1990. [Google Scholar]
- 38.Anselmi Fabio, Rosasco Lorenzo, Tan Cheston, and Poggio Tomaso. Deep convolutional networks are hierarchical kernel machines. arXiv preprint arXiv:1508.01084, 2015. [Google Scholar]
- 39.Wang Binxu and Ponce Carlos R. Tuning landscapes of the ventral stream. Cell Reports, 41(6):111595, 2022. [DOI] [PubMed] [Google Scholar]
- 40.Schubert Ludwig, Voss Chelsea, Cammarata Nick, Goh Gabriel, and Olah Chris. High-low frequency detectors. Distill, 2021. doi: 10.23915/distill.00024.005. https://distill.pub/2020/circuits/frequency-edges. [DOI] [Google Scholar]
- 41.Schnabel Ulf H, Bossens Christophe, Lorteije Jeannette AM, Self Matthew W, de Beeck Hans Op, and Roelfsema Pieter R. Figure-ground perception in the awake mouse and neuronal activity elicited by figure-ground stimuli in primary visual cortex. Scientific reports, 8(1):17800, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Reimer Jacob, Froudarakis Emmanouil, Cadwell Cathryn R, Yatsenko Dimitri, Denfield George H, and Tolias Andreas S. Pupil fluctuations track fast switching of cortical states during quiet wakefulness. neuron, 84(2):355–362, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Sofroniew Nicholas James, Flickinger Daniel, King Jonathan, and Svoboda Karel. A large field of view two-photon mesoscope with subcellular resolution for in vivo imaging. elife, 5:e14472, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mathis Alexander, Mamidanna Pranav, Cury Kevin M., Abe Taiga, Murthy Venkatesh N., Mathis Mackenzie Weygandt, and Bethge Matthias. DeepLabCut: markerless pose estimation of user-defined body parts with deep learning. Nature Neuroscience, 21(9):1281–1289, 2018. ISSN 15461726. doi: 10.1038/s41593-018-0209-y. [DOI] [PubMed] [Google Scholar]
- 45.Pnevmatikakis Eftychios A, Soudry Daniel, Gao Yuanjun, Machado Timothy A, Merel Josh, Pfau David, Reardon Thomas, Mu Yu, Lacefield Clay, Yang Weijian, et al. Simultaneous denoising, deconvolution, and demixing of calcium imaging data. Neuron, 89(2):285–299, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Giovannucci Andrea, Friedrich Johannes, Gunn Pat, Kalfon Jeremie, Brandon L Brown Sue Ann Koay, Taxidis Jiannis, Najafi Farzaneh, Jeffrey L Gauthier Pengcheng Zhou, Khakh Baljit S, Tank David W, Chklovskii Dmitri B, and Pnevmatikakis Eftychios A. Caiman: An open source tool for scalable calcium imaging data analysis. eLife, 8:e38173, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.