Stabilizing the return to normal behavior in an epidemic

Abstract

Predicting the interplay between infectious disease and behavior has been an intractable problem because behavioral response is so varied. We introduce a general framework for feedback between incidence and behavior in an epidemic. By identifying stable equilibria, we provide policy end-states that are self-managing and self-maintaining. We prove mathematically the existence of two new endemic equilibria depending on the vaccination rate: one in the presence of low vaccination but with reduced societal activity (the “new normal”), and one with return to normal activity but with vaccination rate below that required for disease elimination. This framework allows us to anticipate the long-term consequence of an emerging disease and design a vaccination response that optimizes public health and limits societal consequences.

One Sentence Summary:

Incidence-dependent behavioral feedback to epidemic dynamics generates novel equilibria in response to vaccination.

1. Introduction

To understand and control epidemics, models have been developed that reflect the fundamental properties of infectious disease transmission (1). To embody biological understanding and develop effective policy these models rely on abstractions of complicated phenomena: mortality, reinfection, vaccination, loss of immunity and spatial networks (2). Nevertheless, a substantial barrier to progress has been that transmission depends on human behavior, which is impossible to model in detail. To meet this challenge, we must consider all possible responses with minimal assumptions about the behavioral response to disease.

Exogenous effects on spread of disease include seasonality or long-established societal patterns of behavior. These are distinguished by a lack of dependence on the state of the disease (number of susceptible, infected, or recovered people) and can be modeled as external covariates; e.g. transmission rate as a function of relative humidity (4) or contact rates as a function of time of year (5). In contrast, endogenous effects are dependent on the state of the system (e.g. incidence), including individual choices to modify behavior or policy changes that influence behavior in response to incidence or mortality.

Modern technology such as cell phone data has enabled exogenous modeling of behavior (6–8). However, disease forecasting is impossible unless those external variables can also be predicted. Modeling behavior as a function of exogenous forces only permits retrospective evaluation of the interaction between behavior and transmission. Policy decisions need to anticipate future changes in behavior and thus require a framework that can account for future behavioral change.

We show how a wide range of possible endogenous behavioral responses (e.g. distancing, masking, hygiene) can be introduced in a compartmental modeling framework (eg. susceptible, infectious, and recovered, or SIR (3)) in a completely general way. Rather than specify a particular model of behavioral response, we choose reasonable and intuitive properties as assumptions to constrain the form of the behavioral response.

There has been significant work analyzing models with feedback between incidence and vaccination behavior (willingness or hesitancy) (9, 10). Bauch and Earn (9) showed the existence of stable equilibrium vaccination demand that can explain the challenge of attaining univerisal coverage. There has comparatively little work modeling feedback between incidence and activity (11, 12) as applied to behavioral interventions to limit transmission. Current methods typically rely on choosing a particular model for the feedback (13–20). The key advance here is that we avoid the problematic issue of model specification, so the conclusions we reach are widely applicable, including novel emergence scenarios in unknown behavioral contexts.

Consider a standard disease modeling framework (1, 3) for a single well-mixed population that includes vaccination and loss of immunity. We reflect the endogenous/exogenous dichotomy by decomposing the transmission rate, β, into a product of exogenous and endogenous components. The endogenous response is represented with a single variable, a, (the instantaneous activity of individuals averaged over the population) that quantifies the instantaneous rate of effective behavioral interactions. Rather than specify an exact model for the activity dynamics, we assume that the rate of change of activity is determined by an unspecified reactivity function. Without specifying the reactivity function, we base our results on the following three assumptions:

• A1. Reactivity: Change of activity depends on the current level of activity and incidence of infection.

• A2. Resilience: When incidence of infection is zero, activity will return to a baseline level.

• A3. Boundedness: Activity does not exceed the baseline level.

Reactivity reflects the assumption that the population chooses its aggregate activity level based on information available; specifically the currently observed activity level and knowledge of disease incidence. This means that the reactivity function, F, is a function of activity, a, and disease incidence, c, or F(a, c), and does not depend on other variables. Thus, reactivity does not reflect exogenous influences.

We define a baseline activity level as the level of activity that the population would go to if the disease were removed and the activity was allowed to stabilize.

Resilience is here defined as the ability of the activity to spring back to the previous condition when distorting forces are removed. In this case, new infections are a distorting force, so resilience is the assumption that when disease incidence is zero the activity averaged over the population will return towards the baseline level. We also assume that, when there is no incidence, the baseline activity level is stationary.

Boundedness asserts that the baseline activity level of the population that exists in the absence of infection is also the maximum activity level. We assign this maximum level to be 1 in arbitrary units, so that the activity level a is always between 0 and 1.

Using only these assumptions, we show that the disease equilibria and stability are determined almost entirely by the vaccination rate, v, regardless of the behavioral model. We illustrate that accounting for an endogenous behavioral feedback gives rise to a novel equilibrium en route to the classical vaccine-based elimination threshold. The existence of this novel equilibrium can be used as a way-point to guide policy to achieve a return to normal behavior coincident with disease control.

2. Results

Starting from the reactivity assumption (A1), we first developed a framework for incorporating any reactive behavioral dynamics into the compartmental disease modeling paradigm (see Supplementary Materials and Methods). The state of the modeled disease at any given time can be characterized by three variables (Fig 1): the percentage of the population that is susceptible, s, the percentage infected, i, and the activity relative to the baseline, a. The novelty here is that the reactivity function, F, which determines the feedback between activity and infection rate, is left completely unspecified. This means our results will apply very broadly to any behavioral response that satisfies our basic assumptions.

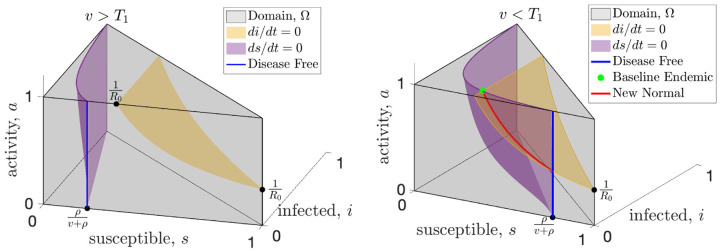
Figure 1: Universal equilibria of resilient behavioral responses with high (left) and low (right) vaccination.

The state space (gray shading) of the SIR model with endogenous behavioral feedback plotted on the susceptible (s), infected (i), and activity (a, where a = 1 represents the baseline activity level) axes. The susceptible and infected population sizes are instantaneously constant along the purple and yellow surfaces, respectively. An equilibrium must occur along the blue line that shows the intersection of the purple surface with the front of the domain (the i = 0 plane) or along the red curve that shows the intersection of these surfaces. When vaccine rates, v, are greater than the critical threshold, T₁ (see left panel), the only equilibrium is disease-free (blue) and resilience will drive the activity to baseline which is the top of the blue line. When vaccination rates drop below the T₁ (right panel), the baseline endemic equilibrium (green dot) is created, along with at least one new normal endemic equilibrium which can be anywhere along the red curve.

First, for any model with reactivity (Assumption A1), we find a universal vaccination threshold, T₁, that is independent of the feedback between activity and incidence. When the vaccination rate is above this threshold any equilibrium must be disease-free. Fig. 1 illustrates the surfaces where the infected population (yellow) and the susceptible population (purple) are not changing; an equilibrium can only happen at the intersection of these two surfaces, or where the purple surface intersects the i = 0 plane (disease-free). When the vaccination rate is greater than T₁ the only equilibrium is disease-free (Fig. 1a, and supplementary figure Fig. S.1a).

Second, by assuming resilience (Assumption A2), we prove that when the vaccination rate is above T₁ the disease-free equilibrium is stable in the face of baseline activity (Fig. S.1a). Resilience assumes that when incidence is zero (disease-free) and activity is below baseline, then activity will increase. While this seems intuitive it does not imply stability by itself. Stability requires that even if we perturb the disease-free equilibrium by introducing a small number of infections, the system must return to the disease-free equilibrium. In Theorem 3 (Supplementary Material), we prove that the disease-free equilibrium is in fact stable, as long as the vaccination rate is above T₁.

Assuming both reactivity (A1) and resilience (A2), when the vaccination rate drops below the universal threshold T₁, the disease-free equilibrium becomes unstable, and endemic equilibria become possible (Fig. 1b). One novel equilibrium, which we call the baseline endemic equilibrium, is stable even when activity is at baseline (a = 1). For a baseline endemic equilibrium to exist, we only require that normal activity be stationary for this incidence level, meaning that F(1, c) = 0. Not every reactivity function, F, will have a baseline endemic equilibrium, and we give several examples in Section 3 of reactivity functions that show the range of possibilities. If the baseline endemic equilibrium does exist, the infection rate at equilibrium depends on the vaccination rate, but is independent of the behavioral model.

While not as desirable as a disease-free equilibrium, an endemic equilibrium with baseline activity (a = 1) may still be preferred to permanently modifying behavior, so it is important to determine its stability. Recall that a bounded behavioral response limits the average activity, a, to be at most the baseline level, a = 1, by imposing A1. In Theorem 4 (Supplementary Material), we show that for any bounded behavioral response, there will be a second vaccination threshold, T₂, which determines the stability of the baseline endemic equilibrium. The T₂ threshold is given by (Supplementary Material),

$$T_2=T_1-{\xi }_F{R}_0(\rho /\gamma +1)$$ (1)

where ξ_F is a constant that depends on the properties of the reactivity function, F, near the baseline endemic equilibrium, R₀ is the average number of infections after contact in a fully susceptible population or basic reproduction number, and ρ and γ are rates (see Supplementary Material). The ξ_F constant will often be positive, and in these cases the T₂ vaccination threshold will be lower than the T₁ threshold. In these cases, when the vaccination rate is higher than T₂ but less than T₁, the baseline endemic endemic will be stable. For some reactivity functions, the constant ξ_F can be negative or zero, and for these reactivity functions the baseline endemic equilibrium will not be stable for any vaccination rate. Once the reactivity function, F, is specified, T₂ can be computed explicitly and we show how to compute T₂ along with several examples in the Supplementary Material. This shows that even when the classical threshold for effective vaccination cannot be achieved, there can still be a substantial benefit at a lower vaccination rate. As long as the vaccination rate exceeds the new T₂ threshold, the baseline activity level will be stable (see examples Fig. 2).

Figure 2: Vaccination may increase or decrease infection rate depending on the form of the behavioral response.

Relationship between activity, incidence, and vaccination rate for three example reactivity functions (columns). In the top row we illustrate zones of increasing (brown) and decreasing (purple) activity as a function of incidence; white indicates regions where activity is stationary (at least instantaneously). In the middle row the equilibrium activity is shown as a function of vaccination rate with colors indicating the disease-free, baseline endemic, and new normal regimes. The bottom row indicates the equilibrium incidence as a function of vaccination; stable equilibria are shown as solid lines and unstable equilibria as dashed lines. Note that when vaccination is less than T₂ (the new normal), increased vaccination may lead to either higher (bottom right) or lower (bottom left) infection rates depending on the reactivity function.

When the vaccination rate is below both the T₁ and T₂ thresholds (e.g. early stages of a novel disease before a vaccination, v = 0) both the disease-free equilibrium and the baseline endemic are unstable and there is no stable equilibrium with baseline activity. In Theorem 6 (Supplementary Material) we prove that there is at least one new equilibrium (Fig. 1b), which we term a “new normal” endemic equilibrium. Unlike the disease-free and baseline endemic equilibrium, the incidence rate at the new normal endemic equilibrium depends on the form of the behavioral feedback and implies long-term behavioral changes with activity level below baseline. When vaccination is below both thresholds, the stability of the new normal endemic cannot be determined universally, and it may have a complicated dependence on the details of the behavioral feedback and exhibit periodic cycles or chaos.

3. Examples

We emphasize that our results apply to any reactivity function, F, that satisfies A1 - A3. To illustrate our results we introduce three basic examples of reactivity functions.

$$F_{\text{linear}}(a,c)=w_1(1-a)-w_{2}c$$ (2)

$$F_{\text{quadratic}}(a,c)=(1-a)(w_1-w_{2}c)$$ (3)

$$F_{\text{bilinear}}(a,c)=(1-a)(w_1-w_{2}c/a)$$ (4)

These functions all satisfy resilience and boundedness for any w₁, w₂ > 0 and we illustrate them in the top row of Fig. 2 for w₁ = 0.1 and w₂ = 10. The first two functions (2, 3) are important because they are the leading order approximation of any reactivity function. Note that the function F_quadratic is quadratic in a since c = aBsi and similarly F_bilinear is bilinear in a and i. In the Supplement we show that the simplest model, F_linear, does not have a baseline endemic equilibrium because T₂ = T₁. Both F_quadratic and F_bilinear have T₂ < T₁, so for vaccination rates between these thresholds the baseline endemic is stable.

The primary difference between the three example reactivity functions is how quickly the equilibrium level of activity falls off as vaccination rate decreases (Fig. 2). For F_linear the activity versus vaccination curve is concave down, and this moderate response results in a new normal infection rate that increases rapidly as vaccination rate decreases (Fig. 2). For F_quadratic equilibrium activity increases linearly with vaccination rate. This model has the interesting feature that a decrease in vaccination rate leads to a decrease in activity that maintains a constant level of infection in the new normal endemic. Finally, F_bilinear has the most robust behavioral response, with a concave up increase in activity as vaccination rate increases. This response results in infection rate increasing as vaccination rates increase. Thus, when initially introducing a vaccination to a population the infection rate may initially increase until the critical vaccination rate threshold T₂ is reached and the baseline endemic is stabilized. This will especially be the case for a new vaccination that is being gradually rolled out, since a slow change in the vaccination rate can help keep the system near equilibrium as the new normal shifts.

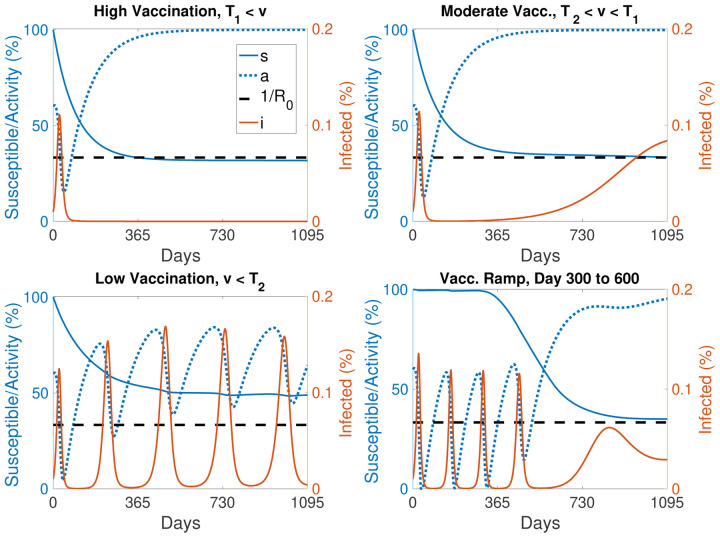
Finally, we note a fascinating feature of F_bilinear. If we consider the fraction of the population that remains susceptible to infection as approximately constant and set 1−a as ‘distancing’, then we recover a form equivalent to the Lotka-Volterra predator-prey model where infections, i, play the role of prey and distancing, 1−a, plays the role of the predator (Supplement equation (12)). Oscillations are present at the beginning of the epidemic, when the susceptible population is large and almost constant. The oscillations are not damped, but they have a very slow decay due to the slow decrease in the susceptibles. Finally, the model exhibits a phase transition when the the susceptible population drops below $\frac{1}{R_0}$, at which point the predator-prey oscillations cease and the system reverts to a more typical epidemic trajectory allowing the system to come to equilibrium. These oscillations depend on the vaccination rate (Fig. 3, Fig. S.2). This illustrates how behavioral feedback can lead to a wide range of epidemic dynamics including oscillations that are independent of any external (e.g. seasonal) forcing.

Figure 3: Introducing resilient activity accounts for a wide range of epidemic dynamics.

Examples of the dynamics of the reactivity function F_bilinear with high vaccination (top left, v > T₁), moderate vaccination (top right, v between T₂ and T₁), and low vaccination (bottom left, v < T₂). Finally (bottom right) we simulate 300 days without any vaccination followed by a linear ramp up in vaccination between days 300 and 600 to a fixed moderate vaccination rate after day 600. Susceptible population, s (solid blue), activity level, a (dotted blue), and the phase transition level $R_0^{-1}$ (dashed black) are scaled to the left axis while the infected population, i (solid red) is scaled to the right axis. (See equation (17) in the Supplement for details and Fig. S.2 for more examples.)

4. Discussion

We have shown that for a broad range of behavioral feedbacks between the incidence of infection and activity that contributes to transmission (e.g. contact rates or hygiene) there exist two novel equilibria in addition to the classic vaccine-based herd immunity threshold. While coordinated behavioral interventions may be sufficient to drive incidence to 0, e.g. as was seen for SARS-CoV-1 in 2004 (24), and Ebola outbreaks (25) prior to the incorporation of vaccination in outbreak response 2017 (26), such interventions alone cannot stabilize the disease-free equilibrium if behavior exhibits resilience. In the absence of vaccination there are no stable equilibria that have a return to normal activity. SARS-CoV-1 is the rare example of a pathogen that emerged and was eradicated in the absence of a vaccine; however, reintroduction from an animal reservoir remains possible (23) and the relaxation of the behavioral interventions (24) render the current disease-free state unstable (27).

The newly identified regime with vaccination between T₂ and T₁ has substantial policy implications for emerging infections and eradication. In the absence of vaccines, non-pharmaceutical interventions remain an important part of pandemic response for emerging infections and can be onerous. The SARS-CoV-2 pandemic led to dramatic economic (28) and educational (29, 30) consequences. Planning for a safe return to pre-emergence activity can minimize these off-target effects. While eradication may still be a goal, vaccination at a level T₂ lower than the classic herd immunity threshold T₁ permits a return to pre-emergence activity while maintaining a stable, non-zero incidence. Furthermore, attaining T₁ may be challenging, particularly in the face of vaccine hesitancy, vaccine administration logistics, or uncertainty about the rate of loss of immunity. The existence of T₂ suggests a midpoint goal for vaccination rate that can be used to motivate vaccination efforts.

The existence of the vaccination regime between T₂ and T₁ may further be useful in policies for endemic infections. The only benefits to vaccination in the standard SIR modeling framework without behavioral feedbacks are reductions in morbidity and mortality. This new model implies additional societal change, in the form of the increased activity, that may be stabilized at or above a lower vaccination threshold T₂. Whether this represents a societal benefit or not will be highly epidemic specific. For example, vaccination rates above T₂ may allow for relaxation of pre-screening requirements and the costs inherent in such programs. Alternatively, one could imagine an increase in risky behaviors, e.g. decreased mask usage as vaccination increases. The positive correlation between vaccination rate and equilibrium incidence under the F_bilinear function could lead to population level assessment of vaccine failure driven by the behavioral response. Any specific predictions of such phenomena is speculative without a mechanistic understanding of the explicit nature of the feedbacks. For example Funk et al. (19) considered that information, and thus behavioral response, may only be available locally rather than globally and Weitz et al. (13) considered that behavioral response may react to the incidence of mortality rather than infection. The general extension of the standard modeling framework for infectious diseases that we have proposed offers a pathway to guide more specific mechanistic investigations.

The description of these new equilibria represents a novel advance for infectious disease and vaccination policy development. A stable equilibrium provides a policy target where the system is self-managing and self-maintaining. The existence of such a stable target allows optimal policy strategies to be formulated to reach that point. Policy formulation without such an explicit goal requires iterative trial-and-error which may incur economic or societal costs that can undermine support for the process. Such adaptive control strategies built upon iterative learning have a long history (31–33) and are useful tools complemented by our results showing that there are multiple advantageous stable equilibria (disease-free or endemic) allowing a return to normal behavior. In the face of uncertainty about the feasibility of elimination, the endemic state with return to normal behavior provides a valuable new policy target to motivate action and guide policy development.