On a barrier height problem for RNA branching

Abstract

The branching of an RNA molecule is an important structural characteristic yet difficult to predict correctly, especially for longer sequences. Using plane trees as a combinatorial model for RNA folding, we consider the thermodynamic cost, known as the barrier height, of transitioning between branching configurations. Using branching skew as a coarse energy approximation, we characterize various types of paths in the discrete configuration landscape. In particular, we give sufficient conditions for a path to have both minimal length and minimal branching skew. The proofs offer some biological insights, notably the potential importance of both hairpin stability and domain architecture to higher resolution RNA barrier height analyses.

1. Introduction

An RNA sequence is said to fold into a secondary structure via the formation of (noncrossing, canonical) base pairings. There are many possible secondary structures for a given sequence, but the most biologically relevant typically have a low free energy approximation under the nearest neighbor thermodynamic model (NNTM). The barrier height problem [18] then considers the thermodynamic cost of transitioning between low-energy configurations. Progress has typically focused on steps consisting of adding/removing a base pair, c.f. [7, 16, 26] and related work discussed therein. Here, we take a complementary approach, focusing on larger structural rearrangements by using plane trees as a combinatorial model of RNA branching configurations.

A plane tree is a rooted tree whose subtrees are linearly ordered [25]. Also know as ordered or linear trees, they are one of the many combinatorial families enumerated by the Catalan numbers. Depending on the question of interest, there are different ways¹ of associating RNA secondary structures with trees in general, e.g. [8], and plane trees in particular, e.g. [24]. As done in other branching analyses [1, 2, 10, 13], we take a low-resolution approach, associating helices to edges and loops to vertices with the external loop as the distinguished root vertex.

A plane tree is thus an abstract representation of an arbitrary RNA secondary structure. By focusing on the overall arrangement of edges/helices and vertices/loops, mathematical results have provided insight into the challenge of designing RNA sequences with a particular branching structure [10], configurations which minimize loop energy costs [1, 2], and a parametric analysis of the branching entropy approximation [13]. This work has lead both to better understanding of RNA prediction accuracy [3, 20, 21] as well as some new combinatorics [12].

Here, we extend this theoretical branching analysis to consider folding pathways between plane trees. We move from one tree to another under a “pairing exchange” operation inspired by the challenge of encoding a particular branched structure in a sequence [11, 10]. Under a coarse approximation to the thermodynamics (branching skew), combinatorial analysis of different types of transition paths is possible in this model of RNA folding. The proofs offer some biological insights.

First, there is a direct path between any two trees, i.e. one where each step increases the number of edges from the final tree by at least one. The edges incident on a leaf are the crucial first steps in such a path, and indeed the stability of RNA hairpins is a critical component of biological function [4] and modeling accuracy [28]. Hence, a suitable model for hairpin rearrangements [29] may be an important component of a higher resolution barrier height analysis.

Second, the branching skew of a direct path is provably bounded when the edges of the two trees decompose into consistent blocks that can rearrange from initial to final configurations independent of each other. This suggests that modeling the domain architecture of RNA secondary structures, which emerges in the folding of longer sequences [14, 19, 23], may be critical to the analysis of optimal folding pathways.

2. Pairing exchanges and branching skew

Let 𝒯_n denote the set of plane trees with n edges. Then $\left|{𝒯}_n\right|=\frac{1}{n+1}\left(\begin{array}{c}2n\\ n\end{array}\right)$, the n-th Catalan number. Motivated by RNA secondary structures, we consider T ∈ 𝒯_n to be a set of paired half-edges. For i, $j\in \mathbb{N}$, let $[i,j]=\{k\in \mathbb{N}\mid i\le k\le j\}$. Label the boundary of T counter-clockwise from the root with [1, 2n] in increasing order. Let (i, j) denote the edge in T which has i as the label on its left side and j on the right for 1 ≤ i < j ≤ 2n.

Lemma 1. A set I = {(i, j) | 1 ≤ i < j ≤ 2n} is a plane tree when each index appears in exactly one ordered pair and there do not exist (i, j),(i′, j′) ∈ I with i < i′ < j < j′.

Proof. Consider (1, k) ∈ I. If k is odd, then either there exists an (i, j) ∈ I with 1 < i < k < j or an index in [2, k − 1] that is unpaired or in more than one pairing. Since k must be even, induct on the pairings with indices in [2, k − 1] and [k + 1, 2n]. □

In other words, there is a simple bijection between noncrossing perfect matchings on 2n endpoints and plane trees with n edges. Previous work [12] considered the comparable operation on matchings to the pairing exchange defined below with the goal of better understanding meanders (interpreted as pairs of noncrossing perfect matchings which form a single closed loop).

Here we consider plane trees as a low-resolution model of RNA secondary structures, and analyze (very approximately) the thermodynamic cost of moving around this branching configuration landscape. Inspired by the challenge of minimizing alternative lower-energy configurations when designing RNA secondary structures (c.f. Fig. 1 in [10]), we transition from one tree to the next by breaking apart and “repairing” two edges.

We start by applying to edges in T the common familial terminology for vertices in rooted trees, i.e. parent/child, siblings, ancestor/descendent, etc. Additionally, an edge incident on the root vertex is called an orphan. Two edges in T are unobstructed if they are incident on the same vertex, in which case they are either parent/child or siblings.

We define a pairing exchange on unobstructed edges E = {(i, j), (i′, j′)} ⊆ T as

$${\mu }_E(T)=(T\backslash E)\cup \left\{\begin{array}{ll}\left(i,i^{\prime }\right)\text{and}\left(j^{\prime },j\right)\hfill & \text{if}i<i^{\prime }<j^{\prime }<j\hfill \\ \left(i,j^{\prime }\right)\text{and}\left(j,i^{\prime }\right))\hfill & \text{if}i<j<i^{\prime }<j^{\prime }\hfill \end{array}\right\}$$

and claim that converting a parent/child into siblings, or vice versa, introduces no crossings.

Lemma 2. The pairing exchange operation is well-defined.

Proof. Let 1 ≤ a < b < c < d ≤ 2n be the indices of two edges in T. Let A = [1, a − 1] ∪ [d + 1, 2n], B = [a + 1, b − 1], C = [b + 1, c − 1], and D = [c + 1, d − 1]. Observe that if the edges are (a, d) and (b, c), then all other edges must have indices in either A or in B ∪ D or in C exclusively. However, if (a, d) and (b, c) are parent and child, then there cannot be an edge (k, l) with k ∈ B and l ∈ D. A similar argument holds if (a, b) and (c, d) are siblings. □

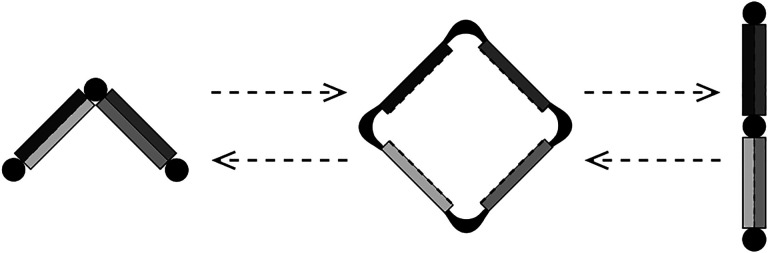
As illustrated in Figure 1, pairing exchanges are reversible operations. Let 𝒢_n be the (undirected) graph with vertex set 𝒯_n and edges which connect two plane trees that differ by a single pairing exchange.

Figure 1:

A pairing exchange on unobstructed edges with indices 1 ≤ a < b < c < d ≤ 2n converts siblings (a, b), (c, d) into parent/child (a, d), (b, c), and vice versa. Note how the incident vertices split and merge. However, edges in the four subtrees with indices exclusively in A = [1, a − 1] ∪ [d + 1, 2n], B = [a + 1, b − 1], C = [b + 1, c − 1], or D = [c + 1, d − 1] are unaltered.

Before proving that 𝒢_n is connected, we distinguish two trees which have the maximum degree of $\left(\begin{array}{l}n\hfill \\ 2\hfill \end{array}\right)$ in 𝒢_n. Let U_n = {(2i − 1, 2i) | 1 ≤ i ≤ n} and L_n = {(1, 2n)} ∪ {(2i, 2i + 1) | 1 ≤ i ≤ n − 1}. Then U₁ = L₁, and 𝒢₁ consists of a single vertex. For n ≥ 2, U_n and L_n differ in the choice of root; both are “star” trees with n unobstructed edges.

Lemma 3. The graph 𝒢_n is connected.

Proof. We claim there is a path in 𝒢_n from T to U_n. If (1, 2) ∈ T, then inductively the subtree with indices in [3, 2n] is connected by pairing exchanges to U_n−1. Else the edges (1, k),(2, l) ∈ T are unobstructed, and there is an edge in 𝒢_n between T and [T \{(1, k),(2, l)}]∪{(1, 2),(k, l)}. □

Dually, T is connected to L_n by first considering the edge (1, 2n), and then successive (2i, 2i + 1). Thus, any two trees are connected by a path through U_n or one through L_n. Unless a star tree is one of the endpoints, the path is indirect since it effectively erases most pairing information in the first tree before replacing it with second. Moreover, although mathematically simple, these are the highest possible barrier paths in terms of branching thermodynamics.

Previous results [2, 11, 13] demonstrated that branching is locally favorable but globally balanced by increasing the number of leaves — since hairpins are the most energetically expensive type of loop structures [27]. Hence, a low barrier path in 𝒢_n passes through trees with a low degree of branching. Since tracking changes in branching degree under pairing exchanges is complicated, we instead consider “branching skew.”

We start by defining the parity of an edge. Since (i, j) ∈ T has $\frac{j-i-1}{2}$ descendents, exactly one of i and j is odd. Call the edge odd if i is, and even otherwise. Let c(T) denote the number of odd edges in T. Then 1 ≤ c(T) ≤ n, with c(T) = 1 exactly when T = L_n and n only if U_n. Moreover, a pairing exchange alters the number of odd edges by exactly one. An example is seen in Figure 2.

Figure 2:

The graph 𝒢₃ with L₃ on left, U₃ on right, and the three plane trees T ∈ 𝒯₃ with c(T) = 2 in the middle. Dashed lines are pairing exchanges. The number of odd edges increases by 1 moving left to right.

Note that edge parity along a path in T from the root vertex to a leaf must alternate, and all orphan edges are odd. Hence, if c(T) = k, then the maximum possible vertex degree in T is either k or n − k + 1. A tree which achieves this is k orphans with one having n − k even children. Thus, c(T) is well-behaved under pairing exchanges, and yields an upper bound, seldom tight, on vertex degree.

More precisely, we are interested in minimizing the maximum possible vertex degree over paths in 𝒢_n. Define the skew of T to be $\left|c(T)-\frac{n+1}{2}\right|$. This is maximal at both U_n and L_n, and decreases to a minimum of 0 or 1/2 when the number of odd and even edges are most evenly balanced. The skew of a path T = T₀, T₁, …, T_k = T′ is ${\text{max}}_{0\le m\le k}\left|c\left(T_m\right)-\frac{n+1}{2}\right|$.

Call a pairing exchange a forward move if c(T) increases, and backward otherwise. In Section 4, we characterize when there is a path from T to T′ consisting only of forward moves. Call this a forward path, and the reverse a backward one. Such a path has the least increase in skew possible given the start and end.

Lemma 3 showed that, even if there is not a forward path from T to T′, they are still connected by a pair of forward paths through U_n. Dually, backward through L_n. More generally, we call a path from T to T′ a forward V-path (respectively backward) if there exists S ∈ 𝒯_n with S ≠ T, T′ such that there is a forward (resp. backward) path from T to S and also from T′ to S. In Section 5, we characterize the minimal skew V-paths, and make explicit in Section 6 the connection with the well-studied lattice of noncrossing partitions.

In Section 7, we show that when forward and backward moves are interspersed, it is possible to have paths in 𝒢_n whose skew exceeds the start and end by at most 1. We conclude in Section 8 by characterizing shortest paths, and proving that their skew is similarly bounded under certain conditions.

3. Introducing tree partitions

Since a plane tree T is specified as a collection of paired half-edges {(i, j) | 1 ≤ i < j ≤ 2n}, we distinguish when a subset S ⊆ T is a subtree, denoted S ⊑ T. When S is connected, by a generalization of Lemma 2, an edge in T \ S has either both or neither indices in an interval between the ordered indices of S. Hence, pairing exchanges on S and its subsequent images are independent of all other edges in T.

Because each edge has exactly one odd index, subsets of T ∈ 𝒯_n are in bijection with subsets of O_n = {1, 3, …, 2n − 1}. For P ⊆ O_n, let σ(T, P) = {(i, j) ∈ T | i ∈ P or j ∈ P}. Let 𝒫 be a (set) partition of O_n. We distinguish when the parts of 𝒫 decompose T into subtrees.

Definition 1. Say 𝒫 splits T if σ(T, P) ⊑ T for every P ∈ 𝒫.

The trees U_n and L_n are split by any 𝒫, since all edges are incident on a common vertex. However, suppose there exists P ∈ 𝒫 and odd integers i < j < k (circularly ordered) such that i, k ∈ P and j ∉ P. Let T = μ_E(U_n) for E = {(j, j + 1), (k, k + 1)}. Then (j, k + 1) obstructs (j + 1, k) from (i, i+1) in T, and so 𝒫 does not split T. Hence, there are exactly two partitions which split every T ∈ 𝒯_n: {O_n} and {{2i − 1} | 1 ≤ i ≤ n}. The latter will be referred to as the singleton partition, and the former as the trivial one.

To characterize paths in 𝒢_n from T to T′, we consider partitions of O_n which split both trees. However, we must insure that the even indices also partition in the same way. For S ⊆ T, let $\alpha (S)={\cup }_{(i,j)\in S}\{i,j\}$ be the collection of indices. Denote the odd ones by α₁(S), respectively α₂(S) for the even.

Definition 2. The subsets S ⊆ T, S′ ⊆ T′ are aligned if α(S) = α(S′). The alignment is simple if no proper subsets of S and S′ are also aligned.

The simply aligned subsets correspond to connected components in the graph with vertices in [1, 2n] and edges in T ∪ T′. It is known [12] that a pairing exchange either splits a connected component into two or joins two disjoint ones. Hence, the number of simply aligned subsets changes by exactly 1 across each edge {T, T′} ∈ 𝒢_n.

Observe that if T and T′ decompose into k pairs of aligned subtrees S_m ⊑ T, $S_m^{\prime }⊑T^{\prime }$, then there is a path in 𝒢_n from T = T₀ to T′ = T_k through $T_m=\left(T_{m-1}\backslash S_m\right)\cup S_m^{\prime }$. In other words, pairing exchanges on distinct aligned subtrees are independent.

Since σ(T, P) and σ(T′, P) have the same odd indices by definition, let ϵ(T, P) = α₂(σ(T, P)). Then the induced subtrees are aligned exactly when ϵ(T, P) = ϵ(T′, P).

Definition 3. Let 𝒫 be a partition of O_n and 𝒮 ⊆ 𝒯_n. Suppose 𝒫 splits every T ∈ 𝒮. Suppose further that ϵ(T, P) = ϵ(T′, P) for every T, T′ ∈ 𝒮 and P ∈ 𝒫. Then 𝒫 is a tree partition of 𝒮.

While the trivial partition meets the alignment criteria for any T and T′, the singleton one fails unless T = T′.

Recall that set partitions form a lattice, partially ordered under refinement. Here we take the singleton partition of O_n as the minimum element since it induces subtrees with the fewest number of edges. The trivial partition, which is a tree partition for any 𝒮 ⊆ 𝒯_n, is then the maximum. This lattice will be denoted (O_n, ∩).

Lemma 4. For 𝒮 ⊆ 𝒯_n, there is a unique tree partition of 𝒮, denoted π(𝒮), minimal in (O_n, ∩).

Proof. Suppose 𝒬 ≠ 𝒬′ are both minimal and let 𝒫 be their greatest lower bound under refinement. Let P ∈ 𝒫. Then P = Q ∩ Q′ for some Q ∈ 𝒬, Q′ ∈ 𝒬′.

Let T ∈ 𝒮, and suppose (k, l) ∈ T lies on the path between (i, j), (i′, j′) ∈ σ(T, P). Since σ(T, X) ⊑ T for X = Q, Q′, then (k, l) ∈ σ(T, P). Since the edges in T with odd endpoints in P are connected, 𝒫 splits T.

Let i ∈ ϵ(T, P). Let T′ ∈ 𝒮, and suppose i pairs with j in T′. Since ϵ(T, P) = ϵ(T′, P), then j ∈ Q. Likewise for Q′. Hence j ∈ P, and i ∈ ϵ(T′, P). Since the induced subtrees are aligned, 𝒫 is a tree partition of 𝒮. Contradiction. □

When 𝒮 = {T, T′}, write π(T, T′). To produce π(T, T′), we can start with the simply aligned subsets. For example, consider T = {(1, 8), (2, 7), (3, 6), (4, 5)} and T′ = {(1, 4), (2, 3), (5, 8), (6, 7)}. The aligned subsets have α(S) = {1, 4, 5, 8}, α(S′) = {2, 3, 6, 7} and induce the partition of O_n with parts α₁(S), α₁(S′). However, σ(T, {1, 5}) ⋢ T and σ(T′, 3, 7) ⋢ T′. To obtain a partition which also splits these trees, it suffices to take the union of α₁(S) and α₁(S′).

More generally, let {S_i} be the simply aligned subsets for 𝒮 ⊆ 𝒯_n, i.e. connected components in the graph on [1, 2n] with all edges from T ∈ 𝒮. Then 𝒫 = {α₁(S_i)} satisfies the tree partition alignment condition by definition. Moreover, any enlargement of 𝒫 in (O_n, ∩) is still aligned. If σ(T, P) is not connected for some T ∈ 𝒮, P ∈ 𝒫, then there is an edge (k, l) ∉ σ(T, P) on the path in T between some (i, j), (i′, j′) ∈ σ(T, P). But this can be addressed by enlarging P to include α₁(S_i) where (k, l) ∈ σ(T, α₁(S_i)). Inductively, π(𝒮) is the unique least enlargement of 𝒫 where the induced subtrees are all connected. Note also that π(S) is an enlargement of π(S′) for every S′ ⊂ S.

4. Characterizing forward paths

We consider when T is connected to T′ by a sequence of forward moves, i.e. pairing exchanges which increase c(T) by 1. As proved in Lemma 3, there is a forward path from T to U_n, and dually one backward down to L_n. Since pairing exchange alters c(T) by exactly 1, with c(L_n) = 1 and c(U_n) = n, then the former has length n − c(T), and the latter c(T) − 1.

Call two trees, like U_n and L_n, complementary if there is only one simply aligned subset. Such trees will be considered more generally in Section 8. Now we show there is a forward path from T to T′ exactly when there is a tree partition which splits them into pairs of complementary “star” subtrees.

For S ⊆ T, let c(S) denote the number of odd edges. If S is connected, then S ⊑ T is isomorphic to S′ ∈ 𝒯_|S| under an order-preserving bijection on its indices. We distinguish whether edge parity is preserved or reversed, denoted S ≃₀ S′ or S ≃₁ S′ respectively. When preserved, c(S) = c(S′). If reversed, c(S) = |S| − c(S′).

Definition 4. The tree T has a minmax decomposition with T′, denoted T → T′, if there exists a tree partition 𝒫 such that, for every P ∈ 𝒫 with |P| = p, σ(T, P) ≃₀ L_p, σ(T′, P) ≃₀ U_p or σ(T, P) ≃₁ U_p, σ(T′, P) ≃₁ L_p.

In other words, if the odd (and even) indices of T and T′ partition so that the induced subtrees are isomorphic to the star tree, with opposite choices of root determined by the edge parity, then they have a minmax decomposition. Note that T → T under the singleton partition and U₁ = L₁ = {(1, 2)}. Dually, L_n → U_n under the trivial partition. If T → T′, then the induced subtree of T′ has p − 1 more odd edges than the one in T. Hence, c(T) ≤ c(T′).

Call (i, j) ∈ T ∩ T′ a common edge. Equivalently, {(i, j)} is a simply aligned subset, or the induced subtree for a singleton part of π(T, T′).

Theorem 1. There is a forward path from T to T′ in 𝒢_n if and only if T → T′.

Proof. Let T = T₀, T₁, …, T_k−1, T_k = T′ be a forward path in 𝒢_n. At each step, either an odd parent/even child are converted into two odd siblings, or two even siblings are changed into an even parent/odd child.

Let 𝒫₁ be the partition which is all singletons, except for a doubleton P which consists of the odd indices involved in the pairing exchange on T. If the exchange started with parent/child, then σ(T, P) ≃₀ L₂ and σ(T₁, P) ≃₀ U₂. Otherwise, σ(T, P) ≃₁ U₂ and σ(T₁, P) ≃₁ L₂.

Assume after m steps that T has a minmax decomposition with T_m for tree partition 𝒫_m. Then an induced subtree in T_m contains either no even edges or exactly one even parent. Hence the next forward pairing exchange necessarily involves edges associated with distinct parts. Let T_m+1 = μ_E(T_m) for E = {(i, j),(i′, j′)}. Then (i, j) ∈ σ(T_m, P) and (i′, j′) ∈ σ(T_m, P′) for P, P′ ∈ 𝒫_m with P ≠ P′, |P| = p and |P′| = p′.

Suppose (i, j),(i′, j′) ∈ T_m are even siblings with i < j < i′ < j′. Then j ∈ P and (i, j) is the parent in σ(T_m, P) ≃₁ L_p, and similarly for (i′, j′) and P′. After the pairing exchange, we have T_m+1 = (T_m \ {(i, j), (i′, j′)}) ∪ {(i, j′), (j, i′)}. The even edge (i, j′) is the parent of (j, i′) as well as of all the odd children of (i, j) in σ(T_m, P) and of (i′, j′) in σ(T_m, P′). Hence σ(T_m+1, P ∪ P′) is a subtree of T_m+1 and by construction ≃₁ L_p+p′.

Consider the partition 𝒫_m+1 = (𝒫_m\{P, P′})∪{P ∪ P′}. If the even siblings comprising σ(T, P) and σ(T, P′) have the same parent, then σ(T, P ∪ P′) ⊑ T. By construction the subtree is aligned with σ(T_m+1, P ∪ P′) and ≃₁ U_p+p′.

Otherwise, let (k, l) ∈ T be the odd parent of σ(T, P) ≃₁ U_p. By the alignment criteria, P ∪ ϵ(T, P) ⊆ [i, j] since (i, j) ∈ σ(T_m, P) is the even parent. Hence, 1 ≤ k < i < j < l ≤ 2n. Without loss of generality, (k, l) is not an ancestor of σ(T, P′). But then, since i < i′ by assumption, l ∈ [j + 1, i′ − 1].

Let Q ∈ 𝒫_m such that (k, l) ∈ σ(T, Q). By induction, an induced subtree of T has either zero or one odd edge. Hence, σ(T, Q) ≃₀ L_|Q| and so σ(T_m, Q) ≃₀ U_|Q|. Let K = [k, i − 1] and L = [j + 1, l]. Suppose there is (k′, l′) ∈ σ(T_m, Q) with k′ ∈ K, l′ ∈ L. But this obstructs (i, j) from (i′, j′). Hence there are an even number of indices from σ(T_m, Q) in K and in L. But then by counting there is a child (k′, l′) ∈ σ(T, Q) with k′ ∈ K and l′ ∈ L, contradicting the choice of (k, l). Thus, if the pairing exchange on T_m began with two even siblings, then T → T_m+1.

Suppose instead (i, j) is the odd parent of (i′, j′) in T_m. Then i < i′ < j′ < j and T_m+1 = (T_m \ {(i, j), (i′, j′)}) ∪ {(i, i′), (j′, j)}. Before the pairing exchange, although σ(T_m, P′) ≃₁ L_p′ as before, σ(T_m, P) may be either ≃₀ U_p or ≃₁ L_p. In either case, the new edges in T_m+1 are odd siblings, along with the former odd siblings of (i, j) and odd children of (i′, j′). Hence, σ(T_m+1, P ∪ P′) ≃₁ L_p+p′ or ≃₀ U_p+p′ according to whether the even parent of (i, j) is in σ(T_m, P) or not.

If the edges of σ(T, P ∪ P′) are not connected in T, then by the same type of argument as above, we arrive at a contradiction. Since σ(T, P ∪ P′) ⊑ T, then either ≃₁ U_p+p′ or ≃₀ L_p+p′ respectively. Since all other parts of the partition were unchanged, 𝒫_m+1 is a tree partition yielding a minmax decomposition for T with T_m+1.

Conversely, suppose T → T′ with tree partition 𝒫. Let S = σ(T, P) and S′ = σ(T, P′) for P ∈ 𝒫 with |P| = p ≥ 2. Suppose S ≃₀ L_p and S′ ≃₀ U_p. There is a forward path of length p − 1 from L_p to U_p in 𝒢_p. Operating on the corresponding edges in S, while keeping T \ S fixed, there is a forward path from T to T″ = (T \ S) ∪ S′ in 𝒢_n. Dually, the backward path in 𝒢_p becomes a forward one when S ≃₁ U_p and S′ ≃₁ L_p. Then T″ has p more common edges with T′ than T does. Inductively, the other pairs of induced subtrees are unchanged. Hence T″ → T for the tree partition 𝒬 = (𝒫 \ {P}) ∪ {{q} | q ∈ P}. □

Suppose T → T′. Then the forward path’s branching skew is $\text{max}\left\{\left|c(T)-\frac{n+1}{2}\right|,\left|c\left(T^{\prime }\right)-\frac{n+1}{2}\right|\right\}$ depending on whether c(T) − 1 < n − c(T′). Hence, it has the least possible barrier height given the start and end points. In this case, by construction, there is a bijection between parts of π(T, T′) and simply aligned subsets. So the path’s length is ∑|P| − 1 = n − k, when there are k parts P ∈ π(T, T′). This is the shortest possible, and is generalized to geodesics between all trees in Section 8. However, bounding the branching skew when T ↛ T′ is more challenging, and we consider several different types of paths.

5. Characterizing minimal skew V-paths

Even if T ↛ T′, they are still connected by a forward V-path of length 2n − c(T) − c(T′) through U_n, respectively backward of length c(T) + c(T′) − 2 through L_n. These paths have the maximum possible skew of $\frac{n-1}{2}$, and hence represent the highest barrier in branching thermodynamics. However, this can be reduced in many cases by restricting the rearrangements to suitable subtrees.

We beging by introducing some additional notation and terminology. Let 𝒫 be a tree partition of 𝒮 ⊆ 𝒯_n. For P ∈ 𝒫, let min P be the least index in P ∪ ϵ(T, P) and max P the greatest. By the alignment criteria, these are well-defined. Note they have opposite parity. Call P odd if min P is, and even otherwise. Let (i, j), (i′, j′) ∈ T. Call (i′, j′) the first child of (i, j) if i′ = i + 1, respectively last if j′ + 1 = j. Say (i′, j′) is the next sibling of (i, j) if i′ = j + 1, or previous if j′ + 1 = i.

Theorem 2. Suppose T → T′. Then π(L_n, T′) is a tree partition of T and T′.

Proof. Let 𝒫 = π(T, T′), 𝒬 = π(L_n, T′), and Q ∈ 𝒬. We show that 𝒬 is an enlargement of 𝒫, which implies ϵ(T, Q) = ϵ(T′, Q), and that σ(T, Q) ⊑ T.

To start, we characterize how 𝒬 splits T′. Let S′ = σ(T′, Q). Since L_n → T′, then S′ ⊑ T′ consists of some odd siblings or an even parent with some odd children. We claim that an odd edge is in the same induced subtree as all its sibling along with its even parent (if it has one).

Let 1 ∈ Q. Then S′ ≃₀ U_|Q|. Consider orphan (i, j) ∈ T′ \ S′ with least i > 1. But then its previous sibling (k, i − 1) ∈ S′ which contradicts alignment of 𝒬 since (i − 1, i) ∈ L_n. Hence S′ consists of all orphans in T′. By a similar argument, if 1 ∉ Q, then S′ ≃₁ L_|Q| consists of an even parent and all its odd children.

Suppose (i, j) ∈ T′ is an even edge with j ∈ P ∩ Q for P ∈ 𝒫. But then σ(T′, P) ≃₁ L_|P| since T → T′ by assumption. Hence (i, j) is the parent in σ(T′, P) ⊆ S′, so P ⊆ Q. If P = Q, then σ(T, Q) ⊑ T also, and ϵ(T, Q) = ϵ(T′, Q).

Otherwise, let (i′, j′) ∈ S′ \ σ(T′, P) with least i′ > i, and consider P′ ∈ 𝒫 with i′ ∈ P′. Since (i′, j′) is an odd child of (i, j) ∈ T′, then σ(T′, P′) ≃₀ U_|P′|. Thus, P′ ⊂ Q. Moreover, σ(T′, P ∪ P′) ⊑ T′ and ≃₁ L_|P|+|P′| by construction.

We claim that σ(T, P ∪ P′) ⊑ T also. Note min P′ = i′ odd. Let max P′ = j″ for 1 < i < i′ < j′ ≤ j″ < j < 2n. Since σ(T, P′) ≃₀ L_|P′|, then (i′, j″) ∈ T is the odd parent. By choice of i′, there exists (i′ − 1, k) ∈ σ(T, P) ≃₁ U_|P| with j″ < k ≤ j. Hence, (i′, j″) is the first child of (i − 1, k), and σ(T, P′) is connected to σ(T, P).

Inductively, Q is the union of P ∈ 𝒫. Since ϵ(T, P) = ϵ(T′, P), then σ(T, Q) is aligned with σ(T′, Q). Connectivity of σ(T, Q) follows by building the enlargement in order of the missing odd children of (i, j) ∈ T′. Such a child belongs to σ(T′, P) ≃₀ U_|P| for odd P ∈ 𝒫. But then σ(T, P) ≃₀ L_|P|. By choice of P, the odd parent in each additional σ(T, P) must be the first child of some even child, or the next sibling of an odd parent, already in the growing induced subtree. The case when 1 ∈ Q proceeds along similar lines beginning with P ∋ 1. □

Corollary 3. Let S ∈ 𝒯_n. Then T → S and T′ → S if and only if there exists a tree partition 𝒫 of T, T′, and S such that, for P ∈ 𝒫, σ(S, P) ≃₀ U_|P| for P odd and ≃₁ L_|P| otherwise.

Proof. Suppose T, T′ → S. Let 𝒫 = π(L_n, S). Then by the proof of Theorem 2, 𝒫 splits S as desired. Also σ(T, P) ⊑ T, σ(T′, P) ⊑ T′, and ϵ(T, P) = ϵ(S, P) = ϵ(T′, P′). For the converse, it suffices to observe that pairing exchanges on distinct aligned subtrees are independent. □

Note that π(L_n, S) is an enlargement of both π(L_n, T) and π(L_n, T′). However, it is not necessarily the least enlargement in (O_n, ∩). For example, consider again T = {(1, 8), (2, 7), (3, 6), (4, 5)} and T′ = {(1, 4), (2, 3), (5, 8), (6, 7)}. Then π(L_n, T) = {{1}, {3, 7}, {5}} whereas π(L_n, T′) = {{1, 5}, {3}, {7}}. Their only forward V-path is through U_n.

Theorem 4. There is a unique S ∈ 𝒯_n with c(S) minimal such that T → S and T′ → S.

Proof. Let 𝒫 = π(T, T′). For P ∈ 𝒫 with |P| = p, let P = {i₁, …, i_p} and ϵ(T, P) = {j₁, …, j_p} in increasing order. If P odd, then i₁ < j₁ < i₂ < …i_p < j_p. Otherwise, j₁ < … < i_p. Define λ(P) = {(i_k, j_k) | 1 ≤ k ≤ p} for P odd, else {(j₁, i_p)} ∪ {(i_k, j_k+1) | 1 ≤ k < p}. Let $S={\cup }_{P\in 𝒫}\lambda (P)$.

We claim S ∈ 𝒯_n. As constructed, each index from [1, 2n] appears in exactly one ordered pair, and λ(P) contains no crossing. Suppose there are (i, j),(i′, j′) ∈ S with 1 ≤ i < i′ < j < j′ ≤ 2n for distinct P, P′ ∈ 𝒫 with I, j ∈ P ∪ ϵ(T, P), i′; j′ ∈ P′ ∪ ϵ(T, P′).

Let J = [i + 1, j − 1]. Consider (k, l) ∈ σ(T, P′). Suppose either k ∈ J, l ∈ [j + 1, 2n] or k ∈ [1, i − 1], l ∈ J. However, such an edge obstructs the edge in σ(T, P) with index i from the one with j. Hence an edge from σ(T, P′) has both or neither indices in J which implies that σ(T, P′ ∩ J) ⊑ T. The same reasoning holds for T′, contradicting minimality of P′.

By construction, 𝒫 is a tree partition of S as well as T and T′. Moreover, σ(S, P) ≃₀ U_p for P odd, and ≃₁ L_p otherwise. Hence T, T′ → S. Furthermore, S is the only tree which meets the isomorphism requirements in Corollary 3 using 𝒫 as the tree partition.

Let k be the number of even P ∈ 𝒫. Then c(S) = ∑_{P odd} p + ∑_{P even}(p − 1) = n − k. We claim this is least possible.

Suppose T, T′ → S′ for S′ ≠ S. Let 𝒬 be a tree partition satisfying Corollary 3 for S′. Then 𝒬 must be a strict enlargement of 𝒫 in (O_n, ∩). Also c(S′) = n − k′ for 𝒬 with k′ even parts. Let Q = P ∪ P′ for Q ∈ 𝒬, P, P′ ∈ 𝒫. If P and P′ are both odd, then σ(S′, Q) = λ(P) ∪ λ(P). Hence, by choice of S′, k′ < k. □

Exchanging backward moves for forward, and the roles of the star trees, we have the following dual versions of these results.

Corollary 5. Suppose T → T′. Then π(T, U_n) is a tree partition of T and T′.

Proof. Subtrees in T induced by π(T, U_n) consist of an odd parent and all its even children. A similar argument to Theorem 2 shows that π(T, U_n) is an enlargement of π(T, T′), and that the corresponding induced subsets of T′ are subtrees aligned with those in T.

Corollary 6. Let S ∈ 𝒯_n. Then S → T and S → T′ if and only if there exists a tree partition 𝒫 of T, T′, and S such that, for P ∈ 𝒫, σ(S, P) ≃₀ L_|P| for P odd and ≃₁ U_|P| otherwise.

Corollary 7. There is a unique S ∈ 𝒯_n with c(S) maximal such that S → T and S → T′.

Proof. Let 𝒫 = π(T, T′) and define γ(P) = {(i₁, j_p)} ∪ {(j_k, i_k+1) | 1 ≤ k < p} for odd P ∈ 𝒫, and {(j_k, i_k) | 1 ≤ k ≤ p} otherwise. A similar argument to Theorem 4 for $S={\cup }_{P\in 𝒫}\gamma (P)$ holds with c(S) = ∑_{P odd} 1 + ∑_{P even} 0 = k where k is now the number of odd P.

Let λ(T, T′) denote the tree from Theorem 4 and γ(T, T′) the one from Corollary 7. Then these are the “apex” of the forward and backward V-paths with the lowest branching barrier. If the apex of a V-path is S, then its branching skew is $\left|c(S)-\frac{n+1}{2}\right|$ and length is |c(T) + c(T′) − 2 · c(S)|. Hence, the minimal skew one is a function of the number of even and odd parts in π(T, T′), and so is the length. At least one of the V-paths through λ(T, T′) or γ(T, T′) has length at most n − 1, although the other orientation (i.e. forward/backward) could be longer.

6. Connection with noncrossing partitions

The relation T → T′ is a partial order on 𝒯_n with 𝒢_n as its Hasse diagram and c(T) as a rank function. In other words, T′ covers T if T′ = μ_E(T) where E is either an odd parent and even child or two even siblings, i.e. the pairing exchange is a forward move and c(T′) = c(T) + 1. When viewed as a poset, λ(T, T′) and γ(T, T′) are the least upper bound and greatest lower bound, respectively. It is worth noting the symmetry in their construction.

We show that this partial order is isomorphic to the well-known lattice of noncrossing partitions, NC(n). A partition of [1, n] is noncrossing if there does not exists 1 ≤ a < b < c < d ≤ n such that a, c are in one part and b, d in another. Noncrossing partitions are still ordered under refinement. The greatest lower bound remains the largest refinement. However, the least upper bound is the smallest enlargement that is also noncrossing.

Theorem 8. There is an order preserving bijection from 𝒯_n under T → T′ to NC(n).

Proof. Let 𝒩_T be the partition of [1, n] obtained by projecting π(L_n, T) down under θ: 2i−1 → i. Let P, P′ ∈ π(L_n, T). Recall that σ(T, P) consist of an even parent and all its odd children, or all the orphan edges.

Suppose 𝒩_T has a crossing 1 ≤ a < b < c < d ≤ n with a, c ∈ θ(P), b, d ∈ θ(P′), and a, b least possible. Let i′ = min P′, j′ = max P′. Then (i′, j′) is the even parent in σ(T, P′) ≃₁ L_|P′| with 2a − 1 < i′ = 2b − 2 and 2d − 1 ≤ j′ ≤ 2n − 1. But then (i′, j′) obstructs the edge with index 2c − 1 from the one with 2a − 1 in σ(T, P) ⊑ T. Contradiction. Hence 𝒩_T ∈ NC(n).

Suppose now 𝒩 ∈ NC(n). Let N ∈ 𝒩 and consider I_N = {2i − 1, 2i − 2 (mod 2n) | i ∈ N}. Then min I_N is odd exactly when 1 ∈ N. Define the pairings λ(N) on the ordered indices in I_N as in the proof of Theorem 4, and let $T_{𝒩}={\cup }_{N\in 𝒩}\lambda (N)$. We claim that T_𝒩 ∈ 𝒯_n. If so, then π(L_n, T_𝒩 ) projects down to 𝒩 by construction since λ(N) ≃₀ U_|N| when 1 ∈ N and ≃₁ L_|N| otherwise.

Suppose there is (i, j) ∈ λ(N), (k, l) ∈ λ(N′) with 1 ≤ i < k < j < l ≤ 2n. For x ∈ {i, j, k, l}, let x′ be $\frac{x+1}{2}$ in x is odd, and $\frac{x+2}{2}(\text{mod}n)$ otherwise. Then i′, j′ ∈ N, k′, l′ ∈ N′ and either 1 ≤ i′ < k′ < j′ < l′ ≤ n if l ≠ 2n or 1 = l′ < i′ < k′ < j′ ≤ n otherwise. Contradiction. Thus T_𝒩 ∈ 𝒯_n is the unique pre-image of 𝒩.

Let E be two unobstructed edges in T and T′ = μ_E(T). Given how π(L_n, T) splits T, this is a forward move if and only if distinct P, P′ ∈ π(L_n, T) are involved. As in the proof of Theorem 1, π(L_n, T′) \ π(L_n, T) = {P ∪ P′} as a result. But then 𝒩_T′ covers 𝒩_T in NC(n), and the bijection is order-preserving. □

An immediate consequence is that plane trees with k odd edges are equinumerous with noncrossing partitions with n − k + 1 parts, which are counted by the Narayana number $N(n,k)=\frac{1}{n}\left(\begin{array}{l}n\hfill \\ k\hfill \end{array}\right)\left(\begin{array}{c}n\\ k-1\end{array}\right)$. This partition of 𝒯_n differs from the common one according to k leaves [5], yielded by the classic bijections [6, 22] with NC(n). However, a more recent enumerative result [17] gives a bijection via vertices of odd distance from the root, and hence a Narayana decomposition with the same sets.

The correspondence has three related bijections: taking the minimal tree partition with U_n and/or using the even indices to partition T ∈ 𝒯_n. Moreover, the connection between π(L_n, T) and π(T, U_n) yields insight into counting orbits in NC(n) under Kreweras complementation [9, 15].

7. Existence of bounded skew paths

Although V-paths are well-characterized mathematically, their branching skew is biologically unfavorable. Hence, we now show there are paths in 𝒢_n, other than forward ones, having the minimum possible branching skew.

Call a path from T to T′ through T_m bounded if c(T) − 1 ≤ c(T_m) ≤ c(T′) + 1 and tightly bounded if c(T) ≤ c(T_m) ≤ c(T′). The distinction accounts for c(T′) − c(T) ≤ 1. In other words, such a path is bounded away from high branching skew trees to the extent possible given its start and end.

A planted plane tree T has a monovalent root vertex so (1, 2n) ∈ T. Call T doubly planted if (2, 2n − 1) ∈ T also.

Lemma 5. If 1 < c(T) < n, then there is a bounded path from T to a doubly planted T′ with c(T′) = c(T).

Proof. Suppose (1, 2n) ∈ T. If (2, 2n − 1) ∉ T, then a forward move on (2, i), (j, 2n − 1) ∈ T yields a doubly planted T″ with c(T″) = c(T) + 1. There is a backward move on T″ to yield a suitable T′ unless T″ \ {(1, 2n), (2, 2n − 1)} ≃₀ L_n−2. But then T = L_n and c(T) = 1.

Otherwise, a backward move on (1, i), (j, 2n) ∈ T yields a planted T″ with c(T″) = c(T) − 1. If T″ is doubly planted, there is a suitable forward move unless T″ \ {(1, 2n), (2, 2n − 1)} ≃₀ U_n−2. But then T = U_n and c(T) = n. Else, 2 < i < j < 2n − 1 and a forward move on the first and last children of (1, 2n) ∈ T″ yields T′. □

Lemma 6. If c(T′) − c(T) ≤ 1, then there is a bounded path from T to T′. Otherwise, there is a tightly bounded one.

Proof. Any forward path is tightly bounded. Hence, consider T ↛ T′ where c(L_n) = 1 < c(T) ≤ c(T′) < n = c(U_n). The result holds for n = 3, 4 since there is either a bounded forward V-path through U_n or backward one through L_n.

Suppose c(T′) − c(T) > 1. Then there are S, S′ ∈ 𝒯_n with T → S, S′ → T′, and c(T) < c(S) = c(S′) < c(T′). The existence of a bounded path from S to S′ implies a tightly bounded one from T to T′. By the previous lemma, we may assume S and S′ are doubly planted. Keeping (1, 2n) and (2, 2n − 1) fixed, inductively there is a bounded path from 𝒢_n−2 connecting S and S′ in 𝒢_n. If c(T′) = c(T) + 1, then the same reasoning holds as for c(S) = c(S′). □

While the skew of these paths is well-characterized, the length is not straightforward since the recursion has various dependencies. A forward path not involving L_n or U_n has length at most n − 3. Let g_n be the maximum length of a bounded path, or tightly bounded if possible, for T ↛ T′ in 𝒢_n. Then g₃ = 2, g₄ = 3, and g_n ≤ (n − 3) + 4 + g_n−2.

8. Existence of geodesics with bounded skew

Finally, we consider shortest paths, also called geodesics, in 𝒢_n. We show their length is determined by the number of simply aligned subsets, which ranges from n (when T = T′) down to 1.

When there is only one, the two trees are called complementary, consistent with lattice terminology. The simplest example is U_n and L_n, and all other complementary pairs likewise [12] have c(T) + c(T′) = n + 1. Moreover [12], the diameter of 𝒢_n is n − 1, and is achieved by complementary trees. Their V-paths necessarily pass through U_n and L_n, so we are interested in alternative geodesics with bounded skew.

Note that removing the edge (i, j) splits T into two subtrees — its descendents and the rest of T. Denote the former as δ_T (i, j) and latter as ${\overline{\delta }}_T(i,j)$. One may be empty; vacuously ∅ ⊑ T.

Lemma 7. Let (i, j) ∈ T \ T′. Suppose either δ_T (i, j) ⊑ T′ or ${\overline{\delta }}_T(i,j)⊑T^{\prime }$. Then the edges in T′ with indices i and j are unobstructed.

Proof. Suppose i pairs with k and j with l in T′. If ${\overline{\delta }}_T(i,j)⊑T^{\prime }$, then i < k < l < j. An obstructing edge must have one index in [k + 1, l − 1] and the other in [1, i − 1] ∪ [j + 1, 2n]. But the latter is not possible, since any edges in T′ with an index < i or > j agrees with T by assumption. When the ordering of indices is considered circularly, the case δ_T (i, j) ⊑ T′ is symmetric. □

Lemma 8. If T and T′ have k simply aligned subsets, then their geodesic has length n − k.

Proof. Construct a path T = T₀, T₁, …, T_n−k = T′ inductively by considering (i, j) ∈ T′ \ T_m with minimal j − i ≥ 1. Then δ_T′(i, j) ⊑ T_m. Let E ⊂ T_m have i, j ∈ α(E). Hence (i, j) ∈ T_m+1 = μ_E(T_m). Since the number of common edges increases monotonically to n, the path is a geodesic with length ∑_S(|S|−1) = n − k where S ⊆ T are the k original simply aligned subsets with T′. □

Call an edge (k, k + 1) a stem. Also define (1, 2n) to be one. Let e be a pairing between index 1 ≤ i ≤ 2n and j = i + 1 (mod 2n). If e ∉ T, then Lemma 7 applies. Call e a forward stem if i is odd, since the move is a forward one. Dually, e and the move are both backward if i is even. Note that (1, 2n) is an odd edge but a backward stem.

For technical reasons, T = {(1, 2)} is considered both a forward and backward stem. Since every unrooted tree has at least two leaves, T ∈ 𝒯_n has two or more stems when n > 1.

Lemma 9. If $c(T)\ge \frac{n+1}{2}$, then T has at least one forward stem. Dually, T has a backward stem when $c(T)\le \frac{n+1}{2}$.

Proof. Let n ≥ 2. Suppose $c(T)\ge \frac{n+1}{2}$, and consider T′ = {(1, 2k)} ∪ δ_T (1, 2k). Assume T″ = T \ T′ ≠ ∅ ⊑ T, then the result holds by induction on either $c\left(T^{\prime }\right)\ge \frac{k+1}{2}$ or $c\left(T^{\prime \prime }\right)\ge \frac{n-k+1}{2}$. If $c(T)=\frac{n+1}{2}$, then n is odd and, we may assume, so is k. Then $c\left(T^{\prime }\right)<\frac{k+1}{2}$ and $c\left(T^{\prime \prime }\right)<\frac{n-k+1}{2}$ implies $c\left(T^{\prime }\right)\le \frac{k-1}{2}$ and $c\left(T^{\prime \prime }\right)\le \frac{n-k}{2}$, a contradiction. When k = n, the result holds by induction on δ_T (1, 2n) ≃₁ T″ ∈ 𝒯_n−1 with $c\left(T^{\prime \prime }\right)=n-c(T)\le \frac{n-1}{2}$. The dual result follows from the mapping i → i + 1 (mod 2n) on the half-edge indices, which is a bijection on 𝒯_n. The image has n − c(T) + 1 odd edges, and the forward/backward orientation of stems reversed. □

Lemma 10. If T, T′ are complementary with c(T) = c(T′), then they have a bounded geodesic.

Proof. Since c(T) + c(T′) = n + 1, consider odd n ≥ 3. By Lemma 9, T′ has both a forward and backward stem. The corresponding moves on E ⊂ T and F ⊂ μ_E(T) yield T″ = μ_F (μ_E(T)) with $c\left(T^{\prime \prime }\right)=\frac{n+1}{2}$. Then π(T″, T′) has three parts, two of which are singletons. Let P be the non-singleton. Then σ(T″, P) and σ(T′, P) are complementary with $\frac{n-1}{2}$ odd edges. Inductively, their images in 𝒢_n−2 have a bounded geodesic. Keeping common edges fixed, so do T and T′. □

In other words, it is possible to “zigzag” between complementary T and T′ when c(T) = c(T′). Since the two moves can be made in either order, when c(T) < c(T′), they can be sequenced not to exceed the original skew.

Lemma 11. If T, T′ are complementary with c(T) ≠ c(T′), they have a tightly bounded geodesic.

Proof. Suppose n ≥ 4 and $c(T)<\frac{n+1}{2}<c\left(T^{\prime }\right)$. There is a forward move on E ⊂ T corresponding to (i, i + 1) ∈ T′. Let S = μ_E(T)\{(i, i + 1)} and S′ = T′\{(i, i + 1)} be the resulting complementary subtrees. If $c(T)=c(S)<\frac{n}{2}<c\left(S^{\prime }\right)=c\left(T^{\prime }\right)-1$, the result holds inductively. Else, ${\mu }_E(T)=\frac{n}{2}+1=c\left(T^{\prime }\right)$, and Lemma 10 applies to S and S′. By applying the backward move first to μ_E(T), the geodesic from T to T′ will be tightly bounded. □

These results extend directly when there is a bijection between simply aligned subsets and parts of the minimal tree partition. Call simply aligned S ⊆ T, S′ ⊆ T′ a block if S ⊑ T and S′ ⊑ T′. Say T and T′ have a block decomposition when the induced subtrees from π(T, T′) are simply aligned, i.e. complementary. Call a pairing exchange a geodesic move if it maintains a block decomposition while increasing the number of common edges.

Lemma 12. Suppose T and T′ have a block decomposition. If c(T′) = c(T), then there is a bounded geodesic from T to T′. Otherwise, there is a tightly bounded one.

Proof. Let S_i ⊆ T, $S_i^{\prime }\subseteq T^{\prime }$ be the simply aligned pairs. Since S_i ⊑ T and $S_i^{\prime }⊑T^{\prime }$, each pair can be treated independently.

Suppose c(T) = c(T′). If $c\left(S_i\right)\ne c\left(S_i^{\prime }\right)$, then Lemma 11 applies. Since $\sum c\left(S_i\right)=\sum c\left(S_i^{\prime }\right)$, alternate a geodesic forward move for T on S_i where $c\left(S_i\right)<c\left(S_i^{\prime }\right)$ with a backward one on S_j where $c\left(S_j\right)>c\left(S_j^{\prime }\right)$ until Lemma 10 applies to all pairs.

If c(T) = c(T′) − 1, again alternate moves until Lemma 10 applies to all pairs but $c\left(S_i\right)=c\left(S_i^{\prime }\right)-1$. Then, as in the proof of Lemma 11, the geodesic moves on S_i and the other pairs can be sequenced so that the path is tightly bounded.

Suppose c(T′) − c(T) > 1. Then either $c\left(S_i\right)+2\le c\left(S_i^{\prime }\right)$ or $c\left(S_i\right)+1\le c\left(S_i^{\prime }\right)$ and $c\left(S_j\right)+1\le c\left(S_j^{\prime }\right)$. But then there is a geodesic forward move on T and a backward one on T′ which decreases c(T′) − c(T) by 2. Keeping common edges fixed, inductively applying any of these cases will not increase the skew beyond the original bounds. □

The case when c(T′) − c(T) = 1 differs from Lemma 6 because the moves for Lemma 5 are ordered, unlike Lemma 10. When T and T′ do not have a block decomposition, moves on simply aligned subsets are not necessarily independent. Hence, the sequencing becomes more complicated, and such bounds may not hold in general.