Abstract
Glioma grading is critical for treatment selection, and the fine classification between glioma grades II and III is still a pathological challenge. Traditional systems based on a single deep learning (DL) model can only show relatively low accuracy in distinguishing glioma grades II and III. Introducing ensemble DL models by combining DL and ensemble learning techniques, we achieved annotation-free glioma grading (grade II or III) from pathological images. We established multiple tile-level DL models using residual network ResNet-18 architecture and then used DL models as component classifiers to develop ensemble DL models to achieve patient-level glioma grading. Whole-slide images of 507 subjects with low-grade glioma (LGG) from the Cancer Genome Atlas (TCGA) were included. The 30 DL models exhibited an average area under the curve (AUC) of 0.7991 in patient-level glioma grading. Single DL models showed large variation, and the median between-model cosine similarity was 0.9524, significantly smaller than the threshold of 1.0. The ensemble model based on logistic regression (LR) methods with a 14-component DL classifier (LR-14) demonstrated a mean patient-level accuracy and AUC of 0.8011 and 0.8945, respectively. Our proposed LR-14 ensemble DL model achieved state-of-the-art performance in glioma grade II and III classifications based on unannotated pathological images.
Keywords: Glioma grading, Deep learning, Ensemble learning, Pathology
1. Introduction
Glioma is one of the most common primary brain tumors in humans. The World Health Organization (WHO) classified gliomas into glioma Ⅰ–IV based on their pathological characteristics and malignancy level [[1], [2], [3]]. Accurate assessment of the glioma grade is of great significance for both diagnosis and treatment options, especially distinguishing between low-grade glioma (LGG) and high-grade glioma (HGG). Pathology is considered the gold standard for tumor diagnosis, and pathological whole-slide images (WSIs) can provide detailed and intuitive features for diagnosis. However, diagnosing tumors based on pathology is still challenging [[4], [5], [6]]. First, a pathological WSI usually occupies up to gigabytes, and it is difficult for the pathologist to check all contexts of the WSI, leading to a higher risk of misdiagnosis. In addition, interpreting pathological images is a highly objective and labor-intensive task and is sensitive to the operator's objectivity. Furthermore, there is a crucial unmet demand for access to pathology services, especially in low- and middle-income countries (LMICs) [7,8]. In all, an intelligent system should be introduced to assist pathologists in improving the accuracy and efficiency of the diagnostic process. Embracing deep learning (DL) is a promising way to achieve intelligent pathological diagnosis, and many repetitive and tedious tasks can be effectively solved by DL models.
Pathological image–based DL models have shown great performance in diagnosing various tumors [[9], [10], [11], [12], [13]]. There are also several reported glioma grading DL models based on pathology images [14,15]. In an image tile–level dataset extracted from 22 WSIs, a convolutional neural network (CNN)-based DL model yielded an accuracy of 96% and 71% in LGG versus HGG classification and grade II versus III classification, respectively [16]. However, this study has the limitation that several image tiles in the training and testing datasets may come from the same WSI. Patient–level and WSI–level experiments would be more reliable. In another WSI–level dataset, the developed CNN models achieved an accuracy of 73% in distinguishing HGG from others and an accuracy of 53% in grade II versus III classification [17]. Recently, a DL model based on a residual neural network (ResNet) showed an accuracy of 73.95% in grade II versus III classification tasks using pathological WSIs [18]. These reported systems exhibited relatively poor performance in grade II versus III classification than in LGG versus HGG classification.
In the grade II versus III classification task, traditional methods based on a single DL model are still not sufficiently accurate. Integrating the diagnostic results from multiple DL models using the ensemble learning technique is a possible way to solve this problem [[19], [20], [21]]. Ensemble DL frameworks usually have higher accuracy than a single DL model and are widely used in medical and health areas, such as epileptic prediction from EEG [22], Alzheimer's disease classification [23], and pneumonia disease classification from medical images [24,25].
In this study, we investigated a pathological image–based glioma grading system using an ensemble DL framework to solve the grade II versus III classification task, achieving higher accuracy and requiring no manual annotation. Most of the reported histopathology-based DL systems usually require tumor region annotations, i.e., manually delineating tumor regions’ contours. However, tumor region annotation is not only costly but also subjective to the operators. Here, we developed a glioma grading system based on unannotated pathological images, i.e., the original WSIs without tumor region annotation. We combined the diagnostic results of multiple image tile–level DL models using ensemble learning to generate a patient-level machine learning model. The ensemble DL system exhibited high performance in distinguishing glioma grade II versus III from unannotated pathological WSIs.
2. Materials and methods
2.1. Patient cohorts
Hematoxylin and eosin (HE) staining pathological images and clinical data were obtained from the Cancer Genome Atlas (TCGA) for patients with LGG [26]. The histological grades Ⅱ and Ⅲ were considered in this study. All subjects with pathological WSI were further screened by two pathologists to implement HE staining image quality control. In total, 507 subjects were included to develop a glioma grading system. All subjects were randomly separated into balanced training and testing cohorts. The training cohort consisted of 195 grade Ⅱ patients and 208 grade Ⅲ patients. The testing cohort consisted of 52 grade Ⅱ patients and 52 grade Ⅲ patients (Table 1).
Table 1.
Patients’ demographics in training and testing cohorts.
| Training cohort | Testing cohort | |
|---|---|---|
| Patient count | 403 | 104 |
| Gender (male/female) | 214/189 | 66/38 |
| Grade (grade II/III) | 195/208 | 52/52 |
| Age (median [IQR Q1–Q3]) | 41.1 [IQR 32.5–52.6] | 41.5 [IQR 33.8–55.2] |
IQR: interquartile range; Q1: 25th percentile; Q3: 75th quartile.
2.2. Image tile extraction
The computer is usually unable to directly process WSIs, which may occupy up to gigabytes, and we therefore used the OpenSlide tool to segment WSIs into small image tiles for further analysis [27,28]. All image preprocessing and tile extraction methods have been previously described [12,13]. All WSIs were segmented into image tiles with a size of 512 × 512 pixels and a spatial resolution of 0.50 μm/pixel. Adjacent image tiles overlapped by 100 pixels.
There was usually only a part of the valid region with tissue samples in the WSI, and the other regions were seen as the background. In the background region, WSIs in this study tend to be white. In the image tile extraction process, we used the thresholding method to screen the valid image tiles and abandon the background tiles. If the mean value for all channels was less than 200, the image tile was considered invalid. All segmented image tiles were further screened by two pathologists to ensure the quality of the image tile dataset. No additional annotations were made for WSI and image tiles. The glioma grade for each patient was assigned as a label for all image tiles of that patient.
2.3. Developing a tile-level DL model
To achieve glioma grading, we developed tile-level DL models using a pretrained ResNet-18 model based on ImageNet [29]. Similar to our previous DL-based biomedical image studies, all DL models were trained using transfer learning techniques [12,13,30,31]. We modified the output layer of the ResNet-18 model to fit the glioma-grade binary classification problem and used the transfer learning technique to fine-tune the parameters of the model.
During model training, we randomly divided the training image tiles into two parts: 80% of the tiles were used to train the DL model, and 20% of the tiles were unused. We repeated the process of training the DL model 30 times independently and obtained 30 DL models. When training each DL model, the randomly selected 80% training image tiles would increase the difference between the developed DL models, facilitating the performance of subsequent ensemble learning. Other parameter settings in the training process were as follows: maximum epochs, 1; batch size, 256; learning rate, 10−2; L2 normalization, 10−4; and optimizer, adaptive moment estimation (ADAM) algorithm. The DL architectures and experiments were implemented on a computer with MATLAB 2021a and configured with a Nvidia GeForce GTX 1080 Ti GPU with 11 GB of memory.
2.4. Patient-level feature vectors
First, we calculated the mean glioma grade score for each DL model and for each patient in the testing cohort. The DL model can calculate the glioma grade scores (including scores of grades Ⅱ and Ⅲ) for each image tile. We used the mean grade Ⅱ score as the patient-level diagnosis by averaging the grade Ⅱ scores of the patients’ all image tiles. With 30 developed tile-level DL models, we obtained 30 mean grade Ⅱ scores for each patient.
Then, the mean grade Ⅱ scores for each model were used as the elements of the patient-level feature vector. Each patient's feature vector had 30 elements, corresponding to each patient's 30 mean grade Ⅱ scores.
2.5. DL model feature vector and cosine similarity analysis
Assume we have N (N = 104) patients in the testing cohorts and M (M = 30) tile-level DL models. After calculating patient-level feature vectors, we got a grade Ⅱ score matrix with the size of M × N. Each row of the grade Ⅱ score matrix was seen as a DL model feature vector, representing each DL model's diagnostic results for all patients in the testing cohort. Each DL model feature vector has the size of 1 × N. We then calculated the cosine similarity (CS) of the patient-level recognition results between multiple DL models. The threshold of the CS was 1, which denoted that the two DL models had completely similar diagnostic results for all patients in the testing cohort.
2.6. Developing a patient-level machine learning model by ensemble learning
The developed tile-level DL models usually have different diagnostic results, even for the same patient. Ensemble learning refers to the technique of combining a diverse set of component classifiers into a stronger classifier. Ensemble learning can improve the stability of the overall diagnosis, leading to more reliable and accurate predictions. We used these 30 different tile-level DL models as component classifiers to create optimal glioma grading models using different machine learning models. Four machine learning models were considered in this study: the naïve Bayes (NB) model, logistic regression (LR) model, linear discriminant (LD) model, and decision tree (DT) model.
When constructing ensemble DL models, the grade Ⅱ scores from component classifiers were used as the features to develop subsequent machine learning models. The ensemble model with various m (m = 2, 3, …, 20) component classifiers (i.e., m dimensional features) was explored. The NB-, LR-, LD-, and DT-based ensemble models with m component models were marked as NB-m, LR-m, LD-m, and DT-m, respectively. For a given m value and a given machine learning method, there were mainly two steps to construct an ensemble DL model: 1) randomly selecting m component classifiers from the 30 developed DL models, calculating grade Ⅱ score–based patient-level feature vectors using the m selected component classifiers, and getting a grade Ⅱ score matrix with the size of m × N (where N denotes the number of patients in the testing cohorts); and 2) using the grade Ⅱ score matrix as input to train a classification model (grade Ⅱ vs. grade Ⅲ) based on a given machine learning method (NB, LR, LD, or DT), considering each row of the score matrix with a size of 1 × N elements as a feature, integrating the diagnosis of all m selected component classifiers by the trained model (i.e., the ensemble DL model), and using a fivefold cross-validation method to develop the classification model. Notably, there were many combinations to select m-component classifiers from 30 developed DL models. To increase validity and reliability, the training process for each experiment setting was repeated 200 times independently.
2.7. Evaluation of glioma grading models
There are two kinds of glioma grading models: tile-level and patient-level models. We used the receiver operating characteristic (ROC) curve and the area under the curve (AUC) to evaluate the tile-level performance of the tile-level DL models. In tile-level modeling, the label of tiles was inherited from their corresponding patient. We used ROC, AUC, accuracy, precision, and recall to evaluate patient-level performance.
2.8. Statistics
Statistical analyses were performed using GraphPad Prism software. In box-and-whisker plots, the box denotes the 25th and 75th quartiles, the horizontal line denotes the median, and the whiskers show the 5th and 95th percentiles. The D'Agostino–Pearson test was used to test the normality of datasets. Datasets that passed the normality test were presented as mean ± SD (standard deviation). Datasets that could not be assumed normal distribution were presented as median [IQR Q1–Q3] (IQR: interquartile range; Q1: 25th percentile; Q3: 75th quartile). Statistical differences among these groups were evaluated using the nonparametric Mann–Whitney test and Kruskal–Wallis test. Dunn's test was used to correct for multiple comparisons. Statistical significance was set at *p < 0.05.
3. Results
3.1. Establishment of an annotation-free glioma grading system
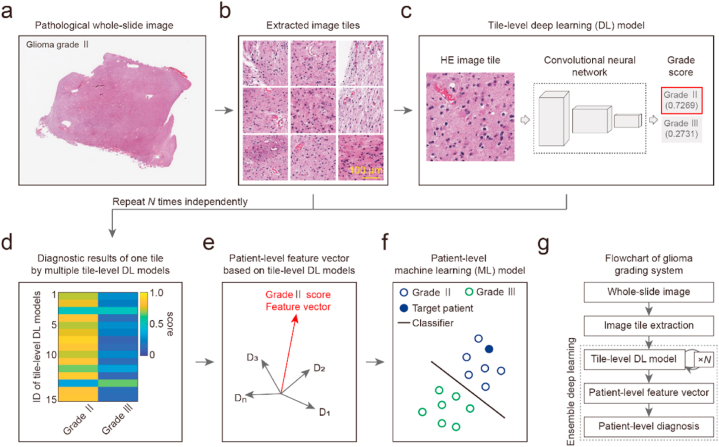
To achieve high performance in distinguishing glioma grades II and III based on unannotated pathological images, we developed an ensemble DL system (Fig. 1). The system was developed using pathological WSIs of 507 subjects with LGG (WHO grades Ⅱ and Ⅲ) from TCGA. To overcome the subjectivity and high workload of manual tumor contour annotation, the original unannotated WSIs were directly extracted as image tiles (Fig. 1a and b). Based on the image tile dataset, we developed tile-level DL models to classify each tile into grade II or III classes (Fig. 1c). The DL modeling processes were repeated for N times independently, and we obtained N tile-level DL models. For each image tile, multiple tile-level DL models were used to calculate the probabilities of grade II and III classes (Fig. 1d). Because DL modeling processes have randomness and are sensitive to the initial condition, the diagnostic results of the same image tile by different DL models usually have certain variances. Combining the diagnostic results of all DL models, we constructed patient-level feature vectors. The dimension of the patient-level feature vector equals the number of DL models, and each element corresponds to the average diagnostic results of all tiles by one DL model (Fig. 1e). Finally, we developed patient-level machine learning models based on these patient-level feature vectors and achieved final glioma grading (Fig. 1f and g). By incorporating the advantages of both DL and ensemble learning, the proposed ensemble DL system can eliminate the interference of nontumor regions and realize glioma grading based on unannotated pathological images.
Fig. 1.
Architecture of annotation-free glioma grading from the pathological image using ensemble deep learning. (a) Original pathological whole-slide image (WSI) of a patient with glioma grade Ⅱ. (b) Extracted image tiles from the WSI. The size of each tile is 512 × 512 pixels with a spatial resolution of 0.5 μm/pixel. Scale bar, 100 μm. (c) Developing a tile-level deep learning (DL) model to recognize the glioma grade of tiles. Left panel, hematoxylin-eosin (HE) staining image tile. Middle panel, deep learning model. Right panel, glioma grading results. The illustrated image tile was classified into the class of grade Ⅱ with a score of 0.7269. (d) The heat map of scores calculated by multiple tile-level DL models versus classes of grade Ⅱ and grade Ⅲ. The DL modeling process in panel (c) was repeated N times independently to obtain multiple tile-level DL models. Scores of grades Ⅱ and Ⅲ for one image tile from 15 tile-level DL models are shown. (e) Patient-level feature vector based on the tile-level DL model using grade Ⅱ score. The average grade Ⅱ score of all image tiles for each patient was used as the element of the patient-level feature vector. Each patient's feature vector contains N elements corresponding to the N tile-level DL model. (f) Developing a machine learning model to achieve patient-level glioma grading. Schematic diagram of patient-level glioma grade classification. Blue circle, grade Ⅱ. Filled blue circle, target patient with grade Ⅱ glioma. Green circle, grade Ⅲ. Blackline, classifier model. (g) Flow chart of the annotation-free glioma grading system. The ensemble learning technique was used to fuse the multiple tile-level DL models into a stronger machine learning model.
3.2. Performance of tile-level glioma grading models
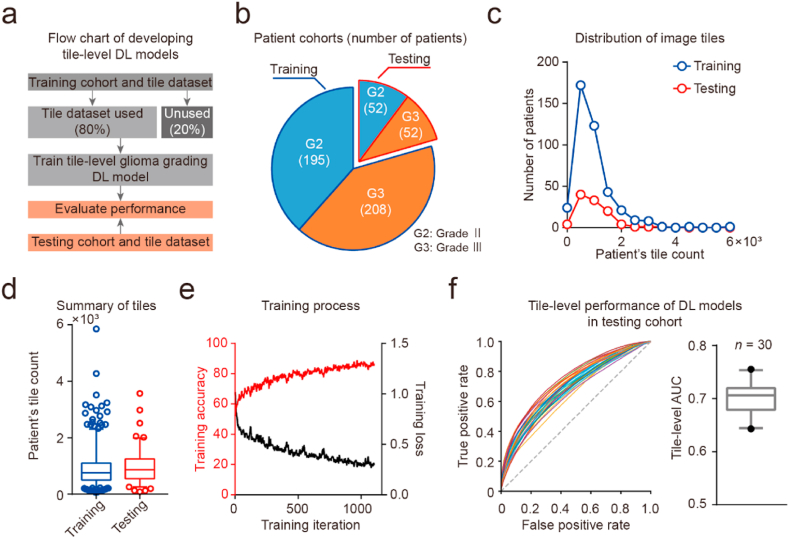
To achieve tile-level glioma grading, we developed 30 DL models based on the ResNet-18 architecture using transfer learning (Fig. 2a). The number of patients with grades II and III in both training and testing cohorts was almost balanced (training cohorts, grade II:III = 1:1.07; testing cohorts, grade II:III = 1:1; Fig. 2b; Table 1). Furthermore, the count of each patient's tiles in the training and testing dataset showed no significant difference (count of patient's tiles: median [IQR Q1–Q3], training dataset 762 [IQR 502–1104]; testing dataset 868 [IQR 554–1254]; Mann–Whitney test, p > 0.05; Fig. 2c and d). The training and testing datasets that were balanced at both the patient level and the tile level provided a solid foundation for subsequent DL modeling. Using a randomly selected 80% of the tiles in the training dataset, we developed 30 different tile-level models independently (Fig. 2e and f). The AUC measurements between these DL models in the testing dataset showed a normal distribution (tile-level AUC: mean ± SD, 0.7001 ± 0.0301, n = 30). Our experimental results showed that the developed DL models achieved tile-level glioma grading, and these DL models exhibited performance variances.
Fig. 2.
Development and validation of DL models to achieve tile-level glioma grading. (a) Flow chart of developing tile-level DL models. (b) Pie graph of patient cohorts. (c) Plot of patient count versus each patient's tile count. Blue circle and line, training cohort. Red circle and line, testing cohort. (d) Box-and-whiskers plots of patient's tile counts. Blue, training cohorts. Red, testing cohorts. (e) Plot of training accuracy and loss versus training iteration. (f) Tile-level performance of multiple DL models in the testing cohort. Left panel, the plot of receiver operating characteristic (ROC) curve for 30 DL models. Right panel, box-and-whiskers plots of tile-level area under the curve (AUC) values.
3.3. Performance of patient-level glioma grading models
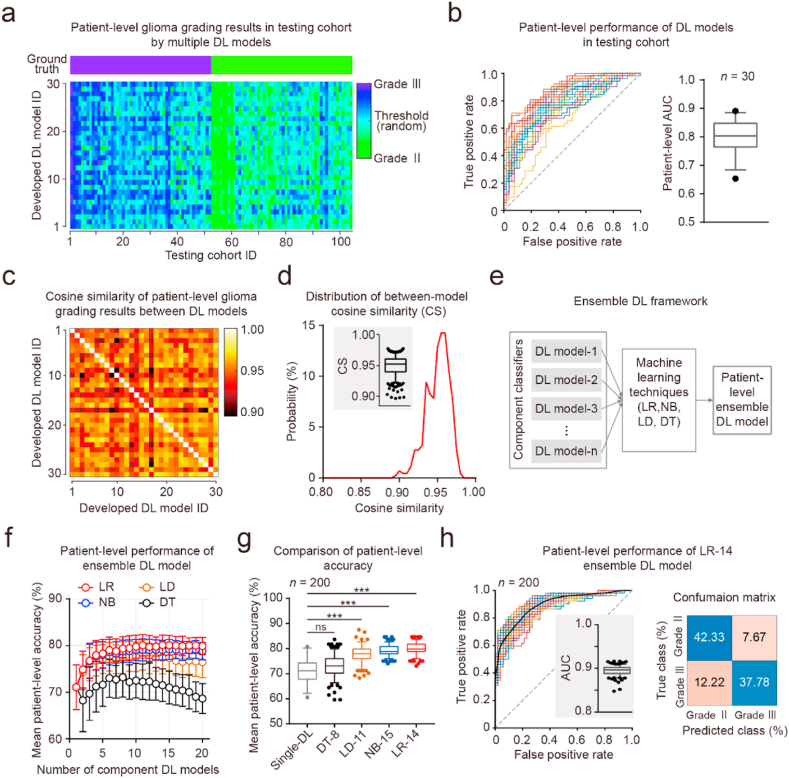
To achieve accurate patient-level glioma grading, we integrated the developed tile-level DL models using ensemble learning techniques and developed an ensemble DL system (Fig. 3). First, we averaged the diagnostic results of all tiles for each patient to obtain the patient-level diagnosis (patient-level AUC: mean ± SD, 0.7991 ± 0.0575, n = 30; Fig. 3a and b). We measured the similarity between the patient-level diagnostic results of DL models using CS criteria (Fig. 3c). Between-model CS was significantly less than the threshold of 1.0 (between-model CS, median [IQR Q1–Q3], 0.9524 [IQR 0.9399–0.9608]; compared to the threshold of 1.0: Wilcoxon signed-rank test, p < 0.001; Fig. 3d). Second, we used these DL models as component classifiers to generate ensemble DL models and developed various patient-level machine learning models (Fig. 3a, e). All these NB, LR, LD, and DT models were developed and validated based on the patient-level glioma grading results in the testing cohort using fivefold cross-validation. For the NB, LR, and LD models, the mean patient-level accuracies increased as the number of component classifiers increased until a bottleneck was reached (Fig. 3f). The single DL model without ensemble learning showed relatively low patient-level accuracy (mean ± SD, 0.7106 ± 0.0481, n = 30). Four kinds of ensemble models reached the highest mean patient-level accuracy with different component classifiers (DT-8, LD-11, NB-15, and LR-14; Fig. 3f). The LD-11, NB-15, and LR-14 models showed significantly higher patient-level accuracy than the single DL model (LD-11, p < 0.001; NB-15, p < 0.001; LR -14, p < 0.001; Kruskal–Wallis test, p < 0.001; Dunn's multiple comparisons test; Fig. 3f and g; Table 2). Furthermore, the LR-14 ensemble DL model showed significantly higher patient-level accuracy than the other ensemble DL models (LR-14 vs. DT-8, p < 0.001; LR-14 vs. LD-11, p < 0.001; LR-14 vs. NB-15, p < 0.01; Kruskal–Wallis test, p < 0.001; Dunn's multiple comparisons test; Fig. 3f and g; Table 2). The optimal LR-14 ensemble DL model achieved an AUC of 0.8945 ± 0.0101 (Table 2); the precisions for grades II and III were 0.7760 and 0.8465, respectively; and the recalls for grades II and III were 0.8312 and 0.7556, respectively (Fig. 3h). Our experimental results showed that the LR ensemble DL models achieved high performance in patient-level glioma grade II and III recognition.
Fig. 3.
Development and validation of patient-level machine learning models using ensemble learning techniques. (a) Ground truth and patient-level feature vectors for the testing cohorts. Upper panel, ground truth. Down panel, the heat map of each patient's feature vector was calculated from 30 developed tile-level DL models. (b) Patient-level performance of multiple DL models in the testing cohort. Left panel, the plot of the ROC curve for 30 DL models. Right panel, box-and-whiskers plots of patient-level AUC values. (c) Heat map of the cosine similarity matrix for patient-level glioma grading results between 30 DL models. (d) Distribution of between-model cosine similarity (CS) values in panel (c). Plot of probability versus CS value. Insert graph, box-and-whiskers plots of between-model CS. Threshold of CS value, 1.0. (e) Schematic diagram of developing ensemble DL models. Multiple DL models were seen as component classifiers and were integrated using ensemble learning techniques to develop further machine learning models. NB, naïve Bayes; LR, logistic regression; LD, linear discriminant; DT, decision tree. (f) Patient-level performance of ensemble DL models in the testing cohort. Plot of patient-level accuracy versus the number of component DL models. Fivefold cross-validation was used. Red, LR model. Blue, NB model. Green, LD model. Black, DT model. Data are presented as mean ± SD. (g) Box-and-whiskers plots of patient-level accuracy. Gray, single DL model; DT-8, DT ensemble DL model with 8 component models; LD-11, LD ensemble DL model with 11 component models; NB-15, NB ensemble DL model with 15 component models; LR-14, LR ensemble DL model with 14 component models. (h) Patient-level performance of the LR-14 ensemble DL model. Left panel, plot of the ROC curve for 200 LR-14 ensemble DL models. Right panel, average confusion matrix for LR-14 ensemble DL models.
Table 2.
Patient-level diagnostic performance of ensemble DL models.
| Model | Accuracy | AUC |
|---|---|---|
| Single DL model (n = 30) | 0.7106 ± 0.0481 | 0.7991 ± 0.0575 |
| Ensemble model: DT-8 (n = 200) | 0.7320 ± 0.0423 | 0.7557 ± 0.0461 |
| Ensemble model: LD-11 (n = 200) | 0.7794 ± 0.0319 | 0.8614 ± 0.0253 |
| Ensemble model: NB-15 (n = 200) | 0.7916 ± 0.0214 | 0.8885 ± 0.0103 |
| Ensemble model: LR-14 (n = 200) | 0.8011 ± 0.0215 | 0.8945 ± 0.0101 |
Data are presented as mean ± SD. AUC, area under the curve; DT-8, DT ensemble DL model with 8 component models; LD-11, LD ensemble DL model with 11 component models; NB-15, NB ensemble DL model with 15 component models; LR-14, LR ensemble DL model with 14 component models.
4. Discussion
We investigated the pathological image–based ensemble DL framework to classify glioma grades II and III. We developed multiple tile-level glioma grading DL models and then established four kinds of patient-level ensemble DL models based on these tile-level DL models. The LD, NB, and LR ensemble DL models performed significantly better than the single DL model in the glioma grade II and III recognition task.
In the reported pathological image–based glioma grading work, the accuracy of glioma grade II and III recognition ranged from 53% to 73.95% [[16], [17], [18]]. In this study, the proposed single DL model without ensemble learning exhibited a patient-level accuracy of 0.7106 ± 0.0481 in the glioma grade II and III recognition task. The proposed single DL model's accuracy is comparable to the performance (73.95%) of Pei et al.‘s mostly reported work [18]. By combining the diagnostic results of multiple DL models, the proposed ensemble DL models demonstrated better glioma grading performance. The LR ensemble DL models achieved state-of-the-art accuracy (0.8011 ± 0.0215). The performance improvement brought about by the ensemble DL framework has an upper limit. When the number of component DL classifiers exceeds a threshold, the performance will no longer increase; it will even decrease in the DT and LD ensemble DL models. Furthermore, most of the pathological image–based DL systems in glioma and other tumors usually require image preprocessing to eliminate the interference of noised background and nontumor regions, such as manual annotation of tumor contours or pre-segmentation by other developed models [13,16,18,32]. In this study, the ensemble DL framework was able to eliminate the variance between the data and the DL models and achieved high-performance glioma grading based on unannotated pathological images.
Combining magnetic resonance imaging (MRI) with DL can realize noninvasive glioma diagnosis and grading. Most reported glioma grading systems based on MRI and CNNs can accurately distinguish between LGG and HGG [[33], [34], [35]]. In several testing experiments of the LGG versus HGG classification task, a VGG16-based DL model achieved an AUC of 0.898 and an accuracy of 0.800 [36], and a GoogLeNet-based DL model achieved an AUC of 0.939 and an accuracy of 0.909 [37]. In a further fine classification task to distinguish between grades II and III, MRI-based DL models showed relatively poor performance [38,39]. Although DL models have powerful feature extraction capabilities, it is difficult for MRI-based DL systems to achieve high accuracy in grade II versus III classification tasks because of the low spatial resolution of MRI.
DL and ensemble learning are two important methods in the artificial intelligence field. Traditionally, these two methods have been regarded as separate approaches in practical applications [20,21]. DL is mainly based on deep neural networks (DNNs), which is a highly nonlinear model with extremely high flexibility and strong learning ability. However, DNNs are very sensitive to initial conditions, including the initial weights and statistical noise of the data. In addition, most optimization algorithms introduce randomness when training DL models [40]. Therefore, DL models usually have different weights and produce different prediction results, even if they are developed from the same training dataset. In this study, the developed tile-level DL models showed high variance in glioma grading performance. Establishing ensemble DL frameworks can effectively overcome the variability of the DL method. Ensemble learning is based on the principle of “the wisdom of the crowd,” which denotes that a large group of people with average knowledge of a topic can provide better-than-expert solutions to some questions [41,42]. Ensemble DL models integrate the output of multiple DL models and can overcome variation and noise, leading to better performance than a single DL model [[43], [44], [45]]. In addition, the method of establishing ensemble DL models also greatly impacts final performance. In this study, the NB and LR methods were more suitable and had higher accuracy than the LD and DT methods when developing ensemble DL models.
In this research, all DL models were trained to achieve the same target (grade II vs. grade III classification) and were used as component models to further construct the ensemble DL models. Ertosun and Rubin developed another ensemble DL system (ER-ensemble system) to achieve glioma grading [16]; they assembled two modular CNN components specialized in two different classification tasks (GBM vs. LGG classification and grade II vs. grade III classification) to achieve a glioma grading diagnosis. In the reported ER-ensemble system, segmented nuclei images with reserved original positions were used as the input of the CNN model, showing the advantages of higher interpretability and faster computational efficiency. Benefiting from the advances in DL techniques and well-established pre-trained DL models, the system built in this study adopted the original segmented tiles as the input of CNN models, yielding the advantages of a more informative input with preserved features of cytoplasm as well as the microenvironment. In the future, we plan to extend our proposed ensemble DL framework to both GBM versus LGG classification and grade II versus grade III classification tasks, as reported in the ER-ensemble system [16].
Besides glioma grading, pathological images also play an important role in many other diagnoses, such as glioma subtype identification (oligodendroglioma, oligoastrocytoma, and astrocytoma) [15,46]. As the revised WHO classification standards for gliomas in 2016 encourage the integration of genomic data into standard diagnostic tests, predicting molecular markers and gene mutations from the pathological image using DL techniques has gained increasing attention [2,3,46], especially the prediction of isocitrate dehydrogenase (IDH) mutation [47,48] and 1p/19q codeletion status [46]. Until now, most of these reported studies have developed single DL-based glioma diagnostic models. Extending the ensemble DL framework to these pathological image diagnosis tasks may further facilitate the development of AI pathology in gliomas.
There were two main limitations in this study. First, we investigated how the number of component DL classifiers affected the performance of ensemble DL models but ignored the interaction between component classifiers. Between-model CS analysis showed that the similarity between the diagnostic results of the DL model pairs had a large variation, and how the degree of similarity between the component DL classifiers affects the performance of the ensemble DL model is still unclear. Second, all the tile-level DL models were developed using the ResNet-18 architecture in this study. There are many other high-performance models in the artificial intelligence field, such as ResNet-50, GoogLeNet [49], Inception v3 [50], and Xception [51]. Although the ResNet-18 model is widely used in many pathological image studies for its balanced benefits in performance and speed [13,32], optimizing DL model architectures may also be necessary, which may further improve the performance of the ensemble DL models. Furthermore, using DL models with different architectures as component classifiers is also an issue worth exploring.
In conclusion, we developed the pathological image–based ensemble DL framework for glioma grading and achieved high performance in distinguishing glioma grades II and III using unannotated pathological images, which provided insights into optimizing DL diagnostic systems by improving accuracy and efficiency. This work can potentially promote the practical applications of artificial intelligence in diagnosing and treating human glioma.
Author contribution statement
Feng Su; Ye Cheng; Liang Chang; Leiming Wang; Gengdi Huang: Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Peijiang Yuan; Chen Zhang; Yongjie Ma: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
Gengdi Huang was supported by National Science Foundation of China [82101492].
Ye Cheng was supported by Youth Program of National Natural Science Foundation of China [81802485].
Data availability statement
Data associated with this study has been deposited at the analysis codes are publicly available in Zenodo (https://zenodo.org/record/6830441#.YtC_fsiWnGQ).
Contributor Information
Peijiang Yuan, Email: itr@buaa.edu.cn.
Chen Zhang, Email: czhang@188.com.
Yongjie Ma, Email: mayongjie@xwhosp.org.
References
- 1.Louis D.N., Ohgaki H., Wiestler O.D., Cavenee W.K., Burger P.C., Jouvet A., et al. The 2007 WHO classification of tumours of the central nervous system. Acta Neuropathol. 2007;114:97–109. doi: 10.1007/s00401-007-0243-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Louis D.N., Perry A., Reifenberger G., von Deimling A., Figarella-Branger D., Cavenee W.K., et al. The 2016 world health organization classification of tumors of the central nervous system: a summary. Acta Neuropathol. 2016;131:803–820. doi: 10.1007/s00401-016-1545-1. [DOI] [PubMed] [Google Scholar]
- 3.Wesseling P., Capper D. WHO 2016 Classification of gliomas. Neuropathol. Appl. Neurobiol. 2018;44:139–150. doi: 10.1111/nan.12432. [DOI] [PubMed] [Google Scholar]
- 4.Norgeot B., Glicksberg B.S., Butte A.J. A call for deep-learning healthcare. Nat. Med. 2019;25:14–15. doi: 10.1038/s41591-018-0320-3. [DOI] [PubMed] [Google Scholar]
- 5.Esteva A., Robicquet A., Ramsundar B., Kuleshov V., DePristo M., Chou K., et al. A guide to deep learning in healthcare. Nat. Med. 2019;25:24–29. doi: 10.1038/s41591-018-0316-z. [DOI] [PubMed] [Google Scholar]
- 6.Fogel A.L., Kvedar J.C. Artificial intelligence powers digital medicine. NPJ Digit Med. 2018;1:5. doi: 10.1038/s41746-017-0012-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wilson M.L., Fleming K.A., Kuti M.A., Looi L.M., Lago N., Ru K. Access to pathology and laboratory medicine services: a crucial gap. Lancet. 2018;391:1927–1938. doi: 10.1016/S0140-6736(18)30458-6. [DOI] [PubMed] [Google Scholar]
- 8.Sayed S., Cherniak W., Lawler M., Tan S.Y., el Sadr W., Wolf N., et al. Improving pathology and laboratory medicine in low-income and middle-income countries: roadmap to solutions. Lancet. 2018;391:1939–1952. doi: 10.1016/S0140-6736(18)30459-8. [DOI] [PubMed] [Google Scholar]
- 9.Kather J.N., Heij L.R., Grabsch H.I., Loeffler C., Echle A., Muti H.S., et al. Pan-cancer image-based detection of clinically actionable genetic alterations. Nat. Can. 2020;1:789–799. doi: 10.1038/s43018-020-0087-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Coudray N., Ocampo P.S., Sakellaropoulos T., Narula N., Snuderl M., Fenyö D., et al. Classification and mutation prediction from non-small cell lung cancer histopathology images using deep learning. Nat. Med. 2018;24:1559–1567. doi: 10.1038/s41591-018-0177-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Komori T. AI Neuropathologist: an innovative technology enabling a faultless pathological diagnosis? Neuro Oncol. 2021;23:1–2. doi: 10.1093/neuonc/noaa229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hu Y., Su F., Dong K., Wang X., Zhao X., Jiang Y., et al. Deep learning system for lymph nodes quantification and metastatic cancer identification from whole-slide pathology images. Gastric Cancer. 2021;24:868–877. doi: 10.1007/s10120-021-01158-9. [DOI] [PubMed] [Google Scholar]
- 13.Su F., Li J., Zhao X., Wang B., Hu Y., Sun Y., et al. Interpretable tumor differentiation grade and microsatellite instability recognition in gastric cancer using deep learning. Lab. Invest. 2022;102:641–649. doi: 10.1038/s41374-022-00742-6. [DOI] [PubMed] [Google Scholar]
- 14.Yonekura A., Kawanaka H., Surya Prasath V.B., Aronow B.J., Takase H. 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM) 2017. Improving the generalization of disease stage classification with deep CNN for Glioma histopathological images; pp. 1222–1226. [DOI] [Google Scholar]
- 15.Im S., Hyeon J., Rha E., Lee J., Choi H.-J., Jung Y., et al. Classification of diffuse glioma subtype from clinical-grade pathological images using deep transfer learning. Sensors. 2021;21 doi: 10.3390/s21103500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ertosun M.G., Rubin D.L. Automated grading of gliomas using deep learning in digital pathology images: a modular approach with ensemble of convolutional neural networks. AMIA Annu Symp Proc. 2015:1899–1908. [PMC free article] [PubMed] [Google Scholar]
- 17.Truong A.H., Sharmanska V., Limbӓck-Stanic C., Grech-Sollars M. Optimization of deep learning methods for visualization of tumor heterogeneity and brain tumor grading through digital pathology. Neurooncol Adv. 2020;2:110. doi: 10.1093/noajnl/vdaa110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pei L., Jones K.A., Shboul Z.A., Chen J.Y., Iftekharuddin K.M. Deep neural network analysis of pathology images with integrated molecular data for enhanced glioma classification and grading. Front. Oncol. 2021;11 doi: 10.3389/fonc.2021.668694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ganaie M.A., Hu M., Tanveer M., Suganthan P.N. 2014. Ensemble Deep Learning: A Review. ArXiv 2021. [Google Scholar]
- 20.Cao Y., Geddes T.A., Yang J.Y.H., Yang P. Ensemble deep learning in bioinformatics. Nat. Mach. Intell. 2020;2:500–508. doi: 10.1038/s42256-020-0217-y. [DOI] [Google Scholar]
- 21.Ray A., Chakraborty T., Ghosh D. Optimized ensemble deep learning framework for scalable forecasting of dynamics containing extreme events. Chaos. 2021;31 doi: 10.1063/5.0074213. [DOI] [PubMed] [Google Scholar]
- 22.Muhammad Usman S., Khalid S., Bashir S. A deep learning based ensemble learning method for epileptic seizure prediction. Comput. Biol. Med. 2021;136 doi: 10.1016/j.compbiomed.2021.104710. [DOI] [PubMed] [Google Scholar]
- 23.An N., Ding H., Yang J., Au R., Ang T.F.A. Deep ensemble learning for Alzheimer's disease classification. J. Biomed. Inf. 2020;105 doi: 10.1016/j.jbi.2020.103411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zhou T., Lu H., Yang Z., Qiu S., Huo B., Dong Y. The ensemble deep learning model for novel COVID-19 on CT images. Appl. Soft Comput. 2021;98 doi: 10.1016/j.asoc.2020.106885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.El Asnaoui K. Design ensemble deep learning model for pneumonia disease classification. Int J Multimed Inf Retr. 2021;10:55–68. doi: 10.1007/s13735-021-00204-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Brat D.J., Verhaak R.G.W., Aldape K.D., Yung W.K.A., Salama S.R., Cooper L.A.D., et al. Comprehensive, integrative genomic analysis of diffuse lower-grade gliomas. N. Engl. J. Med. 2015;372:2481–2498. doi: 10.1056/NEJMoa1402121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Herrmann M.D., Clunie D.A., Fedorov A., Doyle S.W., Pieper S., Klepeis V., et al. Implementing the DICOM standard for digital pathology. J. Pathol. Inf. 2018;9:37. doi: 10.4103/jpi.jpi_42_18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Goode A., Gilbert B., Harkes J., Jukic D., Satyanarayanan M. OpenSlide: a vendor-neutral software foundation for digital pathology. J. Pathol. Inf. 2013;4:27. doi: 10.4103/2153-3539.119005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.He K., Zhang X., Ren S., Sun J. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition. 2016:770–778. [Google Scholar]
- 30.Su F., Wei M., Sun M., Jiang L., Dong Z., Wang J., et al. Deep learning-based synapse counting and synaptic ultrastructure analysis of electron microscopy images. J. Neurosci. Methods. 2022 doi: 10.1016/j.jneumeth.2022.109750. [DOI] [PubMed] [Google Scholar]
- 31.Su F., Sun Y., Hu Y., Yuan P., Wang X., Wang Q., et al. Development and validation of a deep learning system for ascites cytopathology interpretation. Gastric Cancer. 2020;23:1041–1050. doi: 10.1007/s10120-020-01093-1. [DOI] [PubMed] [Google Scholar]
- 32.Kather J.N., Pearson A.T., Halama N., Jäger D., Krause J., Loosen S.H., et al. Deep learning can predict microsatellite instability directly from histology in gastrointestinal cancer. Nat. Med. 2019;25:1054–1056. doi: 10.1038/s41591-019-0462-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Tripathi P.C., Bag S. A computer-aided grading of glioma tumor using deep residual networks fusion. Comput. Methods Progr. Biomed. 2022;215 doi: 10.1016/j.cmpb.2021.106597. [DOI] [PubMed] [Google Scholar]
- 34.Zhuge Y., Ning H., Mathen P., Cheng J.Y., Krauze A.V., Camphausen K., et al. Automated glioma grading on conventional MRI images using deep convolutional neural networks. Med. Phys. 2020;47:3044–3053. doi: 10.1002/mp.14168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Özcan H., Emiroğlu B.G., Sabuncuoğlu H., Özdoğan S., Soyer A., Saygı T. A comparative study for glioma classification using deep convolutional neural networks. Math. Biosci. Eng. 2021;18:1550–1572. doi: 10.3934/mbe.2021080. [DOI] [PubMed] [Google Scholar]
- 36.Ding J., Zhao R., Qiu Q., Chen J., Duan J., Cao X., et al. Developing and validating a deep learning and radiomic model for glioma grading using multiplanar reconstructed magnetic resonance contrast-enhanced T1-weighted imaging: a robust, multi-institutional study. Quant. Imag. Med. Surg. 2022;12:1517–1528. doi: 10.21037/qims-21-722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Yang Y., Yan L.-F., Zhang X., Han Y., Nan H.-Y., Hu Y.-C., et al. Glioma grading on conventional mr images: a deep learning study with transfer learning. Front. Neurosci. 2018;12:804. doi: 10.3389/fnins.2018.00804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gutta S., Acharya J., Shiroishi M.S., Hwang D., Nayak K.S. Improved glioma grading using deep convolutional neural networks. AJNR Am J Neuroradiol. 2021;42:233–239. doi: 10.3174/ajnr.A6882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Naser M.A., Deen M.J. Brain tumor segmentation and grading of lower-grade glioma using deep learning in MRI images. Comput. Biol. Med. 2020;121 doi: 10.1016/j.compbiomed.2020.103758. [DOI] [PubMed] [Google Scholar]
- 40.Kingma D., Ba J. Adam: a method for stochastic optimization. Computer Science. 2014 arXiv:1412.6980. [Google Scholar]
- 41.van Dolder D., van den Assem M.J. The wisdom of the inner crowd in three large natural experiments. Nat. Human Behav. 2018;2:21–26. doi: 10.1038/s41562-017-0247-6. [DOI] [PubMed] [Google Scholar]
- 42.Elliott D.L., Anderson C. IEEE Trans Neural Netw Learn Syst; 2021. The Wisdom of the Crowd: Reliable Deep Reinforcement Learning through Ensembles of Q-Functions. [DOI] [PubMed] [Google Scholar]
- 43.Zhou Zhi-Hua. Machine Learning. Springer; Singapore: 2021. Ensemble learning. [DOI] [Google Scholar]
- 44.Efron B. Bootstrap methods: another look at the jackknife. Ann. Stat. 1979;7:1–26. [Google Scholar]
- 45.Polikar R. Bootstrap - inspired techniques in computation intelligence. IEEE Signal Process. Mag. 2007;24:59–72. doi: 10.1109/MSP.2007.4286565. [DOI] [Google Scholar]
- 46.Jin L., Shi F., Chun Q., Chen H., Ma Y., Wu S., et al. Artificial intelligence neuropathologist for glioma classification using deep learning on hematoxylin and eosin stained slide images and molecular markers. Neuro Oncol. 2021;23:44–52. doi: 10.1093/neuonc/noaa163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cui D., Liu Y., Liu G., Liu L. A multiple-instance learning-based convolutional neural network model to detect the IDH1 mutation in the histopathology images of glioma tissues. J. Comput. Biol. 2020;27:1264–1272. doi: 10.1089/cmb.2019.0410. [DOI] [PubMed] [Google Scholar]
- 48.Liu S., Shah Z., Sav A., Russo C., Berkovsky S., Qian Y., et al. Isocitrate dehydrogenase (IDH) status prediction in histopathology images of gliomas using deep learning. Sci. Rep. 2020;10:7733. doi: 10.1038/s41598-020-64588-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Szegedy C., Liu W., Jia Y., Sermanet P., Reed S.E., Anguelov D., et al. Going deeper with convolutions. IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2015:1–9. [Google Scholar]
- 50.Szegedy C., Vanhoucke V., Ioffe S., Shlens J., Wojna Z. Rethinking the inception architecture for computer vision. IEEE ASME Trans. Mechatron. 2016:2818–2826. [Google Scholar]
- 51.Chollet Francois. IEEE; 2017. Xception: Deep Learning with Depthwise Separable Convolutions. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data associated with this study has been deposited at the analysis codes are publicly available in Zenodo (https://zenodo.org/record/6830441#.YtC_fsiWnGQ).