Mode specific dynamics for the acoustic vibrations of a gold nanoplate

Abstract

The vibrational modes of semiconductor and metal nanostructures occur in the MHz to GHz frequency range, depending on dimensions. These modes are at the heart of nano-optomechanical devices, and understanding how they dissipate energy is important for applications of the devices. In this paper ultrafast transient absorption microscopy has been used to examine the breathing modes of a single gold nanoplate, where up to four overtones were observed. Analysis of the frequencies and amplitudes of the modes using a simple continuum mechanics model shows that the system behaves as a free plate, even though it is deposited onto a surface with no special preparation. The overtones decay faster than the fundamental mode, which is not predicted by continuum mechanics calculations of mode damping due to radiation of sound waves. Possible reasons for this effect include frequency dependent thermoelastic effects in the nanoplate, and/or flow of acoustic energy out of the excitation region.

1. Introduction

The past decade has seen considerable advances in the development of nano-optomechanical devices for high sensitivity measurements [1], [2]. Examples of applications include force sensing [3], [4], measurements of the mass of single nano-objects [5], [6], [7], [8], and detection of the optical absorption of single molecules [9]. These devices are typically constructed from thin semiconductor nanostructures, and a significant amount of engineering is needed to actuate and read-out the device [3], [4], [5], [6], [7], [8], [9], [10], [11]. Accurate measurements for these applications require high vibrational quality factors, which means that it is important to understand vibrational damping. A convenient approach to detecting the vibrations of single nano-structures and measure their damping is transient absorption microscopy (TAM) [12], [13], [14]. In these experiments, ultrafast heating from a pump laser excites breathing modes of the nanostructure that are detected by a time delayed probe. Advantages of TAM experiments compared to measurements using nano-optomechanical devices are that highly engineered samples are not needed, and very high frequency vibrations can be interrogated (10–100 GHz). However, the quality factors of the nanostructures that have been examined by TAM are typically much smaller than those that have been measured in conventional nano-optomechanical devices [12], [13], [14]. There are several reasons for this. The majority of TAM measurements for single nanostructures have been performed on metals, which suffer greater dissipation than semiconductor nanostructures [15], [16], [17]. Substrate supported structures have also been interrogated, where the radiation of sound waves into the support reduces the vibrational lifetimes [13], [14], [18], [19], [20].

The different types of samples that have been studied by single particle TAM measurements include nanospheres [21], nanorods [22], nanodisks [13], [14], nanowires [23], [24], [25] and nanoplates [18], [26], [27]. The particles are typically supported through a substrate, although optically trapped particles have also been investigated [28]. The quality factors depend sensitively on the environment: a number of experimental studies have shown that the vibrational modes are strongly damped by interactions with liquids and/or solid surfaces [12], [14], [19], [22], [23]. Recently, it has been found that high quality factors (> 100) can be obtained for Au nanoplates that are either suspended in air or supported by a low density substrate [26], [27]. Thus, these structures are promising for applications. However, the reason why nanoplates display higher quality factors than other metal structures, and whether the quality factors depend on nanoplate dimensions are not well understood.

In this study TAM was used to investigate the breathing modes of a single gold nanoplate supported on a glass substrate. The experiments were performed using Asynchronous Optical Sampling (ASOPS) to avoid problems associated with using a conventional mechanical delay line for TAM measurements [29]. The nanoplate investigated has extremely long lived acoustic vibrational modes (exceeding the 10 ns time between pulses in our experiments), and up to the four overtones of the breathing mode were observed in the vibrational spectrum. Both these observations are unusual for substrate supported structures. The amplitudes and frequencies of the overtones match the results of a simple continuum mechanics model for a free nanoplate. [19], [30] Detailed analysis of the transient absorption data shows that the overtones have shorter lifetimes than the fundamental mode, which is not expected from the continuum mechanics calculations. Possible reasons for the mode specific dynamics for this structure are discussed.

2. Experimental methods

Sample Preparation: Gold nanoplates were synthesized using the recipe adapted from Ref. [31]. All chemicals were purchased from Sigma-Aldrich and were used without further purification. Briefly, 100 μL of 0.1 M Gold (III) Trichloride, AuCl₃, was added to 3 mL of 0.02 M Cetrimonium Bromide (CTAB) and left undisturbed for 10 min. 100 μL of 0.1 M Ascorbic Acid was added to the solution and vigorously agitated for 10 s. The solution was then placed in a hot bath at 90 °C for 1 h, and subsequently decanted and centrifuged at 4000 rpm for 10 min. After centrifugation, the nonpacked layer was decanted off and the precipitant was washed with chloroform in a separation funnel. The washed solution was then dropcast onto a glass coverslip and allowed to dry for 2 h. The remaining liquid was wicked off and the coverslip was washed with DI water and allowed to sit for an additional 2 h, before the water was wicked off and the coverslip dried overnight.

Transient Absorption Measurements: The transient absorption measurements were performed with a Menlo Systems Dual Color 520/780 ASOPS system. The sample was pumped at 780 nm using a Menlo Systems C-Fiber Er:doped fiber laser, and probed at 520 using a Menlo Systems Orange Yb:doped laser. For the experiments in this paper the repetition rate of the probe was locked to $f_r=$100 MHz, and the pump to $f_r+50$ Hz using the Menlo Systems EM100 synchronization electronics. The beams were combined using a dichroic beam splitter, and focused onto the sample with an Olympus 100x objective (immersion oil was not used for these experiments, which limits the NA of the objective, but was necessary due to the orientation of the sample in the microscope). The intensity of the reflected beam was recorded using a New Focus 2107 balanced detector (maximum bandwidth 10 MHz) and the output was digitized using a Tektronics TBS 2000B series digital oscilloscope, which was triggered at the 50 Hz difference frequency for the pump and probe lasers [29], [32]. The ASOPS traces (20,000 points) were averaged 512 times on the oscilloscope, and then dumped to a computer using an in-house LabVIEW program. The averaged traces from the oscilloscope were then further averaged by the software (typical averaging times were 16 min, corresponding to 100 repeats). Vibrational spectra were obtained by Fourier transforming the transient absorption traces using the Fast Fourier Transform (FFT) routine implemented in IgorPro (ver. 9.01). The time scale for the traces, and corresponding Nyquist interval in the Fourier spectra, were determined by recording the number of points between pulses – see the Supporting Information for details.

3. Results and discussion

Fig. 1 shows an example of an ASOPS trace from the Au nanoplate interrogated in this study. The data shows a fast “spike” at zero time, and an oscillating signal on a decaying background. The fast initial signal corresponds to the decay of the hot electrons created by the pump pulse due to electron-phonon coupling. [33] This signal is not resolved in these experiments because of the relatively low bandwidth of the detector. Two types of oscillations can be seen in the data: fast 50 ps oscillations that are assigned to the breathing vibrational mode of the nanoplate [18], [26], [27], and a slower modulation on a few nanoseconds timescale. The low frequency modulations are tentatively assigned to motion of the nanoplate relative to the substrate. [34] The main focus of this study is the breathing modes. It is important to note the following points: First, the signal from the breathing modes appears as a “saw-tooth” pattern at early times, see the inset in Fig. 1, whereas at longer times it appears as a more conventional sine/cosine signal. The saw-tooth pattern implies that multiple modes contribute to the signal, rather than a single mode. Second, the oscillations are clearly present in the signal just before time zero, which means that the lifetime of the breathing mode exceeds the time between pulses for the laser system.

Fig. 1.

Transient absorption trace for a single gold nanoplate. The inserts show how the form of the time-dependent signal changes from a “saw-tooth” pattern to a simple sine/cosine function as time increases.

Fig. 2 shows the Fourier transform of the transient absorption trace from Fig. 1. In this analysis the slowly varying background in the data was removed by fitting and subtracting a double exponential decay function. The main panel plots the FFT magnitude, and the inset shows the real output of the FFT. The spectra has been truncated at frequencies less than 2 GHz. The main peak at 19.4 GHz is assigned to the fundamental breathing mode of the nanoplate ($n=1$), and the higher frequency peaks are assigned to overtones, where the mode number is labeled in the spectrum. The frequencies of the different modes, and their relative amplitudes, are collected in Table 1. The real FFT spectrum shows that the phase of the $n=2$ mode is different to that of the odd-order modes. This indicates that there is a different excitation and/or detection mechanism for the $n=2$ mode. Close inspection of the FFT data shows that the width of the peaks in the spectra are resolution limited: the full-width-at-half-maximum (fwhm) of the fundamental is less than $2\times$ the spacing between points in the frequency domain, see Fig. S3 in the Supporting Information. This implies a vibrational quality factor of $Q>150$ for the fundamental mode. The fwhm of the overtone modes are slightly larger, again see Fig. S3 in the Supporting Information, but still close to the resolution limit in the experiment. These quality factors are much larger than typical values for substrate supported nanoplates [18], and even exceed the values observed for nanoplates on low density substrates [27] or suspended over trenches [35]. It is important to note that the extremely high quality factor observed here is an exception for this sample. Other nanoplates in the sample display smaller quality factors ($Q_1$ on the order of 50–60). Also note that the vibrational frequencies in these experiments are almost exact integer multiples of each other – see Table 1.

Fig. 2.

FFT of the transient absorption trace in Fig. 1 plotted as magnitude versus frequency. The main peak near 20 GHz is assigned to the fundamental breathing mode of the nanoplate. The inset shows the real output of the FFT, which demonstrates that there is a difference in phase between the even and odd modes.

Table 1.

Calculated and measured frequencies and amplitudes of the fundamental and overtone modes of the nanoplate.

Mode #	$f_n$ (GHz)	$A_n/A_1(\mathit{expt}.)$	$A_n/A_1(\mathit{calc}.)$	$f_n/f_1$$(\mathit{expt}.)$
1	19.38 ± 0.11	1	1	1
2	38.76 ± 0.24	0.027	-	2.00
3	57.98 ± 0.31	0.093	0.11	2.99
5	96.87 ± 0.15	0.020	0.04	5.00
7	135.3 ± 0.07	0.007	0.02	6.98

The vibrational frequencies $f$ and quality factors $Q$ for the breathing modes of a nanoplate on a surface can be calculated using the continuum mechanics model described in Refs. [18], [19], [36]. This model assumes an infinitely wide nanoplate separated from the surface by a spacer layer with a different acoustic impedance. Choosing oscillating functions for the displacement of the plate and spacer layer, an outgoing wave for the substrate, and matching the displacement and stress at the different interfaces yields the following eigenvalue equation: ^{20, 19, 36}

$$\tan \left(\xi \right)\frac{c_p{\rho }_p}{c_s{\rho }_s}\left(i+\tan \left(\frac{c_{p}d}{c_{s}h}\xi \right)\frac{c_g{\rho }_g}{c_s{\rho }_s}\right)+i\tan \left(\frac{c_{p}d}{c_{s}h}\xi \right)-\frac{c_g{\rho }_g}{c_s{\rho }_s}=0$$ (1)

where $\xi =\omega h/c_p$ is the complex eigenvalue, $h$ and $d$ are the thickness of the nanoplate and spacer layer, and $c_i$ and ${\rho }_i$ are the longitudinal speeds of sound and densities of the different materials ($p$ = plate, $s$ = spacer layer and $g$ = glass substrate), respectively. The frequencies and quality factors are obtained from $\xi$ by $f=c_p\mathrm{Re}[\xi ]/2\pi h$ and $Q=\mathrm{Re}[\xi ]/2\mathrm{Im}[\xi ]$. Eq. (1) shows that the quality factors depend on the relative acoustic impedances $Z_i=c_i{\rho }_i$ of the nanoplate compared to the spacer laser and the glass substrate.

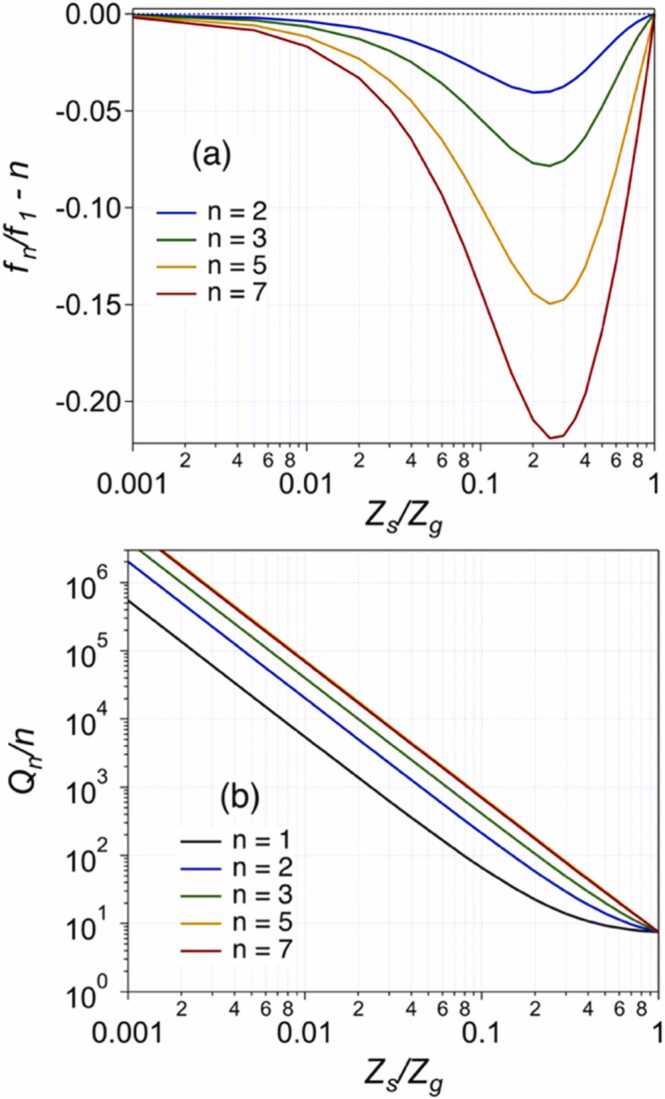
Fig. 3 shows plots of the normalized frequencies and quality factors for a gold nanoplate on a glass surface with a 6 nm spacer layer, as a function of the acoustic impedance of the spacer layer relative to the glass substrate ($Z_s/Z_g$). Varying the acoustic impedance of the spacer layer relative to the glass substrate allows us to investigate the effect of mechanical contact between the nanoplate and the substrate. The nanoplate thickness for these calculations was set to $h=83.5$ nm to match the experimental frequency (for $c_p=3240$ m s⁻¹ $h=83.5$ nm gives $f_1=c_p/2h=19.4$ GHz). In Fig. 3, the frequencies are plotted as $f_n/f_1-n$ to allow easy comparison with the data in Table 1 ( $f_n/f_1-n=0$ means that the overtone frequencies are integer multiples of the fundamental frequency), and the quality factors are plotted as $Q_n/n$. Note that the normalized quality factors $Q_n/n$ are proportional to the vibrational lifetime for this system because $f_n\propto n$.

Fig. 3.

(a) Relative vibrational frequencies ($f_n/f_1-n$) and (b) normalized quality factors ($Q_n/n$) for a nanoplate on a glass surface, as a function of the acoustic impedance of the spacer layer ($Z_s/Z_g$) relative to the glass substrate. The dimensions of the nanoplate and spacer layer are $h=83.5$ nm and $d=6$ nm, respectively. Similar calculations are presented in the Supporting Information for different thickness spacer layers.

The key points from the results in Fig. 3 are: (i) when the spacer layer has the same acoustic impedance as the substrate (i.e., there is effectively no spacer layer and perfect mechanical contact), the eigenvalues are simply multiples of $\pi$ ($\mathrm{Re}\left[\xi \right]=n\pi$, where $n=\mathrm{1,2,3},\dots .)$ so that $f_n/f_1-n=0$, which is consistent with the experiments. However, in this case the calculated quality factors are very low ($Q_1=7.5$) [18], which does not match the experimental results. In this limit the theory also predicts that all the modes have the same decay rate, so that the normalized quality factors $Q_n/n$ are the same for each mode. (ii) As the acoustic impedance of the spacer layer is reduced to values appropriate for organic materials ($Z_s/Z_g\approx 0.25-0.5$), the calculated quality factors become larger, but the relationship between the frequencies of the overtone and fundamental vibrations changes. Specifically, the relative frequencies $f_n/f_1$ are no long integer multiples. The different modes also now have different decay rates: $Q_n/n$ increases as $n$ increases which means that the lower order modes are predicted to decay faster than the higher order modes. (iii) At very low acoustic impedances the model predicts both relative frequencies that are close to integer multiples ($f_n/f_1-n\approx 0$), and high quality factors. Given that the experimental relative frequencies show deviations from integer multiples of less than 1%, the effective acoustic impedance of the spacer layer must be $Z_s/Z_g<0.01$. Note that similar results are obtained for different choices of the spacer layer thickness, which is not known in our experiments, see Fig. S6 of the Supporting Information. This implies that the nanoplate in our experiments must be separated from the substrate by a very low acoustic impedance spacer layer. This situation could arise from an incomplete organic layer at the surface of the nanoplate, and/or roughness of the glass substrate surface.

The very low acoustic impedance inferred from the above analysis implies that the nanoplate examined in this work is essentially “free”, with very little contact with the substrate. For a free nanoplate the vibrational modes are simply given by $u_n\left(z,t\right)=u_n\left(z\right)e^{-i{\omega }_{n}t}$, where $u_n\left(z\right)=-\sqrt{2/h}\cos \left(\frac{n\pi z}{h}\right)$ is the displacement, and the frequencies are ${\omega }_n=n\pi c_p/h$ for $n=1,2,3\dots$ [30]. The even-order modes are symmetric with respect to the geometric center of the NPL and the odd-order modes are antisymmetric, which means that the odd-order modes correspond to changes in volume [30]. The simple form for the displacement for the free nanoplate model allows us to estimate the amplitudes of the different modes in the experiments. Specifically, the overall vibrational response of the nanoplate can be written as $U\left(z,t\right)={\sum }_n{A}_n{u}_n\left(z\right)e^{-i{\omega }_{n}t}$. Assuming that laser excitation causes isotropic expansion, and that the signal is proportional to the volume change, the amplitude coefficients $A_n$ can be obtained by projecting the mode displacements onto the dilation of the nanoplate: $A_n=\int z.u_n\left(z\right)\mathit{dz}/\left(\sqrt{\int z^2\mathit{dz}}\times \sqrt{\int {u_n\left(z\right)}^2\mathit{dz}}\right)$ [23]. This calculation gives amplitudes of $A_n=2\sqrt{6}/{\left(n\pi \right)}^2$ for n = odd, and $A_n=0$ for n = even (see Supporting Information for details). Thus, only the odd-order modes should appear in the Fourier spectra. A possible reason for the appearance of the $n=2$ mode in the vibrational spectrum is non-uniform heating of the nanoplate, which can create a nonuniform initial strain and excite modes with different symmetries than the breathing modes [37]. This effect can occur when the dimensions of the nanostructures are greater than the optical penetration depth in the metal [37], [38], which is certainly the case for the nanoplate studied here. The different phase of the $n=2$ mode is consistent with a different excitation mechanism for this mode. The calculated amplitudes are included in Table 1, and (except for the $n=2$ mode) are in reasonable agreement with the experimental data.

The presence of the overtone modes in the vibrational spectrum of the nanoplate is the reason for the saw-tooth pattern in the early time TAM data. Fig. S5 in the Supporting Information shows the time dependent displacement determined from the calculated $A_n$ values, which matches the experimental results at early times. As noted above, the sawtooth pattern disappears after approximately 3 nanoseconds, while the oscillation due to the fundamental breathing mode continues for the entire length of the trace. This implies that the overtone modes decay faster than the fundamental. To investigate this effect the transient absorption data was Fourier transformed over several different time windows ($0\to 1$ ns, $1\to 2$ ns, etc.). The time-dependent spectra are shown in Fig. S4 of the Supporting Information and the normalized mode amplitudes obtained from the spectra are presented in Fig. 4 for the $n$ = 1, 3 and 5 modes.

Fig. 4.

Normalized amplitudes of the different modes obtained from Fourier transforming the time resolved data in Fig. 1 over different time ranges.

The data in Fig. 4 confirms that the higher order modes decay faster than the fundamental mode, that is, that the nanoplate displays mode specific dynamics. Mode specific dynamics have been previously observed in several transient absorption studies of single nanostructures. For example, Yu et al. investigated chemically synthesized gold nanorods drop cast on a surface, and found that the breathing mode has a different damping compared the extensional mode [22]. Vallee and coworkers also observed mode specific dynamics for the acoustic vibrations of lithographically fabricated Au disks [13]. In both cases, the results could be well explained by continuum mechanics calculations, and the differences in damping were attributed to how the different modes interact with the substrate [13], [20], [22]. However, for our system, there are only weak interactions with the substrate, and the continuum mechanics analysis does not correctly predict the trend in $Q$ with mode number. Thus, a different mechanism from the usual radiation of sound waves into the substrate is needed to explain the results.

Several explanations for the faster damping of the overtone modes of the nanoplate are considered here. First, the stronger damping of the higher frequency modes could be due to viscoelastic effects in the spacer layer. This has been observed in recent experiments by Hettich et al. for thin gold films with polymer spacer layers [36]. However, this seems unlikely for our system because of the weak substrate interactions. A second possibility is that flow of acoustic energy out of the excitation region might be faster for the higher frequency modes [24], [25]. A control experiment for this effect would be to examine the overtone dynamics with different spot sizes of the pump and probe beams. Unfortunately, we do not yet have this data. The faster decay for the overtone modes could be an effect from thermoelastic damping in the metal [39], or from interactions with defects [40]. Experiments are underway to unravel which of these effects are important.

4. Conclusion

Transient absorption microscopy has been used to examine the breathing vibrational modes of a gold nanoplate that has minimal contact with the substrate. The very high quality factors for this system allow the observation of multiple overtones: up to the $n=7$ overtone of the breathing mode. The relative frequencies and amplitudes of the overtones match the prediction of a simple continuum mechanics model of a free plate, with the exception of the $n=2$ mode. This mode is not expected to contribute to the vibrational response of the nanoplate under homogeneous excitation conditions. Its presence is attributed to non-uniform heating [37], which breaks symmetry and is not accounted for in our simple model. Analysis of the transient absorption data shows that the higher order modes decay at a faster rate than the fundamental mode. This effect has not been previously observed, and does not match the predictions of a model for damping due to radiation of sound waves into the substrate [13], [20], [22]. Possible reasons for the faster decay of the overtone modes include frequency dependent thermoelastic effects [39], [40], and/or flow of acoustic energy out of the excitation region [24], [25].

Declaration of Competing Interest

The authors declare that there are no conflicts of interest for the present manuscript.

Biographies

Cameron Wright received his B.S. degree in Chemistry from Butler University in 2019. He is currently pursuing a Ph.D. at the University of Notre Dame. His research interest lies in the development of time-resolved spectroscopy techniques to study the relaxation of single nanostructures.

Prof. Hartland obtained a Ph. D. from UCLA in 1991, and performed postdoctoral studies at the University of Pennsylvania with Prof. Hai-Lung Dai before joining the Department of Chemistry and Biochemistry at the University of Notre Dame in 1994. His research interests are in developing and applying novel spectroscopy techniques to study energy relaxation processes in single nanoparticles. Prof. Hartland is a Fellow of the AAAS, the American Chemical Society and the Royal Society of Chemistry.

Appendix A. Supplementary material

Supplementary material.

.

Data Availability

Data will be made available on request.