Implementation of a practical Markov chain Monte Carlo sampling algorithm in PyBioNetFit

Abstract

Summary

Bayesian inference in biological modeling commonly relies on Markov chain Monte Carlo (MCMC) sampling of a multidimensional and non-Gaussian posterior distribution that is not analytically tractable. Here, we present the implementation of a practical MCMC method in the open-source software package PyBioNetFit (PyBNF), which is designed to support parameterization of mathematical models for biological systems. The new MCMC method, am, incorporates an adaptive move proposal distribution. For warm starts, sampling can be initiated at a specified location in parameter space and with a multivariate Gaussian proposal distribution defined initially by a specified covariance matrix. Multiple chains can be generated in parallel using a computer cluster. We demonstrate that am can be used to successfully solve real-world Bayesian inference problems, including forecasting of new Coronavirus Disease 2019 case detection with Bayesian quantification of forecast uncertainty.

Availability and implementation

PyBNF version 1.1.9, the first stable release with am, is available at PyPI and can be installed using the pip package-management system on platforms that have a working installation of Python 3. PyBNF relies on libRoadRunner and BioNetGen for simulations (e.g. numerical integration of ordinary differential equations defined in SBML or BNGL files) and Dask.Distributed for task scheduling on Linux computer clusters. The Python source code can be freely downloaded/cloned from GitHub and used and modified under terms of the BSD-3 license (https://github.com/lanl/pybnf). Online documentation covering installation/usage is available (https://pybnf.readthedocs.io/en/latest/). A tutorial video is available on YouTube (https://www.youtube.com/watch?v=2aRqpqFOiS4&t=63s).

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Given a model structure, a dataset and a prior distribution for model parameter values, Bayesian inference (Gelman et al., 2014) is a dataset-dependent transformation from the prior distribution, which encodes pre-existing knowledge (external to the dataset of interest) about parameter values, to a posterior distribution, which probabilistically quantifies new data-informed parameter estimates. The posterior is typically characterized through Markov chain Monte Carlo (MCMC) sampling (Andrieu et al., 2003). The MCMC sampling problems that arise in biological modeling applications of Bayesian inference are often challenging, because the posterior is typically far from Gaussian and multidimensional. A major benefit of Bayesian inference is the ability to quantify uncertainties in parameter estimates (in terms of the parameter posterior), and also in predictions, which is accomplished by performing an array of simulations based on different samples from the parameter posterior. Thus, practical MCMC sampling methods are important for assessing the reliability of predictions obtained from data-driven model parameterizations.

Few software tools provide implementations of MCMC sampling methods that enable fast setup of Bayesian inference jobs through compatibility with standardized model-specification formats used in biological modeling, such as SBML (Keating et al., 2020), BNGL (Faeder et al., 2009) and PySB (Lopez et al., 2013). Examples of such software tools include BayesSB (Eydgahi et al., 2013), PyDREAM (Shockley et al., 2018), PTEMPEST (Gupta et al., 2018) and PyBioNetFit (PyBNF) (Thomas et al., 2016; Mitra et al., 2019).

In recent work (Lin et al., 2021), we used an adaptive MCMC sampling method described by Andrieu and Thoms (2008) to make daily 7-day ahead forecasts of newly detected Coronavirus Disease 2019 (COVID-19) cases with Bayesian quantification of forecast uncertainties. In this work, we found the sampling method to be easy to use and efficient. Thus, we implemented this method in PyBNF, a general-purpose software package designed to support parameterization of biological models. We also added various other features, such as support for a negative binomial likelihood function $\text{NB}(r,\mathrm{ }p)$ wherein the hyperparameter $r$ may be specified before inference or jointly inferred with model parameters. We evaluated new PyBNF features by solving an array of test problems and comparing the results against independently generated results.

2 Methods and implementation

PyBNF’s new MCMC sampler, am, is based on the pseudocode labeled ‘Algorithm 4’ in Andrieu and Thoms (2008). See also Supplementary Methods. The am method is adaptive, meaning that the covariance matrix of the multivariate Gaussian proposal distribution (i.e. the distribution used to stochastically generate move proposals), is learned/optimized on-the-fly during sampling. Both the starting point for sampling and the algorithmic parameters of the proposal distribution are initialized on the basis of user-supplied inputs. Warm starts and continuation are supported. Multiple chains may be generated in an embarrassingly parallel fashion on a computer cluster and combined to decrease the wall-clock time required to complete an inference job. If this approach is used, each chain should be evaluated to check for efficient sampling as recommended in Supplementary Methods. Usage of the am method is fully explained in the online PyBNF documentation.

Inference job setup files for test problems are included in the latest PyBNF distribution. The files are also provided as Supplementary Files S1–S4, which are ZIP archives. As described in Mitra et al. (2019), inference job setup requires a configuration file (marked by a CONF filename extension), a model-definition file compatible with either BioNetGen (Harris et al., 2016) or libRoadRunner (Somogyi et al., 2015) (marked by a BNGL or XML filename extension), and one or more files containing data in a tabular format (marked by an EXP filename extension). PyBNF is compatible with models available in BNGL (Faeder et al., 2009) and SBML (Keating et al., 2020) formats. BNGL and SBML files can be generated by diverse tools, including BioNetGen (Harris et al., 2016), PySB (Lopez et al., 2013) and Tellurium (Choi et al., 2018).

3 Results

To assess the correctness and practicality of the am method, we used it to solve a series of increasingly challenging test problems. We evaluated am relative to mh, a sampler implemented in PyBNF version 1.01 (Mitra et al., 2019) that uses a fixed move proposal distribution, and against PyBNF-independent problem-specific solutions.

We started with a linear regression problem involving synthetic data (Supplementary File S1 and Supplementary Methods). For this problem, an analytical expression for the posterior exists. PyBNF’s am method was able to reconstruct the analytical posterior nearly exactly (Supplementary Fig. S1), whereas mh failed with the same computational budget.

We next considered a non-linear regression problem: inferring the values of four parameters in a two-phase exponential decay model for viral dynamics under therapy (Ho et al., 1995; Perelson et al., 1996; Supplementary File S2 and Supplementary Methods). Results generated using PyBNF’s am method were found to be consistent with results generated using problem-specific code (Supplementary Figs S2–S4).

Using a previously established benchmark problem (Harmon et al., 2017; Mitra et al., 2019; Supplementary File S3 and Supplementary Methods), we evaluated the efficiency of am relative to mh. Results obtained using the two methods are consistent (Supplementary Fig. S5). For each of the 16 adjustable parameters in the benchmark problem, we calculated the effective sample size (ESS) for an equal-length chain of parameter values obtained using either am or mh (Supplementary Methods and Supplementary Table S1). ESS for am was typically larger than for mh, indicating greater efficiency. The ratio ESS_am/ESS_mh ranged from 3.03 to 27.7, with a mean (median) of 11.5 (10.5).

Finally, we used PyBNF’s am method to reproduce inferences performed in the epidemiological forecasting study of Lin et al. (2021; Supplementary File S4 and Supplementary Methods). As illustrated in Figure 1, marginal posteriors found using the problem-specific code of Lin et al. (2021) and am are indistinguishable. Supplementary Figures S6–S20 show the full results of our comparison of am against the code of Lin et al. (2021).

Fig. 1.

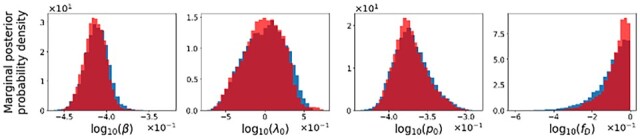
A comparison of selected marginal posteriors was obtained using PyBNF’s am method (blue) and the problem-specific code of Lin et al. (2021; light red). Dark red indicates overlap. The inference problem is that considered in Supplementary Figure S7, which is related to a forecast of COVID-19 incidence for the metropolitan statistical area encompassing Los Angeles, CA. Nomenclature is the same as that of Lin et al. (2021)

4 Conclusions

We find that the new am method available in PyBNF version 1.1.9 is significantly more efficient than the mh method available in earlier versions of PyBNF. We also find that the adaptive sampler is practical, in that it can be used to solve real-world inference problems, including challenging inference problems that arose in a recent COVID-19 forecasting effort (Lin et al., 2021; Fig. 1 and Supplementary Figs S6–S20).

Funding

This work was supported by NIH/NIGMS grant [R01GM111510] and the LDRD program at Los Alamos National Laboratory.

Conflict of Interest: none declared.