Meiotic Crossover Interference: Methods of Analysis and Mechanisms of Action

Abstract

Segregation of chromosomes during meiosis, to form haploid gametes from diploid precursor cells, requires in most species formation of crossovers physically connecting homologous chromosomes. Along with sister chromatid cohesion, crossovers allow tension to be generated when chromosomes begin to segregate; tension signals that chromosome movement is proceeding properly. But crossovers too close to each other might result in less sister chromatid cohesion and tension and thus failed meiosis. Interference describes the non-random distribution of crossovers, which occur farther apart than expected from independence. We discuss both genetic and cytological methods of assaying crossover interference and models for interference, whose molecular mechanism remains to be elucidated. We note marked differences among species.

Introduction

Eukaryotes are typically generated by fusion of two special cells, one coming from each parent. Examples of these cells, called gametes, are eggs and sperm in mammals, eggs and pollen in flowering plants, and spores (or cells resulting from spore germination and growth) in fungi such as yeasts and molds. Gametes contain one copy of each chromosome and are thus haploids. Fusion of two gametes regenerates a diploid organism. The generation of haploid gametes from diploid precursors, called meiosis, requires the accurate segregation of the chromosomes, which in turn requires the pairing of the two copies of each chromosome (called homologs) and their segregation into separate cells. This process occurs with two sequential cell divisions but only one replication of the chromosomes, so that during meiosis diploids give rise to haploids (Figure 1).

Fig. 1.

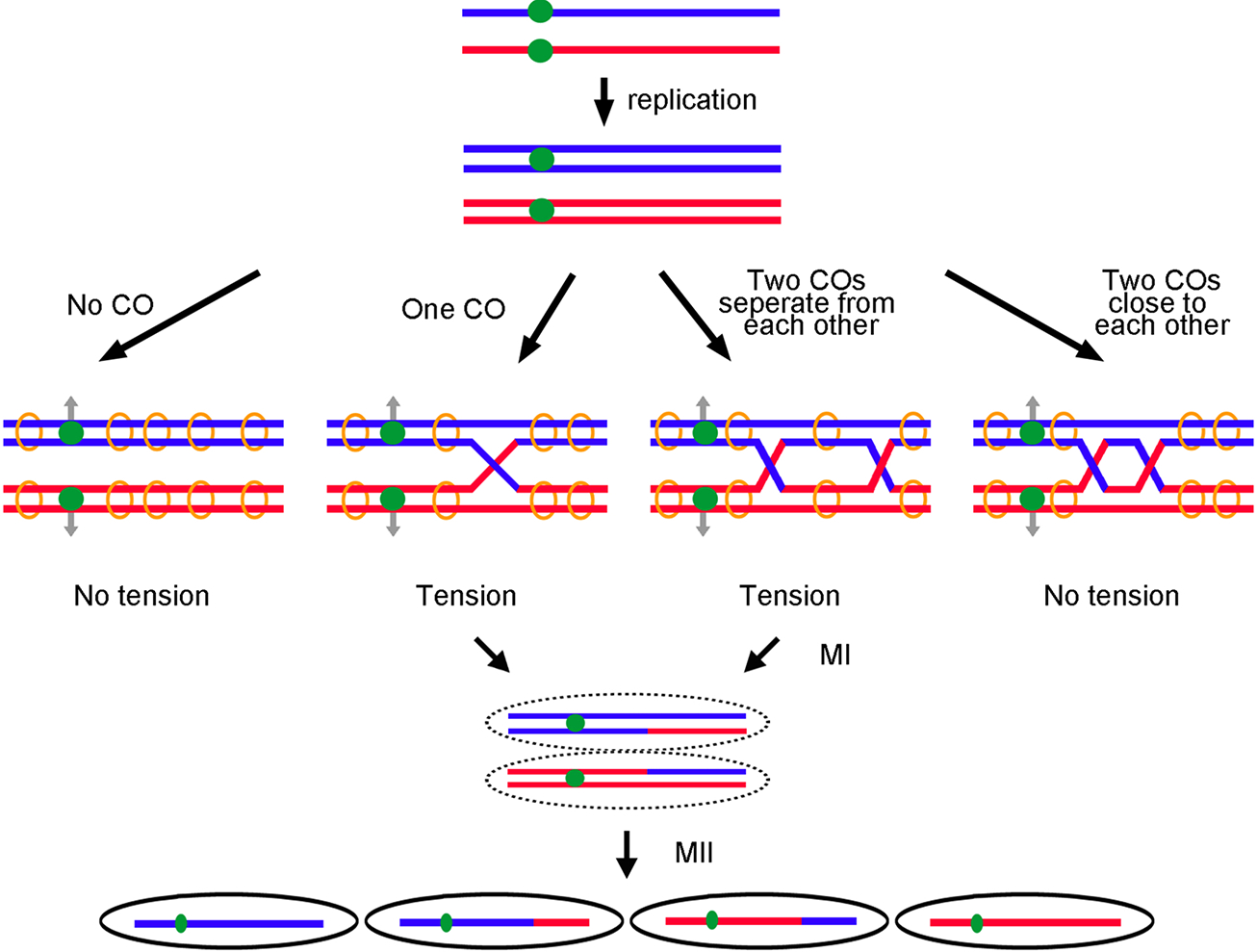
Crossovers are needed for proper chromosome segregation in meiosis. Red and blue lines indicate replicated homologs from each parent. Each line indicates a double-stranded DNA of one chromatid. Green dots represent centromeres. After replication, sister chromatids are held together by cohesins (orange circles). Gray arrows indicate the direction of homologous centromere separation at the first meiotic division (MI). (Left panel) No tension is generated between homologs when no CO is formed. (Middle two panels) Tension is formed between homologs when one CO or two well-separated COs arise. (Right panel) Two COs too close to each other may have too little sister chromatid cohesion between the crossovers to produce tension between homologs to aid segregation. The tension ensures homologous centromeres segregate properly in MI. Crossovers also generate recombinant haploid gametes after the second meiotic division (MII).

Accurate chromosome segregation at the first meiotic division (MI) requires that the two homologs, one from each of the previous parents, find each other and move to opposite sides (poles) of the cell (Figure 1). First, each chromosome is replicated, forming sister chromatids. Then, the replicated chromosomes pair, forming a bivalent (four copies in all). In many species this pairing occurs by homologous recombination between the two copies; there is extensive DNA sequence homology only between homologs, ensuring that each chromosome pairs with its proper partner. Recombination by reciprocal exchange generates a crossover (a cytological chiasma), which connects the two chromosome pairs. When the centromeres of one pair are pulled away from the centromeres of the other pair, tension is generated if there is at least one crossover connecting them and if the sister chromatids are held together by the cohesin complex. Tension appears to be the signal that homologs are properly moving to opposite poles (Nicklas, 1997). Thus, crossovers and cohesion are critical for proper segregation and gamete formation.

Crossovers can occur at most places along a chromosome, but some regions have crossovers much more frequently than others (reviewed in Nambiar et al., 2019). For example, crossovers are rare in or near centromeres, presumably because a crossover there interrupts proper attachment of the fibers (the spindle) to the centromere (via the kinetochore) or the proper pulling of the centromeres to opposite poles (e.g., Nambiar and Smith, 2018). In addition, two crossovers too close together may leave too little cohesin between the crossovers to firmly hold the bivalent together to generate tension upon centromere movement.

This last feature – the placement of crossovers not too close together – is called crossover interference. This chapter discusses the occurrence of interference, ways it can be measured, and models for its action. Interference was first observed in the fruit fly Drosophila melanogaster (Sturtevant, 1915; Muller, 1916) and has been found in nearly all species examined (Perkins, 1962; Mortimer and Fogel, 1974; Barnes et al., 1995; Anderson et al., 2001; Copenhaver et al., 2002; Meneely et al., 2002; de Boer et al., 2006; Baudat and de Massy, 2007; Fowler et al., 2018). The molecular mechanism of interference is still a matter of speculation, although many gene products required for interference have been identified. We first describe methods for assaying interference and discuss complications in interpreting the data, especially given differences among species. We then present proteins required for interference and finally discuss various models for interference.

Methods for measuring crossover interference

Genetic analysis

Two genetic methods to measure crossover interference use either random gametes (spores or next generation progeny) or complete meiotic tetrads. The former has been used with essentially all species investigated, and tetrad analysis is common with fungi. Recently, tetrad analysis has been done in other species, including Arabidopsis thaliana (see below) (Francis et al., 2006), Zea maize (Li et al., 2015), and Mus musculus (Cole et al., 2014). It is generally easier to get more data from random gametes than from tetrads, but in tetrads chromatid relations can be assessed and crossovers can be distinguished from gene conversions (transfer of a genetic marker from one homolog to the other with or without formation of an associated crossover). Tetrads with fewer than four viable spores are often excluded from the analyses; this bias may overlook important events associated with crossovers that, when disrupted, lead to spore death.

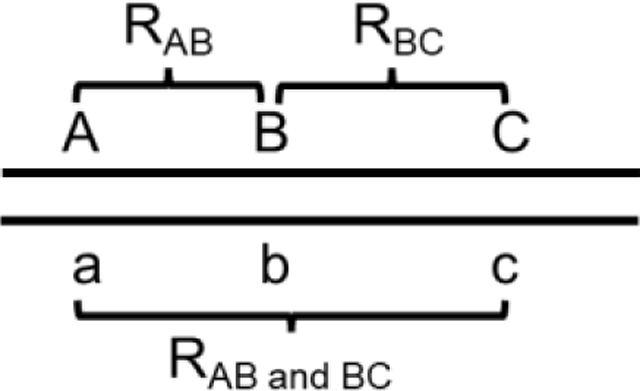
Using random gametes, the coefficient of coincidence (CoC) compares the observed frequency of double crossovers with that expected from independent crossovers. First used in D. melanogaster (Sturtevant, 1915; Muller, 1916) and subsequently in many species, it assumes recombinant chromosomes reflect crossovers and not gene conversion and it assumes no chromatid interference (i.e., that 2-, 3-, and 4-strand double crossovers occur 1:2:1; Figure 2A). CoC using three linked markers is given by the formula

$$CoC\left(S_3\right)=\frac{\text{observed}\text{double}\text{crossover}\text{frequency}}{\text{expected}\text{double}\text{crossover}\text{frequency}}=\frac{R_{AB\text{and}BC}}{R_{AB}\times R_{BC}}$$

where $R$ values are the frequencies of single ($R_{AB}$ and $R_{BC}$) and double ($R_{ABandBC}$) crossovers from a cross of this form:

Fig. 2.

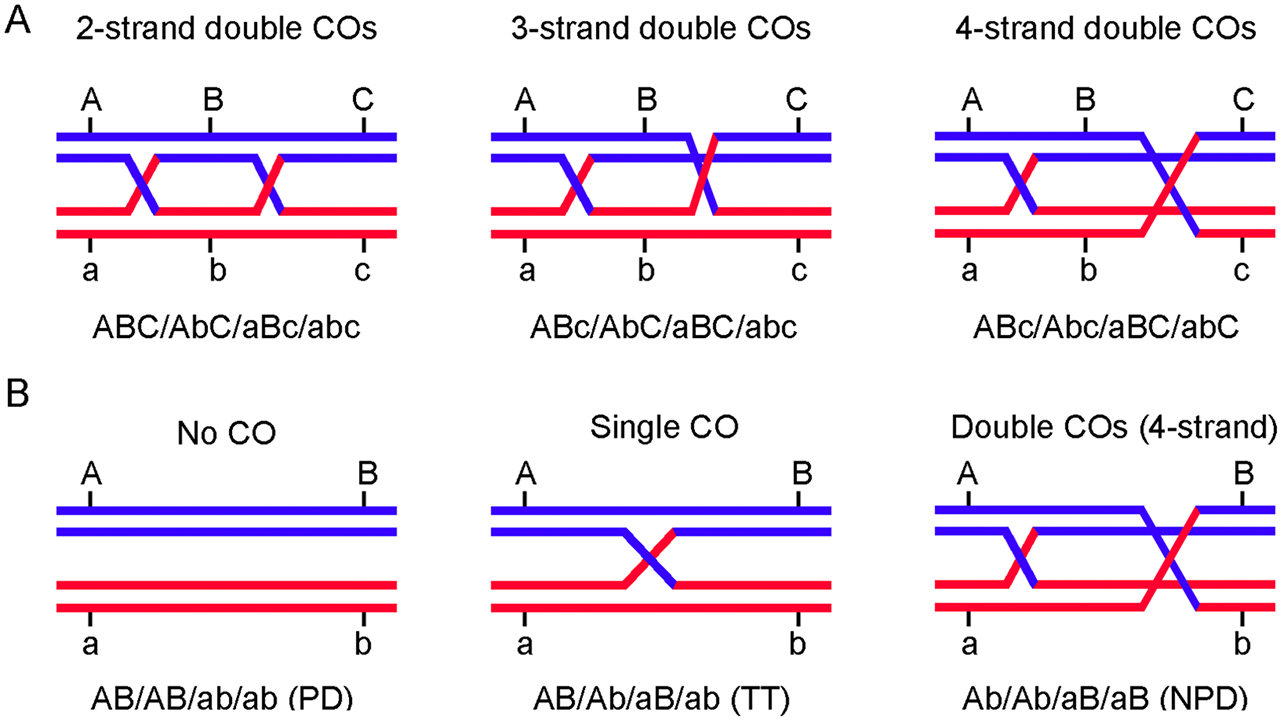
Characterizing crossovers in meiotic tetrads with genetic markers. (A) Three-marker tetrad analysis can identify two-, three-, or four-strand (chromatid) double crossovers. (B) Three types of tetrads in two-marker tetrad analysis. PD, parental di-type; TT, tetra-type; NPD, non-parental di-type. The genotypes of the four gametes are indicated below each panel.

A variation uses a fourth marker to allow comparisons with the two intervals assayed for crossovers (A-B and C-D) to be kept nearly constant in size but moved farther and farther apart.

$$CoC\left(S_4\right)=\frac{\text{observed}\text{double}\text{crossover}\text{frequency}}{\text{expected}\text{double}\text{crossover}\text{frequency}}=\frac{R_{AB\text{and}CD}}{R_{AB}\times R_{CD}}$$

In both cases, interference (I) = 1 – CoC. In D. melanogaster and Neurospora crassa S₄ is lowest at short genetic distances and increases to near unity at ~40 – 50 centiMorgans (cM); in other words, in these species interference is strong at short distances and disappears at about the distance of one crossover per meiotic cell (50 cM) (Foss et al., 1993) (Figure 3).

Fig. 3.

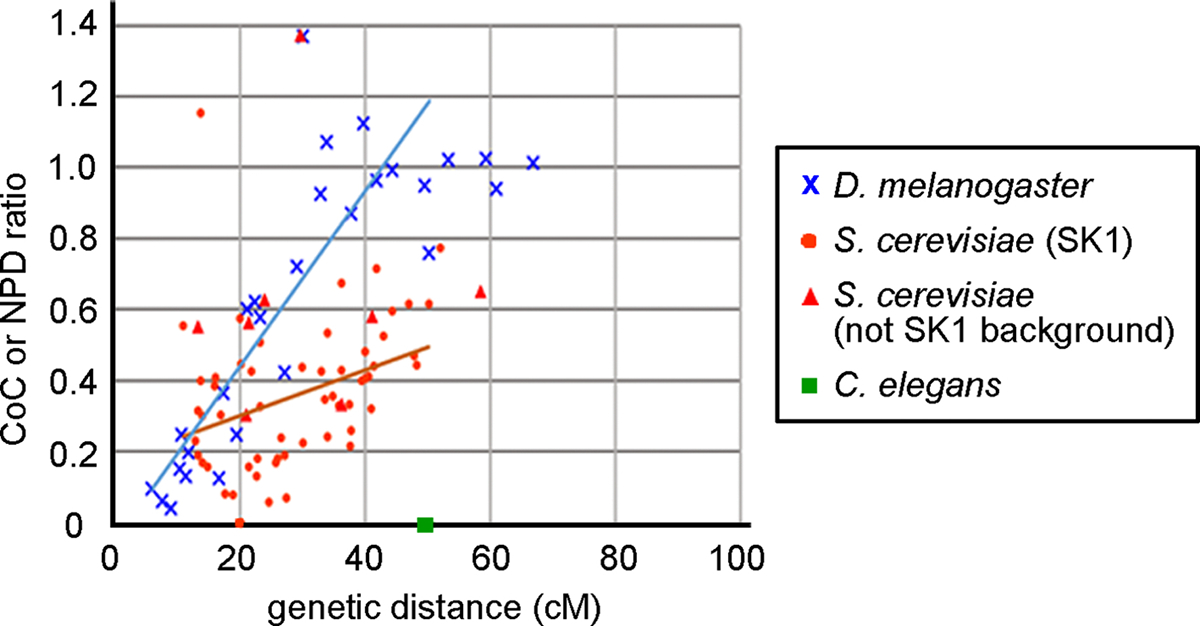
Correlation between crossover interference and genetic distance in D. melanogaster, S. cerevisiae and C. elegans. D. melanogaster CoC (S4) data (Foss et al., 1993; Morgan, Bridges, & Schultz, 1935), S. cerevisiae NPD ratio data (Argueso et al., 2003; Argueso, Wanat, Gemici, & Alani, 2004; Chua and Roeder, 1997; He et al., 2020; Novak, Ross-Macdonald, & Roeder, 2001; Oh et al., 2007; Shinohara, Sakai, Shinohara, & Bishop, 2003; Stahl et al., 2004; Sym & Roeder, 1994; Tsubouchi, Zhao, & Roeder, 2006; Zanders & Alani, 2009) and the genetic distance of each interval are plotted. C. elegans makes only one crossover per chromosome (Barnes et al., 1995; Meneely et al., 2002), indicating it has complete interference up to 50 cM, the genetic length of each chromosome. Most S. cerevisiae data were analyzed in the SK1 background (red circles), and eight data points were analyzed in other strain backgrounds (red triangles). N. crassa data are similar to those of D. melanogaster (Foss et al., 1993). D. melanogaster data with < 5 double recombinants and S. cerevisiae data with < 5 expected and < 5 observed NPD tetrads were not included. S. cerevisiae data were re-analyzed using the “better way” of Stahl (2008). The blue and orange lines, respectively, show the linear regression analysis of data from D. melanogaster (y = 0.025x − 0.053; r2 = 0.72) and S. cerevisiae (y = 0.0064x + 0.17; r2 = 0.17); for this analysis, data with > 50 cM and S. cerevisiae data with NPD ratio > 1 were omitted.

Fungi and some non-vascular plants allow convenient tetrad analysis, as does the flowering plant A. thaliana mutant qrt1, which retains the four pollen from one meiosis in a single cell (Rhee and Somerville, 1998; Francis et al., 2006). CoC analysis, as above, could be used with tetrad data, but a simpler alternative uses only two markers denoting the three tetrad classes (Figure 2B). The observed frequency of non-parental ditype (NPD) tetrads reflects 4-strand double crossovers (Figure 2A). Assuming no chromatid interference, as is the case where tested (Emerson and Beadle, 1933; Mortimer and Fogel, 1974; Munz, 1994; Zhao et al., 1995; Stahl and Housworth, 2009; Miller et al., 2016), and no crossover interference, the expected frequency (f) of NPD, tetratypes (T; single crossover) and parental ditypes (PD; no crossover) can be calculated from the Haldane relation of genetic distance (in Morgans) and the observed recombinant frequency R.

$$\text{Recombinant}\text{frequency}(R)=fNP{D}_{observed}+\frac{1}{2}f{T}_{observed}$$

$$\text{genetic}\text{distance}(\text{X})=-\frac{1}{2}\ln (1-2R)$$

The NPD ratio = NPD_observed/NPD_expected, and I = 1 – NPD ratio.

Papazian (1952) used Haldane’s formula to calculate the expected NPD frequency from the observed T frequency.

$$fNP{D}_{expected}=\frac{1}{2}[1-f{T}_{observed}-{(1-\frac{3}{2}f{T}_{observed})}^{2/3}$$

Stahl (2008) extended this analysis to include the expected frequencies of each of the three classes based on the observed recombinant frequency and Haldane’s equation.

$$f{T}_{expected}=\frac{2}{3}\left(1-e^{-3X}\right)$$

$$fNP{D}_{expected}=\frac{1}{2}\left[\left(1-e^{-2X}\right)-f{T}_{expected}\right]$$

$$f{P}_{expected}=1-fNP{D}_{expected}-f{T}_{expected}$$

Papazian’s analysis is not valid for T close to 2/3, but Stahl’s “better way” is valid for all values. In addition, Stahl’s analysis, based on all three tetrad classes, gives more reliable statistical analysis of the data than Papazian’s (Stahl, 2008).

Two studies in yeasts (Munz, 1994; Shinohara et al., 2003) found similar degrees of interference using both random spore and tetrad (NPD; Papazian method) analyses, as expected.

Cytological analysis

A physical (cytological) method determines the position of fluorescent markers, seen as foci in a microscope, along a chromosome. Typically, the chromosomal axis is labeled uniformly, to allow distance measurements along the chromosome, and a chromosomal end is labeled uniquely, to identify an individual chromosome. A chromosome is divided into many equal-length intervals, and the frequencies of foci in each interval and the frequencies of two foci in each pair of intervals are determined. Interference is seen as foci being farther apart than expected from random positioning. Fung et al. (2004) found that synapsis initiation complex proteins (e.g., Saccharomyces cerevisiae Zip2 and Zip3) showed interference. Similar markers used are those thought to indicate “crossover designation,” for example Caenorhabditis elegans COSA-1, mouse MLH1, and A thaliana MLH1 (Anderson et al., 1999; Chelysheva et al., 2010; Yokoo et al., 2012). S. cerevisiae Zip3 promotes CO formation, is required for CO interference (Table 1), and has been proposed to bind to DSB sites after they are “designated” by an unknown factor for CO formation (Agarwal and Roeder, 2000; Serrentino et al., 2013). C. elegans COSA-1 and A. thaliana MLH1 are located between bivalents at or near a chiasma (Chelysheva et al., 2010; Yokoo et al., 2012). COSA-1 is also needed for CO formation (Yokoo et al., 2012). The chromosomal distribution of mouse and A. thaliana MLH1 foci reflect the number and distribution of crossovers (Anderson et al., 1999; Chelysheva et al., 2010). These observations support these foci being a valid proxy for crossovers.

Table 1.

Proteins with diverse functions are required for crossover interference

Protein	Species	Function	Interference assay	Reference
Synaptonemal complex (SC)
Zip1	S. cerevisiae	Transverse filament of the SC	NPD ratio	Sym and Roeder, 1994
SYP-1	C. elegans		Cytology	Libuda et al., 2013
Zyp1	A. thaliana		Cytology	Capilla-Pérez et al., 2021
Asy1	A. thaliana		Cytology	Lambing et al. 2020
Zep1	O. sativa		Cytology	Wang et al., 2010
Sycp1	M. musculus		Cytology	de Boer et al., 2006
DPY-28	C. elegans	Condensin I subunit; chromosomal axis formation	Cytology	Tsai et al., 2008
Regulating CO formation
Msh4-Msh5	S. cerevisiae	Binds Holliday junctions; facilitates CO formation	NPD ratio	Novak et al., 2001; Argueso et al,. 2004; Getz et al., 2008
			NPD ratio and CoC	Nishant et al., 2010
			CoC	Anderson et al., 2015
Zip3	S. cerevisiae	SUMO E3 ligase; required for SC formation and CO formation	CoC	Anderson et al., 2015
Mlh1-Mlh3	S. cerevisiae	Endonuclease; binds and resolves Holliday junctions	NPD ratio	Argueso et al,. 2003
Slx4	S. cerevisiae	Endonuclease; resolves Holliday junctions	NPD ratio	Higashide and Shinohara, 2016
Sgs1	S. cerevisiae	DNA helicase; chromosome synapsis; meiotic joint molecule and CO formation	NPD ratio	Oh et al., 2007
			CoC	Anderson et al., 2015
Blm	D. melanogaster		CoC	Hatkevich et al., 2017
Mer3	S. cerevisiae	DNA helicase; promotes CO formation	NPD ratio	Nakagawa and Ogawa, 1999
Spo16	S. cerevisiae	Facilitates SC and CO formation	NPD ratio	Shinohara et al., 2008
Spo22 (Zip4)	S. cerevisiae	TPR-like repeat protein; facilitates SC formation and CO formation	NPD ratio	Tsubouchi et al., 2006; Shinohara et al., 2008
Pch2	S. cerevisiae	Regulating chromosome synapsis and CO formation	NPD ratio	Joshi et al., 2009; Zanders and Alani, 2009
Pch2	A. thaliana		CoC	Lambing et al., 2015
RTEL-1	C. elegans	CO formation	Cytology	Youds et al., 2010
DNA damage check point
Tel1	S. cerevisiae	Protein kinase regulating DNA double-strand-break response	CoC	Anderson et al., 2015
Tel1	S. pombe		CoC	Fowler et al., 2018
ATM	M. musculus		Cytology	Barchi et al., 2008
Topoisomerase II and SUMOylation
Top2	S. cerevisiae	DNA topoisomerase; binds axial cores	Cytology	Zhang et al., 2014b
Ndj1	S. cerevisiae	Regulating meiotic SPB cohesion and telomere clustering	NPD ratio	Chua and Roeder, 1997
Slx5/8	S. cerevisiae	SUMO-targeted ubiquitin ligase (STUbL)	Cytology	Zhang et al., 2014b
Sir2	S. cerevisiae	Activation of STUbL activity of Slx5/8	Cytology	Zhang et al., 2014b

Interference is measured as in CoC analysis: I = 1 – CoC, where

$$CoC=\frac{\text{observed}\text{double}\text{focus}\text{frequency}}{\text{expected}\text{double}\text{focus}\text{frequency}}=\frac{F_{AB}}{F_A\times F_B}$$

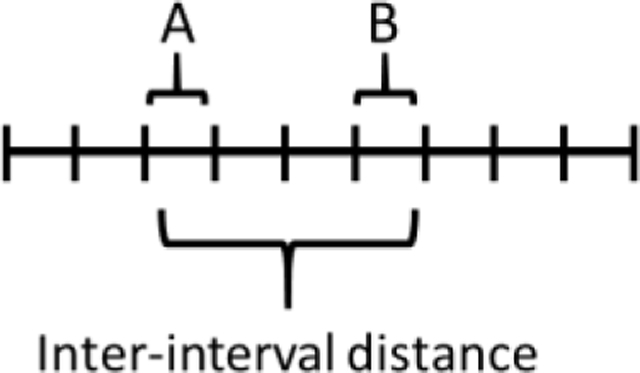
This cytological method does not require genetic markers and can be used in mutants that do not complete meiosis. But it requires spreading nuclei and high-resolution microscopy, which may be difficult for large numbers of cells. In addition, distance is measured as physical distance along the chromosomal axis, which may not be proportional to genetic map or DNA length. In S. cerevisiae, however, cytological interference extends over ~0.45 microns of axis, which corresponds to ~44 cM (Zhang et al., 2014), indicating equivalence of cytological and genetic interference. In A. thaliana and humans, the data are ~25 microns (~61 cM) and ~5 microns (~50 – 60 cM), respectively (Gruhn et al., 2013; White et al., 2017; Capilla-Pérez et al., 2021). [See Table 2 for relations between DNA length (Mb), genetic distance (cM), and axis length (microns) in various species.] It should be noted that several S. cerevisiae mutants (e.g., zip1Δ, sgs1Δ, and msh4Δ) show cytological interference but not genetic interference (Sym and Roeder, 1994; Novak et al., 2001; Fung et al., 2004; Oh et al., 2007). Simple explanations are that a) S. cerevisiae strains from different genetic backgrounds were used to test the two methods and b) these proteins may be required at a stage of crossover formation after crossover “designation” (e.g., Zip3 binding) (De Muyt et al., 2012; Zakharyevich et al., 2012; Zhang et al., 2014b). Nevertheless, these mutants indicate some difference in cytological vs. genetic interference.

Table 2.

Ratio of genetic distance to physical distance varies >500-fold among species

Species	Genetic map length (cM)	Physical map length (Mb)	Axis length (μm)§	Genetic length/ physical length (cM/Mb)	Axis length/physical length (μm/Mb)	Genetic length/axis length (cM/μm)
S. cerevisiae	4206a	12a	43b	350	3.6	98
S. pombe	2100c	13.8d	--	150	--	--
N. crassa	1075e	43f	--	25	--	--
A. thaliana	597g	135h	240i	4.4	1.8	2.5
D. melanogaster	287j	180k	--	1.6	--	--
D. melanogaster Chr X	65.3j	24k	15l	2.8	0.63	4.4
C. elegans	300	103m	29n	2.9	0.28	10
Humans	3630o	3019o	--	1.2	--	--
Human autosomes	3451o	2740o	260 –320p	1.3	0.09 – 0.12	11 – 13
M. musculus	1373o	2577o	--	0.53	--	--
M. musculus autosomes	1316o	2320o	150 – 162q	0.56	0.06 – 0.07	8.1 – 8.8

^§Axis length was measured by light microscopy of formaldehyde-fixed samples.

^aCherry et al. (1997); Mortimer et al. (1992)

^b Song et al. (2021)

^c Egel (2004)

^dWood et al. (2003)

^e Perkins and Barry (1977)

^f Galagan et al. (2003)

^gLister and Dean (1993),

^hThe Arabidopsis Genome Initiative (2000)

^I Morgan et al. (2021)

^j Comeron et al. (2012)

^k Adams et al. (2000)

^l Page et al. (2001)

^m C. elegans Sequencing Consortium. (1998)

ⁿLascarez, Lagunas and Colaiácovo, unpublished data

^o Jensen-Seaman et al. (2004)

^p Codina-Pascual et al. (2006)

^q Vranis et al. (2010)

Complications in interpreting interference data

While it is often said that this or that species has crossover interference, the reported strengths clearly differ among species and often across a given genome (Figure 3). Some, such as C. elegans, appear to have absolute interference – two crossovers on one chromosome do not appear (Barnes et al., 1995; Meneely et al., 2002). Extensive data show strong interference for short intervals (<10 cM) in D. melanogaster (~0.95) and in N. crassa (~0.8), gradually decreasing for longer intervals, and becoming negligible at ~40 -- 50 cM (Foss et al., 1993) (Figure 3). S. cerevisiae interference ranges from near 0 up to ~0.8, but among data analyzed in Figure 3 there is a less distinct trend with distance: intervals of similar genetic size can have different degrees of interference. According to the only report of which we are aware (Strickland, 1958), Aspergillus nidulans has no detectable crossover interference. Schizosaccharomyces pombe has statistically highly significant but weak crossover interference (0.26 ± 0.051) in the one pair of adjacent intervals assayed extensively (Fowler et al., 2018); other intervals may have no interference, but the data for most individual intervals reported are limited (Munz, 1994).

The ratio of genetic distance (cM) to DNA length (Mb) differs by a factor of >500 among species (Table 2), indicating that a similar level of interference in two species may reflect vastly different DNA distances. In addition, each micron of cytological axis length corresponds to different lengths of DNA. A simple interpretation is that DNA loops of increasing size extend from the axis as the parameter (micron of axis length/Mb) decreases. Consequently, different genetic distances correspond to different axis lengths among species. In multicellular species the parameter (cM/micron of axis) ranges from about 2 to 10; in S. cerevisiae, the value is about 100 (Table 2).

Interpreting these data is complicated by additional considerations (see also Berchowitz and Copenhaver, 2010). Gene conversions, whose formation is closely related to that of crossovers, are often stated not to interfere with each other. Mortimer and Fogel (1974) and Foss and Stahl (1995) report CoC = 1.0 (95% confidence interval, or CI, = 0.75 – 1.45 or wider) for gene conversions at the closely linked ARG4 and THR1 genes of S. cerevisiae. Because the number of double gene conversions is small (13 and 28, respectively), the data do not rule out weak interference, either positive or negative. Sequencing 980 chromatid arms from progeny of D. melanogaster hybrids, Miller et al. (2016) found 291 chromatid arms with one or more gene conversions and 33 with two or more gene conversions. 86 doubles are expected from independence; thus, CoC = 0.38 (CI = 0.28 – 0.49), indicating highly significant positive interference of gene conversions. Using a different method of analysis, the authors, however, concluded that gene conversions do not show interference. Miller et al. (2016) found 541 crossovers and 52 double crossovers; CoC = 0.17 (CI = 0.13 – 0.22), indicating strong crossover interference, as concluded by Miller et al. (2016) and others cited above for D. melanogaster. Similarly, for crossovers and non-crossovers (124 such doubles observed), CoC = 0.77 (CI = 0.63 – 0.91), indicating weak but significant interference of these events. Some but not other classes of gene conversion (6:2, 5:3, or aberrant 4:4) with an associated crossover also interfere with a nearby crossover in another interval in some species but not in others (Kitani, 1978; Mancera et al., 2008; Getz et al., 2008; Stahl and Foss, 2008). These results may reflect different relative activities of two pathways of recombination, one with and one without interference, as discussed in the next paragraph. Although the original definition of interference referred to genetic crossovers, more recently emphasis has been put on spatial interference of cytological markers along chromosomes, as described above. These foci are inferred to mark “designated” crossover sites, which may be closely related to, but not guaranteed to become, crossovers, as noted above. Thus, it is important to specify what is measured to indicate interference.

An added complication is the possibility of two or more types of meiotic recombination occurring in the same species. In S. cerevisiae, A. thaliana, and mice two pathways of crossover formation have been shown – one with and one without interference (e.g., Ross-Macdonald and Roeder, 1994; Copenhaver et al., 2002; de los Santos et al., 2003; Argueso et al., 2004; Higgins et al., 2004; Stahl et al., 2004). Direct support for this view comes from studies of S. cerevisiae zip1 and msh5 mutants, in which the residual crossovers (20 – 40% of wt frequency) show little if any interference (Sym and Roeder, 1994; de los Santos et al., 2003). In an mms4 mutant, defective in another postulated pathway, interference is not significantly different from that in wt (de los Santos et al., 2003). Some authors have proposed that the non-interfering pathway acts early, to establish chromosome pairing, and the interfering pathway acts late, to facilitate chromosome disjunction (de los Santos et al., 2001; de los Santos et al., 2003; Getz et al., 2008). In some species, crossing over aids both events, but the degree to which the pathways differ is unclear. They could diverge at the beginning of the recombination pathway (before DSB formation) or at the end (resolution of Holliday junctions). For example, nicked Holliday junctions could arise in the “early” pathway and be resolved by Mus81-Mms4, while non-nicked (ligated) Holliday junctions could arise in the “late” pathway and be resolved by Msh4-Msh5 and Mlh1 and its partners (e.g., Getz et al., 2008; Berchowitz and Copenhaver, 2010). These pathways could act differentially in different genomic intervals, further complicating the interpretation of interference strength in a given species.

Important to keep in mind is that species differ. For example, Mus81-Eme1 is essential for Holliday junction resolution and >95% of crossover formation in S. pombe (Boddy et al., 2001; Smith et al., 2003; Cromie et al., 2006), but its homolog Mus81-Mms4 is required for only ~20% of crossovers in S. cerevisiae (de los Santos et al., 2003; Argueso et al., 2004), although it is required for abundant viable spore-formation in both species. Some proteins essential for recombination in some species, such as Dmc1 DNA strand-exchange protein, are not apparent in other species. [Among tested species, those with Dmc1 require recombination for chromosome synapsis, but those without it do not (Stahl et al., 2004)]. We know of no species in different genera in which the same set of orthologous proteins is required for meiotic recombination, emphasizing that species differ. Thus, it is risky to use data from one species in interpreting data from another species. Rather, one should state the species under discussion and not dismiss a view proposed for one species because of counter data in another species. Observations and models of interference in any species are nevertheless important for thinking about the mechanism of interference in other species.

Proteins Required for Crossover Interference

Mutants with altered crossover interference have been identified in a variety of species. Table 1 groups the corresponding proteins according to their known functions in meiotic recombination and DNA metabolism. Homologs of some of these proteins are found in widely divergent species, suggesting some underlying similarity in interference. The molecular mechanisms by which these proteins impart interference remain largely unknown.

Models of Crossover Interference

Numerous models for crossover interference have been proposed. Many have led to mathematical models that account for existing data, such as the relation of interference and genetic or cytological distance, but few have specified a molecular mechanism, including roles for proteins required for interference (Table 1). Some models can be considered genetic, in the sense of having properties related to genetic distance, or physical, in the sense of measuring kb of DNA or microns of chromosome axis in fully condensed chromosomes. In both cases, however, the features of the models often account for interference allowing exactly one crossover in the genetic distance (50 cM) required by the definition of cM and over which interference acts, at least in D. melanogaster and N. crassa (Figure 3). (50 cM, or 0.5 Morgan, is the genetic separation generated by one crossover in a bivalent, in which half the chromosomes are recombinant in the defined interval; Figure 2B). Here, we discuss models in several classes. Words or phrases in quotation marks below are from the references cited.

Trigger model

Fox (1973) postulated that a “chiasma determination mechanism passes along the chromosome at a constant rate” and is “triggered” to form a chiasma. It continues to move along the chromosome and “requires a fixed time to become recharged” to form another chiasma. The trigger was proposed to be “some feature of the secondary structure of the chromosome,” which is rare in chromosomal regions with few chiasmata, such as the heterochromatic centromeres. Although further descriptions and predictions of the mechanism were not provided, this may be the first model postulating an entity moving along the chromosome to promote a limited number of crossovers in a given region.

Polymerization models

Egel (1978) proposed that “nodes” (required for the “establishment of an exchange possibility”) are formed only before chromosome synapsis and “serve as initiation centres at which synapsis is started.” One node, presumably activated at random, starts polymerization of the synaptonemal complex (SC). As the SC grows by polymerization, it inactivates additional nodes, thereby preventing further crossovers in the region over which there was SC polymerization.

King and Mortimer (1990) also proposed a model involving polymerization, but one in which the polymer (separate from the SC) both promotes and inhibits rather than simply inhibits crossover formation. In their model, “early structures” bind randomly along the already established SC and are held within it, thereby preventing interaction with another chromosome. Each structure initiates bidirectional polymerization and “give[s] rise to the late recombination nodules,” which initiate crossover formation. The growing polymer then prevents other early structures from binding or ejects those already bound but not yet polymerizing. The ejected structures can act on other SC regions without a structure-induced polymer. This feature assures that all chromosomal regions have the opportunity for crossovers, provided there are enough structures present. The nature of the early structures, the ensuing polymer, and nodules was not specified.

Reaction-diffusion models

In this class of models, a factor, such as a protein, diffuses in one dimension along a chromosome or bivalent for a limited distance and affects crossover formation, either positively or negatively. This factor may be restricted by the SC from moving to another bivalent. Its effect is thus limited to the chromosome or bivalent it is on, as expected for imposition of interference along but not between chromosomes.

Holliday (1977) proposed that an activating factor, limited in amount, converts an unstable crossover into a stable chiasma. The factor is proposed to be a protein that binds DNA cooperatively and forms a complex with the crossover to stabilize it. It does not interact with a non-crossover structure. Diffusion of the protein along the chromosome to the crossover site depletes the surrounding region and prevents formation of a second stable chiasma in that region. Although not stated in the model, presumably the factor is initially randomly distributed along the chromosome. Organisms that lack interference, such as A. nidulans (Strickland, 1958), are proposed to have an unusually high level of the activating protein. To account for interference not extending across centromeres in some species, Holliday proposed that the centromere is a barrier to diffusion of the protein.

Fujitani et al. (2002) proposed that “random walkers” are randomly distributed along chromosomes; each diffuses randomly in one dimension and with a set rate “becomes immobilized and matures into a crossover point.” Collision of two random walkers inactivates both; collision of a moving walker with an immobilized walker inactivates the moving one. This model, like those above, generates exactly one crossover in an interval of 50 cM. Mathematical models built on two parameters (the initial density of walkers and the rate at which a walker becomes immobilized) account for data in D. melanogaster and N. crassa. As in other models above, the nature of the walkers and the means by which they mature into crossovers were not stated.

Rog et al. (2017) found that proteins of the C. elegans SC behave as though they are in liquid crystals – they are sensitive to 1,6-hexanediol, which disrupts such structures, and quickly diffuse from the surrounding area into a particular region (as observed after localized irradiation of a photoconvertible derivative of the SC protein SYP-3). The latter property of liquid crystals is similar to that of lipid membranes, in which proteins can readily diffuse within, but not out of, the membrane. This property would allow a protein to diffuse along the chromosome and interact with sites on that chromosome but not with those on another chromosome, as demanded for crossover interference. Thus, Zhang et al. (2018) propose that SC proteins, including ZHP-3, diffuse in one dimension and a combination of positive and negative effects allows only limited numbers of crossovers (one for C. elegans) to form along a chromosome. Additional proteins required for interference include the SC protein SYP-1, the condensin subunit DPY-28, and the protein kinase RTEL-1 (Table 1). Homologs of SYP-1 and RTEL-1 are also required for interference in other species, suggesting that the C. elegans mechanism may be widespread.

Morgan et al. (2021) showed that the HEI10 protein of A. thaliana behaves as predicted by a reaction-diffusion model for an activator of crossover formation. HEI10 is initially nearly uniformly distributed along each bivalent and then condenses into several small foci and eventually into one to three foci, approximating the number of genetic crossovers per bivalent in other experiments. How HEI10, a putative ubiquitin E3 ligase and Zip3 homolog, promotes crossovers is unclear.

Counting models

Foss et al. (1993), like previous authors, pointed out that interference in D. melanogaster and N. crassa is strong for short genetic intervals but diminishes to nearly zero for intervals ~40 – 50 cM or greater (Figure 3). Note that 50 cM corresponds to about 20 Mb in D. melanogaster but only 2 – 3 Mb in N. crassa (Table 2). Foss et al. (1993) therefore sought an interference mechanism that measures genetic, not physical, distance. In their model “recombination-initiation events” are randomly placed along chromosomes. By unstated mechanisms, one is matured into a crossover, the next m events in one direction along the chromosome are matured into non-crossovers (gene conversions or sister chromatid interaction), and the next event is matured into a crossover. The authors developed mathematical equations with the variable m and found that data for D. melanogaster and N. crassa were fit well with m = 4 and 2, respectively. Mortimer and Fogel (1974) proposed that “recombinogenic events are distributed along the chromosome in an independent fashion” but with alternating crossovers and non-crossovers; this model is equivalent to the counting model of Foss et al. (2003) with m = 1.

The counting model predicts that between two neighboring crossovers there should be m non-crossovers. Short intervals between two crossovers should be enriched for non-crossovers relative to the same intervals on chromosomes without flanking crossovers. Foss and Stahl (1995) tested this prediction in S. cerevisiae and found it did not hold. Rather, there were fewer non-crossovers (gene conversions) in the short interval in tetrads with flanking crossovers compared to those without flanking crossovers, suggesting interference between crossovers and non-crossovers, as noted above.

Mechanical models

Interference might result from a purely mechanical, rather than biochemical, property of a chromosome. Muller (1916) proposed that a chromosome is too stiff to bend near an existing crossover and thus allow formation of another crossover nearby. Kleckner et al. (2004) compared a chromosome to a stiff beam coated with a brittle ceramic film. Bending the beam would put increasing stress on the film until it cracked and relieved the surrounding stress in the film. By analogy, they proposed that formation (or designation) of a crossover requires stress (the opposite of Muller’s proposal) resulting from chromosome expansion and that stress in turn is relieved by crossover formation. Thus, a crossover would not form until stress built up, but once a crossover formed, there would be no stress nearby to allow formation of a second crossover. Stress would monotonically increase with distance from the first crossover, thus allowing, with increasing probability, another crossover some distance away. Support for this model comes from the partial reduction of interference, measured as inter-focus distance between Zip3 foci, in a top2 mutant deficient in DNA topoisomerase II, which relaxes supercoiled DNA (Zhang et al., 2014b).

In an expansion of the beam-film model (Zhang et al., 2014a), certain “precursors” are “designate[d] to eventually mature as a crossover.” Thus, the act of designation imposes interference. “The precursors for CO patterning are generally assumed to be the total array of double strand break (DSB)-initiated interactions between homologs,” and “yeast DSBs are evenly spaced.” DSBs become “designated” to become crossovers by an unstated mechanism but are reflected by the distribution of Zip3 foci (see Cytological analysis above). The probability (frequency) curve resembles that of CoC vs. cM in D. melanogaster (Figure 3). In S. cerevisiae, the distance at which adjacent Zip3 foci occur at the frequency expected for independence is roughly 100 kb or about 50 cM. Kleckner et al. (2004) emphasize, however, that crossover designation (interference) measures axis length, not kb of DNA or cM of genetic map length.

The beam-film model has been used to formulate mathematical models for interference (Zhang et al., 2014a). These models use multiple parameters reflecting such features as the average number of precursors per chromosome, their distribution along chromosomes (random or even or intermediate), and the “designation driving force.” Data from various species fit the model when appropriate values for these parameters are chosen. With nine adjustable parameters, the model fits the data from various species (Zhang et al., 2014a).

Because few molecular (biochemical) features of the beam-film model are specified, it is hard to test this model genetically. The presumed even spacing, by an unstated mechanism, of precursors (DSBs) in yeast would seem to be interference itself, perhaps one of several factors leading to crossover interference. In addition, it seems counterintuitive that crossovers rather than DSBs would relieve stress in a chromosome. The model does, however, offer a different way of thinking about the problem of crossover interference.

Chromosome oscillatory movement model

Hultén (2011) viewed chromosomes as long flexible entities that move with wave-like motions. Chromosome ends (telomeres, attached to the nuclear membrane) and centromeres (attached to the kinetochore and spindle apparatus) move vigorously as the homologs pair. These movements create waves along each chromosome (univalent). When the “nodes” (crests) of two waves on homologs meet, they engage and form a crossover. Because the adjacent chromosome regions are not juxtaposed, no crossovers occur there. This model accounts for chromosomal translocations and other large rearrangements, such as deletions and inversions, blocking recombination and interference in the flanking regions.

Clustering models

Most of the models above do not specify the proteins involved in interference. The clustering model proposed by Fowler et al. (2018) specifies particular proteins involved in several steps. This model is based on their finding that S. pombe linear element proteins (LinE proteins; Rec25, Rec27, and Mug20), in conjunction with another linear element protein Rec10, bind to DSB hotspots with high specificity and are required for DSB formation at most hotspots (Fowler et al., 2013). Rec10 is more uniformly distributed and is required for all DSB formation. Loading of LinE proteins onto chromosomes is promoted by cohesins containing meiosis-specific subunits Rec8 and Rec11. These six proteins are required for full levels of recombination. A type of Hi-C analysis showed that Rec27-bound DSB hotspots form 3D clusters over ~200 kb (Fowler et al., 2018). A DSB at one hotspot interferes with DSB formation at surrounding hotspots; this DSB interference, like hotspot clustering, is strongest for nearby hotspots and decreases to an undetectable level at ~200 kb, corresponding to ~35 cM (Fowler et al., 2018) (Table 2). DSB interference also occurs in S. cerevisiae, extending ~20 – 50 kb, corresponding to ~7 – 20 cM (Garcia et al., 2015). Fowler et al. (2018) proposed that DSB interference gives rise to crossover interference, just as DSBs give rise to crossovers.

In the model of Fowler et al. (2018) a protein complex, such as condensin or cohesin or both, binds to a site on a chromosome and, while remaining bound to that site, moves unidirectionally along the chromosome and forms an ever-growing loop (Hyppa et al., 2021). Upon encountering a potential DSB hotspot in the chromosome (or pair of sister chromatids or pair of homologs) being moved along, the protein complex loads a LinE complex onto the hotspot(s), holds onto that site, and continues moving. Upon encountering the next potential hotspot, it loads another LinE complex with a probability proportional to the strength of that hotspot. After it has loaded a set number of LinE complexes at hotspots, perhaps only two, it ceases loading. A DSB formed at random in the cluster of hotspot-LinE complexes activates the Tel1 protein kinase, which blocks further DSB formation in that cluster by phosphorylating a member of the DSB-forming complex (Rec12 and its half dozen essential partners). The DSB is repaired to a crossover. Because additional DSB formation in the surrounding area (the chromosomal region in the loop) is blocked, so is crossover formation. Formation of clusters encompassing only one homolog (paired chromatids) would allow independent DSBs on the other homolog, and interference would be limited to 0.5, but clusters encompassing both homologs would allow complete interference (I = 1). Formation of clusters over different regions in individual cells would make a gradient, from complete interference to none, in the population of cells, as typically used for assessing crossover interference genetically.

In mitotic S. pombe cells, condensin forms topologically associated domains (TADs) over chromosomal regions of ~300 kb; cohesin forms TADs over ~80 kb (Kim et al., 2016). These distances are about the distance over which DSB interference is observed (~200 kb, as noted above). An S. pombe meiotic cell forms about 60 DSBs over its 13 Mb genome, or 1 DSB per ~200 kb (Fowler et al., 2014). Thus, these numbers are consistent with the model. In a tel1Δ mutant, both DSB interference and crossover interference become negative (Fowler et al., 2018), indicating that Tel1 is required for interference. Negative interference may arise from two or more DSBs being formed in a cluster when Tel1 is not present to inactivate the DSB-forming complex. The result is coordinated action of the DSB-forming complex within a cluster and coordinated crossover formation (negative interference). This model predicts interference between gene conversions, which to our knowledge has not been reported in S. pombe. In the one report of which we are aware, noted above, gene conversions do not show interference in S. cerevisiae (Foss and Stahl, 1995), but the data do not exclude low level interference (i.e., CoC = 1.0 ± 0.3).

Stahl et al. (2004) proposed that “neighboring intermediates (-to-be) [also called “attempts”] are gathered into clusters of more or less fixed size” and that exactly one member of this cluster is converted into a crossover. These clusters were proposed to be foci of Zip2-Zip3 or “late nodules” observed by electron microscopy on the SC in D. melanogaster (Carpenter, 2003). The mode of clustering and the molecular mechanism limiting crossovers to one per cluster were not specified.

Conclusions and future research

Crossover interference has been well documented in many species and to require a variety of proteins. The molecular mechanism remains to be determined in any species. Given the differences in interference strength (Figure 3) and protein requirements (Table 1) in various species, it seems likely that there are multiple mechanisms. Interference strength is clearly distance-dependent in D. melanogaster but less so in S. cerevisiae and C. elegans (Figure 3), suggesting that the mechanisms of interference may be quite different. Determining the mechanisms is a challenge requiring a combination of methods, including genetic and biochemical as well as cytological analyses.