Directional sensitivity of dynamic cerebral autoregulation during spontaneous fluctuations in arterial blood pressure at rest

Abstract

Directional sensitivity, the more efficient response of cerebral autoregulation to increases, compared to decreases, in mean arterial pressure (MAP), has been demonstrated with repeated squat-stand maneuvers (SSM). In 43 healthy subjects (26 male, 23.1 ± 4.2 years old), five min. recordings of cerebral blood velocity (bilateral Doppler ultrasound), MAP (Finometer), end-tidal CO₂ (capnograph), and heart rate (ECG) were obtained during sitting (SIT), standing (STA) and SSM. A new analytical procedure, based on autoregressive-moving average models, allowed distinct estimates of the autoregulation index (ARI) by separating the MAP signal into its positive (MAP_+D) and negative (MAP_−D) derivatives. ARI_+D was higher than ARI_−D (p < 0.0001), SIT: 5.61 ± 1.58 vs 4.31 ± 2.16; STA: 5.70 ± 1.24 vs 4.63 ± 1.92; SSM: 4.70 ± 1.11 vs 3.31 ± 1.53, but the difference ARI_+D–ARI_−D was not influenced by the condition. A bootstrap procedure determined the critical number of subjects needed to identify a significant difference between ARI_+D and ARI_−D, corresponding to 24, 37 and 38 subjects, respectively, for SSM, STA and SIT. Further investigations are needed on the influences of sex, aging and other phenotypical characteristics on the phenomenon of directional sensitivity of dynamic autoregulation.

Introduction

The mechanism of cerebral autoregulation (CA), which tends to attenuate changes in cerebral blood flow (CBF) caused by changes in mean arterial blood pressure (MAP), ¹ is usually regarded as an evolutionary advantage that prevents cerebral hypoperfusion during changes in posture or other physiological conditions causing hypotension. ² CA is also regarded as protective against surges in MAP, by restricting rises in CBF that could cause intracranial hypertension, with subsequent edema and/or capillary damage.^3,4 More recently, the protective role of CA against the risks of hyperperfusion have received considerable attention in studies showing the presence of directional sensitivity, whereby increases in MAP lead to a more efficient response of dynamic CA, the transient behavior of CBF following a sudden change in MAP, ⁵ as compared to what is observed during a reduction in MAP.

To observe the differential effects of increases versus reductions in MAP, these studies have focussed on relatively large changes in MAP, or cerebral perfusion pressure (CPP), induced by the infusion of vasoactive drugs, ⁶ repetitive compression/decompression of thigh cuffs,^7,8 selection of large transients,^9,10 or repeated squat-stand maneuvers (SSM).^11–14 Although not all studies have detected the presence of directional sensitivity, ⁸ it is reassuring that differences in dynamic CA efficiency between episodes of increasing MAP, versus those with decreasing MAP, have been identified using different analytical techniques, such as correlation coefficients,^6,9 autoregressive-exogenous models, ¹⁰ increment ratios, ¹¹ rates of change,^12,14,15 or autoregressive-moving average models. ¹³ What is most relevant though, is the potential, that taking directional sensitivity into account, might improve our understanding of CBF regulation in humans, and the possibility that it might also improve the sensitivity of detecting abnormalities of dynamic CA in clinical studies. ¹⁶

Despite the feasibility of employing different maneuvers to induce relatively large changes in MAP, and some methodological advantages of this approach, ¹⁷ it is important to acknowledge that the dominant method for obtaining estimates of dynamic CA is based on recordings of spontaneous fluctuations of MAP and CBF at rest.^18–20 Characteristically, spontaneous fluctuations have a random temporal pattern that make it difficult to study directional sensitivity using the techniques mentioned above that rely on the identification of segments of data with uninterrupted increasing or decreasing MAP. In a pioneering study, Simpson et al used a complex method to analyse distinct segments of data with spontaneous fluctuations, and obtained indications that directional sensitivity might be present at rest. ¹⁰ They have also acknowledged the difficulty of separating periods with rising or falling MAP. ¹⁰ To address this problem, we are proposing a new analytical approach that is independent of the identification of segments of data with increasing or decreasing MAP, and hence can be applied to continuous data, including recordings with spontaneous fluctuations of MAP and CBF. Moreover, using a single method to express directional sensitivity at rest and during induced changes in MAP, allows for comparative studies between these two modalities and the mechanisms underlying the directional sensitivity phenomenon. To demonstrate the feasibility of our new method, we have compared estimates of directional sensitivity obtained during repeated SSM, with those at rest, either in the sitting or standing positions, to test the hypotheses that i) directional sensitivity can be identified in the dynamic CA response to spontaneous fluctuations of MAP at rest, and ii) the strength of directional sensitivity at rest is similar to that observed during SSM.

Methods

Ethical approval

Ethical approval was obtained from the University of Leicester Ethics Committee (Refs: 8442-vjh12-cardiovascularsciences and 18199-ab786-ls:medicine,schoolof). All participants provided written, informed consent. Both studies were carried out according to the latest approved protocols, the International Conference on Harmonisation-Good Clinical Practice (ICH-GCP), and in accordance with the Declaration of Helsinki.

Participants

The study is a secondary analysis based on the amalgamation of two sets of data that have been reported previously.^21,22 In summary, to be included, participants had to be aged 18 years or older; to be a member of staff or student at the University of Leicester; and to be willing to participate, and able and willing to comply with all the study requirements. Female participants who were pregnant, lactating or planning pregnancy were excluded from the study, as well as participants with a history of cardiovascular, neurological or pulmonary disease.

Mathematical background

The dynamic relationship between MAP and MCAv can be expressed in the time domain as a linear autoregressive-moving average (ARMA) process:

$$v\left(n\right)=\sum _{i=1}^{Nv}{a}_{i}v\left(n-1\right)+\sum _{j=0}^{Np}{b}_{j}p(n-j)$$ (1)

where n is the discrete sample number and [Nv, Np] are the model orders for the autoregressive (AR) and moving-average (MA) terms in equation (1), with the MCAv time-series represented by v(n) and MAP by p(n). a _i are the AR coefficients and b_j are the MA coefficients.

Any time-varying quantity can be expressed as the time-integral of its time-derivative. Applying this to the MAP signal:

$$p\left(t\right)={\int }_{-\mathrm{\infty }}^t\frac{dp\left(t\right)}{dt}\text{d}t$$ (2)

The time derivative of p(t), can then be expressed as the sum of its positive and negative values, that is:

$$\frac{dp\left(t\right)}{dt}={\frac{dp}{dt}}^{+}dt+\mathrm{ }{\frac{dp}{dt}}^{-}\left(t\right)$$ (3)

where dp⁺(t)/dt and dp⁻(t)/dt are the positive and negative values of dp(t)/dt, respectively (Figure 1). Replacing equation (3) into equation (2) results:

$$p\left(t\right)={\int }_{-\mathrm{\infty }}^t{\frac{dp}{dt}}^{+}\text{d}t+{\int }_{-\mathrm{\infty }}^t{\frac{dp}{dt}}^{-}\text{d}t$$ (4)

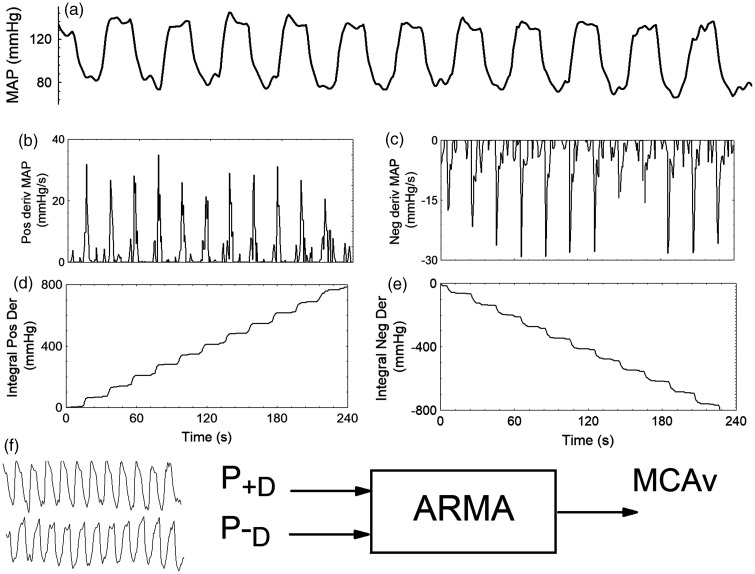
Figure 1.

Separation of the original mean arterial blood pressure (MAP) signal (a) into its positive (b) and negative (c) derivatives for a 22 year-old male subject during the repeated squat-stand maneuver at 0.05 Hz. (d) time-integral of the positive derivative signal; (e) time-integral of the negative derivative signal. After linear detrending of the signals in (d) and (e), (f) shows the integrated positive (P_+D) and negative (P_−D) derivative signals used as inputs to a multivariate autoregressive-moving average (ARMA) model with middle cerebral artery velocity (MCAv) as output. The mathematical derivation of P_+D and P_-D is described in Methods (Mathematical background).

To simplify representation, each of the integrals in equation (4) is expressed by a different pressure component:

$$p\left(t\right)=p^{+}\left(t\right)+p^{-}\left(t\right)$$ (5)

Since p⁺(t) is the integral of the positive derivative of p(t), and p⁻(t) the corresponding integral of the negative derivative, each of these time-series is representing only the rising and falling components of p(t) (Figure 1). To remove the trends introduced by integration (Figure 1), a linear regression was performed and its slope was subtracted from each of the p⁺(t) and p⁻(t), signals (Figure 1).

With the derivative and integral operations performed with discrete operators, equation (5) can be replaced into equation (1), leading to:

$$v\left(n\right)=\sum _{i=1}^{Nv}{a}_{i}v\left(n-1\right)+\sum _{j=0}^{Np}{b}_j^{+}{p}^{+}\left(n-j\right)+\sum _{j=0}^{N\mathrm{p}}{b}_j^{-}{p}^{-}(n-j)$$ (6)

Accordingly, equation (6) is now representing a multivariate ARMA process with inputs p⁺(n) and p⁻(n), respectively (Figure 1).

The model coefficients a_i, b⁺_j and b⁻_j were calculated by least-squares for model orders [2,4,4] based on extensive previous work.^23–27

For each of the input functions, the corresponding MCAv step response was calculated as:

$$S\left(n\right)=\sum _{i=1}^{Nv}{a}_{i}S\left(n-i\right)+\sum _{k=0}^n{b}_k$$ (7)

with the duration of the response set to 20 s (Figure 2).

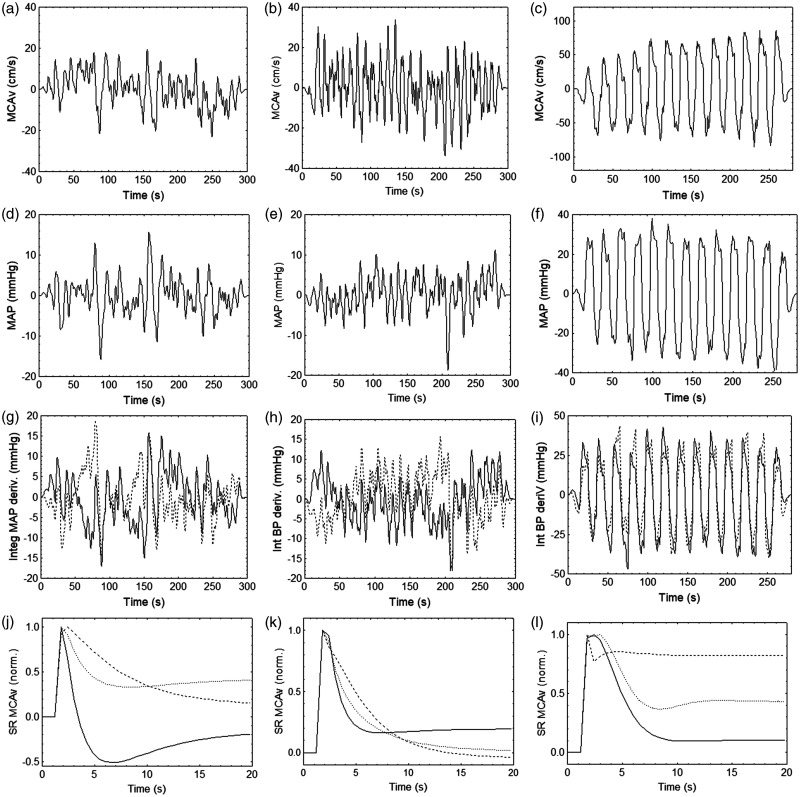
Figure 2.

Representative results from the same subject as in Figure 1 for the right middle cerebral artery during sitting (a,d,g,j), standing (b,e,h,k) and repeated squat-stand maneuver at 0.05 Hz (c,f,i,l). (a–c) middle cerebral artery velocity (MCAv), (d–f) original mean arterial blood pressure, (g–i) integrated positive (continuous line) and negative (dashed line) derivatives of mean arterial blood pressure (BP), and (j–l) normalized MCAv responses to a step change in the original MAP (dotted line) and to the integrated positive (continuous line) and negative (dashed line) derivatives of MAP. Signals in (a–i) have been windowed (Hanning) after removing their mean values. The corresponding values of the autoregulation index (ARI) for the MCAv step responses were, 7.7, 3.7, and 2.7 (j); 5.2, 4.6, and 4.0 (k); and 4.0, 3.1, and 1.5 (l) for the original, integrated positive and negative derivatives of MAP, respectively.

In summary, by replacing the MAP term in the single input ARMA model of equation (1), with the time-integral of the separate positive and negative derivatives, we obtain a 2-input ARMA, where the two separate inputs allow estimation of distinct MCAv step responses, thus expressing the dynamic CA response to increasing or decreasing MAP. As described below, the temporal pattern of the two distinct step responses can then be expressed by the Autoregulation Index (ARI) metric. ²⁸

Experimental protocol

All study participants attended a dedicated cardiovascular research laboratory, which was controlled at a temperature of 20–24°C and was free from distraction. Participants were asked to refrain from heavy meals, strenuous exercise, smoking, alcohol and caffeine for at least 4 hours prior to attending the lab.

Once satisfactory signals had been obtained for all equipment, baseline brachial arterial blood pressure (BP), heart rate (HR), and end-tidal CO₂ (EtCO₂) measurements were taken. Participants were shown how to perform the SSM and asked to avoid a Valsalva-like maneuver when in the squat position. A 5 min recording was performed with subjects resting in the sitting position and breathing normally. This was followed by another 5 min recording with participants standing up. A third recording started with a period of 90 s of quiet standing, followed by a maximum of fifteen SSM at a frequency of 0.05 Hz (10 s standing, 10 s squatting) with the squatting and standing prompted by visual cues provided via a computer program. When performing the SSM, subjects were instructed to squat down as low as they felt able, usually having their thigh parallel to the floor. Participants were provided with a high chair on their side, which they could touch lightly, to maintain balance, if needed. After the fifteen SSM were concluded, the recording was terminated with another period of 90 s of quiet standing.

Instrumentation

A tilt-sensor attached to the participant’s right thigh measured the efficiency and depth of squat (QG-KI-090AI-K, DIS Sensors, Oostergacht, The Netherlands). HR was measured using three-lead electrocardiogram. Beat-to-beat, non-invasive BP measurements were recorded using the Finometer cuff device, attached to the middle finger of the right hand (Finapres® Medical Systems; Amsterdam, The Netherlands). The right arm was held steady using an arm sling, in order to minimize movement and keep the Finometer cuff at heart level. The PhysioCal mechanism was switched off during recordings to ensure a continuous BP trace. Brachial BP was measured before the recording using electrosphygmomanometry (UA 767 BP monitor). Simultaneous bilateral insonation of the middle cerebral arteries (MCAs) through the temporal windows was performed using transcranial Doppler ultrasound (TCD, DWL Doppler Box 10.5.1) with 2 MHz probes, held in place by a bespoke head frame. Respiratory rate and EtCO₂ were monitored using nasal cannulae (Salter Labs, ref 4000) attached to a capnograph (Capnocheck Plus). All signals were simultaneously recorded onto the Physiological Data Acquisition System (PHYSIDAS, Leicester Medical Physics Department), at a sampling rate of 500 samples/s, for subsequent offline analysis.

Data analysis

Data were edited and analysed using in-house software written in Fortran. Under visual inspection, narrow spikes (<100 ms) and artefacts in the recordings were manually removed by linear interpolation. The Finometer readings were calibrated using the brachial BP values. The middle cerebral artery velocity (MCAv) signal was passed through a median filter and all recordings were filtered in the forward and reverse direction using an eighth-order Butterworth low-pass filter with a 20 Hz cut-off frequency. The beginning and end of each cardiac cycle were marked from the ECG signal, and mean values for BP (MAP), HR and MCAv were calculated for every heartbeat. The end of expiration was detected in the EtCO₂ signal, linearly interpolated, and re-sampled in synchronism with the cardiac cycle. Beat-to-beat parameters were interpolated with a third-order polynomial and then resampled at 5 Hz to produce signals with a uniform time base.

The temporal relationship between MAP and MCAv was modelled in the time-domain with an autoregressive-moving average (ARMA) structure, as described above and in previous studies.^27,29,30 In summary, at each point in time, MCAv is expressed by a combination of past values of MCAv (AR terms) and current and past values of MAP (MA terms). Based on extensive previous studies,^23–27,31 the order of the AR terms was set to two past samples, and the order of the MAP input (MA terms) was set to four, corresponding to the present sample and three past samples. After model coefficients were estimated by singular value decomposition, they were used to obtain the MCAv response to a step change in MAP, henceforth referred to as the MCAv step response (SRMCAv-MAP). SRMCAv-MAP were estimated at each measurement condition (sitting, standing, SSM) for the original MAP signal (SRMCAv-MAP_ORIG) and also for the integrated positive (SRMCAv-MAP_+D) and negative (SRMCAv-MAP_−D) time derivatives of MAP as described above. Therefore, SRMCAv-MAP_+D represents the MCAv step response to increases in MAP, whilst SRMCAv-MAP_−D corresponds to the step response to reductions in MAP (Figure 1).

For each of these three different types of step responses, the Autoregulation Index (ARI) was extracted by fitting the estimated responses to the model templates proposed by Tiecks et al. ²⁸ The ARI ranges from zero (absence of autoregulation) to nine (best autoregulation observed) and it has been widely used in physiological and clinical studies to express the efficiency of dynamic CA.^13,19,32 For the analysis of SSM, the three first maneuvers were removed, to avoid the initial phase of non-uniform behavior described previously.^13,33

Statistical analysis

Normality of data was tested with the Shapiro-Wilk W statistic. Differences in the temporal pattern of SRMCAv-MAP were assessed using the ARI as described above. Inter-hemispherical differences in ARI were tested with the dependent t-test and values were averaged in the absence of a significant difference. The effects of different conditions (sitting, standing, SSM) on physiological parameters were tested with repeated-measures one-way ANOVA. For the ARI, the General Linear Model (GLM) was used when testing the effects of different conditions combined with those due to different MAP inputs (ARI_ORIG, ARI_+D, ARI_−D). Following significant values of the F-test, post hoc analysis was performed with Tukey’s test.

A bootstrap exercise was performed to determine the critical number (N_crit) of participants required to detect significant differences between ARI_+D and ARI_−D. For each tested number (N) of participants, 10,000 random samples were taken from the entire population and a dependent t-test was performed between values of ARI_+D and ARI_−D. N was varied from 2 to 42 (see Results) and complete curves were constructed for the percent number of significant differences. N_crit was determined as the value of N ≥ 95% of significant tests.

Statistical significance was assumed for P < 0.05.

Results

Complete sets of data suitable for analysis were obtained from 43 participants (26 male) aged 23.1 ± 4.2 years. All main physiological parameters were elevated during SSM, as compared to sitting and standing at rest (Table 1). No differences in the depth of squatting were detected between participants based on the minimum angle indicated by the tilt-sensor attached to the right thigh.

Table 1.

Main physiological parameters averaged during sitting and standing at rest and during the squat-stand maneuver.

Parameter	Sitting	Standing	SSM	p-value
MAP (mmHg)	89.4 ± 10.8	89.4 ± 11.4	97.8 ± 14.2	<0.0001
Psys (mmHg)	122.0 ± 16.5	118.0 ± 15.9	136.2 ± 24.8	<0.0001
Pdias (mmHg)	76.2 ± 9.9	78.2 ± 10.9	81.9 ± 11.5	0.024
MCAv-R (cm/s)	60.5 ± 12.3	56.5 ± 12.4	63.4 ± 13.4	<0.0001
MCAv-L (cm/s)	57.6 ± 11.9	53.9 ± 12.0	60.6 ± 11.9	<0.0001
EtCO2 (mmHg)	37.8 ± 3.1	35.7 ± 3.3	39.8 ± 4.0	<0.0001
HR (bpm)	73.2 ± 11.2	84.4 ± 12.2	93.6 ± 11.8	<0.0001

Values are mean ± SD. MAP: mean arterial blood pressure; P_sys: systolic blood pressure; P_dias: diastolic blood pressure; MCAv-R: middle cerebral artery velocity, right hemisphere; MCAv-L: left hemisphere; EtCO₂: end-tidal CO₂: HR, heart rate; bpm: beats per minute.

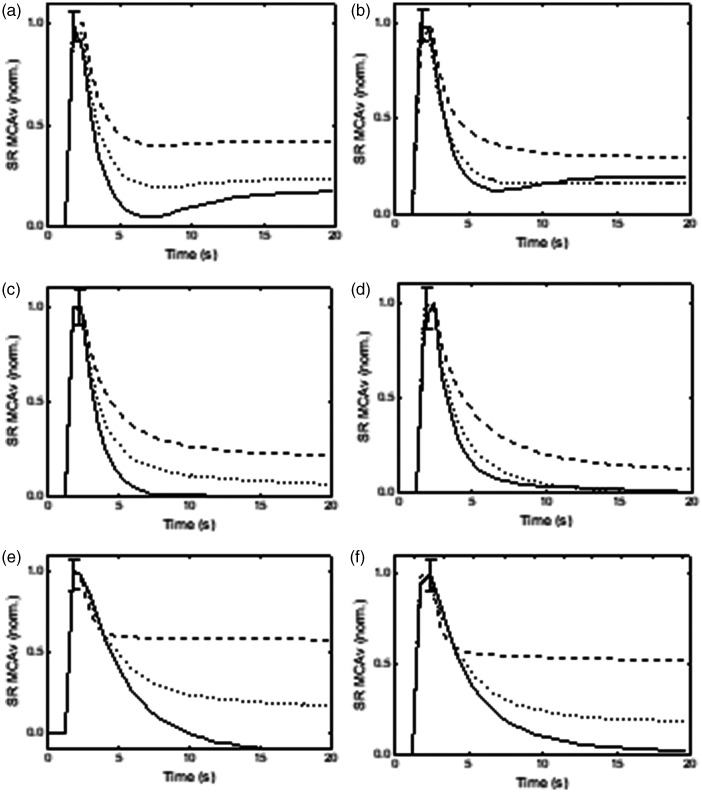
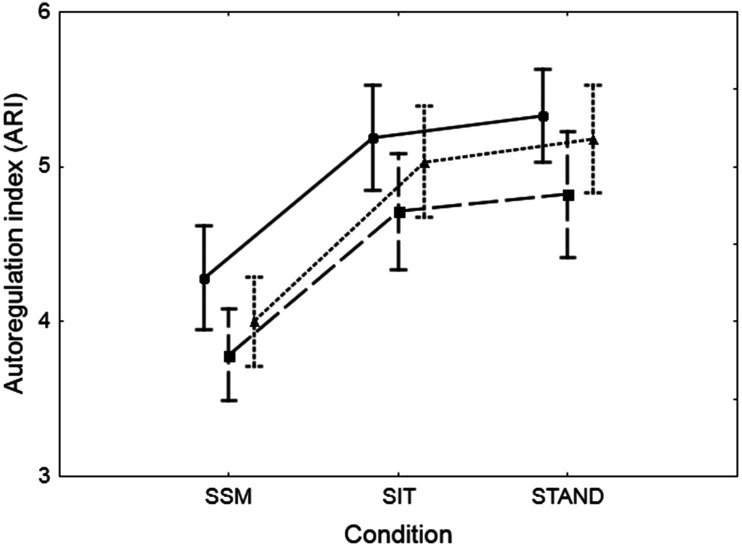
In most subjects, visual inspection of the SRMCAv-MAP suggested more efficient dynamic CA for the MAP_+D input when compared to the MAP_−D case, with intermediary values for MAP_ORIG (Figure 2). For population averaged normalised responses (Figure 3), there is the suggestion of differences between the three responses, and similar step responses from the right and left MCA. ARI values did not show inter-hemispherical differences; all subsequent analyses were performed for values averaged for both sides. Both condition (p < 0.0001) and MAP directionality (p < 0.0001) had highly significant effects on the ARI (Table 2, Figure 4), without showing an interaction. Post hoc testing (Tukey) showed highly significant differences between ARI_+D and ARI_−D, but, in general, ARI_ORIG was not different from ARI_+D or ARI_−D, for any of the conditions, with the exception of the comparison between ARI_ORIG, and ARI_−D when sitting. Moreover, the condition of being seated, standing, or performing SSM, did not influence the difference between ARI_+D and ARI_−D or their individual differences in relation to ARI_ORIG (Table 2). On the other hand, averaging ARI_+D and ARI_−D provided values that were highly dependent on the condition (ARI_AVER, Table 2), but in close approximation to ARI_ORIG, as shown by the very small differences (bias) and correlation coefficients in Table 2.

Figure 3.

Population averages of normalized middle cerebral artery velocity step responses (SRMCAv) estimated from the integrated positive (continuous line) and negative (dashed line) derivatives of mean arterial blood pressure (MAP), compared with the responses obtained with the original MAP signal (dotted line), for the right (a,c,e) and left (b,d,f) hemispheres. (a,b) sitting position, (c standing position and (e,f) repeated squat-stand maneuver at 0.05 Hz. The error bars correspond to the largest ±1 SE of the three responses, at the point of occurrence.

Table 2.

Mean ± SD values of ARI for sitting, standing and squat-stand maneuver.

ARI	Sitting	Standing	SSM	P-value
ARI+D	5.61 ± 1.58	5.70 ± 1.24	4.70 ± 1.11	0.001
ARI−D	4.31 ± 2.16	4.63 ± 1.92	3.31 ± 1.53	0.002
ARIORIG	5.03 ± 1.16	5.18 ± 1.13	4.00 ± 0.93	<0.0001
ARI+D–ARI−D	1.29 ± 3.05	1.07 ± 2.45	1.38 ± 2.18	0.81
ARI+D–ARIORIG	0.58 ± 1.57	0.52 ± 1.29	0.70 ± 0.96	0.77
ARIORIG–ARI−D	0.72 ± 1.79	0.55 ± 1.34	0.69 ± 1.46	0.83
ARIAVER	4.96 ± 1.12	5.16 ± 1.06	4.01 ± 0.82	<0.0001
ARIAVER–ARIORIG	−0.072 ± 0.707	−0.013 ± 0.484	0.006 ± 0.634	0.78
correlationARIAVER–ARIORIG	0.81#	0.90#	0.75#	–

Values are mean ± SD. SSM: repetitive squat-stand maneuver; ARI: autoregulation index; ARI_+D: ARI for the integrated positive derivative of mean arterial blood pressure (MAP); ARI_−D: ARI for the integrated negative derivative of MAP; ARI_ORIG: ARI for the original MAP values; ARI_AVER: intra-subject averaged values of ARI_+D and ARI_−D. P-values from one-way ANOVA for differences between sitting, standing and SSM; ^#p < 0.0001 with significant values in bold.

Figure 4.

Population (n = 43) mean values of the autoregulation index (ARI) averaged for both hemispheres, estimated from the original mean arterial blood pressure (BP) signal (dotted line) and the integrated positive (continuous line) and negative (dashed line) derivatives of BP. The error bars correspond to ±1 SE. Both effects of condition (SSM, SIT, STAND) and estimation source were highly significant (p < 0.0001) in a 2-way ANOVA, without the interaction of effects.

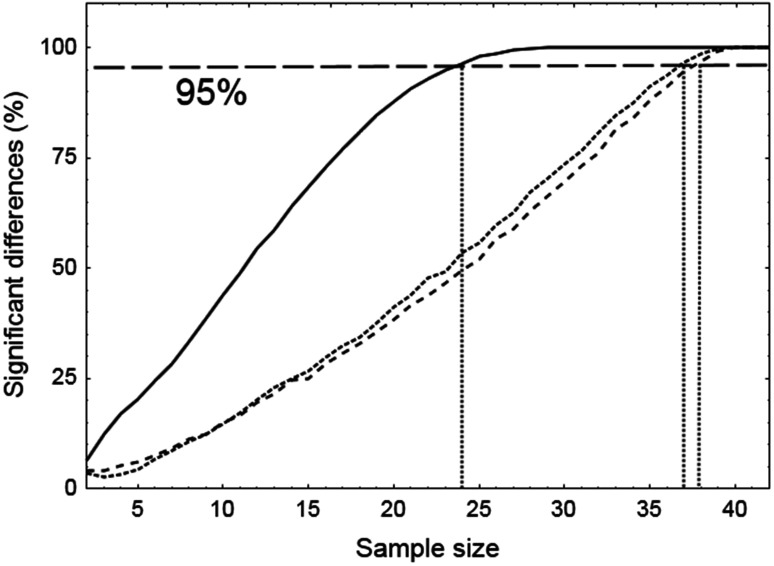
Differences between ARI_+D and ARI_−D proved to be very robust for SSM, with a smaller margin for reductions in sample size for sitting and standing, when sub-samples were extracted with the bootstrap method (Figure 5). Corresponding values of N_crit were 38, 37 and 24 subjects, for sitting, standing and SSM, respectively (Figure 5).

Figure 5.

Number of significant differences between ARI values derived from the integrated positive and negative derivatives of mean arterial blood pressure, expressed in percent of the 10,000 runs performed with the bootstrap method. The critical sample size (N_crit) for each condition, is given by the intercept of the horizontal 95% line (long dashed line) with each curve, corresponding to repeated squat-stand maneuver (continuous line, N_crit= 24), standing (dotted line N_crit= 37) and sitting (dashed line, N_crit= 38).

Discussion

Main findings

The results described above support the acceptance of the two main hypotheses of the study. Using a new approach, based on the integrated MAP signal for the separated positive (MAP_+D) and negative (MAP_−D) derivatives, we have shown significant differences in the efficiency of dynamic CA for increasing or decreasing MAP at rest. Moreover, directional sensitivity of dynamic CA, as expressed by the difference in ARI values extracted from SRMCAv-MAP_+D and SRMCAv-MAP_−D, did not show any changes for sitting, standing or SSM. Both, the occurrence of directional sensitivity at rest, and its lack of difference from what is observed during SSM, have considerable implications for our conceptual models of CBF regulatory mechanisms, and corresponding methodological approaches that can be adopted for its assessment in physiological and clinical studies.

Directional sensitivity of dynamic CA

The finding that directional sensitivity is a feature of dCA is not surprising, given the evolutionary protective advantages offered by this type of control mechanism, as previously demonstrated for other physiological regulatory functions, such as the control of the pupil diameter ³⁴ or the baroreflex. ³⁵ The initial observations of directional sensitivity in dCA, obtained from SSM protocols,^11–16 fitted well with teleological expectations, given the large swings in MAP induced by repeated SSM. Following those findings, the immediate question was if directional sensitivity is dependent on the amplitude of MAP changes, or if it is an inherent feature of the myogenic mechanisms underlying the dCA response. Our study, demonstrating the occurrence of directional sensitivity at rest, where much smaller fluctuations in MAP take place, confirming the early observations of Simpson et al, ¹⁰ and showing that the strength of directional sensitivity, as expressed by the differences between ARI_+D and ARI_−D, was not different from those during SSM, has thus provided an answer to this question. Nevertheless, further questions arise. What is the source of the directional sensitivity of the myogenic mechanism? Previous studies pointed the finger at increases in cerebral sympathetic nervous activity (SNA) during SSM,^11,15 following the demonstration that SNA from the superior cervical ganglia increases with rises in MAP, but does not respond to reductions in MAP. ⁴ Our results, showing the presence of directional sensitivity at rest, calls for alternative explanations. As shown by Cassaglia et al, a substantial change in MAP is needed, of the order of 50% of baseline values, to trigger increased SNA. ⁴ Fluctuations in MAP at rest are usually of less than 10% of baseline values, which makes SNA less likely to be the source of directional sensitivity at rest. Instead, we speculate that directional sensitivity is an intrinsic property of the vascular smooth muscle, where contraction, leading to vasoconstriction caused by increases in MAP, acts faster than the relaxation needed for vasodilation, following reductions in MAP. In-vitro studies of diameter changes in small arteries during constriction and dilation, as well as the dynamics of calcium currents, are examples that can substantiate our hypothesis.^36,37

Methodological considerations

In human studies, directional sensitivity was first reported in patients with traumatic brain injury.^7,9 In both cases, the methods employed to assess directional sensitivity make it difficult to compare results with other studies. Aaslid et al. induced large changes in MAP with the cyclic compression and decompression of thigh cuffs, expressing dCA with a gain metric, extracted from the relationship between MAP and critical closing pressure. ⁷ The gain parameter indicated the presence of directional sensitivity in 14 patients with traumatic brain injury, but not in 10 normal subjects, suggesting that the gain metric was inadequate for the purposes of their study, or, alternatively, the occurrence of Type-II error in the healthy group. Schmidt et al. analysed data from 210 patients with traumatic brain injury and used the Mx index (a correlation coefficient) to express the efficiency of autoregulation during episodes of increasing and decreasing CPP. ⁹ Due to strict criteria requiring a minimum change in CPP of more than 10 mmHg in either direction, they could only extract the Mx from 53 of the patients, with the number of available recordings dropping from 727 to 84. The mean values of Mx for episodes with rising CPP was different from those with falling CPP, but the difference became non-significant when the analysis was performed with MAP, instead of CPP. The conclusion from these two studies is that the identification of directional sensitivity might be masked by methodological choices and that there is a need for standardization of analytical tools that are fit-for-purpose. ¹⁰ Similarly to Aaslid et al., ⁷ Katsogridakis et al. induced perturbations in MAP by means of cycling compression/release of thigh cuffs in 30 healthy subjects, during normocapnia and hypercapnia. ⁸ They used the slope of linear regressions during separate rising and falling phases of MAP and did not detect the presence of directional sensitivity, although the slope was highly sensitive to the effects of hypercapnia. Again, it is possible that a lack of sensitivity of the slope metric, combined with an insufficient number of subjects, led to a Type-II error.

Studies based on the SSM have provided more consistent identification of the presence of directional sensitivity, but methodological differences should also be considered. To date, most studies based on the SSM have used the ratio of absolute changes in MCAv, divided by the corresponding change in MAP (ΔMCAv/ΔMAP), ¹¹ or the ratio of their rates of change, that is, taking into account the duration (Δt) of the changes (ΔMCAv/Δt_V/ΔMAP/Δt_P).^12,14,15 One limitation of these metrics though is that they do not take into account the phase differences between MCAv and MAP. ³⁸ In other words, the variable time delays between MCAv and MAP might lead to the detection of maxima and minima taking place at different points in time, potentially distorting estimates of these metrics. This limitation was overcome with the use of the ARMA model applied to each individual squat or stand maneuver. ¹³ The lack of consideration for phase differences might be the reason why directional sensitivity was detected with SSM at 0.10 Hz, but not at 0.05 Hz,^12,14,15 since the phase tends to be higher with the latter frequency, compared to the former. ³⁹

One advantage of the novel approach that we are proposing is that the ARMA model is applied only once, to the entire recording, and hence does not need the visual marking for the separation of individual squat and stand cycles, leading to 30 different estimates of ARMA parameters (15 SSM cycles with two segments per cycle). ¹³ Of note, in the present study, after removing the first three cycles of SSM, we have obtained differences between ARI_+D and ARI_−D (∼1.4, Table 2) that are in excellent agreement with corresponding values obtained with the ARMA of each SSM cycle, during the steady-state phase, despite the different number of subjects involved. ¹³ Nevertheless, further work is needed on the potential distortions that could be introduced by running two ARMA models in parallel, due to the presence of interspersed segments of data with null-signal and sudden transitions to either positive or negative derivative values of MAP (Figure 1). The use of model simulation might be particularly suited for this purpose.

The bootstrap analysis of N_crit (Figure 5) clearly shows the risks of Type-II errors in studies that are under-powered. Extending this approach to other metrics of dCA, such as the Mx, or the use of slope ratios ^{15 ,} would be important to allow comparisons between different approaches to quantify directional sensitivity. Of particular interest, would be the ability of other metrics to detect directional sensitivity at rest, given the larger sample sizes required (Figure 5). Moreover, we did not have supine recordings in this cohort; including this condition in future studies would be key to obtaining reference values to underpin clinical studies. Although SSM was a more robust approach to detect directional sensitivity, compared to sitting or standing (Figure 5), independently of the metric adopted, we can speculate that studies using only 12 subjects could be under-powered to detect the presence of directional sensitivity. ¹⁴

Clinical perspectives

Disturbances in dCA have been reported in a range of cerebrovascular conditions, chiefly stroke and other forms of brain injury.^19,40–42 On the other hand, classical methods of dCA assessment, such as transfer function analysis,^18,43 have not provided consistent evidence of dCA alterations in conditions such as transient ischemic attack, ⁴⁴ Alzheimer’s disease, ⁴⁵ or arterial hypertension. ⁴⁰ Further studies, using methods that could quantify directional sensitivity of dCA, have the potential to improve detection of CBF regulatory disturbances that could lead to better patient management and outcomes. Given our limited understanding of the physiological pathways underpinning the source(s) of directional sensitivity, at this stage it is not possible to predict if differences in dCA responses between increasing and decreasing MAP would be reduced or enhanced by pathology. The findings that directional sensitivity could be detected in patients with head trauma,^7,9 suggests that the latter might be the case, but replication of these early studies is needed, ideally with sample sizes with adequate statistical power, as proposed by our bootstrap results (Figure 5).

Despite its potential, we are not advocating that methods aimed at quantifying the directional sensitivity of dCA become the norm, until considerable more evidence is available to justify its widespread use in clinical, as well as physiological studies. In particular, much more information is needed about the influences of sex, aging, blood gases, posture, and other phenotypical characteristics, on this phenomenon, before attempts at methodological standardization.^18,43

Limitations of the study

The use of transcranial Doppler ultrasound generates concerns about the stability of the insonated artery diameter, in our case the MCA, that could lead to distorted results, due to alterations in the relationship between CBFv and absolute flow. ⁴⁶ In our case, changes in MCA diameter were unlikely to have occurred within each recording, since measurements were obtained during stable poikilocapnia ^21,22,47 and significant changes in MCA diameter were only reported at elevated values of hypercapnia.^48,49 Moreover, the ARI index is only dependent on the temporal pattern of the SRMCAv-MAP, and would not be affected by amplitude changes in MCAv or MAP, unless there were relatively fast changes in MCA diameter, say over 2-10 s, something that has never been demonstrated.

Despite its relevance, we have not been able to describe the influences of sex and aging on the directional sensitivity of dCA, due to the insufficient number of cases in our database, ²² taking into account the results in Figure 5. For similar reasons, ⁴⁷ we have not been able to perform a reproducibility study and this should be a priority for future work. Also, we have not been able to ascertain the state of physical fitness of our subjects, as this could have influenced the strength of directional sensitivity.^14,50 Previous studies of directional sensitivity based on the SSM have performed repeated maneuvers at both 0.05 Hz and 0.10 Hz, often finding that directional sensitivity was present at one of these frequencies, but not both.^12,14,15 We could not test our new method at 0.10 Hz as our data were limited to the 0.05 Hz condition only. For this reason, future studies are warranted to allow comparison of directional sensitivity estimates at both frequencies with the new method we are proposing. In addition to potential differences in directional sensitivity, the use of more rapid changes in MAP, as would be observed with SSM at 0.10 Hz, also raises the prospect that dynamic CA might be a rate-sensitive phenomenon, something that also deserves further investigation.

All the recordings we analysed had the duration of five minutes. Differently from transfer function analysis, that often uses the Welch method to superpose shorter segments of data,^18,43 the ARMA model used the entire five minute recording and one relevant question, that deserves further investigation, is how the method we are proposing would perform with shorter segments of data. ⁵¹

A sensitivity analysis of the effects of the ARMA model orders was not performed. Our choice of model orders was based on several previous studies, but it is possible that for the purposes of quantifying directional sensitivity, different model orders could have led to larger effects, thus modifying the conclusions from the bootstrap analysis (Figure 5).

Conclusions

A new signal processing procedure, based on the separation of the positive and negative derivatives of the beat-to-beat MAP signal, was able to detect the presence of directional sensitivity at rest and during repeated SSM at 0.05 Hz. Entire recordings of 5 min duration, could be utilised, without the need to identify separate segments of data with rising or falling MAP. This new approach brings considerable simplification to the study of directional sensitivity, paving the way for further research onto the phenotypical determinants of directional sensitivy and its potential application to clinical conditions.

ORCID iDs

Ronney B Panerai https://orcid.org/0000-0001-6983-8707

Samuel C Barnes https://orcid.org/0000-0001-6009-406X