Finite Element Model-Computed Mechanical Behavior of Femurs with Metastatic Disease Varies Between Physiologic and Idealized Loading Simulations

Abstract

Background and objectives:

Femurs affected by metastatic bone disease (MBD) frequently undergo surgery to prevent impending pathologic fractures due to clinician-perceived increases in fracture risk. Finite element (FE) models can provide more objective assessments of fracture risk. However, FE models of femurs with MBD have implemented strain- and strength-based estimates of fracture risk under a wide variety of loading configurations, and “physiologic” loading models typically simulate a single abductor force. Due to these variations, it is currently difficult to interpret mechanical fracture risk results across studies of femoral MBD. Our aims were to evaluate (1) differences in mechanical behavior between idealized loading configurations and those incorporating physiologic muscle forces, and (2) differences in the rankings of mechanical behavior between different loading configurations, in FE simulations to predict fracture risk in femurs with MBD.

Methods:

We evaluated 9 different patient-specific FE loading simulations for a cohort of 54 MBD femurs: strain outcome simulations—physiologic (normal walking [NW], stair ascent [SA], stumbling), and joint contact only (NW contact force, excluding muscle forces); strength outcome simulations—physiologic (NW, SA), joint contact only, offset torsion, and sideways fall. Tensile principal strain and femur strength were compared between simulations using statistical analyses.

Results:

Tensile principal strain was 26% higher (R² = 0.719, P < .001) and femur strength was 4% lower (R² = 0.984, P < .001) in simulations excluding physiologic muscle forces. Rankings of the mechanical predictions were correlated between the strain outcome simulations (ρ = 0.723 to 0.990, P < .001), and between strength outcome simulations (ρ = 0.524 to 0.984, P < .001).

Conclusions:

Overall, simulations incorporating physiologic muscle forces affected local strain outcomes more than global strength outcomes. Absolute values of strain and strength computed using idealized (no muscle forces) and physiologic loading configurations should be used within the appropriate context when interpreting fracture risk in femurs with MBD.

Introduction

The annual prevalence of metastatic bone disease (MBD) in the US is over 280 000, and the femur is a commonly affected skeletal site.^1,2 Patients with MBD often undergo prophylactic surgery to prevent impending pathologic fractures and alleviate pain. Mirels’ score³ is a radiographic metric used clinically to predict impending fracture risk and inform surgical treatment decisions. Mirels’ score is a sensitive predictor of fracture risk (71%-100%); however, over half of low-risk MBD femurs potentially receive nonessential surgical treatment due to Mirels’ low specificity (13%-50%).² Unfortunately, inherent proximal femur strength and/or subsequent strength reductions resulting from MBD are difficult to evaluate directly from diagnostic (radiographic or computed tomography (CT)) imaging.^4,5

The need for accurate fracture prediction in MBD patients has led to early clinical implementation of engineering methods that can provide more objective assessments of true mechanical vulnerability and subsequent fracture risk.^6,7 To date, CT-based rigidity analysis^8,9 has been the most useful engineering-based augment to improve fracture risk assessment in MBD patients. However, this technique makes several significant simplifying assumptions for clinical utility, including basic loading and geometry assumptions. Finite element (FE) models have been shown to predict bone strength better than quantitative density-only methods,¹⁰ and FE analyses have also indicated that the applied loading configurations affect model-predicted bone mechanics.^11,12 Though validated FE models of the femur simulating sideways fall,^{13 -15} single-limb stance,¹⁶ or physiologic loading,¹¹ have provided great insight into age/non-traumatic/injury-related mechanical changes in bone strength and fracture risk, FE modeling has not yet seen widespread clinical implementation for fracture risk prediction in MBD.

FE models of femoral MBD have mainly been utilized in experiments with simulated lytic lesions that only modestly replicate the heterogeneous lesions (lytic/mixed/diffuse/blastic) present in MBD patients. Those various FE studies have implemented local strain- and global strength-based estimates of fracture risk under a variety of loading configurations such as offset torsion,^17,18 axial compression,^{5,19 -22} single-limb stance,^{23 -27} and physiologic activity like level walking and stair ascent.^{28 -31} While termed “physiologic” loading, these models only simulate a single hip abductor force, and the forces and displacements are typically applied to the model through plastic pots.^{29 -31} This has implications for MBD as locally acting muscle forces would be expected to influence local strains, particularly for lesions located near muscle insertion sites. Femur strength, which considers global/whole-bone interactions, would expect to be less severely affected by such a modeling assumption. It is currently difficult to interpret mechanical fracture risk results across studies due to the variations in FE simulations of femoral MBD.

Our main aim was to evaluate differences in mechanical behavior between idealized loading configurations and those incorporating physiologic muscle forces, in FE simulations of femoral MBD with patient-specific lesions. Our primary hypothesis was that realistic physiologic muscle forces would affect simulations with local strain-dependent outcomes, rather than simulations with global/whole-bone strength outcomes. A secondary aim was to evaluate differences in the rankings of mechanical behavior between different loading configurations in FE simulations of femoral MBD. We hypothesized that MBD femurs would be ranked similarly from weakest to strongest between the strain outcome simulations, and between the strength outcome simulations.

Materials and Methods

Patient information

A retrospective analysis was performed on 48 MBD patients (27-90 years old; 21 females, 27 males) with Institutional Review Board approval. We analyzed 54 (6 bilateral) femurs from whole-femur diagnostic CT scans (Siemens, Forchheim, Germany; 120 kVp, 150 mAs, 0.3906 mm × 0.3906 mm × 0.6 mm voxel size) that were collected consecutively over a period of 3 years, prior to any prophylactic surgery was performed. Due to the timeframe of acquiring patient data, our only enrollment restrictions were MBD lesions in the distal half of the femur and femoral fracture at initial presentation. We focused on proximal femur lesions due to their proximity to the maximum strained region of the femur. Most patients were diagnosed with the common cancers that metastasize to bone, that is, lung (13), kidney (7), prostrate (7), breast (3). There were 22 lytic, 15 mixed, 6 diffuse, and 5 blastic metastatic cases. Twenty-two out of the 54 femurs underwent prophylactic surgery. A single, fellowship-trained orthopedic oncologist (BJM) with 10 years of clinical experience managed all patients. Patient age (66 ± 11 vs 63 ± 15 years, P = .453) and BMI (25 ± 7 vs 28 ± 7 kg/m², P = .187) were similar between those that underwent fixation and those that did not. Mirels’ score was 11 ± 1 (range 9-12) and 9± 1 (range 6-10) for femurs that underwent fixation and those that did not, respectively.

FE geometry and meshing

Patient-specific femur geometries were extracted from CT images (Figure 1) using Mimics (Materialise, Leuven, Belgium) using a fixed density threshold (0.15 g/cm³).^13,17 Low density region boundaries were manually corrected only as necessary. Using custom code (Matlab, Mathworks, Natick, MA), femur geometries were converted into voxel meshes (8-node hexahedral elements) with 1.5 mm isotropic edge length based on prior validation.^13,17 The resulting meshes contained 171 500 ± 34 881 elements on average. Changing element edge length from 1.5 mm to 1.0 mm changed elastic modulus, tensile, and compressive principal strains by less than 1.75%, independently confirming convergence. We evaluated 9 different patient-specific FE models for each femur (486 total). Whole or partial-femur lengths were implemented based on the model evaluated (Figure 1).

Figure 1.

Cross-section of a sample femur geometry with lytic metastasis and elastic modulus distribution acquired from computed tomography scans (left), and the 9 loading configurations simulated using finite element models (right). The normal walking, stair ascent, and stumbling physiologic simulations included the abductor (ABD), proximal and distal ilio-tibial tract (ITTP, ITTD), proximal and distal tensor fascia lata (TFLP, TFLD), vastus medialis (VM), and vastus lateralis (VL) muscle forces, in addition to the hip joint contact force (CF). Posterior view shown. Please refer to the online version for interpretation of color.

FE material behavior

Bone was assigned element-based, isotropic (ν = 0.3),³² inhomogeneous modulus values specific to cortical (apparent density>1.0 g/cm³) and trabecular (apparent density ⩽ 1.0 g/cm³) bone.^15,33 CT scans included a calibration phantom (QRM, Moehrendorf, Germany) allowing for extrapolation of patient-specific bone densities from Hounsfield units (Figure 2; R² = 0.99). Modulii were determined from the patient-specific bone densities and femur-specific empirical relationships (Table 1; r ⩾ .82). Our methodology of voxel mesh modulus assignment can result in partial volume artifacts at the cortical surface elements of the femoral shaft. However, this methodology has been validated for estimation of global/whole-bone mechanical behavior.^13,15,17 A modulus of 0.01 MPa was assigned to elements with values <0.01 MPa.¹⁶ To conform with existing MBD femur FE models, we simulated both linear elastic material behavior and nonlinear material properties that incorporated post-yield behavior (Table 1). FE models incorporating post-yield behavior used the von Mises yield criterion to simulate bone yield.³⁴

Figure 2.

Average calibration relationship relating CT Hounsfield units to density using a calibration phantom included in each femur CT scan. Dotted line indicates a linear fit.

Table 1.

Femur-specific empirical relationships for assigning material properties.

Model	Material behavior	Relationships	Reference
Physiologic strain (NW, SA, ST)	Linear elastic	$E=6850{\rho }_{app}^{1.49}$	Morgan et al35
		${\rho }_{app}={\rho }_{HA}/0.626$	Dalstra et al33
Joint contact only strain (NW)	Same as physiologic strain
Physiologic strength (NW, SA)	Elastic-perfectly plastic until a defined plastic strain, followed by strain softening until a minimum stress, followed by indefinite perfectly plastic	$E=14900{\rho }_{ash}^{1.86}$ $S=102{\rho }_{ash}^{1.80}$ ${\sigma }_{min}=43.1{\rho }_{ash}^{1.81}$ ${\rho }_{ash}=0.887{\rho }_{HA}+0.0633$	Keyak et al34
Joint contact only strength (NW)	Same as physiologic strength
Offset torsion	Linear elastic	$E=\{\begin{array}{c}33900{\rho }_{ash}^{2.20},{\rho }_{ash}\le 0.27\\ 5307{\rho }_{ash}+469,0.27<{\rho }_{ash}<0.6\\ 10200{\rho }_{ash}^{2.01},{\rho }_{ash}\ge 0.6\end{array}$	Keyak et al16
		${\rho }_{ash}=0.694{\rho }_{HA}+0.111$	Vivanco et al36
Sideways fall	Elastic-perfectly plastic	$E=6850{\rho }_{app}^{1.49}$	Morgan et al35
		${\rho }_{app}={\rho }_{HA}/0.626$	Dalstra et al33
		0.9% homogeneous yield strain	Edwards et al13

Abbreviations: NW, normal walking, SA, stair ascent, ST, stumbling, E, elastic modulus (MPa), S, ultimate strength (MPa), σ_min, minimum stress (MPa), ρ_HA, hydroxyapatite equivalent density (g/cm³), ρ_app, apparent density (g/cm³), ρ_ash, ash density (g/cm³).

FE loads and boundary conditions

Physiologic Models—Strain (walking/stair ascent/stumbling): boundary conditions replicated the instant of peak hip joint contact force at heel-strike during normal level walking (NW), or the instant of peak hip joint torque during stair ascent (SA), or the instant of peak hip joint contact force during stumbling (ST).^37,38 This represented progressively more strenuous levels of physiologic loading activities likely experienced in this patient population. Patient-specific femurs were aligned to the Bergmann et al instrumented dataset coordinate system,^38,39 and patient-specific bodyweight-scaled⁴⁰ muscle forces specific to each loading activity (Table 2) were applied as concentrated loads to FE model surface nodes that corresponded to muscle insertion locations. The abductor, tensor fascia lata, and vastus lateralis muscle forces were applied during physiologic NW (Figure 1). FE simulation of SA included the ilio-tibial tract and vastus medialis muscle forces, in addition to the abductor, tensor fascia lata, and vastus lateralis muscle forces.³⁹ Muscle forces during ST are unclear, hence we applied the same muscle forces during NW to simulate ST, assuming that stumbling would occur during walking. Patient-scaled joint contact force during each activity (Table 2) was applied to the femoral head surface in the direction of the resultant hip joint contact force and passing through the femoral head center. To prevent excessive local mesh distortion, a modulus of 25 GPa was assigned to load application elements.^31,34 The femur was physiologically constrained at the location of hip contact on the femoral head, lateral epicondyle, and below the patella groove center.⁴¹

Table 2.

Applied muscle forces, joint contact forces, and displacements for the different loading activities simulated.

	Normal walking			Stair ascent			Stumbling
	x	y	z	x	y	z	x	y	z
Abductor (%BW)	58.0	4.3	86.5	70.1	28.8	84.9	Same as normal walking
Ilio-tibial tract proximal (%BW)	–	–	–	10.5	−3.0	12.8	–	–	–
Ilio-tibial tract distal (%BW)	–	–	–	−0.5	−0.8	−16.8	–	–	–
Tensor fascia lata proximal (%BW)	7.2	11.6	13.2	3.1	4.9	2.9	Same as normal walking
Tensor fascia lata distal (%BW)	−0.5	−0.7	−19.0	−0.2	−0.3	−6.5	Same as normal walking
Vastus lateralis (%BW)	−0.9	18.5	−92.9	−2.2	22.4	−135.1	Same as normal walking
Vastus medialis (%BW)	–	–	–	−8.8	39.6	−267.1	–	–	–
Hip contact force (%BW)	−77.9	−26.6	−240.3	−102.3	−56.9	−249.9	−294.8	−182.4	−1270
Hip contact displacement magnitude (mm)	5			5			–

Abbreviations: BW, body weight.

Physiologic Models—Strength (walking/stair ascent): because muscle forces are unclear for ST, only the NW and SA activities were simulated. Boundary conditions were the same as the physiologic strain models, except that a compressive contact displacement was applied incrementally to the femoral head surface³⁴ in the direction of the resultant hip joint contact force passing through the femoral head center.

Joint Contact Only Models—Strain/Strength (walking): boundary conditions were the same as the physiologic strain/strength models, except that muscle forces were excluded, which replicated a single-limb stance/axial compression-type loading configuration. Only NW joint contact loads were simulated since this is likely the common activity in the patient population.

Offset Torsion Models—Strength: boundary conditions replicated a mechanism of low-energy failure under torsional loading such as encountered when getting out of bed.¹⁷ Loading platens were modeled as a conforming mesh at the anterior femoral head and distal femur, and assigned a linear elastic PMMA material with a modulus of 2500 MPa and ν = 0.3.⁴² An anterior-posterior displacement was applied incrementally to the surface of the femoral head platen to produce a torsional moment about the femur long axis, while constraining whole-bone bending. The distal femur was constrained in all translations.

Sideways Fall Models—Strength: boundary conditions replicated a mechanism of fragility fracture such as during a fall from hip level.¹³ Loading platens were modeled as a conforming mesh at the medial femoral head and lateral greater trochanter. A medial-lateral displacement was applied incrementally to the surface of the femoral head platen, while the base of the greater trochanter platen was constrained in medial-lateral translation. The femur distal to the lesser trochanter was constrained in rotation (torsion, bending) and axial (shear) translation.

FE postprocessing

All simulations were performed in Abaqus 2018 (Dassault Systemes Simulia Corp, Johnston, RI) using a static analysis. FE analyses terminated prior to femur strength evaluation for 2 NW and 3 SA physiologic models, and 1 NW joint contact only model, which were excluded from further analysis.

Tensile (maximum) principal strains for physiologic (NW, SA, ST) and joint contact only (NW) strain loading configurations were determined from lesion regions²³ that included bone 2 voxels adjacent to the segmented lesion (accounting for partial volume effects at the lesion interface). Average strain from the lesion region, rather than peak strain, was used for comparison to minimize effects of local numerical artifacts. Load application elements and elements in their immediate vicinity were excluded from the analysis to remove strain concentrations.⁴³

Femur strengths for physiologic (NW, SA) and joint contact only (NW) strength loading configurations were determined as the peak resultant reaction force at the femoral head.³⁴ To provide an intra-patient assessment of fracture risk accounting for confounding inter-patient covariates, we also evaluated patient-specific load-to-strength ratios (LSR), defined as the ratio of activity-specific contact force to activity-specific femur strength.^4,29

Femur strengths for offset torsion and sideways fall were determined using the maximum principal strain criterion,¹⁷ and deformation of the femoral head relative to the greater trochanter,¹³ respectively.

Model verification

A direct validation of our femoral MBD FE model strains and strengths was beyond the current scope. However, the methods used for model generation were based on validated, published procedures.^13,17,34 Therefore, we presently compared our model results with published data to additionally verify our simulation procedures.

Statistical analyses

To test the hypothesis that physiologic muscle forces would affect local strain rather than global strength-based simulations, we compared the tensile strain relationship between NW physiologic and joint contact only loading models using linear regression, and we also compared bias using a Bland-Altman plot. Femur strengths were similarly compared between NW physiologic and joint contact only loading models. Mean differences between NW physiologic and joint contact only loading simulations were compared using either a paired T-test or Wilcoxon signed-rank test (non-normal data).

To test the hypothesis that MBD femurs would be ranked similarly, we evaluated the concordance of mechanical predictions between strain outcome simulations. For each loading configuration, the femurs were ranked from weakest (high strain) to strongest (low strain), and correlations between distributions of femur rankings were compared using Spearman rank correlation. The concordance of mechanical predictions between strength outcome simulations was similarly compared. We also used a percentile analysis to compare the distributions of femur strains/strengths between the different loading configurations. Percentile group means were compared using either a one-way ANOVA or Kruskal–Wallis test (non-normal data). Bonferroni adjustments were made for post hoc comparisons. The strength of the relationship between lesion tensile strain and femur strength, and between LSR and femur strength, was compared using Spearman correlation (non-normal data) for the NW physiologic loading simulation. Alpha level of .05 was defined as significant for all comparisons (SPSS, IBM Analytics, NY).

Results

Our NW physiologic loading model-predicted tensile strains (154-2447 μstrain range) corroborated well the range of reported femur tensile principal strains during level walking (~300-2300 μstrain).^37,41,43 Similarly, our 863 to 9210 N range of femur strengths compared well with the range of reported femur strengths (~500-15 000 N).^15,16,34

While NW joint contact only loading explained most of the variance in femur strength in relation to physiologic loading (R² = 0.984, P < .001; slope = 0.992; intercept = −169 N, P = .04 [significantly different from 0]), there was a bias for lower femur strengths (Figure 3). NW joint contact only loading explained variance in tensile principal strain in relation to physiologic loading to a lesser degree (R²=0.719, P < .001; slope = 1.055; intercept = 137 μstrain, P = .08), with a bias for higher strains (Figure 3). Femur strengths were 4% lower (4166 ± 1411 vs 4333 ± 1422 N, P < .001), while tensile strains were 26% higher (842 ± 637 vs 668 ± 512 μstrain, P < .001) for NW joint contact only loading compared to physiologic loading.

Figure 3.

Femur strength and lesion tensile principal strain relationships between normal walking joint contact only and physiologic loading configurations (left column). Dashed lines indicate y = x relationship and dotted lines indicate linear fit. Outcome bias between loading configurations was evaluated using Bland-Altman plots (right column). Solid lines indicate means of the differences and dotted lines indicate 95% confidence interval limits.

The rankings of the mechanical predictions were strongly correlated between the strain outcome simulations (ρ = 0.723 to 0.990, P < .001), and moderately-to-strongly correlated between the strength outcome simulations (ρ = 0.524 to 0.984, P < .001). Femur strengths and strains followed a generally comparable distribution between loading configurations (Figures 4 and 5), with a trend for the strongest percentile group mostly including femurs that were not surgically fixed. Femurs within the strongest percentile were at lower fracture risk (lower LSR) on average than femurs within the weakest percentile (P < .001, Figure 4 top) for both the NW and SA physiologic loading configurations. Lesion tensile strain was moderately related to femur strength (Figure 6).

Figure 4.

Distribution of femur strengths according to the weakest (33rd), middle, and strongest (67th) percentiles for physiologic, offset torsion, and sideways fall loading configurations. Surgically and non-surgically treated femurs are indicated. Error bars indicate percentile standard deviation. LSR – load-to-strength ratio, a – weakest percentile average significantly different from middle, b – weakest percentile average significantly different from strongest, c – middle percentile average significantly different from strongest, all P < .001. The insets show force-displacement curves from a sample femur. Please refer to the online version for interpretation of color.

Figure 5.

Distribution of lesion tensile principal strains according to the strongest (33rd), middle, and weakest (67th) percentiles for physiologic loading configurations. Surgically and non-surgically treated femurs are indicated. Error bars indicate percentile standard deviation. a – weakest percentile average significantly different from middle, b – weakest percentile average significantly different from strongest, c – middle percentile average significantly different from strongest, all P < .001. The insets show distribution of tensile principal strain through the cross-section of a sample femur. Please refer to the online version for interpretation of color.

Figure 6.

Relationship between femur strength and lesion tensile principal strain for normal walking physiologic loading, showing a moderate correlation. Dotted line indicates a linear fit. ρ – Spearman correlation coefficient.

LSR was strongly related to femur strength (Figure 7). As expected, LSR trended higher under the more strenuous SA physiologic loading activity (Figure 4). Except for one case, femurs observed to be at higher fracture risk (LSR > 1) during NW physiologic loading were also at higher fracture risk during SA physiologic loading.

Figure 7.

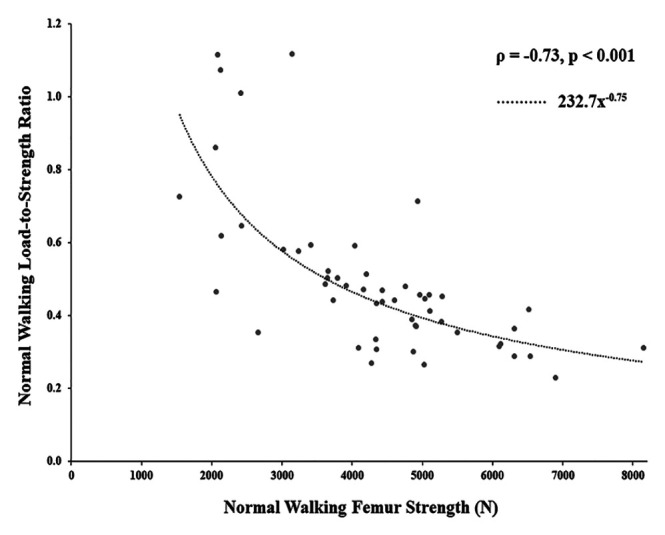
Relationship between femur strength and load-to-strength ratio for normal walking physiologic loading, showing a strong correlation. Dotted line indicates a power fit. ρ – Spearman correlation coefficient.

Discussion

Using data from 48 patients, we evaluated differences in mechanical behavior between idealized loading configurations and those incorporating physiologic muscle forces, and differences in the rankings of mechanical behavior between different loading configurations, in FE simulations of femurs with MBD. We found that tensile strain was 26% higher and femur strength was 4% lower in simulations excluding physiologic muscle forces. We also found that the rankings of the mechanical predictions were correlated between the strain outcome simulations, and between the strength outcome simulations.

Excluding muscle forces has previously been shown to result in higher computed tensile strains in femurs without MBD.^11,43 We similarly found incorporating physiologic muscle forces affected NW simulations with strain, rather than strength, outcomes. Strains for NW with joint contact only loading (excluding muscles) were similar in magnitude to strains in the more strenuous SA physiologic loading activity, indicating that muscle loading effects (ie, bending) are not fully accounted for when only simulating compressive joint loads. Excluding muscle force in single abductor simulations has been shown to result in small (0.5%-1.3%) decreases in femur strength in femurs with MBD.³⁴ We found the same femurs had a higher fracture risk (LSR > 1) for both NW physiologic and joint contact only loading. However, due to the lower magnitudes estimated with joint contact only loading, there is potential for predicting higher fracture risk based on femur strength given the calculation of LSR with reference to constant joint loads. Conversely, strain-based evaluation of fracture risk, like the strain ratio (lesion region strain/contralateral normal region strain),²³ would be less prone to error from systematic bias. Regardless, absolute values should be used within the appropriate context when interpreting fracture risk calculated with idealized and physiologic loading configurations.

Loads during activities of daily living are important for fracture risk prediction,⁴ and pathologic fractures predominantly occur during non-traumatic activities of daily living.^25,30 Prior femur MBD FE models simulating physiologic loading only focus on the abductor muscle, with loads typically applied through plastic pots.^{29 -31} Loads applied through plastic pots preferentially load cortical bone, thereby altering the load transfer mechanism to the underlying trabecular compartment and result in overestimation of bone strength.⁴⁴ The abductor is only one of several muscles active during level walking and stair ascent; therefore, our physiologic simulations incorporated all dominantly active muscles.³⁹ We currently focused on proximal femur lesions and musculature and the effects of distal lesions and including distal muscles warrant further investigation.

While strain concentrations were observed at and in the vicinity of lesion locations (Figure 5), only the weakest percentile strains during the ST loading simulation approached the tensile yield limit of bone (~6000 μstrain).⁴⁵ Strain-dependent outcome simulations provide an indirect estimate of fracture risk (only moderately correlated with femur strength) that requires correlation with prospective incidences of fracture for accurate interpretation.²³ Also, implementation of the strain-dependent approach requires well-defined lytic lesions to evaluate lesion region strain as mixed/diffuse metastatic lesion geometries/boundaries are harder to identify.⁴⁶ However, identifying lesion boundaries is not critical in nonlinear material-based global femur strength outcome simulations, which inherently account for change in material behavior resulting from MBD. Also, nonlinear models have been shown to explain more variance in failure load.²⁶ On the other hand, offset torsion/sideways fall loading simulations may be more relevant for predictions of fragility fracture risk,¹⁵ resulting from osteoporosis-related systemic global weaking of the femoral head-neck regions, versus localized MBD structural effects. The strong concordance of mechanical predictions between the strain outcome simulations, and between the strength outcome simulations suggests that it may be possible to compare the ranking of femur mechanics within a cohort across studies implementing various loading configurations. Further, given the (mostly) automated modeling process and strong concordance of mechanical predictions, combinations of fracture risk outcomes from different FE model types may potentially be processed using a machine/deep learning approach to improve predictions of fracture risk and assist clinical decision making for surgical management in patients with femur MBD.

Limitations

Our study was not without limitations. We were limited to a relative comparison of mechanical differences between loading configurations due to lack of a true reference. However, our modeling methods were based on validated, published procedures and our results corroborated well with published data, thereby providing a level of confidence in our simulation outcomes. Only 2/32 non-surgically treated femurs experienced a pathologic fracture. Therefore, it was also presently not possible to evaluate model performance against prospective incidences of fractures. Additionally, a surgeon’s decision to treat may be prone to bias and may not be an ideal substitute outcome option to evaluate model performance. When making treatment decisions surgeons also consider clinical factors such as diagnostic need apart from mechanical factors, evident from the few treated cases within the strongest percentile (Figure 4). We also did not explicitly model the constitutive behavior of the bone-metastatic tissue interface. However, given the similar order of magnitude of metastatic tissue modulus as trabecular bone,^47,48 our model can account for variations in modulus distribution at the macro-scale due to the local alterations, which are expected to contribute to the variation in whole-bone mechanics. Incorporating a metastasis-specific constitutive model would be expected to systematically affect the mechanical predictions, which, given the parametric nature of our study, would not be expected to change the interpretation of our results. Mechanical assessment was made at the timepoint the CT scans were acquired. While mechanical integrity may vary over time due to the dynamic disease process, we expect similar conclusions due to our parametric evaluation of loading configurations. Because muscle forces during a fracture event are undocumented, for femur strength outcome physiologic loading simulations, activity-specific scaled muscle forces were applied incrementally in proportion together with the contact displacements to achieve the peak reaction force.²⁹ We did not explicitly adjust for covariates due to the relatively low sample size. However, demographics were similar between treated and untreated cases, and we limited our analyses to paired comparisons to test our primary hypothesis.

Conclusions

Despite the limitations, we showed that FE simulations of patient-specific MBD femurs incorporating physiologic muscle forces affect local strain outcomes more than global strength outcomes. Based on a comprehensive evaluation of common loading simulations pertinent to MBD femurs, we also showed that mechanical predictions were ranked (weakest to strongest) similarly between the strain outcome simulations, and between the strength outcome simulations. The resulting differences from the variability in FE model loading indicated absolute values computed using idealized (no muscle forces) and physiologic loading configurations should be used within the appropriate context when interpreting fracture risk.