Abstract
The coronavirus disease (COVID-19) pandemic has already caused enormous damage to the global economy and various industries worldwide, especially the tourism industry. In the post-pandemic era, accurate tourism demand recovery forecasting is a vital requirement for a thriving tourism industry. Therefore, this study mainly focuses on forecasting tourist arrivals from mainland China to Hong Kong. A new direction in tourism demand recovery forecasting employs multi-source heterogeneous data comprising economy-related variables, search query data, and online news data to motivate the tourism destination forecasting system. The experimental results confirm that incorporating multi-source heterogeneous data can substantially strengthen the forecasting accuracy. Specifically, mixed data sampling (MIDAS) models with different data frequencies outperformed the benchmark models.
Keywords: Tourism demand forecasting, Online news, Search query data, MIDAS, GDFM
1. Introduction
In 2019, the coronavirus disease (COVID-19) pandemic ravaged the world, with a huge negative impact on countries, including their social and economic aspects (Zhang, Song, Wen, & Liu, 2021). The tourism and hospitality industries of several countries have been hit hard by embargo measures and restrictive policies (Wu, Hu, & Chen, 2022; Yang, Fan, Jiang, & Liu, 2022). Due to the unexpected and severe mobility restrictions brought on by the COVID-19 epidemic, the tourism industry is currently in an unprecedented situation and needs assistance on how quickly different destinations will recover (Liu et al., 2021a, Liu et al., 2021b). Accurate and timely tourism demand forecasting as a prerequisite for allocating resources, emergency management, tourism policy design and implementation, and tourism recovery judgment plays an important role during the COVID-19 pandemic (Liu et al., 2021a, Liu et al., 2021b; Yang et al., 2022). Therefore, tourism demand recovery forecasting in the post-epidemic era has become a key focus and a topic of concern for tourism management research (Qiu et al., 2021). Various forecasting models have been leveraged to improve the forecasting accuracy. Examples include combined econometric and judgemental models (Li et al., 2022a, Li et al., 2022b, Li et al., 2022c, Li et al., 2022d; Zhang et al., 2021); scenario-based judgemental forecasting models (Kourentzes et al., 2021; Qiu et al., 2021; Liu, Vici, et al., 2021); artific ial neural networks (ANNs) technique (Li et al., 2022a, Li et al., 2022b) and expert judgement-based probabilistic forecasting models (Athanasopoulos, Hyndman, Kourentzes, & O'Hara-Wild, 2022).
Previous literature on tourism demand forecasting has highlighted the importance of exogenous factors in enhancing the accuracy of tourism forecasting. These exogenous factors mainly involve economy-related variables, search query index, social media posts (tweets, online reviews, online news, and tourist sharing photos), and many other factors (Hu, Li, Song, Li, & Law, 2022; Park, Park, & Hu, 2021; Sun, Li, Guo, & Wang, 2021; Sun, Wei, Tsui, & Wang, 2019; Yang et al., 2022). However, online news data is rarely taken into account when predicting a destination's tourism demand (Park et al., 2021; Önder, Gunter, & Scharl, 2019). As is well known, economic factors represent tourist income and destination consumption level, search query index shows tourists' attention to tourism destinations, and online news represents real-time policies of tourism destinations (Li et al., 2020a, Li et al., 2020b, Li et al., 2020c; Sun et al., 2021; Önder et al., 2019). In particular, in the post-COVID-19 era, tourists can explore real-time policies regarding the epidemic through the destination's online news, which can influence the tourists' decision to travel there. Furthermore, the economic factors published by the National Bureau of Statistics are low-frequency monthly, quarterly, or annual data, whereas search query data and online news data are real-time. Hence, it poses a challenge for extant models to deal with multi-source heterogeneous data with different frequencies. To the best of the author's knowledge, this is the first research work that integrates these exogenous factors into models to achieve better performance in the tourism demand forecasting. If these exogenous factors are simultaneously considered with different frequencies, the forecasting performance of extant methods may be limited to a certain extent. This is mainly due to the fact that how to deal with these factors with different frequencies, the existing methods typically maintain all variables at the same frequency by aggregating a high-frequency variable into a low-frequency one which can lead to the loss of data information. To address this issue, the seasonal autoregressive integrated moving average-mixed data sampling (SARIMA-MIDAS) approach has been introduced into tourism demand forecasting (Hu et al., 2022; Wen, Liu, Song, & Liu, 2020). Thus, an interesting research question arises as to whether multi-source heterogeneous data with different frequencies can improve the forecasting performance of tourism demand amid COVID-19 era.
To address this research question and the research gaps of previous studies, this study proposed SARIMA-MIDAS approach for Hong Kong tourism demand recovery forecasting amid COVID-19 by fusing multi-source heterogeneous predictors with different frequencies, including monthly economic index, daily search query index, and weekly online news data. Hong Kong has cultural diversity and shopping opportunities attracting thousands of tourists each year (Zhang et al., 2021), especially those from mainland China. Additionally, the tourist volume of Hong Kong from mainland China is very typical and has been adopted in many other studies, such as Wen, Liu, and Song (2019) and Wen et al. (2020). Therefore, an empirical analysis of the tourist volume of Hong Kong from Mainland China is conducted in this study to verify the effectiveness of our proposed approach.
The experimental results prove that this study proposed SARIMA-MIDAS approach using multi-source heterogeneous predictors with different frequencies significantly outperforms all other benchmarks. These findings show that this study proposed approach is a promising paradigm for tourism demand recovery forecasting during COVID-19. The contributions of this research work are threefold: (1) for online news data, we utilise structure topic models (STM) and linguistic inquiry and word count (LIWC) to generate the topic distribution and sentiment score, respectively; (2) this study is the first to integrate the topic intensity and sentiment intensity of online news for tourism demand recovery forecasting during COVID-19; and (3) we constructed an economic index, visitor attention index, and topic intensity using a generalised dynamic factor model (GDFM) from economic factors, search query data, and topic distribution.
The remainder of this article is organised as follows. A literature review is provided in Section 2. Section 3 introduces the methodology and forecasting framework. The empirical study and discussion are given in Section 4 and Section 5, respectively. Finally, Section 6 presents the conclusions, practical implications, limitations, and future research.
2. Literature review
2.1. Tourism demand forecasting
As a critical part of tourism management, various models have been proposed during the past several decades to generate more accurate results in the tourism demand forecasting. These proposed models mainly include non-causal time series models, causal econometric models, artificial intelligence (AI) techniques (Kulshrestha, Krishnaswamy, & Sharma, 2020; Li et al., 2020a, Li et al., 2020b, Li et al., 2020c; Song, Qiu, & Park, 2019; Xie, Qian, & Wang, 2020; Zhang, Li, Muskat, & Law, 2020; Zhao, Du, Azaglo, Wang, & Sun, 2022). Table 1 summarises some representative research on tourism demand forecasting in recent years.
Table 1.
Overview of typical research works related to tourism demand forecasting.
| References | Destination | Data frequency | Models | Performance measure | Independent variables | Forecasting context |
|---|---|---|---|---|---|---|
| Sun et al. (2019) | Beijing | Monthly |
KELM, ARIMAX, ARIMA, ANN, SVR, LSSVR |
NRMSE, MAPE, DM | Tourist arrivals, Baidu index, and Google trends data | Tourist arrivals in Beijing from Mainland and overseas |
| Bi et al. (2021) | Jiuzhaigou and Mount Siguniang | Daily |
GAF/MTF/RP-CNN-LSTM, SVM,BPNN,CNN,LSTM,CNN-LSTM |
MAE, MAPE, RMSE | Tourist arrivals | Tourist arrivals at two well-known attractions in China, Jiuzhaigou, and Mount Siguniang |
| Kulshrestha et al. (2020) | Singapore | Quarterly | BBiLSTM, LSTM, SVR, RBFNN, ADLM | RMSE, MAE, MAPE, RRMSE | Tourist arrivals and economic variables | Tourist arrivals to Singapore from five major source countries, namely Australia, France, Germany, Netherlands, and New Zealand |
| Law, Li, Bayesian and Han (2019) | Macau | Monthly | LSTM-AM, Naïve, SVR, ANN, ARIMA, ARIMAX | RMSE, MAE, MAPE | Tourist arrivals, Baidu index, and Google trends data | Tourism arrivals in Macau from the global market and mainland China |
| Sun et al. (2021) | Beijing | Monthly | SN, SARIMA, SES, ARDL, SARIMAX, MLP, B-MLP, KELM, B-KELM, SAKE, B-SAKE | MAPE, NRMSE, DS, DM, PT | Tourist arrivals, economic variables and Baidu index | Tourist arrivals in Beijing from origin countries of the United States, the United Kingdom, Germany, and France |
| Silva, Hassani, Heravi, and Huang (2019) | European | Monthly | NNAR, DNNAR, ARIMA, ETS | RMSE, RRMSE, MAPE, DM, HS | Tourist arrivals | International tourism demand for tourist arrivals of ten European countries,namely, Germany, Greece, Spain, Italy, Cyprus, Netherlands, Austria, Portugal, Sweden, United Kingdom |
| Park et al. (2021) | Hong Kong | Monthly | SARIMAX, SARIMA, SNAIVE, ETS | MAE, MAPE, RMSE, RMSPE, RI | Tourist arrivals and online news data | Tourism arrivals in Macau from the US and mainland China |
| Hu et al. (2021) | Jiuzhaigou, Kulangsu and Siguniang Mountain | Daily | SN, SARIMA, ETS, SARIMAX, TBATS, k-NN and HPR | MAPE and MASE | Tourist arrivals and dummy variables for holidays | Tourist visits to three attractions in China |
| Höpken et al. (2020) | Sweden | Monthly | ARIMAX, ARIMA, ANN, ANNX | RMSE and Shapiro-Wilk test | Tourist arrivals and Google trends data | Inbound tourist arrivals to Sweden from major sending countries (Denmark, Finland, Norway, the Russian Federation, and the United Kingdom) |
| Li et al., 2019a, Li et al., 2019b | Hong Kong | Quarterly | Naïve, ES, SARIMA, STS, ADL, VAR, EC, TVP, Interval combination model | MAPE and Winkler scores | Tourist arrivals, economic variables, seasonal dummies and one-off event dummies | Hong Kong's inbound tourism demand from its eight key source markets: mainland China, Taiwan, South Korea, Japan, Macao, the Philippines, Singapore and the US |
| Bi, Liu, and Li (2020) | Jiuzhaigou and Huangshan Mountain |
Daily | Naïve, ARIMA, SVR, ANN and LSTM | MAE, RMSE and MAPE | Tourism volume data, Baidu index and weather data | Forecasting the daily tourism volume of Jiuzhaigou and Huangshan Mountain Area, two famous tourist attractions in China |
Notes: Models: Kernel extreme learning machine (KELM); Support vector regression (SVR); Autoregressive integrated moving average (ARIMA); Autoregressive integrated moving average with exogenous variables (ARIMAX); Artificial neural network (ANN); Least squares support vector regression (LSSVR); Gramian angular field (GAF); Markov transition field (MTF); Recurrence plot (RP); Convolutional neural network (CNN); Long short-term memory (LSTM); Support vector machine (SVM); Back propagation neural network (BPNN); Bidirectional long short-term memory optimized by Bayesian (BBiLSTM); Radial basis function neural network (RBFNN); Autoregressive distributed lag model (ADLM); LSTM augmented with the attention mechanism (LSTM-AM); Seasonal naïve (SN); Seasonal exponential smoothing (SES); Autoregressive distributed lag (ARDL); Multilayer perceptron (MLP); Bagging-based MLP (B-MLP); Bagging-based KELM (B-KELM); Stacked auto-encoder with KELM (SAKE); Bagging-based SAKE (B-SAKE); Neural networks auto-regression (NNAR); Denoised neural networks auto-regression (DNNAR); Hierarchical pattern recognition (HPR); Exponential smoothing state space model with Box-Cox transformation, ARMA errors, trend, and seasonal components (TBATS); k-Nearest neighbour (k-NN); Artificial neural network with exogenous variables (ANNX); Seasonal autoregressive integrated moving average (SARIMA); Seasonal autoregressive integrated moving average with exogenous variables (SARIMAX); Exponential smoothing (ETS); Structural time series (STS); Autoregressive distributed lag (ADL); Vector autoregressive (VAR); Error correction (EC); Time-varying parameter (TVP). Performance measures: Normalized root mean square error (NRMSE); Mean absolute percentage error (MAPE); Mean absolute error (MAE); Root mean square error (RMSE); The ratio of RMSE (RRMSE); Root mean square percentage error (RMSPE); Mean absolute scaled error (MASE); Diebold and Mariano statistic (DM); Pesaran and Timmermann statistic (PT); Hassani and Silva statistic (HS); Directional symmetry (DS); Relative improvement (RI). The bold font indicates the highest forecasting accuracy among the models.
Time series models mainly include generalised autoregressive conditional heteroskedasticity (GARCH), structural time series model (STSM), naïve and exponential smoothing (ETS), autoregressive moving average (ARMA), and its variants: autoregressive integrated moving average model (ARIMA), seasonal ARIMA (SARIMA), and autoregressive fractionally integrated moving average (ARFIMA). According to historical patterns, there models generate forecasting values of tourism demand and they are widely used as benchmarks (Hu, Qiu, Wu, & Song, 2021). An inherent disadvantage of time series models is that many factors that may profoundly affect tourism volumes are largely ignored. Whereas, econometric models incorporate exogenous factors to enhance the accuracy of tourism forecasting, such as economy-related indicators, weather indicators, holiday indicators, and big data indicators (search query data, online reviews, online news). Commonly used econometric models include the autoregressive distributed lag model (ADLM), error correction model (ECM), time-varying parameter (TVP) model, system-of-equation model, mixed-data sampling, and Bayesian vector autoregressive (BVAR) model. These two models rely on the stability of historical patterns and economic structures. However, these models may not fully utilise complex and nonlinear data.
With the impressive performance, AI-based techniques have been popular in tourism demand forecasting (Höpken, Eberle, Fuchs, & Lexhagen, 2020; Sun et al., 2019). The most commonly models include artificial neural networks (ANNs), fuzzy logic theory, grey theory, support vector machines (SVM), genetic algorithms (GA), and rough set models. Although AI-based models have higher prediction accuracy than statistical models and econometric models, they still have several limitations. Firstly, as the frequency of data increases, these models become exceedingly difficult to process the data given its non-stationarity, seasonality, and complexity (Zhang et al., 2021). Secondly, AI-based models generally have problems of overfitting or local optima (Zhang, Li, MUSKAT, & Law, 2021). In contrast, deep learning approaches can extract discriminative features without requiring a lot of human effort and domain knowledge, which has become a research hotspot in recent years (Bi, Li, & Fan, 2021; Kulshrestha et al., 2020; Li & Law, 2019; Zhang et al., 2020).
Since COVID-19 pandemic is sudden, uncertain, and volatile and directly affect tourism demand, accurate tourism demand forecasting poses more challenges. Tourism demand recovery forecasting has attracted interests of plenty researchers and various forecasting models have been leveraged to improve the forecasting accuracy. Examples include combined econometric and judgemental models (Zhang et al., 2021); scenario-based judgemental forecasting models (Kourentzes et al., 2021; Liu et al., 2021a, Liu et al., 2021b; Qiu et al., 2021) artificial neural networks (ANNs) technique (Li et al., 2022a, Li et al., 2022b, Li et al., 2022c, Li et al., 2022d) and expert judgement-based probabilistic forecasting models (Athanasopoulos et al., 2022).
After analysing the existing literature, there is not a model that consistently outperforms others in all situations. The forecasting accuracy of tourism demand is affected by multiple factors, such as the data frequency and explanatory variables. To consider different frequency data and multiple explanatory variables simultaneously, this study proposes SARIMA-MIDAS-based multi-source heterogeneous data with different frequencies for tourism demand forecasting.
2.2. Tourism demand forecasting with search query data
Before starting a journey, people generally search for the information related to the destination online and plan their travel route. Such search query data, covering customers’ digital footprints, reflects the consumption preferences and desires of tourists and can be used as a powerful predictor in the prediction. A lot of researches in several areas have explored the role of search query data in the forecasting and these researches can be classified into three categories: industry market (Chen, Xu, Jia, & Gao, 2021; Hand & Judge, 2012; Lu, Li, Chai, & Wang, 2020; Petropoulos, Siakoulis, Lazaris, & Vlachogiannakis, 2021; Yang, Guo, Sun, & Li, 2021; Zhang, Tian, & Fan, 2022), macroeconomic indicators forecasting (Smith, 2016; Aaronson et al., 2022), public health and disease surveillance (Ginsberg et al., 2009; Liu, Feng, Tsui, & Sun, 2021; Song et al., 2014). Table 2 summarises the basic information of some representative studies of tourism demand forecasting recent years.
Table 2.
Summary of selected tourism demand forecasting studies using search query data.
| Author (Year) | Data frequency | Data categories | Search data preprocessing | Analysis method | Predicted context |
|---|---|---|---|---|---|
| Li et al. (2018) | Monthly | Baidu Index | PCA | PCA-ADE-BPNN | Beijing in-bound tourist volume |
| Li and Law (2019) | Monthly | Google Trends | EEMD | ARX | Tourist arrivals from nine countries to Hong Kong |
| Liu, Zhang, Zhang, Sun, & Qiu (2019) | Daily | Baidu Index | NA | VAR | Tourist arrivals to Tianmu lake in China |
| Law et al. (2019) | Monthly | Google Trends | MIC | DL | Tourist arrivals in Macau |
| Hu and Song (2019) | Monthly | Google Trends | AIC | ANN | Short-haul travel from Hong Kong to Macau |
| Sun et al. (2019) | Monthly | Google Trends and Baidu Index | Correlation analysis | KELM | Tourist arrivals to Beijing |
| Wen and Liu (2019) | Monthly | Baidu Index | PCA | Hybrid models | Tourist arrivals in Hong Kong from mainland China |
| Li, Hu, and Li (2020) | Weekly | Baidu Index | GDFM | ARIMAX, SVM, and RF | Tourist arrivals to Mount Siguniang |
| Li, Li, et al. (2020) | Weekly and Monthly | Google Trends and Baidu Index | Machine learning-based feature selection models | ARMAX | Monthly domestic tourist arrivals to Beijing, China and weekly forecasting of hotel occupancy in Charleston, SC |
| Wen et al. (2020) | Daily | Baidu Index | GDFM | SARIMA-MIDAS | Tourist arrivals in Hong Kong from mainland China |
| Bi et al. (2020) | Daily | Baidu Index | Pearson correlation coefficient | LSTM | Daily tourism volume of Jiuzhaigou and Huangshan Mountain Area |
| Tang, Zhang, Li, and Li (2021) | Monthly | Baidu Index | Pearson correlation coefficient and PCA | SED-BEMD-LR, SED-BEMD-SARIMA, SED-BEMD-SVR, SED-BEMD-ELM, and SED-BEMD-RVFL | Tourist arrivals to Hainan, China |
| Xie, Li, Qian and Wang (2020) | Baidu Index and Google Trends | KPCA | ARIMAX, BPNN, SVR, LSSVR, MA-LSSVR | Tourist arrivals to Hong Kong from Chinese Mainland and United Stated | |
| Bi, Li, Xu and Li (2021) | Daily | Baidu Index | Correlation analysis | Ensemble LSTM with CPS | Daily tourism demand forecasting for the Huangshan Mountain Area |
| Hu, Xiao and Li (2021) | Weekly | Baidu Index | Boruta algorithm | ARIMAX | Weekly tourist arrivals to Mount Siguniang and Kulangsu |
| Xie, Qian, and Wang (2021) | Monthly | Baidu Index | Correlation analysis | LSSVR-GSA | The volume of cruise tourism in China |
| Tian, Yang, Mao and Tang (2021) | Daily | Baidu Index | Lasso and elastic net | ARMAX and MSAR | Daily tourist arrivals to Mount Longhu in China |
| Yang, Guo and Sun (2021) | Monthly | Baidu Index | Correlation analysis | LR | Domestic tourist arrivals to Chongqing |
| Sun et al. (2021) | Monthly | Google Trends | Pearson correlation coefficient | B-SAKE | Inbound tourist arrivals in Beijing from origin countries of United States, the United Kingdom, Germany, France |
| Yang et al. (2022) | Daily | Google Trends | LASSO | ARX | Tourism demand across 74 countries |
Notes: Adaptive differential evolution algorithm (ADE); Principal component analysis (PCA); Kernel principal component analysis (KPCA); Autoregressive exogenous model (ARX); Ensemble empirical mode decomposition(EEMD); Maximal information coefficient (MIC); Deep learning (DL); Akaike Information Criterion (AIC); Generalised dynamic factor model (GDFM); Bivariate empirical mode decomposition (BEMD); Least absolute shrinkage and selection operator (LASSO); Markov-switching auto-regression (MSAR); Random forest (RF); Least squares support vector regression model with gravitational search algorithm (LSSVR-GSA); Moving average–least squares support vector regression (MA-LSSVR); Bivariate empirical mode decomposition (BEMD); Seasonal autoregressive integrated moving Average–Mixed data sampling (SARIMA-MIDAS); correlation-based predictor selection(CPS).
In tourism demand, a more recent trend is forecasting using search query data. For instance, by employing Baidu search index as a predictor, Li, Chen, Wang, and Ming (2018) predict the tourist arrivals in Beijing and overnight tourist arrivals of Hainan. Li, Pan, Law, and Huang (2017) also utilized Baidu search data in the prediction of Beijing's tourism demand and their results confirmed that the prediction performance is improved when the dimension of keywords in the Baidu index data was reduced using GDFM. Wen et al. (2019) exploited Baidu index data and hybrid models to improve the prediction accuracy for tourist arrivals. To explore the effect of decomposed search data in improving the prediction accuracy, Li and Law (2019) present forecasting for the tourism arrivals of nine source in Hong Kong by employing the Google Trend as a predictor and the results demonstrated it suppose.
Using the ARMA model, Yang, Pan, Evans, and Lv (2015) examined the predictive power of Google Trend and Baidu search data in the tourism demand forecasting and the results showed that Baidu search query had a better performance owing to its larger market share in China. Sun et al. (2019) integrated the search engine data with tourist arrivals and proposed kernel extreme learning (KELM) models. Taking the tourist arrivals in Beijing as an example, this study demonstrated that the proposed models significantly enhanced forecasting performance. Li et al., 2020a, Li et al., 2020b, Li et al., 2020c forecasted the number of visitors to Mount Siguniang and indicated that tourism demand forecasting based on internet big data from a search engine and online review platforms could significantly improve forecasting performance. Amid COVID-19 era, Yang et al. (2022) applied the lasso method to predict daily tourism demand across 74 countries in 2020 and evaluated the usefulness of online search queries in boosting forecasting accuracy.
Before integrating the search query data into the forecasting model, Li et al., 2020a, Li et al., 2020b, Li et al., 2020c extracted useful feature from it by utilizing feature selection method. And the forecasting results of tourist volume in China and hotel occupancy in USA shown that the models with feature selection performed better than the benchmarks without it. By studying and summarising existing relevant studies, it was found that almost all studies on tourism demand forecasting mainly considered six aspects: tourism, traffic, recreation, shopping, dining, and lodging. Since 2019, the COVID-19 pandemic has profoundly impacted the whole tourism industry. In addition to the six aspects mentioned above, we also considered epidemic-related influence factors in this study.
2.3. Forecasting with online news data
A rising body of researches investigate news-based metric as information sources for forecasting in light of the advantage of big data. Researchers have examined the valence of news data for forecasting in many fields, including industry market forecasting, macroeconomic indicator forecasting, public health and disease surveillance, and economic policy. Table 3 summarises the selected literature that incorporates online news data for forecasting.
Table 3.
Summary of the selected literature that incorporated online news data to forecast.
| Category | Research object | Author (Year) | Data set | Model | Evaluation criteria |
|---|---|---|---|---|---|
| Industry market forecasting | Tourism demand forecasting | Park et al. (2021) | China Daily and CNN online news | STM- SARIMAX | MAE, MAPE, RMSE, RMSPE,RI |
| Önder et al. (2019) | Online news | R-MIDAS | RMSE, MAE, MAPE, SMAPE, Theil's U | ||
| Stock returns forecasting | Narayan (2019) | Oil price news | OCR-Time series regression | MSFE, R2 | |
| Agricultural futures prices forecasting | Li et al. (2022) | Agricultural futures online news headlines | DP-Sent-LDA- BiLSTM-SVR/RF/BPNN | MAPE, RMSE | |
| Crude oil price forecasting | Li, Shang, and Wang (2019) | Crude oil news headlines | LDA–CNN–RFE-SVR/RF | MAE, RMSE | |
| Oil futures returns and volatility forecasting | Li, Jiang, Li, and Wang (2021) | Crude oil news headlines | VMD-BiLSTM | MSE, RMSE, MAE, HMSE, HMAE | |
| Oil market forecasting | Wu, Wang, Wang, and Zeng (2021) | Online oil news | CNN-BPNN/MLR/SVM/LSTM/RNN | MAE, MAPE, RMSE | |
| Macroeconomic indicators forecasting | Economic indicators forecasting | Song and Shin (2019) | Online economic news articles | Lexicon approach-MA/ARMA | RMSE, MAE,R2 |
| Macroeconomic forecasting | Tilly, Ebner, and Livan (2021) | Newspaper articles | BiLSTM-AR | RMSE, DM | |
| Economic index forecasting | Shapiro, Sudhof, and Wilson (2022) | Economic and financial newspaper articles | NLP text sentiment analysis techniques-regression | Adjusted R2 | |
| Economic forecasting | Ardia, Bluteau, and Boudt (2019) | Economic newspaper articles | Lexicons-Penalized least squares regression- | RMSFE, MAFE | |
| Elections and Politics | Elections forecasting | Fronzetti Colladon (2020) | Voting events online news | Social network analysis/text mining/Semantic brand score | MAPE, MAE |
| Public health and disease surveillance | Health-care stock prices forecasting | Shynkevich, McGinnity, Coleman, and Belatreche (2016) | Stocks news articles | GICS-MKL | Accuracy, Return |
| Economic policy | Economic policy uncertainty forecasting | Tobback, Naudts, Daelemans, Junquéde Fortuny, and Martens (2018) | Economic news | SVM-OLS | RMSPE |
Notes: Models: Structural topic models (STM); Ordinary least squares regression (OLS); Restricted MIDAS (R-MIDAS); Optical character recognition (OCR); Dependency parsing sentence latent dirichlet allocation (DP-Sent-LDA); Bi-directional long short-term memory (BiLSTM); Latent dirichlet allocation (LDA); Convolutional neural network (CNN); Recursive feature elimination (RFE); Moving average (MA); Global industry classification standard (GICS); Multiple kernel learning (MKL). Performance measure: Symmetric mean absolute percentage error (SMAPE); Mean squared forecast errors (MSFE); Mean Square Error (MSE); Heteroscedasticity adjusted mean squared error (HMSE); Heteroscedasticity adjusted mean absolute error (HMAE); Root mean squared forecast error (RMSFE); Mean absolute forecast error (MAFE).
Online news represents real-time policies of tourism destinations; thus, it has also been used as a predictor in tourism demand forecasting. Park et al. (2021) proposed a new model by integrating the news topic variables into the SARIMA and confirmed the usefulness of news topic in the tourism demand forecasting. Önder et al. (2019) employed the MIDAS model and used the web sentiment of news media as a predictor to forecast tourism arrivals in four European cities. The result indicated that the web sentiment of social media is a powerful predictor for the tourism demand forecasting. Especially in the post-COVID-19 era, some COVID-19-related policies have affected the tourism and hospitality industries. Therefore, tourists can capture real-time policies about the epidemic through the destination's online news, which can influence tourists' decision to travel to this tourism destination. In this study, we fused the topics and sentiments recognized from online news into tourism demand recovery forecasting.
2.4. Mixed data sampling model
Time series data often contain different frequencies. To estimate models with different frequencies variables, researchers typically maintain all variables at the same frequency by aggregating a high-frequency variable into a low-frequency one which can lead to the loss of data information. To handle this issue, Ghysels, Santa Clara, and Valkanov (2004) proposed the MIDAS model which allowed the variables with different frequencies to appear in the model simultaneously. Since then, the MIDAS model has gained popularity in several research fields. Table 4 summarises some studies that employ the MIDAS model.
Table 4.
Summary of selected studies of MIDAS regressions.
| Research object | Author (Year) | Dependent variable data frequency | Independent variable data frequency | Analysis methods |
|---|---|---|---|---|
| Gross domestic product | Pan, Wang, Wang, and Yang (2018) | Quarterly GDP | Monthly crude oil prices | TVP |
| Tourism demand | Bangwayo-Skeete and Skeete (2015) | Monthly tourist arrivals | Weekly Google search data | AR |
| Gunter, Önder, and Gindl (2018) | Monthly tourist arrivals | Daily LIKES and monthly Google trends data | ADL | |
| Hirashima, Jones, Bonham, and Fuleky (2017) | Quarterly tourist arrivals and quarterly labor income | Monthly tourist arrivals; monthly passenger counts; monthly airline passenger seats outlook; monthly consumer price index; monthly accommodation; food services jobs; and monthly tourist days | ADL | |
| Wen, Liu, Song and Liu (2021) | Monthly tourist arrivals | Daily Baidu search data | SARIMA | |
| Hu et al. (2022) | Monthly tourist arrivals | Weekly online review volume and average review rating | SARIMA | |
| Liu et al., 2021a, Liu et al., 2021b | Monthly visitor arrivals | Daily Baidu index, monthly visitor arrival data and macroeconomic variables | LASSO | |
| Wu, Hu and Chen (2022) | Monthly hotel occupancy rates | Daily visitor arrivals and search query data, monthly historical hotel occupancy rates | U-MIDAS, MIDAS-Almon | |
| Oil future volatility | Mei, Ma, Liao, and Wang (2020) | 5min oil futures price volatility | Daily geopolitical risk index | RV |
| Crude oil prices | Zhang and Wang (2019) | Monthly WTI and Brent crude oil spot prices | Daily stock market indices | ADL |
Notes: Realised volatility (RV); Generalised autoregressive conditional heteroscedastic (GARCH); Simple MIDAS models by using an unweighted polynomial function (U-MIDAS).
Currently, only a few studies have applied the MIDAS model to tourism demand modelling and forecasting. Bangwayo-Skeete and Skeete (2015) applied the AR-MIDAS with Google Trend to forecast the tourist volume of Caribbean. The result shown that the MIDAS models significantly outperformed most of their baseline time series models combining with weekly Google data. Wen et al. (2020) proposed an improved approach integrating the MIDAS model with the SARIMA process and utilized it to forecast tourism volume in Hong Kong. The forecasting results suggested that their model performed better than the benchmark models. Hu et al. (2022) employed MIDAS model to take online review data, a kind of high-frequency data, as a predictor of the tourist arrivals. Taking the tourist arrivals in Hong Kong, the experimental results shown that MIDAS model achieved more accurate forecasting than other benchmarks. In this study, we employ the SARIMA-MIDAS model to address the data information loss problem. Since the SARIMA-MIDAS model considers more information of data, it is logical to believe that this model can predict tourism demand more accurately.
3. Methodology
3.1. Data collection and pre-processing
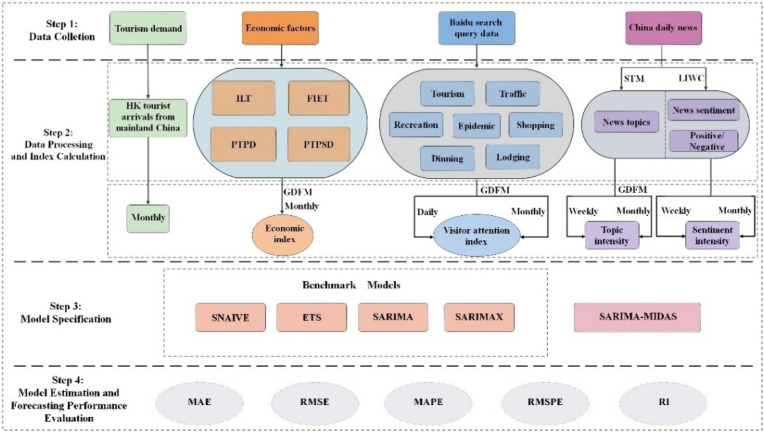
This study integrates data of different time frequencies and different structures, such as daily search query data, weekly online news data, monthly economic variables and monthly tourist arrival data, as input variables for the forecasting approaches (as Fig. 1 ). This study framework involves four steps: (1) collect data from multiple data sources; (2) data pre-processing for different data types; (3) constructing an index, and (4) building a forecasting approach and evaluating its performance.
Fig. 1.
The framework of this study.
3.1.1. Data collection
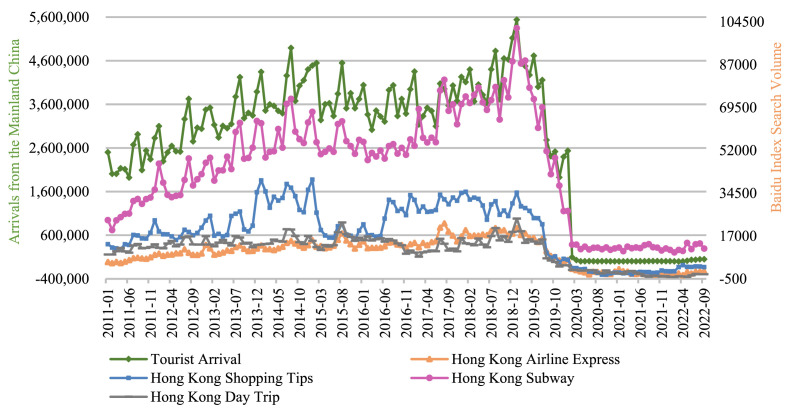
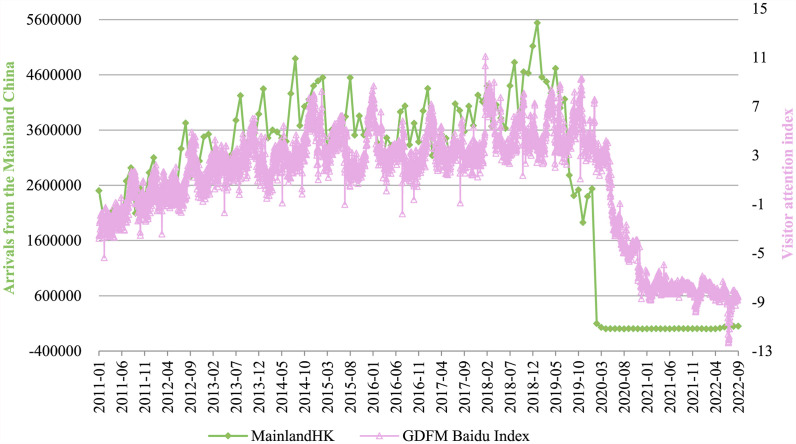
Tourist arrival data. Hong Kong is a tourist hotspot with its cultural diversity and shopping opportunities attracting thousands of tourists each year, especially those from mainland China. Fig. 2 shows monthly tourist arrivals data from mainland China to Hong Kong from January 2011 to September 2022. This study uses data from January 2011 to September 2020 as the training set to estimate the model, and data from October 2020 to September 2022 as the test set to test the predictive performance of the model. From Fig. 2, it can be preliminarily seen that tourist arrivals exhibit seasonality and cliff volatility. Since the Baidu Index data provides data from 2011 to the present, we selected the data from 2011 to 2022 in the Wind database (http://www.wind.com.cn/).
Fig. 2.
Monthly tourist arrivals and daily Baidu index search volume.
Search query data. Baidu is the most popular search engine in mainland China (Yang et al., 2015). People are used to using Baidu to search for various content they want to know. Since this study is a forecast of the number of tourists from mainland China to Hong Kong, the Baidu index is chosen instead of the Google search index. Daily Baidu index data were collected from January 2011 to September 2022 from the Baidu index (http://index.baidu.com/). According to the rules of travel, the first step for travellers is to choose a destination. The second step is to search for information about hotels, weather, shopping, and attractions related to the destination. Following this pattern of tourism, we next define all of these aspects: travel, accommodation, entertainment, transportation, dining, and shopping. Owing to the COVID-19 outbreak, travellers pay more attention to these criteria and consider this the primary factor in their coming trip. For this reason, we select seven aspects of tourism planning. First, we chose 25 seed keywords based on seven aspects of tourism planning, including travel, traffic, lodging, dining, recreation, shopping and epidemic. Then, we added keywords highly correlated to the initial keywords using a demand map interface provided by Baidu. This step was iterated until keywords with unavailable or extremely low volume data. Finally, we obtained 100 Baidu search queries. The seed keywords are listed in Table 5 reflected in different categories.
Table 5.
Seed Search keywords related to Hong Kong tourism.
| No. | Search queries | No. | Search queries | No. | Search queries |
|---|---|---|---|---|---|
| Tourism | Traffic | Recreation | |||
| 1 | Hong Kong tourism | 11 | Hong Kong subway | 19 | Hong Kong tourist attraction |
| 2 | Hong Kong weather | 12 | Hong Kong Airport | 20 | Hong Kong Victoria Harbour |
| 3 | Hong Kong map | 13 | Hong Kong subway price | 21 | Hong Kong Disneyland |
| 4 | Hong Kong travel agency | 14 | Hong Kong and Macau passport | 22 | Hong Kong recreation |
| Shopping | Dinning | Lodging | |||
| 5 | Hong Kong shopping | 15 | Hong Kong snacks | 23 | Hong Kong hotels |
| 6 | Hong Kong shopping duty free shop | 16 | Hong Kong food | 24 | Hong Kong accommodation |
| 7 | Hong Kong shopping tips | 17 | Hong Kong food tips | 25 | Hong Kong hotels booking |
| 8 | Hong Kong shopping list | 18 | Hong Kong restaurant | ||
| Epidemic | |||||
| 9 | HK COVID-19 | ||||
| 10 | Hong Kong epidemic |
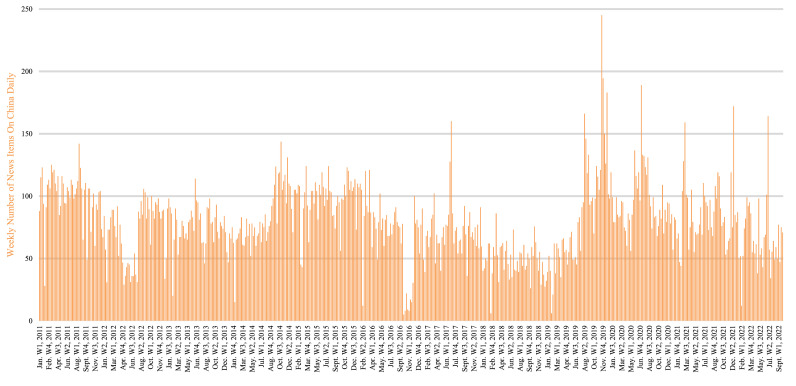
Online news data. Destination-related information published in the news will generate image perception of the destination for tourists, which in turn affects their choice. The news involves local related cultural, political and social issues, including epidemics and other related reports, more or less influence the decision-making of tourists. Therefore, this study builds a web crawler using the Python programming language to collect English online news data from China Daily. The keywords “Hong Kong, HongKong and HK” were used to search for destination-related online news articles from online news sources. By removing duplicate online news articles, we collected 48,634 related news items from China Daily from January 2011 to September 2022. Fig. 3 shows the distribution of weekly news in China. The data were collected from China Daily (http://www.chinadaily.com.cn/).
Fig. 3.
Weekly news distribution for China Daily.
Economic variable data Income and price are the main influencing variables in the theory of economic demand, and there are four income-like and price-like variables that have been widely verified in tourism demand: (1) income level of tourists (ILT); (2) future income expectations of tourists (FIET); (3) prices of tourism products in the destination (PTPD); (4) prices of tourism products in substitute destination (PTPSD). Hong Kong and Macao are very close to Mainland, integration of Hong Kong and Macao passport, and both have a large number of places of interest. Especially most of mainland tourists went to visit both destinations at the same time, so we choose Macao as substitute destination. In this study, we incorporated these four variables into tourism demand forecasting. Specific variable definitions can be found in (Sun et al., 2021). These economic-related variables are also downloaded from the Wind database (https://www.wind.com.cn).
3.1.2. Data processing and variable generation
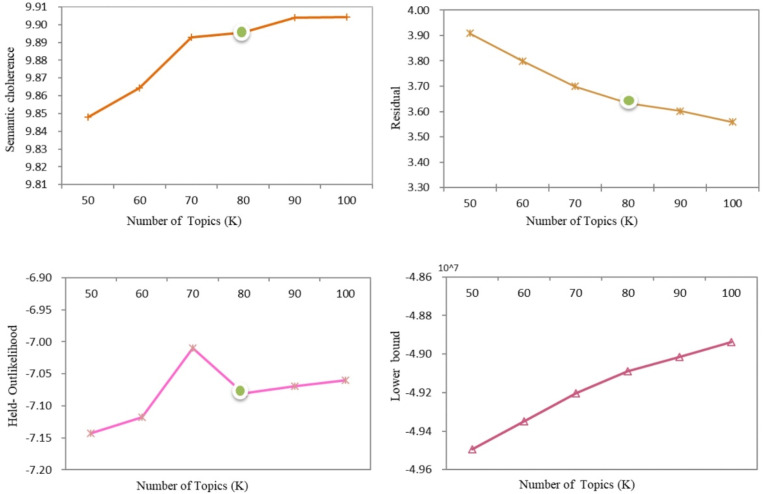
Cleaning of text data can improve the performance of text mining when analyzing text corpora. Therefore, in this study, the Python Natural Language Tool Kit (NLTK) package was utilized to perform a series of pre-processing steps on the text data, specifically, removing non-alphanumeric characters and lowercase conversion. The second is to mark the part of speech, marking out nouns, verbs, adjectives and adverbs for subsequent selection. In addition to NLTK, stopwords, this study also customized to include stopwords (e.g., “also”, “could”, “get”, “may”, “still”) for each news dataset. We then employed STM to extract latent topics from pre-processed online news texts. Ultimately, as depicted in Fig. 4 , we employ semantic coherence and held out likelihood and residuals to find the optimum value for K, as depicted in Fig. 4. The optimal K dataset for online news was 80. Topic prevalence (topic distribution of document topics) reflects the main topics covered in each sampled article. As tourist demand explanations are not continuous nor steady, weekly and monthly subject distributions were created.
Fig. 4.
Selection of the optimum number of topics k based on semantic coherence and held out likelihood and residuals optimisation.
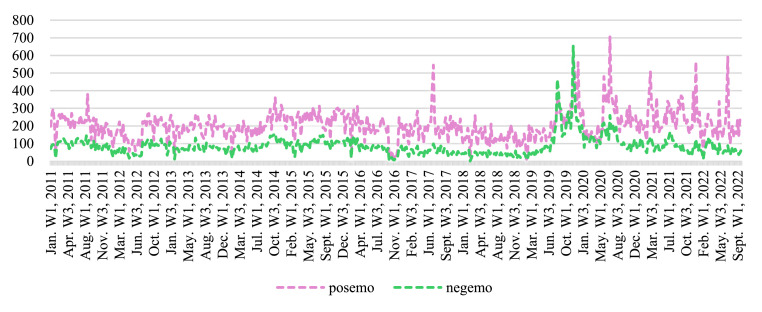
Meanwhile, this study exploits LIWC to analyse the sentiment of online news data; weekly and monthly sentiment intensities (, ) were generated. First, consider the first, second, and third seventh days of each month to be the first, second, and third weeks of the month, respectively, and the remaining days to be the fourth week. Second, the weekly or monthly variables are generated by summing the topic distributions or sentiment intensities in the corresponding weeks or months (identified by timestamps). Typically, the values for the first three weeks of the weekly variable could well be determined, and weekly topic distribution or sentiment intensity value for the fourth week of each month can be computed as 7 times the average topic distribution or sentiment intensity for the remaining days. The weekly positive and negative sentiment scores for China Daily news are plotted in Fig. 5 .
Fig. 5.
Weekly positive score and negative score of China Daily news calculated by LIWC.
Artificial intelligence models (for example, deep learning models) can directly integrate a large number of economic factors, search query data and topic distribution and identify the most relevant search queries. Nonetheless, most of econometric models, such as the MIDAS model used in this study, cannot perform as this. Therefore, we must reduce the dimensions of economic factors, search queries, and topic distributions before modelling. In this study, the GDFM was used to construct monthly economic index (EIMonthly) and daily and monthly visitor attention index (VAIDaily, VAIMontly) from economic factors and Baidu search query data, respectively, meanwhile weekly and monthly topic intensity (TIWeekly, TIMonthly) are constructed by GDFM from the 80-topic distribution. The relationship between the daily visitor attention index and monthly tourist arrivals is shown in Fig. 6 .
Fig. 6.
Daily visitor attention index constructed by GDFM model and monthly tourist arrivals.
3.2. Structural topic models (STM) and sentiment analysis
As the most important Bayesian generation topic models, both LDA and STM assume that each text is represented by a multinomial distribution of topics, and each topic is a distribution of words. More accurately, STM is an extension of LDA due to its introduction of document-level structural information in the form of covariates which make it can influence topic prevalence and topic content. Roberts, Stewart, and Airoldi (2016) proposed a hierarchical mixed membership model and demonstrated that STM has a better performance than LDA in topic modelling. The feature of allowing topic prevalence probability to be modelled with other covariates makes STM more suitable to treat online new because news articles are more likely to discuss multiple topics, such as the impact of COVID-19 on the tourism industry. Therefore, STM was deemed appreciate for this study.
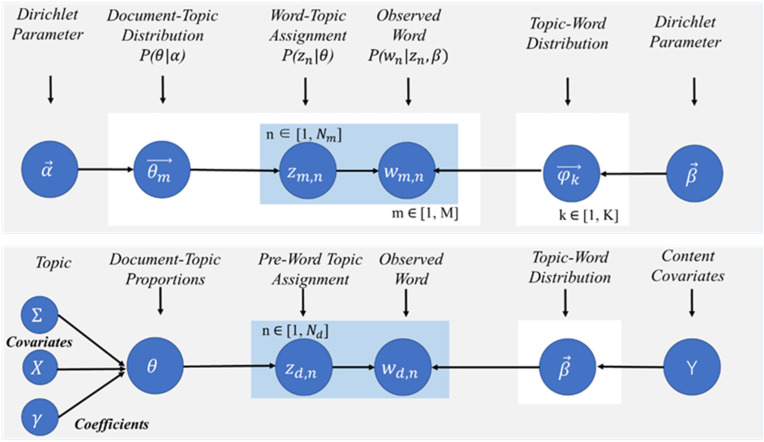
The STM and LDA processes are graphically shown in Fig. 7 by plate notation which visualises technical differences. The generative process for computing topic models using STM is as follows.
Step 1
Generating regression coefficient of covariate X affecting subject distribution:
Given its prior distribution as normal distribution, the posterior distribution is update according to the data.
(1)
Step 2
Generating the topic distribution vector of document d:
In order to introduce the correlation between different topics, the topic distribution vector is extracted from a logistic normal distribution.
(2) where denotes a matrix of the coefficients generated in the Step 1, is a matrix of topic prevalence covariates, and is an covariance matrix.
Step 3
Generating word distribution vector under topic k and document d:
(3) This is equivalent to doing a multinomial logistic regression, where the dependent variables are the observed words, and the independent variables are the different topics, the different values of the covariates, and the interaction terms between the topics and the values of the covariates.
In equation (3), represents the intercept term, is coefficient estimation of words under different topics, represents coefficient estimation of words with different covariate values, and denotes the interaction between the topic and covariate.
Step 4
Generating word set.
Firstly, topics are extracted from a multinomial distribution:
Then, the probability of an observed word in a document to be attributed to this topic is given by
(4) As one of the most important parameters of STM the number of topics K is chosen to allow for a meaningful interpretation of the results instead of maximizing the fit. To make the “K” decision, there has three criteria to select the number of topics: (i) Held out likelihood (To what extent does the candidate number of topics explain the overall variability in the corpus); (ii) Semantic coherence of words to each topic; (iii) Exclusivity of topic words to the topic.
Most of prior researches on sentiment analysis in the tourism field have concentrated on issues like online reviews of tourism products. Few studies have exploited the sentiment of online news to analyse tourism visitor volume. Noteworthy, Önder et al. (2019) were the first to use web sentiments from online news sources to forecast tourism demand. As a destination's coverage may influence its image, sentiment analysis may indicate potential travel behaviour. To fill this gap, this study employs sentiment regarding online news to meet tourism demand. Sentiment data were analysed using LIWC.
LIWC is a software that can quantitatively analyse the word categories (especially psychological words) of text content. Specially, LIWC can calculate the usage percentage of different categories of words in the text, such as causal words, emotional words, cognitive words and so on in the whole text.
Fig. 7.
Comparison of the plate notations of LDA and STM.
3.3. Generalised dynamic factor model (GDFM)
Owing to multi-collinearity and over-fitting concerns in the model estimation, retaining all the variables in the model can be problematic when the number of variables is large. Therefore, constructing indices using many variables is a feasible solution. To do this, common components can be extracted using a variety of factor models, including static and dynamic factor models and the former represents common components as a linear combination of a few concurrently loaded, unobserved static factors.
The GDFM model proposed by Forni, Hallin, Lippi, and Reichlin (2000) has been widely used because of its superior performance. In this study, is the observed variables are driven by common component and idiosyncratic component , where can be expressed as the linear combination of unobservable common factors, . The model is formulated as follows:
| (5) |
| (6) |
where is the time-varying factor loading, is the lag operator, and indicates the number of common factors. Before estimating the GDFM, must be determined.
Forni et al. (2000) suggested that the number of is determined by the cumulative variance contribution rate usually taking the number of factors when the cumulative variance reaches more than 90%. The GDFM has two salient features in the analysis data with many variables: (1) the model's parameters can be updated dynamically, and (2) Cross-correlation between idiosyncratic components is allowed by the GDFM. Specifically, GDFM represents the common states of the observed variables by generating a coincident index. Li et al. (2017), Li, Hu, and Li (2020), and Wen et al. (2020) used the GDFM to generate a composite index from online data. Li et al. (2017) applied the GDFM model to create a composite index and the experimental results demonstrated its validity. Therefore, in this study, we adopt the GDFM model to analyse economic factors, Baidu search query data, and topic distribution related to online news.
3.4. Seasonal autoregressive integrated moving average–mixed data sampling (SARIMA-MIDAS) model
Search query data and online news data generally have a higher frequency than tourist volumes. When high- and low-frequency variables coexist, most existing models combine high-frequency data into low-frequency variables, which may result in inefficient and skewed model estimation. To solve this issue, Ghysels, Santa-Clara, and Valkanov (2006) proposed the MIDAS model which realizes the regression and prediction of low-frequency variables by automatically weighting the high-frequency variables. The application of the MIDAS in tourism research is still in its infancy, and only a few of researches have used it, such as Bangwayo-Skeete and Skeete (2015), Gunter et al. (2018), Hirashima et al. (2017), Wen, Liu, Song, and Liu (2021), and Hu et al. (2022). The MIDAS model is perfect for this study which use the daily visitor attention index, weekly topic and sentiment intensity, and monthly economic indices (, , , and ).
| (7) |
| (8) |
where represents current tourist arrivals, represents a constant, represents the error of the MIDAS regression model, represents backshift operator, and refer to the components of non-seasonal and , respectively, and is the components of seasonal and , respectively, , and constitute the MIDAS component, , and are the coefficients of the high-frequency exogenous variables , and ,respectively, is the coefficient of the low-frequency exogenous variables, is polynomials determining the aggregate weights of high-frequency variables. The most ubiquitous specifications of include exponential Almon lag polynomial, beta, the Almon lag polynomial and Nakagam models. Some researchers, for example, Bangwayo-Skeete and Skeete (2015), Wen, Liu, Song, and Liu (2021), and Hu et al. (2022) have validated that different weighting methods have a little difference in the estimation of MIDAS model. The exponential Almon-lag polynomial method has been suggested by Wen, Liu, Song, and Liu (2021) and Hu et al. (2022) owing to its superior performance. In this study, the ranking of the different weighting schemes generated by the model confidence set (MCS) test in this study's dataset in order is as follows, Exponential Almon lag polynomial, Nakagami, Beta, Almon lag polynomial, therefore, we utilized the exponential Almon-lag polynomial model.
3.5. Benchmark models
3.5.1. SARIMA/SARIMAX
Belonging to the ARMA family, the SARIMA model introduces the seasonal term on the basis of ARIMA which makes it more powerful in the modelling of time series, and it has been popular in recent years (Song, Qiu, & Park, 2019; Li, Hu, & Li, 2020). SARIMA can be exploited to forecast tourist arrivals because of the seasonality among it and the generally expression is SARIMA (p, d, q) (P, Q, D). In this study, the SARIMA model is estimated by the “forecast package” (Hyndman et al., 2020) in the R software. Specifically, the auto. arima () function of it is used to determine p, d, q, P, D, and Q according to the AIC criteria. Forecast () helps generate the forecast value.
The SARIMAX model further extends the SARIMA model by introducing exogenous variables in the model. In this study, the exogenous variables include the economic index, visitor attention index, topic intensity and sentiment intensity. The SARIMAX model can be expressed as
| (9) |
where is the monthly delayed composite visitor attention index, is the monthly delayed - topic intensity, is the monthly delayed sentiment intensity, is the monthly delayed economic index, , , and represent the coefficients for , , and , respectively.
3.5.2. Exponential smoothing
Taking the average of historical values with exponentially decreasing weights as the predicted value, Exponential Smoothing (ETS) model includes the level, trend, seasonality, and smoothing components expressing as , where e, t and s are the error term, trend term and the seasonality term, respectively. Generally, the parameters of ETS are determined by the ets () function in R (Hyndman et al., 2020).
3.5.3. Seasonal naïve
The seasonal NAÏVE (SNAÏVE) model takes the most recent historical observations for the corresponding season as predictions. To forecast monthly tourist arrivals, the general model can be specified as:
| (10) |
where represents the forecast value of tourist arrivals, denotes tourist arrivals, t is time, and m is 12. The SNAÏVE model uses the data from the previous period as the forecast value. In this study, the data from October 2019 to September 2020 was used as the predicted value. This is the predicted value without considering the prediction time step.
3.6. Evaluation criteria of forecasting performance
To verify the performance of proposed model, the mean absolute error (MAE), mean absolute percentage error (MAPE), root mean square error (RMSE), and root mean square percentage error (RMSPE) were adopted as follows (Hu et al., 2022; Bi, Li, Xu, & Li, 2022):
| (11) |
| (12) |
| (13) |
| (14) |
where and are the actual value and forecasting value of tourist volume, respectively. For the above measures, the smaller the value, the better the prediction effect of the model. To compare two models intuitively, this research work further introduced a measure named RI which is build based on MAPE and represents the relative improvement of Model A over Model B (Park et al., 2021).
| (15) |
A larger RI value indicates that Model B outperforms Model A.
Not only in terms of error, this study will also evaluate the performance of the model from a statistical perspective. This study chosed the Superior Predictive Ability (i.e., SPA) test (Hansen, 2005). The SPA test compares favorably to the reality check (RC) for data snooping, because it is more powerful and less sensitive to poor and irrelevant alternatives. It is widely used in tourism demand forecasting for forecasting model performance evaluation (Tang et al., 2021; Li et al., 2022d, Li et al., 2022c, Li et al., 2022b, Li et al., 2022a). The null hypothesis of the SPA test is expressed mathematically as follows:
| (16) |
where Li is the loss from model i and L bm is the loss from the benchmark model.
4. Empirical study
In this section, we first compare the forecasting results of SNAΪVE, ETS, and SARIMA models. After that, we add the three variables of the economic index, visitor attention index, topic and sentiment intensity related online news to SARIMA to examine the forecasting performance of different features. Finally, we consider three feature variables with different frequencies and rely on the SARIMA-MIDAS algorithm for input to obtain the final mixed-frequency model. The empirical evidence of this study is completed and compared across six horizons (For example, we use X1, X2, …. X10 to train the model; if we use the model to forecast X11, then we are forecasting 1 step ahead (h = 1); if we use the model to forecast X13, then we are forecasting 3 steps ahead (h = 3); and so on.).
Specifically, we perform three sets of comparisons to validate the research questions. The first comparison group is presented to examine the performance of SARIMA in a set of benchmark models (include SNAΪVE, ETS and SARIMA). The second comparison group tests whether incorporating the economic index with Internet big data (i.e., visitor attention index, topic and sentiment intensity) into a single forecasting model can improve the forecasting accuracy, while the third one tests whether incorporating big data with different frequencies into the SARIMA-MIDAS model can get a better performance.
To achieve the above three comparisons, nine models were constructed and estimated for SNAÏVE, ETS, SARIMA, SARIMAX1, SARIMAX2, SARIMAX3, SARIMAX4, SARIMA-MIDAS1, SARIMA-MIDAS2, and SARIMA-MIDAS3, as shown in Table 6 . The SNAΪVE, ETS, and SARIMA are time series models, whereas SARIMAX1 is a SARIMAX model with an economic index for fusion. SARIMAX2 is a SARIMAX model that combines a visitor attention index and an economic index. SARIMAX3 is a SARIMAX model that combines topic, sentiment intensity, and an economic index. SARIMAX4 is a SARIMAX model that combines topic, sentiment intensity, visitor attention and an economic index. SARIMA-MIDAS3 is a mixed-frequency SARIMAX model that adds different frequencies (i.e. daily) of a topic and sentiment intensity, and visitor attention index.
Table 6.
Variables setting in the forecasting models.
| Models | Historical series (Monthly) | Economic index (Monthly) | Visitor attention index (Monthly) | Visitor attention index (Daily) | Topic and Sentiment intensity (Monthly) | Topic and Sentiment intensity (Weekly) |
|---|---|---|---|---|---|---|
| SNAÏVE | ✓ | |||||
| ETS | ✓ | |||||
| SARIMA | ✓ | |||||
| SARIMAX1 | ✓ | ✓ | ||||
| SARIMAX2 | ✓ | ✓ | ✓ | |||
| SARIMAX3 | ✓ | ✓ | ✓ | |||
| SARIMAX4 | ✓ | ✓ | ✓ | ✓ | ||
| SARIMA-MIDAS1 | ✓ | ✓ | ✓ | |||
| SARIMA-MIDAS2 | ✓ | ✓ | ✓ | |||
| SARIMA-MIDAS3 | ✓ | ✓ | ✓ | ✓ |
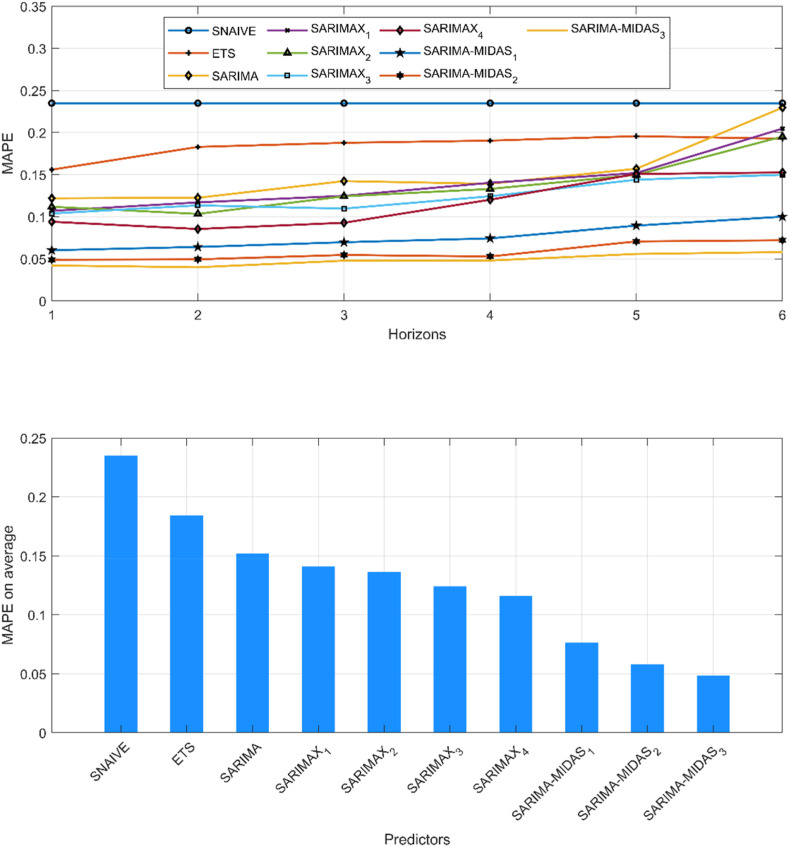
The results of the error indicators (i.e. MAPE, RMSPE, RMSE, and MAE) are shown in Table 7 , and the MAPE is visualised in Fig. 8 . From these results, we can draw some meaningful conclusions. First, among the benchmark models, SNAÏVE possessed the worst results, while SARIMA had better accuracy at forecasting 1 to 4 steps ahead however, inferior to the ETS model at 5 to 6 steps ahead. Second, all four SARIMAX models improve in accuracy compared to SARIMA after adding exogenous variables, which indicates that the economic index, visitor attention index, topic and sentiment intensity all influence tourism demand and can guide better forecasting results. Using SARIMA as a benchmark, the SARIMAX1 model achieves an error reduction of 12.31% (MAPE) in just one step ahead, whereas the rest of the models incorporating more effective variables yield greater accuracy gains. Third, data from the visitor attention index were added to the economic index to further contribute to forecasting accuracy.
Table 7.
H-steps-ahead forecasting accuracy comparisons ().
| Models |
SNAÏVE |
ETS |
SARIMA |
SARIMAX1 |
SARIMAX2 |
SARIMAX3 |
SARIMAX4 |
SARIMA-MIDAS1 |
SARIMA-MIDAS2 |
SARIMA-MIDAS3 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1-step-ahead forecasting | ||||||||||
| MAPE | 0.2349 | 0.1559 | 0.1219 | 0.1069 | 0.1118 | 0.1038 | 0.0940 | 0.0602 | 0.0489 | 0.0421 |
| RMSPE | 0.2514 | 0.193 | 0.1407 | 0.1345 | 0.1403 | 0.1266 | 0.1156 | 0.0789 | 0.0678 | 0.0478 |
| RMSE | 2.9541 | 1.6801 | 0.5007 | 0.5875 | 0.5011 | 0.4609 | 0.4353 | 0.2987 | 0.2458 | 0.1812 |
|
MAE |
1.9938 |
1.3488 |
0.4502 |
0.4381 |
0.4141 |
0.3872 |
0.3558 |
0.2279 |
0.1803 |
0.1598 |
| 2-steps-ahead forecasting | ||||||||||
| MAPE | 0.2349 | 0.1829 | 0.1225 | 0.1170 | 0.1033 | 0.1134 | 0.0854 | 0.0641 | 0.0494 | 0.0400 |
| RMSPE | 0.2514 | 0.2086 | 0.1448 | 0.1391 | 0.1399 | 0.1355 | 0.1149 | 0.0865 | 0.0628 | 0.0517 |
| RMSE | 2.9541 | 1.7682 | 0.6265 | 0.5263 | 0.6180 | 0.5084 | 0.5036 | 0.3607 | 0.2685 | 0.2180 |
|
MAE |
1.9938 |
1.5781 |
0.4977 |
0.4444 |
0.4284 |
0.4281 |
0.3516 |
0.2566 |
0.2007 |
0.1618 |
| 3-steps-ahead forecasting | ||||||||||
| MAPE | 0.2349 | 0.1878 | 0.1423 | 0.1248 | 0.1242 | 0.1096 | 0.0928 | 0.0697 | 0.0546 | 0.0478 |
| RMSPE | 0.2514 | 0.2393 | 0.1625 | 0.1429 | 0.1419 | 0.1463 | 0.1131 | 0.0898 | 0.0645 | 0.0559 |
| RMSE | 2.9541 | 2.1505 | 0.5658 | 0.5145 | 0.5103 | 0.6460 | 0.4376 | 0.3428 | 0.2350 | 0.2032 |
|
MAE |
1.9938 |
1.6908 |
0.5184 |
0.4631 |
0.4606 |
0.4545 |
0.3556 |
0.2667 |
0.2034 |
0.1776 |
| 4-steps-ahead forecasting | ||||||||||
| MAPE | 0.2349 | 0.1904 | 0.1391 | 0.1403 | 0.1330 | 0.1243 | 0.1202 | 0.0743 | 0.0528 | 0.0480 |
| RMSPE | 0.2514 | 0.2275 | 0.1628 | 0.1634 | 0.1510 | 0.1585 | 0.1425 | 0.0946 | 0.0643 | 0.0615 |
| RMSE | 2.9541 | 1.9607 | 0.7006 | 0.6265 | 0.5339 | 0.5726 | 0.5564 | 0.3633 | 0.2655 | 0.2598 |
|
MAE |
1.9938 |
1.6625 |
0.5653 |
0.5343 |
0.4890 |
0.4635 |
0.4632 |
0.2847 |
0.2084 |
0.1956 |
| 5-steps-ahead forecasting | ||||||||||
| MAPE | 0.2349 | 0.1957 | 0.1570 | 0.1519 | 0.1497 | 0.1439 | 0.1508 | 0.0894 | 0.0707 | 0.0558 |
| RMSPE | 0.2514 | 0.2307 | 0.1892 | 0.1788 | 0.1773 | 0.1689 | 0.1810 | 0.1204 | 0.0975 | 0.0747 |
| RMSE | 2.9541 | 2.1198 | 0.8189 | 0.7672 | 0.7645 | 0.6919 | 0.6309 | 0.4706 | 0.3528 | 0.2657 |
|
MAE |
1.9938 |
1.7605 |
0.6428 |
0.6185 |
0.6105 |
0.5659 |
0.5423 |
0.3441 |
0.2584 |
0.2053 |
| 6-steps-ahead forecasting | ||||||||||
| MAPE | 0.2349 | 0.1927 | 0.2296 | 0.2047 | 0.1952 | 0.1498 | 0.1525 | 0.1000 | 0.0720 | 0.0580 |
| RMSPE | 0.2514 | 0.2383 | 0.2633 | 0.2333 | 0.2214 | 0.1924 | 0.1914 | 0.1183 | 0.0855 | 0.0695 |
| RMSE | 2.9541 | 2.0357 | 0.9212 | 0.8119 | 0.7701 | 0.8400 | 0.7851 | 0.4144 | 0.3074 | 0.2568 |
| MAE | 1.9938 | 1.6604 | 0.8255 | 0.7345 | 0.7023 | 0.6180 | 0.6029 | 0.3616 | 0.2686 | 0.2156 |
Fig. 8.
Performance comparison of different models.
Online tourism service platforms can provide a range of tourism-related information through information collection and interaction with tourists, and this information can further influence tourists’ decision-making. To test the impact of online reviews, we compared SARIMAX2-4, in which both the economic and visitor attention indices were added to the topic and sentiment intensity. According to the values of the four indices in the table, SARIMAX4 consistently outperforms SARIMAX2 and SARIMAX3. Therefore, it is possible that the accuracy of tourism demand forecasting can be improved by extracting the topic and sentiment intensity from big data, for example, online reviews, and then adding it to the forecasting sequence. It is worth noting that the fusion model with the addition of topic and sentiment intensity to the economic index (i.e., SARIMAX2) outperforms SARIMAX1 only at a low horizon, which is related to the potency of the topic and sentiment intensity, which is not significantly enhanced compared to the visitor attention index.
Next, we considered the inclusion of variable data with different frequencies (daily and monthly) to enable the application of the mixing frequency model. From the results of the evaluation metrics in the table, the inclusion of daily data with more complex information produces a further reduction in the overall forecasting error. Meanwhile, it can be seen in the comparison between SARIMA-MIDAS2 and SARIMA-MIDAS3 that the optimal performance is obtained for both at different time steps, which indicates that when the information sampling interval is low, the content of online news causes profound effects at different time steps and does not yield an accuracy improvement at either time step. These conclusions are reflected in Fig. 8. The figure above in Fig. 8 shows the changes in MAPE under different horizons, whereas the below figure shows the average MAPE performance under multiple horizons, all of which confirm the above conclusions.
To illustrate the superiority of the proposed model based on mixing data, we provide the RI values in Table 8 . Compared with the proposed model, the errors of each single benchmark model and hybrid benchmark model are significantly reduced, and the fewer exogenous variables added, the greater the improvement. Meanwhile, it can be observed that at h = 1, 2, SARIMA-MIDAS3 has a negative improvement compared to SARIMA-MIDAS1. The specific reason: in most cases, tourism is an activity that requires time planning, and short-term sentiment may not immediately affect the traffic at the current time, but will be reflected several periods later. This leads to the inclusion of ‘Topic and Sentiment intensity (Weekly)’ under some horizon to have an impact on the forecast, to the point where the effect becomes poorer. Combining the results of the above indicators, considering the proposed indicators (i.e. visitor attention index, topic and sentiment intensity) in the forecasting model can make a great contribution to the forecasting of the COVID-19 recovery period, and can largely grasp the development trend of tourist volume in the post-epidemic period, thereby improving the forecast precision. In addition, the consideration of mixed data also supports the forecasting effect of this particular period.
Table 8.
RI results: SARIMA-MIDAS3 vs. other benchmark models.
|
Models |
SNAÏVE |
ETS |
SARIMA |
SARIMAX1 |
SARIMAX2 |
SARIMAX3 |
SARIMAX4 |
SARIMA-MIDAS1 |
SARIMA-MIDAS2 |
|---|---|---|---|---|---|---|---|---|---|
| 1-step-ahead forecasting | |||||||||
| MAPE | 0.8208 | 0.7300 | 0.6546 | 0.6062 | 0.6234 | 0.5944 | 0.5521 | 0.3007 | 0.1391 |
| RMSPE | 0.8099 | 0.7523 | 0.6603 | 0.6446 | 0.6593 | 0.6224 | 0.5865 | 0.3942 | 0.2950 |
| RMSE | 0.9387 | 0.8921 | 0.6381 | 0.6916 | 0.6384 | 0.6069 | 0.5837 | 0.3934 | 0.2628 |
|
MAE |
0.9199 |
0.8815 |
0.6450 |
0.6352 |
0.6141 |
0.5873 |
0.5509 |
0.2988 |
0.1137 |
| 2-steps-ahead forecasting | |||||||||
| MAPE | 0.8297 | 0.7813 | 0.6735 | 0.6581 | 0.6128 | 0.6473 | 0.5316 | 0.3760 | 0.1903 |
| RMSPE | 0.7944 | 0.7522 | 0.6430 | 0.6283 | 0.6305 | 0.6185 | 0.5500 | 0.4023 | 0.1768 |
| RMSE | 0.9262 | 0.8767 | 0.6520 | 0.5858 | 0.6472 | 0.5712 | 0.5671 | 0.3956 | 0.1881 |
|
MAE |
0.9188 |
0.8975 |
0.6749 |
0.6359 |
0.6223 |
0.6221 |
0.5398 |
0.3694 |
0.1938 |
| 3-steps-ahead forecasting | |||||||||
| MAPE | 0.7965 | 0.7455 | 0.6641 | 0.6170 | 0.6151 | 0.5639 | 0.4849 | 0.3142 | 0.1245 |
| RMSPE | 0.7776 | 0.7023 | 0.6560 | 0.6088 | 0.6061 | 0.6179 | 0.5057 | 0.3775 | 0.1333 |
| RMSE | 0.9312 | −0.0820 | 0.6409 | 0.6051 | 0.6018 | 0.6854 | 0.5356 | 0.4072 | 0.1353 |
|
MAE |
0.9109 |
0.0543 |
0.6574 |
0.6165 |
0.6144 |
0.6092 |
0.5006 |
0.3341 |
0.1268 |
| 4-steps-ahead forecasting | |||||||||
| MAPE | 0.7957 | 0.7479 | 0.6549 | 0.6579 | 0.6391 | 0.6138 | 0.6007 | 0.3540 | 0.0909 |
| RMSPE | 0.7554 | 0.7297 | 0.6222 | 0.6236 | 0.5927 | 0.6120 | 0.5684 | 0.3499 | 0.0435 |
| RMSE | 0.9121 | 0.8675 | 0.6292 | 0.5853 | 0.5134 | 0.5463 | 0.5331 | 0.2849 | 0.0215 |
|
MAE |
0.9019 |
0.8823 |
0.6540 |
0.6339 |
0.6000 |
0.5780 |
0.5777 |
0.3130 |
0.0614 |
| 5-steps-ahead forecasting | |||||||||
| MAPE | 0.7625 | 0.7149 | 0.6446 | 0.6327 | 0.6273 | 0.6122 | 0.6300 | 0.3758 | 0.2108 |
| RMSPE | 0.7029 | 0.6762 | 0.6052 | 0.5822 | 0.5787 | 0.5577 | 0.5873 | 0.3796 | 0.2338 |
| RMSE | 0.9101 | 0.8747 | 0.6755 | 0.6537 | 0.6525 | 0.6160 | 0.5789 | 0.4354 | 0.2469 |
|
MAE |
0.8970 |
0.8834 |
0.6806 |
0.6681 |
0.6637 |
0.6372 |
0.6214 |
0.4034 |
0.2055 |
| 6-steps-ahead forecasting | |||||||||
| MAPE | 0.7531 | 0.6990 | 0.7474 | 0.7167 | 0.7029 | 0.6128 | 0.6197 | 0.4200 | 0.1944 |
| RMSPE | 0.7235 | 0.7084 | 0.7360 | 0.7021 | 0.6861 | 0.6388 | 0.6369 | 0.4125 | 0.1871 |
| RMSE | 0.9131 | 0.8739 | 0.7212 | 0.6837 | 0.6665 | 0.6943 | 0.6729 | 0.3803 | 0.1646 |
| MAE | 0.8919 | 0.8702 | 0.7388 | 0.7065 | 0.6930 | 0.6511 | 0.6424 | 0.4038 | 0.1973 |
In this study, SPA tests were used to statistically evaluate the strengths and weaknesses of the forecasting performance of each model. The p-values for the results are listed in Table 9 . The p-value shows if there is a statistically significant association of superiority between the two selected models. What is striking from the results are: (1) All p-values are larger than 0.95 when the approach provided in this study, SARIMA-MIDAS3, is regarded the benchmark model, indicating that the proposed strategy considerably outperforms all other comparison models at the 95% confidence level; (2) SARIMA-MIDAS1 and SARIMA-MIDAS2 validate their superiority in statistical terms compared to the five benchmark models and prove the utility of the availability of mixing data.
Table 9.
Results of the SPA test.
| SARIMA | SARIMAX1 | SARIMAX2 | SARIMAX3 | SARIMAX4 | SARIMA-MIDAS1 | SARIMA-MIDAS2 | |
|---|---|---|---|---|---|---|---|
| SARIMA | |||||||
| SARIMAX1 | 0.9750 | ||||||
| SARIMAX2 | 0.9870 | 0.9970 | |||||
| SARIMAX3 | 0.9510 | 1.0000 | 0.9710 | ||||
| SARIMAX4 | 0.9000 | 1.0000 | 0.9920 | 1.0000 | |||
| SARIMA-MIDAS1 | 1.0000 | 0.9520 | 0.9850 | 1.0000 | 1.0000 | ||
| SARIMA-MIDAS2 | 0.9060 | 1.0000 | 0.9560 | 0.9200 | 0.9670 | 0.9910 | |
| SARIMA-MIDAS3 | 0.9580 | 1.0000 | 0.9970 | 0.9670 | 0.9680 | 0.9960 | 0.9990 |
5. Discussion
In this study, by combining historical series, economic index, visitor attention index and topic intensity and sentiment intensity data to forecast the monthly tourist arrivals using SARIMA-MIDAS model, the following four major conclusions are obtained from the experimental study.
The proposed SARIMA-MIDAS model with mixed frequency characteristics significantly outperforms all considered benchmark models in tourism demand forecasting, even during the COVID-19 pandemic. This may be related to the fact that the SARIMA-MIDAS model simultaneously considers the mixed-frequency qualities of different exogenous variables, which can effectively reduce the loss of information from the conversion of high-frequency data into low-frequency data (Wen et al., 2020).
The strong forecasting power of the mixed-frequency feature can be tested using various metrics to verify its superiority in tourism demand forecasting relative to the corresponding benchmark that lacks the mixed-frequency feature. The reason for this is that high-frequency data such as weekly data contain information that is more useful for forecasting, and that the mixture of low and high frequency data increases the forecasting power of the data (Hu et al., 2022).
The results also reveal that the topic and sentiment intensity are more instructive than the visitor attention and economic indices in terms of the characteristics included. The underlying factor for this may be that people are more sensitive to commentary and news data in the Internet era, and data on the Web play a large role in influencing visitors' decisions (Park et al., 2021; Önder et al., 2019).
With information-rich mixed-frequency data and the MIDAS algorithm, the proposed model can serve as an effective tool to analyse and forecast complex systems during times of turmoil (i.e., during a pandemic), such as tourism demand. The main advantage of the proposed model is that it can both fully consider the characteristics of different frequency data and obtain timely and effective information that affects the forecasting accuracy in different environments.
6. Conclusions and implications
In the face of the lasting impact of the 2019 coronavirus pandemic (COVID-19), accurate forecasting of tourism demand recovery is an important prerequisite for tourism-related decisions. In this study, we use the SARIMA-MIDAS model to forecast monthly tourism demand to improve forecasting accuracy. For the predictor variables, we used economic variables data, Baidu index data, online news data, etc., and combined them in different combinations to fit the MIDAS model, which in turn guided decision-making. We also considered forecasting performance in multiple horizon cases. Our study covers the COVID-19 period and evaluates the potential role of multimodal data with different frequencies in travel forecasting during this chaotic period. First, we collect the original visitor data using the above-mentioned multiple feature data. Second, we pre-process the different data, including topic modelling using the STM model for text data and index aggregation using the GDFM model for time series. Third, we introduce different combinations of various features (including co-frequency and mixed frequency) into the model to obtain the forecasting results. Finally, we evaluate the forecasting results using several indexes, such as MAE.
This study makes two methodological contributions to the existing literature. First, three features (i.e. economic index, visitor attention index, and topic and sentiment intensity) are simultaneously introduced into tourist arrival forecasting at the same time. These three features contribute to the forecasting system in different forms, with the economic index providing support from a macro perspective: the visitor attention index, which shows the travel behaviour of consumers, and the topic and sentiment intensity, taking into account the emotions of tourists. The empirical results show that under the traditional time series model, a model with multiple features has better forecasting ability. Second, this study provides new insights into the mixed use for the characteristics of tourism demand series, and has achieved excellent results. Different frequencies of data reflect the information contained in the features from different levels and are also considered in the forecasting model, which can more effectively extract relevant information to guide accurate forecasts.
The final findings of this study have several useful practical implications. First, accurate forecasting of tourist volumes can help tourism practitioners optimise resource allocation and rationalise pricing strategies. Second, user-generated data, including search and news data, are freely available in this era of big data. Research has shown that it can significantly improve the forecasting accuracy of tourism volume. Therefore, it can be utilized as an alternative data source in future forecasting frameworks. In conclusion, managers and practitioners in the tourism industry can use our proposed forecasting framework to make accurate judgments, which can guide strategic decisions in practical applications. In addition, the forecasting framework based on MIDAS with user-generated data proposed in this study can be used to solve complex forecasting problems in other fields, such as crude oil and stock price forecasting.
However, this study also has some limitations. For the first thing, we only used the Hong Kong tourism market as a test case, and in addition to the three features mentioned above, other variables such as weather conditions, safety conditions, and social media data can also be included in the forecasting process to expand the proposed model. Second, we do not have options for more innovative machine-learning models, such as LSTM and Transformer. Third, more complex user-generated data can be considered, such as photo, video, and speech data. To address these limitations, further research is necessary to explore the use of user-generated data in other destinations and empirical studies with larger samples. These interesting questions will be investigated in the future.
Impact statement
The coronavirus disease (COVID-19) pandemic has had a huge negative impact on the world economy, with tourism suffering a devastating blow in many regions. Under such extreme conditions, how to effectively make accurate forecasts of tourism volumes is an important issue. In this study, three variables, the economic index, visitor attention index and topic and sentiment intensity, are simultaneously considered into the forecasting model, while data of different frequencies (daily and monthly) are planned with the support of mixed data sampling model (MIDAS), which finally significantly improves the accuracy of tourism demand forecasting compared with the benchmark model. Using Hong Kong visitor volume as an example, multiple horizons are considered simultaneously to obtain robust and accurate forecasting performance, and in turn, it can provide effective advice to managers and practitioners to guide the recovery of the tourism industry amid COVID-19.
Credit author statement
Jing Wu and Shaolong Sun: Idea, Conceptualization, Writing-review & editing. Jing Wu and Mingchen Li: Methodology, Software, Visualization, Writing-original draft. Erlong Zhao: Writing-review & editing. Shouyang Wang: Writing-review & editing, Project administration. All authors provided critical feedback and helped shape the research, analysis and manuscript. All authors read and approved the manuscript.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This research work was partly supported by the National Key R&D Program of China under Grant No. 2022YFF0903000, and the National Natural Science Foundation of China under Grants No. 72101197 and No. 71988101.
Biographies

Jing Wu received the M.S. degree from School of Mathematics and Statistics, Lanzhou University, Lanzhou, China, in 2016. She is currently pursuing the Ph.D. degree in Management Science and Engineering at School of Management, Xi'an Jiaotong University, Xi'an, China. Her research interests include big data analysis, UGC, and tourism demand forecasting.

Mingchen Li received the M.S. degree from School of Mathematics and Statistics, Lanzhou University, Lanzhou, China, in 2020. He is currently pursuing the Ph.D. degree in Management Science and Engineering at Academy of Mathematics and Systems Sciences, Chinese Academy of Sciences, Beijing, China. His research interests include artificial intelligence, big data analysis, and tourism management.

Erlong Zhao received the M.S. degree from School of Information Science and Technology, Northwestern University, Xi'an, China, in 2018. He is currently pursuing the Ph.D. degree in Management Science and Engineering at School of Management, Xi'an Jiaotong University, Xi'an, China. His research interests include big data analysis, tourism management, knowledge management and forecasting. He has published four journal papers in Expert Systems with Applications, Current Issues in Tourism, Energy, and Energy for Sustainable Development.

Shaolong Sun received the Ph.D. degree majoring in Management Science and Engineering from Academy of Mathematics and Systems Sciences, Chinese Academy of Sciences, Beijing, China. He is currently a Professor with the Department of Management Science, School of Management, Xi'an Jiaotong University, Xi'an, China. His research interests include big data mining, business intelligence, smart tourism, economic forecasting and financial management. He has authored or coauthored more than 40 papers in leading journals including Tourism Management, Journal of Travel Research, International Journal of Contemporary Hospitality Management, Tourism Management Perspectives, Current Issues in Tourism, Tourism Economics and Journal of Environmental Management.

Shouyang Wang received his PhD degree in Operations Research from the Institute of Systems Science, Chinese Academy of Sciences, China, in 1986. He is currently a Bairen Distinguished Professor of Management Science at the Academy of Mathematics and Systems Science, Chinese Academy of Sciences. He has received many research related awards and honors. He has published 42 monographs and published more than 450 papers in international academic journals. He is/was a co-editor of 16 journals and a guest editor of special issues/volumes of more than 15 journals. His research interests include decision analysis, risk management, economic analysis and forecasting.
References
- Aaronson D., Brave S.A., Butters R.A., Fogarty M., Sacks D.W., Seo B. Forecasting unemployment insurance claims in realtime with Google trends. International Journal of Forecasting. 2022;38(2):567–581. [Google Scholar]
- Ardia D., Bluteau K., Boudt K. Questioning the news about economic growth: Sparse forecasting using thousands of news-based sentiment values. International Journal of Forecasting. 2019;35(4):1370–1386. [Google Scholar]
- Athanasopoulos G., Hyndman R.J., Kourentzes N., O'Hara-Wild M. Probabilistic forecasts using expert judgment: The road to recovery from COVID-19. Journal of Travel Research. 2022 doi: 10.1177/00472875211059240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bangwayo-Skeete P.F., Skeete R.W. Can Google data improve the forecasting performance of tourist arrivals? Mixed-Data sampling approach. Tourism Management. 2015;46:454–464. doi: 10.1016/j.tourman.2023.104759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bi J.-W., Li H., Fan Z.-P. Tourism demand forecasting with time series imaging: A deep learning model. Annals of Tourism Research. 2021;90 [Google Scholar]
- Bi J.-W., Liu Y., Li H. Daily tourism volume forecasting for tourist attractions. Annals of Tourism Research. 2020;83 [Google Scholar]
- Chen W., Xu H., Jia L., Gao Y. Machine learning model for Bitcoin exchange rate prediction using economic and technology determinants. International Journal of Forecasting. 2021;37(1):28–43. [Google Scholar]
- Forni M., Hallin M., Lippi M., Reichlin L. The generalized dynamic-factor model: Identification and estimation. The Review of Economics and Statistics. 2000;82(4):540–554. [Google Scholar]
- Fronzetti Colladon A. Forecasting election results by studying brand importance in online news. International Journal of Forecasting. 2020;36(2):414–427. [Google Scholar]
- Ghysels E., Santa-Clara P., Valkanov R.I. Predicting volatility: Getting the most out of return data sampled at different frequencies. Journal of Econometrics. 2006;131(1–2):59–95. [Google Scholar]
- Ghysels E., Valkanov R. The MIDAS touch: Mixed data sampling regression models. CIRANO Working Papers. 2004;5(1):512–517. [Google Scholar]
- Ginsberg J., Mohebbi M.H., Patel R.S., Brammer L., Smolinski M.S., Brilliant L. Detecting influenza epidemics using search engine query data. Nature. 2009;457(7232):1012–1014. doi: 10.1038/nature07634. [DOI] [PubMed] [Google Scholar]
- Gunter U., Önder I., Gindl S. Exploring the predictive ability of LIKES of posts on the Facebook pages of four major city DMOs in Austria. Tourism Economics. 2018;25(3):375–401. [Google Scholar]
- Hand C., Judge G. Searching for the picture: Forecasting UK cinema admissions using Google trends data. Applied Economics Letters. 2012;19(11):1051–1055. [Google Scholar]
- Hansen P.R. A test for superior predictive ability. Journal of Business & Economic Statistics. 2005;23(4):365–380. [Google Scholar]
- Hirashima A., Jones J., Bonham C.S., Fuleky P. Forecasting in a mixed up world: Nowcasting Hawaii tourism. Annals of Tourism Research. 2017;63:191–202. [Google Scholar]
- Höpken W., Eberle T., Fuchs M., Lexhagen M. Improving tourist arrival prediction: A big data and artificial neural network approach. Journal of Travel Research. 2020;60(5):998–1017. [Google Scholar]
- Hu M., Li H., Song H., Li X., Law R. Tourism demand forecasting using tourist-generated online review data. Tourism Management. 2022;90 [Google Scholar]
- Hu M., Qiu R.T.R., Wu D.C., Song H. Hierarchical pattern recognition for tourism demand forecasting. Tourism Management. 2021;84 [Google Scholar]
- Hyndman R.J., Athanasopoulos G., Bergmeir C., Caceres G., Chhay L., O'Hara-Wild M., et al. 2020. Package ‘forecast’.https://cran.r-project.org/web/packages/forecast/forecast.pdf retrieved from. [Google Scholar]
- Kourentzes N., Saayman A., Jean-Pierre P., Provenzano D., Sahli M., Seetaram N., et al. Visitor arrivals forecasts amid COVID-19: A perspective from the africa team. Annals of Tourism Research. 2021;88 doi: 10.1016/j.annals.2021.103197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulshrestha A., Krishnaswamy V., Sharma M. Bayesian BILSTM approach for tourism demand forecasting. Annals of Tourism Research. 2020;83 [Google Scholar]
- Law R., Li G., Fong D.K.C., Han X. Tourism demand forecasting: A deep learning approach. Annals of Tourism Research. 2019;75:410–423. [Google Scholar]
- Li S., Chen T., Wang L., Ming C. Effective tourist volume forecasting supported by PCA and improved BPNN using Baidu index. Tourism Management. 2018;68:116–126. [Google Scholar]
- Li C., Ge P., Liu Z., Zheng W. Forecasting tourist arrivals using denoising and potential factors. Annals of Tourism Research. 2020;83 [Google Scholar]
- Li H., Hu M., Li G. Forecasting tourism demand with multisource big data. Annals of Tourism Research. 2020;83 [Google Scholar]
- Li Y., Jiang S., Li X., Wang S. The role of news sentiment in oil futures returns and volatility forecasting: Data-decomposition based deep learning approach. Energy Economics. 2021;95 [Google Scholar]
- Li X., Law R. Forecasting tourism demand with decomposed search cycles. Journal of Travel Research. 2019;59(1):52–68. [Google Scholar]
- Li J., Li G., Liu M., Zhu X., Wei L. A novel text-based framework for forecasting agricultural futures using massive online news headlines. International Journal of Forecasting. 2022;38(1):35–50. [Google Scholar]
- Li X., Li H., Pan B., Law R. Machine learning in internet search query selection for tourism forecasting. Journal of Travel Research. 2020;60(6):1213–1231. [Google Scholar]
- Li X., Pan B., Law R., Huang X. Forecasting tourism demand with composite search index. Tourism Management. 2017;59:57–66. [Google Scholar]
- Li X., Shang W., Wang S. Text-based crude oil price forecasting: A deep learning approach. International Journal of Forecasting. 2019;35(4):1548–1560. [Google Scholar]
- Liu P, Zhang H, Zhang J, Sun Y, Qiu M. Spatial-temporal response patterns of tourist flow under impulse pre-trip information search: From online to arrival. Tourism Management. 2019;73:105–114. [Google Scholar]
- Liu Y., Feng G., Tsui K.-L., Sun S. Forecasting influenza epidemics in Hong Kong using Google search queries data: A new integrated approach. Expert Systems with Applications. 2021;185 [Google Scholar]
- Liu A., Vici L., Ramos V., Giannoni S., Blake A. Visitor arrivals forecasts amid COVID-19: A perspective from the europe team. Annals of Tourism Research. 2021;88 doi: 10.1016/j.annals.2021.103182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G., Wu D.C., Zhou M., Liu A. The combination of interval forecasts in tourism. Annals of Tourism Research. 2019;75:363–378. [Google Scholar]
- Li M., Zhang C., Sun S., Wang S. A novel deep learning approach for tourism volume forecasting with tourist search data. International Journal of Tourism Research. 2022 doi: 10.1002/jtr.2558. [DOI] [Google Scholar]
- Li M., Zhang C., Wang S., Sun S. Multi-scale analysis-driven tourism forecasting: Insights from the peri-COVID-19. Current Issues in Tourism. 2022 doi: 10.1080/13683500.2022.2144151. [DOI] [Google Scholar]
- Li C., Zheng W., Ge P. Tourism demand forecasting with spatiotemporal features. Annals of Tourism Research. 2022;94 [Google Scholar]
- Lu Q., Li Y., Chai J., Wang S. Crude oil price analysis and forecasting: A perspective of “new triangle”. Energy Economics. 2020;87 [Google Scholar]
- Mei D., Ma F., Liao Y., Wang L. Geopolitical risk uncertainty and oil future volatility: Evidence from MIDAS models. Energy Economics. 2020;86 [Google Scholar]
- Narayan P.K. Can stale oil price news predict stock returns? Energy Economics. 2019;83:430–444. [Google Scholar]
- Önder I., Gunter U., Scharl A. Forecasting tourist arrivals with the help of web sentiment: A mixed-frequency modeling approach for big data. Tourism Analysis. 2019;24(4):437–452. [Google Scholar]
- Pan Z., Wang Q., Wang Y., Yang L. Forecasting U.S. Real gdp using oil prices: A time-varying parameter MIDAS model. Energy Economics. 2018;72:177–187. [Google Scholar]
- Park E., Park J., Hu M. Tourism demand forecasting with online news data mining. Annals of Tourism Research. 2021;90 [Google Scholar]
- Petropoulos A., Siakoulis V., Stavroulakis E., Lazaris P., Vlachogiannakis N. Employing Google trends and deep learning in forecasting financial market turbulence. The Journal of Behavioral Finance. 2021;10:1–13. [Google Scholar]
- Qiu R.T.R., Wu D.C., Dropsy V., Petit S., Pratt S., Ohe Y. Visitor arrivals forecasts amid COVID-19: A perspective from the asia and pacific team. Annals of Tourism Research. 2021;88 doi: 10.1016/j.annals.2021.103155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts M.E., Stewart B.M., Airoldi E.M. A model of text for experimentation in the social sciences. Journal of the American Statistical Association. 2016;111(515):988–1003. [Google Scholar]
- Shapiro A.H., Sudhof M., Wilson D.J. Measuring news sentiment. Journal of Econometrics. 2022;228:221–243. [Google Scholar]
- Shynkevich Y., McGinnity T.M., Coleman S.A., Belatreche A. Forecasting movements of health-care stock prices based on different categories of news articles using multiple kernel learning. Decision Support Systems. 2016;85:74–83. [Google Scholar]
- Silva E.S., Hassani H., Heravi S., Huang X. Forecasting tourism demand with denoised neural networks. Annals of Tourism Research. 2019;74:134–154. [Google Scholar]
- Smith P. Google's MIDAS touch: Predicting UK unemployment with internet search data. Journal of Forecasting. 2016;35(3):263–284. [Google Scholar]
- Song H., Qiu R.T.R., Park J. A review of research on tourism demand forecasting: Launching the annals of tourism research curated collection on tourism demand forecasting. Annals of Tourism Research. 2019;75:338–362. [Google Scholar]
- Song M., Shin K.S. Forecasting economic indicators using a consumer sentiment index: Survey‐based versus text‐based data. Journal of Forecasting. 2019;38:504–518. [Google Scholar]
- Song T.M., Song J., An J.Y., Hayman L.L., Woo J.M. Psychological and social factors affecting internet searches on suicide in korea: A big data analysis of Google search trends. Yonsei Medical Journal. 2014;55(1):254–263. doi: 10.3349/ymj.2014.55.1.254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun S., Li Y., Guo J.-e., Wang S. Tourism demand forecasting: An ensemble deep learning approach. Tourism Economics. 2021 doi: 10.1177/13548166211025160. [DOI] [Google Scholar]
- Sun S., Wei Y., Tsui K.-L., Wang S. Forecasting tourist arrivals with machine learning and internet search index. Tourism Management. 2019;70:1–10. [Google Scholar]
- Tang L., Zhang C., Li T., Li L. A novel BEMD-based method for forecasting tourist volume with search engine data. Tourism Economics. 2021;27(5):1015–1038. [Google Scholar]
- Tilly S., Ebner M., Livan G. Macroeconomic forecasting through news, emotions and narrative. Expert Systems with Applications. 2021;175 [Google Scholar]
- Tobback E., Naudts H., Daelemans W., Junqué de Fortuny E., Martens D. Belgian economic policy uncertainty index: Improvement through text mining. International Journal of Forecasting. 2018;34(2):355–365. [Google Scholar]
- Wen L., Liu C., Song H. Forecasting tourism demand using search query data: A hybrid modelling approach. Tourism Economics. 2019;25(3):309–329. [Google Scholar]
- Wen L., Liu C., Song H., Liu H. Forecasting tourism demand with an improved mixed data sampling model. Journal of Travel Research. 2020;60(2):336–353. [Google Scholar]
- Wu B., Wang L., Wang S., Zeng Y.R. Forecasting the U.S. oil markets based on social media information during the COVID-19 pandemic. Energy. 2021;226 doi: 10.1016/j.energy.2021.120403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie G., Qian Y., Wang S. A decomposition-ensemble approach for tourism forecasting. Annals of Tourism Research. 2020;81 doi: 10.1016/j.annals.2020.102891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie G., Qian Y., Wang S. Forecasting Chinese cruise tourism demand with big data: An optimized machine learning approach. Tourism Management. 2021;82 [Google Scholar]
- Yang Y., Fan Y., Jiang L., Liu X. Search query and tourism forecasting during the pandemic: When and where can digital footprints be helpful as predictors? Annals of Tourism Research. 2022;93 [Google Scholar]
- Yang Y., Guo J.E., Sun S., Li Y. Forecasting crude oil price with a new hybrid approach and multi-source data. Engineering Applications of Artificial Intelligence. 2021;101 [Google Scholar]
- Yang X., Pan B., Evans J.A., Lv B. Forecasting Chinese tourist volume with search engine data. Tourism Management. 2015;46:386–397. [Google Scholar]
- Zhang Y., Li G., Muskat B., Law R. Tourism demand forecasting: A decomposed deep learning approach. Journal of Travel Research. 2020;60(5):981–997. [Google Scholar]
- Zhang H., Song H., Wen L., Liu C. Forecasting tourism recovery amid COVID-19. Annals of Tourism Research. 2021;87 doi: 10.1016/j.annals.2021.103149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C., Tian Y.X., Fan Z.-P. Forecasting sales using online review and search engine data: A method based on PCA–DSFOA–BPNN. International Journal of Forecasting. 2022;38:1005–1024. [Google Scholar]
- Zhang Y.J., Wang J.L. Do high-frequency stock market data help forecast crude oil prices? Evidence from the MIDAS models. Energy Economics. 2019;78:192–201. [Google Scholar]
- Zhao E., Du P., Azaglo E.Y., Wang S., Sun S. Forecasting daily tourism volume: A hybrid approach with CEMMDAN and multi-kernel adaptive ensemble. Current Issues in Tourism. 2022 doi: 10.1080/13683500.2022.2048806. [DOI] [Google Scholar]