Stress‐dependent macromolecular crowding in the mitochondrial matrix

Abstract

Macromolecules of various sizes induce crowding of the cellular environment. This crowding impacts on biochemical reactions by increasing solvent viscosity, decreasing the water‐accessible volume and altering protein shape, function, and interactions. Although mitochondria represent highly protein‐rich organelles, most of these proteins are somehow immobilized. Therefore, whether the mitochondrial matrix solvent exhibits macromolecular crowding is still unclear. Here, we demonstrate that fluorescent protein fusion peptides (AcGFP1 concatemers) in the mitochondrial matrix of HeLa cells display an elongated molecular structure and that their diffusion constant decreases with increasing molecular weight in a manner typical of macromolecular crowding. Chloramphenicol (CAP) treatment impaired mitochondrial function and reduced the number of cristae without triggering mitochondrial orthodox‐to‐condensed transition or a mitochondrial unfolded protein response. CAP‐treated cells displayed progressive concatemer immobilization with increasing molecular weight and an eightfold matrix viscosity increase, compatible with increased macromolecular crowding. These results establish that the matrix solvent exhibits macromolecular crowding in functional and dysfunctional mitochondria. Therefore, changes in matrix crowding likely affect matrix biochemical reactions in a manner depending on the molecular weight of the involved crowders and reactants.

The mitochondrial matrix solvent exhibits macromolecular crowding, which is increased under stress conditions.

Introduction

Mitochondria host a large variety of biochemical reactions, including the ATP‐generating oxidative phosphorylation (OXPHOS) system (Smeitink et al, 2001; Rath et al, 2021). Structurally, mitochondria consist of an inner (MIM) and outer membrane (MOM), which surround the mitochondrial matrix compartment. The MIM contains many folds (cristae) that protrude into the matrix thereby providing a large surface area for biochemical reactions. Alterations in metabolic state are generally paralleled by dynamic changes in mitochondrial internal and external structure, matrix volume, and physicochemical properties of the matrix solvent (Hackenbrock, 1966; Perkins & Ellisman, 2011; Willems et al, 2015; Bulthuis et al, 2019). It is to be expected that these changes are functionally relevant through affecting matrix solute diffusion and biochemical reaction dynamics (Scalettar et al, 1991; Lizana et al, 2008; Perkins & Ellisman, 2011; Dieteren et al, 2011a; Cogliati et al, 2016; Sprenger & Langer, 2019).

Diffusion‐limited bioreactions often involve “target finding” by (partially) mobile enzymes and/or substrates that need to diffuse towards a binding partner (Haggie & Verkman, 2002; Wilkens et al, 2013; Dey & Bhattacherjee, 2019). An example of such a system is the biogenesis of OXPHOS Complex I (CI), which involves matrix diffusion of an 100–200 kDa assembly intermediate in search of a MIM‐attached scaffold (Dieteren et al, 2008, 2011b; Koopman et al, 2010; Guerrero‐Castillo et al, 2017). However, our quantitative understanding of solute diffusion in the mitochondrial matrix is still limited. A key parameter in this respect is the solvent‐dependent diffusion constant of the solute (D_solvent; Weiss, 2014). For any given solute, the value of D_solvent is linked to the physicochemical properties of the solvent like viscosity (η_solvent), absolute temperature (T), and solute properties like molecular structure and molecular weight (MW). The former is quantitatively described by the radius of gyration (R_G) and hydrodynamic radius (R_H) of the solute (Einstein, 1905; Sutherland, 1905; von Smoluchowski, 1906; Young et al, 1980; Tyn & Gusek, 1990; He & Niemeyer, 2003; Saxton, 2014). With respect to solute diffusion in the mitochondrial matrix, it has been previously demonstrated that mitochondrial cristae can act as diffusion barriers that impede the free diffusion of fluorescent proteins (FPs; Ölveczky & Verkman, 1998; Partikian et al, 1998; Dieteren et al, 2011a).

In addition to cristae, macromolecular crowding is also a potential key factor influencing solute diffusion by increasing effective solvent viscosity and reducing the water‐accessible volume via volume exclusion, the extent of which increases with crowder size (Boersma et al, 2015; Rivas & Minton, 2016). In this way, macromolecular crowding can alter the hydrodynamic volume (compaction, shape, folding, structure, and conformational stability) and/or association state (protein–protein interactions, aggregation, oligomerization, and phase separation) of proteins (Kuznetzova et al, 2014). This will affect their chemical reaction rates and/or molecular target finding (Dey & Bhattacherjee, 2019; Weilandt & Hatzimanikatis, 2019). Macromolecular crowding can also induce “molecular sieving” effects, which alter the translational mobility of biomolecules in an MW/size‐dependent manner (Papadopoulos et al, 2000; Mika et al, 2010; Junker et al, 2019; Van Tartwijk & Kaminski, 2022). In this sense, macromolecular crowding will reduce the diffusion coefficient of larger tracer molecules to a greater extent than predicted by the Stokes–Einstein equation (Mika et al, 2010; Delarue et al, 2018; Junker et al, 2019). Experimental and theoretical studies suggest that modulation of macromolecular crowding can act as a (patho)physiological control mechanism in prokaryotes and eukaryotes (Scalettar et al, 1991; Akabayov et al, 2013; Poggi & Slade, 2015; Cravens et al, 2015; Joyner et al, 2015; Hansen et al, 2016; Delarue et al, 2018; Schavemaker et al, 2018; Fuentes‐Lemus et al, 2021; Hochmair et al, 2022; Vorontsova et al, 2022). The mitochondrial matrix compartment is classically recognized as highly protein‐rich. For instance, 46% of all mitochondrial proteins were predicted to be matrix‐localized in humans (Rath et al, 2021) and 20% of the mitochondrial proteins were classified as matrix‐soluble in Saccharomyces cerevisiae (Vögtle et al, 2017). Therefore, it appears likely that the mitochondrial matrix fluid displays macromolecular crowding‐related phenomena. However, given the biological functions of these matrix proteins (e.g., metabolism, mtDNA maintenance, OXPHOS assembly; Rath et al, 2021), they might not always be expressed at the same levels and/or could be (transiently) MIM‐attached or otherwise immobilized. For example, four of the most abundant mitochondrial proteins (ATP5A1, ATP5B, ANT1, and ANT2) are membrane‐bound (Calvo & Mootha, 2010). In addition, TCA cycle enzymes and subunits of the fatty acid β‐oxidation multienzyme complex appear to be organized in (MIM‐attached) multiprotein complexes with restricted mobility (Robinson & Srere, 1985; Partikian et al, 1998; Haggie & Verkman, 2002; Fernie et al, 2018). This suggests that the protein concentration of the mitochondrial matrix solvent might be (substantially) lower than generally assumed. Moreover, quantitative live‐cell evidence demonstrating the existence of macromolecular crowding‐related phenomena in the mitochondrial matrix fluid is lacking. Here, we aimed at providing such evidence by quantifying the mobility of matrix‐targeted fluorescent protein (FP) concatemers of increasing MW (AcGFP1, AcGFP1², AcGFP1³, and AcGFP1⁴). To this end, fluorescence recovery after photobleaching (FRAP) experiments and Brownian dynamics (BD) simulations were integrated to obtain quantitative estimates of D_solvent and η_solvent in functionally active and dysfunctional mitochondria. The obtained results support the conclusion that the mitochondrial matrix fluid displays macromolecular crowding and that this crowding is increased during chloramphenicol (CAP)‐induced mitochondrial dysfunction.

Results

A key phenomenon associated with macromolecular crowding is that it reduces the translational mobility of solutes with a similar or larger size than the crowder to a greater extent than the mobility of smaller solutes (e.g., Mika et al, 2010; Delarue et al, 2018; Junker et al, 2019; Van Tartwijk & Kaminski, 2022). The solvent‐dependent translational mobility of a solute in the mitochondrial matrix is quantitatively described by its solvent‐dependent diffusion constant (D_solvent). Therefore, we here quantified D_solvent values of mitochondria‐targeted AcGFP1 concatemers of increasing MW (AcGFP1, AcGFP1², AcGFP1³, and AcGFP1⁴) in HeLa cells. To this end, fluorescence recovery after photobleaching (FRAP) analysis of these fluorescent proteins (FPs) was combined with predictive, experimentally constrained, Brownian dynamics (BD) computer simulations. This strategy aimed at delivering quantitative estimates for D_solvent and matrix solvent viscosity (η_solvent) in functional mitochondria, as well as in dysfunctional mitochondria treated with the mitochondrial RNA (mtRNA) translation inhibitor chloramphenicol (CAP). Interpretation of these estimates was used to gain insight into macromolecular crowding, concatemer structural conformation, and η_solvent in the mitochondrial matrix (Fig 1).

Figure 1. Integrated strategy for quantifying the solvent‐dependent diffusion constants of mitochondrial matrix‐targeted fluorescent proteins and mitochondrial matrix solvent viscosity.

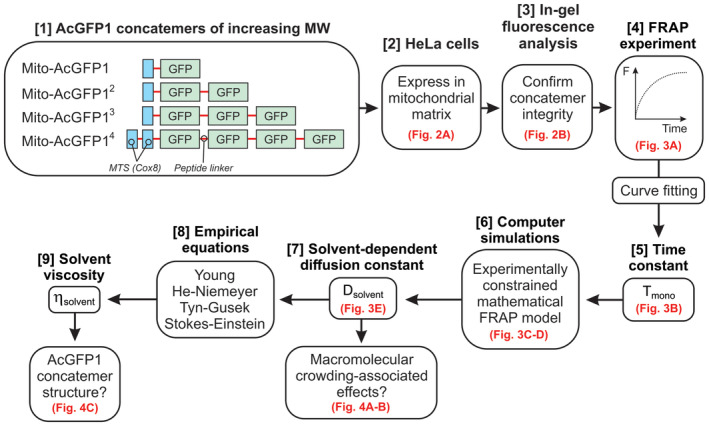
Corresponding figures are highlighted in red. Four mitochondrial matrix‐targeted concatemers of the monomeric fluorescent protein AcGFP1 [1] were stably expressed in HeLa cells [2]. The integrity and mobility of these fluorescent proteins (FPs) was investigated by in‐gel fluorescence analysis [3] and fluorescence recovery after photobleaching (FRAP) recordings [4], respectively. Curve fitting was applied to obtain a mono‐exponential FRAP time constant for each concatemer (T_mono) [5]. The latter were fed into an experimentally constrained mathematical FRAP model [6] to compute solvent‐dependent diffusion constants (D_solvent; [7]). By inserting these constants into four empirical equations [8], the viscosity of the mitochondrial matrix solvent (η_solvent) was determined [9]. Finally, the obtained η_solvent and D_solvent values were interpreted to draw conclusions on the structural conformation of the concatemers and the presence of macromolecular crowding phenomena in the mitochondrial matrix.

Expression, localization, and integrity of mitochondrial matrix‐targeted FPs

Four HeLa cell lines were created that stably expressed matrix‐targeted AcGFP1 concatemers. These proteins were targeted to the mitochondrial matrix using N‐terminal fusions with a mitochondrial targeting sequence (MTS), consisting of a 25‐residue Cox8 sequence. In case of AcGFP1⁴, a double MTS was used to improve mitochondrial matrix delivery (Filippin et al, 2005). AcGFP1 and MTS domains were connected by flexible peptide linkers (Appendix Table S1), and FP expression was controlled by a doxycycline (DOX)‐inducible promoter. Following induction, all FPs displayed a mitochondrial localization as demonstrated by confocal microscopy and MitoTracker Red co‐staining (Fig 2A). Western blot analysis of mitochondrial fractions demonstrated that DOX treatment increased the in‐gel fluorescence and expression of the FPs (Fig 2B; marked by *). AcGFP1 and AcGFP1² displayed a single major fluorescent product, compatible with our previous findings with DOX‐inducible HEK293 cells (Dieteren et al, 2008, 2011a, 2011b). Similarly, AcGFP1³‐expressing cells displayed a single fluorescence band albeit of much lower intensity. By contrast, mitochondria in AcGFP1⁴‐expressing cells contained two fluorescence products, one of the expected size (Fig 2B; marked by *) and another of lower MW (marked by #). Fluorescence analysis by flow cytometry (Fig 2C) correlated well with in‐gel fluorescence signals (Fig 2D). This demonstrates that all inducible FP cell lines exhibit a low fluorescence signal in their noninduced state and strongly suggests that the cellular fluorescence intensities reflect mitochondria‐specific signals. The former observation is compatible with low‐level induction (“leakage”) of FP expression in the mitochondrial matrix occurring in the absence of added DOX, as observed previously in our DOX‐inducible HEK293 cell models (Dieteren et al, 2011b).

Figure 2. Expression and localization of the mitochondrial matrix‐targeted fluorescent proteins.

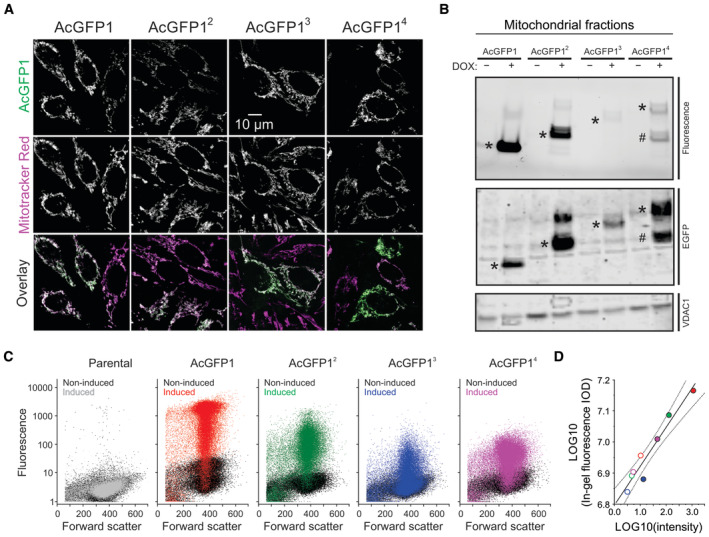
1. Cellular localization of the four AcGFP1 concatemers (AcGFP1, AcGFP1², AcGFP1³, AcGFP1⁴) in HeLa cell lines cultured in the presence of the expression inducer doxycycline (DOX). Images were acquired by confocal microscopy and depict typical fluorescence signals of AcGFP1 (upper row), the mitochondrial marker Mitotracker Red CM‐H₂XROS (middle row), and an overlay of these signals (lower row; AcGFP1 in green; Mitotracker Red CM‐H₂XROS in magenta; colocalization in white).
2. Analysis of FP expression and concatemer integrity in mitochondrial fractions isolated from HeLa cells cultured in the absence (−) and presence (+) of DOX. The panels display AcGFP1 fluorescence (SDS–PAGE fluorogram; upper panel), AcGFP1 protein signals (SDS–PAGE; anti‐EGFP immunodetection; middle panel) and VDAC1 protein signals (SDS–PAGE; loading control; lower panel). Bands for AcGFP1, AcGFP1², AcGFP³ and AcGFP1⁴ are marked by asterisks (*). For AcGFP1⁴, also a substantial band of lower MW was detected (marked #). Individual panels were contrast‐optimized for visualization purposes. Original blots are presented in Appendix Fig S1A.
3. Flow cytometry analysis of the parental and FP‐expressing HeLa cell lines. Fluorescence intensity is plotted against forward scatter. The noninduced condition (i.e., in absence of DOX) is depicted by black symbols. The effects of DOX are marked in gray (parental cells) and various colors (FP‐expressing cells). For AcGFP1, AcGFP1² (noninduced), AcGFP1³ and AcGFP1⁴ a total of n = 40,000 cells from four technical replicates were analyzed on a single day (N = 1). For the AcGFP1²‐induced condition n = 30,000 cells from three technical replicates are depicted (N = 1).
4. Correlation between the average AcGFP1 fluorescence intensity in panel (C) (x‐axis) and the integrated optical density (IOD; y‐axis) for each condition (full lane) in panel (B) (in‐gel fluorescence signal; the original gel was used for quantification). Noninduced cells are marked by open symbols; induced cells are marked with colored symbols (similar to panel C). The continuous line represents a linear fit to the data (R = 0.966; P < 0.0001). Dotted lines indicate the 95% confidence limits of the fit.

Experimental FRAP analysis of mitochondrial matrix‐targeted FP mobility

FP mobility in the mitochondrial matrix was determined by confocal FRAP analysis of individual mitochondria. In this approach, mitochondrial fluorescence is rapidly bleached in a square region of interest (ROI) placed at one end of a single mitochondrial filament (Fig 3A; inset), followed by quantification of fluorescence recovery (Appendix Fig S2). As a quality control measure, this analysis included only individual mitochondria: (i) that were fully located within the focal plane (confirmed by an axial scan), and (ii) in which FRAP was paralleled by fluorescence loss in photobleaching (FLIP) in a part distal to the FRAP region (Appendix Fig S2), indicating that these mitochondria possessed a continuous matrix. Combining multiple experiments yielded an average FRAP curve for each FP (Fig 3A), which was adequately fitted by a mono‐exponential equation (Table 1). The recovery time constant of this fit (T_mono), representing the FRAP rate, increased with increasing MW (Table 1 and Fig 3B). This agrees with our previous results with mitochondrial matrix‐targeted AcGFP1¹ and AcGFP1² in HEK293 cells (Dieteren et al, 2011a) and demonstrates that FRAP is slower for FPs with a larger MW. The FP mobile fraction (F_m) somewhat decreased with increasing MW (Table 1 and Fig 3A), suggesting that the FPs became progressively immobilized. A proper comparison of T_mono between the different FPs requires that their MW is taken into account (Sprague & McNally, 2005). In case of AcGFP1⁴, the fluorescent product of lower MW (Fig 2B) accelerated the average FRAP rate for this FP leading to an underestimation of T_mono. To correct for this effect, a straight line was fitted through the origin and the T_mono data points for AcGFP1, AcGFP1², and AcGFP1³ (Fig 3B). Next, the measured T_mono value for AcGFP1⁴ was projected on the fitted line yielding a corrected (“AcGFP1⁴‐corr”) value (Fig 3B; dotted line and open symbol). This corrected T_mono value was used in the remainder of the study.

Figure 3. Solvent‐dependent mobility of the mitochondrial matrix‐targeted fluorescent proteins.

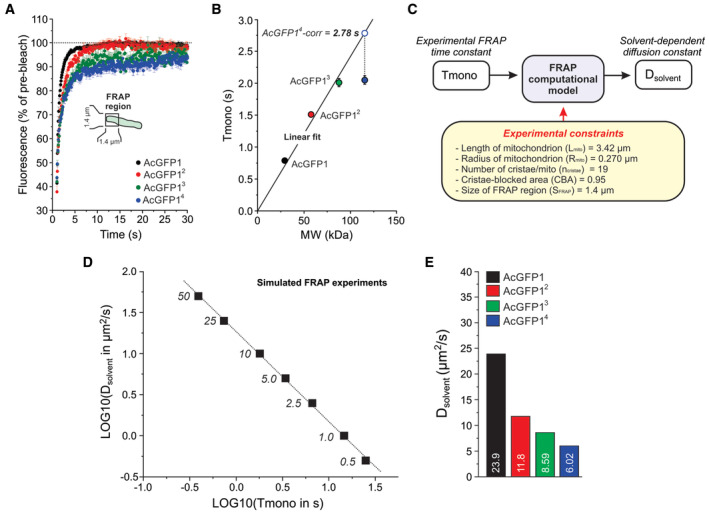
1. Average mitochondrial fluorescence recovery after photobleaching (FRAP) curves for the four FPs. These curves were fitted using a mono‐exponential function to determine the FRAP recovery time constant T_mono. Symbols and error bars indicate mean ± SEM. Data was obtained in at least N = 3 independent experiments for n = 76 mitochondria (AcGFP1), n = 30 (AcGFP1²), n = 37 (AcGFP1³) and n = 68 (AcGFP1⁴).
2. Relationship between the molecular weight (MW) of the FPs and their FRAP time constant (T_mono; numerical data are provided in Table 1). A linear fit was calculated through the origin and the data points for AcGFP1, AcGFP1² and AcGFP1³ (R = 0.993, P = 0.022; T_mono = B·MW; B (slope) = 0.0241 ± 0.00118 (SE)). The experimental T_mono value for AcGFP⁴ (filled blue symbol) was corrected using this linear fit (dotted line; see Results for details) yielding a new T_mono value (“AcGFP1⁴‐corr”). Symbols and error bars reflect mean ± SE (standard error) values from the mono‐exponential fit.
3. Strategy to compute D_solvent from the experimental T_mono value for each FP using an experimentally constrained BD simulation model (see Results and Appendix Supplementary Methods for details).
4. Linear relationship between LOG10 (T_mono) and LOG10 (D_solvent) predicted by the model for a mitochondrion containing 19 cristae and with a cristae‐blocked area (CBA) of 0.95. Parameters of the linear fit (LOG10 (D_solvent) = A + B·LOG10 (T_mono)) are: R = −0.999, P < 0.0001; A (intercept) = 1.27 ± 0.0123 (SE); B (slope) = −1.10 ± 0.0154 (SE)). Numerals indicate the D_solvent values (μm²/s) used in the model (the corresponding FRAP data are presented in Appendix Fig S3B).
5. D_solvent values of the four FPs (numerals) obtained using the relationship in panel (D) by inserting the experimental T_mono values in the fitting equation for panel (D) (see Results for details). Numerical data are provided in Table 1.

Table 1.

Experimental data and BD modeling results.

	−CAP				+CAP
Cell line	AcGFP1	AcGFP12	AcGFP13	AcGFP14	AcGFP1	AcGFP12	AcGFP13	AcGFP14
MW (kDa) a	29.155	57.586	87.705	115.337	29.155	57.586	87.705	115.337
LOG10 (MW)	1.4641	1.7603	1.9430	2.06197	1.4641	1.7603	1.9430	2.06197
Mitochondrial length, diameter and radius determined using confocal laser scanning microscopy (CLSM) b
Lmito (μm)	3.42 (N = 55)	3.42 (N = 30)	3.42 (N = 37)	3.42 (N = 68)	3.40 (N = 31)	ND	ND	3.42 (N = 26)
Dmito (μm)	0.562 ± 0.025 (N = 26)	0.524 ± 0.012 (N = 41)	0.549 ± 0.020 (N = 33)	0.525 ± 0.017 (N = 29)	0.552 ± 0.015 (N = 24)	ND	ND	0.546 ± 0.017 (N = 20)
Rmito (μm)	0.281	0.262	0.275	0.263	0.276	ND	ND	0.273
Vmito (μm3)	0.848	0.738	0.813	0.743	0.819	ND	ND	0.801
Vmito (l)	0.848·10−15	0.738·10−15	0.813·10−15	0.743·10−15	0.819·10−15	ND	ND	0.801·10−15
Mitochondrial diameter, radius and cristae per mitochondrion determined using electron microscopy (EM) c
Dmito (μm)	0.510 ± 0.019 (N = 52)	ND	ND	0.504 ± 0.015 (N = 59)	0.490 ± 0.017 (N = 51)	ND	ND	0.494 ± 0.018 (N = 53)
Rmito (μm)	0.255	ND	ND	0.252	0.245	ND	ND	0.247
ncristae (1/μm)	5.620 ± 0.155 (N = 244)	ND	ND	5.462 ± 0.174 (N = 314)	2.705 ± 0.130 (N = 295)	ND	ND	3.50 ± 0.145 (N = 260)
ncristae/mito	19	ND	ND	19	9	ND	ND	12
Mono‐exponential fitting parameters of the fluorescence recovery after photobleaching (FRAP) curve d
N	76	30	37	68	40	24	26	33
R 2	0.922	0.971	0.932	0.921	0.962	0.947	0.780	0.951
y0	−80.0 ± 5.85	−0.677 ± 2.42	24.7 ± 2.29	30.7 ± 2.17	39.1 ± 1.20	30.9 ± 0.800	44.2 ± 0.920	47.5 ± 0.767
Amono	178 ± 5.84	98.9 ± 2.40	68.6 ± 2.26	60.5 ± 2.14	55.4 ± 1.17	45.1 ± 0.667	23.6 ± 0.763	39.0 ± 0.706
Tmono (s)	0.789 ± 0.015	1.51 ± 0.031	2.01 ± 0.065	2.05 ± 0.066	2.75 ± 0.099	8.76 ± 0.357	9.31 ± 0.883	5.43 ± 0.168
Tmono‐corr (s)				2.78
F0	41.4 ± 1.61%	37.7 ± 2.40%	42.0 ± 1.80%	43.6 ± 1.22%	42.0 ± 2.60%	22.7 ± 3.38%	40.2 ± 4.51%	42.6 ± 2.50%
F∞	98.8 ± 11.7%	98.2 ± 4.82%	93.3 ± 4.55%	91.2 ± 4.31%	94.5 ± 2.37%	76.0 ± 1.47%	67.8 ± 1.68%	86.5 ± 1.47%
Fm	0.979	0.972	0.885	0.844	0.904	0.689	0.462	0.765
Parameters and results regarding the BD model e
1. Simulation parameters for Dsolvent prediction
Identical for all simulations	Lmito = 3.42 μm; Rmito = 0.270 μm; SFRAP = 1.4 μm; CBA = 0.95
ncristae	19	19	19	19	9	ND	ND	12
2. Predicted Dsolvent
Dsolvent (μm2/s)	23.9	11.8	8.59	6.02	2.91	NA	NA	NA
LOG10 (Dsolvent)	1.378	1.072	0.9340	0.7796	0.464	NA	NA	NA
3. Computation of radius of gyration (RG), hydrodynamic radius (RH) and ηsolvent (cP) at 293 K
MW (kDa)	29.155	57.586	87.705	115.337	29.155	57.586	87.705	115.337
Assuming that the FP has a compact conformation
Radius of molecule R (Å)	15	20	20	20	15	NA	NA	NA
Length of molecule L (Å)	40	60	60	60	40	NA	NA	NA
RG (Å)	15.5	20	20	20	15.5	NA	NA	NA
RH (Å)	20	23	23	23	20	NA	NA	NA
ηsolvent (Young)	3.32	5.36	6.40	8.34	27.3	NA	NA	NA
ηsolvent (He–Niemeyer)	3.69	5.88	7.53	10.3	30.3	NA	NA	NA
ηsolvent (Tyn–Gusek)	4.57	7.18	9.86	14.1	37.5	NA	NA	NA
ηsolvent (Stokes–Einstein)	4.49	7.91	10.9	15.5	36.9	NA	NA	NA
Assuming that the FP has an extended conformation
Radius of molecule R (Å)	15	15	35	35	15	NA	NA	NA
Length of molecule L (Å)	40	130	247	349	40	NA	NA	NA
RG (Å)	15.5	38	73	102	15.5	NA	NA	NA
RH (Å)	20	30	61	75	20	NA	NA	NA
ηsolvent (Young)	3.32	5.36	6.40	8.34	27.3	NA	NA	NA
ηsolvent (He–Niemeyer)	3.69	4.27	3.94	4.55	30.3	NA	NA	NA
ηsolvent (Tyn–Gusek)	4.57	3.78	2.70	2.76	37.5	NA	NA	NA
ηsolvent (Stokes–Einstein)	4.49	6.06	4.10	4.75	36.9	NA	NA	NA

BD, Brownian dynamics; CAP, chloramphenicol; D_solvent, solvent‐dependent diffusion constant; η_solvent, solvent‐dependent viscosity; NA, not appropriate; ND, not determined; R_G, radius of gyration; R_H, hydrodynamic radius; S_FRAP, size of the experimental FRAP region in the BD model; T, temperature; T_mono, experimental FRAP mono‐exponential time constant.

^a Molecular weight (MW) was calculated directly from the protein sequences given in Appendix Table S1 (excluding the N‐terminal mitochondrial targeting sequence) using the pI/Mw tool (web.expasy.org/compute_pi). One (1) Dalton (Da) equals 1 g/mol.

^b Confocal laser scanning microscopy (CLSM) analysis: The data are presented as mean ± SEM. N indicates the number of mitochondria analyzed in at least two independent experiments. Mitochondrial length (L_mito) and mitochondrial diameter (D_mito) were determined from the FRAP images by quantifying the frame width at half‐maximal height (FWHM; equaling 2∙R_mito) of a Gaussian curve fitted to a 1 pixel wide intensity profile perpendicular to the short and long axis of the mitochondrial filament (see Appendix Fig S2F). Mitochondrial volume (V_mito) was calculated using a cylindrical approximation: V_mito = π ·(R_mito)²·L_mito. One (1) μm³ equals 10⁻¹⁵ liter, 0.001 picoliter (1 picoliter = 10⁻¹² liter) and 1,000 attoliter (1 attoliter = 10⁻¹⁸ liter). Average V_mito values equaled 0.786 ± 0.0540(SD) μm³ = 786 attoliter (−CAP) and 0.810 μm³ = 810 attoliter (+CAP).

^c Electron microscopy (EM) analysis: The data are presented as mean ± SEM. N indicates the number of mitochondria analyzed in two independent experiments. D_mito and R_mito indicate the mitochondrial diameter and radius, respectively.

^d Fitting of the fluorescence recovery after photobleaching (FRAP) curve: y = y₀ + A_mono[1−EXP(−t/T_mono)]. N indicates the number of mitochondria analyzed in at least three independent experiments. The coefficient of determination (R²) is used as a measure of the goodness of fit (the closer R² is to a value of one, the closer the fit is to the data points). The parameter errors reflect the standard error (SE) value from the fit, as reported by the fitting software. F₀ indicates the fluorescence signal at the start of the fluorescence recovery (expressed as % of the prebleach value). F_∞ indicates the fluorescence signal to which the fluorescence signal recovers given by: y₀ + A_mono (expressed as % of the prebleach value). The error in F_∞ was calculated by summation of the errors in y₀ and A_mono. F_m indicates the mobile fraction given by: [(F_∞−F₀+)/(F_i−F₀)], with F_i being the prebleach fluorescence equaling 100%.

^e Mathematical modeling: One (1) Angstrom (Å) equals 1·10⁻¹⁰ m. CBA, cristae‐blocked area (fraction of total transecting area). See Results for further details.

Brownian dynamics simulations of FRAP experiments

To convert the experimental T_mono data into D_solvent values, we developed a Brownian dynamics (BD) simulation model (Fig 3C). This quantitative model generated synthetic FRAP curves, used a cristae‐containing cylindrical structure to represent mitochondria, and was constrained by experimental data. The latter included mitochondrial length (L_mito), mitochondrial radius (R_mito), size of the FRAP region (S_FRAP), the number of cristae per mitochondrion (n_cristae), and the “cristae‐blocked area” (CBA; expressed as a fraction of the total transecting area). Validated by EM analysis and data on HeLa cristae structure from the literature (Appelhans et al, 2011; Wilkens et al, 2013; Wolf et al, 2019; Hu et al, 2020; Segawa et al, 2020; Weissert et al, 2021) we assumed in the model that (Appendix Fig S3A): (i) mitochondria contained regularly arranged cristae perpendicular to the longitudinal axis of the mitochondrion, (ii) the positions of the cristae alternated, with consecutive cristae being opposite of each other, (iii) cristae were equidistant, partially overlapping and of negligible thickness (Partikian et al, 1998), and (iv) CBA equaled 0.95. The presence of cristae increased the effective length of the “channel” that connected the two ends of the mitochondrion thereby increasing FP diffusion length. In addition, the presence of cristae reduced the diffusive flow between consecutive mitochondrial subcompartments. Therefore, as indicated previously (Ölveczky & Verkman, 1998; Partikian et al, 1998), FRAP was slower when more cristae were present (Appendix Fig S3B and C). Further details of the BD model are presented in the Appendix Supplementary Methods.

Determining the D_solvent value of mitochondria‐targeted FPs

Confocal microscopy analysis of living FP‐expressing cells yielded values for L_mito and R_mito of 3.42 and 0.262–0.281 μm, respectively (Table 1). Similar R_mito values (0.252–0.255 μm) were obtained by electron microscopy (EM) analysis of fixed AcGFP1 and AcGFP1⁴ cells (Table 1). EM quantification of the number of cristae yielded values of 5.620 cristae/μm (AcGFP1‐expressing cells) and 5.462 cristae/μm (AcGFP1⁴‐expressing cells). This reflects an average n_cristae value of 19 (Table 1) and an intercrista distance between 177 and 183 nm. The latter lies within a range of experimental values previously reported for HeLa cells (51–250 nm; Wilkens et al, 2013; Stephan et al, 2019; Wang et al, 2019). Applying these experimental constraints, BD simulations were carried out using the following parameters (Table 1): L_mito = 3.42 μm, R_mito = 0.270 μm, n_cristae = 19 and S_FRAP = 1.4 μm. Model output was determined for several values of D_solvent (0.5–50 μm²/s) to establish the relationship between T_mono and D_solvent. On a logarithmic scale, these parameters displayed a linear correlation (Fig 3D), allowing calculation of D_solvent for the experimental T_mono values (Fig 3E). This yielded values of 23.9 μm²/s (AcGFP1), 11.8 μm²/s (AcGFP1²), 8.59 μm²/s (AcGFP1³), and 6.02 μm²/s (AcGFP1⁴).

The mitochondrial matrix solvent reduces FP mobility in a manner compatible with macromolecular crowding

The obtained D_solvent values (Fig 3E) reflect solvent‐dependent FP diffusion in the mitochondrial matrix. To address our primary research question on macromolecular crowding, we first compared these values with empirical data sets of free 3D diffusion of globular biomolecules in aqueous media (Fig 4A; details are provided in Appendix Tables S2 and S3). The LOG10 (D_solvent) value of these molecules decreased linearly as a function of their LOG10 (MW) value, with a slope of −0.36 (Fig 4B). The latter is compatible with the theoretical proportionality of D_solvent with the molecular radius, and hence MW^−0.33, for globular molecules (Dross et al, 2009). Analysis of EGFP concatemer diffusion in aqueous solution suggested that these molecules display a globular conformation, that is, the open blue circles (Fig 4A) appear to be on the line fitted for the globular proteins (black symbols). However, the underlying experimental studies provided evidence that EGFP concatemers display an elongated molecular structure in aqueous solution (Pack et al, 2006; Vámosi et al, 2014). Therefore, we added the EGFP concatemers to the data set of the elongated molecules in aqueous solution (Fig 4A; open and filled blue symbols). For elongated molecules (Saxton, 2014), D_solvent decreased faster as a function of MW than for globular molecules (Fig 4A; black vs. blue line) and a slope of −0.72 was found (Fig 4B). The latter is compatible with experimental data for elongated (i.e., supercoiled) plasmid DNA molecules in dilute aqueous solution where D_solvent is proportional to MW^−0.66 (Prazeres, 2008). Quantification of EGFP concatemer diffusion in HeLa cell nuclei and cytosol yielded steeper slopes relative to aqueous solution (Fig 4A; open red squares, filled red circles, and Fig 4B; open red bars). These slopes were relatively close to the theoretical value for elongated molecules (−0.66), suggesting that these EGFP concatemers displayed an elongated molecular structure. The latter was experimentally confirmed in the underlying studies (Pack et al, 2006; Dross et al, 2009). In case of mitochondrial matrix‐targeted FPs, a slope of −0.98 was obtained (Fig 4A; filled red squares, and Fig 4B; filled red bar). This decline was faster than for globular molecules in aqueous solution (2.7‐fold), elongated molecules in aqueous solution (1.4‐fold), elongated EGFP concatemers in the HeLa cell nucleus (1.3‐fold), and elongated EGFP concatemers in HeLa cytosol (1.5‐fold). Of note, the LOG10 (D_solvent) value for AcGFP1⁴ fell exactly on the fitted line (Fig 4A; filled red square for highest MW), supporting the validity of the applied T_mono correction (Fig 3B). Because the data points for the mitochondrial matrix‐targeted FPs are not parallel to the “aqueous” lines for the globular and elongated molecules (Fig 4A and B), the steeper decline in D_solvent for the matrix‐targeted concatemers cannot be explained by differences in solvent viscosity. The steeper decline is also not due to cristae‐induced diffusion hindrance, since n_cristae was similar for AcGFP1‐ and AcGFP1⁴‐expressing cells (Table 1) and our modeling approach delivers cristae‐independent D_solvent values. Integrating the above results, we conclude that the MW‐dependent mobility reduction of AcGFP1 concatemers in the mitochondrial matrix is not only due to their elongated structure but also involves macromolecular crowding.

Figure 4. Relationship between D_solvent and MW for the mitochondrial matrix‐targeted fluorescent proteins, viscosity analysis and protein structure prediction.

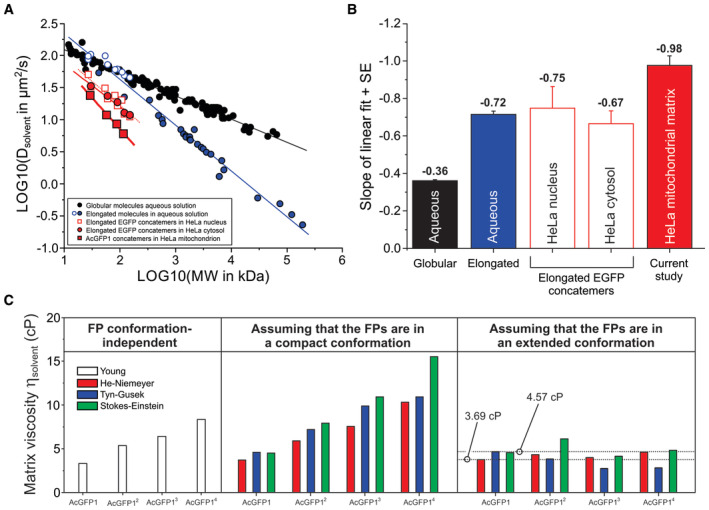
1. Linear relationship between experimental D_solvent and MW values for various biomolecules in a double logarithmic plot. Data obtained in aqueous solution is separated into globular biomolecules (filled black symbols; continuous black line), elongated EGFP concatemers (open blue symbols; continuous blue line) and elongated biomolecules (filled blue symbols; continuous blue line). Red symbols reflect intracellular diffusion measurements with EGFP concatemers in HeLa cell nuclei (open red squares; dotted red line), EGFP concatemers in HeLa cytosol (filled red circles; continuous thin red line) and AcGFP1 concatemers in the mitochondrial matrix (filled red squares; continuous thick red line; current study). Full numerical data, fitting parameters using (LOG10 (D_solvent) = A + B·LOG10 (MW) and background information are provided in Appendix Tables S2 and S3.
2. Slopes of the linear fits depicted in panel (A) for the different classes of biomolecules measured in aqueous solution and intracellular compartments. Individual bars reflect mean ± SE (standard error) values from the linear fit.
3. The viscosity of the mitochondrial matrix solvent (η_solvent) was calculated from the D_solvent values of the FPs using four empirical equations (Young, He–Niemeyer, Tyn–Gusek and Stokes–Einstein). This allowed the prediction of η_solvent as well as FP structural conformation (“compact” or “extended”; Fig EV1). The estimated η_solvent ranged between 3.69 and 4.57 cP. See Results for details.

Quantifying the viscosity of the mitochondrial matrix solvent and predicting FP structural conformation

To gain further insight into the structural conformation of the mitochondrial matrix‐targeted FPs, we next determined mitochondrial matrix solvent viscosity (η_solvent). To this end, we applied four empirical equations allowing prediction of η_solvent from D_solvent (Appendix Supplementary Methods): “Young” (Young et al, 1980), “He–Niemeyer” (He & Niemeyer, 2003), “Tyn–Gusek” (Tyn & Gusek, 1990), and “Stokes–Einstein” (Einstein, 1905; Sutherland, 1905; von Smoluchowski, 1906; Perrin, 1936). These equations also accounted for the effects of MW (Young, He–Niemeyer), radius of gyration (R_G; He–Niemeyer, Tyn–Gusek), and hydrodynamic radius (R_H; Stokes–Einstein) of the FPs. The MW of each concatemer was computed from its protein sequence (Appendix Table S1), whereas R_G and R_H were derived from structural information (see Table 1 and Fig EV1, and Appendix Supplementary Methods). In case of AcGFP1², AcGFP1³, and AcGFP1⁴, two extreme conformations of minimal size (“compact”) and maximal size (“extended,” i.e., elongated) were considered (Fig EV1B–G). The Young equation, which is independent of FP conformation, predicted that η_solvent increased as a function of concatemer MW (Fig 4C; left panel). Similarly, when assuming that the FPs displayed a “compact” structural conformation also the He–Niemeyer, Tyn–Gusek and Stokes–Einstein equations predicted that η_solvent increased as a function of MW (Fig 4C; middle panel). By contrast, the predicted η_solvent values for AcGFP1², AcGFP1³, and AcGFP1⁴ were highly similar when assuming that these FPs displayed an “extended” structural conformation (Fig 4C; right panel). This strengthens our above conclusion that the FPs have an extended structure in the mitochondrial matrix solvent. The D_solvent value of AcGFP1 is the most reliable and easy‐to‐interpret predictor of η_solvent because AcGFP1‐expressing cells display a single protein band (Fig 2B), and no assumptions regarding AcGFP1 structure are required (Fig EV1A). For AcGFP1 (Fig 4C; right panel) the He–Niemeyer, Tyn–Gusek, and Stokes–Einstein equations predicted η_solvent values between 3.69 and 4.57 cP (dotted lines). Taken together, these results support the conclusion that AcGFP1², AcGFP1³, and AcGFP1⁴ have an elongated structural conformation in the mitochondrial matrix and that the mitochondrial matrix fluid displays a three to five‐fold higher viscosity than water.

Figure EV1. Compact and extended structural conformations of AcGFP1 concatemers.

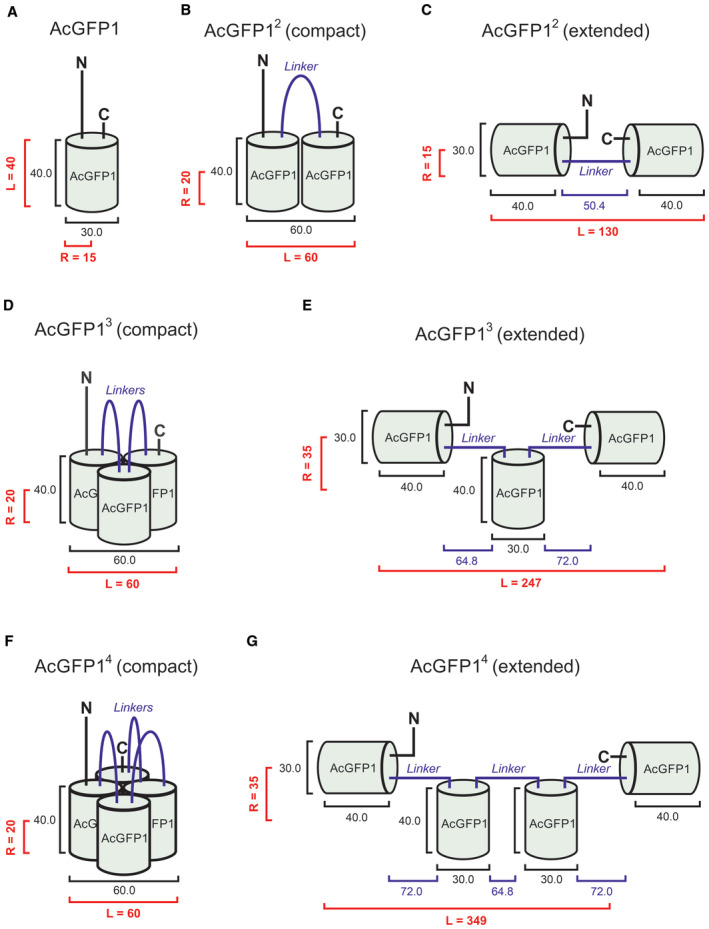
1. Dimensions (numerals) of AcGFP1 in Angstrom (Å) based upon GFP crystal structure. R and L indicate the radius and length of the protein, respectively. Geometric data are summarized in Table 1.
2. Same as panel (A) but now for AcGFP1² displaying a minimal structural conformation (“compact”).
3. Same as panel (A) but now for AcGFP1² displaying a structural conformation of maximal size (“extended”).
4. Same as panel (A) but now for AcGFP1³ displaying a compact structure.
5. Same as panel (A) but now for AcGFP1³ displaying an extended structure.
6. Same as panel (A) but now for AcGFP1⁴ displaying a compact structure.
7. Same as panel (A) but now for AcGFP1⁴ displaying an extended structure.

Chloramphenicol decreases the number of cristae, increases matrix electron density, and partially immobilizes matrix‐targeted FPs

Although the above data provide evidence that FP diffusion in the mitochondrial matrix is reduced by macromolecular crowding, this effect appears to be relatively small. Therefore, we aimed to increase matrix macromolecular crowding levels by treating the cells with chloramphenicol (CAP), which inhibits the biosynthesis of mitochondrial DNA (mtDNA)‐encoded OXPHOS subunits. The latter normally function as MIM‐embedded binding platforms for nDNA‐encoded OXPHOS subunits and/or assembly intermediates during OXPHOS biogenesis (Guerrero‐Castillo et al, 2017; Hock et al, 2020). As such, CAP treatment induces the formation of stable subassemblies of mitochondrial CI with MWs of 170‐, 67‐, and 72‐kDa (Guerrero‐Castillo et al, 2017). Compositional analysis of these subassemblies demonstrated that the 72‐kDa subassembly consisted of the NDUFV1 and NDUFV2 subunit. Previous analysis of mitochondrial matrix protein diffusion in HEK293 cells demonstrated that CAP treatment: (i) particularly increased the F_m of AcGFP1‐tagged NDUFV1 subunits and/or NDUFV1‐containing assembly intermediates, (ii) slowed the FRAP rate of AcGFP1 and AcGFP1², and (iii) did not slow the FRAP rate of the integral MIM protein adenine nucleotide translocase 1 (ANT1; Dieteren et al, 2011b). This demonstrates that NDUFV1 subunits and/or NDUFV1‐containing subassemblies are not MIM‐attached but diffusing in the mitochondrial matrix solvent. Considering the currently known mechanisms of OXPHOS biogenesis (Hock et al, 2020; Fernández‐Vizarra & Ugalde, 2022), it is to be expected that CAP treatment also increases the amount of nDNA‐encoded subunits and/or assembly intermediates from other OXPHOS complexes (i.e., III, IV, and V) in the matrix solvent. CAP treatment did not alter mitochondrial dimensions and FP expression patterns (Table 1 and Appendix Fig S1B). EM analysis demonstrated that the number of cristae/μm was ~twofold reduced (Fig 5A and B, and Table 1), compatible with previous studies in HeLa and HEK293 cells (Lenk & Penman, 1971; Kislev et al, 1973; Dieteren et al, 2011b). Moreover, the mitochondrial matrix was more electron‐dense in CAP‐treated cells (Fig 5C). The FRAP signal recovered slower, that is, T_mono was larger for all FPs in CAP‐treated relative to untreated cells (Fig 5D and E, and Table 1). CAP treatment further induced a substantial decrease in F_m (Fig 5D and Table 1) and F_∞ (i.e., the predicted FP fluorescence intensity at t = t_∞; Fig 5F), in particular for AcGFP1² and AcGFP1³. By contrast, CAP treatment was much less effective in reducing T_mono, F_m, and F_∞ for AcGFP1⁴, compatible with the detected fluorescent degradation product of smaller MW (Appendix Fig S1B). CAP‐treated AcGFP1²‐ and AcGFP1³‐expressing cells displayed a substantial decrease in F_m and F_∞, which could not be quantitatively reproduced by the BD simulation model (Appendix Fig S3). In light of the above, prediction of D_solvent values for AcGFP1², AcGFP1³, and AcGFP1⁴ using BD simulations was not possible. However, AcGFP1 displayed T_mono and F_m values that were still reasonably compatible with BD simulations, predicting a D_solvent of 2.91 μm²/s for an experimental n_cristae value of 9 (Table 1; Appendix Fig S3C and D). This predicted an η_solvent value between 27.3 and 37.5 cP (Fig 5G and Table 1). Collectively, our FRAP analysis of CAP‐treated cells demonstrates that mitochondrial matrix‐targeted FPs become progressively immobilized as a function of MW, associated with an eightfold increase in η_solvent. These phenomena are compatible with increased macromolecular crowding.

Figure 5. Chloramphenicol decreases the number of cristae, increases matrix electron density, reduces the mobility of mitochondrial matrix‐targeted fluorescent proteins and increases matrix viscosity.

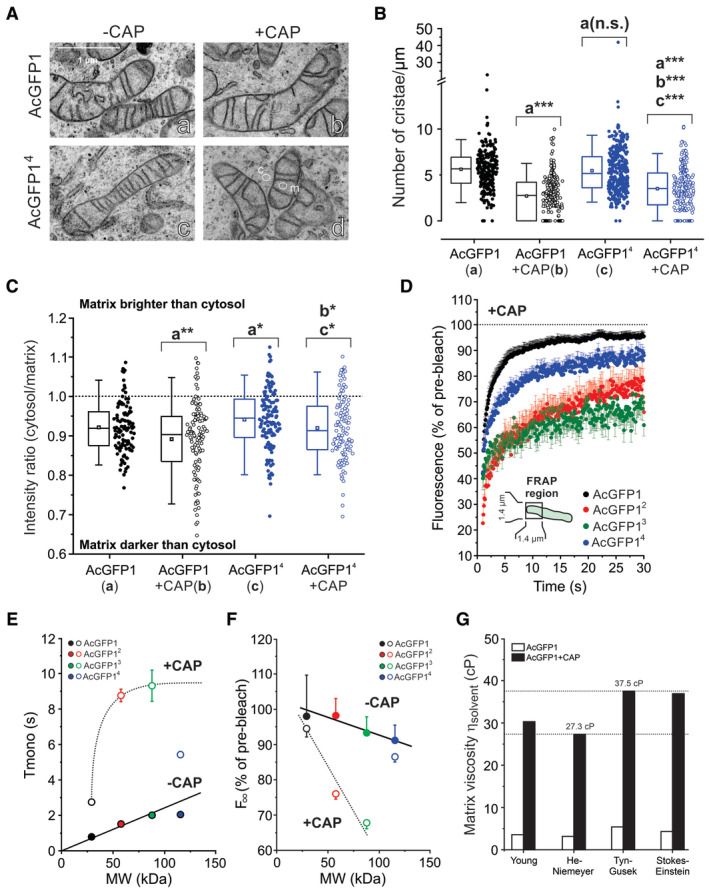
1. Transmission electron microscopy (EM) images of AcGFP1 and AcGFP1⁴‐expressing HeLa cells cultured in the absence and the presence of chloramphenicol (CAP). Images were contrast‐optimized to better visualize cristae. Cytosolic and mitochondrial regions of interest typically used for electron density analysis (panel C) are marked by “c” and “m,” respectively.
2. Effect of CAP on the average number of cristae/μm calculated by dividing the number of cristae by the mitochondrial length for individual mitochondria. Data was obtained in N = 2 independent EM experiments for n = 244 mitochondria (AcGFP1), n = 295 (AcGFP1 + CAP), n = 314 (AcGFP1⁴) and n = 259 (AcGFP1⁴ + CAP).
3. Effect of CAP on the electron density of the mitochondrial matrix quantified from EM images (original images were used). The y‐axis depicts the intensity ratio between a cytosolic region of interest (ROI; e.g., panel A‐d, marked “c”) and a close by ROI in the mitochondrial matrix (e.g., panel A‐d, marked “m”). Equal intensities of these ROIs are marked by the dotted line. Only mitochondria with clearly visible cristae (i.e., that were fully within the EM section) were included (N = 2 independent experiments) from n = 112 mitochondria (AcGFP1), n = 119 (AcGFP1 + CAP), n = 134 (AcGFP1⁴) and n = 116 (AcGFP1⁴ + CAP).
4. Average FRAP curves (mean ± SEM) for mitochondrial matrix‐targeted FPs in the presence of CAP (Table 1). Data was obtained in at least N = 3 independent experiments for n = 40 mitochondria (AcGFP1 + CAP), n = 24 (AcGFP1² + CAP), n = 26 (AcGFP1³ + CAP) and n = 33 (AcGFP1⁴ + CAP).
5. Relationship between MW and T_mono in the absence of CAP (−CAP; data taken from Fig 3B) and in the presence of CAP (+CAP; curve manually drawn). Symbols and error bars reflect mean ± SE (standard error) values from the mono‐exponential fit. For data points without error bar, the latter fell within the size of the symbol.
6. Same as panel (E) but now for the relationship between MW and the fluorescence intensity (F_∞) of the FPs by extrapolating the fitted exponential recovery to t = t_∞ (lines manually drawn). Symbols and error bars for F_∞ reflect mean ± SEM and were computed from the mono‐exponential fit parameters as described in Table 1.
7. Impact of CAP on the solvent‐dependent viscosity (η_solvent) of the mitochondrial matrix fluid determined using the D_solvent values of AcGFP1 (see Results for details). The estimated η_solvent ranged between 27.3 and 37.5 cP.

Data information: In panels (B and C) each symbol represents an individual mitochondrion, error bars mark the 95% (upper) and 5% (lower) percentile, the boundary boxes mark the 75% (upper) and 25% (lower) percentile, the square marks the mean value of the data, and the horizontal line within the box indicates the median value of the data. Data in panel (B and C) was compared using an independent Student's t‐test and significant differences are indicated by *P < 0.05, **P < 0.01, ***P < 0.001 between the marked conditions (a–c). Not significant is marked by n.s. The exact P‐values for panel (B) were: AcGFP1 (a) vs. AcGFP1 + CAP (b): P = 1.894·10⁻⁴⁰; AcGFP1 (a) vs. AcGFP1⁴ + CAP: P = 1.458·10⁻²¹; AcGFP1 + CAP (b) vs. AcGFP1⁴ + CAP: P = 4.846·10⁻⁵; AcGFP1⁴ (c) vs. AcGFP1⁴ + CAP: P = 2.725·10⁻¹⁶. The exact P‐values for panel (C) were: AcGFP1 (a) vs. AcGFP1 + CAP (b): P = 0.00545; AcGFP1 (a) vs. AcGFP1⁴ (c): P = 0.0348; AcGFP1 + CAP (b) vs. AcGFP1⁴ + CAP: P = 0.0142; AcGFP1⁴ (c) vs. AcGFP1⁴ + CAP: P = 0.0366.

Chloramphenicol impairs mitochondrial function, but neither induces the mitochondrial unfolded protein response, not alters mtDNA copy number and mitochondrial fission/fusion protein levels

Evidence in the literature suggests that both DOX and CAP inhibit mitochondrial function, thereby potentially inducing the mitochondrial unfolded protein response (UPR^mt; Houtkooper et al, 2013; Moullan et al, 2015; Shpilka & Haynes, 2018). The latter is classically linked to the accumulation of misfolded proteins in the mitochondrial matrix, which could hinder FP diffusion in our experiments by increasing macromolecular crowding. In case of DOX, cellular oxygen consumption rate (OCR) was not reduced (Appendix Supplementary Results and Fig EV2A–C) and the levels of proteinaceous UPR^mt‐linked markers (LONP1, mtHSP70, mtHSP60, CLPP, and CHOP) were not affected (Figs EV2E, and EV3A and B). This makes it unlikely that DOX treatment induces mitochondrial dysfunction and UPR^mt in our experiments. CAP treatment greatly reduced OCR values and increased extracellular acidification rate (ECAR), potentially suggesting induction of a glycolytic switch (Schmidt et al, 2021; Bulthuis et al, 2022; Divakaruni & Jastroch, 2022). Further analysis demonstrated that CAP‐treated cells do not display UPR^mt activation (Appendix Supplementary Results and Fig EV2A–C) and exhibit lower and higher TMRM fluorescence signals in the nucleus and mitochondrion, respectively (Appendix Supplementary Results and Fig EV2D). The latter suggests that CAP induces mitochondrial membrane potential (Δψ) hyperpolarization. FP diffusion might potentially be altered by changes in mtDNA organization and the function of the mitochondrial MIM fusion protein Optic Atrophy 1 (OPA1). However, no CAP‐induced changes in mtDNA copy number and expression of mitochondrial fission/fusion proteins were detected (Appendix Supplementary Results, and Fig EV2F and G). The latter is compatible with CAP not altering mitochondrial length and diameter. Taken together, these results suggest that the progressive FP immobilization observed in CAP‐treated cells is neither caused by UPR^mt induction nor by alterations in the level of mtDNA and mitochondrial fission/fusion proteins. This supports our conclusion that CAP treatment affects FP mobility by increasing macromolecular crowding.

Figure EV2. Functional consequences of chloramphenicol (CAP) treatment in HeLa parental cells.

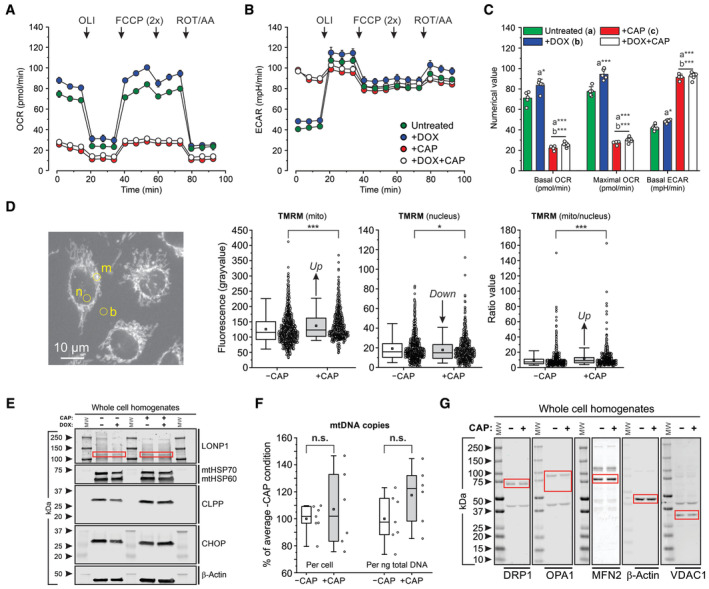
1. Average oxygen consumption rate (OCR) in untreated cells, and cells treated with DOX, CAP, or DOX + CAP (for legend see panel B). Oligomycin (OLI), mitochondrial uncoupler (FCCP), and antimycin A + rotenone (AA/ROT) were added at the indicated time points.
2. Same as panel (A) but now for the average extracellular acidification rate (ECAR).
3. Statistical analysis of the data in panel (A and B) with respect to the basal OCR, maximal OCR and basal ECAR.
4. Effect of CAP on the TMRM fluorescence signal in mitochondria and nucleus. Left panel: Typical example of fluorescence microscopy image of TMRM‐stained cells. Fluorescence signals were manually determined in two regions of interest (yellow) defined in a mitochondria‐dense (“m”) and nucleoplasmic part (“n”) of the cell and corrected for background using a close by ROI outside of the cell (“b”). Data panels: numerical values for the mitochondrial fluorescence signal (mito), nuclear fluorescence signal (nucleus) and fluorescence ratio value (mito/nucleus).
5. Effect of DOX, CAP or DOX + CAP on the cellular protein levels of LONP1 (specific bands marked by red boxes), mtHSP70, mtHSP60, CLPP and CHOP. β‐actin was used as cellular loading control. Arrowheads indicate molecular weight in kDa. Individual panels were contrast‐optimized for visualization purposes. Original blots are presented in Appendix Fig S5B.
6. Effect of CAP on mitochondrial DNA (mtDNA) levels expressed as number of mtDNA copies per cell and per nanogram (ng) of total DNA.
7. Effect of CAP on the cellular levels of key mitochondrial fission and fusion proteins (specific bands are marked by red boxes): DRP1 (Dynamin‐related protein 1, OPA1 (Optic atrophy protein 1), MFN2 (Mitofusin 2). β‐actin and VDAC1 were used as cellular and mitochondrial loading controls, respectively. Arrowheads indicate molecular weight in kDa. Individual panels were contrast‐optimized for visualization purposes. Original blots are presented in Appendix Fig S5A.

Data information: OCR and ECAR data (panels A–C) was obtained in a single (N = 1) experiment and the following number (n) of technical replicates: Untreated (n = 5), +DOX (n = 5), +CAP (n = 4), +DOX+CAP (n = 6). TMRM data (Panel D) was obtained in N = 2 independent experiments for n = 991 cells (−CAP) and n = 668 cells (+CAP). MtDNA data (panel F) was obtained in N = 2 independent experiments in n = 7 assays (−CAP) and n = 6 assays (+CAP). Each symbol represents an individual well (panel C), cell (panel D) or assay (panel F). In panels (A and B), individual data points reflect mean ± SEM. In panel (C), bars and errors reflect mean ± SEM. In panels (D and F), error bars mark the 95% (upper) and 5% (lower) percentile, the boundary boxes mark the 75% (upper) and 25% (lower) percentile, the square marks the mean value of the data, and the horizontal line within the box indicates the median value of the data. Significant differences, obtained using an independent Student's t‐test, are indicated by *P < 0.05, **P < 0.01, ***P < 0.001 between the marked conditions (a–c) in panel (C) and between the −CAP and +CAP condition (panel D and F). Not significant is marked by n.s. The exact P‐values for panel (C) (basal OCR) were: Untreated (a) vs. +DOX (b): P = 0.0126; Untreated (a) vs. +CAP (c): P = 1.554·10⁻⁶; Untreated (a) vs. +DOX+CAP: P = 4.082·10⁻⁸; +DOX (b) vs. +CAP (c): P = 2.671·10⁻⁷; +DOX (b) vs. +DOX + CAP: P = 3.806·10⁻⁹. The exact P‐values for panel (C) (maximal OCR) were: Untreated (a) vs. +DOX (b): P = 6.509·10⁻⁴; Untreated (a) vs. +CAP (c): P = 2.019·10⁻⁷; Untreated (a) vs. +DOX+CAP: P = 4.900·10⁻⁹; +DOX (b) vs. +CAP (c): P = 4.558·10⁻⁸; +DOX (b) vs. +DOX + CAP: P = 5.713·10⁻¹⁰. The exact P‐values for panel (C) (basal ECAR) were: Untreated (a) vs. +DOX (b): P = 0.0023; Untreated (a) vs. +CAP (c): P = 4.571·10⁻⁸; Untreated (a) vs. +DOX+CAP: P = 7.784·10⁻¹⁰; +DOX (b) vs. +CAP (c): P = 2.412·10⁻⁸; +DOX (b) vs. +DOX+CAP: P = 7.039·10⁻¹⁰. The exact P‐value for panel (C) (mito) was: P = 7.145·10⁻⁶. The exact P‐value for panel (C) (nucleus) was: P = 0.0237. The exact P‐value for panel (C) (mito/nucleus) was: P = 5.702·10^–5. The exact P‐value for panel (F) (per cell) was: P = 0.556. The exact P‐value for panel (F) (per ng total DNA) was: P = 0.139.

Figure EV3. Chloramphenicol (CAP) and doxycycline (DOX) do not increase protein markers typically associated with induction of the mitochondrial unfolded protein response (UPR^mt) in parental and FP‐expressing cells.

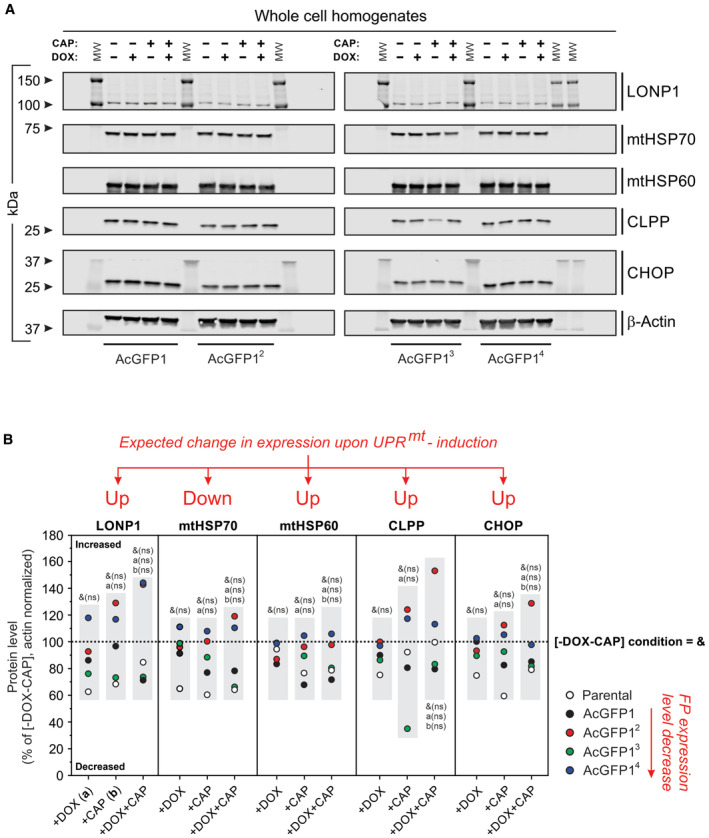
1. Western blot analysis (SDS–PAGE) of whole‐cell homogenates was used to assess the levels of the following proteins: LONP1, mtHSP70, mtHSP60, CLPP, and CHOP. β‐actin was used as a cellular loading control. MW indicates molecular weight in kDa. Effect of the expression inducer DOX (1 μg/ml, 24 h) and CAP (40 μg/ml, 72 h), alone and in combination (i.e., 48‐h CAP treatment followed by 24 h CAP + DOX treatment), on protein levels in FP‐expressing HeLa cell lines (AcGFP1, AcGFP1², AcGFP1³, and AcGFP1⁴). Individual panels were contrast‐optimized for visualization purposes. Original blots are presented in Appendix Fig S4.
2. Quantitative analysis of protein levels in panel A and in HeLa parental cells (the open symbols reflect data for the parental cells in Appendix Fig S5B). All signals were normalized on β‐actin and expressed as % of the condition without DOX and CAP (“−DOX−CAP”). Effects previously associated with UPR^mt induction are marked: “Up” indicates proteins that are expected to be upregulated upon UPR^mt induction, “Down “indicates proteins that are expected to be downregulated upon UPR^mt induction.

Data information: The effects of DOX, CAP, and DOX + CAP were compared with the “−DOX−CAP” (untreated) condition (i.e., with the dotted line marked “&”) by testing whether the mean value for each protein (i.e., within each gray box in panel B) differed from 100% (using a one‐sample Student's t‐test). Comparisons with the DOX only condition (+DOX; marked “a”) and CAP‐only condition (+CAP; marked “b”) were performed using an independent two‐population t‐test (i.e., between each gray box for each protein). Not significant is marked by n.s.

Discussion

The primary aim of this study was to determine whether the mitochondrial matrix solvent displays macromolecular crowding. To this end, we studied the diffusional behavior of four inert monomeric FPs of increasing MW in the mitochondrial matrix of HeLa cells in the absence and presence of CAP. Mitochondrial FP fluorescence intensity per cell decreased as a function of concatemer MW (Fig 2C) and correlated well with in‐gel fluorescence signals (Fig 2D). This strongly suggests that the latter signals faithfully reflect the cellular situation and that AcGFP1 concatemers are not denatured during mitochondrial isolation. Similar to the current findings, the fluorescence signal and expression of nucleus‐targeted EGFP concatemers (containing up to 12 monomers) decreased as a function of MW in H1299 cells (Böhm et al, 2017). The latter study also demonstrated the presence of minor amounts of fluorescent degradation products of smaller MW. Similarly, expression of EGFP concatemers in Escherichia coli cytoplasm (containing up to eight monomers) was paralleled with the formation of degradation products of smaller MW (Nenninger et al, 2010). By contrast, FP concatemers of up to four EGFP molecules remained intact when expressed in the nucleus of HeLa cells (Dross et al, 2009), whereas concatemers of up to five EGFP molecules remained intact in the cytosol of HEK293 cells (Pack et al, 2006). Inspection of MW marker positions (Appendix Fig S1A and B) revealed that AcGFP1‐expressing cells contained a single fluorescent product with an estimated MW between 25 and 37 kDa (predicted: 29‐kDa; Table 1). The fluorescent product in AcGFP1²‐expressing cells displayed an MW between 37 and 50 kDa (predicted: 58‐kDa). For AcGFP1³ a product of 50–75 kDa was observed (predicted: 88‐kDa). In case of AcGFP1⁴ (predicted: 115‐kDa), two fluorescent products with MWs between 37 and 50 kDa (smaller product) and 75–100 kDa (larger product) were detected. With the exception of AcGFP1, these data highlight a discrepancy between the marker‐reported MW of the FPs and their predicted MW. This is probably due to the fact that the structural dimensions of the FPs, which co‐determine gel migration distance, scale differently with their MW than for the MW markers. Moreover, SDS binding to the various FPs might be different, since samples were not heated (to prevent FP fluorescence loss), thereby affecting their migration behavior. In this context, our SDS–PAGE analysis suggests that the smaller fluorescent product in AcGFP1⁴‐expressing cells is similar to AcGFP1². This might indicate that AcGFP1⁴, once imported in the mitochondrial matrix, is cleaved by a mitochondrial protease at the position of its 2^nd linker (DIPPHPAFLYKVVDDPPV; Appendix Table S1). However, an identical linker connected the 1^st and 2^nd AcGFP1 monomer within AcGFP1³ but no fluorescent breakdown product was detected. This suggests that the size and/or MW of AcGFP1⁴ is responsible for its partial breakdown within mitochondria, in both the presence and absence of CAP.

Viscosity of the mitochondrial matrix solvent in the absence of CAP

Analysis of AcGFP1 experiments predicted a D_solvent of 23.9 μm²/s (Fig 3E). This is within the range of previous FP‐employing FRAP and fluorescence correlation spectroscopy (FCS) studies (Partikian et al, 1998; Verkman, 2002; Koopman et al, 2007, 2008b; Dieteren et al, 2011a). Free EGFP in aqueous solution displayed a D_solvent value between 87 and 104 μm²/s (Appendix Table S2). This means that the D_solvent of AcGFP1 is between 3.6‐ and 4.4‐fold lower in the mitochondrial matrix than in aqueous solution. As a consequence, computed matrix η_solvent values were between 3.69 and 4.57 cP (Fig 4C), being three to five‐fold higher than pure water and similar to those observed previously in HEK293 cells (Dieteren et al, 2011a) and E. coli cytoplasm (Chen et al, 2018). In the literature, mitochondrial matrix viscosity was also analyzed using viscosity‐sensitive fluorescent rotor molecules (Xiao et al, 2021; Yin et al, 2021). In the case of HeLa cells, these studies reported heterogeneous and relatively high viscosity values between 20.7 and 275 cP (Yang et al, 2013; Jímenez‐Sánchez et al, 2018; Ren et al, 2018, 2020; Steinmark et al, 2019). Similarly, variable high mitochondrial viscosity values between < 100 and > 900 cP were reported in rat hepatic tissue slices (Liu et al, 2018), whereas COS7 cells displayed a viscosity value of 325 cP, measured with a BODIPY‐HaloTag rotor molecule targeted to mitochondria using the mitochondrial Cox8a targeting sequence (Chambers et al, 2018). It is currently unknown why the rotor‐based viscosity values exceed those reported in the current study and earlier FP‐based research (Partikian et al, 1998; Verkman, 2002; Koopman et al, 2007, 2008b; Dieteren et al, 2011a). Potentially, the observed discrepancy in cP values could be due to the BODIPY and/or TPP⁺‐containing part of the rotors displaying a (transient) physical or electrochemical interaction with the inside‐negative MIM. In this context, and to the best of our knowledge, there is currently no information regarding the translational mobility of these rotors in the mitochondrial matrix. Therefore, the rotor properties in the mitochondrial matrix might differ from those in solution, meaning that the viscosity reporting behavior of the sensor is altered (Puchkov, 2013; Chen et al, 2018). This hypothesis is supported by the observation that some of the rotor‐reported matrix viscosities are close to that of the MIM (i.e., 900–950 cP; Chazotte & Hackenbrock, 1988) and that a plasma membrane‐directed BODIPY‐based rotor‐reported viscosity values between 270 and 380 cP (Kubankova et al, 2019). This means that the rotor‐reported mitochondrial matrix viscosity values are similar to those of the plasma membrane, which is unrealistic. It was further argued that accurate viscosity analysis with BODIPY‐C₁₀‐based probes requires calibration in the same polarity environment as the sample of interest and that the size of the surrounding molecules should not exceed that of BODIPY‐C₁₀ (Polita et al, 2020). We here demonstrate that CAP‐induced impairment of mitochondrial function is associated with an eightfold increase in η_solvent (Fig 5G). Therefore, differences in rotor‐ and FP‐reported matrix viscosities might also be due to interstudy differences in mitochondrial functional state.

Evidence for matrix macromolecular crowding in the absence of CAP

Applying empirical relationships, we provided evidence that AcGFP1², AcGFP1³ and AcGFP1⁴ display an elongated (structurally extended) conformation in the mitochondrial matrix solvent (Fig 4C). Similarly, EGFP concatemers displayed an elongated structure in the nucleus and cytosol of HeLa cells (Pack et al, 2006; Dross et al, 2009). This is compatible with the behavior of single DNA molecules in nanochannels, which displayed an elongated structure at low crowding levels but, when exceeding a certain volume fraction of the crowding agent, condensed into a compact form (Zhang et al, 2009). Interestingly, analyzing the dependency of D_solvent on MW revealed a steeper linear decline for matrix‐targeted FPs, than for globular/elongated molecules in aqueous solution and elongated EGFP concatemers in the nucleus/cytoplasm of HeLa cells (Fig 4B). This means that the elongated structure of the matrix‐targeted FPs cannot fully explain the steeper decline. In addition, our BD modeling approach renders D_solvent cristae‐independent and both F_m and F_∞ increased as a function of MW (Table 1 and Fig 5F). Therefore, we conclude that matrix FP mobility is reduced by the combined impact of their elongated structure and macromolecular crowding. This latter probably is low level, since substantial crowding is associated with molecule compaction (Zhang et al, 2009; Kuznetzova et al, 2014).

CAP treatment slows solute diffusion and increases mitochondrial matrix viscosity

Triggered by our previous findings (see Results), cells were treated with CAP to increase the protein concentration of the matrix solvent. Although technical limitations prevented assessing D_solvent for AcGFP1², AcGFP1³, and AcGFP1⁴, analysis of AcGFP1 mobility demonstrated that CAP treatment eightfold decreased and increased D_solvent and η_solvent, respectively (Table 1 and Fig 5G). By itself, this viscosity increase is highly relevant, since it will slow down any diffusion‐limited process, including metabolite diffusion and macromolecular association/dissociation reactions (Van den Bogaart et al, 2007; Molines et al, 2022). Mitochondria in CAP‐treated cells displayed a progressive immobilization of AcGFP1² and AcGFP1³ (Fig 5D–F), contained three to five‐fold cristae and displayed a more electron‐dense matrix (Fig 5C). This strongly suggests that matrix macromolecular crowding is increased in CAP‐treated cells (Mika et al, 2010; Mittal et al, 2015; Delarue et al, 2018; Junker et al, 2019). Electron density analysis was performed on EM images of osmium tetroxide‐treated samples, which preferentially binds to unsaturated fatty acids (Belazi et al, 2009). However, it appears that osmium tetroxide also can react with proteins (e.g., Porter & Kallman, 1953) and that electron density increases when proteins with a relatively high affinity for this fixative are present (Bisht et al, 2016). In this context, it has been argued that differences in electron density of cryo‐electron tomograms can be interpreted as differences in macromolecular density and that mitochondrial matrices are expected to display a higher density than the surrounding cytoplasm (Ader et al, 2019). Therefore, we propose that the increased electron density in CAP‐treated cells (Fig 5C) represents a minor though significant increase in the concentration of soluble matrix macromolecules. This conclusion is supported by the fact that mitochondria in AcGFP1⁴‐expressing cells displayed a lower fluorescent signal (Fig 2B–D), as well as a less electron‐dense matrix relative to AcGFP1‐expressing cells (Fig 5C). Compatible with a previous study in CAP‐treated mouse embryonic fibroblasts (Sasaki et al, 2020), CAP‐treated HeLa cells lacked a detectable increase in proteinaceous UPR^mt‐linked markers (Figs EV2E and EV3). Although this suggests that the increase in matrix protein levels is relatively small, such an increase can substantially elevate macromolecular crowding levels due to the relatively small matrix volume.

CAP treatment does not induce mitochondrial orthodox‐to‐condensed transition

Classically, changes in matrix electron density are linked to alterations in mitochondrial bioenergetic state during mitochondrial “orthodox‐to‐condensed transition” (Hackenbrock, 1966, 1972). Orthodox mitochondria are characterized by a low OCR, Δψ hyperpolarization and a relatively large matrix volume, whereas condensed mitochondria display a high OCR and a relatively small matrix volume (Perkins & Ellisman, 2011). During orthodox‐to‐condensed transition, matrix volume decrease is accompanied by an increase in electron density without alterations in total mitochondrial volume (Hackenbrock, 1966). In CAP‐treated cells, mitochondria displayed functional properties typical of orthodox mitochondria (i.e., a low OCR and Δψ hyperpolarization; Fig EV2A–D) but a more electron‐dense (darker) matrix (typical of condensed mitochondria; Fig 5C). Although CAP did reduce the number of cristae, mitochondrial dimensions and volume were not detectably affected (Table 1). With respect to CAP‐induced Δψ hyperpolarization, we observed that mitochondrial TMRM fluorescence was increased, whereas nucleoplasmic TMRM fluorescence was decreased. Since TMRM accumulates in the cytoplasm and mitochondrial matrix according to the plasma membrane and MIM electrical potential, respectively, this suggests that Δψ is more negative (Koopman et al, 2008a). Similarly, CAP pretreatment (48 h) induced Δψ hyperpolarization in HepG2 cells, as reported by fluorescence analysis of mitochondrial DiOC₆ accumulation (Li et al, 2005). However, when the rotational motion of fluorescent molecules is impeded their fluorescence quantum yield might increase (Dragan et al, 2014; Vyšniauskas et al, 2015). Therefore, it cannot be ruled out that the increased mitochondrial TMRM fluorescence signal in CAP‐treated cells is due to a higher viscosity/crowding environment within the mitochondrial matrix. Taken together, our results indicate that CAP treatment might hyperpolarize Δψ and does not induce mitochondrial orthodox‐to‐condensed transition.

Predicting the degree of macromolecular crowding and volume exclusion in the mitochondrial matrix

As stated above, macromolecular crowding will reduce the translational mobility of solutes with a similar or larger size than the crowder to a greater extent than the mobility of smaller solutes. Therefore, to gain some theoretical insight into how CAP might quantitatively affect matrix crowding levels, we analyzed the predicted effect of human serum albumin (HSA) as a model crowding protein (Appendix Supplementary Results). HSA was selected because its MW (≈92‐kDa) is relatively close to that of the expected NDUFV1/NDUFV2 assembly intermediates, potentially acting as (co)crowders (see Results), and similar to the MW of AcGFP1³ (≈88‐kDa), which was demonstrated to be substantially immobilized in CAP‐treated cells. Using the obtained η_solvent values, and assuming that HSA is the sole crowding entity, it was predicted that HSA would occupy between ~20% (absence of CAP) and ~33% (presence of CAP) of the total mitochondrial matrix volume (Appendix Supplementary Results and Fig 6A). Obviously, the magnitude of this volume exclusion effect will increase with the number/size of the crowding macromolecules and with decreasing matrix volume.

Figure 6. Key results and interplay between mitochondrial (ultra)structure, matrix solvent macromolecular crowding/viscosity and mitochondrial function.

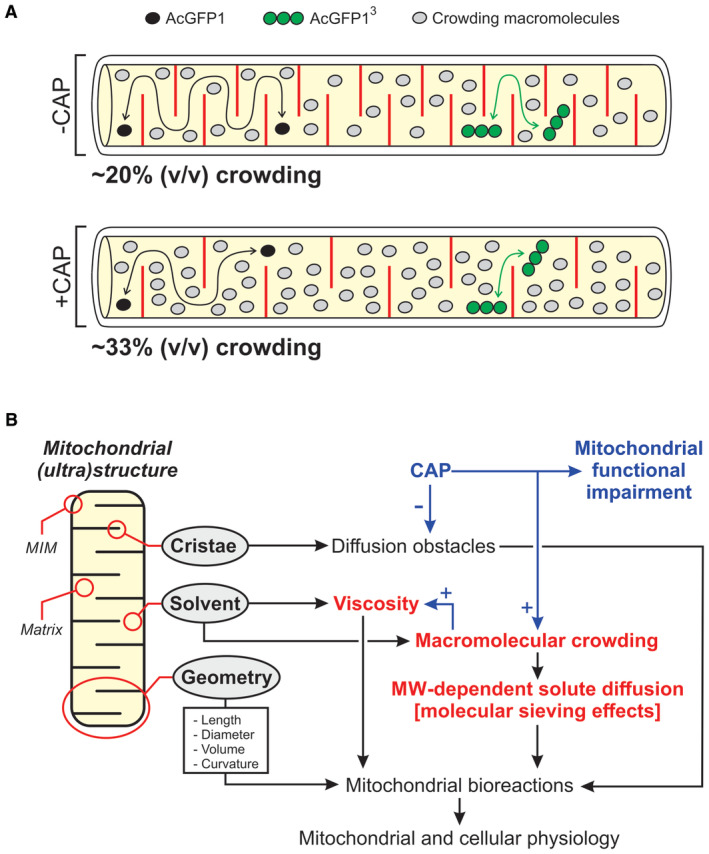
1. Graphical representation (not to scale) of the key results of this study, illustrating the hindrance effect of cristae (red lines) and crowding macromolecules (gray symbols) on the mobility of AcGFP1 (black symbols) and AcGFP1³ (green symbols) in the mitochondrial matrix (yellow). In the absence of chloramphenicol (−CAP), low levels of macromolecular crowding reduce the mobility of AcGFP1³ to a greater extent than the mobility of AcGFP1. In the presence of CAP (+CAP), the number of cristae is reduced but crowding is increased. This impedes the mobility of AcGFP1 and AcGFP³, although the latter is affected to a greater extent. In this panel, the number of crowding macromolecules approximately reflects the predicted maximal degree of crowding determined using human serum albumin (HSA) as a model crowder (see Discussion).
2. Integration of mitochondrial morphofunction. The mitochondrial matrix is surrounded by the mitochondrial inner membrane (MIM), which contains matrix‐protruding folds (cristae). Biochemical reactions in the mitochondrial matrix are affected by hindrance of solute diffusion by cristae, the physicochemical properties of the mitochondrial matrix solvent (e.g., viscosity) and the geometry of the mitochondrial compartment (e.g., volume). We here demonstrate that the mitochondrial matrix solvent can reduce the diffusion of fluorescent proteins in an MW‐dependent manner typical of macromolecular crowding. The latter appeared only minor during “normal” conditions but increased during CAP‐induced mitochondrial functional impairment. We propose that crowding‐induced molecular sieving effects, in combination with alterations in matrix solvent viscosity, impact on mitochondrial bioreactions and thereby on mitochondrial and cellular physiology.

Summary and conclusion

The results presented in this study support the conclusion that the mitochondrial matrix solvent displays macromolecular crowding phenomena, particularly during conditions of CAP‐induced mitochondrial dysfunction. In analogy to the cytosol (Delarue et al, 2018), it is therefore likely that (changes in) matrix crowding will induce molecular sieving effects that will affect matrix bioreactions dependent on the size of the involved crowding molecules and reactants. It is expected that macromolecular crowding will decrease the rate of diffusion‐limited, fast association reactions whereas it will increase this rate for slow, transition‐state‐limited association reactions (Zhou et al, 2008). Therefore, crowding impacts on complex formation, surface binding, aggregation and folding/compaction of matrix proteins and, via volume exclusion, on the diffusion and (local) concentration of metabolites, ions, and other small reactants (Minton, 1990; Yu et al, 2016; Andrews, 2020). Crowding‐induced effects on the Michaelis–Menten mechanism were predicted in silico (Weilandt & Hatzimanikatis, 2019) and demonstrated experimentally for the mitochondrial matrix enzymes malate hydrogenase (Poggi & Slade, 2015) and citrate synthase (Wilcox et al, 2020). We hypothesize that alterations in mitochondrial matrix crowding level, cristae number/architecture, and/or mitochondrial geometry exert control over mitochondrial bioreactions, which exemplifies the intricate link between mitochondrial (ultra)structure and function (Fig 6B). In this sense, the combined crowding and cristae‐induced hindrance of matrix Ca²⁺ diffusion might be involved in heterogeneous spreading of mitochondrial Ca²⁺ signals (Gerencser & Adam‐Vizi, 2005) and compartmentalization of matrix reaction networks (Kekenes‐Huskey et al, 2015).

Materials and Methods

Generation of inducible HeLa cell lines

HeLa T‐REx Flp‐in cell lines stably expressing mitochondria‐targeted concatemers of monomeric AcGFP1 (AcGFP¹, AcGFP1², AcGFP1³, and AcGFP1⁴) were generated as described in the Appendix Supplementary Methods and cultured at 37°C in a humid atmosphere (95% air, 5% CO₂). Expression of these fluorescent proteins (FPs) was induced by adding 1 μg/ml doxycycline (DOX) to the culture medium for 24 h. In certain experiments, cells were treated with 40 μg/ml chloramphenicol (CAP) for 72 h.

Mitochondrial staining and flow cytometry

Localization of the FPs and the mitochondrial marker MitoTracker Red CM‐H₂XROS was visualized using confocal microscopy. Flow cytometry was applied to analyze the cellular fluorescence intensity of the AcGFP1 concatemers and forward scatter. Details are provided in the Appendix Supplementary Methods.

Fluorescence recovery after photobleaching (FRAP) analysis

Mitochondrial FRAP experiments were performed as described previously (Dieteren et al, 2008, 2009, 2011a, 2011b). Details are provided in the Appendix Supplementary Methods.

Western blotting

Mitochondrial fractions or whole‐cell lysates were used for SDS–PAGE, in‐gel fluorescence analysis, and Western blotting as described in the Appendix Supplementary Methods.

Electron microscopy (EM)

Electron microscopy was performed as described previously (Koopman et al, 2008a). Details are provided in the Appendix Supplementary Methods.

Functional cell analysis

Oxygen consumption rates (OCR) and extracellular acidification rates (ECAR) were quantified using a Seahorse XFe96 flux Analyzer (Agilent, Santa Clara, CA, USA). Mitochondrial membrane potential (Δψ) was analyzed using the fluorescent cation TMRM (tetramethylrhodamine methyl ester). Mitochondrial DNA (mtDNA) copy number was quantified using real‐time quantitative PCR (qPCR) analysis. Details are provided in the Appendix Supplementary Methods.

Numerical simulations

A Brownian dynamics (BD) computer model was developed to determine the solvent‐dependent diffusion constant (D_solvent) of the AcGFP1 concatemers. This model was constrained by experimental data and implemented in GNU Fortran (https://gcc.gnu.org) under Ubuntu 20.04 LTS (https://releases.ubuntu.com). Details are provided in the Results section and in the Appendix Supplementary Methods.

Image analysis

Image visualization, processing, and quantification were carried out using Image Pro Plus software (Media Cybernetics, Rockville, MD, USA), Zeiss LSM 510 Meta software (Carl Zeiss AG, Oberkochen, Germany) and FIJI (https://imagej.net/Fiji).

Statistical analysis

Curve fitting and statistical analyses were performed using Origin Pro software (Originlab Corp., Northampton, MA, USA). Levenberg–Marquardt and least squares algorithms were used for nonlinear and linear regression, respectively. Average data were expressed as mean ± SEM (standard error of the mean), and significance was tested using an independent Student's t‐test unless stated otherwise.

Author contributions

Elianne P Bulthuis: Formal analysis; supervision; validation; investigation; visualization; writing – original draft; writing – review and editing. Cindy E J Dieteren: Formal analysis; supervision; funding acquisition; validation; investigation; visualization; writing – original draft; writing – review and editing. Jesper Bergmans: Data curation; investigation; writing – review and editing. Job Berkhout: Formal analysis; investigation. Jori A Wagenaars: Formal analysis; investigation; visualization. Els M A van de Westerlo: Formal analysis; supervision; investigation; visualization. Emina Podhumljak: Investigation. Mark A Hink: Resources; formal analysis; supervision; investigation; writing – original draft. Laura F B Hesp: Investigation. Hannah S Rosa: Formal analysis; investigation. Afshan N Malik: Formal analysis; supervision; investigation; writing – original draft. Mariska Kea‐te Lindert: Formal analysis; investigation; writing – original draft. Peter H G M Willems: Funding acquisition; writing – original draft. Han J G E Gardeniers: Writing – original draft; writing – review and editing. Wouter K den Otter: Conceptualization; resources; software; validation; visualization; methodology; writing – review and editing. Merel J W Adjobo‐Hermans: Conceptualization; supervision; validation; investigation; visualization; writing – original draft; writing – review and editing. Werner J H Koopman: Conceptualization; data curation; formal analysis; supervision; funding acquisition; validation; visualization; methodology; writing – original draft; project administration; writing – review and editing.

Disclosure and competing interests statement

WJHK is an ad hoc scientific advisor of Khondrion B.V. (Nijmegen, The Netherlands). This SME had no involvement in the data collection, analysis and interpretation, writing of the manuscript, and in the decision to submit the manuscript for publication.

Supporting information

Appendix

Expanded View Figures PDF

Source Data for Appendix

PDF+

The EMBO Journal (2023) 42: e108533

Data availability

Source data, materials, and computer code are available from the corresponding authors at reasonable request. All other data are contained in the main manuscript, Expanded View and Appendix. This study includes no data deposited in external repositories.