Multi-attribute decision-making based on novel Fermatean fuzzy similarity measure and entropy measure

Abstract

To deal with situations involving uncertainty, Fermatean fuzzy sets are more effective than Pythagorean fuzzy sets, intuitionistic fuzzy sets, and fuzzy sets. Applications for fuzzy similarity measures can be found in a wide range of fields, including clustering analysis, classification issues, medical diagnosis, etc. The computation of the weights of the criteria in a multi-criteria decision-making problem heavily relies on fuzzy entropy measurements. In this paper, we employ t-conorms to suggest various Fermatean fuzzy similarity measures. We have also discussed all of their interesting characteristics. Using the suggested similarity measurements, we have created some new entropy measures for Fermatean fuzzy sets. By using numerical comparison and linguistic hedging, we have established the superiority of the suggested similarity metrics and entropy measures over the existing measures in the Fermatean fuzzy environment. The usefulness of the proposed Fermatean fuzzy similarity measurements is shown by pattern analysis. Last but not least, a novel multi-attribute decision-making approach is described that tackles a significant flaw in the order preference by similarity to the ideal solution, a conventional approach to decision-making, in a Fermatean fuzzy environment.

Introduction

To solve problems involving uncertainty more precisely, a new notion known as the Pythagorean fuzzy set (PFS) was put forward by Yager (2013). PFS is a generalized version of fuzzy (Zadeh 1965) and intuitionistic fuzzy sets (Atanassov 1986) (IFSs). A membership $\left(\sigma \right)$ and a non-membership $\left(\varsigma \right)$ degree whose maximum square sum is one $\left({\sigma }^2,+,{\varsigma }^2,\le ,1\right)$ is assigned to each element in a PFS. The Pythagorean fuzzy number and the technique for order of preference by similarity to the ideal solution (TOPSIS) in a Pythagorean fuzzy (PF) environment were proposed by Zhang and Xu (2014). Yager (2014) provided several PF aggregating functions and their usefulness in decision-making. Wei and Lu (2018) developed some PF power aggregation functions. Garg (2016) suggested some new aggregating functions for the PF environment utilizing Einstein operations. Wei (2017) proposed many PF interaction aggregation functions and discussed their applicability to multi-attribute decision-making (MADM). The literature has numerous studies (Garg 2017; Lu et al. 2017; Wei et al. 2017; Wei and Lu 2017) on the PF aggregating functions and their applicability. The TODIM (multi-criteria decision-making in Portuguese) in the PF setting was developed by Ren et al. (2016). Many PF measures of information were proposed by Peng et al. (2017). A new PF distance metric was proposed by Peng and Dai (2017). Singh and Ganie (2020) developed a few PF metrics of correlation with their utility. PFSs have been examined and implemented by numerous researchers (Garg 2019a, b; Khan et al. 2019a, b; Akram and Ali 2020; Ejegwa 2020a, b; Rahman et al. 2020; Zhang et al. 2021; Olgun et al. 2021; Mishra et al. 2021; Zeb et al. 2022; Wang et al. 2022; Ganie 2022, 2023; Ganie et al. 2022; Akram and Bibi 2023; Ejegwa et al. 2023; Aldring and Ajay 2023; Kirişci 2023; Akram et al. 2023b; Akram et al. 2023a, c) in various uncertain situations. Chen and Chiou (2015) and Zeng et al. (2020) discussed the applicability of interval-valued IFSs to MADM problems. Although PFSs have many uses in a variety of domains, they are unable to handle circumstances where ${\sigma }^2+{\varsigma }^2>1$. For instance, if $\sigma =0.8$ and $\varsigma =0.7$, then ${\sigma }^2+{\varsigma }^2=1.13>1$. Senapati and Yager’s (2020) concept of Fermatean fuzzy sets was thus proposed (FFSs). We have ${\sigma }^3+{\varsigma }^3\le 1$ in a Fermatean fuzzy set (FFS). FFSs are more robust and effective than FSs, IFSs, and PFSs because these all fall in the space of FFSs. Senapati and Yager (2019) provided a list of FFS aggregation operators and their potential applications in decision-making. Mishra and Rani (2021) proposed the weighted aggregated sum product assessment (WASPAS) method in the Fermatean fuzzy (FF) environment. Keshavarz-Ghorabaee et al. (2020) presented an innovative FF decision-making approach. Garg et al. (2020) demonstrated the use of FF aggregating functions in the COVID-19 testing facility. The continuities and derivatives of FF functions were researched by Yang et al. (2021). Sergi and Sari (2021) suggested a few FF capital budgeting strategies. Sahoo (2021a, b) suggested a few score functions for FFSs and discussed their use in solving transportation-related problems and making decisions. Aydemir and Yilmaz (2020) introduced the FF TOPSIS technique. Some FF aggregating functions based on Einstein’s norm were proposed by Akram et al. (2020). There are some investigations of FFSs and their real-world applications in the literature (Salsabeela and John 2021; Aydın 2021; Gul et al. 2021; Hadi et al. 2021; Shit and Ghorai 2021; Rani and Mishra 2021; Akram et al. 2022, 2023d; Mishra et al. 2022a, b, 2023; Ali and Ansari 2022; Zhou et al. 2022; Luqman and Shahzadi 2023). The creation of several FF similarity and entropy measurements is discussed in this study.

Based on the content of equality, two things can be compared very effectively using similarity measurements. Zhang (2016) introduced a PF metric of similarity and applied it to a decision-making problem. Many novel PF measurements of distance and similarity were given by Peng (2019). Based on the cosine function, some PF measurements of similarity were proposed by Wei and Wei (2018). Mohd and Abdullah (2018) created several innovative PF similarity metrics by fusing the Euclidean distance measure with cosine similarity measures. By considering all three membership grades Ejegwa (2020a) presented many PF metrics of similarity and distance. The applicability of some PF metrics of similarity and distance in MADM was shown by Zeng et al. (2018). A Hausdorff PF similarity metric was suggested by Hussain and Yang (2019). Zhang et al. (2019) developed some exponential PF similarity metrics and showed how they may be used for pattern identification, MADM, and medical diagnostics. Li and Lu (2019) provided a few complement-based, matching function-based, and set theoretic-based PF similarity measurements. Wang et al. (2019) provided some PF Dice similarity measures with applications in decision-making. Some trigonometric function-based PF metrics of similarity were created by Verma and Merigo (2019). Peng and Garg (2019) highlighted how several multi-parametric PF measures of similarity can be used in classification challenges.

A PFS’s ambiguous content determines its entropy. In a MADM problem involving PF information, the attribute weights are computed using entropy measures. Xue et al. (2018) defined the entropy function for PFSs and its usage in decision-making. Yang and Hussain (2018) provided some probabilistic and nonprobabilistic PF entropy measurements. Thao and Smarandache (2019) introduced the CORPAS MADM approach in the PF environment with the use of a new PF entropy measure. Five FF entropy measurements were introduced by Mishra and Rani (2021).

The following are the main causes that motivated us to carry out this study.

• Several domains, including clustering, decision-making, pattern detection, etc., use fuzzy sets' similarity metrics and their various extensions. The FFS similarity measures, however, have not yet been properly investigated.

• The majority of the proposed formula-level fuzzy similarity metrics, both standard and non-standard, do not adhere to the axiomatic requirements. Thus, there is no technique that can be applied repeatedly to assess similarity.

• The five FF entropy measurements (Olgun et al. 2021) are worthless from the standpoint of linguistic hedging, and there is no standard method for creating the FF entropy measurements.

• The conventional MADM technique i.e., TOPSIS provides a compromise solution that is most similar to the PIS (positive ideal solution), but not the least similar to the NIS (negative ideal solution). So, a new decision-making method is desirable.

The contribution of this paper is given below:

• We suggest four metrics of similarity for FFSs along with their weighted equivalents.

• We suggest four metrics of entropy for FFSs using the suggested FF metrics of similarity.

• We contrast the performance of the proposed FF information measures with the available measures.

• We apply the FF similarity metrics in classification problems.

• We introduce an innovative decision-making method in the FF setting.

Section 2 of the paper is preliminary. Section 3 lists many unique FF similarity measurements along with desirable characteristics. A few similarity-based FF entropy measurements are introduced in Sect. 4. Section 5 displays a comparison of the proposed FF entropy and similarity metrics with the current FF/PF compatibility metrics. The use of the suggested similarity measures in pattern identification is illustrated in Sect. 6. In Sect. 7, a new MADM technique for the FF environment is proposed. The benefits and implications of the suggested FF similarity metrics, entropy measures, and the new MADM method are covered in Sect.  8. Section 9 provides the conclusion and recommendations for further research.

Preliminaries

Let $FFS(B)$ denote the collection of all FFSs of the universal set $B=\left\{b_1,,,b_2,,,\cdots ,,,b_p\right\}$.

Definition 1

(Yager 2013) A PFS $C_1$ in $B$ is defined as

$$C_1=\left\{\left(b_t,,,{\sigma }_{C_1},\left(b_t\right),,,{\varsigma }_{C_1},\left(b_t\right)\right),;,b_t,\in ,B\right\}.$$

Here, ${\sigma }_{C_1}\left(b_t\right)$ is the grade of membership and ${\varsigma }_{C_1}\left(b_t\right)$ is the grade of non-membership of the element $b_t$ in $C_1$ with the conditions that $0\le {\sigma }_{C_1}\left(b_t\right),{\varsigma }_{C_1}\left(b_t\right)\le 1$ and $0\le {\sigma }_{C_1}^2\left(b_t\right)+{\varsigma }_{C_1}^2\left(b_t\right)\le 1$. Further, ${\tau }_{C_1}\left(b_t\right)=\sqrt{1-{\sigma }_{C_1}^2\left(b_t\right)-{\varsigma }_{C_1}^2\left(b_t\right)}$ is the grade of the hesitancy of the element $b_t$ in $C_1$.

An example of a PFS is $C_1=\left\{\left(b_1,,,0.5,,,0.6\right),,,\left(b_2,,,0.1,,,0.3\right),,,\left(b_3,,,0.2,,,0.6\right)\right\}.$ Here, we see that ${\sigma }_{C_1}\left(b_1\right)+{\varsigma }_{C_1}\left(b_1\right)=0.5+0.6=1.1>1,$ but ${\sigma }_{C_1}^2\left(b_1\right)+{\varsigma }_{C_1}^2\left(b_1\right)=0.25+0.36=0.61<1$.

Definition 2

(Senapati and Yager 2020) An FFS $C_1$ in $B$ is defined as

$$C_1=\left\{\left(b_t,,,{\sigma }_{C_1},\left(b_t\right),,,{\varsigma }_{C_1},\left(b_t\right)\right),;,b_t,\in ,B\right\}.$$

Here, ${\sigma }_{C_1}\left(b_t\right)$ is the grade of membership and ${\varsigma }_{C_1}\left(b_t\right)$ is the grade of non-membership of the element $b_t$ in $C_1$ with the conditions that $0\le {\sigma }_{C_1}\left(b_t\right),{\varsigma }_{C_1}\left(b_t\right)\le 1$ and $0\le {\sigma }_{C_1}^3\left(b_t\right)+{\varsigma }_{C_1}^3\left(b_t\right)\le 1$. Further, ${\tau }_{C_1}\left(b_t\right)=\sqrt[3]{1-{\sigma }_{C_1}^3\left(b_t\right)-{\varsigma }_{C_1}^3\left(b_t\right)}$ is the grade of the hesitancy of the element $b_t$ in $C_1$.

An example of an FFS is $C_1=\left\{\left(b_1,,,0.2,,,0.4\right),,,\left(b_2,,,0.7,,,0.8\right),,,\left(b_3,,,0.6,,,0.5\right)\right\}$. Here, we see that ${\sigma }_{C_1}^2\left(b_2\right)+{\varsigma }_{C_1}^2\left(b_2\right)=0.49+0.64=1.13>1$, but ${\sigma }_{C_1}^3\left(b_1\right)+{\varsigma }_{C_1}^3\left(b_1\right)=0.343+0.512=0.855<1$.

Definition 3

(Senapati and Yager 2020) Let $C_1,C_2\in FFS(B)$, then some operations are listed below.

1. $C_1\cup C_2=\left\{\left(b_t,,,\max ,\left({\sigma }_{C_1},\left(b_t\right),,,{\sigma }_{C_2},\left(b_t\right)\right),,,\min ,\left({\varsigma }_{C_1},\left(b_t\right),,,{\varsigma }_{C_2},\left(b_t\right)\right)\right),;,b_t,\in ,B\right\}.$

2. $C_1\cap C_2=\left\{\left(b_t,,,\min ,\left({\sigma }_{C_1},\left(b_t\right),,,{\sigma }_{C_2},\left(b_t\right)\right),,,\max ,\left({\varsigma }_{C_1},\left(b_t\right),,,{\varsigma }_{C_2},\left(b_t\right)\right)\right),;,b_t,\in ,B\right\}.$

3. $C_1\subseteq C_2.$ iff ${\sigma }_{C_1}\left(b_t\right)\le {\sigma }_{C_2}\left(b_t\right)$ and ${\varsigma }_{C_1}\left(b_t\right)\ge {\varsigma }_{C_2}\left(b_t\right)\forall b_t\in B$.

4. ${\left(C_1\right)}^c=\left\{\left(b_t,,,{\varsigma }_{C_1},\left(b_t\right),,,{\sigma }_{C_1},\left(b_t\right)\right),;,b_t,\in ,B\right\}.$

For example, consider the two FFSs $C_1,C_2\in FFS\left(B\right)$ given as

$$C_1=\left\{\left(b_1,,,0.2,,,0.4\right),,,\left(b_2,,,0.6,,,0.8\right),,,\left(b_3,,,0.6,,,0.5\right)\right\},$$

$$C_2=\left\{\left(b_1,,,0.8,,,0.4\right),,,\left(b_2,,,0.7,,,0\right),,,\left(b_3,,,0.7,,,0.2\right)\right\}.$$

Then,

1. $C_1\cup C_2=\left\{\begin{array}{c}\left(b_1,,,\max ,\left(0.2,,,0.8\right),,,\min ,\left(0.4,,,0.4\right)\right),\left(b_2,,,\max ,\left(0.6,,,0.7\right),,,\min ,\left(0.8,,,0\right)\right),\\ \left(b_3,,,\max ,\left(0.6,,,0.7\right),,,\min ,\left(0.5,,,0.2\right)\right)\end{array}\right\}=\left\{\left(b_1,,,0.8,,,0.4\right),,,\left(b_2,,,0.7,,,0\right),,,\left(b_3,,,0.7,,,0.2\right)\right\}.$

2. $C_1\cap C_2=\left\{\begin{array}{c}\left(b_1,,,\min ,\left(0.2,,,0.8\right),,,\max ,\left(0.4,,,0.4\right)\right),\left(b_2,,,\min ,\left(0.6,,,0.7\right),,,\max ,\left(0.8,,,0\right)\right),\\ \left(b_3,,,\min ,\left(0.6,,,0.7\right),,,\max ,\left(0.5,,,0.2\right)\right)\end{array}\right\}=\left\{\left(b_1,,,0.2,,,0.4\right),,,\left(b_2,,,0.6,,,0.8\right),,,\left(b_3,,,0.6,,,0.5\right)\right\}.$

3. $C_1\subseteq C_2$ because ${\sigma }_{C_1}\left(b_t\right)\le {\sigma }_{C_2}\left(b_t\right)$ and ${\varsigma }_{C_1}\left(b_t\right)\ge {\varsigma }_{C_2}\left(b_t\right)\forall t=1,2,3$.

4. ${\left(C_1\right)}^c=\left\{\left(b_1,,,0.4,,,0.2\right),,,\left(b_2,,,0.8,,,0.6\right),,,\left(b_3,,,0.5,,,0.6\right)\right\}.$

Definition 4

(Peng et al. 2017) A PF similarity measure $S_{\mathrm{PF}}$ is a function $S_{\mathrm{PF}}:\mathrm{PFS}\left(B\right)\times \mathrm{PFS}\left(B\right)\to \left[0,,,1\right]$ such that $\forall C_1,C_2$ and $C_3\in \mathrm{PFS}\left(B\right)$,

1. $0\le S_{\mathrm{PF}}\left(C_1,,,C_2\right)\le 1$.

2. $S_{\mathrm{PF}}\left(C_1,,,C_2\right)=S_{\mathrm{PF}}\left(C_2,,,C_1\right)$.

3. $S_{\mathrm{PF}}\left(C_1,,,C_2\right)=1$ iff $C_1=C_2$.

4. $S_{\mathrm{PF}}\left(C_1,,,{\left(C_1\right)}^c\right)=0$ iff $C_1$ is a crisp set, where $c$ denotes the complement.

5. If $C_1\subseteq C_2\subseteq C_3$, then $S_{\mathrm{PF}}\left(C_1,,,C_2\right)\ge S_{\mathrm{PF}}\left(C_1,,,C_3\right)$ and $S_{\mathrm{PF}}\left(C_2,,,C_3\right)\ge S_{\mathrm{PF}}\left(C_1,,,C_3\right)$.

An example of a PF similarity measure is given below:

$$S_{\mathrm{PF}}\left(C_1,,,C_2\right)=1-\frac{1}{2p}\sum _{t=1}^p\left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,+,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|,+,\left|{\tau }_{C_1}^2,\left(b_t\right),-,{\tau }_{C_2}^2,\left(b_t\right)\right|\right).$$

Definition 5

(Peng et al. 2017) A PF distance measure $D_{\mathrm{PF}}$ is a function $D_{\mathit{PF}}:\mathrm{PFS}\left(B\right)\times \mathrm{PFS}\left(B\right)\to \left[0,,,1\right]$ such that $\forall C_1,C_2$ and $C_3\in PFS\left(B\right)$,

1. $0\le D_{\mathit{PF}}\left(C_1,,,C_2\right)\le 1$.

2. $D_{\mathrm{PF}}\left(C_1,,,C_2\right)=D_{\mathrm{PF}}\left(C_2,,,C_1\right)$.

3. $D_{\mathrm{PF}}\left(C_1,,,C_2\right)=0$ iff $C_1=C_2$.

4. $D_{\mathrm{PF}}\left(C_1,,,{\left(C_1\right)}^c\right)=1$ iff $C_1$ is a crisp set, where $c$ denotes the complement.

5. If $C_1\subseteq C_2\subseteq C_3$, then $D_{\mathit{PF}}\left(C_1,,,C_2\right)\le D_{\mathit{PF}}\left(C_1,,,C_3\right)$ and $D_{\mathit{PF}}\left(C_2,,,C_3\right)\le D_{\mathrm{PF}}\left(C_1,,,C_3\right)$.

An example of a PF similarity measure is given below:

$$D_{\mathit{PF}}\left(C_1,,,C_2\right)=\frac{1}{2p}\sum _{t=1}^p\left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,+,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|,+,\left|{\tau }_{C_1}^2,\left(b_t\right),-,{\tau }_{C_2}^2,\left(b_t\right)\right|\right).$$

Definition 6

(Mishra and Rani 2021) An FF entropy measure $E_{\mathrm{FF}}$ is a function $E_{\mathrm{FF}}:\mathrm{FFS}\left(B\right)\to \left[0,,,1\right]$ such that $\forall C_1,C_2$ and $C_3\in \mathrm{FFS}\left(B\right)$,

1. $0\le E_{\mathrm{FF}}\left(C_1\right)\le 1$

2. $E_{\mathrm{FF}}\left(C_1\right)=0$iff $C_1$ is a crisp set.

3. $E_{\mathrm{FF}}\left(C_1\right)=1$ iff ${\sigma }_{C_1}\left(b_t\right)={\varsigma }_{C_1}\left(b_t\right)\forall b_t\in B$.

4. $E_{\mathrm{FF}}\left(C_1\right)=E_{\mathrm{FF}}\left({\left(C_1\right)}^c\right)$ where $c$ denotes the complement.

5. $E_{\mathrm{FF}}\left(C_1\right)\le E_{\mathrm{FF}}\left(C_2\right)$, if ${\sigma }_{C_1}\left(b_t\right)\le {\sigma }_{C_2}\left(b_t\right)\le {\varsigma }_{C_2}\left(b_t\right)\le {\varsigma }_{C_1}\left(b_t\right)$ or ${\sigma }_{C_1}\left(b_t\right)\ge {\sigma }_{C_2}\left(b_t\right)$ $\ge {\varsigma }_{C_2}\left(b_t\right)\ge {\varsigma }_{C_1}\left(b_t\right)\forall b_t\in B$.

An example of FF entropy is given below:

$$E_{\mathrm{FF}}\left(C_1\right)=\frac{1}{\left(\sqrt{2},-,1\right)p}\sum _{t=1}^p\left(\cos ,\left(\frac{\pi \left(1,+,{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right)}{4}\right),+,\cos ,\left(\frac{\pi \left(1,-,{\sigma }_{C_1}^3,\left(b_t\right),+,{\varsigma }_{C_1}^3,\left(b_t\right)\right)}{4}\right),-,1\right).$$

Definition 7

(Weber 1983) A t-conorm is a function $h:\left[0,1\right]\times \left[0,1\right]\to \left[0,1\right]$ if $\forall i,j,k,l\in \left[0,1\right]$

1. $h\left(i,,,j\right)=h\left(j,,,i\right)$.

2. $h\left(i,,,j\right)\le h\left(k,,,l\right),$ whenever $i\le k$ and $j\le l$.

3. $h\left(i,,,0\right)=i$.

4. $h\left(i,,,h,\left(j,,,k\right)\right)=h\left(h,\left(i,,,j\right),,,k\right)$.

An example of a t-conorm is $h\left(b_1,,,b_2\right)=\frac{b_1+b_2-2b_1{b}_2}{1-b_1{b}_2}$.

We offer some innovative similarity measures for FFSs along with their characteristics in the following section.

New Fermatean fuzzy similarity measures

Here, we suggest a few FF similarity measurements. A similarity metric is first defined in the FF environment.

Definition 8

An FF similarity measure $S_{\mathrm{FF}}$ is a function $S_{\mathrm{FF}}:\mathrm{FFS}\left(B\right)\times \mathrm{FFS}\left(B\right)\to \mathbb{R}$ such that $\forall C_1,C_2$ and $C_3\in \mathrm{FFS}\left(B\right)$:

1. $0\le S_{\mathrm{FF}}\left(C_1,,,C_2\right)\le 1$.

2. $S_{\mathrm{FF}}\left(C_1,,,C_2\right)=S_{\mathrm{FF}}\left(C_2,,,C_1\right)$.

3. $S_{\mathrm{FF}}\left(C_1,,,C_2\right)=1$ iff $C_1=C_2$.

4. $S_{\mathrm{FF}}\left(C_1,,,{\left(C_1\right)}^c\right)=0$ iff $C_1$ is a crisp set, where $c$ denotes the complement.

5. If $C_1\subseteq C_2\subseteq C_3$, then $S_{\mathrm{FF}}\left(C_1,,,C_2\right)\ge S_{\mathrm{FF}}\left(C_1,,,C_3\right)$ and $S_{\mathit{FF}}\left(C_2,,,C_3\right)\ge S_{\mathrm{FF}}\left(C_1,,,C_3\right)$.

We now present a novel technique for deriving FF similarity metrics from t-conorms.

Definition 9

For $C_1,C_2\in \mathrm{FFS}\left(B\right),$ let $S_G:\mathrm{FFS}\left(B\right)\times \mathrm{FFS}\left(B\right)\to \mathbb{R}$ be a function defined as

$$S_G\left(C_1,,,C_2\right)=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right).$$ 1

Here, $h$ is a t-conorm.

Theorem 1

$S_G$ in Eq.  ( 1 ) is a valid measure of similarity for FFSs.

Proof

We will establish that $S_G$ satisfies the characteristic of a metric of similarity for FFSs listed in Definition 8.

(SM1) It is obvious.

(SM2) $S_G\left(C_1,,,C_2\right)=S_G\left(C_2,,,C_1\right)$ follows from the definition of $S_G$.

(SM3) $S_G\left(C_1,,,C_2\right)=1⟺h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)=0\forall t,$ $⟺\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|=0$ and $\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|=0\forall t$, $⟺{\sigma }_{C_1}^3\left(b_t\right)={\sigma }_{C_2}^3\left(b_t\right)$ and ${\varsigma }_{C_1}^3\left(b_t\right)={\varsigma }_{C_2}^3\left(b_t\right)\forall t$, $⟺C_1=C_2$.

(SM4) $S_G\left(C_1,,,{\left(C_1\right)}^c\right)=0⟺h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_1}^3,\left(b_t\right)\right|\right)=1\forall t,$ $⟺\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|=1$ and $\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_1}^3,\left(b_t\right)\right|=1\forall t$, $⟺\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|=1\forall t$, $⟺{\sigma }_{C_1}^3\left(b_t\right)=1$ and ${\varsigma }_{C_1}^3\left(b_t\right)=0$ or ${\sigma }_{C_1}^3\left(b_t\right)=0$ and ${\varsigma }_{C_1}^3\left(b_t\right)=1\forall t,$ $⟺{\sigma }_{C_1}\left(b_t\right)=1$ and ${\varsigma }_{C_1}\left(b_t\right)=0$ or ${\sigma }_{C_1}\left(b_t\right)=0$ and ${\varsigma }_{C_1}\left(b_t\right)=1\forall t,$ $⟺C_1$ is a crisp set.

(SM5) Let $C_1\subseteq C_2\subseteq C_3$, then ${\sigma }_{C_1}^3\left(b_t\right)\le {\sigma }_{C_2}^3\left(b_t\right)\le {\sigma }_{C_3}^3\left(b_t\right)$ and ${\varsigma }_{C_1}^3\left(b_t\right)\ge {\varsigma }_{C_2}^3\left(b_t\right)\ge {\varsigma }_{C_3}^3\left(b_t\right)\forall t$. Then, we have

$$\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\le \left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_3}^3,\left(b_t\right)\right|,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\le \left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_3}^3,\left(b_t\right)\right|,$$

and

$$\left|{\sigma }_{C_2}^3,\left(b_t\right),-,{\sigma }_{C_3}^3,\left(b_t\right)\right|\le \left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_3}^3,\left(b_t\right)\right|,\left|{\varsigma }_{C_2}^3,\left(b_t\right),-,{\varsigma }_{C_3}^3,\left(b_t\right)\right|\le \left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_3}^3,\left(b_t\right)\right|.$$

So, $h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)\le h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_3}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_3}^3,\left(b_t\right)\right|\right)$ and

$$h\left(\left|{\sigma }_{C_2}^3,\left(b_t\right),-,{\sigma }_{C_3}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_2}^3,\left(b_t\right),-,{\varsigma }_{C_3}^3,\left(b_t\right)\right|\right)\le h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_3}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_3}^3,\left(b_t\right)\right|\right).$$

Thus $S_G\left(C_1,,,C_2\right)\ge S_G\left(C_1,,,C_3\right)$ and $S_G\left(C_2,,,C_3\right)\ge S_G\left(C_1,,,C_3\right)$. Hence, $S_G$ is a similarity measure for FFSs.

Theorem 2

The measure of similarity $S_G$ in Eq. (1) possesses the following characteristics.

1. $S_G\left({\left(C_1\right)}^c,,,{\left(C_2\right)}^c\right)=S_G\left(C_1,,,C_2\right)\forall C_1,C_2\in \mathrm{FFS}\left(B\right)$.

2. $S_G\left(C_1,,,{\left(C_2\right)}^c\right)=S_G\left({\left(C_1\right)}^c,,,C_2\right)\forall C_1,C_2\in \mathrm{FFS}\left(B\right)$.

3. $S_G\left(C_1,,,{\left(C_1\right)}^c\right)=1$ if and only if ${\sigma }_{C_1}\left(b_t\right)={\varsigma }_{C_1}\left(b_t\right)\forall t$.

4. $S_G\left(C_1,\cap ,C_2,,,C_2\right)\ge S_G\left(C_1,,,C_2\right)$, for every $C_1,C_2\in \mathrm{FFS}\left(B\right)$.

5. $S_G\left(C_1,\cup ,C_2,,,C_2\right)\ge S_G\left(C_1,,,C_2\right)$, for every $C_1,C_2\in \mathrm{FFS}\left(B\right)$.

Proof 1. $S_G\left({\left(C_1\right)}^c,,,{\left(C_2\right)}^c\right)=1-\frac{1}{p}{\sum }_{t=1}^{p}h\left(\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\right)$

$$=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

$$=S_G\left(C_1,,,C_2\right).$$

2. $S_G\left(C_1,,,{\left(C_2\right)}^c\right)=1-\frac{1}{p}{\sum }_{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\right)$

$$=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

$$=S_G\left({\left(C_1\right)}^c,,,C_2\right)$$

3.

$$S_G\left(C_1,,,{\left(C_1\right)}^c\right)=1⟺1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_1}^3,\left(b_t\right)\right|\right)=1$$

$$⟺h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_1}^3,\left(b_t\right)\right|\right)=0\forall t$$

$⟺\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|=0$ and $\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_1}^3,\left(b_t\right)\right|=0\forall t$

$$⟺\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|=0\forall t$$

$$⟺{\sigma }_{C_1}^3\left(b_t\right)={\varsigma }_{C_1}^3\left(b_t\right)\forall t$$

$$⟺{\sigma }_{C_1}\left(b_t\right)={\varsigma }_{C_1}\left(b_t\right)\forall t.$$

4. $S_G\left(C_1,\cap ,C_2,,,C_2\right)=1-\frac{1}{p}{\sum }_{t=1}^{p}h\left(\begin{array}{c}\left|m,i,n,\left({\sigma }_{C_1}^3,\left(b_t\right),,,{\sigma }_{C_2}^3,\left(b_t\right)\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,\\ \left|m,a,x,\left({\varsigma }_{C_1}^3,\left(b_t\right),,,{\varsigma }_{C_2}^3,\left(b_t\right)\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\end{array}\right)$.

Now, there are the following cases:

1. When ${\sigma }_{C_1}\left(b_t\right)\ge {\sigma }_{C_2}\left(b_t\right)$ and ${\varsigma }_{C_1}\left(b_t\right)\ge {\varsigma }_{C_2}\left(b_t\right)\forall t$, then

   $$S_G\left(C_1,\cap ,C_2,,,C_2\right)=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_2}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$=1-\frac{1}{p}\sum _{t=1}^{p}h\left(0,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$\ge 1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$=S_G\left(C_1,,,C_2\right).$$
2. When ${\sigma }_{C_1}\left(b_t\right)\ge {\sigma }_{C_2}\left(b_t\right)$ and ${\varsigma }_{C_1}\left(b_t\right)\le {\varsigma }_{C_2}\left(b_t\right)\forall t$, then

   $$S_G\left(C_1,\cap ,C_2,,,C_2\right)=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_2}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_2}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$=1-\frac{1}{p}\sum _{t=1}^{p}h\left(0,,,0\right)=1\ge S_G\left(C_1,,,C_2\right).$$
3. When ${\sigma }_{C_1}\left(b_t\right)\le {\sigma }_{C_2}\left(b_t\right)$ and ${\varsigma }_{C_1}\left(b_t\right)\ge {\varsigma }_{C_2}\left(b_t\right)\forall t$, then

   $$S_G\left(C_1,\cap ,C_2,,,C_2\right)=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)=S_G\left(C_1,,,C_2\right).$$
4. When ${\sigma }_{C_1}\left(b_t\right)\le {\sigma }_{C_2}\left(b_t\right)$ and ${\varsigma }_{C_1}\left(b_t\right)\le {\varsigma }_{C_2}\left(b_t\right)\forall t$, then

   $$S_G\left(C_1,\cap ,C_2,,,C_2\right)=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_2}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,0\right)$$

   $$\ge 1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$=S_G\left(C_1,,,C_2\right).$$

5. $S_G\left(C_1,\cup ,C_2,,,C_2\right)=1-\frac{1}{p}{\sum }_{t=1}^{p}h\left(\begin{array}{c}\left|\max ,\left({\sigma }_{C_1}^3,\left(b_t\right),,,{\sigma }_{C_2}^3,\left(b_t\right)\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,\\ \left|\min ,\left({\varsigma }_{C_1}^3,\left(b_t\right),,,{\varsigma }_{C_2}^3,\left(b_t\right)\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\end{array}\right)$.

Now, there are the following cases:

1. When ${\sigma }_{C_1}\left(b_t\right)\ge {\sigma }_{C_2}\left(b_t\right)$ and ${\varsigma }_{C_1}\left(b_t\right)\ge {\varsigma }_{C_2}\left(b_t\right)\forall t$, then

   $$S_G\left(C_1,\cup ,C_2,,,C_2\right)=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_2^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,0\right)$$

   $$\ge 1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$=S_G\left(C_1,,,C_2\right).$$
2. When ${\sigma }_{C_1}\left(b_t\right)\ge {\sigma }_{C_2}\left(b_t\right)$ and ${\varsigma }_{C_1}\left(b_t\right)\le {\varsigma }_{C_2}\left(b_t\right)\forall t$, then

   $$S_G\left(C_1,\cup ,C_2,,,C_2\right)=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)=S_G\left(C_1,,,C_2\right).$$
3. When ${\sigma }_{C_1}\left(b_t\right)\le {\sigma }_{C_2}\left(b_t\right)$ and ${\varsigma }_{C_1}\left(b_t\right)\ge {\varsigma }_{C_2}\left(b_t\right)\forall t$, then

   $$S_G\left(C_1,\cup ,C_2,,,C_2\right)=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_2}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_2}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$=1-\frac{1}{p}\sum _{t=1}^{p}h\left(0,,,0\right)=1\ge S_G\left(C_1,,,C_2\right).$$
4. When ${\sigma }_{C_1}\left(b_t\right)\le {\sigma }_{C_2}\left(b_t\right)$ and ${\varsigma }_{C_1}\left(b_t\right)\le {\varsigma }_{C_2}\left(b_t\right)\forall t$, then

   $$S_G\left(C_1,\cup ,C_2,,,C_2\right)=1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_2}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$=1-\frac{1}{p}\sum _{t=1}^{p}h\left(0,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$\ge 1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right)$$

   $$=S_G\left(C_1,,,C_2\right).$$

Example 1

Table 1 provides some examples of FF similarity measurements.

Table 1.

FF similarity measurements

t-Conorms	FF similarity measures
$h\left(b_1,,,b_2\right)=\frac{b_1+b_2-2b_1{b}_2}{1-b_1{b}_2}$	$S_{G1}\left(C_1,,,C_2\right)=1-\frac{1}{p}{\sum }_{t=1}^p\left[\frac{\begin{array}{c}\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|+\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\\ -2\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\end{array}}{1-\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|}\right]$
$h\left(b_1,,,b_2\right)=b_1+b_2-b_1{b}_2$	$S_{G2}\left(C_1,,,C_2\right)=1-\frac{1}{p}{\sum }_{t=1}^p\left[\begin{array}{c}\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|+\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\\ -\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\end{array}\right]$
$h\left(b_1,,,b_2\right)=\min \left(1,,,b_1,+,b_2\right)$	$S_{G3}\left(C_1,,,C_2\right)=1-\frac{1}{p}{\sum }_{t=1}^p\min \left(\begin{array}{c}1,\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\\ +\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\end{array}\right)$
$h\left(b_1,,,b_2\right)=\frac{b_1+b_2}{1+b_1{b}_2}$	$S_{G4}\left(C_1,,,C_2\right)=1-\frac{1}{p}{\sum }_{t=1}^p\left[\frac{\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|+\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|}{1+\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|}\right].$

Next, we construct the weighted metrics of similarity for FFSs.

Definition 10

For $C_1,C_2\in \mathrm{FFS}\left(B\right),$ let the function $S_G^W:\mathrm{FFS}\left(B\right)\times \mathrm{FFS}\left(B\right)\to \mathbb{R}$ be defined as

$$S_G^W\left(C_1,,,C_2\right)=1-\frac{1}{p}\sum _{t=1}^p{w}_{t}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\right),$$ 2

where $h$ is a t-conorm.

Theorem 2

$S_G^W$ given in Eq. (1) is a valid weighted measure of similarity for FFSs.

Proof

Same as Theorem 1.

Example 2

Table 2 provides some examples of weighted FF similarity measurements.

Table 2.

Some examples of weighted FF similarity measurements

t-Conorms	FF-weighted similarity measures
$h\left(b_1,,,b_2\right)=\frac{b_1+b_2-2b_1{b}_2}{1-b_1{b}_2}$	$S_{G1}^W\left(C_1,,,C_2\right)=1-\frac{1}{p}{\sum }_{t=1}^p{w}_t\left[\frac{\begin{array}{c}\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|+\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\\ -2\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\end{array}}{1-\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|}\right]$
$h\left(b_1,,,b_2\right)=b_1+b_2-b_1{b}_2$	$S_{G2}^W\left(C_1,,,C_2\right)=1-\frac{1}{p}{\sum }_{t=1}^p{w}_t\left[\begin{array}{c}\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|+\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\\ -\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\end{array}\right]$
$h\left(b_1,,,b_2\right)=min\left(1,,,b_1,+,b_2\right)$	$S_{G3}^W\left(C_1,,,C_2\right)=1-\frac{1}{p}{\sum }_{t=1}^p{w}_{t}min\left(\begin{array}{c}1,\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\\ +\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|\end{array}\right)$
$h\left(b_1,,,b_2\right)=\frac{b_1+b_2}{1+b_1{b}_2}$	$S_{G4}^W\left(C_1,,,C_2\right)=1-\frac{1}{p}{\sum }_{t=1}^p{w}_t\left[\frac{\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|+\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|}{1+\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\sigma }_{C_2}^3,\left(b_t\right)\right|\left|{\varsigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|}\right].$

Some similarity-based metrics of entropy for FFSs are given in the next section.

Entropy measures based on FF similarity measures

The degree of ambiguity in an FFS is determined using the entropy measures. In this section, we present a technique for creating FF entropy measurements using FF similarity measures.

Definition 11

For $C_1\in \mathrm{FFS}\left(B\right)$, let the function $E_G:FFS\left(B\right)\to \left[0,,,1\right]$ be defined as

$$E_G\left(C_1\right)=S_G\left(C_1,,,{\left(C_1\right)}^c\right),$$ 3

with $S_G$ a similarity measure of FFSs.

Theorem 3

$E_G$ in Eq. (3) is a valid measure of entropy for FFSs.

Proof

We demonstrate that the function $E_G$ has the characteristics of an FF measure of entropy listed in Definition 6.

(EM1) It is obvious as $0\le S_G\left(C_1,,,{\left(C_1\right)}^c\right)\le 1$.

(EM2) $E_G\left(C_1\right)=0⟺S_G\left(C_1,,,{\left(C_1\right)}^c\right)⟺C_1$ is a crisp set.

(EM3) $E_G\left(C_1\right)=1⟺S_G\left(C_1,,,{\left(C_1\right)}^c\right)=1⟺{\sigma }_{C_1}\left(b_t\right)={\varsigma }_{C_2}\left(b_t\right)\forall t$.

(EM4) $E_G{\left(C_1\right)}^c=E_G\left(C_1\right)$ follows by the definition of $E_G$.

(EM5) Consider $C_1$ to be less fuzzy than $C_2$, i.e., ${\sigma }_{C_1}\left(b_t\right)\le {\sigma }_{C_2}\left(b_t\right)\le {\varsigma }_{C_2}\left(b_t\right)\le {\varsigma }_{C_1}\left(b_t\right)$ or ${\sigma }_{C_1}\left(b_t\right)\ge {\sigma }_{C_2}\left(b_t\right)$ $\ge {\varsigma }_{C_2}\left(b_t\right)\ge {\varsigma }_{C_1}\left(b_t\right).$

When ${\sigma }_{C_1}\left(b_t\right)\le {\sigma }_{C_2}\left(b_t\right)\le {\varsigma }_{C_2}\left(b_t\right)\le {\varsigma }_{C_1}\left(b_t\right)$, we have $\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|\ge \left|{\sigma }_{C_2}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|$. So, $S_G\left(C_1,,,{\left(C_1\right)}^c\right)=1-\frac{1}{p}{\sum }_{t=1}^{p}h\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|,,,\left|{{\varsigma }_{C_1}^3\left(b_t\right)-\sigma }_{C_1}^3,\left(b_t\right)\right|\right)$

$$\le 1-\frac{1}{p}\sum _{t=1}^{p}h\left(\left|{\sigma }_{C_2}^3,\left(b_t\right),-,{\varsigma }_{C_2}^3,\left(b_t\right)\right|,,,\left|{{\varsigma }_{C_2}^3\left(b_t\right)-\sigma }_{C_2}^3,\left(b_t\right)\right|\right)=S_G\left(C_2,,,{\left(C_2\right)}^c\right).$$

Thus, $E_G\left(C_1\right)\le E_G\left(C_2\right)$.

Similarly, for ${\sigma }_{C_1}\left(b_t\right)\ge {\sigma }_{C_2}\left(b_t\right)$ $\ge {\varsigma }_{C_2}\left(b_t\right)\ge {\varsigma }_{C_1}\left(b_t\right)$, we have $E_G\left(C_1\right)\le E_G\left(C_2\right)$. Hence, $E_G$ in Eq. (3) is a valid measure of entropy for FFSs.

Some FF measurements of entropy are provided in Table 3 below using Eq. (3) and the recommended FF measures of similarity.

Table 3.

Some examples of FF entropy measures

Recommended FF similarity measures	FF entropy measures
$S_{G1}$	$E_{G1}\left(C_1\right)=1-\frac{1}{p}{\sum }_{t=1}^p\frac{2\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|,-,{\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|}^2\right)}{1-{\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|}^2}$
$S_{G2}$	$E_{G2}\left(C_1\right)=1-\frac{1}{p}{\sum }_{t=1}^{p}2\left(\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|,-,{\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|}^2\right)$
$S_{G3}$	$E_{G3}\left(C_1\right)=1-\frac{1}{p}{\sum }_{t=1}^{p}min\left(1,,,2,\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|\right)$
$S_{G4}$	$E_{G4}\left(C_1\right)=1-\frac{1}{p}{\sum }_{t=1}^p\frac{2\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|}{1+{\left|{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right|}^2}$

Now, we contrast several existing PF/FF measures of information with the suggested FF measures of similarity and entropy.

Comparative analysis

In this part, we demonstrate that the proposed FF measures of similarity and entropy outperform the majority of existing PF/FF measures of information in terms of accuracy.

Comparability of the proposed metrics of similarity for FFSs with the several available metrics

For comparability, we first recall the available metrics of distance and similarity. These are shown in Tables 4 and 5 respectively.

Table 4.

Some existing PF measures of similarity (Peng et al. 2017)

Similarity measure	Expression
$S_1\left(C_1,,,C_2\right)$	$1-\frac{1}{2p}{\sum }_{t=1}^p\left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,+,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|,+,\left|{\tau }_{C_1}^2,\left(b_t\right),-,{\tau }_{C_2}^2,\left(b_t\right)\right|\right)$
$S_2\left(C_1,,,C_2\right)$	$1-\frac{1}{2p}{\sum }_{t=1}^p\left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right),-,\left({\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right)\right|\right)$
$S_3\left(C_1,,,C_2\right)$	$1-\frac{1}{4p}\left[\begin{array}{c}{\sum }_{t=1}^p\left(\begin{array}{c}\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|+\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\\ +\left|{\tau }_{C_1}^2,\left(b_t\right),-,{\tau }_{C_2}^2,\left(b_t\right)\right|\end{array}\right)\\ +{\sum }_{t=1}^p\left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right),-,\left({\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right)\right|\right)\end{array}\right]$
$S_4\left(C_1,,,C_2\right)$	$1-\frac{1}{p}{\sum }_{t=1}^p\max \left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\right)$
$S_5\left(C_1,,,C_2\right)$	$\frac{1}{p}{\sum }_{t=1}^p\frac{1-\max \left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\right)}{1+\max \left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\right)}$
$S_6\left(C_1,,,C_2\right)$	$\frac{{\sum }_{t=1}^{p}1-\max \left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\right)}{{\sum }_{t=1}^{p}1+\max \left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\right)}$
$S_7\left(C_1,,,C_2\right)$	$x\frac{{\sum }_{t=1}^p\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)}{{\sum }_{t=1}^p\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)}+y\frac{{\sum }_{t=1}^p\min \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}{{\sum }_{t=1}^p\max \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)},x+y=,x,y\in \left[0,1\right]$
$S_8\left(C_1,,,C_2\right)$	$\frac{x}{p}{\sum }_{t=1}^p\frac{\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)}{\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)}+\frac{y}{p}{\sum }_{t=1}^p\frac{\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)}{\max \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)},x+y=,x,y\in \left[0,1\right]$
$S_9\left(C_1,,,C_2\right)$	$\frac{1}{p}{\sum }_{t=1}^p\frac{\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\min \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}{\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\max \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}$
$S_{10}\left(C_1,,,C_2\right)$	$\frac{{\sum }_{t=1}^p\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\min \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}{{\sum }_{t=1}^p\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\max \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}$
$S_{11}\left(C_1,,,C_2\right)$	$\frac{1}{p}{\sum }_{t=1}^p\frac{\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\min \left(1,-,{\varsigma }_{C_1}^2,\left(b_t\right),,,{1-\varsigma }_{C_2}^2,\left(b_t\right)\right)}{\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\max \left({1-\varsigma }_{C_1}^2,\left(b_t\right),,,{1-\varsigma }_{C_2}^2,\left(b_t\right)\right)}$
$S_{12}\left(C_1,,,C_2\right)$	$\frac{{\sum }_{t=1}^p\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\min \left(1,-,{\varsigma }_{C_1}^2,\left(b_t\right),,,{1-\varsigma }_{C_2}^2,\left(b_t\right)\right)}{{\sum }_{t=1}^p\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\max \left({1-\varsigma }_{C_1}^2,\left(b_t\right),,,{1-\varsigma }_{C_2}^2,\left(b_t\right)\right)}$

Table 5.

Some existing PF measures of distance (Peng et al. 2017)

Distance measures	Expression
$D_1\left(C_1,,,C_2\right)$	$\frac{1}{2p}{\sum }_{t=1}^p\left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,+,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|,+,\left|{\tau }_{C_1}^2,\left(b_t\right),-,{\tau }_{C_2}^2,\left(b_t\right)\right|\right)$
$D_2\left(C_1,,,C_2\right)$	$\frac{1}{2p}{\sum }_{t=1}^p\left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right),-,\left({\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right)\right|\right)$
$D_3\left(C_1,,,C_2\right)$	$\frac{1}{4p}\left[\begin{array}{c}{\sum }_{t=1}^p\left(\begin{array}{c}\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|+\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\\ +\left|{\tau }_{C_1}^2,\left(b_t\right),-,{\tau }_{C_2}^2,\left(b_t\right)\right|\end{array}\right)\\ +{\sum }_{t=1}^p\left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right),-,\left({\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right)\right|\right)\end{array}\right]$
$D_4\left(C_1,,,C_2\right)$	$\frac{1}{p}{\sum }_{t=1}^p\max \left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\right)$
$D_5\left(C_1,,,C_2\right)$	$\frac{2}{p}{\sum }_{t=1}^p\frac{\max \left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\right)}{1+\max \left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\right)}$
$D_6\left(C_1,,,C_2\right)$	$\frac{2{\sum }_{t=1}^p\max \left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\right)}{{\sum }_{t=1}^{p}1+\max \left(\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\sigma }_{C_2}^2,\left(b_t\right)\right|,,,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_2}^2,\left(b_t\right)\right|\right)}$
$D_7\left(C_1,,,C_2\right)$	$1-x\frac{{\sum }_{t=1}^p\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)}{{\sum }_{t=1}^p\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)}-y\frac{{\sum }_{t=1}^p\min \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}{{\sum }_{t=1}^p\max \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)},x+y=,x,y\in \left[0,1\right]$
$D_8\left(C_1,,,C_2\right)$	$1-\frac{x{\sum }_{t=1}^p\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)}{p{\sum }_{t=1}^p\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)}-\frac{y{\sum }_{t=1}^p\min \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}{p{\sum }_{t=1}^p\max \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)},x+y=,x,y\in \left[0,1\right]$
$D_9\left(C_1,,,C_2\right)$	$1-\frac{1}{p}{\sum }_{t=1}^p\frac{\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\min \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}{\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\max \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}$
$D_{10}\left(C_1,,,C_2\right)$	$1-\frac{{\sum }_{t=1}^{p}min\left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\min \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}{{\sum }_{t=1}^p\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\max \left({\varsigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_2}^2,\left(b_t\right)\right)}$
$D_{11}\left(C_1,,,C_2\right)$	$1-\frac{1}{p}{\sum }_{t=1}^p\frac{\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\min \left(1,-,{\varsigma }_{C_1}^2,\left(b_t\right),,,{1-\varsigma }_{C_2}^2,\left(b_t\right)\right)}{\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\max \left(1,-,{\varsigma }_{C_1}^2,\left(b_t\right),,,{1-\varsigma }_{C_2}^2,\left(b_t\right)\right)}$
$D_{12}\left(C_1,,,C_2\right)$	$1-\frac{{\sum }_{t=1}^p\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\min \left(1,-,{\varsigma }_{C_1}^2,\left(b_t\right),,,{1-\varsigma }_{C_2}^2,\left(b_t\right)\right)}{{\sum }_{t=1}^p\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\sigma }_{C_2}^2,\left(b_t\right)\right)+\max \left(1,-,{\varsigma }_{C_1}^2,\left(b_t\right),,,{1-\varsigma }_{C_2}^2,\left(b_t\right)\right)}$

Now, we examine three distinct FFS situations, each of which consists of two distinct FFSs. Table 6 displays the values of comparability.

Table 6.

Values of comparability

Compatibility measure	Case I $C_1=\left(0.5,,,0.3\right)$ $C_2=\left(0.4,,,0.3\right)$	Case I $C_1=\left(0.5,,,0.2\right)$ $C_2=\left(0.4,,,0.3\right)$	Case I $C_1=\left(0,,,0\right)$ $C_2=\left(0.5,,,0.5\right)$
$S_1$	0.9100	0.9100	0.5000
$S_2$	0.9550	0.9300	1
$S_3$	0.8650	0.8150	0.7500
$S_4$	0.9100	0.9100	0.7500
$S_5$	0.8349	0.8349	0.6000
$S_6$	0.8349	0.8349	0.6000
$S_7$	− 0.5080	− 0.1191	0
$S_8$	− 0.5080	− 0.1191	0
$S_9$	0.6400	0.6400	0
$S_{10}$	0.6400	0.6400	0
$S_{11}$	0.9224	0.8843	0.6000
$S_{12}$	0.9224	0.8843	0.6000
$D_1$	0.0900	0.0900	0.5000
$D_2$	0.0450	0.0700	0
$D_3$	0.1350	0.1850	0.2500
$D_4$	0.0900	0.0900	0.2500
$D_5$	0.1651	0.1651	0.4000
$D_6$	0.1651	0.1651	0.4000
$D_7$	0.1080	0.4969	1
$D_8$	0.1080	0.4969	1
$D_9$	0.3600	0.3600	1
$D_{10}$	0.3600	0.3600	1
$D_{11}$	0.0776	0.1157	0.4000
$D_{12}$	0.0776	0.1157	0.4000
$S_{G1}$	0.9390	0.9222	0.7778
$S_{G2}$	0.9390	0.9212	0.7656
$S_{G3}$	0.9390	0.9200	0.7500
$S_{G4}$	0.9390	0.9201	0.7538

Unreasonable results are indicated by bold values

From Table 6, we observe

1. The similarity metrics $S_1,S_4,S_5,S_6,S_9,S_{10}$ and distance metrics $D_1,D_4,D_5,D_6,D_9,D_{10}$ consider the FFSs $C_1,C_2$ (Case I) and $C_1,C_2$ (Case II) to be the same, which is unreasonable.

2. The similarity metric $S_2$ gives 1 as the similarity level between the FFSs (Case III), which is unreasonable as $C_1\ne C_2$.

3. The level of similarity between the FFSs (Case I and Case II) comes out to be negative by the similarity metrics $S_7\mathrm{and}{S}_8$ and thus violates the non-negativity property of a similarity metric.

4. The similarity metrics $S_7,S_8,S_9$, and $S_{10}$ gives 0 as the similarity level between the FFSs (Case III), which is unreasonable as $C_2$ is not a complement of $C_1$.

5. The distance metrics $D_7,D_8,D_9$, and $D_{10}$ gives 1 as the similarity level between the FFSs (Case III), which is unreasonable as $C_2$ is not a complement of $C_1$.

6. The suggested metrics of similarity produce satisfactory results in all three cases.

Thus, we conclude that most of the available compatibility measures produce unreasonable results as shown by bold values, whereas the newly suggested measures of similarity $S_{\mathit{Gt}},t=1,2,3,4$ give satisfactory results in all three cases. This establishes the effectiveness of the suggested similarity measures.

Next, we contrast the proposed FF entropy measures with the existing PF/FF entropy metrics.

Comparison of the proposed FF entropy measurements with the existing PF/FF entropy measures

For comparability, we first enumerate the available metrics of entropy for FFSs/PFSs as shown in Table 7.

Table 7.

Some existing PF/FF measures of entropy (Xue et al. 2018; Yang and Hussain 2018; Thao and Smarandache 2019; Senapati and Yager 2020; Mishra and Rani 2021)

Entropy measure	Expression
$E_1$	$\frac{-1}{p\times \ln 2}{\sum }_{t=1}^p\left(\begin{array}{c}{\sigma }_{C_1}^3\left(b_t\right)ln\left({\sigma }_{C_1}^3,\left(b_t\right)\right)+{\varsigma }_{C_1}^3\left(b_t\right)ln\left({\varsigma }_{C_1}^3,\left(b_t\right)\right)\\ -\left(1,-,{\tau }_{C_1}^3,\left(b_t\right)\right)ln\left(1,-,{\tau }_{C_1}^3,\left(b_t\right)\right)-{\tau }_{C_1}^3\left(b_t\right)ln2\end{array}\right)$
$E_2$	$\frac{1}{2p}{\sum }_{t=1}^p\left(\sin ,\left(\frac{{\sigma }_{C_1}^3\left(b_t\right)+1-{\varsigma }_{C_1}^3\left(b_t\right)}{2}\right),\pi ,+,\sin ,\left(\frac{{\varsigma }_{C_1}^3\left(b_t\right)+1-{\sigma }_{C_1}^3\left(b_t\right)}{2}\right),\pi \right)$
$E_3$	$\frac{1}{\left(\sqrt{2},-,1\right)p}{\sum }_{t=1}^p\left(\cos ,\left(\frac{\pi \left(1,+,{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right)}{4}\right),+,\cos ,\left(\frac{\pi \left(1,-,{\sigma }_{C_1}^3,\left(b_t\right),+,{\varsigma }_{C_1}^3,\left(b_t\right)\right)}{4}\right),-,1\right)$
$E_4$	$\frac{1}{\left(\sqrt{2},-,1\right)p}{\sum }_{t=1}^p\left(\sin ,\left(\frac{\pi \left(1,+,{\sigma }_{C_1}^3,\left(b_t\right),-,{\varsigma }_{C_1}^3,\left(b_t\right)\right)}{4}\right),+,\sin ,\left(\frac{\pi \left(1,-,{\sigma }_{C_1}^3,\left(b_t\right),+,{\varsigma }_{C_1}^3,\left(b_t\right)\right)}{4}\right),-,1\right)$
$E_5$	$1-\sqrt{\frac{1}{p}{\sum }_{t=1}^p{\left({\sigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_1}^2,\left(b_t\right)\right)}^2}$
$E_6$	$\frac{1}{p}{\sum }_{t=1}^p\left(1,-,\left|{\sigma }_{C_1}^2,\left(b_t\right),-,\frac{1}{3}\right|,-,\left|{\varsigma }_{C_1}^2,\left(b_t\right),-,\frac{1}{3}\right|\right)$
$E_7$	$\frac{1}{p}{\sum }_{t=1}^p\left(1,-,\left({\sigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_1}^2,\left(b_t\right)\right),\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_1}^2,\left(b_t\right)\right|\right)$
$E_8$	$\frac{1}{p}{\sum }_{t=1}^p\tan \left(\frac{\pi }{4},-,\frac{\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_1}^2,\left(b_t\right)\right|}{4\left(1,+,{\tau }_{C_1}^2,\left(b_t\right)\right)},\pi \right)$
$E_9$	$\frac{1}{p}{\sum }_{t=1}^p\cot \left(\frac{\pi }{4},+,\frac{\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_1}^2,\left(b_t\right)\right|}{4\left(1,+,{\tau }_{C_1}^2,\left(b_t\right)\right)},\pi \right)$
$E_{10}$	$\frac{1}{\left(\sqrt{2},-,1\right)p}{\sum }_{t=1}^p\left(\cos ,\left(\frac{1+{\sigma }_{C_1}^2\left(b_t\right)-{\varsigma }_{C_1}^2\left(b_t\right)}{4},\pi \right),+,\cos ,\left(\frac{1-{\sigma }_{C_1}^2\left(b_t\right)+{\varsigma }_{C_1}^2\left(b_t\right)}{4},\pi \right),-,1\right)$
$E_{11}$	$\frac{1}{\left(\sqrt{2},-,1\right)p}{\sum }_{t=1}^p\left(\sin ,\left(\frac{1+{\sigma }_{C_1}^2\left(b_t\right)-{\varsigma }_{C_1}^2\left(b_t\right)}{4},\pi \right),+,\sin ,\left(\frac{1-{\sigma }_{C_1}^2\left(b_t\right)+{\varsigma }_{C_1}^2\left(b_t\right)}{4},\pi \right),-,1\right)$
$E_{12}$	$\frac{1}{p}{\sum }_{t=1}^p\frac{\min \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_1}^2,\left(b_t\right)\right)}{\max \left({\sigma }_{C_1}^2,\left(b_t\right),,,{\varsigma }_{C_1}^2,\left(b_t\right)\right)}$
$E_{13}$	$1-\frac{1}{p}{\sum }_{t=1}^p\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_1}^2,\left(b_t\right)\right|$
$E_{14}$	$\frac{{\sum }_{t=1}^p\left(1,-,\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_1}^2,\left(b_t\right)\right|\right)}{{\sum }_{t=1}^p\left(1,+,\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_1}^2,\left(b_t\right)\right|\right)}$
$E_{15}$	$\frac{1}{p}{\sum }_{t=1}^p\frac{{\tau }_{C_1}^2\left(b_t\right)+1-\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_1}^2,\left(b_t\right)\right|}{{\tau }_{C_1}^2\left(b_t\right)+1+\left|{\sigma }_{C_1}^2,\left(b_t\right),-,{\varsigma }_{C_1}^2,\left(b_t\right)\right|}$

Now, we demonstrate the usefulness of the recommended FF measurements of entropy using linguistic hedges.

Definition 12

(Senapati and Yager 2020) The modifier of an FFS $C_1\in FFS\left(B\right)$ is given by

$${\left(C_1\right)}^{\delta }=\left\{\left(b_t,{\left({\sigma }_{C_1}^3\left(b_t\right)\right)}^{\delta },{\left(1-{\left(1-{\varsigma }_{C_1}^3\left(b_t\right)\right)}^{\delta }\right)}^{\frac{1}{3}}\right),b_t\in B\right\}.$$ 4

Now, we consider the following FFSs:

LARGE: $C_1$, very LARGE: ${\left(C_1\right)}^2$, quite very LARGE: ${\left(C_1\right)}^3$, very very LARGE: ${\left(C_1\right)}^4$, more or less LARGE: ${\left(C_1\right)}^{\frac{1}{2}}$.

$E$, the entropy must meet the following criteria since it computes the ambiguity content in an FFS.

$$E\left({\left(C_1\right)}^{\frac{1}{2}}\right)>E\left(C_1\right)>E\left({\left(C_1\right)}^2\right)>E\left({\left(C_1\right)}^3\right)>E\left({\left(C_1\right)}^4\right)$$ 5

We now take a look at an illustration of how the aforementioned FFSs compute ambiguity.

Example 3

Consider $C_1\in FFS\left(B\right)$ as

$$C_1=\left\{\left(b_1,,,0.48,,,0.56\right),,,\left(b_2,,,0.80,,,0.35\right),,,\left(b_3,,,0.21,,,0.60\right),,,\left(b_4,,,0.45,,,0.72\right),,,\left(b_5,,,0.33,,,0.47\right)\right\}.$$

We form the FFSs ${\left(C_1\right)}^{\frac{1}{2}},{\left(C_1\right)}^2,{\left(C_1\right)}^3$, and ${\left(C_1\right)}^4$ with the aid of Definition 12. Table 8 displays the amount of ambiguity present in these FFSs.

Table 8.

Computed values of several measures of entropy concerning Example 3

	${\left(C_1\right)}^4$	${\left(C_1\right)}^3$	${\left(C_1\right)}^2$	$C_1$	${\left(C_1\right)}^{\frac{1}{2}}$
$E_1$	0.5229	0.6056	0.7101	0.8650	0.8455
$E_2$	0.1422	0.1598	0.1782	0.1919	0.1829
$E_3$	0.6867	0.7717	0.8602	0.9266	0.8831
$E_4$	0.6867	0.7717	0.8602	0.9266	0.8831
$E_5$	0.2731	0.3612	0.4943	0.6880	0.6248
$E_6$	0.3155	0.4224	0.5296	0.6782	0.6670
$E_7$	1.5283	1.4081	1.2429	0.9902	0.8592
$E_8$	0.3640	0.4785	0.5750	0.7412	0.7209
$E_9$	0.3640	0.4785	0.5750	0.7412	0.7209
$E_{10}$	12.0414	12.0963	12.1659	12.2385	12.2186
$E_{11}$	1.2769	1.2909	1.3087	1.3275	1.3222
$E_{12}$	0.0836	0.1677	0.1497	0.3864	0.4849
$E_{13}$	0.3155	0.4260	0.5296	0.7311	0.7176
$E_{14}$	0.1873	0.2706	0.3602	0.5762	0.5596
$E_{15}$	0.3050	0.4183	0.5062	0.6900	0.6761
$E_{G1}$	0.3849	0.4778	0.5188	0.6659	0.6692
$E_{G2}$	0.3241	0.4210	0.4680	0.6339	0.6404
$E_{G3}$	0.2212	0.3082	0.3731	0.5636	0.6046
$E_{G4}$	0.2939	0.3890	0.4325	0.6094	0.6238

From Table 8, we observe that

1. $E_1{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_1\left(C_1\right)$

2. $E_2{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_2\left(C_1\right).$

3. $E_3{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_3\left(C_1\right)$

4. $E_4{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_4\left(C_1\right)$

5. $E_5{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_5\left(C_1\right)$

6. $E_6{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_6\left(C_1\right)$

7. $E_6{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_6\left(C_1\right)\ngtr E_6{\left(C_1\right)}^2\ngtr E_6{\left(C_1\right)}^3\ngtr E_6{\left(C_1\right)}^4$

8. $E_8{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_8\left(C_1\right)$

9. $E_9{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_9\left(C_1\right)$

10. $E_{10}{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_{10}\left(C_1\right)$

11. $E_{11}{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_{11}\left(C_1\right)$

12. $E_{12}{\left(C_1\right)}^2\ngtr E_{12}{\left(C_1\right)}^3$

13. $E_{13}{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_{13}\left(C_1\right)$

14. $E_{14}{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_{14}\left(C_1\right)$

15. $E_{15}{\left(C_1\right)}^{\frac{1}{2}}\ngtr E_{15}\left(C_1\right)$

16. $E_{\mathit{Gt}}{\left(C_1\right)}^{\frac{1}{2}}>E_{\mathit{Gt}}\left(C_1\right)>E_{\mathit{Gt}}{\left(C_1\right)}^2>E_{\mathit{Gt}}{\left(C_1\right)}^3>E_{\mathit{Gt}}{\left(C_1\right)}^4,t=1,2,3,4.$

Therefore, it follows that none of the PF/FF measurements of entropy $E_t,1\le t\le 15$ that are currently available satisfy the condition stated in Eq. (5). All of our FF entropy metrics $E_{\mathit{Gt}},1\le t\le 4$, however, adhere to the specification outlined in Eq. (5). This demonstrates that the recommended measurements of entropy are more reliable than the ones that are already available from the perspective of a linguistic hedge.

The applicability of the proposed similarity metrics in pattern identification

Here, we demonstrate how the suggested FF measures of similarity can be applied to address pattern classification-related issues. In pattern analysis, an unidentified pattern is categorized into one of the recognized patterns by applying several compatibility criteria, such as “similarity”, “distance”, “correlation”, etc. We also compare our findings to the various similarity metrics.

Now, using the examples below, we will solve several pattern analysis-related issues.

Example 4

(Jiang et al. 2019) Consider $C_1,C_2,C_3$, and $C$ representing patterns in terms of FFSs.

$$C_1=\left\{\left(b_1,,,0.01,,,0.13\right),,,\left(b_2,,,0.21,,,0.46\right),,,\left(b_3,,,0.33,,,0.35\right)\right\},$$

$$C_2=\left\{\left(b_1,,,0,,,0.14\right),,,\left(b_2,,,0.20,,,0.47\right),,,\left(b_3,,,0.35,,,0.33\right)\right\},$$

$$C_3=\left\{\left(b_1,,,0.02,,,0.12\right),,,\left(b_2,,,0.19,,,0.48\right),,,\left(b_3,,,0.34,,,0.34\right)\right\},$$

$$C=\left\{\left(b_1,,,0.04,,,0.10\right),,,\left(b_2,,,0.23,,,00.44\right),,,\left(b_3,,,0.37,,,0.31\right)\right\}.$$

The challenge is to determine which pattern $C_t,t=1,2,3$ shares the most similarities with $C$. We use the existing metrics of similarity with the recommended FF similarity measurements for this aim. Table 9 displays the computed results. Table 9 makes it obvious that $C$ should be assigned to $C_2$ based on the majority of similarity metrics, including the specified FF metrics.

Table 9.

Computed values of several similarity metrics about Example 4

Similarity measure	$\left(C_1,,,C\right)$	$\left(C_2,,,C\right)$	$\left(C_3,,,C\right)$	Result
$S_1$	0.9824	0.9829	0.9792	$C_2$
$S_2$	0.9851	0.9869	0.9833	$C_2$
$S_3$	0.9837	0.9849	0.9813	$C_2$
$S_4$	0.9824	0.9829	0.9792	$C_2$
$S_5$	0.9655	0.9665	0.9595	$C_2$
$S_6$	0.0173	0.0168	0.0204	$C_3$
$S_7$	0.8431	0.8560	0.8242	$C_2$
$S_8$	0.7237	0.7152	0.7494	$C_3$
$S_9$	0.5639	0.5503	0.5923	$C_3$
$S_{10}$	0.8348	0.8547	0.8188	$C_2$
$S_{11}$	0.9694	0.9719	0.9643	$C_2$
$S_{12}$	0.9690	0.9728	0.9654	$C_2$
$S_{G1}$	0.9854	0.9872	0.9827	$C_2$
$S_{G2}$	0.9854	0.9872	0.9826	$C_2$
$S_{G3}$	0.9853	0.9872	0.9825	$C_2$
$S_{G4}$	0.9853	0.9872	0.9825	$C_2$

Example 5

Consider $C_1,C_2,C_3$, and $C$ representing patterns in terms of FFSs.

$$C_1=\left\{\left(b_1,,,0.5,,,0.3\right),,,\left(b_2,,,0.2,,,0.5\right),,,\left(b_3,,,0.3,,,0.4\right),,,\left(b_4,,,0.4,,,0.3\right),,,\left(b_5,,,0.1,,,0.3\right)\right\},$$

$$C_2=\left\{\left(b_1,,,0.3,,,0.3\right),,,\left(b_2,,,0.1,,,0.4\right),,,\left(b_3,,,0.2,,,0.1\right),,,\left(b_4,,,0.2,,,0.3\right),,,\left(b_5,,,0.7,,,0.1\right)\right\},$$

$$C_3=\left\{\left(b_1,,,0.6,,,0.1\right),,,\left(b_2,,,0.7,,,0\right),,,\left(b_3,,,0.4,,,0.3\right),,,\left(b_4,,,0.5,,,0.3\right),,,\left(b_5,,,0.4,,,0.3\right)\right\},$$

$$C=\left\{\left(b_1,,,0.4,,,0.2\right),,,\left(b_2,,,0.7,,,0.1\right),,,\left(b_3,,,0.4,,,0.3\right),,,\left(b_4,,,0.3,,,0.4\right),,,\left(b_5,,,0.6,,,0.2\right)\right\}.$$

The challenge is to determine which pattern $C_t,t=1,2,3$ shares the most similarities with $C$. We use the existing metrics of similarity with the recommended FF similarity measurements for this aim. Table 10 and Fig. 1 both display the computed results. As can be seen from Table 10, the majority of the measures indicate that $C$ should be assigned to $C_3$.

Table 10.

Computed values of several similarity metrics concerning Example 5

Similarity measure	$\left(C_1,,,C\right)$	$\left(C_2,,,C\right)$	$\left(C_3,,,C\right)$	Result
$S_1$	0.7840	0.8000	0.8860	$C_3$
$S_2$	0.8590	0.9030	0.9280	$C_3$
$S_3$	0.8215	0.8515	0.9070	$C_3$
$S_4$	0.7940	0.8260	0.8860	$C_3$
$S_5$	0.6868	0.7291	0.8075	$C_3$
$S_6$	0.1708	0.1482	0.1023	$C_1$
$S_7$	0.3429	0.3147	0.6027	$C_3$
$S_8$	0.4036	0.3094	0.4911	$C_3$
$S_9$	0.3749	0.4024	0.6498	$C_3$
$S_{10}$	0.3041	0.3627	0.6418	$C_3$
$S_{11}$	0.7707	0.8130	0.8870	$C_3$
$S_{12}$	0.7545	0.8026	0.8873	$C_3$
$S_{G1}$	0.8321	0.8619	0.9096	$C_3$
$S_{G2}$	0.8257	0.8585	0.9083	$C_3$
$S_{G3}$	0.8158	0.8534	0.9068	$C_3$
$S_{G4}$	0.8197	0.8552	0.9070	$C_3$

Fig. 1.

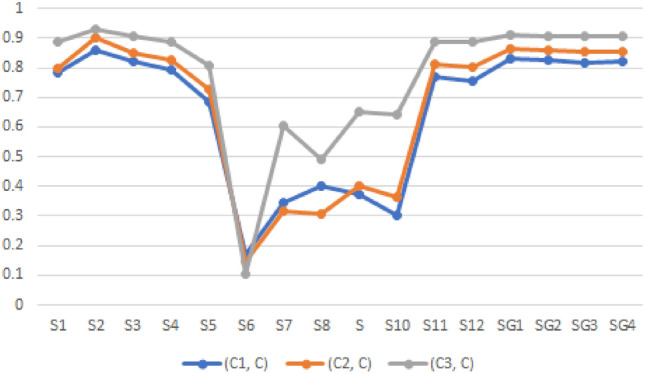
Similarity values regarding Example 5

From examples 4 and 5, we conclude that the recommended similarity metrics of FFSs are compatible with the current similarity metrics in terms of pattern recognition.

We now demonstrate the usefulness of the FF entropy and similarity measurements in decision-making.

An innovative Fermatean fuzzy MADM approach

In this section, we first go over the shortcomings of the conventional Fermatean fuzzy TOPSIS method. Then, under the FF circumstances, we present a novel MADM approach that is similar to TOPSIS.

Flaws of Fermatean fuzzy TOPSIS method

One of the most popular and efficient approaches for solving MADM problems is the methodology for order preference by similarity to ideal solution (TOPSIS), which was first put out by Hwang and Yoon (1981) and then extended to the fuzzy environment by Chen (2000). The TOPSIS method is predicated on the notion that the best choice should be the one that is farthest from the NIS and closest to the PIS. The selected alternative should have the lowest similarity to NIS and the highest similarity to PIS if we use the similarity metric in TOPSIS rather than the distance measure. The TOPSIS-selected alternative, however, does not have a minimum similarity to NIS, as can be shown in the examples below.

Example 6

Take into consideration a FF decision matrix $A_1$ with three options $B_t,t=1,2,3$, and two characteristics $C_k,k=1,2$.

$$A_1=\left(\begin{array}{cc}\left(0.7,,,0.6\right)& \left(0.5,,,0.4\right)\\ \left(0.5,,,0.6\right)& \left(0.7,,,0.8\right)\\ \left(0,,,0.2\right)& \left(0.8,,,0.4\right)\end{array}\right).$$

Then, PIS $B^{+}$ and NIS $B^{-}$ are $B^{+}=\left\{\left(0.7,,,0.2\right),,,\left(0.8,,,0.4\right)\right\}$ and $B^{-}=\left\{\left(0,,,0.6\right),,,\left(0.5,,,0.8\right)\right\}$. Table 11 and Fig. 2 display how similar each alternative is to $B^{+},$ i.e., $S_{G1}\left(B_t,,,B^{+}\right)$ and $B^{-}$ i.e., $S_{G1}\left(B_t,,,B^{-}\right)$ and their closeness coefficient ${\mu }_t=\frac{S_{G1}\left(B_t,,,B^{+}\right)}{S_{G1}\left(B_t,,,B^{+}\right)+S_{G1}\left(B_t,,,B^{-}\right)},t=1,2,3.$ The same Table 11 also displays the alternatives’ final rankings. Table 11 makes it evident that there is no minimum similarity between the best alternative $B_3$ and the NIS $B^{-}$ as $S_{G1}\left(B_3,,,B^{-}\right)>S_{G1}\left(B_1,,,B^{-}\right)$.

Table 11.

Computed values related to Example 6

Alternative	$S_{G1}\left(B_t,,,B^{-}\right)$	$S_{G1}\left(B_t,,,B^{+}\right)$	${\mu }_t$	Ranking
$B_1$	0.8085	0.8620	0.5160	2
$B_2$	0.9198	0.7954	0.4637	3
$B_3$	0.8232	0.8037	0.5205	1

Fig. 2.

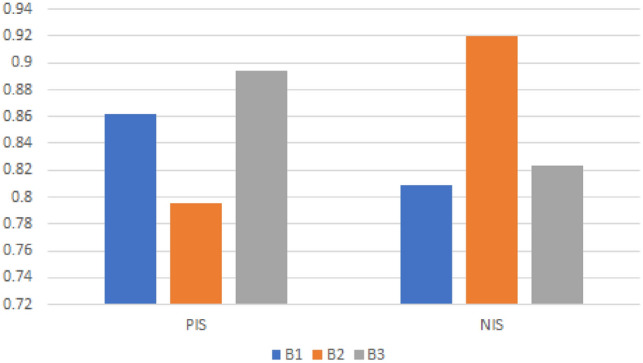
Alternatives’ similarity with PIS and NIS concerning Example 6

Example 7

Take into consideration an FF decision matrix $A_2$ with three options $B_t,t=1,2,3$, and two characteristics $C_k,k=1,2$.

$$A_2=\left(\begin{array}{cc}\left(0.9,,,0.2\right)& \left(0.1,,,0.9\right)\\ \left(0.7,,,0.8\right)& \left(0.6,,,0.5\right)\\ \left(0.1,,,0.2\right)& \left(0.4,,,0.5\right)\end{array}\right).$$

Then PIS $B^{+}$ and NIS $B^{-}$ are $B^{+}=\left\{\left(0.9,,,0.2\right),,,\left(0.6,,,0.5\right)\right\}$ and $B^{-}=\left\{\left(0.1,,,0.8\right),,,\left(0.1,,,0.9\right)\right\}$. Table 12 and Fig. 3 display how similar each alternative is to $B^{+},$ i.e., $S_{G1}\left(B_t,,,B^{+}\right)$ and $B^{-},$ i.e., $S_{G1}\left(B_t,,,B^{-}\right)$ and their closeness coefficient ${\mu }_t=\frac{S_{G1}\left(B_t,,,B^{+}\right)}{S_{G1}\left(B_t,,,B^{+}\right)+S_{G1}\left(B_t,,,B^{-}\right)},t=1,2,3.$ The same Table 12 also displays the alternatives’ final rankings. Table 12 makes it evident that there is no minimum similarity between the best alternative $B_2$ and the NIS $B^{-}$ as $S_{G1}\left(B_2,,,B^{-}\right)>S_{G1}\left(B_3,,,B^{-}\right)$.

Table 12.

Computed values related to Example 7

Alternative	$S_{G1}\left(B_t,,,B^{-}\right)$	$S_{G1}\left(B_t,,,B^{+}\right)$	${\mu }_t$	Ranking
$B_1$	0.8051	0.8378	0.5099	3
$B_2$	0.7531	0.8460	0.5291	1
$B_3$	0.7202	0.7814	0.5204	2

Fig. 3.

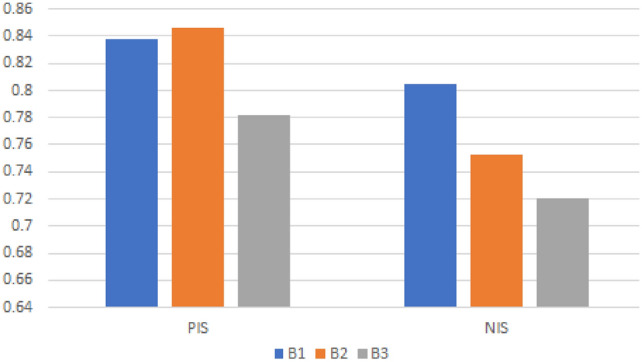
Alternatives’ similarity with PIS and NIS concerning Example 7

The ideal TOPSIS alternative does not possess low similarity with NIS, as seen in Examples 6 and 7. To overcome this severe issue, we suggest the inferior ratio method in the FF environment known as the Fermatean fuzzy inferior ratio (FFIR) method. This is based on the same principle as that of TOPSIS.

Fermatean fuzzy inferior ratio (FFIR) method

Our suggested method produces an alternative that is the least identical to NIS and the most similar to PIS. The algorithm for solving an MCDM problem with $p$ choices $B_t,t=1,2,\cdots ,p$ and $q$ criteria $C_k,k=1,2,..,q$ and $w_k,k=1,2,\cdots ,q$ as criteria weights, where $0\le w_k\le 1$ and ${\sum }_{k=1}^q{w}_k=1$ is given below.

Algorithm

Step 1: Create the decision matrix $A={\left[\left({\sigma }_{\mathit{tk}},,,{\varsigma }_{\mathit{tk}}\right)\right]}_{p\times q}$ to convey information about the options concerning the criteria.

Step 2: Create the normalized decision matrix $D={\left[\left({\sigma }_{\mathit{tk}}^{{}^{\prime }},,,{\varsigma }_{\mathit{tk}}^{{}^{\prime }}\right)\right]}_{p\times q}$ with

$$\left({\sigma }_{\mathit{tk}}^{{}^{\prime }},,,{\varsigma }_{\mathit{tk}}^{{}^{\prime }}\right)=\left\{\begin{array}{c}\left({\sigma }_{\mathit{tk}},,,{\varsigma }_{\mathit{tk}}\right),\text{for benefit criteria}{C}_k\\ \left({\varsigma }_{\mathit{tk}},,,{\sigma }_{\mathit{tk}}\right),\text{for cost criteria}{C}_k.\end{array}\right)$$

Step 3: Find the criteria weights $w_k,k=1,2,\cdots ,q$ using the FF entropy measure as $w_k=\frac{E\left(C_k\right)}{{\sum }_{k=1}^{q}E\left(C_k\right)},$ $k=1,2,\cdots ,q$, with $E$ being a FF measure of entropy.

Step 4: Find the PIS

$$B^{+}=\left\{\left({\sigma }_1^{+},,,{\varsigma }_1^{+}\right),,,\left({\sigma }_2^{+},,,{\varsigma }_2^{+}\right),,,\cdots ,,,\left({\sigma }_q^{+},,,{\varsigma }_q^{+}\right)\right\}$$

and the NIS

$$B^{-}=\left\{\left({\sigma }_1^{-},,,{\varsigma }_1^{-}\right),,,\left({\sigma }_2^{-},,,{\varsigma }_2^{-}\right),,,\cdots ,,,\left({\sigma }_q^{-},,,{\varsigma }_q^{-}\right)\right\},$$

where ${\sigma }_k^{+}=\underset{t}{\max }\left({\sigma }_{\mathit{tk}}\right)$, ${\varsigma }_k^{+}=\underset{t}{\min }\left({\sigma }_{\mathit{tk}}\right)$ and ${\sigma }_k^{-}=\underset{t}{\min }\left({\sigma }_{\mathit{tk}}\right)$, ${\varsigma }_k^{-}=\underset{t}{\max }\left({\sigma }_{\mathit{tk}}\right),k=1,2,\cdots ,q.$

Step 5: Determine the similarity of each alternative $B_t,t=1,2,\cdots ,p$ with the PIS $B^{+}$ and NIS $B^{-}$ with the help of the newly introduced FF-weighted measures of similarity, i.e., find $S_{\mathit{Gj}}^W\left(B_t,,,B^{+}\right)$ and $S_{\mathit{Gj}}^W\left(B_t,,,B^{-}\right),t=1,2,\cdots ,p,$ and $j=1,2,3,4.$

Step 6: Determine $S_{\mathit{Gj}}^W\left(B^{+}\right)$, where $S_{\mathit{Gj}}^W\left(B^{+}\right)=\underset{1\le t\le p}{\max }{S}_{\mathit{Gj}}^W\left(B_t,,,B^{+}\right)$ and so if $S_{\mathit{Gj}}^W\left(B^{+}\right)=S_{\mathit{Gj}}^W\left(B_t,,,B^{+}\right)$, the alternative $B_t$ has maximum similarity with PIS.

Step 7: Determine $S_{\mathit{Gj}}^W\left(B^{-}\right)$, where $S_{\mathit{Gj}}^W\left(B^{-}\right)=\underset{1\le t\le p}{\min }{S}_{\mathit{Gj}}^W\left(B_t,,,B^{-}\right)$ and so if $S_{\mathit{Gj}}^W\left(B^{-}\right)=S_{\mathit{Gj}}^W\left(B_t,,,B^{-}\right)$, the alternative $B_t$ has minimum similarity with NIS.

Step 8: Determine ${\nu }_t=\frac{S_{\mathit{Gj}}^W\left(B_t,,,B^{+}\right)}{S_{\mathit{Gj}}^W\left(B^{+}\right)}-\frac{S_{\mathit{Gj}}^W\left(B_t,,,B^{-}\right)}{S_{\mathit{Gj}}^W\left(B^{-}\right)},1\le t\le p.$ It is obvious that ${\nu }_t$ represents the amount to which an option $B_t,t=1,2,\cdots ,p$ has the least and greatest similarity with NIS and PIS, respectively, at the same time. The option for which ${\nu }_t=0$ is the best choice.

Step 9: Compute the FFIR ${\lambda }_t=\frac{{\nu }_t}{\underset{1\le t\le p}{\min }{\nu }_t}$.

Step 10: In the increasing order of the values of ${\lambda }_t$, we rank the alternatives.

In the example that follows, we apply the suggested FFIR approach to resolve a MADM issue with FF data.

Example 8

(Singh and Ganie 2022) Consider the issue of choosing a home among the five homes $B_t,t=1,2,3,4,5$. Take into account the following factors: $C_1$: Ventilation, $C_2$: Purchase price, $C_3$: Location, $C_4$: Design, $C_5$: Ceiling height. The decision matrix $A$ below illustrates how the information regarding the five houses in relation to the five aforementioned criteria is expressed as FFSs.

$$A=\left(\begin{array}{ccccc}\left(0.6,,,0.5\right)& \left(0.8,,,0.3\right)& \left(0.4,,,0.7\right)& \left(0.6,,,0.8\right)& \left(0.7,,,0.5\right)\\ \left(0.1,,,0.7\right)& \left(0.4,,,0.6\right)& \left(0.2,,,0.7\right)& \left(0.7,,,0.3\right)& \left(0.6,,,0.6\right)\\ \left(0.1,,,0.3\right)& \left(0.71,,,0.3\right)& \left(0.6,,,0.8\right)& \left(0.21,,,0.9\right)& \left(0.29,,,0.8\right)\\ \left(0.4,,,0.7\right)& \left(0.5,,,0.6\right)& \left(0.1,,,0.6\right)& \left(0.2,,,0.8\right)& \left(0.2,,,0.9\right)\\ \left(0.3,,,0.4\right)& \left(0.6,,,0.6\right)& \left(0.4,,,0.8\right)& \left(0.32,,,0.9\right)& \left(0.3,,,0.9\right)\end{array}\right).$$

Given that the criteria $C_2$ is a cost attribute, the normalized decision matrix $D$ is provided below using Step 2:

$$D=\left(\begin{array}{ccccc}\left(0.6,,,0.5\right)& \left(0.3,,,0.8\right)& \left(0.4,,,0.7\right)& \left(0.6,,,0.8\right)& \left(0.7,,,0.5\right)\\ \left(0.1,,,0.7\right)& \left(0.6,,,0.4\right)& \left(0.2,,,0.7\right)& \left(0.7,,,0.3\right)& \left(0.6,,,0.6\right)\\ \left(0.1,,,0.3\right)& \left(0.3,,,0.71\right)& \left(0.6,,,0.8\right)& \left(0.21,,,0.9\right)& \left(0.29,,,0.8\right)\\ \left(0.4,,,0.7\right)& \left(0.6,,,0.5\right)& \left(0.1,,,0.6\right)& \left(0.2,,,0.8\right)& \left(0.2,,,0.9\right)\\ \left(0.3,,,0.4\right)& \left(0.6,,,0.6\right)& \left(0.4,,,0.8\right)& \left(0.32,,,0.9\right)& \left(0.3,,,0.9\right)\end{array}\right).$$

We acquire the following criteria weights using Step 3 and the suggested entropy measure $E_{G1}$ presented in Table 3:$w_1=0.2714,w_2=0.2464,w_3=0.1897,w_4=0.1250,$ and $w_5=0.1675$.

The FF PIS $B^{+}$ and FF NIS $B^{-}$ are then provided using Step 4.

$$B^{+}=\left\{\left(0.6,,,0.3\right),,,\left(0.6,,,0.4\right),,,\left(0.6,,,0.6\right),,,\left(0.6,,,0.4\right),,,\left(0.6,,,0.3\right)\right\}$$

$$B^{-}=\left\{\left(0.1,,,0.7\right),,,\left(0.3,,,0.8\right),,,\left(0.1,,,0.8\right),,,\left(0.2,,,0.9\right),,,\left(0.2,,,0.9\right)\right\}.$$

Then using the suggested similarity measure $S_{G1}^W$ we calculate the similarity values of each alternative $B_t,t=1,2,3,4,5$ with the FF PIS $B^{+}$ and FF NIS $B^{-}$. Then we get $S_{G1}^W\left(B^{+}\right)=\underset{1\le t\le p}{\max }{S}_{G1}^W\left(B_t,,,B^{+}\right)=0.9594=S_{G1}^W\left(B_2,,,B^{+}\right)$ and $S_{G1}^W\left(B^{-}\right)=\underset{1\le t\le p}{\min }{S}_{G1}^W\left(B_t,,,B^{-}\right)=0.9307=S_{G1}^W\left(B_2,,,B^{-}\right)$

Then for each alternative, we determine ${\nu }_t$ and ${\lambda }_t,t=1,2,3,4,5$. Finally, we rank the alternatives in increasing order of the values of ${\lambda }_t$. All these computations are listed in Table 13 and shown in Fig. 4. Table 13 also provides the ranking results for the other there suggested weighted similarity measures $S_{\mathit{Gj}}^W,j=2,3,4$.

Table 13.

Computed values for Example 8 based on the suggested FF similarity measure $S_{\mathit{Gj}}^W,j=1,2,3,4$

Similarity measure	Alternative	$S_{\mathit{Gj}}^W\left(B_t,,,B^{-}\right)$	$S_{\mathit{Gj}}^W\left(B_t,,,B^{+}\right)$	${\mu }_t$	Ranking
$S_{G1}^W$(proposed)	$B_1$	0.9414	0.9472	− 0.0243	2
	$B_2$	0.9307	0.9594	0	1
	$B_3$	0.9595	0.9216	− 0.0703	5
	$B_4$	0.9571	0.9304	− 0.0586	3
	$B_5$	0.9610	0.9260	− 0.0674	4
$S_{G2}^W$(proposed)	$B_1$	0.9365	0.9438	− 0.0248	2
	$B_2$	0.9255	0.9562	0	1
	$B_3$	0.9594	0.9165	− 0.0781	5
	$B_4$	0.9551	0.9249	− 0.0648	3
	$B_5$	0.9590	0.9210	− 0.0730	4
$S_{G3}^W$(proposed)	$B_1$	0.9256	0.9374	− 0.0285	2
	$B_2$	0.9128	0.9512	0	1
	$B_3$	0.9592	0.9047	− 0.0998	3
	$B_4$	0.9515	0.9115	− 0.0842	4
	$B_5$	0.9559	0.9047	− 0.0932	5
$S_{G4}^W$(proposed)	$B_1$	0.9325	0.9409	− 0.0520	2
	$B_2$	0.9216	0.9534	0	1
	$B_3$	0.9593	0.9125	− 0.0838	5
	$B_4$	0.9535	0.9208	− 0.0688	3
	$B_5$	0.9573	0.9174	− 0.0765	4

Fig. 4.

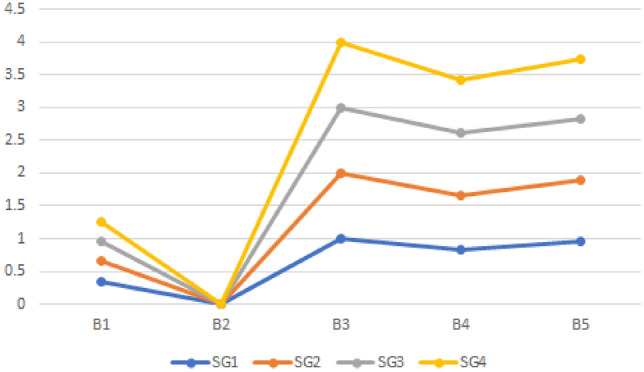
FFIR values corresponding to the proposed four FF similarity measures

We conclude from Table 13 and Figs. 5, 6, 7 and 8 that $B_2$ is the most practical choice because all recommended FF similarity measures show the same results. We can see from Table 13 and Figs. 5, 6, 7 and 8 that the optimal alternative $B_2$ is most similar to PIS $B^{+}$ while being least similar to NIS $B^{-}$.

Fig. 5.

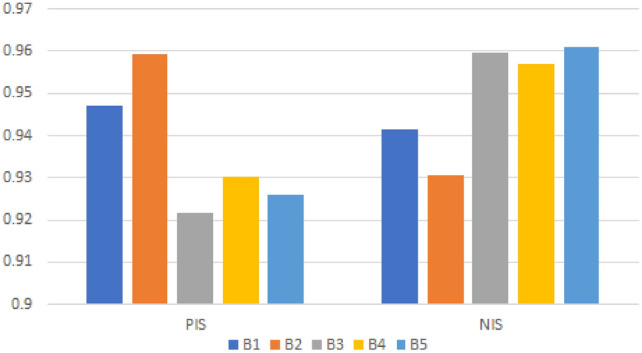
Alternatives’ similarity using $S_{G1}^W$

Fig. 6.

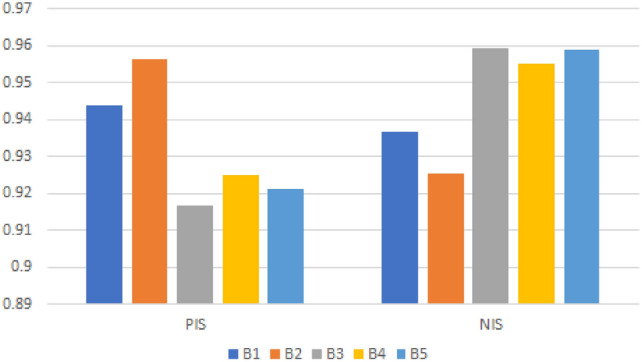
Alternatives’ similarity using $S_{G2}^W$

Fig. 7.

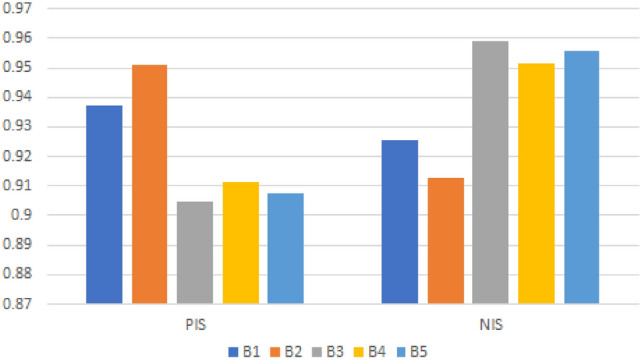
Alternatives’ similarity using $S_{G3}^W$

Fig. 8.

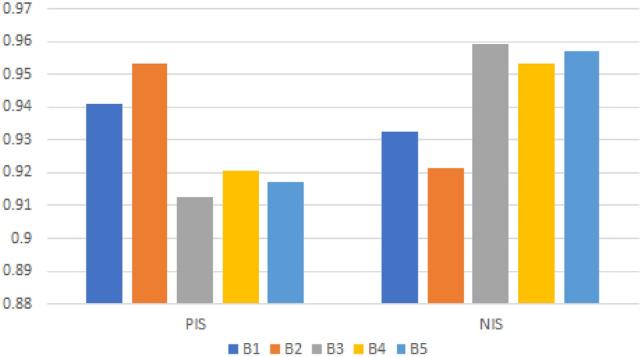
Alternatives’ similarity using $S_{G4}^W$

Discussion and comparative analysis

In the vast quantity of studies on the topic, applications for fuzzy and non-standard fuzzy information measures can be found in MADM, pattern recognition, clustering analysis, picture segmentation, etc. In a certain situation, both activities appear to have the same outcome. Yet, it could provide a variety of results. For instance, in a MADM situation, the ranks of the alternatives may vary depending on the fuzzy entropy or fuzzy knowledge metrics used. When evaluating the compatibility of two fuzzy sets, we may obtain different results with alternate fuzzy similarity/distance/accuracy metrics. This seems to be due to the fuzzy/non-standard fuzzy information measure's failure to accurately represent the ambiguity or precision present in the fuzzy/non-standard fuzzy sets under consideration. As a result, when modeling a specific fuzzy system, we must carefully assess the fuzzy/non-standard fuzzy information measurements. There are many reasons given in the literature for picking a fuzzy information/compatibility measure in a certain situation. The noteworthy ones involve computations for weight, similarity/distance, and linguistic hedging, among other things. The significance of our recommended similarity and entropy metrics are then justified.

We have devised a method for creating the FF similarity measures from t-conorms in Sect. 3 . In Theorem 2, we went through a few of their fresh features. By computing the similarity between several FFSs, we have demonstrated in Sect. 5 that the suggested similarity metrics are preferable. Table 6 has three different FFS situations, each of which consists of two different FFSs. In these three circumstances, while calculating the degree of similarity between the FFSs, we found that the majority of the existing distance and similarity metrics did not produce the desired results, and some of them even failed to meet the necessary axiomatic requirements. Nonetheless, the suggested similarity measures handled all three scenarios correctly and without creating any illogical circumstances. We have demonstrated in Sect. 6 how the recommended similarity measures can be applied to the classification problems and we have also noted that the suggested similarity metrics produce satisfactory results.

With the suggested FF similarity measures, we have demonstrated how to create several innovative FF entropy measures in Sect. 4. Additionally, we have proven that these entropy measurements meet all axiomatic constraints for FF entropy measures. We used linguistic hedges in Sect. 5.2 to demonstrate how the suggested entropy metrics outperform the current entropy measures. Only the suggested entropy measures are found to perform in accordance with the desired condition stated in Eq. (5) in the numerical example studied in this Sect. 5.2. Also, we've shown how to use them to calculate attribute weights in a MADM problem in Sect. 7.2 (Step 3 of Algorithm).

Finding the best option out of all those that are offered is the ultimate goal of a MADM technique. The alternative that is most similar to the positive ideal solution (PIS) and least similar to the negative ideal solution is the ideal alternative (NIS). In contrast, we have demonstrated in Examples 6 and 7 that the optimal option resulting from TOPSIS has maximum similarity to PIS but not least resemblance to NIS. However, the suggested FFIR method gives us the optimal option that is close to PIS and at the same time is far from the NIS as can be seen in Table 13.

The benefits of the novel MADM technique, the suggested entropy metrics, and similarity measures are outlined below.

• The suggested method of obtaining the new similarity measures from t-conorms can be used in many recent generalizations of fuzzy sets.

• Since the present entropy methods yield inaccurate results, the ambiguity content of FFSs can be calculated using similarity-based entropy measurements.

• The suggested similarity metrics can be used for image processing, identifying construction materials, and bidirectional approximate reasoning, among other things.

• The TOPSIS method has a significant flaw that causes it to provide irrational results, hence the newly developed MADM approach, the FFIR method, can be used in its substitute.

In addition to the benefits already described, one drawback of the suggested methods is that they are challenging to implement in real-world situations with the crisp data found in repositories and other websites that are similar to them. The suggested actions can be put into practice by either developing a linguistic database or applying certain conversion procedures.

Conclusion

This article presents a novel method for the creation of various similarity metrics and entropy measures for FFSs. First, four new similarity measures were created, and then utilizing the suggested similarity measurements, four new entropy measures were established. The proposed measures of similarity outperform the majority of the PF distance/similarity metrics reported in the literature in terms of the distance or degree of similarity between different PFSs/FFSs. The suggested entropy metrics for FFSs are also more dependable than the existing PF/FF entropy measures from the linguistic hedge standpoint. The suggested FF similarity measurements have achieved satisfactory results in pattern analysis. A compromise solution that has the most similarity to PIS and the least similarity to NIS was created using the recently proposed MADM methodology, commonly known as the FFIR method.

We will further present examples of clustering and medical diagnostics using the proposed FFS similarity metrics. Additionally, we will add some more recent generalizations of FSs, such as picture fuzzy sets (Cuong and Kreinovich 2013), spherical fuzzy sets (Mahmood et al. 2019), complex fuzzy sets (Ramot et al. 2002), etc., into the suggested method for calculating similarity and entropy measurements. We will also extend the newly introduced MADM method to the recent extensions of fuzzy sets.

Author contributions

All authors contributed equally.

Data availability

All data generated or analyzed during this study are included in this published article.

Declarations

Conflict of interest

The authors declare that they do not have any conflict of interest.