Significance
Foraging requires individuals to compare a local option to the distribution of alternatives across the environment. While foraging is a putatively core, evolutionarily “old” behavior, foragers, across a range of species, systematically deviate from optimality by “overharvesting”—staying too long in a patch. We introduce a computational model that explains overharvesting as a by-product of two mechanisms: 1) statistically rational learning about the distribution of alternatives and 2) planning that adapts to uncertainty over this learned representation. We test the model using a variant of a serial stay–leave task and find that human foragers behave consistently with both mechanisms. Our findings suggest that overharvesting, rather than reflecting a deviation from optimal decision-making, is instead a consequence of optimal learning and adaptation.
Keywords: foraging, structure learning, reinforcement learning, decision-making
Abstract
Patch foraging presents a sequential decision-making problem widely studied across organisms—stay with a current option or leave it in search of a better alternative? Behavioral ecology has identified an optimal strategy for these decisions, but, across species, foragers systematically deviate from it, staying too long with an option or “overharvesting” relative to this optimum. Despite the ubiquity of this behavior, the mechanism underlying it remains unclear and an object of extensive investigation. Here, we address this gap by approaching foraging as both a decision-making and learning problem. Specifically, we propose a model in which foragers 1) rationally infer the structure of their environment and 2) use their uncertainty over the inferred structure representation to adaptively discount future rewards. We find that overharvesting can emerge from this rational statistical inference and uncertainty adaptation process. In a patch-leaving task, we show that human participants adapt their foraging to the richness and dynamics of the environment in ways consistent with our model. These findings suggest that definitions of optimal foraging could be extended by considering how foragers reduce and adapt to uncertainty over representations of their environment.
Many real-world decisions are sequential in nature. Rather than selecting from a set of known options, a decision-maker must choose between accepting a current option or rejecting it for a potentially better future alternative. Such decisions arise in a variety of contexts, including choosing an apartment to rent, a job to accept, or a website to browse. In ethology, these decisions are known as patch-leaving problems. Optimal foraging theory suggests that the current option should be compared to the quality of the overall environment (1). An agent using the optimal choice rule given by the marginal value theorem MVT (2) will leave once the local reward rate of the current patch, or concentration of resources, drops below the global reward rate of the environment.
Foragers largely abide by the qualitative predictions of MVT but deviate quantitatively in systematic ways—staying longer in a patch relative to MVT’s prescription. Known as overharvesting, this bias to overstay is widely observed across organisms (3–10). Despite this, how and why it occurs remains unclear. Proposed mechanisms include a sensitivity to sunk costs (9, 10), diminishing marginal utility (3), discounting of future rewards (3, 10, 11), and underestimation of postreward delays (5). Critically, these all share MVT’s assumption that the forager has accurate and complete knowledge of their environment, implying that deviations from MVT optimality emerge in spite of this knowledge. However, an assumption of accurate and complete knowledge often fails to be met in dynamic real-world environments (12). Relaxing this assumption, how might foragers learn the quality of the local and global environment?
Previously proposed learning rules include recency-weighted averaging over all previous experiences (3, 13) and Bayesian updating (14). In this prior work, learning of environment quality is foregrounded while knowledge of environment structure is assumed. In a homogeneous environment, as is nearly universally employed in these experiments, this is a reasonable assumption as a single experience in a patch can be broadly generalized from across other patches. However, it may be less reasonable in more naturalistic heterogeneous environments with regional variation in richness. To make accurate predictions within a local patch, the forager must learn the heterogeneous structure of the broader environment. How might they rationally do so? Here, we show that apparent overharvesting in these tasks can be explained by combining structure learning with adaptive planning, a combination of mechanisms with potentially broad applications to many complex behaviors performed by humans, animals, and artificial agents (15).
We formalize this combination of mechanisms in a computational model. For the structure learning mechanism, we use an infinite capacity mixture model (16, 17), and for the adaptive planning mechanism, we use a dynamically adjusting, uncertainty-sensitive discounting factor (18). The infinite capacity mixture model assumes that the forager treats structure learning as a categorization problem—one in which they must discover not only a particular patch’s type but also the number of patch types there are in the environment. The categorization problem is itself cast as Bayesian inference in which these environmental features can be inferred only from rewards received. Within a patch, the forager infers the probability of a patch being of type k. This inference is dependent on their experience in the current patch, D, and in previous patches.
| [1] |
where J is the number of patch types created up until the current patch, D is a vector of all the depletions observed in the current patch, and all probabilities are conditioned on prior cluster assignments of patches, p1 : N.
A priori, a patch type, k, is more likely if it has been commonly encountered. However, there is always some probability, proportional to α, of the current patch being a novel type.
where nk is the number of patches assigned to cluster k, α is a clustering parameter that can be interpreted as a forager’s prior over environment complexity, and N is the total number of patches encountered.
The parameter α is key for allowing the representation of the environment to grow in complexity as experience warrants it. In a heterogeneously rich environment, allowing for the possibility of multiple patch types enables better predictions of future rewards (Fig. 1 A and B). Specifically, this informs prediction of the upcoming decay rate and hence determines the value of staying in the current patch:
| [2] |
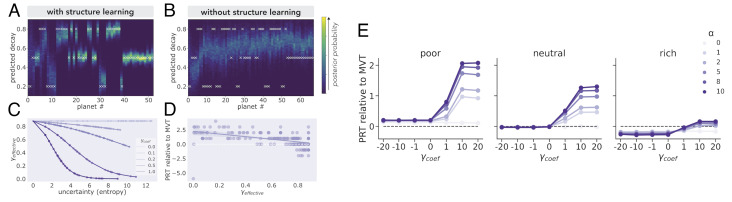
Fig. 1.
Structure learning improves prediction accuracy. (A) With structure learning. A simulated agent’s posterior probability over the upcoming decay rate on each planet is plotted. If the forager’s prior allows for the possibility of multiple clusters (α > 0), they learn with experience the cluster-unique decay rates. Initially, the forager is highly uncertain of their predictions. However, with more visitations to different planets, the agent makes increasingly accurate and precise predictions. (B) Without structure learning. If the forager’s prior assumes a single cluster (α = 0), the forager makes inaccurate and imprecise predictions—either over or underestimating the upcoming decay, depending on the planet type. This inaccuracy persists even with experience because of the strong initial assumption. Uncertainty adaptive discounting. (C) The effect of γcoef. The entropy of the posterior distribution over patch type assignment is taken as the forager’s internal uncertainty and is used to adjust their discounting rate, γeffective. The direction and magnitude of uncertainty’s influence on the discounting rate are determined by the parameter, γcoef. The more positive the parameter is, the more the discounting rate is reduced with increasing uncertainty, formalized as entropy. If negative, the discounting rate increases with greater uncertainty. (D) The effect of γeffective on overharvesting. Increasing γbase increases the baseline discounting rate, while increasing the slope term increases the extent the discounting rate adapts in response to uncertainty. (E) Overharvesting increases with α and γcoef in single patch type environments. Simulating the model in multiple single patch type environments with varying richness, we find that increasing α and γcoef, holding γbase constant, increases the extent of overharvesting (PRT relative to MVT). The richness of the environment determines the extent of the parameters’ influence, with it being greatest in the poor environment.
where rt is the reward received on the last dig, dk is the predicted upcoming decay, and k is the inferred patch type or cluster.
| [3] |
Unless foragers have strong prior assumptions that there is a single patch type, they will be uncertain regarding their assignment of patches to types.
A rational decision-maker should account for this uncertainty. Thus, we adjusted the discount factor on each choice proportionally, capturing the suggestion that it is optimal for a decision-maker using a mental model of the world to set their planning horizon only as far as is justified by their model certainty (18). We implemented this principle by setting the effective discount factor on each choice to be a linear function of the representational uncertainty, U, with intercept (γbase) and slope (γcoef) terms fit to each participant (Fig. 1 C and D).
| [4] |
We quantified representational uncertainty as the entropy of the posterior distribution over the current patch type given their experience in the current patch and previous assignments of patches to types:
| [5] |
This discounting formulation allowed us to test the nested null hypothesis that discount factors would not be sensitive to the agent’s fluctuating representational uncertainty.
The computed discounting rate is applied to the value of leaving.
| [6] |
where is the overall reward rate of the environment computed by diving the total reward earned and the total time spent. tdig is the time required to dig or harvest the current patch. Together, these reflect the opportunity cost of foregoing the current patch.
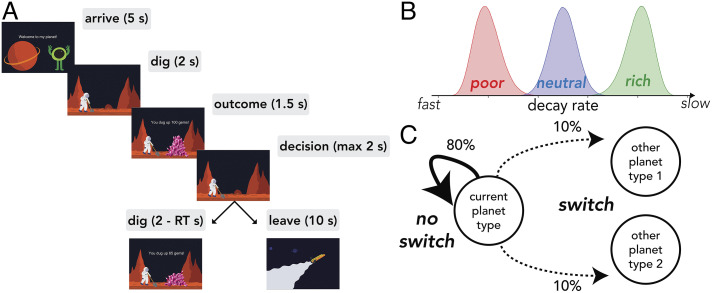
We tested the model’s predictions with a variant of a serial stay-switch task Fig. 2A; (3, 19). Participants visited different planets to mine for “space treasure” and were tasked to collect as much space treasure as possible over the course of a fixed-length game. On each trial, they had to decide between staying on the current planet to dig from a depleting treasure mine or traveling to a new planet with a replenished mine at the cost of a time delay. To mimic naturalistic environments, we varied planet richness across the broader environment while locally correlating richness in time. More concretely, planet richness was drawn from a trimodal distribution (Fig. 2B), and transitions between planets of a similar richness were more likely (Fig. 2C). Our model predicted distinct behavioral patterns from structure-learning individuals versus their nonstructure-learning counterparts in our task. Specifically, within the multimodal environment, nonstructure learners are predicted to underharvest on average, while structure learners overharvest. Furthermore, structure learners’ extent of overharvesting is predicted to vary across the task, fluctuating with their changing uncertainty—decreasing with experience and increasing following rare transitions between planets. In contrast, nonstructure learners should consistently underharvest. We also compared the model’s predictions to those of two other models—an MVT model that learns the global and local reward rates through trial and error and a temporal-difference learning model (3). Both models assume a unimodal distribution of decay rates.
Fig. 2.
(A) Serial stay-switch task. Participants traveled to different planets and mined for space gems across five 6-min blocks. On each trial, they had to decide between staying to dig from a depleting gem mine or incurring a time cost to travel to a new planet. (B) Environment structure. Planets varied in their richness or, more specifically, the rate at which they exponentially decayed with each dig. There were three planet types: poor, neutral, and rich—each with its own characteristic distribution over decay rates. (C) Environment dynamics. Planets of a similar type clustered together. A new planet had an 80% probability of being the same type as the prior planet (“no switch”). However, there was a 20% probability of transitioning or “switching” to a planet of a different type.
We found that principled inference of environment structure and adaptation to this structure can 1) produce key deviations from MVT that have been widely observed in participant data across species and 2) capture patterns of behavior in a novel patch foraging task that cannot be explained by previously proposed models. Taken together, these results reinterpret overharvesting: Rather than reflecting irrational choice under a fixed representation of the environment, it can be seen as a rational choice under a dynamic representation.
Results
Structure Learning and Adaptive Discounting Increase Overharvesting in Single Patch Type Environments.
We examined the extent of overharvesting and underharvesting as a function of the richness of the environment and the parameters governing structure learning (α) and uncertainty adaptive discounting (γcoef). We simulated the model in single patch type environments to demonstrate that overharvesting could be produced through these two mechanisms in an environment commonly used in patch foraging tasks. It is important to note that, because of our definition of uncertainty, discounting adaptation is dependent on the structure learning parameter. We take uncertainty as the entropy of the posterior distribution over the current patch type. If a single patch type is assumed (α = 0), then the entropy will always be zero and the discounting rate will be static. In our exploration of the parameter space, we find that as α increases, overharvesting increases. Similarly, increasing γcoef also increases overharvesting, however, only if α > 0 (Fig. 1E). Additionally, the overall richness of the environment interacts with the influence of these parameters on overharvesting—α and γcoef’s influence is attenuated with increasing richness. The environment’s richness also determines the baseline (when α = 0 and γcoef ≤ 0) extent of overharvesting and underharvesting. Because our model begins with a prior over the decay rate centered on 0.5, this produces overharvesting in the poor environment (mean decay rate = 0.2), optimal harvesting in the neutral (mean decay rate = 0.5), and underharvesting in the rich (mean decay rate = 0.8). In sum, we have shown, in multiple single patch type environments varying in richness, that overharvesting can be produced through a combination of mechanisms—structure learning and uncertainty adaptive discounting.
Model-Free Analyses.
Participants adapt to local richness.
We first examined a prediction of MVT—foragers should adjust their patch leaving to the richness of the local patch. In the task environment, planets varied in their richness or how quickly they depleted. Slower depletion causes the local reward rate to more slowly approach the global reward rate of the environment. Thus, MVT predicts that stay times should increase as depletion rates slow. As predicted, participants stayed longer on rich planets relative to neutral (t(115) = 19.77, P < .0001) and longer on neutral relative to poor (t(115) = 12.57, P < .0001).
Experience decreases overharvesting.
Despite modulating stay times in the direction prescribed by MVT, participants stayed longer or overharvested relative to MVT when averaging across all planets (t(115) = 3.88, P = .00018). However, the degree of overharvesting diminished with experience. Participants overharvested more in the first two blocks relative to the final two (t(115) = 3.27, P = .0014). Our definition of MVT assumes perfect knowledge of the environment. Thus, participants approaching the MVT optimum with experience is consistent with learning the environment’s structure and dynamics.
Local richness modulates overharvesting.
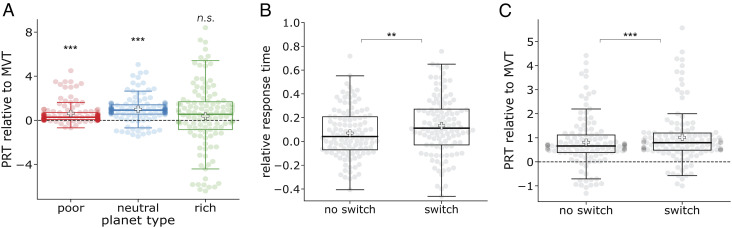
We next considered how participants’ overharvesting varied with planet type. As a group, participants overharvested only on poor and neutral planets while behaving MVT optimally on rich planets (Fig. 3A; poor - t(115) = 6.92, P < .0001; neutral - t(115) = 9.00, P < .0001; rich - t(115) = 1.38, P = .17).
Fig. 3.
Model-free results. (A) Planet richness influences overharvesting and underharvesting behavior. Planet residence times (PRT) relative to the marginal value theorem’s (MVT) prediction are plotted as the median (± one quartile) across participants. The gray line indicates the median, while the white cross indicates the mean. Individuals’ PRTs relative to MVT are plotted as shaded circles. In aggregate, participants overharvested on poor and neutral planets and acted MVT optimally on rich planets. (B) Decision times are longer following rare switch transitions. If a participant has knowledge of the environment’s planet types and the transition structure between them, then they should be surprised following a rare transition to a different type. Consequently, they should take longer to decide following these transitions. As predicted, participants spent longer making a decision following transitions to different types (“switch”) relative to when there was transition to a planet of the same type (“no switch”). This is consistent with having knowledge of the environment’s structure and dynamics. (C) Overharvesting increases following rare switch transitions. On poor and neutral planets, participants overhavested to a greater extent following a rare “switch” transition relative to when there was a “no switch” transition. This is consistent with uncertainty adaptive discounting. Switches to different planet types should be points of greater uncertainty. This greater uncertainty produces heavier discounting and in turn staying longer with the current option.*P < 0.05, **P < 0.01, ***P < 0.001.
Environment dynamics modulate decision time and overharvesting.
We also asked how participants adapted their foraging strategy to the environment’s dynamics or transition structure. Upon leaving a planet, it was more common to transition to a planet of the same type (80%, “no switch”) than transition to a planet of a different type (“switch”). Thus, we reasoned that switch transitions should be points of maximal surprise and uncertainty given their rareness. However, this would be the case only if the participant could discriminate between planet types and learned the transition structure between them.
If surprised, a participant should take longer to make a choice following a rare “switch” transition. So, we next examined participants’ reaction times (z-scored and log-transformed) for the decision following the first depletion on a planet. We compared when there was a switch in planet type versus where there was none. As predicted, participants showed longer decision times following a “switch” transition suggesting that they were sensitive to the environment’s structure and dynamics (Fig. 3B; t(115) = 2.65, P = .0093).
If uncertain, our adaptive discounting model predicts that participants should discount remote rewards more heavily and, consequently, overharvest to a greater extent. To test this, we compared participants overharvesting following rare “switch” transitions to their overharvesting following the more common “no switch” transitions. Following the model’s prediction, participants marginally overharvested more following a change in planet type (t(115) = 1.86, P = .065). When considering only planets that participants overharvested on average (poor and neutral), overharvesting was significantly greater following a change (Fig. 3C; t(115) = 4.67, P < .0001).
Computational Modeling.
Structure learning with adaptive discounting provides the best account of participant choice.
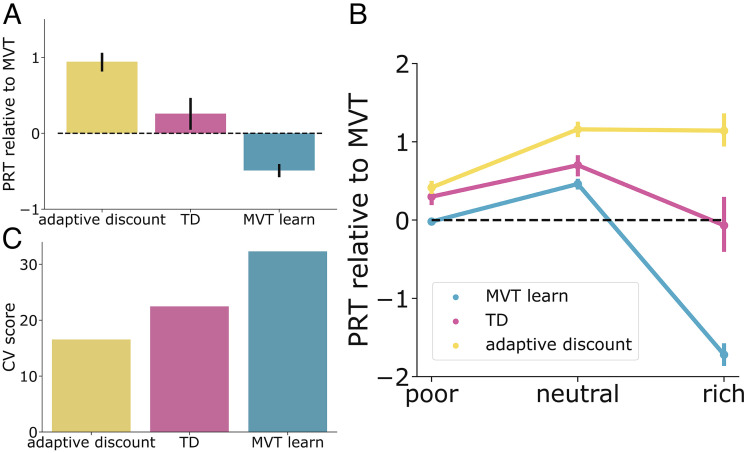
To check the models’ goodness of fit, we asked whether the compared models could capture key behavioral results found in the participants’ data. For each model and participant, we simulated an agent with the best-fitting parameters estimated for them under the given model. Only the adaptive discounting model was able to account for overharvesting when averaging across all planets (Fig. 4A, t(115) = 8.87, P < .0001). The temporal-difference learning model predicted MVT optimal choices on average (t(115) = 1.30, P = .19), while the MVT learning model predicted underharvesting (t(115) = −7.26, P < .0001). These differences were primarily driven by predicted behavior on the rich planets (Fig. 4B).
Fig. 4.
Modeling results. (A) The adaptive discounting model predicts overharvesting. Averaging across all planets, only the adaptive discounting model predicts overharvesting, while the temporal-difference learning model predicts MVT optimal behavior, and the MVT learning model predicts underharvesting. This demonstrates that overharvesting, a seemingly suboptimal behavior, can emerge from principled statistical inference and adaptation. (B) Model predictions diverge most on rich planets. Similar to participants, the greatest differences in behavior between the models occurred on rich planets. (C) The adaptive discounting model provides the best account for participant choices. The adaptive discounting model had the lowest mean cross-validation score, indicating that it provided the best account of participant choice at the group level.
Model fit was also assessed at a more granular level (stay times on individual planets) using 10-fold cross-validation. Comparing cross-validation scores as a group, participants’ choices were best captured by the adaptive discounting model (Fig. 4C; mean cross-validation scores—adaptive discounting: 16.55, TD: 22.47, MVT learn: 32.31). At the individual level, 64% of participants were best fit by the adaptive discounting model, 14% by TD, and 22% by MVT learn.
Adaptive discounting model parameter distribution.
Because the adaptive discounting model provided the best account of choice for most participants, we examined the distribution of individuals’ best-fitting parameters for the model. Specifically, we compared participants’ estimated parameters to two thresholds. These thresholds were used to identify whether a participant 1) inferred and assigned planets to multiple clusters and 2) adjusted their overharvesting in response to internal uncertainty.
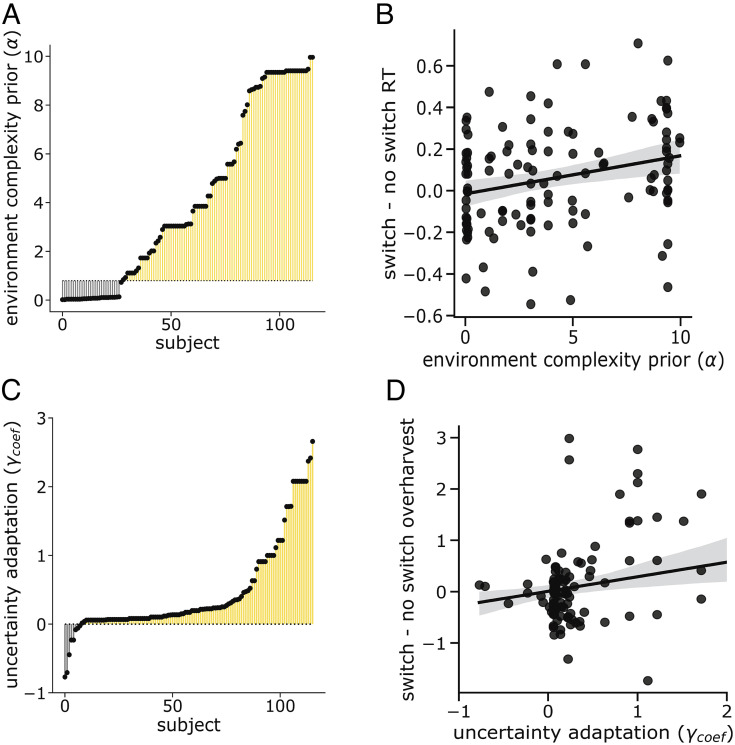
The threshold for multicluster inference, 0.8, was computed by simulating the adaptive discounting model 100 times and finding the lowest value that produced multicluster inference in 90% of simulations. Of note, 76% of participants were above this threshold (Fig. 5A). Thus, most participants were determined to be “structure learners” using our criteria.
Fig. 5.
Parameter distributions. (A) Participants learned the structure of the environment. Distribution of participants’ priors over environment complexity, α. Each individual’s parameter is shown relative to a baseline threshold, 0.8. This threshold is the lowest value that produced multicluster inference in simulation. Most participants (76%) fall above this threshold, indicating that a majority learned the environment’s multicluster structure. (B) Environment complexity parameters were positively related to reaction time sensitivity to transition frequency. An individual must infer multiple planet types to be sensitive to the transition structure between them. In terms of the model, this would correspond to having a sufficiently high environment complexity parameter. Validating this parameter, it was positively correlated with the individual’s modulation of reaction time following a rare transition to a different planet type. (C) Participants adapted their discounting computations to their uncertainty over environment structure. Distribution of the participant’s uncertainty adaptation parameter, γcoef. Each individual’s parameter is shown relative to a baseline of 0. A majority were above this threshold (93%), indicating that most participants dynamically adjusted their discounting, increasing it when they experienced greater internal uncertainty. (D) Uncertainty adaptation parameters were positively related to overharvesting sensitivity to transition frequency. If individuals increase their discounting to their internal uncertainty over environment structure, then they should discount more heavily following rare transitions and consequently, stay longer with the current option. Consistent with this, we found that the extent to which individuals increased their overharvesting following a rare transition was related to their uncertainty adaptation parameter.
The threshold for uncertainty-adaptive discounting was assumed to be 0. A majority of participants, 93%, were above this threshold (Fig. 5C). These participants were determined to be “adaptive discounters,” those who dynamically modulated their discounting factor in accordance with their internal uncertainty.
We next looked for relationships between parameters. Uncertainty should be greatest for individuals who have prior expectations that do not match the environment’s true structure, whether too complex or too simple. Consistent with this, there was a nonmonotonic relationship between the structure learning and discounting parameters. γbase and γcoef were greatest when α was near its lower bound, 0, and upper bound, 10 (γbase: β = 0.080, P < .0001; γcoef: β = 0.021, P < .0001). An individual’s base level discounting constrains the range over which uncertainty can adapt effective discounting. Reflecting this, the two discounting parameters were positively related to one another (τ = −0.33, P < .0001).
Parameter validation.
Correlations with model-free measures of task behavior confirmed the validity of the model’s parameters. We interpret α as reflecting an individual’s prior expectation of environment complexity. α must reach a certain threshold to produce inference of multiple clusters and, consequently, sensitivity to the transitions between clusters. Validating this interpretation, participants with higher fit α demonstrated greater switch costs between planet types (Fig. 5B, Kendall’s τ = 0.17, P = .00076). Moreover, this relationship was specific to α. γbase and γcoef were not significantly correlated with switch cost behavior (γbase: τ = −0.036, P = .57; γcoef: τ = -0.10, P = .11). This is a particularly strong validation as the model was not fit to reaction time data. Validating γcoef as reflecting uncertainty-adaptive discounting, the parameter was correlated with the extent to which overharvesting increased following a rare transition or “switch” between different planet types (Fig. 5D, τ = 0.15, P = .016). This was not correlated with α nor the baseline discounting factor γbase (α: τ = −0.011, P = .86; γbase: τ = 0.082, P = .20).
Discussion
While marginal value theorem (MVT) provides an optimal solution to patch-leaving problems, organisms systematically deviate from it, staying too long or overharvesting. A critical assumption of MVT is that the forager has accurate and complete knowledge of the environment. Yet, this is often not the case in real-world contexts—the ones to which foraging behaviors are likely to have been adapted (20). We propose a model of how foragers could rationally learn the structure of their environment and adapt their foraging decisions to it. In simulation, we demonstrate how seemingly irrational overharvesting can emerge as a by-product of a rational dynamic learning process. In a heterogeneous, multimodal environment, we compared how well our structure learning model predicted participants’ choices relative to two other models—one implementing an MVT choice rule with a fixed representation of the environment and the other a standard temporal-difference learning algorithm. Importantly, only our structure learning model predicted overharvesting in this environment. Participants’ choices were most consistent with learning a representation of the environment’s structure through individual patch experiences. They leveraged this structured representation to inform their strategy in multiple ways. One way determined the value of staying. The representation was used to predict future rewards from choosing to stay in a local patch. The other modulated the value of leaving. Uncertainty over the accuracy of the representation was used to set the discount factor over future value. These results suggest that in order to explain foraging as it occurs under naturalistic conditions, optimal foraging may need to provide an account of how the forager learns to acquire accurate and complete knowledge of the environment and how they adjust their strategy as their representation is refined with experience.
In standard economic choice tasks, humans have been shown to act in accordance with rational statistical inference of environment structure. Furthermore, by assuming that humans must learn the structure of their environment from experience, seemingly suboptimal behaviors can be rationalized, including prolonged exploration (21), melioration (22), social biases (23), and overgeneralization (24). Here, we extend this proposal to decision tasks with sequential dependencies, which require simultaneous learning and dynamic integration of both the distribution of immediately available rewards and the underlying contingencies that dictate future outcomes. This form of relational or category learning has long been associated with distinct cognitive processes and neural substrates from those thought to underlie reward-guided decisions (25), including the foraging decisions we investigate here (7). However, a network of neural regions thought to support relational learning is more recently thought to play a role in deliberative, goal-directed decisions (26, 27).
If foragers are learning a model of the environment and using it to make decisions for reward, this suggests that they may be doing something like model-based reinforcement learning (RL). In related theoretical work, patch-leaving problems have been cast as a multiarmed bandit problem from RL. Which actions are treated as the “arms” is determined by the nature of the environment. In environments where the next patch is unknown to the foragers, the two arms become staying in the current patch and leaving for a new patch. In environments in which the forager does have control over which patch to travel to next, the arms can become the individual patches themselves. Casting patch leaving as an RL problem allows for the use of RL’s optimal solutions as benchmarks for behavior. Applications of these optimal solutions in foraging have been found to capture search patterns (28, 29), choice of lower-valued options (30), and risk aversion (31). In contrast to this work and our own, Constantino & Daw (3) found human foragers’ choices to be better explained by an MVT model augmented with a learning rule than a standard reinforcement learning model. However, importantly, their task environment was homogeneous, and the RL model tested was model-free (temporal-difference learning). Thus, the difference in results could be attributed to differences in task environments and the class of models considered. A key way our model deviates from a model-based RL approach is that prospective prediction is applied in computing only the value of staying, while the value of leaving is similar to MVT’s threshold for leaving—albeit discounted proportionally to the agent’s internal uncertainty over their representation’s accuracy. In the former respect, our model parallels the framework discussed by Kolling & Akam (15) to explain humans’ sensitivity to the gradient of reward rate change during foraging observed by Wittman et al. (32). Given that computing the optimal exit threshold under a pure model-based strategy would be highly computationally expensive, Kolling & Akam (15) suggest pairing model-based patch evaluation with a model-free, MVT-like exit threshold. Under their proposal, the agent leaves once the local patch’s average predicted reward rate over n time steps in the future falls below the global reward rate. We build on, formally test, and extend this proposal by explicitly computing the representational uncertainty at each trial and adjusting the planning horizon accordingly.
While learning a model of the environment is beneficial, it is also challenging and computationally costly. With limited experience and computational noise, an inaccurate model of the environment may be inferred. An inaccurate model, however, can be counteracted by adapting certain computations. In this way, lowering the temporal discounting factor acts as a form of regularization or variance reduction (18, 33–36). Empirical work has found humans appear to do something like this in standard intertemporal choice tasks. Gershman & Bhui (37) found evidence that individuals rationally set their temporal discounting as a function of the imprecision or uncertainty of their internal representations. Here, we found that humans while foraging act similarly, overharvesting to a greater extent at points of peak uncertainty. While temporal discounting has been proposed as a mechanism of overharvesting previously (3, 10, 11), the discounting factor is usually treated as a fixed, subject-level parameter, inferred from choice. Thus, it provides no mechanism for how the factor is set let alone dynamically adjusted with experience. In contrast, our model proposes a mechanism through which the discounting factor is rationally set in response to both the external and internal environments. To further test the model, future work could examine the model’s prediction that overharvesting should increase as the environment’s stochasticity (observation noise) increases. In the current task environment, noise comes from the variance of the generative decay rate distributions. An additional source of noise could be from the reward itself. After the decay rate has been applied to the previously received reward, white Gaussian noise could be added to the product. As a result, the distribution of observed decay rates would have higher variance than the generating decay rate distributions. This reward generation process should elicit greater uncertainty for the forager than the current reward generation process and, consequently, greater overharvesting.
Finally, our observation that humans adjust their planning horizons dynamically in response to state-space uncertainty may have practical applications in multiple fields. In psychiatry, foraging has been proposed as a translational framework for understanding how altered decision-making mechanisms contribute to psychiatric disorders (38). An existing body of work has examined how planning and temporal discounting are impacted in a range of disorders from substance use and compulsion disorders (39, 40) to depression (41) to schizophrenia (42, 43). This wide range has led some to suggest that these abilities may be a useful transdiagnostic symptom and a potential target for treatment (44). However, it remains unclear why they are altered in these disorders. Our findings may provide further insight by way of directing attention toward identifying differences in structure learning and uncertainty adaptation. How uncertainty is estimated and negotiated has been found to be altered in several mood and affective disorders (45, 46); theoretical work has suggested that symptoms of bipolar disorder and schizophrenia may be explained through altered structure learning (47), and finally, in further support, compulsivity has been empirically associated with impaired structure learning (48). Our model suggests a rationale for why these phenotypes co-occur in these disorders. Alternatively, myopic behavior may not reflect differences in abilities but rather in the environment. Individuals diagnosed with these disorders, rather, may more frequently have to negotiate volatile environments. As a result, their structure learning and uncertainty estimation are adapted for these environments. Potential treatments, rather than targeting planning or temporal discounting, could address its possible upstream cause of uncertainty—increasing the individual’s perceived familiarity with the current context or increasing their self-perceived ability to act efficaciously in it. Another application could be in the field of sustainable resource management, where it has recently been shown that, in common pool resource settings (e.g., waterways, grazing fields, fisheries), the distribution of individual participants’ planning horizons strongly determines whether resources are sustainably managed (49). Here, we show that the discount factor, set as a rational response to uncertainty about environmental structure, directly impacts the degree to which an individual tends to (over)harvest their locally available resources. The present work suggests that policymakers and institution designers interested in producing sustainable resource management outcomes should focus on reducing uncertainty—about the contingencies of their actions and the distribution of rewards that may result—for individuals directly affected by resource availability, thus allowing them to rationally respond with an increased planning horizon and improved outcomes for all participants.
Materials and Methods
Participants.
We recruited 176 participants from Amazon Mechanical Turk (111 males, age 23 to 64, mean = 39.79, SD = 10.56). Participation was restricted to workers who had completed at least 100 prior studies and had at least a 99% approval rate. This study was approved by the institutional review board of the University of California, Irvine, under Institutional Review Board (IRB) Protocol 2019-5110 (“Decision-making in time”). All participants gave informed consent in advance. Participants earned $6 as a base payment and could earn a bonus contingent on performance ($0–$4). We excluded 60 participants according to one or more of three criteria: 1) having average planet residence times 2 standard deviations above or below the group mean (36 participants), 2) failing a quiz on the task instructions more than 2 times (33 participants), or 3) failing to respond appropriately to one or more of the two catch trials (17 participants). On catch trials, participants were asked to press the letter “Z” on their keyboard. These questions were meant to “catch” any participants repeatedly choosing the same option (using key presses “A” or “L”) independent of value.
Task Design.
Participants completed a serial stay-switch task adapted from previous human foraging studies (3, 50). With the goal of collecting as much space treasure as possible, participants traveled to different planets to mine for gems. Upon arrival at a new planet, they performed an initial dig and received an amount of gems sampled from a Gaussian distribution with a mean of 100 and SD of 5. Following this initial dig, participants had to decide between staying on the current planet to dig again or leaving to travel to a new planet (Fig. 2A). Staying would further deplete the gem mine, while leaving yielded a replenished gem mine at the cost of a longer time delay. They made these decisions in a series of five blocks, each with a fixed length of 6 min. Blocks were separated by a break of participant-controlled length, up to a maximum of 1 min.
On each trial, participants had 2 s to decide via key press whether to stay (“A”) or leave (“L”). If they decided to stay, they experienced a short delay before the gem amount was displayed (1.5 s). The length of the delay was determined by the time the participant spent making their previous choice (2 - RT s). This ensured that participants could not affect the environment reward rate via their response time. If they decided to leave, they encountered a longer time delay (10 s) after which they arrived on a new planet and were greeted by a new alien (5 s). On trials where a decision was not made within the allotted time (2 s), participants were shown a timeout message for 2 s.
Unlike previous variants of this task, planets varied in their richness within and across blocks, introducing greater structure to the task environment. Richness was determined by the rate at which the gem amount exponentially decayed with each successive dig (Fig. 2B). If a planet was “poor,” there was steep depletion in the amount of gems received. Specifically, its decay rates were sampled from a beta distribution with a low mean (mean = 0.2; sd = 0.05; α = 13 and β = 51). In contrast, rich planets depleted more slowly (mean = 0.8; sd = 0.05; α = 50 and β = 12). Finally, the quality of the third planet type—neutral—fell in between rich and poor (mean = 0.5; sd = 0.05; α = 50 and β = 50). The environment dynamics were designed such that planet richness was correlated in time. When traveling to a new planet, there was an 80% probability of it being the same type as the prior planet (“no switch”). If not of the same type, it was equally likely to be of one of the remaining two types (“switch”, Fig. 2C). This information was not communicated to participants, requiring them to infer the environment’s structure and dynamics from rewards received alone.
Comparison to Marginal Value Theorem.
Participants’ planet residence times, or PRTs, were compared to those prescribed by MVT. Under MVT, agents are generally assumed to act as though they have accurate and complete knowledge of the environment. For this task, that would include knowing each planet type’s unique decay rate distribution and the total reward received and time elapsed across the environment.
Knowledge of the decay rate distributions is critical for estimating Vstay, the anticipated reward if the agent were to stay and dig again.
| [7] |
where rt is the reward received on the last dig, and d is the upcoming decay.
Vleave is estimated using the total reward accumulated, rtotal, total time passed in the environment, ttotal, and the time delay to reward associated with staying and digging, tdig.
| [8] |
estimates the average reward rate of the environment. Multiplying it by tdig gives the opportunity cost of the time spent exploiting the current planet.
Finally, to make a decision, the MVT agent compares the two values and acts greedily, always taking the higher-valued option.
| [9] |
Model.
Making the stay–leave decisions.
We assume that the forager compares the value for staying, Vstay, to the value of leaving Vleave, to make their decision. Similar to MVT, we assume that foragers act greedily with respect to these values.
Learning the structure of the environment.
Learning the structure of the environment affords more accurate and precise predictions which support better decision-making. Here, the forager predicts how many gems they will receive if they stay and dig again, and this determines the value of staying, Vstay. To generate this prediction, a forager could aggregate over all past experiences in the environment (3). This may be reasonable in homogeneous environments but less so in heterogeneous ones where it could introduce substantial noise and uncertainty. Instead, in these varied environments, it may be more reasonable to cluster patches based on similarity and only generalize from patches belonging to the same cluster as the current one. This selectivity enables more precise predictions of future outcomes.
Clusters are latent constructs. Thus, it is not clear how many clusters a forager should divide past encounters into. Nonparametric Bayesian methods provide a potential solution to this problem. They allow for the complexity of the representation—as measured by the number of clusters—to grow freely as experience accumulates. These methods have been previously used to explain phenomena in category learning (16, 51), task set learning (24), fear conditioning (17), and event segmentation (23).
To initiate this clustering process, the forager must assume a model of how their observations, decay rates, are generated by the environment. The generative model we ascribe to the forager is as follows. Each planet belongs to some cluster, and each cluster is defined by a unique decay rate distribution:
| [10] |
where k denotes the cluster number. The generative model takes the form of a mixture model in which normal distributions are mixed together according to some distribution P(k), and observations are generated from sampling from the distribution P(d|k).
Before experiencing any decay on a planet, the forager has prior expectations regarding the likelihood of a planet belonging to a certain cluster. We assume that the prior on clustering corresponds to a “Chinese restaurant process” (52). If previous planets are clustered according to p1 : N, then for the current planet,
where nk is the number of planets assigned to cluster k, α is a clustering parameter, and N is the total number of planets encountered. The probability of a planet belonging to an old cluster is proportional to the number of planets already assigned to it. The probability of it belonging to a new cluster is proportional to α. Thus, α controls how dispersed the clusters are—the higher α is, the more new cluster creation is encouraged. The ability to incrementally add clusters as experience warrants it makes the generative model an infinite capacity mixture model.
After observing successive depletions on a planet, the forager computes the posterior probability of a planet belonging to a cluster:
| [11] |
where J is the number of clusters created up until the current planet, D is a vector of all the depletions observed on the current planet, and all probabilities are conditioned on prior cluster assignments of planets, p1 : N.
The exact computation of this posterior is computationally demanding as it requires tracking all possible clusterings of planets and the likelihood of the observations given those clusterings. Thus, we approximate the posterior distribution using a particle filter (53). Each particle maintains a hypothetical clustering of planets which are weighted by the likelihood of the data under the particle’s chosen clustering. All simulations and fitting were done with 1 particle, which is equivalent to Anderson’s local MAP algorithm (54).
With 1 particle, we assign a planet definitively to a cluster. This posterior then determines a) which cluster’s parameters are updated and b) the inferred cluster on subsequent planet encounters.
If the planet is assigned to an old cluster, k, the existing μk and σk are updated analytically using the standard equations for computing the posterior for a normal distribution with unknown mean and variance:
| [12] |
where d is a decay observed on the current planet, n is the total number of decays observed on the current planet, n0 is the total number of decays observed across the environment before the current planet, μ0 is the prior mean of the cluster-specific decay rate distribution, and ν0 is its precision. μ′0 and ν′0 are the posterior mean and variance, respectively.
If the planet is assigned to a new cluster, then a new cluster is initialized with the following distribution:
| [13] |
This initial distribution is updated with the depletions encountered on the current planet upon leaving.
The goal of this learning and inference process is to support accurate prediction. To generate a prediction of the next decay, the forager samples a cluster according to P(k) or P(k|D) depending on whether any depletions have been observed on the current planet. Then, a decay rate is sampled from the cluster-specific distribution, dk. The forager averages over these samples to produce the final prediction.
To demonstrate structure learning’s utility for prediction, we show in simulation the predicted decay rates on each planet with structure learning (Fig. 1A) and without (Fig. 1B). With structure learning, the forager’s predictions approach the mean decay rates of the true generative distributions. Without structure learning, however, the forager is persistently inaccurate, underestimating the decay rate on rich planets and overestimating it on poor planets.
Adapting the model of the environment.
Because the inference process is an approximation and foragers’ experience is limited, their inferred environment structure may be inaccurate. Theoretical work has suggested that a rational way to compensate for this inaccuracy is to discount future values in proportion to the agent’s uncertainty over their representation of the environment (18). We quantified an agent’s uncertainty by taking the entropy of the approximated posterior distribution over clusters (Fig. 1 C and D). We sample clusters 100 times proportional to the posterior. These samples are multinomially distributed. We represent them with the distribution X:
| [14] |
where K is a vector containing the counts of clusters from sampling 100 times from the distribution, P(k) or P(k|d), depending on whether depletions on the planet have been observed. Uncertainty is quantified as the Shannon entropy of distribution X.
We implemented this proposal in our model by discounting the value of leaving as follows:
| [15] |
| [16] |
where γbase and γcoef are free parameters, and H(X) is the entropy of the distribution X.
Model simulation: parameter exploration.
For each combination of α, γcoef, and environment richness, we simulated the model 100 times, with γbase held constant at 5. Decay rates in each patch in an environment were drawn from the same beta distribution. Critically, the parameters of the beta distribution varied between environments but not patches (poor - a = 13, b = 51; neutral - a = 50, b = 50; poor - a = 50, b = 12). This was done to create single patch type environments, similar to those commonly used in prior work on overharvesting (3–5, 55–58). Simulated agents’ choices were compared to those that would be made if acting with an MVT policy (Comparison to Marginal Value Theorem). The difference was taken between the agent’s stay time in a patch and that prescribed by MVT, and these differences were averaged over to compute a single average patch residence time (PRT) relative to MVT for each agent.
Model fitting.
We compared participant PRTs on each planet to those predicted by the model. A model’s best-fitting parameters were those that minimized the difference between the true participant’s and simulated agent’s PRTs. We considered 1,000 possible sets of parameters generated by quasi-random search using low-discrepancy Sobol sequences (59). Prior work has demonstrated random and quasi-random search to be more efficient than grid search (60) for parameter optimization. Quasi-random search is particularly efficient with low-discrepancy sequence, more evenly covering the parameter space relative to true random search.
Because cluster assignment is a stochastic process, the predicted PRTs vary slightly with each simulation. Thus, for each candidate parameter setting, we simulated the model 50 times and averaged over the mean squared error (MSE) between participant PRTs and model-predicted PRTs for each planet. The parameter configuration that produced the lowest MSE on average was chosen as the best fitting for the individual.
Model comparison.
We compared three models: the structure learning and adaptive discounting model described above, a temporal difference model previously applied in a foraging context, and an MVT model that learns the mean decay rate and global reward rate of the environment.
MVT-learning.
In this model, the agent learns a threshold for leaving, which is determined by the global reward rate, ρ (3). ρ is learned with a simple delta rule with α as a learning rate and taking into account the temporal delay accompanying an action τ. The value of staying is d * rt, where d is the predicted decay and rt is the reward received on the last time step. The value of leaving,Vleave, is the opportunity cost of the time spent digging, ρ * tdig. The agent chooses an action using a softmax policy with temperature parameter, β, which determines how precisely the agent represents the value difference between the two options.
| [17] |
TD-learning.
The temporal difference (TD) agent learns a state-specific value of staying and digging, Q(s, dig), and a non-state-specific value of leaving, Q(leave). The state, s, is defined by the gem amounts offered on each dig. The state space is defined by binning the possible gems that could be earned from each dig. The bins are spaced according to log(bj + 1) - log(bj) = , where bj + 1 and bj are the upper and lower bounds of the bins, and is the mean decay rate. This state space specification is taken from ref. 3. We set bj + 1 to 135 and bj to 0 as these were the true bounds on gems received per dig. We set to 0.5 because this would be the mean decay rate if one were to average the depletions experienced over all planets. The agent compares the two values and makes their choice using a softmax policy.
| [18] |
where c, α, β, andγ are free parameters, and t is the current time step. c is a perseveration term, α is the learning rate, β is the softmax temperature, and γ is the temporal discounting factor.
Cross-validation.
Each model’s fit to the data was evaluated using a 10-fold cross-validation procedure. For each participant, we shuffled their PRTs on all visited planets and split them into 10 separate training/test datasets. The best-fitting parameters were those that minimized the sum of squared error (SSE) between the participant’s PRT and the model’s predicted PRT on each planet in the training set. Then, with the held-out test dataset, the model was simulated with the best-fitting parameters, and the SSE was calculated between the participant’s true PRT and the model’s PRT. To compute the model’s final cross-validation score, we summed over the test SSE from each fold.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
We thank Catherine Hartley for extensive helpful discussions and Mark Steyvers and Frederick Callaway for consulting on the particle filter fitting procedure. This work was supported by a NIMH P50MH096889 (PI: Tallie Z. Baram) seed grant and a NARSAD Young Investigator Award by the Brain and Behavior Research Foundation to A.M.B. N.C.H. was supported by a National Defense Science and Engineering Graduate fellowship.
Author contributions
N.C.H. and A.M.B. designed research; performed research; analyzed data; and wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
All data, data analysis, and model fitting code will be deposited in a public GitHub repository which can be found at https://github.com/noraharhen/Harhen-Bornstein-2023-Overharvesting-as-Rational-Learning.
Supporting Information
References
- 1.Mobbs D., Trimmer P. C., Blumstein D. T., Dayan P., Foraging for foundations in decision neuroscience: Insights from ethology. Nat. Rev. Neurosci. 19, 419–427 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Charnov E. L., Optimal foraging, the marginal value theorem. Theor. Popul. Biol. 9, 129–136 (1976). [DOI] [PubMed] [Google Scholar]
- 3.Constantino S. M., Daw N. D., Learning the opportunity cost of time in a patch-foraging task. Cogn. Affect. Behav. Neurosci. 15, 837–853 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hayden B. Y., Pearson J. M., Platt M. L., Neuronal basis of sequential foraging decisions in a patchy environment. Nat. Neurosci. 14, 933–939 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kane G. A., et al. , Rats exhibit similar biases in foraging and intertemporal choice tasks. Elife 8 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nonacs P., State dependent behavior and the marginal value theorem. Behav. Ecol. 12, 71–83 (2001). [Google Scholar]
- 7.Kolling N., Behrens T. E., Mars R. B., Rushworth M. F., Neural mechanisms of foraging. Science 336, 95–98 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shenhav A., Straccia M. A., Cohen J. D., Botvinick M. M., Anterior cingulate engagement in a foraging context reflects choice difficulty, not foraging value. Nat. Neurosci. 17, 1249–1254 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wikenheiser A. M., Stephens D. W., Redish A. D., Subjective costs drive overly patient foraging strategies in rats on an intertemporal foraging task. Proc. Natl. Acad. Sci. U.S.A. 110, 8308–8313 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Carter E. C., Redish A. D., Rats value time differently on equivalent foraging and delay-discounting tasks. J. Exp. Psychol. Gen. 145, 1093–1101 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Blanchard T. C., Hayden B. Y., Monkeys are more patient in a foraging task than in a standard intertemporal choice task. PLoS One 10, e0117057 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kaelbling L. P., Littman M. L., Cassandra A. R., Planning and acting in partially observable stochastic domains. Artif. Intell. 101, 99–134 (1998). [Google Scholar]
- 13.Garrett N., Daw N. D., Biased belief updating and suboptimal choice in foraging decisions. Nat. Commun. 11, 3417 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kilpatrick Z. P., Davidson J. D., El Hady A., Uncertainty drives deviations in normative foraging decision strategies (2021). [DOI] [PMC free article] [PubMed]
- 15.Kolling N., Akam T., (reinforcement?) learning to forage optimally. Curr. Opin. Neurobiol. 46, 162–169 (2017). [DOI] [PubMed] [Google Scholar]
- 16.Griffiths T. L., Navarro D. J., Sanborn A. N., A more rational model of categorization. Proc. Ann. Meeting Cognit. Sci. Soc. 28 (2006). [Google Scholar]
- 17.Gershman S. J., Blei D. M., Niv Y., Context, learning, and extinction. Psychol. Rev. 117, 197–209 (2010). [DOI] [PubMed] [Google Scholar]
- 18.Jiang N., Kulesza A., Singh S., Lewis R., The dependence of effective planning horizon on model accuracy in Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI, 2016). [Google Scholar]
- 19.Decker J. H., Otto A. R., Daw N. D., Hartley C. A., From creatures of habit to goal-directed learners: Tracking the developmental emergence of model-based reinforcement learning. Psychol. Sci. 27, 848–858 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hayden B. Y., Time discounting and time preference in animals: A critical review. Psychon. Bull. Rev. 23, 39–53 (2016). [DOI] [PubMed] [Google Scholar]
- 21.Acuña D. E., Schrater P., Structure learning in human sequential decision-making. PLoS Comput. Biol. 6, e1001003 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sims C. R., Neth H., Jacobs R. A., Gray W. D., Melioration as rational choice: Sequential decision making in uncertain environments. Psychol. Rev. 120, 139–154 (2013). [DOI] [PubMed] [Google Scholar]
- 23.Shin Y. S., DuBrow S., Structuring memory through Inference-Based event segmentation. Top. Cogn. Sci. 13, 106–127 (2021). [DOI] [PubMed] [Google Scholar]
- 24.Collins A. G. E., Frank M. J., Cognitive control over learning: Creating, clustering, and generalizing task-set structure. Psychol. Rev. 120, 190–229 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Poldrack R. A., et al. , Interactive memory systems in the human brain. Nature 414, 546–550 (2001). [DOI] [PubMed] [Google Scholar]
- 26.Bornstein A. M., Daw N. D., Cortical and hippocampal correlates of deliberation during model-based decisions for rewards in humans. PLoS Comput. Biol. 9, e1003387 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vikbladh O. M., et al. , Hippocampal contributions to model-based planning and spatial memory. Neuron 102, 683–693 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Srivastava V., Reverdy P., Leonard N. E., “On optimal foraging and multi-armed bandits” in 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton) (2013), pp. 494–499.
- 29.Morimoto J., Foraging decisions as multi-armed bandit problems: Applying reinforcement learning algorithms to foraging data. J. Theor. Biol. 467, 48–56 (2019). [DOI] [PubMed] [Google Scholar]
- 30.Keasar T., Rashkovich E., Cohen D., Shmida A., Bees in two-armed bandit situations: Foraging choices and possible decision mechanisms. Behav. Ecol. 13, 757–765 (2002). [Google Scholar]
- 31.Niv Y., Joel D., Meilijson I., Ruppin E., Evolution of reinforcement learning in uncertain environments: A simple explanation for complex foraging behaviors. Adapt. Behav. 10, 5–24 (2002). [Google Scholar]
- 32.Wittmann M. K., et al. , Predictive decision making driven by multiple time-linked reward representations in the anterior cingulate cortex. Nat. Commun. 7, 12327 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Petrik M., Scherrer B., “Biasing approximate dynamic programming with a lower discount factor” in Advances in Neural Information Processing Systems, Koller D., Schuurmans D., Bengio Y., Bottou L., Eds. (Curran Associates, Inc., 2008), vol. 21. [Google Scholar]
- 34.Francois-Lavet V., Rabusseau G., Pineau J., Ernst D., Fonteneau R., On overfitting and asymptotic bias in batch reinforcement learning with partial observability. J. Artif. Intell. Res. 65, 1–30 (2019). [Google Scholar]
- 35.van Seijen H., Fatemi M., Tavakoli A., Using a logarithmic mapping to enable lower discount factors in reinforcement learning. CoRR abs/1906.00572 (2019).
- 36.Amit R., Meir R., Ciosek K., Discount factor as a regularizer in reinforcement learning. CoRR abs/2007.02040 (2020).
- 37.Gershman S. J., Bhui R., Rationally inattentive intertemporal choice. Nat. Commun. 11, 3365 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Addicott M. A., Pearson J. M., Sweitzer M. M., Barack D. L., Platt M. L., A primer on foraging and the Explore/Exploit Trade-Off for psychiatry research. Neuropsychopharmacology 42, 1931–1939 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Amlung M., Vedelago L., Acker J., Balodis I., MacKillop J., Steep delay discounting and addictive behavior: A meta-analysis of continuous associations. Addiction 112, 51–62 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gillan C. M., Kosinski M., Whelan R., Phelps E. A., Daw N. D., Characterizing a psychiatric symptom dimension related to deficits in goal-directed control. Elife 5 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Pulcu E., et al. , Temporal discounting in major depressive disorder. Psychol. Med. 44, 1825–1834 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Heerey E. A., Robinson B. M., McMahon R. P., Gold J. M., Delay discounting in schizophrenia. Cogn. Neuropsychiatry 12, 213–221 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Culbreth A. J., Westbrook A., Daw N. D., Botvinick M., Barch D. M., Reduced model-based decision-making in schizophrenia. J. Abnorm. Psychol. 125, 777–787 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Amlung M., et al. , Delay discounting as a transdiagnostic process in psychiatric disorders: A meta-analysis. JAMA Psychiatry 76, 1176–1186 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Aylward J., et al. , Altered learning under uncertainty in unmedicated mood and anxiety disorders. Nat. Hum. Behav. 3, 1116–1123 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pulcu E., Browning M., The misestimation of uncertainty in affective disorders. Trends Cogn. Sci. 23, 865–875 (2019). [DOI] [PubMed] [Google Scholar]
- 47.Radulescu A., Niv Y., State representation in mental illness. Curr. Opin. Neurobiol. 55, 160–166 (2019). [DOI] [PubMed] [Google Scholar]
- 48.Seow T. X. F., et al. , Model-based planning deficits in compulsivity are linked to faulty neural representations of task structure. J. Neurosci. 41, 6539–6550 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Barfuss W., Donges J. F., Vasconcelos V. V., Kurths J., Levin S. A., Caring for the future can turn tragedy into comedy for long-term collective action under risk of collapse. Proc. Natl. Acad. Sci. U.S.A. 117, 12915–12922 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lenow J. K., Constantino S. M., Daw N. D., Phelps E. A., Chronic and acute stress promote overexploitation in serial decision making. J. Neurosci. 37, 5681–5689 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sanborn A. N., Griffiths T. L., Navarro D. J., Rational approximations to rational models: Alternative algorithms for category learning. Psychol. Rev. 117, 1144–1167 (2010). [DOI] [PubMed] [Google Scholar]
- 52.Antoniak C. E., Mixtures of Dirichlet processes with applications to Bayesian nonparametric problems. Ann. Stat. 2, 1152–1174 (1974). [Google Scholar]
- 53.Fearnhead P., Particle filters for mixture models with an unknown number of components. Stat. Comput. 14, 11–21 (2004). [Google Scholar]
- 54.Anderson J. R., The adaptive nature of human categorization. Psychol. Rev. 98, 409–429 (1991). [Google Scholar]
- 55.Crowley P. H., DeVries D. R., Sih A., Inadvertent errors and error-constrained optimization: Fallible foraging by bluegill sunfish. Behav. Ecol. Sociobiol. 27, 135–144 (1990). [Google Scholar]
- 56.Cuthil I. C., Haccou P., Kacelnik A., Starlings (sturnus vulgaris) exploiting patches: Response to long-term changes in travel time. Behav. Ecol. 5, 81–90 (1994). [Google Scholar]
- 57.Cuthill I. C., Kacelnik A., Krebs J. R., Haccou P., Iwasa Y., Starlings exploiting patches: The effect of recent experience on foraging decisions. Anim. Behav. 40, 625–640 (1990). [Google Scholar]
- 58.Kacelnik A., Todd I. A., Psychological mechanisms and the marginal value theorem: Effect of variability in travel time on patch exploitation. Anim. Behav. 43, 313–322 (1992). [Google Scholar]
- 59.Sobol I. M., Distribution of points in a cube and approximate evaluation of integrals. Zh. Vych. Mat. Mat. Fiz. 7, 784–802 (1967). [Google Scholar]
- 60.Bergstra J., Bengio Y., Random search for hyper-parameter optimization (2012). https://www.jmlr.org/papers/volume13/bergstra12a/bergstra12a.pdf. Accessed 6 May 2021.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
All data, data analysis, and model fitting code will be deposited in a public GitHub repository which can be found at https://github.com/noraharhen/Harhen-Bornstein-2023-Overharvesting-as-Rational-Learning.