Teacher efforts towards the development of students’ mathematical reasoning skills

Abstract

Research shows that improved mathematical reasoning results in improved conceptual understanding and the application of mathematical knowledge to a variety of real-world contexts. The assessment of teacher efforts to help students develop their mathematical reasoning, however, and the identification of classroom practices that encourage this growth have received less attention in previous studies. A descriptive survey was conducted with 62 mathematics teachers from six randomly chosen public secondary schools in one district. Lesson observations were carried out in six randomly selected grade 11 classrooms from all participating schools to supplement teachers' questionnaire replies. Results show that more than 53% of the teachers believed that they had been making enormous efforts towards the development of students' mathematical reasoning skills. Nonetheless, some teachers were not found to be as supportive of students' mathematical reasoning as they believed they were. Additionally, the teachers did not leverage all of the opportunities that arose during instruction to support students’ mathematical reasoning. These results show the need for greater professional development opportunities geared towards orienting both in-service and prospective teachers on useful teaching strategies for fostering students' mathematical reasoning.

1. Introduction

Today’s world is characterised by calls for the provision of educational experiences that are bound to meet the demands of the 21st century. Students need to possess relevant skills to solve challenging problems that society is faced with. For instance, separating important information from misinformation requires them to possess critical thinking skills. The evolution of new technologies also comes with a renewed emphasis on mathematics curriculum that promotes critical thinking skills among students. However, the current instructional approaches in most mathematics classrooms seem to be flawed and ineffective in responding to the challenges that are unique to specific contexts such as the sub-sahara Africa [1,2].

Mathematical reasoning emerges as one such skill that has a significant contribution to students’ overall critical thinking in the sense that it enables them to reason logically when confronted with challenging tasks in the classroom and beyond. This demonstrates a need for instructional practices that emphasize the development of mathematical reasoning, a skill that provides opportunities for students to engage with mathematics at a deeper and thought-provoking intellectual level. Mathematical reasoning, according to Mata-Pereira and da Ponte [3], enables students to move beyond the normal application of processes and learn concepts, properties, and procedures as being logical, interrelated, and coherent aspects of mathematics. It also gives students the opportunities to engage in proving. As such, students engaged in mathematical reasoning gain familiarity with the mathematical structure/language that eventually increases their conceptual understanding and application of mathematics to real-world scenarios. This aligns well with the Zambian curriculum for school mathematics that expects learners to develop logical reasoning, abstract thought processes and being able to solve real-world problems with related mathematical knowledge [4].

This study, which was inspired by earlier studies [3,[5], [6], [7], [8], [9]], identifies key practices for the development of mathematical reasoning skills as involving students in solving challenging problems, modeling with mathematics, examining mathematical structures, using multiple representations, and teamwork, among others. According to Battista [10], mathematical thinking necessarily consists of creating and testing conjectures, making sense of objects, and forming and defending judgments, inferences, and conclusions. Battista [10] adds that mathematical behavior can be demonstrated through the recognition and observation of patterns or in the development of symbol systems that can be used to describe, manipulate, and solve. Similarly, the Australian Curriculum [11] highlights that:

When students explain their thinking, infer and support the logic behind their methods and conclusions, adapt the known to the unknown, transfer learning from one context to another, compare and contrast similar concepts, and justify their decisions, they are engaging in mathematical reasoning.

This demonstrates that students’ enhanced mathematical reasoning leads to increased sense-making, conceptual understanding and application of mathematical knowledge to real-life situations.

Despite its centrality in every school mathematics curriculum, mathematical reasoning is a skill whose development has been quite challenging for many teachers [3,5,12]. Worse still, there is little emphasis, in mathematics education literature (especially in the context of Zambia), on the ways through which teachers of mathematics can teach students to reason logically. A study on pre-service teachers’ mathematical reasoning with number concepts revealed that student teachers exhibited a narrow view and limited comprehension of what consititutes valid mathematical justification and proof [13]. Another study conducted on some Zambian grade 11 students [14] revealed that majority of learners failed to provide logical justifications when explaining the validity of a mathematical statement, “x² + 1 can never be zero if x ∈ R”. The study further revealed that students have limited understanding and comprehension of quadratic equations judging from the nature of responses they gave when assessing and justifying the validity of suggested solutions to the quadratic equation, (x+2)(x+3) = 14.

Students' failure to present valid mathematical arguments and justification may be attributed to their lack of appreciation of the importance of mathematical definitions and proof. Errors or mistakes may also come from the fact that school mathematics does not prepare learners on how to present valid mathematical arguments and justification. One way to develop mathematical reasoning is the provision of opportunities for students to practise writing proofs [13]. However, one question that remains (especially in the context of Zambia) pertains to “how many teachers challenge their students this way?”. This is why it is necessary to conduct an empirical investigation into the efforts that teachers have been making towards the development of students’ mathematical reasoning, a skill that all learners of school mathematics are expected to possess for them to engage with the subject at a desired level.

This research highlights the observed classroom activities that could improve students' mathematical reasoning in addition to reporting teacher efforts to promote that skill in the classroom. The results of this study are expected to serve as a foundation for additional treatments aimed at enhancing students' mathematical reasoning abilities, both in Zambian secondary schools and other settings. With this background, the following research questions were posed.

• (i)What initiatives do teachers from selected public secondary schools take to help students in their classes improve their capacity for mathematical reasoning?
• (ii)What are the observed opportunities for fostering and evaluating students' mathematical reasoning skills in the classrooms?

2. Classroom activities to improve students' mathematical reasoning

The term “mathematical reasoning” refers to a variety of abilities. Some scholars have likened it to a skill with a high degree of deductive and logical quality [3,6]. Similar to this, Lithner [15] defines mathematical reasoning as a logical chain of premises that a learner adopts in order to draw a conclusion when completing a mathematical activity. Therefore, developing effective mathematical reasoning requires putting students through stimulating, demanding, and interesting learning scenarios. The following classroom activities and viewpoints are seen to be essential for the development of students' mathematical reasoning skills in light of the aforementioned and the examined literature.

2.1. Communication

In a classroom setting, communication is a way through which teachers and students share or clarify ideas. When students are encouraged or challenged to share ideas with others either orally or in writing, they get the hang of being clear, convincing, and decisive in their mathematical expressions. A classroom community that aims at promoting students' mathematical reasoning should not only concentrate on procedural descriptions or mimicking examples but ought to encourage mathematical justification of students' ideas both orally and written. Goos [16] suggests encouraging students to participate in dialogues in which they can put forth and support arguments, as well as respond to, criticise, and/or evaluate the ideas of their peers or group members. Additionally, Tong et al. [9] emphasize that communicating mathematical ideas among students (and with the teacher) enables them to be more confident towards learning as well as being open to accepting other people’s ideas.

2.2. Teacher’s talk

The teacher's talk in this study refers to the queries or comments made to the students during the lesson. The way a teacher asks questions during a lesson has a big impact on how far students can take their understanding of mathematics. According to Mueller et al. [7], teachers can better grasp how students build their mathematical ideas and contribute to students' mathematical growth by “skillfully probing students' reasoning and observing students' problem-solving.” This shows that a teacher's discussion or inquiry should be intended to support students in reflecting on and expanding upon their prior knowledge as they produce new knowledge. Leatham et al. [17] propose that teachers should continuously look for evidence of student thinking while making appropriate pedagogical shifts in pushing them to elaborate, explain, and justify their thinking. This is known as the mathematically significant pedagogical opportunities to build on student thinking (MOST) model.

2.3. Multiple representation

In mathematics teaching, multiple representations are used for understanding, describing, developing as well as communicating different mathematical features of the same concept. Multiple representations may include words, symbols, diagrams, formulas, grids and tables, manipulatives, graphs, pictures, and many more. Stylianou [8] highlights that gaining access to mathematical representations enables learners to acquire a set of thinking tools that enhances their problem-solving skills not only in mathematics classrooms but also in other sciences where mathematical tools are applicable. Multiple representations have also been recognized as an important aspect of the MERLO (Meaning Equivalent Reusable Objects) framework for promoting higher-order thinking as well as learners' ability to explore mathematical ideas and relations [18]. In acknowledging the benefits of multiple representations on students’ mathematical reasoning, Dreher et al. [19] stressed that students ought to be supported and encouraged to construct meaning concerning different mathematical representations and make connections among various representations.

2.4. Modelling with mathematics

Literature is well-stocked with studies that have persistently advocated for making mathematics education to be realistic [[20], [21], [22]]. It has been recommended that school mathematics should be relevant to the workplace and real-world experiences. Promotion of mathematical modelling competency is critical to the development of mathematical reasoning skills in the sense that it enables learners to explain, and/or predict the behaviours of related quantities [23]. A teachers' guide by Reboot Foundation [24] highlights that mathematical modeling offers mathematical tools for solving real-world problems thereby helping students to develop deeper mathematical reasoning and critical thinking skills. For instance, a topic like ‘functions’ should aim at increasing students' reasoning ability in relating one quantity of interest to another. Allowing students to put real-world experiences into mathematical terms or relating mathematical content to various practical situations is bound to enhance their mathematical reasoning skills.

2.5. Mathematical tasks

Administration of appropriate tasks is regarded as one of the most essential aspects of stimulating students’ mathematical reasoning. Therefore, teachers should pose questions that give students opportunities to interact with a variety of thinking and sense-making processes rather than assigning exercises that just require students to follow well-known procedures or imitate worked examples [3,5,6,12]. This is because student feedback to the tasks and activities posed by the teacher may reveal the level and nature of mathematical reasoning skill that learners possess [25]. Therefore, teachers ought to pose tasks and activities that are bound to trigger higher-order thinking among students because their reasoning is shaped by the tasks they encounter in the classroom. It is also evident that thought-provoking tasks initiate specific moves to promote reasoning and understanding as they encourage students to begin to build their justifications and sharing of ideas [7].

3. Methods

3.1. Research design and setting

This study employed a multimethod quantitative research approach that enabled the collection of data using both a self-administered questionnaire and a structured classroom observation protocol. A descriptive survey research design was employed. Consistent with the pragmatic worldview [26,27], a multimethod research approach was deemed appropriate considering that no single point of view could have given a complete picture of the prevailing situation regarding teacher efforts towards the development of students' mathematical reasoning skills. Amidst all the advantages of self-administered questionnaires such as anonymity of respondents and less costly in terms of time and resources, there was no guarantee that all teachers reported what they practiced in the real classrooms. As such, teachers’ written responses were complemented by lesson observations to provide further insights about the prevailing situation in the real classrooms. This is consistent with the guidelines by Saunders and Tossey [27] who highlight that triangulation of data sources enables a researcher to collect in-depth information that may be required to address the research question(s) fully.

Data to address the aforementioned research questions were collected from six public secondary schools in Ndola district of Zambia. To ensure that the selected sample was representative of the target population, cluster random sampling was used. Schools were clustered into three categories based on their average academic performance in national examinations at the school certificate level. Schools that had achieved a pass rate of 75% or more were categorised as “high performing” while schools that attained a pass rate of between 50% and 75% were categorised as “moderate performing” schools. Schools that scored an average pass rate below 50% were categorised as “low performing”. Thereafter, two schools were randomly selected from each cluster and all the available mathematics teachers for each selected school were included in the sample. Sixty-two teachers of mathematics completed the questionnaire. Out of the 62 respondents, 43 (69.4%) were male while 19 (30.6%) were female. Respondents' mathematics teaching experience at secondary school level ranged from 1 to 27 years (M = 11.37, SD = 7.03). A larger proportion of these teachers (30 or 48.4%) were Bachelor’s degree holders while 27 (43.5%) were diploma holders and only 5 (8.1%) were Masters degree holders. It was further revealed that 37 teachers representing 59.7% were teaching both junior (grade 8 to 9) and senior (grade 10 to 12) classes, while 22 (35.5%) were teaching senior classes only and 3 (4.8%) were teaching junior classes only. After questionnaire administration, mathematics lesson observations were carried out in one randomly selected grade 11 class from each of the six participating schools.

3.2. Development and validation of instruments

Both the teachers' questionnaire and a mathematics classroom observation protocol (MCOP²) were used to collect data that provided answers to the two research questions. Apart from complementing teachers' questionnaire responses, lesson observations were used to establish whether teachers’ questionnaire responses were a true reflection of what transpired in the real classrooms.

3.2.1. Questionnaire for teachers

After the formulation of questionnaire items, a pilot study was conducted on 33 teachers of mathematics from 4 secondary schools. Data collection for the pilot study and refinement of the questionnaire were undertaken in the month of June 2019 before commencement of the actual data collection that took place from July to the first week of August 2019. While the four public schools were randomly selected, participation of 33 mathematics teachers in the pilot study was voluntary. These four secondary schools were selected from a different district, about 60 km from the district where the actual study was undertaken. A pilot study was undertaken for purposes of testing the validity and reliability of the research instruments. Of the 33 teachers, 17 (53.1%) were male while 15 (46.9%) were female and 1 teacher did not disclose. While Yurdugül [28] guides that a sample size of 30 is sufficient, it suffices to point out that the first eigenvalue of the Principal Component Analysis (PCA) for this pilot study was 3.75, contrary to the recommended first eigenvalue of more than 6. However, a study by Bujang et al. [29] et al. concluded that a sample size of 31 can measure reliability using Cronbach’s alpha provided the item loadings of the extracted components are large enough. As such, a sample size of 33 was considered sufficient for establishing the content validity and reliability of the questionnaire items.

To optimize the number of factors, the default number in SPSS given by Kaiser’s criterion (eigenvalue >1) was used. Four (04) components were extracted and none of the 10 items had a communality score of less than 0.2. Despite that, a principal component analysis matrix (Refer to Table 1) showed that only one component had more than 3 items with factor loadings greater than 0.4.

Table 1.

Principal component analysis matrix (factor loadings).

Item Code	Item Description	Component
		1	2	3	4
Item1	I encourage the use of mathematics vocabulary during mathematics lessons	.597	−.086	−.025	−.553
Item2	I require students to share their thinking with peers by observing patterns, arguing, and justifying ideas	.721	.311	.138	−.385
Item3	I encourage students to explain the reasoning behind their ideas both orally and in writing	.556	.290	.051	.463
Item4	I encourage students to ask questions when difficulties or misunderstandings arise	.359	−.649	.439	.097
Item5	I ask students to construct graphs arising from real life situations	−.187	.656	.501	.343
Item6	I aim at helping students acquire procedural mathematical knowledge, give them a task, and provide feedback	.275	−.175	−.727	.324
Item7	I ask students to construct simple algebraic and geometric proofs based on what they already know	.819	.152	−.282	.228
Item8	I give tasks that require students to formulate, explore and investigate mathematical conjectures	.855	.102	−.115	.019
Item9	I ask students to interpret results from graphs, charts, or tables and use multiple representations	.832	.161	.210	−.088
Item10	I ask students to relate classroom mathematics to the real-life situations	.482	−.573	.367	.332

Following recommendations by different scholars [[30], [31], [32]], the principal component analysis was repeated with one fixed factor and all the 10 items were loaded. At that point, only 7 items had factor loadings greater than 0.4 and were all retained. This means that items 4, 5, and 6 did not meet the criteria and were not included in the refined questionnaire as per the recommended guidelines. Table 2 displays the data analysis codes, full statements (as they appear in the questionnaire), and factor loadings for all the seven retained items.

Table 2.

Factor loadings of the retained items.

Code	Full Statement	Factor Loadings
MR1	I encourage the use of mathematics vocabulary terms during mathematics lessons	.592
MR2	I require students to share their thinking with peers by observing patterns, arguing, and justifying ideas	.753
MR3	I encourage students to explain the reasoning behind their ideas both orally and in writing	.583
MR4	I ask students to construct simple algebraic and geometric proofs based on what they already know	.824
MR5	I give tasks that require students to formulate, explore and investigate mathematical conjectures	.860
MR6	I ask students to interpret results from graphs, charts, or tables and use multiple representations	.849
MR7	I ask students to relate classroom mathematics to the real-life situations	.429

A further check for multicollinearity indicated that all the retained items were independent since none of the inter-item correlations was above the recommended maximum value of 0.8 [31]. Table 3 shows the inter-item correlation coefficients among the retained items.

Table 3.

Inter-item correlation coefficient matrix.

	MR1	MR2	MR3	MR4	MR5	MR6	MR7
MR1	1.00
MR2	.455	1.00
MR3	.255	.236	1.00
MR4	.290	.505	.511	1.00
MR5	.485	.510	.477	.731	1.00
MR6	.380	.760	.300	.609	.642	1.00
MR7	.141	.087	.212	.310	.290	.390	1.00

After ensuring that no pair of the retained items were highly correlated (since all correlation coefficients were below 0.8), reliability analysis was undertaken and Cronbach alpha of .829 was found. This means that all the seven items were internally consistent in measuring the same construct since the computed Cronbach alpha was above 0.7, the recommended minimum value [33,34].

3.2.2. Mathematics classroom observation protocol (MCOP²)

Regarding lesson observations, 12 items for measuring two distinct factors of Teacher Facilitation and Student Engagement were extracted from the Mathematics Classroom Observation Protocol (MCOP²) that was developed by Gleason et al. [35,36]. Since the original authors had already validated the instrument, no other changes were made outside the order in which the items appear in the original manual and a few minor wording adjustments. The “Student Engagement subscale” (α = 0.887) measured students' activities in the classroom throughout the session, whereas the “Teacher Facilitation subscale” (α = 0.850) measured teacher-related actions in the classroom. The adapted observation protocol elements were put through a pilot study with three observers watching the identical lecture, despite the fact that the instrument had already been verified by the original authors. This was done to determine the degree of interobserver agreement. The researcher and two mathematics teacher educators made up the group of three observers. The two mathematics teacher educators were chosen because of their familiarity with the secondary school mathematics curriculum in Zambia and their background in lesson observations.

Spearman’s rank correlation coefficient was used at 5% level of significance to establish consistency levels among the three observers. The Spearman’s rank correlation coefficient was used because it is a non-parametric statistic that is not affected by the normality assumption as opposed to the most recommended intraclass correlation coefficient that requires data to be normally distributed. It was found that the level of agreement between observers 1 and 2 was significant (r = .83, p < .001). Agreement level between observers 1 and 3 was significant (r = .68, p = .01) and that of observers 2 and 3 was also significant (r = .69, p = .009). These statistics assured that different raters or observers were bound to observe similar classroom activities using the same instrument. Table 5 gives the adapted MCOP² items associated with teacher facilitation and student engagement activities.

Table 5.

Student engagement and teacher facilitation activities.

MCOP2 Item	Lesson 1	Lesson 2	Lesson 3	Lesson 4	Lesson 5	Lesson 6
Student Engagement Activities
Exploration, investigation, and/or problem-solving	1	1	1	3	1	1
Use of multiple representations	1	0	0	0	0	0
Perseverance in problem-solving activities	1	2	1	2	1	1
The climate of respect for other people’s opinions	2	2	2	2	1	1
Communicating ideas to others (peer-to-peer)	1	3	1	1	0	1
Teacher Facilitation Activities
Promotes conceptual understanding	2	1	1	3	1	1
Promotes modelling with mathematics	0	0	0	0	0	0
Engages students in examining mathematical structures	0	0	0	3	0	0
Tasks that have multiple paths to a solution	2	2	3	2	1	1
Promotes precision of mathematical language	2	3	2	3	1	1
Promotes higher-order thinking	2	3	1	3	2	2
The climate of respect for other people’s opinions	2	2	2	2	1	1

3.3. Ethical considerations

The Directorate of Research and Innovations at the University of Rwanda's College of Education gave its ethical approval of research tools prior to data collection. The Zambian Ministry of General Education then gave the necessary approval for the collection of data from teachers. Before any data was gathered from the participants, they all supplied written consent.

3.4. Data analysis

Lesson observations concentrated on preparation and delivery of lessons while ensuring that classroom practices recognized as essential for improving students' mathematical reasoning skills were implemented. Based on the replies from teachers to a questionnaire, Table 4 shows the average frequency with which each of the classroom activities listed in Table 2 was used. Table 5 shows the scores for each of the observed classroom practices, which range from 0 (not engaged at all) to 3 (frequently engaged), reflecting the frequency with which a certain practice or activity happened in each of the six 80-minute lessons that were observed. The scoring was carried out in accordance with the advice of the authors of the observation protocol that was modified [35,36]. The instrument's creators also recommended that “would-be” users of the protocol observe at least three lessons. Since most of the qualitative remarks on what happened in those classrooms were included in the discussion section, only quantitative data have been presented in the “results” section.

Table 4.

Descriptive statistics, factor loadings and inter-item correlations.

Items	Factor Loadings	M	SD	Inter-Item Correlations
				MR1	MR2	MR3	MR4	MR5	MR6	MR7
MR1	.474	3.35	0.81	1.00
MR2	.706	3.26	0.72	.165	1.00
MR3	.806	3.26	0.90	.180	.564	1.00
MR4	.818	2.73	0.87	.268	.478	.712	1.00
MR5	.562	2.27	1.01	.362	.227	.256	.314	1.00
MR6	.651	3.00	0.99	.141	.305	.437	.558	.406
MR7	.677	3.39	0.78	.420	.487	.458	.376	.293	.204	1.00

4. Results

4.1. Teachers' self-reported efforts towards developing students’ mathematical reasoning

Respondents were requested to indicate the frequency with which they employed classroom activities aimed at deepening students’ mathematical reasoning on a five-point scale rating from 0 (never) to 4 (always).

After questionnaire administration to the intended participants (n = 62), item reliability was assessed in terms of the Principal Component Analysis (PCA), Cronbach Alpha, and inter-item correlations as illustrated in Table 4. Results show that item reliability for the main study (Cronbach alpha, α = 0.799) did not deviate much from that of a pilot study in the sense that the extracted component showed the first eigen value of 3.24 accounting for 46.3% extraction sums of squared loadings. Reliability analysis further showed that none of the factor loadings for the seven items was below the recommended threshold of 0.4 and that all the inter-item correlation coefficients were below 0.8. This shows that the items were internally consistent in measuring the same construct and no pair of items were highly correlated implying that all the explanatory items were independent.

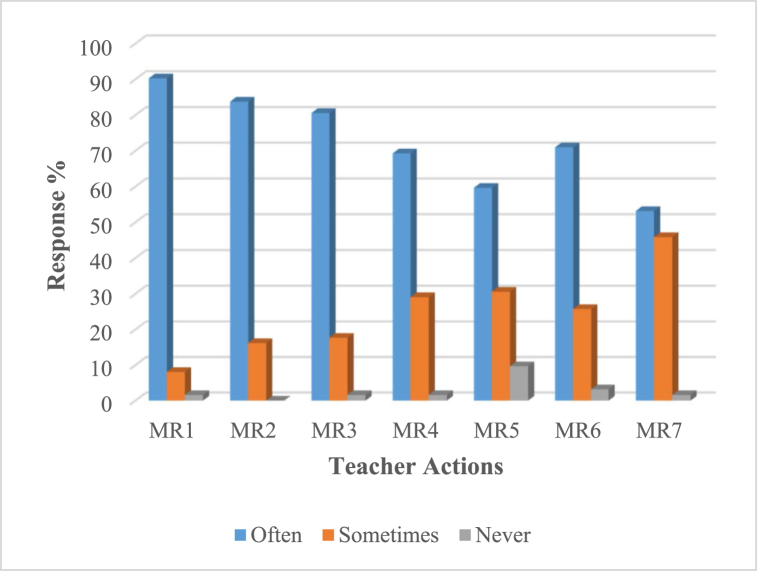
Results displayed in Fig. 1 reflect that only a minority (below 10%) of the respondents indicated that they had never employed any of the classroom practices that were perceived to deepen students' mathematical reasoning skills. Based on Table 4 results, a minimum mean value of 2.27 and maximum mean value of 3.39 reflect that majority of teachers believed that they had been making enormous efforts towards the development of students’ mathematical reasoning skills. This is also reflected in the pictorial presentation of teacher responses displayed in Fig. 1, which shows that more than 53% of the teachers believed they regularly engaged their students in classroom activities that are perceived to enhance mathematical reasoning skills.

Fig. 1.

Reported frequencies regarding teachers' efforts towards developing students' mathematical reasoning.

By re-defining “often” as an aggregate of the “always” and “often” responses, results displayed in Fig. 1 show that 53.2% of the teachers often encouraged their students to relate classroom mathematics to real-life situations (MR7). Similarly, 57.9% of the respondents indicated having administered tasks that required students to formulate, explore and investigate mathematical conjectures (MR5).

Results displayed in Fig. 1 further reveal that 69.3% of the teachers had been encouraging students to construct simple algebraic and geometric proofs where appropriate (MR4) while 71% had often engaged their students in interpreting results from graphs, charts, or tables, and the use of multiple representations (MR6). It has also been shown that 80.6% of the teachers had been encouraging their students to explain the reasoning behind their ideas both orally and in writing (MR3) while 83.8% required students to share their thinking with peers by observing patterns, arguing, and justifying ideas (MR2). The most prominent classroom activity that was reported by 90.3% of the teachers is that of encouraging the use of mathematics vocabulary during mathematics lessons (MR1).

4.2. Student engagement and teacher facilitation activities in the classroom

Among the 6 lessons that were observed, lessons 1, 2, 3, and 5 were based on graphs of quadratic functions while lesson 4 was based on angle properties of a circle, and lesson 6 was on equations of straight lines and their graphs. In lessons 1, 2, 3, and 5, the focus was on determining the nature and coordinates of the turning point of a given function (parabola), x- and y-intercepts, and curve sketching. Lesson 4 was based on angles of a cyclic quadrilateral and their relationship with the associated exterior angles. Lesson 6 was based on the determination of the equation of a straight line and sketching the graph of a straight line based on the sign of the gradient (negative or positive) and the position of the y-intercept.

Table 5 illustrates the scores ranging from 0 to 3 indicating the extent to which a particular practice or activity occurred in each of the six 80-minute lessons that were observed. These numbers give the weightings with which a particular activity occurred during each lesson:

0 = Not engaged at all, 1 = seldom engaged, 2 = sometimes engaged, and 3 = regularly engaged.

Regarding student engagement activities, results displayed in Table 5 indicate that most of the activities seldom occurred during the observed lessons. For instance, none of the six observed lessons had students manipulate multiple representations of mathematical concepts. In situations where at least one representation was used (like in lesson 1), it was exclusively manipulated by the teacher only.

Table 5 also reflect that only lesson 4 had students regularly engaging in exploration, investigation, and/or problem-solving is another noteworthy finding. A small number of learners participated actively in the remaining lessons, while the most were inactive. Despite the fact that students regularly engaged in sharing their views with others in lesson 2, it should be noted that this activity was unusual in other classes and did not occur at all in lesson 5. This somewhat contradicts what several teachers claimed in the questionnaire replies (see to MR2 in Table 4 and Fig. 1), that they had been encouraging their students to express their ideas and provide explanations for their decisions. The outcomes shown in Table 5 further reveal that the small number of students who frequently engaged in exploration, investigation, or problem-solving also displayed some persistence in problem-solving as well as consideration for other people's opinions.

Results displayed in Table 5 for teacher facilitation actions show that most of the observed teachers created lessons that encouraged mathematical language precision and made use of students' queries or answers to strengthen conceptual understanding. The findings also demonstrate that teachers had some regard for what students had to say. Another encouraging finding was that teachers made an effort to incorporate exercises with many solution options into virtually all of their lesson plans in order to increase conceptual knowledge of the subject matter. The degree to which teachers used several of these activities in the observed sessions was not as great as it was depicted, despite the fact that these results are partially compatible with the teachers' questionnaire replies (Table 4 and Fig. 1). For instance, none of the teachers who were observed made an effort to get pupils involved in mathematical modeling activities. Additionally, none of the observed lessons (with the exception of lesson 4) involved students in examining mathematical structures (I.e., conjecturing, justifying, and generalising).

5. Discussion

The overall impression from questionnaire responses is that teachers believed they had been making enormous efforts to employ classroom activities aimed at developing students’ mathematical reasoning skills. Some of the answers on these self-reported questionnaires matched what was noticed during lesson observations. For instance, encouraging the use of mathematical language in the classroom, formulation of tasks that had multiple solution paths, and encouraging communication of ideas with others were not only self-reported by teachers but were also witnessed during lesson observations.

It was further highlighted that teachers missed certain opportunities to improve the reasoning abilities of their pupils despite all the encouraging and good outcomes from their questionnaire replies as well as lesson observations. The lack of or minimal emphasis placed on thought-provoking tasks, mathematical modeling, an examination of mathematical structure (i.e., noticing patterns, conjecturing, justification, and generalization), use of multiple representations, and student collaboration are notable examples of these opportunities.

The lack of emphasis or special focus on the “why” behind any of the procedures and facts that were presented to the learners provided few opportunities for them to engage in conjecturing, justification and generalisation activities. This was more prevalent in lessons 1, 2, 3, and 5 on sketching graphs of quadratic functions. Emphasis on memorising the formula $\left(\frac{-b}{2a},\frac{4ac-b^2}{4a}\right)$ for finding the turning point was one of the common features observed in those lessons. This was a good opportunity for teachers to present different ways of obtaining the turning point of the function $y={ax}^2+bx+c$. As an alternative to depending solely on the formula, which is easily forgotten, learners may have been encouraged to apply other methods to arrive at the same solution, such as the calculus notion of gradient function, completing the square, or the usage of the mid-point between the x-intercepts. Instead of having learners memorize information without completely grasping the notion, the derivation of the formula might have been done to help them see and understand the underpinning mathematical concepts.According to some scholars’ recommendations [13,37], there is a need to inform both pre-service and in-service teachers about the benefits of having students participate in mathematical proofs in order to develop their mathematical reasoning abilities.

While the majority of teachers self-reported that they had been encouraging students to collaborate in problem-solving activities, it has been noted that most observed lessons were primarily teacher-directed as little or no opportunities were available for student-to-student conversations. This is consistent with the results of another study conducted in Zambia [38], which revealed that more than 64% of the teacher participants preferred expository teaching to cooperative learning approaches. However, this is contrary to the social constructivist view of learning that encourages classrooms where students are provided with opportunities to “learn to talk and work together by participating in mathematical discussions, proposing and defending arguments and responding to the ideas and conjectures of their peers” [16]. A review by Alegre et al. [39] also established that peer tutoring improved conceptual understanding and academic achievement among learners of school mathematics. Similarly, Chazan and Ball [40] acknowledge that deepening the reasoning ability of students in mathematics classrooms requires that students are provided with opportunities to voice their mathematical thinking to peers during group discussions. The lack of such discourse in most of the observed classrooms in the present study deprived learners of an opportunity to reflect on their own and other peoples’ views and then correct misconceptions collectively.

The other aspect that was missing in almost all the observed class sessions is modelling with mathematics. This could be attributed to teachers' failure to design tasks that help students to use classroom mathematics in solving real-world problems (i.e., problems arising from everyday life experiences, society, and workplaces). For example, those lessons that focused on sketching graphs of linear and quadratic functions could have incorporated tasks aimed at enabling students to use that knowledge to determine how one real-world quantity varies with another [23,35]. There is also evidence on the need for the design of lessons that incorporate practical situations to stimulate higher-order thinking, which is bound to foster students’ mathematical reasoning [41].

While self-reported questionnaire responses revealed that 71% of the teachers had regularly engaged their students with the use of multiple representations, none of the six observed lessons had incorporated this activity adequately. In instances (like lesson 1) where multiple representations were included, they were restrictive to teacher manipulation and use. This led to students being stuck with only one way of representing a concept. Meaningful problem-posing and the use of multiple representations should be encouraged as they aid the process of developing students’ mathematical reasoning skills [42]. Similarly, Gleason et al. [36] highlight that, while representations can be student-generated (a drawing or a graph) or provided by the teacher (manipulatives or a table), it is the students that must then use the representation” (p.125). This is why some scholars [22,43,44] have stressed a need for designing professional development programmes whose aim is to support teachers of mathematics in what and how they teach.

6. Conclusion

This study is important and impacts the field of mathematics education in the sense that it highlights several opportunities for enhancing students' mathematical reasoning skills. Although this study was contextually bound, its findings are beneficial to all mathematics educators, researchers, and learners at all levels of education in different settings. Findings of the study revealed that the majority of teachers believed that they had been making enormous efforts in supporting their students to reason mathematically. Nonetheless, this paper highlights three major concerns regarding teacher efforts towards the development of students' mathematical reasoning skills. First, the teachers were not found (via observation of their teaching) to be as supportive of students' mathematical reasoning as they believed they were (as indicated in analysis of their responses to questionnaire items). Second, the teachers did not leverage all of the opportunities that arose during instruction to support students’ mathematical reasoning. Third, it has been noted that most of the observed lessons were primarily teacher-directed as little or no opportunities were available for student-to-student conversations.

One obvious implication is that we have to be very careful with opinion polls about what and how one teaches. Another implication is the enormous challenge of getting teachers to teach to promote mathematical reasoning. As such, there is a serious need to design professional development activities through which both pre-service and in-service teachers could be supported on classroom practices that are effective for enhancing students' mathematical reasoning skills. This is attributed to the fact that enhanced mathematical reasoning is associated with better performance, increased self-efficacy, and increased application of mathematical knowledge to various practical (real-world) scenarios. While lesson observations complemented the self-reported questionnaire responses, observing six teachers might not be enough to detect a robust pattern of how teachers promoted students’ mathematical reasoning in their classrooms. As such, future studies may consider increasing the number of classes to be observed along with video and/or audio recordings that could be examined in detail to have a complete understanding of the prevailing situation.

Author contribution statement

Angel Mukuka: Conceived and designed the experiment; Performed the experiment; Analyzed and interpreted the data; Wrote the paper. Sudi Balimuttajjo, Vedaste Mutarutinya: Performed the experiment; Analyzed and interpreted the data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

Data will be made available on request.

Originality statement

This is to certify that this paper is an outcome of the independent and original work of the lead author under the supervision of the coauthors. All of the sources from which the thoughts and passages were derived have been properly credited. Other than a preprint that is accessible at SSRN, the manuscript has not been submitted anywhere else for publication.

Declaration of competing interest

The authors declare no conflict of interest.

Appendix A. Supplementary data

The following are the Supplementary data to this article: