Mechanistic modelling for African swine fever transmission in the Republic of Korea

Abstract

Under the current African swine fever (ASF) epidemic situation, a science-based ASF-control strategy is required. An ASF transmission mechanistic model can be used to understand the disease transmission dynamics among susceptible epidemiological units and evaluate the effectiveness of an ASF-control strategy by simulating disease spread results with different control options. The force of infection, which is the probability that a susceptible epidemiological unit becomes infected, could be estimated by applying an ASF transmission mechanistic model. The government needs to plan an ASF-control strategy based on an ASF transmission mechanistic model.

ASF TRANSMISSION MECHANISTIC MODEL

African swine fever (ASF) is a notifiable disease in the Republic of Korea because it can be transmitted easily between domestic pigs and wild boars and potentially cause catastrophic economic damage to the pork industry. The first ASF virus-infected wild boar carcass was found in October 2019 in the Republic of Korea [1]. Since the first detection of an ASF virus-infected case, the Korean government has been implementing intensive ASF-control measures, including fencing, capture-and-removing for wild boars, or enforcing biosecurity measures for domestic pig farms. On the other hand, ASF outbreaks in wild boars or domestic pigs occurred in 2022. Most of the Republic of Korea is mountainous, making it difficult to control ASF [2]. Thus, the government requires a science-based intervention strategy to control ASF outbreaks in wild boars and domestic pigs under challenging environmental conditions. An understanding of ASF transmission dynamics is required to evaluate the effectiveness of ASF-control strategies.

A mechanistic model of ASF transmission is to simulate the kinematics of disease spread in the real world [3]. A biological representation of livestock disease transmission dynamics includes explicit hypotheses about the infection process, such as susceptible, infectious, or removed. In the disease transmission model, the infection process is carried out on an epidemiological unit (e.g., infectious host or infectious area). In addition, parameters such as contact rate with the infectious unit, latent period, infectious period, death rate, and transmission to susceptible host are included in the model. The deterministic or stochastic characteristics of the parameters can be derived from experimental or observational studies or estimated by fitting the model into the observed dataset. If the constructed mechanistic model can represent the disease transmission pattern in the real world, it can help understand the epidemiological aspects, such as transmission rate or reproduction number. Furthermore, the effectiveness of disease control options can be evaluated using the mechanistic model. The simulated epidemiological consequences, such as the number of infected herds or epidemic duration from different disease control options, can be compared. Given the limited human or material resources, policymakers can plan the most efficient ASF control strategy by comparing the simulated ASF spread results from different control options in ASF mechanistic models. The approaches for building an ASF mechanistic model aim to fit the model to the observed dataset from wild boars and domestic pig farms.

The first step of ASF mechanistic model building is to define an epidemiological unit. The epidemiological unit in the mechanistic model should match the unit in the disease control policy. For an ASF mechanistic model, a domestic pig farm, wild boar, or administrative province can be the epidemiological unit. The infection process of epidemiological units is driven by a function, the force of infection (FOI), which is defined as the rate (or probability) that the susceptible units become infected. The FOI should reflect the epidemiological context, which includes transmission 1) between wild boars, 2) between wild boars and domestic pig farms, and 3) between domestic pig farms. The FOI of transmission type would be specified based on disease spread dynamics between epidemiological units.

First, an ASF transmission among wild boars is associated with the host population dynamics. Unfortunately, there is a lack of knowledge about the wild boar population dynamics in the Republic of Korea. Therefore, approximating methods for the knowledge gap are required. Multiple layers could be included in the ASF mechanistic model, and the wild boar population dynamics were simulated on one of the layers. In the layer, the density or the number of wild boars, death rate, birth rate, home range, and reproduction rate can be used to simulate wild boar population dynamics. The number of wild boars, which is a key parameter for wild boar population dynamics, would be estimated using the proxy variables for the intensity of the forest, such as the normalized difference vegetation index. The knowledge of wild boar experts can be summarized using a quantitative decision analysis, such as multiple-criteria decision analysis for estimating the wild boar population density. The other method for approximating the number of wild boars is to apply a statistical approach. For example, a species distribution model can be used to estimate the wild boar density in the Republic of Korea. Environmental factors, such as the standard normalized difference vegetation index, the enhanced vegetation index, the solar zenith angle, and the daytime or nighttime land surface temperature, could be used to predict the distribution of wild boars in South Korea [4]. Most information for estimating the wild boar population dynamics is obtained from passive or active surveillance. On the other hand, the surveillance system has limitations of delayed detection and underreporting [2]. Thus, an additional method is required to adjust the limits of the surveillance results. A hidden Markov model, which assumes the observation at a certain time, was generated considering that “hidden from the observer” could be used to adjust the delayed detection or underreporting of wild boars.

ASF transmission between wild boars and domestic pigs is related to human behaviors and at-farm biosecurity practices [1]. Transmission between wild boars and domestic pigs would be because the pathogen is geographically located adjacent to susceptible animals, resulting in local spread. A grid-based compartment simulation model would be appropriate to simulate the local spread of ASF based on a mechanistic model. The study area could be comprised of a component, and the probability of ASF infection per component can be estimated. The wild boar population dynamics, ASF transmission rate, biosecurity level of pig farms, or other environmental factors could be added to the model as parameters. The Markov Chain Monte Carlo (MCMC) algorithm could estimate the probability of ASF infection per component, considering variable parameter values. The goodness of the model can be evaluated by examining the converged values of parameters by calculating potential scale reduction or effective sample size. In the ASF local spread simulation model, the wild boar population dynamics is a key parameter. Thus, the knowledge gap of the ecological characteristics of wild boars in the Republic of Korea should be complimented [5]. Unfortunately, the number of ASF virus-infected domestic pig farms until October 2022 was 25 cases, which might not be sufficient to converge the model parameter.

ASF transmission among domestic pigs is associated with livestock vehicle movements, including feed delivery, livestock transport, or manure hauling [6]. In the Republic of Korea, livestock vehicles are mandatorily registered to the national surveillance system, Korea Animal Health Integrated Systems. The epidemiological relationship between the risk of ASF transmission and the frequency of vehicle movement can be explored using a mechanistic model [7]. The FOI for a farm on a day could be estimated using a Bayesian method [8]. Livestock movement factors, such as the risk of infection resulting from ASF-contaminated vehicle movement or the infection probability of a vehicle due to visiting an ASF-contaminated area, would be parameterized in the model to estimate the posterior distribution of the FOI for a farm on a day. The convergence of the model is evaluated using MCMC trace plots or Gelman–Rubin convergence diagnostics. On the other hand, the risk of ASF infection due to the frequency of livestock vehicle movement can be calculated using a spatial regression model. The integrated nested Laplace approximation method would be appropriate for the spatial regression model because the number of livestock vehicle movements is enormous. If there are a number of areas without ASF outbreak, then a Bayesian zero-inflated Poisson model would be applicable to consider the influence of areas without ASF infection. The structured spatial autocorrelation of ASF virus-infected areas will be explored using a Morans’ I or Getis-Ord Gi statistics for the residuals of the model. A mixed-effects Poisson model could estimate the unstructured random effect of spatial autocorrelation.

Within-farm transmission would be added as a parameter in the model to simulate ASF spread between wild boars and domestic pigs or among domestic pigs. A reproduction number within a pen or between pens would be useful for estimating the within-farm transmission rate. A reproduction number of ASF could be calculated using the Wallinga and Teunis method with incubation period and serial interval of ASF or estimating the epidemic doubling time with infectious period and the observed number of ASF infections. On the other hand, there are still knowledge gaps in the epidemiological characteristics of the ASF virus in the Republic of Korea. Therefore, transmission experiments or intensive outbreak investigation for the previous ASF-infected farms are needed to understand the within-farm transmission dynamics [9]. In addition, the ASF virus can be transmitted via a vector, genus Ornithodoros [10]. The ASF FOI for a farm due to ASF virus-infected soft ticks could be parameterized as a probability distribution in an ASF virus transmission mechanistic model.

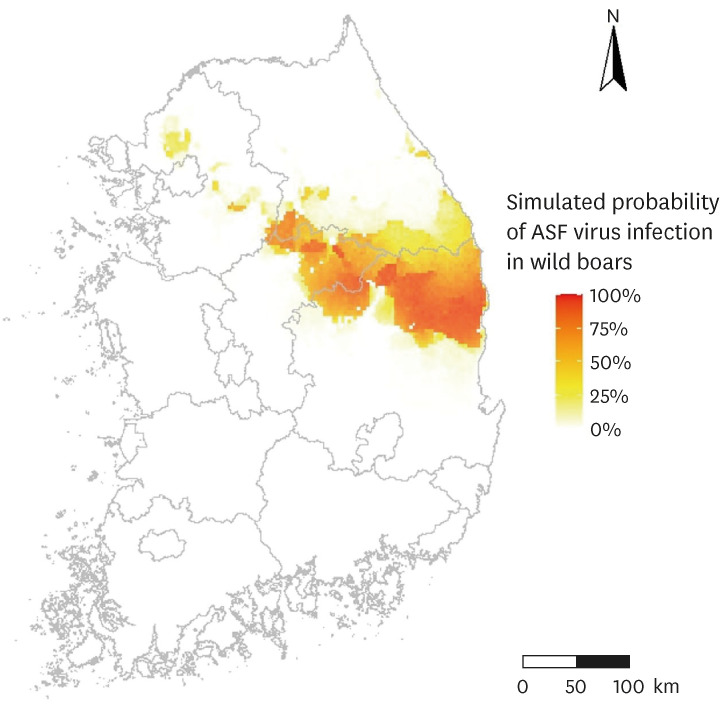
Under the ongoing ASF epidemics in wild boars or domestic pig farms in the Republic of Korea, an ASF virus transmission mechanistic model should be applied to planning an ASF control strategy. A science-based ASF control strategy would be implemented by comparing the simulated ASF spread results with different control options (Fig. 1). For example, a decision maker could increase or decrease a wild boar hunting intensity in the ASF virus transmission mechanistic model and the ASF control option with the most effective simulated result, such as the lowest number of ASF virus-infected wild boars or duration of ASF epidemics would be selected as the ASF control strategy. The epidemiological or environmental context for ASF transmission is different for each country. Therefore, a pig farming system or geographical characteristics of a country should be reflected in the ASF transmission mechanistic model. For example, epidemiological research on ASF virus characteristics in the Republic of Korea should be performed, including the incubation period, infectious period, environmental resistance, or serial interval. In addition, ecological research on wild boar habitat suitability, wild boar movement, or ASF virus-infected wild boar carcass decomposition will also be needed. With the research results, an ASF virus transmission mechanistic model can be applied as an ASF-control strategy decision support tool.

Fig. 1. Hypothetical African swine fever transmission among wild boars for three years of simulation in the Republic of Korea by using a grid-based mechanistic model (the percentage indicated the probability that wild boars in each grid would be infected with African swine fever virus).