Covariate-specific evaluation of continuous biomarker

Summary

Diagnostic tests usually need to operate at a high sensitivity or specificity level in practice. Accordingly, specificity at the controlled sensitivity, or vice versa, is a clinically sensible performance metric for evaluating continuous biomarkers. Meanwhile, the performance of a biomarker may vary across sub-populations as defined by covariates, and covariate-specific evaluation can be informative. In this article, we develop a novel modeling and estimation method for covariate-specific specificity at a controlled sensitivity level. Unlike existing methods which typically adopt elaborate models of covariate effects over the entire biomarker distribution, our approach models covariate effects locally at a specific sensitivity level of interest. We also extend our proposed model to handle the whole continuum of sensitivities via dynamic regression and derive covariate-specific ROC curves. We provide the variance estimation through bootstrapping. The asymptotic properties are established. We conduct extensive simulation studies to evaluate the performance of our proposed methods in comparison with existing methods, and further illustrate the applications in two clinical studies for aggressive prostate cancer.

1 ∣. INTRODUCTION

Evaluation of biomarkers for their diagnostic ability is a common task in biomedical research. It is relatively straightforward to evaluate binary biomarkers using metrics such as sensitivity and specificity. The evaluation of continuous biomarkers, however, is more complicated as a threshold is needed to define the normal and abnormal ranges of the measurement for disease diagnosis. The threshold for a diagnostic test usually needs to attain a high sensitivity or specificity level to keep false negatives or positives, respectively, to minimal e.g., Sanda (2017).¹ As a result, specificity at a controlled sensitivity (or vice versa) has been used as a clinically sensible metric.^2,3

Meanwhile, covariates, such as age, race, and sample collection conditions, may influence biomarkers. Given a desired sensitivity or specificity level, the diagnostic threshold of a biomarker may change in sub-populations as defined by these covariates. Moreover, the diagnostic ability of a biomarker at a fixed threshold may also associate with or be influenced by covariates. Consequently, covariates can confound the assessment of continuous biomarkers, biasing the results if ignored. For example, if the covariates affect the distribution of the biomarker but not the covariate-specific ROC curves, Pepe (2003)⁴ showed that ignoring covariate effects may lead to underestimated diagnostic ability of a biomarker comparing to its actual performance. Therefore, as already recognized and discussed by many existing studies^5,6,7,4, it is important to adjust for covariate effects in the evaluation of continuous biomarkers.

Many existing methods imposed models on both the case and the control biomarker distributions to subsequently induce the covariate effects on the ROC curves.^8,9,10,11,12 For example, Faraggi (2003) adopted the normal linear regression models for both the case and control biomarker distributions.¹¹ The approach of Pepe (1998) was more general by adopting semiparametric models.⁹ Additionally, Inácio de Carvalho et al. (2013)¹² and Inácio and Rodriguez-Álvarez (2021)¹³ developed Bayesian methods based on dependent dirichlet process mixtures to target the whole conditional distribution. Nevertheless, all these methods modeled the covariate effects on the ROC curves in an indirect fashion. Thus their coefficients cannot be directly interpreted with respect to the ROC curve. To address that, several parametric distribution-free (PDF) methods that directly model the ROC curve have been proposed.^5,14,15,16 These PDF methods can accommodate multiple test types and continuous covariates, and they may also target restricted portions of the ROC curve that are of interest. In particular, Alonzo and Pepe (2002) and Cai and Pepe (2002) developed generalized linear models for covariate effects on the ROC curve.^15,16 Even with these PDF methods, the models are still restrictive because they presume covariate effects, as measured in regression coefficients, to be constant over the ROC curve of interest.

As a related problem, covariate adjustment has been developed for test thresholds so as to keep a controlled sensitivity or specificity level uniform across patient sub-populations. Janes and Pepe (2009) developed a non-parametric estimator in the circumstance of discrete covariates.⁶ Our previous work generalized the method by imposing a parsimonious quantile regression model for the thresholds.¹⁷ These methods may provide a biomarker evaluation at covariate-adjusted thresholds for the overall population, but do not permit subpopulation-specific evaluation, as focused on in this article.

In this work, we develop a novel modeling and estimation method for covariate-specific specificity at a controlled sensitivity level. It generalizes the PDF methods by targeting the particular controlled sensitivity level of interest only or accommodating potential varying covariate effects at different sensitivity levels. At the same time, The proposed approach extends our previous work¹⁷ to provide covariate-specific biomarker assessment. We first model the covariate effects among the diseased population by quantile regression, locally at a sensitivity of interest. Subsequently, the covariate-specific specificity is modeled among the non-diseased population by logistic regression. This formulation uses covariate-adjusted thresholds to equally control the sensitivity among sub-populations, meanwhile providing flexibility to estimate specificity for given covariate values. The proposed method starts with a local model for specificity at a controlled sensitivity level, and it extends naturally to covariate-specific ROC curves by addressing the continuous spectrum of sensitivity levels. It is worthwhile to point out that the same method directly applies to covariate-specific sensitivity at controlled specificity by switching the roles of cases and controls.

The subsequent sections are organized as follows. Section 2 considers the covariate-specific specificity locally at a controlled sensitivity level. Inference and asymptotic properties are established. Section 3 extends the proposal to covariate-specific ROC curve with related inference and asymptotic properties. We evaluate the performance of our proposed estimator and inference in the simulation studies presented in Section 4. Section 5 illustrates our proposals with applications to aggressive prostate cancer. Discussions and remarks are presented in Section 6. Technical proofs are relegated to the Appendix. The software of our proposed methods is available through R/CRAN package caROC.

2 ∣. COVARIATE-ADJUSTED SPECIFICITY AT A CONTROLLED SENSITIVITY LEVEL

Denote the continuous biomarker of interest by $M_1$ and $M_0$ for cases and controls, respectively. Let their associated covariates be ${\mathit{Z}}_1$ and ${\mathit{Z}}_0$, respectively. The covariates could be discrete or continuous. Write the conditional biomarker distribution for cases as $F_1(t;\mathit{z})\equiv \text{Pr}(M_1\le t\mid {\mathit{Z}}_1=\mathit{z})$ and for controls as $F_0(t;\mathit{z})\equiv \text{Pr}(M_0\le t\mid {\mathit{Z}}_0=\mathit{z})$. The corresponding conditional quantile function for the cases is $F_1^{-1}(\cdot ;\mathit{z})$. To control the sensitivity level at ${\rho }_0$, we adopt a quantile regression model on the cases as follows:

$$F_1^{-1}(1-{\rho }_0;{\mathit{z}}_1)=(1,{\mathit{z}}_1^T)\beta ,$$ (1)

where $\beta$ is the regression coefficient. One is added to the covariate vector to incorporate an intercept. Denote the true value of $\beta$ by ${\beta }_0$.

Since the covariate-specific performance of the biomarker is of interest, we further model specificity over covariates in the control population. A logistic regression model is adopted, with the threshold $(1,{\mathit{Z}}_0^T){\beta }_0$ imposed on the biomarker to control sensitivity at ${\rho }_0$ uniformly among the subpopulations:

$$\text{Pr}\{M_0\le (1,{\mathit{Z}}_0^T){\beta }_0\mid {\mathit{Z}}_0={\mathit{z}}_0,\gamma \}=\frac{\text{exp}\{(1,{\mathit{z}}_0^T)\gamma \}}{1+\text{exp}\{(1,{\mathit{z}}_0^T)\gamma \}},$$ (2)

where $\gamma$ is the regression coefficient of interest. A logit link function is used here but it can be replaced by other link functions, e.g., probit link. Write the true value of $\gamma$ as ${\gamma }_0$. The measure ${\varphi }_0(\mathit{z}\mid {\beta }_0,{\gamma }_0)\equiv \text{Pr}\{M_0\le (1,{\mathit{Z}}_0^T){\beta }_0\mid {\mathit{Z}}_0=\mathit{z},{\gamma }_0\}$ gauges the covariate-adjusted specificity at the controlled sensitivity level for the subpopulation with covariate value $\mathit{z}$.

Observe that our model is more general than existing methods in many aspects. Pepe (1998) estimated the biomarker distribution $F_0(\cdot ;\mathit{z})$ and $F_1(\cdot ;\mathit{z})$ using semiparametric location-scale regression models⁹, whereas Faraggi (2003) adopted normal linear regression models for both distributions.¹¹ It is easy to see that both models on $F_1$ are more restrictive than our quantile regression model (1). The normal linear regression model on $F_0$ of Faraggi (2003) implies the probit counterpart of our model (2).¹¹ Thus, our model (2) is also more general than the model of Faraggi (2003) on $F_0$.¹¹ In comparison with the PDF methods of Alonzo et al. (2002)¹⁵ and Cai and Pepe (2002)¹⁶, our model (2) is much less restrictive in that the covariate effects are modeled for the controlled sensitivity level only, rather than assumed the same across various sensitivity levels.

2.1 ∣. Estimation

Consider a case cohort study. Suppose the data contain $n_1$ i.i.d. case samples, $(M_{1i},{\mathit{Z}}_{1i})$, $i=1,\cdots ,n_1$ and $n_0$ i.i.d. control samples, $(M_{0j},{\mathit{Z}}_{0j})$, $j=1,\cdots ,n_0$. The point estimator for ${\beta }_0$ could be obtained using the standard quantile regression method by Koenker and Bassett (1978).¹⁸ After ${\beta }_0$ is estimated by $\widehat{\beta }$, a binary diagnostic result based on the estimated threshold is computed for every control sample, $I\{M_{0j}\le (1,{\mathit{Z}}_{0j}^T)\widehat{\beta }\}$, $j=1,\cdots ,n_0$. The logistic regression is then performed with the binary result over the covariates in the control sample to obtain the point estimation for ${\gamma }_0$. The estimator $(\widehat{\beta },\widehat{\gamma })$ is the solution to the following set of estimating equations:

$${\mathit{G}}_n\{\beta ,\gamma \}=\left(\begin{array}{c}\hfill n_1^{-1}\sum _{i=1}^{n_1}{\tilde{\mathit{Z}}}_{1i}[I\{M_{1i}>{\tilde{\mathbf{Z}}}_{1i}^T\beta \}-{\rho }_0]\hfill \\ \hfill n_0^{-1}\sum _{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}\left([I\{M_{0j}\le {\tilde{\mathbf{Z}}}_{0j}^T\beta \}-\text{exp}\{{\tilde{\mathbf{Z}}}_{0j}^T\gamma \}∕\left[1+\text{exp}\{{\tilde{\mathbf{Z}}}_{0j}^T\gamma \}\right]\right)\hfill \end{array}\right),$$

where ${\tilde{\mathbf{Z}}}_{1i}=(1,{\mathbf{Z}}_{1i}^T{)}^T$ and ${\tilde{\mathbf{Z}}}_{0j}=(1,{\mathbf{Z}}_{0j}^T{)}^T$. To estimate the variance for the proposed estimators, the standard non-parametric bootstrap can be applied to cases and controls separately. That is, within cases or controls, the pairs of biomarker and covariates are resampled.

2.2 ∣. Asymptotic study

We study the asymptotic properties of the estimators $\widehat{\beta }$ and $\widehat{\gamma }$. The regularity conditions are given as follows:

Condition 1. The control and case size ratio $n_0∕n_1$ approaches a constant $c>0$ as $n_0+n_1\to \infty$.

Condition 2. Covariates ${\mathbf{Z}}_1$ and ${\mathbf{Z}}_0$ are bounded.

Condition 3. Both $E({\tilde{\mathbf{Z}}}_1^{\otimes 2})$ and $E({\tilde{\mathbf{Z}}}_0^{\otimes 2})$ are nonsingular, where ${\mathit{v}}^{\otimes 2}=\mathit{v}{\mathit{v}}^T$ for vector $\mathit{v}$.

Condition 4a. Both $F_1(t;\mathbf{z})$ and $F_0(t;\mathbf{z})$ are differentiable at the threshold $t={\tilde{\mathit{z}}}^T{\beta }_0$ with derivative bounded away from 0 and ∞ uniformly in $\mathbf{z}$ over the supports of ${\tilde{\mathit{Z}}}_1$ and ${\tilde{\mathit{Z}}}_0$, respectively.

All these conditions are standard and mild. Previous works using quantile regression have adopted similar assumptions.^19,17

Theorem 1. Suppose that the quantile regression model for the cases given in (1) and the logistic regression model for the controls given in (2) hold locally at the controlled sensitivity level ${\rho }_0$, along with Conditions 1, 2, 3, and 4a. Then, $({\widehat{\beta }}^T,{\widehat{\gamma }}^T{)}^T$ is consistent almost surely for $({\beta }_0^T,{\gamma }_0^T{)}^T$. In addition, $\sqrt{n_0}\{(\widehat{\beta }-{\beta }_0{)}^T$, $(\widehat{\gamma }-{\gamma }_0{)}^T{\}}^T$ converges to a bivariate normal distribution with mean 0 and variance

$$V=\left(\begin{array}{cc}\hfill V_{\beta }\hfill & \hfill C_{\beta ,\gamma }\hfill \\ \hfill C_{\beta ,\gamma }\hfill & \hfill V_{\gamma }\hfill \end{array}\right),$$

where $V_{\beta }=c{\rho }_0(1-{\rho }_0){\mathit{D}}_1^{-1}{\mathit{D}}_0{\mathit{D}}_1^{-1}$, $C_{\beta ,\gamma }=c{\rho }_0(1-{\rho }_0){\mathit{D}}_3^{-1}{\mathit{D}}_2{\mathit{D}}_1^{-1}{\mathit{D}}_0{\mathit{D}}_1^{-1}$,

$$V_{\gamma }={\mathit{D}}_3^{-1}+c{\rho }_0(1-{\rho }_0){\mathit{D}}_3^{-1}{\mathit{D}}_2{\mathit{D}}_1^{-1}{\mathit{D}}_0{\mathit{D}}_1^{-1}{\mathit{D}}_2^T({\mathit{D}}_3^{-1}{)}^T,$$

and ${\mathit{D}}_0=E{\tilde{\mathit{Z}}}_1^{\otimes 2}$, ${\mathit{D}}_1=E\{F_1^{\prime }({\tilde{\mathit{Z}}}_1^T{\beta }_0){\tilde{\mathit{Z}}}_1^{\otimes 2}\}$, ${\mathit{D}}_2=E\{F_0^{\prime }({\tilde{\mathit{Z}}}_0^T{\beta }_0){\tilde{\mathit{Z}}}_0^{\otimes 2}\}$, and ${\mathit{D}}_3=E[{\tilde{\mathit{Z}}}_0^{\otimes 2}\text{exp}({\tilde{\mathit{Z}}}_0^T{\gamma }_0)∕\{1+\text{exp}({\tilde{\mathit{Z}}}_0^T{\gamma }_0){\}}^2]$.

Note that $V_{\gamma }$ has two components. The second component, $c{\rho }_0(1-{\rho }_0){\mathit{D}}_3^{-1}{\mathit{D}}_2{\mathit{D}}_1^{-1}{\mathit{D}}_0{\mathit{D}}_1^{-1}{\mathit{D}}_2^T({\mathit{D}}_3^{-1}{)}^T$, is the additional variabilities in $\widehat{\gamma }$, due to the estimation of ${\beta }_0$. For given covariate $\mathit{z}$, since $\varphi (\mathit{z}\mid \widehat{\beta },\widehat{\gamma })$ is a continuous function of $\widehat{\gamma }$, the asymptotic properties for $\varphi (\mathit{z}\mid \widehat{\beta },\widehat{\gamma })$ can be established by applying the continuous mapping theorem and delta method.

3 ∣. COVARIATE-SPECIFIC ROC CURVE

The local model in (1) and (2) pertains to a given sensitivity level ${\rho }_0$. This can be naturally extended to the whole spectrum of sensitivity values $\rho \in (0,1)$ to obtain a global model. For cases, the quantile regression model for any sensitivity $\rho \in (0,1)$ becomes

$$F_1^{-1}(1-\rho ;\mathit{z})={\tilde{\mathit{z}}}_1^T\beta (\rho ),\forall \rho \in (0,1),$$ (3)

and for controls, the coefficients of logistic regression also vary with $\rho$

$$\text{Pr}\{M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T\beta (\rho )\mid {\tilde{\mathit{Z}}}_{0j}={\tilde{\mathit{z}}}_{0j}\}=\frac{\text{exp}\{{\tilde{\mathit{z}}}_{0j}^T\gamma (\rho )\}}{1+\text{exp}\{{\tilde{\mathit{z}}}_{0j}^T\gamma (\rho )\}},\forall \rho \in (0,1).$$ (4)

Again, the logit link here can be replaced by other link functions. Since $F_1(\cdot ,\mathit{z})$ and $F_0(\cdot ,\mathit{z})$ are distribution functions for all $\mathit{z}$, there are natural constraints on the coefficient processes, $\beta (\rho )$ and $\gamma (\rho )$ in the preceding models. Obviously, $\beta (\rho {)}^T\tilde{\mathit{z}}$ needs to be non-increasing in $\rho$ for all $\tilde{\mathit{z}}$ in Equation (3). With $\beta (\rho )$ being differentiable, that is equivalent to ${\beta }^{\prime }(\rho {)}^T\tilde{\mathit{z}}\le 0$ for all $\tilde{\mathit{z}}$. For the controls with any $\tilde{\mathit{z}}$,

$$\frac{\partial \text{Pr}(M_0\le t\mid \tilde{\mathit{z}})}{\partial t}\ge 0.$$

Plugging the right-hand side of (4), we have $[{\gamma }^{\prime }(\rho {)}^T\tilde{\mathit{z}}]∕[{\beta }^{\prime }(\rho {)}^T\tilde{\mathit{z}}]\ge 0$, $\forall \tilde{\mathit{z}}$. Given (3) holds, the constraint simplifies to ${\gamma }^{\prime }(\rho {)}^T\tilde{\mathit{z}}\le 0$ for all $\tilde{\mathit{z}}$.

Of course, the above general model is more restrictive than the earlier local model. Nevertheless, the covariate effects are allowed to vary over various sensitivity levels. Thus, it remains to be more general than the existing methods^9,11,15,16, just like the local model as discussed before.

We could apply the estimation procedure developed for local model to estimate the parameters of (3) and (4) in a pointwise way based on the estimating equations:

$${\mathit{G}}_n\{\beta (\rho ),\gamma (\rho )\}=\left(\begin{array}{c}\hfill n_1^{-1}\sum _{i=1}^{n_1}{\tilde{\mathit{Z}}}_{1i}[I\{M_{1i}>{\tilde{\mathbf{Z}}}_{1i}^T\beta (\rho )\}-\rho ]\hfill \\ \hfill n_0^{-1}\sum _{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}\left([I\{M_{0j}\le {\tilde{\mathbf{Z}}}_{0j}^T\beta (\rho )\}-\text{exp}\{{\tilde{\mathbf{Z}}}_{0j}^T\gamma (\rho )\}∕\left[1+\text{exp}\{{\tilde{\mathbf{Z}}}_{0j}^T\gamma (\rho )\}\right]\right)\hfill \end{array}\right).$$

The computational burden may seem heavy as the solutions may be needed for each and every $\rho \in (0,1)$. However, the estimator $\widehat{\beta }(\rho )$ is actually a step function and can be efficiently solved by the parametric programming algorithm described in Koenker (2005).¹⁹ Portnoy (1991)²⁰ showed that the number of breakpoints is ${\mathit{O}}_p(n\log n)$, where $p$ is the number of covariates and $n$ is the sample size. For logistic regression, one only needs to solve the estimator $\widehat{\gamma }(\rho )$ when $I\{M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T\beta (\rho )\}$ changes, which is a subset of the breakpoints in quantile regression. Our R/CRAN package, caROC, provides efficient implementations for both local and global models.

3.1 ∣. An asymptotic analysis

To derive the asymptotic properties of the global model, we strengthen Condition 4a.

Condition 4b. Both $F_1(t;\mathit{z})$ and $F_0(t;\mathit{z})$ have density functions $f_1(t;\mathit{z})$ and $f_0(t;\mathit{z})$, respectively, which are continuous in $t$ for given $\mathit{z}$ and bounded uniformly in $t$ and $\mathit{z}$ over the supports of ${\mathit{Z}}_1$ and ${\mathit{Z}}_0$, respectively. Meanwhile, ${\beta }_0(\cdot )$ is continuously differentiable on $[{\rho }_1,{\rho }_2]$ for any ${\rho }_1$ and ${\rho }_2$ such that $0<{\rho }_1<{\rho }_2<1$.

This condition is also standard and has been used before. For example, Janes and Pepe (2009) used similar conditions for the existence of density function when the ROC curve was of interest.⁶ Similarly, the differentiability of the quantile regression estimand has been adopted in Koenker (2005).¹⁹

Theorem 2. Suppose that the quantile regression model for the cases given in (3) and the logistic regression model for controls given in (4) holds globally over sensitivity levels ${\rho }_1$ through ${\rho }_2$ with $0<{\rho }_1<{\rho }_2<1$, along with Conditions 1, 2, 3, and 4b. Then, $\{\widehat{\beta }(\rho {)}^T,\widehat{\gamma }(\rho {)}^T{\}}^T$ converges almost surely to $\{{\beta }_0(\rho {)}^T,{\gamma }_0(\rho {)}^T{\}}^T$ uniformly over $\rho \in [{\rho }_1,{\rho }_2]$. Furthermore, $\sqrt{n_0}[\{\widehat{\beta }(\rho )-{\beta }_0(\rho ){\}}^T$, $\{\widehat{\gamma }(\rho )-{\gamma }_0(\rho ){\}}^T{]}^T$ converges weakly to a Gaussian process over $\rho \in [{\rho }_1,{\rho }_2]$.

3.2 ∣. Monotonization and inference

There is inherent monotonicity in covariate-specific ROC curves for all $\mathit{z}$, and accordingly ${\beta }_0(\cdot )$ and ${\gamma }_0(\cdot )$ are necessarily monotonicity-respecting. However, as both quantile regression and logistic regression are solved in a point-wise fashion, lack of respect for such monotonicity may arise in $\widehat{\beta }$, $\widehat{\gamma }$, and subsequently the estimated covariate-specific ROC curves and so do illogical results. The monotonicity-respecting restoration method of Huang (2017)²¹ may be used, targeting either $\widehat{\beta }(\cdot )$ and $\widehat{\gamma }(\cdot )$ or the estimated covariate-specific ROC curves. In our related work¹⁷, the regression-based and the ROC-based monotonization method demonstrate comparable accuracy in the estimations, but ROC-based method has better computational performance. In this work, we shall adopt ROC-based monotonization. Consider an estimated covariate-specific ROC curve $1-\widehat{\varphi }(\cdot )$, which is a step function; note that we view an ROC curve as 1-specificity versus sensitivity in this article. Denote the set of break points along with boundary points, i.e., 0 and 1, by $\Pi$. From a starting point ${\rho }_0$, we find the left nearest monotonicity-respecting neighbor in $\Pi$ as $\max \{\rho \in \Pi :\rho <{\rho }_0,\widehat{\varphi }(\rho )-\widehat{\varphi }({\rho }_0)>0\}$. Each identified point then has its own left nearest monotonicity-respecting neighbor, and we repeat this procedure until no such neighbor exists. In the opposite direction, we can similarly identify the right nearest monotonicity-respecting neighbor of ${\rho }_0$, $\text{min}\{\rho \in \Pi :\rho >{\rho }_0,\widehat{\varphi }(\rho )-\widehat{\varphi }({\rho }_0)<0\}$, and recursively identify all the right monotonicity-respecting points. We denote the set containing all these points including the starting one ${\rho }_0$ by $ℳ$. A monotonized covariate-specific ROC curve is obtained by linear interpolating $1-\widehat{\varphi }(\rho )$ over the points in $ℳ$. As discussed in Huang (2017)²¹, the monotonicity-restored estimator is robust to the potential tail instability of the original estimators as long as ${\rho }_0$ is selected away from the tails. Additionally, Huang (2017)²¹ established the asymptotic equivalence between the monotonized and original esitmators. Therefore, our asymptotic theory applies for estimators with monotonicity restoration as well.

For inference, the procedures described for the local model could be adopted if a point on the ROC curve is of interest. When inference of the whole ROC curve is needed, one may construct a confidence band using a non-parametric bootstrap. Conditional on the data, the distribution of $n_0^{1∕2}\{{\varphi }^{\ast }(\cdot \mid \mathit{z})-\widehat{\varphi }(\cdot \mid \mathit{z})\}$ is asymptotically the same as $n_0^{1∕2}\{\widehat{\varphi }(\cdot \mid \mathit{z})-{\varphi }_0(\cdot \mid \mathit{z})\}$. Thus, given a set of interested covariates $\mathit{z}$, the $\alpha$-level equal-precision confidence band of $\widehat{\varphi }(\rho \mid \mathit{z})$ can be constructed by

$$\widehat{\varphi }(\rho \mid \mathit{z})\pm {\eta }_{\alpha }\text{SE}\{\widehat{\varphi }(\rho \mid \mathit{z})\},$$

where $\rho \in [{\rho }_1,{\rho }_2]$ with $0<{\rho }_1<{\rho }_2<1$ and $\text{SE}\{\widehat{\varphi }(\rho \mid \mathit{z})\}$ is the standard error of $\widehat{\varphi }(\rho \mid \mathit{z})$. ${\eta }_{\alpha }$ is the estimated $\alpha$-percentile of ${\text{sup}}_{\rho \in [{\rho }_1,{\rho }_2]}[\mid {\varphi }^{\ast }(\rho \mid \mathit{z})-\widehat{\varphi }(\rho \mid \mathit{z})\mid ∕\text{SE}\{\widehat{\varphi }(\rho \mid \mathit{z})\}]$. $\text{SE}\{\widehat{\varphi }(\rho \mid \mathit{z})\}$ is the standard error obtained from bootstrap resamples. For a monotonized ROC curve, the confidence band can be similarly obtained by replacing the $\widehat{\varphi }(\rho \mid \mathit{z})$ and $\text{SE}\{\widehat{\varphi }(\rho \mid \mathit{z})\}$ with their monotonized versions.

4 ∣. SIMULATIONS

We evaluate the finite sample properties of the proposed method through two simulation studies. In each study, we compare the proposed method with three existing covariate-specific ROC estimation methods: Pepe (1998)⁹, Faraggi (2003)¹¹, and Inácio de Carvalho et al. (2013)¹², which have been implemented in R/CRAN package ROCnReg.²² These existing methods are adapted for covariate-specific specificity at controlled sensitivity levels by switching the roles of cases and controls. Unfortunately, many other methods do not have their software readily available and thus are not included for comparison.

Suppose that the biomarker in cases and controls rely on two continuous covariates $Z_1$ and $Z_2$, both of which follow uniform distribution in region [0, 1]. In the first simulation setting, the biomarker in cases $M_1$ is associated with the two covariates under the quantile regression model (1) with coefficients $\beta ({\rho }_0)=[\log \{-\log ({\rho }_0)\}$, $1-{\rho }_0$, $(1-{\rho }_0{)}^2{]}^T$, $\forall {\rho }_0\in [0,1]$. The biomarker in controls $M_0$ is associated with the two covariates under the logistic regression model (2) with coefficients $\gamma ({\rho }_0)=(\log \text{it}[\Phi \{1-{\Phi }^{-1}({\rho }_0)\}]\phantom{)}$, $5(1-{\rho }_0)$, ${\phantom{(}5(1-{\rho }_0{)}^2)}^T$, $\forall {\rho }_0\in [0,1]$, where $\log \text{it}(x)=\log \{x∕(1-x)\}$ and $\Phi (\cdot )$ is the cumulative density function for standard normal distribution. The true specificities at controlled sensitivity levels for given observation $\tilde{\mathit{z}}$ could be obtained from ${\varphi }_0(\tilde{\mathit{z}})=\text{exp}\{{\tilde{\mathit{z}}}^T\gamma ({\rho }_0)\}∕[1+\text{exp}\{{\tilde{\mathit{z}}}^T\gamma ({\rho }_0)\}]$.

The first simulation setting uses the modeling assumptions that our proposed model holds but not the three existing ones. To provide a fair comparison with the three existing methods, we design the second simulation setting that all three models hold. In the second setting, the case biomarkers is associated with the two covariates through normal distribution $Y_{1j}\sim N(0.3+Z_{1j}+2\cdot Z_{2j},1^2)$ and control biomarkers $Y_{0i}\sim N(0.2+0.5\cdot Z_{1i}+Z_{2i},{0.5}^2)$. Denote the distribution functions for $Y_1$ and $Y_0$ by $F_1(\cdot ;\mathit{z})$ and $F_0(\cdot ;\mathit{z})$. For a given sensitivity $\rho$ and covariates $\mathit{z}$, the covariate-specific specificity is $F_0\left[F_1^{-1}(1-\rho ;\mathit{z});\mathit{z}\right]$.

The estimation accuracy of the proposed method and the performance of the bootstrap inference are evaluated at three different covariate values and four sensitivity levels. Table 1 reports the performance using the proposed method with bootstrap-based inference as well as using the semiparametric method proposed by Pepe (1998)⁹ and Faraggi (2003)¹¹, respectively, under covariate value $\tilde{\mathit{z}}=(1,0.5,0.5{)}^T$. The four blocks of rows correspond to the results under different specified sensitivity levels. All presented results are summarized over 5000 Monte Carlo datasets. First, our proposed method overall achieves good accuracy for all covariate values. The estimation accuracy is higher when the controlled sensitivity is away from the 1 (${\rho }_0=0.80,0.85$) compared to near the border (${\rho }_0=0.95$). Our confidence intervals have good coverage rates in most sample sizes and covariate settings. A logit-transformation based 95% confidence interval is adopted here, as the logit-transformation based confidence interval is more stable than the regular confidence interval when sensitivity ${\rho }_0$ is near 0 or 1. Second, the bootstrap inference has a stable and good variance estimation as well as coverage rate even when sample size is relatively small. The standard errors are very close to the empirical standard deviations. Lastly, compared with the proposed method, Pepe (1998)⁹ and Faraggi (2003)¹¹ overall have larger bias, worse standard error estimations and lower coverage probabilities. The semiparametric method by Pepe (1998)⁹ has much better performance than the results by Faraggi (2003)¹¹.

TABLE 1.

Estimation and inference results under the first simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at covariate value $\mathit{z}=(0.5,0.5{)}^T$.

n1 = n0	Proposed method				Pepe (1998)				Faraggi (2003)
	Bias	SD	SE	LCov	Bias	SD	SE	LCov	Bias	SD	SE	LCov
${\rho }_0=0.95$
100	174	1061	1126	96.0	348	992	936	91.4	1250	866	782	59.0
200	78	710	779	96.4	181	687	660	92.7	1250	622	571	41.3
500	22	435	469	96.1	47	429	415	94.1	1230	391	371	12.2
1000	21	306	323	95.2	6	298	292	94.0	1230	275	264	1.22
5000	3	136	140	95.1	−22	135	130	93.6	1230	124	119	0
${\rho }_0=0.90$
100	134	1086	1184	97.2	256	1030	963	92.1	876	769	704	68.1
200	71	752	807	96.0	123	728	693	93.1	886	543	506	55.4
500	20	457	492	96.0	19	459	443	94.3	872	342	326	27.9
1000	19	329	343	95.2	−11	326	313	93.8	871	240	231	6.32
5000	2	147	150	95.3	−34	144	140	93.8	874	108	104	0
${\rho }_0=0.85$
100	93	1035	1113	97.2	173	985	901	92.9	406	665	614	81.6
200	53	711.4	766	96.6	85	692	659	93.8	415	464	437	76.9
500	17	441	473	96.0	2	440	424	93.9	406	292	280	64.9
1000	15	320	329	94.8	−23	314	303	94	405	206	198	45.8
5000	−1	142	145	95.1	−38	141	136	92.8	408	92.4	88.7	0.8
${\rho }_0=0.80$
100	63	928	998	97.4	106	869	799	93.3	−19	573	532	90.9
200	44	648	685	96.5	41	622	587	93.9	−11	397	377	92.2
500	10	399	424	96.0	−12	391	381	94.6	−18	250	240	93.0
1000	12	286	297	95.2	−31	282	272	93.7	−19	177	170	93.2
5000	−2	128	131	95.3	−39	126	122	92.5	−16	79.1	75.9	93.3

Bias, $(\widehat{\varphi }-{\varphi }_0)\times {10}^4$; SD, standard deviation ×10⁴; SE, standard error estimated using bootstrap ×10⁴; LCov (%), coverage rates of logit transformation-based 95% confidence interval.

Table S1-S3 presents the performance of all three methods with three different covariate selections. The results are also summarized over the same 5000 simulation datasets as in Table 1. As discussed in the introduction, Pepe (1998)⁹ and Faraggi (2003)¹¹ adjusted covariate effects using a general model over the entire ROC curve, which may not be able to handle the changing covariate effects well. We find the proposed method has good accuracy and superior coverage probabilities compared to the two existing methods in all covariate selections. This comparison may not be completely fair since the data is generated based on our model. However, it shows that the methods by Pepe (1998)⁹ and Faraggi (2003)¹¹ may not provide accurate ROC estimation and inference when the covariate effect changes with specificity levels, as is the situation in our simulation setting.

Table 2 presents the performance of the three methods at covariate value $\tilde{\mathit{z}}=(1,0.5,0.5{)}^T$ in the second simulation setting. Table S4-S6 present the simulation results using our proposed method and the two existing methods in this setting at the other two covariate values. The model assumption holds for all methods in this setting. All the results are summarized over 5000 Monte Carlo datasets. As expected, we observe that the two existing methods show improved biases results compared to the ones from the previous setting. Meanwhile, our proposed method demonstrates comparable and sometimes even better results in comparison to the two existing methods, suggesting the favorable performance and robustness of the proposed method. The existing methods of Pepe (1998)⁹ and Faraggi (2003)¹¹ have slightly higher efficiency compared to the proposed method. This is not surprising as our proposal uses a non-parametric approach to model the covariate effect on the case population.

TABLE 2.

Estimation and inference results under the second simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.5,0.5{)}^T$ by our proposed method and two existing methods^9,11 are estimated and presented.

$n_1=n_0$	Proposed method				Pepe (1998)				Faraggi (2003)
	Bias	SD	SE	LCov	Bias	SD	SE	LCov	Bias	SD	SE	LCov
${\rho }_0=0.95$
100	136	1025	1073	93.5	468	1000	932	91.1	130	695	654	91.1
200	63	658	734	95.7	242	672	644	93.4	68	475	456	92.7
500	−16	401	432	96.7	88	406	389	94.1	21	294	282	93.3
1000	−40	281	297	95.9	49	280	275	94.2	13	206	200	93.5
5000	−50	125	128	94.0	8	126	122	93.4	2	91.7	89	93.3
${\rho }_0=0.90$
100	87	1377	1495	97.4	389	1300	1180	92.6	76	1030	944	91.3
200	37	957	1039	97.1	210	915	861	93.5	46	727	686	92.8
500	−42	622	642	95.5	68	578	557	94.2	8	457	439	93.1
1000	−55	432	449	95.3	42	409	394	94.2	9	322	313	93.5
5000	−60	193	196	94.0	9	184	178	93.3	1	145	141	93.0
${\rho }_0=0.85$
100	90	1395	1514	97.8	244	1270	1160	92.8	9	1060	959	91.5
200	54	976	1045	96.7	135	911	857	93.5	15	746	701	92.9
500	11	625	652	95.5	48	577	558	94.1	−6	468	451	93.1
1000	11	440	454	95.5	27	407	398	94.4	3	330	321	93.1
5000	8	195	200	95.0	3	187	179	93.6	0	149	144	93.3
${\rho }_0=0.80$
100	78	1206	1328	98.2	139	1100	1010	93.4	−33	931	844	91.9
200	82	845	909	96.6	87	801	750	93.4	−7	656	614	93.0
500	58	540	562	95.4	22	504	483	93.8	−13	410	395	93.1
1000	63	381	393	94.9	16	353	346	94.1	−1	289	281	93.2
5000	63	170	171	93.3	3	160	156	93.8	−1	131	126	93.1

Bias, $(\widehat{\varphi }-{\varphi }_0)\times {10}^4$; SD, standard deviation ×10⁴; SE, standard error estimated using bootstrap ×10⁴; LCov (%), coverage rates of logit transformation-based 95% confidence interval.

The comparison between our proposed method and Inácio de Carvalho et al. (2013)¹² is presented in Table S5-10 and Figure S1-8. The implementation of Inácio de Carvalho et al. (2013) is slower than our proposed and two other existing methods for the construction of confidence interval. Thus we only perform 100 Monte Carlo iterations and summarize the results in supplementary materials, not 5000 Monte Carlo iterations as shown in Table 1 and 2. In the first simulation setting (Table S5-7), we observe that the proposed method generally has smaller bias and better coverage probability for the setting (0.5,0.5)^T, (0.25,0.75)^T, and (0.75,0.75)^T. In settings of (0.25,0.25)^T and (0.75,0.25)^T, Inácio de Carvalho et al. (2013) are better in some sample sizes. In the second simulation setting with Gaussian data (Table S8-10), the two methods are mostly comparable in bias and covarage probability. However, Inácio de Carvalho et al. (2013) has a smaller estimation variance compared to our proposed method, as our method has less assumptions. The advantage of the proposed method in computational performance is substantial. For the sample size of 5000, the Inácio de Carvalho et al. (2013) method takes about 3.8 minutes to construct confidence interval at a given sensitivity level (Time_CI) while the proposed method with bootstrap confidence interval construction only takes about 3 seconds. However, the construction of confidence band using bootstrap by our method (Time_CB) is slower than Inácio de Carvalho et al. (2013) when the sample size is very large (e.g., 1000 or 5000).

We also evaluate the performance our method with monotonicity restoration under the two simulations. Table S11 shows the bias, standard deviation, standard error, and the coverage probability. As shown in Huang (2017)²¹, the monotonized and the original estimators are asymptotically equivalent. Comparing Table S11 versus Table 1 and 2 in the main manuscript, we find that the results using the proposed method with monotonicity restoration have similar performance as the method without monotonicity restoration, which is consistent with the previous findings²¹. Overall, the results using our method with monotonicity restoration show good variance estimation and coverage probability.

5 ∣. ILLUSTRATION WITH TWO CLINICAL DATASETS

Many previous studies have reported improved outcomes from treating aggressive prostate cancer patients at an early stage.^23,24 However, such survival benefits can be undermined by harms from treating over-diagnosed indolent prostate cancer patients. To improve the diagnostic accuracy, biomarkers for aggressive prostate cancer usually need to achieve high specificity while maintaining sensitivity at a desirable level to provide clinical utility. Below, we illustrate the usage of the proposed method through a multi-center clinical study for aggressive prostate cancer.

The whole NCI-EDRN dataset was collected by researchers from Harvard University, Cornell University and Michigan University over the past two decades.^1,25 It enrolled a total of 2261 men and collected their pre-diagnosis biomarkers, characteristics and the biopsy-confirmed diagnosis. Among them, 615 were aggressive prostate cancer patients with Gleason scores ≥ 7 and the rest had indolent prostate cancer or were normal controls. We provide evaluations of two biomarkers, prostate-specific antigen (PSA) and prostate health index (phi). In the first part of the analysis, we will use all patients and apply the proposed method to evaluate PSA. Since phi is a much newer biomarker than the PSA, only a subset of 502 men in the data has phi measurement and will be included in the second part of the analysis.

5.1 ∣. Covariate-specific evaluation of PSA

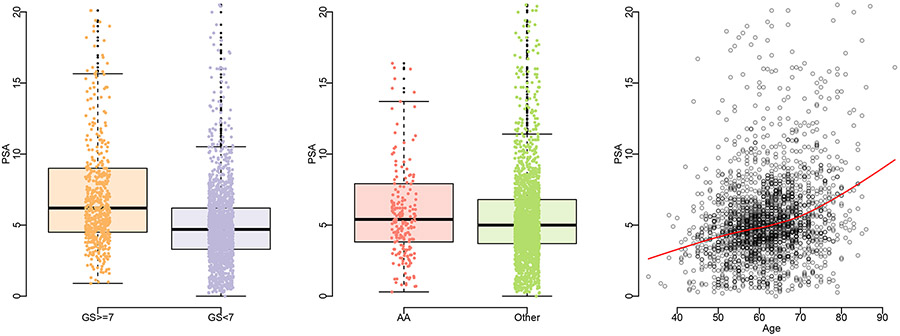
The data from the total 2261 men are used for the evaluation of PSA. The left panel of Figure 1 shows that the subjects with Gleason score equal to or greater than 7 tend to have higher PSA values. The impacts of patient characteristics on PSA have been reported before in many publications. For example, it is known that elder men and African American men tend to have elevated PSA values.^26,27 The right panel of Figure 1 demonstrates a clear trend of higher PSA for elder men. Although we have a very unbalanced distribution of being African American (AA) - only 219 out of 2261 men are African American men, we still observe consistent covariate effects of AA on PSA as shown in the middle panel of Figure 1. As a nonlinear trend of age on PSA can be observed in Figure 1, we also consider including squared age into the modeling. However, the term is not significant in both the quantile regression and logistic regression, and thus we exclude the squared term from the final analysis. Motivated by all the observations, we include age and being African American (AA) as covariates in the following evaluation of PSA.

FIGURE 1.

Exploratory plots of PSA versus patient characteristics in the NCI-EDRN cohort.

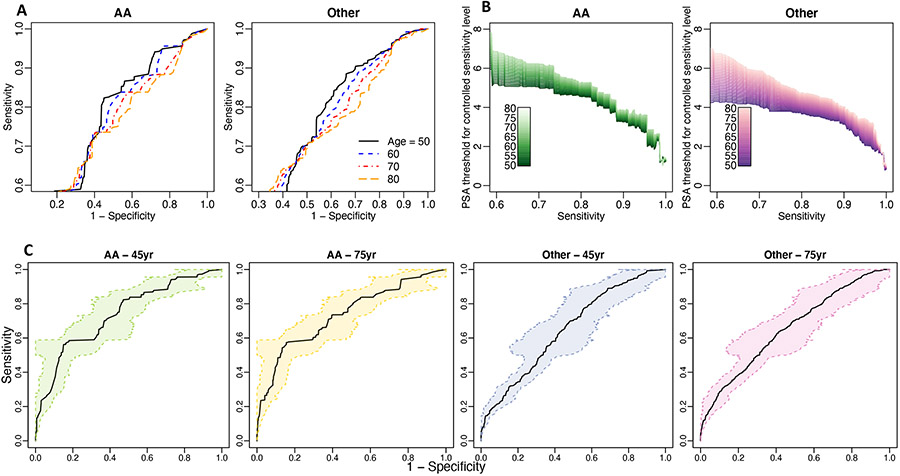
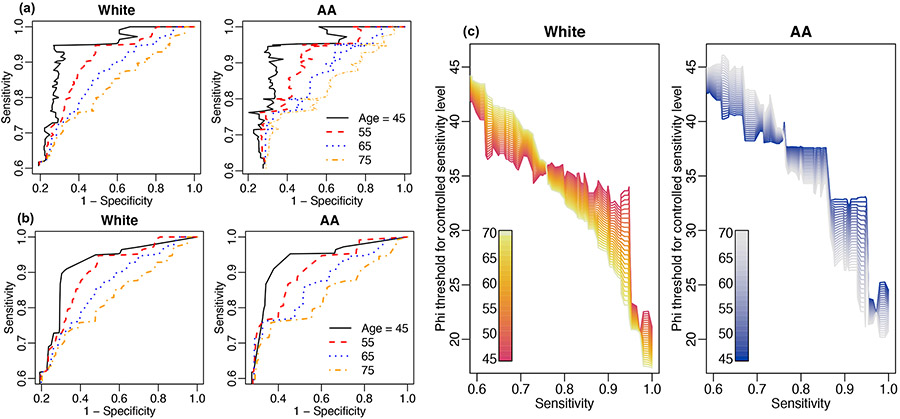
Figure 2 presents the results obtained from applying the proposed methods. Panel A demonstrates that PSA has better specificity at high controlled sensitivity levels for younger patients (age = 50) than older patients (age = 80) in both African American and other races. Our results indicate that older and African American men need higher PSA thresholds to achieve the same controlled sensitivity level (Figure 2 Panel B). This figure could help clinicians to make diagnostic decisions for patients in different age and race groups controlling sensitivity at the same high level. We then obtain the 95% bootstrap-based confidence bands of the monotonized ROC curves for age 45 and 75 years old in both African American and other subpopulations (Figure 2 Panel C).

FIGURE 2.

Results from applying the proposed method to PSA of the NCI-EDRN cohort. Panel A is the monotonized ROC curve. Panel B is the PSA threshold for controlled sensitivity level for different race and age groups. Panel C is the 95% bootstrap-based confidence band for the monotonized ROC curve in different subpopulations.

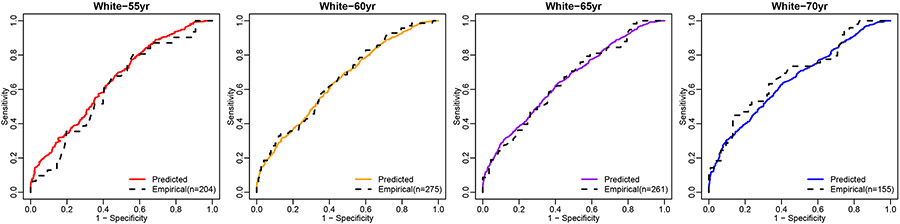
We also perform a model check with this relatively large dataset. Without model specification, calculating covariate-specific ROC curve requires sub-setting the data at each of the covariate values. When datasets have limited sample sizes, sub-setting data to each age level generally results in too few data points to construct an ROC curve. The large sample size of this NCI-EDRN dataset provides an opportunity for us to scrutinize our model fitting by comparing the model-based ROC curves with empirical ROC curves. Figure 3 shows that the predicted ROC curves using our proposed method are very close to the empirical ROC curves, especially when a good number of data points for the specific covariate are available. For example, there are a total of 275 patients being both White and around 60 years old (59 ≤ age ≤ 61). The constructed empirical ROC curve aligns well with our predicted ROC curve for this subpopulation (yellow curve). These results confirm that the proposed method provides a good fit for the data.

FIGURE 3.

The covariate-specifc ROC curve estimated from the proposed method and the empirical ROC curve based on NCI-EDRN data for the biomarker PSA.

5.2 ∣. Covariate specific evaluation of phi

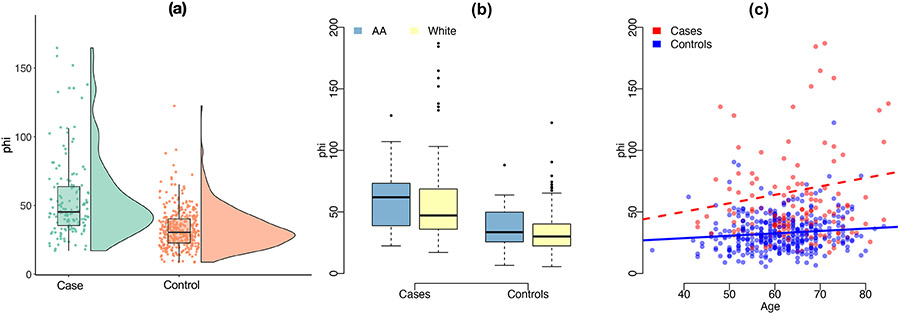
The Beckman Coulter^® Prostate Health Index or phi is an FDA-approved multi-analyte blood test for more accurate prostate cancer detection. Proposed in 2010, phi combines three measurements, total prostate-specific antigen (PSA), free PSA and p2PSA, into a mathematical formula $(p2PSA∕freePSA)\times \sqrt{totalPSA}$.²⁸ It has been reported that the men with a higher total PSA and p2PSA as well as a lower free PSA are more likely to have clinically significant prostate cancer.^29,30,31 As a result, a larger phi value indicates more risk for aggressive prostate cancer. The prostate health index may be more accurate in detecting prostate cancer than PSA.^32,33,34 Among the 502 patients, a total of 352 patients are biopsy-confirmed aggressive prostate cancer patients. Figure 4(a) shows the distributions of phi in cases and controls, respectively. It can clearly be seen that aggressive prostate cancer patients tend to have higher phi values than the controls.

FIGURE 4.

Exploratory plots for the aggressive prostate cancer clinical study with the biomarker phi.

The covariates under consideration here are again age and being AA. The subjects analyzed in this part also have very unbalanced distributions in both covaraites. The majority of the patients are between age 50 and 70. Only 49 of the subjects are African Americans. Nonetheless, the observations in Figure 4(b) and (c) confirm the covariate effect of age and AA on phi. We observe that African-American men have higher phi values than White men in both cases and controls. In addition, elder men are more likely to have higher phi, especially in the case subjects (p=0.0498 for the interaction of age and disease status in linear regression model).

Figure 5 presents the results of applying the proposed method to this clinical data. Controlling equal sensitivity levels among different covariate groups, we evaluate the diagnostic accuracy of phi for specific sub-populations. Figure 5(a) shows the covariate-specific ROC curves and (b) is the smoothed covariate-specific ROC curves after applying ROC-based monotonization. The presented ROC curves are truncated to sensitivity levels greater than 0.6, as high sensitivity levels are usually desired for clinical utility. We observe phi has better diagnostic performance in younger patients, for example, around age 45 years old, than older patients around age 75. The raw ROC curves of AA men are bumpier than the curves in White men, because this study has fewer AA men than White men, as discussed above. The trend is similar for both raw and monotonized ROC curves. Figure 5(c) is the estimated phi threshold at controlled sensitivity levels for different age groups in White and AA men, respectively.

FIGURE 5.

Covariate-adjusted ROC curve for specific sub-populations from the aggressive prostate cancer clinical trial data by controlling sensitivity levels for the biomarker phi.

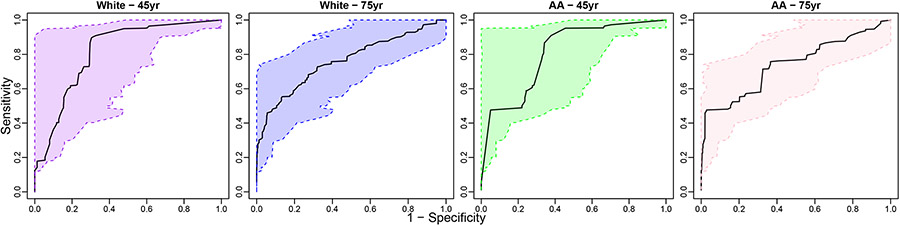
We also obtain the 95% bootstrap-based confidence band for the covariate-specific ROC curves (Figure 6). The presented ROC curves and the related confidence intervals have been monotonized by ROC-based monotonization methods. Compared to the first part, the confidence bands are wider in the current application due to the limited sample size.

FIGURE 6.

The estimated covariate-adjusted ROC curve (black solid curves) with ROC-based monotonization and bootstrap-based confidence bands (colored areas between the dashed lines) for the biomarker phi.

6 ∣. DISCUSSION

In this work, we develop an approach to evaluate the performance of continuous biomarkers at specific covariate levels. It extends our previous work on pooled evaluation with covariate-adjusted threshold¹⁷. Although the modeling for the diseased population under quantile regression framework is similar to Li et al. 2021¹⁷, the covariate-specific evaluation requires further modeling on the controls, which substantially increases the model complexity.

Compared with existing methods, our contribution is twofold. First, by adopting a combined framework of quantile regression and logistic regression, our method allows flexible local covariate adjustment and covariate-specific evaluation for continuous biomarkers. The proposed method is more general than previous methods in many aspects and demonstrates favorable performance. Second, the establishment of asymptotic properties and inference procedures lays a solid foundation to the applications of the proposed method. Our R implementations, wrapped in the R/CRAN package caROC, contain efficient estimation procedures and graphical functions. These allow researchers to easily apply the proposed method for clinical biomarker evaluation. The package provides options for users to control sensitivity or specificity, as well as to specify covariate values of interest. In this era of precision medicine, our method offers a useful tool to improve subpopulation-specific diagnosis.

Supplementary Material

Supplementary material

Table S1. Estimation and inference results under the first simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.25,0.75{)}^T$ by our proposed method and two existing methods (Pepe, 1998; Faraggi, 2003) are estimated and presented.

Table S2. Estimation and inference results under the first simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.75,0.25{)}^T$ by our proposed method and two existing methods (Pepe, 1998; Faraggi, 2003) are estimated and presented.

Table S3. Estimation and inference results under the second simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.25,0.75{)}^T$ by our proposed method and two existing methods (Pepe, 1998; Faraggi, 2003) are estimated and presented.

Table S4. Estimation and inference results under the second simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.75,0.25{)}^T$ by our proposed method and two existing methods (Pepe, 1998; Faraggi, 2003) are estimated and presented.

Table S5. Estimation and inference results under the first simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.50,0.50{)}^T$ by our proposed method and an existing Bayesian method (Inácio de Carvalho et al. 2013) are estimated and presented. Results were summarized over 500 Monte Carlo iterations.

Table S6. Estimation and inference results under the first simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.25,0.25{)}^T$ and $\mathit{z}=(0.25,0.75{)}^T$ by our proposed method and an existing Bayesian method (Inácio de Carvalho et al. 2013) are estimated and presented. Results were summarized over 100 Monte Carlo iterations.

Table S7. Estimation and inference results under the first simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.75,0.25{)}^T$ and $\mathit{z}=(0.75,0.75{)}^T$ by our proposed method and an existing Bayesian method (Inácio de Carvalho et al. 2013) are estimated and presented. Results were summarized over 100 Monte Carlo iterations.

Table S8. Estimation and inference results under the second simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.50,0.50{)}^T$ by our proposed method and an existing Bayesian method (Inácio de Carvalho et al. 2013) are estimated and presented. Results were summarized over 100 Monte Carlo iterations.

Table S9. Estimation and inference results under the second simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.25,0.25{)}^T$ and $\mathit{z}=(0.25,0.75{)}^T$ by our proposed method and an existing Bayesian method (Inácio de Carvalho et al. 2013) are estimated and presented. Results were summarized over 100 Monte Carlo iterations.

Table S10. Estimation and inference results under the first simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.75,0.25{)}^T$ and $\mathit{z}=(0.75,0.75{)}^T$ by our proposed method and an existing Bayesian method (Inácio de Carvalho et al. 2013) are estimated and presented. Results were summarized over 100 Monte Carlo iterations.

Table S11. Evaluation of the proposed method with monotonicity restoration under the first and second simulation setting. Specificity ${\varphi }_0(\mathit{z})$ under controlled sensitivity level ${\rho }_0$ at the covariate selection $\mathit{z}=(0.50,0.50{)}^T$ by our proposed method with monotonization are estimated and presented. Results were summarized over 5000 Monte Carlo iterations.

Figure S1. Simulation results in the first simulation setting of the proposed method (red box) and the Inácio de Carvalho et al. (2013) (blue). From top panel to the bottom panel, the sample sizes are 100, 200, 500, 1000, and 5000. The Sensitivity level is fixed at 0.8. The title of each figure shows the covariate combination for $Z_1$ and $Z_2$. All results are summarized over 100 Monte Carlo datasets.

Figure S2. Simulation results in the first simulation setting of the proposed method (red box) and the Inácio de Carvalho et al. (2013) (blue). From top panel to the bottom panel, the sample sizes are 100, 200, 500, 1000, and 5000. The Sensitivity level is fixed at 0.85. The title of each figure shows the covariate combination for $Z_1$ and $Z_2$. All results are summarized over 100 Monte Carlo datasets.

Figure S3. Simulation results in the first simulation setting of the proposed method (red box) and the Inácio de Carvalho et al. (2013) (blue). From top panel to the bottom panel, the sample sizes are 100, 200, 500, 1000, and 5000. The Sensitivity level is fixed at 0.90. The title of each figure shows the covariate combination for $Z_1$ and $Z_2$. All results are summarized over 100 Monte Carlo datasets.

Figure S4. Simulation results in the first simulation setting of the proposed method (red box) and the Inácio de Carvalho et al. (2013) (blue). From top panel to the bottom panel, the sample sizes are 100, 200, 500, 1000, and 5000. The Sensitivity level is fixed at 0.95. The title of each figure shows the covariate combination for $Z_1$ and $Z_2$. All results are summarized over 100 Monte Carlo datasets.

Figure S5. Simulation results in the second simulation setting of the proposed method (red box) and the Inácio de Carvalho et al. (2013) (blue). From top panel to the bottom panel, the sample sizes are 100, 200, 500, 1000, and 5000. The Sensitivity level is fixed at 0.80. The title of each figure shows the covariate combination for $Z_1$ and $Z_2$. All results are summarized over 100 Monte Carlo datasets.

Figure S6. Simulation results in the second simulation setting of the proposed method (red box) and the Inácio de Carvalho et al. (2013) (blue). From top panel to the bottom panel, the sample sizes are 100, 200, 500, 1000, and 5000. The Sensitivity level is fixed at 0.85. The title of each figure shows the covariate combination for $Z_1$ and $Z_2$. All results are summarized over 100 Monte Carlo datasets.

Figure S7. Simulation results in the second simulation setting of the proposed method (red box) and the Inácio de Carvalho et al. (2013) (blue). From top panel to the bottom panel, the sample sizes are 100, 200, 500, 1000, and 5000. The Sensitivity level is fixed at 0.90. The title of each figure shows the covariate combination for $Z_1$ and $Z_2$. All results are summarized over 100 Monte Carlo datasets.

Figure S8. Simulation results in the second simulation setting of the proposed method (red box) and the Inácio de Carvalho et al. (2013) (blue). From top panel to the bottom panel, the sample sizes are 100, 200, 500, 1000, and 5000. The Sensitivity level is fixed at 0.95. The title of each figure shows the covariate combination for $Z_1$ and $Z_2$. All results are summarized over 100 Monte Carlo datasets.

Abbreviations:

ROC

Receiver Operating Characteristic

PDF

parametric distribution-free

PSA

prostate-specific antigen

phi

prostate health index

Biographies

Ziyi Li is an Assistant Professor in the Department of Biostatistics at The University of Texas MD Anderson Cancer Center, Houston, TX. She is a a statistician and data scientist who develops statistical and machine learning methods and applies them to different high-dimensional biomedical data. She is also interested in collaboration projects with Biologist and Physicians. Her previous collaboration project involves the study of cancer, Alzheimer’s disease, autism, obesity and cardiovascular diseases.

Yijian (Eugene) Huang is Professor in the Department of Biostatistics and Bioinformatics at Rollins School of Public Health of Emory University. His methodological research interests include survival analysis, measurement errors in covariates, and disease diagnosis using biomarkers. He has collaborated in clinical research of HIV/AIDS, cancer, renal disease, and cardiovascular diseases.

Dattatraya Patil is a senior Biostatistician in the Department of Urology at Emory University School of Medicine. He is the co-author of more than 200 manuscripts for Urological cancers, biomarker detections, and health services research.

Mark Rubin is Professor and Director, Department for BioMedical Research, University of Bern, Switzerland; Project Leader for Precision Medicine, University Hospital of Bern, Switzerland; Professor, Pathology and Laboratory Medicine, Weill Cornell Medical College, New York, NY. His laboratory focuses on understanding prostate cancer disease progression, taking a functional genomics approach. Most recently, he has been trying to understand therapy resistance in the context of lineage plasticity which implicates epigenetic as well as genomic alterations.

Martin G Sanda is an internationally recognized prostate cancer surgeon and scientist. He is the appointed Chair of the Department of Urology at Emory University School of Medicine and service chief for Emory Healthcare. Dr. Sanda’s clinical practice, which includes robotic prostatectomy and robotic cystectomy, is focused on developing new surgical and non-surgical approaches to cancer care and to improving the quality of life among cancer survivors.

APPENDIX

A PROOF FOR THEOREM 1

The asymptotic properties of the quantile regression estimator have been established before, e.g. Koenker (2005, Section 4.1.1 and Theorem 4.1),

$$\widehat{\beta }\stackrel{\text{a.s.}}{\to }\beta \text{and}{n}_1^{1∕2}(\widehat{\beta }-{\beta }_0)\stackrel{\mathrm{d}}{\to }N(0,{\rho }_0(1-{\rho }_0){\mathit{D}}_1^{-1}{\mathit{D}}_0{\mathit{D}}_1^{-1}),$$ (A1)

where ${\mathit{D}}_0$ and ${\mathit{D}}_1$ are defined in Theorem 1.

Write

$${\mathit{G}}_n(\beta ,\gamma )=n_0^{-1}\sum _{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}\left(I(M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T\beta )-\frac{\text{exp}({\tilde{\mathit{Z}}}_{0j}^T\gamma )}{1+\text{exp}({\tilde{\mathit{Z}}}_{0j}^T\gamma )}\right).$$

Note that $\widehat{\gamma }$ is the solution to

$${\mathit{G}}_n(\widehat{\beta },\gamma )=0.$$

By the Glivenko-Cantelli theorem, $n_0^{-1}{\sum }_{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}I(M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T\beta )$ converges to $E\{{\tilde{\mathit{Z}}}_{0j}I(M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T\beta )\}$ almost surely and uniformly in $\beta$. Then it follows that $n_0^{-1}{\sum }_{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}I(M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T\widehat{\beta })$ converges to $E\{{\tilde{\mathit{Z}}}_{0j}I(M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T{\beta }_0)\}$ almost surely under Condition 4a.

On the other hand, $n_0^{-1}{\sum }_{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}\text{exp}({\tilde{\mathit{Z}}}_{0j}^T\gamma )∕\{1+\text{exp}({\tilde{\mathit{Z}}}_{0j}^T\gamma )\}$ converges to $E[{\tilde{\mathit{Z}}}_0\text{exp}({\tilde{\mathit{Z}}}_0^T\gamma )∕\{1+\text{exp}({\tilde{\mathit{Z}}}_0^T\gamma )\}]$ almost surely by Strong Law of Large Numbers for a fixed $\gamma$. This convergence holds uniformly in $\gamma$ because of the monotonicity of the function.

Combining the two results, we have shown that ${\mathit{G}}_n(\widehat{\beta },\gamma )$ converges to $E\{{\mathit{G}}_n({\beta }_0,\gamma )\}$ almost surely and uniformly in $\gamma$. Since $E\{{\mathit{G}}_n({\beta }_0,\gamma )\}$ has a unique solution at ${\gamma }_0$, $\widehat{\gamma }$ converges to ${\gamma }_0$ almost surely.

Meanwhile, define

$$A_n(\beta )=n_0^{-1∕2}\sum _{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}I(M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T\beta )-n_0^{1∕2}E\{Z_{0}I(M_0\le {\tilde{\mathit{Z}}}_0^T\beta )\}.$$

Since ${\tilde{\mathit{Z}}}_{0j}I(M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T\beta )$ is Donsker, $A_n(\beta )$ converges weakly to a Gaussian process. Under Conditions 2 and 4a, $A_n(\beta )$ is asymptotically uniformly equicontinuous in probability using an argument similar to Huang (2017, appendix). Together with the consistency result of $\widehat{\beta }$, it follows that

$$A_n(\widehat{\beta })-A_n({\beta }_0)=o_p(1).$$ (A2)

By component-wise Taylor Expansion, one then obtains

$$\begin{gathered} n_0^{-1}\sum _{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}I(M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T\widehat{\beta })-n_0^{-1}\sum _{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}I(M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T{\beta }_0) \\ =\{{\mathit{D}}_2+o_p(1)\}(\widehat{\beta }-{\beta }_0)+o_p(n_0^{-1∕2}). \end{gathered}$$

Thus

$${\mathit{G}}_n(\widehat{\beta },\widehat{\gamma })={\mathit{G}}_n({\beta }_0,\widehat{\gamma })+\{{\mathit{D}}_2+o_p(1)\}(\widehat{\beta }-{\beta }_0)+o_p(n_0^{-1∕2}).$$

Note that the left hand side is equal to 0. We apply the component-wise Taylor expansion on the part involving $\widehat{\gamma }$ and obtain

$$n_0^{1∕2}(\widehat{\gamma }-{\gamma }_0)=n_0^{1∕2}{\mathit{D}}_3^{-1}\left[{\mathit{G}}_n({\beta }_0,{\gamma }_0)+\{{\mathit{D}}_2+o_p(1)\}(\widehat{\beta }-{\beta }_0)\right]+o_p(1).$$

By the Central Limit Theorem,

$$n_0^{1∕2}{\mathit{G}}_n({\beta }_0,{\gamma }_0)\stackrel{d}{\to }N\left(0,E\left[{\tilde{\mathit{Z}}}_0^{\otimes 2}\frac{\text{exp}({\tilde{\mathit{Z}}}_0^T{\gamma }_0)}{\{1+\text{exp}({\tilde{\mathit{Z}}}_0^T{\gamma }_0){\}}^2}\right]\right).$$

The asymptotic normality of $\widehat{\beta }$ has been established in (A1). Meanwhile, ${\mathit{G}}_n({\beta }_0,\gamma )$ is independent of $\widehat{\beta }$. Therefore,

$$\sqrt{n_0}\left(\begin{array}{c}\hfill \widehat{\beta }-{\beta }_0\hfill \\ \hfill \widehat{\gamma }-{\gamma }_0\hfill \end{array}\right)\stackrel{d}{\to }N\left(\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{cc}\hfill V_{\beta }\hfill & \hfill C_{\beta ,\gamma }\hfill \\ \hfill C_{\beta ,\gamma }\hfill & \hfill V_{\gamma }\hfill \end{array}\right)\right).$$

B PROOF FOR THEOREM 2

Write

$$\begin{gathered} {\eta }_n(\beta ,\rho )=n_1^{-1}\sum _{i=1}^n{\tilde{\mathit{Z}}}_{1i}\{I(M_{1i}>{\tilde{\mathit{Z}}}_{1i}^T\beta )-\rho \}, \\ \eta (\beta ,\rho )=E\left[{\tilde{\mathit{Z}}}_1\{I(M_1>{\tilde{\mathit{Z}}}_1^T\beta )-\rho \}\right], \\ {\psi }_n(\beta )=n_0^{-1}\sum _{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}I(M_{0j}\le {\tilde{\mathit{Z}}}_{0j}^T\beta ), \\ \psi (\beta )=E\{{\tilde{\mathit{Z}}}_{0}I(M_0\le {\tilde{\mathit{Z}}}_0^T\beta )\}, \\ {\xi }_n(\gamma )=n_0^{-1}\sum _{j=1}^{n_0}{\tilde{\mathit{Z}}}_{0j}\frac{\text{exp}({\tilde{\mathit{Z}}}_{0i}^T\gamma )}{1+\text{exp}({\tilde{\mathit{Z}}}_{0i}^T\gamma )}, \\ \xi (\gamma )=E\left({\tilde{\mathit{Z}}}_0\frac{\text{exp}({\tilde{\mathit{Z}}}_{0i}^T\gamma )}{1+\text{exp}({\tilde{\mathit{Z}}}_{0i}^T\gamma )}\right). \end{gathered}$$

With the cases, the consistency of $\widehat{\beta }(\rho )$ has been shown previously, e.g., Li et al. (2021+). Turning to the controls, note that $\{{\tilde{\mathit{Z}}}_{0}I(M_0\le {\tilde{\mathit{Z}}}_0^T\beta ):\beta \in {\mathbb{R}}^p\}$ is Donsker. By the Glivenko-Cantelli theorem, almost surely,

$$\underset{\beta }{\text{sup}}\Vert {\psi }_n(\beta )-\psi (\beta )\Vert =o(1).$$ (B3)

With the consistency of $\widehat{\beta }(\rho )$ and the continuity of $\psi (\cdot )$, we have

$$\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\Vert \psi \{\widehat{\beta }(\rho )\}-\psi \{{\beta }_0(\rho )\}\Vert =o(1)$$

almost surely. As a result, almost surely,

$$\begin{gathered} \underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\Vert {\psi }_n\{\widehat{\beta }(\rho )\}-\psi \{{\beta }_0(\rho )\}\Vert \le \underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\Vert {\psi }_n\{\widehat{\beta }(\rho )\}-\psi \{\widehat{\beta }(\rho )\}\Vert \\ +\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\Vert \psi \{\widehat{\beta }(\rho )\}-\psi \{{\beta }_0(\rho )\}\Vert \\ =o(1). \end{gathered}$$ (B4)

The uniform convergence of ${\xi }_n(\gamma )$ to $\xi (\gamma )$ holds following the same arguments in the proof of Theorem 1. Thus, almost surely,

$$\underset{\gamma }{\text{sup}}\Vert {\xi }_n(\gamma )-\xi (\gamma )\Vert =o(1).$$ (B5)

By definition, for any $\rho \in [{\rho }_1,{\rho }_2]$,

$${\psi }_n\{\widehat{\beta }(\rho )\}={\xi }_n\{\widehat{\gamma }(\rho )\}.$$

Results (B4) and (B5) then lead to, almost surely,

$$\begin{gathered} \underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\Vert \xi \{\widehat{\gamma }(\rho )\}-\xi \{{\gamma }_0(\rho )\}\Vert \le \underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\Vert \xi \{\widehat{\gamma }(\rho )\}-{\xi }_n\{\widehat{\gamma }(\rho )\}\Vert \\ +\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\Vert {\psi }_n\{\widehat{\beta }(\rho )\}-\psi \{{\beta }_0(\rho )\}\Vert \\ +\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\Vert \psi \{{\beta }_0(\rho )\}-\xi \{{\gamma }_0(\rho )\}\Vert \\ =o(1). \end{gathered}$$

By component-wise Taylor Expansion, almost surely,

$$\xi \{\widehat{\gamma }(\rho )\}=\xi \{{\gamma }_0(\rho )\}+\left[{\xi }^{\prime }\{{\gamma }_0(\rho )\}+o(1)\right]\{\widehat{\gamma }(\rho )-{\gamma }_0(\rho )\}.$$

Since the minimum eigen value of ${\xi }^{\prime }\{{\gamma }_0(\rho )\}$ is bounded away from 0 and ${\gamma }_0(\rho )$ is also bounded by Condition 4b,

$$\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\Vert \widehat{\gamma }(\rho )-{\gamma }_0(\rho )\Vert =o(1),$$

almost surely.

Now we prove the weak convergence of the proposed estimators. The weak convergence of $\widehat{\beta }(\rho )$ has been obtained in Li et al. (2021+):

$$n_1^{1∕2}\{\widehat{\beta }(\rho )-{\beta }_0(\rho )\}=n_1^{1∕2}{\left(E[{\tilde{\mathit{Z}}}_1^{\otimes 2}{f}_1\{{\tilde{\mathit{Z}}}_1^T{\beta }_0(\rho ){\tilde{\mathit{Z}}}_1\}]\right)}^{-1}{\eta }_n\{{\beta }_0(\rho ),\rho \}+o_p(1),$$ (B6)

uniformly in $\rho \in [{\rho }_1,{\rho }_2]$.

With the afore given Donsker result, $n_0^{1∕2}\{{\psi }_n(\beta )-\psi (\beta )\}$ converges weakly to a Gaussian process. Under Conditions 2 and 4b, $n_0^{1∕2}\{{\psi }_n(\beta )-\psi (\beta )\}$ is asymptotically uniformly equicontinuous in probability using arguments similar to those given by Huang (2017, appendix). Therefore,

$$\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}{n}_0^{1∕2}\Vert {\psi }_n\{\widehat{\beta }(\rho )\}-{\psi }_n\{{\beta }_0(\rho )\}-\psi \{\widehat{\beta }(\rho )\}+\psi \{{\beta }_0(\rho )\}\Vert =o_p(1).$$ (B7)

Since ${\psi }_n\{\widehat{\beta }(\rho )\}={\xi }_n\{\widehat{\gamma }(\rho )\}$ and $\psi \{{\beta }_0(\rho )\}=\xi \{{\gamma }_0(\rho )\}$,

$$\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}{n}_0^{1∕2}\Vert {\xi }_n\{\widehat{\gamma }(\rho )\}-{\psi }_n\{{\beta }_0(\rho )\}-\psi \{\widehat{\beta }(\rho )\}+\xi \{{\gamma }_0(\rho )\}\Vert =o_p(1).$$ (B8)

Using the similar uniform equicontinuous argument for ${\xi }_n(\cdot )$, we have

$$\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}{n}_0^{1∕2}\Vert {\xi }_n\{\widehat{\gamma }(\rho )\}-{\xi }_n\{{\gamma }_0(\rho )\}-\xi \{\widehat{\gamma }(\rho )\}+\xi \{{\gamma }_0(\rho )\}\Vert =o_p(1).$$ (B9)

Results (B8) and (B9) togerther lead to

$$\begin{gathered} \underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}{n}_0^{1∕2}\Vert [{\psi }_n\{{\beta }_0(\rho )\}-{\xi }_n\{{\gamma }_0(\rho )\}]+[\psi \{\widehat{\beta }(\rho )\}-\xi \{\widehat{\gamma }(\rho )\}]\Vert \\ \le \underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}{n}_0^{1∕2}\Vert {\xi }_n\{\widehat{\gamma }(\rho )\}-{\psi }_n\{{\beta }_0(\rho )\}-\psi \{\widehat{\beta }(\rho )\}+\xi \{{\gamma }_0(\rho )\}\Vert \\ +\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}{n}_0^{1∕2}\Vert {\xi }_n\{\widehat{\gamma }(\rho )\}-{\xi }_n\{{\gamma }_0(\rho )\}-\xi \{\widehat{\gamma }(\rho )\}+\xi \{{\gamma }_0(\rho )\}\Vert \\ =o_p(1). \end{gathered}$$ (B10)

To build the connection between $\psi \{\widehat{\beta }(\rho )\}$ and $\widehat{\beta }(\rho )$, $\xi \{\widehat{\gamma }(\rho )\}$ and $\widehat{\gamma }(\rho )$, respectively, we apply the component-wise Taylor expansion. Almost surely,

$$\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\frac{\Vert \psi \{\widehat{\beta }(\rho )\}-\psi \{{\beta }_0(\rho )\}-E[{\tilde{\mathit{Z}}}_0^{\otimes 2}{f}_0\{{\tilde{\mathit{Z}}}_0^T{\beta }_0(\rho )\}]\{\widehat{\beta }(\rho )-{\beta }_0(\rho )\}\Vert }{\Vert \widehat{\beta }(\rho )-{\beta }_0(\rho )\Vert }=o(1)$$ (B11)

and

$$\underset{\rho \in [{\rho }_1,{\rho }_2]}{\text{sup}}\frac{\Vert \xi \{\widehat{\gamma }(\rho )\}-\xi \{{\gamma }_0(\rho )\}-E[{\tilde{\mathit{Z}}}_0^{\otimes 2}\frac{\text{exp}\{{\tilde{\mathit{Z}}}_0^T{\gamma }_0(\rho )\}}{[1+\text{exp}\{{\tilde{\mathit{Z}}}_0^T{\gamma }_0(\rho )\}{]}^2}]\{\widehat{\gamma }(\rho )-{\gamma }_0(\rho )\}\Vert }{\Vert \widehat{\gamma }(\rho )-{\gamma }_0(\rho )\Vert }=o(1).$$ (B12)

Combining results (B10), (B11) and (B12) leads to

$$\begin{gathered} n_0^{1∕2}\left(-E[{\tilde{\mathit{Z}}}_0^{\otimes 2}{f}_0\{{\tilde{\mathit{Z}}}_0^T{\beta }_0(\rho )\}]\{\widehat{\beta }(\rho )-{\beta }_0(\rho )\}+E[{\tilde{\mathit{Z}}}_0^{\otimes 2}\frac{\text{exp}\{{\tilde{\mathit{Z}}}_0^T{\gamma }_0(\rho )\}}{[1+\text{exp}\{{\tilde{\mathit{Z}}}_0^T{\gamma }_0(\rho )\}{]}^2}]\{\widehat{\gamma }(\rho )-{\gamma }_0(\rho )\}\right) \\ =n_0^{1∕2}[{\psi }_n\{{\beta }_0(\rho )\}-{\xi }_n\{{\gamma }_0(\rho )\}]+o_p(1). \end{gathered}$$

Together with (A1), we have

$$\begin{gathered} n_1^{1∕2}\left(\begin{array}{c}\hfill \widehat{\beta }(\rho )-{\beta }_0(\rho )\hfill \\ \hfill \widehat{\gamma }(\rho )-{\gamma }_0(\rho )\hfill \end{array}\right)={\left(\begin{array}{cc}\hfill E[{\tilde{\mathit{Z}}}_1^{\otimes 2}{f}_1\{{\tilde{\mathit{Z}}}_1^T{\beta }_0(\rho )\}]\hfill & \hfill 0\hfill \\ \hfill -E[{\tilde{\mathit{Z}}}_0^{\otimes 2}{f}_0\{{\tilde{\mathit{Z}}}_0^T{\beta }_0(\rho )\}]\hfill & \hfill E[{\tilde{\mathit{Z}}}_0^{\otimes 2}\frac{\text{exp}\{{\tilde{\mathit{Z}}}_0^T{\gamma }_0(\rho )\}}{[1+\text{exp}\{{\tilde{\mathit{Z}}}_0^T{\gamma }_0(\rho )\}{]}^2}]\hfill \end{array}\right)}^1 \\ \times \left(\begin{array}{c}\hfill n_1^{1∕2}{\eta }_n\{{\beta }_0(\rho )\}\hfill \\ \hfill n_1^{1∕2}[{\psi }_n\{{\beta }_0(\rho )\}-{\xi }_n\{{\gamma }_0(\rho )\}]\hfill \end{array}\right)+o_p(1), \end{gathered}$$

uniformly in $\rho \in [{\rho }_1,{\rho }_2]$. Then $n_1^{1∕2}\left(\begin{array}{c}\hfill \widehat{\beta }(\cdot )-{\beta }_0(\cdot )\hfill \\ \hfill \widehat{\gamma }(\cdot )-{\gamma }_0(\cdot )\hfill \end{array}\right)$ over $[{\rho }_1,{\rho }_2]$ converges weakly to a Gaussian process.

Data availability statement

The proposed methods together with sample simulation data have been wrapped in R/CRAN package caROC. This software is freely available from the CRAN website https://cran.r-project.org/web/packages/caROC/index.html. The prostate data that were analyzed in this study are not publicly available due to privacy or ethical restrictions. The data are available upon reasonable request from Dr. Martin Sanda at the Department of Urology of Emory University.