Modeling incomplete penetrance in long QT syndrome type 3 through ion channel heterogeneity: an in silico population study

Abstract

Many cardiac diseases are characterized by an increased late sodium current, including heart failure, hypertrophic cardiomyopathy, and inherited long QT syndrome type 3 (LQT3). The late sodium current in LQT3 is caused by a gain-of-function mutation in the voltage-gated sodium channel Nav1.5. Despite a well-defined genetic cause of LQT3, treatment remains inconsistent because of incomplete penetrance of the mutation and variability of antiarrhythmic efficacy. Here, we investigate the relationship between LQT3-associated mutation incomplete penetrance and variability in ion channel expression, simulating a population of 1,000 individuals with the O’Hara–Rudy model of the human ventricular myocyte. We first simulate healthy electrical activity (i.e., in the absence of a mutation) and then incorporate heterozygous expression for three LQT3-associated mutations (Y1795C, I1768V, and ΔKPQ), to directly compare the effects of each mutation on individuals across a diverse population. For all mutations, we find that susceptibility, defined by either the presence of an early afterdepolarization (EAD) or prolonged action potential duration (APD), primarily depends on the balance between the conductance of I_Kr and I_Na, for which individuals with a higher I_Kr-to-I_Na ratio are less susceptible. Furthermore, we find distinct differences across the population, observing individuals susceptible to zero, one, two, or all three mutations. Individuals tend to be less susceptible with an appropriate balance of repolarizing currents, typically via increased I_Ks or I_K1. Interestingly, the more critical repolarizing current is mutation specific. We conclude that the balance between key currents plays a significant role in mutant-specific presentation of the disease phenotype in LQT3.

NEW & NOTEWORTHY An in silico population approach investigates the relationship between variability in ion channel expression and gain-of-function mutations in the voltage-gated sodium channel associated with the congenital disorder long QT syndrome type 3 (LQT3). We find that ion channel variability can contribute to incomplete penetrance of the mutation, with mutant-specific differences in ion channel conductances leading to susceptibility to proarrhythmic action potential duration prolongation or early afterdepolarizations.

INTRODUCTION

Between 300,000 and 450,000 cases of sudden cardiac death (SCD) are annually reported in the United States, with as many as one-third attributed to ventricular fibrillation (VF), the largest cause of SCD (1). There are many triggers for VF, including those of both structural and electrical origin (2, 3). Several of the underlying electrical causes are associated with an increase in the late component of the sodium current (I_Na,L), including conditions such as heart failure, hypertrophic cardiomyopathy, oxidative stress, and inherited long QT syndrome type 3 (LQT3), one of 15 forms of inherited long QT syndrome (LQTS) (4).

LQTS is characterized by a significant prolongation of the QT interval on a surface electrocardiogram (ECG). Although the prevalence of LQT3 is relatively low among LQTSs, third in prevalence behind LQT1 and LQT2, it has the highest mortality risk, with a 20% chance of death during a cardiac event in individuals with LQT3 versus 4% in either LQT1 or LQT2 (5). LQT3 is associated with a mutation in the SCN5A gene encoding for the α-subunit of the voltage-gated sodium channel Nav1.5, the primary carrier of the depolarizing sodium current in human ventricular myocytes. Critically, several Nav1.5 variants have been identified and linked to LQT3, with some associated with both Brugada syndrome and LQT3 (6). Furthermore, LQT3, like all LQTSs, exhibits genetic heterozygosity and incomplete penetrance, leading to heterogeneous expression of the LQTS phenotype and associated symptoms, thus making clinical classification and arrhythmia risk assessment difficult (7).

Prior studies have considered the cause of incomplete penetrance in LQT3 (8–12). Clinical studies have shown that an additional mutation to the SCN5A genome can protect from the effects of LQT3 (10). Regulation of LQT3 phenotype has been seen at multiple levels, ranging from common polymorphisms in the primary structure of Nav1.5 (13) to alterations in SCN5A intron sequence (14). Even alteration in the gene encoding for a different voltage-gated sodium channel (Nav1.8) has been linked to differential expression of SCN5A (15, 16). Similarly, differences in phenotype have been observed in LQT2 (linked to potassium channel gene KCNH2) because of a common variant in a different gene KCNK17, which encodes for a two-pore domain potassium channel. These findings highlight that changes in ion channel activity impact the presentation of the LQTS phenotype, physiological evidence that variable ion channel expression plays a critical role in the LQT3-associated arrhythmias.

More broadly, variable ion channel expression has been observed in myocyte cell cultures as well. In in vitro studies measuring current activity, variability has been observed in the measurements of peak and plateau current density and total carried charge of specific ionic currents, e.g., sodium current (I_Na), rapid delayed rectifier (I_Kr), slow delayed rectifier (I_Ks), etc., between cells from different individuals of the same species, age, and sex paced with the same self-action potential (AP) clamp protocol (17–19).

Weiss and colleagues (20) suggested an explanation for population variation in ionic current expression as “good enough solutions” to the cardiac AP, following work from neuroscientists Marder and Goaillard (21) on the bursting behavior in neurons. Marder and Goaillard showed in crustaceans that similar neural bursting patterns could emerge, despite the densities of key ion channels substantially differing between lobsters. Similarly, the good enough solution framework posits that similar cardiac AP morphology can be conserved between individuals within a population, with different expression of key ion channels. The assumption that ionic current expression varies between individuals under the same condition has been adopted for many in silico studies in the cardiac electrophysiology field (22–29). A “population approach,” in which ionic current expression is varied within a wide range, can recapitulate the diverse physiological characteristics of a population; that is, a wide range of ionic current conductance combinations can reproduce a physiological AP in conjunction with multiple constraints that narrow the range of appropriate parameters (30).

Applying a population approach at the cellular level can contribute toward an explanation of incomplete penetrance of patients with LQT3, as this approach can link ionic current expression to phenotype variability. Prior work from Paci and colleagues used such an approach to simulate phenotypic variability in LQT3; however, as the authors note, there were drawbacks to the use of a human induced pluripotent stem cell-derived cardiomyocyte (hiPSC-CM) model including an immature phenotype (8). Additionally, the authors only considered LQT3 associated with one specific mutation. However, differences between different LQT3-associated mutations can have distinct effects on Nav1.5 kinetics, potentially impacting whether an individual is susceptible to their respective LQT3-associated mutation. This is supported by previous work by Ruan et al. (31) illustrating that the response to mexiletine is mutation specific, pointing to genotype-specific risk stratification and management of LQT3 (32). More broadly, multiple studies have shown the importance of maintaining a balance between ionic currents in cardiac cells, where deviations from this balance are observed in diseased phenotypes (19, 26, 33, 34) of which, to our knowledge, no study has explored in LQT3 beyond functional increases in I_Na,L.

We hypothesize that incomplete penetrance in a population of simulated human ventricular myocytes with LQT3-associated mutations can result from specific ion channel combinations that are more “resistant” to the perturbation of a specific LQT3-associated mutation. In this study, we generate a population of cells with variable ionic current expression, represented as variable maximal current conductance in silico, and perturb each population member with multiple LQT3-associated mutations to discern why some individuals, but not all, are susceptible to a specific LQT3-associated mutation. Furthermore, we determine whether there are specific combinations of ionic current expression that can be protective against all LQT3 mutations or, alternatively, whether specific combinations of ionic currents are protective against susceptibility for specific LQT3 mutations.

We find that in a group of LQT3-associated mutations (Y1795C, I1768V, and ΔKPQ) the resulting phenotype of the individual depends on both the combined expression of multiple currents (the individual’s good enough solution) as well as the specific mechanism for QT prolongation from a given LQT3-associated mutation. For all LQT3-associated mutations, the balance between I_Na and I_Kr was a strong predictor of action potential duration (APD) prolongation. Beyond these two currents, susceptibility depended on the relative contribution of different potassium currents contributing to repolarization for a given cell, reminiscent of the repolarization reserve concept (35, 36). A strong dependence on the inward rectifier potassium channel current I_K1 was an indicator of “resistance” to rapid sodium channel reactivation for the I1768V mutation, due to rapid sodium channel reactivation occurring concurrent with I_K1 activation. In contrast, a strong dependence on the slow delayed rectifier potassium current I_Ks was protective against both Y1795C and ΔKPQ mutations, which prolong the AP primarily through increased persistent late sodium current I_Na,L during the plateau phase, concurrent with I_Ks activation. This work thus establishes a foundation for further studies of incomplete penetrance in the presence of variable mechanisms underlying specific disease-associated mutations.

METHODS

Computational Model Formulation

Model structure.

For our study, we simulate a single-cell model of a human ventricular epicardial myocyte using the O’Hara–Rudy model (ORd) (37). We replace the baseline ORd Na⁺ channel model, based on Hodgkin–Huxley gating dynamics, with a Markov chain-based model incorporating either wild-type (WT) or LQT3-associated mutated Na⁺ channel dynamics (Y1795C, I1768V, or ΔKPQ). We also removed the ORd late sodium current, as the Markov chain models represent both peak and late current components. Simulations of mutant myocyte included heterozygous expression of the mutant Na⁺ channel variant, modeled as a 1-to-1 ratio of WT to mutant channels. Na⁺ channel dynamics were governed by a 13- or 10-state Markov model for Y1795C (38) and I1768V (39) or ΔKPQ (40), respectively. As described previously (38–40), these models reproduce mutant channel dynamics that lead to an increased late Na⁺ current. Channel states represent gating of a baseline background mode and a noninactivating burst mode. Both 13-state Markov models contain the same states, whereas the 10-state Markov model lacks closed-inactivation states (UIC2 and UIC3) and intermediate inactivation states (UIM1 and UIM2) but includes a slow inactivation state (IS).

Population Generation

To study the role of ion channel expression heterogeneity in incomplete penetrance of LQT3 mutations, we generated a population of 1,000 individuals, with scaled maximal conductance of the 13 ionic currents, similar to previous studies (27, 41, 42), by multiplying each current conductance by a scaling factor θ. To generate an individual in the population, we first generate 13 scaling factors (for each ionic current) using a log-uniform distribution from 0.25 to 4. This ensured an equal likelihood that an ionic current is defined as 4× the baseline (θ = 4) or 1/4× the baseline (θ = 0.25). We note that each Markov chain model of an LQT3-associated mutation was published with a corresponding WT channel model (38–40). All three WT models were incorporated in the myocyte, for a given set of scaling factors, and the individual was included in the population only if all three simulations yielded AP and calcium transient characteristics within the epicardial myocyte biomarker range, given in Table 1 (27). This process was repeated until a population of 1,000 individuals with distinct combinations of scaled current conductances and physiologically relevant action potential characteristics was established. Note that throughout this study, all three WT models are used to establish a direct comparison between the WT and mutant model. Simulations of mutant myocytes incorporated the respective mutant model in heterozygous expression, as described above.

Table 1.

Physiological biomarker ranges for AP and calcium transient characteristics in human epicardial ventricular myocytes

Biomarker	Minimum Value	Maximum Value
APD50, ms	110	350
APD90, ms	180	440
CTD50, ms	120	420
CTD90, ms	220	785
RMP, mV	−95	−80

APD₅₀ and APD₉₀, action potential (AP) duration at 50% and 90% repolarization, respectively; CTD₅₀ and CTD₉₀, Ca²⁺ transient duration at 50% and 90% decay, respectively; RMP, resting membrane potential.

As described further below, we also generated a second population where the sodium conductance G_Na was unvaried. Generation of this population was performed in the same manner as generation of the first; however, θ_Na was held at the median value of the first population (θ_Na = 0.5741).

Model fitting.

With baseline values for sodium channel conductance, cells simulated with both the WT and mutant Na⁺ channel Markov model for I1768V and ΔKPQ failed to repolarize. This issue has been reported previously when incorporating Markov chain-based dynamics in place of a Hodgkin–Huxley formulation for the sodium current, with past studies resolving this issue by adjusting overall sodium channel conductance G_Na (43, 44). Therefore, we adjusted the maximal conductance for the Na⁺ current conductance G_Na for I1768V and ΔKPQ in a systematic manner: Specifically, we implemented a bisection algorithm to find the threshold value of a relative sodium conductance value ${\widehat{G}}_{\mathrm{Na}}$ that resulted in mutant heterozygous cells that successfully repolarized. We next halved these values, anticipating that using the threshold value would produce a population of cells that are unrealistically proarrhythmic when incorporating scaling of G_Na. Individual-specific scaling factors θ_Na were multiplied by the mutant-specific ${\widehat{G}}_{\mathrm{Na}}$ values to determine the overall Na⁺ channel conductance. Simulations incorporating the Y1795C resulted in repolarizing action potentials when using the baseline G_Na value, and G_Na was therefore unchanged. Bisection and final values of ${\widehat{G}}_{\mathrm{Na}}$ are shown in Supplemental Table S1 (https://github.com/SHWeinberg/Miller-LQT3-IncompletePenetrance/blob/main/Miller_AJP_Supplement.pdf).

Simulation parameters, pacing protocol, and analysis.

Cells were simulated with a stimulation current of 30 µA/µF for a duration of 1 ms. Ordinary differential equations for membrane potential and state variables (given in full detail in Ref. 37) were solved using the built-in MATLAB function ode15s. The initial conditions for all state variables and ion concentrations, except for those pertaining to the sodium channel, are set as in the original O’Hara–Rudy model (37). Initial conditions for the sodium channel Markov chain state variables (which replace the Hodgkin–Huxley sodium channel gating variables) are set as the Markov chain steady-state values at the initial membrane potential.

Parameters for cell size were set to match those of an adult cardiomyocyte, with a length of 100 µm and radius of 11 µm. To mimic normal heart rate, a basic cycle length (BCL) of 1,000 ms (corresponding to 60 beats/min) was used for all simulations. Cells were paced for 50 beats or 50 s of simulation of time. After pacing for 50 beats, a large majority of cells (between 90% and 95%, depending on the mutation) reached an equilibrium. Specifically, either the beat-to-beat APD difference was <1 ms or a stable alternating pattern formed, with a prolonged APD with several early afterdepolarizations (EADs) alternating with a short APD. For the remaining 5–10%, APD dynamics present as in a chaotic system, in which APD varies substantially on a beat-to-beat pattern in a chaotic manner, because of a different number of EADs each beat. This chaotic behavior has been previously shown to occur in cardiac cells in the presence of EADs (35, 45). To account for this potential variation yet still quantify the degree of APD prolongation for a given cell and mutation, APD at 90% repolarization (APD₉₀) was measured as the maximum value over the final five beats.

Characterizing Susceptibility to LQT3 Mutations

Clinically, patients are diagnosed with LQTS based on the Schwartz score, with ratings based on ECG findings, clinical history, and family history (46). The resulting score can indicate low, intermediate, or high probability of the patient having LQTS, with an individual being diagnosed with high probability of LQTS regardless of the Schwartz score if they have a repeated measured corrected QT (QTc) interval of 500 ms. QTc intervals can be calculated with a number of methodologies, with the Bazett formula $\left(\text{QTc\hspace{0.17em}}=\frac{\text{QT}}{\sqrt{\text{R}-\text{R}}}\right)$ being used most commonly (47), where the QTc is the heart rate-corrected QT interval used for clinical diagnosis, QT is the measured time between the onset of the QRS complex and the end of the T wave, and the R-R interval is the time between consecutive R waves (with units in seconds). The condition of QTc ≥ 500 ms is considered a “powerful predictor of short-term mortality overruling comorbidities” (48) and an immediate qualifier for high likelihood of LQTS. To compare clinical diagnostic criteria with single-cell measurement, we assumed that the APD₉₀ for an individual cell was a realistic approximation of the QTc interval.

For each of the LQT3 mutations, individuals were categorized as either “susceptible” or “not susceptible” based on the presence of at least one of the following conditions: 1) severe APD₉₀ prolongation, defined as APD₉₀ ≥ 500 ms, or 2) the presence of EADs, a known mechanism promoting arrhythmias in LQTS (49). EAD formation was defined via the presence of a local minimal following the notch phase of the action potential and before full repolarization. For presentation and analysis, APD₉₀ was reported as 1,000 ms (the value of the BCL) for cells that did not repolarize. After simulating all three mutations in all 1,000 individuals, the population was divided into eight groups: individuals susceptible to no mutations, susceptible to only one mutation (Y1795C only, ΔKPQ only, I1768V only), susceptible to a pair of mutations (Y1795C and I1768V, Y1795C and ΔKPQ, I1768V and ΔKPQ), or susceptible to all three mutations.

Model Comparison

To determine model dependence on our conclusions, we perform a subset of the above simulations and analysis using a different model of the human ventricular myocyte, the ten Tusscher, Noble, Noble, and Panlov (TNNP) model (50), similarly incorporating a Markov chain model to represent LQT3-associated Na⁺ channel mutant dynamics. Specifically, we generated a population of 1,000 individuals for which AP and calcium transient characteristics are within the biomarker range with the WT channel models, as described above. We then performed simulations with each population member with heterozygous expression of one of the three mutant channels and determined susceptibility as described above.

Statistical Analysis

Significant differences between groups were calculated with a one-way ANOVA, with P < 0.05 being considered statistically significant. Correlations between data sets were calculated with Pearson’s correlation coefficient r, for which 0.5 < r < 0.7 was considered moderately correlated and r > 0.7 was considered strongly correlated.

RESULTS

Variable θ_Na Population

APD prolongation and EAD depend on specific mutations.

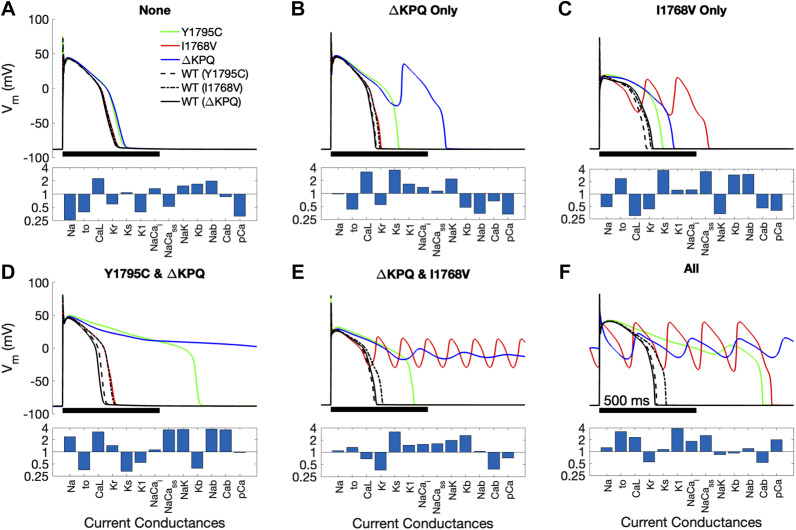
The transmembrane voltage (V_m) time course for representative example cells incorporating LQT3 mutations [Y1795C (green), I1768V (red), and ΔKPQ (blue)] are shown in Fig. 1, with V_m from the cells incorporating the wild-type (WT) channel models (black lines) published with each of the associated mutant models (denoted in parentheses) also shown, and the corresponding current conductance scaling factors shown below each set of traces. We present the six conditions of susceptibility that were observed: 1) susceptible to no mutations (“none”), 2) susceptible to ΔKPQ only, 3) susceptible to I1768V only, 4) susceptible to ΔKPQ and Y1795C, 5) susceptible to ΔKPQ and I1768V, or 6) susceptible to all three mutations (“all”).

Figure 1.

Example cells from the variable θ_Na population representing each case of susceptibility observed. Top: transmembrane voltage (V_m) trace over 1 beat for the example cell. Bottom: scaled conductance (θ) of the 13 ionic currents for the example cell. The 6 conditions of susceptibility are susceptible to no mutations (A), susceptible to ΔKPQ only (B), susceptible to I1768V only (C), susceptible to both Y1795C and ΔKPQ (D), susceptible to ΔKPQ and I1768V (E), and susceptible to all mutations (F). Wild-type (WT) traces are shown in black for each individual, incorporating 1 of the WT channel model published with each mutant model (denoted in parentheses).

We note variability in the characteristics of the V_m time course and the manner of APD prolongation. For example, we observe significant APD prolongation that arises through one or two EADs (Fig. 1, B, blue and C, red), significant prolongation without EADs (Fig. 1D, green), and action potentials that fail to repolarize (Fig. 1, D, blue, E, red and blue, and F, blue). Importantly, these traces illustrate that not all cells modeled with a given mutation show proarrhythmic changes to the action potential (i.e., all 3 mutants exhibit incomplete penetrance) and further that susceptibility to one mutation does not necessitate susceptibility to a different mutation. Additionally, we find that in all cases, the mutations prolong APD relative to WT channels, however with varying degrees depending on both the mutation and individual cell.

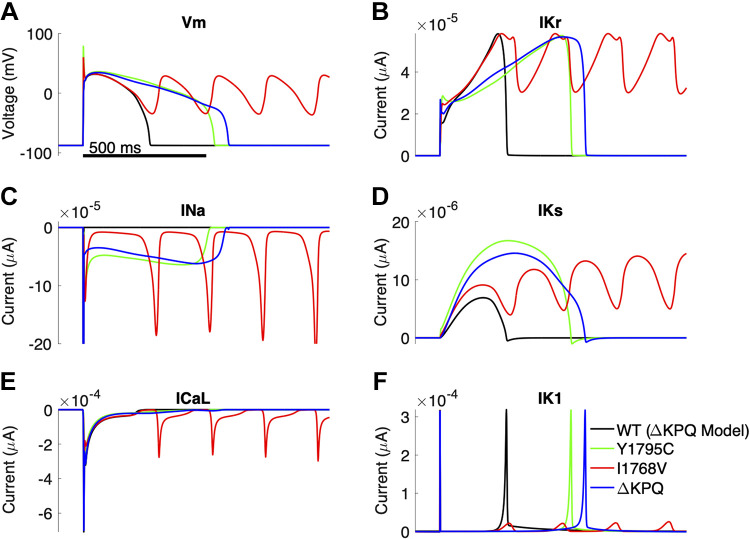
We next investigated the role of different ionic currents in prolonging APD and/or promoting EADs for each mutation, in comparison with WT conditions, considering a cell that is susceptible to all three mutations (Fig. 2). Note that scaling values for all currents are the same for all three mutation cases shown. As expected, all three mutations exhibit a more pronounced I_Na,L current compared with WT (Fig. 2C). However, the time course of the late current differs, with Y1795C and ΔKPQ exhibiting a more persistent current, whereas I1768V exhibits a low-amplitude baseline with “spiking” repetitive reactivation of the current. These differences are reflected in the V_m time course, with Y1795C and ΔKPQ exhibiting a prolonged APD without EADs, whereas I1768V presents with pronounced EADs.

Figure 2.

Example cell susceptible to all mutations, with wild type (WT) shown for reference. Transmembrane voltage (V_m; A), rapid delayed potassium rectifier current (I_Kr; B), sodium current (I_Na; C), slow delayed rectifier potassium current (I_Ks; D), long-lasting calcium current (I_Ca,L; E), and inwardly rectifying potassium current (I_K1; F) are shown as functions of time.

The changes in V_m in turn impact I_Ca,L and potassium currents. Specifically, for Y1795C and ΔKPQ cases, I_Ca,L is moderately enhanced during the late stage of the AP plateau, whereas I_Ca,L for I1768V exhibits spiking-like reactivation paralleling I_Na,L. Interestingly, all three mutation cases exhibit larger-magnitude I_Ks current compared with WT. I_Kr and I_Ks have similar time courses for ΔKPQ (blue) and Y1795C (green), although we note that small changes in V_m during the plateau result in differences in both potassium currents, in particular the peak I_Ks magnitude (Fig. 2, C and D). Furthermore, we observe that EADs for the I1768V case (red) result in transient I_K1 current (Fig. 2F). To isolate the differences between the different mutations, we also simulate I_Na,L under action potential-clamp conditions for the three mutations and WT channels, specifically for the three cases of an AP with normal APD, a prolonged APD without an EAD, and a prolonged APD with an EAD (Supplemental Fig. S1). We find that for all three APs, I_Na,L for Y1795C and ΔKPQ exhibit similar plateaulike dynamics, with Y1795C slightly larger early in the AP and smaller later in the AP. In contrast, I_Na,L for I1768V exhibits a low-amplitude late current that increases in magnitude during late repolarization, consistent with the reactivation kinetics of this mutant.

Susceptibility differs between mutations and individual cells.

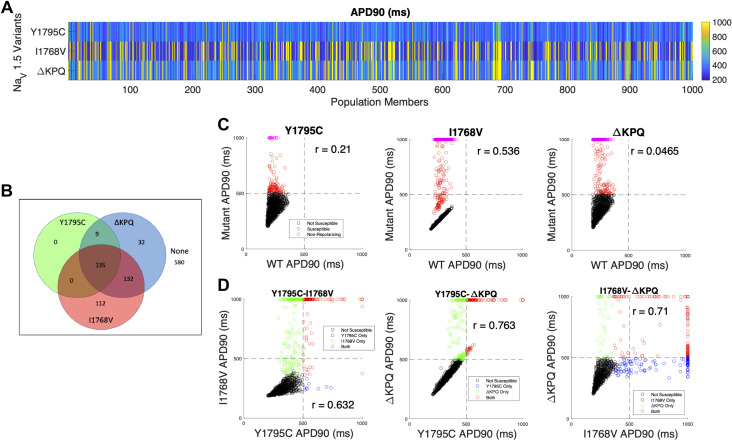
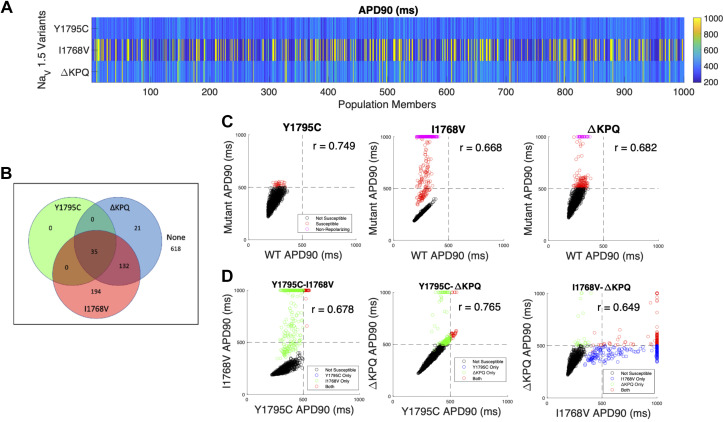
As described in methods, we first investigate the prevalence of incomplete penetrance through a population with all conductances varying, including the scaling factor for sodium conductance θ_Na. APD₉₀ for all 1,000 cells is shown, incorporating each of the three mutants (Fig. 3A). We find a high degree of variability in APD prolongation across the full population, with more prolonged APD generally observed for cells with the I1768V (379/1,000) and ΔKPQ (308/1,000) mutations compared with Y1795C (144/1,000). Note that, for presentation purposes, APD is reported as 1,000 ms (the pacing cycle length) for cells that failed to repolarize.

Figure 3.

Variable θ_Na population overview illustrating action potential duration (APD) prolongation for different mutations. A: APD at 90% repolarization (APD₉₀) for 1,000 cells, shown by row for Y1795C, I1768V, and ΔKPQ (top to bottom). B: Venn diagram illustrating susceptibility categorization for all 3 mutations. C: comparison between wild-type (WT) and mutant APD₉₀ for each mutation. Weak or no correlation was observed between WT and mutants. D: direct comparison of APD₉₀ for all cells in the population with 2 different mutations. Horizontal and vertical lines at 500 ms indicate the threshold of APD prolongation for cells susceptible or not susceptible to a given mutation. Note that the inclusion of early afterdepolarizations (EADs) in the susceptibility criteria results in some cells with APD < 500 ms also in the susceptible quadrants.

The Venn diagram in Fig. 3B illustrates the distribution of cells susceptible to one or more mutations. For example, we find that the majority of the population (580/1,000) are not susceptible to any mutation, while just over 10% (135/1,000) are susceptible to all three mutations. Additionally, although there is a small population of cells that are only susceptible to either I1768V (112/1,000) or ΔKPQ (32/1,000), no cells are only susceptible to Y1795C; that is, any cells that are susceptible to the Y1795C mutation are also susceptible to other mutations (either ΔKPQ or both ΔKPQ and I1768V).

We next plot the relationship between APD₉₀ for each mutation and the corresponding APD₉₀ for a WT channel, i.e., each point in the scatterplot corresponds to one cell with either WT or heterozygous mutant channel expression (Fig. 3C). There is a range of relationships depending on the mutation, with almost no correlation (r = 0.0465) for ΔKPQ to moderately positive (r = 0.536) for I1768V. Thus, depending on the specific mutation, APD₉₀ in the absence of a mutation (WT) is either not predictive or only moderately predictive of APD prolongation in the presence of the mutation. We also consider whether there is a relationship between APD prolongation for different mutants. In Fig. 3D, we plot APD₉₀ for each pair of mutations, i.e., each point in the scatterplot corresponds to one cell with either of the two mutations in the pair. For all three pairs, we observe a moderate correlation between APD₉₀, with the strongest correlation between Y1795C and ΔKPQ (r = 0.763), consistent with the similar mechanism of APD prolongation observed in Fig. 2. Thus, we find that although susceptibility to one mutation does not necessarily correspond with susceptibility to a different mutation, there is a positive correlation between APD prolongation in response to different mutations.

Current conductances and susceptibility.

We begin investigating the role of individual currents in incomplete penetrance of LQT3 by considering the distribution of current conductances in the population and susceptibility subgroups. First, we note that for the entire population of 1,000 cells, scaling factors for each current are typically not centered around 1 (Supplemental Fig. S2), indicating that the “median” cell parameters do not correspond to the baseline model parameters. Importantly, we note that these are the scaling factor combinations that result in APs and calcium transients within the WT biomarker ranges (as described in methods).

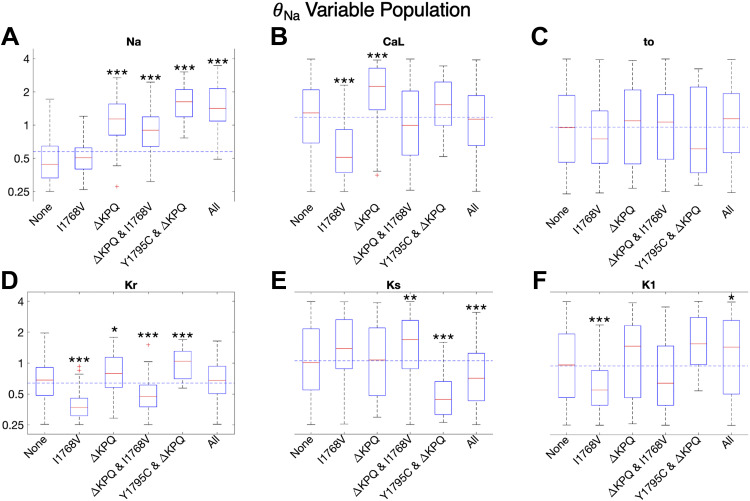
In Fig. 4, we show the box plots for the scaling factor distributions for each of the six identified cases for susceptibility (as described in Fig. 1) for six key ionic currents (I_Na, I_Ca,L, I_to, I_Kr, I_Ks, and I_K1). Note that the scaling factor distributions for the remaining fluxes (background currents, pumps, and exchangers) are shown in Supplemental Fig. S3 and in general show minimal differences across susceptibility groups and with the overall population median.

Figure 4.

Distribution of scaling factors θ for each of 6 major currents depicted on a logarithmic scale. A–F: cells are separated into subgroups based on mutation susceptibility. Trends for all other varied current conductances are shown in Supplemental Fig. S3. *P < 0.05, **P < 0.01, and ***P < 0.001. Significance is in reference to the subpopulation of cells susceptible to no mutations. Dashed horizontal lines represent population median.

First, considering cells that are not susceptible to any mutations (“None”), we find that the most significant factor is that θ_Na is significantly reduced compared with the population median (horizontal dashed line) and with all other susceptibility groups (Fig. 4A). Interestingly, all other key ionic current conductance scaling factors have distributions comparable to the overall population (Fig. 4, B–F), demonstrating that θ_Na is the most critical factor for cells without susceptibility to any mutations. Indeed, this is not surprising, as θ_Na directly impacts the magnitude of I_Na,L, which in turn drives APD prolongation. We further find that, for all three mutations, the correlation between APD₉₀ and θ_Na ranges from moderate to strongly positive correlation (r = 0.462 to 0.748) (Supplemental Fig. S4A).

Interestingly, we find distinct differences between the scaling factor distributions for cells that are susceptible to only one mutation, specifically I1768V versus ΔKPQ. Cells susceptible to only I1768V tend to have lower levels of both θ_Ca,L and most of the potassium currents (θ_to, θ_Kr, θ_K1), except θ_Ks. This combination of currents leads to EADs and APD prolongation in particular driven by the I_Na,L characteristics consistent with the I1768V mutation, i.e., reactivation of the current, as shown in Fig. 2. Specifically, relatively low θ_Ca,L requires an overall balance of lower potassium currents to maintain normal APs and calcium transients in the WT cell. However, in the presence of the I1768V mutation, low θ_K1 specifically fails to counterbalance the reactivation of I_Na,L that occurs late in the plateau phase, which ultimately results in EADs. In contrast, higher θ_Ks likely arises to compensate for the lower levels of intracellular calcium activation of I_Ks (due to lower θ_Ca,L). Interestingly, the median θ_Na for cells only susceptible to I1768V is slightly lower than the population median, demonstrating that it is actually the balance of calcium and potassium currents that tends to determine EADs in this subgroup. In contrast, cells susceptible to only ΔKPQ tend to have elevated θ_Na, θ_Ca,L, θ_Kr, and θ_K1. Whereas elevated θ_Na and θ_Ca,L tend to promote susceptibility to all mutations, high levels of θ_Kr and θ_K1 result in a subgroup of cells in which APD prolongation is suppressed for Y1795C and I1768V mutations but not ΔKPQ. As described above, high θ_K1 suppresses susceptibility to I1768V, whereas differences between Y1795C and ΔKPQ gating result in a shorter I_Na,L that suppresses susceptibility to Y1795C.

Cells that are susceptible to two or all three mutations tend to exhibit similarities (and some differences) in their current conductance scaling factor distributions. In particular, all of these cells exhibit high levels of θ_Na, consistent with the corollary of cells exhibiting susceptibility to no mutations exhibiting low θ_Na. Each of these susceptibility subgroups exhibits low levels of one or more potassium currents: specifically, cells susceptible to ΔKPQ and I1768V exhibit low θ_Kr; cells susceptible to Y1795C and ΔKPQ exhibit low θ_to and θ_Ks; and cells susceptible to all three mutations exhibit low θ_Ks. Interestingly, high levels of θ_K1 in cells susceptible to Y1795C and ΔKPQ are consistent with high θ_K1 suppressing susceptibility to the I1768V mutation. Furthermore, although the θ_Ca,L distributions for these three groups were either near or slightly above the population distribution, it does not appear that high θ_Ca,L is required for enhanced susceptibility, demonstrated by the presence of cells with θ_Ca,L below the population median that are still susceptible to all three mutations. Rather, these results suggest that it is the particular balance of potassium currents, in conjunction with the I_Na,L dynamics, that results in EADs and APD prolongation.

Relationships between current conductances across the population and susceptibility subgroups.

As noted above, the overall population distribution (fit to match WT biomarkers) exhibited differences from the baseline model (corresponding with scaling factors of 1). We next considered whether there exist correlations between the current conductance scaling factors both across the entire population and within the different susceptibility subsets (Fig. 5). Conceptually, we expect some correlations within the overall population, as the overall balance of ionic currents must be defined to yield physiological APs and calcium transients in the initial WT population. (Note that the correlation coefficient matrix is by definition symmetric, and all currents have a perfect +1 correlation with themselves.) Viewing trends across the whole population (Fig. 5A), we find several moderate positive and negative correlations: a positive correlation between θ_Kr and θ_Ca,L; a positive correlation between θ_Na and θ_Kr; a negative correlation between θ_to and θ_Ca,L; and a negative correlation between θ_Kr and θ_Ks. Ultimately, all these correlations arise to maintain a physiological balance of ionic currents. For example, the negative correlation between θ_Kr and θ_Ks arises as a decrease in one current can be compensated for by an increase in the other (i.e., the concept of repolarization reserve). Interestingly, a decrease in θ_to, and thus lower level of I_to, reduces the driving force for I_Ca,L, requiring a higher level of θ_Ca,L to compensate.

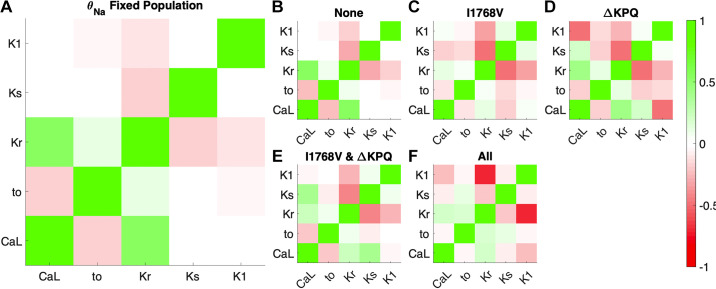
Figure 5.

Pearson’s correlation coefficient between pairs of current scaling factors θ in the variable θ_Na population. Dark red indicates a strong negative correlation, lack of color (white) indicates no correlation, and bright green indicates strong positive correlation. Correlation coefficients between scaling factors for whole generated variable θ_Na population (A), cells susceptible to no mutations (B), cells susceptible to I1768V only (C), cells susceptible to ΔKPQ only (D), cells susceptible to Y1795C and ΔKPQ (E), cells susceptible to ΔKPQ and I1768V (F), and cells susceptible to all 3 mutations (G) are shown.

In general, many of the trends that hold at the level of the entire population are also true in subgroups susceptible to different mutations (Fig. 5, B–G). However, some additional relationships are observed in specific subgroups. In cells susceptible to ΔKPQ (including ΔKPQ only and groups with 2 or 3 susceptibilities), there tends to be a stronger positive correlation between θ_Na and θ_Ca,L. Furthermore, in these cells, there tends to be a negative correlation between θ_to and several conductances, including θ_Na and θ_Kr. Interestingly, whereas θ_Kr and θ_Ks tend to be negatively correlated in the whole population and most subgroups, there is a weak but positive correlation between these conductances in cells susceptible to all three mutations. Correlations for all currents and fluxes, including background currents, pumps, and exchangers, are shown in Supplemental Fig. S5.

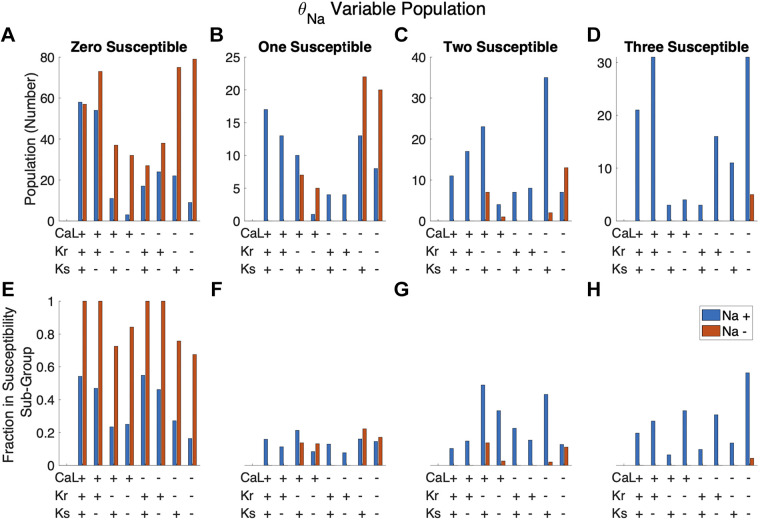
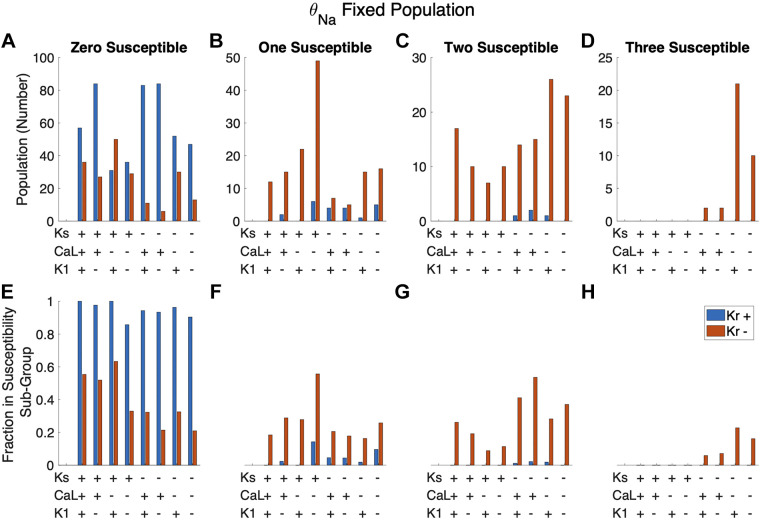
We next explored the relationship between the expression level of multiple current conductances and susceptibility to mutations (Fig. 6). For each cell, we define the conductance of each current as either “high” or “low” (denoted as “+” or “−”) if the conductance is above or below the population median, respectively. Figure 6, A–D, show the number of cells in a given conductance combination group. For example, the first blue bar in the “zero susceptible” group (Fig. 6A) indicates that there are 59 cells with the combination high θ_Ca,L, high θ_Kr, high θ_Ks, and high θ_Na that are not susceptible to any mutations. Figure 6, E–H, indicate what fraction of cells in a combination group are in a given susceptibility subgroup. Considering the same combination group (high θ_Ca,L, high θ_Kr, high θ_Ks, high θ_Na), these 59 cells not susceptible to any mutations represent 54% (or a fraction of 0.54) of all 108 cells in this combination group. The first blue bar in Fig. 6, E–H, thus indicates that 54%, 16%, 10%, and 20% of this combination group are susceptible to zero, one, two, and three mutations, respectively (for a total of 100%).

Figure 6.

Trends in susceptibility based on the combined scaling factors of 4 major currents: I_Na, I_Ca,L, I_Kr, and I_Ks. For a given cell, current conductance scaling factors below and above the population median were labeled as low (−) and high (+) conductance, respectively. A–D: number of cells in a given subgroup with 1 of 16 combinations of high and low conductance. E–H: fraction of cells with a given high- and low-conductance combination that are in the given subpopulation.

Figure 6 illustrates trends in susceptibility based on the combined expression of I_Na, I_Ca,L, I_Kr, and I_Ks conductances. Most striking is the relationship between θ_Na and susceptibility, with the majority of cells with low θ_Na (orange bars) susceptible to no mutations, whereas all cells susceptible to all three mutations have high θ_Na (blue bars). For cells with low θ_Na, susceptibility to one or more mutations tends to occur with low θ_Kr. A scatterplot of APD₉₀ versus the ratio of θ_Kr to θ_Na for each mutation similarly demonstrates that low values of this ratio are associated with prolonged APD for all three mutations (Supplemental Fig. S4B). We observe a similar but weaker relationship between susceptibility and low θ_Ks: the corresponding scatterplot of APD₉₀ versus the θ_Ks-to-θ_Na ratio exhibits a negative correlation that tends to be weaker compared with the θ_Kr-to-θ_Na ratio (Supplemental Fig. S4C).

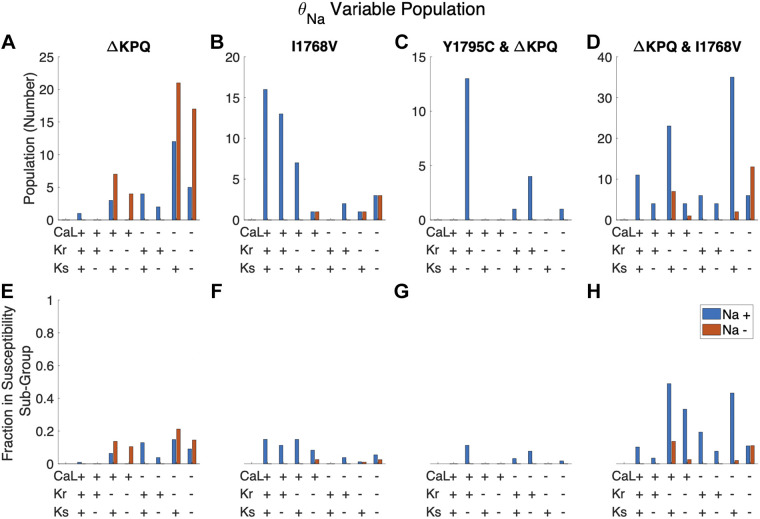
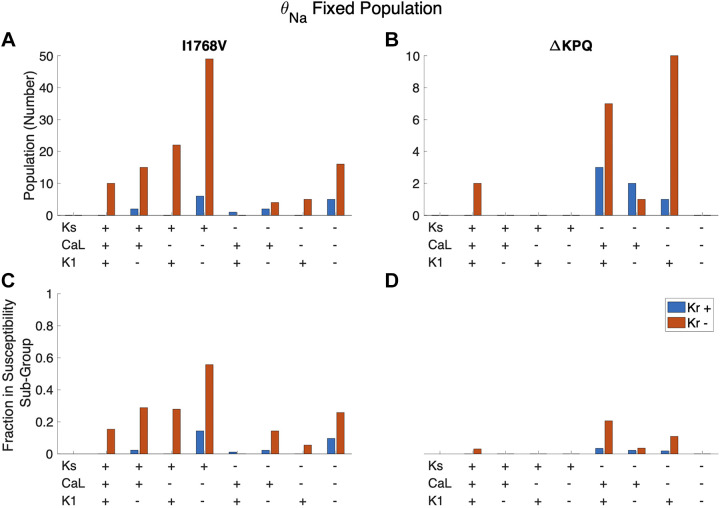
Additionally, we can consider whether there are conductance “signatures” for cells susceptible to only a single mutation or specific combinations, i.e., considering the specific groups within the “One susceptible” (Fig. 7, A and B) or “two susceptible” (Fig. 7, C and D) groups. Here, we find interesting results; specifically, the largest groups of cells susceptible to only ΔKPQ have low θ_Kr and low θ_Na, whereas the largest groups of cells susceptible to only I1768V have high θ_Ca,L and high θ_Na. Similarly, although both “two susceptible” groups are associated with high θ_Na, the largest group of cells susceptible to both Y1795C and ΔKPQ have high θ_Ca,L and high θ_Kr, whereas the largest group susceptible to both ΔKPQ and I1768V have low θ_Ca,L and low θ_Kr. Thus, we find that individual subgroups of cells susceptible to a specific mutation or mutations can exhibit very different characteristics or signatures. Additional comparisons of susceptible and nonsusceptible cells for each mutant in the θ_Na variable population are shown in Supplemental Figs. S6–S8.

Figure 7.

Trends in mutation-specific susceptibility subgroups based on the combined scaling factors of 4 major currents: I_Na, I_Ca,L, I_Kr, and I_Ks. For a given cell, current conductance scaling factors below and above the population median were labeled as low (−) and high (+) conductance, respectively. A–D: number of cells in a given subgroup with one of 16 combinations of high and low conductance. E–H: fraction of cells with a given high- and low-conductance combination that are seen in the given subpopulation.

Generation of a Fixed θ_Na Population

Results of this first analysis collectively indicate that θ_Na is the primary determinant for susceptibility. To further elucidate the role other currents play in APD prolongation and EAD formation, we simulated a second population with θ_Na fixed at the median of the first population (θ_Na = 0.5741). In this fixed θ_Na population, the distribution of other ionic conductances was similar to the first (Supplemental Fig. S9). We find that fixing θ_Na at this median level resulted in an overall decrease in susceptibility. However, we still observe several subgroups of cells susceptible to zero, one, two, or all three mutations (Fig. 8). Unlike in the previous population, in which all conductances including θ_Na vary, here we find a consistent strong positive correlation between WT and mutant APD₉₀ for all three mutations (Fig. 8C), which can be explained as follows. In the original population, θ_Na significantly impacted APD in mutant cells but had minimal influence on WT cells. With θ_Na fixed, the combinations of other ionic currents play a larger role in determining APD in mutant cells, which in turn also impacts APD in the corresponding WT cells. As in the first population, we find positive correlations between APD for cells with different mutations (Fig. 8D).

Figure 8.

Fixed θ_Na population overview illustrating action potential duration (APD) prolongation for different mutations. A: APD at 90% repolarization (APD₉₀) for 1,000 cells, shown by row for Y1795C, I1768V, and ΔKPQ (top to bottom). B: Venn diagram illustrating susceptibility categorization for all 3 mutations. C: comparison between wild-type (WT) and mutant APD₉₀ for each mutation. Unlike in the variable θ_Na population, there is a strong correlation between WT and mutant APD₉₀ for all mutations. D: direct comparison of APD₉₀ for all cells in the population with 2 different mutations. Horizontal and vertical lines at 500 ms indicate the threshold of APD prolongation between cells susceptible or not susceptible to a given mutation. Note that the inclusion of early afterdepolarizations (EADs) in the susceptibility criteria results in some cells with APD < 500 ms also in the susceptible quadrants.

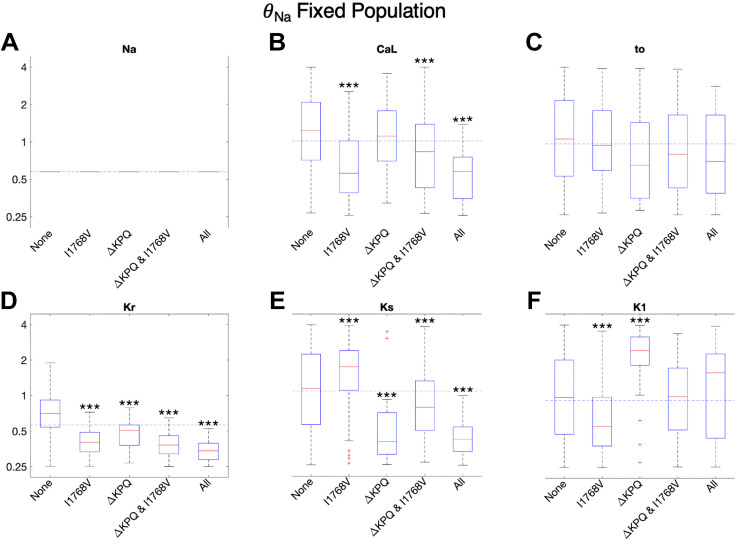
Current conductances and susceptibility.

In Fig. 9, we show box plots for the conductance scaling factor distributions for the different susceptibility subgroups for this population. Interestingly, cells susceptible to only I1768V had lower θ_Ca,L and θ_K1 and higher θ_Ks, whereas cells susceptible to only ΔKPQ had lower θ_Ks and higher θ_K1, again highlighting different characteristics of cells susceptible to distinct mutations. Furthermore, susceptibility to any mutations is associated with lower θ_Kr, suggesting this conductance as an additional critical determinant (as in the first population). Consistent with this finding, θ_Kr is negatively correlated with APD₉₀ across all mutations in this population (Supplemental Fig. S11). Perhaps most unexpected, cells susceptible to all mutations have lower distribution of θ_Ca,L; however, this occurs in conjunction with the lowest levels (relative to the population median) of θ_Kr and θ_Ks, and also low levels of θ_to. Collectively, these results suggest that enhanced susceptibility may be more closely related to lower levels of all plateau currents, such that the presence of a mutation cannot be counterbalanced.

Figure 9.

Distribution of conductances for each of 6 major currents in the fixed θ_Na population. A–F: cells are separated into subgroups based on to which mutations they are susceptible. Trends for the other 7 scaled currents are shown in Supplemental Fig. S10. D: subgroups susceptible to 1 or more mutations have significantly lower θ_Kr. ***P < 0.001.

Relationships between current conductances across the population and susceptibility subgroups.

Across the whole population, correlation between pairs of current conductances in the fixed θ_Na population were remarkably similar to those in the variable θ_Na population (Fig. 10A). For specific susceptibility subgroups, a few correlations between current conductances became stronger. For example, for cells susceptible to ΔKPQ only there was an increase in the magnitude of the negative correlation between θ_Kr and θ_Ks, as well as between θ_Ca,L and θ_K1. For cells susceptible to both ΔKPQ and I1768V, the correlation between θ_Kr and θ_Ks is similarly more negative. In cells susceptible to all mutations, the correlation between θ_Ca,L and θ_Kr is weaker, whereas the correlation between θ_Kr and θ_K1 is much more negative. Collectively, these trends are perhaps not surprising, as the same currents are playing similar roles in both populations; however, the lack of differences in θ_Na (fixed in these cells) results typically in stronger relationships between the currents in individual cells. Correlations for all currents and fluxes, including background currents, pumps, and exchangers, are shown in Supplemental Fig. S12.

Figure 10.

Pearson’s correlation coefficient between conductance between pairs of currents in the fixed θ_Na population. Red indicates a strong negative correlation, lack of color (white) indicates no correlation, and green indicates strong positive correlation. Correlation coefficients between current conductance for whole generated population (A), cells susceptible to no mutations (B), cells susceptible to I1768V only (C), cells susceptible to ΔKPQ only (D), cells susceptible to I1768V and ΔKPQ (E), and cells susceptible to all mutations (F) are shown.

Figure 11 shows the susceptibility of different combinations of high/low levels of θ_Kr, θ_Ks, θ_Ca,L, and θ_K1 in this population with fixed θ_Na. We find here that the vast majority of cells with high θ_Kr are not susceptible to any mutation. In contrast, as noted above, cells susceptible to all mutations tend to also have low θ_Ks and θ_Ca,L, in addition to low θ_Kr. Interestingly, we find that cells susceptible to one or two mutations are associated with both high and low θ_Ks.

Figure 11.

Trends in susceptibility from the fixed θ_Na population based on the combined expression of four major currents: I_Kr, I_Ks, I_Ca,L, and I_K1. A–D: number of cells in a given subgroup with one of 16 combinations of high and low conductance. E–H: fraction of cells with a given high- and low-conductance combination that are seen in the given subpopulation. Cells with high θ_Kr are almost exclusively seen in the zero susceptible subgroup. Cells are susceptible to all mutations only when θ_Kr and θ_Ks are both low (−) and, more frequently, when θ_Ca,L is low (−).

When we separate cells susceptible to only one mutation (Fig. 11, B and F) into susceptible to I1768V only and ΔKPQ only, we find distinct differences in these two groups (Fig. 12). Although both groups are associated with low θ_Kr, susceptibility to only I1768V is primarily comprised of cells with low θ_K1, high θ_Ks, and low θ_Ca,L; in contrast, cells susceptible to only ΔKPQ tend to have low θ_Ks and high θ_K1.

Figure 12.

Trends for cells susceptible to only I1768V (A and C) and only ΔKPQ (B and D) in the fixed θ_Na population based on the combined expression of 4 major currents: I_Kr, I_Ks, I_Ca,L, and I_K1. Cells are most likely to be susceptible to I1768V only when θ_Kr, θ_Ca,L, and θ_K1 are low (−) and θ_Ks is high (+). Cells are most likely to be susceptible to ΔKPQ only when θ_Kr, θ_Ca,L and θ_Ks are low (−) and θ_K1 is high (+). Cells are also frequently susceptible to ΔKPQ only when θ_Ca,L is high (+).

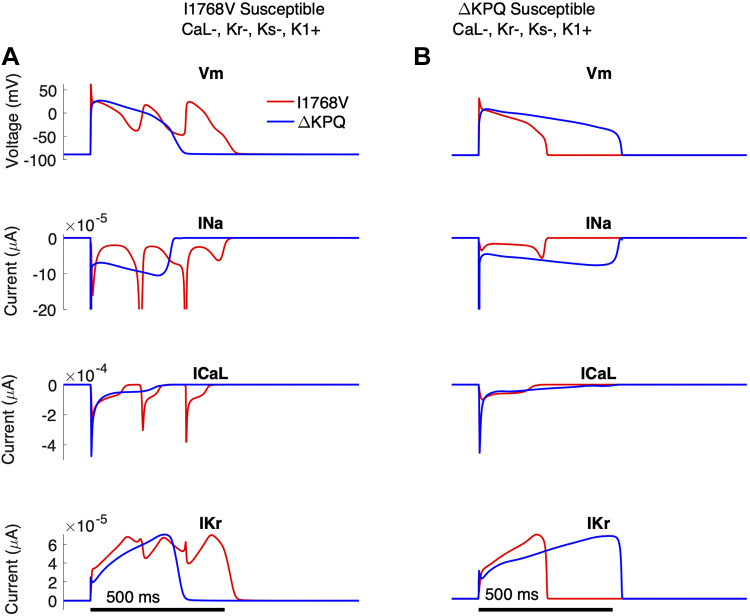
Finally, we selected two individual cells in the fixed θ_Na population from the same current expression level combination, specifically the low θ_Ca,L, low θ_Kr, low θ_Ks, and high θ_K1 group, one of which was only susceptible to I1768V and one only susceptible to ΔKPQ (Fig. 13). We show the transmembrane voltage and corresponding I_Na, I_Ca,L, and I_Kr traces for that individual, simulated with either the I1768V (red) and ΔKPQ (blue) mutations. For the individual cells susceptible to only I1768V (Fig. 13A), the I1768V mutation resulted in reactivation of I_Na, which triggered reactivation of I_Ca,L and driving EADs. In contrast, the same cell with the ΔKPQ mutation illustrates APD prolongation close to, but below, the 500-ms threshold.

Figure 13.

Distinct individuals, susceptible to either I1768V (A) or ΔKPQ (B), from the same combination of current expression [low θ_Ca,L (−), low θ_Kr (−), low θ_Ks (−), and high θ_K1 (+)]. Top to bottom: transmembrane voltage(V_m), I_Na (magnified to highlight the late sodium current), I_Ca,L, and I_Kr as functions of time.

The second individual from the same combined expression group of low θ_Ca,L, low θ_Kr, low θ_Ks, and high θ_K1 was susceptible to ΔKPQ but not I1768V (Fig. 13B). The ΔKPQ mutation (blue) yields a significant I_Na,L, leading to prolongation of APD greater than the 500-ms threshold. The same cell with the I1768V mutation (red) shows no significant prolongation and is not characterized by EAD formation or I_Na,L reactivation. Traces for additional potassium currents and I_Na Markov state changes are shown in Supplemental Fig. S13. Importantly, this figure illustrates that, as also observed in Fig. 2, APD prolongation in cells with the ΔKPQ mutation is primarily driven by a sustained late sodium current throughout the plateau phase. In contrast, APD prolongation in cells with I1768V is driven by reactivation of the late sodium current, which in turn reactivates I_Ca,L, triggering an EAD, even for the same individual in the same current expression combination groups.

DISCUSSION

Main Findings

In this study, we demonstrate in human cardiac ventricular myocytes incorporating LQT3-associated mutations that presentation of the disease phenotype depends on the specific mutation genotype and combinations of ionic current conductance levels. Notably, there was a common trend in which the balance between I_Kr and I_Na determines the individual disease phenotype, frequently more important than the specific genotype and the expression of other major currents. Individuals with deviations from the typical I_Kr-I_Na balance were able to protect against significant prolongation in a genotype-specific manner based on established repolarization reserve. Individuals with mutations characterized by a persistent late sodium current through the plateau phase (i.e., Y1795C and ΔKPQ) were less prone to susceptibility if they had elevated conductance of the slow delayed rectifier potassium current I_Ks. In contrast, individuals with the I1768V mutation, characterized by a reactivating late current, were less prone with high expression of the inward rectifier potassium channel current I_K1.

Interestingly, we expected to find a positive correlation between θ_Ca,L and mutation susceptibility. Instead, we found that increases in θ_Ca,L were either uncorrelated with susceptibility or carried an inverse correlation because of θ_Ca,L being generally proportional to potassium currents, in particular θ_Kr. That is, the inherent balance between I_Ca,L and I_Kr currents in the WT population resulted in individuals with high I_Ca,L also expressing high I_Kr, and the high I_Kr was more critical, opposing significant APD prolongation and EADs in the presence of a LQT3-associated mutation.

Contributions to the Field

Correlations in the healthy population.

In this population approach, each individual healthy cell’s conductance combination was generated by randomly varying each conductance within a defined range and then only including individuals that met electrophysiological criteria characteristic of a healthy ventricular cell. With this approach, we were able to directly compare the same individual with three distinct LQT3-associated mutations. A similar approach has been applied by other groups (22–29). The establishment of a population of healthy individuals resulted in a set of correlations between channel conductances akin to correlated channel expression levels in vitro. Increases in either major depolarizing current, I_Na or I_Ca,L, led to a correlated increase in I_Kr, consistent with I_Kr as a major repolarizing current in the human ventricle, an observation that has been made by others (51).

Our population demonstrates a limited range for the ratio of I_Kr to I_Na, indicating that lower levels of I_Kr-I_Na are nonphysiological. The requirement for balance between I_Na and I_Kr has been observed in rabbit and porcine tissue samples in a study by Hegyi and colleagues (19), for which a healthy AP is restricted to a narrow range of the ratio between these two currents. When cells include a gain of function in the late sodium current I_Na,L because of heart failure, there is a deviation from the balance between I_Na and I_Kr, prolonging APD. In our study, we observe that cells with a lower I_Kr-to-I_Na ratio present with similar prolongation. In contrast, those with higher I_Kr-I_Na ratios resist the increase in I_Na,L from the LQT3-associated mutations.

Similarly, a correlation between I_Ca,L and I_Kr has been observed previously in canine ventricular cells (17) and has been linked to proportional gene expression in human induced pluripotent stem cell-derived cardiomyocytes (hiPSC-CMs) (33). The correlation is important for the unexpected result in which θ_Ca,L is inversely correlated with APD in the setting of LQT3-associated mutations. Note that this result does not imply that increasing I_Ca,L decreases APD; indeed, with all other current conductances held constant, increasing I_Ca,L increases APD as expected. Rather, this result implies that within a healthy population higher I_Ca,L is associated with higher I_Kr, and this higher I_Kr is more protective in the presence of enhanced I_Na,L, such that this overall balance results in shorter APD.

We also observed a negative correlation or lack of correlation among potassium currents I_Kr, I_Ks, and I_K1. Increased conductance from one repolarizing current would require less contribution from other currents. In agreement with this, we find a strong negative correlation between repolarizing currents primarily active during the same phase, such as plateau-phase currents I_Kr and I_Ks, and slightly negative to no correlation between repolarizing currents active during different phases, namely between I_K1 and either I_Kr or I_Ks (although there is overlap between the active periods of these currents).

Trends in susceptible individuals.

We observe distinct differences in ionic current conductance in individuals not susceptible to any LQT3 mutations. In the variable θ_Na population, we see elevated I_Na and I_K1 conductance in individuals susceptible to all mutations, in agreement with an observation in simulated hiPSC-CMs by Paci and colleagues (8) studying the LQT3-associate mutation V1763M, characterized by an increase in a persistent late sodium current. This is similar to the mechanism observed in the ΔKPQ genotype and to a lesser extent Y1795C but dissimilar to I1768V, which is characterized by both increased late sodium current and rapid sodium channel recovery (52).

When directly comparing the characteristics of susceptible versus nonsusceptible cells in our study with human ventricular myocytes modeled with ΔKPQ to hiPSC-CMs modeled with V1763M by Paci et al. (8), we see similarity in the high levels of I_Na and I_K1 in susceptible cells (Supplemental Fig. S8). However, Paci and colleagues observed high levels of I_Ca,L and low-level expression of I_Kr in susceptible cells; in contrast, we saw no significant differences in these currents. Furthermore, comparing their V1763M results to our study of the Y1795C mutation (Supplemental Fig. S6), we find more dissimilarities: we observed a relationship between susceptibility and I_Ks conductance, where Paci et al. observed no significant difference. A similar analysis of susceptible versus nonsusceptible cells for I1768V is shown in Supplemental Fig. S7 and for all three mutants in the fixed θ_Na population in Supplemental Figs. S14–S16.

We hypothesize that the differences in results can be attributed to three causes: model, genotype, and population variability. Although hiPSC-CMs are a powerful tool to characterize patient-specific cells, they have been shown to poorly translate the disease phenotype of LQTS because of developmental immaturity. Quantitative characterization shows that they are functionally closer to prenatal cardiomyocytes than adult cardiomyocytes (53). Specifically, they present with immature calcium handling and reduced repolarization reserve, leading to greater sensitivity to alterations in I_Kr. This could explain why Paci et al. observed correlations between susceptibility and both I_Ca,L and I_Kr expression that were not seen in our study. Notably, in silico modeling of hiPSC-CMs shows insensitivity to I_Ks, which we find plays an integral role in determining susceptibility to the Y1795C mutation characterized by persistent late sodium current.

Furthermore, we emphasize that the mutation modeled by Paci et al., although presenting similar I_Na,L to the ΔKPQ and Y1795C mutations, exhibits different Nav1.5 kinetics and as a result changes the interplay between ionic currents in a distinct way. Here, we have shown genotype to alter the interplay between ionic currents, and work by Zhu et al. (9) has demonstrated further implications of genotype, particularly that different mutations predictably alter the efficacy of the sodium channel blocker mexiletine, emphasizing the importance of genotype in understanding and treating LQT3. More broadly, the differences in the findings between our studies strongly agree with the hypothesis that there are genotype-specific balances of ionic currents that result in susceptibility or protection from disease presentation.

Finally, our population simulates a wider range of ionic current conductance scaling factors (0.25–4) compared with that of Paci et al. (0.5–2). Our wider range of variability leads to more diverse good enough solutions to the cardiac AP and potentially recapitulates a wider variability expressed in the population (20); however, to our knowledge, no study has characterized on a large scale the range of expression levels for each ionic current. As such, the appropriate range to properly mimic physiological population variability is unknown.

Clinical relevance.

Clinical observations have shown that up to 40% of genotype-confirmed LQTS patients may have a normal range-corrected QT interval (QTc) (46), a lower prevalence of LQT individuals with a normal QTc than we observe in our study (58%). Although not exact quantitative agreement, our predicted penetrance within the simulated population was remarkably close to what is observed clinically. This result is notable, considering the lack of a number of factors in our population model that certainly also contribute to the degree of penetrance. In particular, our study considers specifically trends observed in a single cell, whereas in vivo the QT interval is determined by the summed activity of cardiac tissue. Additionally, we categorized susceptibility based on the criteria of an APD₉₀ ≥ 500 ms; however, clinical diagnosis is based on a sliding score as opposed to an all-or-none threshold as was used in our study (46).

In addition to phenotype variability (i.e., incomplete penetrance), LQT3 demonstrates treatment variability, such that pharmacological intervention does not predictably shorten the QT interval. Work by others has shown that response to antiarrhythmics is due to both patient variability such as differences in ionic current expressions (8, 24) and genotype or the specific mutation (9). Although sodium channel blockers are the typical first option for treatment, our work indicates that potassium channel agonists could also be used to restore healthy ventricular APD. Our work suggests that understanding the properties of an individual’s specific mutation is critical to determining an optimal treatment, since the specific potassium current best suited to act as a rescue mechanism is genotype dependent. Our work suggests that I_Kr agonists may be used similarly to I_Na channel blockers in all LQT3 patients to restore the I_Kr-I_Na balance, consistent with previous work showing that I_Kr agonists can restore the QT interval for LQT (54). Our work further indicates that I_Ks and I_K1 could be considered as pharmacological targets. An I_Ks agonist may be able to restore a healthy phenotype in patients with a mutation characteristic of a persistent late sodium current (such as Y1795C and ΔKPQ), and an I_K1 agonist may restore healthy phenotype in patients with a mutation characterized by rapid sodium channel recovery from inactivation (such as I1768V); however, further studies are needed to assess potential off-target effects on conduction or transmural gradients in tissue.

Experimental and clinical comparisons between mutations.

Experimental evidence supports the observed sodium channel dynamics of each mutation, specifically the increased channel reactivation of I1768V and ΔKPQ, and the increased late sodium current from Y1795C and ΔKPQ. Detailed Markov chain-based models of the LQT3-associated mutation sodium channels were developed for Y1795C (38), ΔKPQ (40), and I1768V (39) based on heterologous expression of the corresponding mutant channel in HEK293 cells or Xenopus oocytes (55, 56). However, as these are nonexcitable cells, there is not a direct comparison between APD from our simulations and from these experimental systems. A mouse model of the ΔKPQ mutation has been developed, which demonstrates APD prolongation qualitatively consistent with our results (57); however, cross-species differences between mice and humans make numerical comparisons impractical.

Clinical patient data comparing the different LQT3-associated mutations are relatively sparse. More generally, our study assumption that there is inherent diversity in ion channel expression that results in a wide range of APD for all three mutations is consistent with the broad clinical manifestation of LQT3, mimicking individuals ranging from no QT prolongation to those with severe arrhythmia risk (58). Regarding clinical data comparing mutations, one multicenter study (59) annotated the prevalence of specific mutations in 406 LQT3 patients, indicating 3, 64, and 58 individuals with Y1795C, ΔKPQ, and I1768V mutations, respectively; however, QTc data were only available for a small subset of these patients. A few prior studies have suggested relationships between the biophysical properties of specific LQT3-associated mutations and clinical drug responses in patients: Based on a study of five symptomatic patients with four different mutations, Ruan and colleagues (31) proposed that shifts in steady-state inactivation in different mutations are associated with drug responsiveness. In an analysis of eight patients with five different mutations, Zhu and colleagues (9) showed that a regression model incorporating properties of voltage-sensing domain kinetics was predictive of mexiletine QTc correction. Two studies assessed drug responses in small patient groups with the ΔKPQ mutation (5 individuals in both), finding QTc ranges of 534–672 ms (60) and 500–630 ms (61). Interestingly, in these two studies that include patients all with the same mutation, there was a wide range of baseline QT prolongation and responsiveness to drug treatment. Thus, although clinical data are limited, these studies all consistently demonstrate differences in individuals with different mutations and individuals with the same mutation, consistent with our results. Future work is needed to focus on understanding how ion channel heterogeneity may also impact drug responsiveness in different individuals.

Limitations and Future Directions

Model specificity of ionic current balance and incomplete penetrance.

As with all computational models, there is the possible concern that results are limited to a specific model formulation. As a final analysis of the model specificity of our results, we performed simulations using a different human ventricular myocyte model, specifically the TNNP ionic model (50), similarly integrating the sodium channel Markov chain model, representing mutant channel dynamics, as described above. We performed a similar population study, first generating 1,000 “healthy” individual parameter sets (based on the WT channel models) and then incorporating the three mutant models.

Interestingly, we find that susceptibility rates were similar between the two models, as 498 individuals were susceptible to at least one mutation with the TNNP model compared with 420 in the simulated ORd population, with similar qualitative but differing quantitative overlap between susceptibilities to two or more mutations (Supplemental Fig. S17). Notably, the mutation with the highest rate of susceptibility differed between ionic models, as the ΔKPQ mutation had the highest susceptibility rate in the TNNP model compared with the I1768V mutation in the ORd model.

In addition, we find differences in the role of the specific potassium currents in predicting overall susceptibility. As noted above, the relationship between θ_Na and θ_Kr is the strongest predictor of APD₉₀ in the ORd model across mutations (Supplemental Fig. S4), consistent with the relatively larger magnitude of I_Kr current compared with I_Ks in the ORd model (Fig. 2). However, in the TNNP model, I_Kr and I_Ks are closer in amplitude (Supplemental Fig. S18). Correspondingly, APD₉₀ tends to exhibit a stronger correlation with the θ_Ks-to-θ_Na ratio in the TNNP model, with a weaker relationship between APD₉₀ and the θ_Kr-to-θ_Na ratio (Supplemental Fig. S19). Note that the I1768V mutation in the TNNP model typically resulted in a binary outcome, in which individuals had either a healthy APD₉₀ or failed to repolarize, which resulted in a poor estimate of correlations for this mutation. Importantly, as in the ORd model, we find that different currents are associated with susceptibility depending on the mutation, including low I_Ks for Y1795C and ΔKPQ and low I_K1 for I1768V (Supplemental Figs. S20–S22). Collectively, these results highlight that model formulation differences can account for differing conclusions as to the role of specific currents in contributing to susceptibility and incomplete penetrance. However, the overall conclusion that different currents contribute to incomplete penetrance in a mutation-specific manner is consistent across models.

Limitations.

Although our modeling approach uses a well-validated model based on experimental findings, it is still a simplified version of the level of detail observed in vivo. Specifically, we simulate a model of a single cardiac cell, which does not fully capture the detailed interaction between cells in the native cardiac tissue environment. Direct electrical coupling via gap junctions can mitigate or suppress APD prolongation and EADs in heterogeneous tissue by so-called “source-sink” effects (62); however, these issues in tissue may be less prominent in congenital disorders, such as LQT3, in which all cells are present with the dysfunctional mutation. Additionally, our group has previously shown in cardiac tissue that the localization of sodium channels at the intercalated disk can drive transient depletion of sodium in the intercellular cleft space, which in turn can regulate the LQT3 phenotype (63–65). Thus, although we expect that the clinical presentation of LQT3-associated symptoms, such as QT prolongation and arrhythmias, will be influenced by a host of factors, including tissue-scale properties, our present study shows that single-cell-level factors, specifically ion channel expression and mutation-specific dynamics, are also critical regulators of incomplete penetrance.

Additionally, we categorize cell susceptibility based on the presence of an EAD or an APD₉₀ ≥ 500 ms, as EADs are established arrhythmic triggers (49) and ventricular APD₉₀ translates into QT interval, respectively. Both presence of arrhythmia and QT interval ≥ 500 ms lead to clinical categorization of “high risk” long QT patients (46). Although this mimics clinical classification, studies have shown that mutant cells that present with a healthy-range APD can still form arrhythmia significantly more often than healthy tissue, which our work at present does not capture. Future work including additional criteria, such as AP morphology and the calcium transient (24), could provide a more accurate prediction of arrhythmic risk.

Future directions.

Ongoing and future work is needed for a more thorough understanding of the cause of incomplete penetrance in LQT3. Investigating these trends in a tissue model (66), which more realistically recreates conditions in vivo, will provide more clinically translatable conclusions. In addition, results have indicated that potassium channel (I_Kr, I_Ks, and I_K1) agonists could be used as therapeutic targets in a genotype-specific manner. More mechanistic work characterizing the effects of increasing potassium currents on individuals susceptible to LQT3 could further support targeting these currents for potential LQT3 treatment. Finally, although our study demonstrates the population-level investigation of a gain of function in the late sodium current, similar approaches as used in this study can be applied to other gain-of-function or loss-of-function cardiac diseases.

SUPPLEMENTAL DATA

Supplemental data can be accessed here: https://github.com/SHWeinberg/Miller-LQT3-IncompletePenetrance/blob/main/Miller_AJP_Supplement.pdf.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grant R01HL138003 (to S.H.W.) and American Heart Association Postdoctoral Fellowship Grant 908824 (to N.M.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.A.M., N.M. and S.H.W. conceived and designed research; J.A.M. performed experiments; J.A.M. analyzed data; J.A.M., N.M., and S.H.W. interpreted results of experiments; J.A.M. prepared figures; J.A.M. drafted manuscript; J.A.M., N.M., and S.H.W. edited and revised manuscript; J.A.M., N.M., and S.H.W. approved final version of manuscript.