Spontaneous glutamatergic postsynaptic currents recorded in developing cerebellar interneurons are enhanced by presynaptic depolarization. In response to depolarization, they are organized in bursts. Le Guellec, Gomez et al. propose that bursts signal simultaneous pre- and postsynaptic calcium elevation in single synapses, and that they help synapse formation or stabilization.
Abstract
In central synapses, spontaneous transmitter release observed in the absence of action potential firing is often considered as a random process lacking time or space specificity. However, when studying miniature glutamatergic currents at cerebellar synapses between parallel fibers and molecular layer interneurons, we found that these currents were sometimes organized in bursts of events occurring at high frequency (about 30 Hz). Bursts displayed homogeneous quantal size amplitudes. Furthermore, in the presence of the desensitization inhibitor cyclothiazide, successive events within a burst displayed quantal amplitude occlusion. Based on these findings, we conclude that bursts originate in individual synapses. Bursts were enhanced by increasing either the external potassium concentration or the external calcium concentration, and they were strongly inhibited when blocking voltage-gated calcium channels by cadmium. Bursts were prevalent in elevated potassium concentration during the formation of the molecular layer but were infrequent later in development. Since postsynaptic AMPA receptors are largely calcium permeant in developing parallel fiber-interneuron synapses, we propose that bursts involve presynaptic calcium transients implicating presynaptic voltage-gated calcium channels, together with postsynaptic calcium transients implicating postsynaptic AMPA receptors. These simultaneous pre- and postsynaptic calcium transients may contribute to the formation and/or stabilization of synaptic connections.
Introduction
It is well known that neurotransmitter release occurs in two very different modes: evoked release, where release is sharply timed with presynaptic action potentials (APs), and spontaneous release, where release occurs near resting conditions and is more broadly distributed in time (Fatt and Katz, 1952). Whereas the functional role and the Ca2+ dependence of evoked release have been well characterized, those of spontaneous release are emerging only recently (review: Williams and Smith, 2018). A series of studies suggest that spontaneous release plays a key role in the establishment and in the stabilization of synapses (McKinney et al., 1999; Choi et al., 2014; Cho et al., 2015; review: Andreae and Burrone, 2018). However, whether spontaneous release is modulated by specific signals during development remains unknown. In several subtypes of central neurons, elevating either the extracellular Ca2+ concentration (Cao) or the external K+ concentration (Ko) results in an increase in the frequency of spontaneous synaptic currents (cerebellar Purkinje cells: Llano et al., 2000; Yamasaki et al., 2006; hippocampal granule cells: Goswami et al., 2012). Since these results were obtained in the presence of tetrodotoxin, they suggest that neurotransmitter release may be modulated by Ca2+ independently of the short presynaptic Ca2+ rise resulting from Na+-dependent APs. The enhanced neurotransmitter release observed when elevating either Cao or Ko has been attributed to an increase in the presynaptic Ca2+ concentration that may result either from the release of Ca2+ ions from intracellular Ca2+ stores in the presynaptic axon (Llano et al, 2000; Emptage et al, 2001; Yamasaki et al, 2006) or from the activation of voltage-gated Ca2+ channels (VGCCs) in the subthreshold range of presynaptic membrane potential (Awatramani et al., 2005; Goswami et al., 2012; Williams et al., 2012; Ermolyuk et al., 2013; Lee et al., 2022).
These studies leave the question open as to whether the increased rate of transmitter release occurs randomly, or whether it is structured in space and/or in time. Whereas the first option would suggest that the synaptic events carry little information and have little functional significance, the second option would suggest the opposite, but it has been rarely investigated so far. An early study in hypogastric ganglia showed that the timing of miniature excitatory postsynaptic currents (mEPSCs) did not obey a Poisson process (Bornstein, 1978). In hippocampal cultures, Abenavoli et al. (2002) found that mEPSC occurrence times were clustered in bursts, and the authors suggested that each burst reflected repetitive glutamate release from a single synaptic site. Bursts of miniature inhibitory postsynaptic currents were reported in hypothalamic magnocellular neurons (Popescu et al., 2010). In spite of their potential importance these studies remained isolated. Furthermore, they did not investigate whether bursting could be modulated by specific experimental manipulations, and they did not reveal the cellular mechanisms underlying bursting.
In the present work, we examine signaling mechanisms linked to mEPSCs in cerebellar slice preparations. We focus on the synapse between parallel fibers (PFs) and molecular layer interneurons (MLIs), taking advantage of the very large quantal size of mEPSCs at this synapse (Llano and Gerschenfeld, 1993). In PF-MLI synapses, mEPSCs originating from different synapses may readily be distinguished on the basis of peak amplitude differences (Crowley et al., 2007; Malagon et al., 2016). Differences in mEPSC amplitudes are thought to arise because individual synapses differ in the size of postsynaptic density and in the associated number of postsynaptic receptors (Auger and Marty, 2000; Masugi-Tokita et al., 2007; Miki et al., 2017). In this preparation, we have examined the effects of elevating Cao and Ko on mEPSCs. Our results reveal a high degree of temporal and spatial separation of mEPSCs under these conditions, suggesting that AP-independent neurotransmitter release conveys spatiotemporally precise neuronal signaling. In addition, we find that the prevalence of bursts decreases with age, suggesting a possible role for bursts during development.
Materials and methods
Slice preparation
Slices (200 µm thick) were prepared from the cerebellar vermis of Sprague Dawley rats of either sex following the animal care guidelines of our host institution (Université Paris Cité; approval number A-750607). Experiments were performed at postnatal days 13–16 except for those described in Fig. 8. Rats were anesthetized in isoflurane and beheaded using a guillotine. Cerebellar vermis was isolated and placed in a Leica VT1200S vibratome. Slices were cut in ice-cold sucrose solution (in mM: 75 sucrose, 75 NaCl, 0.5 CaCl2, 7 MgCl2, 2.5 KCl, 1.25 NaH2PO4, 26 NaHCO3, 25 glucose, 5 Na pyruvate, and 0.5 ascorbic acid). In most cases, slices were cut in the direction parallel to the sagittal plane. In these conditions, MLI dendrites were contained in a plane parallel to the cutting plane, whereas PFs were orthogonal to that plane. In addition, some control experiments were conducted where slices were cut in the orthogonal, coronal direction, as indicated. After cutting, slices were incubated for 25 min in a 34°C bath of sucrose solution, and they were then transferred to a bicarbonate buffered solution (in mM: 130 NaCl, 2.5 KCl, 26 NaHCO3, 1.25 NaH2PO4, 10 glucose, 1.5 CaCl2, and 1 MgCl2; osmolarity 300 mosm). They were kept in this solution first at 34°C for 30 min, and then at room temperature, before transfer to the recording chamber. Recorded MLIs were 10–50 µm below the slice surface. When using solutions with a high concentration of K+ ions, the concentration of Na+ ions was diminished to preserve osmolarity.
Figure 7.
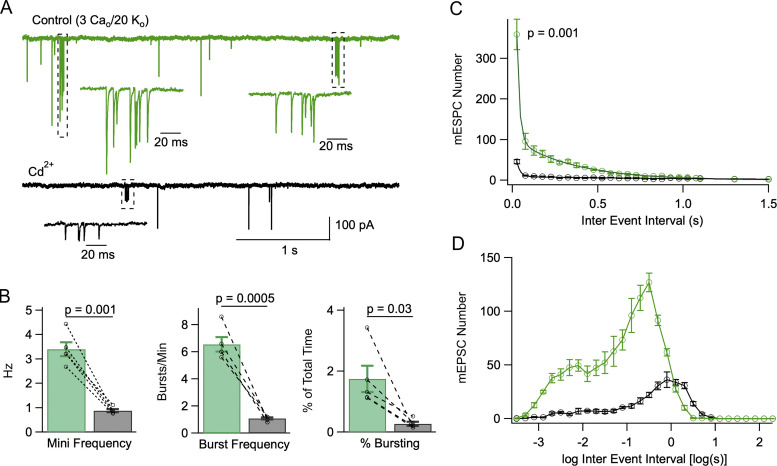
Cd2+ blocks mEPSC bursts. (A) A recording in control solution (3 Cao/20 Ko) displaying two bursts (green; dotted areas and expanded traces below), and after addition of 100 μM Cd2+ (black trace, containing one burst). (B) Summary data showing that Cd2+ reduces overall mEPSC frequency (left), burst frequency (center), and percentage time of bursting (right). (C and D) Comparison of IEI histograms in linear (C; bin size: 50 ms) and logarithmic (D; bin size: 0.2 log unit) coordinates before and after addition of 100 μM Cd2+ (n = 5 cells). P values represent the results of paired t tests for mEPSC frequency, burst frequency, and percent bursting time in Cd2+ vs. control in B, and that of a paired-test comparison between the first 50 ms bin of IEI histograms in Cd2+ vs. control (C). Data obtained from n = 5 cells from 4 animals.
Recording procedures
Patch-clamp whole-cell recordings were obtained from MLIs in rat cerebellar slices visualized through an upright binocular Zeiss microscope (magnification 630×) with water immersion optics. MLIs were selected as having a soma diameter of 8–15 µm located within the molecular layer. MLIs comprise stellate cells, located in the upper part of the molecular layer, and basket cells, located in the lower part. Similar proportions of stellate cells and basket cells were collected for each set of data. Slices were perfused at a rate of 1 ml/min with the bicarbonate buffered solution previously mentioned; this solution was equilibrated with a 95% oxygen, 5% CO2 mixture. Recording pipettes displayed a 3–7 MΩ resistance when filled with internal solution (in mM: 144 K-gluconate, 6 KCl, 4.6 MgCl2, 1 EGTA, 0.1 CaCl2, 10 HEPES-K, 4 ATP-Na2, and 0.4 GTP-Na, pH 7.3, osmolarity 300 mosm). Currents were recorded through a HEKA patch-clamp amplifier EPC10. Holding potentials were kept at −70 mV. Recordings were made at 30–36°C. Uncompensated series resistance values were 15–30 MΩ during recording. A series resistance compensation of up to 60% was applied. The standard recording solution was the bicarbonate-buffered solution described above, supplemented with tetrodotoxin (100 nM, to block action potentials), gabazine (15 μM, to block gabaergic inputs), and 2-amino-5-phosphovaleric acid (APV, 50 μM, to block N-methyl-D-aspartate [NMDA] receptors).
Granule cells contact MLIs at the level of PFs. In addition, the “ascending axon,” the part of the axon comprised between soma exit and branching point, contains presynaptic varicosities that may contact MLIs (Palay and Chan-Palay, 1974). If slices are cut parallel to the sagittal plane, ascending axons are well preserved and PFs are cut; by contrast, if they are cut parallel to the coronal plane, PFs are well preserved and ascending axons are cut. The proportion of mEPSCs in MLI recordings originating from PF and ascending axon may change depending on which structure is preserved and which one is cut. Therefore, if mEPSCs have different amplitudes for the two kinds of synapses, mean EPSC amplitudes may differ depending on cutting orientation. However, we found similar mEPSC amplitudes (measured in standard Ko and Cao conditions) for coronal slices (102 ± 10 pA, n = 9 cells) and for sagittal slices (101 ± 12 pA, n = 9 cells; P = 0.93, t test). These results indicate that differences in peak amplitudes of mEPSCs outlined in Results do not depend on whether synapses originate in an ascending axon or in a PF. In view of these results, mEPSC measurements were routinely carried out in sagittal slices in the present work.
Burst analysis
Histograms of inter-event intervals (IEIs) are presented in two formats, one with linear abscissa axis (as in Fig. 1 E, upper panel), and one with logarithmic abscissa axis (as in Fig. 1 E, lower panel). The rationale of using the linear x-axis is that this plot may be fitted with a double exponential, and that it gives numbers that are directly relevant to burst analysis (see below). Amplitudes of exponential components depend on the duration of the recording and on the bin size. To facilitate comparisons between different figures, they have been normalized to a total duration of 300 s and to a bin size of 50 ms. The rationale of using the logarithmic x-axis as well is that this plot gives an overview of IEIs over a broader range of time domains than would be possible with the linear x-axis (Sigworth and Sine, 1987). Like the linear axis plot, the logarithmic axis plot provides a visual representation of the relative contributions of bursting and non-bursting components to the overall mEPSC distribution.
Figure 1.
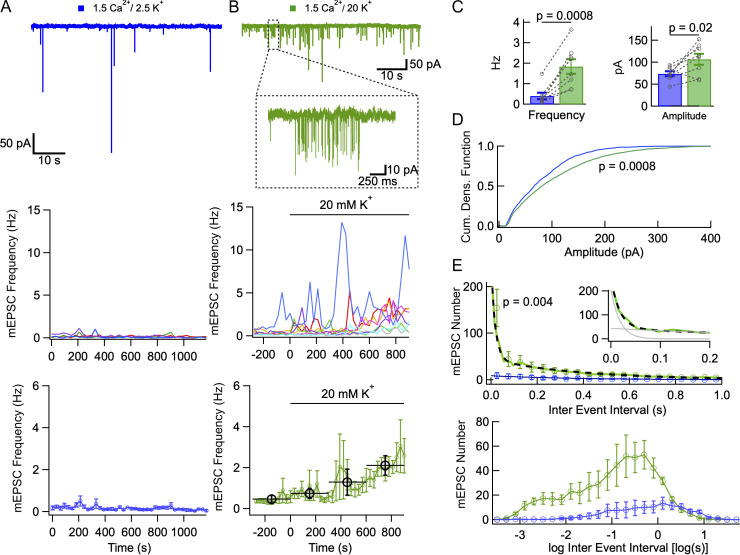
Increasing the external K+ concentration elicits mEPSC bursts. (A) mEPSCs under control conditions (1.5 mM Cao, 2.5 mM Ko saline, containing tetrodotoxin, gabazine, and APV). Upper: Example trace. Middle: mEPSC frequency remains small and stable over a period of 20 min (time bins: 30 s duration). Lower: Mean mEPSC frequency ± SEM, over 30 s long time bins. (B) Effect of elevating Ko. Upper: Example trace in 20 mM Ko, with individual mEPSC burst enlarged. Middle: mEPSC frequency shows large, slow fluctuations in individual recordings, and large cell-to-cell variability. Time 0 marks the transition to the higher Ko. Lower: Plotting mean mEPSC frequency as a function of time (error bars: ± SEM) reveals a slow increase in the higher Ko solution (green: 30 s bins; black: 5 min bins). (C) Summary plots comparing mEPSC frequencies and amplitudes in 2.5 mM Ko (blue) and 10–15 min after switching to 20 mM Ko (green). (D) Cumulative amplitude distributions for 2.5 mM Ko and 20 mM Ko, showing a stronger contribution of large amplitude events in 20 mM Ko. (E) IEI histograms in 2.5 mM Ko and in 20 mM Ko. Histograms reflect 5 min long data taken either in control saline (blue), or 10–15 min after switching to 20 mM Ko (green). The upper plot uses linear coordinates. Circles and associated error bars are calculated for 50 ms bins. For 20 mM Ko data, data are displayed with 10 ms resolution up to 100 ms to highlight the initial part of the histogram (green trace). In 2.5 mM Ko, the interval distribution displays a single exponential component (blue trace) with initial amplitude 9 events/50 ms bin and time constant 370 ms. In 20 mM Ko, IEI distribution is fitted with a double exponential (black dots), where the fast component has an amplitude of 204 events/50 ms bin and a time constant of 18 ms, and the slow component has an amplitude of 44 events/50 ms bin and a time constant of 393 ms (inset: fit of the initial part of the histogram with fast and slow exponential components in gray). The lower plot shows the same data with logarithmic abscissa (bins: 0.2 log unit). P values indicate paired t tests for cell data in C, Kolmogorov-Smirnov test in D, and Wilcoxon signed-rank test for first 50 ms bin in E. Dotted lines link individual cell data together in C. Number of independent experiments: n = 4 cells from 2 animals in A; n = 8 cells from 4 animals in B–E.
Inspection of experimental traces under various experimental conditions indicated that bursts typically contained four mEPSCs or more, and that the time separation between consecutive mEPSCs within bursts was on the order of 20 ms. Consistent with these evaluations, plots of mEPSC numbers as a function of burst duration can be approached with a line having a slope of 29 Hz and a y-intersect of 4.6 (see Fig. 4 C, below). In addition, the time separation between consecutive mEPSCs showed a tendency to increase as a function of time inside individual bursts, as illustrated in Fig. 4 D. Based on these observations, bursts were defined using the following criteria: (i) Bursts consist of at least four consecutive mEPSCs separated by <50 ms from one another; (ii) once a burst is started, it continues as long as time intervals between consecutive events remain below 200 ms.
Figure 4.
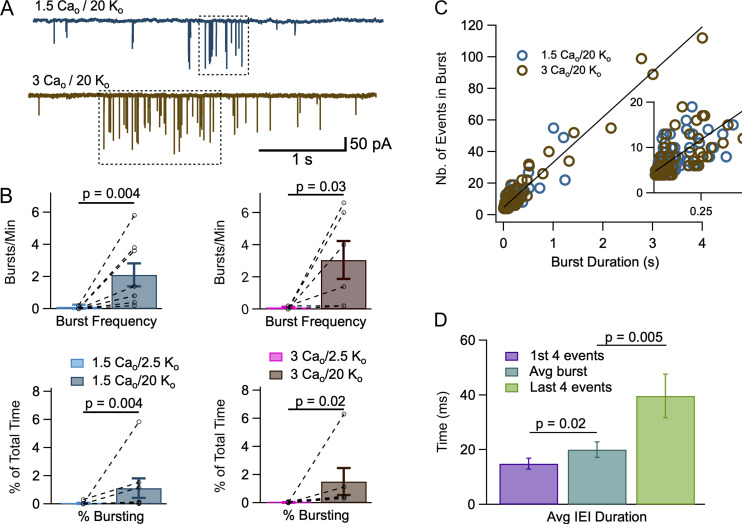
Individual mEPSC bursts in high Ko. (A) Individual mEPSC bursts (dotted boxes) were identified as explained in Materials and methods in recordings obtained in 1.5 Cao/20 Ko (upper trace) and in 3 Cao/20 Ko (lower trace). (B) Comparison of burst frequency (number of bursts per minute: upper panels) and burst occurrence (the percentage of recording time when a burst was observed: lower panel) in 2.5 Ko and in 20 Ko solutions (left: 1.5 Cao; right: 3 Cao). Dashed lines link results of individual experiments together. (C) A plot of the number of mEPSCs inside a burst as a function of burst duration (blue: 1.5 Cao/20 Ko; brown: 3 Cao/20 Ko) reveals a linear relationship. The slope of the regression line corresponds to an intraburst mEPSC frequency of 28.6 Hz. It intersects the ordinate axis at an initial value of 4.6 events. The relation shown is for all blue and brown points; separate regression lines for blue and brown points were almost identical to the line shown. (D) Comparison of mEPSC IEIs for the first four events in a burst (purple), for the entire burst (blue), and for the last four events in a burst (green). Mean values between the three groups are significantly different, showing a gradual frequency adaptation during a burst. P values represent the results of Wilcoxon signed-rank tests in B, and of paired t tests in D. Number of independent experiments: n = 8 cells from 6 animals in B, left; n = 6 cells from 5 animals in B, right; n = 14 bursts from 7 cells taken from 6 animals in D.
The effectiveness of criterion (i) may be assessed when considering the biexponential shape of IEI histograms in Fig. 1 E and Fig. 2 D. In these histograms the fast component time constant, with values of 18 ms (Fig. 1 E) or 10 ms (Fig. 2 D), represents the mean separation between consecutive events inside a burst, while the slow component time constant, with values of 393 ms (Fig. 1 E) or 220 ms (Fig. 2 D), represents the mean separation between consecutive events outside a burst. Applying these numbers to criterion (i) above, it can be estimated that the percentage of false positives (four consecutive non-bursting events classified as bursting) is <0.2%, while the percentage of false negatives (four consecutive bursting events classified as non-bursting) is <0.06%.
Figure 2.
Effects of external Ca2+ concentration on mEPSC bursts. (A) Summary data showing a significant mean mEPSC frequency increase and no significant mean amplitude change when increasing Cao from 1.5 to 3 mM. (B) Increasing Cao from 1.5 to 3 mM elicits bursting. Upper: IEI distributions shift from monoexponential in control conditions (1.5 mM Cao, blue; circles: experimental; continuous line: exponential fit with initial amplitude 0.34 event/bin, and time constant 8.5 s) to biexponential 10–15 min after shifting to 3 mM Cao (purple; fast component: amplitude 14 events/bin, time constant 66 ms; slow component: amplitude 1.7 event/bin, time constant 2.4 s). Bin durations are 50 ms up to 1.1 s, and 200 ms (with appropriate ordinate scaling) thereafter. Lower: Same data presented with logarithmic abscissa axis (bins: 0.2 log units). (C) Summary data showing a significant mean mEPSC frequency increase and a significant mean amplitude increase when raising Ko from 2.5 to 20 mM (3 mM Cao in both solutions). (D) Analysis of bursts elicited by elevating Ko, starting with 3 mM Cao. IEI histograms are displayed in linear (upper graph, with 50 ms bins) and logarithmic (lower graph, with 0.2 log unit bins) coordinates. Upper: In 20 mM Ko, the distribution follows a biexponential curve (black dots) with a fast component (amplitude 725 events/50 ms bin, time constant 10 ms) and a slow component (amplitude 78 events/50 ms bin, time constant 220 ms). Histogram resolution is enhanced to 10 ms/bin in the 0–100 ms range to better document the fast component (green line). Inset: fit of the initial part of the histogram with fast and slow exponential components in gray. Lower: The 3 Cao/20 Ko distribution (green) is clearly distinct from the 3 Cao/2.5 Ko distribution over a wide range of interval durations (purple), but it is not significantly different from the 1.5 Cao/20 Ko distribution (dashed red, from Fig. 1). Results are shown as mean ± SEM for n = 6 experiments from 4 animals comparing 1.5 Cao and 3 mM Cao (A and B), and n = 6 other experiments from 5 animals comparing 3 Cao/2.5 Ko with 3 Cao/20 Ko (C and D). P values indicate the results of paired t tests for cell data in A and C, and of Wilcoxon signed-rank test for first 50 ms bin in D. Dotted lines link individual cell data together in A and C.
The effectiveness of criterion (ii) in identifying burst end may be assessed by considering the plot of Fig. 4 D, showing the evolution of the mean IEI duration from the beginning to the end of a burst. In the beginning of a burst, the estimated inter-event duration from this plot is close to 15 ms, that is, close to the value expected from the time constant of the first exponential in Fig. 1 E and Fig. 2 D. This shows that our burst analysis is self-consistent. At the end of a burst, the estimated interval is close to 40 ms, and in this condition the percentage of false negatives (continuing bursts classified as stopping) expected from criterion (ii) is <2%.
Burst modeling
To model mEPSC bursts in high Ko conditions, we neglect the minor mEPSC population (about 10% of all mEPSCs, see Fig. 3) that have a slow risetime and small amplitude, because these mEPSCs contribute very little to bursts (Fig. 5). For the remaining major population of fast-rising mEPSCs, we postulate that any PF presynaptic terminal can assume two different states, a resting state where mEPSCs occur at very low frequency, and a bursting state where mEPSCs occur much more frequently. We call P the probability that a given synapse is in the bursting state. We assume that a given MLI receives n PF-MLI synapses, and that all of these synapses behave in the same manner and are independent of each other. Calling F the fraction of time when at least one presynaptic site is active for a given postsynaptic MLI, the relation F = nP applies in the limit of small F values. This assumption is consistent with F estimates obtained from direct burst analysis (F = 1.12% in 1.5 Cao/20 Ko, and F = 1.62% in 3 Cao/20 Ko; see Results). On the basis of these numbers, and under the above assumption that presynaptic terminals are independent of each other, the percentage of bursts that reflect simultaneous activation of multiple terminals is only on the order of 1%. We further assume that both in the resting and in the bursting state, mEPSCs follow a Poisson process, with probability densities pr and pb, respectively, in one presynaptic varicosity. Following these assumptions, cellularly recorded mEPSCs follow a Poisson process, with a probability density that equals npr when all presynaptic terminals are in the resting state, and ([n −1] pr + pb) when one presynaptic terminal is active. Corresponding mean IEI values are 1/(npr) and 1/([n −1] pr + pb), respectively. Under the assumptions that F << 1 (active states are rare) and that npr << pb (mEPSCs occurring in one bursting synapse are much more frequent than the combined mEPSCs contributed by n resting synapses), IEIs are distributed along the sum of two exponentials, with time constants that can be approximated to τ1 = 1/pb (fast component) and τ2 = 1/(npr) (slow component), and with corresponding amplitudes A1 and A2.
Figure 3.
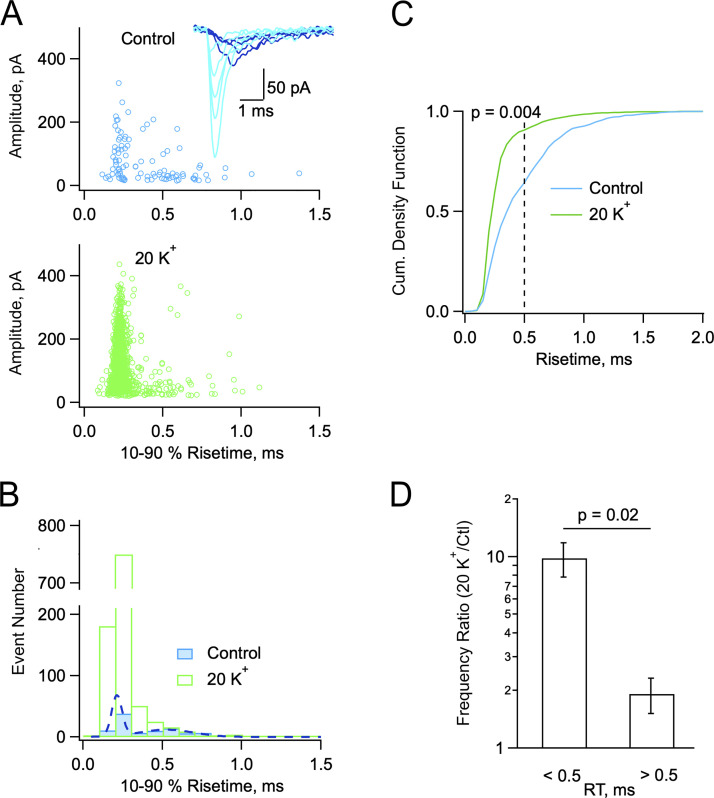
mEPSCs display two populations with differential sensitivities to Ko. (A and B) Exemplar experiment illustrating two groups of mEPSCs in control (blue: 2 Cao/2.5 Ko) and in high Ko (green: 2 Cao/20 Ko). (A) Plot of peak amplitude versus 10–90% risetime for individual mEPSCs in control (above) and in 20 Ko (below; 300 s recording duration in each case). Insert: Superimposed representative mEPSCs in control (light blue: fast rising; deep blue: slow rising). (B) Corresponding risetime histograms with double Gaussian fit to the control data (dots). (C) Cumulative risetime histograms from a group of five cells as in A and B. The control histrogram displays a major component with risetimes <0.5 ms and a minor component with risetimes >0.5 ms. In elevated Ko the weight of the <0.5 ms component is greatly enhanced (P = 0.004, Kolmogorov-Smirnov test). (D) Comparison of frequency ratios (20 Ko vs. control) for the two mEPSCs components (P = 0.02, paired t test). Number of independent experiments: n = 5 from 4 animals (C and D), one of which is illustrated in A and B.
Figure 5.
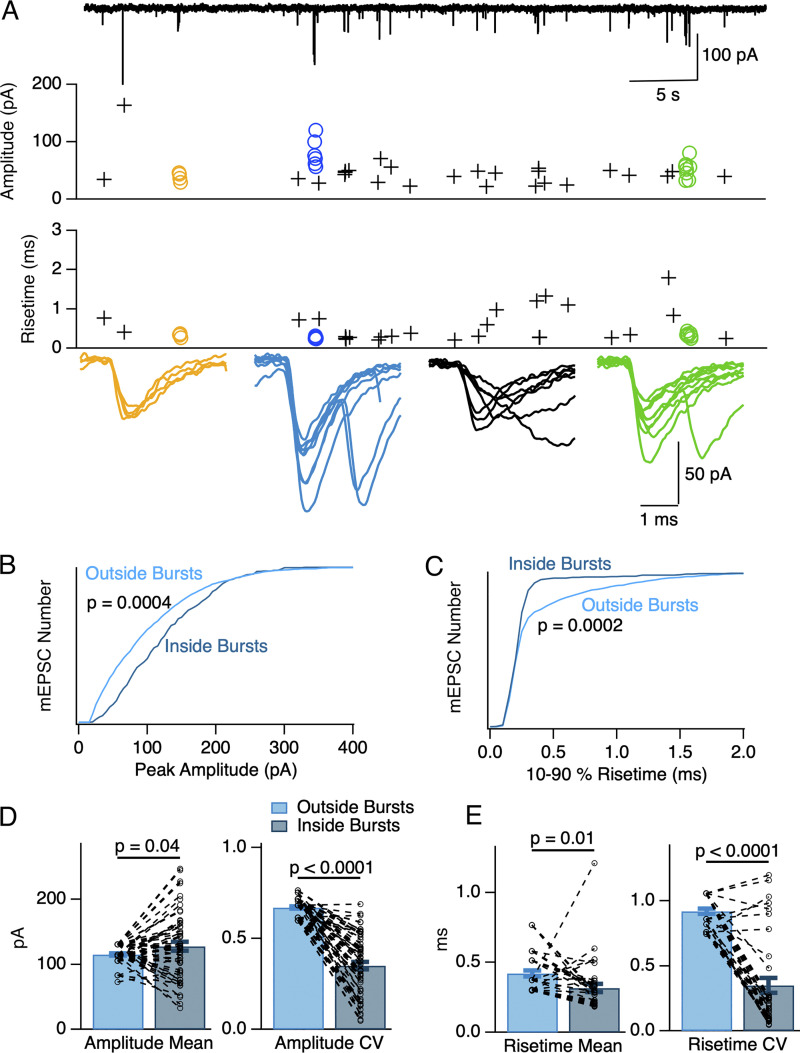
Different mEPSC characteristics inside and outside bursts. (A) A 50 s long recording in 1.5 Cao/20 Ko (upper trace) containing three bursts (yellow, blue, and green symbols). Within each burst, mEPSCs display homogeneous peak amplitude values (upper plot) as well as homogeneous and low risetime values (lower plot). Superimposed synchronized mEPSCs are shown below for each burst. In contrast to mEPSCs inside bursts, mEPSCs outside bursts display variable peak amplitude and risetime values (crosses). A plot of seven superimposed consecutive mEPSCs (black) occurring between the blue and the green burst is shown in addition to the burst traces. (B and C) Normalized cumulative histograms from six cells as in A showing larger peak amplitudes for mEPSCs inside bursts compared to mEPSCs outside bursts (P = 0.0004, B), and faster mEPSC risetimes for mEPSCs inside bursts compared to mEPSCs outside bursts (P = 0.0002, C; Kolmogorov-Smirnov test). (D and E) Individual burst analysis of the same data. D, left: mEPSCs inside bursts (dark blue) had on average a higher peak amplitude than mEPSCs outside bursts (light blue; paired t test: P = 0.04). Dotted lines link together results for individual bursts to corresponding non-bursting events data in the same recording. D, right: mEPSCs inside bursts have a lower peak amplitude CV than mEPSCs outside bursts (paired t test: P = 2 × 10−21). E, left: mEPSCs inside bursts had on average a lower 10–90% risetime than mEPSCs outside bursts (paired t test: P = 0.01). E, right: mEPSCs inside bursts have a lower risetime CV than mEPSCs outside bursts (paired t test: P = 1 × 10−11). Number of independent experiments: n = 6 cells from 5 animals in B–E.
In each burst, the number of events is equal to the number of IEIs plus 1. In each recording, the total number of IEIs belonging to bursts can be obtained by integrating the fast component of the IEI histogram, giving A1τ1. Likewise, the total number of events in bursts is approximately A1τ1. This number can alternatively be estimated from the product of the total recording duration (T) times the fraction of time when a presynaptic terminal is bursting (F), times the bursting frequency (pb), giving
Since τ1 = 1/pb, the above equation can be rewritten as:
| (1) |
Statistical analysis
To compare results across two experimental conditions, we usually employed the following method. In a first step, a relevant parameter (such as peak mEPSC amplitude) was averaged for each recording. Mean values of this parameter were collected for several cells in the two conditions, and overall means were calculated across cells. A statistical test was performed to compare overall means across cells. When each experiment included each of the two conditions, a paired comparison was performed. Alternatively, an unpaired comparison was performed. A t test was used when data were distributed along a Gaussian. If the data distribution clearly deviated from a Gaussian, a non-parametric test was used instead. n values reflected the number of cells recorded in each condition, with equal n values in the case of paired comparison. Differences between the two conditions were considered statistically significant if the P value returned by the test was <0.05.
A different procedure was employed to compare parameters inside and outside bursts. In this case, average values were obtained for individual bursts in each experiment. Events that did not belong to a burst provided an outside-burst average for each experiment. A paired comparison was performed by comparing each burst value to the corresponding outside-burst value for the same experiment. Therefore, for each experiment, several inside-burst values were compared to a single outside-burst value. In this case, n reflected the total number of bursts analyzed, rather than the number of recorded cells.
Results
Increase in mEPSC frequency and mEPSC amplitude from a 1.5 Cao/2.5 Ko solution to a 1.5 Cao/20 Ko solution
mEPSCs in MLIs are thought to originate from the axons of granule cells, PFs (this point will be further discussed below). They are characterized by a large peak amplitude (reaching up to 100 s of pA) and a short decay, with a time constant on the order of 1 ms (Llano and Gerschenfeld, 1993). For most of the experiments, we recorded MLIs in cerebellar slices derived from rats aged 13–16 d, as mEPSCs are relatively frequent in this age group. Experiments concerning an older age group will be described below. Having blocked APs with tetrodotoxin, GABAergic inputs with gabazine, and NMDA receptors with APV, we observed mEPSCs ranging in amplitude from ∼10 pA to several 100 s of pA (Fig. 1 A). As previously noted, these mEPSCs appeared to occur randomly at low frequency (Llano and Gerschenfeld, 1993). Our main goal in the present work was to find conditions where mEPSCs would be enhanced, and to characterize the spatiotemporal pattern of mEPSCs under these conditions. In view of previous data showing a rise of the mEPSC frequency as a function of Ko (e.g., in cochlear hair cell afferent boutons [Glowatzki and Fuchs, 2002] and in the calyx of Held [He et al., 2009]), we tested the effects of elevating Ko on mEPSCs. In 20 mM Ko, we observed a general elevation of the mEPSC frequency, together with a striking shift from a random pattern to a bursting pattern (Fig. 1 B, upper panel). Individual cells displayed bursts lasting for several tens of milliseconds to several seconds (see inset in Fig. 1 B, upper panel, and the more detailed description of burst results below). When plotting mEPSC frequency during 30 s long durations as a function of time, periods with elevated frequency were observed. These periods contained several bursts. They lasted 1 to a few minutes, with marked cell-to-cell differences (Fig. 1 B, middle panel). They were in all cases (n = 8 cells) enhanced in high Ko (individual traces in middle panel, Fig. 1 B). Note that one cell (blue trace in middle panel, Fig. 1 B) displayed one high-frequency period before switching over to the high Ko solution. Average data indicated a gradual frequency increase following an elevation of Ko (t = 0 in Fig. 1 B), from 0.46 ± 0.19 Hz in control to 0.75 ± 0.24 Hz during the first 5 min period in 20 Ko, up to 2.11 ± 0.47 Hz during the third 5 min period in 20 Ko. The slow rise in frequency likely reflects a delayed equilibration of the effective Ko concentration when washing in the 20 Ko solution (Kocsis et al., 1983). In contrast to the 20 Ko experiments, no increase was observed under control conditions (2.5 Ko) over the same time period (Fig. 1 A, lower panel).
Group results indicated that exposure to 20 mM Ko resulted in an increase both of the mEPSC frequency (control: 0.40 ± 0.16 Hz; 20 mM Ko: 1.84 ± 0.35 Hz; n = 8 cells; P = 0.0008, paired t test; Fig. 1 C, left) and of the mean mEPSC amplitude (control: 74.0 ± 5.5 pA; 20 mM Ko: 107.0 ± 12.3 pA; n = 8 cells; P = 0.02, paired t test; Fig. 1 C, right).
Consistent with the results of Fig. 1 C, right, cumulative amplitude histogram analysis revealed that in the presence of 20 mM Ko, large amplitude mEPSCs were more prevalent than in the control (Fig. 1 D; Kolmogorov-Smirnov test, P = 0.0008). The mechanisms underlying the preferential enhancement of large mEPSCs by 20 mM Ko will be investigated below.
Biexponential IEI histograms in high K0 solution
To gain insight into the mechanisms underlying the potentiating effects of Ko elevation, we next compared in individual experiments the time separation between consecutive mEPSCs before and after Ko increase (Abenavoli et al., 2002). Under control conditions, a plot of IEIs during the control period could be fitted with a single exponential component with a time constant of 369 ms (blue data points and superimposed exponential fit; Fig. 1 E, upper panel). This is consistent with a random process where mEPSCs occur at all times with a constant probability. In the presence of 20 mM Ko however, the distribution of IEIs was biphasic, and could be fitted with the sum of two exponentials with widely different time constants (green data and superimposed biexponential fit in Fig. 1 E, upper panel; fast component: A1 = 204 events/50 ms bin, τ1 = 18 ms; slow component: amplitude A2 = 44 events/50 ms bin, time constant τ2 = 393 ms; total analysis duration: 300 s; biexponential fit better than monoexponential fit with P < 0.001; F-test). As explained in Materials and methods, we model these results by assuming that individual synapses fluctuate between a basal state with low mEPSC frequency and an active state with high mEPSC frequency (bursts). With these assumptions, the fast time constant of the IEI histogram reflects the spacing of events for one active synapse, while the slow time constant reflects the spacing of combined events contributed by the sum of synapses converging on the recorded cell, all in their basal state. The fraction of time when at least one presynaptic terminal was active is F = A1 τ12/T (Materials and methods, Eq. 1). Since A1 = 204/50 events/ms, τ1 = 18 ms, and T = 300 000 ms, F = 0.44%. These results indicate that the fraction of time when at least one presynaptic terminal is bursting is small.
In 20 mM Ko, estimates of the numbers of events within and outside bursts can be obtained by integrating the fast and slow components, respectively. This gives for our standard 300 s (5 min) long recording time a number of 204 × 18/50 = 73 events inside bursts, and 44 × 393/50 = 346 events outside bursts. These results indicate that in 20 mM Ko, 17% of the mEPSCs belong to bursts, while the remaining 83% are randomly distributed. By contrast in 2.5 Ko, all events may be considered as randomly distributed.
In another display of the same results, using logarithmic time intervals, it can be seen that time intervals are more numerous after Ko elevation in a broad time domain ranging from ∼1 ms to ∼1 s (Fig. 1 E, lower panel). In this display bursts appear as a first component ranging roughly between 1 and 10 ms, and randomly occurring mEPSCs appear as a second component ranging roughly between 100 ms and 1 s. For interval durations on the order of 10 s, the relative numbers of events in low and high Ko was reversed, with more events at the low Ko value.
In conclusion, IEI histograms display a single exponential component in control, consistent with randomly occurring mEPSCs, and a double exponential in high K0, consistent with distinct periods when mEPSCs occur at high frequency (bursts). A more detailed description of individual bursts will be presented below.
mEPSC bursts are sensitive to the external Ca2+ concentration
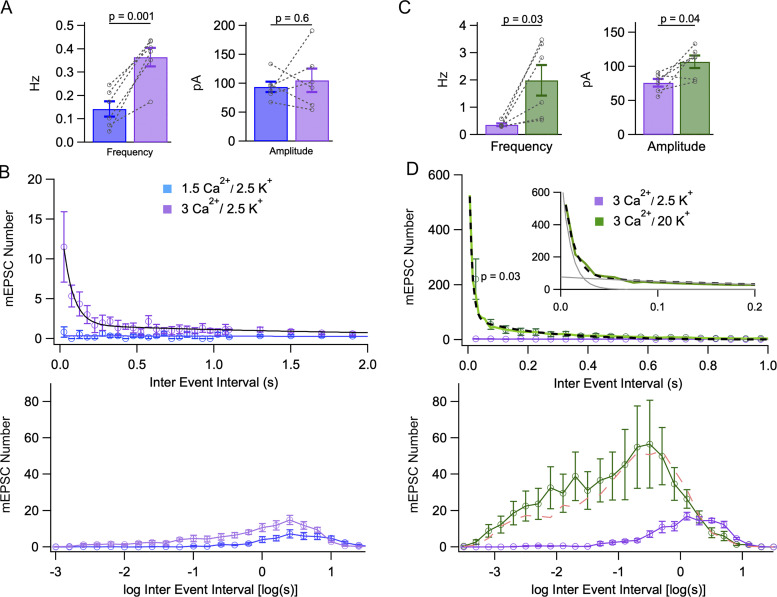
In certain preparations, miniature current frequency depends on extracellular Ca2+ concentration (Cao), suggesting a role of Cao in the regulation of the presynaptic Ca2+ concentration (miniature inhibitory postsynaptic currents: Llano et al., 2000; Goswami et al., 2012; miniature EPSCs: Ermolyuk et al., 2013; Lee et al., 2022; review: Williams and Smith, 2018). In MLIs, mEPSC frequency increased more than twofold when raising Cao from 1.5 to 3 mM (from 0.14 ± 0.03 Hz to 0.36 ± 0.04 Hz; n = 6 cells; P = 0.001, paired t test; Fig. 2 A, left) while Ko was kept at the reference value of 2.5 mM. Mean mEPSC amplitude remained constant (93.6 ± 9.1 pA in control vs. 105.3 ± 20.4 pA in 3 mM Cao; P = 0.6; Fig. 2 A, right).
IEI histograms were clearly biphasic at the higher Cao (fast component: amplitude 14 events/50 ms bin, time constant 66 ms; slow component: amplitude 1.7 events/50 ms bin, time constant 2.4 s; Fig. 2 B, upper panel) whereas control data showed a single component (amplitude 0.3 event/50 ms bin, time constant 8.4 s). Histograms with logarithmic abscissa showed increases for intervals ranging from ∼10 ms to ∼1 s, suggesting an enhancement of event numbers both inside and outside bursts (Fig. 2 B, lower panel). The enhancement of mEPSC numbers linked to Cao elevation was clear, but it was not as marked as that obtained after Ko elevation (compare Fig. 2 B with Fig. 1 E; note that the vertical scales are the same for the logarithmic plots, but that they differ for the linear plots).
To quantify the proportions of events inside and outside bursts as a function of Cao, we integrated as before the exponential components apparent in Fig. 2 B. In 1.5 Cao, randomly occurring events added to 0.3 × 8,400/50 = 50 events per recording (recording duration: 300 s), corresponding to a mean frequency of 0.17 Hz. In 3 mM Cao, randomly occurring events added to 1.7 × 2,400/50 = 82 events per recording, corresponding to a mean frequency of 0.27 Hz, while events inside bursts added to 14 × 66/50 = 18 events per recording, corresponding to a mean frequency of 0.06 Hz. Thus, 18% of the events (= 18/[18 + 82]) occurred in bursts in 3 mM Cao—almost the same proportion as in the 20 mM Ko experiments of Fig. 1—whereas as before, the proportion of events occurring in bursts in 1.5 mM Cao/2.5 mM Ko was negligible.
Increase in mEPSC frequency and mEPSC amplitude from a 3 Cao/2.5 Ko solution to a 3 Cao/20 Ko solution
Having established that elevating Ko from 2.5 to 20 mM, or elevating Cao from 1.5 to 3 mM induces bursting, we next combined together high Ko and high Cao conditions, increasing the external K+ from a 3 mM Cao control condition. Again, mEPSC frequency as well as mean amplitude increased (respectively, from 0.36 ± 0.05 Hz to 1.99 ± 0.56 Hz; n = 6 cells; P = 0.03, and from 75.8 ± 5.6 pA to 106.6 ± 9.2 pA; P = 0.04; paired t tests; Fig. 2 C). As previously observed with 1.5 mM Cao, increasing the external K+ concentration in 3 mM Cao increased bursting, producing a sharply biphasic IEI histogram (Fig. 2 D). Comparison of the biexponential fits to the mean IEI histograms in 3 mM Cao/20 mM Ko and 1.5 mM Cao/20 mM Ko (noted, respectively, 3 Cao/20 Ko and 1.5 Cao/20 Ko hereafter) suggested faster and more prominent bursts in the first case (fast component: amplitude, 725 events/50 ms bin in 3 Cao/20 Ko vs. 204 events/50 ms bin in 1.5 Cao/20 Ko; time constant, 10 ms in 3 Cao/20 Ko vs. 18 ms in 1.5 Cao/20 Ko; slow component: amplitude, 78 events/50 ms bin in 3 Cao/20 Ko vs. 44 events/50 ms bin in 1.5 Cao/20 Ko; time constant, 220 ms in 3 Cao/20 Ko vs. 393 ms in 1.5 Cao/20 Ko; percentage of events in bursts: 30% in 3 Cao/20 Ko vs. 17% in 1.5 Cao/20 Ko; compare Fig. 1 E and Fig. 2 D). Nevertheless, due to large variations between individual experiments, the two sets of data did not display any significant difference, as can be seen when comparing mean IEI histograms in logarithmic coordinates in 3 Cao/20 Ko and 1.5 Cao/20 Ko (lower panel of Fig. 2 D, continuous green curve vs. dashed red curve). Likewise, the mean frequency and mean amplitude values were similar under the two conditions (frequency: 2.63 ± 0.39 Hz in 3 Cao/20 Ko vs. 1.84 ± 0.35 Hz in 1.5 Cao/20 Ko, n.s.; amplitude: 101.3 ± 7.3 pA in 3 Cao/20 Ko vs. 107.0 ± 12.3 pA in 1.5 Cao/20 Ko, n.s.; statistics in 3 Cao/20 Ko were obtained by pooling together the two series of experiments in this condition presented in Table 1, with overall number n = 11). These results indicate that differences between 3 Cao/20 Ko and 1.5 Cao/20 Ko conditions are relatively minor, and that the effects of external Ca2+ and K+ are occlusive rather than additive.
Table 1.
Summary of paired comparisons for experiments performed with animals aged 13–16 d
| Condition | mEPSC amplitude (pA) | mEPSC frequency (Hz) | Burst frequency (/min) | F (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.5 Cao/2.5 Ko | 74.0 ± 5.5 n = 8 |
93.6 ± 9.1 n = 6 |
0.40 ± 0.16 n = 8 |
0.14 ± 0.03 n = 6 |
0.025 ± 0.025 n = 8 |
0.037 ± 0.037 n = 8 |
||||||||
| 3 Cao/2.5 Ko | 105.3 ± 20.4 n = 6 |
75.8 ± 5.6 n = 6 |
0.36 ± 0.04 n = 6 |
0.36 ± 0.05 n = 6 |
0.067 ± 0.042 n = 6 |
0.022 ± 0.013 n = 6 |
||||||||
| 1.5 Cao/20 Ko | 107.0 ± 12.3 n = 8 |
1.84 ± 0.35 n = 8 |
2.10 ± 0.72 n = 8 |
1.12 ± 0.70 n = 8 |
||||||||||
| 3 Cao/20 Ko | 106.6 ± 9.2 n = 6 |
95.0 ± 12.2 n = 5 |
1.99 ± 0.56 n = 6 |
3.40 ± 0.29 n = 5 |
3.06 ± 1.18 n = 6 |
6.56 ± 0.54 n = 5 |
1.51 ± 0.96 n = 6 |
1.75 ± 0.43 n = 5 |
||||||
| 3 Cao/20 Ko + Cd2+ |
68.8 ± 8.3 n = 5 |
0.88 ± 0.06 n = 5 |
1.08 ± 0.08 n = 5 |
0.27 ± 0.07 n = 5 |
||||||||||
Key parameters (mEPSC peak amplitude, mEPSC frequency, burst frequency, and F, the fraction of time when bursts are observed) were measured under various experimental conditions. For each parameter, vertically aligned columns of six numbers (separated in two groups including in each group mean, SEM, and number of independent experiments) represent a paired comparison between two different conditions (e.g., 74.0 ± 5.5 pA, n = 8 in 1.5 Cao/2.5 Ko vs. 107.0 ± 12.3 pA, n = 8 in 1.5 Cao/20 Ko).
A separate population of mEPSCs with small peak amplitudes and long risetimes contributes little to bursting
The finding that high Ko solutions increases not only the mEPSC frequency but also the mean peak mEPSC amplitude was surprising. As individual PF-MLI synapses display distinct mEPSC sizes (Malagon et al., 2016; Miki et al., 2017), the shift of amplitude distributions associated with Ko elevation (Fig. 1, C and D; and Fig. 2 C) suggests that bursts may preferentially target synapses with large quantal sizes. This indicates that all mEPSCs do not contribute equally to bursts, and that large amplitude mEPSCs are more likely to produce bursts than small amplitude mEPSCs.
As illustrated for a representative experiment in Fig. 3, A and B, close examination of mEPSCs in control conditions (2 Cao/2.5 Ko) suggested the presence of two distinct populations of events: mEPSCs with heterogeneous peak amplitudes and fast onset kinetics (light blue traces in inset to Fig. 3 A) and mEPSCs with small peak amplitudes and slow onset kinetics (deep blue traces in Fig. 3 A). Under control conditions, a plot of peak mEPSC amplitudes as a function of risetime duration exhibits a first distinct component with risetimes comprised between 0.1 and 0.3 ms and a mean peak amplitude near 100 pA (Fig. 3 A, upper panel). This was followed by another broader component with risetimes mostly comprised between 0.3 and 1 ms, and a mean amplitude around 50 pA. In the 20 Ko solution, a strong enhancement in the number of fast-rising events was observed, but slow-rising mEPSCs were less affected (Fig. 3 A, lower panel). Two distinct peaks centered at 0.21 and 0.52 ms values were apparent in mEPSC risetime histogram in 2 Cao/2.5 Ko (Fig. 3 B, blue histogram; dotted curve: fit with the sum of two Gaussians, one centered at 0.21 ms and the other centered at 0.52 ms; F-test comparing single Gaussian and double Gaussian fits favors double Gaussian with P < 0.001). In the 20 Ko solution, the component centered at 0.21 ms was strongly potentiated, while that centered at 0.52 ms remained similar to control (Fig. 3 B, green histogram).
We next gathered group results from five selected cells similar to that of Fig. 3, A and B, with low and stable series resistance values, ensuring good resolution of the mEPSC risetime throughout the experiments. These results confirmed the presence of two components in the histogram distribution under control conditions (Fig. 3 C, blue curve). The two components correspond to mEPSCs having risetimes <0.5 ms and >0.5 ms, respectively, with respective approximate weights of 60 and 40%. Group results further indicated a shift in favor of shorter risetimes in the 20 Ko solution, as the proportion of the fast component rose to about 90% (Kolmogorov-Smirnov test, P = 0.004; Fig. 3 C, green curve). They finally showed that fast-rising events were far more potentiated in the 20Ko solution than slow-rising events (ratio: 9.8 ± 2.0 for risetimes <0.5 ms; 1.9 ± 0.4 for risetimes <0.5 ms; paired t test, P = 0.02; Fig. 3 D). In the same set of data, in agreement with data shown in Figs. 1 and 2, mean mEPSC amplitudes calculated across experiments were larger in 2 Cao/20 Ko than in 2 Cao/2.5 Ko (respectively, 118.1 ± 10.6 pA and 77.5 ± 6.0 pA, n = 5; paired t test: P = 0.04). These results suggest that the main reason underlying the mEPSC amplitude increase upon Ko elevation is a shift in the proportion of fast-rising vs. slow-rising events.
The origin of the second component of mEPSCs with slow risetimes is intriguing. When using extracellular stimulation in juvenile preparations, consistently fast risetimes are observed (e.g., 0.19 ± 0.1 ms in Clark and Cull-Candy, 2002). Likewise, when sampling individual dendritic synapses with minimal extracellular stimulation, only short risetimes were observed (rising phase time constant ranging from 50 to 300 μs across various synapses when fitting quantal events with a multiexponential; this corresponds to a range of 40–250 μs when using 10–90% amplitude risetime; Malagon et al., 2016). The corresponding mean amplitude was 105 pA (Malagon et al., 2016), markedly larger than that of the second component of mEPSCs described here. These results indicate that the second component of mEPSCs with small amplitude and slow risetime does not have a counterpart in evoked EPSCs (see also Miki et al., 2017). They suggest in turn that the second component of mEPSCs does not originate at normally functional PF-MLI synapses.
It may be asked to what extent dendritic filtering might account for small amplitude, slow-rising mEPSCs. In juvenile rats, as used in the present study, MLIs have short and thick dendrites, and dendritic filtering is considered to exert only minimal effects on postsynaptic current amplitudes or kinetics (Pouzat and Marty, 1999). By contrast, MLI dendrites in adult animals are long and thin, giving rise to an increase in 10–90% risetimes in single synapse EPSCs from about 150 μs for somatic synapses up to 500 μs for the most distant dendritic sites (Abrahamsson et al., 2012). Thus, dendritic filtering is measurable in adult preparations, but it is then insufficient to convert EPSCs from the first to the second component. The same must also apply for the less severely filtered data in juvenile MLIs.
Overall, these results suggest the presence of a separate population of mEPSCs with small amplitudes and slow risetimes that are probably not arising at fully functional PF-MLI synapses, and that are little affected by the 20 Ko solution. The lower weight of this population in 20 Ko solution compared to control is a likely explanation for the finding that the mean mEPSC amplitude increases in 20 Ko.
Increased burst frequency and increased burst occurrence in high Ko solutions
So far, we have used a global description of bursting based on IEI histograms, and on the simple burst model outlined in Materials and methods. This initial approach is valuable as it avoids any possible bias that could be associated with the definition of what is considered a burst. To study individual bursts, we next developed a criterion to classify mEPSCs as belonging to a burst or occurring randomly. We based this classification on the mean time intervals of events inside and outside bursts in the experiments of Figs. 1 and 2, as explained under Materials and methods. With this classification, we could define specific sequences of mEPSCs as bursts in each experiment (Fig. 4 A).
Once individual bursts were identified, we could compare burst frequency in low and high Ko conditions (Fig. 4 B, upper panels). The burst frequency increased from 0.025 ± 0.025 burst/min in 1.5 Cao/2.5 Ko to 2.1 ± 0.7 burst/min in 1.5 Cao/20 Ko (n = 8; P = 0.004, Wilcoxon signed-rank test), and it likewise increased from 0.067 ± 0.042 burst/min in 3 Cao/2.5 Ko to 3.06 ± 1.18 burst/min in 3 Cao/20 Ko (n = 6; P = 0.03, Wilcoxon signed-rank test; Table 1). We also compared the fraction of recording time when bursts were observed (parameter F of Materials and methods) in low and high Ko conditions (Fig. 4 B, lower panels). This bursting percentage increased from 0.037 ± 0.037% in 1.5 Cao/2.5 Ko to 1.12 ± 0.70% in 1.5 Cao/20 Ko (n = 8; P = 0.004, Wilcoxon signed-rank test), and it also increased from 0.022 ± 0.013% in 3 Cao/2.5 Ko to 1.51 ± 0.96% in 3 Cao/20 Ko (n = 6; P = 0.02, Wilcoxon signed-rank test; Table 1). These results are in line with the conclusions of the above analysis of the same data based on IEI histograms.
Event frequency within bursts is reproducible and displays adaptation
When plotting the number of EPSCs inside a burst as a function of burst duration, data fall along a linear relation with a slope of 28.1 Hz for 1.5 Cao/20 Ko and of 28.7 Hz for 3 Cao/20 Ko, suggesting that the pattern of events within a burst is reproducible (Fig. 4 C). As results were similar for the two sets of data (blue and brown circles in Fig. 4 C), a single regression line for the grouped data is displayed in Fig. 4 C with a slope of 28.6 ± 0.7 Hz (95% confidence interval for slope value).
Mean numbers of mEPSCs per burst from this set of data were 10.6 ± 11 (n = 68 bursts) in 1.5 Cao/20 Ko and 17.4 ± 2.9 (n = 59 bursts) in 3 Cao/20 Ko (unpaired t test, P < 0.05). Corresponding mean burst durations were 192 ± 30 ms in 1.5 Cao/20 Ko and 418 ± 101 ms in 3 Cao/20 Ko (unpaired t test, P < 0.05). As can be seen in Fig. 4 C, the larger values for the number of events per burst and for burst duration in 3 Cao/20 Ko compared to 1.5 Cao/20 Ko reflect a tendency for bursts to last longer while the intra-burst frequency remained constant. Like burst duration, burst frequency was smaller in 1.5 Cao/20 Ko (2.10 ± 0.72 bursts/min, n = 8 cells) than in 3 Cao/20 Ko (4.65 ± 0.86 bursts/min, n = 11 cells; P < 0.05, unpaired t test). Nevertheless, the fraction of time when bursts were obtained (F) was similar in 1.5 Cao/20 Ko (1.12 ± 0.70%, n = 8 cells) and in 3 Cao/20 Ko (1.62 ± 0.54%, n = 11 cells; n.s., unpaired t test).
These numbers indicate that some burst parameters (number of mEPSCs per burst, burst duration, and burst frequency) differ in 1.5 Cao/20 Ko and in 3 Cao/20 Ko, while another burst parameter (F) is similar in 1.5 Cao/20 Ko and in 3 Cao/20 Ko conditions (Table 1). This is consistent with the above analysis of mEPSC frequency and IEIs suggesting weak or no differences between the same conditions.
Compared to the estimate of F = 0.44% based on IEI histogram analysis by application of Eq. 1 in 1.5 Cao/20 Ko, the estimate of F obtained by summing individual burst durations is somewhat higher (1.12%). A similar discrepancy appeared in 3 Cao/20 Ko (0.48 and 1.62%, respectively). The differences are likely due to the frequency adaptation occurring during bursts, to be described below. IEI histogram analysis does not take this adaptation into account and as a consequence fails to attribute many late bursting events to the first IEI histogram component representing bursts. By contrast, when using individual burst analysis, the IEI threshold changes within each burst from 50 to 200 ms (Materials and methods). For this reason, individual burst analysis includes the contribution of late burst events with relatively low frequency. Overall, individual burst analysis provides a more realistic F estimate than IEI histogram analysis.
In Fig. 4 C, the regression line intersects the ordinate axis at a positive value (4.6 ± 0.4 events; insert in Fig. 4 C). Two effects were considered as possible sources of the positive y-intercept. Firstly, since we put a threshold at four events to define a burst, it seemed possible that exclusion of bursts with <4 events may have led to a bias toward high ordinates near the plot origin. Alternatively, very short bursts may have had a tendency to display a higher mEPSC frequency, so that the threshold of four was rapidly reached. To distinguish between these two possibilities, we determined in individual bursts the mean IEI for the first four events, the mean IEI across the burst, and the mean IEI for the last four events. We observed significant differences between the three classes of IEIs (first four events: 14.9 ± 2.0 ms; average along burst: 20.0 ± 2.8 ms; last four events: 39.6 ± 8.0 ms; n = 14 bursts from 7 cells; P = 0.02 for first vs. average; P = 0.005 for last vs. average; paired t tests). These results indicate a strong adaptation of mEPSC frequency within each burst (Fig. 4 D), with a gradual frequency decrease by more than twofold inside individual bursts. They also indicate that the positive y-intercept of the linear regression results from a genuine tendency of short bursts to display a high event frequency, rather than from a sampling artefact linked to the definition of a burst.
Differences in mEPSC amplitudes and risetimes inside and outside bursts
As a rule, quantal sizes differ between individual synapses, so that the coefficient of variation (CV) of quantal amplitudes is larger when sampling from several synapses than when sampling from a single synapse (Auger and Marty, 2000). On this basis, Abenavoli et al. (2002) concluded that bursts in hippocampal cultured neurons originated from individual synapses.
As illustrated in the recording of Fig. 5 A, mEPSCs differed within bursts and outside bursts. Within bursts, risetimes were short, amplitudes were large and homogeneous. By contrast, outside bursts, risetimes were on average longer, amplitudes were on average smaller, and both risetimes and amplitudes displayed large variations among consecutive mEPSCs.
These differences are quantified in a group analysis (n = 6 cells) in Fig. 5, B and C. Cumulative amplitude histograms carried out on all mEPSCs recorded in these cells showed larger amplitudes inside bursts compared to outside bursts (Fig. 5 B), and shorter risetimes inside bursts compared to outside bursts (Fig. 5 C; P < 0.001 in both cases, Kolmogorov-Smirnov tests).
A paired analysis of mean burst results from the same recordings showed that mean amplitudes were larger inside bursts than the corresponding means of amplitudes outside bursts (mean amplitude inside bursts: 127.8 ± 6.6 pA; outside bursts: 115.1 ± 2.0 pA; P = 0.04, paired t test) and that amplitude CV was markedly smaller inside bursts than outside (respective mean values: 0.35 ± 0.02 and 0.67 ± 0.01; p = 2 × 10−21, paired t test; n = 54 bursts from 6 cells; Fig. 5 D; see analysis procedure in Materials and methods). Mean 10–90% risetimes were smaller inside bursts than outside (respectively, 0.32 ± 0.03 ms and 0.42 ± 0.02 ms; P = 0.02, paired t test), while risetime CV was markedly smaller inside bursts compared to outside (respectively, 0.35 ± 0.06 and 0.92 ± 0.02; p = 1 × 10−11, paired t test; n = 37 bursts from 6 cells; Fig. 5 E).
Individual PF-MLI synapses typically contain a single presynaptic active zone and a single associated postsynaptic density (Masugi-Tokita et al., 2007), and they are called for this reason “simple synapses.” As the number of α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid receptors (AMPARs) varies greatly across simple synapses, mEPSC amplitudes CV values are larger when recording from several simple synapses compared to one simple synapse. The CV values for mEPSC amplitudes in bursts are similar to those previously obtained in the same preparation with three different manipulations that are all thought to stimulate release from simple synapses (0.29 with α-latrotoxin applications: Crowley et al., 2007; 0.36 with local GABA applications: Stell et al., 2007; 0.34 when giving trains of presynaptic APs from a single PF: Malagon et al., 2016). In all of these studies, the amplitude CV across unselected EPSCs—arising from multiple synapses—was comprised between 0.6 and 0.7. Again, these values are similar to the CV value of 0.67 found outside bursts in the present experiments (Fig. 5 D, right). Altogether, the close similarity between CV values found here inside and outside bursts with previous estimates of CV values inside and across simple synapses strongly suggests that most of the bursts originate from a single PF terminal.
A detailed inspection of the results in Fig. 5, D and E, suggests a larger dispersion of burst parameters inside bursts compared to outside bursts. This is because outside burst values were taken from all outside burst events in a given recording, and they were therefore averaged over a large number of events (see Materials and methods). By contrast, inside burst parameters were averaged inside individual bursts, sometimes containing as few as four events.
While bursts usually displayed fast risetimes and small risetime CVs, some bursts reported a high mean risetime value (Fig. 5 E). The same bursts displayed a large risetime CV value. When examining closely these unusual bursts, we found that they consisted of a normal looking burst together with a single contaminant mEPSC with slow risetime. Artificially removing the contaminant mEPSC restored normal mean risetime and risetime CV values. Altogether, these odd burst results are readily explained by the superimposition of a normal burst provided by one synapse and of a slow event contributed by another synapse.
mEPSC amplitude occlusion during bursts
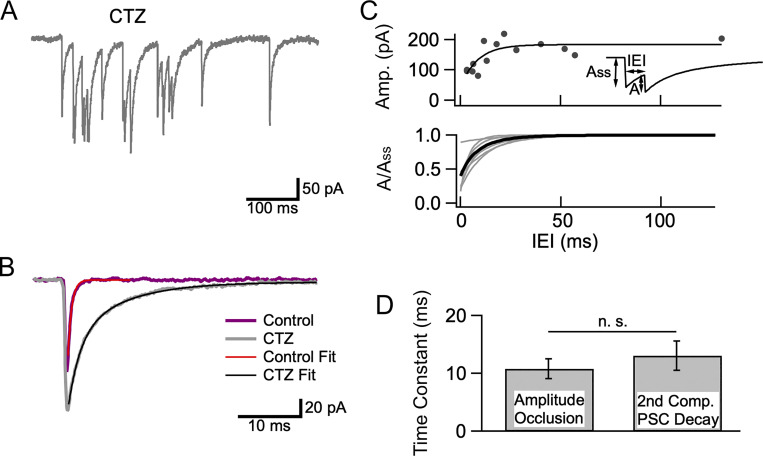
If a simple synapse is stimulated by the release of two synaptic vesicles (SVs) at short time intervals, consecutive postsynaptic currents display “amplitude occlusion,” as postsynaptic receptors that are engaged in the response to the first SV do not participate in the response to the second SV. Amplitude occlusion is a hallmark of simple synapses. It can be demonstrated by plotting the amplitude of the second postsynaptic current in a pair as a function of the time interval from the first postsynaptic current (Auger and Marty, 1997). As time interval increases, receptors disengage from the first response, and the amplitude of the second response gradually recovers. We next examined whether amplitude occlusion was apparent in mEPSC bursts.
Amplitude occlusion is difficult to analyze under the conditions of Figs. 1, 2, 3, 4, and 5 because the time interval between mEPSCs inside bursts (∼15 ms at the onset: Fig. 4 D) is too large compared to the time constant of mEPSC decay (∼1 ms) to produce significant overlap between consecutive mEPSCs. To reveal amplitude occlusion, and to derive an estimate of the percentage of receptor occupancy at the peak of mEPSCs, we studied bursts in the presence of the AMPAR modifier cyclothiazide (CTZ; Fig. 6 A). CTZ is known to slow down EPSC decay, as well as to block AMPAR desensitization (Crowley et al., 2007). Therefore, it seemed possible that CTZ application would bring mEPSC decay into a time range where amplitude occlusion should become measurable. In control conditions the mEPSC decay was fit to a single exponential with a time constant of 0.66 ms (Fig. 6 B, purple curve and superimposed exponential fit). In the presence of 100 μM CTZ, a double exponential fit was needed, with time constants 1.86 ± 0.04 ms (fast) and 8.01 ± 0.13 ms (slow; Fig. 6 B, gray curve and superimposed biexponential fit; 95% confidence intervals to fit time constants).
Figure 6.
mEPSC amplitude occlusion in CTZ. (A) Example of a burst recorded in 3 Cao/20 Ko in the presence of CTZ (100 μM). (B) Superimposed average recordings of mEPSCs under control condition (purple; time constant of decay 0.6 ms) and after addition of CTZ (gray) showing slower, biphasic decay in CTZ (fast component time constant 1.9 ms; slow component time constant 8.0 ms; % slow component 53%). (C) Upper: Amplitude occlusion analysis (A as a function of IEI, see insert) for a burst in CTZ, showing a drop of peak amplitudes at short IEIs. An exponential fit to the data describes the recovery kinetics of mEPSC amplitudes. Extrapolation of this exponential to an interval duration of 0 provides an estimate of 75% receptor occupancy at mEPSC peak, while the time constant of recovery is 8.5 ms. Lower: Fits of normalized A(IEI) plots as in the upper plot for seven bursts (gray), with average in black. (D) Similarity between the kinetics of receptor deactivation (given by the time constant of the second component of mEPSC decay; n = 13 mEPSCs from 5 recordings) and those of amplitude occlusion recovery (n = 7 bursts from 6 recordings) indicates that mEPSC occlusion is driven by receptor deactivation.
In line with former results with α-latrotoxin (Crowley et al., 2007), we found that in CTZ, plots of mEPSC amplitude as a function of IEIs displayed a reduction at short times (Fig. 6 C, upper panel). Such results at simple synapses have been interpreted as reflecting amplitude occlusion following repeated stimulation of a common set of AMPARs (Auger and Marty, 1997; Crowley et al., 2007). After fitting the amplitude (A) vs. IEI plot with an exponential, receptor occupancy at the peak of mEPSCs can be calculated as ω = 1 − A0/Ass, where A0 represents the back-extrapolated value of A for an IEI of 0, and Ass represents the amplitude of a stand-alone mEPSC (insert in Fig. 6 C, upper panel; Auger and Marty, 1997; Crowley et al., 2007). In the example of Fig. 4 C, upper panel, the A0/Ass ratio was 0.25, giving a receptor occupancy of 0.75 at the peak of an mEPSC. The time constant of the exponential (here 8.5 ms) reflects the rate of recovery of receptors available for renewed activation by glutamate.
Results from seven bursts similar to that illustrated in the upper panel are shown in the lower panel of Fig. 6 C (gray: fits of individual A(IEI) plots; black: average of gray curves, with a time constant of 9.5 ms). The average receptor occupancy value found with this method was 0.60 ± 0.09 (n = 7 bursts), close to the value of 0.62 found with the same method in the absence of CTZ for evoked EPSCs in simple synapses (Malagon et al., 2016). As amplitude occlusion rests on receptor availability in simple synapses, these results confirm that most bursts originate in simple synapses.
In CTZ, the average time constant of the exponential fit to the A(IEI) plot was 10.8 ± 1.7 ms (n = 7 bursts), close to the slow time constant of mEPSC decay (13.1 ± 2.5 ms; Fig. 6 D). Since CTZ blocks desensitization, the slow time constant of mEPSC decay in CTZ presumably reflects receptor deactivation rather than receptor desensitization. As receptors become available following receptor deactivation, they can contribute to increasing mEPSC amplitude upon renewed glutamate release. The results therefore suggest that the kinetics of recovery of amplitude occlusion for paired mEPSCs match those of receptor deactivation following a single mEPSC. A similar conclusion was reached earlier concerning receptor occlusion in the absence of CTZ (Malagon et al., 2016).
Bursts are inhibited by Cd2+
In 20 mM Ko the Nernst potential for K+ is about −51 mV, a potential sufficiently depolarized to activate certain presynaptic VGCCs and to induce a significant basal Cai rise in presynaptic terminals (Awatramani et al., 2005; Bouhours et al., 2011). To test whether VGCC activation was involved in the activation of presynaptic PF terminals, we examined the effects of the broad spectrum VGCC antagonist Cd2+ on mEPSCs in 3 Cao/20 Ko (Fig. 7). As illustrated in Fig. 7 A, application of 100 μM Cd2+ exerted a marked inhibitory effect on mEPSCs in these conditions. The peak mEPSC amplitude was reduced from 95.0 ± 12.2 to 68.8 ± 8.3 pA (P = 0.003; n = 5 cells; paired t test). Cd2+ ions act on open VGCCs by interfering with calcium permeation and reducing calcium entry (Swandulla and Armstrong, 1989). As AMPARs in MLIs of juvenile rodents are calcium permeant (Liu and Cull-Candy, 2000; Soler-Llavina and Sabatini, 2006), it is plausible that Cd2+ ions likewise act on these AMPAR channels to reduce their conductance. The overall mEPSC frequency was reduced more than threefold by Cd2+ (from 3.40 ± 0.29 Hz down to 0.88 ± 0.06 Hz; P = 0.001; n = 5 cells; paired t test; Fig. 7 B, left). The burst frequency was reduced from 6.56 ± 0.54 bursts/min to 1.08 ± 0.08 bursts/min (P = 0.0005; paired t test; Fig. 7 B, center), and the percentage bursting time (F) was reduced from 1.75 ± 0.43 to 0.27 ± 0.07% (P = 0.03; paired t test; Fig. 7 B, right). These results indicate an even stronger inhibitory effect of Cd2+ on bursting than on overall mEPSC frequency.
Consistent with the results of Cd2+ observed with individual burst analysis, Cd2+ inhibited both the fast component (amplitude: 1,204 events/50 ms bin in control vs. 126 events/50 ms bin in Cd2+; time constant: 16 ms in control vs. 21 ms in Cd2+; total number in 300 s recording period: 285 events in control vs. 53 in Cd2+) and the slow component (amplitude: 104 events/50 ms bin in control vs. 9 events/50 ms bin in Cd2+; time constant: 351 ms in control vs. 1.25 s in Cd2+; total number in 300 s recording period: 730 events in control vs. 225 in Cd2+; Fig. 7 C) of IEI histograms. A strong decrease of the two components of the IEI histogram is also apparent when using logarithmic time coordinates (Fig. 7 D). These results suggest that voltage-gated Ca2+ entry plays a major role in the generation of mEPSC bursts.
Bursts are developmentally regulated
Results so far have been gathered in preparations from rats aged 13–16 d. This age group corresponds to the last days of the formation of the molecular layer, during which many of the PF-MLI synapses are established (Altman, 1972). We next tested Ko-dependent mEPSC bursting would also be present at a more mature stage of PF-MLI synapses.
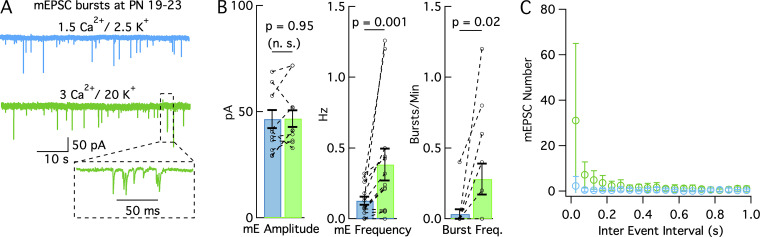
To this end, we investigated the effect of the 3 Cao/20 Ko solution in a higher age group (19–23 d, compared to 13–16 d hitherto; Fig. 8). At 19–23 d, the definitive molecular layer circuitry is established (Altman, 1972). In this age group, as may be seen in the representative experiment of Fig. 8 A, mEPSCs were only moderately enhanced in 3 Cao/20 Ko conditions compared with 1.5 Cao/2.5 Ko (green and blue traces, respectively). Furthermore, bursting was not prominent in this experiment, as no burst was observed in control and a single burst (illustrated in the inset to Fig. 8 A) was observed in the 3 Cao/20 Ko solution (during recording durations of 3 min in each case).
Figure 8.
mEPSC bursts are infrequent at PN 19–23 d. mEPSCs were examined in control conditions and in elevated K0/Ca0 at PN 19–23 d instead of PN 13–16 d. (A) Example recordings in 1.5 Ca0/2.5 K0 solution (blue) and in 3 Ca0/20 K0 solution (green) from the same cell obtained from a 19-d-old rat. During total recording times of 3 min in each solution, no burst was obtained in control, and a single burst was obtained in 3 Ca0/20 K0 solution (inset). (B) Peak mEPSC amplitude (left), mEPSC frequency (center), and mEPSC burst frequency (right) in the two solutions (blue: 1.5 Ca0/2.5 K0; green: 3 Ca0/20 K0). P values represent the results of paired t test for mEPSC amplitudes (left), and of Wilcoxon signed-rank test for mEPSC frequency and burst frequency (center and right). (C) Inter-event histograms in 1.5 Ca0/2.5 K0 solution (blue) and in 3 Ca0/20 K0 solution (green; data normalized to a recording duration of 300 s as in Figs. 1, 2, and 7). The fast time constant component of the 3 Ca0/20 K0 histogram at PN 19–23 d has a small mean amplitude and a high variability compared with corresponding PN 13–16 d data (Figs. 1, 2, and 7). Data are from n = 12 cells from 5 animals in B left, and from n = 13 cells from 5 animals in B center/right and in C.
Group results are shown in Fig. 8, B and C. In control solution (1.5–2 Cao/2.5 Ko), mEPSC peak amplitudes were markedly smaller at postnatal days 19–23 (PN 19–23 d) than at 13–16 PN d (46.5 ± 4.3 pA, n = 12 cells, vs. 81.1 ± 3.6 pA, n = 19 cells; P < 0.001, unpaired t test; the cells at PN 13–16 d include the two series tabulated in Table 1 plus five additional cells in 2 Cao/2.5 Ko). Mean mEPSC frequencies were also smaller at the higher age group (0.13 ± 0.03 Hz, n = 13 cells vs. 0.32 ± 0.06 Hz, n = 19 cells; P < 0.05, unpaired t test). As in the lower age group, shifting to the 3 Cao/20 Ko solution significantly increased mEPSC frequency at 19–23 d (from 0.13 ± 0.03 Hz to 0.38 ± 0.11 Hz, n = 13 cells; P = 0.001, Wilcoxon signed-rank test; Fig. 8 B, center). However, there was no change in the mean amplitude in the higher age group when shifting to the 3 Cao/20 Ko solution (46.7 ± 3.9 pA vs. 46.5 ± 4.3 pA; n = 12 cells; P = 0.95, paired t test; Fig. 8 B, left). In addition, the frequency reached in the 3 Cao/20 Ko solution was smaller at 19–23 d than at 13–16 d (0.28 ± 0.11 Hz, n = 13 cells vs. 2.63 ± 0.39 Hz, n = 11 cells; P < 0.01, unpaired t test). These results indicate that mEPSCs at 19–23 d have smaller amplitudes, lower frequency, and lower sensitivity to elevated Ko/Cao than at 13–16 d (Table 1).
As already noted in the case of the experiment of Fig. 8 A, bursts were occasionally observed at 19–23 d in control conditions (1/13 cells) and in 3 Cao/20 Ko solution (6/13 cells). In fact, they were more readily recognizable at the higher age group because they contrasted more strikingly against what was a lower mEPSC background rate. As in the younger age group, burst numbers increased significantly in the 3 Cao/20 Ko solution (from 0.03 ± 0.03/min to 0.23 ± 0.10/min; n = 13 cells; P = 0.02, Wilcoxon signed-rank test; Fig. 8 B, right). However, bursts were much less frequent than at 13–16 d, when all cells displayed bursting in the 3 Cao/20 Ko solution (n = 11 cells; mean number of bursts of 3.06 ± 1.14/min; P < 0.001, unpaired t test comparison with corresponding data at 19–23 d). These results indicate that burst frequency in the 3 Cao/20 Ko solution is about 13-fold lower at 19–23 d compared to 13–16 d, whereas the corresponding ratio for mean mEPSC frequency is about ninefold. Bursts were not only less frequent, but also more variable at 19–23 d than at 13–16 d. The larger cell-to-cell variability at the higher age group can be appreciated by comparing inter-event histograms in 3 Cao/20 Ko at 19–23 d (Fig. 8 C) and at 13–16 d (Fig. 2 D and Fig. 7 C). Compared to 13–16 d data, error bars are comparatively larger at 19–23 d, such that differences for individual bins to the control solution (here 1.5 Cao/2.5 Ko) are not significant. Altogether, Ko-dependent bursting is less marked and more variable at 19–23 d than at 13–16 d.
Discussion
The main findings of the present work are that in elevated Ko or Cao conditions, (i) mEPSCs of MLIs are organized in bursts, and (ii) individual bursts originate in single synapses.
mEPSCs of MLIs are organized in bursts
In the present work, mEPSC bursts were characterized using two complementary approaches. A first approach was based on the analysis of IEI histograms. In 20 Ko solutions, these histograms could be accurately fitted with a biexponential curve. The fast and slow components were interpreted as reflecting events occurring within bursts and outside bursts, respectively. Time constants values for the fast component varied between 10 and 21 ms (Fig. 1 E, Fig. 2 D, and Fig. 7 C), a narrow range that suggested a reproducible minimal IEI value of 10–21 ms within bursts.
A second approach was based on direct identification of individual bursts, using criteria detailed in Materials and methods. This approach provided a more detailed view of bursts. It revealed that during an initial phase, mEPSC frequency is high (around 60 Hz, consistent with the results of IEI histogram analysis), and that mEPSC frequency displays adaptation during bursts. While individual bursts follow a common pattern of frequency adaptation, they differ markedly in terms of their total duration (Fig. 4 C).
Individual bursts originate in single synapses
Our conclusion that bursts originate in single synapses is consistent with previous work on hippocampal cultures (Abenavoli et al., 2002), and is based on two lines of evidence. First, the CV of mEPSC amplitudes is lower when comparing events inside individual bursts to events outside bursts, with respective mean values of 0.35 and 0.67. Both values are consistent with previous estimates of intrasynaptic and intersynaptic variability in the same preparation, suggesting that each burst arises at a single synapse (Crowley et al, 2007; Malagon et al., 2016). The low value of intrasynaptic amplitude CV at PF-MLI synapses may come from the small size and high receptor density at these synapses, while the larger value for intersynaptic CV may come from variations in postsynaptic density sizes across synapses (Masugi-Tokita et al., 2007; Miki et al., 2017). By comparison, earlier estimates of intrasynaptic CV in hippocampal cultures tend to be higher than at PF-MLI synapses (0.4 to 0.5 vs. 0.37: Liu et al., 1999; Abenavoli et al., 2002).
The second line of evidence comes from experiments performed in the presence of CTZ, showing amplitude occlusion for consecutive mEPSCs at short intervals within bursts. Amplitude occlusion is diagnostic of a single synapse origin (Crowley et al, 2007; Malagon et al., 2016). Furthermore, the value estimated in the present experiments for receptor occupancy at the peak of individual mEPSCs (0.60) is in agreement with that obtained in earlier work (0.62, Malagon et al., 2016), confirming that bursts originate in single synapses.
Intense presynaptic stimulation during bursts
When elevating Ko or Cao, spontaneous synaptic currents occur along two very distinct modes. The first mode, corresponding to the slow component of Fig. 1 C, reflects a low probability release contributed by many synapses, with a global mean frequency around 0.3 Hz. It was reported that individual stellate cells receive >100 synapses from granule cells (Abrahamsson et al., 2012). Since basket cells tend to have larger dendritic trees than stellate cells, the global MLI population, comprising stellate and basket cells, can be considered to likewise receive >100 synapses per cell. Therefore, the basal mini rate from each of these synapses is on average <0.003 Hz. The second mode, corresponding to the fast component of Fig. 1 E, is due to bursts having a mean duration of a few hundreds of milliseconds and a mean intraburst frequency near 30 Hz. The analysis of Figs. 4 and 5 shows that the extent of burst overlap between different synapses is minimal, and that bursts primarily reflect the separate activation of single synapses. Therefore, when a burst occurs in a synapse, the rate of SV release presumably increases in that synapse from <0.003 to 30 Hz, a ratio of >10,000-fold. As discussed in Materials and methods, the fraction of time when at least one terminal is bursting, F, is only 0.4–1.1% (depending on the method used to estimate F) in the conditions of Fig. 1 (1.5 Cao/20 Ko); when taking into account that each cell potentially receives signals from >100 terminals, this means that the fraction of time when an average individual terminal is active is < 4 × 10−5–1.1 × 10−4.
The number of events inside a burst is highly variable, but in most cases, this number falls in the range between 4 and 20 (Fig. 4 C). When stimulating a PF-MLI synapse with an AP train at high frequency, SVs are released at an average rate near 1 SV per AP (Malagon et al., 2020). Therefore, the mean frequency of 50 Hz observed during a burst roughly corresponds to the response to an AP train at 50 Hz, indicating that a burst involves an intense presynaptic stimulation.
Slowly rising mEPSCs
Our results show that a distinct category of mEPSCs exhibiting slowly rising phases and low peak amplitudes is little involved in bursting. As discussed earlier, these events do not appear to be merely the consequence of dendritic filtering. In addition, individual PF-MLI recordings only display fast-rising, large-amplitude EPSCs, suggesting that slow and small mEPSCs do not originate at fully functional PF-MLI synapses.
We considered the possibility that slowly rising mEPSCs could originate from climbing fiber terminals. Consistent with this idea, Matsui and Jahr (2003) found that spontaneous glutamate release from climbing fibers produces mEPSCs in Bergman glial cells, and Szapiro and Barbour (2007) found that climbing fiber stimulation elicits AMPAR-mediated EPSCs in MLIs that display onset kinetics similar to those of the slow mEPSC component described here. But Szapiro and Barbour failed to find asynchronous quantal EPSCs after stimulating a climbing fiber in a strontium containing solution, indicating that slowly rising mEPSCs do not reflect spontaneous glutamate release from climbing fibers.
Another possible scenario would be that slowly rising mEPSCs originate from PF synapses onto Purkinje cells. Glutamate originating from these synapses would activate nearby PF-MLI synapses by spillover, similarly to what is observed at mossy fiber-granule cell synapses (Nielsen et al., 2004). If this were the case, stimulation of a presynaptic PF should, in certain cases, elicit a mix of fast and large EPSCs originating at a PF-MLI synapse, and of slow and small EPSCs originating at a nearby PF-Purkinje cell synapse (Nielsen et al., 2004). Contrary to this prediction, only fast and large EPSCs are observed (Malagon et al., 2016; Miki et al., 2017). Therefore, the hypothesis of spillover from PF-Purkinje cell synapses is unlikely.
A final possibility could be that slow and small mEPSCs originate at deficient PF-MLI synapses that would lack a normal complement of presynaptic VGCCs and/or of postsynaptic AMPARs. Such synapses could provide spillover signals in neighboring fully functional synapses in response to spontaneous glutamate release.
Further work is needed to explore these possibilities.
Sensitivity of bursts to Ko and to Cao
Our results show that bursts are sensitive to Ko and to Cao. Increasing Ko to 20 mM reliably produced bursts. In vivo data show a rise of Ko inside the cerebellar molecular layer to several mM following a few PF stimulations (Kocsis et al., 1983), suggesting that the amount of elevation used in our experiments can occur under physiological conditions. Ko elevation presumably acts by depolarizing presynaptic terminals (to a potential estimated at about −50 mV for 20 Ko based on the Nernst potential for K+) and by activating presynaptic VGCCs. The block of bursts by external Cd2+ (Fig. 7) suggests that presynaptic VGCC activation is necessary for burst generation, and the facilitatory effects of Cao elevation (Fig. 2) is consistent with the same notion.
While elevating Ko or Cao stimulate bursts in the presence of tetrodotoxin, such conditions are not necessary for bursting to occur. A previous study reported EPSC bursts with similar properties with and without tetrodotoxin (Popescu et al., 2010).
What could be the mechanism of burst initiation in normal Ko conditions (e.g., in 3 Cao/2.5 Ko)? As depolarizations to −50 mV fall in the normal range of fluctuation of resting membrane potentials, it is not surprising that bursts occur, albeit with very low frequency, in unstimulated preparations. In addition, spontaneous or evoked neurotransmitter release may lead to local elevations of various substances susceptible to depolarize PF terminals. These substances include GABA since local GABA applications induce EPSC bursts in MLI following activation of excitatory presynaptic GABAARs (Stell et al., 2007; Stell, 2011; note that these studies were performed in the absence of tetrodotoxin). They also include glutamate since PF-MLI synapses possess presynaptic kainate and NMDA receptors (Delaney and Jahr, 2002; Falcon-Moya et al., 2018; Bidoret et al., 2009; Bouvier et al., 2016). Presynaptic ionotropic glutamate receptors could provide bursts with a positive feedback mechanism, as glutamate released from a presynaptic terminal would bind back to the same terminal, leading to a depolarization of its membrane potential, an increase in presynaptic calcium concentration, and enhanced glutamate release.
Effect of Cd2+ on bursts
Addition of Cd2+ strongly inhibited bursts, without abolishing them altogether (Fig. 7). The inhibitory effect of Cd2+ indicates that presynaptic VGCCs play a key role in the generation of bursts. To explain that the block was not total, we note that the blocking action of Cd2+ is steeply voltage-sensitive, and that Cd2+ is much less effective at hyperpolarized than at depolarized potentials (Swandulla and Armstrong, 1989). Since our estimate of the presynaptic membrane potential during bursts is rather hyperpolarized (near −50 mV), it is plausible that the residual bursts observed in the presence of Cd2+ reflect a partial reduction of Ca2+ flux through VGCCs at this voltage. Another possible source of the residual bursts observed in Cd2+ could be a positive feedback loop implicating the activation of calcium-permeant presynaptic ionotropic glutamate receptors and glutamate release.
Simultaneous pre- and postsynaptic calcium signals in developing PF-MLI synapses
In regenerating hippocampal circuits, spontaneous activation of AMPARs has been shown to facilitate synapse maintenance, an effect that has been attributed to the activation of postsynaptic receptors (McKinney et al., 1999). Likewise, spontaneous release contributes to synapse maturation at fly neuromuscular junctions (Choi et al., 2014; Cho et al., 2015). More generally, it is accepted that mEPSC activity contributes to the establishment and stabilization of excitatory synapses (Andrae and Burrone, 2018). The present results in developing PF-MLI synapses suggest that bursts could provide these effects with temporal and spatial organization. Because most postsynaptic AMPARs are calcium permeant at these synapses, bursts are presumably accompanied by a postsynaptic calcium transient (Liu and Cull-Candy, 2000; Soler-Llavina and Sabatini, 2006). As postsynaptic calcium transients are sharply delimited in space due to the high concentration of parvalbumin in MLIs (Collin et al., 2005; Soler-Llavina and Sabatini, 2006), this transient could provide a synapse-specific signal facilitating synapse formation/stabilization. Interestingly, postsynaptic AMPARs lose their permeability to calcium later in development (Bao et al., 2020), suggesting a specific role of AMPAR-mediated postsynaptic calcium rises in synapse formation/stabilization.
On the presynaptic side, activation of VGCCs likely provides a simultaneous presynaptic excitatory signal. Given the high frequency of mEPSCs during bursts, the local presynaptic calcium concentration must reach the micromolar range (Miki et al., 2018). It is possible that activation of presynaptic ionotropic glutamate receptors, as discussed earlier, could contribute to elevating the presynaptic calcium concentration both directly, by allowing calcium influx through glutamate-gated channels, and indirectly, by inducing depolarization of the presynaptic membrane potential and enhancing activation of VGCCs.
Altogether, our results suggest the presence of large, sustained, and simultaneous elevations of presynaptic and postsynaptic calcium concentration during mEPSC bursts at developing PF-MLI synapses. They offer a solution to the conendrum of how the classically envisaged mEPSC signaling, only involving rare and short activation of postsynaptic AMPARs, could possibly lead to any effect on synapse formation. We therefore suggest that the pre- and postsynaptic calcium signals associated with bursts serve as a homosynaptic plasticity signal for synapse establishment and/or for synapse stabilization. Consistent with this hypothesis, our recordings taken after full formation of the molecular layer indicate much weaker mEPSC bursting than during the formation of the molecular layer (Fig. 8).
Acknowledgments
Jeanne M. Nerbonne served as editor.
We thank Van Tran for helpful comments on the manuscript.
This work was supported by Centre national de la recherche scientifique (UMR 8118, and UMR 8003) and by the European Community (European Research Council Advanced Grant “Single Site” to A. Marty, nb. 294509).
Authors contributions: B. Le Guellec and L.C. Gomez performed most of the experiments and analyzed results. G. Malagon supervised the experimental and analysis work of B. Le Guellec and L.C. Gomez. T. Collin and A. Marty performed additional control experiments, revised the analysis of the results, and wrote the manuscript. All authors revised the manuscript.
References
- Abenavoli, A., Forti L., Bossi M., Bergamaschi A., Villa A., and Malgaroli A.. 2002. Multimodal quantal release at individual hippocampal synapses: Evidence for no lateral inhibition. J. Neurosci. 22:6336–6346. 10.1523/JNEUROSCI.22-15-06336.2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abrahamsson, T., Cathala L., Matsui K., Shigemoto R., and Digregorio D.A.. 2012. Thin dendrites of cerebellar interneurons confer sublinear synaptic integration and a gradient of short-term plasticity. Neuron. 73:1159–1172. 10.1016/j.neuron.2012.01.027 [DOI] [PubMed] [Google Scholar]
- Altman, J. 1972. Postnatal development of the cerebellar cortex in the rat, I, II, III. J. Comp. Neurol. 145:353–514. 10.1002/cne.901450305 [DOI] [PubMed] [Google Scholar]
- Andreae, L.C., and Burrone J.. 2018. The role of spontaneous neurotransmission in synapse and circuit development. J. Neurosci. Res. 96:354–359. 10.1002/jnr.24154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auger, C., and Marty A.. 1997. Heterogeneity of functional synaptic parameters among single release sites. Neuron. 19:139–150. 10.1016/S0896-6273(00)80354-2 [DOI] [PubMed] [Google Scholar]
- Auger, C., and Marty A.. 2000. Quantal currents at single-site central synapses. J. Physiol. 526:3–11. 10.1111/j.1469-7793.2000.t01-3-00003.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Awatramani, G.B., Price G.D., and Trussell L.O.. 2005. Modulation of transmitter release by presynaptic resting potential and background calcium levels. Neuron. 48:109–121. 10.1016/j.neuron.2005.08.038 [DOI] [PubMed] [Google Scholar]
- Bao, J., Graupner M., Astorga G., Collin T., Jalil A., Indriati D.W., Bradley J., Shigemoto R., and Llano I.. 2020. Synergism of type 1 metabotropic and ionotropic glutamate receptors in cerebellar molecular layer interneurons in vivo. Elife. 9:e56839. 10.7554/eLife.56839 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bidoret, C., Ayon A., Barbour B., and Casado M.. 2009. Presynaptic NR2A-containing NMDA receptors implement a high-pass filter synaptic plasticity rule. Proc. Natl. Acad. Sci. USA. 106:14126–14131. 10.1073/pnas.0904284106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bornstein, J.C. 1978. Spontaneous multiquantal release at synapses in Guinea-pig hypogastric ganglia: Evidence that release can occur in bursts. J. Physiol. 282:375–398. 10.1113/jphysiol.1978.sp012470 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouhours, B., Trigo F.F., and Marty A.. 2011. Somatic depolarization enhances GABA release in cerebellar interneurons via a calcium/protein kinase C pathway. J. Neurosci. 31:5804–5815. 10.1523/JNEUROSCI.5127-10.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouvier, G., Higgins D., Spolidoro M., Carrel D., Mathieu B., Léna C., Dieudonné S., Barbour B., Brunel N., and Casado M.. 2016. Burst-dependent directional plasticity in the cerebellum is driven by presynaptic NMDA receptors. Cell Rep. 15:104–116. 10.1016/j.celrep.2016.03.004 [DOI] [PubMed] [Google Scholar]
- Cho, R.W., Buhl L.K., Volfson D., Tran A., Li F., Akbergenova Y., and Littleton J.T.. 2015. Phosphorylation of complexin by PKA regulates activity-dependent spontaneous neurotransmitter release and structural synaptic plasticity. Neuron. 88:749–761. 10.1016/j.neuron.2015.10.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi, B.J., Imlach W.L., Jiao W., Wolfram V., Wu Y., Grbic M., Cela C., Baines R.A., Nitabach M.N., and McCabe B.D.. 2014. Miniature neurotransmission regulates Drosophila synaptic structural maturation. Neuron. 82:618–634. 10.1016/j.neuron.2014.03.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark, B.A., and Cull-Candy S.G.. 2002. Activity-dependent recruitment of extrasynaptic NMDA receptor activation at an AMPA receptor-only synapse. J. Neurosci. 22:4428–4436. 10.1523/JNeurosci.22-11-04428.2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collin, T., Chat M., Lucas M.G., Moreno H., Racay P., Schwaller B., Marty A., and Llano I.. 2005. Developmental changes in parvalbumin regulate presynaptic Ca2+ signaling. J. Neurosci. 25:96–107. 10.1523/JNEUROSCI.3748-04.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crowley, J.J., Carter A.G., and Regehr W.G.. 2007. Fast vesicle replenishment and rapid recovery from desensitization at a single synaptic release site. J. Neurosci. 27:5448–5460. 10.1523/JNEUROSCI.1186-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delaney, A.J., and Jahr C.E.. 2002. Kainate receptors differentially regulate release at two parallel fiber synapses. Neuron. 36:475–482. 10.1016/S0896-6273(02)01008-5 [DOI] [PubMed] [Google Scholar]
- Emptage, N.J., Reid C.A., and Fine A.. 2001. Calcium stores in hippocampal synaptic boutons mediate short-term plasticity, store-operated Ca2+ entry, and spontaneous transmitter release. Neuron. 29:197–208. 10.1016/S0896-6273(01)00190-8 [DOI] [PubMed] [Google Scholar]
- Ermolyuk, Y.S., Alder F.G., Surges R., Pavlov I.Y., Timofeeva Y., Kullmann D.M., and Volynski K.E.. 2013. Differential triggering of spontaneous glutamate release by P/Q-, N- and R-type Ca2+ channels. Nat. Neurosci. 16:1754–1763. 10.1038/nn.3563 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falcón-Moya, R., Losada-Ruiz P., Sihra T.S., and Rodríguez-Moreno A.. 2018. Cerebellar kainate receptor-mediated facilitation of glutamate release requires Ca2+-calmodulin and PKA. Front. Mol. Neurosci. 11:195. 10.3389/fnmol.2018.00195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fatt, P., and Katz B.. 1952. Spontaneous subthreshold activity at motor nerve endings. J. Physiol. 117:109–128. 10.1113/jphysiol.1952.sp004735 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glowatzki, E., and Fuchs P.A.. 2002. Transmitter release at the hair cell ribbon synapse. Nat. Neurosci. 5:147–154. 10.1038/nn796 [DOI] [PubMed] [Google Scholar]
- Goswami, S.P., Bucurenciu I., and Jonas P.. 2012. Miniature IPSCs in hippocampal granule cells are triggered by voltage-gated Ca2+ channels via microdomain coupling. J. Neurosci. 32:14294–14304. 10.1523/JNEUROSCI.6104-11.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- He, L., Xue L., Xu J., McNeil B.D., Bai L., Melicoff E., Adachi R., and Wu L.-G.. 2009. Compound vesicle fusion increases quantal size and potentiates synaptic transmission. Nature. 459:93–97. 10.1038/nature07860 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kocsis, J.D., Malenka R.C., and Waxman S.G.. 1983. Effects of extracellular potassium concentration on the excitability of the parallel fibres of the rat cerebellum. J. Physiol. 334:225–244. 10.1113/jphysiol.1983.sp014491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, B.J., Yang C.H., Lee S.Y., Lee S.-H., Kim Y., and Ho W.-K.. 2022. Voltage-gated calcium channels contribute to spontaneous glutamate release directly via nanodomain coupling or indirectly via calmodulin. Prog. Neurobiol. 208:102182. 10.1016/j.pneurobio.2021.102182 [DOI] [PubMed] [Google Scholar]
- Liu, G., Choi S., and Tsien R.W.. 1999. Variability of neurotransmitter concentration and nonsaturation of postsynaptic AMPA receptors at synapses in hippocampal cultures and slices. Neuron. 22:395–409. 10.1016/S0896-6273(00)81099-5 [DOI] [PubMed] [Google Scholar]
- Liu, S.-Q., and Cull-Candy S.G.. 2000. Synaptic activity at calcium-permeable AMPA receptors induces a switch in receptor subtype. Nature. 405:454–458. 10.1038/35013064 [DOI] [PubMed] [Google Scholar]
- Llano, I., and Gerschenfeld H.M.. 1993. Inhibitory synaptic currents in stellate cells of rat cerebellar slices. J. Physiol. 468:177–200. 10.1113/jphysiol.1993.sp019766 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llano, I., González J., Caputo C., Lai F.A., Blayney L.M., Tan Y.P., and Marty A.. 2000. Presynaptic calcium stores underlie large-amplitude miniature IPSCs and spontaneous calcium transients. Nat. Neurosci. 3:1256–1265. 10.1038/81781 [DOI] [PubMed] [Google Scholar]
- Malagon, G., Miki T., Llano I., Neher E., and Marty A.. 2016. Counting vesicular release events reveals binomial release statistics at single glutamatergic synapses. J. Neurosci. 36:4010–4025. 10.1523/JNEUROSCI.4352-15.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malagon, G., Miki T., Tran V., Gomez L.C., and Marty A.. 2020. Incomplete vesicular docking limits synaptic strength under high release probability conditions. Elife. 9:e52137. 10.7554/eLife.52137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsui, K., and Jahr C.E.. 2003. Ectopic release of synaptic vesicles. Neuron. 40:1173–1183. 10.1016/S0896-6273(03)00788-8 [DOI] [PubMed] [Google Scholar]
- Masugi-Tokita, M., Tarusawa E., Watanabe M., Molnár E., Fujimoto K., and Shigemoto R.. 2007. Number and density of AMPA receptors in individual synapses in the rat cerebellum as revealed by SDS-digested freeze-fracture replica labeling. J. Neurosci. 27:2135–2144. 10.1523/JNEUROSCI.2861-06.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McKinney, R.A., Capogna M., Dürr R., Gähwiler B.H., and Thompson S.M.. 1999. Miniature synaptic events maintain dendritic spines via AMPA receptor activation. Nat. Neurosci. 2:44–49. 10.1038/4548 [DOI] [PubMed] [Google Scholar]
- Miki, T., Kaufmann W.A., Malagon G., Gomez L., Tabuchi K., Watanabe M., Shigemoto R., and Marty A.. 2017. Numbers of presynaptic Ca2+ channel clusters match those of functionally defined vesicular docking sites in single central synapses. Proc. Natl. Acad. Sci. USA. 114:E5246–E5255. 10.1073/pnas.1704470114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miki, T., Nakamura Y., Malagon G., Neher E., and Marty A.. 2018. Two-component latency distributions indicate two-step vesicular release at simple glutamatergic synapses. Nat. Commun. 9:3943. 10.1038/s41467-018-06336-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen, T.A., DiGregorio D.A., and Silver R.A.. 2004. Modulation of glutamate mobility reveals the mechanism underlying slow-rising AMPAR EPSCs and the diffusion coefficient in the synaptic cleft. Neuron. 42:757–771. 10.1016/j.neuron.2004.04.003 [DOI] [PubMed] [Google Scholar]
- Palay, S.L., and Chan-Palay V.. 1974. Cerebellar Cortex. Springer, Berlin. 10.1007/978-3-642-65581-4 [DOI] [Google Scholar]
- Popescu, I.R., Morton L.A., Franco A., Di S., Ueta Y., and Tasker J.G.. 2010. Synchronized bursts of miniature inhibitory postsynaptic currents. J. Physiol. 588:939–951. 10.1113/jphysiol.2009.181461 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pouzat, C., and Marty A.. 1999. Somatic recording of GABAergic autoreceptor currents in cerebellar stellate and basket cells. J. Neurosci. 19:1675–1690. 10.1523/JNeurosci.19-05-01675.1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigworth, F.J., and Sine S.M.. 1987. Data transformations for improved display and fitting of single-channel dwell time histograms. Biophys. J. 52:1047–1054. 10.1016/S0006-3495(87)83298-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soler-Llavina, G.J., and Sabatini B.L.. 2006. Synapse-specific plasticity and compartmentalized signaling in cerebellar stellate cells. Nat. Neurosci. 9:798–806. 10.1038/nn1698 [DOI] [PubMed] [Google Scholar]
- Stell, B.M., Rostaing P., Triller A., and Marty A.. 2007. Activation of presynaptic GABA(A) receptors induces glutamate release from parallel fiber synapses. J. Neurosci. 27:9022–9031. 10.1523/JNEUROSCI.1954-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stell, B.M. 2011. Biphasic action of axonal GABA-A receptors on presynaptic calcium influx. J. Neurophysiol. 105:2931–2936. 10.1152/jn.01125.2010 [DOI] [PubMed] [Google Scholar]
- Swandulla, D., and Armstrong C.M.. 1989. Calcium channel block by cadmium in chicken sensory neurons. Proc. Natl. Acad. Sci. USA. 86:1736–1740. 10.1073/pnas.86.5.1736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szapiro, G., and Barbour B.. 2007. Multiple climbing fibers signal to molecular layer interneurons exclusively via glutamate spillover. Nat. Neurosci. 10:735–742. 10.1038/nn1907 [DOI] [PubMed] [Google Scholar]
- Williams, C., Chen W., Lee C.H., Yaeger D., Vyleta N.P., and Smith S.M.. 2012. Coactivation of multiple tightly coupled calcium channels triggers spontaneous release of GABA. Nat. Neurosci. 15:1195–1197. 10.1038/nn.3162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams, C.L., and Smith S.M.. 2018. Calcium dependence of spontaneous neurotransmitter release. J. Neurosci. Res. 96:335–347. 10.1002/jnr.24116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamasaki, M., Hashimoto K., and Kano M.. 2006. Miniature synaptic events elicited by presynaptic Ca2+ rise are selectively suppressed by cannabinoid receptor activation in cerebellar Purkinje cells. J. Neurosci. 26:86–95. 10.1523/JNEUROSCI.2258-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]