Abstract
Training end-to-end unrolled iterative neural networks for SPECT image reconstruction requires a memory-efficient forward-backward projector for efficient backpropagation. This paper describes an open-source, high performance Julia implementation of a SPECT forward-backward projector that supports memory-efficient backpropagation with an exact adjoint. Our Julia projector uses only ~5% of the memory of an existing Matlab-based projector. We compare unrolling a CNN-regularized expectation-maximization (EM) algorithm with end-to-end training using our Julia projector with other training methods such as gradient truncation (ignoring gradients involving the projector) and sequential training, using XCAT phantoms and virtual patient (VP) phantoms generated from SIMIND Monte Carlo (MC) simulations. Simulation results with two different radionuclides (90Y and 177Lu) show that: 1) For 177Lu XCAT phantoms and 90Y VP phantoms, training unrolled EM algorithm in end-to-end fashion with our Julia projector yields the best reconstruction quality compared to other training methods and OSEM, both qualitatively and quantitatively. For VP phantoms with 177Lu radionuclide, the reconstructed images using end-to-end training are in higher quality than using sequential training and OSEM, but are comparable with using gradient truncation. We also find there exists a trade-off between computational cost and reconstruction accuracy for different training methods. End-to-end training has the highest accuracy because the correct gradient is used in backpropagation; sequential training yields worse reconstruction accuracy, but is significantly faster and uses much less memory.
Keywords: End-to-end learning, regularized model-based image reconstruction, backpropagatable forward-backward projector, quantitative SPECT
I. INTRODUCTION
Single photon emission computerized tomography (SPECT) is a nuclear medicine technique that images spatial distributions of radioisotopes and plays a pivotal role in clinical diagnosis, and in estimating radiation-absorbed doses in nuclear medicine therapies [1, 2]. For example, quantitative SPECT imaging with Lutetium-177 (177Lu) in targeted radionuclide therapy (such as 177Lu DOTATATE) is important in determining dose-response relationships in tumors and holds great potential for dosimetry-based individualized treatment. Additionally, quantitative Yttrium-90 (90Y) bremsstrahlung SPECT imaging is valuable for safety assessment and absorbed dose verification after 90Y radioembolization in liver malignancies. However, SPECT imaging suffers from noise and limited spatial resolution due to the collimator response; the resulting reconstruction problem is hence ill-posed and challenging to solve.
Numerous reconstruction algorithms have been proposed for SPECT reconstruction, of which the most popular ones are model-based image reconstruction algorithms such as maximum likelihood expectation maximization (MLEM) [3] and ordered-subset EM (OSEM) [4]. These methods first construct a mathematical model for the SPECT imaging system, then maximize the (log-)likelihood for a Poisson noise model. Although MLEM and OSEM have achieved great success in clinical use, they have a trade-off between recovery and noise. To address that trade-off, researchers have proposed alternatives such as regularization-based (or maximum a posteriori in Bayesian setting) reconstruction methods [5–7]. For example, Panin et al. [5] proposed total variation (TV) regularization for SPECT reconstruction. However, TV regularization may lead to “blocky” images and over-smoothing the edges. One way to overcome blurring edges is to incorporate anatomical boundary side information from CT images [8], but that method requires accurate organ segmentation. Chun et al. [9] used non-local means (NLM) filters that exploit the self-similarity of patches in images for regularization, yet that method is computationally expensive and hence less practical. In general, choosing an appropriate regularizer can be challenging; moreover, these traditional regularized algorithms may lack generalizability to images that do not follow assumptions made by the prior.
With the recent success of deep learning (DL) and especially convolutional neural networks (CNN), DL methods have been reported to outperform conventional algorithms in many medical imaging applications such as in MRI [10–12], CT [13, 14] and PET reconstruction [15–17]. However, fewer DL approaches to SPECT reconstruction appear in the literature. Reference [18] proposed “SPECTnet” with a two-step training strategy that learns the transformation from projection space to image space as an alternative to the traditional OSEM algorithm. Reference [19] also proposed a DL method that can directly reconstruct the activity image from the SPECT projection data, even with reduced view angles. Reference [20] trained a neural network that maps non-attenuation-corrected SPECT images to those corrected by CT images as a post-processing procedure to enhance the reconstructed image quality.
Though promising results were reported with these methods, most of them worked in 2D whereas 3D is used in practice [18, 19]. Furthermore, there has yet to be an investigation of end-to-end training of CNN regularizers that are embedded in unrolled SPECT iterative statistical algorithms such as CNN-regularized EM. End-to-end training is popular in machine learning and other medical imaging fields such as MRI image reconstruction [21], and is reported to meet data-driven regularization for inverse problems [22]. But for SPECT image reconstruction, end-to-end training is nontrivial to implement due to its complicated system matrix. Alternative training methods have been proposed, such as sequential training [23–26] and gradient truncation [27]; these methods were shown to be effective, though they could yield sub-optimal reconstruction results due to approximations to the training loss gradient. Another approach is to construct a neural network that also models the SPECT system matrix, like in “SPECTnet” [18], but this approach lacks interpretability compared to algorithms like unrolled CNN-regularized EM, i.e., if one sets the regularization parameter to zero, then the latter becomes identical to the traditional EM.
As an end-to-end training approach has not yet been investigated for SPECT image reconstruction, this paper first describes a SPECT forward-backward projector written in the open-source and high performance Julia language that enables efficient auto-differentiation. Then we compare the end-to-end training approach with other non-end-to-end training methods.
The structure of this article is as follows. Section II describes the implementation of our Julia projector and discusses end-to-end training and other training methods for the unrolled EM algorithm. Section III compares the accuracy, speed and memory use of our Julia projector with Monte Carlo (MC) and a Matlab-based projector, and then compares reconstructed images with end-to-end training versus sequential training and gradient truncation on different datasets (XCAT and VP phantoms), using qualitative and quantitative evaluation metrics. Section IV and V conclude this paper and discuss future works.
Notation:
Bold upper/lower case letters (e.g., ) denote matrices and column vectors, respectively. Italics (e.g., ) denote scalars. and denote the ith element in vector and , respectively. and denote N-dimensional real/complex normed vector space, respectively. (·)* denotes the complex conjugate and (·)′ denotes Hermitian transpose.
II. METHODS
This section summarizes the Julia SPECT projector, a DL-based image reconstruction method as well as the dataset used in experiments and other experiment setups.
A. Implementation of Julia SPECT projector
Our Julia implementation of SPECT projector is based on [28], modeling parallel-beam collimator geometries. Our projector also accounts for attenuation and depth-dependent collimator response. We did not model the scattering events like Compton scatter and coherent scatter of high energy gamma rays within the object. Fig. 1 illustrates the SPECT imaging system modeled in this paper.
Fig. 1:
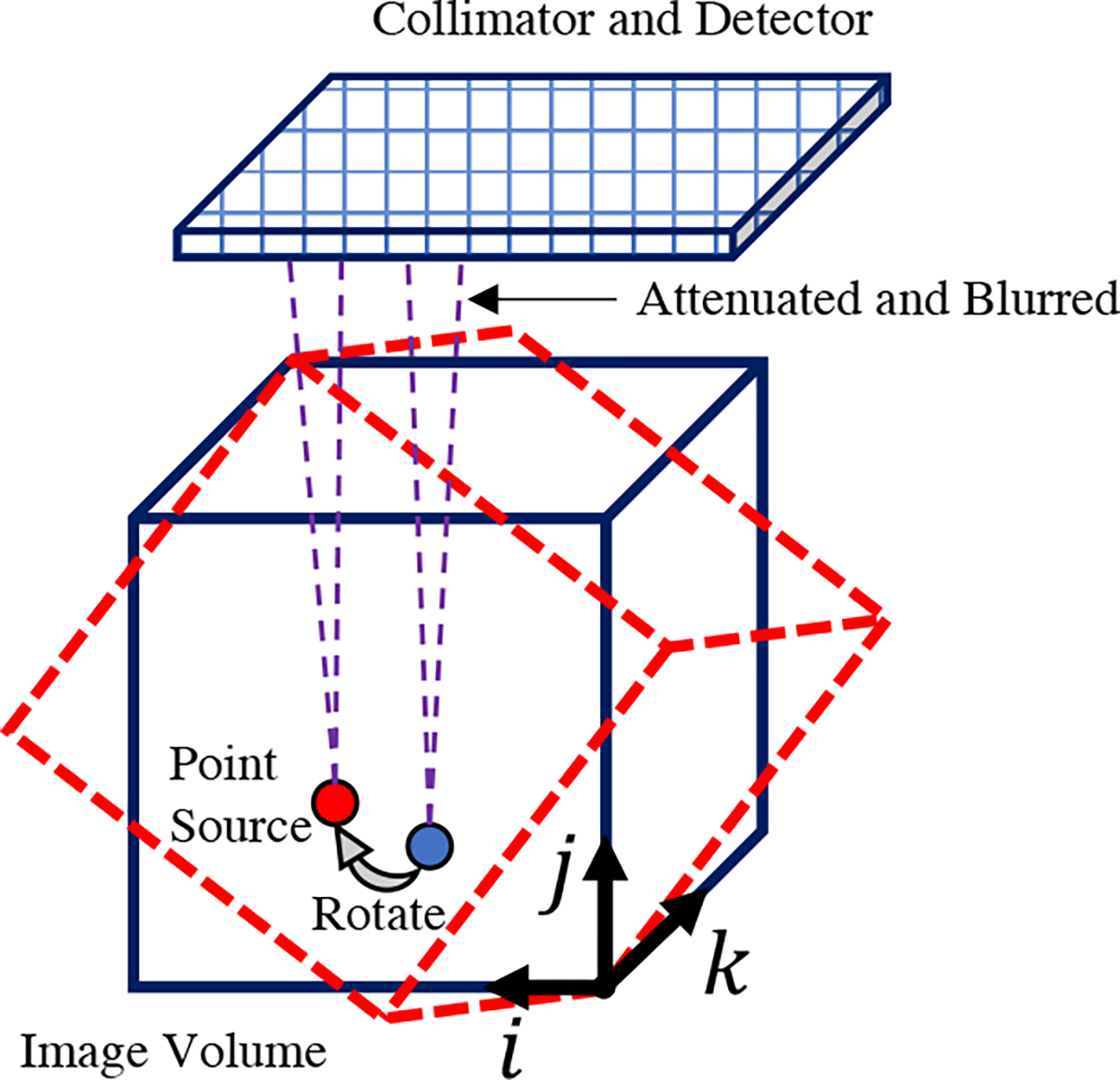
SPECT imaging model for parallel-beam collimators, with attenuation and depth-dependent collimator point spread response.
For the forward projector, at each rotation angle, we first rotate the 3D image matrix according to the third dimension by its projection angle (typically denotes the view index, which ranges from 1 to and denotes the total number of projection views. We implemented and compared (results shown in Section III) both bilinear interpolation and 3-pass 1D linear interpolation [29] with zero padding boundary condition for image rotation. For attenuation correction, we first rotated the 3D attenuation map (obtained from transmission tomography) also by , yielding a rotated 3D array , where denotes the 3D voxel coordinate. Assuming is the index corresponding to the closest plane of to the detector, then we model the accumulated attenuation factor for each view angle as
| (1) |
where denotes the voxel size for the (first and) second coordinate. Next, for each slice (an plane for a given index) of the rotated and attenuated image, we convolve with the appropriate slice of the depth-dependent point spread function using a 2D fast Fourier transform (FFT). Here we use replicate padding for both the and coordinates. The view-dependent PSF accommodates non-circular orbits. Finally, the forward projection operation simply sums the rotated, blurred and attenuated activity image along the second coordinate . Algorithm 1 summarizes the forward projector, where denotes a 2D convolution operation.

|
All of these steps are linear, so hereafter, we use to denote the forward projector, though it is not stored explicitly as a matrix. As each step is linear, each step has an adjoint operation. So the backward projector is the adjoint of that satisfies
| (2) |
The exact adjoint of (discrete) image rotation is not simply a discrete rotation of the image by . Instead, one should also consider the adjoint of linear interpolation. For the adjoint of convolution, we assume the point spread function is symmetric along coordinates and so that the adjoint convolution operator is just the forward convoluation operator along with the adjoint of replicate padding. Algorithm 2 summarizes the SPECT backward projector.

|
To accelerate the for-loop process, we used multi-threading to enable projecting or backprojecting multiple angles at the same time. To reduce memory use, we pre-allocated necessary arrays and used fully in-place operations inside the for-loop in forward and backward projection. To further accelerate auto-differentiation, we customized the chain rule to use the linear operator or as the Jacobian when calling or during backpropagation. We implemented and tested our projector in Julia v1.6; we also implemented a GPU version in Julia (using CUDA.jl) that runs efficiently on a GPU by eliminating explicit scalar indexing. For completeness, we also provide a PyTorch version but without multi-threading support, in-place operations nor the exact adjoint of image rotation.
B. Unrolled CNN-regularized EM algorithm
Model-based image reconstruction algorithms seek to estimate image from noisy measurements with imaging model . In SPECT reconstruction, the measurements are often modeled by
| (3) |
where denotes the vector of means of background events such as scatters. Combining regularization with the Poisson negative log-likelihood yields the following optimization problem:
| (4) |
where is the data fidelity term and denotes the regularizer. For deep learning regularizers, we follow [23] and formulate as
| (5) |
where denotes the regularization parameter; denotes a neural network with parameter that is trained to learn to enhance the image quality.
Based on (4), a natural reconstruction approach is to apply variable splitting with and then alternatively update the images and as follows
| (6) |
where subscript denotes the iteration number. To minimize (6), we used the EM-surrogate from [30] as summarized in [23], leading to the following vector update:
| (7) |
| (8) |
where and denote element-wise multiplication and division, respectively. To compute , one must substitue back into in (8), and repeat. Hereafter, we refer to (6) as one outer iteration and (7) as one inner EM iteration. Algorithm 3 summarizes the CNN-regularized EM algorithm.

|
To train , the most direct way is to unroll Algorithm 3 and train end-to-end with an appropriate target; this supervised approach requires backpropagating through the SPECT system model, which is not trivial to implement with previous SPECT projection tools due to the memory issues. Non-end-to-end training methods, e.g., sequential training [23], first train by the target and then plug into (7) at each iteration. This method must use non-shared weights for the neural network per each iteration. Another method is gradient truncation [27] that ignores the gradient involving the system matrix and its adjoint during backpropagation. Both of these training methods, though reported to be effective, may be sub-optimal because they approximate the overall training loss gradients.
C. Phantom dataset and simulation setup
We used simulated XCAT phantoms [31] and virtual patient phantoms for experiment results presented in Section III. Each XCAT phantom was simulated to approximately follow the activity distributions observed when imaging patients after 177Lu DOTATATE therapy. We set the image size to 128×128×80 with voxel size 4.8×4.8×4.8mm3. Tumors of various shapes and sizes (5–100mL) were located in the liver as is typical for patients undergoing this therapy.
For virtual patient phantoms, we consider two radionuclides: 177Lu and 90Y. For 177Lu phantoms, the true images were from PET/CT scans of patients who underwent diagnostic 68Ga DOTATATE PET/CT imaging (Siemens Biograph mCT) to determine eligibility for 177Lu DOTATATE therapy. The 68Ga DOTATATE distribution in patients is expected to be similar to 177Lu and hence can provide a reasonable approximation to the activity distribution of 177Lu in patients for DL training purposes but at higher resolution. The PET images had size 200 × 200 × 577 and voxel size 4.073 × 4.073 × 2 mm3 and were obtained from our Siemens mCT (resolution is 5–6 mm FWHM [32]) and reconstructed using the standard clinic protocol: 3D OSEM with three iterations, 21 subsets, including resolution recovery, time-of-flight, and a 5mm (FWHM) Gaussian post-reconstruction filter. The density maps were also generated using the experimentally derived CT-to-density calibration curve.
For 90Y phantoms, the true activity images were reconstructed (using a previously implemented 3D OSEM reconstruction with CNN-based scatter estimation [33]) from 90Y SPECT/CT scans of patients who underwent 90Y microsphere radioembolization in our clinic.
In total, we simulated 4 XCAT phantoms, 8 177Lu and 8 90Y virtual patient phantoms. We repeated all of our experiments 3 times with different noise realizations. All image data have University of Michigan Institutional Review Board (IRB) approval for retrospective analysis. For all simulated phantoms, we selected the center slices covering the lung, liver and kidney corresponding to SPECT axial FOV (39cm).
Then we ran SIMIND Monte Carlo (MC) program [34] to generate the radial position of SPECT camera for 128 view angles. The SIMIND model parameters for 177Lu were based on 177Lu DOTATATE patient imaging in our clinic (Siemens Intevo with medium energy collimators, a 5/8” crystal, a 20% photopeak window at 208 keV, and two adjacent 10% scatter windows) [35]. For 90Y, a high-energy collimator, 5/8” crystal, and a 105 to 195 keV acquisition energy window was modeled as in our clinical protocol for 90Y bremsstrahlung imaging. Next we approximated the point spread function for 177Lu and 90Y by simulating point source at 6 different distances (20, 50, 100, 150, 200, 250mm) and then fitting a 2D Gaussian distribution at each distance. The camera orbit was assumed to be non-circular (auto-contouring mode in clinical systems) with the minimum distance between the phantom surface and detector set at 1 cm.
III. EXPERIMENT RESULTS
A. Comparison of projectors
We used an XCAT phantom to evaluate the accuracy and memory-efficiency of our Julia projector.
1). Accuracy:
We first compared primary (no scatter events included) projection images and profiles generated by our Julia projector with those from MC simulation and the Matlab projector. For results of MC, we ran two SIMIND simulations for 1 billion histories using 177Lu and 90Y as radionuclide source, respectively. Each simulation took about 10 hours using a 3.2 GHz 16-Core Intel Xeon W CPU on MacOS. The Matlab projector was originally implemented and compiled in C99 and then wrapped by a Matlab MEX file as a part of the Michigan Image Reconstruction Toolbox (MIRT) [36]. The physics modeling of the Matlab projector was the same as our Julia projector except that it only implemented 3-pass 1D linear interpolation for image rotation. Unlike the memory-efficient Julia version, the Matlab version pre-rotates the patient attenuation map for all projection views. This strategy saves time during EM iterations for a single patient, but uses considerable memory and scales poorly for DL training approaches involving multiple patient datasets.
Fig. 2 compared the primary projections generated by different methods without adding Poisson noise. Visualizations of image slices and line profiles illustrate that our Julia projector (with rotation based on 3-pass 1D interpolation) is almost identical to the Matlab projector, while both give a reasonably good approximation to the MC. Using MC as reference, the NRMSE of Julia1D/Matlab/Julia2D projectors were 7.9%/7.9%/7.6% for 177Lu, respectively; while the NRMSE were 8.2%/8.2%/7.9% for 90Y. We also compared the OSEM reconstructed images using Julia (2D) and Matlab projectors, where we did not observe notable difference, as shown in Fig. 3. The overall NRMSD between Matlab and Julia (2D) projector for the whole 3D OSEM reconstructed image ranged from 2.5% to 2.8% across 3 noise realizations.
Fig. 2:
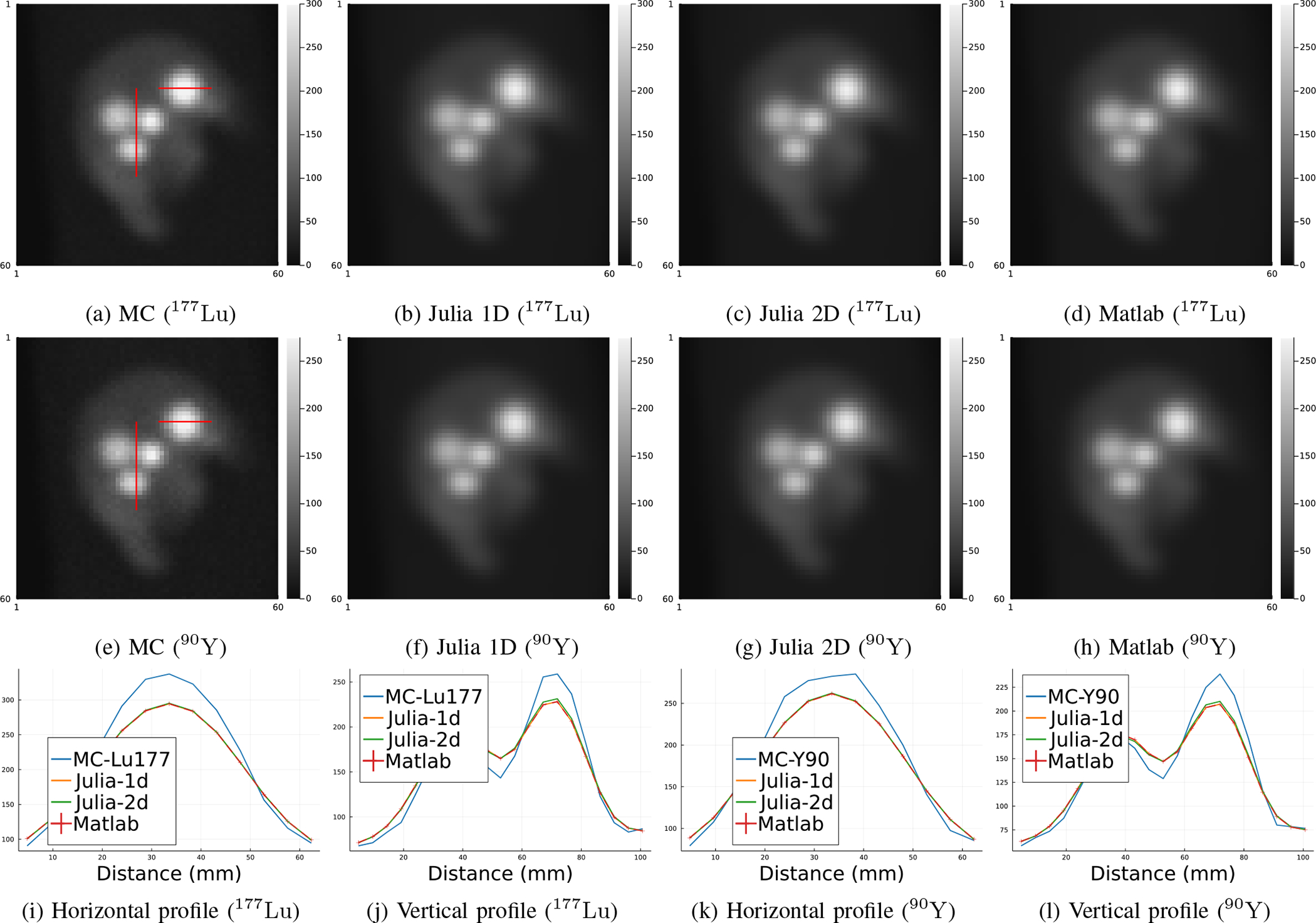
Primary (scatter-free) projections generated by MC simulation, Matlab projector and our Julia projector with 3-pass 1D linear interpolation and 2D bilinear interpolation for image rotation, using 177Lu and 90Y radionuclides. Subfigure (i)-(l) show line profiles across tumors as shown in subfigure (a) and (e), respectively. MC projections were scaled to have the same total activities as the Matlab projector per field-of-view.
Fig. 3:
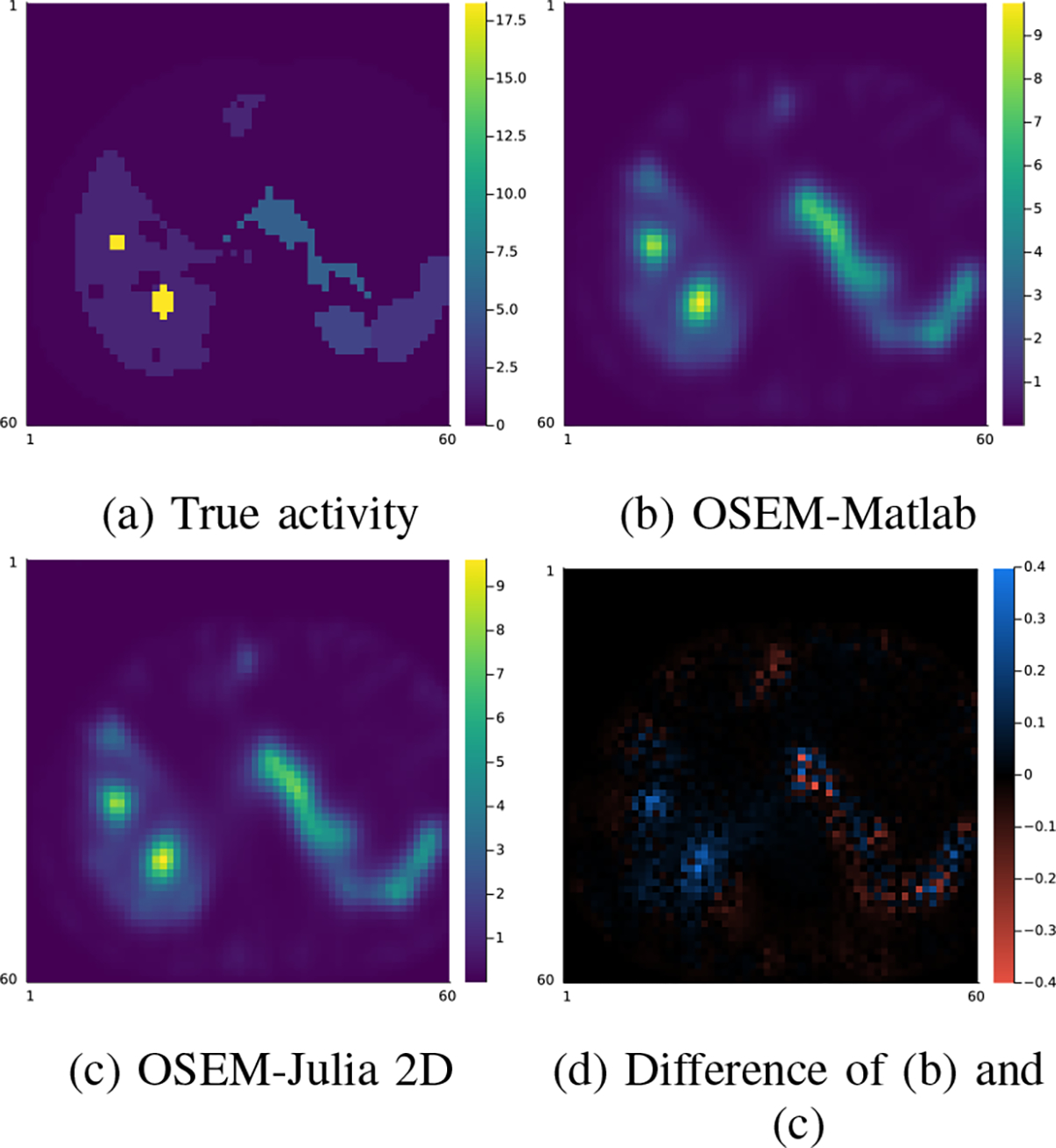
Comparison of one slice of the 128 × 128 × 80 OSEM reconstruction (16 iterations, 4 subsets) using Matlab and Julia (2D interpolation) projectors.
2). Speed and memory use:
We compared the memory use and compute times between our Julia projector (with 2D bilinear interpolation) and the Matlab projector using different number of threads when projecting a 128 × 128 × 80 image. Fig. 4 shows that our Julia projector has comparable computing time for a single projection with 128 view angles using different number of CPU threads, while using only a very small fraction of memory (~5%) and pre-allocation time (~1%) compared to the Matlab projector.
Fig. 4:
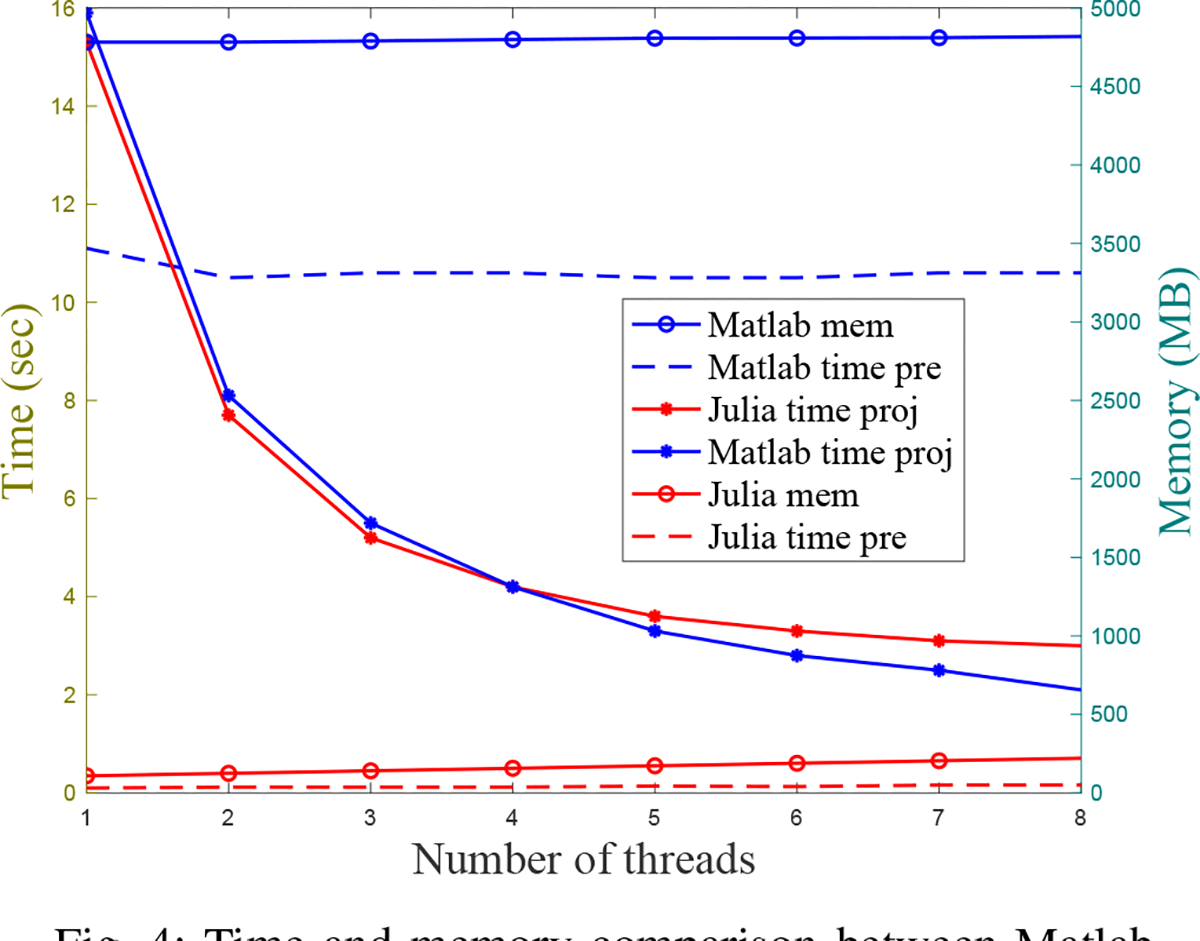
Time and memory comparison between Matlab projector and our Julia projector for projecting 128 view angles of a 128 × 128 × 80 image. “time pre” denotes the time cost for pre-allocating necessary arrays before projection; “time proj” denotes the time cost for a single projection; “mem” denotes the memory usage. All methods were tested on MacOS with a 3.8 GHz 8-Core Intel Core i7 CPU.
3). Adjoint of projector:
We generated a set of random numbers to verify that the backprojector is an exact adjoint of the forward projector. Specifically, we generated the system matrix of size (8 × 6 × 7) × (8 × 8 × 6) using random (nonnegative) attenuation maps and random (symmetric) PSF. Fig. 5 compares the transpose of the forward projector to the backprojector. As shown in Fig. 5 (d), the Frobenius norm error of our backprojector agrees well with the regular transpose within an accuracy of 10−6 across 100 different realizations, as expected for 32-bit floating point calculations. A more comprehensive comparison is available in the code tests at https://github.com/JuliaImageRecon/SPECTrecon.jl.
Fig. 5:
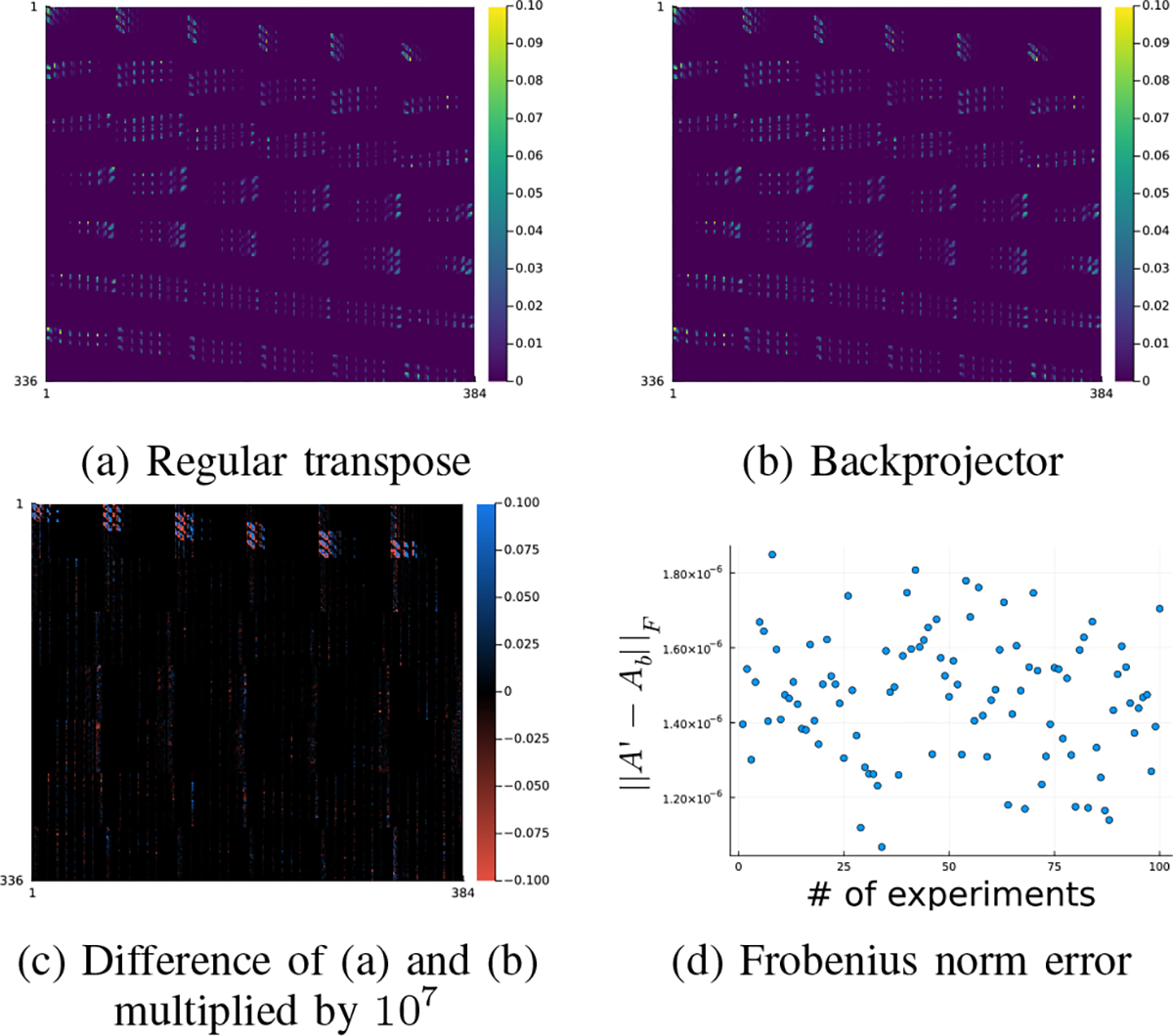
Accuracy of the backprojector. In subfigure (d), denotes regular transpose of denotes the backprojector.
B. Comparison of CNN-regularized EM using different training methods
This section compares end-to-end training with other training methods that have been used previously for SPECT image reconstruction, namely the gradient truncation and sequential training. The training targets were simulated activity maps on 177Lu XCAT phantoms and 177Lu & 90Y virtual patient phantoms. We implemented an unrolled CNN-regularized EM algorithm with 3 outer iterations, each of which had one inner iteration. Only 3 outer iterations were used (compared to previous works such as [27]) because we used the 16-iteration 4-subset OSEM reconstructed image as a warm start for all reconstruction algorithms. We set the regularization parameter (defined in (5)) as . The regularizer was a 3-layer 3D CNN, where each layer had a 3 × 3 × 3 convolutional filter followed by ReLU activation (except the last layer), and hence had 657 trainable parameters in total. We added the input image to the output of CNN following the common residual learning strategy [37]. End-to-end training and gradient truncation could also work with a shared weights CNN approach, but were not included here for fair comparison purpose, since the sequential training only works with non-shared weights CNN. All the neural networks were initialized with the same parameters (drawn from a Gaussian distribution) and trained on an Nvidia RTX 3090 GPU for 600 epochs by minimizing mean square error (loss) using AdamW optimizer [38] with a constant learning rate 0.002.
Besides line profiles for qualitative comparison, we also used mean activity error (MAE) and normalized root mean square error (NRMSE) as quantitative evaluation metrics, where MAE is defined as
| (9) |
where denotes number of voxels in the voxels of interest (VOI). and denote the reconstructed image and the true activity map, respectively. The NRMSE is defined as
| (10) |
All activity images were scaled by a factor that normalized the whole activity to 1 MBq per field of view (FOV) before comparison. All quantitative results (Table I, Table II, Table III) were averaged across 3 different noise realizations.
TABLE I:
The average(± standard deviation) MAE(%) and NRMSE(%) across 3 noise realizations of 177Lu XCAT phantoms.
| MAE(%) | ||||
| Lesion/Organ | OSEM | Sequential | Truncation | End2end |
| Lesion 1 (67mL) | 12.5 ± 0.6 | 6.7 ± 1.8 | 2.8 ± 0.9 | 2.1 ± 1.1 |
| Lesion 2 (10mL) | 20.2 ± 0.9 | 11.5 ± 4.1 | 10.8 ± 0.9 | 9.7 ± 1.1 |
| Lesion 3 (9mL) | 25.6 ± 0.6 | 18.8 ± 0.4 | 15.2 ± 0.9 | 12.8 ± 1.0 |
| Lesion 4 (5mL) | 43.0 ± 0.6 | 40.0 ± 1.2 | 38.8 ± 0.8 | 38.7 ± 0.7 |
| Liver | 6.4 ± 0.7 | 6.2 ± 1.5 | 4.6 ± 1.1 | 3.7 ± 1.2 |
| Lung | 2.4 ± 0.7 | 2.2 ± 0.4 | 0.7 ± 0.6 | 0.9 ± 0.5 |
| Spleen | 14.2 ± 0.9 | 12.6 ± 2.4 | 8.9 ± 0.7 | 9.3 ± 1.5 |
| Kidney | 15.9 ± 1.0 | 15.1 ± 1.2 | 14.4 ± 1.4 | 13.6 ± 1.6 |
| NRMSE(%) | ||||
| Lesion/Organ | OSEM | Sequential | Truncation | End2end |
| Lesion 1 (67mL) | 27.3 ± 0.3 | 21.7 ± 1.3 | 18.9 ± 0.6 | 18.3 ± 0.6 |
| Lesion 2 (10mL) | 26.8 ± 0.6 | 19.2 ± 2.2 | 16.4 ± 0.4 | 16.3 ± 0.8 |
| Lesion 3 (9mL) | 28.4 ± 0.4 | 22.8 ± 0.8 | 18.3 ± 0.7 | 16.3 ± 0.7 |
| Lesion 4 (5mL) | 43.5 ± 0.5 | 41.1 ± 1.3 | 40.0 ± 0.7 | 40.2 ± 0.6 |
| Liver | 28.5 ± 0.1 | 25.0 ± 0.8 | 24.3 ± 0.3 | 24.5 ± 0.3 |
| Lung | 32.1 ± 0.1 | 31.2 ± 1.1 | 29.5 ± 0.3 | 30.4 ± 0.4 |
| Spleen | 25.7 ± 0.3 | 22.8 ± 1.1 | 20.4 ± 0.4 | 19.9 ± 0.6 |
| Kidney | 40.8 ± 0.3 | 39.7 ± 0.4 | 39.7 ± 0.2 | 39.2 ± 0.3 |
TABLE II:
The average(± standard deviation) MAE(%) and NRMSE(%) across 3 noise realizations of 177Lu VP phantoms.
| MAE(%) | ||||
| Lesion/Organ | OSEM | Sequential | Truncation | End2end |
| Lesion (6–152mL) | 11.1 ± 2.5 | 9.4 ± 3.2 | 6.7 ± 2.4 | 7.3 ± 2.8 |
| Liver | 4.8 ± 0.1 | 4.5 ± 0.2 | 3.4 ± 0.6 | 4.0 ± 0.2 |
| Healthy liver | 4.1 ± 0.1 | 4.1 ± 0.1 | 3.5 ± 0.6 | 4.1 ± 0.2 |
| Lung | 3.4 ± 0.1 | 3.0 ± 0.2 | 2.4 ± 0.7 | 3.0 ± 0.5 |
| Kidney | 5.2 ± 0.3 | 4.3 ± 0.1 | 2.6 ± 0.1 | 2.3 ± 0.2 |
| Spleen | 0.8 ± 0.2 | 0.6 ± 0.1 | 1.3 ± 0.6 | 1.2 ± 0.4 |
| NRMSE(%) | ||||
| Lesion/Organ | OSEM | Sequential | Truncation | End2end |
| Lesion (6–152mL) | 16.1 ± 2.2 | 14.9 ± 2.4 | 14.3 ± 1.7 | 14.2 ± 2.1 |
| Liver | 15.9 ± 0.2 | 15.3 ± 0.1 | 15.5 ± 0.6 | 15.3 ± 0.1 |
| Healthy liver | 16.8 ± 0.1 | 16.6 ± 0.1 | 17.3 ± 0.5 | 17.1 ± 0.3 |
| Lung | 22.3 ± 0.3 | 22.1 ± 0.4 | 22.0 ± 0.4 | 21.9 ± 0.5 |
| Kidney | 17.4 ± 0.1 | 16.8 ± 0.1 | 16.4 ± 0.3 | 16.3 ± 0.5 |
| Spleen | 13.5 ± 0.2 | 12.4 ± 0.3 | 12.3 ± 0.7 | 12.3 ± 0.5 |
TABLE III:
The average(± standard deviation) MAE(%) and NRMSE(%) across 3 noise realizations of 90Y VP phantoms.
| MAE(%) | ||||
| Lesion/Organ | OSEM | Sequential | Truncation | End2end |
| Lesion (3–356mL) | 32.5 ± 1.3 | 25.3 ± 1.3 | 24.9 ± 1.0 | 23.1 ± 1.8 |
| Liver | 25.0 ± 0.1 | 18.7 ± 0.1 | 17.8 ± 1.3 | 15.6 ± 3.6 |
| Healthy liver | 25.1 ± 0.2 | 23.8 ± 0.5 | 21.8 ± 1.2 | 19.4 ± 3.1 |
| Lung | 88.4 ± 2.1 | 64.9 ± 1.6 | 58.3 ± 6.6 | 48.9 ± 8.4 |
| NRMSE(%) | ||||
| Lesion/Organ | OSEM | Sequential | Truncation | End2end |
| Lesion (3–356mL) | 35.3 ± 1.5 | 29.6 ± 1.4 | 28.9 ± 1.1 | 27.8 ± 1.2 |
| Liver | 29.9 ± 0.4 | 22.7 ± 0.1 | 22.1 ± 0.9 | 21.2 ± 1.5 |
| Healthy liver | 31.6 ± 0.4 | 27.9 ± 0.3 | 27.0 ± 0.9 | 25.9 ± 2.0 |
| Lung | 62.4 ± 1.3 | 59.2 ± 1.1 | 57.3 ± 3.0 | 55.6 ± 4.6 |
1). Loss function, computing time and memory use:
We compared the training and validation loss using sequential training, gradient truncation and end-to-end training. We ran 1800 epochs for each method on 177Lu XCAT phantoms with the AdamW optimizer [38]. Fig. 6 shows that the end-to-end training achieved the lowest validation loss while it had comparable training loss with the gradient truncation (which became lower at around 1400 epochs). For visualization, we concatenated the first 600 epochs of each outer iteration for the sequential training method, as shown by the spikes in sequential training curve. We ran 600 epochs for each algorithm for subsequent experiments because the validation losses were pretty much settled at around 600 epochs.
Fig. 6:
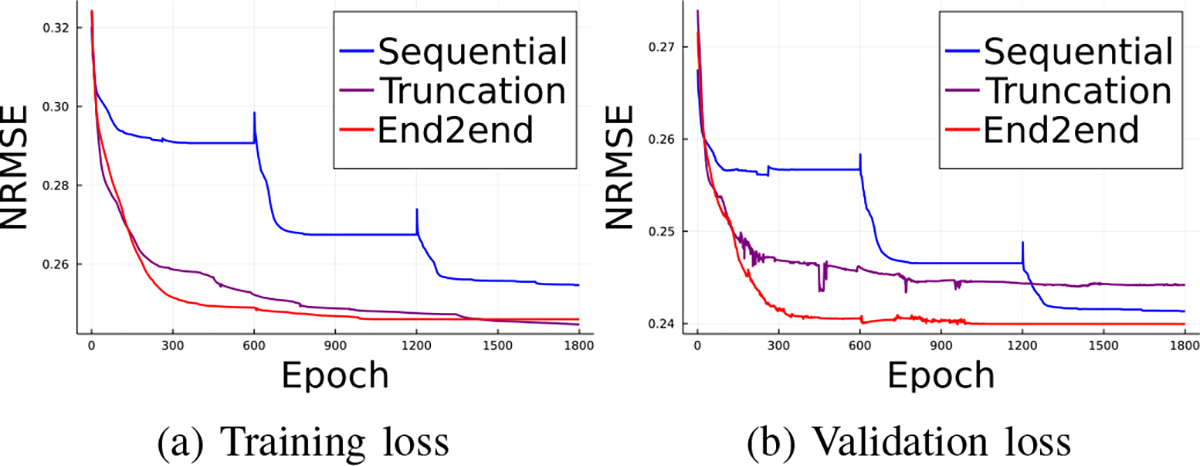
Training and validation loss of three backpropagation methods.
We also compared the computing time of each training method. We found that for MLEM with 3 outer iterations and 1 inner iteration, where each outer iteration had a 3-layer convolutional neural network, sequential training took 48.6 seconds to complete a training epoch; while gradient truncation took 327.1 seconds and end-to-end training took 336.3 seconds. Under the same experiment settings, we found sequential training took less than 1GB of memory to backpropagate through one outer iteration; compared to approximately 6GB used in gradient truncation and end-to-end training that backpropagated through three outer iterations.
2). Results on 177Lu XCAT phantoms:
We evaluated the CNN-regularized EM algorithm with three training methods on 4 177Lu XCAT phantoms we simulated. We generated the primary projections by calling forward operation of our Julia projector and then added uniform scatters with 10% of the primary counts before adding Poisson noise. Of the 4 phantoms, we used 2 for training, 1 for validation and 1 for testing.
Fig. 7 shows that the end-to-end training yielded incrementally better reconstruction of the tumor in the liver center over OSEM, sequential training and gradient truncation. Fig. 7 (g) also illustrates this improvement by the line profile across the tumor. For the tumor at the top-right corner of the liver, all methods had comparable performance; this can be attributed to the small tumor size (5mL) for which partial volume (PV) effects associated with SPECT resolution are higher; and hence its recovery is even more challenging.
Fig. 7:
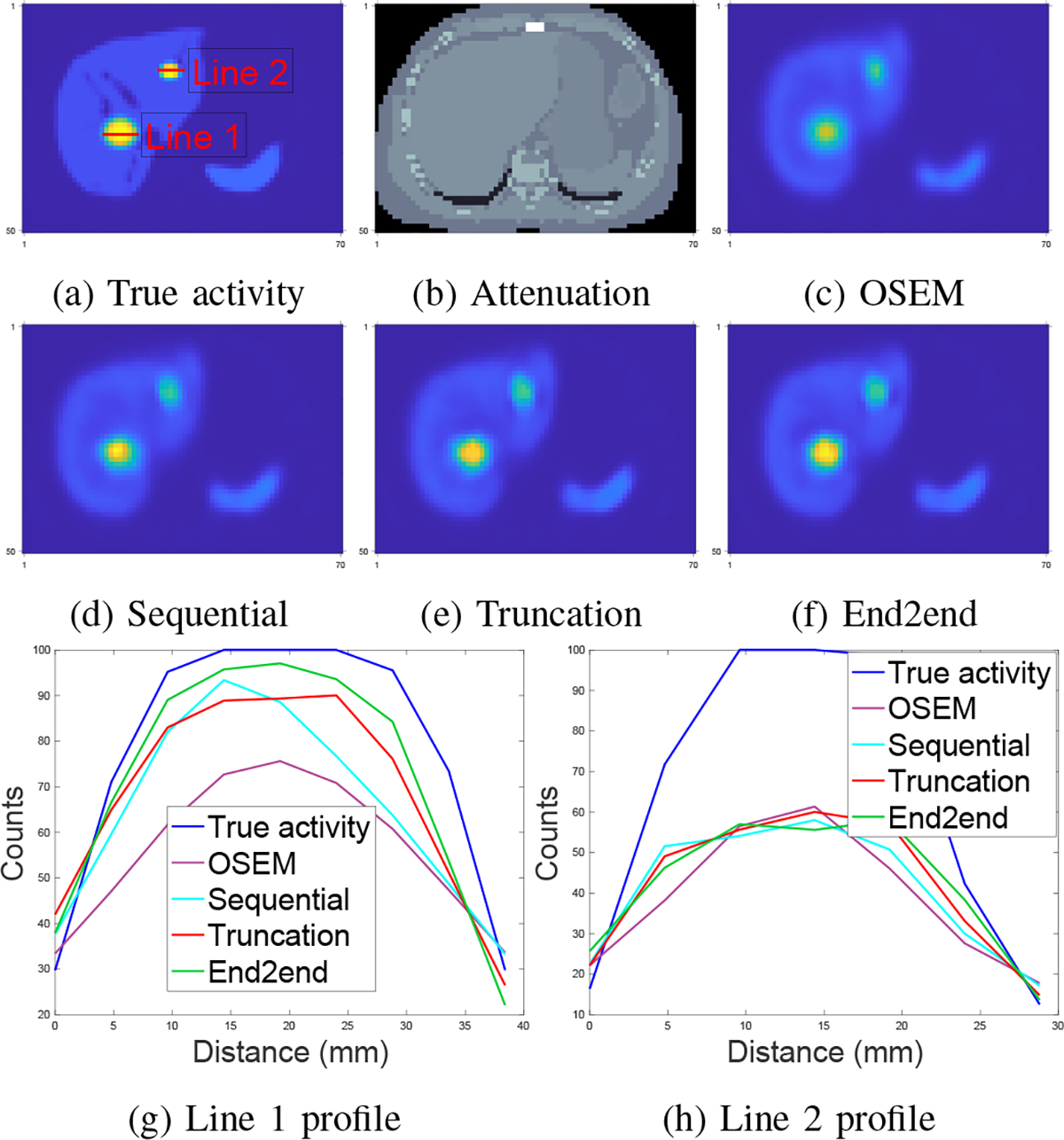
Qualitative comparison of different training methods and OSEM tested on 177Lu XCAT phantoms. Subfigure (a)-(c): true activity map, attenuation map and OSEM reconstruction (16 iterations and 4 subsets); (d)-(f): regularized EM using sequential training, gradient truncation, end-to-end training, respectively; (g) and (h): line profiles in (a).
Table I demonstrates that the CNN-regularized EM algorithm with all training methods (sequential training, gradient truncation and end-to-end training) consistently had lower reconstruction error than the OSEM method. Among all training methods, the proposed end-to-end training had lower MAE over nearly all lesions and organs than other training methods. The relative reduction in MAE by the end-to-end training was up to 32% (for lesion 3) compared to sequential training. End-to-end training also had lower NRMSE for most lesions and organs, and was otherwise comparable to other training methods. The relative improvement compared to sequential training was up to 29% (for lesion 3).
3). Results on 177Lu VP phantoms:
Next we present test results on 8 177Lu virtual patient phantoms. Out of 8 177Lu phantoms, we used 4 for training, 1 for validation and 3 for testing.
Fig. 8 shows that the improvement of all learning-based methods was limited compared to OSEM, which was also evident from line profiles. For example, in Fig. 8 (g), where the line profile was drawn on a small tumor. We found that OSEM yielded a fairly accurate estimate already, and we did not observe as much improvement as we had seen on 177Lu XCAT phantoms for end-to-end training or even learning-based methods. Table II also demonstrates this observation. The OSEM method had substantially lower MAE and NRMSE compared to the errors shown for 177Lu XCAT data (cf Table I). Moreover, the end-to-end training method had comparable accuracy with gradient truncation. For example, gradient truncation was the best on lesion, liver and lung in terms of MAE; end-to-end training had the lowest NRMSE on lesion, liver, lung, kidney and spleen. Perhaps this could be due to the loss function used for training, i.e., MSE loss was used in our experiments so that end-to-end training might yield lower NRMSE. A more comprehensive study would be needed to verify this conjecture.
Fig. 8:
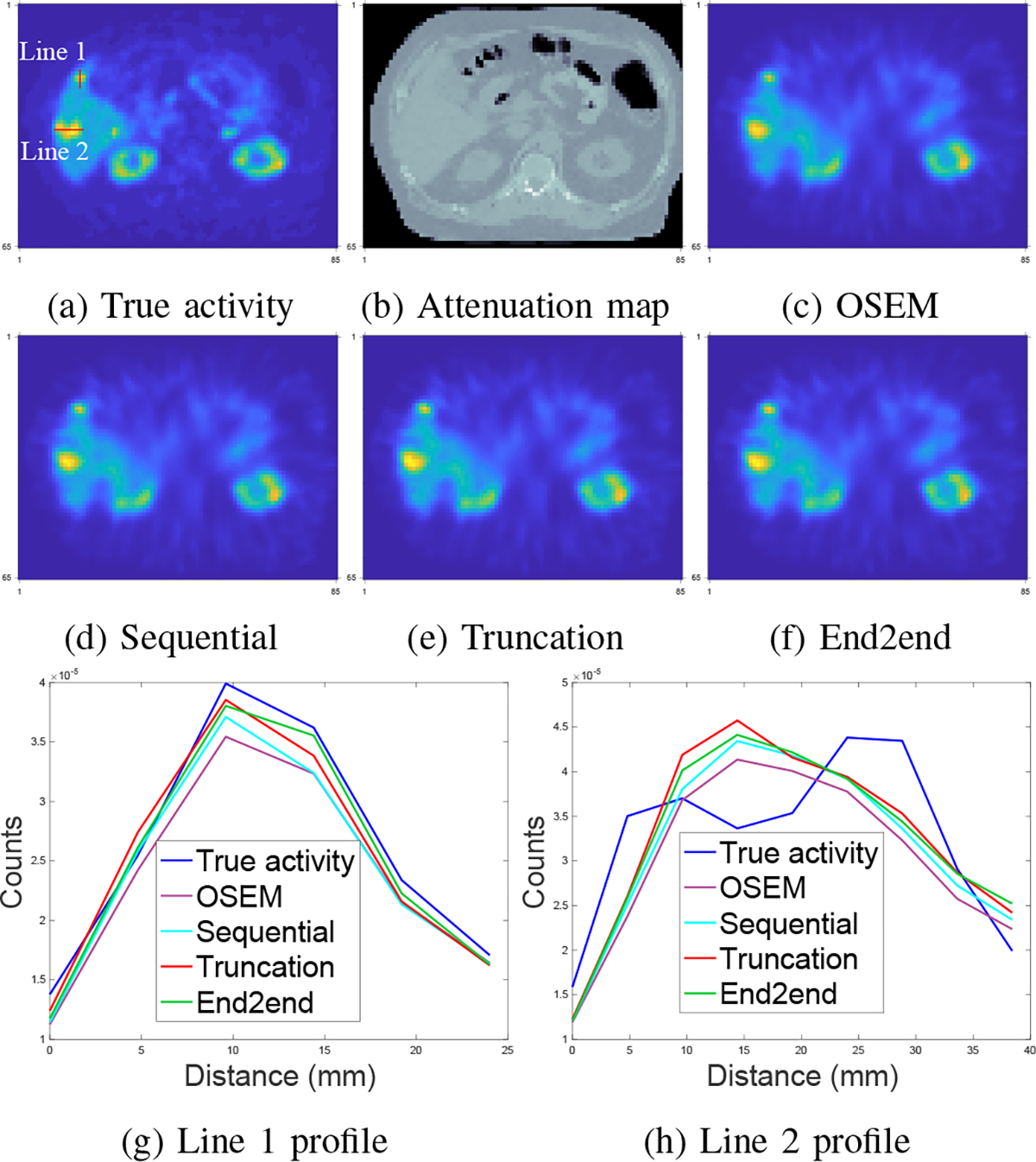
Qualitative comparison of different training methods and OSEM tested on 177Lu VP phantoms. Subfigure (g) and (h) correspond to line profiles marked in (a).
4). Results on 90Y VP phantoms:
We also tested with 8 90Y virtual patient phantoms. Of the 8 phantoms, we used 4 for training, 1 for validation and 3 for testing.
Fig. 9 compares the reconstruction quality between OSEM and CNN-regularized EM algorithm using sequential training, gradient truncation and end-to-end training. Visually, the end-to-end training reconstruction yields the closest estimate to the true activity. This is also evident through the line profiles (subfigure (m) and (n)) across the tumor and the liver.
Fig. 9:

Qualitative comparison of different training methods and OSEM tested on 90Y VP phantoms. Subfigure (a)-(f) and (g)-(l) show two slices from two testing phantoms. Subfigure (m) and (n) correspond to line profiles in (a) and (g), respectively.
Table III reports the mean activity error (MAE) and NRMSE for lesions and organs across all testing phantoms. Similar to the qualitative assessment (Fig. 9), the end-to-end training also produced lower errors consistently across all testing lesions and organs. For instance, compared to sequential training/gradient truncation, the end-to-end training relatively reduced MAE on average by 8.7%/7.2%, 18.5%/11.0% and 24.7%/16.1% for lesion, healthy liver and lung, respectively. The NRMSE was also relatively reduced by 6.1%/3.8%, 7.2%/4.1% and 6.1%/3.0% for lesion, healthy liver and lung, respectively. All learning-based methods consistently had lower errors than the OSEM method.
C. Results at intermediate iterations
One potential problem associated with end-to-end training (and gradient truncation) is that the results at intermediate iterations could be unfavorable, because they are not directly trained by the targets [39]. Here, we examined the images at intermediate iterations and did not observe such problems as illustrated in Fig. 10, where images at each iteration gave a fairly accurate estimate to the true activity. Perhaps under the shallow-network setting (e.g., 3 layers used here, with only 3 outer iterations), the network for each iteration was less likely to overfit the training data. Another reason could be due to the non-shared weights setting so that the network could learn suitable weights for each iteration.
Fig. 10:
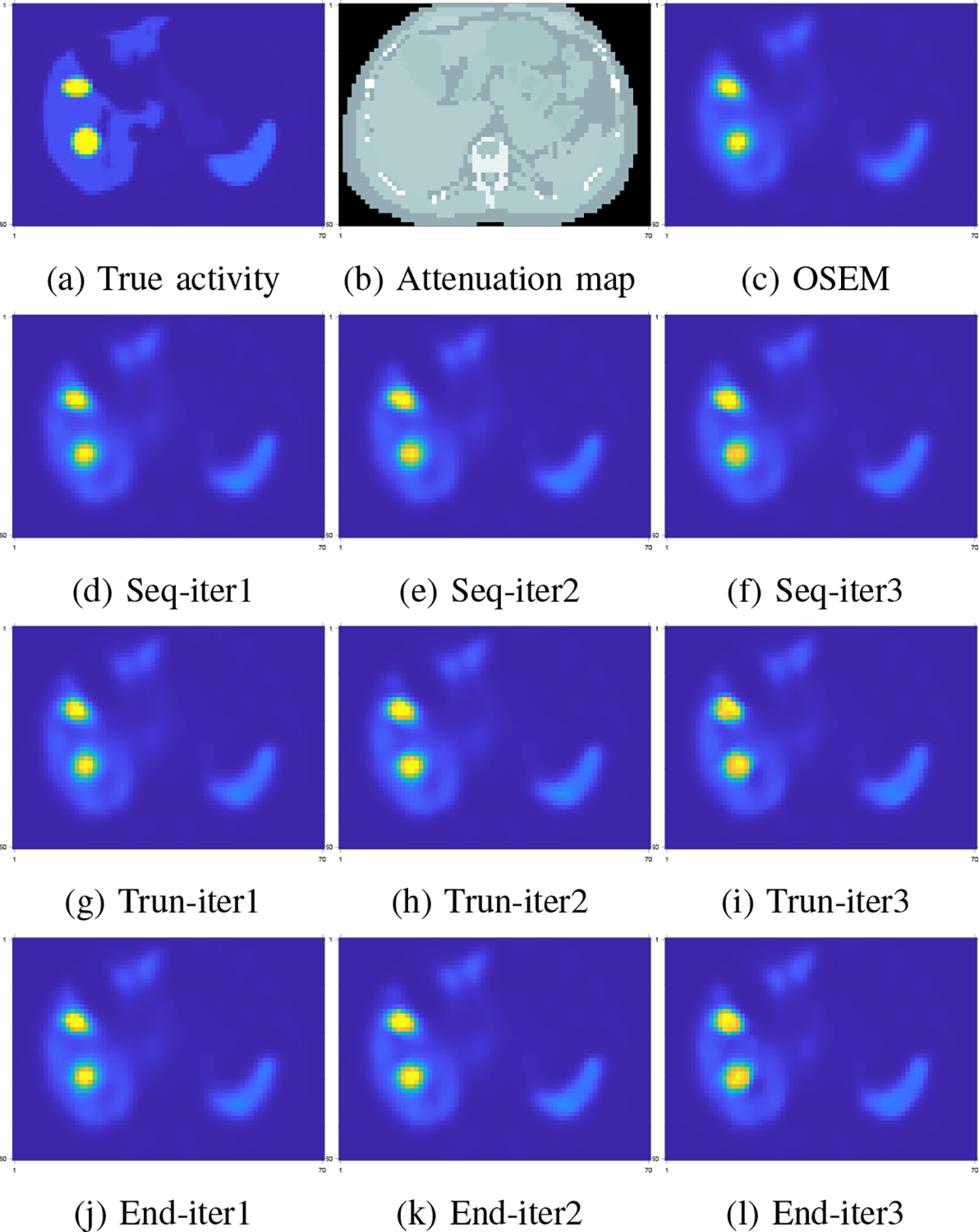
Visualization of intermediate iteration results of different training methods. Subfigure (d)-(f): sequential training; (g)-(i): gradient truncation; (j)-(l): end-to-end training.
IV. DISCUSSION
Training end-to-end CNN-based iterative algorithms for SPECT image reconstruction requires memory efficient forward-backward projectors so that backpropagation can be less computationally expensive. This work implemented a new SPECT projector using Julia that is an open-source, high performance and cross-platform language. With comparisons between Monte Carlo (MC) and a Matlab-based projector, we verified the accuracy, speed and memory-efficiency of our Julia projector. These favorable properties support efficient backpropagation when training end-to-end unrolled iterative reconstruction algorithms. Most modern DL algorithms process multiple data batches in parallel, so memory efficiency is of great importance for efficient training and testing neural networks. To that extent, our Julia projector is much more suitable than the Matlab-based projector.
We used the CNN-regularized EM algorithm as an example to test end-to-end training and other training methods on different datasets including 177Lu XCAT phantoms, 177Lu and 90Y virtual patient phantoms. Simulation results demonstrated that end-to-end training improved reconstruction quality on these datasets. For example, end-to-end training improved the MAE of lesion/liver in 90Y phantoms by 8.7%/16.6% and 7.2%/12.4% compared to sequential training and gradient truncation. This improvement could be attributed to the correct gradient was used in backpropagation. Although the end-to-end training yielded the lowest reconstruction error on both 177Lu XCAT phantoms and 90Y VP phantoms, the reconstruction errors on 177Lu VP phantoms were comparable with the gradient truncation. This could be due to the choice of loss functions and CNN architectures in the EM algorithm, which we will explore in the future. Also we noticed that the recovery of the nonuniform activity in VP phantoms was generally higher than activity for the XCAT phantom (MAE reported in Table I and Table II) because the assigned “true” activities at the boundaries of organs did not drop sharply, and instead, were blurred out. And therefore the OSEM algorithm was fairly competitive as reported in Table II; in 90Y VP results, the OSEM performed worse than learning-based methods, which could be attributed to the high downscatter associated with 90Y SPECT due to the continuous bremsstrahlung energy spectrum. We found all learning methods did not work very well for small tumors (e.g., 5mL), potentially due to the worse PV effect. Reducing PV effects in SPECT images has been studied extensively [40, 41]. Recently, Xie et al. [42] trained a deep neural network to learn the mapping between PV-corrected and non-corrected images. Incorporating their network into our reconstruction model using transfer learning is an interesting future direction.
Although promising results were shown in previous sections, this work has several limitations. First, we did not test numerous hyperparameters and CNN architectures, nor with a wide variety of phantoms and patients for different radionuclides therapies. Secondly, our experiments used OSEM images as warm start to the CNN-regularized EM algorithm, where the OSEM itself was initialized with a uniform image. We did not investigate using other images such as uniform images as the start of the EM algorithm. Using a uniform image to initialize the network would likely require far more network iterations which would be very expensive computationally and therefore impractical. Additionally, this paper used fixed regularization parameter ( in (5)) rather than declaring as a trainable parameter. We compared different methods for backpropagation, which requires using the same cost function (4) for a fair comparison. If one set as a trainable parameter, then different methods could learn different values, leading to different cost functions. However, the investigation of trainable values is an interesting future work. Another limitation is that we did not investigate more advanced parallel computing methods such as distributed computing using multiple computers to further accelerate our Julia implementation of SPECT forward-backward projector. Such acceleration is feasible using existing Julia packages if needed. The compute times reported in Fig. 4 show that the method needs a few seconds per 128 projection views using 8 threads, which is already feasible for scientific investigation.
We also found there exists a trade-off between computational cost and reconstruction accuracy for different training methods. End-to-end training yielded reconstruction results with the lowest MAE and NRMSE because the correct gradient was used during backpropagation. Sequential training yielded worse results, but it was significantly faster and more memory efficient than the end-to-end training method. It is notably faster because it splits the whole training process and trains each of neural networks separately, and its backpropagation does not involve terms associated with the MLEM algorithm, so sequential training is actually equivalent to training that neural network alone without considering MLEM. Sequential training also used much less memory because the training was performed iteration by iteration, one network by one network, and hence the memory limitation did not depend on the number of unrolled iterations in the MLEM algorithm.
V. CONCLUSION
This paper presents a Julia implementation of backpropagatable SPECT forward-backward projector that is accurate, fast and memory-efficient compared to Monte Carlo (MC) and a previously developed analytical Matlab-based projector. Simulation results based on 177Lu XCAT phantoms, 90Y and 177Lu virtual patient (VP) phantoms demonstrate that: 1) End-to-end training yielded reconstruction images with the lowest MAE and NRMSE when tested on XCAT phantoms and 90Y VP phantoms, compared to other training methods (such as sequential training and gradient truncation) and OSEM. 2) For 177Lu VP phantoms, end-to-end training method yielded better results than sequential training and OSEM; but was rather comparable with gradient truncation. We also found there exists a trade-off between computational cost and reconstruction accuracy in different training methods (e.g., end-to-end training and sequential training). These results indicate that end-to-end training, which is feasible with our developed Julia projector, is worth investigating for SPECT reconstruction.
ACKNOWLEDGEMENT
All authors declare that they have no known conflicts of interest in terms of competing financial interests or personal relationships that could have an influence or are relevant to the work reported in this paper.
This work involved human subjects in its research. Approval of all ethical and experimental procedures and protocols was granted by University of Michigan Institutional Review Board (IRB).
This work was supported in part by NIH Grants R01 EB022075 and R01 CA240706.
Footnotes
Code for reproducing the results is available at https://github.com/ZongyuLi-umich/end-to-end-spect.
Contributor Information
Zongyu Li, Department of Electrical Engineering and Computer Science, University of Michigan.
Yuni K. Dewaraja, Department of Radiology, University of Michigan.
Jeffrey A. Fessler, Department of Electrical Engineering and Computer Science, University of Michigan.
REFERENCES
- [1].James S. S, Bednarz B, Benedict S, et al. “Current Status of Radiopharmaceutical Therapy”. In: Int. J. Radiat. Oncol. Biol. Phys. 109.4 (2021). DOI: 10.1016/j.ijrobp.2020.08.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Dewaraja Y, Frey E, Sgouros G, Brill A, Roberson P, Zanzonico P, and Ljungberg M. “MIRD pamphlet No. 23: quantitative SPECT for patient-specific 3-dimensional dosimetry in internal radionuclide therapy”. In: J. Nucl. Med. 53.8 (2012). DOI: 10.2967/jnumed.111.100123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Shepp LA and Vardi Y. “Maximum Likelihood Reconstruction for Emission Tomography”. In: IEEE Trans. Med. Imaging 1.2 (1982), pp. 113–122. DOI: 10.1109/TMI.1982.4307558. [DOI] [PubMed] [Google Scholar]
- [4].Hudson H and Larkin R. “Accelerated image reconstruction using ordered subsets of projection data”. In: IEEE Trans. Med. Imaging 13.4 (1994), pp. 601–609. DOI: 10.1109/42.363108. [DOI] [PubMed] [Google Scholar]
- [5].Panin V, Zeng G, and Gullberg G. “Total variation regulated EM algorithm [SPECT reconstruction]”. In: IEEE Transactions on Nuclear Science 46.6 (1999), pp. 2202–2210. DOI: 10.1109/23.819305. [DOI] [Google Scholar]
- [6].Fessler J. “Penalized weighted least-squares image reconstruction for positron emission tomography”. In: IEEE Trans. Med. Imaging 13.2 (1994), pp. 290–300. DOI: 10.1109/42.293921. [DOI] [PubMed] [Google Scholar]
- [7].Lalush D and Tsui B. “A generalized Gibbs prior for maximum a posteriori reconstruction in SPECT”. In: Phys. Med. Biol. 38.6 (1993), pp. 729–741. DOI: 10.1088/0031-9155/38/6/007. [DOI] [PubMed] [Google Scholar]
- [8].Dewaraja Y, Koral K, and Fessler J. “Regularized reconstruction in quantitative SPECT using CT side information from hybrid imaging”. In: Phys. Med. Biol. 55.9 (2010), pp. 2523–2539. DOI: 10.1088/0031-9155/55/9/007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Chun SY, Fessler JA, and Dewaraja YK. “Non-local means methods using CT side information for I-131 SPECT image reconstruction”. In: 2012 IEEE Nuclear Science Symposium and Medical Imaging Conference Record (NSS/MIC). 2012, pp. 3362–3366. DOI: 10.1109/NSSMIC.2012.6551766. [Google Scholar]
- [10].Zeng G, Guo Y, Zhan J, et al. “A review on deep learning MRI reconstruction without fully sampled k-space”. In: BMC Med. Imaging 21.1 (2021). DOI: 10.1186/s12880-021-00727-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Yang G et al. “DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction”. In: IEEE Transactions on Medical Imaging 37.6 (2018), pp. 1310–1321. DOI: 10.1109/TMI.2017.2785879. [DOI] [PubMed] [Google Scholar]
- [12].Quan TM, Nguyen-Duc T, and Jeong W-K. “Compressed Sensing MRI Reconstruction Using a Generative Adversarial Network With a Cyclic Loss”. In: IEEE Transactions on Medical Imaging 37.6 (2018), pp. 1488–1497. DOI: 10.1109/TMI.2018.2820120. [DOI] [PubMed] [Google Scholar]
- [13].Minnema J, Ernst A, van EM, et al. “A review on the application of deep learning for CT reconstruction, bone segmentation and surgical planning in oral and maxillofacial surgery”. In: Dentomaxillofac Radiol (2022). DOI: doi: 10.1259/dmfr.20210437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Chen H, Zhang Y, Chen Y, Zhang J, Zhang W, Sun H, Lv Y, Liao P, Zhou J, and Wang G. “LEARN: Learned Experts’ Assessment-Based Reconstruction Network for Sparse-Data CT”. In: IEEE Transactions on Medical Imaging 37.6 (2018), pp. 1333–1347. DOI: 10.1109/TMI.2018.2805692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Reader AJ, Corda G, Mehranian A, Costa-Luis C. d., Ellis S, and Schnabel JA. “Deep Learning for PET Image Reconstruction”. In: IEEE Transactions on Radiation and Plasma Medical Sciences 5.1 (2021), pp. 1–25. DOI: 10.1109/TRPMS.2020.3014786. [DOI] [Google Scholar]
- [16].Kim K, Wu D, Gong K, Dutta J, Kim JH, Son YD, Kim HK, El Fakhri G, and Li Q. “Penalized PET Reconstruction Using Deep Learning Prior and Local Linear Fitting”. In: IEEE Transactions on Medical Imaging 37.6 (2018), pp. 1478–1487. DOI: 10.1109/TMI.2018.2832613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Mehranian A and Reader AJ. “Model-Based Deep Learning PET Image Reconstruction Using Forward–Backward Splitting Expectation–Maximization”. In: IEEE Transactions on Radiation and Plasma Medical Sciences 5.1 (2021), pp. 54–64. DOI: 10.1109/TRPMS.2020.3004408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Shao W, Rowe S, and Du Y. “SPECTnet: a deep learning neural network for SPECT image reconstruction”. In: Ann Transl Med 9.9 (2021). DOI: 10.21037/atm-20-3345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Shao W, Pomper MG, and Du Y. “A Learned Reconstruction Network for SPECT Imaging”. In: IEEE Transactions on Radiation and Plasma Medical Sciences 5.1 (2021), pp. 26–34. DOI: 10.1109/TRPMS.2020.2994041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Mostafapour S, Gholamiankhah F, Maroufpour S, Momennezhad M, Asadinezhad M, Zakavi SR, Arabi H, and Zaidi H. “Deep learning-guided attenuation correction in the image domain for myocardial perfusion SPECT imaging”. In: J. Comp. Design and Engineering 9.2 (Mar. 2022), pp. 434–447. DOI: 10.1093/jcde/qwac008. [DOI] [Google Scholar]
- [21].Shen G, Dwivedi K, Majima K, Horikawa T, and Kamitani Y. “End-to-End Deep Image Reconstruction From Human Brain Activity”. In: Front. Comput. Neurosci. (2019). DOI: 10.3389/fncom.2019.00021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Mukherjee S, Carioni M, Öktem O, and Schönlieb C-B. “End-to-end reconstruction meets data-driven regularization for inverse problems”. In: Advances in Neural Information Processing Systems. Ed. by Ranzato M, Beygelzimer A, Dauphin Y, Liang P, and Vaughan JW. Vol. 34. Curran Associates, Inc., 2021, pp. 21413–21425. URL: https://proceedings.neurips.cc/paper/2021/file/b2df0a0d4116c55f81fd5aa1ef876510-Paper.pdf. [Google Scholar]
- [23].Lim H, Chun IY, Dewaraja YK, and Fessler JA. “Improved Low-Count Quantitative PET Reconstruction With an Iterative Neural Network”. In: IEEE Trans. Med. Imaging 39.11 (2020), pp. 3512–3522. DOI: 10.1109/TMI.2020.2998480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Sahiner A, Mardani M, Ozturkler B, Pilanci M, and Pauly JM. “Convex Regularization behind Neural Reconstruction”. In: International Conference on Learning Representations. 2021. URL: https://openreview.net/forum?id=VErQxgyrbfn. [Google Scholar]
- [25].Ozturkler B, Sahiner A, Pilanci M, Vasanawala S, Pauly J, and Mardani M. “Scalable and interpretable neural MRI reconstruction via layer-wise training”. In: International Society for Magnetic Resonance in Medicine. 2021. URL: https://index.mirasmart.com/ISMRM2021/PDFfiles/1953.html. [Google Scholar]
- [26].Corda-D’Incan G, Schnabel JA, and Reader AJ. “Memory-Efficient Training for Fully Unrolled Deep Learned PET Image Reconstruction With Iteration-Dependent Targets”. In: IEEE Transactions on Radiation and Plasma Medical Sciences 6.5 (2022), pp. 552–563. DOI: 10.1109/TRPMS.2021.3101947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Mehranian A and Reader AJ. “Model-Based Deep Learning PET Image Reconstruction Using Forward-Backward Splitting Expectation Maximisation”. In: 2019 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). 2019, pp. 1–4. DOI: 10.1109/NSS/MIC42101.2019.9059998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Zeng G and Gullberg G. “Frequency domain implementation of the three-dimensional geometric point response correction in SPECT imaging”. In: Conference Record of the 1991 IEEE Nuclear Science Symposium and Medical Imaging Conference. 1991, 1943–1947 vol.3. DOI: 10.1109/NSSMIC.1991.259256. [Google Scholar]
- [29].Di Bella EVR, Barclay AB, Eisner RL, and Schafer RW. “A comparison of rotation-based methods for iterative reconstruction algorithms”. In: IEEE Trans. Nuc. Sci. 43.6 (Dec. 1996), 3370–6. DOI: 10.1109/23.552756. [DOI] [Google Scholar]
- [30].De Pierro AR. “A modified expectation maximization algorithm for penalized likelihood estimation in emission tomography”. In: IEEE Trans. Med. Imag. 14.1 (Mar. 1995), 132–7. DOI: 10.1109/42.370409. [DOI] [PubMed] [Google Scholar]
- [31].Segars W, Sturgeon G, Mendonca S, Grimes J, and Tsui B. “4D XCAT phantom for multimodality imaging research”. In: Med. Phys. 37.9 (2010), pp. 4902–4915. DOI: 10.1118/1.3480985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Soderlund A, Chaal J, Tjio G, et al. “Beyond 18F-FDG: Characterization of PET/CT and PET/MR Scanners for a Comprehensive Set of Positron Emitters of Growing Application–18F, 11C, 89Zr, 124I, 68Ga, and 90Y”. In: J. Nucl. Med. 56.8 (2015), pp. 1285–1291. DOI: 10.2967/jnumed.115.156711. [DOI] [PubMed] [Google Scholar]
- [33].Xiang H, Lim H, Fessler J, and Dewaraja Y. “A deep neural network for fast and accurate scatter estimation in quantitative SPECT/CT under challenging scatter conditions”. In: Eur. J. Nucl. Med. Mol. Imaging 47.13 (2020), pp. 2956–2967. DOI: 10.1007/s00259-020-04840-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Ljungberg M. The SIMIND Monte Carlo program. 2012. DOI: 10.1201/b13073-8. [DOI]
- [35].Dewaraja Y, Mirando D, Peterson A, et al. “A pipeline for automated voxel dosimetry: application in patients with multi-SPECT/CT imaging following 177Lu peptide receptor radionuclide therapy”. In: J. Nucl. Med. (2022). DOI: 10.2967/jnumed.121.263738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Fessler J. Michigan Image Reconstruction Toolbox. URL: https://github.com/JeffFessler/mirt.
- [37].He K, Zhang X, Ren S, and Sun J. “Deep residual learning for image recognition”. In: Proc. IEEE Conf. on Comp. Vision and Pattern Recognition. 2016, 770–8. DOI: 10.1109/CVPR.2016.90. [Google Scholar]
- [38].Loshchilov I and Hutter F. “Decoupled Weight Decay Regularization”. In: ICLR. 2019. [Google Scholar]
- [39].Knoll F. “Rise of the machines (in MR image reconstruction)”. In: IMA workshop on Computational Imaging. 2019. URL: https://www.ima.umn.edu/2019-2020/SW10.14-18.19. [Google Scholar]
- [40].Pretorius P and King M. “Diminishing the impact of the partial volume effect in cardiac SPECT perfusion imaging”. In: Med. Phys. 36.1 (2009). DOI: 10.1118/1.3031110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Grings A, Jobic C, Kuwert T, et al. In: EJNMMI Phys. (2022). DOI: 10.1186/s40658-022-00446-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Xie H, Liu Z, Shi L, et al. “Segmentation-free Partial Volume Correction for Cardiac SPECT using Deep Learning”. In: Journal of Nuclear Medicine (supplement 2) 63 (2022). [Google Scholar]


