Estimation of the overall treatment effect in the presence of interference in cluster-randomized trials of infectious disease prevention

Abstract

An issue that remains challenging in the field of causal inference is how to relax the assumption of no interference between units. Interference occurs when the treatment of one unit can affect the outcome of another, a situation which is likely to arise with outcomes that may depend on social interactions, such as occurrence of infectious disease. Existing methods to accommodate interference largely depend upon an assumption of “partial interference” - interference only within identifiable groups but not among them. There remains a considerable need for development of methods that allow further relaxation of the no-interference assumption.

This paper focuses on an estimand that is the difference in the outcome that one would observe if the treatment were provided to all clusters compared to that outcome if treatment were provided to none – referred as the overall treatment effect. In trials of infectious disease prevention, the randomized treatment effect estimate will be attenuated relative to this overall treatment effect if a fraction of the exposures in the treatment clusters come from individuals who are outside these clusters.

This source of interference – contacts sufficient for transmission that are with treated clusters – is potentially measurable. In this manuscript, we leverage epidemic models to infer the way in which a given level of interference affects the incidence of infection in clusters. This leads naturally to an estimator of the overall treatment effect that is easily implemented using existing software.

1. Introduction

An issue that remains challenging in the field of causal inference is relaxing one critical assumption: the absence of interference between units – an important component of the stable unit treatment value assumption (SUTVA) in the potential outcomes framework for causal inference (see, e.g. Neyman (1923), Rubin (1974)). Interference arises when the treatment status of one unit can influence the outcome of another. This issue arises in areas as diverse as social interventions (Sobel, 2006, Verbitsky-Savitz and Raudenbush, 2012), education (Hong and Raudenbush, 2006), or infectious disease (Hudgens and Halloran, 2008, Perez-Heydrich, Hudgens, Halloran, Clemens, Ali, and Emch, 2014), among others.

In the presence of interference, one cannot assume that the outcomes of the control units represent the outcomes of the treated units had they not received treatment. In this setting, the observed treatment effect is a function not only of the direct effect of treatment but also indirect effects from spillover or contamination (Halloran and Struchiner, 1991). This paper deals specifically with the context of cluster-randomized trials of an intervention intended to prevent the transmission of an infectious disease. A reduction in incidence can occur through both direct protection of the index subject and the reduction in the prevalence of infection in contacts of the index. The latter effect will tend to be attenuated if cluster members have contacts with individuals from a cluster randomized to a different treatment condition than that of the index.

Our motivation arises from a large community-randomized trial of a combination HIV prevention intervention in Botswana, the Botswana Combination Prevention Project (BCPP) (ClinicalTrials.gov, 2016, Wang, Goyal, Lei, Essex, and De Gruttola, 2014). We wish to estimate the reduction in incidence due to the inervention, which comprises efforts to increase testing coverage (and thereby treatment coverage for those who qualify), treatment for subjects with high viral load regardless of CD4 count (the usual metric used to determine eligibility), prevention of mother-to-child transmission (PMTCT), and promotion of male circumcision. Of these, only the last will have a protective effect for the individual receiving the treatment. The rest operate by treating those who are already infected, thus reducing their viral burden, and hence the probability of onward transmission Quinn, Wawer, Sewankambo, Serwadda, Li, Wabwire-Mangen, Meehan, Lutalo, and Gray (2000), Attia, Egger, Müller, Zwahlen, and Low (2009), Lingappa, Hughes, Wang, Baeten, Celum, Gray, Stevens, Donnell, Campbell, Farquhar et al. (2010), Novitsky and Essex (2012). Therefore, the bulk of the effect will be due to indirect mechanisms. We also expect a considerable fraction of sexual relationships to be with members of other communities, thus violating the assumption of no interference between clusters. Although PMTCT is included in the treatment package, the outcome (reduction in incidence) is measured only on the adult population.

In many cluster-randomized trials, ensuring that clusters are sufficiently distant from each other by some metric (usually geographic), can help support the assumption of no interference (see, e.g. (Kamali, Quigley, Nakiyingi, Kinsman, Kengeya-Kayondo, Gopal, Ojwiya, Hughes, Carpenter, and Whitworth, 2003, Jewkes, Nduna, Levin, Jama, Dunkle, Puran, and Duwury, 2008, Small, Ten Have, and Rosenbaum, 2008)). This design strategy, however, may not be sufficient in all cases. For example, it was not feasible in Botswana to include only villages (the unit of randomization) within which all residents can be assumed to have sexual contacts only within others in the village. Hence in this trial, information is collected about the number of sexual contacts that occur with residents of villages outside that of the index subject. Regardless of distance between clusters, if a fraction of the exposures among subjects in the treatment clusters come from outside the cluster the estimate of the randomized treatment effect of an infectious disease prevention strategy will be attenuated compared to what it would have been had the treatment been implemented throughout the population of interest (Tiono, Ouédraogo, Ogutu, Diarra, Coulibaly, Gansané, Sirima, O’Neil, Mukhopadhyay, and Hamed, 2013, Wang et al., 2014).

For individually-randomized interventions and when interference is contained within clusters of individuals, several causal effects are identifiable using two-stage randomization (Halloran and Struchiner, 1991, Hudgens and Halloran, 2008, Tchetgen Tchetgen and Vander Weele, 2012). At the first stage, clusters are randomized to treatment allocation programs; at the second, individuals within clusters are randomized to treatment or control according to the assigned allocation program. Such a design permits randomized comparison of the outcomes of non-treated individuals in non-treated clusters to those of non-treated individuals in treated clusters, thereby permitting estimation of direct, indirect and overall effects. When the desired outcome of the trial is at the cluster level, however, a comparable two-stage randomization would involve identifying super-clusters (groups of clusters) that do not interference with one another for the first stage of randomization, then randomizing clusters within super-clusters at the second stage. The required resources to perform such a design make it generally infeasible.

Given this concern, other approaches are required to investigate transmission dynamics between clusters. In this paper, we make use of epidemic models to account for one form of interference: cross-cluster exposures due to contacts between clusters. Contact here refers to an interaction between individuals that is sufficient to transmit the infection (for sexually-transmitted infections, this would be sexual contact; for respiratory illness it might simply be sharing air space). This cross-cluster contact leads to spillover effects in control clusters, which consequently receive less infectious pressure from treatment clusters than they would in the absence of an intervention. Conversely, treatment clusters receive infectious pressure from control clusters that are unaffected by treatment. An effective intervention is likely to be rolled out across entire populations within administrative units rather than in randomly selected clusters. Therefore, the estimand of interest in this paper is the difference in incidence between what one would observe if the treatment were provided to all clusters (including those not included in the study if they have contacts with clusters in the study) and what one would observe if treatment were not provided to any cluster. We refer to this estimand as the overall treatment effect, though (as discussed in Section 2), this elides the dependence on the specific treatment programs being compared. In some settings, it is possible to measure the source of the interference – the proportion of contacts that occur outside the cluster. In fact, the BCPP is collecting information about the locations of residence of sexual partners of subjects in participating villages (Max Essex, personal communication). We make use of such information in leveraging mathematical models of epidemics to investigate how a given level of cross-cluster contact is likely to affect the transmission dynamics in the presence of an intervention.

In Section 2 we define our estimand of interest in the counterfactual framework. Section 3 outlines a simple epidemic model for disease transmission within and between clusters. In Section 4 we relate this epidemic model to an additive hazards model for survival, and derive an estimator of the overall treatment effect. The usefulness of the method is shown via simulation in Section 5, and an application to design studies for the BCPP appears in Section 6.

2. Estimand of Interest

We are interested in comparing rates of new HIV infections in treated and untreated clusters; hence the event of interest is acquisition of infection by a new individual. Thus, for each individual j in cluster i, the outcome is time of infection, T_ij. Treatment Z_i is assigned at the cluster level. In the counterfactual framework without interference, there is one possible outcome for each unit under each treatment condition: T_ij(Z_i). In the presence of interference among units, each unit’s outcome depends on the treatment assignments of other units, called the treatment program, $\mathbb{S}$. The treatment program is the vector of treatment assignments, $\mathbb{S}=\left(S_1,\cdots ,S_C\right)$, where S_i ∈ {0, 1} for binary treatments. This formulation implies 2^C potential outcomes for each unit.

Halloran and Struchiner (1991) define four different treatment effects in the presence of interference – direct, indirect, total, and overall – in the individual context; we restate them here in the cluster-randomized context. For clarity, we state them in the context of comparing an intervention to no intervention; all comparisons apply equally when comparing two more general intervention programs.

• The direct effect of the cluster-level intervention is the difference between the outcome in that cluster under the intervention condition and the outcome in that cluster under no intervention, holding the rest of the treatment program constant.

• The indirect effect of the intervention program for a cluster is the difference between the outcome in that cluster under the intervention program and the outcome in that cluster under no intervention program, given that the cluster does not receive treatment in either setting.

• The total effect in the cluster is the difference between the outcome for the cluster when it receives treatment under an intervention program and the outcome when the cluster is untreated under no intervention program.

• The overall effect is averaged over the population of clusters, and contrasts the outcome of an average cluster under the intervention with an average cluster under no intervention.

Of interest in this paper is the difference between two specific treatment programs, namely $\mathbb{S}\equiv 1$ and $\mathbb{S}\equiv 0$: the expected difference in outcome under the condition that none of the population is treated compared to that when the entire population is treated. This can be thought of as the difference in outcomes obtained by continuing the current standard of care and those obtained by implementing the intervention program throughout the population of interest. This corresponds to the overall treatment effect above.

Under $\mathbb{S}\equiv 1(\mathbb{S}\equiv 0)$, all exposures arise from contacts with a treated (untreated) cluster. Neither of these potential outcomes is observed for any unit in the study by design. We require observations of outcomes under both treated and untreated conditions to be able to make any comparison, leading to a realized $\mathbb{S}$ that is a mixture of 0 and 1. Nonetheless, if cross-cluster contact rates are measured, we can use them to compute the fraction of exposures that come from treated clusters and use the resulting fractional treatment variable, which is a function of those rates and the treatment program $\mathbb{S}$.

The overall treatment effect has been investigated in the literature on design and analysis of experiments on networks when the effect of interest is a difference in mean outcomes. Choi (2015) derives bounds for the outcome under the two treatment programs of interest here, which can be combined to give a lower bound for the overall treatment effect. Eckles, Karrer, and Ugander (2014) show that, under a linear model for outcomes, the overall treatment effect will be underestimated if interference is not taken into account through the design and/or analysis of the study.

3. A simple epidemiological model for disease transmission between clusters

Suppose that we have clusters 1, ⋯ , C that form a closed system of contacts (all contacts are within cluster or with other clusters in the study), with 1, …, c₁ receiving the control and the rest treatment. We begin with a simple Susceptible-Infectious (SI) model of disease transmission between clusters, defined by the following system of equations:

$$\frac{d{S}_i}{dt}=\upsilon -\sum _{j=1}^C{\alpha }_{ij}{S}_i{I}_j-{\mu }_S{S}_i$$

$$\frac{d{I}_i}{dt}=\sum _{j=1}^C{\alpha }_{ij}{S}_i{I}_j-{\mu }_I{I}_i$$

Here S_i(t) and I_i(t) are the proportions of the entire population that are susceptible and infectious individuals in cluster i (∑_i S_i(t) + I_i(t) = 1) with parameters:

• υ, the birth rate

• μ_S and μ_I, the death rate in the susceptible and infectious populations

• α_ij, the rate of new infections among susceptibles in cluster i from infectives in cluster j

This model is appropriate for a life-long infection such as HIV, although epidemic models can take many other forms: with an exposed but noninfectious phase; with recovery and subsequent immunity; with recovery and return to the susceptible population; etc. (Anderson and May, 1991, Keeling and Rohani, 2008). The following results rely only on the dynamics of interactions between susceptibles and infectives. Exposure of susceptibles to infectious individuals determines the incidence of new infections; therefore rates of contacts and population sizes for the S and I groups determine the infection process regardless of the existence of any exposed (E) or recovered (R) states. Thus an expansion to SIR, SEIR, SIS, etc. would not alter the following development (see Appendix for SEIR example). A model with multiple infectious states, on the other hand, would have implications that we do not describe here.

We include births in the model for full generality. In the particular setting of the BCPP, the population of interest is the at-risk adult population residing in the communities under study over the course of the trial. Individuals will age into this group over the three years of the trial. The birth rate could alternatively be set to zero for studies using a closed cohort, with no modification in the procedure for estimation of the overall treatment effect discussed in Section 2.

Following Watson (1972), α_ij is the infection rate in cluster i due to infectives in cluster j. In the absence of cross-cluster mixing, α_ij = 0 ∀i ≠ j, and the remaining α_ii are equivalent to the total rate of new infections per infective in their respective clusters. We decompose α_ij into three components: α_ij = κm_ijη_j, where κ is the overall average rate of contacts, m_ij is the percentage of contacts of individuals in cluster i that are with cluster j and η_j is the per-contact transmission probability of infectives in j. We assume that infection status does not affect the rate of contact. If, in addition, we assume that the probability of selecting a contact in a different cluster does not vary by infection status, then the m_ij can be estimated from the full population. Note that, since this is a closed system, m_ii = 1−∑_j≠i mij.

Let the counts of individuals in the infectious states at time t, I_i(t), be denoted Y_i(t), and the total population in cluster i N_i(t). The hazard function in cluster i is ${\lambda }_i(t)={\sum }_{j=1}^C{\alpha }_{ij}{Y}_j(t)/N_j(t)$. We assume that cluster sizes do not vary significantly over time, and that the m_ij account for relative sizes of clusters (i.e., m_ijN_i = m_jiN_j). Time-varying cluster sizes could be accommodated by allowing the m_ij to vary with time.

4. The additive hazards model and the epidemic framework

Note that the hazard function λ_i(t) = α_ijY_j(t)/N_j(t) is assumed to follow a linear additive form in the epidemic model described in Section 3. The additive hazards model, described in nonparametric form by Aalen (1989, 1993) and in semiparametric form by Lin and Ying (1994), has several nice properties for causal inference applications in general that are particularly useful for this application. One is collapsibility (Martinussen and Vansteelandt, 2013), which permits a straightforward handling of cluster effects (Pan, Liu, and Wu, 2015).

The general Aalen additive hazards model, incorporating covariates X, takes the form

$$\lambda (t\mid Z,X)={\beta }_0(t)+{\beta }_Z(t)z(t)+{\beta }_X(t)x(t),$$ (1)

where β₀(t) is the baseline hazard, β_Z (t) and β_X (t) are the coefficients (possibly vector-valued) of the treatment variable Z and any covariates X, respectively. Note that all parameters are time-varying and all variables are permitted to be time-varying. The parameter β_Z (t) represents a population-averaged overall causal effect of the treatment Z (Lange and Hansen, 2011, Martinussen and Vansteelandt, 2013) under assumptions of no unmeasured confounding.

For each individual j in cluster i we observe the infection time T_ij or censoring time W_ij. For each cluster, we have the treatment status Z_i and a measure m_ik of the percent of contacts of infected people in cluster i that are with people in cluster k. Under the assumed epidemic process $\lambda \left(t_{ij}\mid m,\mathbb{S}\right)={\sum }_{k=1}^C{\alpha }_{ik}{Y}_k(t)/N_k(t)={\sum }_{k=1}^C\kappa m_{ik}{\eta }_k{Y}_k(t)/N_k(t)$ In the following, we let κη_kY_k(t)/N_k(t) = ν_k(t) for clarity.

$$\begin{gathered} \lambda \left(t_{ij}\mid m,\mathbb{S}\right)=\sum _{k=1}^C{m}_{ik}{\nu }_k(t) \\ =\sum _{k=c_1+1}^C{m}_{ik}{\nu }_k(t)+\sum _{l=1}^{c_1}{m}_{il}{\nu }_l(t) \\ ={\overline{\nu }}^{ctr}(t)+m_i^{trt}\left({\overline{\nu }}^{trt}(t)-{\overline{\nu }}^{ctr}(t)\right)+ \\ +\sum _{k=c_1+1}^C{m}_{ik}\left({\nu }_k(t)-{\overline{\nu }}^{trt}(t)\right)+\sum _{l=1}^{c_1}{m}_{il}\left({\nu }_l(t)-{\overline{\nu }}^{ctr}(t)\right), \end{gathered}$$ (2)

where $m_i^{trt}$ is the total percentage of contacts of susceptibles in cluster i that are with infectives in treated clusters, and ${\overline{\nu }}^X(t)$ is the average (infection rate × prevalence) in clusters with treatment status X at time t. Under assumptions of no differential contact rate or partner choice by infection status, $m_i^{trt}$ represents the total percentage of contacts in cluster i that are with treated clusters. When there are no contacts between clusters, m_ij = 0 ∀i ≠ j and m_ii = 1, or equivalently $m_i^{trt}=1$ [i treated]. Note that this is also true under the two counterfactual treatment programs of interest, $\mathbb{S}\equiv 1$ and $\mathbb{S}\equiv 0$.

The expected value of the remainder term in Equation 2 is zero over the randomization distribution. This, with the consistency of the estimator (Lin and Ying, 1994, Aalen, 1989), gives

$$\text{E}\left[\widehat{\lambda }\left(t_{ij}\mid m,\mathbb{S}\right)\right]={\overline{\nu }}^{ctr}(t)+m_i^{trt}\left({\overline{\nu }}^{trt}(t)-{\overline{\nu }}^{ctr}(t)\right).$$ (3)

This result implies that in an additive hazards model using total contact with treated clusters $\left(m_i^{trt}\right)$ as the treatment variable (rather than treatment assignment), the corresponding coefficient estimate will provide a consistent estimator of $\left({\overline{V}}^{trt}(t)-{\overline{V}}^{ctr}(t)\right)$, the population-averaged overall causal effect associated with a change from 0% to 100% exposure to treatment.

We have written the $m_i^{trt}$ as constant values because we expect to have estimates from a single point in time of cross-cluster contact rates. The additive hazard model accommodates non-constant mixing through specifying treatment exposure as a function of time, $m_i^{trt}\left(t\right)$, but this creates an additional burden of data collection.

Inclusion of other covariates that impact the hazard rate is also compatible with the epidemic model framework; we focus here on the treatment alone for clarity of presentation. In the presence of other categorical covariates, the compartments or sub-populations of the epidemic model can be further subdivided by them. For example, one could divide the groups presented in Section 3 (S_i, and I_i) by sex s, yielding S_is and I_is. In this case, the summation would be over clusters as well as covariates; the m_ij could be either assumed to be constant over covariates or estimated within subgroups. Unless there is an association between the covariate and either infectivity or contact rate, however, this expansion will have no effect on the estimator. In addition, the collapsibility property of the additive hazards model assures that excluding these covariates will not create bias in the treatment effect estimate – in contrast to approaches based on the proportional hazards model (Martinussen and Vansteelandt, 2013).

Collapsibility also implies that the identifiability result extends directly to a model with clustered survival times, although standard errors would be estimated differently (Pan et al., 2015).

The model described here can be fit either to a single system of multiple clusters, or multiple sets of closed systems (i.e., pairs of clusters).

5. Simulation study

We assess the properties of our approach by simulating pairs of interacting clusters: one that receives treatment and one that does not. This approach captures the fundamental issue under study – exposures arising from both treated and untreated clusters – without requiring specification of a large stochastic network model for interactions between multiple clusters. Disease spread is modeled by a stochastic epidemic model with varying population size over time. We consider both an SI epidemic model, as described above, and an SEIR model.

We begin with 500 individuals in each of two clusters; total population size varies stochastically over time as individuals enter and leave the population (birth/death rate μ = 1/(5·365) per day). The intensity of contacts is set so that individuals have an average of two contacts on any given day. In the SI model, transmission is driven by an infectivity parameter η₀ = 0.0008 in the untreated cluster and η₁ = 0.0004 in the treated cluster. In the SEIR model, individuals spend an average of 5 days in the exposed state and 1500 days in the infectious state, with infectivity parameters η₀ = 0.0007 and η₁ = 0.0004. Together, these generate a reproductive rate of 2.5 new infections per case at the start of the epidemic. We generate random effects by cluster with mean zero, normally–distributed perturbations on the infectivity parameter. Mixing is established by forcing 0 to 30% of contacts of members of cluster 1 to be with members of cluster 0; in settings with any positive chance of cross-cluster contacts, contact rates are slightly perturbed for each pair of clusters. Disease spread starts with 5% initial infectives, and data are “collected” over a three-year period. We then record the rates of mixing between clusters, infection times and censoring status for individuals. This is repeated for 20 simulated pairs of clusters. We fit additive hazard models with adjustment for within-cluster correlation using (1) the randomized treatment assignment and (2) the realized proportion of treated exposures given mixing rates.

Because the coefficients of interest are time-varying in these simulations, we present a summary measure of the resulting hazard: the difference in the cumulative incidence over the first 3 years of the epidemic. The expected difference in cumulative incidence between the setting where all contacts are with treated clusters and that where all contacts are with untreated clusters is calculated via simulation; the estimated value and standard error over 5000 replicates are −0.038(0.00006) for the SI model and −0.037(0.00007) for the SEIR model. Each point in Figure 1 represents the average difference over 500 simulated data sets, and the average 95% confidence interval is given by the vertical lines. Note the rapid attenuation of the estimated treatment effect as the mixing rate increases for the randomized effect in both cases. The estimates of the overall treatment effect for all levels of mixing are within the confidence bounds for the no-mixing case, though there may be some over-correction at the highest level of mixing. The latter is also reflected in a slight increase in the root mean squared error (RMSE, Figure 2).

Figure 1: Simulation results from true SI and SEIR epidemic.

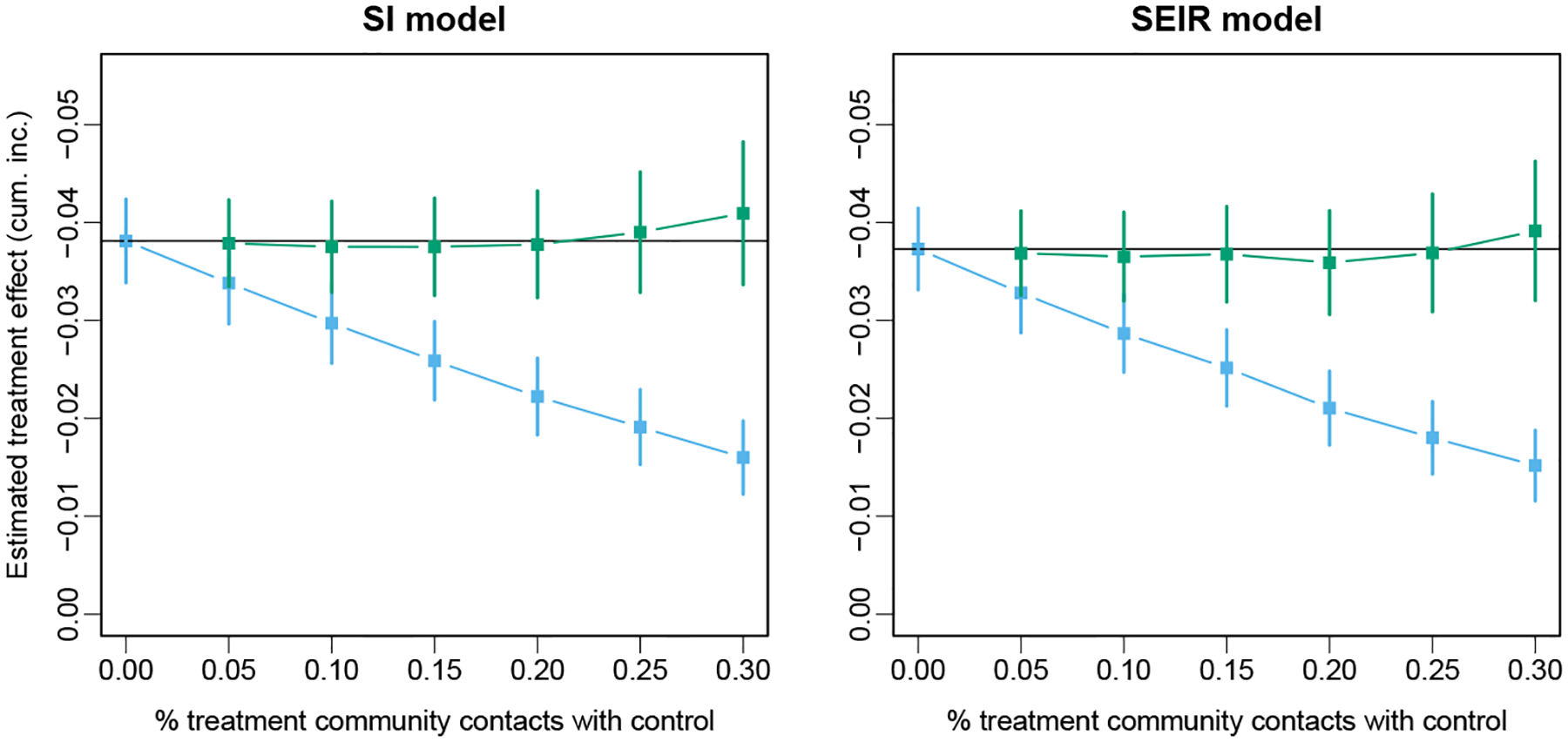
Average point estimate and 95% confidence interval for the estimates of randomized and overall treatment effects over 500 simulated data sets with SI and SEIR models. The horizontal black line indicated the expected value of the treatment effect in the absence of interference.

Figure 2: Simulation results from true SI and SEIR epidemic.

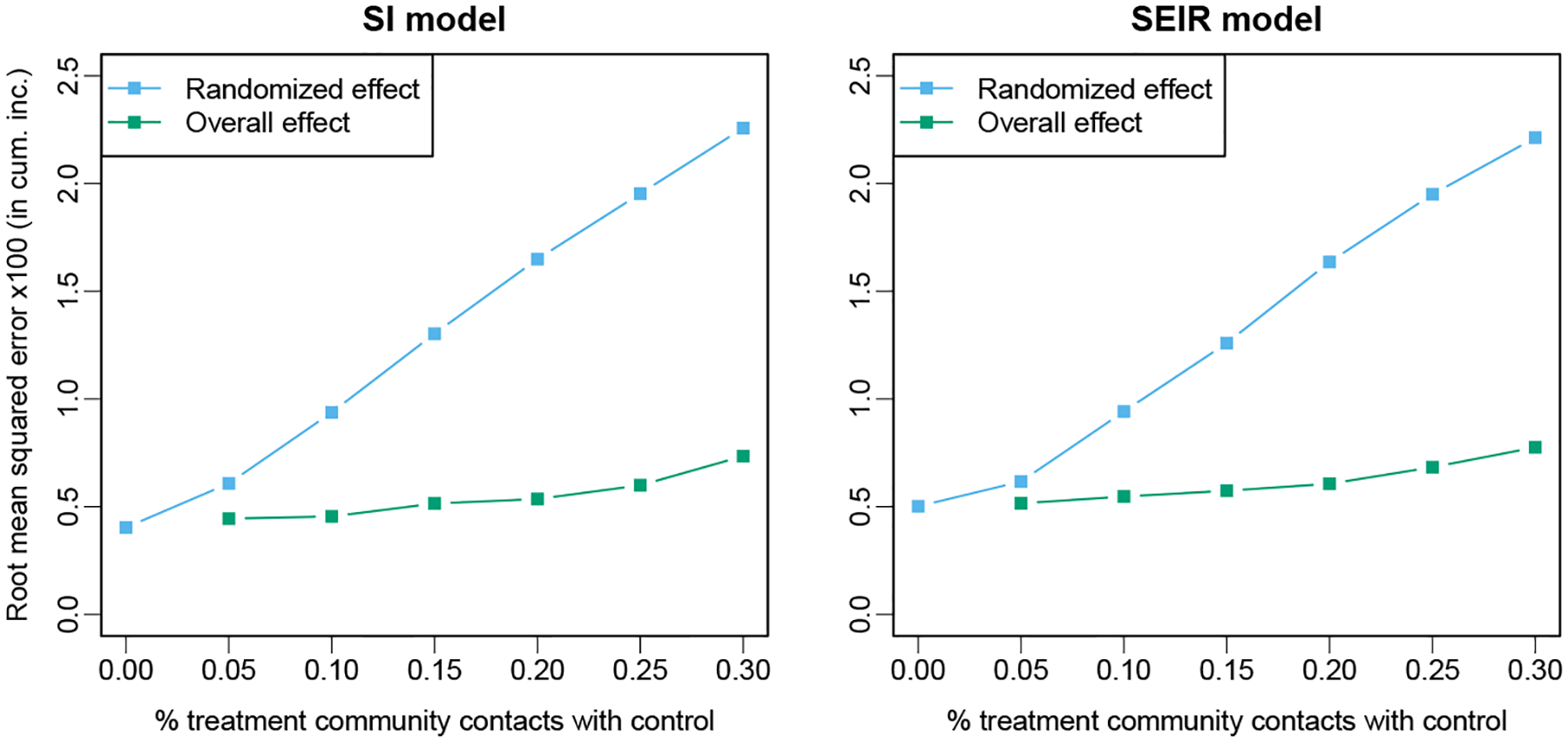
Root mean squared error relative to the expected value of the treatment effect in the absence of interference for the estimates of randomized and overall treatment effects over 500 simulated data sets with SI and SEIR models.

6. Application to design issues in Botswana CRT

To demonstrate the performance of the estimator in an actual research setting, we apply the method to the results of an agent-based simulation of a cluster randomized trial of HIV prevention (Wang et al., 2014). In that model, the epidemic spreads over dynamic networks in pairs of interacting clusters of equal size. The proportion of relationships that are between clusters in a pair range from 0 (no mixing) to 50% (clusters are effectively indistinguishable). For each mixing level there are 1000 simulated pairs of clusters. See the original article for details of the epidemic model and intervention.

We bootstrap the 1000 pairs into simulated CRTs by randomly sampling (with replacement) 200 sets of 20 pairs. For each simulated trial we compute the randomized treatment effect estimate and standard error as well as the overall treatment effect estimate and standard error using a random-effects additive hazard model.

Because prevalence is roughly constant over time in this setting, we can compare results for the cumulative incidence reported in Section 5 and the hazard difference in the additive hazard model. Figure 3 shows the decline in the randomized treatment effect as mixing increases from 0 to 50% of relationships and the estimates of the overall treatment effect. Note that we cannot estimate the overall treatment effect at 50% mixing, because this level of mixing implies no difference between treated and control communities in the total contact with treated communities. The dashed black line gives the treatment effect in the absence of mixing, while the dashed red line at 0 is included for reference when assessing the significance of the result. Although the estimation of the overall effect induces a cost in terms of variability, the mean squared error is nonetheless reduced compared to using the randomized effect to estimate overall effect, because of the latters greater bias, even at low levels of mixing (Figure 4).

Figure 3: Community–randomized trial model study results.

Randomized and overall treatment effect estimates over a range of mixing rates for Botswana CRT simulation. Vertical bars give the mean 95% CI from the additive hazards model with random effects for each estimate (note that mixing values are slightly jittered to prevent overlap of CIs).

Figure 4: Community–randomized trial model study results.

Root Mean Squared Error (relative to the expected value of the treatment effect in the absence of interference) of randomized and overall treatment effect estimates over a range of mixing rates for Botswana CRT simulation.

The confidence intervals in Figure 3 are the 95% CIs obtained from the average point estimate and SE over simulations from the appropriate model. Another measure of performance is the coverage of the 95% intervals. We take the true value to be the mean estimated treatment effect under the case of no mixing, which is approximately −0.000025, and calculate the percentage of simulated data sets for which the fitted models include that value. Coverage declines rapidly using the randomized estimator, and is conservative across mixing rates for the proposed estimator (Table 1).

Table 1:

Coverage of nominal 95% confidence intervals for hazard difference when targeting the treatment effect in the absence of mixing.

Mixing rate	Randomized estimator	Proposed estimator
0	1.00	1.00
0.1	1.00	1.00
0.2	0.83	1.00
0.3	0.16	1.00
0.4	0.00	1.00
0.5	0.00	N/A

In this application, the underlying assumption of the compartmental model described in Section 3 that any individual can come into contact with any other at any moment in time is violated, as contacts are contained within relationships that are sustained over time. In addition, the treatment effect is not a population-wide additive change in the transmissibility (η) parameter, but rather a heterogeneous treatment effect within the cluster arising from differing levels of exposure to different components of the intervention. Nonetheless, the model accounting for mixing accurately estimates the overall treatment effect, even for relatively large mixing rates, even though the uncertainty increases substantially with mixing rate.

7. Discussion

Interference between units presents a challenging problem for causal inference. While trials using two-stage randomization can identify causal effects in the presence of interference, this approach may be infeasible for cluster- or community-level outcomes for two reasons. First, as mentioned above, it requires randomization of super-clusters and of smaller clusters within them, which may require more experimental units than are available or feasible to include. Second, it would still require an assumption of no interference between super-clusters, which may not be more reasonable than assuming no interference between clusters. This paper presents an alternative approach to estimate the overall treatment effect using data from a traditional cluster-randomized trial design in which interference between clusters takes place, when the interactions between clusters causing the interference can be measured. We use an alternative measure of exposure to treatment, the fraction of contacts that are with a treated cluster, in an additive hazards model that is compatible with the structure of an epidemic model. This approach can be implemented readily using standard software, such as (Scheike and Zhang, 2011, Therneau, 2015). The approach assigns each cluster a fractional treatment exposure to reflect the actual exposure to treated contacts of subjects in both treated and untreated clusters.

This method is applicable in many settings, but may fail if the fraction of contacts with clusters of opposite treatment status is approximately 50% for all clusters. This situation is unlikely to arise, however, if clusters are defined with sufficient consideration of the issue of mixing across them. While the clusters in a study may not comprise a closed system of contacts, this could be addressed by the inclusion of a “pseudo-cluster” representing anyone who is not included in the study but may have a contact with someone included in the study. This would be particularly useful in a setting where the intervention is only delivered to study communities.

The development presented here requires the assumption that any individual can come into contact with any other at any moment in time–a common assumption in epidemic models that does not allow for repeated contacts within social relationships. This is not unreasonable for diseases such as respiratory infections which require little direct contact for transmission and can be well captured by deterministic compartmental models such as those used here (see, e.g. Anderson and May (1991)). Pathogens spread by more intimate contact may be difficult to model in this framework (see, e.g., Goodreau (2011)). However, in our simulation using the design study for the BCPP (Section 6) estimation of the overall treatment effect is not sensitive to violations of the epidemic model assumptions.

When the additive hazard model coefficients are constant, as would be the case under this epidemic model when prevalence is constant, the additive hazards model is equivalent to a proportional hazards model with form λ(t | Z) = λ₀(t)exp(1+γ₀Z(t)). The assumption of constant prevalence over the duration of the study is a reasonable one in the case of HIV in a mature epidemic. Because HIV infection is of such long duration, even if new infections were sharply reduced, it would take considerable time for the prevalence to decline measurably from deaths in the HIV-infected. In an epidemic with rapidly changing prevalence or for which an effective prevention program would significantly alter prevalence, the equivalency to proportional hazards breaks down.

The fraction of social contacts sufficient for transmission that occur within treatment clusters can be obtained from a survey of sexual behavior (a standard tool in STI prevention research) by asking respondents to identify the community/cluster of residence of their partners, as is being done for the BCPP (Max Essex, personal communication). This self-reported measure could potentially be validated using genetic linkage data from HIV positive participants. In either case, it is likely to be subject to measurement error. This error in the exposure of interest will further attenuate the estimate of the treatment effect (Thomas, Stram, and Dwyer, 1993), so we recommend consideration of the use of an errors-in-variables adjustment in the implementation of the model, such as in Kulich and Lin (2000).

The methods discussed here allow estimation of the overall treatment effect in cases where contacts sufficient for transmission occur between treatment and control clusters. Another potential source of treatment effect attenuation that we do not address is the adoption of the treatment in control clusters. This may be particularly likely to occur in educational interventions, where social contacts between clusters can spread the intended message into the control clusters.

This work deals with an idealized situation that captures fundamental features of the problem of interactions between clusters and could be extended in many ways. These include allowing for more complex behavioral patters (non-homogeneous mixing), allowing changes to susceptibility as well as infectivity in response to treatment, and non-homogeneous treatment effects. The application of Section 6 suggests that the last issue may not cause biases in the estimator of the overall effect, as long as the distribution of effects within clusters in the same and treatment effect is not associated with mixing behavior.

Appendix

A. Other epidemic model forms: Susceptible-Exposed-Infectious-Recovered

Suppose that we have clusters 1, ⋯, C that form a closed population, with 1, …, c₁ receiving the control and the rest treatment. We consider a simple SEIR model of disease transmission between clusters, defined by the following system of equations:

$$\frac{d{S}_i}{dt}=\upsilon -\sum _{j=1}^C{\alpha }_{ij}{S}_i{I}_j-{\mu }_S{S}_i$$

$$\frac{d{E}_i}{dt}=\sum _{j=1}^C{\alpha }_{ij}{S}_i{I}_j-\xi E_i-{\mu }_E{E}_i$$

$$\frac{d{I}_i}{dt}=\xi E_i-\gamma I_i-{\mu }_I{I}_i$$

$$\frac{d{R}_i}{dt}=\gamma I_i-{\mu }_R{R}_i$$

Here S_i, E_i, I_i and R_i are the proportions of the entire population that are susceptible, exposed, infectious, and recovered individuals in cluster i with parameters:

• υ, the birth rate

• μ_S, μ_E, μ_I and μ_R, the death rate in the susceptible, exposed, infectious and recovered populations

• α_ij, the rate of new infections among susceptibles in i from infectives in j

• ξ, the rate of transition from the exposed to infectious state

• γ, the rate of recovery for infectious individuals

As in the SI model case α_ij = κm_ijη_j, and the incidence rate in cluster i is ${\lambda }_i(t)={\lambda }_i(t)={\sum }_{j=1}^C{\alpha }_{ij}{Y}_j(t)/N_j(t)$, where Y_i(t) and N_i(t) denote the count of individuals in the infectious state and total population in cluster i at time t, respectively. Note that the transition parameters ξ and γ do not play a role here. Since they do not affect the incidence rate, they are irrelevant to the modeling of disease-free survival.