Abstract
Patient-specific quality assurance (PSQA) of volumetric modulated arc therapy (VMAT) to assure accurate treatment delivery is resource-intensive and time-consuming. Recently, machine learning has been increasingly investigated in PSQA results prediction. However, the classification performance of models at different criteria needs further improvement and clinical validation (CV), especially for predicting plans with low gamma passing rates (GPRs). In this study, we developed and validated a novel multi-task model called autoencoder based classification-regression (ACLR) for VMAT PSQA. The classification and regression were integrated into one model, both parts were trained alternatively while minimizing a defined loss function. The classification was used as an intermediate result to improve the regression accuracy. Different tasks of GPRs prediction and classification based on different criteria were trained simultaneously. Balanced sampling techniques were used to improve the prediction accuracy and classification sensitivity for the unbalanced VMAT plans. Fifty-four metrics were selected as inputs to describe the plan modulation-complexity and delivery-characteristics, while the outputs were PSQA GPRs. A total of 426 clinically delivered VMAT plans were used for technical validation (TV), and another 150 VMAT plans were used for CV to evaluate the generalization performance of the model. The ACLR performance was compared with the Poisson Lasso (PL) model and found significant improvement in prediction accuracy. In TV, the absolute prediction error (APE) of ACLR was 1.76%, 2.60%, and 4.66% at 3%/3 mm, 3%/2 mm, and 2%/2 mm, respectively; whereas the APE of PL was 2.10%, 3.04%, and 5.29% at 3%/3 mm, 3%/2 mm, and 2%/2 mm, respectively. No significant difference was found between CV and TV in prediction accuracy. ACLR model set with 3%/3 mm can achieve 100% sensitivity and 83% specificity. The ACLR model could classify the unbalanced VMAT QA results accurately, and it can be readily applied in clinical practice for virtual VMAT QA.
Keywords: VMAT QA, patient-specific QA, deep learning, radiotherapy
1. Introduction
With the rapid development of radiotherapy planning and delivery techniques, intensity-modulated radiation therapy (IMRT) improved the target coverage conformity and normal tissue sparing compared with three-dimensional conformal radiotherapy (Popescu et al 2010, Nicolini et al 2012). Volumetric modulated arc therapy (VMAT) plans have better delivery efficiency with the equivalent or better plan quality compared with IMRT. However, VMAT plans created by inverse planning algorithms often consist of highly modulated beams with significant dosimetric uncertainty (Fog et al 2011). The accuracy of plan delivery is heavily dependent on the treatment planning system (TPS) dose calculation and linear accelerator (Linac) performance (Ong et al 2011). Comprehensive quality assurance (QA) and quality control (QC) programs have been developed to assure the delivery accuracy of VMAT plans (Klein et al 2009, Van Esch et al 2011, Smilowitz et al 2015, Miften et al 2018). Despite improving the safety and reliability of treatment delivery, patient-specific QA (PSQA) is resource-intensive and time-consuming. With limited accessible information from TPS, the delivery accuracy of VMAT plans are difficult to predict and interpret before QA measurements. Recently, machine learning techniques have rapidly emerged in PSQA results prediction and causal factors analysis (Valdes et al 2016, 2017, Interian et al 2018, Tomori et al 2018, Granville et al 2019, Lam et al 2019, Mahdavi et al 2019, Ono et al 2019, Wall and Fontenot 2020).
Valdes et al first reported that Poisson regression with Lasso regularization model was trained using 78 complexity metrics and the PSQA results of 498 IMRT plans from multiple treatment sites (Valdes et al 2016). They found that the Poisson Lasso (PL) model could accurately predict 3%/3 mm gamma passing rates (GPRs) with maximum errors smaller than 3%. However, in the multi-institutional validation study, the generalization performance of the PL model decreased, only about 86.33% (120 of 139) predictions had error smaller than 3.5% (Valdes et al 2017). Interian et al (2018) developed a convolution neural network (CNN) model using fluence maps of IMRT plans as input, with comparable prediction accuracy obtained with previously developed PL model, which used 78 metrics as input. However, about 15 to 20 plans with prediction error higher than 3% were observed in both CNN model and PL model and the maximum prediction error was higher than 5%. Deep learning models were also used for IMRT PSQA. Deep networks (CNN with transfer learning) were found to be comparable to the PL model based on the expert-designed features (Interian et al 2018).
Instead of predicting GPR for plans from multiple treatment sites, Tomori et al (2018) trained the CNN model with 60 prostate IMRT plans. Planar dose distributions, geometric features of planning target volume (PTV) and rectum, and MU for each field were used as inputs. The maximum prediction errors were 3.0%, 4.5%, and 5.8% at 3%/3 mm, 3%/2 mm, and 2%/2 mm, respectively. The Spearman rank correlation coefficients between the measured and predicted GPRs of 0.32–0.62 were found in the test set. CNN model also achieved slightly better results in the prediction of dosimetric accuracy of VMAT plans using plan complexity parameters, compared with regression tree analysis and multiple regression analysis by (Ono et al 2019) Linac QC metrics were also added into treatment plan characteristics to improve the prediction accuracy for VMAT PSQA (Granville et al 2019). Artificial neural network (ANN) was investigated as an application for the pretreatment dose verification of IMRT fields using two-dimensional fluence maps acquired by an electronic portal imaging device (EPID) (Mahdavi et al 2019).
Deep learning with convolutional neural networks was also used to classify the presence or absence of introduced radiotherapy treatment delivery errors from patient-specific gamma images. The performance of the CNN was superior to a handcrafted approach with texture features, and radiomic approaches were better than threshold-based passing criteria in classifying introduced radiotherapy treatment delivery errors from patient-specific gamma image (Wootton et al 2018, Nyflot et al 2019). Some recent studies have used three tree-based machine learning algorithms (AdaBoost, Random Forest, and XGBoost) (Lam et al 2019) and SVM models (Wall PDH et al 2020) in predicting the plan QA GPRs, providing a helpful guide for physicists to better identify the failed plans.
To date, several studies have shown the feasibility of predicting PSQA results with machine learning models. When deciding whether the plan can be delivered accurately enough to be used for patient treatment, it is critical to select the appropriate gamma criteria and tolerance/action limits. The AAPM TG 218 report recommended 95% and 90% as the tolerance and action limits under 3%/2 mm gamma criteria, respectively (Miften et al 2018). Therefore, the most important function of a machine learning model is to find plans that may fail to pass the tolerance/action limits before QA measurements. We have investigated the impact of delivery characteristics on the dose delivery accuracy of VMAT (Li et al 2019b), the prediction and classification accuracy of machine learning models under different gamma criteria and tolerance/action limits for VMAT QA (Li et al 2019a). The performance of prediction and classification was affected by the measured GPRs level (‘high’ GPRs and ‘low’ GPRs, or ‘failed’ or ‘passed’ plans) of the VMAT plans. Good prediction accuracy was obtained for plans with higher GPR. However, the prediction accuracy needs to be improved for the plans with lower GPR. Whereas the distribution of the data is unbalanced in the VMAT plans, most of the plans have higher GPR and only small portion of plans have lower GPR. The VMAT plans with lower GPRs are the failed plans, so the improvement of prediction accuracy for plans with lower GPR would help physicists to take proactive action, thereby reducing QA workload while still assuring the delivery fidelity and safety. If the model predicted the failed plans as passed (false negative), then the delivery fidelity and safety would be compromised. If the model predicted the passed plans as failed (false positive), then the physicists’ workload would be increased. Besides, prediction and classification models were used separately in the previous study (Li et al 2019a).
In this study, a novel deep learning model called autoencoder based classification-regression (ACLR) was developed for VMAT QA from multiple treatment sites. We can consider the task of solving regression and classification problems under three different gamma criteria through a single deep learning model as multi-task learning (MTL). MTL uses related task-sharing representations to parallelize the specific domain information contained in the training signal of the training task, thereby improving generalization (Caruana 1997). The deep neural network for object detection like Fast R-CNN (Girshick 2015) also used a model that combining classification and regression model into a single-model and using multi-task loss. Inspired by this, we proposed the classification and regression combined model. The classification model was used as an intermediate result to improve the performance of the regression model by providing the measured GPRs level label information. On the other hand, the regression model could naturally guide the classification results for its ability to provide the prediction of the GPRs. By integrating classification and regression into a multi-task model, the neural network architecture would also be simplified and training would be accelerated because the two models share the same main network architecture. Different tasks of GPRs prediction based on different criteria were solved in one model.
The aims of this study are: (1) to develop and validate a novel multi-task classification and prediction model for patient-specific virtual VMAT QA; (2) to improve the prediction and classification accuracy for unbalanced data compared with previous models.
2. Materials and methods
2.1. Clinical data collection
426 VMAT plans previously used for patient treatment in our department, were retrospectively selected for model training and technical validation (TV). Among these plans, 148 were gynecological cancer (GYN) plans, 117 were head and neck cancer (H&N) plans, 69 were prostate cancer plans, and 92 were rectal cancer plans. Additionally, a new independent prospectively collected cohort of 150 VMAT plans (from four different treatment sites: 52 GYN, 41 H&N, 24 prostate, and 33 rectal plans) without cross validation were used for clinical validation (CV).
All plans were generated using two full arcs with Eclipse TPS (Varian Medical Systems, Palo Alto, CA, USA), each plan has 178 control points per arc. The prescription dose to the PTV for GYN and rectal cancer patients was 50.4 Gy (1.8 Gy f−1), and 50 Gy (2.0 Gy f−1). For H&N cases, prescription doses of 60.04 Gy (1.82 Gy f−1) and 69.96 Gy (2.12 Gy f−1) were delivered to PTV and planning gross target volume (PGTV), respectively. For Prostate cases, prescription doses of 72 Gy (2.40 Gy f−1) were delivered to PTV. All plans were delivered with Trilogy Linac and Millennium 120 MLC (Varian Medical Systems, Palo Alto, CA, USA), the maximum gantry speed was 4.8 deg s−1 and the maximum dose rate was 600 MU min−1.
The PSQA measurement was performed with a MatriXX ion chamber array together with a Multicube phantom (IBA Dosimetry, Schwarzenbruck, Germany). The dose calculation algorithm for the VMAT plan was Analytical Anisotropic Algorithm (AAA, Eclipse TPS V.10.0), with a calculation grid of 2.0 mm. The dose-effect of the treatment couch was taken into account in the dose calculation. Before the measurements, the output of the Linac was calibrated, and the absolute dose calibration of MatriXX was performed. The plan was delivered using true composite method, the radiation beams are delivered to a stationary detector array on the couch using the actual treatment parameters for the patient, including MUs, gantry, collimator, couch angle, jaws, and MLC leaf positions, recommended by AAPM TG 218 report (Miften et al 2018). The reference field (20 cm*20 cm) was used to evaluate setup errors in the VMAT QA measurement. The gamma passing rate of the reference field was compared with the baseline. If the gamma passing rate of the reference field was equal to or close to the baseline, we believed that the setup errors were small and we could continue following measurements. If the gamma passing rate of reference field deviated from the baseline, we believed that the setup errors were large and we would adjust the position of the phantom and repeat the above steps. The angular dependence of the detector array was corrected using a gantry angle sensor (IBA Dosimetry, Schwarzenbruck, Germany) during measurement. The measured dose distribution was set as a reference. Gamma criteria of 3%/3 mm, 3%/2 mm, and 2%/2 mm with a 10% dose threshold, absolute dose mode, and global normalization were used for gamma evaluations.
In this study, 54 metrics were used to characterize the modulation complexity of VMAT plans, a full summary was given in table A1 (Li et al 2019a). To extract MLC leaf position and MU weights of all control points in the VMAT plans, RT plans were exported from the TPS and converted into ASCII format. Then, an in-house developed Matlab script was used to extract information and calculate the complexity metrics. In the pre-processing, the 54 metrics were standardized by removing the mean and scaling the standard deviation to unity before the training, cross validation, and testing process.
In TV, 84.7% of the measured GPRs were distributed between 95% and 100% at 3%/3 mm, 69.3% at 3%/2 mm and 24.7% at 2%/2 mm gamma criteria; In CV, about 89.0% of the measured GPRs were distributed between 95% and 100% at 3%/3 mm, 84.0% at 3%/2 mm and 66.0% at 2%/2 mm gamma criteria (as shown in table 1 and figure 1). The minority of the GPRs were distributed in the range below 90% at 3%/3 mm, below 90% at 3%/2 mm, below 80% at 2%/2 mm gamma criteria.
Table 1.
Summary of measured gamma passing rate (GPRs) under different gamma criteria.
| Measured GPR(%) | 3%/3 mm |
3%/2 mm |
2%/2 mm |
|||
|---|---|---|---|---|---|---|
| TV, % (N) | CV, % (N) | TV, % (N) | CV, % (N) | TV, % (N) | CV, % (N) | |
|
| ||||||
| 100 – 95 | 84.7 (361) | 89.3 (134) | 69.3 (295) | 84.0 (126) | 24.7 (105) | 66.0 (99) |
| 95 – 90 | 11.2 (48) | 5.3 (8) | 20.7 (88) | 8.0 (12) | 31.7 (135) | 18.0 (27) |
| <90 | 4.0 (17) | 5.3 (8) | 10.0 (43) | 8.0 (12) | 43.6 (186) | 16.0 (24) |
Abbreviations: TV = technical validation; CV = clinical validation; % = percentage in this column; N = number of plans.
Figure 1.
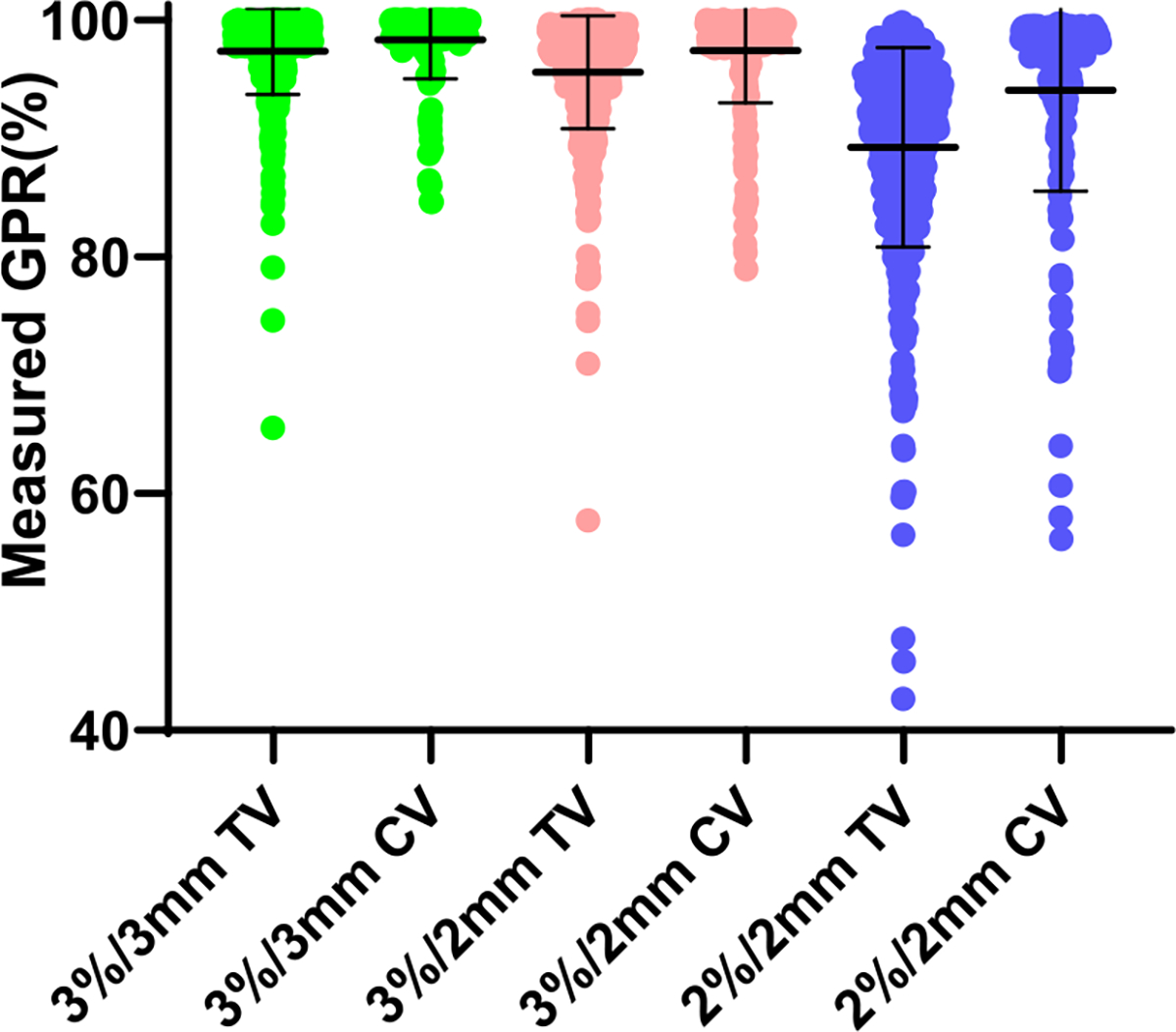
The distribution of GPRs of volumetric modulated arc therapy plans at different gamma criteria. Abbreviations: CV = clinical validation; TV = technical validation. Error bar = mean ± standard deviation.
2.2. Deep learning model design and validation
The Schematic of the model design, TV, and CV were given in figure 2(A). In TV, 426 VMAT plans with cross validation were used for model training and exploring the model performance under different gamma criteria. In CV, a new independent prospectively collected cohort of 150 VMAT plans without cross validation was used for further validating the generalization performance of the proposed deep learning model and the reliability and feasibility as a clinical tool.
Figure 2.
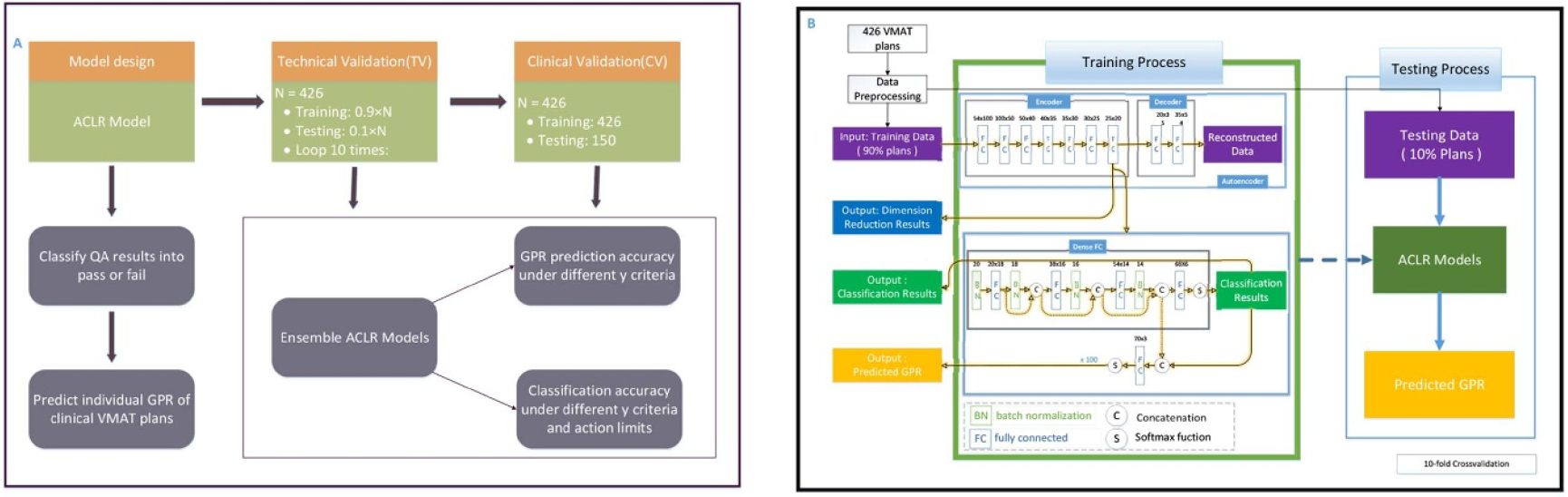
Schematic of the model design, technical validation, and clinical validation (A) and training process and testing process of ACLR in technical validation (B). Abbreviations: GPR = gamma passing rate; ACLR = autoencoder based classification-regression deep learning model. The blocks in the Training Process box show the training process of ACLR.
The PL model was used as a baseline model to compare the prediction performance of GPRs (Li et al 2019a). For QA results classification (Li et al 2019a), action limits for 3%/3 mm, 3%/2 mm, and 2%/2 mm gamma criterion in the models were 90%, 90%, and 80%, respectively.
2.3. Model framework
In this section, we explained the details of the proposed model framework. We first introduced several techniques used to improve the prediction results. Then the ACLR model was described in detail.
‘Parameter norm penalties’ is one of the most common regularizations for machine learning models. and regularization as one of parameter norm penalties was used to improve machine learning models’ generalization performance, which is used widely in many fields by adding penalties on parameters:
| (1) |
| (2) |
| (3) |
where is a combination of -norm and -norm of parameters of the deep learning models.
During the training process, ACLR has four losses: (Softmax Loss) for classification branch, (MSE Loss) for regression branch, and L1, L2 for regularization penalty. The total loss is the sum of all these losses:
| (4) |
The balanced sampling technique is an intuitive method that can help balance training data to classify QA results during the classification training process. The balanced sampling technique is used here to improve the sensitivity of the model. In the VMAT plans, the distribution of the data is unbalanced, most of the plans have higher GPR and only a few plans have lower GPR. Hence, we used a random under-sampling strategy to have the number of different GPR plans balanced. Through the under-sampling strategy, the size of the majority class was down-sampled to the same size as the minority class in the training subprocess. In every batch of the training process, balanced sampling techniques were used to balance the size of minority and majority class, and the deep learning model can achieve better performance by combining the process with the architecture we designed.
As we often observe, validation and training errors of the model are not always reduced synchronously, because the deep learning model tends to over-fit as the maximum number of iterations increases to a certain degree. ‘Early stopping’ technique was used in the process of model training to stop the model training when the error on the validation set did not improve for some amount of time. The optimal stop epoch for the deep model was determined by cross validation in the training process. In the training process, the models were run until the loss in the validation set has not improved in 20 consecutive epochs. We chose the model with the minimum loss as the optimal model and recorded the optimal stop epoch.
Autoencoder is an unsupervised ANN architecture to learn a low-dimensional representation of the dataset (Hinton and Salakhutdinov 2006). A deep autoencoder, an improvement over an autoencoder that has been trained on dimensionality reduction, was used to pre-train our deep network to improve performance and speed up the training process (figure 2(B) Autoencoder). The entire training process of a deep autoencoder was divided into two steps. A shallow autoencoder was first trained, and its encoder was then used as a pre-trained network to train a deeper autoencoder. This process was repeated several times to build a deep autoencoder with sufficient depth. And, the final encoder of the deep autoencoder was used as the backbone of our deep learning models.
Data augmentation and dense fully connected layers were also implemented to improve the performance of the model. We enhanced the dataset four times by adding Gaussian white noise to the data to alleviate the problem of limited data volume. Inspired by DenseNet (Huang et al 2017), dense fully connected layers were used between feature layers by concatenation operator (figure 2(B) Dense FC).
We proposed a multi-task classification and regression combined model, called ACLR (figure 2(B) Training Process). Ten-fold cross validation was used to divide the data into ten folds. The training and testing processes were repeated ten times. Each time nine-fold data were used for the training process and one-fold for the testing process. In the training process, the classification part and regression part could be trained alternately or simultaneously. If the main goal is to get better classification results, we recommend that the classification part and the regression part should be trained simultaneously. If the main goal is to get better regression results, we recommend alternate training for the classification part and the regression part, and in the last epoch, only the regression part is trained. Inspired by PL regression, in order to limit the range of the regression branch between 0 and 100, a softmax activation function (the range of the softmax function between 0 and 1) multiplied by 100 was added to the last layer before the output results of prediction branch.
The network architecture of the blocks we used in our models was shown in figure 2(B). All deep learning models were trained by the Adam learning rate optimizer through different initialization parameters and initial learning rates. The weights of ACLR were randomly initialized from a zero-mean Gaussian distribution with a standard deviation of 0.01. We selected multiple sets of optimal initialization parameters to train different models to predict QA results and performed ensemble learning by averaging the results of the three models to obtain more stable results. This was implemented using the open-source machine learning framework, PyTorch.
We used student t test to compare the prediction error between ACLR and PL models on MAE values in both TV and CV data. In TV, the MAE was calculated by collecting all the prediction errors of the ten-fold cross validation. In CV, the MAE was calculated by averaging the absolute value of the prediction error.
3. Results
3.1. Prediction accuracy
The prediction accuracies of the ACLR and PL model under different gamma criteria were given in table 2. ACLR model significantly outperformed the PL model in both TV and CV, in terms of MAE (mean absolute error) and RMSE (root-mean-square error) at 3%/3 mm, 3%/2 mm, and 2%/2 mm.
Table 2.
Prediction accuracy of ACLR and Poisson Lasso model under different gamma criteria.
| MAE(%) |
RMSE(%) |
||||||
|---|---|---|---|---|---|---|---|
| ACLR | PL | Improved | ACLR | PL | Improved | ||
|
| |||||||
| TV | 3%/3 mm | 1.76** | 2.10 | 16 | 2.50 | 2.99 | 16 |
| 3%/2 mm | 2.60** | 3.04 | 17 | 3.50 | 4.23 | 17 | |
| 2%/2 mm | 4.66** | 5.29 | 12 | 6.08 | 6.95 | 13 | |
| CV | 3%/3 mm | 1.73 | 2.07 | 16 | 2.61 | 3.04 | 14 |
| 3%/2 mm | 2.75 | 2.99 | 8 | 3.87 | 4.12 | 6 | |
| 2%/2 mm | 5.93* | 7.12 | 17 | 7.39 | 8.91 | 17 | |
Abbreviations: MAE = mean absolute error, RMSE = root mean squared error; TV = technical validation; CV = clinical validation. ACLR = autoencoder based classification-regression deep learning model; PL = Poisson Lasso. Student t test was performed on MAE values between ACLR and PL in TV and CV. Improved = the percentage improvement between ACLR and PL. Bold number in table 2 = absolute prediction errors have significant differences between ACLR and PL
in table 2 = (p < 0.01)
= (p < 0.05)
The summary of absolute prediction errors (APEs) distribution under different gamma criteria for ACLR and PL model in TV was shown in table 3. In TV, for ACLR model, 405 (95.1%) plans had APE below 5% at 3%/3 mm; 375 (88.0%) plans had APE below 5% at 3%/2 mm while only 265 (62.2%) plans had APE below 5% at 2%/2 mm. For PL model, 397 (93.2%) plans had APE below 5% at 3%/3 mm; 367 (86.2%) plans had APE below 5% at 3%/2 mm while only 247 (58.0%) plans had APE below 5% at 2%/2 mm. In CV, for ACLR model, 138 (92.0%) plans had APE below 5% at 3%/3 mm; 134 (89.3%) plans had APE below 5% at 3%/2 mm while only 69 (46.0%) plans had APE below 5% at 2%/2 mm. For PL model, 133 (88.6%) plans had APE below 5% at 3%/3 mm; 132 (88.0%) plans had APE below 5% at 3%/2 mm while only 53 (35.3%) plans had APE below 5% at 2%/2 mm.
Table 3.
Summary of APE distribution under different gamma criteria for ACLR and Poisson Lasso models in TV and CV.
| Metrics | 3%/3 mm |
3%/2 mm |
2%/2 mm |
||||
|---|---|---|---|---|---|---|---|
| ACLR, N (%) | PL, N (%) | ACLR, N (%) | PL, N (%) | ACLR, N (%) | PL, N (%) | ||
|
| |||||||
| TV | APE ⩽ 3.5% | 386 (90.6) | 369 (86.6) | 334 (78.4) | 304 (71.4) | 202 (47.4) | 186 (43.7) |
| APE ⩽ 5% | 405 (95.1) | 397 (93.2) | 375 (88.0) | 367 (86.2) | 265 (62.2) | 247 (58.0) | |
| APE ⩽ 10% | 419 (98.4) | 415 (97.4) | 416 (97.7) | 411 (96.5) | 385 (90.4) | 370 (86.9) | |
| MAE (SD) | 1.76% (1.8) | 2.10% (2.1) | 2.60 (2.4) | 3.04 (2.9) | 4.66% (3.9) | 5.28% (4.6) | |
| CV | APE ⩽ 3.5% | 135 (90.0) | 131 (87.3) | 113 (75.3) | 102 (68.0) | 39 (26.0) | 35 (23.3) |
| APE ⩽ 5% | 138 (92.0) | 133 (88.6) | 134 (89.3) | 132 (88.0) | 69 (46.0) | 53 (35.3) | |
| APE ⩽ 10% | 146 (95.3) | 143 (95.3) | 144 (96.0) | 142 (94.7) | 147 (98.0) | 141 (94) | |
| MAE (SD) | 1.73% (1.5) | 2.07% (1.7) | 2.99% (1.9) | 2.36% (2.1) | 5.93% (2.3) | 7.12% (3.2) | |
Abbreviations: APE = absolute prediction error; MAE = mean absolute error; SD = standard deviation; ACLR = autoencoder based classification-regression deep learning model; PL = Poisson Lasso; TV = technical validation
As shown in table 4, the prediction accuracy of ACLR and PL models were compared under different ranges of measured GPRs, which affects the prediction accuracy. According to the results of the ACLR and PL models in TV, under the gamma standards of 3%/3 mm and 3%/2 mm, APE that measure GPR above 90% are significantly lower than APE that measure GPR below 90% (3%/3 mm ACLR: 1.28 ± 0.81% vs. 5.3 ± 4.64%, p < 0.0001; 3%/3 mm PL: 1.43 ± 0.79% vs. 6.8 ± 5.0%, p < 0.0001; 3%/2 mm ACLR: 1.94 ± 1.35% vs. 4.58 ± 4.64%, p < 0.0001; 3%/2 mm PL: 2.13 ± 1.43% vs. 5.65 ± 5.44%, p < 0.0001); At 2%/2 mm GPR prediction, the APE of the plans with a measured GPR of 80% to 100% was significantly lower than the plan with a measured GPR of less than 80%. (ACLR: 2.46 ± 1.86% vs. 7.53 ± 5.58%, p < 0.0001; PL: 3.04 ± 2.65% vs. 8.21 ± 6.22%, p < 0.0001). The bold number in table 4 showed the significant differences of APEs between ACLR and PL models.
Table 4.
Summary of absolute prediction error under different measured gamma passing rate (GPR) for ACLR and Poisson Lasso model in TV and CV.
| Measured GPR | 3%/3 mm |
3%/2 mm |
2%/2 mm |
||||
|---|---|---|---|---|---|---|---|
| ACLR, Mean (SD) | PL, Mean (SD) | ACLR, Mean (SD) | PL, Mean (SD) | ACLR, Mean (SD) | PL, Mean (SD) | ||
|
| |||||||
| TV | 100 – 95 | 1.28 (0.81) | 1.43 (0.79) | 1.94 (1.35) | 2.13 (1.43) | 5.84 (1.76) | 6.35 (2.44) |
| 95 – 90 | 3.66 (1.81) | 4.56 (1.27) | 2.76 (1.56) | 3.02 (1.42) | 2.01 (1.35) | 2.97 (2.47) | |
| <90 | 7.72 (3.83) | 10.95 (2.47) | 7.10(4.14) | 9.84 (4.56) | 5.94 (5.03) | 6.39 (5.86) | |
| CV | 100 – 95 | 1.25 (0.45) | 1.51 (0.74) | 2.15 (1.21) | 2.35 (1.25) | 5.77 (1.76) | 7.03 (2.28) |
| 95 – 90 | 1.53 (1.32) | 2.66 (1.21) | 1.90 (1.46) | 1.79 (1.34) | 2.37 (1.24) | 2.81 (2.14) | |
| <90 | 10.16 (3.42) | 10.96 (2.36) | 9.97 (4.28) | 10.89 (7.42) | 10.62 (4.37) | 12.40 (3.32) | |
Abbreviations: SD = standard deviation; ACLR = autoencoder based classification-regression deep learning model; PL = Poisson Lasso; TV = technical validation. Bold number in table 4 = absolute prediction errors have significant differences between ACLR and PL (p < 0.01). Student t test was performed here.
3.2. Classification accuracy
The classification accuracy of VMAT QA at 3%/3 mm gamma criteria in TV with the ACLR model was also evaluated. The results were obtained through the ensemble models and have greater weight for classification loss.
In TV, for the ACLR’s ensemble model, the sensitivity was 100% and specificity was 83% at 3%/3 mm gamma criteria, the sensitivity was 90% and specificity was 72% at 3%/2 mm gamma criteria and the sensitivity was 90% and specificity was 70% at 2%/2 mm gamma criteria. For PL model, the sensitivity was 0% and specificity was 100% at 3%/3 mm gamma criteria, the sensitivity was 0% and specificity was 99% at 3%/2 mm gamma criteria and the sensitivity was 68% and specificity was 63% at 2%/2 mm gamma criteria.
In CV, for the ACLR’s ensemble model, the sensitivity was 100% and specificity was 72% at 3%3 mm gamma criteria, the sensitivity was 92% and specificity was 69% at 3%/2 mm gamma criteria and the sensitivity was 100% and specificity was 67% at 2%/2 mm gamma criteria. For PL model, the sensitivity was 0% and specificity was 100% at 3%/3 mm gamma criteria, the sensitivity was 0% and specificity was 100% at 3%/2 mm gamma criteria and the sensitivity was 0% and specificity was 100% at 2%/2 mm gamma criteria.
4. Discussion
Aiming to improve the accuracy of the GPR prediction, a new deep learning model called ACLR was developed and validated, which has significantly higher accuracy than the current state-of-art model in TV and CV. Compared with the regression PL model, the accuracy improved 12%–17% and 6%–17% in TV and CV. The ACLR model achieved sensitivity of 100% and specificity of 83% at 3%/3 mm gamma criteria.
In this study, we studied VMAT QA plans of multi-disease-sites (GYN, H&N, prostate, and rectum) and proposed a novel machine learning model, ACLR, which can significantly improve the predictive performance of VMAT QA. The consistent results were obtained for CV and cross validation. Our method has better performance than the PL method by comparing APE and RMSE as shown in table 2. At three different criteria (3%/3 mm, 3%/2 mm, and 2%/2 mm) of the predicted errors, our method also outperformed PL as demonstrated in table 3.
The prediction results of ACLR are more accurate compared to those of PL. The prediction of low GPRs plan (Measured GPRs <90) was significantly improved (table 4) at 3%/3 mm, 3%/2 mm, and 2%2 mm. ACLR will be useful for improving the efficiency of VMAT QA. It can help physicists to determine the failed plans more accurately and spend more time on the failed plans and investigate the causes.
The classification results show that the sensitivity of PL model is too low for classification and ACLR model has advantages in classification. For classification results, the sensitivity of ACLR was higher than PL. Classification is a more important problem that needs to be solved considering the decision making of PSQA. Previous work has done little in classification research and has not used a better classification model. The previous PL model is mainly used for regression that did not deal with unbalanced data.
In this study, a novel deep learning model was proposed to predict the GPR by combining four different treatment sites, which GPR of these four VMAT plans can be predicted with the same model. Compared with the previous method PL (Li et al 2019a), our proposed model used more useful information by training a two-branch deep learning model called ACLR and performs better in QA predictions. In Interian et al study (Interian et al 2018), PL was also used as a baseline model and a CNN-based depth model was established with comparable results compared to PL.
Several techniques were used in the ACLR model to improve the prediction accuracy. Data augmentation was used to improve the accuracy and robustness of the model. Since Gaussian white noise was added to the training data during the training process, the model may be more stable in noisy data. The autoencoder was trained to simplify the training of the model and reduce parameters. Ensemble techniques were also used in the process of results handling to help the system be more stable. To our knowledge, this is the first time that a hybrid deep learning model of prediction and classification has been introduced to predict GPR. The prediction results were significantly improved compared with the baseline model. The regression model and the classification model share the same main network architecture, which makes the model more simplified and the training speed faster. The idea of sharing network architecture from regression models and classification models also improved the performance of ACLR.
It is hard to compare this study with previous studies directly due to the differences in the treatment equipment, planning systems, verification systems, GPRs criteria, as well as different inputs of prediction models. The distribution of measured GPR also differed across the studies, especially the number of low GPR data varied much across studies. Specifically, Valdes et al had 8% IMRT plans with GPR lower than 95% at 3%/3 mm (Valdes et al 2016), Tomori et al had very few plans with GPR lower than 95%, and the lowest GPR was 94% at 3%/3 mm (Tomori et al 2018). as reported in (Lam et al 2019), the lowest GPR is about 91%, and most of the IMRT plans had GPR more than 96% at 2%/2 mm. Despite the different GPR measurements among studies, the data distribution of all previous studies and this study were unbalanced. In order to improve the prediction accuracy of low GPR plans, multi-institutional cooperation research should be conducted, which is also what we did here.
The comprehensive comparison of previous relevant studies was listed in table 5. Compared with previous work, we used 54 expert designed features, a new ACLR method to predict and classify VMAT plans. Our algorithm has several advantages. An autoencoder could reduce the dimension of features. The data balance method was useful to alleviate overfitting and classification bias due to unbalanced training data before training the classification branch of the ACLR model. In classification, balanced sampling techniques are necessary to improve the sensitivity of machine learning models. Machine learning algorithms optimize the loss function by reducing the total loss of all samples, which will result in a classifier with higher classification accuracy in majority classes (‘high’ GPRs classes) and lower classification accuracy in minority classes (‘low’ GPRs classes), which means that the sensitivity of the model is low. In this study, we pay more attention to the classification effect of minority classes. The balanced sampling technique may slightly affect the classification accuracy, resulting in a slightly lower classification accuracy but a higher sensitivity, which was demonstrated in the cross validation and test results. Here the model’s sensitivity means the ability to detect the failed PSQA plans.
Table 5.
A comprehensive comparison of previous related studies.
| Group | Training Data, Testing Data | Input Feature | QA Tool | GPR/Targets | ML Model | Measured GPR/Results |
|---|---|---|---|---|---|---|
|
| ||||||
| Ono et al Med Phys, 2019 | 500 VMAT plans, 100 VMAT plans | N = 28 complexity, machine type, photons | ArcCHECK | DD5%, 3%/3 mm | RTA, MRA, NNs | 92.3% (9.1%), 96.8% (3.1%) |
| Interian et al Med Phys, 2018 | 498 IMRT plans, 10-fold-CV | Fluence maps, 78 features | MapCHECK2 | 3%/3 mm | CNN(VGG-16), Poisson regression | MAE of 0.70 |
| Tomori et al Med Phys, 2018 | 60 IMRT Plans, 5-fold-cross-validation | Dose distributionin prostate CA | EBT3 film | 2%/2 mm, 3%/2 mm, 2%/3 mm, 3%/3 mm. | CNN | Spearman rank correlation coefficients in validation |
| Granville et al PMB 2019 | 1215 VMAT Beam, 405 VMAT Beams | Planning complexity, Linac metrics | Delta4 | Median dose deviation | svc | ROC 0.88–0.93 |
| Mahdavi et al BIR 2019 | 60 IMRT GZP beams, 20 IMRT GZP beams | 2D fluence map | EPID | 2D-dose map | ANN | 3%/2 mm,90% |
| Lam et al Med Phys, 2019 | 1269 IMRT beams, 228 IMRT beams | 31 features | EPID | 2%/2 mm | AdaBoost, Random Forest, XGBoost | 98%, 98%, 95% |
| Wall et al Informatics in Medicine Unlocked 2020 | 500 VMAT plans | 100 selected features | MapCHECK2 | 3%/3 mm | linear models, SVMs, tree-based, neural networks | MAE 3.75% |
| Our Studies 2019, present | 426 VMAT (TV), 10-fold-CV; 150 VMAT (CV) | 54 expert designed features | MatriXX | 2%/2 mm, 3%/2 mm, 3%/3 mm | PL,RF,ACLR | 3%/2 mm,90% |
Compared with models with regression branches alone, ACLR with regression branches and classification branches can achieve better regression performance. Before the output layer of the regression branch, a softmax activation function is used to limit the range of the regression output and improve the regression performance. By this manually designed neural network structure process, we achieved a way of combining more informative features, which benefit from both dimension reduction and classification information at the same time to help us to achieve more stable and accurate results with a limited amount of data that can be collected. Our model has better prediction accuracy than PL under three different gamma criteria and unbalanced data conditions as demonstrated in table 4.
ACLR provided a new way and better performance for virtual VMAT QA. By combining deep learning models with clinical QA data, there is greater potential to make VMAT QA more efficient and effective. There are many practical values in solving VMAT QA prediction problems. For one thing, through using a deep learning model predicting PSQA results, physicists could know whether a QA plan would pass or fail before delivery. With deep learning models, physicists could narrow PSQA efforts on the plans that may fail instead of all plans. Also, deep learning models could save a lot of time and resources by improving the efficiency of VMAT QA, so that physicists could spend more time on failed plans and investigate; and thus, prevent failures.
For deep learning models or more complex models, more data are needed than those were used in this study, which will lead to overfitting of the model. Our method has almost fully used the information that we can obtain now, which may still be not enough to give us a total prediction of all VMAT QA plans. To a certain extent, the generalization performance of the deep learning model is not so good as the fitting data performance with limited training data and prior information.
In this study, 54 metrics were used as input data. The source and calculation process of these 54 metrics had corresponding QC to ensure their high integrity. Firstly, the daily, monthly, and annual QA items of the accelerator were implemented strictly. Secondly, the reference field (20 cm*20 cm) was used to evaluate the setup errors of the phantom. Finally, the fully verified Matlab script was used to extract information from the RT plans and calculate the complexity metrics. These 54 metrics were all related to the plan complexity and accelerator delivery accuracy. In the following study, other information, such as anatomy information of targets and OARs, could be added as metrics.
426 VMAT plans previously used for patient treatment in our department, were retrospectively selected for model training and validation in this study. All of the PSQA measurements were performed with MatriXX, a commonly used dosimetric verification device. For gamma pass rate calculation, the measured dose distribution was set as a reference considering the pixel size of MatriXX according to the recommendation of AAPM TG 218. The model performance may be different for different dosimetric verification device. We will perform further investigation in future study, including the use of EPID. Next, we will continue to investigate the ACLR model for virtual VMAT QA, to improve and validate the performance of the model in more clinical scenarios. Multi-institutions validation study involving different delivery modalities and dosimetric verification techniques is underway.
5. Conclusions
A new deep learning framework based on autoencoder and ensemble learning was developed and validated for virtual VMAT QA under different gamma criteria and unbalanced data conditions. By integrating a hybrid deep learning model of prediction and classification, significantly better predictive performance was achieved compared with PL models alone for virtual VMAT QA plans from multiple treatment sites. This model of virtual VMAT QA can be readily implemented in clinical practices.
Acknowledgments
This work was partly supported by the Strategic Priority Research Program of Chinese Academy of Science Capital’s Funds for Health Improvement and Research (Grant No. XDB32040100), National Natural Science Foundation of China (No. 81071237; 61773380), Beijing Municipal Commission of science and technology collaborative innovation project Z201100005620012, Capital’s Funds for Health Improvement and Research (2020-2Z-40919), the Natural Science Foundation of Beijing (7202223), Interdisciplinary Medicine Seed Found of Peking University (Grant No. BMU20160585), and the NIH/NCI P30 Cancer Center Support Grant (Grant No. CA008748).
Abbreviations:
- TV
technical validation
- CV
clinical validation
- %
percentage in this column
- N
number of plans
Appendix
The complexity metrics contains aperture complexity metrics, plan-normalized monitor units (PMU), aperture area metrics, leaf speed metrics and gantry speed metrics. Aperture complexity metrics was (Younge and Matuszak, 2012) the ratio of the aperture perimeter defined by the MLC (multi-leaf collimater) leaf sides to the aperture area. PMU (Park et al 2015) were computed by dividing the total MU of VMAT plans by the fractional target dose and then multiplying by 2 Gy. Aperture area metrics contains field area (MFA) and small aperture score (SAS). The MFA (Crowe et al 2015) was calculated by averaging the area of all individual apertures in a VMAT plan, each aperture area weighted by the number of MU delivered. SAS (Crowe et al 2015) was used to calculate the proportions of apertures defined as small where the MLC leaf separation was less than a certain value (5, 10 and 20 mm).Leaf speed for individual MLC leaves in each control point was calculated by dividing leaf travel distance by delivery time (Park et al 2014, 2015). Gantry speed metrics was calculated by dividing control point spacing by delivery time.
Table A1.
Summary of complexity metrics used in this study.
| Number | Metrics | Reference |
|---|---|---|
|
| ||
| 1 | Modulation index for leaf speed f = 2 (MIs 2) | Park et al (2014) |
| 2 | Modulation index for leaf speed f = 1 (MIs 1) | Park et al (2014) |
| 3 | Modulation index for leaf speed f = 0.5 (MIs 0.5) | Park et al (2014) |
| 4 | Modulation index for leaf speed f = 0.2 (MIs 0.2) | Park et al (2014) |
| 5 | Modulation index for leaf acceleration f = 2 (MIa 2) | Park et al (2014) |
| 6 | Modulation index for leaf acceleration f = 1 (MIa 1) | Park et al (2014) |
| 7 | Modulation index for leaf acceleration f = 0.5 (MIa 0.5) | Park et al (2014) |
| 8 | Modulation index for leaf acceleration f = 0.2 (MIa 0.2) | Park et al (2014) |
| 9 | Modulation index for total modulation f = 2 (MIt 2) | Park et al (2014) |
| 10 | Modulation index for total modulation f = 1 (MIt 1) | Park et al (2014) |
| 11 | Modulation index for total modulation f = 0.5 (MIt 0.5) | Park et al (2014) |
| 12 | Modulation index for total modulation f = 0.2 (MIt 0.2) | Park et al (2014) |
| 13 | Proportion of leaf speed ranging from 0 to 0.4 cm s−1 (S0–0.4) | Park et al (2015) |
| 14 | Proportion of leaf speed ranging from 0.4 to 0.8 cm s−1 (S0.4–0.8) | Park et al (2015) |
| 15 | Proportion of leaf speed ranging from 0.8 to 1.2 cm s−1 (S0.8–1.2) | Park et al (2015) |
| 16 | Proportion of leaf speed ranging from 1.2 to 1.6 cm s−1 (S1.2–1.6) | Park et al (2015) |
| 17 | Proportion of leaf speed ranging from 1.6 to 2.0 cm s−1 (S1.6–2) | Park et al (2015) |
| 18 | Proportion of leaf acceleration ranging from 0 to 1 cm s−2 (A0–1) | Park et al (2015) |
| 19 | Proportion of leaf acceleration ranging from 1 to 2 cm s−2 (A1–2) | Park et al (2015) |
| 20 | Proportion of leaf acceleration ranging from 2 to 4 cm s−2 (A2–4) | Park et al (2015) |
| 21 | Proportion of leaf acceleration ranging from 4 to 6 cm s−2 (A4–6) | Park et al (2015) |
| 22 | Average leaf speed (ALS) | Park et al (2015) |
| 23 | Standard deviation of leaf speed (SLS) | Park et al (2015) |
| 24 | Average leaf acceleration (ALA) | Park et al (2015) |
| 25 | Standard deviation of leaf acceleration (SLA) | Park et al (2015) |
| 26 | Small aperture score 5 mm (SAS 5 mm) | Crowe et al (2015) |
| 27 | Small aperture score 10 mm (SAS 10 mm) | Crowe et al (2015) |
| 28 | Small aperture score 20 mm (SAS 20 mm) | Crowe et al (2015) |
| 29 | Mean asymmetry distance (MAD) | Crowe et al (2015) |
| 30 | Modulation complex score (MCS) | Mcniven et al (2010) |
| 31 | Leaf sequence variability (LSV) | Mcniven et al (2010) |
| 32 | Aperture area variability (AAV) | Mcniven et al (2010) |
| 33 | Plan area (PA) | Du et al (2014) |
| 34 | Plan irregularity (PI) | Du et al (2014) |
| 35 | Plan modulation (PM) | Du et al (2014) |
| 36 | Plan normalized MU (PMU) | Du et al (2014) |
| 37 | Union aperture area (UAA) | Du et al (2014) |
| 38 | Edge metric (EM) | Younge et al (2012) |
| 39 | Converted aperture metric (CAM) | Götstedt et al (2015) |
| 40 | Edge area metric (EAM) | Götstedt et al (2015) |
| 41 | Circumference/area (C/A) | Götstedt et al (2015) |
| 42 | Average leaf travel distance (LT) | Masi et al (2013) |
| 43 | Combination of LT and MCS (LTMCS) | Masi et al (2013) |
| 44 | Average leaf gap (ALG) | Nauta et al (2011) |
| 45 | Standard deviation of leaf gap (SLG) | Nauta et al (2011) |
| 46 | Average dose rate (ADR) | — |
| 47 | Standard deviation of dose rate (SDR) | — |
| 48 | MU value in first arc (MU 1) | — |
| 49 | MU value in second arc (MU 2) | — |
| 50 | Prescribed dose to primary target per fraction (Dose) | — |
| 51 | Field length at X direction in first arc (Field X1) | — |
| 52 | Field length at Y direction in first arc (Field Y1) | — |
| 53 | Field length at X direction in second arc (Field X2) | — |
| 54 | Field length at Y direction in second arc (Field Y2) | — |
Complexity metrics that have ‘—’ in the reference column can be easily extracted or calculated based on plan information in the TPS.
References
- Caruana R 1997. Multitask learning Mach. Learn. 28 41–75 [Google Scholar]
- Crowe SB, Kairn T, Middlebrook N, Sutherland B, Hill B, Kenny J, Langton CM and Trapp JV 2015. Examination of the properties of IMRT and VMAT beams and evaluation against pre-treatment quality assurance results Phys. Med. Biol. 60 2587–601 [DOI] [PubMed] [Google Scholar]
- Du W, Cho SH, Zhang X, Hoffman KE and Kudchadker RJ 2014. Quantification of beam complexity in intensity-modulated radiation therapy treatment plans Med. Phys. 41 021716. [DOI] [PubMed] [Google Scholar]
- Fog LS, Rasmussen JF, Aznar M, Kjaer-Kristoffersen F, Vogelius IR, Engelholm SA and Bangsgaard JP 2011. A closer look at RapidArc(R) radiosurgery plans using very small fields Phys. Med. Biol. 56 1853–63 [DOI] [PubMed] [Google Scholar]
- Girshick R 2015. Fast R-CNN Proc. of the Int. Conf. on Computer Vision (ICCV) [Google Scholar]
- Götstedt J, Karlsson HA and Bäck A 2015. Development and evaluation of aperture-based complexity metrics using film and EPID measurements of static MLC openings Med. Phys. 42 3911–21 [DOI] [PubMed] [Google Scholar]
- Granville DA, Sutherland JG, Belec JG and La Russa D J 2019. Predicting VMAT patient-specific QA results using a support vector classifier trained on treatment plan characteristics and linac QC metrics Phys. Med. Biol. 64 095017 [DOI] [PubMed] [Google Scholar]
- Hinton GE and Salakhutdinov RR 2006. Reducing the dimensionality of data with neural networks Science 313 504–7 [DOI] [PubMed] [Google Scholar]
- Huang G, Liu Z, Van Der Maaten L and Weinberger KQ 2017. Densely connected convolutional networks 2017 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR) pp 2261–9 [Google Scholar]
- Interian Y, Rideout V, Kearney VP, Gennatas E, Morin O, Cheung J, Solberg T and Valdes G 2018. Deep nets vs expert designed features in medical physics: an IMRT QA case study Med. Phys. 45 2672–80 [DOI] [PubMed] [Google Scholar]
- Klein EE et al. 2009. Task Group 142 report: Quality assurance of medical accelerators Med. Phys. 36 4197–212 [DOI] [PubMed] [Google Scholar]
- Lam D, Zhang X, Li H, Deshan Y, Schott B, Zhao T, Zhang W, Mutic S and Sun B 2019. Predicting gamma passing rates for portal dosimetry-based IMRT QA using machine learning Med. Phys. 46 4666–75 [DOI] [PubMed] [Google Scholar]
- Li J, Wang L, Zhang X, Liu L, Li J, Chan MF, Sui J and Yang R 2019a. Machine learning for patient-specific quality assurance of VMAT: prediction and classification accuracy Int. J. Radiat. Oncol. Biol. Phys. 105 893–902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Zhang X, Li J, Jiang R, Sui J, Chan MF and Yang R 2019b. Impact of delivery characteristics on dose delivery accuracy of volumetric modulated arc therapy for different treatment sites J. Radiat. Res. 60 603–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahdavi SR, Tavakol A, Sanei M, Molana SH, Arbabi F, Rostami A and Barimani S 2019. Use of artificial neural network for pretreatment verification of intensity modulation radiation therapy fields Br. J. Radiol. 92 20190355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masi L, Doro R, Favuzza V, Cipressi S and Livi L 2013. Impact of plan parameters on the dosimetric accuracy of volumetric modulated arc therapy Med. Phys. 40 071718. [DOI] [PubMed] [Google Scholar]
- Mcniven AL, Sharpe MB and Purdie TG 2010. A new metric for assessing IMRT modulation complexity and plan deliverability Med. Phys. 37 505–15 [DOI] [PubMed] [Google Scholar]
- Miften M et al. 2018. Tolerance limits and methodologies for IMRT measurement-based verification QA: recommendations of AAPM task group no. 218 Med. Phys. 45 e53–83 [DOI] [PubMed] [Google Scholar]
- Nauta M, Villarreal-Barajas JE and Tambasco M 2011. Fractal analysis for assessing the level of modulation of IMRT fields Med. Phys. 38 5385–93 [DOI] [PubMed] [Google Scholar]
- Nicolini G et al. 2012. Volumetric modulation arc radiotherapy with flattening filter-free beams compared with static gantry IMRT and 3D conformal radiotherapy for advanced esophageal cancer: a feasibility study Int. J. Radiat. Oncol. Biol. Phys. 84 553–60 [DOI] [PubMed] [Google Scholar]
- Nyflot MJ, Thammasorn P, Wootton LS, Ford EC and Chaovalitwongse WA 2019. Deep learning for patient-specific quality assurance: identifying errors in radiotherapy delivery by radiomic analysis of gamma images with convolutional neural networks Med. Phys. 46 456–64 [DOI] [PubMed] [Google Scholar]
- Ong CL, Cuijpers JP, Senan S, Slotman BJ and Verbakel WF 2011. Impact of the calculation resolution of AAA for small fields and rapidarc treatment plans Med. Phys. 38 4471–9 [DOI] [PubMed] [Google Scholar]
- Ono T, Hirashima H, Iramina H, Mukumoto N, Miyabe Y, Nakamura M and Mizowaki T 2019. Prediction of dosimetric accuracy for VMAT plans using plan complexity parameters via machine learning Med. Phys. 46 3823–32 [DOI] [PubMed] [Google Scholar]
- Park JM, Park SY, Kim H, Kim JH, Carlson J and Ye SJ 2014. Modulation indices for volumetric modulated arc therapy Phys. Med. Biol. 59 7315–40 [DOI] [PubMed] [Google Scholar]
- Park JM, Wu HG, Kim JH, Carlson JNK and Kim K 2015. The effect of MLC speed and acceleration on the plan delivery accuracy of VMAT Br. J. Radiol. 88 20140698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popescu CC, Olivotto IA, Beckham WA, Ansbacher W, Zavgorodni S, Shaffer R, Wai ES and Otto K 2010. Volumetric modulated arc therapy improves dosimetry and reduces treatment time compared to conventional intensity-modulated radiotherapy for locoregional radiotherapy of left-sided breast cancer and internal mammary nodes Int. J. Radiat. Oncol. Biol. Phys. 76 287–95 [DOI] [PubMed] [Google Scholar]
- Smilowitz JB et al. 2015. AAPM medical physics practice guideline 5.a.: Commissioning and QA of treatment planning dose calculations - megavoltage photon and electron beams J. Appl. Clin. Med. Phys. 16 14–34 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomori S, Kadoya N, Takayama Y, Kajikawa T, Shima K, Narazaki K and Jingu K 2018. A deep learning-based prediction model for gamma evaluation in patient-specific quality assurance Med. Phys. 45 4055–65 [DOI] [PubMed] [Google Scholar]
- Valdes G, Chan MF, Lim SB, Scheuermann R, Deasy JO and Solberg TD 2017. IMRT QA using machine learning: a multi-institutional validation J. Appl. Clin. Med. Phys. 18 279–84 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valdes G, Scheuermann R, Hung CY, Olszanski A, Bellerive M and Solberg TD 2016. A mathematical framework for virtual IMRT QA using machine learning Med. Phys. 43 4323. [DOI] [PubMed] [Google Scholar]
- Van Esch A, Huyskens DP, Behrens CF, Samsoe E, Sjolin M, Bjelkengren U, Sjostrom D, Clermont C, Hambach L and Sergent F 2011. Implementing RapidArc into clinical routine: a comprehensive program from machine QA to TPS validation and patient QA Med. Phys. 38 5146–66 [DOI] [PubMed] [Google Scholar]
- Wall PDH and Fontenot JD 2020. Application and comparison of machine learning models for predicting quality assurance outcomes in radiation therapy treatment planning Inform. Med. Unlocked 18 100292 [Google Scholar]
- Wootton LS, Nyflot MJ, Chaovalitwongse WA and Ford E 2018. Error detection in intensity-modulated radiation therapy quality assurance using radiomic analysis of gamma distributions Int. J. Radiat. Oncol. Biol. Phys. 102 219–28 [DOI] [PubMed] [Google Scholar]
- Younge KC, Matuszak MM, Moran JM, Mcshan DL, Fraass BA and Roberts DA 2012. Penalization of aperture complexity in inversely planned volumetric modulated arc therapy Med. Phys. 39 7160–70 [DOI] [PMC free article] [PubMed] [Google Scholar]


