A fly inspired solution to looming detection for collision avoidance

Summary

Dodging rapidly approaching objects is a fundamental skill for both animals and intelligent robots. Flies are adept at high-speed collision avoidance. However, it remains unclear whether the fly algorithm can be extracted and is applicable to real-time machine vision. In this study, we developed a computational model inspired by the looming detection circuit recently identified in Drosophila. Our results suggest that in the face of considerably noisy local motion signals, the key for the fly circuit to achieve accurate detection is attributed to two computation strategies: population encoding and nonlinear integration. The model is further shown to be an effective algorithm for collision avoidance by virtual robot tests. The algorithm is characterized by practical flexibility, whose looming detection parameters can be modulated depending on factors such as the body size of the robots. The model sheds light on the potential of the concise fly algorithm in real-time applications.

Graphical abstract

Highlights

• •We model the fast escape circuit of the fruit fly
• •LPLC2 neurons nonlinearly integrate EMD inputs and jointly extract looming features
• •Looming-size threshold is determined by the receptive field size of LPLC2 neurons
• •The fly algorithm enables robust collision avoidance in virtual robot tests

Applied computing; Biomimetics; Robotics

Introduction

Collision detection ability is of significance to both biological and machine vision systems. Biologically inspired looming detection has long aroused research interest. One recent example is the realization of moving-obstacle detection based on bioinspired vision sensors, i.e., event cameras.¹ Neuromorphic sensors greatly shorten the algorithm’s perception latency to moving obstacles. Except for bioinspired event cameras, however, their detection framework was still established upon a traditional approach, such as the use of a Kalman filter and artificial potential field method. Could the solution of biological vision systems for looming detection be accurately extracted and borrowed in real time?

Looming responses are ubiquitous across a wide variety of animal species, including humans, mice, zebrafish, and flies.^2,3,4,5,6 While neural substrates of looming responses have been extensively identified,^{3,5,6,7,8,9,10,11,12,13} the underlying neural computation in many species, especially those having visual cortexes, is still unclear.

The best-understood circuit mechanisms are from studies on flying insects, which have superb motion vision but tiny and relatively simple brains. In the locust visual system, a highly specialized neuron, i.e., the lobula giant motion detector (LGMD), was identified to be involved in looming detection and related escape behaviors.^10,14 A number of models have been proposed to elucidate the neural computation underlying LGMD-based looming detection.^15,16,17,18 Another circuit in the Drosophila visual system, which connects T4/T5 cells to the giant fiber (GF) descending neuron via lobula plate/lobula columnar, type 2 (LPLC2) visual projection neurons, was recently identified by a series of experimental studies.^19,20,21,22 Differing from LGMD-based circuits that do not receive directionally selective inputs, the fly LPLC2-GF circuit critically depends on the inputs of local motion detectors, i.e., T4/T5 cells.

Different from motion detection techniques used in computer vision such as differential methods and region-based matching methods, and so forth,²³ biological vision uses correlation-based motion detection.^24,25,26 A widely accepted model of local motion detectors for biological vision is correlation-type elementary motion detector (EMD), which was formulated more than half a century ago.²⁷ Given that visual motion measurement by the EMD is sensitive to nonmotion-related factors such as luminance contrast and texture properties,^28,29 it remains unclear how the visual motion-based LPLC2-GF circuit performs accurate looming detection. Another significant question is whether the fly algorithm is applicable to real-time collision avoidance.

In this study, we addressed these issues by developing a computational model constrained by the anatomical properties of the LPLC2-GF circuit. By assuming that individual LPLC2 neurons perform a nonlinear integration of inputs, we show that the model reproduces the physiological response properties of the circuit neurons. The model suggests that the key to fly looming detection lies in looming feature extraction by a population coding strategy. The population coding is a means to represent information by using the joint activities of a group of individual neurons.³⁰ Specifically, looming features cannot be restored by independently analyzing the activity of each LPLC2 neuron that responds to the looming stimulus. By contrast, looming features such as the looming size is able to be extracted from the dynamics of the population activity of all LPLC2 neurons that are simultaneously activated by the stimulus, although the responses of the individual LPLC2 neurons themselves could be noisy.

We further tested the model by setting a virtual robot with the task of moving around obstacles. To endow the model with adaptability to robots having a definite body size, we identified a specific parameter in the model that could be adjusted depending on the robot size. Robot simulations show that the model is a robust and effective algorithm for guiding the robot for timely collision avoidance. The superiority of the brain-inspired algorithm over optic flow-based algorithms such as the flow divergence algorithm is examined in the discussion. To the best of our knowledge, the model is the first fly inspired algorithm that can be applicable to real-time collision avoidance.

Results

Nonlinear integration causes LPLC2 units to selectively respond to radial expansion stimuli

Inspired by the circuit connecting T4/T5 cells to single GF descending neuron via LPLC2 neurons in Drosophila,^19,20 we developed a three-layered feedforward network model (Figure 1A). The first layer is an array of EMD units simulating T4/T5 cells, which estimate visual motion based on visual inputs. Detailed structure of individual EMD units (Figure 1B) was developed based on the model proposed by Eichner et al.,³¹ which reproduced a variety of experimental datasets (Figure 4A in Eichner et al.³¹) (see STAR Methods). Significant progress has been made in models of the fly EMD over the past decade.³² Individual EMDs have been revealed to be three-armed rather than two-armed in both the ON and the OFF motion pathway in Drosophila.^33,34 We chose, however, to retain the two-armed EMD structure in the present study. The reason is that the two-armed Hassenstein-Reichardt model yields a high degree of directional selectivity that is characteristic of a three-armed EMD model. Compared with the three-armed EMD model, however, two-armed EMD models have been extensively studied. Their pattern-dependent response properties have been clearly known (Buchner 1984; Reichardt 1987)^28,29, which would greatly simplify and facilitate the present study.

Figure 1.

An overview of the looming detection model

(A) Schematic of the EMD-LPLC2-GF network. The biological neurons simulated by the model are denoted in parentheses inside each module, and the simulated function is indicated beside each layer.

(B) Detailed structure of individual EMD units (left) with symbolic representations defined (right). The hollow and solid arrows denote the output of motion detectors simulating T4 and T5 cells, respectively.

(C) Four convolution kernels of the LPLC2 layer in (A). Each kernel consists of binary elements responsible for extracting the flow feature in the corresponding cardinal direction. The four kernels together comprise a cross shape, simulating the RF of individual LPLC2 neurons.

(D) Schematic of dendritic arbor spread found in individual LPLC2 neurons in Drosophila (Klapoetke et al.²⁰). The representative LPLC2 neuron (green) extends dendrites into four layers of the lobular plate (denoted by LP1, LP2, LP3, and LP4) to extract looming features. Each layer’s preferred direction is indicated as an arrow array.

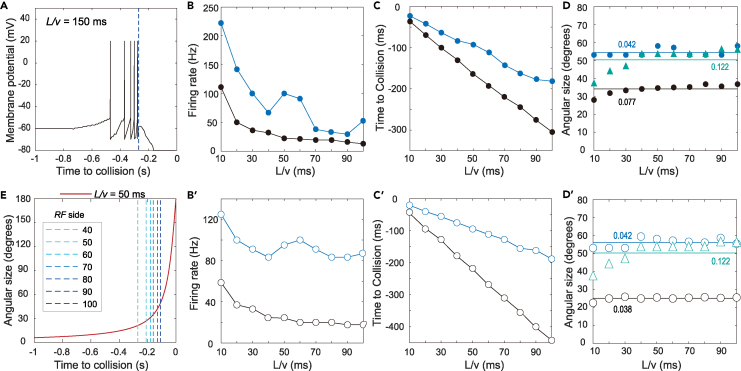
Figure 4.

Emergence of an angular-size threshold in the GF unit

(A) The simulated membrane potential of the GF unit simultaneously recorded with the data in Figure 3B. The dashed line marks the peak time of $N_{\text{act}}\left(t\right)$.

(B) Instantaneous firing rates of the GF unit across looming L/v values at the time of its first spike (black solid circles) and the time of its peak response (blue solid circles).

(C) The first spike time (black solid circles) and the peak response time (blue solid circles) of the GF unit across looming L/v values.

(D) Instantaneous looming size when the GF unit fired its first spike (black solid circles) or reached peak firing (blue solid circles) and when the $N_{act}\left(t\right)$ peaked (green triangles) across looming L/v values. The color-coded lines denote the average values for each sample. The color-coded numbers beside the lines indicate the corresponding coefficient of variation.

(E) The peak time of $N_{\text{act}}\left(t\right)$ (dashed lines) under different conditions of the RF side length of LPLC2 units. The same looming stimulus (L/v value, at the top of the panel) was used for all the simulations, whose temporal characteristics of the looming size are displayed (red curve).

(B′, C′, D′) Same as (B), (C), and (D), respectively, except that the multiplicative integration of the looming size and velocity information in the GF unit was replaced by a summation operation. The circles represent the same meaning as the solid circles with the corresponding color between each pair of panels.

The second layer is an array of LPLC2 units simulating LPLC2 neurons, which extract looming features based on visual motion. The last layer consists of a GF unit simulating the single GF descending neuron, which integrates the approaching features of the looming object. The model’s working hypothesis is that individual LPLC2 units nonlinearly integrate visual motion expanding in the four cardinal directions multiplicatively (see Equation 5 in STAR Methods).

For a given LPLC2 unit, its receptive field (RF) consists of four layers, in each of which the sub-RF forms one arm of a cross shape (Figure 1C). The four-layered RF qualitatively mimics the four-lobe structure found in the RF of individual LPLC2 neurons²⁰ (Figure 1D). According to the model ((Equation 1), (Equation 2), (Equation 3), (Equation 4) in STAR Methods), motion in a preferred and null direction in each of the sub-RFs gives excitatory and inhibitory inputs to the LPLC2 unit, respectively. The inputs in the four sub-RFs are finally combined through a multiplication operation (Equation 5 in STAR Methods), causing the LPLC2 unit to activate only if it detects preferred direction motion simultaneously in all four cardinal directions from the upstream EMD array. In other words, as local looming detectors, individual LPLC2 units should remain silent when facing nonexpansive stimuli such as unidirectional movement or radial contraction motion.

To test the above assumption, we reproduced a variety of visual stimuli used in a previous study²⁰ (Figure 2A). Among these stimuli, only the one shown in the first column and first row in Figure 2A is a looming stimulus (see STAR Methods). The expanding square with a constant edge speed is not a looming stimulus (Figure 2A, the panel in the second column and first row). The parameter L/v, i.e., a size-to-velocity ratio was used to characterize a looming object’s approaching kinematics.¹⁶ The object’s half-size is L, and its approaching velocity is v (Figure 2C).

Figure 2.

Response properties of the LPLC2 model units

(A) Responses of the centrally located unit in the LPLC2 layer to a variety of motion stimuli, including outward square motion (first and second col.), unidirectional motion (a bar: third and fifth col.; an edge: fourth and sixth col.; a square-wave grating: seventh and eighth col.), and outward (ninth col.) or inward (10th col.) cross motion. It is worth noting that the outward motion in the first col. and first row is a looming stimulus with L/v = 50 ms, whereas the other outward motion (in the second and ninth col. and first row) is not looming but expanding with a constant edge speed, as illustrated by their temporal characteristics (two panels at the top of the first and second col.). All the stimuli had a constant edge velocity of 50 pixels per second except for the looming one. Simulation parameters are the same for the results in the second and third row except for the integration operation by the LPLC2 units, as indicated under each row.

(B) Same as (A) except that each stimulus in (A) was replaced by a corresponding motion-defined stimulus, whose texture consists of randomly distributed black and white dots (leftmost panel in the first row). The foreground figure is invisible unless it is moving relative to the background. The texture in all the motion-defined stimulus is represented by a uniform gray color for drawing clarity. The foreground is outlined by straight lines, and the square-wave grating is represented by three parallel arrows for drawing clarity.

(C) Top view diagram illustrating the presentation of looming stimuli. The approaching square objects (half-size, L in both horizontal and vertical directions; velocity, v) projected on the screen were fed into the network model (model input, black square on the green area), giving the model a 118°×103°-field of view. θ is the object’s horizontal angle subtended to the modeled eye, whose maximal value (denoted as θ_max) is reached when the object moves to the location marked by the gray area.

We fed the stimuli to the model and recorded the response of the downstream LPLC2 unit that was retinotopically aligned with the focus of expansion (FOE) motion (denoted as unit O below). The results show that although the EMD array was activated by each type of stimulus, unit O remained silent except for three radial expansion stimuli (Figure 2A, second row). The model responses to the looming square (first col.), the expanding square (second col.), a variety of unidirectional motion (third to eighth col.), and outward (ninth col.) or inward (10th col.) cross-motion are qualitatively consistent with the essential responses of LPLC2 neurons shown in Figure 2D (upper panel) in Klapoetke et al.,²⁰ in the first panel of Figure 2F in Klapoetke et al.,²⁰ in the second to seventh panel of Figure 2F in Klapoetke et al.,²⁰ in the panel b and c of Figure 4A in Klapoetke et al.,²⁰ respectively.

The results were qualitatively unchanged if we fed motion-defined stimuli, whose texture consists of randomly distributed black and white dots and thus makes the foreground figure invisible unless it is moving relative to the background (Figure 2B, first row: motion-defined stimuli; second row: responses of the unit O).

To probe whether a multiplicative integration of EMD inputs is critical for the selectivity of individual LPLC2 units to radial expansion stimuli, we replaced the multiplicative operation in Equation 5 by a summation operation. Specifically, the state of individual LPLC2 units was simulated as an additive integration of visual motion in the four cardinal directions in their RFs, i.e., ${LPLC2}_{\mathrm{i},\mathrm{j}}\left(t\right)={\left[L_{\mathrm{i},\mathrm{j}}^1\left(t\right)-L_0\right]}^{+}+{\left[L_{\mathrm{i},\mathrm{j}}^2\left(t\right)-L_0\right]}^{+}+{\left[L_{\mathrm{i},\mathrm{j}}^3\left(t\right)-L_0\right]}^{+}+{\left[L_{\mathrm{i},\mathrm{j}}^4\left(t\right)-L_1\right]}^{+}$. The function ${\left[x\right]}^{+}$ is defined as $\mathit{max}\left(x,0\right)$, and $L_{\mathrm{i},\mathrm{j}}^K$ indicates visual motion in the cardinal direction K (see STAR Methods for detailed parameter definition). Repeating the above simulations, we found that the LPLC2 unit O responded to nearly all of the stimuli, including wide-field grating motion and unidirectional motion of a bar or edge (Figure 2A, third row). The results were qualitatively unchanged if the stimuli were replaced by motion-defined stimuli (Figure 2B, third row). These results indicate that nonlinear integration makes LPLC2 units selectively respond to radial expansion stimuli.

Looming features are extracted in the LPLC2 layer by a population coding strategy

Our simulations found that looming stimuli always induced population activity in the LPLC2 array, whose central unit O retinotopically pointed to the FOE (Figure 3A, panel A7). The activity spatial scope rapidly reached the boundary of an inner area within the RF of unit O, after which the activation began to retract and then vanished (see Video S1). The inner area was found to have a side length that is approximately half the side length of the RF. The underlying reason was that individual LPLC2 units were activated only if four arms of their RFs were simultaneously swept by expanding visual motion (Figure 3A). Even if three of the four arms of an RF were swept by expanding visual motion, the corresponding unit could not be activated (Figure 3A, panel A4).

Figure 3.

LPLC2 population coding

(A) Schematic of the activation state of representative LPLC2 units (A1‒A6) and the LPLC2 array (A7) under a looming stimulus. The black square denotes an instantaneous snapshot of the looming object projected on the modeled eye, whose FOE is marked by a red dot. Individual LPLC2 units (green dots at cross centers) were activated (yellow dot) only if their RFs (light green area in A1‒A6) were swept by expanding visual motion simultaneously in the four cardinal directions. Consequently, a population of LPLC2 units constrained only within a limited area (dotted boundary) could be activated (yellow dot and dark yellow dots) on the collision course of the looming object (A7) (see also Video S1). The limited area has a side length of half of the RF side. The RF of the center unit of the activated population is marked by the red boundary (A7).

(B) Number of instantaneously activated LPLC2 units (denoted as $N_{\text{act}}\left(t\right)$) induced by a looming stimulus with the L/v value indicated in the panel. Peak time is marked by the dashed line. On the x axis, $t=0$ represents the time of expected collision when the looming size reaches 180° and $t<0$ before collision.

(C and D) Temporal characteristics of the angular size subtended by the looming object and the GF firing under different L/v conditions. The looming size was separately measured by plane angle (C) and solid angle (D). The black and blue solid circles show the first spike time and the peak response time of the GF unit, respectively. The L/v value of the stimulus was systematically varied as specified in the panel.

(E) The number $N_{act}\left(t\right)$ of instantaneously activated LPLC2 units versus time under each stimulus given in (C).

(F and G) Same data as in (E) except for being replotted to display a relationship between $N_{act}\left(t\right)$ and looming size. $N_{act}\left(t\right)$ is more linearly correlated with the solid angle (G), although $N_{act}\left(t\right)$ is also positively correlated with the plane angle (F).

Video S1. LPLC2 array activity induced by a looming stimulus, related to Figure 3A

The stimulus is a dark looming square on a white background with L/v = 150 ms (left panel). The looming stimulus induced spreading activation in the LPLC2 array, whose center was retinotopically aligned with the focus of expanding optic flow (right panel). The spreading activation (yellow) rapidly reached the boundary of an inner area (red inner boundary) within the RF of the central LPLC2 unit (red outer boundary), after which the spreading activation began to retract and then vanished. The inner area had a side length that was approximately half of the side length of the RF. The video is shown at 0.5× actual speed.

We examined the number of instantaneously activated LPLC2 units (denoted as $N_{\text{act}}\left(t\right)$ below) in the population. The number showed a negatively skewed unimodal curve over time (Figure 3B). An obvious question to ask is whether the spatially limited population activity encoded approaching features of the looming object.

We created a set of looming stimuli, whose parameter L/v fell within the range [10 ms, 100 ms]. The looming object’s subtended angle, measured by both plane angle (Figure 3C) and solid angle (Figure 3D), rapidly increased with time on its collision course. By feeding each of the stimuli to the model, our simulations showed that within the rising part of the $N_{\text{act}}\left(t\right)$ curve, the number of instantaneously activated LPLC2 units increased with time in a trend similar to the looming size on visual inspection (Figure 3E vs. Figures 3C and 3D). The rising part of the unimodal curve shifted each other along the time axis in an L/v value-dependent way. The larger the L/v value was, the earlier the curve peak was.

We further plotted $N_{\text{act}}\left(t\right)$ against the looming size measured by plane angle (Figure 3F) and solid angle (Figure 3G). Both plots confirmed that within the rising part of the curves, the number of instantaneously activated LPLC2 units increased with the looming size across all the L/v values tested. Compared with the plane angle, the solid angle was almost perfectly linearly related to $N_{\text{act}}\left(t\right)$, especially for $N_{\text{act}}\left(t\right)<\mathrm{1,000}$. In summary, these results indicate that the looming size was well extracted by the LPLC2 units in a population coding strategy.

The giant fiber unit normalizes various looming stimuli into its firing response occurring at a consistent angular-size threshold

Driven by presynaptic LPLC2 units, the GF unit was depolarized to spike firing during looming, as illustrated by an example in Figure 4A. To examine the relationship between the GF peak responses and approaching kinematics, we plotted the GF peak firing rate (Figure 4B, blue dots), the corresponding peak time (Figure 4C, blue dots), and peak looming size (Figure 4D, blue dots) against the L/v value. The results showed that the GF peak firing rate monotonically decreased with the L/v value except for an abnormal elevation at medium L/v (50−60 ms). The peak firing time was almost linearly related to the L/v ratio and corresponded to a particular looming size. In other words, the GF peak firing occurred at a consistent angular-size threshold that was independent of the L/v value. The specific angular-size threshold was consistently at approximately θ_peak = 55° across all the L/v values tested.

The linear dependence of the GF peak firing time on the L/v ratio (Figure 4C, blue dots) is qualitatively consistent with the linear relationship between the latency of the GF peak response and L/v (e.g., Figure 8B (black squares) in von Reyn et al.²²). Except for the peak time, a direct comparison of the GF unit’s spiking in our model (e.g., the example in Figure 4A) with the GF response data is irrational. This is because looming stimuli usually induced a gradual GF depolarization but not GF spikes in most flies.^21,22 The GF response under the condition of LC4 silencing should be, however, comparable to the number of instantaneously activated LPLC2 units $N_{\text{act}}\left(t\right)$ in our model, because the remaining GF responses after LC4 silencing derive from LPLC2 input.¹⁹ The unimodal curve $N_{\text{act}}\left(t\right)$ in our model (e.g., Figure 3B) is qualitatively consistent with the non-LC4 component of the GF response (red curves in Figure 7A in von Reyn et al.²²). The rising part of the $N_{\text{act}}\left(t\right)$ curve vs. the looming object’s subtended angle in our model (Figure 3F) is qualitatively consistent with the rising part of the non-LC4 component of the GF response plotted with respect to the instantaneous angular size (Figure 7C in von Reyn et al.²²). These aligned properties of our results with the observation of looming responses of the GF cell indicate that our model qualitatively mimics the LPLC2−GF circuit at the algorithmic level. Meanwhile, the properties (such as the consistent angular-size threshold that was independent of the L/v value) are also consistent with findings in locust¹⁶ and zebrafish larvae,⁵ indicating that different animal species share a similar neural mechanism.

Figure 8.

Obstacle detection and avoidance facing real-world objects

(A) Scene arrangement in the test arena (10 × 10 m) taken from two different viewpoints. Around the robot (marked by the blue boundary), four objects were placed: two fire hydrants, a postbox, and a cabinet. A spotlight source is placed over the ground center.

(B) Trajectories of the robot moving through the arena. Different trials were color-coded, each of which lasted 5 min. The robot successfully avoided the obstacles (black spots) most of the time. A few collision events (red circles) were mainly caused by uneven illumination.

(C and D) Contrast effect on obstacle detection. The robot performed successful collision avoidance when approaching the rear of the golden cabinet (D), but it failed to avoid the same object when approaching from the opposite side (C). Compared with the former case (D, inset), the cabinet in the latter case (C, inset) was too weak to be discriminated from its background. One snapshot of the robot’s field of view is displayed in the inset, in which the cabinet is marked by the yellow rectangle.

Figure 7.

Obstacle detection and avoidance in cluttered environments

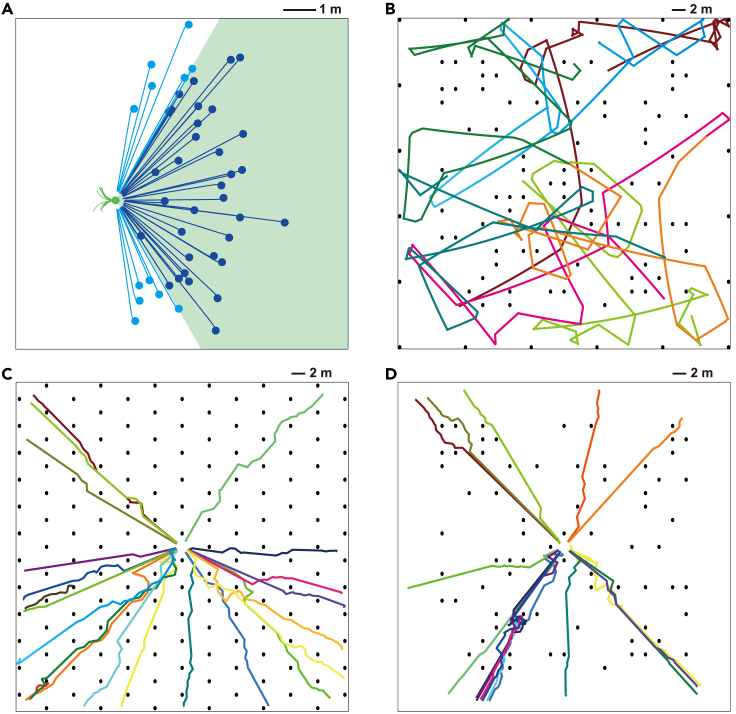
(A) Detection Scope. Robot 1 (green filled circle) was equipped with the model and kept stationary except for avoiding an obstacle (green curves: avoiding trajectories). Robot 2 without the model was moving toward robot 1 from various starting positions at a constant speed within a range of 0.1-0.9 m/s (light and dark blue filled circles and lines). Robot 1 successfully avoided robot 2 as long as robot 2 was within its 120-degree field of view (green area).

(B) Trajectories of a robot moving around obstacles. Ninety-two black cylinders with a diameter and height of 0.5 m were randomly arranged in the arena as obstacles with a minimum distance of 2 m (black spots). The robot has a size of 0.25 × 0.25 × 0.25 m. The trajectories with different starting positions are color-coded.

(C and D) The same as (B) except that a goal location was set for the robot. The goal location is a 2 × 2 m region around the area center. Cylinder obstacles were either regularly arranged (C, 162 obstacles with a minimum distance of 4 m) or randomly placed (D, 72 obstacles with a minimum distance of 2 m).

An important question is whether the angular-size threshold is totally determined by the $N_{\text{act}}\left(t\right)$ input. We then calculated the coefficient of variation (CV) of two samples: the looming size when $N_{\text{act}}\left(t\right)$ peaked (Figure 4D, green triangles) and the looming size when the GF peak firing occurred (Figure 4D, blue dots). The analysis showed that the CV of the looming size corresponding to the $N_{\text{act}}\left(t\right)$ peaks was approximately 3 times as large as that of the looming size corresponding to the GF peak firing (the numbers in Figure 4D). The results indicate that the looming velocity input ($\Delta N_{\mathrm{a}\mathrm{c}\mathrm{t}}\left(t\right)/\Delta \mathrm{t}$ in Equation 7) makes an indispensable contribution to making the angular-size threshold consistent across various L/v values, especially at small L/v (fast looms), although the $N_{\text{act}}\left(t\right)$ input plays an essential role in the emergence of the angular-size threshold.

Since a neuron’s first spike represents a significant increase in the degree of its depolarization, we thus checked how the first spike changes with the L/v value. The simultaneously recorded data showed that the GF firing rate around its first spike monotonically decreased with the L/v value (Figure 4B, black dots). The first spike time of the GF unit was linearly related to the L/v ratio as was its peak firing time (Figure 4C, black dots). The first spike also occurred at a consistent angular-size threshold θ_first-spike = 34° which was independent of the L/v value (Figure 4D, black dots). Considering that the GF first spike provided an earlier time for looming detection than its peak firing (black versus blue dots in Figures 3C, 3D, and 4C), we chose the former rather than the latter as the avoidance time in virtual robot simulations below.

By further changing the RF of the LPLC2 units, our simulations showed that the peak time of the $N_{\text{act}}\left(t\right)$ curve was determined by the RF size (Figure 4E, dashed lines). The smaller the RF is, the earlier the $N_{\text{act}}\left(t\right)$ peak is, and the smaller the angular-size thresholds (θ_first-spike and θ_peak) should be. The RF was set as a cross in a square of 100 × 100 pixels (i.e., 80°×80°) in our simulations, unless otherwise specified. This RF size is larger than the real size of 60°×60° measured in LPLC2 neurons,²⁰ which was chosen to ensure a reasonable θ_first-spike in our model. The curves of a looming object’s subtended angular size versus time could be split into three phases: early, middle, and late (Figures 3C and 3D). Compared with the other two, the middle phase, approximately falling within 20°−50°, shows the largest sensitivity to different L/v conditions on visual inspection. The θ_first-spike = 34° (Figure 3C, black dots) fell within the phase having the largest sensitivity.

To examine whether a multiplicative integration of looming size and velocity in the GF unit is critical for its firing properties above, we replaced the multiplicative operation in Equation 7 by a summation operation. Repeating the above simulations, the results showed that the GF firing properties were qualitatively the same as those obtained above (Figures 4B′, 4C′, 4D′), indicating that the emergence of the angular-size thresholds was not affected by the specific integration operation of looming size and velocity in the GF unit.

Taken together, the postsynaptic GF unit normalized the approaching kinematics with various L/v values into its first spike firing or its peak firing that occurred at a consistent angular-size threshold, to which not only the looming size but also the looming velocity played an indispensable role.

Looming detection under moving background conditions

All looming stimuli in the above simulations feature a static background. It is necessary to ask whether the model works when the background is not stationary as in the real-world. To this end, either a translational natural scene (Figure 5A) or a scene captured by a driving recorder mounted on a vehicle moving forward³⁵ (Figure 5B) was used as a background. By superimposing a dark or bright looming square with various L/v values upon each of these backgrounds, we synthesized image sequences or Video clips as new stimuli (see Videos S2 and S3).

Figure 5.

Looming detection by the model is robust to moving background and object texture

(A) The simulated membrane potential of the GF unit (second and fourth col.) on a direct collision course of a dark (first col.) or bright (third col.) looming square. The background of the stimulus was moving leftwards at a constant speed of 1200 pixels per second (see Video S2). The frame images were preprocessed to a size of $N\times M=400\times 300$ pixels by downsampling. Representative frames at the time stamp marked are displayed, at the top of which the corresponding L/v value is specified.

(B) The simulated membrane potential of the GF unit (second and fourth col.) on a direct collision course of a dark (first col.) or bright (third col.) looming square. The expanding background Video was taken by a driving recorder mounted on a vehicle moving forward³⁵ (see Video S3).

(C) The simulated membrane potential of the GF unit (second and fourth col.) on a direct collision (first col.) or receding (third col.) course of a textured square consisting of randomly distributed black and white dots. The background is the same as used in (A) except that its speed is 1,440 pixels per second (see Video S4). The GF unit remained silent during the receding course as predicted by the model.

Video S2. Visual stimulus, related to Figure 5A

Each image sequence was synthesized by superimposing a dark (left panel) or bright (right panel) looming square (L/v = 50 ms) upon a leftward translating natural scene. The video is shown at 0.5× actual speed.

Video S3. Visual stimulus, related to Figure 5B

Each image sequence was synthesized by superimposing a dark (left panel) or bright (right panel) looming square (L/v = 50 ms) upon an expanding background scene. The video is shown at 0.5× actual speed. The background scene was taken by a driving recorder mounted on a vehicle moving forward³⁵.

By presenting the synthetic stimuli to the model one by one, our simulations show that for nearly all of the stimuli tested, the looming object was successfully detected, which was indicated by the appearance of spike firing in the GF unit (Figures 5A and 5B). Even if the background was slowly expanding, the model capably detected the looming foreground object (Figure 5B). A few exceptions occurred for the stimuli that were not only very fast but also had a low contrast, such as the case with a dark looming object with L/v = 5 ms in Figure 5A.

Does the model only detect objects with a solid texture from a moving natural scene? We next created a textured looming square consisting of randomly distributed black and white dots. By superimposing the square with various L/v values upon a translational natural scene, we synthesized a set of new stimuli (e.g., Video S4, the left side of the screen). By presenting the synthetic stimuli to the model one by one, our simulations show that the textured object was successfully detected in most cases, except for the condition of very fast looming stimuli (Figure 5C, fourth row in the left half). To further confirm that the model output should remain silent when facing a receding textured object, we replaced the textured square by the same but receding one in each of the stimuli above (e.g., Video S4, the right side of the screen). The repeated simulations show that the LPLC2 units did not respond to the receding textured object as expected, which was indicated by the inactivated or silent GF unit (Figure 5C, the right half).

Video S4. Visual stimulus, related to Figure 5C

Each image sequence was synthesized by superimposing a looming (left panel) or receding (right panel) square (L/v = ±50 ms) upon a leftward translating natural scene. The textured square consists of randomly distributed black and white dots. The video is shown at 0.5× actual speed.

In short, the model is qualified for detecting a looming object from a moving natural scene background.

Collision avoidance in a virtual robot based on estimated visual motion

Compared with the open-loop conditions above, looming detection is much more challenging in real physical scenes because of a critical requirement for collision avoidance. Collision avoidance actions bring a rapid and sudden change in visual inputs to the agent, making real-time looming detection harder. By equipping TurtleBot 3.0 robots with the model (see STAR Methods), we investigated whether the model could be an efficient algorithm for real-time collision avoidance.

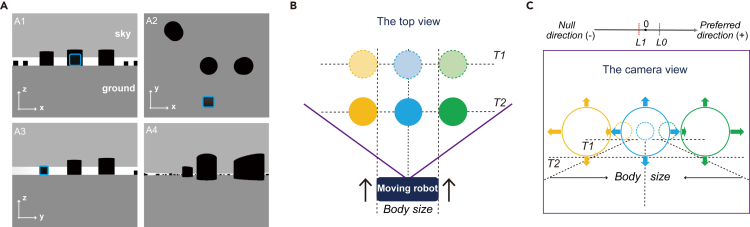
The robot saw surrounding obstacles within its 120-degree field of view through a camera mounted on it (Figure 6A). We first take an example of the robot that kept moving straight ahead toward three stationary obstacles (Figures 6B and 6C). In addition to obstacles straight ahead (blue object in Figures 6B and 6C), objects on front-left or front-right, which induce optic flow expanding in three cardinal directions but slightly contracting in the fourth cardinal direction (orange and green objects in Figures 6B and 6C), probably collided with the moving robot. This is because the robot is not an ideal mass point but has a definite body size. To solve the problem, we proposed that the parameter $L_1$ in the state function of LPLC2 units should be negative (Equation 5), whose specific value should depend on the robot’s body size and moving speed (Figure 6C). In our simulations with constant robot speed and body size below, the values of parameters $L_1$ and $L_0$ were kept unchanged (Table 1). Therefore, in closed-loop conditions, the model operated in the same way as in open-loop conditions except for a two-step flow detection. First, the LPLC2 layer kept detecting a flow pattern that expanded simultaneously in any three cardinal directions. Once such a flow pattern was caught, the layer then checked whether the pattern satisfied the condition ${\left[L_{\mathrm{i},\mathrm{j}}^4\left(t\right)-L_1\right]}^{+}>0$ in another cardinal direction (Equation 5).

Figure 6.

Closed-loop tests by applying the model to a virtual robot

(A) Simulation arena viewed separately from the positive y axis (A1), negative z axis (A2), negative x axis (A3), and from a camera mounted on the robot (A4). The robot (marked by a blue boundary) saw its environment (A4) by receiving a real-time Video stream from the camera. Frame images were preprocessed to $N\times M=300\times 250$ pixels by downsampling. Randomly placed cylindrical objects were used as obstacles.

(B) Top view of three stationary obstacles (orange, blue, and green circles) experienced by the moving robot (arrows: moving direction). The obstacles were arranged along a line (horizontal dashed lines) perpendicular to the robot’s heading direction (vertical dashed lines). The obstacles at time T2 (solid circles) were nearer to the robot than at an earlier time T1 (dashed circles). Vertical lines illustrate that the robot will be next to but not touch the orange and green objects.

(C) The same scene as that in (B) except that the view is from the robot camera itself. From the robot’s field of view (purple boundary), the obstacle sizes changed from small (dashed circles) at time T1 to large (solid circles) at time T2. If the robot was a mass point, only the blue object that induced expanding optic flow in all four cardinal directions (blue arrows) was detected as a looming object. However, it had a definite body size and thus would probably collide with the orange and green objects. The threshold $L_1$ in Equation 5 should be tuned as negative (top), so that the model can detect obstacles whose optic flow amplitudes are larger than $L_0$ in three cardinal directions and simultaneously larger than $L_1$ in another direction.

Table 1.

Parameter values for the model

Parameter	Value
${\mathit{L}}_{\mathbf{0}}$a	$2$
${\mathit{L}}_{\mathbf{0}}$b	$1.5$
${\mathit{L}}_{\mathbf{1}}$a	$2$
${\mathit{L}}_{\mathbf{1}}$b	$-2$
RF (in pixels)	40 × 40∼100 × 100
w	5∼250
τ(ms)	30∼300
${\mathit{E}}_{\text{leak}}\left(\text{mV}\right)$	$-60$
${\mathit{V}}_{\text{th}}\left(\text{mV}\right)$	$-50$
${\mathit{V}}_{\text{re}}\left(\text{mV}\right)$	$-70$

^aUsed for open-loop simulations except for those with real-world looming animals.

^bUsed for both closed-loop simulations on virtual robots and open-loop simulations with real-world looming animals.

Once an obstacle was detected, the model triggered a control module by giving the robot an avoidance command with two messages. One was the avoidance time signaled by the first spike timing of the GF unit. The other was the direction of impending collision, which was signaled by the relative location of the center of the activated LPLC2 population. If the center unit was located at the left side of the LPLC2 array, the robot should turn right to avoid the obstacle and vice versa.

We then checked the visual field scope of obstacle detection by using two robots. The simulation experiment was designed to make robot 2 (without the model) move straight toward stationary robot 1 (equipped with the model) at a constant speed. By testing various starting positions of robot 2, the simulation results found that robot 1 successfully avoided approaching robot 2 as long as robot 2 did not exceed the 120-degree field of view of robot 1 (Figure 7A).

We next examined the model’s performance in a moving robot through a cluttered environment. One hundred cylindrical objects were randomly placed within a $50\times 50\mathrm{m}$ square arena as obstacles (Figure 7B). The robot started from a randomly given position and did not change the moving direction except when necessary to avoid an obstacle. Simulation results found that the robot performed collision avoidance very well in most cases, irrespective of the starting condition (Figure 7B), which was considered a high success rate (Table 2). The success rate is defined as $N_a/\left(N_a+N_m\right)$, where $N_a$ is the collision avoidance time and $N_m$ is the miss detection time.

Table 2.

Success rate of a moving robot without a goal direction

Collision avoidance task	Avoidance times (Na)	Miss times (Nm)	Success rate
Figure 7B	99	2	98.0%
Figure 8B	41	4	91.1%

Since the only purpose was to avoid collisions, the robot tended to stay in a relatively small area. To ensure that the robot travels through the environment, we set a goal location. Collision avoidance tasks during goal-directed traveling are more general in application. In each trial, the robot kept moving in a straight line toward the goal unless an obstacle was detected. After each collision avoidance action, the robot decided a goal-constrained movement direction. Simulation results found that the robot traveled through obstacles and reached the goal location with a high success rate, regardless of how these obstacles were distributed (Figures 7C and 7D) (Table 3). The success rate for the goal-directed tasks was defined as $N_s/\left(N_s+N_f\right)$, where $N_s$ is the number of times the robot successfully reached the goal and $N_f$ the number of times the robot failed to reach the goal.

Table 3.

Success rate of a moving robot with a goal direction

Collision avoidance task	Success times (Ns)	Failure times (Nf)	Success rate
Figure 7C	20	2	90.9%
Figure 7D	16	1	94.1%

Last, we examined the model’s performance when facing obstacles more like real-world objects. Different from the black cylinders used above, four virtual obstacles mimicking real objects were disposed within a 10 × 10 m square arena (Figure 8A). A light above the arena center provided ample illumination. The scene contrast varied between the objects and even between different views of the same individual objects, causing the measurement efficiency of visual motion by the model to vary across the arena. Simulation results found that although a failure occurred in rare cases, the moving robot successfully avoided collisions most of the time (Figure 8B) (Table 2). The failure was mainly because the contrast of the front of an obstacle was too weak to be distinguished by the robot from that of its surrounding background (Figure 8C). In contrast, a successful collision avoidance was performed once the robot approached the rear of the same obstacle where the contrast was higher than that of its front surface (Figure 8D).

In summary, the tests show that the model is a robust and efficient algorithm for real-time collision avoidance that relies only on visual motion measured by an EMD array. Adjustable parameters of visual motion detection make the model adaptable to various robot speeds and body sizes.

Looming detection is robust to real-world objects

Looming objects used in the above open- and closed-loop simulations are not real-world objects. Real-world objects vary in features such as shape, texture, contrast, and luminance, just like those experienced by prey organisms. An obvious question to ask is whether the model works with real-world looming objects. To this end, we next tested the model on Videos taken in various real-world scenes, in each of which an animal was flying or running toward frame.

By presenting each of the Videos (see Videos S5, S6, S7, S8, S9, and S10) to the model, the simulations show that the looming animals were successfully detected (black curves in Figures 9B, 9C, 9D, 9E, 9F, and 9G) provided that the threshold parameter L₁ in Equation 5 was set as L₁ < 0 (see Table 1 for parameter values). Our simulations under the condition of L₁ > 0 (see Table 1 for the values of parameters with superscript “a”) show that the model was not able to guarantee a successful detection of looming animals, as shown by the red curves in Figures 9B, 9C, 9D, 9E, 9F, and 9G, indicating the significance of the setting of L₁ parameter. This is because the approaching animal was usually not flying or running straight toward camera. The animal thus induced visual motion patterns that expanded in three directions {1, 2, 3} but expanded more weakly or even contracted slightly in another direction {4}. For example, the cat during the time interval between two representative frames induced a visual motion pattern that slightly contracted in the leftward direction but expanded in the other three directions (left, Figure 9A; middle, Figure 9A). Similarly, another looming animal induced a visual motion pattern that expanded more weakly in the upward direction than in the other three directions (right, Figure 9A). To ensure a successful detection of approaching animals with a small deviation angle relative to the camera, the model must relax the detection range in one cardinal direction. Therefore, when facing these real-world looming objects, the model took a two-step detection in the same manner as described under closed-loop conditions. First, the LPLC2 layer kept detecting a flow pattern that expanded simultaneously in any three cardinal directions. Once such a flow pattern was caught, the layer then checked whether the pattern satisfied the condition ${\left[L_{\mathrm{i},\mathrm{j}}^4\left(t\right)-L_1\right]}^{+}>0$ in another cardinal direction (Equation 5).

Figure 9.

Looming detection is robust to real-world objects taken in various real-world scenes

(A) Schematic of a change in the area occupied by a looming animal in the visual field. Three pairs of frames on the left, middle, and right side were taken from Videos S5, S6, and S9, respectively. For each pair, the looming animal in the later frame (outlined by the green boundary) was nearer to the camera than in the earlier frame (outlined by the red boundary). During the time interval between the two frames, the animal induced a visual motion pattern that expanded strongly in three directions (three arrows) but either expanded more weakly (right) or contracted slightly (left; middle) in another direction.

(B) The simulated membrane potential of the GF unit on a direct collision course of the looming animal in Video S5. Representative frames at the time stamp marked are displayed at the top. There are two steps of input preprocessing. First, the Video frames in color were converted to grayscale. Second, the size of the grayscale images was reduced to 25 percent of the original images by downsampling. The preprocessed frames were then fed to the EMD array consisting of N × M units, whose resolution matched the size of the preprocessed frames. Since the time step of the EMD array is 10 ms, the Video presented to the model was equivalently speeded up from 30 frames per second (fps) to 100 fps, as shown in the horizontal x axis.

(C, D, E, F, and G) Same as (B) except that the visual input to the model was replaced by Videos S6, S7, S8, S9, and S10, respectively.

Video S5. Visual stimuli, related to Figures 9A (left) and 9B

The video was taken and provided by Xiaodan Zhang. The video is shown at 3.3× actual speed.

Video S6. Visual stimuli, related to Figures 9A (middle) and 9C

The video was taken and provided by Daniel Ocean. The video is shown at 3.3× actual speed.

Video S7. Visual stimuli, related to Figure 9D

The video was taken and provided by Meikun. The video is shown at 3.3× actual speed.

Video S8. Visual stimuli, related to Figure 9E

The video was taken and provided by Qiyue Jiang. The video is shown at 3.3× actual speed.

Video S9. Visual stimuli, related to Figures 9A (right) and Figure 9F

The video was taken and provided by Qiyue Jiang. The video is shown at 3.3× actual speed.

Video S10. Visual stimuli, related to Figure 9G

The video was taken and provided by Xiaodan Zhang. The video is shown at 3.3× actual speed.

Our results with the setting of L₁ < 0 predicts that an individual LPLC2 neuron is able to be activated when the expandance strength of the visual motion pattern within its four-layered RF is not uniform across four cardinal directions, even if the pattern is slightly contracting in one of the four directions. To the best of our knowledge, existing experimental recordings on LPLC2 cells were not performed under the condition of stimuli charactering the real-world looming objects (e.g., Klapoetke et al.²⁰). Future studies, especially using electrophysiological approaches, are expected to test the prediction by designing such stimuli.

In summary, the model is robust and efficient for detecting looming animals in Videos taken in real-world scenes.

Discussion

Testable predictions

Previous studies have shown that it is an angular-size threshold reached by the looming stimulus on the retina but not a fixed time before collision with the approaching object that determines the initiation of looming-mediated escape behaviors in animals including locusts,¹⁶ zebrafish⁵ and flies.^19,22 Although types of angular-size threshold detectors (a neuron or population of neurons) have been identified, the circuit mechanism for the emergence of such an angular size threshold is still unclear. A prediction of the model is that the threshold angular-size is determined by the RF size of neurons upstream of the angular-size threshold detectors. The prediction suggests that the angular-size threshold, which initiates the rapid escape behaviors in flies,^19,22 should be determined by the RF size of LPLC2 neurons.

LPLC2 and LC4 visual projection neurons provide the GF descending neuron with two types of information about a looming object: its subtended angular size and its angular velocity.^19,22 How the information is specifically encoded still remains elusive. The model did not explicitly include LC4 units. Our simulations demonstrated that the looming velocity, inferred from the temporally dynamic change of the instantaneous number of activated LPLC2 population (Equation 9 in STAR Methods), ensured the model a looming detection. We thus speculate that LC4 neurons might extract the looming velocity from two input sources: the motion pathway via the direct postsynaptic projections from LPLC2 onto LC4 neurons¹⁹ and another unidentified non-LPLC2 pathway. The remaining velocity tuning of the GF neuron in LPLC2-silenced flies¹⁹ might originate from the non-LPLC2 pathway, which might primarily depends on luminance and contrast. Future investigations are expected to provide insights into the neural computation underlying the encoding of looming velocity.

Comparison with previous bioinspired models

To solve collision avoidance, an elegant model sought to extract a relative nearness map from visual motion, i.e., the relative distance of an agent to objects in the surrounding environment.³⁶ The challenging extraction was achievable provided that the agent was confined to move in a plane and the eye of the agent was spherical. Our model seeks to extract expanding visual motion and is thus insensitive to the conditions. The nearness map must cover the visual field. Therefore, their model requires strongly textured images as inputs, and the FOE of the optic flow field must be dealt with separately as a singular point. By contrast, our model readily detects a uniform looming object whose surface lacks optic flow, during which the FOE is naturally detected as the location of impending collision. Both models were established upon EMD-based visual motion measurement. The essential difference between two models can be attributed to the fact that our model is further inspired by the fly LPLC2‒GF pathway that is downstream of the EMD circuit.

Another type of looming detection models is inspired by the lobula giant motion detectors (LGMDs) of locusts.^15,18,37 The wide-field neurons LGMD1¹⁰ and LGMD2¹³ have no directionally selective inputs. Their motion sensitivity is derived from luminance temporal changes integrated by their giant dendritic arbor. This characteristic makes LGMD-inspired models respond not only to looming stimuli but also to receding and translating stimuli, which are different from our model that does not respond to non-looming stimuli. These models include various improvement mechanisms, such as parameter optimization, to increase their selectivity to looming stimuli.^18,37

Different from most LGMD-inspired models, the connectionist model proposed by Bermúdez i Badia et al.¹⁵ can identify the direction of an impending collision at the LGMD’s presynaptic layer, i.e., the second chiasma. Their model did not explicitly include any local motion detectors, but the pairwise combination of ON and OFF cells in the medulla layer actually detected visual motion. Leaving aside the different visual systems on which the two models are based, their model exhibits similar characteristics to ours from an computational point of view. Their second chiasma layer (i.e., the LGMD presynaptic fan-in) and the LGMD neuron unit computationally corresponds to our LPLC2 layer and GF unit, respectively. In addition, similar to the dependence of the angular-size threshold on the RF of the LPLC2 units in our model, the larger the RF of projection neurons in the second chiasma layer was, the larger the angular-size threshold was in their model. However, their model did not address how the individual projection neurons integrated the oriented contrast boundaries or directional visual moion in the four cardinal directions. Therefore, it is unclear whether the model proposed by Bermúdez i Badia et al.¹⁵ could completely suppress the responses to non-looming stimuli such as translating stimuli.

A recent study trained a two-layer network to detect impending collision objects.³⁸ Similar to our model, the first and second layer of their network mimicked an EMD array and a LPLC2 population, respectively. Unlike our model, the receptive field (i.e., its four spatial filters) of their individual LPLC2 units was not predefined but determined by a training procedure using artificial visual stimuli. Both their model and ours support that LPLC2 neurons employ a population strategy to ensure an efficient detection of impending collision. However, their model suggests that individual LPLC2 neurons additively integrate visual motion flow expanding in the four cardinal directions, whereas ours argues for multiplicative integration. Future studies, especially using electrophysiological approaches, are expected to provide new insight into the integration property across LPLC2 dendrites.

Comparison with optic flow-based algorithms

Optic flow-based algorithms for collision detection feature lightweight and low-cost sensors such as single cameras, making them advantageous in applications where constraints in weight and computational power are important.³⁹ A typical algorithm measures flow field divergence at the image center (assumed to be the FOE) and then acquires an estimation of the time-to-contact (TTC).^40,41,42 TTC is the time it would take an agent to make contact with a surrounding obstacle if the agent’s velocity is maintained constant. Positive flow divergence indicates the presence of potential obstacles with a TTC inversely proportional to the divergence magnitude.

Measuring flow divergence is equivalent to extracting expansive visual motion in our model, but the two algorithms are essentially different in the implementation method (Figure 10). The flow divergence algorithm calculates the sum of partial spatial derivatives of optic flow components in orthogonal directions, whereas our model argues for a multiplication integration of visual motion across the four cardinal directions. Moreover, the flow divergence algorithm relies entirely on the FOE’s divergence, whereas our model lets LPLC2 neurons around the FOE make a collective voting. The RF of LPLC2 neurons naturally determines an RF-dependent peak firing in the GF unit for signaling the anticipated timing of impending collisions in our model, whereas the flow divergence is continuously increasing on the collision course of the looming object. Finally, the flow divergence algorithm measures only instantaneous divergence values, whereas our model utilizes the GF unit to accumulate the looming confidence over time up to a firing threshold.

Figure 10.

Comparison between the flow divergence algorithm and the fly inspired model

Schematic of the flow divergence algorithm (A) and the fly inspired Model (B) for collision detection. Their differences are reflected in the 3 steps. Step 1: Gradient-based methods for measuring optic flow (A) vs. the EMD method for analyzing visual motion (B). Step 2: a summation of partial spatial derivatives of optic flow components in orthogonal directions (A, “+” sign) vs. a multiplication integration of visual motion across the four cardinal directions (B, “o” signs); relying on the FOE’s flow divergence alone (A, concentric circles) vs. adopting a distributed coding strategy (B, green cross symbols). Step 3: Transforming an instantaneous measurement of flow divergence into a TTC value (A) vs. accumulating the looming confidence over time up to a firing threshold by the GF unit (B). The gray shadow in (A) and (B) represents the pathway activated by a looming stimulus.

The flow divergence algorithm relies considerably on rich texture information and is susceptible to optic flow noise. To make an accurate TTC estimation, the flow divergence algorithm was improved by introducing either an extra stabilization mechanism to keep the FOE aligned with the camera’s optic axis⁴¹ or an extra temporal module to integrate the confidence of a TTC estimation over time.⁴⁰ This is in contrast to our model, which is robust even when facing textureless looming obstacles. On the other hand, the shortcoming of our model is its inability to detect a textureless looming object once its angular size on the modeled eye exceeds the RF of LPLC2 units. Therefore, our model is more applicable for detecting objects approaching from a distance, even if the objects are textureless.

Correlation-type EMDs are generally adopted by biological vision for visual motion measurement and have a much lower computational complexity than computer vision methods such as gradient-based algorithms.²³ However, EMDs are seldom used in real-time applications because of their well-known sensitivity to nonmotion-related factors such as luminance contrast and texture properties. Our model proposes a fly inspired solution to cope with EMD sensitivity in looming detection, thus shedding light on real-time applications of EMDs.

Limitations of the study

As a first limitation, the model cannot quantitatively reproduce the physiological response properties of individual LPLC2 neurons under some specially laboratory-designed stimuli. For instance, one-dimensional narrow bar expanding toward two but not four cardinal directions (at the top of Figure 3E in Klapoetke et al.²⁰) is a laboratory-designed stimulus, which is different from the real profile of an object’s subtended angle during looming in the physical world. Under this stimulus condition, the response strength of our LPLC2 model units will depend on the bar expansion direction. By contrast, the observed LPLC2’s responses were nearly uniform across all the expansion directions (at the top of Figure 3E in Klapoetke et al.²⁰). In another instance, the response strength of our LPLC2 model units will not be strongly affected by tangential motion at the periphery of the LPLC2’s RF. On the contrary, the observed LPLC2’s responses were significantly inhibited by the presence of tangential motion at RF edges (Figures 4G, 4C and 4D in Klapoetke et al.²⁰). The discrepancy between the model and experimental recordings at the level of individual LPLC2 neurons suggests that for each of the four sub-RFs, visual motion inducing directionally selective inhibition to the LPLC2 is not restricted to the null direction of the corresponding sub-RF. Other visual motion orthogonal to the sub-RF’s null direction may induce inhibitory input to the LPLC2, too. A surrounding inhibitory region at the boundaries of the four-layered RF of individual LPLC2 units, which was not considered in our model, should play a role in the observed LPLC2’s responses to the specially designed stimuli. Predefining the detailed structure or the fine spatiotemporal characteristics of the hypothesized RF, however, is a daunting task. Training the model network using the specially designed stimuli, in a manner similar to that adopted by Zhou et al.,³⁸ could be helpful for determining the hypothesized RF. Future investigations are expected to provide insights into the additional mechanisms involved in the visual feature processing of LPLC2.

As a second limitation, we used a planar screen as the modeled eye for simplicity (Figure 2C), whose field of view was smaller than that of the hemispherical compound eyes of the fly. The planar screen introduced spatial distortions in the peripheral field of view. This can be illustrated by the example of distorted cylindrical objects shown in Figure 6A4, which were saw by the planar camera of the virtual robot . The distortions could make the model have different optimal parameter values between the central and peripheral field of view. Therefore, it is the spherical but not planar array of visual sensors that can take full advantage of the model algorithm.

Finally, we did not test the model under high-speed collision conditions due to the limitations of our existing software and hardware resources. The current study mainly focuses on establishing the fly inspired algorithm and demonstrating its effectiveness and potential advantage in real-time scenarios. Future studies should exploit the speed advantage of the algorithm in real walking or flying robots by optimizing the algorithm and using airborne computer programs.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and algorithms
MATLAB 2019b	MathWorks	RRID: SCR_001622
Ubuntu 16.04 LTS	Canonical Ltd	https://ubuntu.com/
Robot Operating System (ROS)	Open Robotics	https://www.ros.org/
Gazebo	Open Robotics	https://www.ros.org/
Code	This paper	https://github.com/zhaojunyu01/EMD-LPLC2-GF-model.git
Deposited data
Data	This paper	https://github.com/zhaojunyu01/EMD-LPLC2-GF-model.git

Resource availability

Lead contact

Requests for further information regarding resources used in this study should be directed to the lead contact, Zhihua Wu (wuzh@shu.edu.cn).

Materials availability

This study did not generate new unique reagents.

Method details

Visual stimuli

Four types of stimuli were created for simulations. The resolution of each frame image is denoted as $N\times M$ pixels. Iuput images have the same size as the entire frame. The first type shares a static background and were used for simulations, the results of which are shown in Figures 2, 3, and 4. The input images were preprocessed to $N\times M=200\times 150$ pixels (i.e., 118^o⨯103^o) by downsampling. Except for the stimuli used in the 2nd–10th column of Figures 2A and 2B that had a constant edge speed, all the other stimuli in Figures 2, 3 and 4 mimicked a looming square object approaching the modeled eye with a constant velocity. We use the parameter L/v size-to-velocity ratio to characterize the looming object’s approaching kinematics.¹⁶ The object’s half-size is L, and its approaching velocity is v (Figure 2C). In the 2nd column of Figures 2A and 2B, the square expands from 6 × 6 pixels to 105 × 105 pixels, and all the cross arms of the stimuli in Figures 2A and 2B have a width of 30 pixels.

The second type of stimuli was created by superimposing a looming square upon a scene captured by a driving recorder mounted on a vehicle moving forward³⁵ or a translational natural scene. The input images were preprocessed to $N\times M=400\times 300$ pixels by downsampling and used for simulations, the results of which are shown in Figure 5. The third type of stimuli was a series of images captured by the camera of a virtual robot while moving within its surrounding environment. The input images were preprocessed to $N\times M=300\times 250$ pixels by downsampling and used for simulations, the results of which are shown in Figures 6, 7, and 8. The fourth type of stimuli was Videos S5, S6, S7, S8, S9, and S10. They were used as the visual input to the model for simulations, the results of which are shown in Figure 9. The six Videos were taken in various indoor and outdoor scenes.

EMD array

The EMD array was developed with each unit receiving two inputs separated in visual space. The array consists of $N\times M$ units, whose resolution matches the size of the input images. Individual EMD units comprise parallel ON and OFF detector subunits (Figure 1B), whose detailed structure and parameter values are in accordance with a previous work by Eichner et al.³¹ (see Figure 4A in Eichner et al.³¹). Significant progress has been made in models of the fly EMD over the past decade.^32,34 Our EMD model does not include the DC components of the Eichner model,³¹ which has no longer been justified by the progress. Visual inputs were first processed by a first-order high-pass filter with time constant τ_HP = 250 ms. The filtered components were fed into two parallel half-wave rectifiers, one forming the ON pathway and the other the OFF pathway. The cutoff for ON and OFF rectifiers was set at zero and 0.05, respectively. First-order low-pass filters with τ_LP = 50 ms were used in both ON and OFF subunits. The two mirror-symmetrical half-detectors of each horizontal full EMD units were modeled to detect rightward and leftward motion, respectively. The two mirror-symmetrical half-detectors of each vertical full EMD units were modeled to detect downward and upward motion, respectively.

To further simplify the problem, outputs of the two EMD arrays in the ON and OFF pathways were retinotopically added to give the final output of the ON+OFF EMD array. The rightward and leftward motion components detected by the ON+OFF EMD array are denoted as matrices $H_{\mathrm{i},\mathrm{j}}^r\left(t\right)$ and $H_{\mathrm{i},\mathrm{j}}^l\left(t\right)$, respectively. The downward and upward motion components detected by the ON+OFF EMD array are denoted as matrices $V_{\mathrm{i},\mathrm{j}}^d\left(t\right)$ and $V_{\mathrm{i},\mathrm{j}}^u\left(t\right)$, respectively. The four visual motion patterns were then projected to the LPLC2 layer (Figure 1), mimicking the four-layered projection from T4/T5 cells to the four distinct fields formed by dendritic arbors of individual LPLC2 neurons in the lobula plate.²⁰

LPLC2 layer

The LPLC2 layer consists of $N\times M$ units. Each LPLC2 unit integrates inputs from the EMD array in its receptive field (RF) with a four-layered structure denoted as $K_{\mathrm{r}}$, $K_{\mathrm{l}}$, $K_{\mathrm{d}}$, and $K_{\mathrm{u}}$ (Figure 1C). The subscripts {r, l, d, u} denote rightward, leftward, downward, and upward, respectively. The RF is a cross in a square, and the arm width of the cross is one-third the length of the side of the square. The square was set as 100×100 pixels, i.e., 80^o×80^o, unless otherwise specified. The adjacent units have highly overlapping RFs. Four input matrices to the LPLC2 layer were specifically calculated as $\left\{H_{\mathrm{i},\mathrm{j}}^r\left(t\right)-H_{\mathrm{i},\mathrm{j}}^l\left(t\right)\right\}\text{,}$ $\left\{H_{\mathrm{i},\mathrm{j}}^l\left(t\right)-H_{\mathrm{i},\mathrm{j}}^r\left(t\right)\right\}$, $\left\{V_{\mathrm{i},\mathrm{j}}^d\left(t\right)-V_{\mathrm{i},\mathrm{j}}^u\left(t\right)\right\}$, and $\left\{V_{\mathrm{i},\mathrm{j}}^u\left(t\right)-V_{\mathrm{i},\mathrm{j}}^d\left(t\right)\right\}$ to simulate motion opponency induced by inhibitory inputs of lobula plate LPi interneurons in Drosophila.^20,43 By convolving each of the four matrices with an RF kernel in the corresponding directions, we obtained inputs to LPLC2 units denoted as $L_{\mathrm{i},\mathrm{j}}^{\mathrm{r}}\left(t\right)$, $L_{\mathrm{i},\mathrm{j}}^{\mathrm{l}}\left(t\right)$, $L_{\mathrm{i},\mathrm{j}}^{\mathrm{d}}\left(t\right)$, and $L_{\mathrm{i},\mathrm{j}}^{\mathrm{u}}\left(t\right)$.

$$L_{\mathrm{i},\mathrm{j}}^{\mathrm{r}}\left(t\right)=\left\{H_{\mathrm{i},\mathrm{j}}^r\left(t\right)-H_{\mathrm{i},\mathrm{j}}^l\left(t\right)\right\}\ast K_{\mathrm{r}}$$ (Equation 1)

$$L_{\mathrm{i},\mathrm{j}}^{\mathrm{l}}\left(t\right)=\left\{H_{\mathrm{i},\mathrm{j}}^l\left(t\right)-H_{\mathrm{i},\mathrm{j}}^r\left(t\right)\right\}\ast K_{\mathrm{l}}$$ (Equation 2)

$$L_{\mathrm{i},\mathrm{j}}^{\mathrm{d}}\left(t\right)=\left\{V_{\mathrm{i},\mathrm{j}}^d\left(t\right)-V_{\mathrm{i},\mathrm{j}}^u\left(t\right)\right\}\ast K_{\mathrm{d}}$$ (Equation 3)

$$L_{\mathrm{i},\mathrm{j}}^{\mathrm{u}}\left(t\right)=\left\{V_{\mathrm{i},\mathrm{j}}^u\left(t\right)-V_{\mathrm{i},\mathrm{j}}^d\left(t\right)\right\}\ast K_{\mathrm{u}}$$ (Equation 4)

The state of individual LPLC2 units was simulated as a function of their total inputs, which are hypothesized to be a multiplicative integration of visual motion expanding in the four cardinal directions in their RFs.

$${LPLC2}_{\mathrm{i},\mathrm{j}}\left(t\right)={\left[L_{\mathrm{i},\mathrm{j}}^1\left(t\right)-L_0\right]}^{+}·{\left[L_{\mathrm{i},\mathrm{j}}^2\left(t\right)-L_0\right]}^{+}·{\left[L_{\mathrm{i},\mathrm{j}}^3\left(t\right)-L_0\right]}^{+}·{\left[L_{\mathrm{i},\mathrm{j}}^4\left(t\right)-L_1\right]}^{+}$$ (Equation 5)

where the function ${\left[x\right]}^{+}$ is defined as $\mathit{max}\left(x,0\right)$, and $L_0$ and $L_1$ are input thresholds with $L_0$ >0. The superscripts {1, 2, 3, 4} in Equation 5 indicate {r, l, d, u} via one-to-one correspondence.

For open-loop simulations in Figures 2, 3, 4, and 5, we set L₁ = L₀. Therefore, the four input channels were equivalent, causing an LPLC2 unit to be activated only when it detects visual motion simultaneously expanding in all four cardinal directions. For open-loop simulations with real-world animals in Figure 9, we set L₁ < 0. This is because visual motion patterns, induced by the looming animals, usually simultaneously expand in three directions {1, 2, 3} but either expand more weakly or contract slightly in another direction {4}. Once the model was operating in the modality of closed-loop simulations (Figures 6, 7, and 8), we also set L₁ < 0 by considering that the robot is not an ideal mass point but has a definite body size (Figure 6C). The negative L₁ makes an LPLC2 unit activated when it detects visual motion patterns simultaneously expanding in three directions {1, 2, 3} and either expanding more weakly or contracting slightly in another direction {4}.

GF unit

The single GF neuron unit comprises the last layer of the model (Figure 1A). We used the leaky integrate-and-fire model to simulate the unit without loss of generality. By integrating inputs from the LPLC2 layer, the simulated membrane potential V(t) of the unit obeyed the following dynamics.

$${\tau }_{\mathrm{m}}\frac{dV\left(t\right)}{dt}={-V\left(t\right)+E}_{\text{Leak}}+R{I}^{\text{syn}}\left(t\right)$$ (Equation 6)

in which an action potential is generated whenever $V\left(t\right)$ reaches a threshold value $V_{\text{th}}$. After an action potential, the potential is reset to a value $V_{\text{re}}$ with $V_{\text{re}}<V_{\text{th}}$. Parameter $R$ was set to be one as the simulated membrane resistance, and τ_m is the simulated membrane time constant. $I^{\text{syn}}\left(t\right)$ is the input current that is hypothesized to be proportional to a multiplicative integration of two quantities extracted from the LPLC2 layer: the number $N_{\text{act}}\left(t\right)$ of instantaneously activated LPLC2 units and its changing speed $\Delta N_{\mathrm{a}\mathrm{c}\mathrm{t}}\left(t\right)/\Delta \mathrm{t}$.

$$I^{\text{syn}}\left(t\right)=w·N_{\text{act}}\left(t\right)·\frac{\Delta N_{\text{act}}\left(t\right)}{\Delta \mathrm{t}}$$ (Equation 7)

$$N_{\text{act}}\left(t\right)=\sum _{\mathrm{i},\mathrm{j}}{S}_{\mathrm{i},\mathrm{j}}\left(t\right)$$ (Equation 8)

$$\frac{\Delta N_{\text{act}}\left(t\right)}{\Delta \mathrm{t}}=\left(N_{\text{act}}\left(t\right)-N_{\text{act}}\left(t-1\right)\right)/step$$ (Equation 9)

where $step=10\text{ms}$ is the time interval between frames in visual stimulus inputs. Parameter $w$ was used as a coefficient for scaling the input current $I^{\text{syn}}\left(t\right)$ to a reasonable range. To prevent a meaningless decrease in the simulated GF membrane potential induced by a negative changing speed $\Delta N_{\mathrm{a}\mathrm{c}\mathrm{t}}\left(t\right)/\Delta \mathrm{t}$ after the peak time of $N_{\text{act}}\left(t\right)$, a minimum potential of –80 mV was set for the model V(t). $S_{\mathrm{i},\mathrm{j}}\left(t\right)$ is the output of the LPLC2 layer, which was simulated to be a binary value matrix depending on the state of LPLC2 units in a nonlinear way.

$$S_{\mathrm{i},\mathrm{j}}\left(t\right)=\{\begin{array}{c}1,{LPLC2}_{\mathrm{i},\mathrm{j}}\left(t\right)>0\\ 0,{LPLC2}_{\mathrm{i},\mathrm{j}}\left(t\right)\le 0\end{array}$$ (Equation 10)

Model simulations

Simulation programs were run on a Dell Precision T7920 workstation under Windows 10. The EMD array and LPLC2 layer were simulated as a discrete-time system with a step of 10 ms, while the GF unit was a continuous-time system that was integrated using the fourth-order Runge–Kutta method with a time step of 0.5 ms. To link up different time scales, the EMD array and LPLC2 layer were updated every 10 ms, during which the GF unit was successively integrated for 20 steps. All the parameters are summarized in Table 1.

The open-loop simulations were coded in MATLAB 2019b (MathWorks). The closed-loop simulations were performed by communications between the EMD‒LPLC2‒GF model under Windows and virtual robots under Ubuntu 16.04. Specifically, we installed Ubuntu 16.04 into Windows via VMware Workstation Pro, into which the Robot Operating System (ROS) and physical simulation environment Gazebo were then installed. By utilizing the ROS interface of the MATLAB ROS toolbox, the EMD‒LPLC2‒GF model programmed in MATLAB was able to collect real-time visual input signals from a camera mounted on ROS controlled TurtleBot 3.0 virtual robots (specific type: turtlebot3_waffle_pi). The robot camera has a 120-degree field of view.

Published: March 5, 2023

Data and code availability

• •Data necessary to reproduce the figures have been deposited at the GitHub repository: https://github.com/zhaojunyu01/EMD-LPLC2-GF-model.git and are publicly available as of the date of publication. The URL is listed in the key resources table.
• •Code necessary to reproduce the figures has been deposited at the GitHub repository: https://github.com/zhaojunyu01/EMD-LPLC2-GF-model.git and is publicly available as of the date of publication. The URL is listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.