SUMMARY
The genomic positions of nucleosomes are a defining feature of the cell’s epigenomic state, but signal-dependent transcription factors (SDTFs), upon activation, bind to specific genomic locations and modify nucleosome positioning. Here we leverage SDTFs as perturbation probes to learn about nucleosome dynamics in living cells. We develop Markov models of nucleosome dynamics and fit them to time-course sequencing data of DNA accessibility. We find that 1) the dynamics of DNA unwrapping are significantly slower within cells than reported from cell-free experiments, 2) only models with cooperativity in wrapping and unwrapping fit the available data, 3) SDTF activity produces highest eviction probability when its binding site is adjacent to but not on the nucleosome dyad, and 4) oscillatory SDTF activity results in high location variability. Our work uncovers the regulatory rules governing SDTF-induced nucleosome dynamics in live cells, which can predict chromatin accessibility alterations during inflammation at single nucleosome resolution.
INTRODUCTION
Nucleosomes are critical to packaging the eukaryotic genome into the nucleus: 2m of human DNA must be packed into a 1μm nucleus (Alberts et al., 2002). As a consequence of packing, access to the DNA is limited, yet selective access is important for gene expression (Allfrey et al., 1963). Hence, nucleosomes have evolved to be highly dynamic. Dynamic nucleosome repositioning, including histone assembly, disassembly, and eviction, are important for generating dynamic chromatin states that are ultimately permissive or non-permissive to gene expression (Lee et al., 2004; Shivaswamy et al., 2008).
Early biophysical in vitro studies of histone octamer-DNA interactions focused on high resolution studies of static interactions (culminating in x-ray or cryo-EM structures), as well as dynamic interactions of nucleosomal DNA sequences bound to reconstituted histones in cell-free experimental systems (Zhou et al., 2019). High-resolution structures elucidated the interaction points between the histone octamer (H2A–H2B pairs and H3–H4 pairs) and the DNA wrapped around it (Luger et al., 1997). In vitro studies of nucleosome unwrapping and rewrapping determined with a variety of methods, including FRET, revealed quantities such as the average time taken for spontaneous DNA unwrapping (Li et al., 2005), the differences in timescales of dissociation and reassociation of the different DNA-histone contact regions on the nucleosome (Tims et al. 2011), and a fundamental asymmetry in the process such that the unwrapping of one side helped to stabilize the other side (Ngo et al., 2015).
Mathematical models have explored the dynamic behavior of nucleosomes and their role in chromatin biology, including the effect of chromatin remodeling proteins on nucleosome sliding (Chou, 2007) and the deposition of histone marks along nucleosome arrays for epigenetic memory (Dodd et al., 2007). Nucleosomes have also been modeled with biophysical accuracy by incorporating the nucleosomal structure of 14 DNA-histone contact points and describing how DNA unwrapping/rewrapping depends on particular rate parameters (Cheng et al., 2021; Dobrovolskaia and Arya, 2012; Möbius et al., 2006). These theoretical approaches show that a mathematical model, especially those involving Markov chains and Brownian motion, can be used to reproduce in vitro experimental measurements and to provide insights such as an analytic form of the mean DNA detachment time, DNA bending angles, and bistability in histone modifications.
However, little is known about nucleosome dynamics as they occur on native chromatin in living cells. These “in vivo” dynamics are likely markedly different from dynamics measured in cell-free systems “in vitro” because the interactions between DNA polymer and histone octamer are constrained, and because additional protein factors that are not present in biochemical studies may further stabilize or destabilize the nucleosome. For example, linker histones present in vivo also bind to nucleosomal core particles close to the DNA entry and exit sites, and enzymatic machines such as SWI/SNF (Dechassa et al., 2010) or FACT complexes facilitate nucleosome repositioning (Chen et al., 2018; Liu et al., 2020). However, we know little about these dynamics quantitatively because there has not been a straightforward way to measure nucleosome positioning in vivo and no controlled way to perturb steady-state positions.
Two recent advances have allowed us to probe nucleosome dynamics. First, next generation sequencing (NGS) has provided ways to measure nucleosome accessibility and positioning with DNAse1, and more recently with ATAC-seq. These genome-wide measurements revealed that nucleosome positions in vivo are to a large degree determined by DNA sequence (Segal and Widom, 2009; Segal et al., 2006). Second, the identification of DNA-binding proteins termed pioneer factors, that may displace nucleosomes by competing with histones for DNA contacts, provides a means to perturb nucleosomes. The discovery that stimulus-induced signal-dependent transcription factors (SDTFs) may also initiate nucleosome re-positioning now allows them to be used as a probe to study in vivo dynamics, as they provide a trigger to perturb DNA-histone interactions within the cell at controllable start times (Ostuni et al., 2013; Sen et al., 2020; Weinmann et al., 1999). In particular, the dynamics of inflammation-activated SDTF activity has been shown to determine the propensity for nucleosome repositioning in both macrophages and fibroblasts (Cheng et al., 2021; Sen et al., 2020). This suggests that SDTF activation with stimulus-specific dynamics may be used as a probe to study the histone-DNA interaction dynamics within the nucleosome, via NGS measurements at stimulus start and end points.
We here present stochastic models for epigenetic remodeling, which in this paper refers to changes in chromatin accessibility. These math models are based on structural features of the nucleosome to investigate the regulatory rules behind nucleosome eviction. Using probability theory, we calculated the probability of histone eviction and the resulting mean chromatin accessibility under various dynamical SDTF signaling patterns. We report that oscillatory SDTF signals potentially induce greater variability of cell fate in heterogeneous cell environments than constant SDTF signals. Then, by experimentally tracking nucleosomes at different genomic locations and counting the number of nucleosome evictions between two time points, we found that optimal eviction takes place when the SDTF binds adjacent to the dyad, defined as the center position of nucleosomal DNA, rather than directly on top of it, indicative of the cooperativity of histone-DNA contacts. Thus our modeling approach allows us to derive quantitative insights from NGS chromatin accessibility data, provides a framework for understanding location-specific, SDTF-induced chromatin accessibility changes in different cellular contexts, and constitutes a tool to predict eviction probability for single nucleosomes in live cells responding to inflammation.
RESULTS
A stochastic model accounts for nucleosome dynamics upon SDTF binding in vivo
When SDTFs bind to DNA, their stimulus-specific temporal dynamics disrupt the resting state distribution of nucleosomes, affecting chromatin accessibility (Figure 1A). Epigenetic dynamics can be modeled as a continuous system - for example, deterministic ordinary differential equation models describing chromatin accessibility in bulk have been used to describe chromatin opening steps that result in enhancer formation (Cheng et al., 2021). However, DNA unwrapping/rewrapping of individual nucleosomes is subject to molecular stochasticity. Moreover, the binding of SDTFs to DNA can be regarded as a time-dependent on/off switch dramatically influencing chromatin dynamics – this binding is discrete and stochastic. To incorporate such noisy behavior and discreteness, we used a continuous time, discrete-state Markov chain to model chromatin accessibility with time-dependent SDTF binding. This model is time-inhomogeneous as the transitions given by SDTF binding/unbinding are time-dependent (STAR METHODS Section S1).
Figure 1: A stochastic model accounts for nucleosome eviction by dynamic SDTF activity.

A. Immune responses activate SDTFs with different temporal dynamics, ultimately affecting chromatin accessibility. B. Schematic for the unwrapping/rewrapping model for nucleosome dynamics under SDTF signaling dynamics. C. State configuration of the stochastic nucleosome model, where ai, bi, ci, di represent rate parameters. (See also Figure S1 and S7).
To reflect the biophysical structure of the nucleosome, we assumed that each nucleosome consists of 14 step-wise unwrapping and rewrapping transitions, consistent with structural data on the number of contact points between the histone and DNA (Luger et al., 1997), as well as previous nucleosome unwrapping models (Figure 1B) (Cheng et al., 2021; Mobius et al., 2013). Approximately 147bp of DNA wrap one and three-quarter times around the core histone octamer (Luger et al., 2012), resulting in 14 main non-covalent DNA-histone contact points (Luger et al., 1997). To fully displace the nucleosome from any particular genomic location, multiple steps may be required. Hence, based on structural and biophysical measurements performed on single nucleosomes in vitro, we used a coupled stochastic process (X(t), N(t)), where X(t) represents the number of disassembled DNA-histone contact regions, and N(t) takes either 0 or 1 to represent the on/off state of the SDTF binding (Figure 1C). We considered the spontaneous, step-wise unwrapping behavior of DNA from a single histone, which originates at the locations furthest from the nucleosome dyad (state 7).
Regarding the symmetry of the model, we assumed a one-sided unwrapping model where DNA unpacks from state 0. Prior experimental cryo-EM or atomic force microscopy studies investigated whether the nucleosome unwraps from one-side at a time or two-sides simultaneously. The results suggested that one-sided unwrapping is more likely, as opening of one nucleosomal end stabilizes the other end (de Bruin et al., 2016; Konrad et al., 2021; Mauney et al., 2018). In addition, structural studies on the H1 linker histone showed that the H1 globular domain bound directly on the dyad and associated with both sides of the linker DNA, while the H1 C-terminal domain attached to just one of the two linker DNA segments (Bednar et al., 2017). We surmised that the asymmetry of linker histones may also further promote one-sided asymmetrical unwrapping in vivo. Although unwrapping and wrapping of the nucleosome is primarily unidirectional (Bilokapic et al., 2018; Li et al., 2005; Ngo et al., 2015), we also considered and analyzed the possibility that it takes place simultaneously at both ends of the DNA (STAR METHODS Section S2 and Figure S1), and we found that the qualitative behavior of both 1-sided and 2-sided stochastic models were similar. Hence, we settled on using the 1-sided model in the main results of this paper.
The amount of energy released by re-establishing hydrogen bonds between histone and DNA is greater than the energy released by the straightening of the DNA polymer during unwrapping, so the rates of rewrapping exceed that of unwrapping, which in our model corresponds to setting ai < bi (Tims et al., 2011). We set the unwrapping/rewrapping parameters as an = a1hn−1[min−1] and bn = b1h−n+1[min−1] with a cooperativity constant h so that DNA unwraps more easily the more unwrapped it already is. Biophysical and structural measurements on single nucleosomes support the cooperative and multistep transitions in DNA unwrapping from the histone (Li et al., 2005; Polach and Widom, 1995; Tims et al., 2011), but the extent of such cooperativity remains a free parameter that can be later fit to data. We note that evidence for cooperativity in the literature is measured in isolated nucleosomes in vitro, whereas our measurements below were carried out within the full cellular chromatin environment.
We then considered the effect of a dynamic signaling protein that competes for DNA binding with the histone core octamer. Short periods of DNA accessibility may be stabilized by the binding of transcription factors if their cognate binding sequence is present in that stretch of DNA and they are present at sufficiently high concentrations (Klemm et al., 2019). Spontaneous nucleosome dynamics, also known as nucleosome breathing, allow transient exposure of nucleosomal DNA, and the binding of SDTFs provide steric hindrance that occludes the rewrapping of DNA-histone contacts within the nucleosome. The on-state of the SDTF makes the nucleosome rewrapping parameter dn much less than bn around the SDTF binding site (Figure 1C), while cn is set to be identical to an. Once a histone is fully evicted it detaches entirely from the DNA and might not dock to the same genomic location again. Thus, we assumed that b14 = d14 = 0 so that state 14 is an absorbing state of X(t). That is, if X(s) = 14 for some s, then X(t) = 14 for all t > s. We also analyzed the alternative assumption that state 14 is non-absorbing, which represents reattachment of an evicted histone, and found the models produced similar behavior (STAR METHODS Section S5.1).
It is known that transcription factor binding operates at a faster timescale than DNA wrapping or unwrapping (Callegari et al., 2019). Hence for a given SDTF concentration f(t), we used the SDTF binding rate κon(t) = cf(t) with a large constant c, and the unbinding rate κoff is proportional to κon(0). Indeed, the stochastic system behaves almost identically with any choice of large c, and this was proved in STAR METHODS Section S1.2 using a timescale decomposition argument. For large values of c, the ratio BF = κoff/(κon + κoff) approximately determines the fraction of time that the SDTF is unbound. Note that the ratio BF could depend on time if the SDTF signal is oscillatory, and it can also depend on the strength of the SDTF input.
In further difference from previous models, we considered the SDTF binding position in relation to the original nucleosome dyad. As the nucleosome encompasses ~147 base pairs of DNA, and SDTF binding motifs typically stretch 8–10 base pairs (Stewart et al., 2012), the stochastic binding and unbinding of the SDTF from DNA at the site of its motif is modeled with genome location-specific resolution by incorporating the relative location of binding motifs from the nucleosome dyad. When the SDTF binds to its cognate motif, it tends to disrupt DNA-histone contacts in its vicinity. The effect of SDTF binding on the rewrapping parameter is highest near the SDTF binding site and decreases with distance. See STAR METHODS Section S1.1 and Table S1 for a mathematical derivation of statistical quantities, the definition of the parameters, and the choice of parameter values of the stochastic process (X(t), N(t))
Periodicity of SDTF oscillations affects DNA accessibility
In inflammation signaling, the importance of signaling dynamics is well appreciated (Behar and Hoffmann, 2010; Purvis and Lahav, 2013; Werner et al., 2005). A prominent SDTF that is activated during immune responses is NFκB. For NFκB signaling, the amplitude (Lee et al., 2014) and duration (Hoffmann et al., 2002; Sen et al., 2020) of the signal controls which genes are activated. However, only recently has the importance of oscillatory versus non-oscillatory signaling been revealed in remodeling the epigenome (Cheng et al., 2021), rather than in primary response gene expression (Barken, 2005). Previously published experimental systems involving mutations of NFκB feedback regulators allowed comparison of oscillatory (WT) and non-oscillatory (Mut) NFκB activity after TNF stimulation of macrophages (Figure 2A) (Adelaja et al., 2021; Cheng et al., 2021), but there is currently no experimental system that allows altering the period of NFκB oscillations (Longo et al., 2013). Thus, we used the stochastic model to examine how the period of SDTF oscillations alters the chromatin accessibility; we analyzed the results of numerical computations with the probability distribution of the full histone eviction time.
Figure 2: Periodicity of SDTF oscillations affects DNA accessibility.

A. Experimental knowledge of SDTF signaling dynamics in single cells (top: two individual single cells, bottom: hundreds of single cells). WT and Mut cells activate NFκB with different temporal dynamics (Adelaja et al., 2021). B-D. Chromatin response to oscillatory SDTF dynamics with different frequency. B. SDTF dynamics with rapid (top) or slow oscillation (bottom). C. 50 sample traces of DNA dynamics under the oscillatory SDTF inputs of half-period=10min (top) and 60min (bottom). Red traces reach the fully evicted state, and black traces do not. D. Time evolution of histone eviction probability. E-G. Parameter sensitivity under oscillatory vs. constant SDTF signals. E. Oscillatory and constant SDTF signal inputs. F. Full eviction probability vs unwrap parameter cooperativity (h = 1.3). m represents the fold-change increase in unwrapping/rewrapping parameters. G. Mean chromatin accessibility distribution at t = 500 min with the oscillatory or constant SDTF dynamics. To model heterogeneous cell environment, we randomly perturb the system parameters. Coefficient variation (standard deviation/mean) of the distributions under oscillatory SDTF and constant SDTF are 0.35 and 0.12, respectively. (See also Figure S2).
The period of the oscillation quantitatively affects the time-course dynamics of chromatin accessibility. We set the cooperativity constant h = 1.3, and we set the unwrapping/rewrapping parameters as an = 0.2hn−1, bn = 3 h−n+1 for each state n in the stochastic nucleosome model. For simplicity, we used zero rewrapping rates under the SDTF binding, meaning that dn = 0 at each state n. We considered two oscillatory SDTF inputs of 10 min and 60 min half-periods, respectively, that have the same aggregate signal within the time interval [0,500] min (Figure 2B). We sampled 50 timecourses of our stochastic model under each of these two oscillatory inputs, using the Extrande method (Voliotis et al, 2016), which is a stochastic simulation algorithm for Markov chains with time-dependent transition rates. The rapid oscillatory SDTF signal with a half-period of 10 min unwrapped the nucleosome completely in 19 out of 50 samples within 500 min, while 40 out of 50 samples are fully unwrapped by 500 min when the half-period is 60 min (Figure 2C). This result reflected experimental results where SDTF dynamics of longer continuous duration resulted in increased nucleosome eviction (Cheng et al., 2021).
To further analyze this system modeled under the two different dynamic SDTF signals, we described the DNA wrapping process as a ‘success-or-failure game’ (Figure S2A–C), which can be analyzed with a geometric distribution. In the case of a cooperative system with h = 1.3, when X(t) reaches state 6 or above, the unwrapping parameters an+1 are greater than the rewrapping parameters bn so that X(t) can easily reach state 14 (state of full eviction) even without the support of SDTF binding. Hence success of X(t) is reaching state 6, and we used the probability of the success to analyze the distinct behaviors of DNA under two oscillatory inputs.
If nucleosomes are exposed to an SDTF signal at amplitude 10 for 10 min, then only about 2.5% of nucleosomes reach state 6 (Figure S2C). Hence during the on-phase (i.e. SDTF signal at amplitude 10), nearly 2.5% of DNA segments can successfully unwrap from the entire histone octamer under this rapid oscillation. After the first 10 min oscillation, when the SDTF signal is turned off, most remaining nucleosomal DNA which failed to reach state 10 during the previous on-phases, rapidly rewraps around the histone because the rewrapping parameter bn is much greater than the unwrapping parameter an for n < 6, likely returning back to state 0. Therefore, in the next on-phase, about 2.5% of the remaining free DNA can be fully unwrapped, and DNA undergoes this process 25 times by 500 min. This success-or-failure game under the oscillatory SDTF signal can be described using the geometric distribution Geo(0.025) with the success probability 0.025 (Figure S2A–B). Similarly, the full eviction probability by 500 min under the SDTF signal of 60 min half-period can be estimated with Geo(0.24) since the success probability is about 24% during 60 min on-phase. The full eviction probabilities computed with the geometric distributions Geo(0.025) and Geo(0.24) are about 0.47 and 0.7 respectively, which closely estimate the actual eviction probabilities shown in Figure 2D. The detailed computations of the full eviction probabilities using these two geometric distributions are shown in STAR METHODS S3.1.
In our simulations, very fast oscillations of the SDTF signal did not necessarily render the DNA less accessible. Indeed, when the half-period was 0.3 sec, the SDTF signal is interpreted as a constant signal with half the amplitude. Therefore, despite the extremely short on-phase of the oscillation, about 50% of DNA temporal trajectories were fully unwrapped by 500 min (Figure 2C bottom), which is higher than when the half-period was 10 min. Intuitively, this phenomenon occurs because the optimal scenario for the least unwrapping is based on the SDTF oscillation frequency matching the relative unwrapping/rewrapping frequency of the nucleosome. The time evolutions of histone eviction probability under these three different SDTF signals are displayed in Figure 2D. See STAR METHODS Section S3.1 and Figure S2 for more detailed mathematical analysis about the full eviction probability under different frequencies of the SDTF signal.
Oscillatory SDTF inputs can lead to heterogeneous chromatin accessibility responses
While our computational investigation of different SDTF oscillatory frequencies cannot be tested in experimental systems (as the period is hardwired by the IκBα-NFκB negative feedback loop (Longo et al., 2013)), we now considered that the same oscillatory SDTF dynamics may affect different nucleosomes within a cell differently because of differences in kinetic parameters determined by location-specific molecular mechanisms.
To explore the capacity for differential responses of various chromatin regions to the same dynamic signal, we scanned the nucleosome unwrapping/rewrapping parameters and computed the probability of histone eviction using the stochastic model under non-oscillatory or oscillatory inputs with a fixed period (Figure 2E). We found that the system was more sensitive to the unwrapping/rewrapping parameters under oscillatory than non-oscillatory SDTF dynamics (Figure 2F). We used the same parameters as used in previous simulations and they are shown in Table S1.
Under oscillatory and constant SDTF dynamics, we calculated the probability of histone eviction at T=360 minutes after multiplying each of the unwrapping/rewrapping parameters an and bn by a fold-change parameter m (Figure 2F). Under oscillatory SDTF dynamics, the full DNA eviction probability rapidly grows for m ∈ [2,4]. In fact, this graph has a sigmoidal shape, indicative of a higher sensitivity with respect to fold change increases, so that the same oscillatory input can lead to widely different responses for different parameter values. In STAR METHODS Section S3.2, using simple matrix exponentials, we explored sensitivity analysis with our stochastic model under both constant transition rates and time-dependent oscillatory transition rates.
We may speculate that the greater variability of chromatin accessibility under an oscillatory SDTF input allows more cell-to-cell variability of cell fate decisions. For instance, if the cell type is determined by a threshold mean accessibility at particular chromatin regions, then an oscillatory SDTF may produce both type A and type B, whereas a non-oscillatory SDTF may more consistently convert cells to type B (Figure 2G).
Eviction Probability Profiles characterize the in vivo nucleosome unwrapping process
We next sought to use the nucleosome model to investigate how the location of the SDTF binding site relative to each nucleosome might affect nucleosome eviction. We utilized ATAC-seq data from an IκBα knockout mutant macrophage experimental system (Cheng et al., 2021) at a 0 hour baseline and at 4 hours after NFκB has been activated by TNF stimulation. Using paired-end ATAC-sequencing to separate nucleosomal read fragments from nucleosome-free read fragments, we calculated nucleosome dyad positions across the genome (Schep et al., 2015), (Figure S3). We assessed nucleosome dyad locations relative to κB sites before and after stimulation and observed a reduction in the number of κB-site-associated nucleosomes following NFκB activation, but this reduction depended on the distance between the κB site and the nucleosome dyad (Figure 3A).
Figure 3: Modeling SDTF binding sites, range of SDTF effect, and cooperativity in unwrapping steps reveals potential Eviction Probability Profiles.

A. Summary of NFκB motifs adjacent to nucleosome dyads. Shown are NFκB motifs in relation to each nucleosome dyad called by NucleoATAC (Schep et al., 2015) at 0 hours and 4 hours after TNF stimulation, in male mouse BMDMs (no replicates used, n=1 for each timepoint, validation experiment performed in Figure 6). Locations shown have an NFκB motif +/− 100bp of the nucleosome dyad. B. SDTFs locally affects the DNA-histone contact regions near the SDTF binding site. C. The range parameter σ determines how widely the SDTF affects the rewrapping parameters. D. Computation of the full eviction probability via the stochastic model shows that motifs at the dyad promote greater nucleosome unwrapping probability under a non-oscillatory SDTF signal and non-cooperative open/close parameters. E. The full eviction probability is maximal at the SDTF binding location between the edge and dyad under cooperative unwrap/rewrap parameters. Assuming 50% of right edge-unwrapping and 50% of left edge-unwrapping, the average full eviction probability displays a center valley. (See also Figure S3, S4, and S6).
To understand why the location of the binding motif relative to nucleosome dyad position affects nucleosome eviction, we added mechanistic detail to the nucleosome model. We allowed the rewrapping parameters to depend on the SDTF binding site location along the 147 base pair stretch of DNA that encompasses the nucleosome. Hence DNA locations lying within a certain range around the SDTF binding site have a rewrapping parameter dn that is smaller than bn. For simplicity we used a Gaussian formula, which allowed us to center the effect at the SDTF binding site and control the range of its influence. We used the formula dn = bn (1 – exp(−(s − n)2/2σ2)), where s is the SDTF binding location and the standard deviation σ represents the SDTF effect range (Figure 3B). In this way, dn ≈ bn for a state n far from the binding site s, and dn ≈ 0 when n is close to s (Figure 3C).
In the nucleosome model the unwrapping and rewrapping parameters may describe cooperativity within the unwrapping mechanism, meaning that every unwrapping step facilitates further unwrapping (i.e. an increases and bn decreases in n). If the system is non-cooperative, then each state n has constant parameters an and bn. Prior evidence suggests that the unwrapping process may be highly cooperative, either due to an inherent cooperativity of contact points within the nucleosome, or due to the collaborative mechanism between DNA binding proteins that promote nucleosome eviction (Miller and Widom, 2003). To achieve such behavior, the unwrapping and rewrapping parameters were modeled as an = a1hn−1 and bn = b1h−n+1 for each n with cooperativity constant h. The special case of h = 1 indicates non-cooperative behavior.
Notice that while the unwrapping parameters are increasing, the average timescales for site exposure from state n to state n + 1, or from state 0 to state n, still become progressively longer as experimentally observed (Tims et al., 2011). This is because the opening process from state n to state n + 1 could involve multiple steps of unwrapping and rewrapping. For example, one possible trajectory of DNA from state 5 to state 6 consists of the path 5 → 4 → 3 → 4 → 5 → 6 (STAR METHODS Section S6).
We then tested which binding location is optimal for nucleosome eviction under constant SDTF activity. SDTF binding motifs were distributed across the DNA strand in the range [−100 bps, 100 bps] centered at the histone dyad (state 7 in Figure 3B). We assumed that the SDTF binds at one of the states s in {−3,−2,…,16,17}, which is an extended range from the original state space {0,1,…,14} (Figure 1C), so that we can consider SDTF binding motifs lying slightly outside the nucleosome. Then for each distance relative to the nucleosome dyad, computed as |7 − s| × 10 (bps), we calculated the full eviction probability. The resulting behaviors under various levels of cooperativity of the parameters an and bn are distinct, as the optimal binding site is either in the center of the nucleosome or toward the extremes. Under non-cooperative rates (h = 1), the optimal binding site is at the nucleosome dyad so that the full eviction probability is symmetric about the relative distance between SDTF binding site and dyad (Figure 3D). In contrast, when the parameters model cooperative behavior (h > 1), the optimal site is closer to the unwrapping edge, and hence the full eviction graph has a peak close to this edge (Figure 3E left). This is because once the first few contacts between DNA and histone are unwrapped, the cooperativity of the system facilitates the unwrapping of the remainder. After averaging multiple cells, due to the symmetry of nucleosomes unwrapping from either end, the probability-binding site plot has a center dip (Figure 3E right). Given such different patterns of eviction probability vs. the distance of the SDTF binding site from the dyad, we termed the graph the “Eviction Probability Profile” and concluded that it may be used to characterize the in vivo nucleosome unwrapping process. In STAR METHODS Section S4.1 and Figure S4, we provide a mathematical analysis of the effect of the SDTF binding site on the probability of nucleosome eviction.
Model predicts cooperativity based on Eviction Probability Profiles
The shape of the Eviction Probability Profile is altered not only by wrapping cooperativity (parameter h) but also by the range of the SDTF binding effect (parameter σ), which is likely to be SDTF-specific. If the range is wider, all the rewrapping parameters dn are equally affected so that the probability plot becomes more flattened. We first examined computationally how different values of the cooperativity parameter h and the SDTF range parameter σ could alter the chromatin accessibility (Figure 4A). We tested multiple potential values of this range parameter, as well as cooperativity parameters h = 1 (non-cooperative), 1.1 and 1.2 (high cooperativity). We also used σ2 = 2.5, 10 and 50 for the range of the SDTF binding effect. It is notable that for higher cooperativity and narrower SDTF binding effect range, the plot of full DNA eviction probability displays a clearer center valley.
Figure 4: Fitting the model Eviction Probability Profiles to SDTF binding location data provides evidence of cooperativity and estimates model parameters.

A. Probabilities of full eviction with respect to relative motif position from the nucleosome dyad, and SDTF binding effect range for the macrophage system under non-oscillatory NFκB signal. Three different ranges (σ2 = 1.5, 10, and 50) and cooperativity parameters (h = 1, 1.1 and 1.2) are chosen. B. Left: Nucleosome counts from male mouse BMDM ATAC-seq samples under non-oscillatory TNF-induced NFκB activity at NFκB motifs at 0 hours and 4 hours (no replicates used, n=1 for each timepoint, validation experiment performed in Figure 6). Right: Full eviction probability vs. SDTF binding locations. Experiment-based Eviction Probability Profile (red curves). Model-based Eviction Probability Profile before and after parameter fitting by gradient descent (blue curves). C. Full DNA eviction probability under a steady NFκB input signal of different durations. Red: Experimental measurements shown in Cheng et al., 2021. Blue: Simulated values using the stochastic model with the fitted parameters in Table S1. D. Left: Fold change (WT/Mut) of resulting chromatin accessibility after activation of SDTFs with different dynamics. Two biological replicates were used for each genotype (n=2). Right: Reproduction of the experimental measurements using the stochastic nucleosome model under the fitted parameters listed in Table S1. Counts are converted to proportion due to simulation of a different number of nucleosome locations. E. Left: Variance in chromatin accessibility across genomic locations at 4 hours in WT and Mut cells, as measured by bulk ATACseq. Two biological replicates were used for each genotype (n=2). Right: Reproduction of the experimental measurements using the stochastic nucleosome model. (See also Figure S5).
Using this relation between the model parameters and the Eviction Probability Profile, we next compared these computational results to experimental measurements. We fit model parameters to data on nucleosome eviction probabilities given the SDTF binding motif location relative to the dyad. The parameter σ corresponds to the standard deviation of the Gaussian curve describing the influence of the SDTF binding, in units of number of binding sites. Since these binding sites are approximately 10 base pairs away from each other, a value of σ = 2 would correspond to a standard deviation of around 20 base pairs, or a range of 40 base pairs around the SDTF binding site.
We returned to the time-course experimental data from macrophages responding to TNF stimulation (Figure 3A). As ATAC-seq data can provide an estimate of the nucleosome positions, we assigned nucleosomes to their nearest TSS at the baseline time point 0 hours and tracked whether the nucleosomes matching to the same TSS changed in position or disappeared at the later time point of 4 hours – quantified by having fewer or no nucleosomes mapping to that TSS (Methods). Using the difference of the nucleosome counts between two time points, we computed experimental full nucleosome eviction probability for each relative motif distance by 240 min after TNF stimulation as
We used this data to fit values of the different parameters in our model by approximating an initial set of parameters, followed by gradient descent (CourantRichard, 1994) to find the optimal parameter set. Fitted parameters included the cooperativity parameter, SDTF range parameter, unwrapping/rewrapping parameters, and SDTF binding/unbinding rates. For IκBα knockout macrophages treated with TNF for 4 hours (Cheng et al, 2021), fitting these parameters resulted in the best-fit Eviction Probability Profile (Figure 4B). (See STAR METHODS Section S4.2 for additional details, and Table S1 for the resulting parameter values.) Based on the shape of the fitted Eviction Probability Profile, we found that the nucleosome unwrapping/rewrapping parameters are likely cooperative. The range of SDTF effect was fitted at σ = 2.1, which corresponds to a radius of around 20 base pairs from the SDTF binding site, or 40 base pairs around the binding site. The initial unwrapping parameter a1 = 0.16 indicates that the first DNA unwrapping from the fully wrapped configuration takes approximately 1/0.16 = 6.25 minutes on average. See Figure S5 for an analysis of the error between the Eviction Probability Profiles of the data and the model. Furthermore, recent studies have shown that nucleosome eviction is likely to take place under a long NFκB signal pulse of approximately 120 minutes, but that it rarely occurs under a shorter NFκB signal pulse of less than 45 minutes (Cheng et al., 2021), and similar observations were made in fibroblasts after 60 minutes and 150 minutes, respectively (Sen et al., 2020). These observations can be reproduced with our stochastic model under the fitted parameters (Figure 4C).
To further compare the model with experimental data, we examined several properties of the chromatin locations. We hypothesized that the ATAC-seq distributions across genomic locations in both WT and Mut macrophages could be reproduced by simulating the stochastic model using the fitted parameters. Indeed, under fitted parameter values (Table S1), simulations of the stochastic model reproduced two experimental findings (Figure 4D–E). First, comparing the two systems, WT and Mut, allowed us to assess the distribution of stimulus-induced fold changes for each genomic location that are attributable to differences in signaling dynamics (Figure 4D). Second, the two experimental systems displayed differences in the amount of post-stimulation chromatin accessibility among genomic locations, which was recapitulated by the model (Figure 4E). We also computed the total variation distance, one of the most common measurements for similarity of given distributions (Levin & Peres, 2017), between the two experimentally measured distributions (see STAR METHODS) and found it to be 0.25. The distance between the two modeled distributions was 0.22, showing that modeled difference between the DNA accessibility under WT and Mut signals was similar to that from experiments. This comparison with experimental data helped validate the dynamic rates of DNA wrapping and unwrapping in the model.
Eviction Probability Profiles under more general parameter settings
We next found that the Eviction Probability Profiles showed consistent shapes even under more biophysically nuanced SDTF binding parameters κon. We first allowed κon(s) to vary as a function of the binding location s. We set κon(s) to be smallest at the most inaccessible site, the nucleosome dyad (Figure 5A). Under such spatially inhomogeneous SDTF binding rates, the full Eviction Probability Profile has the same characteristic shape as before: In the cooperative case one can see two peaks, and in the non-cooperative case there is only a single peak (Figure 5B). Second, we assumed that the SDTF binding rate κon(n) depends on the state n of the nucleosome for a fixed SDTF binding location s. It is reasonable to assume that when the SDTF binding location is exposed by DNA unwrapping, the SDTF has higher binding rate than when the binding site is buried by wrapped DNA (Figure 5C). Under this general setting, the Eviction Probability Profile robustly showed the characteristic shapes for both the cooperative and non-cooperative cases (Figure 5D). The consistency of the model predictions to different parameter assumptions supports the robustness of the behaviors generated by our stochastic epigenome model as shown in Figure S6 and is mathematically verified in STAR METHODS Section S5.
Figure 5: Consistency of the Eviction Probability Profiles under more general parameter settings.

A. Generalization of the model where SDTF binding rate κon(s) is a function of the binding location s. B. Resulting Eviction Probability Profiles based on the binding rates illustrated in A. C. Generalization of the model where SDTF binding rate κon(n) is a function of the DNA opening state n. D. Resulting Eviction Probability Profiles based on the binding rates illustrated in C. (See also Figure S6).
Fitting the model to a different dataset results in consistent behavior
We hypothesized that the model parameters associated with nucleosome dynamics should be consistent in a second experiment with the same SDTF activated, but by a different ligand. We thus stimulated wild-type macrophages with LPS for 4hrs to generate non-oscillatory NFκB dynamics (Figure 6A), analogous to the non-oscillatory NFκB dynamics generated by TNF stimulation in IκBα knockout mutant macrophages. We again performed paired-end ATAC-sequencing and identified the location of NFκB binding sites relative to the nucleosome dyad (Figure 6B). Comparing nucleosome positions at 0hrs and 4hrs resulted in the experimental Eviction Probability Profile, and the mathematical model was again fit to this data.
Figure 6: Stimulation of macrophages with LPS leads to consistent modeling results.

A. Schematic of SDTF activation in response to TNF or LPS. TNF stimulation results in NFκB activity, while LPS stimulation results in both NFκB and IRF activity. B. Top: Experimental and simulated nucleosome counts after LPS stimulation, for NFκB-associated nucleosome locations after 0hrs and 4hrs (n=1 for each timepoint). Bottom: Analogous counts for IRF-associated nucleosome locations (n=1 for each timepoint). C. Eviction Probability Profiles associated with LPS-induced NFκB activity, using the same model parameters as the TNF-induced data (green) and direct fit (blue). D. Eviction Probability Profiles associated with LPS-induced IRF3 activity. *: All the parameters are the same as the fitted parameters with the TNF data (Figure 4) except for the SDTF unbinding fraction, BF. (See also Figure S5).
Experiments were all performed in macrophages, but LPS stimulation may activate greater amounts of NFκB than TNF. Hence, we first fit the model to the LPS-stimulated dataset with all the same parameters obtained from the previous fit to TNF-simulated data, but slightly adjusted SDTF unbinding fraction (BF) reflecting greater amount of NFκB. Remarkably, the model closely reproduced the Eviction Probability Profile given by the LPS-stimulated dataset (Figure 6C). We next fit the Eviction Probability Profile to the LPS-stimulated data using gradient descent, and the resulting parameters closely matched the parameters obtained from fitting to the TNF-stimulated dataset (Figure 6C, Table S1). We found a remarkable similarity in the estimated nucleosome unwrapping and rewrapping parameters, as well as in the range of NFκB effect. For example, the cooperativity constant is estimated at h = 1.4 with this new data, while it was measured at h = 1.35 with the previous TNF-stimulated data. This value is exponentiated to specify the unwrapping parameters at each step, and even at step 13, this difference between gives a fold change in parameters of only (1.413 × 0.15)/(1.3513 × 0.16) = 1.48.
The unwrapping/rewrapping parameters and the cooperativity may be specific to a set of nucleosomes, but the range of the SDTF effect may be SDTF-specific. We therefore next asked to what extent the Eviction Probability Profiles remained consistent under another SDTF. Interferon-regulatory factors (IRFs) are also activated by LPS (Figure 6A), affecting chromatin accessibility and enhancer formation at genomic positions containing IRF binding motifs (Cheng et al, 2021). We mapped the locations of IRF motifs in relation to the nucleosome dyads estimated from ATAC-seq data (Figure 6B), and we plotted the Eviction Probability Profile by comparing nucleosomes before stimulation and 4hrs after. We again noted a double-peaked profile suggestive of cooperativity in nucleosome unwrapping/ rewrapping parameters. To quantify this, we fit the stochastic model to the profile and obtained new parameter estimations for these IRF-affected epigenomic regions (Figure 6D, Table S1). A key difference between the parameters previously fit to NFκB data was the unwrapping parameter an = 0.07, compared with an = 0.15 for the previous model. As NFκB and IRF bind to their motifs with distinct biophysical characteristics, stereochemistries, and to different locations of the genome, our results suggest that such differences also determine their nucleosome eviction characteristics.
The Eviction Probability Profile is a fingerprint for kinetic features of nucleosome dynamics
We asked how different model parameters might affect the features of the Eviction Probability Profile, and we found that changes in model parameters could be directly mapped to changes in particular geometrical characteristics of the Eviction Probability Profile (Figure 7). The unwrapping and rewrapping rates vertically translate the Eviction Probability Profile, since larger unwrapping parameters lead to larger eviction probabilities. Adjusting the SDTF unbinding fraction BF stretches the peaks up and down because the strength of the SDTF binding effect is determined by the SDTF binding fraction parameter (See STAR METHODS Section S1.2 and Figure S7 for a mathematical proof for this fact). More DNA-histone contact regions are influenced if the range of the SDTF binding effect is wide. Hence the range parameter σ changes the depth of the center dip in the Eviction Probability Profile. The other parameter, BF, controls the depth of the center dip as well, but a small σ particularly can create plateaus at both ends since the DNA around ±100 relative base pairs is never affected by the SDTF binding when the effect range is narrow. The optimal SDTF binding location tends to shift towards the edges under strong cooperativity, so that the distance between two peaks in the Eviction Probability Profile increases as the cooperativity parameter h increases. Based on this one-to-one correspondence, we can systematically find a good initial prediction for the parameter fitting to given data, and this prediction can be used as an initial condition of the gradient descent searching algorithm for finer parameter fitting.
Figure 7: The Eviction Probability Profile is a fingerprint for kinetic features of nucleosome dynamics.
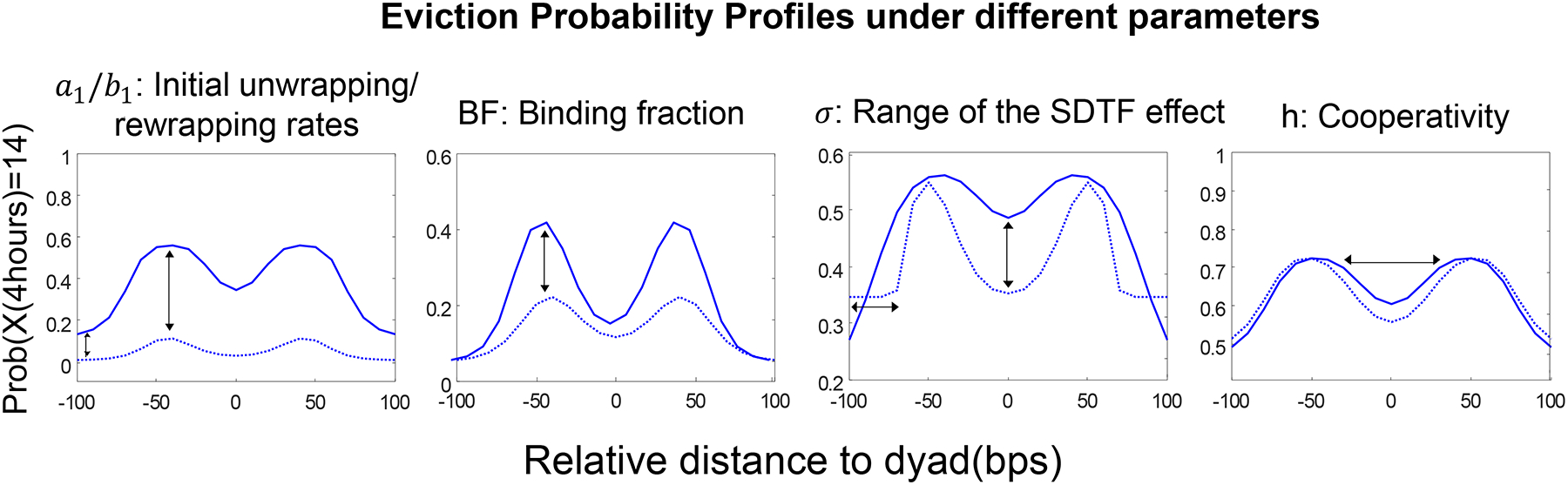
The geometric characteristics of the Eviction Probability Profile has one-to-one correspondence to the parameters of the stochastic epigenome model. For a given location-specific nucleosome eviction profile, this correspondence can be used to identify epigenetic features such as the DNA unwrapping parameter, the SDTF binding fraction, and the cooperativity. (See also Figure S5).
DISCUSSION
Our study pairs stochastic modeling and epigenomic chromatin accessibility measurements from primary cells to investigate the biophysical regulatory rules of histone octamer-DNA interactions that determine nucleosome positioning. Using probability theory, we described nucleosome eviction as a success-or-failure game scheme, as DNA has a chance of full eviction only under the on-phase of the SDTF signal. This scheme revealed the role of oscillatory inputs in nucleosome eviction, and heterogeneity in DNA accessibility under oscillatory SDTF dynamics. Nucleosome positioning data provided the nucleosome Eviction Probability Profile as a function of SDTF motif location, and fitting model parameters to the Eviction Probability Profile revealed quantitative features of nucleosome dynamics: 1) 30–40 base pairs of DNA-histone contacts around the SDTF binding site are disrupted, 2) the expected initial DNA unwrapping time from the fully wrapped state is about 7 minutes, and 3) evidence of cooperativity in the DNA unwrapping steps. Supportive of this model, these quantitative features of our model are consistent with previous experimental observations (Cheng et al., 2021).
Naturally, as with all mathematical models, the in vivo cellular system is more complex than the model describes, and our model is necessarily an abstraction describing one aspect of the dynamic epigenome that results when mammalian cells encounter an inflammatory threat. Nucleosome dynamics at each location along the genome are influenced by multiple factors, including but not limited to the stiffness of the local DNA, the histone marks or histone variants that are present, the density of nucleosomes at that region, and the binding motif location in relation to the position of the nucleosome (Brahma and Henikoff, 2020). However, our model is able to assess several characteristics of nucleosome dynamics that may govern the rules and parameter rates at which nucleosomes are evicted across the epigenome. These predictions help formulate hypotheses that are compared to time-course epigenomic sequencing data, which allows the selection of one of the hypotheses or the establishment of parameter ranges.
Notably, the model can be used to evaluate numerous different stimulus-response systems, including those with different SDTFs activated (Calderon et al., 2019), or different cell types and genomic locations that may have different kinetic rates governing the unwrapping and rewrapping of the nucleosome. Here we focused on immune responses and the resulting epigenome of innate immune macrophages, but the modeling approach can be applied to other contexts as well where cells encounter an inflammatory signal that produces stimulus-induced epigenomic changes (for example, cancer cell plasticity during immunotherapy). For innate immune responses particularly, the variation in the baseline epigenome that results from a prior exposure, rather than variation in genetically-encoded receptors like for T- and B-cells, may be a critical component of innate immune memory and response to future inflammatory threats (Netea et al., 2016). Thus, a predictive mechanistic understanding of how SDTF activity can evict nucleosomes can guide further investigation into epigenomic reprogramming events induced by inflammation.
The development and parameterization of this mechanistic model has several implications. First, the model may allow predictions of nucleosome eviction probabilities in response to any SDTF and any activation dynamics. Second, because the relationship of the motif location and nucleosome dyad correlates with eviction probability, the model can make a prediction on the probability for nucleosome eviction in a location-specific manner. Third, the model arrives at biological insights related to the nucleosome parameters themselves: by comparing pre- and post-stimulation nucleosome distributions, we can calculate experimental nucleosome eviction probabilities and fit the model to estimate the degree of cooperativity within the nucleosome and the range of effect of SDTF binding on disrupting nucleosomal contact-points.
This stochastic model describes the nucleosome, which is the fundamental unit of chromatin containing multi-step dynamic processes, and serves as a starting point for describing other epigenomic features (Bilokapic et al., 2018; Eslami-Mossallam et al., 2016; Hall et al., 2009; Henikoff, 2016). Future work incorporating other key elements of nucleosome dynamics, such as the structure of nucleosome arrays and the effect of histone modifications, or behaviors such as nucleosome sliding or rolling, which we have not yet considered here, may reveal further insights. In addition, although here we use an optimization approach to analyze this model topology and initial conditions with respect to the data, model parameters can also be further trained with machine learning approaches that incorporate additional layers of epigenomic data as training data in order for the parameters to incorporate more elements of the epigenomic complexity that exists in vivo. Our modeling framework and these further possibilities support the feasibility of combining biophysically-detailed mechanistic models of epigenetic processes, with next generation sequencing epigenome-wide measurements, to characterize kinetic rules controlling cellular responses to inflammation.
Limitations of the Study
Our stochastic model describes one process of how epigenomic states may be altered – through the activation of SDTFs and the effect of their DNA binding in disrupting the positions of nucleosomes. Within cells however, other proteins and enzymes also play key roles in how readily nucleosomes are evicted, for example the deposition of histone modifications, the presence of histone chaperones, or histone variants substituting for the canonical histone subunits. The activity of these other processes likely varies across different cell types and different cell states, for example in cancer cells vs. immune cells vs. epithelial cells. The models we present here, while biophysically detailed, still represent an abstraction of more complex interplay among many chromatin remodeling proteins. In another system, an increase in the estimated cooperativity, or range of SDTF effect, may suggest not simply a direct biophysical change in the modeled components, but rather could also indicate the activity of unmodeled proteins. Yet, using mathematical models such as those described here to estimate such parameters across different experimental systems will suggest further hypotheses that motivate the continual inclusion of additional mechanisms into future models.
STAR METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and materials should be directed to and will be fulfilled by the Lead Contact, German Enciso (enciso@uci.edu).
Materials Availability
No materials were generated in this paper.
Data and Code Availability
ATAC-seq data have been deposited at GEO and are publicly available as of the date of publication. Accession numbers are listed in the key resources table.
This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table.
Model and analysis code includes MATLAB code for running the stochastic model, and bioinformatic analysis of sequencing data. All original code has been deposited to Github and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Chemicals, Peptides, and Recombinant Proteins | ||
| LPS | Sigma, B5:055 | L2880 |
| murine TNF | Roche | 11271156001 |
| Experimental Models: Cell lines | ||
| Immortalized Myeloid Progenitor-derived macrophages | (Singh et al., 2022) | N/A |
| Experimental Models: Organisms | ||
| C57Bl/6 mouse Nfkbia−/− Rel−/− Tnf−/− Nfkbie−/− BMDMs | (Cheng et al., 2021) | N/A |
| Deposited Data | ||
| Macrophage PE ATACseq | This paper | GSE156385 |
| Macrophage SE ATACseq | (Cheng et al., 2021) | GSE146068 |
| Software and Algorithms | ||
| MATLAB 2016b | https://matlab.mathworks.com/ | |
| R (version 4.0.3) | https://www.r-project.org/ | |
| ENCODE-DCC ATACseq Pipeline | https://github.com/ENCODE-DCC/atac-seq-pipeline | |
| bedtools | (Quinlan and Hall, 2010) | https://bedtools.readthedocs.io/en/latest/ |
| NucleoATAC | (Schep et al., 2015) | https://github.com/GreenleafLab/NucleoATAC |
| HOMER | (Heinz et al., 2010) | http://homer.ucsd.edu/homer/ngs/peakMotifs.html |
| Nucleosome Model Code | This paper | DOI: 10.5281/zenodo.6503369 (https://github.com/signalingsystemslab/nucleosome_stochasticModel) |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Macrophage cell culture
All mouse experiments were approved by the UCLA animal research committee under protocols ARC2014–110 and ARC-2014–126. Macrophages were obtained via two methods: (1) differentiating bone-marrow-derived monocytes from male C57BL/6 mice in DMEM/10% FBS + 30% L929 supernatant for a total of 7 days, or (2) differentiating immortalized myeloid progenitors (iMPs) originally derived from male C57BL/6 mice, in DMEM/10% FBS + 30% L929 supernatant for a total of 10 days. BMDM data was obtained from paired-end resequencing of the same libraries that had been sequenced single-ended in Cheng et al., 2021, so no additional mice were used for this paper. As described in Cheng et al., 2021, sex-matched bone marrow-derived macrophages (BMDMs) were prepared by culturing bone marrow monocytes from femurs of 8–12-week-old mice in DMEM/10% FBS + 30% L929 supernatant medium using standard methods (Cheng et al., 2021, Adelaja et al., 2021). BMDMs were re-plated in experimental dishes on day 4, and stimulated on day 7 with 10ng/mL murine TNF (Roche 11271156001) for 4 hours. For iMP-derived macrophages (iMPDMs), cells were replated into 6cm plates with new media on day 7, at a density of ~20k cells/cm2. On day 10, cells were stimulated 100ng/mL lipopolysaccharide (LPS, Sigma Aldrich) for 4 hours.
METHOD DETAILS
ATAC sequencing
Control and stimulated immortalized myeloid progenitor derived macrophages (iMPDMs) were dissociated with Accutase (Thermo Fisher Scientific), and 50,000 cells were used per sample. Cell membranes were lysed using cold lysis buffer (10mM Tris-HCl pH7.5, 32 3mM MgCl2, 10mM NaCl and 0.1% IGEPAL CA-630). Nuclei were pelleted by centrifugation for 10 minutes at 500 × g and suspended in transposase reaction mixture (25 μl of 2X TD Buffer (Illumina), 2.5 μl of TD Enzyme 1 (Illumina), and 22.5 μl of nuclease-free water), and the transposase reaction was performed for 30 minutes at 37C in a thermomixer shaker. DNA was purified using MinElute PCR purification kit (QIAGEN, Hilden, Germany). Libraries were prepared for sequencing using Nextera DNA Library Preparation Kit (Illumina, FC-121). The libraries were purified using MinElute PCR purification kit (QIAGEN) and quantified using KAPA Library Quantification Kit (KAPA Biosystems). Libraries were sequenced paired end 2×100 on Illumina Novaseq.
QUANTIFICATION AND STATISTICAL ANALYSIS
Model simulations
Model implementation and simulations were performed in MATLAB 2016b. Further detailed description of the model can be found in the METHOD DETAILS.
Coefficients Variation
The coefficient variation for a probability distribution or a random variable is calculated with the standard deviation divided with the mean. Since this quantity gives a normalized degree of variation of a given probability distribution, we can use them to compare the variabilities of two probability distributions as described in Figure 2G.
Total variation distance
We used the total variation distance to measure similarities between the distributions of chromatin accessibilities under an oscillatory signal and a constant signal shown in Figure 4E. For probability distribution P1 and P2 defined on the same finite state space, the total variation distance is defined as . The usage of this distance can be found in “Model predicts cooperativity based on Eviction Probability Profiles” in Results.
ATAC-seq data processing
Macrophage ATAC-seq samples were generated as previously described (Buenrostro et al., 2015), and single-end data was obtained from (Cheng et al., 2021). Macrophage ATAC-seq libraries of the IκBα knockout mouse from Cheng et al., 2021 were re-sequenced paired-end 2×150 on HiSeq4000. Only paired-end sequencing allows the separation of nucleosomal fragments from non-nucleosomal fragments, as read fragments with lengths shorter than the nucleosome footprint of ~150 basepairs can be classified as nucleosome-free accessible regions, while read fragments of ~150bp, or a multiple of 150bp, can be classified as accessible nucleosomal genomic regions, with cut sites flanking nucleosome boundaries. ATAC-seq fastqs were processed through the ENCODE-DCC ATAC-seq pipeline (https://github.com/ENCODE-DCC/atac-seq-pipeline). The reads were trimmed using cutadapt, and aligned to mm10 or hg38 using bowtie2. Picard was used to de-duplicate reads, which were then filtered for high quality, paired reads using samtools. Peak calling was performed using macs2. The optimal Irreproducible Discovery Rate (IDR) thresholded peak output was used for all downstream analyses, with a threshold p-value of 0.05. Other ENCODE3 parameters were enforced with the flag --encode3. Reads that mapped to mitochondrial genes or blacklisted regions, as defined by the ENCODE pipeline, were removed. The peak files were merged using bedtools merge to create a consensus set of peaks across all samples.
ATAC-seq nucleosome analysis
Nucleosome positions were called using the merged regions, from paired-end ATAC-sequencing data, using the published software NucleoATAC (Schep et al., 2015). An example genomic location Cxcl2, illustrates the information obtained is orthogonal to simply chromatin accessibility (Figure S6). The output of this software provides putative nucleosomal and nucleosome-free regions of accessible chromatin, by analyzing the patterns of ATAC-seq read fragment sizes. As described in full detail in Schep et al, 2015, nucleosome occupancy is called by maximum likelihood estimation, and nucleosome dyad positions are called by considering the local maxima of candidate nucleosome positions. Genomic locations of nucleosome positions called were annotated, and NFκB motifs were found using the tool HOMER (Heinz et al., 2010). Motif searching was done using the three NFκB motif position weight matrices within the HOMER database, for length 9, 10, 11. Motifs were listed if they occurred within +/−200 basepairs of the nucleosome dyad. Nucleosomes across timepoints were matched by assigning them to their closest transcription start site for each sample. Nucleosomes assigned to a TSS for the baseline time point, and subsequently not found at that TSS at the later time point, were considered evicted. For analyses where the model calculated a probability of nucleosome eviction, nucleosomes that appeared, and matched to a new gene at the second time point but not in the first, were ignored. Probabilities of eviction p with respect to location of the binding motif and distance from nucleosome dyad were calculated by taking bins of distance from dyad, and using the following formula for each bin: , where nt=h is the number of nucleosomes at h hours.
Supplementary Material
ACKNOWLEDGEMENTS
JK and GE were partially supported by NSF grants DMS1763272, DMS1616233 and Simons Foundation grant 594598 (Qing Nie). JK is supported by Basic Science Research Institute Fund, whose NRF grant number is 2021R1A6A1A10042944. KMS is supported by the UCLA Medical Scientist Training Program (NIH NIGMS T32-GM008042) and Systems and Integrative Biology Training Grant (T32-GM008185). AH was funded by R01AI127864. We thank Sho Ohta for early access to the macrophage sequencing data and paired-end resequencing of the macrophage ATAC-seq libraries published in Cheng et al, 2021. Sequencing data from this paper was performed with the services of the UCLA Technology Center for Genomics and Bioinformatics Sequencing Core. We also thank the NSF-Simons Center for Multiscale Cell Fate for an Interdisciplinary Opportunity Award that initiated this project.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
References
- Adelaja A, Taylor B, Sheu KM, Liu Y, Luecke S, and Hoffmann A (2021). Six distinct NFκB signaling codons convey discrete information to distinguish stimuli and enable appropriate macrophage responses. Immunity 54, 916–930.e7. 10.1016/j.immuni.2021.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberts B, Johnson A, Lewis J, Raff M, Roberts K, and Walter P (2002). Chromosomal DNA and Its Packaging in the Chromatin Fiber. Molecular Biology of the Cell. 4th Edition. [Google Scholar]
- Allfrey VG, Littau VC, and Mirsky AE (1963). ON THE ROLE OF HISTONES IN REGULATING RIBONUCLEIC ACID SYNTHESIS IN THE CELL NUCLEUS*. Proc Natl Acad Sci U S A 49, 414–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Al-Radhawi MA, Vecchio DD, and Sontag ED (2019). Multi-modality in gene regulatory networks with slow promoter kinetics. PLOS Computational Biology 15, e1006784. 10.1371/journal.pcbi.1006784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barken D (2005). Comment on “Oscillations in NF- B Signaling Control the Dynamics of Gene Expression.” Science 308, 52a–52a. 10.1126/science.1107904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bednar J, Garcia-Saez I, Boopathi R, Cutter AR, Papai G, Reymer A, Syed SH, Lone IN, Tonchev O, Crucifix C, et al. (2017). Structure and Dynamics of a 197 bp Nucleosome in Complex with Linker Histone H1. Molecular Cell 66, 384–397.e8. 10.1016/j.molcel.2017.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behar M, and Hoffmann A (2010). Understanding the temporal codes of intra-cellular signals. Current Opinion in Genetics & Development 20, 684–693. 10.1016/j.gde.2010.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bilokapic S, Strauss M, and Halic M (2018). Histone octamer rearranges to adapt to DNA unwrapping. Nat Struct Mol Biol 25, 101–108. 10.1038/s41594-017-0005-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brahma S, and Henikoff S (2020). Epigenome Regulation by Dynamic Nucleosome Unwrapping. Trends in Biochemical Sciences 45, 13–26. 10.1016/j.tibs.2019.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Bruin L, Tompitak M, Eslami-Mossallam B, and Schiessel H (2016). Why Do Nucleosomes Unwrap Asymmetrically? J. Phys. Chem. B 120, 5855–5863. 10.1021/acs.jpcb.6b00391. [DOI] [PubMed] [Google Scholar]
- Buenrostro JD, Wu B, Chang HY, and Greenleaf WJ (2015). ATAC‐seq: A Method for Assaying Chromatin Accessibility Genome‐Wide. Current Protocols in Molecular Biology 109. 10.1002/0471142727.mb2129s109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calderon D, Nguyen MLT, Mezger A, Kathiria A, Müller F, Nguyen V, Lescano N, Wu B, Trombetta J, Ribado JV, et al. (2019). Landscape of stimulation-responsive chromatin across diverse human immune cells. Nat Genet 1–12. 10.1038/s41588-019-0505-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callegari A, Sieben C, Benke A, Suter DM, Fierz B, Mazza D, and Manley S (2019). Single-molecule dynamics and genome-wide transcriptomics reveal that NF-kB (p65)-DNA binding times can be decoupled from transcriptional activation. PLOS Genetics 15, e1007891. 10.1371/journal.pgen.1007891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen P, Dong L, Hu M, Wang Y-Z, Xiao X, Zhao Z, Yan J, Wang P-Y, Reinberg D, Li M, et al. (2018). Functions of FACT in Breaking the Nucleosome and Maintaining Its Integrity at the Single-Nucleosome Level. Mol Cell 71, 284–293.e4. 10.1016/j.molcel.2018.06.020. [DOI] [PubMed] [Google Scholar]
- Cheng QJ, Ohta S, Sheu KM, Spreafico R, Adelaja A, Taylor B, and Hoffmann A (2021). NF-κB dynamics determine the stimulus specificity of epigenomic reprogramming in macrophages. Science 372, 1349–1353. 10.1126/science.abc0269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou T (2007). Peeling and Sliding in Nucleosome Repositioning. Phys. Rev. Lett 99, 058105. 10.1103/PhysRevLett.99.058105. [DOI] [PubMed] [Google Scholar]
- Dechassa ML, Sabri A, Pondugula S, Kassabov SR, Chatterjee N, Kladde MP, and Bartholomew B (2010). SWI/SNF has intrinsic nucleosome disassembly activity that is dependent on adjacent nucleosomes. Mol Cell 38, 590–602. 10.1016/j.molcel.2010.02.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobrovolskaia IV, and Arya G (2012). Dynamics of Forced Nucleosome Unraveling and Role of Nonuniform Histone-DNA Interactions. Biophys J 103, 989–998. 10.1016/j.bpj.2012.07.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodd IB, Micheelsen MA, Sneppen K, and Thon G (2007). Theoretical Analysis of Epigenetic Cell Memory by Nucleosome Modification. Cell 129, 813–822. 10.1016/j.cell.2007.02.053. [DOI] [PubMed] [Google Scholar]
- Eslami-Mossallam B, Schiessel H, and van Noort J (2016). Nucleosome dynamics: Sequence matters. Advances in Colloid and Interface Science 232, 101–113. 10.1016/j.cis.2016.01.007. [DOI] [PubMed] [Google Scholar]
- Hall MA, Shundrovsky A, Bai L, Fulbright RM, Lis JT, and Wang MD (2009). High resolution dynamic mapping of histone-DNA interactions in a nucleosome. Nat Struct Mol Biol 16, 124–129. 10.1038/nsmb.1526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heinz S, Benner C, Spann N, Bertolino E, Lin YC, Laslo P, Cheng JX, Murre C, Singh H, and Glass CK (2010). Simple Combinations of Lineage-Determining Transcription Factors Prime cis-Regulatory Elements Required for Macrophage and B Cell Identities. Molecular Cell 38, 576–589. 10.1016/j.molcel.2010.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henikoff S (2016). Mechanisms of Nucleosome Dynamics In Vivo. Cold Spring Harb Perspect Med 6. 10.1101/cshperspect.a026666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann A, Levchenko A, Scott ML, and Baltimore D (2002). The IkappaB-NF-kappaB signaling module: temporal control and selective gene activation. Science 298, 1241–1245. 10.1126/science.1071914. [DOI] [PubMed] [Google Scholar]
- Kim J, and Enciso G (2020). Absolutely robust controllers for chemical reaction networks. J R Soc Interface 17, 20200031. 10.1098/rsif.2020.0031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klemm SL, Shipony Z, and Greenleaf WJ (2019). Chromatin accessibility and the regulatory epigenome. Nature Reviews Genetics 20, 207–220. 10.1038/s41576-018-0089-8. [DOI] [PubMed] [Google Scholar]
- Konrad SF, Vanderlinden W, Frederickx W, Brouns T, Menze BH, Feyter SD, and Lipfert J (2021). High-throughput AFM analysis reveals unwrapping pathways of H3 and CENP-A nucleosomes. Nanoscale 13, 5435–5447. 10.1039/D0NR08564B. [DOI] [PubMed] [Google Scholar]
- Kurtz TG (1980). Representations of Markov Processes as Multiparameter Time Changes. The Annals of Probability 8, 682–715. [Google Scholar]
- Lee C-K, Shibata Y, Rao B, Strahl BD, and Lieb JD (2004). Evidence for nucleosome depletion at active regulatory regions genome-wide. Nat Genet 36, 900–905. 10.1038/ng1400. [DOI] [PubMed] [Google Scholar]
- Lee RE, Walker SR, Savery K, Frank DA, and Gaudet S (2014). Fold change of nuclear NF-kappaB determines TNF-induced transcription in single cells. Mol Cell 53, 867–879. 10.1016/j.molcel.2014.01.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Levitus M, Bustamante C, and Widom J (2005). Rapid spontaneous accessibility of nucleosomal DNA. Nature Structural & Molecular Biology 12, 46–53. 10.1038/nsmb869. [DOI] [PubMed] [Google Scholar]
- Liu Y, Zhou K, Zhang N, Wei H, Tan YZ, Zhang Z, Carragher B, Potter CS, D’Arcy S, and Luger K (2020). FACT caught in the act of manipulating the nucleosome. Nature 577, 426–431. 10.1038/s41586-019-1820-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longo DM, Selimkhanov J, Kearns JD, Hasty J, Hoffmann A, and Tsimring LS (2013). Dual Delayed Feedback Provides Sensitivity and Robustness to the NF-kB Signaling Module. PLOS Computational Biology 9, 15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luger K, Mäder AW, Richmond RK, Sargent DF, and Richmond TJ (1997). Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature 389, 251–260. 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- Luger K, Dechassa ML, and Tremethick DJ (2012). New insights into nucleosome and chromatin structure: an ordered state or a disordered affair? Nature Reviews Molecular Cell Biology 13, 436–447. 10.1038/nrm3382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauney AW, Tokuda JM, Gloss LM, Gonzalez O, and Pollack L (2018). Local DNA Sequence Controls Asymmetry of DNA Unwrapping from Nucleosome Core Particles. Biophys J 115, 773–781. 10.1016/j.bpj.2018.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Méléard S, and Villemonais D (2011). Quasi-stationary distributions and population processes. ArXiv:1112.4732 [Math] 10.1214/11-PS191. [DOI] [Google Scholar]
- Miller JA, and Widom J (2003). Collaborative Competition Mechanism for Gene Activation In Vivo. Molecular and Cellular Biology 23, 1623–1632. 10.1128/MCB.23.5.1623-1632.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Möbius W, Neher RA, and Gerland U (2006). Kinetic Accessibility of Buried DNA Sites in Nucleosomes. Physical Review Letters 97. 10.1103/PhysRevLett.97.208102. [DOI] [PubMed] [Google Scholar]
- Mobius W, Osberg B, Tsankov AM, Rando OJ, and Gerland U (2013). Toward a unified physical model of nucleosome patterns flanking transcription start sites. Proceedings of the National Academy of Sciences 110, 5719–5724. 10.1073/pnas.1214048110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Netea MG, Joosten LAB, Latz E, Mills KHG, Natoli G, Stunnenberg HG, ONeill LAJ, and Xavier RJ (2016). Trained immunity: A program of innate immune memory in health and disease. Science 352, aaf1098–aaf1098. 10.1126/science.aaf1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngo TTM, Zhang Q, Zhou R, Yodh JG, and Ha T (2015). Asymmetric Unwrapping of Nucleosomes under Tension Directed by DNA Local Flexibility. Cell 160, 1135–1144. 10.1016/j.cell.2015.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostuni R, Piccolo V, Barozzi I, Polletti S, Termanini A, Bonifacio S, Curina A, Prosperini E, Ghisletti S, and Natoli G (2013). Latent Enhancers Activated by Stimulation in Differentiated Cells. Cell 152, 157–171. 10.1016/j.cell.2012.12.018. [DOI] [PubMed] [Google Scholar]
- Polach KJ, and Widom J (1995). Mechanism of Protein Access to Specific DNA Sequences in Chromatin: A Dynamic Equilibrium Model for Gene Regulation. Journal of Molecular Biology 254, 130–149. 10.1006/jmbi.1995.0606. [DOI] [PubMed] [Google Scholar]
- Purvis JE, and Lahav G (2013). Encoding and Decoding Cellular Information through Signaling Dynamics. Cell 152, 945–956. 10.1016/j.cell.2013.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinlan AR, and Hall IM (2010). BEDTools: a flexible suite of utilities for comparing genomic features. Bioinformatics 26, 841–842. 10.1093/bioinformatics/btq033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schep AN, Buenrostro JD, Denny SK, Schwartz K, Sherlock G, and Greenleaf WJ (2015). Structured nucleosome fingerprints enable high-resolution mapping of chromatin architecture within regulatory regions. Genome Research 25, 1757–1770. 10.1101/gr.192294.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segal E, and Widom J (2009). What controls nucleosome positions? Trends in Genetics 25, 335–343. 10.1016/j.tig.2009.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segal E, Fondufe-Mittendorf Y, Chen L, Thåström A, Field Y, Moore IK, Wang J-PZ, and Widom J (2006). A genomic code for nucleosome positioning. Nature 442, 772–778. 10.1038/nature04979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen S, Cheng Z, Sheu KM, Chen YH, and Hoffmann A (2020). Gene Regulatory Strategies that Decode the Duration of NFκB Dynamics Contribute to LPS- versus TNF-Specific Gene Expression. Cell Syst 10, 169–182.e5. 10.1016/j.cels.2019.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shinar G, and Feinberg M (2010). Structural sources of robustness in biochemical reaction networks. Science 327, 1389–1391. 10.1126/science.1183372. [DOI] [PubMed] [Google Scholar]
- Shivaswamy S, Bhinge A, Zhao Y, Jones S, Hirst M, and Iyer VR (2008). Dynamic remodeling of individual nucleosomes across a eukaryotic genome in response to transcriptional perturbation. PLoS Biol 6, e65. 10.1371/journal.pbio.0060065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shoval O, Goentoro L, Hart Y, Mayo A, Sontag E, and Alon U (2010). Fold-change detection and scalar symmetry of sensory input fields. Proc Natl Acad Sci U S A 107, 15995–16000. 10.1073/pnas.1002352107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh A, Sen S, Adelaja A, and Hoffmann A (2022). Stimulus-Response signaling dynamics characterize macrophage polarization states. 2022.03.27.485991. 10.1101/2022.03.27.485991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelling J, Gilles ED, and Doyle FJ (2004). Robustness properties of circadian clock architectures. Proc Natl Acad Sci U S A 101, 13210–13215. 10.1073/pnas.0401463101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart AJ, Hannenhalli S, and Plotkin JB (2012). Why Transcription Factor Binding Sites Are Ten Nucleotides Long. Genetics 192, 973–985. 10.1534/genetics.112.143370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tims HS, Gurunathan K, Levitus M, and Widom J (2011). Dynamics of Nucleosome Invasion by DNA Binding Proteins. Journal of Molecular Biology 411, 430–448. 10.1016/j.jmb.2011.05.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinmann AS, Plevy SE, and Smale ST (1999). Rapid and Selective Remodeling of a Positioned Nucleosome during the Induction of IL-12 p40 Transcription. Immunity 11, 665–675. 10.1016/S1074-7613(00)80141-7. [DOI] [PubMed] [Google Scholar]
- Werner SL, Barken D, and Hoffmann A (2005). Stimulus specificity of gene expression programs determined by temporal control of IKK activity. Science 309, 1857–1861. 10.1126/science.1113319. [DOI] [PubMed] [Google Scholar]
- Zhou K, Gaullier G, and Luger K (2019). Nucleosome structure and dynamics are coming of age. Nature Structural & Molecular Biology 26, 3–13. 10.1038/s41594-018-0166-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
ATAC-seq data have been deposited at GEO and are publicly available as of the date of publication. Accession numbers are listed in the key resources table.
This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table.
Model and analysis code includes MATLAB code for running the stochastic model, and bioinformatic analysis of sequencing data. All original code has been deposited to Github and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Chemicals, Peptides, and Recombinant Proteins | ||
| LPS | Sigma, B5:055 | L2880 |
| murine TNF | Roche | 11271156001 |
| Experimental Models: Cell lines | ||
| Immortalized Myeloid Progenitor-derived macrophages | (Singh et al., 2022) | N/A |
| Experimental Models: Organisms | ||
| C57Bl/6 mouse Nfkbia−/− Rel−/− Tnf−/− Nfkbie−/− BMDMs | (Cheng et al., 2021) | N/A |
| Deposited Data | ||
| Macrophage PE ATACseq | This paper | GSE156385 |
| Macrophage SE ATACseq | (Cheng et al., 2021) | GSE146068 |
| Software and Algorithms | ||
| MATLAB 2016b | https://matlab.mathworks.com/ | |
| R (version 4.0.3) | https://www.r-project.org/ | |
| ENCODE-DCC ATACseq Pipeline | https://github.com/ENCODE-DCC/atac-seq-pipeline | |
| bedtools | (Quinlan and Hall, 2010) | https://bedtools.readthedocs.io/en/latest/ |
| NucleoATAC | (Schep et al., 2015) | https://github.com/GreenleafLab/NucleoATAC |
| HOMER | (Heinz et al., 2010) | http://homer.ucsd.edu/homer/ngs/peakMotifs.html |
| Nucleosome Model Code | This paper | DOI: 10.5281/zenodo.6503369 (https://github.com/signalingsystemslab/nucleosome_stochasticModel) |


