A real-time feedback system stabilises the regulation of worker reproduction under various colony sizes

Simeon Adejumo; Tomonori Kikuchi; Kazuki Tsuji; Kana Maruyama-Onda; Ken Sugawara; Yoshikatsu Hayashi

doi:10.1371/journal.pcbi.1010840

. 2023 Mar 24;19(3):e1010840. doi: 10.1371/journal.pcbi.1010840

A real-time feedback system stabilises the regulation of worker reproduction under various colony sizes

Simeon Adejumo ^1,^*, Tomonori Kikuchi ², Kazuki Tsuji ³, Kana Maruyama-Onda ⁴, Ken Sugawara ⁵, Yoshikatsu Hayashi ^1,^¤,^*

Editor: Christian Hilbe⁶

PMCID: PMC10075462 PMID: 36961874

Abstract

Social insects demonstrate adaptive behaviour for a given colony size. Remarkably, most species do this even without visual information in a dark environment. However, how they achieve this is yet unknown. Based on individual trait expression, an agent-based simulation was used to identify an explicit mechanism for understanding colony size dependent behaviour. Through repeated physical contact between the queen and individual workers, individual colony members monitor the physiological states of others, reflecting such contact information in their physiology and behaviour. Feedback between the sensing of physiological states and the corresponding behaviour patterns leads to self-organisation with colonies shifting according to their size. We showed (1) the queen can exhibit adaptive behaviour patterns for the increase in colony size while density per space remains unchanged, and (2) such physical constraints can underlie the adaptive switching of colony stages from successful patrol behaviour to unsuccessful patrol behaviour, which leads to constant ovary development (production of reproductive castes). The feedback loops embedded in the queen between the perception of internal states of the workers and behavioural patterns can explain the adaptive behaviour as a function of colony size.

Author summary

In the ant Diacamma cf. Indicum (from Japan), the queen spends more effort on queen pheromone-transmitting behaviour (patrolling) in response to the growth of colony size to inhibit worker ovary development. We used an agent-based simulation to understand the mechanism of the colony size dependent behaviour of the queen. The queen simply follows a feedback loop mediated by the mutual contact between her and the workers. In other words, the queen patrols the workers more often when she has recently encountered workers with developed ovaries.

We found that this self-regulatory mechanism works even when the worker density per space was kept constant. We also found that despite the presence of such feedback, the effectiveness of the queen patrol, and thus, the suppression of worker ovarian activity decreased with increasing colony size. This indicates that a colonial phase shift from the ergonomic stage to the reproductive stage, a general phenomenon in social insect colonies, emerged as the colony grew.

Introduction

Various collective behaviours in social insects are regulated by self-organisation [1]. While many studies have addressed questions about how short-term (finite) collective behaviour (foraging, moving, etc., dynamics from the beginning to the end of behaviour) is autonomously controlled, there is relatively scant knowledge about the homeostatic mechanisms of societies. Namely, while the homeostatic mechanisms of individual organisms, such as breathing, thermoregulation, and osmoregulation have been thoroughly studied, how society is autonomously maintained has attracted less attention.

Each species or population of social insects may have a characteristic value in social traits such as colony size and caste ratios. However, the colony size can dramatically change over time as the colony grows (like in the body size of multicellular organisms [2]), and the caste composition and age composition also can show much shorter-term fluctuations [3–5]. The reproductive division of labour through suppression of worker reproduction, which is a hallmark of insect eusociality, is maintained even during such changes in the internal environment of the colony. This implies the existence of a size-free autonomous control mechanism, but their detailed mechanisms have not been clarified [6].

From a phylogenetic point of view, physical suppression via dominance behaviour is considered an ancestral state of insect eusociality and has changed to chemical suppression using the queen pheromone [7] as the colony size increases. The reason is likely due to a physical constraint since direct interference would be difficult if the colony size increased above a certain point. However, control problems could still arise as the colony size increases. There are also control problems which could arise during the process of colony development (colonial ontogeny) where physical suppression is still practical as a form of controlling worker ovary development.

So far, mechanisms of the reproductive division of labour, such as dominance behaviour, queen pheromones and worker policing, have been extensively studied [8–10], but less about the robustness and effectiveness of the regulation mechanisms against the increase in colony size [11–14].

Based on a computer simulation model, we examined how robust the regulation system for worker reproduction is when colony size changes. Workers in many Hymenoptera are prevented from laying eggs in the presence of the queen, instead engaging in non-reproductive work. For workers, this reproductive altruism is considered to be an adaptive tactic in terms of inclusive fitness optimisation [15, 16].

In many species, when the queen dies or becomes absent for any reason, the worker’s ovaries begin to develop and eventually lay male-destined haploid eggs. This switch in reproduction is triggered by the perception of the queen’s presence. Therefore, the transmission of information on the existence of the queen is the key to understanding the mechanism of the reproductive division of labour [10, 17–19].

Information about the queen’s existence has been considered to be transmitted by a chemical substance (queen pheromone). Empirical studies in recent years revealed that the main body of the queen pheromone is low volatility cuticular hydrocarbons (CHCs) that are conserved widely in social Hymenopteran taxa such as ants, bees and wasps [20]. Analogous solutions has also been found in termites in the form of 9-ODA [21, 22]. In an environment where the queen pheromone has low volatility, its transmission is thought to require direct physical contact between the queen and her nest mates.

In this study, we focused on Diacamma ants as a model system [23]. Specifically the Japanese Diacamma, Diacamma.cf. Indicum, the only Japanese species. The information transmission mechanism of the gamergate worker of this species (known henceforth as the queen) has been well established [24]. This information is coded by CHCs and transmitted by direct contact between the queen and workers [25]. The queen is reported to exhibit specific behaviours to improve the information transmission efficiency of her presence. The locomotory activity of the ant queen in the nest is generally not as high as that of workers, but in the Japanese Diacamma, the queen frequently roams the nest (this is called patrol [26]).

Importantly, in large colonies, the queen’s patrol is more active than that in small colonies [24]. In other words, the queen is buffering the possible decrease in the transmission efficiency (contact probability) of the queen pheromone to workers. Since in Diacamma the physiological effect (suppression of ovarian development of workers) of the queen pheromone can last only 3 hours or so [24], stable control of worker reproduction seems to require the perception of ever-changing colony size, thereby the queen can adjust her patrol effort. However, a question remains about how the queen obtains colony size information and reflects it in her actions.

In ants, the frequency of contacts between individuals is a local population-size proxy, and such contact frequency is used for behavioural switching in various contexts such as moving the nest [27, 28]. Note, however, that the fundamental mechanisms which can link different types of perception such as the frequency of contacts, local density perception and colony size perception have been largely unclear.

In general, the feedback mechanism is essential for system stability and has been identified in various collective actions created by self-organisation [29–31]. In Diacamma, it is known that the queen acts aggressively towards reproductive workers and when she encounters an egg-laying worker during her patrol, she steals and destroys the egg (queen policing) [32]. Therefore, we assume the queen can detect the reproductive status of the worker when she contacts it during her patrol. There is at least some circumstantial evidence that the queen can detect the reproductive state of workers from Shimoji et al. [33]. The queen can suppress worker reproduction through dominance interactions. The ability to sense worker reproductive status is a necessary precursor to determine if and when these dominance interactions should take place.

Previous work by Sugawara et al. [34] theoretically suggested that a feedback mechanism could play a role in the colony size dependant patrol of Diacamma queens. Their model had three assumptions: (1) A worker that has lost contact with the queen for a significant period is released from the inhibitory effects of the queen pheromone; (2) such a worker starts ovarian development and also starts herself emission of the queen pheromone (or other chemicals associated with ovarian development); (3) when the queen, on patrol, comes into contact with a worker who emits such chemicals, the queen increases her future patrol effort according to the chemical concentration she perceives.

As the colony size increases, the contact efficiency of the queen decreases, and the workers have more chances to develop their ovaries and emit the associated chemicals. The colony-size-dependent behaviour of the queen would be a result of feedback mechanisms in response to changes in the worker’s physiological condition (Fig 1).

Fig 1 — A feedback loop between the queen’s patrol behaviour and the reproductive activity of workers.

Sugawara et al.’s model assumed that the queen contacts the workers at a constant rate (number of contacts per unit time), and as the colony grows, the contact rate with the queen per worker decreases linearly, increasing the patrol frequency of the queen (Fig 1). It is, however, not self-evident that the queen and workers have a constant contact rate. For instance, workers’ behaviour may change as the density of workers in a given space increases. This itself is thought to be a response to changes in contact frequency to reduce the probability of contact between individuals [35].

However, the average individual density for a given space in the ant’s nest may not change very much, even if the colony size changes. Franks et al. [36] found that ants changed the size of their nest space to fit with the colony size, making changes to the nest as required. Though others [37] found that the increase in nest space is slower than the increase in colony size, the largest variation in worker density occurred due to seasonal changes. Inter-individual distance also appears to be regulated [38]. Indeed in Diacamma the worker density per space in the nest remains almost constant (see the experimental results in Appendix 4, S4 Fig in appendix).

As the previous method by Sugawara et al. did not include the spatial aspect, our approach to this problem is to use an agent-based simulation in which the queen and workers can move around and interact in a defined space. Regardless of the colony size, the worker density per space (surface area) was assumed to remain constant. Thus, the queen was simulated under the condition that the absolute contact rate with other individuals (workers) would not be an indicator of colony size. The mathematical model by Sugawara et al. [34] focused only on the queen’s patrol and did not investigate changes in worker reproductive status. We need to keep in mind that queen pheromones suppress worker reproduction, so the queen needs to evaluate the internal state of the workers. That is, if activated, the patrol behaviour of the queen results in the inactivation of the workers’ ovaries, suppressing the development of ovaries. Furthermore, since the contact between the queen and the workers is a stochastic event, the contact interval tends to vary from individual to individual. Therefore, it is unclear whether a simple increase in patrol time or frequency is effective in limiting the reproduction of workers at a colony-wide level.

This is the first time that an agent-based has been used to investigate the effectiveness of the queen’s patrol behaviour via the tracking of the internal state of workers. Although simulations have been used in other biological contexts such as Boids. Boids are an agent-based simulation [39] that replicates the complex flight patterns observed in groups of flocking birds by simulating the interaction between the individuals of the flock. The agent-based simulation can also be used for predicting the behaviour of the flock given simple rules the individuals follow. However, the Boids do not use feedback between individual agents to determine the flight path of the flock, instead, monitoring their neighbours.

Previous studies were also able to successfully simulate the nest quality assessment behaviour of ants. These include Şahin and Franks [40], which utilised a free mobile robot simulator to study nest assessment dynamics in a similar way to the current paper. Similar approaches were used by Perna et al. [31], Marshall et al. [41], and Shiraishi et al. [42] which were able to reproduce results observed in the literature for trail formation. For the agent-based simulation proposed in this paper, the agents have an internal state which modulates the behaviour of the agents and reacts to the mutual interactions which occur between agents to form a negative feedback loop. This leads to control over the division of reproductive labour in the colony.

Using an agent-based simulation has substantial advantages in studying our hypothesis of a negative feedback mechanism. As a result, it is possible to program an individual organism’s behaviour and its interactions with other organisms with certain degrees of freedom, such as density. In other words, group behaviour arises as a result of the contact between agents and between the agents and their environment, rather than attempting to represent system-level phenomena [43, 44]. Also, it gives other advantages such as allowing a closer examination of how the internal dynamics which characterise individual behaviour are coupled with the more complex group behaviour [45, 46].

In this study, using an agent-based simulation, we investigated how the reproductive state (ovarian development) of the workers and the patrol behaviour of the queen are affected by the change in colony size. We set the condition that the individual density per nest space is constant even if the colony size changes. We also provide experimental evidence and results supporting the constant-density assumption and validating simulation results. We propose a feedback mechanism between the internal states and the patrol behaviour of the queen. We discuss how the feedback mechanism contributes to the stable suppression of worker reproduction as the colony size increases.

Materials and methods

Maintenance and experimental procedure

The taxonomic status of species of genus Diacamma is still under revision. Since it is known that there are only one species of this genus in Japan that is very closely related to the Indian species Diacamma Indicum, we tentatively use the new name Diacamma cf. Indicum (from Japan) following Fujioka et al. [47](previously described as Diacamma sp. from Japan). The species has no morphological castes among females, that is, all females are wingless and monomorphic. In each colony, a single mated female (queen) functions as the reproductive queen that produces female eggs, whereas the other females play the helper-worker role [48].

New colonies are founded via colony fission. When the queen is absent after fission or due to queen mortality, among the cohort of newly emerged females the most dominant individual (usually the first emerged) copulates and becomes the next queen. In the field, colonies contain 20–300 workers, and alates (males) are produced in large queen-right colonies and orphan colonies [49, 50]. Unmated workers can potentially lay male-destined haploid eggs. However, in colonies at the ergonomic (growing) stage (i.e., ones with fewer than 100 workers), worker reproduction is suppressed by queen pheromone and, queen and worker policing [25, 32, 50, 51]. Whereas in colonies at the reproductive stage (containing 100 workers or more) such suppression is relaxed, and males are produced by worker reproduction [50].

We used colonies of Diacamma cf. indicum collected on the main island of Okinawa during 2001–2014. Those colonies were maintained in a laboratory at 25 ±1°C with a light: dark cycle of 12 h:12 h. Each colony was kept in a plastic container (26.5 cm length × 18.5 cm width × 5 cm height) with a plaster floor (1.5 cm thick), however, in the natural environment, ants would explore the surrounding environments to expand the colony space whenever there is an opportunity. In the middle of the floor, a 13 × 9 cm depression (1 cm deep) covered with a glass plate was prepared for the ants as an artificial nest. Ants were fed honey water and mealworms ad libitum three or four times a week.

Ants were kept in the laboratory. First, all workers and the queen in each of the 15 colonies were marked with enamel paint for individual identification. The number of workers (colony size) was 58, 69, 81, 110, 125, 128, 131, 144, 149, 151, 162, 169, 174, 181, and 214, respectively (mean ± SD = 137.9 ± 42.7). For the video recording, each colony was moved to another artificial nest, which was a plastic container (26.5 cm length × 18.5 cm width × 5 cm height) with a plaster floor (1.5 cm thick). In the middle of the floor, a depression (8 cm length × 16 cm width × 1 cm depth) covered with a glass plate was prepared for the ants as an artificial nest. After acclimatisation for a day, we video-recorded each colony for 12h. By using that video data, we were able to track all queen–worker contacts.

Agent-based simulations

Overview

To validate our hypothesis of the negative feedback loop between the queen and workers, we ran the agent-based simulations in which the queen and workers move randomly within the grid space and contact each other. The internal state of the workers is defined as the hypothetical physiological condition, such as the hormone level, which controls the ovary development in workers and queen pheromone secretion in the queen. Within an ant colony, the queen’s perception of the internal state via contact is largely dependent on the frequency of her contacts with workers as a function of time. Thus, along with the internal dynamics of the queen and workers, the spatial distribution of the workers and the queen as a function of time should play an important role in the patrol behaviour of queens and the reproductive behaviour of workers. Note that the density of workers was kept the same though the number of workers (colony size) increased. This can distinguish the mechanism based on the negative feedback loop from those dependent on the perception of density [35]. To include the spatial degree of freedom, we used an agent-based simulation to model the behaviour of the queen and individual workers within a certain space representing the nest.

We first assumed that the internal state of the workers and the queen would operate differently. For the worker, the internal state would represent their ovary development and demonstrate a steady increase over time. This could be suppressed by the queen via direct contact (perception of the queen pheromone). For the queen, the internal state would represent the probability to become active. That is, the likelihood that the queen will go from an inactive state to an active state, at which point she will begin to patrol the colony. The queen’s internal state steadily decreases (increasing her resting period) but increases when interacting with workers. This increase is proportional to the internal state of the worker who has been contacted. Meaning, a worker with a low internal state has minimal effect on the queen’s internal state but a worker with a high internal state increases the queen’s internal state and therefore her likelihood to begin patrolling the colony.

The queen’s movement [52, 53] around the nest was based on her temporal behaviour: when she is in the active state, she moves around the space, whereas in the inactive state, she halts within the grid she had moved in. The contact behaviour of the queen depended on these temporal behavioural patterns of active–inactive cycles. In this case, the workers also have active-inactive cycles which determined their movement around the space and were determined a priori.

The movement of the queen and workers around the colony was a simple random walk around the nest space. The next position of the agents is generated randomly from one of 4 directions, North, South, East and West. The movements of the agents are asynchronous, with agents only moving when they are in an active state. The queen walks around the nest space to contact all workers in the colony to suppress their internal states. The duration of the simulation was determined by how long it took the queen to contact all workers at least once. The simulation was then terminated. Various variables were recorded for analysis, including the active and inactive period of the queen and the contacts between the queen and workers.

Internal state dynamics

The rhythmic cycle of the active–inactive state was simplified into the two time periods of the active time (t_a) and the inactive time (t_r). For the worker agents, t_a and t_r were kept constant ( $t_{a_{c o n s t a n t}} = 20$ steps, $t_{r_{c o n s t a n t}} = 100$ steps). For the queen agent, t_a was kept constant ( $t_{a_{c o n s t a n t}} = 20$ steps), but t_r(t) was modulated by her internal state, I_q(t), using the dynamics of:

\begin{matrix} t_{r} (t) = t_{r_{c o n s t a n t}} \cdot e^{- δ \cdot I_{q} (t)} \end{matrix}

(1)

where $t_{r_{c o n s t a n t}}$ and δ were constant ( $t_{r_{c o n s t a n t}} = 100$ steps, δ = 20.0). I_q(t) represents the likelihood that the queen will transition to patrolling at time t. Increases in I_q(t) lead to a decrease in the inactive time, t_r(t), of the queen. If the queen has a prolonged period where her internal state is low, then t_r(t) approaches $t_{r_{c o n s t a n t}}$ .

To test our hypothesis about the feedback mechanisms of internal state and behaviour, we model the dynamics of the internal states of the queen and workers in the following manner. The dynamics of the internal state of the queen is given by:

\begin{matrix} I_{q} (t + 1) = (1 - ϵ) \cdot I_{q} (t) + α \cdot δ (\vec{x_{q}}, \vec{x_{w}}) \cdot I_{w} (t) \end{matrix}

(2)

(1 − ϵ) ⋅ I_q(t) is a damping factor, where ϵ = 0.01 and is constant. As the reproductive division of labour enables the queen to be the main producer of offspring in the colony, there is a compromise between patrolling the colony and laying eggs. As the internal state of the queen represents the likelihood she will become active, we use the damping factor to naturally decrease the queen’s internal state over time. This allows the queen to move to a more restful state, where there is minimal patrol, assuming workers have a low internal state. The second term, $α \cdot δ (\vec{x_{q}}, \vec{x_{w}}) \cdot I_{w} (t)$ , is an activation factor. The activation factor increases the probability of the queen becoming active when the queen contacts a worker with a high internal state. It is also proportional to the number of contacts with the workers. α = 0.1 and is constant. $\vec{x_{g}}$ and $\vec{x_{w}}$ denote the position of the queen and worker respectively. The term δ(r) denotes Kronecker’s delta, i.e., its value is zero except when the distance between $\vec{x_{q}}$ and $\vec{x_{w}}$ is zero, then δ(r) = 1.

The dynamics of the internal state of the workers was given by:

\begin{matrix} I_{w} (t + 1) = (1 - β) \cdot I_{w} (t) + γ - κ \cdot δ (\vec{x_{q}}, \vec{x_{w}}) \cdot I_{w} (t) \end{matrix}

(3)

γ and β represent an activation factor that increases the internal state of the worker over time as a function of time. This levels off over time as I_w(t) approaches 1. In this case, γ and β were set to 0.0001. Here we chose the constants of the activation factor to reflect the pace of ovary development in workers observed in previous work where the queen was removed from the colony [24]. The next term only functions to decrease the internal state of the worker, I_w(t), when the worker is contacted by the queen with κ = 0.9009, representing an approximately 90% decrease in the worker’s internal state.

Spatial behavioural dynamics

While we understand that the movement of ants in a real colony are less than random, for simplicity, we implemented spatial dynamics in the following way:

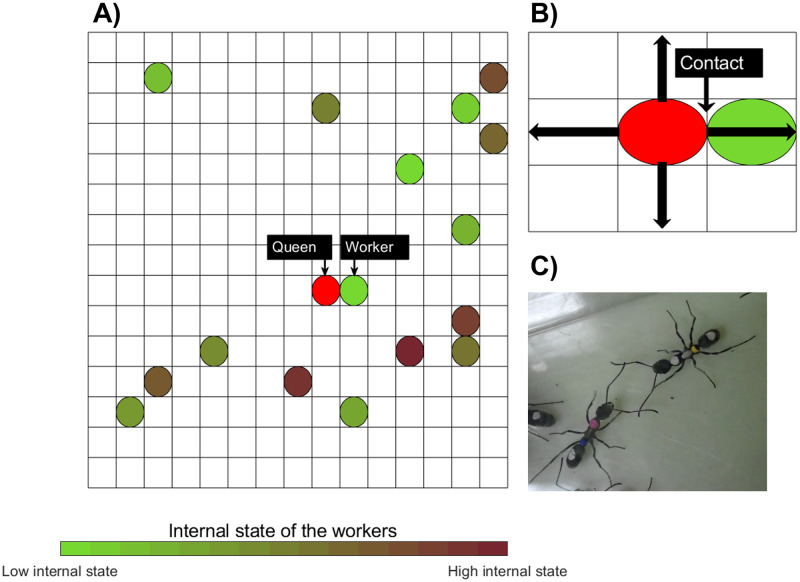
1. The virtual nest was set with a grid size of L × L (Fig 2A) with distance measured in arbitrary units (simply referred to as units). The ants (agents) were distributed randomly throughout the nest space at the start of the simulation. The size of the nest space was dependent on the colony size to keep the density (N/L²) approximately constant (L was set proportional to the square root of N). For example, when N = 20, L = 100 units. We controlled L to keep the ant density per space constant (this assumption was based on empirical evidence as shown in Appendix 3 and Appendix 4).
2. Each agent was set to be 5 units long. Every time step the agents move randomly in one of four directions: north, south, east, or west (Fig 2B) in the grid. The agents are prevented from going outside of the virtual nest space with a simple check of their next position vs the position of the boundaries of the space.
3. Agents are unable to overlap each other within the single grid.
4. A contact is determined when a worker is close to the queen, within the length of 5 units (see evidence of the ant’s morphology Fig 2C). The queen can only contact one worker in each time step. Therefore we decided that the queen would not contact the same worker twice in a row. This is to decrease the prospect of a worker who has already been contacted recently monopolising contact with the queen despite other workers being in range in a short period of time. When the queen contacts the worker, the internal state of the queen and the worker increase and decrease respectively. The increase in the queen’s internal state is proportional to the internal state of the worker, while the decrease in the worker’s internal state is constant (approx. a 90% decrease).

Fig 2 — A) Grid structure with the queen and workers. B) Contact is established when workers are within range of the queen. In this instance, the threshold was set to 5 units of length. C) Two ants contacting each other by touching antennae.

Initial conditions and analysis

Conditions of workers and the queen were initialised with parameters that represent the position, direction, velocity and internal state. The internal states of the workers were randomly assigned a value between 0 and 0.5. The queen was given an initial internal state of 0.1. The number of ant workers, N, was predefined to sample the different colony sizes. The initial rest time of the queen is set to the maximum rest time ( $t_{r_{c o n s t a n t}} = 100$ ). The status of the workers and queen (whether it is active or inactive) were randomly assigned at the beginning of the simulation. Each agent, either a worker or the queen, has its internal state, I_w and I_q, respectively. I_w, the internal state, is assumed to decrease when the worker contacts the queen but to increase otherwise (Eq 3). I_q is assumed to increase when the queen encounters a worker with high I_w and to decrease in the absence of such an encounter (Eq 2). The queen’s internal state is assumed to be correlated with her patrol behaviour, i.e., a higher I_q leads to a shorter resting time, t_r.

The simulation ended when the queen had contacted all the workers in the colony at least once. The simulation was repeated 50 times for each of the colony sizes N = 20−200 increasing N in increments of 20. The colony size coincides with the range of natural Diacamma cf. Indicum colony sizes [24]. In every trial, the positions of the workers are reset to another random value (different initial conditions for spatial distributions of workers). The total time of the simulation, patrol frequency and length of the rest time were recorded. The internal states of the workers and the contacts between agents were recorded. Using these variables, the effect of the queen’s patrol behaviour could be analysed by calculating the average internal state of workers over time, as well as the distribution of these internal states. Contact rates between the queen and workers were also calculated based on the number of contacts made between the queen and the workers within the simulation time. All variables used in the simulation are shown in Table 1.

Table 1. Variables, constants, and initial conditions used in the agent-based simulation.

Variable Symbol	Variable Name	Value
L	Grid length and width	100(when N = 20)
N	Number of workers (colony size)	20,40,60,80,100,120,140,160,180,200
t_r(t = 0)	Resting time for the queen	Randomly assigned between 0 and $t_{r_{c o n s t a n t}}$
$t_{r_{c o n s t a n t}}$	Maximum resting time	100
$t_{a_{c o n s t a n t}}$	Maximum active time	20
δ	Delta(constant)	20
ϵ	Epsilon(constant)	0.01
α	Alpha(constant)	0.1
γ	Gamma(constant)	0.0001
β	Beta(constant)	0.0001
κ	Kappa(constant)	0.9009
I_q(t = 0)	Queen internal state	0.1
I_w(t = 0)	Worker internal state	Randomly assigned between 0 and 0.5
$\vec{x_{q}}$	Queen position	Randomly assigned between 0 and L
$\vec{x_{w}}$	Worker position	Randomly assigned between 0 and L

Open in a new tab

We tested the robustness of our model in several ways. Firstly, we checked the initialisation of parameters. By increasing the initial internal of the queen, we assessed its effect on the system. We found that it had little affect and returned to similar values seen in our original initialisation (see Appendix 8, S8 and S9 Figs). We then standardised the time across the colony sizes which were investigated to mitigate possible effects due to the system not being in a steady state. We also found this to have little effect (possibly strengthening our results, see Appendix 9, S10 Fig). Finally, we increased β and γ to 10x their original values. While we found a significant difference in the results (see Appendix 10, S11 Fig), the dynamics of the system were unchanged.

Results

In the experimental results, overall in small colonies with fewer than 100 workers, the queen was able to contact more than 80% of workers in the 20 bouts of patrols, whereas, in large colonies with more than 100 workers, the queens’ per worker contact frequency dramatically decreased (Fig 3). These results suggest that although the queen increased her patrol effort with increasing colony size, the efficiency of making contacts between the queen and workers dropped in the large colonies.

The first set of simulation results displays colony size dependent features of the queen’s patrol behaviour. Fig 4 showed the patrol frequency and rest time of the queen with respect to colony size. In this case, the patrol frequency refers to how often the queen patrols the colony at a given colony size. The rest time is the total amount of time the queen spends inactive for a given colony size. Fig 4A showed an increase in the patrol frequency of the queen with respect to colony size (see also Appendix 6, S6 Fig) due to the increased internal state of workers. Inversely, Fig 4B showed that the mean resting time for the queen decreased with colony size, i.e., as the colony size increases, the queen increases her patrol effort to contact an increasing number of workers in the colony. The increase in patrol frequency does not lead to constant patrolling by the queen at large colony sizes, which would be impossible for a real queen due to physical restrictions.

These results qualitatively agreed with the experimental data reported by Kikuchi et al. [24]. Kikuchi et al., through colony size manipulation, also showed that the queen increased her patrol effort with increasing colony size. This was also confirmed through our own experiments (Appendix 1, S1 Fig). As a next step, let us determine the effectiveness of the queen’s patrol behaviour in controlling the internal state of workers in the colony.

To determine the effectiveness of the queen’s patrol behaviour, distributions of worker internal states were calculated over time. Fig 5 shows the distributions of the internal states of workers (when N = 20), comparing two cases where real-time feedback was implemented and not implemented (contact with the queen had no impact on worker state as a control). Here, we could quantify the internal states as a function of time in the agent-based simulations, which cannot be obtained experimentally.

These results indicate that the real-time feedback model of the queen’s patrol behaviour suppresses the internal states of the workers effectively with smaller variance than the case when there is no feedback. Results for a larger colony size, N = 120, show that the feedback model can be effective in controlling the internal state of workers when compared to no the feedback case (S5 Fig). However, there appears to be an increase in the mean internal state and the variance of the distribution. Therefore, as colony size increases, the effectiveness of the queen’s patrol behaviour decreases.

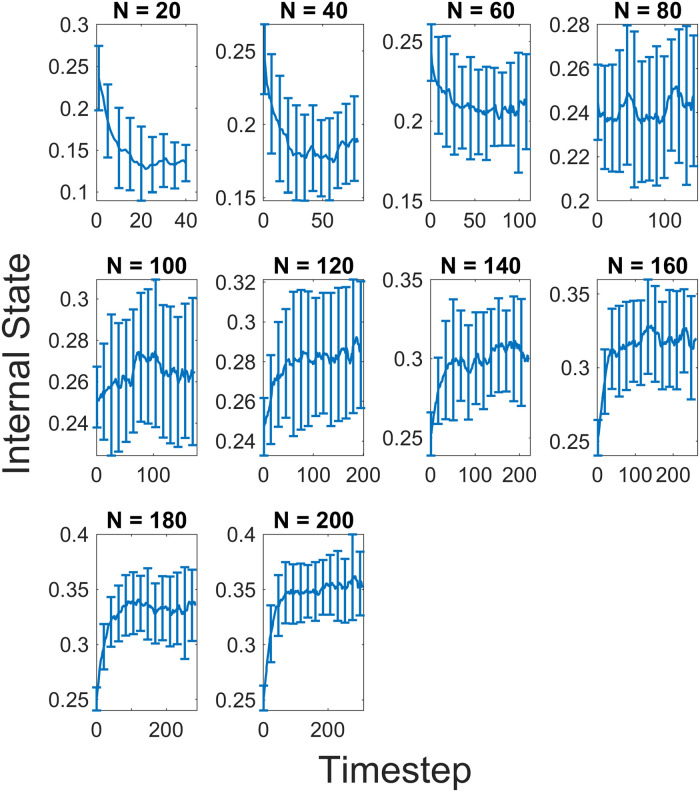
The decrease in the efficiency of the queen’s patrol behaviour can be shown more clearly in Fig 6 which shows the mean internal states of workers over time for different colony sizes ranging from N = 20 to N = 200. In smaller colony sizes, we observe a decrease in the mean internal state of workers as a function of time from the initial random values of the internal states.

This confirms that the suppression of the internal states was realised sufficiently via physical contact by the queen. This indicates that the feedback loops between the perception of the internal states and the decrease of the rest time in patrol worked effectively. Also, in the spatial degree of freedom, the queen (through her random walk) was able to contact all the workers who were also walking around randomly even though the colony size increases.

When the colony size increases further, there appears to be an inflexion point, between N = 80 and N = 100 (Fig 6), where the mean internal state begins to increase rather than decrease as a function of time. This shows a decrease in the effectiveness of the queen’s suppression of worker internal states or the start of the failure of the patrol behaviour. This can be seen more clearly in the larger colony sizes (N = 120 to N = 200). The lack of suppression at this stage is due to the contact between the queen and workers and not the physical limitation of the queen. While there is an increase in the mean internal state with colony size, there appears to be relative stabilisation in the mean after some time. As a next step, let us interrogate the mechanism in the spatial degree of freedom, namely the number of contacts from the queen to the workers, and vice versa.

By logging the number of contacts that occurred during the simulation, various contact rates could be calculated. These are the queen contact rate, the per-worker contact rate and the contact rate between workers. The contact rate is defined as the number of contacts per unit time. Therefore, the queen contact rate is the rate at which the queen contacts workers per unit time. While the per-worker contact rate is the average contact rate of a worker in the colony. The contact rate between workers is the rate workers contact any other worker in the colony. These values were calculated separately, with contacts logged for the queen and individual workers. Theoretically, assuming an even distribution of contacts between workers, the per-worker contact rate is equivalent to the queen contact rate divided by the number of workers. However, the per-worker contact rate conveys the contact efficiency of the queen and, therefore, the effectiveness of the queen’s patrol behaviour.

Fig 7 shows various contact rates between the queen and workers as a function of the colony size. Fig 7A shows the overall contact rate for the queen increasing (black line) while the per-worker contact rate decreases (blue line). Despite the increased patrol effort by the queen (shown in Fig 4), the contact efficiency of the queen decreases with colony size. This is due to the insufficient increase in the queen contact rate. Distinctions were made for the contact rate during the rest cycles (Fig 7B) and patrol cycles (Fig 7C) of the queen. This was to demonstrate that the majority of the contacts by the queen were made when the queen was patrolling.

Note here that all the results obtained in the agent-based simulations were predicated on constant density. The results so far indicate that while the queen contacts more workers in larger colonies, based on more frequent patrols, the lower contact per worker leads to an increase in the mean internal state of workers in the colony due to the decrease in contact efficiency.

The loss of contact efficiency may be due to a colony size dependent effect on the patrol behaviour of the queen. This should not affect how workers contact each other. To test this, we quantified the contact rate between workers, shown in Fig 8. Similar to Fig 7A, the contact rate between workers increases as a function of colony size, but the per-worker contact rate between workers decreases. Note again that the results were obtained based on constant density. The per-worker contact rate decreases for the same reason it decreases for the queen. The contact efficiency is lost at larger colonies because the agent’s movement is insufficient to cover the space. However, for the queen, we can relate this to her behaviour because her internal state is related to her movement.

Fig 8 — The contact rate between workers (black line) increases with colony size. An increased colony means more workers so there will be more contacts in general. When looking at the per-worker contact rate (blue line), there is a decrease with colony size similar to that seen in Fig 7A. There appears to be a decrease in the contact efficiency not just between the queen and workers but also between workers.

In comparison, the worker’s movement stays the same at all times. Hence, the loss in per-worker contact rate between workers is likely more significant than the drop in per-worker contact rate with the queen. Although there are more workers than the queen and as the simulation ends once the queen has contacted every worker at least once, there is a more considerable drop in the per-worker contact rate with the queen in Fig 7A than in Fig 8. The workers do not have to have unique contact with other workers. In contrast, the queen does have unique contacts because she needs to address every worker individually.

Discussion

Our results from the agent-based simulations revealed that the real-time feedback system between a queen and workers can have an influential role in maintaining and stabilising the internal states of the workers under various colony sizes. The simulations showed that, with a constant density, the queen increased her patrol frequency as the colony size grew (Fig 4A), and as a result, she could suppress the internal states of workers effectively (Fig 5). The underlying feedback mechanism is as follows: When the average internal state of workers increases, the queen frequently perceives a larger internal state, leading to an increase in the queen’s internal state (2). This increase in the queen’s internal state in turn leads to an increase in the queen’s patrol frequency by decreasing her resting time (1). In short, as the colony size increases, the per-worker contact rate (Fig 7A, blue line) decreases, which triggers an increase in the queen’s patrol frequency (Fig 4A). Hence, the queen’s sterility-maintaining behaviour in response to an increasing colony size is revealed. However, this was only the case until the colony reached certain colony sizes. In larger colonies, N = 120 to N = 200, the queen contact efficiency became low (Fig 7A), and consequently, the internal states of workers were no longer effectively suppressed, i.e., the average internal states increased as a function of time (Fig 6) and at the end of the run many workers were ready to perform self-reproduction.

This simulation result was qualitatively consistent with what was observed in real Diacamma colonies. Namely, a positive association between the queen patrol effort and colony size (Appendix 1, S1 Fig, see also [24]), and the effective suppression of worker reproduction in small colonies and less effective suppression in larger colonies [49, 50]. The feedback loops through physical contact between queens and workers are sufficient to suppress the internal state of workers in small colonies (Fig 5). In theory, such colony size dependent worker reproduction is adaptive in terms of the inclusive fitness of workers in monogynous and monandrous hymenopteran colonies [16]. Suppression of worker’s reproduction when the colony is small (ergonomic stage) contributes to rapid colony growth. When the colony is large (reproductive stage), worker-produced eggs are less policed and more likely to survive [50], which can imply that the selfish option (worker reproduction) may benefit workers.

We are the first to explicitly state a hypothetical proximate mechanism generating the colony size dependent character expression and the shift from ergonomic to reproductive stages. This is a general pattern in social insects.

More importantly, both the reproductive division of labour among a queen and workers and the switch in the colony stages (from ergonomic to reproductive) are simply achieved by the decision making of member individuals who just rely on personally acquired local information of recently encountered individuals. Decentralised control and self-organisation are thought to be the mechanisms that give rise to various adaptive functions of social insect colonies, such as the allocation of the workforce to various tasks that the colony needs, and selective recruitment of foragers to better food sources among the food sources available [54–56]. These theories commonly argue that single colony members have access to only limited “local” information, but they perform adaptively as a whole [57, 58]. So far, the “overall” frequency of encounters with other individuals related to local density in a nest has been often discussed as a piece of effective colony-size information for each colony member to decide their behaviour [28, 35]. However, in this study, we assumed that the individual density per nest space, thus the contact frequency with other individuals per time per individual, is constant even if the colony size changes. We consider that in real ants a positive correlation of individual density per space with colony size can occur. This can occur in situations in which ants have physical difficulty in expanding their own nest space. However, in the absence of such a spatial constraint, it would be more natural to assume that ants extend the housing architecture of the nest as the colony grows. For this reason, we consider that local density, or the simple frequency of encounters, does not generally serve as reliable information on total colony size. Actually, in Diacamma (Appendix 4, S4 Fig) individual density per nest space is likely regulated to be more or less constant. Also, in some ants, workers change their behaviours depending on density, thereby contact frequency does not linearly increase with density [35].

In this computational study, we show that even at a constant individual density per nest space, colony size dependent behaviours both in queens and workers emerged. This demonstrates that the behavioural changes caused by the feedback loop (which couples the internal state of the queen and workers) code the information regarding the contact rate of the individual worker by the queen. Note that in our simulations all the agents are assumed to exhibit a random walk, i.e., no grouping or clustering, in a constant individual density per space. This demonstrates that it is not the simple overall frequency of encounters, but instead, the two types of specific contact rates that play a role; the contact rate of the queen with reproductive workers and the contact rate of the worker with the queen. The former contact rate is a measure of the inverse of how completely the queen can make contact with workers. The latter is how often individual workers can be contacted by the queen. Due to the contact rate of the individual worker decreasing with colony size, the internal state of the worker increases. Through the resulting change in the internal states, the queen’s patrol behaviour is controlled as if she perceives the colony size as discussed previously. Furthermore, the queen patrol efficiency decreases in very large colonies presumably due to some constraints (see later), which leads to the colony stage shifting from the ergonomic stage to the reproductive one, a general phenomenon considered to be adaptive. This discovery is quite novel in that it reveals a single real-time feedback system can control both suppression of worker reproduction in small colonies and its release in large colonies. In monogynous colonies when the queen pheromone is transmitted by direct physical contact between the queen and workers, we consider that this mechanism can generally operate. When these situations arise, the queen-to-worker ratio in the group can be of key importance.

Now we consider the generality of the model presented in this paper in relation to both Diacamma cf. Indicum and other social insects. As we have shown, our model is able to replicate the patrol behaviour observed in the queen for Diacamma cf. Indicum, with increases in the patrol frequency as a function of colony size. Additionally, previous work [24] has shown the colony size distribution for Diacamma with most colonies containing less than 120 workers. From our results (Fig 6), we show that there is a transition between N = 80 and N = 120 where the queen’s control on worker internal state weakens, with an increase in the internal state of workers. Thus, our model adds value in its explanation of the field observations of real Diacamma colonies. With regards to other social insects, the applicability of our model is dependant on the way information is transmitted across the colony. For Bumblebees and Honeybees [24] where queen presence is transmitted through low volatility CHCs, our model could be relevant and adapted to investigate the effectiveness of the queen presence in those colonies and the suppression of worker reproduction. Other eusocial insects such as Pachycondyla and Dinoponera use dominance interactions from the queen to control worker reproduction in the colony [59, 60]. For such insects, our model could be applicable as a mechanism for the enforcement of the reproductive division of labour. However, for social insects with much larger colonies (such as leaf cutter ants) it would likely be impractical given decreases in queen patrol effectiveness shown in this paper. Queen patrol behaviour would have to be observed in such colonies and other mechanisms would have to be taken into account when determining the importance of such a behaviour in the dynamics of the colony.

Conclusion

A key assumption of our real-time feedback model is that the queen can perceive the reproductive status (an internal physiological state) of a worker when she contacts it. More importantly, the model also assumes that contact with a reproductive worker(s) leads to an increase in the frequency of queen patrols. These are, however, necessary to empirically demonstrate in experiments using Diacamma.

There is another issue that remains to be addressed. Why should the queen’s patrol behaviour peak at a certain rate in real Diacamma colonies, even if the colony size expands further? The peak queen patrol time is only 20% to 30% of the total time available (S1 Fig), and thus, in principle, the queen could afford to increase her patrol effort further. If queens could significantly increase the frequency of their patrol behaviour, the suppression of worker reproduction would be achieved even in large colonies. To understand the adaptive strategies of queens, we must clarify the limiting factor of the queen’s effort investment in patrolling large colonies. One hypothesis is that excessive investment in patrolling might have some fitness costs such as diminished survival and fecundity, which should also be empirically studied in the future.

Also, as to proximate mechanisms of reproductive division of labour in Diacamma, we have to take into account other mechanisms, such as dominance behaviour between workers and worker policing. Dominance behaviour is a worker-worker aggressive interaction over the right to produce own male offspring, which occurs both in the absence of the queen [26] and in the presence of the queen, and finally forms a linear hierarchy among workers [61, 62]. Interestingly, similar to the patrol behaviour of queens, ritualised aggressive behaviours by dominant individuals can have an inhibitory effect on the reproductive physiology of subordinate workers [33]. The frequency of dominance behaviours is known to increase with colony size in queen-right colonies [24], which might have a complementary effect to suppress worker reproduction when the efficiency of queen patrol declines. Worker policing, destruction of worker-produced eggs and aggression to an ovary-developed worker by other workers exist in Diacamma [32, 51], of which occurrence is also colony-size dependent [50]. Future studies need to develop a simulation model that involves these two mechanisms simultaneously operating. We believe that future research directions discussed above will further enhance our understanding of the mechanisms of the reproductive division of labour in social insects.

Appendix 1

The frequency of patrols in 12h was positively associated with the colony size (GLMM, χ² = 9.396, P = 0.002, S1A Fig). The mean resting time (time between two serial patrols) was negatively correlated with the colony size (χ² = 11.202, P = 0.0008, S1B Fig). This finding confirms the results of Kikuchi et al. [24].

Appendix 2

We focused on the first 20 patrol bouts for each queen. The mean patrol duration was 40.6 ± 36.0 sec (SD), and each queen contacted on average 13.1 workers per patrol. The longer the patrol duration, the more workers were encountered during the patrol (GLMM, χ² = 475.42, P < 0.001). However, the mean patrol duration was not significantly correlated with colony size (GLMM, χ² = 1.148, P = 0.264). The cumulative percentage of workers that a queen encountered in 20 patrols was negatively associated with colony size (GLM, colony size: z = −5.93, P < 0.001, S2 Fig).

Appendix 3

Finally, we analysed the spatial distribution of workers and the queen, because we had an impression that worker density in the vicinity of the queen is regulated to be relatively constant. Note that we provided an artificial nest of the same design to all 15 colonies. The nest space (the depression of the plaster floor) seemed wide enough for even the largest colony containing 214 workers. Inside the nest, workers tended to aggregate around the queen. Within such an aggregation, spacing between workers seemed more or less constant irrespective of the colony size: in large colonies, a wide space within the nest was occupied by such an aggregation, whereas in small colonies, the aggregation used only a small portion of the nest space (S3 Fig).

Appendix 4

To test this observation statistically, using the video data for the 15 colonies of Diacamma, we made a snapshot of the inside of a nest every 2h, for a total of five times for each colony. We counted the number of workers inside the circle of 2.5-cm radius, the centre of which was positioned on the petiole of the queen. We only counted workers who had over 50% of the body area inside the circle. We excluded snapshot data in which the queen stayed near the wall (within 2.5-cm). The worker density in the circle was not significantly correlated with the colony size (GLMM, χ² = 1.302, P = 0.24354, S4 Fig), suggesting that the local worker density around the queen was kept roughly constant regardless of colony size (mean ± SD: 7.04 ± 1.89 workers). Thus, for the queen, a simple encounter frequency with workers is not a reliable proxy of the colony size.

Appendix 5

Using data we collected from the agent-based simulation, we plotted the probability distribution of worker internal states for a larger colony size (N = 120) to observe the effect of colony size on the distribution over time. Our real-time feedback was effective in controlling the internal state of workers over time (S5 Fig). With no feedback, workers’ internal states simply increase. Although, at the larger colony size, there is an increase in the mean internal state and the variance of the distribution. This reflects a weakening of the control the queen has on the reproduction of workers at larger colony sizes as opposed to smaller colonies.

Appendix 6

Previous work of Kikuchi et al. [24] found that while the rest time of the queen decreased with colony size, the patrol time did not seem to significantly increase. We reflected this in the simulation by setting the patrol time of the queen to be constant. However, as shown in Fig 4A, the patrol frequency of the queen increases with colony size. S6 Fig shows the queen’s activity cycle for N = 20 and N = 200. In the simulation code, when the queen is active (and therefore patrolling) the variable “QueenActive” is set to 1, otherwise, it is set to 0. Though the active time of the queen stays the same, the decrease in the rest time causes shorter delays between each patrol when the colony size is large. This is demonstrated in S6 Fig where the increased closeness of the patrols can be seen for N = 200.

Appendix 7

The reason for this increase in patrol frequency is the internal state of the queen. The queen’s internal state represents a transition probability. If the queen is inactive and interacts with workers of a high internal state, it increases the probability that the queen will become active and patrol the colony. S7 Fig shows the queen’s internal state over time for colony sizes N = 20, 100 and 200. As the colony size increases, the internal state of the queen also increases, with a similar trend for colony sizes. There are periods where the queen’s internal state is high, followed by significant drops. The larger colony size means that there are more workers to interact with and patrol. From Fig 6 we see that higher colony sizes have a higher average internal state for the workers. This is reflected in the queen also as a higher internal state as she interacts with workers which have an average higher internal state in larger colonies.

Appendix 8

To check that the dynamics are not influenced by the initialisation of the internal state of the queen, we also ran simulations where the internal state of the queen was initialised at 0.8 (instead of the default 0.1). S8 Fig shows that, despite a different initial value, the queen’s internal state mirrors the trends shown in the previous figure, with an increase in the queens internal state as the colony size increases. We also compared directly the internal state of the queen at N = 20 when the initial value was 0.1 and 0.8 (S9 Fig). This confirmed that the queen’s internal state returns to similar values despite the increase in the initial value showing the robustness of the dynamics of the system.

Appendix 9

To further confirm our results, we changed the end criteria of the simulation. Initially, the simulation would end when the queen had contacted all workers in a colony. The time it took to accomplish this differed between colony sizes. Thus, the results may not be reflective of the system at a steady state. To account for this, we simulated 300 timesteps across all colony sizes (shown in S10 Fig). We found that the effectiveness of the queen’s patrol is strengthened. While there is still an increase in the average internal state of workers as the colony size increases, the suppression of the internal state of workers continues for larger colony sizes than what is shown in Fig 6. This means that our results may underestimate the effectiveness of the queen’s patrol behaviour.

Appendix 10

However, the effectiveness of the queen’s patrol behaviour is also linked to how the workers develop their internal state. What would happen if workers developed their internal state more rapidly? To answer this, we increased the constants β and γ. From Eq 3, β and γ control the rate at which workers develop their internal state. By increasing their value to 10x the original value, S11 Fig showed that the effectiveness of the queen’s patrol behaviour in this model is reliant on the rate that workers develop their internal state. The dynamics are similar, with weaker control as the colony size increases, but total loss of control occurs at smaller colony sizes. In the main results β and γ were set to approximate the development rate found in the previous work of Kikuchi et al. [24].

Supporting information

S1 Fig. Changes in the (A) frequency of patrol behaviour and (B) mean resting time of the queen at various colony sizes (N = 3).

(TIF)

Click here for additional data file.^{(20.7KB, tif)}

S2 Fig. Proportion of workers contacted by the queen at least once in 20 patrol bouts at various colony sizes (N = 15).

(TIF)

Click here for additional data file.^{(26.1KB, tif)}

S3 Fig. Aggregation patterns of Diacamma individuals at various colony sizes in the artificial nest.

(TIF)

Click here for additional data file.^{(652.3KB, tif)}

S4 Fig. Density of workers within a 2.5-cm radius of the queen at various colony sizes (N = 15).

(TIF)

Click here for additional data file.^{(32.3KB, tif)}

S5 Fig. Probability distribution of worker’s internal state (N = 120).

(Top) The probability distribution of workers’ internal states over time in a colony with 120 workers with (red) and without (blue) real-time feedback. The average value increases from 0.2473 to 0.2888. (Bottom) The variance is greater at this colony size. This shows a decrease in the effectiveness of the queen’s patrol behaviour at larger colony sizes.

(TIFF)

Click here for additional data file.^{(6.3MB, tiff)}

S6 Fig. Activity cycle of the queen at N = 20 and N = 200.

The activity cycle of the queen changes with colony size. As the colony size increases, the rest time of the queen decreases. This increases the frequency of patrol for the queen at larger colony sizes. Here this is seen as clusters of blue lines, with more clusters when N = 200.

(TIF)

Click here for additional data file.^{(3.6MB, tif)}

S7 Fig. Queen internal state over timestep.

The queen’s internal state changes over time and is coupled with the internal state of workers. Workers in a larger colony have a higher average internal state, causing the internal state of the queen to increase with colony size.

(TIF)

Click here for additional data file.^{(316.7KB, tif)}

S8 Fig. Altered queen internal state with higher initialised value.

The initial value of the queen’s internal state does not affect the dynamics of the system. Given a higher initial value, the queen’s internal state returns to the normal range observed in the previous figure, with larger colony sizes causing an increased internal state as before.

(TIF)

Click here for additional data file.^{(684.4KB, tif)}

S9 Fig. Comparison between different initialised value.

Comparing the internal state of the queen for the same colony size with different initial values, we find that there is a convergence in the queen’s internal state after approximately 400 time steps. This shows that the initialisation of the queen’s internal state does not affect the dynamics.

(TIF)

Click here for additional data file.^{(100.9KB, tif)}

S10 Fig. Running simulation for longer period of time.

By running the simulation for a consistent period of time for each colony size, we guarantee a steady state for each. With this, we see greater control by the queen over the internal state of workers. There is still weakening in the effectiveness of the queen’s patrol behaviour but the reversal of the suppression occurs much later at the largest colony sizes.

(TIF)

Click here for additional data file.^{(172.6KB, tif)}

S11 Fig. Increasing β and γ.

By increasing β and γ, the rate that workers develop their internal state, we showed that the queen has weaker control over the reproduction of workers. Loss of control begins even at smaller colony sizes such as N = 40.

(TIF)

Click here for additional data file.^{(131.6KB, tif)}

Acknowledgments

We would like to thank Melissa Winder for assisting in running the simulations. We would also like to thank Oliver Back for his feedback on improving the clarity of the writing. We would like to thank Yuka Fujito, Nao Fujiwara-Tsuji, Shun-ichi Kawabata and Ryohei Yamaoka for discussions that helped to shape the flow of the text. We appreciate Ken Sugawara for his discussion of the work he did which provided a basis for this paper. We are grateful to Toshiharu Akino for helping with a behavioural bioassay, and to Ryo Hosomi and Nao Shigenari who collected preliminary data in their graduation theses at Toyama University.

Data Availability

All data and code used is available at Zenodo (DOI: 10.5281/zenodo.6759932).

Funding Statement

The author(s) received no specific funding for this work.

References

1. Chittka A, Wurm Y, Chittka L. Epigenetics: The Making of Ant Castes. Current Biology. 2012;22(19):R835–R838. doi: 10.1016/j.cub.2012.07.045 [DOI] [PubMed] [Google Scholar]
2. Bonner JT. Perspective: the size-complexity rule. Evolution. 2004;58(9):1883–1890. doi: 10.1554/04-146 [DOI] [PubMed] [Google Scholar]
3. Hölldobler B, Wilson EO, et al. The ants. Harvard University Press; 1990. [Google Scholar]
4. Kikuchi T, Higashi S. Task allocation and alate production in monogynous, polygynous and orphan colonies of Myrmica kotokui. Ethology Ecology & Evolution. 2001;13(2):151–159. doi: 10.1080/08927014.2001.9522781 [DOI] [Google Scholar]
5. Tschinkel WR. Colony growth and the ontogeny of worker polymorphism in the fire ant, Solenopsis invicta. Behavioral Ecology and Sociobiology. 1988;22(2):103–115. doi: 10.1007/BF00343200 [DOI] [Google Scholar]
6. Smith ML, Kingwell CJ, Böröczky K, Kessler A. Colony-level chemical profiles do not provide reliable information about colony size in the honey bee. Ecological Entomology. 2020;45(3):679–687. doi: 10.1111/een.12841 [DOI] [Google Scholar]
7. Beckers R, Deneubourg JL, Goss S, Pasteels JM. Collective decision making through food recruitment. Insectes Sociaux. 1990;37(3):258–267. doi: 10.1007/BF02224053 [DOI] [Google Scholar]
8. Kikuchi T, Tomizuka F, Higashi S. Reproductive strategy in orphaned colonies of Myrmica kotokui Forel, the Japanese species of the M. ruginodis complex (Hymenoptera, Formicidae). Insectes sociaux. 2000;47(4):343–347. doi: 10.1007/PL00001727 [DOI] [Google Scholar]
9. Thomas ML, Elgar MA. Colony size affects division of labour in the ponerine ant Rhytidoponera metallica. Naturwissenschaften. 2003;90(2):88–92. doi: 10.1007/s00114-002-0396-x [DOI] [PubMed] [Google Scholar]
10. Matsuura K, Himuro C, Yokoi T, Yamamoto Y, Vargo EL, Keller L. Identification of a pheromone regulating caste differentiation in termites. Proceedings of the National Academy of Sciences. 2010;107(29):12963–12968. doi: 10.1073/pnas.1004675107 [DOI] [PMC free article] [PubMed] [Google Scholar]
11. Brian M. Social control over sex and caste in bees, wasps and ants. Biological Reviews. 1980;55(4):379–415. doi: 10.1111/j.1469-185X.1980.tb00699.x [DOI] [Google Scholar]
12. Vargo EL, Passera L. Pheromonal and behavioral queen control over the production of gynes in the Argentine ant Iridomyrmex humilis (Mayr). Behavioral Ecology and Sociobiology. 1991;28(3):161–169. doi: 10.1007/BF00172167 [DOI] [Google Scholar]
13. Keller L, Nonacs P. The role of queen pheromones in social insects: queen control or queen signal? Animal Behaviour. 1993;45(4):787–794. doi: 10.1006/anbe.1993.1092 [DOI] [Google Scholar]
14. Fletcher DJ, Ross KG. Regulation of reproduction in eusocial Hymenoptera. Annual review of entomology. 1985;30(1):319–343. doi: 10.1146/annurev.en.30.010185.001535 [DOI] [Google Scholar]
15. Oster GF, Wilson EO. Caste and ecology in the social insects. Princeton University Press; 1978. [PubMed] [Google Scholar]
16. Ohtsuki H, Tsuji K. Adaptive reproduction schedule as a cause of worker policing in social Hymenoptera: a dynamic game analysis. The American Naturalist. 2009;173(6):747–758. doi: 10.1086/598488 [DOI] [PubMed] [Google Scholar]
17. Van Oystaeyen A, Oliveira RC, Holman L, van Zweden JS, Romero C, Oi CA, et al. Conserved class of queen pheromones stops social insect workers from reproducing. Science. 2014;343(6168):287–290. doi: 10.1126/science.1244899 [DOI] [PubMed] [Google Scholar]
18. Holman L, Jørgensen CG, Nielsen J, d’Ettorre P. Identification of an ant queen pheromone regulating worker sterility. Proceedings of the Royal Society B: Biological Sciences. 2010;277(1701):3793–3800. doi: 10.1098/rspb.2010.0984 [DOI] [PMC free article] [PubMed] [Google Scholar]
19. Holman L, van Zweden JS, Oliveira RC, Van Oystaeyen A, Wenseleers T. Conserved queen pheromones in bumblebees: a reply to Amsalem et al. PeerJ. 2017;5:e3332. doi: 10.7717/peerj.3332 [DOI] [PMC free article] [PubMed] [Google Scholar]
20. Smith AA, Liebig J. The evolution of cuticular fertility signals in eusocial insects. Current opinion in insect science. 2017;22:79–84. doi: 10.1016/j.cois.2017.05.017 [DOI] [PubMed] [Google Scholar]
21. Princen SA, Oliveira RC, Ernst UR, Millar JG, van Zweden JS, Wenseleers T. Honeybees possess a structurally diverse and functionally redundant set of queen pheromones. Proceedings of the Royal Society B. 2019;286(1905):20190517. doi: 10.1098/rspb.2019.0517 [DOI] [PMC free article] [PubMed] [Google Scholar]
22. Wanner KW, Nichols AS, Walden KK, Brockmann A, Luetje CW, Robertson HM. A honey bee odorant receptor for the queen substance 9-oxo-2-decenoic acid. Proceedings of the National Academy of Sciences. 2007;104(36):14383–14388. doi: 10.1073/pnas.0705459104 [DOI] [PMC free article] [PubMed] [Google Scholar]
23. Tsuji K. Reproductive differentiation and conflicts in Diacamma: A model system for integrative sociobiology. Asian Myrmecology. 2021;13:e013007. [Google Scholar]
24. Kikuchi T, Nakagawa T, Tsuji K. Changes in relative importance of multiple social regulatory forces with colony size in the ant Diacamma sp. from Japan. Animal Behaviour. 2008;76(6):2069–2077. doi: 10.1016/j.anbehav.2008.08.029 [DOI] [Google Scholar]
25. Tsuji K, Egashira K, Hölldobler B. Regulation of worker reproduction by direct physical contact in the ant Diacamma sp. from Japan. Animal Behaviour. 1999;58(2):337–343. doi: 10.1006/anbe.1999.1161 [DOI] [PubMed] [Google Scholar]
26. Peeters C, Tsuji K. Reproductive conflict among ant workers in Diacamma sp. from Japan: dominance and oviposition in the absence of the gamergate. Insectes Sociaux. 1993;40(2):119–136. doi: 10.1007/BF01240701 [DOI] [Google Scholar]
27. Gordon DM, Mehdiabadi NJ. Encounter rate and task allocation in harvester ants. Behavioral Ecology and Sociobiology. 1999;45(5):370–377. doi: 10.1007/s002650050573 [DOI] [Google Scholar]
28.Gordon DM. Movement, Encounter Rate, and Collective Behavior in Ant Colonies. Annals of the Entomological Society of America. 2020;. [DOI] [PMC free article] [PubMed]
29. Schmickl T, Karsai I. Integral feedback control is at the core of task allocation and resilience of insect societies. Proceedings of the National Academy of Sciences. 2018;115(52):13180–13185. doi: 10.1073/pnas.1807684115 [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Pagliara R, Gordon DM, Leonard NE. Regulation of harvester ant foraging as a closed-loop excitable system. PLoS computational biology. 2018;14(12):e1006200. doi: 10.1371/journal.pcbi.1006200 [DOI] [PMC free article] [PubMed] [Google Scholar]
31. Perna A, Granovskiy B, Garnier S, Nicolis SC, Labédan M, Theraulaz G, et al. Individual rules for trail pattern formation in Argentine ants (Linepithema humile). PLoS computational biology. 2012;8(7):e1002592. doi: 10.1371/journal.pcbi.1002592 [DOI] [PMC free article] [PubMed] [Google Scholar]
32. Kikuta N, Tsuji K. Queen and worker policing in the monogynous and monandrous ant, Diacamma sp. Behavioral Ecology and Sociobiology. 1999;46(3):180–189. doi: 10.1007/s002650050608 [DOI] [Google Scholar]
33. Shimoji H, Aonuma H, Miura T, Tsuji K, Sasaki K, Okada Y. Queen contact and among-worker interactions dually suppress worker brain dopamine as a potential regulator of reproduction in an ant. Behavioral Ecology and Sociobiology. 2017;71(2):1–9. doi: 10.1007/s00265-016-2263-3 [DOI] [Google Scholar]
34. Sugawara K, Yaegashi K, Hayashi Y, Kikuchi T, Tsuji K. Modeling the patrol behavior of the Diacamma’s gamergate. Artificial Life and Robotics. 2009;14(3):318–320. doi: 10.1007/s10015-009-0731-9 [DOI] [Google Scholar]
35. Gordon DM, Paul RE, Thorpe K. What is the function of encounter patterns in ant colonies? Animal Behaviour. 1993;45(6):1083–1100. [Google Scholar]
36. Franks NR, Wilby A, Silverman BW, Tofts C. Self-organizing nest construction in ants: sophisticated building by blind bulldozing. Animal behaviour. 1992;44:357–375. doi: 10.1016/0003-3472(92)90041-7 [DOI] [Google Scholar]
37. Tschinkel WR. Sociometry and sociogenesis of colony-level attributes of the Florida harvester ant (Hymenoptera: Formicidae). Annals of the Entomological Society of America. 1999;92(1):80–89. doi: 10.1093/aesa/92.1.80 [DOI] [Google Scholar]
38. Gordon DM. Ant encounters. Princeton University Press; 2010. [Google Scholar]
39. Hartman C, Benes B. Autonomous boids. Computer Animation and Virtual Worlds. 2006;17(3-4):199–206. doi: 10.1002/cav.123 [DOI] [Google Scholar]
40.Şahin E, Franks NR. Simulation of nest assessment behavior by ant scouts. In: International Workshop on Ant Algorithms. Springer; 2002. p. 274–281.
41.Marshall JA, Kovacs T, Dornhaus AR, Franks NR. Simulating the evolution of ant behaviour in evaluating nest sites. In: European Conference on Artificial Life. Springer; 2003. p. 643–650.
42. Shiraishi M, Takeuchi R, Nakagawa H, Nishimura SI, Awazu A, Nishimori H. Diverse stochasticity leads a colony of ants to optimal foraging. Journal of theoretical biology. 2019;465:7–16. doi: 10.1016/j.jtbi.2019.01.002 [DOI] [PubMed] [Google Scholar]
43.Drogoul A, Ferber J. Multi-agent simulation as a tool for modeling societies: Application to social differentiation in ant colonies. In: European workshop on modelling autonomous agents in a multi-agent world. Springer; 1992. p. 2–23.
44. Helbing D. Agent-based modeling. In: Social self-organization. Springer; 2012. p. 25–70. [Google Scholar]
45. Reid CR, Latty T. Collective behaviour and swarm intelligence in slime moulds. FEMS Microbiology Reviews. 2016;033:798–806. doi: 10.1093/femsre/fuw033 [DOI] [PubMed] [Google Scholar]
46. Herbert-Read JE, Buhl J, Hu F, Ward AJ, Sumpter DJ. Initiation and spread of escape waves within animal groups. Royal Society open science. 2015;2(4):140355. doi: 10.1098/rsos.140355 [DOI] [PMC free article] [PubMed] [Google Scholar]
47. Fujioka H, Abe MS, Okada Y. Individual Ants Do Not Show Activity-Rest Rhythms in Nest Conditions. Journal of Biological Rhythms. 2021;36(3):297–310. doi: 10.1177/07487304211002934 [DOI] [PubMed] [Google Scholar]
48. Fukumoto Y. A novel form of colony organization in the “queenless” ant Diacamma rugosum. Physiology and Ecology Japan. 1989;26:55–61. [Google Scholar]
49. Nakata K, Tsuji K. The effect of colony size on conflict over male-production between gamergate and dominant workers in the ponerine ant Diacamma sp. Ethology Ecology & Evolution. 1996;8(2):147–156. doi: 10.1080/08927014.1996.9522925 [DOI] [Google Scholar]
50. Shimoji H, Kikuchi T, Ohnishi H, Kikuta N, Tsuji K. Social enforcement depending on the stage of colony growth in an ant. Proceedings of the Royal Society B: Biological Sciences. 2018;285(1875):20172548. doi: 10.1098/rspb.2017.2548 [DOI] [PMC free article] [PubMed] [Google Scholar]
51. Kawabata S, Tsuji K. The policing behavior ‘immobilization’ towards ovary-developed workers in the ant, Diacamma sp. from Japan. Insectes Sociaux. 2005;52(1):89–95. doi: 10.1007/s00040-004-0778-5 [DOI] [Google Scholar]
52. Hayashi Y, Yuki M, Sugawara K, Kikuchi T, Tsuji K. Rhythmic behavior of social insects from single to multibody. Robotics and Autonomous Systems. 2012;60(5):714–721. doi: 10.1016/j.robot.2011.06.016 [DOI] [Google Scholar]
53. Hayashi Y, Yuki M, Kikuchi T, Tsuji K, Sugawara K. Effect of Pair Interactions on Transition Probabilities between Inactive and Active States—Achieving Collective Behaviour via Pair Interactions in Social Insects—. Journal of the Physical Society of Japan. 2015;84(10):104801. doi: 10.7566/JPSJ.84.104801 [DOI] [Google Scholar]
54. Franks NR, Gomez N, Goss S, Deneubourg JL. The blind leading the blind in army ant raid patterns: testing a model of self-organization (Hymenoptera: Formicidae). Journal of Insect Behavior. 1991;4(5):583–607. doi: 10.1007/BF01048072 [DOI] [Google Scholar]
55. Nicolis SC, Deneubourg JL. Emerging patterns and food recruitment in ants: an analytical study. Journal of theoretical biology. 1999;198(4):575–592. doi: 10.1006/jtbi.1999.0934 [DOI] [PubMed] [Google Scholar]
56. Seeley TD. When is self-organization used in biological systems? The Biological Bulletin. 2002;202(3):314–318. doi: 10.2307/1543484 [DOI] [PubMed] [Google Scholar]
57. Bonabeau E, Theraulaz G, Deneubourg JL, Aron S, Camazine S. Self-organization in social insects. Trends in ecology & evolution. 1997;12(5):188–193. doi: 10.1016/S0169-5347(97)01048-3 [DOI] [PubMed] [Google Scholar]
58. Camazine S, Deneubourg JL, Franks NR, Sneyd J, Theraula G, Bonabeau E. Self-organization in biological systems. Princeton university press; 2020. [Google Scholar]
59. Ito F, Higashi S. A linear dominance hierarchy regulating reproduction and polyethism of the queenless antPachycondyla sublaevis. Naturwissenschaften. 1991;78(2):80–82. doi: 10.1007/BF01206263 [DOI] [Google Scholar]
60. Monnin T, Peeters C. Dominance hierarchy and reproductive conflicts among subordinates in a monogynous queenless ant. Behavioral Ecology. 1999;10(3):323–332. doi: 10.1093/beheco/10.3.323 [DOI] [Google Scholar]
61. Shimoji H, Abe MS, Tsuji K, Masuda N. Global network structure of dominance hierarchy of ant workers. Journal of the Royal Society Interface. 2014;11(99):20140599. doi: 10.1098/rsif.2014.0599 [DOI] [PMC free article] [PubMed] [Google Scholar]
62. Sasaki T, Penick CA, Shaffer Z, Haight KL, Pratt SC, Liebig J. A simple behavioral model predicts the emergence of complex animal hierarchies. The American Naturalist. 2016;187(6):765–775. doi: 10.1086/686259 [DOI] [PubMed] [Google Scholar]

PLoS Comput Biol. doi: 10.1371/journal.pcbi.1010840.r001

Decision Letter 0

Natalia L Komarova, Christian Hilbe

26 Aug 2022

Dear Mr Adejumo,

As with all papers reviewed by the journal, your manuscript was reviewed by members of the editorial board and by several independent reviewers.

In this case, the paper has been seen by three expert reviewers. They all agree that the model yields interesting results. However, they also raise some serious concerns. In particular, it remains unclear whether some crucial model assumptions are in fact valid. Moreover, the general exposition needs to be improved. All reviewers provide constructive feedback on how to do so (below this email).

To summarize, it seems like it would take quite some work to address these concerns satisfactorily -- this is a 'Major revision' with the stress being on 'Major'.

We cannot make any decision about publication until we have seen the revised manuscript and your response to the reviewers' comments. Your revised manuscript is also likely to be sent to reviewers for further evaluation.

When you are ready to resubmit, please upload the following:

[1] A letter containing a detailed list of your responses to the review comments and a description of the changes you have made in the manuscript. Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out.

[2] Two versions of the revised manuscript: one with either highlights or tracked changes denoting where the text has been changed; the other a clean version (uploaded as the manuscript file).

Important additional instructions are given below your reviewer comments.

Please prepare and submit your revised manuscript within 60 days. If you anticipate any delay, please let us know the expected resubmission date by replying to this email. Please note that revised manuscripts received after the 60-day due date may require evaluation and peer review similar to newly submitted manuscripts.

Thank you again for your submission. We hope that our editorial process has been constructive so far, and we welcome your feedback at any time. Please don't hesitate to contact us if you have any questions or comments.

Sincerely,

Christian Hilbe

Academic Editor

PLOS Computational Biology

Natalia Komarova

Section Editor

PLOS Computational Biology

***********************

In the meantime, the paper has been seen by three expert reviewers. They all agree that the model yields interesting results. However, they also raise some serious concerns. In particular, it remains unclear whether some crucial model assumptions are in fact valid. Moreover, also the general exposition needs to be improved. All reviewers provide extremely constructive feedback on how to do so.

It seems to me that it would take quite some work to address these concerns satisfactorily (this is a 'Major revision' with the stress being on 'Major'). However, if the authors are willing to do this work, I would be willing to reconsider this manuscript.

Reviewer's Responses to Questions

Comments to the Authors:

Please note here if the review is uploaded as an attachment.

Reviewer #1: SUMMARY

The authors explain a new mechanism through which the queen of the ant Diacamma regulates her patrolling behaviour as a function of the colony size. The behaviour is implemented in a multi-agent simulator and the simulation results show a decrease in patrolling efficiency as the colony size increases. This pattern is in agreement with field observations and thus judged correct by the authors.

COMMENTS

The investigated problem is interesting and multi-agent simulation is a suitable research methodology for this study. The topic is relevant to the journal readership.

However, the paper contribution, the methods, and the results are not clearly presented. The

== Issues with the main contribution ==

The authors present a new mechanism that they indicate to be superior to the mechanism presented in previous literature. The previous method consisted of the queen regulating her patrolling behaviour as a function of the ant density. The authors say that when the colony size increases, the ant density remains constant, therefore it cannot be used by the queen to regulate her behaviour. However, I do not see how the new mechanism will produce results qualitatively different from the old mechanism.

The new mechanism shows that when the colony size increases, the queen is less effective in patrolling, thus leading to a phase transition of the colony where some workers become fertile. This is the only result that the authors use to indicate that their method is correct.

I would expect the ‘old’ mechanism to lead to the same qualitative results, in fact, when the queen regulates her patrolling behaviour as a function of ant density and the density is constant, then the queen will put constant patrolling. When the colony size increases, the constant patrolling (which was effective in small colonies) will now become less effective leading to the same phase transition.

The authors need to provide a clear comparison between the previous mechanisms and the new mechanism and must bring convincing arguments to explain why one is better than the other. This comparison is not present and the arguments pushed forward are not convincing.

== Issues with the methods ==

Each simulation runs for the time necessary for the queen to encounter once all the workers. As the simulation can be relatively short, especially for small-sized colonies, and it is far from equilibrium, the initialisation of the parameters can have a particularly relevant impact on the results. I suggest the authors study the system at equilibrium, i.e. to run the simulations for a longer time and/or make a more principled initialisation of the parameters. In particular, my intuition is that the initialisation value of the parameter I_q can have an important effect on the dynamics.

The details of the random walk are not presented, however, the type of selected random walk can have decisive effects on the results. I suggest the authors indicate with clarity what is the tested random walk behaviour and that they also test other random walks.

It is unclear what the authors mean when they say on Line 224 - “The queen will not make a contact with the same worker twice in a row.”

If two workers are in a range of 5 units with the queen for some number of timesteps would it mean that the contact alternates between the two workers? Because the queen does not make a contact two times with the same ant in a row but at each step with a different one alternating between the same two ants.

Or, instead, do the authors mean that the queen never has a second contact with the same worker throughout a simulation? In the former case, it is not clear what is the rationale behind such a choice, and the latter case will have a big impact on the internal state of the queen and it does not seem a correct design choice. Please explain better what you implemented and why you made that implementation choice.

== Issues with the presentation ==

The multi-agent simulations are not sufficiently clearly presented.

* In Figure 2, it is not clear what the blue circles are; the colour legend shows that states are represented with colours from green to brown but several blue circles are displayed. It is also not possible to understand how the runs will evolve over time. Is the movement of all agents synchronous or asynchronous? What’s their motion and interaction pattern?

* Figure 3 is missing. I suggest the authors carefully double-check their submission files before sending them to review.

* Section Results - Lines 258-265 - This part of the text pertains to the Methods and not to the Results (and the information was in part already presented earlier)

* Section Results - Lines 268-273 - This part of the text is difficult to read and it is not clear what is the difference between CRQW and CRWQ. How is the distinction between the two done? and why is it important? Additionally, the text is not correctly organised, as the concepts of contact rates are introduced here and then ignore for a few pages and then the results about them appear much later in the text. This description should go just before the presentation of the results of Fig. 7.

* Fig. 4 - Unclear what patrol frequency is. Never defined. Please define all metrics clearly in a way that your work is reproducible.

* Fig. 5 is hard to read and not well presented. Rather than a 3D plot which is hard to visualise and understand, I suggest the authors use a 2D colourmap (with colour shades indicating the values of the PDF)

* Fig. 6 - “... before stabilising at a higher value.” - Higher than what?

* Fig. 7 - “during the rest cycles of the simulation.” – It is unclear why the results are presented in distinct groups in relation to the rest cycles. What does this distinction mean? Resting cycles of whom? the queen or the worker? Please specify clearly how you computed these values. It is not clear how this data is extracted from the simulations, which quantity do you report? How do you compute CRQW and CRWQ, is it the same quantity divided by the colony size? If yes, I would use a better name (e.g. CR total and per worker).

Reviewer #2: Summary

In this paper, the authors offer a model to help understand and explain how gamergate workers of the ant Diacamma can suppress ovarian development and reproduction of workers through direct contact signalling of queen presence/reproductive status. I have been asked to focus more on the biology than the model itself, though I thought the model seemed logical and sound. On the biology side, I think the paper could be edited to improve clarity – although primarily a computational paper, the work is primarily of interest to social insect researchers, and so I think it should be as accessible as possible to those without a computational background. I’ve made some specific suggestions below, but I think there is greater need to explain certain assumptions and parameters, and the structure could be improved as often some piece of important biological or computational information that would help to understand the model came much later in the paper. I think two major improvements would be incorporating more of the real data in the within paper methods with more explanation on the biology of the ant, rather than this just being in the supplement/methods section. Secondly, related to this, more thought could be given to the generality of the model and the ant species it is replicating. Given that Diacamma are highly unique in that they lack a true queen, colonies are relatively small, and worker reproduction in larger colonies seems somewhat common (though how common I don’t think was mentioned), it would be good to see some discussion on whether it is likely the model described here could be applied to other social insect colonies. For example, I don’t think it would work in something like a leaf cutter ant or Lasius colony, where it would be simply impossible for the queen to contact every individual; moreover, we know they do not perform such patrolling behaviour. However, I could see it being more important in something like a bumblebee colony where the queens actively aggress and police reproductive workers. Finally, as the authors point out, the entire model rests on the assumption queens can detect the internal state of worker, but no attempt to support this by referring to other social insect taxa has been made. Given this is such a major assumption I think it critical this limitation be addressed in the introduction and some justification given.

Specific comments

Italicisation of species name throughout.

Line 23: I think the argument here is that even with chemical signalling, there can potentially be an issue of control as the colony increases in size. If so, I think this could be made clearer as it’s the pivotal point the paper rests on. You could also highlight how important this is, i.e., in very large colonies where they may be millions of insects – how is worker suppression achieved?

Line 34: In either case, there are inclusive fitness benefits that drive the evolution of the behaviour.

Line 36: Rather the ovaries begin to develop.

Line 41: Unclear how 9-ODA connects then with the next sentence, perhaps point out that 9-ODA is more volatile, but that a class of highly conserved, low volatility CHCs seem to play the pivotal role of ovary suppression in social Hymenoptera and an analogous solution has been found in termites.

Line 44: Better to say “low volatility” CHCs.

Line 50: I feel like everything above is a bit repetitive and laboured and could be more succinctly put together.

Line 54: Could point out that she is not a real queen but a gamergate worker, but that you henceforth refer to her as such.

Line 75: Perhaps could be more specific – is she aggressive?

Line 174: Unclear here if “control the length of the resting (i.e., inactive) period depending on the level of her internal states” refers to the queen or the worker. I assume the worker but if queen then I am not sure if her internal state changes? Edit: I now understand how the queen’s state changes but this needs to be made clearer.

Line 178: Does the active-inactive cycles of workers mean they are also moving around the grid? And they were determined a priori, but what were they based on? Edit: I see now they do move, but again this needs to be clearer sooner.

Line 182: Presumably this is unique to the relatively small colonies and would not be feasible in massive colonies, especially where workers do not come into contact with the queen once they switch from inside to outside of nest tasks? I see now from the methods that the queen only contacts about 80% of the colony – would it make more sense given you know this constraint to update the model so it stops once she has contacted 80% rather than 100?

Line 190: Again, I’m a bit unclear what is changing about the queen’s internal state, is this from inactive to patrolling or some other (perhaps hormone) level? Edit: again, realise now what is changing but needs to be clearer sooner.

Line 211: It would be really nice if this section could be given some biological context, i.e. how much of the model here is assumed and how much is based on approximating the biology of the ants. To ensure that the paper is understandable to social insect researchers that are not familiar with such mathematic notations, placing these into biological context would be really helpful, e.g. what is the damping factor attempting to replicate in in the real biological system? I think this is where you could incorporate more about the real-world data you collected and how it has informed your model.

Line 216: In our experience the distribution of ants is not random but concentrated around the queen or brood piles, particularly in small colonies (Casillas- Pérez et al. 2021) – how might such a distribution affect your results, since it should make it easier for the queen to contact as many workers as possible?

Line 220: I appreciate the need for some simplification, but it might worth pointing out here or later than in a real colony ants do not move randomly and there will be overlap, which could impact the dynamics of the queens patrol.

Line 226: Here it would be better to say in plainer terms what happens to the internal states so non-computational biologists can follow along. I presume this is simply that the workers internal state resets to 0 if they contact the queen but it is less clear to me what happens to the queen’s internal state. My interpretation of the damping and activation factors is that if she contacts a low internal state worker, there’s a damping of her internal state which lowers the need to patrol to the point patrolling might switch off with enough contacts, but if she contacts a high internal state worker, she increases her need to control and so patrolling continues? Edit: I now understand from the results that the internal state of the queen is how long she will rest for, and that the patrol length is the same, but this is not clear here where it needs to be.

Line 251: This took me by surprise as I don’t think it is mentioned earlier that you also studied real ant colonies. Could you mention this in the methods above very briefly, so it is easier to follow?

Line 252: I think calling the patrols iterations is a little confusing as it sounds like you might be referring to the model, better to call them bouts as in the methods.

Line 261: Okay so this explanation is what I needed above when I was trying to understand the equations and it would make much more sense if it were to come in the methods rather than the results.

Line 276: To clarify, is this result because the internal state of the workers increases with time? This is mentioned in the equation but could be spelled out more clearly.

Line 291: Could be framed as when contact with the queen has no impact on worker state as a control

Line 299: should add “relative to smaller colonies”, and perhaps give mean values? Looks something 0.15 vs. 0.3.

Line 301: I find figure 6 much easier to read and wonder if figure 5 and S5 are required, as I had to really study these to see the pattern? The same style of figure could be made to show the “without feedback” results for all colony sizes and included within figure 6 or separately in the supplement, with just results reported in the main text.

Line 326: I find this section on contact rates difficult to follow as graph 7 is a bit of a challenge initially to read. It might be helpful to keep the y-axis the same across these graphs, so that the results are more comparable, and to make the dots smaller so the error bars are visible. In general, though, I found I had to look at this figure for a long time to understand it and I’m still not 100% sure I do. My biggest problem is that I don’t understand how there can be contact by the queen during the rest phase of queen. It might also be better to separate out the black and blue results into separate graphs that are on the same row as one another, as the multiple axis, colours and legends make it tricky to follow. I also generally discourage relying on acronyms since it just makes the text harder to follow. Hence, I think this section could be summarised more succinctly by simply saying: as colony size, and thus number of queen patrols, increases, the queen has a higher contact rate per unit time with her workers, whereas the rate that workers contact the queen at decreases. Again, I wonder if it might be simpler to show just Fig 7C, and put A and B in the supplement, or perhaps here you can explain why it is important whether the contacts occur at rest or on patrol.

Line 404: This assumes that ants distribute themselves evenly across nest space though, which I think is unlikely. If a colony concentrates most of its workers in particular chambers or has a stable proportion of workers dedicated to certain task that interact with one another, then encounter rate might be a predictable estimate of colony size.

Line 425: I’m not sure I follow this argument which seems to imply it’s the lack of queen policing that causes the switch, but queen policing efficiency is colinear with increasing colony size, the benefits of which seems like a more general and simply explanation for this shift (i.e., greater brood to worker ratio, more food coming into the nest etc).

Line 443: this assumption is a major one and something that occurred to me throughout the paper. Is there any evidence in this species, other ants, or in other social insects (perhaps in honeybees/ bumblebees) that queens can do this? I also think this needs to be addressed in the introduction as readers will be left wondering about it througought.

Line 446: It might be worth citing Bear et al 2006 or Camargo et al. 2011 which find such trade-offs between an energetic activity (immune response or digging) and fecundity/survival. Though worth noting these are all in claustral systems.

Reviewer #3: See uploaded document.

**********

Have the authors made all data and (if applicable) computational code underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data and code underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data and code should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data or code —e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Reviewer #3: No

Figure Files:

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email us at figures@plos.org.

Data Requirements:

Please note that, as a condition of publication, PLOS' data policy requires that you make available all data used to draw the conclusions outlined in your manuscript. Data must be deposited in an appropriate repository, included within the body of the manuscript, or uploaded as supporting information. This includes all numerical values that were used to generate graphs, histograms etc.. For an example in PLOS Biology see here: http://www.plosbiology.org/article/info%3Adoi%2F10.1371%2Fjournal.pbio.1001908#s5.

Reproducibility:

To enhance the reproducibility of your results, we recommend that you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. Additionally, PLOS ONE offers an option to publish peer-reviewed clinical study protocols. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols

Attachment

Submitted filename: PLOS_CB_Ver.2.pdf

Click here for additional data file.^{(45.1KB, pdf)}

PLoS Comput Biol. 2023 Mar 24;19(3):e1010840. doi: 10.1371/journal.pcbi.1010840.r002

Author response to Decision Letter 0

10 Nov 2022

Attachment

Submitted filename: Reviewer Response.docx

Click here for additional data file.^{(1.9MB, docx)}

PLoS Comput Biol. doi: 10.1371/journal.pcbi.1010840.r003

Decision Letter 1

Natalia L Komarova, Christian Hilbe

25 Jan 2023

Dear Mr Adejumo,

Thank you very much for submitting your manuscript "A real-time feedback system stabilises the regulation of worker reproduction under various colony sizes" for consideration at PLOS Computational Biology. As noted previously, due to changes to the manuscript file at post-accept your manuscript will need to be sent back to peer-review. In order to do so, we will require you to upload the manuscript file with tracked changes and a new response to reviewers file.

As with all papers reviewed by the journal, your manuscript was reviewed by members of the editorial board and by several independent reviewers. The reviewers appreciated the attention to an important topic. Based on the reviews, we are likely to accept this manuscript for publication, providing that you modify the manuscript according to the review recommendations.

Please prepare and submit your revised manuscript within 30 days. If you anticipate any delay, please let us know the expected resubmission date by replying to this email.

When you are ready to resubmit, please upload the following:

[1] A letter containing a detailed list of your responses to all review comments, and a description of the changes you have made in the manuscript. Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out

[2] Two versions of the revised manuscript: one with either highlights or tracked changes denoting where the text has been changed; the other a clean version (uploaded as the manuscript file).

Important additional instructions are given below your reviewer comments.

Thank you again for your submission to our journal. We hope that our editorial process has been constructive so far, and we welcome your feedback at any time. Please don't hesitate to contact us if you have any questions or comments.

Sincerely,

Christian Hilbe

Academic Editor

PLOS Computational Biology

Natalia Komarova

Section Editor

PLOS Computational Biology

***********************

A link appears below if there are any accompanying review attachments. If you believe any reviews to be missing, please contact ploscompbiol@plos.org immediately:

Reviewer's Responses to Questions

Comments to the Authors:

Please note here if the review is uploaded as an attachment.

Reviewer #1: In their revised manuscript, the authors addressed all my original concerns.

Reviewer #2: The authors have made their manuscript more accessible and justified several points I raised, and I think it is now fit for publication.

Reviewer #3: I consider that, through the revision, almost all issues addressed in my last reviewer’s comments were resolved, and the manuscript deserves publication after minor revisions on the following points,

1. I feel the mechanism for the result shown by the decreasing graph (blue line) in fig.8 is unclear. Why does the per-worker contact rate decrease with the colony size under the assumptions; i) the internal state change of workers does not affect the movement of workers, ii)the number density of workers is kept constant independent of the colony size? Because this result looks (at least for me) against intuition, the authors are desired to suggest some underlying mechanism.

2. This is a small but unignorable issue. In the explanation, in L269-270, of the last terms of eq. (2) and (3), delta(x_q-x_w), authors call this function a “delta function”. This is against the widely accepted definition of the delta function because zero point of the delta function is infinity.

The authors should call this term the “Kronecker’s delta” instead of a “delta function”

and should denote as delta_{x_q, x_w)}.

**********

Have the authors made all data and (if applicable) computational code underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Reviewer #3: Yes: Hiraku Nishimori

Figure Files:

Data Requirements:

Reproducibility:

References:

Review your reference list to ensure that it is complete and correct. If you have cited papers that have been retracted, please include the rationale for doing so in the manuscript text, or remove these references and replace them with relevant current references. Any changes to the reference list should be mentioned in the rebuttal letter that accompanies your revised manuscript.

If you need to cite a retracted article, indicate the article’s retracted status in the References list and also include a citation and full reference for the retraction notice.

PLoS Comput Biol. 2023 Mar 24;19(3):e1010840. doi: 10.1371/journal.pcbi.1010840.r004

Author response to Decision Letter 1

30 Jan 2023

Attachment

Submitted filename: Reviewer Response.docx

Click here for additional data file.^{(15.3KB, docx)}

PLoS Comput Biol. doi: 10.1371/journal.pcbi.1010840.r005

Decision Letter 2

Natalia L Komarova, Christian Hilbe

10 Feb 2023

Dear Mr Adejumo,

We are pleased to inform you that your manuscript 'A real-time feedback system stabilises the regulation of worker reproduction under various colony sizes' has been provisionally accepted for publication in PLOS Computational Biology.

Before your manuscript can be formally accepted you will need to complete some formatting changes, which you will receive in a follow up email. A member of our team will be in touch with a set of requests.

Please note that your manuscript will not be scheduled for publication until you have made the required changes, so a swift response is appreciated.

IMPORTANT: The editorial review process is now complete. PLOS will only permit corrections to spelling, formatting or significant scientific errors from this point onwards. Requests for major changes, or any which affect the scientific understanding of your work, will cause delays to the publication date of your manuscript.

Should you, your institution's press office or the journal office choose to press release your paper, you will automatically be opted out of early publication. We ask that you notify us now if you or your institution is planning to press release the article. All press must be co-ordinated with PLOS.

Thank you again for supporting Open Access publishing; we are looking forward to publishing your work in PLOS Computational Biology.

Best regards,

Christian Hilbe

Academic Editor

PLOS Computational Biology

Natalia Komarova

Section Editor

PLOS Computational Biology

***********************************************************

Because the paper has been revised rather substantially, we decided to ask one of the original reviewers to comment on the changes.

As you will see, this reviewer suggested to publish the article, and we concur.

Ideally, you briefly take into account the reviewer's remaining suggestions when uploading the final manuscript.

Reviewer's Responses to Questions

Comments to the Authors:

Please note here if the review is uploaded as an attachment.

Reviewer #3: Although I consider that the manuscript now deserves publication, a little more precise definition of the term, “per-worker contact rate between workers”, is desired to be added because I still have not completely understood its meaning.

Does the “per-worker contact rate between workers” mean the contact frequency of a worker to a particular worker, or, her contact frequency to any of the other workers in the colony?

I guess that the answer is, most probably, the former, then, I completely understand that the decrease in the per-worker contact rate in fig.8 is explained by the same reason as the decrease in the per-worker contact rate of the queen.

But if the answer is the latter, the per-worker contact rate seems to increase (or is kept unchanged) for the same reason as the increase of the queen contact rate to workers.

In addition, the formal notation of the “Kronecker’s delta” should be “delta_{x_q, x_w}”, rather than “delta_(x_q- x_w)”.

I consider that no further review is needed after these minor revisions.

**********

Have the authors made all data and (if applicable) computational code underlying the findings in their manuscript fully available?

Reviewer #3: Yes

**********

PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #3: Yes: Hiraku Nishimori

PLoS Comput Biol. doi: 10.1371/journal.pcbi.1010840.r006

Acceptance letter

Natalia L Komarova, Christian Hilbe

21 Mar 2023

PCOMPBIOL-D-22-00963R2

A real-time feedback system stabilises the regulation of worker reproduction under various colony sizes

Dear Dr Adejumo,

I am pleased to inform you that your manuscript has been formally accepted for publication in PLOS Computational Biology. Your manuscript is now with our production department and you will be notified of the publication date in due course.

The corresponding author will soon be receiving a typeset proof for review, to ensure errors have not been introduced during production. Please review the PDF proof of your manuscript carefully, as this is the last chance to correct any errors. Please note that major changes, or those which affect the scientific understanding of the work, will likely cause delays to the publication date of your manuscript.

Soon after your final files are uploaded, unless you have opted out, the early version of your manuscript will be published online. The date of the early version will be your article's publication date. The final article will be published to the same URL, and all versions of the paper will be accessible to readers.

Thank you again for supporting PLOS Computational Biology and open-access publishing. We are looking forward to publishing your work!

With kind regards,

Anita Estes

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 Fig. Changes in the (A) frequency of patrol behaviour and (B) mean resting time of the queen at various colony sizes (N = 3).

(TIF)

Click here for additional data file.^{(20.7KB, tif)}

S2 Fig. Proportion of workers contacted by the queen at least once in 20 patrol bouts at various colony sizes (N = 15).

(TIF)

Click here for additional data file.^{(26.1KB, tif)}

S3 Fig. Aggregation patterns of Diacamma individuals at various colony sizes in the artificial nest.

(TIF)

Click here for additional data file.^{(652.3KB, tif)}

S4 Fig. Density of workers within a 2.5-cm radius of the queen at various colony sizes (N = 15).

(TIF)

Click here for additional data file.^{(32.3KB, tif)}

S5 Fig. Probability distribution of worker’s internal state (N = 120).

(TIFF)

Click here for additional data file.^{(6.3MB, tiff)}

S6 Fig. Activity cycle of the queen at N = 20 and N = 200.

(TIF)

Click here for additional data file.^{(3.6MB, tif)}

S7 Fig. Queen internal state over timestep.

(TIF)

Click here for additional data file.^{(316.7KB, tif)}

S8 Fig. Altered queen internal state with higher initialised value.

(TIF)

Click here for additional data file.^{(684.4KB, tif)}

S9 Fig. Comparison between different initialised value.

(TIF)

Click here for additional data file.^{(100.9KB, tif)}

S10 Fig. Running simulation for longer period of time.

(TIF)

Click here for additional data file.^{(172.6KB, tif)}

S11 Fig. Increasing β and γ.

(TIF)

Click here for additional data file.^{(131.6KB, tif)}

Attachment

Submitted filename: PLOS_CB_Ver.2.pdf

Click here for additional data file.^{(45.1KB, pdf)}

Attachment

Submitted filename: Reviewer Response.docx

Click here for additional data file.^{(1.9MB, docx)}

Attachment

Submitted filename: Reviewer Response.docx

Click here for additional data file.^{(15.3KB, docx)}

Data Availability Statement

All data and code used is available at Zenodo (DOI: 10.5281/zenodo.6759932).

[pcbi.1010840.ref001] 1. Chittka A, Wurm Y, Chittka L. Epigenetics: The Making of Ant Castes. Current Biology. 2012;22(19):R835–R838. doi: 10.1016/j.cub.2012.07.045 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref002] 2. Bonner JT. Perspective: the size-complexity rule. Evolution. 2004;58(9):1883–1890. doi: 10.1554/04-146 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref003] 3. Hölldobler B, Wilson EO, et al. The ants. Harvard University Press; 1990. [Google Scholar]

[pcbi.1010840.ref004] 4. Kikuchi T, Higashi S. Task allocation and alate production in monogynous, polygynous and orphan colonies of Myrmica kotokui. Ethology Ecology & Evolution. 2001;13(2):151–159. doi: 10.1080/08927014.2001.9522781 [DOI] [Google Scholar]

[pcbi.1010840.ref005] 5. Tschinkel WR. Colony growth and the ontogeny of worker polymorphism in the fire ant, Solenopsis invicta. Behavioral Ecology and Sociobiology. 1988;22(2):103–115. doi: 10.1007/BF00343200 [DOI] [Google Scholar]

[pcbi.1010840.ref006] 6. Smith ML, Kingwell CJ, Böröczky K, Kessler A. Colony-level chemical profiles do not provide reliable information about colony size in the honey bee. Ecological Entomology. 2020;45(3):679–687. doi: 10.1111/een.12841 [DOI] [Google Scholar]

[pcbi.1010840.ref007] 7. Beckers R, Deneubourg JL, Goss S, Pasteels JM. Collective decision making through food recruitment. Insectes Sociaux. 1990;37(3):258–267. doi: 10.1007/BF02224053 [DOI] [Google Scholar]

[pcbi.1010840.ref008] 8. Kikuchi T, Tomizuka F, Higashi S. Reproductive strategy in orphaned colonies of Myrmica kotokui Forel, the Japanese species of the M. ruginodis complex (Hymenoptera, Formicidae). Insectes sociaux. 2000;47(4):343–347. doi: 10.1007/PL00001727 [DOI] [Google Scholar]

[pcbi.1010840.ref009] 9. Thomas ML, Elgar MA. Colony size affects division of labour in the ponerine ant Rhytidoponera metallica. Naturwissenschaften. 2003;90(2):88–92. doi: 10.1007/s00114-002-0396-x [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref010] 10. Matsuura K, Himuro C, Yokoi T, Yamamoto Y, Vargo EL, Keller L. Identification of a pheromone regulating caste differentiation in termites. Proceedings of the National Academy of Sciences. 2010;107(29):12963–12968. doi: 10.1073/pnas.1004675107 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref011] 11. Brian M. Social control over sex and caste in bees, wasps and ants. Biological Reviews. 1980;55(4):379–415. doi: 10.1111/j.1469-185X.1980.tb00699.x [DOI] [Google Scholar]

[pcbi.1010840.ref012] 12. Vargo EL, Passera L. Pheromonal and behavioral queen control over the production of gynes in the Argentine ant Iridomyrmex humilis (Mayr). Behavioral Ecology and Sociobiology. 1991;28(3):161–169. doi: 10.1007/BF00172167 [DOI] [Google Scholar]

[pcbi.1010840.ref013] 13. Keller L, Nonacs P. The role of queen pheromones in social insects: queen control or queen signal? Animal Behaviour. 1993;45(4):787–794. doi: 10.1006/anbe.1993.1092 [DOI] [Google Scholar]

[pcbi.1010840.ref014] 14. Fletcher DJ, Ross KG. Regulation of reproduction in eusocial Hymenoptera. Annual review of entomology. 1985;30(1):319–343. doi: 10.1146/annurev.en.30.010185.001535 [DOI] [Google Scholar]

[pcbi.1010840.ref015] 15. Oster GF, Wilson EO. Caste and ecology in the social insects. Princeton University Press; 1978. [PubMed] [Google Scholar]

[pcbi.1010840.ref016] 16. Ohtsuki H, Tsuji K. Adaptive reproduction schedule as a cause of worker policing in social Hymenoptera: a dynamic game analysis. The American Naturalist. 2009;173(6):747–758. doi: 10.1086/598488 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref017] 17. Van Oystaeyen A, Oliveira RC, Holman L, van Zweden JS, Romero C, Oi CA, et al. Conserved class of queen pheromones stops social insect workers from reproducing. Science. 2014;343(6168):287–290. doi: 10.1126/science.1244899 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref018] 18. Holman L, Jørgensen CG, Nielsen J, d’Ettorre P. Identification of an ant queen pheromone regulating worker sterility. Proceedings of the Royal Society B: Biological Sciences. 2010;277(1701):3793–3800. doi: 10.1098/rspb.2010.0984 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref019] 19. Holman L, van Zweden JS, Oliveira RC, Van Oystaeyen A, Wenseleers T. Conserved queen pheromones in bumblebees: a reply to Amsalem et al. PeerJ. 2017;5:e3332. doi: 10.7717/peerj.3332 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref020] 20. Smith AA, Liebig J. The evolution of cuticular fertility signals in eusocial insects. Current opinion in insect science. 2017;22:79–84. doi: 10.1016/j.cois.2017.05.017 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref021] 21. Princen SA, Oliveira RC, Ernst UR, Millar JG, van Zweden JS, Wenseleers T. Honeybees possess a structurally diverse and functionally redundant set of queen pheromones. Proceedings of the Royal Society B. 2019;286(1905):20190517. doi: 10.1098/rspb.2019.0517 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref022] 22. Wanner KW, Nichols AS, Walden KK, Brockmann A, Luetje CW, Robertson HM. A honey bee odorant receptor for the queen substance 9-oxo-2-decenoic acid. Proceedings of the National Academy of Sciences. 2007;104(36):14383–14388. doi: 10.1073/pnas.0705459104 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref023] 23. Tsuji K. Reproductive differentiation and conflicts in Diacamma: A model system for integrative sociobiology. Asian Myrmecology. 2021;13:e013007. [Google Scholar]

[pcbi.1010840.ref024] 24. Kikuchi T, Nakagawa T, Tsuji K. Changes in relative importance of multiple social regulatory forces with colony size in the ant Diacamma sp. from Japan. Animal Behaviour. 2008;76(6):2069–2077. doi: 10.1016/j.anbehav.2008.08.029 [DOI] [Google Scholar]

[pcbi.1010840.ref025] 25. Tsuji K, Egashira K, Hölldobler B. Regulation of worker reproduction by direct physical contact in the ant Diacamma sp. from Japan. Animal Behaviour. 1999;58(2):337–343. doi: 10.1006/anbe.1999.1161 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref026] 26. Peeters C, Tsuji K. Reproductive conflict among ant workers in Diacamma sp. from Japan: dominance and oviposition in the absence of the gamergate. Insectes Sociaux. 1993;40(2):119–136. doi: 10.1007/BF01240701 [DOI] [Google Scholar]

[pcbi.1010840.ref027] 27. Gordon DM, Mehdiabadi NJ. Encounter rate and task allocation in harvester ants. Behavioral Ecology and Sociobiology. 1999;45(5):370–377. doi: 10.1007/s002650050573 [DOI] [Google Scholar]

[pcbi.1010840.ref028] 28.Gordon DM. Movement, Encounter Rate, and Collective Behavior in Ant Colonies. Annals of the Entomological Society of America. 2020;. [DOI] [PMC free article] [PubMed]

[pcbi.1010840.ref029] 29. Schmickl T, Karsai I. Integral feedback control is at the core of task allocation and resilience of insect societies. Proceedings of the National Academy of Sciences. 2018;115(52):13180–13185. doi: 10.1073/pnas.1807684115 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref030] 30. Pagliara R, Gordon DM, Leonard NE. Regulation of harvester ant foraging as a closed-loop excitable system. PLoS computational biology. 2018;14(12):e1006200. doi: 10.1371/journal.pcbi.1006200 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref031] 31. Perna A, Granovskiy B, Garnier S, Nicolis SC, Labédan M, Theraulaz G, et al. Individual rules for trail pattern formation in Argentine ants (Linepithema humile). PLoS computational biology. 2012;8(7):e1002592. doi: 10.1371/journal.pcbi.1002592 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref032] 32. Kikuta N, Tsuji K. Queen and worker policing in the monogynous and monandrous ant, Diacamma sp. Behavioral Ecology and Sociobiology. 1999;46(3):180–189. doi: 10.1007/s002650050608 [DOI] [Google Scholar]

[pcbi.1010840.ref033] 33. Shimoji H, Aonuma H, Miura T, Tsuji K, Sasaki K, Okada Y. Queen contact and among-worker interactions dually suppress worker brain dopamine as a potential regulator of reproduction in an ant. Behavioral Ecology and Sociobiology. 2017;71(2):1–9. doi: 10.1007/s00265-016-2263-3 [DOI] [Google Scholar]

[pcbi.1010840.ref034] 34. Sugawara K, Yaegashi K, Hayashi Y, Kikuchi T, Tsuji K. Modeling the patrol behavior of the Diacamma’s gamergate. Artificial Life and Robotics. 2009;14(3):318–320. doi: 10.1007/s10015-009-0731-9 [DOI] [Google Scholar]

[pcbi.1010840.ref035] 35. Gordon DM, Paul RE, Thorpe K. What is the function of encounter patterns in ant colonies? Animal Behaviour. 1993;45(6):1083–1100. [Google Scholar]

[pcbi.1010840.ref036] 36. Franks NR, Wilby A, Silverman BW, Tofts C. Self-organizing nest construction in ants: sophisticated building by blind bulldozing. Animal behaviour. 1992;44:357–375. doi: 10.1016/0003-3472(92)90041-7 [DOI] [Google Scholar]

[pcbi.1010840.ref037] 37. Tschinkel WR. Sociometry and sociogenesis of colony-level attributes of the Florida harvester ant (Hymenoptera: Formicidae). Annals of the Entomological Society of America. 1999;92(1):80–89. doi: 10.1093/aesa/92.1.80 [DOI] [Google Scholar]

[pcbi.1010840.ref038] 38. Gordon DM. Ant encounters. Princeton University Press; 2010. [Google Scholar]

[pcbi.1010840.ref039] 39. Hartman C, Benes B. Autonomous boids. Computer Animation and Virtual Worlds. 2006;17(3-4):199–206. doi: 10.1002/cav.123 [DOI] [Google Scholar]

[pcbi.1010840.ref040] 40.Şahin E, Franks NR. Simulation of nest assessment behavior by ant scouts. In: International Workshop on Ant Algorithms. Springer; 2002. p. 274–281.

[pcbi.1010840.ref041] 41.Marshall JA, Kovacs T, Dornhaus AR, Franks NR. Simulating the evolution of ant behaviour in evaluating nest sites. In: European Conference on Artificial Life. Springer; 2003. p. 643–650.

[pcbi.1010840.ref042] 42. Shiraishi M, Takeuchi R, Nakagawa H, Nishimura SI, Awazu A, Nishimori H. Diverse stochasticity leads a colony of ants to optimal foraging. Journal of theoretical biology. 2019;465:7–16. doi: 10.1016/j.jtbi.2019.01.002 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref043] 43.Drogoul A, Ferber J. Multi-agent simulation as a tool for modeling societies: Application to social differentiation in ant colonies. In: European workshop on modelling autonomous agents in a multi-agent world. Springer; 1992. p. 2–23.

[pcbi.1010840.ref044] 44. Helbing D. Agent-based modeling. In: Social self-organization. Springer; 2012. p. 25–70. [Google Scholar]

[pcbi.1010840.ref045] 45. Reid CR, Latty T. Collective behaviour and swarm intelligence in slime moulds. FEMS Microbiology Reviews. 2016;033:798–806. doi: 10.1093/femsre/fuw033 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref046] 46. Herbert-Read JE, Buhl J, Hu F, Ward AJ, Sumpter DJ. Initiation and spread of escape waves within animal groups. Royal Society open science. 2015;2(4):140355. doi: 10.1098/rsos.140355 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref047] 47. Fujioka H, Abe MS, Okada Y. Individual Ants Do Not Show Activity-Rest Rhythms in Nest Conditions. Journal of Biological Rhythms. 2021;36(3):297–310. doi: 10.1177/07487304211002934 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref048] 48. Fukumoto Y. A novel form of colony organization in the “queenless” ant Diacamma rugosum. Physiology and Ecology Japan. 1989;26:55–61. [Google Scholar]

[pcbi.1010840.ref049] 49. Nakata K, Tsuji K. The effect of colony size on conflict over male-production between gamergate and dominant workers in the ponerine ant Diacamma sp. Ethology Ecology & Evolution. 1996;8(2):147–156. doi: 10.1080/08927014.1996.9522925 [DOI] [Google Scholar]

[pcbi.1010840.ref050] 50. Shimoji H, Kikuchi T, Ohnishi H, Kikuta N, Tsuji K. Social enforcement depending on the stage of colony growth in an ant. Proceedings of the Royal Society B: Biological Sciences. 2018;285(1875):20172548. doi: 10.1098/rspb.2017.2548 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref051] 51. Kawabata S, Tsuji K. The policing behavior ‘immobilization’ towards ovary-developed workers in the ant, Diacamma sp. from Japan. Insectes Sociaux. 2005;52(1):89–95. doi: 10.1007/s00040-004-0778-5 [DOI] [Google Scholar]

[pcbi.1010840.ref052] 52. Hayashi Y, Yuki M, Sugawara K, Kikuchi T, Tsuji K. Rhythmic behavior of social insects from single to multibody. Robotics and Autonomous Systems. 2012;60(5):714–721. doi: 10.1016/j.robot.2011.06.016 [DOI] [Google Scholar]

[pcbi.1010840.ref053] 53. Hayashi Y, Yuki M, Kikuchi T, Tsuji K, Sugawara K. Effect of Pair Interactions on Transition Probabilities between Inactive and Active States—Achieving Collective Behaviour via Pair Interactions in Social Insects—. Journal of the Physical Society of Japan. 2015;84(10):104801. doi: 10.7566/JPSJ.84.104801 [DOI] [Google Scholar]

[pcbi.1010840.ref054] 54. Franks NR, Gomez N, Goss S, Deneubourg JL. The blind leading the blind in army ant raid patterns: testing a model of self-organization (Hymenoptera: Formicidae). Journal of Insect Behavior. 1991;4(5):583–607. doi: 10.1007/BF01048072 [DOI] [Google Scholar]

[pcbi.1010840.ref055] 55. Nicolis SC, Deneubourg JL. Emerging patterns and food recruitment in ants: an analytical study. Journal of theoretical biology. 1999;198(4):575–592. doi: 10.1006/jtbi.1999.0934 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref056] 56. Seeley TD. When is self-organization used in biological systems? The Biological Bulletin. 2002;202(3):314–318. doi: 10.2307/1543484 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref057] 57. Bonabeau E, Theraulaz G, Deneubourg JL, Aron S, Camazine S. Self-organization in social insects. Trends in ecology & evolution. 1997;12(5):188–193. doi: 10.1016/S0169-5347(97)01048-3 [DOI] [PubMed] [Google Scholar]

[pcbi.1010840.ref058] 58. Camazine S, Deneubourg JL, Franks NR, Sneyd J, Theraula G, Bonabeau E. Self-organization in biological systems. Princeton university press; 2020. [Google Scholar]

[pcbi.1010840.ref059] 59. Ito F, Higashi S. A linear dominance hierarchy regulating reproduction and polyethism of the queenless antPachycondyla sublaevis. Naturwissenschaften. 1991;78(2):80–82. doi: 10.1007/BF01206263 [DOI] [Google Scholar]

[pcbi.1010840.ref060] 60. Monnin T, Peeters C. Dominance hierarchy and reproductive conflicts among subordinates in a monogynous queenless ant. Behavioral Ecology. 1999;10(3):323–332. doi: 10.1093/beheco/10.3.323 [DOI] [Google Scholar]

[pcbi.1010840.ref061] 61. Shimoji H, Abe MS, Tsuji K, Masuda N. Global network structure of dominance hierarchy of ant workers. Journal of the Royal Society Interface. 2014;11(99):20140599. doi: 10.1098/rsif.2014.0599 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pcbi.1010840.ref062] 62. Sasaki T, Penick CA, Shaffer Z, Haight KL, Pratt SC, Liebig J. A simple behavioral model predicts the emergence of complex animal hierarchies. The American Naturalist. 2016;187(6):765–775. doi: 10.1086/686259 [DOI] [PubMed] [Google Scholar]

PERMALINK

A real-time feedback system stabilises the regulation of worker reproduction under various colony sizes

Simeon Adejumo

Tomonori Kikuchi

Kazuki Tsuji

Kana Maruyama-Onda

Ken Sugawara

Yoshikatsu Hayashi

Roles

Abstract

Author summary

Introduction

Fig 1. Feedback loop diagram.

Materials and methods

Maintenance and experimental procedure

Agent-based simulations

Overview

Internal state dynamics

Spatial behavioural dynamics

Fig 2. Schematic picture of the simulation environment.

Initial conditions and analysis

Table 1. Variables, constants, and initial conditions used in the agent-based simulation.

Results

Fig 3. Cumulative proportion of workers contacted by the queen during patrols at various colony sizes during laboratory experiments.

Fig 4. Patrol frequency and encounters.

Fig 5. Probability distribution of worker’s internal state (N = 20).

Fig 6. Average internal state of the colony for various colony sizes (N = 20–200 at increments of 20 workers).

Fig 7. Contact rates between the queen and workers.

Fig 8. Contact rate between workers.

Discussion

Conclusion

Appendix 1

Appendix 2

Appendix 3

Appendix 4

Appendix 5

Appendix 6

Appendix 7

Appendix 8

Appendix 9

Appendix 10

Supporting information

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Natalia L Komarova

Christian Hilbe

Roles

Author response to Decision Letter 0

Decision Letter 1

Natalia L Komarova

Christian Hilbe

Roles

Author response to Decision Letter 1

Decision Letter 2

Natalia L Komarova

Christian Hilbe

Roles

Acceptance letter

Natalia L Komarova

Christian Hilbe

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases