Globally distributed subducted materials along the Earth’s core-mantle boundary: Implications for ultralow velocity zones

Abstract

Ultralow velocity zones (ULVZs) are the most anomalous structures within the Earth’s interior; however, given the wide range of associated characteristics (thickness and composition) reported by previous studies, the origins of ULVZs have been debated for decades. Using a recently developed seismic analysis approach, we find widespread, variable ULVZs along the core-mantle boundary (CMB) beneath a largely unsampled portion of the Southern Hemisphere. Our study region is not beneath current or recent subduction zones, but our mantle convection simulations demonstrate how heterogeneous accumulations of previously subducted materials could form on the CMB and explain our seismic observations. We further show that subducted materials can be globally distributed throughout the lowermost mantle with variable concentrations. These subducted materials, advected along the CMB, can provide an explanation for the distribution and range of reported ULVZ properties.

Anomalies along Earth’s core can be explained by former oceanic seafloor that descended 3000 km to the base of the mantle.

INTRODUCTION

The absolute change in physical properties (e.g., temperature, density, and viscosity) from the mantle to the core is greater than that between solid rock and air. Hence, Earth’s core-mantle boundary (CMB) is host to a variety of phenomena, including thin (5 to 50 km), enigmatic regions with strongly reduced P- and S-wave velocities (δV_P and δV_S) and increased density (δρ), dubbed ultralow velocity zones (ULVZs; Fig. 1). Previous studies [see review by (1)] have reported a wide range of ULVZ characteristics, leading to notable debate regarding their origins. One common explanation for ULVZs is partial melt associated with thermal anomalies along the CMB, a concept supported by the approximate 3:1 δV_S:δV_P ratio found by some studies (2–4). However, some ULVZs are found far from the presumably hottest portions of the lowermost mantle, suggesting a compositional component to these CMB anomalies (5).

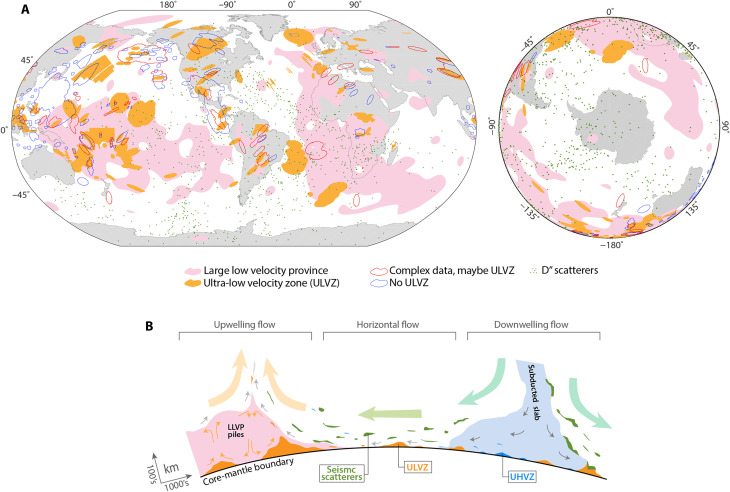
Fig. 1. Prior ULVZ studies and lowermost mantle structures.

(A) Maps showing the locations along the CMB of prior ULVZ and seismic wave scattering investigations (1, 6) in both global view (left) and in the Southern Hemisphere (right). Areas denoted in gold indicate regions where ULVZ evidence was found; those outlined in blue indicate regions where no ULVZ was observed, and those outlined in red mark uncertain regions. Pink shading indicates the LLVPs (61), and green dots mark seismic scatters (6). (B) Cartoon highlighting both upwelling (LLVP) and downwelling (subduction) in the lower mantle along with various CMB anomalies. UHVZ, ultrahigh velocity zones.

While less than 20% of the CMB has been surveyed for the presence of ULVZs (1), seismic wave scattering studies have identified globally distributed small-scale heterogeneities in the lowermost mantle (Fig. 1A) (6). These heterogeneities and ULVZs appear in greater quantities near the Large Low-Velocity Provinces (LLVPs) situated beneath Africa and the Pacific Ocean, but both are found throughout the deep mantle (i.e., away from LLVPs; Fig. 1A) (1). This suggests that compositionally distinct ULVZs and other lower mantle anomalies are part of the large-scale mantle convection cycle (Fig. 1B). Geodynamic modeling studies (7–9) have shown that former mid-ocean ridge basalts (MORBs) and oceanic sediments could be carried into the lowermost mantle by subduction-related downwellings and be advected along the CMB toward regions of mantle upwelling (i.e., toward the LLVPs). Subducted materials can take more than 100 Ma to descend into the lowermost mantle (10), during which time the convergent boundary at the surface may have migrated to a different location. Therefore, portions of the CMB that are not currently beneath active subduction may still have been influenced by mantle downwellings. LLVPs, on the other hand, may be long-lived if they are chemically distinct from and denser than the surrounding mantle [e.g., (11–13)].

Here, we investigate a largely unexplored portion of the lowermost mantle beneath the Southern Hemisphere that is not within or immediately near LLVPs or beneath areas of recent or current subduction, making our study unique compared to prior ULVZ investigations. Using core-reflected PcP waves recorded by the Transantarctic Mountains Northern Network (TAMNNET), a 15-station, broadband seismic array that was deployed in Antarctica from 2012 to 2015 (Fig. 2A) (14), as well as geodynamic simulations, we assess the presence and variability of ULVZ structure and how it relates to plausible mineralogical scenarios. Our seismic results, combined with those from prior investigations (Fig. 1A), and our three-dimensional (3D) geodynamic models provide strong evidence for globally distributed but heterogeneous ULVZ structure throughout Earth’s deep mantle. This widespread ULVZ distribution and the reported range of ULVZ characteristics can be explained by subducted materials along the CMB.

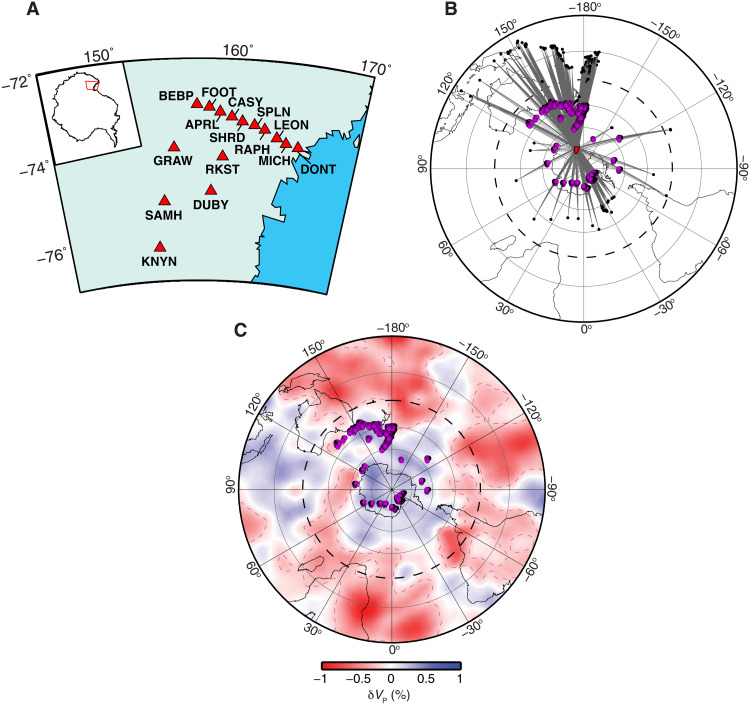
Fig. 2. Stations and events.

(A) TAMNNET stations (red triangles) with corresponding station names. The location of this map in relation to the rest of Antarctica is shown by the red polygon on the inset (upper left). (B) The 227 events (black dots) recorded by the TAMNNET stations (red polygon) used to investigate ULVZ structure beneath the Southern Hemisphere. Gray lines denote the PcP source-receiver ray paths, and purple dots denote the PcP CMB reflection (bounce) points. (C) Same PcP bounce points shown in (B) overlain on the P-wave tomography (δV_P) model from Hosseini et al. (62) at a depth of 2800 km.

RESULTS

Historical interstation pattern referencing

When PcP waves encounter a ULVZ, a reflection off the top of the ULVZ and reverberations inside this layer lead to pre- and post-cursor signals that arrive before and after the main PcP phase, respectively (fig. S1). The travel times and amplitudes of these signals can be modeled to characterize ULVZ structure. However, PcP phases typically have low amplitudes because much of the seismic energy continues into the Earth’s core (e.g., as PKP waves), which can make PcP signals difficult to identify. In addition, complications from complex source signals and scattered energy following the direct P wave can further obscure low-amplitude PcP waves. Stacking (waveform averaging) techniques are typically used to improve the PcP signal-to-noise ratio (SNR); however, if the stacks are based on low-quality waveforms, identification of small amplitude phases can still be challenging.

To improve the robustness of PcP identification and interpretation, we use a recently developed iterative, weighted stacking approach that is based on historical interstation pattern referencing (HIPR) (15). This technique uses both data quality and travel-time measurement differences between every event-station pair to develop historical patterns across a dataset. By referencing individual interstation measurement differences to their historical averages, weights that better reflect station and event quality can be determined. These weights allow us to generate higher-quality waveform stacks than those created with other stacking approaches because they better quantify high- versus low-quality data. Details of the HIPR approach and associated weighting are discussed in Materials and Methods and in the work of Hansen et al. (15).

We collected TAMNNET-recorded data from earthquakes with appropriate distance and magnitude criteria (30° to 75° and 5.0+, respectively) from throughout the Southern Hemisphere and evaluated their P and PcP phases (Materials and Methods). In total, HIPR-weighted, high-SNR PcP waveform stacks were generated for 227 events. We note that an earlier study (16) examined ScP waves recorded by the same network, but the CMB coverage provided by that dataset was limited. As shown in Fig. 2B, the TAMNNET-recorded PcP phases sample a broad section of the CMB beneath the Southern Hemisphere at nearly all azimuths, thereby allowing us to greatly expand upon prior ULVZ investigations. The study region is generally associated with higher-than-average seismic velocities in the lowermost mantle (presumably cooler material) and is dominantly away from LLVPs (Fig. 2C).

Synthetic modeling

Synthetic waveform modeling was used to investigate the lowermost mantle structure sampled by the TAMNNET PcP data. Using the generalized ray method (17), we computed a series of synthetic responses for the P and PcP phases and for ULVZ-generated reflections and reverberations. The synthetic responses were generated for a range of ULVZ characteristics (thickness, δV_S, δV_P, and δρ), where variations are relative to the Preliminary Reference Earth Model (PREM) (18), a 1D radially averaged model that does not contain a ULVZ. The parameter ranges encompass those reported by previous investigations (1), and more than 38,000 1D synthetic models were generated for each epicentral distance covered by the TAMNNET dataset (Materials and Methods). We recognize that the 1D models may not capture structural complexities in the lowermost mantle, such as those associated with CMB and/or ULVZ topography or with ULVZ stratification [e.g., (19)]; however, the range of examined models allows for unambiguous assessment of ULVZ presence and for a general understanding of how the ULVZ structure may change across the study region.

For each event, an attenuation-corrected P wavelet (Materials and Methods) was extracted from the HIPR-weighted P stack and was convolved with each synthetic response to create a series of synthetic PcP waveforms. The fit between the observed and synthetic PcP waveforms was determined with a “comparison quality” (CQ) factor, where a higher CQ value indicates a better match (Materials and Methods). Figure 3 provides an example of our synthetic modeling using the HIPR-weighted P and PcP stacks, with additional examples shown in fig. S2 and in the work of Hansen et al. (15).

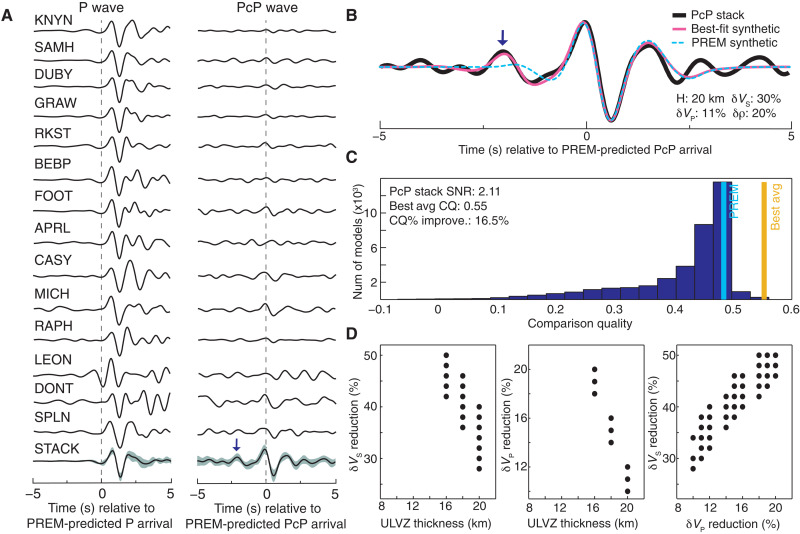
Fig. 3. Example ULVZ modeling.

(A) Example P and PcP waveforms from a TAMNNET-recorded event that occurred on 2 November 2015. All P traces have been normalized so that their maximum amplitudes are ±1.0; however, the PcP traces are normalized by their corresponding, original P amplitude. This emphasizes the difference in amplitude between the two phases. Bottom traces show the corresponding HIPR-weighted stacks, where shading indicates one SD. The stacks are also normalized so their maximum amplitudes are ±1.0. (B) HIPR-based PcP stack (black) along with synthetics from PREM (cyan) and from the best-fit model (pink). ULVZ parameters for the best-fit model are also listed (H: ULVZ thickness). In both (A) and (B), the small arrow indicates a ULVZ precursor on the PcP stack. (C) Histogram showing the range of CQ values across all synthetic models. The CQ values for PREM and the average CQ over the top 100 best-fit models are marked by cyan and orange lines, respectively. For reference, the PcP stack SNR, the average CQ value, and the average percent CQ improvement over PREM are provided (note: averages are again over the top 100 best-fit models). (D) Scatter plots showing the range of ULVZ parameters for the top 100 best-fit models. Models that only differ by δρ plot atop one another. Results were obtained using the method described by Hansen et al. (15).

We enforce two criteria to ensure that our ULVZ modeling and interpretations are based on the most reliable stacking results. First, each HIPR-weighted PcP stack was required to have an SNR ≥ 1.5. Second, the average CQ over the top 100 best-fit synthetic models is required to be > 0.2 (Materials and Methods). These criteria not only help to ensure that observed PcP signals are reliable but also that there is a good match between synthetics and observed PcP waveforms. For events meeting these criteria, we determined the percent CQ improvement for each synthetic PcP compared to that computed for the PREM synthetic. This provides an assessment on whether a given ULVZ model fits the data significantly better than the PREM (i.e., non-ULVZ) model. For a given event, the average CQ value over the top 100 best-fit synthetic models was required to be at least 10% greater than the CQ of PREM for us to confidently interpret that the event robustly displays ULVZ evidence. Events that do not meet this criterion are still best fit by a ULVZ-inclusive model (provided that they meet the SNR and average CQ requirements noted above); however, in such cases, the Earth structure is more ambiguous, meaning a ULVZ is possible but is uncertain (fig. S2).

Of the 227 examined events, 44 did not meet the specified PcP SNR and/or the average CQ criteria noted above; therefore, we focus our ULVZ assessment on the remaining 183 events. Of those, 152 events show robust ULVZ evidence, as defined by the average percent CQ improvement threshold. The remaining 31 events fell below the specified threshold and therefore do not clearly indicate the presence or absence of ULVZ structure (Fig. 4A).

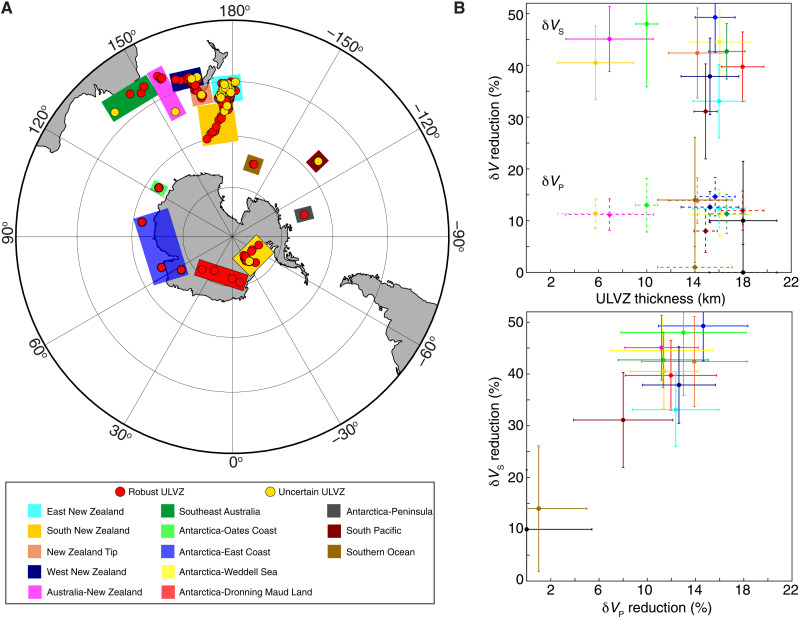
Fig. 4. ULVZ results beneath the Southern Hemisphere.

(A) Average PcP CMB bounce points for examined events. Red dots indicate events that meet all three modeling criteria and show robust ULVZ evidence, and yellow dots denote events that fell below the CQ improvement over PREM threshold and hence provide uncertain ULVZ evidence. Colored rectangles denote geographic families. (B) ULVZ parameters averaged by geographic family with corresponding SDs. Top: Measurements with solid error bars correspond to δV_S, and those with dashed error bars correspond to δV_P. Colors are the same as in (A).

ULVZs beneath the Southern Hemisphere

Given the wide geographic distribution of our PcP CMB sampling, we separated the events into regional families (Fig. 4A). Furthermore, within each family, we grouped the events using a 2° × 2° grid and a moving, circular bin (radius = 2°; fig. S3). This approach provides some geographic overlap between adjacent areas, and any events whose PcP CMB bounce points fell within a particular bin were grouped together. Within each bin, we determined a weighted CQ, which depends on the CQ values computed for each examined synthetic model and for each event in the bin, as well as each event’s average HIPR-based PcP weight and the event’s average PcP CMB bounce point distance from the center of the bin (Materials and Methods). The model with the largest weighted CQ sum is the one that best fits all the events in the bin. This approach illustrates how ULVZ characteristics vary within a given regional family (fig. S3). We also determined the average best-fit ULVZ parameters across all bins for each family, along with corresponding SDs, to represent family-specific models with associated uncertainties, thereby allowing us to examine ULVZ variability between geographic families across the study area as well (Fig. 4B; Materials and Methods).

When modeling the ULVZ structure, it is not uncommon to observe tradeoffs between layer thickness and velocity reduction (Fig. 3D and fig. S2). A model with a thinner and more anomalous ULVZ may provide a comparable fit to data modeled with a thicker, less anomalous ULVZ (20–24). While such modeling tradeoffs preclude specification of exact ULVZ characteristics in any one area, our results suggest stronger ULVZ δV_S reductions than δV_P, even when uncertainties are considered (Fig. 4B). δV_S:δV_P ratios range from about 2.5:1 to 4:1, which are generally consistent with some degree of partial melting [e.g., (2)], even though our study area is associated with a presumably cooler portion of the lowermost mantle (Fig. 2C). Most geographic families have ULVZ thicknesses between about 14 and 20 km, although several show somewhat thinner ULVZs (about 3 to 10 km). Ultimately, our findings provide robust evidence for widespread ULVZs across the study region, including general differences both within and between geographic families (Fig. 4 and fig. S3). Thus, there is a strong indication of variable ULVZ structure throughout our study region.

Geodynamic simulations

As noted previously, our study region is located away from the Pacific and African LLVPs (Fig. 2C), and present-day subduction is not occurring in this portion of the Southern Hemisphere. However, the circum-Pacific subduction system has been active over the past ~200 Ma (25). Therefore, we performed 3D global mantle convection simulations with plate motion history to test whether former subducted materials could have been advected into the study region, thereby providing a source for the imaged ULVZs.

We performed two mantle convection models. In the first model (Fig. 5, Model 1), the LLVPs are represented by intrinsically dense thermochemical piles, while in the second model (Fig. 6, Model 2), the LLVPs are purely thermal structures. Both models use plate motion history over the past 200 Ma (25). Passive tracers are continually introduced beneath subducting regions in the uppermost mantle, which are then advected into the deep mantle by convective flow. These passive tracers are used as a proxy for subducted materials, including oceanic crust (consisting of MORB and sediments) and depleted oceanic lithosphere; we note that we do not separately simulate the advection of each of these components. Further details about the model setup and the tracers are provided in Materials and Methods. The advection of subducted materials into the lowermost 50 km of the mantle is shown in movies S1 and S2 for Models 1 and 2, respectively, with snapshots at the present day shown in Figs. 5 and 6. After ~150 Ma, subducted materials start to consistently reach the lowermost mantle and migrate along the CMB (movies S1 and S2). At present day, the entire CMB outside the thermochemical piles in Model 1 is littered with subducted materials (movie S1 and Fig. 5). In Model 2 (movie S2 and Fig. 6), the subducted materials are even more widespread across the CMB. In both models, the accumulations of subducted materials are highly variable. An examination of the lowermost 300 km of the mantle in both models (fig. S6) similarly shows globally distributed subducted materials above the CMB. Models 1 and 2 also show widespread thermal anomalies above the CMB (Figs. 5 and 6 and fig. S7), which may be related to small-scale convection (26–27).

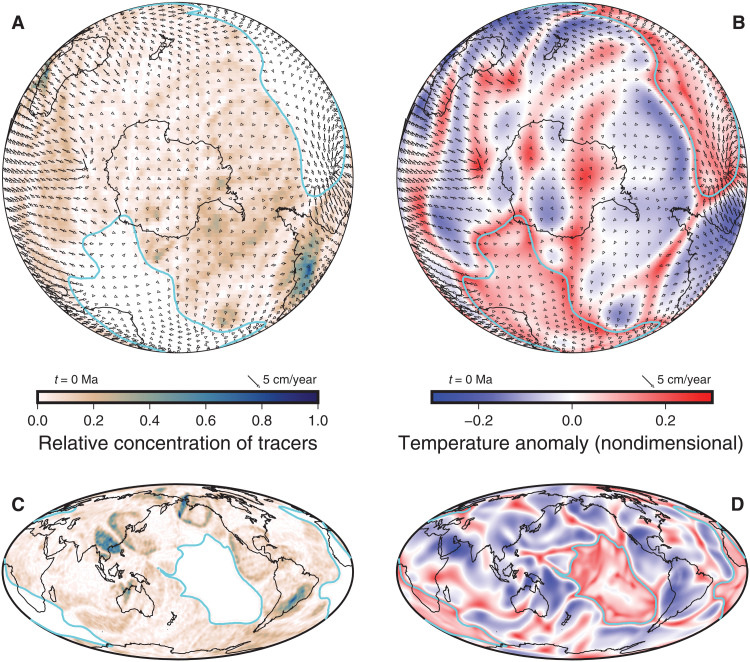
Fig. 5. Distribution of subducted materials and temperature field along the CMB from geodynamic Model 1.

In this model, the LLVPs are simulated by thermochemical piles, the boundaries of which are marked by the cyan lines. (A) Distribution of subducted materials in the lowermost 50 km of the mantle, viewed from South Pole. Colors highlight the relative concentration of tracers, with higher (lower) concentrations representing higher (lower) abundances of subducted materials. (B) Temperature field at a depth of 2800 km, viewed from South Pole. Colors indicate nondimensional temperature anomalies. (C) Same as (A) but in global view. (D) Same as (B) but in global view. Arrows in (A) and (B) indicate mantle flow velocity along the CMB.

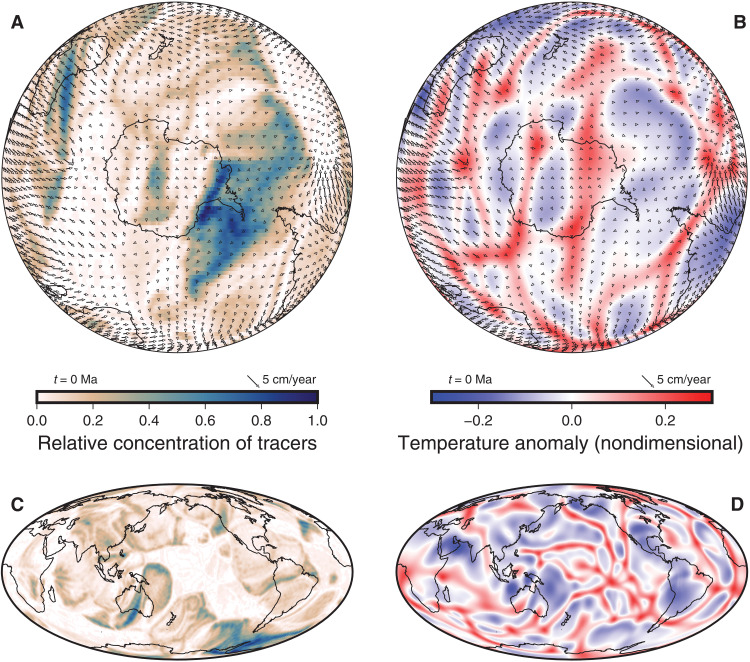
Fig. 6. Distribution of subducted materials and temperature field along the CMB from geodynamic Model 2.

In this model, the LLVPs are assumed to have purely thermal origins. (A) Distribution of subducted materials in the lowermost 50 km of the mantle, viewed from South Pole. Colors highlight the relative concentration of tracers, with higher (lower) concentrations representing higher (lower) abundances of subducted materials. (B) Temperature field at a depth of 2800 km, viewed from South Pole. Colors indicate nondimensional temperature anomalies. (C) Same as (A) but in global view. (D) Same as (B) but in global view. Arrows in (A) and (B) indicate mantle flow velocity along the CMB.

DISCUSSION

Because of its relatively small volume, most subducted MORB may be passively advected into the deep mantle with cold slabs (8, 28). We note that our global-scale geodynamic models cannot resolve thin (< 10 km) oceanic crust; therefore, the models do not incorporate complex, lower mantle processes that may influence the physical properties and separation of subducted materials. For example, prior studies have shown that subducted MORB, which is intrinsically denser than the surrounding mantle, can segregate and accumulate on the CMB (7–8, 29–30). After segregation, the subducted materials could migrate along the CMB, with some materials becoming entrained into LLVPs (8, 31). If LLVPs are purely thermal in origin, then subducted materials could be more easily advected into and across the LLVP regions (Fig. 6). Even the LLVPs themselves may be composed of accumulations of ancient subducted oceanic crust, potentially mixed with other lower mantle materials (8, 29, 31–33).

That said, while segregation and other CMB processes could affect the advection and/or the location of subducted materials on a local scale, such processes would not change their overall broadscale distribution. It is the surface plate motion and the subduction history (25) that drive the mantle convection pattern and, thus, the overall distribution of subducted materials. Our models (Figs. 5 and 6, fig. S6, and movies S1 to S3) demonstrate that subducted materials from over the past 200 Ma could be spread widely across the CMB, not only beneath the Southern Hemisphere but also globally. These materials are advected within the lowermost mantle, migrating from areas of downwelling to areas of upwelling, with lateral variations in accumulation (thickness). Our modeling results and our widespread ULVZ observations, coupled with positively identified ULVZs elsewhere along the CMB (Fig. 1A), collectively suggest that these anomalous CMB structures are principally related to subduction processes.

Besides MORB, other possible origins for widespread, globally distributed ULVZs must be considered. Fractional crystallization of a remnant magma “ocean” (19, 34) is one example. Because these basal remnants represent ancient compositional reservoirs, they were likely advected into upwelling regions of the mantle long ago and thus may not exist outside the LLVPs at present day (5). However, if the remnants have very high intrinsic density and a large viscosity contrast compared to the surrounding mantle, then their advection to LLVP regions may not yet be complete, and a thin, global layer could still be present along the CMB. Under such conditions, the basal remnants could contribute to ULVZs. Some basal remnants could also be entrained into the background mantle and then be advected with subducting slabs into the lowermost mantle (31).

It has been suggested that the seismic properties of the mantle can be explained by a mechanical mixture of basalt and harzburgite, resulting from the subduction of physically and chemically stratified oceanic lithosphere. However, such a mixture cannot explain the seismic properties of the lower mantle, and other mechanisms, such as basalt enrichment (35–37), must be used to reconcile the model with observations. It is also worth noting that ancient subducted materials have likely reached a more uniform mantle composition, resulting from viscous shearing and deformation (35). Alternatively, recent studies (38–39) have suggested that solidus melting of pyrolite, a mineralogical composition thought to exist throughout the lowermost mantle, occurs at ~3500 K, which could be less than the outermost core (and thus CMB) temperature of ~4000 K (40–42). Therefore, partial melting of pyrolite at the base of the mantle could occur globally. Strong partitioning of iron into the silicate partial melt (39, 43) could generate dense and, therefore, gravitationally stable ultralow velocity structures.

However, the presence and degree of pyrolitic partial melt at the CMB would vary with lateral temperature variations: In warmer regions, a thicker accumulation of partial melt would be expected, while a thinner layer would exist in cooler regions. Therefore, if ULVZs were solely associated with pyrolitic partial melt, we would expect to see the thinnest ULVZs outside of LLVPs (e.g., beneath subduction), with thicker ULVZs inside LLVP regions, which is not always the case (1). Furthermore, the melting temperature of pyrolite could be higher (44–45) and remains controversial, but existing studies have consistently shown lower solidus melting temperatures for subducted MORB (46–47). Hydrated subducted lithosphere and subducted ocean sediments could also lower solidus melting temperatures (48), thereby contributing to partially molten subducted materials in the lowermost mantle. Therefore, partial melting of recently subducted materials (i.e., within the past ~200 Ma) near the CMB better explains a global distribution of ULVZs than partially molten pyrolite, although a mixture of both is also plausible. As with pyrolite, the degree of subducted material partial melt would depend on lateral temperature changes.

We favor subducted materials as the origin for broadly distributed ULVZs, although we do not exclude other mechanisms that may locally contribute to anomalous lowermost mantle structure. Accumulations of partially molten, globally distributed subducted materials with variable size and shape (Figs. 5 and 6, Models 1 and 2) would also lead to chemical heterogeneities along the CMB. In turn, this would result in anomalies with varied seismic properties. The distribution of subducted materials in the lowermost mantle would evolve with time, changing with the ever-changing convection system in our planet. Collectively, this could explain the distribution and range of observed ULVZ properties reported here and in other studies (Fig. 1A) (1). It is also worth noting that small-scale (~10 km) scattering heterogeneities detected throughout the deep mantle (Fig. 1A) have been attributed to subducted MORB as well (6); therefore, scatterers and ULVZs may be related features (Fig. 1B).

It is possible that the widespread evidence for ULVZs and the broad distribution of subducted materials highlighted in our study could be associated with a ubiquitous ULVZ above the CMB, with variable characteristics (thickness, δV_S, δV_P, and δρ). While this concept seems to contradict prior seismic investigations that have reported an absence of ULVZ structure in some locations (Fig. 1A) (1), all seismic probes have a ULVZ detectability threshold (typically ~5 km or greater). Therefore, it could be the case that ULVZs are globally present but are too thin to be resolved in some regions. Verifying the existence of such a ubiquitous layer would require global seismic surveys of ultrafine (< 5 km) CMB structures. If present, this layer could also have other notable effects on mantle and core dynamics. For example, subducted materials in the lowermost mantle could strongly influence core heat flux (49), the formation, dynamics, and composition of mantle plumes (29, 50), and/or CMB sedimentation processes that may affect coupling mechanisms between the core and the mantle (51–52).

MATERIALS AND METHODS

Data processing and initial stacking

TAMNNET-recorded waveforms from magnitude 5.0+ earthquakes with event-station distances between 30° and 75° were inspected for PcP energy. All data were band-pass filtered between 0.50 and 1.50 Hz; the vertical and radial components were rotated to their true longitudinal motion directions, and predicted P and PcP arrival times from PREM (18) were marked on the waveforms. A total of 822 events displayed identifiable PcP arrivals, and these events formed the base for our initial analysis (fig. S4).

For each event, both the P and PcP waveforms were initially aligned using the PREM-predicted arrival times. The waveforms were windowed ±25 s around the phase of interest (i.e., P or PcP); their maximum amplitudes were normalized to unity, and the waveforms for each phase were then averaged to create a corresponding linear stack. The individual waveforms were then cross-correlated with the P and PcP linear stacks, respectively, to determine an associated delay time and cross-correlation coefficient (CCC). Individual waveforms were time-shifted by the delay time to improve the alignment of the respective signal (i.e., the P or PcP phase), and the waveforms were weighed by their respective CCC² value and a weight based on the waveform’s SNR (15). The realigned, weighted waveforms for each phase were then restacked. Using the updated stacks, the cross-correlation, realignment, weighting, and restacking scheme was iteratively repeated until the CCC between the newly created stack and the previous one was greater than 0.995. The above approach was applied to all 822 events in our base dataset, thereby optimizing the individual waveform alignments and generating representative P and PcP stacks for each earthquake.

Historical interstation pattern referencing

For a given station, the applied time shift may vary substantially from one event to another given small-scale structures beneath the array, structural heterogeneities between the earthquake and the station, and/or event mislocation errors. It is generally not possible to identify the source(s) of such absolute time-shift variations between individual records, but it is important to assess the corresponding uncertainty to determine whether the prestack time shifts may be erroneous. Time-shift differences between stations, across a large number of events, can be used to better understand which timing variations are similar to historical averages and which deviate from typical values, thereby providing a systematic assessment of time-shift measurement stability at each station. This helps quantify high- versus low-quality data, which can be incorporated into the stacking analysis by means of event and station weights.

For each event-station pair, an interstation time-shift difference (DT_phase) was computed using the total time shift applied to the examined waveform (for the phase of interest, i.e., either P or PcP) and that applied to some reference station (15). The TAMNNET stations were cycled, allowing each to serve as the reference station, and we determined DT for each reference station possibility and for each event. The average and SD of the DT values (μDT_phase and σDT_phase, respectively) across all events were also determined, thereby providing historical averages and corresponding variations for each TAMNNET station based on the differences in a given station’s measurements with respect to those of all other stations in the dataset. Subtracting μDT_phase from DT_phase defines ΔDT_phase, which indicates how differential measurements compare to historical averages. We also determine the L2-norm of the ΔDT_phase values across all stations (𝓁²_ΔDTphase) along with the corresponding averages and SDs (μ𝓁²_ΔDTphase and σ𝓁²_ΔDTphase) across all events (for each reference station). The μ𝓁²_ΔDTphase and σ𝓁²_ΔDTphase values allow us to assess DT_phase for any given event, ultimately allowing an event-specific weight to be defined. For instance, if 𝓁²_ΔDTPcP is large compared to μ𝓁²_ΔDTPcP for a given event (and for a given reference station), then the PcP-wave time shifts for that particular event are substantially different compared to the historical averages of all other events, meaning that they are less reliable and hence should receive a lower event weight. Hansen et al. (15) outlines how weights for different events were assigned on the basis of their 𝓁²_ΔDTphase, μ𝓁²_ΔDTphase, and σ𝓁²_ΔDTphase values.

The historical interstation time-shift differences were also used to determine associated station weights. For each reference station, the L2-norm of the σDT_P values defined above (𝓁²_σDTP) was determined to provide a measure of consistency in the P-wave time shifts. That is, if 𝓁²_σDTP is small, the interstation P-wave time shifts are consistent at a given station and can be reliably used to assess the time shifts of individual events. Hansen et al. (15) specifies how the 𝓁²_σDTP values are used to define weights for each of the TAMNNET stations. We note that the station weights were only based on the P waveforms given their higher SNR compared to the PcP waveforms. Ultimately, the HIPR approach allows us to assign station and event weights (for each phase, P or PcP) to all examined waveforms that better reflect the data quality.

Restacking

Of the 822 events in our base dataset, 15 were removed because their corresponding HIPR event weights were zero. For the remaining events, new P and PcP stacks were generated to incorporate the HIPR-based weights. As before, each P and PcP waveform was weighted by its CCC² value and SNR-based weight; however, the HIPR event and station weights are now also applied, as described by Hansen et al. (15). The iterative stacking approach was again applied to optimize the phase alignment and to update all event-representative stacks. An example is shown in Fig. 3A, with additional examples by Hansen et al. (15).

Following our stacking routine, it was recognized that some events had emergent, low SNR or complex P arrivals, which are not ideal for wavelet extraction (see the “Synthetic modeling” section below); therefore, such events were dismissed from further consideration. Other events were removed from our analysis because there were too few (< 5) station records available to generate a robust stack (fig. S4). While the remaining events had high-quality P arrivals, issues with PcP prevented about half of these events from further consideration. For example, we predicted the arrival times for seismic phases that could potentially overlap with the PcP signal (such as pP, sP, and PP), and all PcP waveforms were visually inspected for such interference. Any waveforms that were “contaminated” by these other phases, thereby making our PcP pre- and/or postcursor analysis ambiguous, were removed from consideration. Other reasons for record dismissal included a low PcP SNR (fig. S5) and/or complex, multipulsed waveshapes. We note that these PcP events may still be associated with anomalous lower mantle structure; therefore, they are denoted separately on fig. S4.

Ultimately, 227 events were considered for our ULVZ assessment (fig. S4). It is worth noting that the HIPR weighting scheme led to higher SNR stacks for ~15% of the considered events, which is notable because the approach allowed us to retain events that would otherwise have been dismissed from further analysis. For all examined data, the HIPR weighting provides further confidence in the events selected for modeling and interpretation because the stacks are based on waveforms whose weights accurately reflect the corresponding station and event quality.

Additional considerations

PcP waves experience more attenuative energy loss compared to direct P waves, and the resultant waveform differences need to be corrected to make the P and PcP stacks more comparable. Each P stack was convolved with a series of t* operators, ranging from 0.2 to 2.0, which represent progressively greater attenuation (16, 21, 53–54). The optimal t* operator is the one that creates an attenuated P-wave response that most closely matches the PcP signal (15).

In some cases, the radiation pattern of an earthquake can lead to opposite P and PcP polarities; therefore, we also examined the polarization of our stacks. Centroid moment tensors (CMTs) (55–56) were used to predict event radiation patterns and the corresponding relative polarities for each phase (57). For any event predicted to have a high likelihood of a polarity reversal (or for any event where a CMT was not available), the t*-convolved P stack was compared to the corresponding PcP stack with both normal and reversed polarity. If the reversed polarity led to a higher similarity between the P and PcP stacks, that polarity was then adopted.

Synthetic modeling

Synthetic responses were generated for ULVZs with thicknesses varying from 2 to 20 km in 2-km increments, δρ varying from −10 to 20% in 5% increments, δV_P varying from 0 to 20% in 1% increments, and δV_S varying from 0 to 50% in 2% increments. All δρ, δV_P, and δV_S values are relative to PREM (18), and a model without a ULVZ was also included. A Hanning-tapered wavelet was extracted from the t*-convolved P-stack for each event (see the “Additional considerations” section above), which was convolved with each synthetic response to generate synthetic PcP waveforms (PcP_syn). The PcP_syn were then correlated with the observed PcP stacks (PcP_obs), and the fit between them was determined with a CQ factor, defined as

$$\mathrm{CQ}=\mathrm{CCC}\times \mathcal{G}$$ (1)

where CCC is the correlation coefficient between PcP_syn and PcP_obs and $\mathcal{G}$ is a measure of the goodness of fit, defined by

$$\mathcal{G}=1-\sqrt{\frac{{\displaystyle \sum _{n=1}^N}{[{\mathrm{PcP}}_{\mathrm{obs}}-{\mathrm{PcP}}_{\mathrm{syn}}]}^2}{{\displaystyle \sum _{n=1}^N}{[{\mathrm{PcP}}_{\mathrm{obs}}]}^2}}$$ (2)

In Eq. 2, N is the number of samples within the examined data. Further details are described by Hansen et al. (15). In practice, the product of CCC and $\mathcal{G}$ (Eq. 2), both of which are less than one, results in CQ values that are commonly below 0.5; therefore, we require that the average CQ is >0.2 to ensure a good match between the synthetic and observed PcP waveforms.

Geographic binning

Our PcP CMB sampling points were grouped using a 2° × 2° grid and a moving, circular bin (radius = 2°). For each event (j) and each examined synthetic model (k) within a given bin, a weighted CQ [CQ(j,k)_weighted] was computed using

$$\mathrm{CQ}{(j,k)}_{\mathrm{weighted}}=\mathrm{CQ}(j,k)\times {\text{Ψ}}_{\mathrm{dist}j}\times {\mathrm{\mu }\mathrm{W}}_{\mathrm{PcP}j}$$ (3)

where CQ(j,k) is the CQ defined by Eq. 1, Ψ_distj is a Gaussian weight based on the event’s average PcP CMB bounce point distance from the center of the examined bin, and μW_PcPj is the average HIRP-based PcP weight for event j (15). The CQ(j,k)_weighted values were summed across all events in the bin for each examined model, and the model with the largest weighted sum is the one that best fits all the events in the bin. That said, given the uncertainties associated with our 1D modeling, it is recognized that the best-fit model may not represent the precise ULVZ characteristics; therefore, we also determine the SD of the ULVZ parameters for each bin (fig. S3). Furthermore, for each geographic family, we determined the average best-fit ULVZ parameters across all bins, along with corresponding SDs (Fig. 4B). Together, these provide reasonable uncertainty estimates for our ULVZ characteristics.

Geodynamic modeling

The geodynamic modeling (Figs. 5 and 6, fig. S6, and movies S1 and S2) is performed by solving the conservation equations of mass, momentum, and energy under the Boussinesq approximation, in a 3D spherical global mantle domain from the surface to the CMB, using the CitcomS code (58). The model domain is split into 12 equal-volume caps, with each cap containing 64 × 64 × 64 elements. Both the surface and the CMB are isothermal with non-dimensional temperatures of 0.0 and 1.0, respectively. The surface is employed with plate motion history from Seton et al. (25), and the CMB has a free-slip velocity boundary condition. The whole mantle initially has a temperature that increases linearly from 0.0 at the surface to 0.558 at a depth of 300 km, and the temperature is maintained at 0.558 below this depth. Models are initially run for 24 Ma using the reconstructed plate motion at 200 Ma (25). After that, the full plate motion history over the past 200 Ma is used on the surface of the model up until present day (e.g., 0 Ma).

The Rayleigh number is 2 × 10⁸ (with Earth’s radius set as the length scale). The temperature (T) dependence of viscosity (η) is given by

$$\mathrm{\eta }(T)=\exp [A(0.5-T)]$$ (4)

where the activation parameter (A) = 9.21. This results in a maximum of 10⁴× changes in η as T increases from 0 to 1. There is a 60× η jump from the upper to the lower mantle and a ~3.4 linear η increase between 660 km depth and the CMB. The model also has a 2.2× linear increase in thermal diffusivity and a 3× linear decrease in thermal expansivity from the surface to the CMB. At every time step from 200 Ma to present day, passive tracers are introduced into regions at a depth of 300 km beneath subduction zones where the plate velocity convergence rate is higher than 0.1 Ma⁻¹ (where the convergence rate is defined as the divergence of velocity, $\mathrm{\nabla }\cdot \overrightarrow{u}$). The tracers are passively advected by mantle flow (i.e., they do not influence the dynamics), and they track the locations of the subducted material (again, consisting of oceanic crust, sediments, and depleted lithosphere) into the deep mantle (movie S3). We note that the subduction zones in our models have widths that are typically on the order of 100s of kilometers, which is much broader than the oceanic crust, which typically has a thickness of ~6 to 7 km. The resolution of our models is not high enough to resolve the dynamics of the thin crustal layer alone; however, previous studies [e.g., (28)] have shown that in most parts of the mantle, the advection of the thin, subducted oceanic crust follows that of the subducted slab. Therefore, the global distribution of subducted oceanic crust is comparable to that of subducted slabs. The number of passive tracers introduced into the model domain is arbitrary; the relative concentration of tracers in the lowermost mantle is more relevant. To calculate the relative concentration of these tracers, we first count the number of tracers per unit area (ξ) in each model element in either the lowermost 50 km (Figs. 5 and 6) or 300 km (fig. S6) of the mantle. The ξ is then normalized by the maximum value to determine the relative tracer concentration.

As noted previously, two different geodynamic models were performed. In Model 1, a global layer of intrinsically dense material with a buoyancy number (B) of 0.15 is initially introduced in the lowermost 150 km of the mantle. This layer is later pushed by convective flow into thermochemical piles that resemble the LLVPs. B is defined as

$$B=\frac{\text{Δ}\mathrm{\rho }}{\mathrm{\rho }\mathrm{\alpha }\text{Δ}T}$$ (5)

where Δρ/ρ is the intrinsic density anomaly, α is the thermal expansivity, and ΔT is the reference temperature. In our models, α = 3 × 10⁻⁵ K⁻¹ and ΔT = 2500 K; therefore, a B = 0.15 is equivalent to a density anomaly of 1.1%. The thermochemical piles and the background mantle are simulated using ~62.9 million active tracers (e.g., 20 tracers per element) using the ratio tracer method (59). Unlike the passive tracers, which are continuously introduced into the model, the active tracers are introduced as an initial condition (i.e., a model input) to Model 1, and the number of active tracers is constant with time. Model 2 uses the same parameters and setup as Model 1 but without the intrinsically dense material in the lowermost mantle. In this scenario, the LLVPs are treated as purely thermal structures. For reference, Models 1 and 2 contain a total of ~2.5 million and ~4.7 million passive tracers, respectively; however, we again emphasize that the number of passive tracers is arbitrary and that only the relative concentration of tracers in the lowermost mantle is relevant to our study. 3D snapshots of the temperature fields at present day are shown in fig. S7 for both models.

Supplementary Materials

This PDF file includes:

Figs. S1 to S7

Movies S1 to S3