Condensed but liquid-like domain organization of active chromatin regions in living human cells

Abstract

In eukaryotes, higher-order chromatin organization is spatiotemporally regulated as domains, for various cellular functions. However, their physical nature in living cells remains unclear (e.g., condensed domains or extended fiber loops; liquid-like or solid-like). Using novel approaches combining genomics, single-nucleosome imaging, and computational modeling, we investigated the physical organization and behavior of early DNA replicated regions in human cells, which correspond to Hi-C contact domains with active chromatin marks. Motion correlation analysis of two neighbor nucleosomes shows that nucleosomes form physically condensed domains with ~150-nm diameters, even in active chromatin regions. The mean-square displacement analysis between two neighbor nucleosomes demonstrates that nucleosomes behave like a liquid in the condensed domain on the ~150 nm/~0.5 s spatiotemporal scale, which facilitates chromatin accessibility. Beyond the micrometers/minutes scale, chromatin seems solid-like, which may contribute to maintaining genome integrity. Our study reveals the viscoelastic principle of the chromatin polymer; chromatin is locally dynamic and reactive but globally stable.

Active chromatin in human cells is rather condensed, but locally dynamic and reactive, and globally stable.

INTRODUCTION

In eukaryotic cells, genomic DNA wraps around core histones to form nucleosomes (1, 2) and functions as chromatin with its associated RNAs and proteins. The spatial and temporal organization of chromatin plays a key role in DNA transactions such as transcription and DNA replication/repair/recombination (3–5). Recent studies suggest that chromatin consists of rather irregular and variable nucleosome arrangements (6–14). Multiscale computational modeling supports this notion (15).

Many studies using various techniques showed that irregularly folded chromatin has higher-order organizations. A large-scale chromatin structure with a diameter of ~200 nm was observed by light and electron microscopic imaging (16–21). Fluorescent pulse labeling during DNA replication has revealed globular DNA replication foci with an average diameter of approximately 110 to 150 nm (22–25). Meanwhile, 3C and related methods like Hi-C (26), which can generate a fine contact probability map of genomic DNA, have suggested that eukaryotic genomes are partitioned into chromatin domains of topologically associating domains (TADs) at the scale of several hundreds of kilobases (kb) (27–29) and smaller contact/loop domains (mean size of ~185 kb) (30, 31). TADs and contact/loop domains are the functional units of the genome, consisting of different epigenetic features (30, 31) and were confirmed visually by super-resolution imaging (32). These domains are clustered as two distinct megabase scale compartments, A and B (26), which supposedly represent open transcriptionally active chromatin and closed inactive chromatin, respectively.

In the hierarchical chromatin organization described above, the loop domain is assumed to be held by cohesin (31, 33–35). However, how the domain looks in a living cell remains unclear (i.e., do loops form a cluster of nucleosomes or extend). While some studies have observed condensed chromatin organization (18, 20), others have suggested the presence of rather loose bundles of fibers or extended loops by electron microscope (EM)-tomography and super-resolution imaging of fixed interphase cells (12, 14). Hi-C studies have shown that contact/loop domains are functional units of the genome in DNA transaction reactions (30, 31). Therefore, it is important to understand which conformation these domains are likely to take in terms of their higher-order regulation.

Dynamic chromatin behavior, or temporal organization of chromatin, plays a critical role in various genome functions (3–5). Our studies of local chromatin motion suggested that chromatin acts like a liquid on a size-scale of about 200 nm (18, 36, 37). Gibson et al. (38) also showed in vitro that nucleosome arrays with cations developed into large chromatin condensates, around 10 μm in size. These condensates behaved like liquid droplets (38) formed by liquid-liquid phase separation (39). Consistently, when a restriction enzyme was injected into mitotic cells to fragment chromatin, chromosomes became round bodies resembling liquid droplets (40). On the other hand, Strickfaden et al. (7) suggested that nucleosome array formed condensates and chromatin in the cell show solid-like properties. The physical nature of chromatin under physiological conditions, whether it is liquid-like or solid-like, is thus still unclear. Chromatin may have viscoelastic properties (41–46), which mean that its physical properties can change depending on the time- and size-scales used for measurements.

To approach the viscoelastic issue of chromatin, it is critical to investigate chromatin in living cells. Chemical fixation with formaldehyde (FA), glutaraldehyde, or methanol can have artifactual effects on chromatin structures, like the formation of chromatin aggregates (47, 48). Moreover, chromatin folding can be altered during the fixation process as environmental conditions, including cations (48, 49) and molecular crowding (50) change. These possible effects can make real chromatin organization and behavior in the cell invisible. High-resolution imaging in living cells is technically challenging because dynamic chromatin movement blurs structural features, as a motion blur effect. This problem is especially prominent in euchromatic regions (A-compartment) (26), which are more actively transcribed and dynamic (18, 51). Thus, we need a novel strategy to visualize and analyze euchromatic chromatin organization in living cells.

In this study, we introduce novel approaches to analyze physical organization and behavior of chromatin domains in living cells. Using previously reported single-nucleosome imaging (18, 37, 52–54), we first visualize local chromatin behavior in the early DNA replicated regions, which corresponds to Hi-C contact domains (TADs) with active chromatin marks (30, 31). Nucleosomes in active chromatin regions are less constrained and more mobile as compared to the average movement of whole chromatin. Next, correlation analysis of motions of two neighbor nucleosomes suggests that nucleosomes form a condensed domain organization with a diameter of ~150 nm. Furthermore, we examine the mean square displacement (MSD) between two neighboring nucleosomes (two-point MSD), which suggests nucleosomes locally fluctuate in the condensed domain like a liquid. On the other hand, fluorescence recovery after photobleaching (FRAP) analysis shows that chromosomes are stable like a solid on the scale of micrometers/minutes. Our findings offer a new physical view of chromatin domains in active euchromatin regions. In living cells, chromatin forms condensed, but flexible, liquid-like domains. At a larger spatiotemporal scale, such as at the chromosome level, chromatin is stable, unmixed, and solid-like. These physical features of chromatin domains contribute to its functional nuclear organization.

RESULTS

Classical early replication foci correspond to Hi-C contact domains with active histone modifications

To approach the physical nature of higher-order chromatin organization in active chromatin regions (A-compartment) of living human cells, we focused on the early DNA replication foci, where fluorescent nucleotides (Cy3-dCTP; fig. S1A) were incorporated during early S phase (Fig. 1, A to C, and fig. S1, A and B). The DNA replication foci have long been used for live-cell imaging to visualize chromatin dynamics (22–25) because these foci patterns are retained throughout several cell cycles. Early and mid-late replication foci correspond to euchromatin and heterochromatin, respectively, but their genomic nature remains unclear, including their relevance to currently well-known Hi-C domains and histone marks.

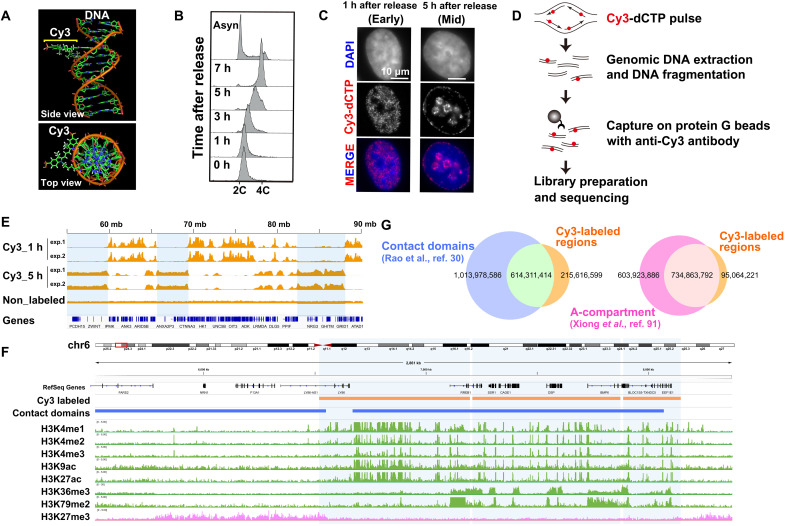
Fig. 1. Analysis of Cy3-labeled genomic regions.

(A) Model of Cy3-labeled DNA structure with a side and top view (provided by Y. Joti at Spring-8). (B) FACS profiles of HeLa cells synchronized at the G1-S boundary, using a double thymidine block, and released in fresh medium at the indicated time point after release. (C) HeLa cell DNA replication foci labeled with a pulse of Cy3-dCTP (second row) 1 hour (first column) and 5 hours (second column) after release from a double thymidine block. The nuclei were stained with DAPI (top row, blue). (D) A scheme of Cy3-dCTP–labeled DNA immuno-purification and analysis. Synchronized HeLa cells in early and mid S phase were pulse-labeled with Cy3-dCTP. DNA from each cell fraction was purified, fragmented, and immunoprecipitated with an anti-Cy3 antibody. The enriched DNA fractions are indexed, amplified, and sequenced. (E) Visualization of Cy3-dCTP–labeled regions on chromosome 10 using the Integrative Genomics Viewer (IGV) Browser. (F) Cy3-labeled genome regions are enriched with active histone marks and excluded from an inactive mark: view from chr6_5512490–8384778 (also see fig. S3, A and B). (G) Venn diagrams show overlapped size (in bp) between Cy3-labeled regions and contact domains (left) and Cy3-labeled regions and A-compartment (right).

We first investigated the genomic nature of early replication foci. HeLa cells highly synchronized at G₁/S (Fig. 1B) and fluorescent nucleotides (Cy3-dCTP) were injected into the cells by electroporation. Concordant with early S-phase progression in the cells (Fig. 1B), the fluorescent nucleotides were incorporated into certain replicated euchromatic regions of the genome, forming early replication foci in the cells (Fig. 1C and fig. S1B). In HeLa cells, each replication focus was assumed to be a genomic region [<1 Mb but including one or a few replication units (replicons)] (fig. S1B) (22), which corresponded to our labeled regions.

To characterize genomic regions of early replication foci, genomic DNA was isolated from the cells after sonication. The Cy3-labeled genomic fragments were purified from genomic DNA with a specific anti-Cy3 antibody (Fig. 1D and fig. S2A) and subjected to sequencing (Fig. 1, E and F, and figs. S2B and S3, A and B). Analysis of the sequencing data identified that 3987 Cy3-labeled regions occupied 29.3% of the annotated HeLa S3 genome (hg19), with median and mean sizes of 129 and 208 kb, respectively (fig. S3C), which agreed with the reported average replicon sizes (inter-origin distance) of 144 kb (22) and 189 kb (24) in HeLa cells. In addition, the regions labeled with Cy3-dCTP in early replication were relatively gene rich and mutually exclusive from those of mid replication (Fig. 1E and fig. S2B).

We next compared Cy3-labeled regions to available data of active chromatin marks (55), inactive chromatin marks (55), and Hi-C contact domains (30). A total of 74.0% of Cy3-labeled regions overlapped with Hi-C contact/loop domains (or TADs) (Fig. 1, F and G, and fig. S3, A, B, and D). A total of 88.6% of the Cy3-labeled regions belong to the A-compartment (Fig. 1G and fig. S3E). Cy3-labeled regions were significantly enriched with active chromatin marks (H3K4me1–3, H3K9ac, H3K27ac, H3K36me3, and H3K79me2) and excluded from an inactive chromatin mark (H3K27me3) (Fig. 1F; figs. S3, A and B, and S4, A to H; and table S1). These results suggested that the early replication focus corresponds to Hi-C contact domains with active chromatin marks (A-compartment), in addition to a cluster of replicons (Fig. 1F and figs. S3, A and B, and S4, A to H). This notion is consistent with the recent findings of Repli-seq (56, 57), establishing a powerful approach to label euchromatic domains with fluorescent nucleotides in living cells.

Single-nucleosome imaging demonstrates nucleosomes in active chromatin regions are highly mobile

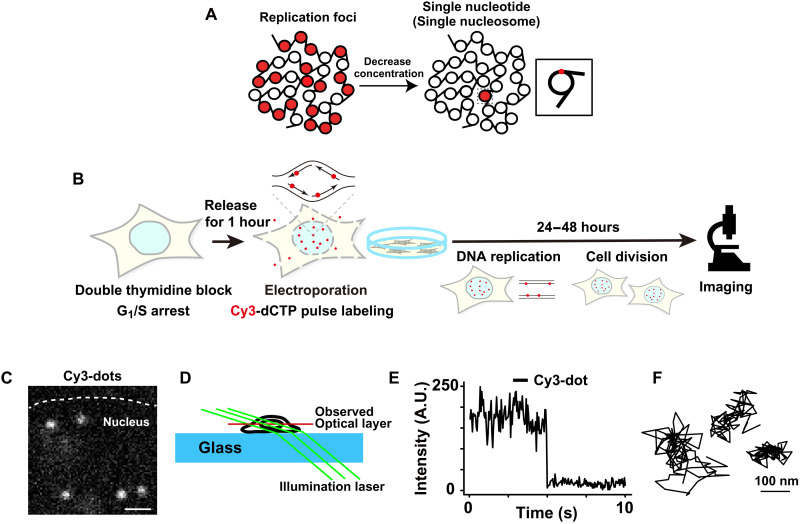
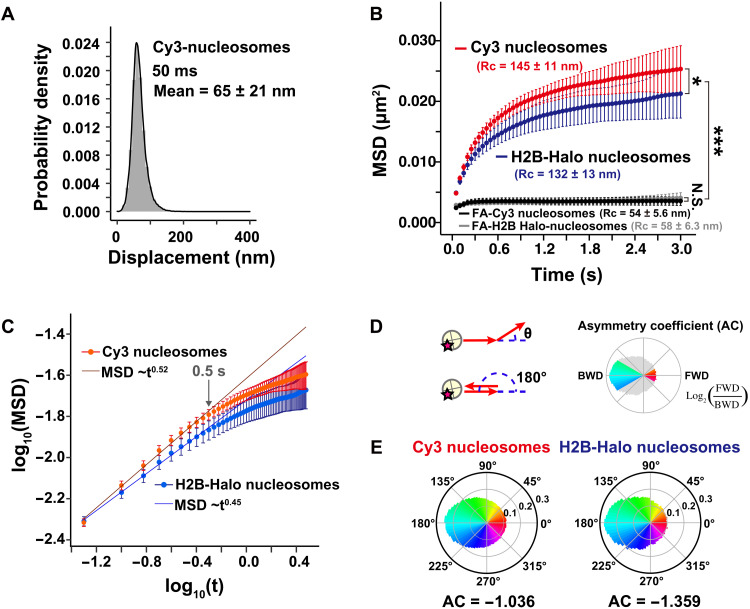
To investigate local chromatin behavior of active chromatin regions, we performed imaging of single nucleosomes sparsely labeled by Cy3-dCTP incorporation. For this purpose, we decreased the concentration of fluorescent nucleotides that were electroporated into the G₁/S-phase–synchronized cells (Fig. 2A). During DNA replication, a very low amount of Cy3-dCTP was incorporated into genomic DNA (Fig. 2A). Although we expected fluorescent nucleotides to incorporate into both nucleosomes and linker DNA regions, here, we referred to both cases as labeled nucleosomes for simplicity (inset, Fig. 2A). After replication and subsequent cell division (Fig. 2B), we observed several bright and clear dots in the cell nuclei (Fig. 2C) using oblique illumination microscopy, which allowed us to illuminate a thin area within a single nucleus (Fig. 2D) (18, 53, 54, 58). We recorded movies of the dots at 50 ms per frame (200 frames, 10 s in total) (movie S1). Each dot showed a single-step photobleaching pattern (Fig. 2E), confirming that each dot represented a single nucleosome containing a single fluorescent nucleotide. We then fitted the dots in each image frame to an assumed Gaussian function to determine the precise center of the dots (59) beyond the diffraction limit (60, 61) and tracked the motion of each nucleosome (Fig. 2F and movie S2). The position determination accuracy of Cy3-dCTP dots was 14.6 nm (fig. S5A and see Materials and Methods). The electroporation did not affect the nucleosome motions (fig. S5, B and C). We only tracked the signals of Cy3-dCTP incorporated into nucleosomes since the free nucleotides moved too fast to detect and track under our imaging conditions. Approximately 65 nm of nucleosome movement for 50 ms was observed (Fig. 3A). Their calculated MSD showed a subdiffusive curve (Fig. 3B). The MSD value was slightly higher than ones obtained in our previous studies using histone H2B-HaloTag–labeled nucleosomes, which represented the averaged motion of nucleosomes incorporated genome-wide (Fig. 3B and fig. S5D) (37). Presumably, this is because only active chromatin (euchromatin) regions, which are more mobile (62), were observed this time. Chemical fixation of the cells with formaldehyde (FA) to cross-link nucleosomes severely suppressed the movements of Cy3-labeled and H2B-Halo–labeled nucleosomes (black and gray lines; Fig. 3B and fig. S5D). When the MSD values began to plateau (P) (Fig. 3B), which is proportional to the square of the radius of constraint [R_c; P = 6/5 × R_c²; (63)], the estimated R_c values of the Cy3-labeled and H2B-Halo–labeled nucleosome motions in living cells were 145 ± 10.8 nm (mean ± SD) and 132 ± 12.7 nm, respectively (Fig. 3B). Furthermore, the MSD exponent in the time range up to 0.5 s (0.52; Fig. 3C and fig. S5E) and asymmetric coefficient (AC) value (64) of the motion angle distribution (−1.036; Fig. 3, D and E) of Cy3-labeled nucleosomes were larger than those of H2B-HaloTag–labeled ones (MSD exponent, 0.45; AC = −1.359). These results reveal that nucleosomes in active chromatin regions were more mobile and less constrained compared to the average of whole chromatin.

Fig. 2. Imaging single-nucleosomes labeled with fluorescent nucleotides in living cells.

(A) Schematic of replication foci labeling with fluorescent nucleotides at high concentrations (left) and single-nucleosome labeling with a low concentration of fluorescent nucleotides (right). The inset shows that single-nucleosome labeling is based on the incorporation of a single nucleotide conjugated with fluorescent dye. This cartoon is simplified and fluorescent labeling can also be in the linker DNA region. (B) Experimental scheme for labeling and imaging. (C) Image of single-nucleosome dots labeled with Cy3-dCTP in a live HeLa nucleus. The bar represents 1 μm. See also movies S1 and S2. (D) Oblique illumination microscopy system. Only a thin optical layer within the nucleus (red) was illuminated with a low background using a sheet light (green). The cartoon was reproduced and modified with permission from (18). (E) Representative single-step photobleaching of a Cy3-labeled nucleosome dot. The vertical axis represents the fluorescence intensity and the horizontal axis is the tracking time series. A.U., arbitrary units. (F) Three representative trajectories of single-nucleosomes. The bar represents 100 nm.

Fig. 3. Single-nucleosome behavior at active chromatin regions.

(A) Displacement (movement) distributions of single-nucleosomes labeled with Cy3-dCTP at active chromatin (euchromatic) regions in live HeLa cells for 50 ms (n = 27 cells). (B) MSD plots (±SD among cells) of Cy3-labeled nucleosomes (red, n = 27 cells) and H2B-Halo–labeled nucleosomes [blue, data were reproduced from (37)] in living HeLa cells from 0 to 3 s. The Kolmogorov-Smirnov test was used to determine P values. *P < 0.05 for Cy3-dCTP versus H2B-Halo (P = 0.049). ***P < 0.0001 for Cy3 nucleosomes versus FA-fixed Cy3 nucleosomes (P = 2.1 × 10⁻¹³), H2B-Halo nucleosomes versus FA-fixed H2B-Halo nucleosomes (P = 5.7 × 10⁻⁶). Not significant (N.S.) for FA-Cy3 nucleosomes versus FA-H2B-Halo nucleosomes (P = 0.37). R_c values (estimated radius of constraint of the nucleosome motion) are also shown. R_c values of Cy3 and H2B-Halo nucleosomes are also significantly different: P = 0.049 by Kolmogorov-Smirnov test. (C) Log-log plots of MSD data shown in (B). The indicated straight lines were fitted using the data from 0.05 to 0.5 s. The plots cannot be fitted linearly beyond this time range, suggesting the motion mode changes over 0.5 s. (D) Schematic for nucleosome motion angle distribution analysis (64). Schematics were reproduced from (37). (E) Angle distributions of Cy3 (left) and H2B-Halo nucleosomes (right). Moving angles of single nucleosomes are biased toward 180° and the AC is negative, indicating that they are often pulled back to their original positions. H2B-Halo data were reproduced from (37).

Two close nucleosomes show highly correlative movements in living cells

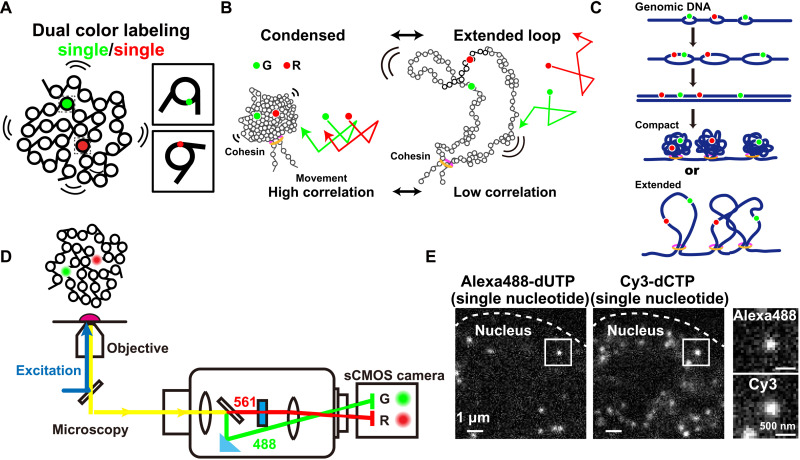
We next introduced dual-color labeling and imaging of two spatially neighboring single-nucleosomes in human cells (Fig. 4A) because we inferred that their movements could distinguish whether the organization of a chromatin domain remained condensed or extended as fiber loops (Fig. 4B); they should be correlated in the condensed loop but not if loops are extended (trajectories in Fig. 4B). This idea was supported by chromatin modeling with Brownian dynamics, which enabled us to characterize the chromatin compaction states using fractal dimensions (see Materials and Methods) (fig. S6, A to C, and movies S3 and S4) (62). Thus, we electroporated very low concentrations of Alexa488–dUTP (fig. S6D) and Cy3-dCTP into early S-phase cells. As DNA was replicated, fluorescently labeled early replicated chromatin regions were created (Fig. 4C), followed by subsequent cell division (Fig. 2B). We performed dual-color imaging of single-nucleosomes labeled with Alexa488-dUTP and Cy3-dCTP in living cells using a beam splitter system (Fig. 4D).

Fig. 4. Dual-color labeling and imaging of single-nucleosomes in living cells.

(A) Diagram of dual-color visualization of single-nucleosome dynamics. (B) Two hypothetical models of higher-order chromatin structure, condensed organization (left), or extended loops (right). In both models, cohesin holds the chromatin fiber to make loop(s). Correlation analysis of the two single-nucleosome movements [G (green) and R (red); their hypothetical movements are shown on the right] can be used to distinguish between these two possible models in living cells. (C) Scheme for Alexa488-dUTP (green) and Cy3-dCTP (red) incorporations during early DNA replication for dual-color labeling of nucleosomes. (D) Schematic for dual-color imaging with a beam splitter system (W-VIEW GEMINI, Hamamatsu Photonics). The images of two single-nucleosomes with different colors were acquired with a single sCMOS camera (left half, green color; right half, red color). (E) Representative images of single-nucleosomes labeled with Alexa488-dUTP (left) or Cy3-dCTP (right) in a living HeLa nucleus. The bar represents 1 μm. The box regions are enlarged to the right. The bar represents 500 nm.

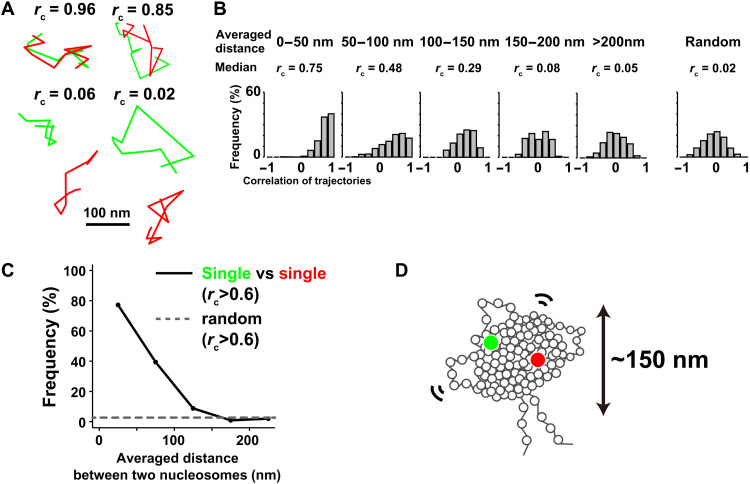
We simultaneously observed clear dots in each color channel (Fig. 4E). There was essentially no cross-talk between the Alexa488 and Cy3 signals in our beam splitter system (fig. S6E). The position determination accuracy of Cy3-dots through the beam splitter was 20.3 nm (fig. S6F). Alexa488- and Cy3-labeled nucleosomes showed similar properties (fig. S6, G and H). Among them, we found many sets in which two close single-nucleosomes were labeled with different fluorescent dyes (insets, Fig. 4E). Two of these closely labeled nucleosomes could localize at either the same replicon/domain (first left replication bubble, Fig. 4C) or at two distinct ones (two from right, Fig. 4C). We collected dynamics information on closely localized pairs of nucleosomes (up to 500 nm) (movies S5 to S8). To evaluate the correlative movements of the pairs, we calculated congruence coefficients (r_c) and averaged distance between two nucleosomes (d) (see details in Materials and Methods) in 10 continuous frames (0.5 s, n = 2071 pairs of trajectories). As shown in Fig. 5A, we found that two nucleosomes near each other commonly showed similar trajectories (r_c = 0.96 and d = 18.31 nm; r_c = 0.85 and d = 35.37 nm), whereas distant nucleosomes did not (r_c = 0.06 and d = 150.04 nm; r_c = 0.02 and d = 170.87 nm).

Fig. 5. Correlation analysis of motions of two neighboring nucleosomes.

(A) Four representative trajectory sets of two nucleosomes labeled with green (Alexa488-dUTP) and red (Cy3-dCTP). While the upper two sets show trajectories of two closely localized nucleosomes, the lower two represent distant nucleosomes. See also movies S5 to S8. (B) Histograms of congruence coefficient r_c calculated between the two single-nucleosomes (green and red) whose averaged distances were in the ranges of 0 to 50 nm (median r_c = 0.75), 50 to 100 nm (median r_c = 0.48), 100 to 150 nm (median r_c = 0.29), 150 to 200 nm (median r_c = 0.08), and over 200 nm (median r_c = 0.05) for 500 ms and the random control (median r_c = 0.02). (C) Frequency plots of nucleosome pairs (green and red) with r_c > 0.6 versus the pair distances. The dashed line shows the frequency of randomly collected nucleosome pairs with r_c > 0.6. (D) Model of nucleosomes formed into a condensed domain with ~150 nm diameter.

Subsequent quantitative correlation analysis at 0.5 s scale (Fig. 5B) revealed that two individual nucleosomes, but closely located (<50 nm), showed high correlations between their movements (median r_c = 0.75). Significant correlative movements were observed between two nucleosomes located at distances of 50 to 100 nm (median r_c = 0.48) or 100 to 150 nm (median r_c = 0.29). On the other hand, almost no movement correlation (median of r_c = 0.05) was observed between two nucleosomes if they were located at a distance of >200 nm, which is similar to that of randomly selected pairs from different cells (median of r_c = 0.02; rightmost panel in Fig. 5B). The plots of correlation frequency with r_c > 0.6 versus nucleosome distance demonstrated significant correlative movements when the distance is 150 nm or less (Fig. 5C). This suggested that two nucleosomes within 150 nm of each other will move similarly and that nucleosomes form condensed domains with ~150 nm diameter, even in euchromatic regions (Fig. 5D).

Note that the obtained value of ~150 nm was a peak value, and condensed domains of various sizes will exist in living cells. We would point out that the value itself might be underestimated because not all pairs of nucleosomes are within the same domain. We also assume that two nucleosomes across neighboring domains, which are likely to move independently with a flexible linker region (25), cannot contribute to, or even perturb, the movement correlation.

Our results are consistent with previous findings of nucleosome clusters/large-scale chromatin structures identified using super-resolution imaging and other methods (16–21). In addition, because our fluorescent labeling was associated with the Hi-C contact domains/TADs in A-compartment (Fig. 1, F and G, and fig. S3, A, B, D, and E) and DNA replication foci (Fig. 1C), our results suggest that they have a physically condensed organization (Fig. 5D).

Nucleosome-nucleosome interactions and cohesin have distinct roles during the condensed domain formation

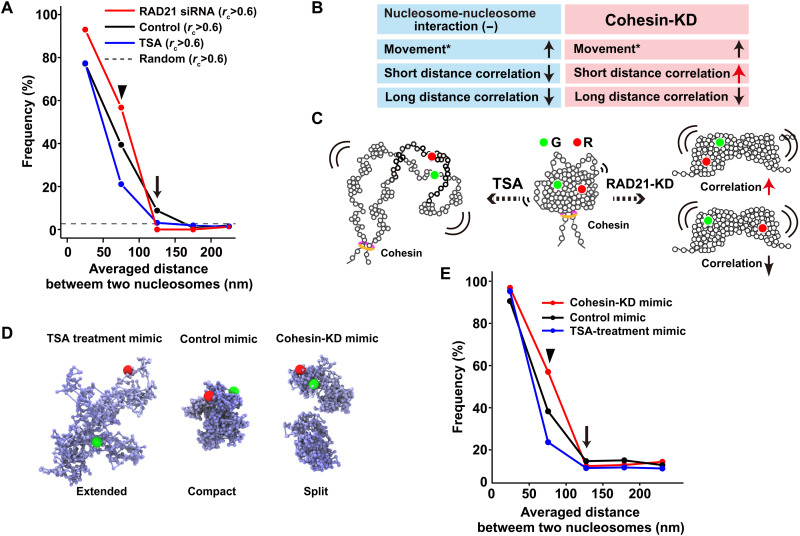
We perturbed nucleosome-nucleosome interactions mediated by histone tails to further investigate the condensed domain organization. Previous treatment of cells with the histone deacetylase inhibitor trichostatin A [TSA; (65)] increased histone H3 and H4 tail acetylation. Histone tail acetylation by TSA treatment weakened nucleosome-nucleosome interactions (66), leading to decondensation of chromatin domains (12, 18, 67). TSA treatment also increased chromatin flexibility and mobility (18). Treating cells with TSA for 3 hours substantially increased the acetylation of H3 and H4 N-terminal tails (asterisks, fig. S7A) and extensively decondensed chromatin as visualized by 3D STED (stimulated emission depletion) super-resolution imaging (fig. S8). The correlation frequency of TSA-treated cells fell sharply compared to that of untreated control cells, as the distance between nucleosomes increased (blue line, Fig. 6A; n = 891 pairs of trajectories), suggesting that inhibiting the interactions of local nucleosomes will decrease their coherent movements within the domains (Fig. 6, B and C).

Fig. 6. Distinct roles of nucleosome-nucleosome interactions and cohesin during condensed domain formation.

(A) Frequency plots of the nucleosome pairs with r_c > 0.6 (congruence coefficient r_c) versus the pair distances in living siRAD21-treated (cohesin-KD) HeLa cells (red), untreated cells (black), and TSA-treated cells (blue). The dashed line shows the frequency of randomly collected nucleosome pairs with r_c > 0.6. Note that closely located nucleosomes (<50 nm) showed high correlations even after TSA treatment since this distance corresponds to a few nucleosomes, possibly with a connected chain. (B) Summary of results in (A). Movement data (*) were obtained from (18, 71). (C) Simplified schematic of possible TSA-treated (left) and cohesin-KD (right) domains. (D) Computational models that mimic TSA-treated, untreated control, and cohesin-KD domains (from left to right). For the cohesin-KD mimic, two split domains were created. (E) Frequency plots of the nucleosome pairs with r_c > 0.2 (congruence coefficient r_c) versus the averaged pair distances in the computationally modeled domains of TSA-treatment mimic (red), untreated control mimic (black), and cohesin-KD mimic (blue) shown in (D).

We next examined the role of the cohesin complex in domain formation. Cohesin can capture chromatin fibers within its ring structure and thereby form loops (34, 35, 68–71). When the cohesin subunit RAD21 was knocked down by small interfering RNA (siRNA) (fig. S7B) (72), increased mobility was observed (18, 34, 35, 73), similar to that detected in TSA-treated domains. Unexpectedly, the nucleosome correlation profile of RAD21-knockdown (KD) cells differed from that of TSA-treated cells (red line, Fig. 6A; n = 1,197 pairs of trajectories). While the nucleosome movement correlation decreased in the range of 100 to 150 nm (arrow in Fig. 6, A and B), an enhanced nucleosome correlation compared to the untreated control was observed in the short distance range (<100 nm) (arrowhead in Fig. 6, A and B).

Our results have led us to the following hypothesis. Chromatin fibers treated with TSA became more stretched, open, and dynamic in the domains (Fig. 6C). Cohesin-KD led to a lower efficiency of loop configurations of the domains (31, 34, 35), while local nucleosome clusters still formed through their nucleosome-nucleosome interactions (Fig. 6C, right). The loss of cohesin increased the movement of the clusters, resulting in the formation of larger trajectories. This then increased the correlation of movement within the shorter range (i.e., within a cluster). On the other hand, long-range correlation (i.e., different clusters within the same domain) markedly decreased because of the loss of global chromatin folding by cohesin (Fig. 6C).

Correlation analysis of the computational model qualitatively recapitulates experimental data

To test the above hypothesis, we computationally generated hierarchical fractal polymer models (62). Our modeling with Brownian dynamics can reveal the behavior of nucleosomes in computationally created structures while allowing the explanation of possible experimental results. The models had 5 domains (or 10 half-sized domains in the case of cohesin depletion), each with 1000 nucleosome beads (cohesin depletion, 500 nucleosome beads) that mimicked three potential types of chromatin organization (extended, compact, or split) (Fig. 6D and fig. S9A). We focused on one or two, among the five domains (or 10 half-sized domains), to measure nucleosome motion (fig. S9A). These simple models might not completely reflect on the chromatin state in live cells because mimic chromatin fibers can pass through one another and have no repulsion between domains. However, they are still useful to qualitatively test our hypothesis. The modeling parameters were fitted with the experimental MSD data (fig. S9B). The ring-polymer models with d_f = 3.3 and d_f = 2.1 mimicked the untreated control and TSA treatment, respectively (center and left in Fig. 6D and fig. S9C). To reconstruct the cohesin-depleted domains, we introduced split domains with d_f = 2.9 (right, Fig. 6D and fig. S9C). We performed simulations of their Brownian dynamics (movies S9 to S14) and monitored the movements of two individual nucleosome beads in one or two domains of each model. We obtained correlation profiles (Fig. 6E and fig. S9, D and E), which were comparable to the experimental data (Fig. 6A), although the overall correlation of paired nucleosomes within the domain was relatively low in the modeling. In the TSA-mimic domains, nucleosome movement correlation substantially decreased compared with that of the control domains as the distance between nucleosome beads increased (blue line, Fig. 6E and fig. S9, D and E). While the nucleosome correlation in RAD21-KD mimic domains decreased in the range from 75 to 150 nm (arrow, red line in Fig. 6E and fig. S9, D and E), the correlation in the short distance range (<100 nm) was even more enhanced than the control correlation (arrowhead, red line in Fig. 6E and fig. S9, D and E). Our modeling qualitatively recapitulated experimental data and provided us with physical pictures of domains treated with TSA (extended loop domains) or depletion of cohesin (split compact domains) (Fig. 6D and fig. S9C). Together, our results suggested that domain formation is governed by both local nucleosome-nucleosome interactions and by global folding through cohesin complexes (Fig. 6C).

Nucleosomes behave like a liquid in the condensed chromatin domain

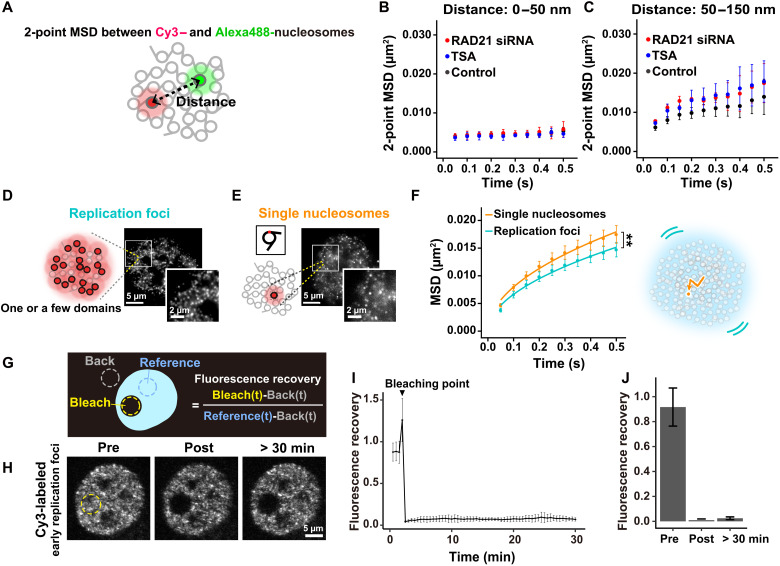
We wondered whether the physical nature of condensed chromatin domains would be solid-like or liquid-like. To address this question, we observed the distances between two neighboring nucleosomes (Fig. 7A) and examined the MSD between them (two-point MSD) like Gabriele et al. (34). We could focus more on local nucleosome motions inside the domain because the distance between nucleosomes is much less affected by either translational or rotational movements of the domain during imaging. Consistent with the correlation analysis (Fig. 6A), two-point MSD between neighboring nucleosomes [averaged distance (d), 0 to 50 nm] only slightly increased over time (Fig. 7B), while two-point MSD plots (d, 50 to 150 nm) showed rather subdiffusive curves (Fig. 7C), suggesting that nucleosomes fluctuate in the domain like a liquid. Here, we define a liquid-like state as one with diffusive movement that does not have a crystal-like long-range order. Such liquid-like chromatin condensates were observed in vitro and in the cell (38, 40). TSA treatment and RAD21 depletion increased the two-point MSD (Fig. 7C), in agreement with previous correlation data (Fig. 6A), demonstrating that both local nucleosome-nucleosome interactions and cohesin constrain the local fluctuation of nucleosomes inside domains.

Fig. 7. Chromatin behaves differently at different spatiotemporal scales.

(A) Schematic for two-point MSD. (B) Two-point MSD plots (±SD among ≥3 clusters) between Cy3- and Alexa488-nucleosomes whose averaged distances (d) were 0 to 50 nm in living siRAD21-treated HeLa cells (red, 54 pairs), untreated cells (black, 84 pairs), and TSA-treated cells (blue, 42 pairs). Ten or more pairs were grouped as a cluster. (C) Two-point MSD plots (±SD among ≥3 clusters; d, 50 to 150 nm) in living siRAD21-treated HeLa cells (red, 33 pairs), untreated cells (black, 95 pairs), and TSA-treated cells (blue, 35 pairs). (D) Schematic for replication foci labeled with Cy3-dCTP at high concentrations (left) and their representative images in a living HeLa nucleus (right). The square region is magnified at lower right. Note that each dot corresponds to one replication focus, consisting of one or a few contact domains. Also see movie S15. (E) Schematic for single-nucleosome imaging and their typical representation. Note that each dot corresponds to a single-nucleosome. (F) MSD plots (±SD among cells) of early replication foci (light blue, n = 12 cells) and single-nucleosomes at the early replicated regions (orange, n = 19 cells) in living HeLa cells. **P < 0.001 by Kolmogorov-Smirnov test for foci versus single nucleosomes (P = 4.8 × 10⁻⁴). (G) Schematic for FRAP. (H) Representative images of Cy3-labeled early replication foci before, just after and 30 min after photobleaching. Photobleached region is shown by a yellow dotted line. XY-movement of the cell is corrected. (I) Mean normalized fluorescence intensity over time (fluorescence recovery curve) for Cy3-labeled early replication foci, n = 10 cells. (J) Mean normalized fluorescence intensity of photobleached region before, just after, and 30 min after photobleaching (n = 11 cells). Also see movie S16.

We focused on early replication foci (Fig. 7D) to further examine this issue. Here, one focus consists of one or a few domains (see Fig. 1F and fig. S3, A and B). We observed the local movements of foci (movie S15) and compared them with individual nucleosome motion (Fig. 7E). Individual nucleosomes have significantly higher mobility than replication foci (left, Fig. 7F). We assume that local movements of foci correspond to centroid movements of domains and our obtained results further support that nucleosomes locally fluctuate inside domains (right, Fig. 7F).

Chromatin is stable at a chromosome scale

Thus far, we have characterized chromatin behavior up to a ~150 nm/~0.5 s scale. To examine chromatin behavior at a larger spatiotemporal scale, we performed FRAP analysis on large areas labeled with early replication foci in the nucleus (Fig. 7G) (7, 74). We bleached a circular area (~6 μm diameter), which roughly corresponds to the size of a chromosome territory. The signals in the bleached area did not return, even 30 min after bleaching (Fig. 7, H to J, and movie S16), suggesting that chromosomes are stable like a solid on the scale of micrometers/minutes, consistent with (7, 74). Our results revealed that chromatin is not globally fluidized on a larger spatiotemporal scale, which complements the previous measurement of the solid-like response of the whole nucleus to applied force (75, 76).

DISCUSSION

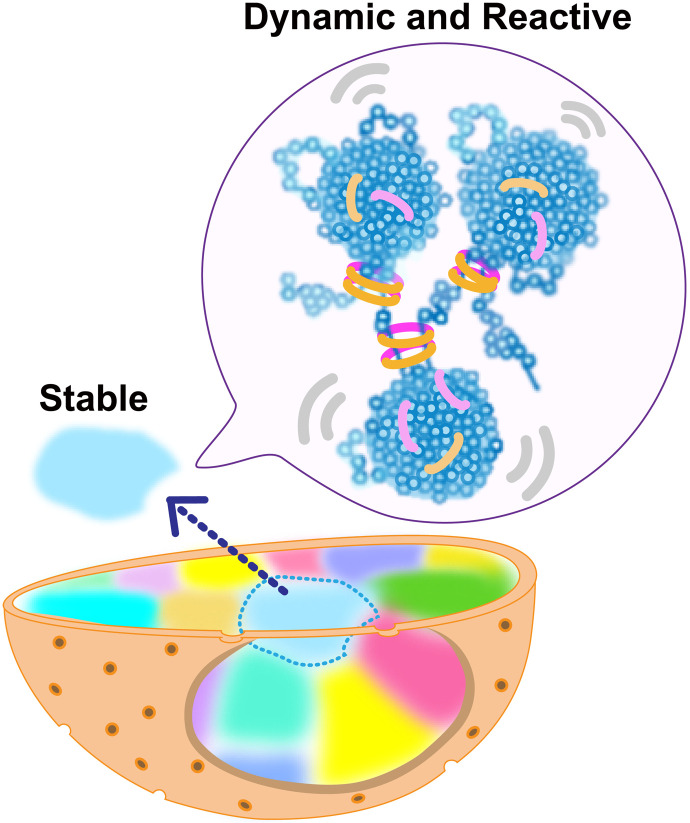
In the present study, we offer a novel approach to investigate dynamic chromatin organization in living cells. We first performed single-nucleosome imaging in the early DNA replicated regions, which corresponded to Hi-C contact domains (TADs) with active chromatin marks (30, 31). The nucleosomes in active chromatin regions are more mobile and less constrained compared to the average of chromatin as a whole. Our correlation analysis of single-nucleosomes suggests that nucleosomes organize into condensed domains (Fig. 8), even in active euchromatic regions. Further, two-point MSD analysis between two neighboring nucleosomes suggested that nucleosomes locally fluctuate in the condensed domain like a liquid (Fig. 7C). On the other hand, FRAP analysis indicated that chromosomes are stable like a solid on the scale of micrometers/minutes (Fig. 7, H to J), consistent with (7, 74). Our study reveals the physical nature of chromatin domains in active chromatin regions (A-compartment).

Fig. 8. Model of euchromatin organization in living cells.

Nucleosomes in active chromatin regions form condensed domains with local nucleosome contacts and cohesin (rings), where nucleosomes fluctuate. A single interphase chromosome is stably occupied in a chromosome territory (highlighted as different colors).

We consider that this condensed liquid-like organization is made of interdigitated 10-nm fibers with local nucleosome contacts via 10 long histone tails of nucleosome. Here, it should be emphasized that chromatin seems very sticky and not an ungummed fiber (e.g., an electric cable or spaghetti). This stickiness facilitates the formation of clusters or domains. Because of this stickiness, the condensed domain organization may not fit well with the Rouse model, which is an ideal chain consisting of beads connected by harmonic springs with an MSD exponent of 0.5 (77). Acetylation of histone tails weakens local nucleosome contacts and chromatin stickiness. Acetylation on the domain surface, which can activate transcription in the corresponding region, may prevent the fusion of chromatin domains and contribute to domain individualization. We estimate that the condensed domains with ~150 nm diameter consist of 500 to 1000 nucleosomes covering 100- to 200-kb genomic regions. This condensed domain view is compatible with other large-scale structures, which have long been observed (16–21). However, this view is at odds with an EM tomography study (14), which reported that chromatin organization largely relies on local nucleosome concentrations but not large-scale structures. The view of condensed domains is also distinct from the yeast chromatin, which is essentially open and forms clusters of only a few nucleosomes (11, 13).

The physically condensed domains can provide higher-order regulation of various DNA transaction reactions, including transcription and DNA replication, while the extended fiber loops cannot. Condensed domains likely hinder the accessibility of large protein complexes, such as transcription factors and replication initiation complexes to their target sequences located in the inner core of chromatin domains (20, 78). Our analyzed domains are also part of DNA replication domains identified using genomic methods (56). Partial decondensation of such domains with histone modifications or the action of other proteins can increase accessibility to the large complexes to turn on gene transcription or other processes. Hyper-histone tail acetylation by TSA treatment seems to transform the condensed domains into rather extended loops. Highly acetylated regions like super-enhancers may also take this kind of organization.

Notably, since the condensed liquid-like domains are the Hi-C contact domains (TADs) in the A-compartment (30, 31), our work provides the Hi-C domains with a physical picture and a new viewpoint of higher-order regulation by the accessibility control mentioned above. This higher-order regulation may also play an important role in cell differentiation processes because mouse embryonic stem cells show less defined domain organization with higher dynamics (18, 79). In addition, condensed domains can be more resistant to radiation and chemical damage than the decondensed forms because condensed chromatin presumably has lower levels of reactive radical generation and access for chemical attacks (80). These two features provide biological relevance to the organization of condensed chromatin.

The present study provides a mechanistic insight into the condensed domain formation. The mechanism revealed may not be well fitted with the loop extrusion model by cohesin (70). Consistent with previous reports (20, 32), cohesin depletion does not destroy the formation of small domains/nucleosome clusters, which are maintained by nucleosome-nucleosome interactions (Fig. 6C). Such sticky physical structures can function as barriers for cohesin to continuously extrude chromatin fibers (69, 71), although partial or discontinuous loop extrusion by cohesin remains possible, especially on the boundary or linker regions between domains. These residual domains/clusters may function as parts for the rapid reassembly of domains, which is consistent with the recent Hi-C data showing rapid reformation of loop domains when cohesin is restored (31).

It is intriguing to compare the condensed domains in euchromatic active regions with heterochromatic regions such as lamina-associated domains (LADs) (81), which are condensed and silenced (82) and less mobile as shown by single-nucleosome imaging (18, 62) and other imaging (51). In this study, we show that euchromatic regions also form physically condensed domains with liquid-like properties, while maintaining their high mobility. On the other hand, the boundary or linker regions between domains, or TAD boundaries (25), can be highly accessible and are often transcribed as housekeeping genes, tRNAs, and SINE elements (28). These actively transcribed regions can be constrained by transcription machinery (83), and they represent functionally intriguing chromatin regions that should be explored in future studies.

Our study strengthens the viscoelastic principle of chromatin (41–46), that is, chromatin is locally dynamic and reactive but globally stable (Fig. 8). Inside the chromatin domain (the ~150 nm/~0.5 s spatiotemporal scale), chromatin behaves like a viscous liquid, allowing smaller proteins, such as transcription factors, to access their target sequences even though chromatin forms condensed domains (Fig. 8). This can increase chromatin accessibility and facilitate DNA transaction reactions such as RNA transcription and DNA replication/repair (5, 52). On the other hand, at a chromosome scale (up to several micrometers), chromatin seems to behave like a solid, presumably because of many local constraints. This property supports that each chromosome is quite stably occupied in the territory (Fig. 8) without excess intermingling of chromosomes, which contributes to keeping genome integrity. With loss of this property, more mixing of chromosomes and subsequent chromosome breaks/fusions may happen, leading to various genetic disorders, including tumorigenesis. Furthermore, the elastic property of chromatin can generate a spring-like restoring force that resists nuclear deformation by mechanical stress and plays an important role in maintaining genomic integrity. Nuclei with condensed chromatin have significant elastic rigidity, while those with decondensed chromatin, including one induced by histone acetylation described above, are considerably softer (75, 76).

Our findings resolve the discrepancy of whether chromatin is liquid-like (38) or solid-like (7). Both reports are consistent with our results. It is very reasonable that the FRAP experiments, including Fig. 7 and (7, 74), suggested that chromatin is rather solid-like because the FRAP spatiotemporal scale was larger than 1 μm and longer than a minute. As shown by Gibson et al. (38), the chromatin condensates might have weak intrinsic droplet properties at a nanoscale (~150 nm) range, given that each nucleosome possesses 10 intrinsically disordered regions as histone tails (2, 84). Since emerging evidence in cell biology revealed that liquid-liquid phase separation (LLPS) forms functional compartmental droplets in the cell (39), it would be exciting to examine how liquid-like chromatin can interplay with the transcription droplets/condensates and how its behaviors can contribute to the transcription, or other DNA transaction processes, and their regulations (85).

MATERIALS AND METHODS

Cell culture

HeLa cells were cultured in Dulbecco’s modified Eagle’s medium (DMEM) (D5796-500ML; Sigma-Aldrich) supplemented with 10% fetal bovine serum (FBS) (FB-1061/500; Biosera) at 37°C in 5% CO₂. For single-nucleosome imaging, cells were plated onto glass-bottomed dishes (3970-035; Iwaki) treated with poly-l-lysine (P1524-500MG; Sigma-Aldrich). Before microscopy imaging, the medium was replaced with DMEM lacking phenol red (21063-029; Thermo Fisher Scientific) and supplemented with 10% FBS.

DNA replication foci labeling by Cy3-dCTP

The electroporation method by Neon Electroporation System (MPK5000; Thermo Fisher Scientific) was used to label DNA replication foci with Cy3-dCTP. HeLa cells were synchronized by a double thymidine block and released into thymidine-free medium and then electroporated with Cy3-dCTP (PA53021; Invitrogen) 1 hour or 5 hours after release. For each electroporation, cells were resuspended in Neon Resuspension Buffer R (10 μl, Neon kit, Invitrogen) to a final concentration of 2.5 × 10⁷ cells/ml and mixed with 1 nmol of Cy3-dCTP. The cells and Cy3-dCTP mixture were pulsed twice with a voltage of 1350 and a width of 20. Cells were grown on coverslips (c018001; Matsunami) coated with poly-l-lysine. After incubation at 37°C overnight, cells were washed twice in phosphate-buffered saline (PBS) and used for further experiments. For Fig. 1C, cells grown on coverslips were fixed with 1.85% FA (064-00406; Wako), permeabilized with 0.5% Triton X-100 (T-9284; Sigma-Aldrich), and stained with 4′,6-diamidino- 2-phenylindole (0.5 μg/ml; DAPI) (10236276001; Roche), followed by PPDI [20 mM Hepes (pH 7.4), 1 mM MgCl₂, 100 mM KCl, 78% glycerol, and paraphenylene diamine (1 mg/ml) (695106-1G; Sigma-Aldrich)] mounting. Optical sectioning images were recorded with a 0.2-μm step size using a DeltaVision microscope (Applied Precision).

Cy3-labeled DNA pulldown assay

For each assay, 200 ng of an enhanced green fluorescent protein (EGFP) gene polymerase chain reaction (PCR) fragment amplified by the Cy3 PCR labeling kit (PP-301S-CY3; Jena Bioscience) and the linearized plasmid (pGEM-T Easy plasmid digested with EcoRI) were resuspended in PBS buffer containing 300 ng of anti-Cy3 antibody (sc-166894; Santa Cruz Biotechnology). The mixture was incubated at 37°C for 1 hour. Protein G Magnetic Beads, 25 μl (10003D; Invitrogen) were pre-equilibrated with citrate buffer and then added. Beads were immobilized on a magnetic stand after incubating the mixture at room temperature for 30 min with shaking. The supernatant was collected as flow-through. Beads were washed three times with 0.5 ml of PBS containing 0.05% Tween-20 (PBST) at room temperature, resuspended in elution buffer [50 mM tris-HCl (pH 8.0), 50 mM NaHCO₃, 1% SDS, and 1 mM EDTA (pH 8.0)], and incubated at 65°C for 30 min before elution. One-tenth volumes of the input, flow-through, and elution fractions were analyzed by agarose gel electrophoresis, followed by ethidium bromide staining.

Immuno-purification of the Cy3-labeled DNA regions in early replication foci

Genomic DNA were extracted from the Cy3-dCTP–transfected and nontreated cells as described above and fragmented with sonication. Five micrograms of Cy3-labeled and nonlabeled DNA samples in PBST were individually incubated with 600 ng of anti-Cy3 antibody at 37°C for 1 hour. The nonlabeled sample was used as a negative control to detect DNAs that nonspecifically bind to the beads. Pre-equilibrated Protein G Magnetic Beads were added and incubated at room temperature for 1 hour with shaking. Beads were washed five times with 1 ml of PBST and finally resuspended in 0.1-ml elution buffer and incubated with shaking at 65°C for 30 min.

DNA extraction and preparation of cDNA libraries for next-generation sequencing

To extract high-purity DNA, input sample (1 ng) and isolated DNA samples (Cy3-labeled and nonlabeled DNAs) were added to an equal volume of phenol:chloroform:isoamylalcohol (25:24:1, v/v) and centrifuged at 16,000g at room temperature for 7 min. The upper aqueous phase was transferred to new tube. One-tenth volume of 3 M sodium acetate, glycogen, and double volume of 100% ethanol were added and incubated at −80°C for 1 hour. The pellets were retained after centrifugation at 20,000g for 30 min at 4°C and washed with 70% ethanol, dried and dissolved in Milli-Q water, and stored at −30°C until use. Complementary DNA (cDNA) libraries were synthesized by the DNA SMART ChIP-seq kit (#634865; Takara) from half of input, Cy3-labeled and nonlabeled samples. The size distribution of the libraries was checked by an Agilent 2100 Bioanalyzer using Agilent High Sensitivity DNA kit. Pooled amplicon library was sequenced with paired-end 2 × 100 bp reads on the Illumina HiSeq and NovaSeq platforms.

Cy3-DNA-seq analysis

Low-quality bases were trimmed from reads using Trimmomatic v0.38 (86), with the parameters “HEADCROP:3 LEADING:20 TRAILING:20 MINLEN:50.” Reads were aligned to the hg19 version of the human reference genome with Bowtie2 (87) using the “--very-sensitive” parameter. From mapped reads, PCR duplicates were discarded using the SAMtools rmdup command (88). To identify broad regions on the chromosomes significantly enriched for the Cy3-dCTP IP sample against the input sample, we used epic2 software (89), using the parameters “--false-discovery-rate-cutoff 0.05 --bin-size 1000 --gaps-allowed 10”. We detected 3987 Cy3-labeled regions. The size distribution of Cy3-labeled regions was shown in fig. S3C.

Overlap between Cy3-labeled regions, domains in the Hi-C map, and histone modification patterns

We evaluated the similarity between the Cy3-labeled regions and contact domains observed in the chromosome conformation capture experiments. The contact domain data from HeLa defined by Rao et al. (30) were downloaded from Gene Expression Omnibus, accession number GSE63525 (GSE63525_HeLa_Arrowhead_domainlist.txt). Overlap of Cy3-labeled regions and contact domains were determined by using the BEDtools intersect (90). As a result, 74% of Cy3-labeled regions (614 Mbp over 830 Mbp of the entire Cy3-labeled regions) were overlapped with contact domains (left, Fig. 1G). To test the statistical significance of the percentage of overlapped regions, we generated the negative control datasets by a random permutation procedure, analogous to the random shuffling control algorithm described in Rao et al. (30). We randomly placed the Cy3-labeled regions throughout the genome such that (i) the size distribution and the number of regions on each chromosome stayed the same with the actual data; (ii) randomly assigned regions did not overlap each other; and (iii) regions did not overlap with any gaps in the assembly (centromeres, telomeres, etc.) and then calculated the overlap between the shuffled data and contact domains. The above procedure was repeated 1000 times to construct a distribution of overlapped percentages in the randomly shuffled dataset. We compared the percentage observed in real data with that distribution and confirmed that the percentage in real data was above the 95th percentile of the distribution (fig. S3D). We next evaluated the overlap between Cy3-labeled regions and A/B-compartment. Compartment annotations on the HeLa cell genome are SNIPER predictions, obtained from (91). Compartments annotated as A1 and A2 were extracted as “A-compartment” and their overlap with Cy3-labeled regions was calculated (right, Fig. 1G). The same procedure described above was also used to evaluate the statistical significance of the overlap percentages by permutation analysis.

We also evaluated the overlap between the Cy3-labeled regions and histone modification patterns throughout the genome. We downloaded eight peak lists on hg19 genome defined by the ChIP-seq analysis for the histone modifications from the ENCODE portal (92, 93) with the following identifiers: H3K4me2 (ENCFF108DAJ), H3K4me3 (ENCFF447CLK), H3K9ac (ENCFF723WDR), H3K27ac (ENCFF144EOJ), H3K79me2 (ENCFF916VLX), H3K36me3 (ENCFF001SVY), H3K4me1 (ENCFF162RSB), and H3K27me3 (ENCFF252BLX). Overlapped percentages with Cy3-labeled regions were calculated for peaks of each histone marker and are shown in table S1. Percentages were compared with the distribution of overlapped percentages with the randomly shuffled Cy3-labeled regions, as was done for the comparisons with contact domains. Figure S4 shows that overlapped percentages of histone markers associated with transcriptional activation (H3K4me1, H3K4me2, H3K4me3, H3K9ac, H3K27ac, H3K79me2, and H3K36me3) were above the 95th percentile of the distribution, while the percentages of the heterochromatin markers (H3K27me3) were below the fifth percentile of the distribution.

Single-nucleosome labeling by Cy3-dCTP and/or Alexa488-dUTP in live cells

The electroporation method was used to fluorescently label single-nucleosomes with Cy3-dCTP and Alexa488-dUTP (CC11397; Invitrogen). Using the Neon electroporation system as described above, 500 fmol of Cy3-dCTP and/or 5 pmol of Alexa488-dUTP were introduced into early S-phase HeLa cells released from thymidine block. Labeled cells were observed after progressing through one or two rounds of their cell cycle/s (Fig. 2B). This process decreased the amount of background signals generated by free fluorescent nucleotides.

Cellular perturbation

To increase the acetylation of histone H3 and H4 tails, cells were treated with 500 nM TSA (203-17561; WAKO) for 3 hours. siRNA transfection was performed with Lipofectamine RNAiMAX (13778075; Invitrogen), in accordance with the manufacturer’s instructions. siRNA oligos of RAD21 were used as described previously (18, 72, 73).

Western blotting

Cells were lysed in Laemmli sample buffer supplemented with 10% 2-mercaptoethanol (133-1457; Wako) and incubated at 95°C for 5 min to denature proteins. The cell lysates, equivalent to 1 × 10⁵ cells per well, were subjected to SDS–polyacrylamide gel electrophoresis (12.5% for histone detection; 10% for RAD21 detection). For Western blotting, the fractionated proteins in the gel were transferred to a polyvinylidene difluoride (PVDF) membrane (IPVH00010; Millipore) by a semi-dry blotter (BE-320; BIO CRAFT). After blocking with 5% skim milk (Morinaga), the membrane-bound proteins were probed by the rabbit anti–acetyl histone H4 (06-866; Millipore), rabbit anti–acetyl histone H3 (06-599; Millipore), rabbit anti-H2B (ab1790; Abcam), mouse anti-RAD21 (05-908; Millipore) or goat anti–lamin A/C (sc-6215; Santa Cruz Biotechnology) antibody, followed by the appropriate secondary antibody: anti-rabbit (170-6515; Bio-Rad), anti-mouse (170-6516; Bio-Rad), or anti-goat (305-035-003; Jackson ImmunoResearch) horseradish peroxidase–conjugated goat antibody. Chemiluminescence reactions were used (WBKLS0100; Millipore) and detected by EZ-Capture MG (AE-9300H-CSP; ATTO).

Microscopy setup for live-cell imaging

Fluorescent nucleotide live-cell imaging was performed using an inverted Nikon Eclipse Ti microscope with a 100-mW Sapphire 488-nm and 561-nm laser (Coherent) and scientific complementary metal-oxide semiconductor (sCMOS) ORCA-Flash 4.0 camera or ORCA-Fusion BT (Hamamatsu Photonics). Cells were exposed to the excitation laser through an objective lens [100× PlanApo total internal reflection fluorescence (TIRF), numerical aperture (NA) 1.49; Nikon]. The images were obtained using an oblique illumination system with the TIRF unit (Nikon) to illuminate a limited thin area in the cell nucleus. Movies of 150 to 200 sequential frames were acquired using MetaMorph software (Molecular Devices) at a frame rate of 50 ms under continuous illumination. To maintain cell culture conditions (37°C, 5% CO₂, and humidity) during imaging, a live-cell chamber and GM-8000 digital gas mixer (Tokai Hit) were used. Dual-color imaging was performed through a beam splitter W-VIEW GEMINI (Hamamatsu Photonics).

Imaging analysis for movements

Sequential microscopy images were converted to 8-bit grayscale and the background signals were subtracted with the rolling ball background subtraction (radius, 50 pixels) and auto-scaled with ImageJ software (National Institutes of Health). The nuclear regions in the images were manually extracted. Single-nucleosome tracking, and single-nucleosome movement analysis were performed as previously described (83). Briefly, the 2D PSF of each fluorescent dot in each image was fitted to a Gaussian function to obtain the center of the distribution, and its trajectory was tracked with u-track [MATLAB package; (59)]. For single-nucleosome movement analysis, the displacement distribution and the MSD of the fluorescent dots were calculated on the basis of their trajectory using a Python program. The originally calculated MSD was in 2D. To obtain the 3D value, the 2D value was multiplied by 1.5 (4 to 6 Dt). Graphs and statistical analyses of the obtained single-nucleosome MSD between various conditions were performed using R. To ascertain the position determination accuracy of the nucleosomes labeled with Cy3-dCTP in FA-fixed cells, distributions of nucleosome displacements from the initial positions in the x- and y-planes in the 50-ms interval (n > 10 molecules) were fitted to Gaussian functions. The mean of SDs of each distribution, the mean of SDx and SDy, was used for position determination accuracy. To analyze movements of two nucleosomes labeled with two colors (Alexa488 and Cy3), we picked a number of closely located pairs of Alexa488 and Cy3 dots from each image movie. The regions including the pairs were cut out from the original movies for further analysis. Detection and tracking were performed using the Fiji package (TrackMate) (94). To analyze movement of early replication foci, the background signals were subtracted as described above. Detection and tracking were performed using TrackMate.

Correlative movement analysis

The position and movement of bright dots were detected and tracked using TrackMate. The correlation of movement trajectories in dual color was calculated over 10 continuous frames (500 ms) based on the congruence coefficient (r_c) (95), as described below

$$r_{\mathrm{c}}=\frac{\sum _{i,j}{a}_{ij}{b}_{ij}}{\sqrt{(\sum _{i,j}{a_{ij}}^2)(\sum _{i,j}{b_{ij}}^2)}}$$

where A = (a_ij) and B = (b_ij) are I-by-J matrices representing nucleosome and replication foci positions. A and B are produced in 10 continuous frames. The first row indicates the time series of x coordinates and the second row indicates the y coordinates; so in this case, we set I to 2 and J to 10. To align the center position of each trajectory in 10 frames, the average positions of A and B were set to (0, 0) by subtracting the average position from each position in each color, respectively. Positions of spots labeled by green and red colors were corrected by affine transformation. Parameters of affine transformation were estimated based on the 0.1-μm TetraSpeck bead (T7279; Thermo Fisher Scientific) imaging and calculations were performed using the R package (vec2dtransf).

Random sampling

To establish the negative control dataset for correlation analysis of trajectories, we generated a pair of nucleosome trajectories randomly chosen from distinct cells and calculated their correlation.

STED imaging

For STED imaging of chromatin, we plated HeLa cells on coverslips and cultured them. Cells were then fixed with 2% FA in 1× PBS for 15 min and neutralized by 50 mM glycine in 1× HMK [10 mM HEPES (pH 7.5), 1 mM MgCl₂, and 100 mM KCl]. Cells were permeabilized with 0.5% Triton X-100 in 1× HMK and stained with 4 μM SiR-Hoechst (CY-SC007; Spirochrome) in 1× HE (10 mM HEPES (pH 7.5) and 1 mM EDTA). After washing with 1× HE, cells were mounted with DABCO (12.5%) + HEPES-KOH (10 mM, pH 7.5) + glycerol (86%) onto a glass slide and sealed. Samples were observed with a STED microscope (SP8-STED3X, Leica) using a glycerol immersion objective lens (HC PL APO CS2 93× NA 1.30). The correction collar was adjusted to minimize the spherical aberrations. The fluorescent dye, SiR, was excited with a laser line of 640 nm from the pulsed white-light laser (WLL, Leica), immediately followed by a pulse of the donut beam of a 775-nm laser for depletion. The latter beam was 3D shaped with the vortex phase plate and the top-hat phase plate at a mixing ratio of 4:6 to balance the lateral resolution and the axial resolution. The signal between the wavelengths of 650 and 710 nm was collected using the hybrid photo detector (HyD, Leica), after rejecting the stray light by a pinhole (86.4 μm, corresponding to 0.5 airy units at 660 nm). The gate of the detector was opened 0.3 ns after the excitation laser pulse to collect photons only from the fluorescent molecules that were not depleted by the donut-shaped STED beam. The image was taken by four-time line averaging with a voxel size of 14 × 14 × 50 nm with a pixel dwell time of 1.11 μs. Raw images were further processed with the deconvolution software package Huygens (SVI) to enhance contrast by removing the haze from incomplete fluorescence depletion.

Two-point MSD analysis

In our single-nucleosome tracking, trajectories of Alexa488- and Cy3-dots on the XY plane, ${\{{\mathbf{S}}_{\mathrm{Alexa}488}(t_m)\}}_{m=0}^{M-1}$ and ${\{{\mathbf{S}}_{\mathrm{Cy}3}(t_m)\}}_{m=0^{\mathrm{\prime }}}^{M-1}$ were simultaneously acquired, where the time interval was Δt = 0.05 s and t_m = m Δt (m = 0,1,2, ⋯, M − 1). To evaluate dynamic fluctuations between two points, we dealt with the relative vector between two trajectories, Q(t_m) = S_Cy3(t_m) − S_Alexa488(t_m). Then, we calculated the two-point MSD for the lag time t_n = n Δt by

$$\mathrm{MSD}(t_n)={⟨\frac{1}{M-n}{\displaystyle \sum _{m=0}^{M-1-n}}{[\mathbf{Q}(t_{m+n})-\mathbf{Q}(t_m)]}^2⟩}_{t_n}\times \frac{3}{2}$$

where ⟨·⟩_tn represents the ensemble average for trajectories at the lag time t_n and the coefficient 3/2 is a correction factor for conversion from 2D to 3D values.

Fluorescence recovery after photobleaching

To label early replication foci, 1 nmol of Cy3-dCTP was introduced into HeLa cells 1 hour after release from a double thymidine block. The transfected cells were grown on fibronectin (163-15591; Fujifilm)–coated glass-bottomed dishes for 1 to 2 days. Photobleaching and time-lapse imaging were carried out under cell culture conditions (37°C, 5% CO₂, and humidity) on a FLUOVIEW FV1000 confocal laser scanning microscope (OLYMPUS) equipped with Olympus UPLANSAPO 40× objective (NA 1.25). A region of interest (ROI) on the nuclear area with Cy3-labeled early replication foci was set in FLUOVIEW FV1000 software and then photobleached by exposing the ROI to 100% power of the 559-nm solid-state laser for 30 s using the Tornado scanning mode. For time-lapse imaging, 60 frames were acquired at 30 s per frame, using 3% power of the 559-nm solid-state laser, with a zoom corresponding to a 207 nm × 207 nm pixel size. Photobleaching was applied when the fourth shot was taken. Cells with excess Z shift due to movements of cells or the microscope were excluded. To minimize the effect of the Z shift, Z scanning was performed 30 min after photobleaching. Z-stack images were taken every 0.4 μm in the z direction, 11 sections in total. Similar Z sections were picked out visually before and after photobleaching. Before normalizing intensity, XY-drifts of cells were corrected by Fiji Plugin StackReg. Fluorescence intensity of the photobleached region was normalized by calculating the ratio of photobleached region to nonbleached region after subtracting background noise (Fig. 7G).

Brownian dynamics simulation of chromatin

Fractal dimension

Our definition of fractal dimension d_f (62) is R ~ N^1/d_f, where R is the size scale of a chromatin domain, and N is the number of nucleosome beads. d_f > 3 is unphysical when N is measured as the number or mass density of spatially distributed beads in the 3D space as discussed in Li et al. (21) because d_f = 3 corresponds to the maximum density of closed-packed beads. On the other hand, d_f > 3 is possible in chromatin when N is measured as the chain length (kilobase) because chromatin is like a heterogeneous polymer with various contact modes. A polymer with a lower contact frequency on short distances in sequence and a higher contact frequency on longer distances can give d_f > 3. Boettiger et al. (82) exhibited power-law scaling between their physical sizes (nanometer) and domain lengths (kilobase) of chromatin domains from Drosophila chromosomes: R_g ~ N^0.22 in silenced chromatin regions and R_g ~ N^0.30 in inactive chromatin regions. Their calculated d_f was 4.54 in silenced chromatin regions and 3.33 in inactive chromatin regions. Their polymer model supported the view that higher contact frequency on longer distances can cause this phenomenon of d_f > 3.

Fractal ring-polymer

In fig. S6 (A to C), we computationally demonstrated 500-nucleosome dynamics belonging to a condensed or extended loop polymer structure using the fractal ring-polymer model. We set ε = 0.01 and calculated 500,000 integration steps for an initial conformation and 100 Brownian dynamics simulations. Here, the spatial length scale was normalized by the monomer size. Then, we randomly selected two monomers for each Brownian dynamics simulation and calculated 10,000 pairs of the congruence coefficient r_c and the average distance d_ave of the two monomers’ trajectories per 50,000 integration steps on the XY-plane (fig. S6, A and B). For a total of 1,000,000 (r_c, d_ave) pairs, we plotted a normalized 2D histogram as a heatmap (fig. S6C).

Hierarchical fractal polymer model

We focused on modeling and simulations for the 1-Mb region composed of 5000 nucleosomes. The genomic region consists of N₂ chromatin domains, and N₁ nucleosome beads form a chromatin domain (fig. S9). Therefore, N₁N₂ (=5000) nucleosome beads hierarchically organize sequentially linked chromatin domains. Each chromatin domain consists of a ring polymer and maintains a compact state characterized by the fractal dimension d_f,1, while the connected chromatin domains form a free-ends polymer and maintain a compact state characterized by the fractal dimension d_f,2. We described mathematical details of the model and algorithm of the Brownian dynamics simulation in the following sections.

Parameters

Performing the Brownian dynamics simulations of the hierarchical fractal polymer model requires the following parameters: the temperature T, the discrete time-step Δt, (N₁, d_f,1, b₁, and γ₁) for the fractal ring-polymer, and (N₂, d_f,2) for the fractal free-ends polymer. As the cells were cultured at 37°C, we set T = 310 K. To simulate the chromatin dynamics within 0.5 sec, we set Δt = 100 ns and calculated 5,000,000 steps for the numerical integration in each simulation. To mimic five chromatin domains (total 1 Mb) with a 200-kb compact state in untreated control cells, we set N₁ = 1000, N₂ = 5 and d_f,1 = 3.3. For simulating five chromatin domains (total 1 Mb) with a 200-kb extended state in TSA-treated cells, we set N₁ = 1000, N₂ = 5, and d_f,1 = 2.1. We set N₁ = 500, N₂ = 10, and d_f,1 = 2.9 for 10 chromatin domains (total 1 Mb) with a 100-kb compact state in cohesin-KD cells. The effective bond length between adjacent nucleosome beads, b₁, is related to the average nucleosome-nucleosome length l, corresponding to the average diameter of chromatin, as $b_1=\sqrt{3\mathrm{\pi }/8}l$. Since the electron microscopy tomography observed l = 14 nm (14), we set b₁ = 15.2 nm. Using the theoretical result of the MSD for the hierarchical fractal polymer model, we obtained the other parameters γ₁ and d_f,2 by fitting the MSD curves for the three types of cells (fig. S9B).

Calculating movements of randomly chosen two beads

First, we carried out 100 Brownian dynamics simulations for both the fractal ring polymer and free-ends polymer models. By combining these simulations, in principle, we can generate a total of $\left(\begin{array}{c}100\\ N_2\end{array}\right)\times 100$ simulations of the hierarchical fractal polymer. For N₂ = 5 and 10, the number is about 7.5 × 10⁹ and 1.7 × 10¹⁵, respectively. For each Brownian dynamics simulation of the fractal free-ends polymer as movements of chromatin domains, we randomly chose two domains from N₂ domains with overlaps, where overlaps occur with the probability 3/4. Therefore, the ratio of the selected two domains belonging to the same domain and the different domains is 3:1. This probability was estimated from our genomics data. Next, for the movements of the selected domain, to calculate the dynamics of the hierarchical fractal polymer, we mounted the fractal ring-polymer randomly chosen from 100 simulations. If the selected domains overlapped and were the same, we analyzed the dynamics of two randomly selected beads within the same fractal ring polymer. If the selected domains were different, we randomly chose two different fractal ring-polymers and mounted on two different domains of the fractal free-ends polymer. Then, we randomly chose a bead in each different fractal ring-polymer. In total, we analyzed the dynamics of 1,000,000 pairs of two randomly selected beads in the hierarchical fractal polymer model to compare with the result of our dual-color imaging of single nucleosomes. For each pair’s trajectories on the XY-plane at 500 ms time step, we calculated the congruence coefficient r_c and the average distance d_ave. We used VMD for the visualization of polymer conformations (96).

Theory of the fractal ring polymer

We briefly give a mathematical description of the dynamics of ring polymers characterized by the fractal dimension d_f. A polymer consists of N monomers. Let (R₀, R₁, ⋯, R_N−1) be the positions of the monomers, and adjacent monomers are connected via a harmonic spring so that the spring constant corresponds to $3k_{\mathrm{B}}T/b_{\mathrm{bond}}^2$, where k_B is the Boltzmann constant, T is the temperature of the environment, and b_bond represents the SD of bond length fluctuations at thermal equilibrium. We assume that long-range interactions exist, such that the phenomenological size scaling of the polymer globule is locally proportional to N^1/d_f. In the continuous limit, the Langevin equation of monomers is described as

$$\mathrm{\gamma }\frac{\mathrm{\partial }\mathbf{R}(n,t)}{\mathrm{\partial }t}=\frac{3k_{\mathrm{B}}T}{b_{\mathrm{bond}}^2}\frac{{\mathrm{\partial }}^2\mathbf{R}(n,t)}{\mathrm{\partial }{n}^2}+{\mathbf{F}}_{\mathrm{long}}(n,t)+\mathbf{g}(n,t)$$

where γ is the friction coefficient of the monomers. The thermal random force g(n, t) satisfies zero mean ⟨g_α(n, t)⟩ = 0 and the fluctuation-dissipation relation (FDR) ⟨g_α(n, t)g_β(m, s)⟩ = 2γk_BTδ_αβδ(n − m)δ(t − s), where ⟨·⟩ stands for the averaging at thermal equilibrium and the suffixes α and β represent x, y, and z. To form a ring polymer, the boundary conditions

$$\mathbf{R}(0)=\mathbf{R}(N)\mathrm{and}\frac{\mathrm{\partial }\mathbf{R}(n)}{\mathrm{\partial }n}\mid {}_{n=0}=\frac{\mathrm{\partial }\mathbf{R}(n)}{\mathrm{\partial }n}\mid {}_{n=N}$$

are imposed in the continuous limit. The long-range interaction force F_long(n, t) includes attractive and repulsive interactions and stands for nonlinear contributions other than the linear spring force. We assume that the long-range interaction force results in the size scaling for fractal ring polymers

$$⟨{[\mathbf{R}(n)-\mathbf{R}(m)]}^2⟩=b^2{N}^{2/d_{\mathrm{f}}}f(n,m)$$

where b is the effective bond length and

$$f(n,m)={\left[\frac{\mid n-m\mid }{N}(1-\frac{\mid n-m\mid }{N})\right]}^{2/d_{\mathrm{f}}}$$

This size scaling relation is an extension of the Rouse ring polymer for the fractal nature.

To analytically calculate, we introduce the normal coordinates

$$\begin{array}{c}{\mathbf{Y}}_p(t)=\frac{1}{N}{\displaystyle {\int }_0^N}dn\cos \left(\frac{2\mathrm{\pi }pn}{N}\right)\mathbf{R}(n,t)(p=0,1,2,\cdots )\\ \mathrm{and}{\mathbf{Z}}_p(t)=\frac{1}{N}{\displaystyle {\int }_0^N}dn\sin \left(\frac{2\mathrm{\pi }pn}{N}\right)\mathbf{R}(n,t)(p=1,2,\cdots )\end{array}$$

and the inverse transformation is

$$\mathbf{R}(n,t)={\mathbf{Y}}_0(t)+2{\displaystyle \sum _{p=1}^{\mathrm{\infty }}}[{\mathbf{Y}}_p(t)\cos \left(\frac{2\mathrm{\pi }pn}{N}\right)+{\mathbf{Z}}_p(t)\sin \left(\frac{2\mathrm{\pi }pn}{N}\right)]$$

These transformations satisfy the boundary conditions.

In the Langevin equation, the long-range interaction force makes the equation nonlinear, and, in general, it is difficult to solve the equation analytically. However, an averaging approximation can make it a linear equation. So, by averaging under thermal equilibrium with respect to the normal coordinates (62), we use an approximation so that the nonlinear Langevin equation is transformed into linear equations

$$\begin{array}{c}\mathrm{\gamma }\frac{d{\mathbf{Y}}_p(t)}{dt}=-{\mathrm{\kappa }}_p{\mathbf{Y}}_p(t)+{\mathbf{\text{ζ}}}_p(t)\\ \mathrm{and}\mathrm{\gamma }\frac{d{\mathbf{Z}}_p(t)}{dt}=-{\mathrm{\kappa }}_p{\mathbf{Z}}_p(t)+{\mathbf{\text{η}}}_p(t)\end{array}$$

The term in the left-hand side and the second term in the right-hand side are straightforwardly derived according to the transformation for the normal coordinates, in which thermal noise terms ${\mathbf{\text{ζ}}}_p(t)=\frac{1}{N}{\int }_0^{N}dn\cos \left(\frac{2\mathrm{\pi }pn}{N}\right)\mathbf{g}(n,t)$ and ${\mathbf{\text{η}}}_p(t)=\frac{1}{N}{\int }_0^{N}dn\sin \left(\frac{2\mathrm{\pi }pn}{N}\right)\mathbf{g}(n,t)$ satisfy zero mean ⟨ζ_pα(t)⟩ = ⟨η_pα(t)⟩ = 0 and the following FDRs

$$⟨{\mathrm{\zeta }}_{p\mathrm{\alpha }}(t){\mathrm{\zeta }}_{q\mathrm{\beta }}(s)⟩=\frac{\mathrm{\gamma }{k}_{\mathrm{B}}T}{N}{\mathrm{\delta }}_{\mathrm{\alpha }\mathrm{\beta }}\mathrm{\delta }(t-s){\mathrm{\delta }}_{pq}(1+{\mathrm{\delta }}_{p0})$$

and

$$⟨{\mathrm{\eta }}_{p\mathrm{\alpha }}(t){\mathrm{\eta }}_{q\mathrm{\beta }}(s)⟩=\frac{\mathrm{\gamma }{k}_{\mathrm{B}}T}{N}{\mathrm{\delta }}_{\mathrm{\alpha }\mathrm{\beta }}\mathrm{\delta }(t-s){\mathrm{\delta }}_{pq}$$

The linear equations implicitly include the nonlinear effect induced by the long-range interactions in the parameter κ_p, and

$${\mathrm{\kappa }}_0=0\mathrm{and}{\mathrm{\kappa }}_p^{-1}=\frac{b^2{N}^{1+2/d_{\mathrm{f}}}}{6k_{\mathrm{B}}T}I(p,d_{\mathrm{f}})\mathrm{for}p\ge 1$$

where

$$I(p,d_{\mathrm{f}})=-{\displaystyle {\int }_0^1}dx\cos (2\mathrm{\pi }px){[x(1-x)]}^{2/d_{\mathrm{f}}}$$

Then, the square radius of gyration of the fractal ring-polymer is

$$R_{\mathrm{g}}^2=b^2{N}^{2/d_{\mathrm{f}}}{\displaystyle \sum _{p=1}^{\mathrm{\infty }}}I(p,d_{\mathrm{f}})$$

and the MSD becomes

$${\mathrm{MSD}}^{\mathrm{ring}}(t)=\frac{6k_{\mathrm{B}}T}{N\mathrm{\gamma }}t+2b^2{N}^{2/d_{\mathrm{f}}}{\displaystyle \sum _{p=1}^{\mathrm{\infty }}}I(p,d_{\mathrm{f}})\{1-\exp [-\frac{6k_{\mathrm{B}}T}{\mathrm{\gamma }{b}^2{N}^{1+2/d_{\mathrm{f}}}I(p,d_{\mathrm{f}})}t]\}$$

Theory of the fractal free-ends polymer

We developed the fractal polymer model with free-ends in our previous work (62). Unlike the fractal ring polymer, the size scaling for the fractal free-ends polymer obeys

$$⟨{[\mathbf{R}(n)-\mathbf{R}(m)]}^2⟩=b^2{\mid n-m\mid }^{2/d_{\mathrm{f}}}$$

and satisfies the free boundary condition at the edges

$$\frac{\mathrm{\partial }\mathbf{R}(n)}{\mathrm{\partial }n}\mid {}_{n=0}=\frac{\mathrm{\partial }\mathbf{R}(n)}{\mathrm{\partial }n}\mid {}_{n=N}=0$$

The normal coordinates are defined as

$${\mathbf{X}}_p(t)=\frac{1}{N}{\displaystyle {\int }_0^N}dn\cos \left(\frac{p\mathrm{\pi }n}{N}\right)\mathbf{R}(n,t)(p=0,1,2,\cdots )$$

and the inverse transformation is

$$\mathbf{R}(n,t)={\mathbf{X}}_0(t)+2{\displaystyle \sum _{p=1}^{\mathrm{\infty }}}{\mathbf{X}}_p(t)\cos \left(\frac{p\mathrm{\pi }n}{N}\right)$$

The dynamics for the normal coordinates X_p(t) is written as

$$\mathrm{\gamma }\frac{d{\mathbf{X}}_p(t)}{dt}=-k_p{\mathbf{X}}_p(t)+{\mathbf{g}}_p(t)$$

where the thermal noise g_p(t) satisfies zero mean ⟨g_pα(t)⟩ = 0 and the FDR

$$⟨g_{p\mathrm{\alpha }}(t)g_{q\mathrm{\beta }}(s)⟩=\frac{\mathrm{\gamma }{k}_{\mathrm{B}}T}{N}{\mathrm{\delta }}_{\mathrm{\alpha }\mathrm{\beta }}\mathrm{\delta }(t-s){\mathrm{\delta }}_{pq}(1+{\mathrm{\delta }}_{p0})$$

and

$$k_0=0\mathrm{and}{k}_p=A_{d_{\mathrm{f}}}\frac{3k_{\mathrm{B}}T}{b^2{N}^{1+2/d_{\mathrm{f}}}}{p}^{1+2/d_{\mathrm{f}}}\mathrm{for}p\ge 1$$

A_df is a dimensionless constant depending on the fractal dimension

$$A_{d_{\mathrm{f}}}=\frac{{\mathrm{\pi }}^{1+2/d_{\mathrm{f}}}}{\text{Γ}(1+2/d_{\mathrm{f}})\sin (\mathrm{\pi }/d_{\mathrm{f}})}$$

Then, the MSD of the fractal free-ends polymer is calculated as

$$\begin{array}{rl}{\mathrm{MSD}}^{\mathrm{f}\mathrm{ree}-\mathrm{ends}}(t)& =\frac{6k_{\mathrm{B}}T}{N\mathrm{\gamma }}t\\ & +\frac{2b^2{N}^{2/d_{\mathrm{f}}}}{A_{d_{\mathrm{f}}}}{\displaystyle \sum _{p=1}^{\mathrm{\infty }}}{p}^{-1-2/d_{\mathrm{f}}}\\ & \times [1-\exp \{-\frac{A_{d_{\mathrm{f}}}3k_{\mathrm{B}}T}{\mathrm{\gamma }{b}^2}{\left(\frac{p}{N}\right)}^{1+2/d_{\mathrm{f}}}t\}]\end{array}$$

Theory of hierarchical fractal polymer model

The hierarchical fractal polymer model is composed of two layers. In the first layer, N₁ nucleosome beads form a chromatin domain modeled by the ring polymer with the fractal dimension d_f,1, where b₁ represents the effective bond length between adjacent beads and γ₁ is the friction coefficient of the beads. Each bead stochastically moves in a thermal environment with temperature T except for the motion of the center of mass. At the second layer, N₂ chromatin domains sequentially connect forming the free-ends polymer with the fractal dimension d_f,2. Therefore, the center-of-mass motion of the domains corresponds to the motion of the fractal free-ends monomers. The effective bond length b₂ between adjacent domains corresponds to the diameter of gyration of the fractal ring polymer

$$b_2=2R_{\mathrm{g}}=2b_1{N}_1^{1/d_{\mathrm{f}}}\sqrt{{\displaystyle \sum _{p=1}^{\mathrm{\infty }}}I(p,d_{\mathrm{f},1})}$$

and the friction coefficient of the domains γ₂ is N₁γ₁. Thus, the following parameters determine the dynamics of our hierarchical fractal model: N₁, N₂, d_f,1, d_f,2, b₁, γ₁, and T. Combining the two MSD equations, we can write the MSD for hierarchical fractal polymer model by

$$\begin{array}{c}\mathrm{MSD}(t)=\frac{6k_{\mathrm{B}}T}{N_1{N}_2{\mathrm{\gamma }}_1}t\\ +\frac{2b_2{N}_2^{2/d_{\mathrm{f},2}}}{A_{d_{\mathrm{f},2}}}{\displaystyle \sum _{p=1}^{\mathrm{\infty }}}{p}^{-1-2/d_{\mathrm{f},2}}[1-\exp \{-\frac{A_{d_{\mathrm{f},2}}3k_{\mathrm{B}}T}{N_1{\mathrm{\gamma }}_1{b}_2^2}{\left(\frac{p}{N_2}\right)}^{1+2/d_{\mathrm{f},2}}t\}]\\ +2b_1^2{N}_1^{2/d_{\mathrm{f},1}}{\displaystyle \sum _{p=1}^{\mathrm{\infty }}}I(p,d_{\mathrm{f},1})[1-\exp (-\frac{6k_{\mathrm{B}}T}{{\mathrm{\gamma }}_1{b}_1^2{N}_1^{1+2/d_{\mathrm{f},1}}I(p,d_{\mathrm{f},1})}t)]\end{array}$$

Algorithm of Brownian dynamics for the fractal polymer models

Before explaining the algorithms, we should obtain a discretized and dimensionless Langevin equation as a stochastic differential equation (SDE). For example, within a time interval ∆t, the Langevin equation of the normal coordinate Y_pα in the fractal ring polymer can be expressed as an SDE integration form with spatial normalization by b

$$\text{Δ}\left(\frac{Y_{p\mathrm{\alpha }}}{b}\right)=-\frac{{\mathrm{\kappa }}_p\text{Δ}t}{\mathrm{\gamma }}\left(\frac{Y_{p\mathrm{\alpha }}}{b}\right)+\sqrt{\frac{k_{\mathrm{B}}T\text{Δ}t}{\mathrm{\gamma }{b}^2}\frac{1+{\mathrm{\delta }}_{p0}}{N}}\mathrm{\xi }+o(\text{Δ}t)(\text{Δ}t\to 0)$$

where the term in the left-hand side means the small displacement, and ξ represents a random variable obeying the normal distribution with mean 0 and variance 1. Here, we can also normalize the time scale by $\mathrm{\epsilon }=\frac{k_{\mathrm{B}}T\text{Δ}t}{\mathrm{\gamma }{b}^2}$, which is a dimensionless parameter and determines the accuracy of the SDE integration. Then, we can obtain a dimensionless SDE integration form

$$\text{Δ}\left(\frac{Y_{p\mathrm{\alpha }}}{b}\right)=-\frac{6\mathrm{\epsilon }}{N^{1+2/d_{\mathrm{f}}}I(p,d_{\mathrm{f}})}\left(\frac{Y_{p\mathrm{\alpha }}}{b}\right)+\sqrt{\mathrm{\epsilon }\frac{1+{\mathrm{\delta }}_{p0}}{N}}\mathrm{\xi }+o(\mathrm{\epsilon })(\mathrm{\epsilon }\to 0)$$

The same normalization steps for the normal coordinate X_pα in the fractal free-ends polymer derive a dimensionless SDE integration form

$$\text{Δ}\left(\frac{X_{p\mathrm{\alpha }}}{b}\right)=-3A_{d_{\mathrm{f}}}\mathrm{\epsilon }{\left(\frac{p}{N}\right)}^{1+2/d_{\mathrm{f}}}\left(\frac{X_{p\mathrm{\alpha }}}{b}\right)+\sqrt{\mathrm{\epsilon }\frac{1+{\mathrm{\delta }}_{p0}}{N}}\mathrm{\xi }+o(\mathrm{\epsilon })(\mathrm{\epsilon }\to 0)$$

The fractal ring polymer

Step 1. The parameters N, d_f, b, γ, ∆t, T, are set. Here, ∆t represents the discrete time step for the numerical integration, then t_j = j∆t for j = 0,1,2, ⋯ is the discrete time. The dimensionless parameter is set as $\mathrm{\epsilon }=\frac{k_{\mathrm{B}}T\text{Δ}t}{\mathrm{\gamma }{b}^2}$. The integration of the function I(p, d_f) is numerically calculated. Since the numerical stability is not good for large p and the asymptotic relation I(p, d_f) ∝ p^{−1 − 2/d_f} for large p is numerically confirmed, the value of the integral are approximately given by calculating I(p, d_f) = I(p_c, d_f)(p_c/p)^{1 + 2/d_f} for p > p_c. We set p_c = 50.

Step 2. An initial state is given: Y₀ = 0 so that the center of mass is the origin, and the normal coordinates with spatial normalization for each freedom ${\{Y_{p\mathrm{\alpha }}/b\}}_{p=1}^{p_{\max }}$ and ${\{Z_{p\mathrm{\alpha }}/b\}}_{p=1}^{p_{\max }}$ are random variables obeying the normal distribution with mean 0 and variance $\frac{k_{\mathrm{B}}T}{2N{\mathrm{\kappa }}_p}\frac{1}{b^2}=\frac{N^{2/d_{\mathrm{f}}}I(p,d_{\mathrm{f}})}{12}$.

Step 3. Numerical integration is calculated by using Heun’s method, which assures the second order convergence in ε. For the dimensionless SDE integration form, the algorithm is defined by first predicting

$${\tilde{x}}_j=x_j-\frac{6\mathrm{\epsilon }}{N^{1+2/d_{\mathrm{f}}}I(p,d_{\mathrm{f}})}{x}_j+\sqrt{\mathrm{\epsilon }\frac{1+{\mathrm{\delta }}_{p0}}{N}}{\mathrm{\xi }}_j$$

and then correcting

$$x_{j+1}=x_j-\frac{6\mathrm{\epsilon }}{N^{1+2/d_{\mathrm{f}}}I(p,d_{\mathrm{f}})}\frac{x_j+{\tilde{x}}_j}{2}+\sqrt{\mathrm{\epsilon }\frac{1+{\mathrm{\delta }}_{p0}}{N}}{\mathrm{\xi }}_j$$

where ξ_j is a random variable obeying the normal distribution with mean 0 and variance 1.

Step 4. To calculate a conformation of the fractal ring polymer, the inverse transformation

$$\mathbf{R}(n,t_j)={\mathbf{Y}}_0(t_j)+2{\displaystyle \sum _{p=1}^{p_{\max }}}[{\mathbf{Y}}_p(t_j)\cos \left(\frac{2\mathrm{\pi }pn}{N}\right)+{\mathbf{Z}}_p(t_j)\sin \left(\frac{2\mathrm{\pi }pn}{N}\right)]$$

is calculated for n = 0,1, ⋯, N − 1 with multiplying the normalized normal coordinates, ${\{Y_{p\mathrm{\alpha }}/b\}}_{p=1}^{p_{\max }}$ and ${\{Z_{p\mathrm{\alpha }}/b\}}_{p=1}^{p_{\max }}$, by b.

The fractal free-ends polymer

Step 1. The parameters N, d_f, b, γ, ∆t, and T are set. Here ∆t represents the discrete time step for the numerical integration, then t_j = j∆t for j = 0,1,2, ⋯ is the discrete time. The dimensionless parameter is set as $\mathrm{\epsilon }=\frac{k_{\mathrm{B}}T\text{Δ}t}{\mathrm{\gamma }{b}^2}$. According to the value of d_f, A_df is calculated.

Step 2. An initial state is given: X₀ = 0 so that the center of mass is the origin, and the normal coordinates with spatial normalization for each freedom ${\{X_{p\mathrm{\alpha }}/b\}}_{p=1}^{p_{\max }}$ are random variables obeying the normal distribution with mean 0 and variance $\frac{k_{\mathrm{B}}T}{2N{k}_p}\frac{1}{b^2}=\frac{N^{2/d_{\mathrm{f}}}}{6A_{d_{\mathrm{f}}}{p}^{1+2/d_{\mathrm{f}}}}$.

Step 3. Numerical integration is calculated by using Heun’s method. For the dimensionless SDE integration form, the algorithm is defined by first predicting

$${\tilde{x}}_j=x_j-3A_{d_{\mathrm{f}}}\mathrm{\epsilon }{\left(\frac{p}{N}\right)}^{1+2/d_{\mathrm{f}}}{x}_j+\sqrt{\mathrm{\epsilon }\frac{1+{\mathrm{\delta }}_{p0}}{N}}{\mathrm{\xi }}_j$$

and then correcting

$$x_{j+1}=x_j-3A_{d_{\mathrm{f}}}\mathrm{\epsilon }{\left(\frac{p}{N}\right)}^{1+2/d_{\mathrm{f}}}\frac{x_j+{\tilde{x}}_j}{2}+\sqrt{\mathrm{\epsilon }\frac{1+{\mathrm{\delta }}_{p0}}{N}}{\mathrm{\xi }}_j$$

where ξ_j is a random variable obeying the normal distribution with mean 0 and variance 1.

Step 4. To calculate a conformation of the fractal free-ends polymer, the inverse transformation

$$\mathbf{R}(n,t_j)={\mathbf{X}}_0(t_j)+2{\displaystyle \sum _{p=1}^{p_{\max }}}{\mathbf{X}}_p(t_j)\cos \left[\frac{\mathrm{\pi }p(2n+1)}{2N}\right]$$

is calculated for n = 0,1, ⋯, N − 1 with multiplying the normalized normal coordinates, ${\{X_{p\mathrm{\alpha }}/b\}}_{p=1}^{p_{\max }}$, by b.

The hierarchical fractal polymer

Step 1. The temperature T and discrete time step ∆t are fixed. The parameters (N₁, d_f,1, b₁, γ₁) for the fractal ring polymer model and (N₂, d_f,2, b₂ = 2R_g, γ₂ = N₁γ₁) for the fractal free-ends polymer model are set.

Step 2. These two fractal polymer models are independently calculated according to the above Brownian dynamics algorithms with setting p_max = N − 1. Note that we do not need to calculate the center-of-mass dynamics of the fractal ring-polymer, Y₀(t).

Step 3. The fractal ring polymer trajectories except for the center of mass are united with the nth monomer movements of the fractal free-ends polymer.

Supplementary Materials

This PDF file includes:

Figs. S1 to S9

Table S1

Legends for movies S1 to S16

Other Supplementary Material for this : manuscript includes the following:

Movies S1 to 16

View/request a protocol for this paper from Bio-protocol.