Compositions and Interior Structures of the Large Moons of Uranus and Implications for Future Spacecraft Observations

Abstract

The five large moons of Uranus are important targets for future spacecraft missions. To motivate and inform the exploration of these moons, we model their internal evolution, present‐day physical structures, and geochemical and geophysical signatures that may be measured by spacecraft. We predict that if the moons preserved liquid until present, it is likely in the form of residual oceans less than 30 km thick in Ariel, Umbriel, and less than 50 km in Titania, and Oberon. The preservation of liquid strongly depends on material properties and, potentially, on dynamical circumstances that are presently unknown. Miranda is unlikely to host liquid at present unless it experienced tidal heating a few tens of million years ago. We find that since the thin residual layers may be hypersaline, their induced magnetic fields could be detectable by future spacecraft‐based magnetometers. However, if the ocean is maintained primarily by ammonia, and thus well below the water freezing point, then its electrical conductivity may be too small to be detectable by spacecraft. Lastly, our calculated tidal Love number (k ₂) and dissipation factor (Q) are consistent with the Q/k ₂ values previously inferred from dynamical evolution models. In particular, we find that the low Q/k ₂ estimated for Titania supports the hypothesis that Titania currently holds an ocean.

Key Points

• Most of the major Uranian moons may host a residual ocean a few tens of kilometers thick at present, except for Miranda

• Thermal metamorphism could create a late, second generation ocean in Titania and Oberon

• These models represent a baseline for the formulation of observations with the Uranus Orbiter and Probe

1. Study Motivations and Goals

The last decade has seen a growing interest in exploration of the ice giant systems, recently culminating with the prioritization of a Uranus Orbiter and Probe (UOP) in the Planetary Science and Astrobiology Decadal Survey for 2023–2032 (Origins, Worlds, Life, NASEM, 2022). This concept includes objectives about understanding the evolution and current state of Uranus' large five moons: Miranda, Ariel, Umbriel, Titania, and Oberon. In particular, UOP would test whether some of these moons are ocean worlds (i.e., host deep, global‐scale oceans at present) (see Roadmap to Ocean Worlds, Hendrix et al., 2019). Recent studies (e.g., Arridge & Eggington, 2021; Cochrane et al., 2021; Weiss et al., 2021) demonstrate that magnetic fields induced in the moons oceans may be detected from flybys. This forms the basis for one of the investigations pursued by the UOP concept.

There have been few studies about the internal evolution of the large Uranian moons. Hussmann et al. (2006) and, more recently, Bierson and Nimmo (2022) predicted that Titania and Oberon could contain thick oceans, whereas Ariel, Umbriel, and Miranda would be frozen at present. These studies concluded that deep oceans, if present, would be maintained by the presence of ammonia, an antifreeze expected in most icy moons (e.g., Kargel, 1998). However, these models did not account for the fate of accreted ammonia in solution: ammonia can speciate into ammonium, which can be the dominant form of nitrogen depending on pH (Fortes, 2012 for Titan; Castillo‐Rogez, Melwani Daswani, & Cockell, 2022; Marion et al., 2012, applicable to a wide range of icy moons), hence diminishing ammonia's antifreeze role significantly. Furthermore, recent studies intended to support the definition of future magnetometer investigations at the Uranian moons (e.g., UOP) did not consider the temperature dependence of electrical conductivity (EC), so that cold oceans sustained by antifreeze may have a very weak or even near‐zero EC.

We revisit the evolution, composition, and structure of the large Uranian moons, motivated by multiple recent advances: surface chemistry and geology (in particular, heat flow estimates), revised dynamical models, and reinterpretation of shape data. Furthermore, we leverage knowledge gained on the geochemistry and geophysics of icy bodies comparable in size to the Uranian moons (i.e., 100–1,000 km in diameter) (Figure 1) derived from recent observations of Enceladus and other moons of Saturn by Cassini, Pluto, and Charon by New Horizons and Ceres by Dawn.

Figure 1.

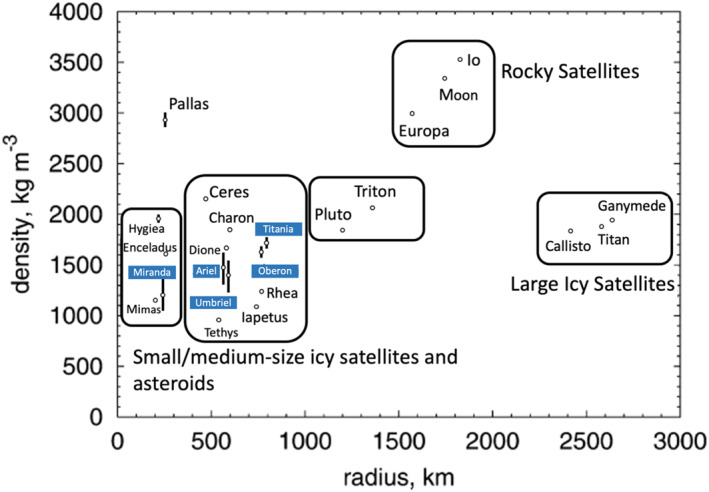
Densities and mean radii of the Uranian moons compared to those of other large moons and dwarf planets. Miranda has a low density similar to Saturn's moon Mimas, whereas the densities of the other Uranian moons are more similar to Saturn's moons Dione and Rhea. After Hussmann et al. (2006).

The goals of this study are to (a) predict the extent of differentiation for the moons based on various heat budget scenarios; (b) assess the conditions for the preservation of deep oceans in the moons until present for various reference temperatures; (c) quantify physical parameters that can be observed by a future spacecraft mission aiming at understanding the moon evolution and current states. These include, for each moon, the shape, moment of inertia, and the amplitude and phase of an induced magnetic field derived from combining interior structure and ocean electric conductivity.

Available observational constraints on the large moon's surface and interior properties are summarized in Section 2. The various models used in this study to model thermal evolution and physical parameters are summarized in Section 3 with their input parameters. The resulting interior structures are presented in Section 4. Alternative assumptions on the moon's origins and evolution pathways are addressed in Section 5. These results serve as a basis for quantifying observation requirements in Section 6. These can serve as a reference for designing future mission investigations targeting these moons in order to assess the extent of differentiation of their interiors and the conditions for detecting an ocean. Relevant knowledge gaps that can be addressed with theoretical and experimental research in preparation for a future mission are briefly addressed in Section 7.

2. Observational Constraints

We review constraints on the large Uranian moons' surface compositions, when available, and inferences from geological analyses (crater‐based geochronology pointing to partial resurfacing and heat flow estimates from flexure analysis) and dynamical modeling. The physical and dynamical properties of the large Uranian moons are gathered in Table 1.

Table 1.

Key Physical and Dynamical Properties of Uranus' Large Moons

Properties	Miranda	Ariel	Umbriel	Titania	Oberon
Mean radius, R (km) (1−σ)	235.8 ± 0.7	578.9 ± 0.6	584.7 ± 2.8	788.9 ± 1.8	761.4 ± 2.6
Mean density (kg/m3) (1−σ)	1,178 ± 53	1,539 ± 26	1,523 ± 41	1,653 ± 32	1,664 ± 50
Suburanian equatorial radius, a (km) (1−σ)	240.4 ± 0.6	581.1 ± 0.9	Not available	Not available	Not available
Along‐orbit equatorial radius, b (km) (1−σ)	234.2 ± 0.9	577.9 ± 0.6	Not available	Not available	Not available
Polar radius, c (km) (1−σ)	232.9 ± 1.2	577.7 ± 1.0	Not available	Not available	Not available
Mean surface temperature (K)	60–70	60–70	70	75	70–80
Central pressure (MPa)	11	111	111	238	225
Semimajor axis, D (km)	129,858	190,930	265,982	436,282	583,449
Orbital eccentricity, e	0.00135	0.00122	0.00394	0.00123	0.00140
Orbital inclination, I (º)	4.4072	0.0167	0.0796	0.1129	0.1478
Radioactive decay power at present (GW)	∼0.8	∼2.8	∼2.8	∼8.4	∼7.7
Solid body power from eccentricity tides at present (GW) Assuming k 2/Q = 10−4	∼8 × 10−3	∼3 × 10−2	∼3 × 10−2	∼3 × 10−4	∼4 × 10−4
Maximum power from obliquity tides in ocean at present (GW) (Chen et al., 2014)	3 × 10−4	∼5 × 10−8	∼2 × 10−6	∼10–4	∼5 × 10−3
k 2/Q	10−5–10−6	10−4–10−5	10−4–10−5	>10−3	10–4
Average, based on orbital parameter evolution since ∼1 Ga (Ćuk et al., 2020)
Tidal dissipation (GW)	∼8 × 10−5–8 × 10−4	∼3 × 10−3–3 × 10−2	∼3 × 10−3–3 × 10−2	>3 × 10−3	∼4 × 10−4
For current values of e and ω = 2π/n (n from above), assuming the Ćuk et al. values
Orbital period n (hours)	33.9	60.6	99.5	208.9	323.1

Note. References for radii and densities are Archinal et al. (2018) and Jacobson (2014). Mean values are used in the simulations presented in this paper. Dynamical properties are provided by https://ssd.jpl.nasa.gov/sats/ephem/ based on Jacobson (2014). References for temperature are Hanel et al. (1986), Janes and Melosh (1988), and Grundy et al. (2006). Q/k ₂ constraints are from Ćuk et al. (2020). Power for obliquity‐driven tides in the ocean is taken from Chen et al. (2014). Eccentricity‐driven tides in the ocean produce several orders of magnitude less heat based on the latter study.

2.1. Constraints on the Interiors of Miranda and Ariel

Assuming no porosity and a rock density of 3,060 kg/m³ (see Section 3), most of the moons have about 30 vol.% of rock (28 vol.% for Ariel and Umbriel, and 34 vol.% for Titania and Oberon). The exception is Miranda with only ∼10 vol.% rock.

Ellipsoidal shape data (equatorial radii, a and b, and polar radius c, with a > b > c) derived from Voyager 2 observations (Thomas, 1988; see also Archinal et al., 2018) are reported in Table 1. The uncertainty in these values is primarily derived from formal errors and does not take into account systematic effects (e.g., variations in topography of areas that were not sampled due to partial coverage by Voyager 2) (Thomas, 1988).

Figure 2 presents values of a, b, and c for different interior structures (differentiated and undifferentiated) assuming hydrostatic equilibrium (e.g., Zharkov et al., 1985, see also Section 6.1).

Figure 2.

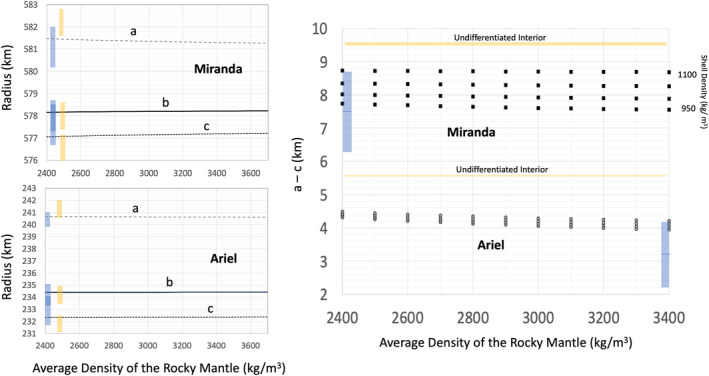
(Left) Ellipsoidal axes (a–c radii) computed for two‐layer (i.e., differentiated structure with rocky core and overlying ice‐rich shell) models for Miranda and Ariel (assuming ρ _shell = 1,050 kg/m³), compared against radii for undifferentiated interiors (yellow) and radii inferred from Voyager 2 observations reported in Archinal et al. (2018) (blue). Observed radii are presented with 1‐sigma error bars. (Right) Differences between (a) and (c) radii with the same color‐coding but for four different shell densities, every 50 kg/m³.

These estimates suggest that the radii inferred from Voyager images are consistent to ≈2σ with differentiated interiors for Ariel and Miranda. However, for both moons, the ratio of (b–c) to (a–c) departs from the ¼ value expected for a body in hydrostatic equilibrium (e.g., Zharkov et al., 1985), about 0.15–0.20 for Miranda and goes from <0 to 0.17 for Ariel. Thomas (1988) pointed out that “a more complete assessment of the significance and accuracy of this shape will eventually be made by comparison with control point and photogrammetric topography.” However, this work has not been performed. Hence there is potential room for improving the analysis of the Voyager data. A future mission arriving in the Uranian system in the 2040s would fill in the coverage gaps.

In the case of Ariel, the mean value of the observed (a–c) is lower than the values predicted for a two‐layer interior. The weak dependence of (a–c) on core density compared against the error bar again precludes further inferences on Ariel's evolution. Altogether, these observations suggest with high (2‐sigma) confidence that the two moons underwent some level of differentiation.

2.2. Surface Evolution From Geological Imaging

Analysis of crater densities for the Uranian moons Umbriel, Titania, and Oberon indicate that they could have largely ancient surfaces (∼3–4 Ga, Zahnle et al., 2003) and, therefore, surface expressions of endogenic activity may be largely relegated to the geologic past on these moons. In contrast, crater densities indicate that Miranda and Ariel have younger surfaces in some regions. As summarized in Kirchoff et al. (2022), surface ages may be as young as 0.1 (−0.1/+0.4) Ga for Inverness Corona on Miranda. The most recent estimates for Ariel's surface age are 1.3 (−0.6/+2.0) Ga with some tectonic features estimated to be as young as 0.8 (−0.5/+1.8) Ga.

Thermal stresses are thought to be responsible for the older extensional tectonic features on the classical Uranian satellites, although some features have likely been erased from impact events (Hillier & Squyres, 1991). Expansion of the lithosphere during freezing of the interior may have also contributed to the formation of extensional faults on these satellites (Croft & Soderblom, 1991; Smith et al., 1986).

Miranda was previously hypothesized to have broken up and reaccreted (e.g., Janes & Melosh, 1988), which would have accelerated cooling. This reaccretion model was proposed to explain Miranda's large deformed regions, termed coronae, under the assumption that the coronae formed by contraction due to subsidence of surface terrains. However, more recent work indicates that the coronae are likely extensional structures formed from uplift, possibly due to diapirism, in contradiction with the reaccretion model (e.g., Hammond & Barr, 2014; Pappalardo et al., 1997). Diapirism, an expression of solid‐state convection, would necessitate tidal heating because radiogenic heating alone is unable to produce sufficiently high temperature gradients and low ice viscosities after a few hundred million years (My).

The relatively high eccentricities observed at all the moons (∼0.1% and up to 0.3% for Umbriel) indicate the average dissipation inside these moons has been small in recent time, which is reflected in the high Q/k ₂ values derived by Ćuk et al. (2020) (gathered in Table 1), within the assumptions (in particular Uranus' Q/k ₂) used in that study. Hence, the moons current heat budget is limited to long‐lived radioisotope decay(see Hussmann et al., 2006; Chen et al., 2014; Table 1) with production power scaled to surface area of the order of 0.1 mW/m² in the case of Miranda, ∼0.7 mW/m² for Ariel and Umbriel, and ∼1 mW/m² for Titania and Oberon.

The surfaces of Miranda and Ariel display evidence for geological activity more recent than 1 Ga (Zahnle et al., 2003). Detailed analysis of geological features have led to constraints on past surface heat flow. Assuming a lithosphere composed of pure water ice, Peterson et al. (2015) estimate Ariel's heat flows range between 29 and 92 mW/m² (almost 1–2 orders of magnitude higher than current heat flows) for a region in the center of Ariel's relatively old “Pixie Group” of chasmata (Peterson et al., 2015), while surrounding chasmata in this group exhibit lower heat flows ranging from 6 to 36 mW/m² (Beddingfield, Cartwright, et al., 2022) and those in the younger “Kachina Group” of chasmata range from 17 to 46 mW/m² (Beddingfield, Cartwright, et al., 2022).

Peterson et al. (2015) and Beddingfield, Cartwright, et al. (2022) interpret their heat flow estimates at Ariel as a result of an eccentricity resonance, likely the 5:3 mean motion resonance (MMR) with Umbriel. Peterson et al. suggest an eccentricity of 20–50 times the current value is needed in order to match the highest estimated heat flows. By comparison, Ćuk et al. find a maximum eccentricity during the 5:3 MMR of ∼0.01, or only about 10 times the current value. Hence, the range of heat flows derived by Peterson et al. and Beddingfield et al. corresponds to Q/k ₂ between 5 and 76.

In the case of Miranda, Beddingfield et al. (2015) inferred a heat flow of 31–112 mW/m² during the formation of Arden Corona, and Beddingfield, Leonard, et al. (2022) inferred a heat flow of 35–140 mW/m² during the formation of Inverness Corona, assuming nonporous lithosphere. Ćuk et al. (2020) showed that secular perturbations exerted by Ariel during the Ariel:Umbriel 5:3 MMR increased Miranda's eccentricity, which could trigger significant tidal heating. Ćuk et al. (2020) suggested that during this resonance, this level of dissipation could be reached if Miranda's Q/k ₂ was ≤10²–10³.

2.3. Surface Composition

Recent ground‐based telescope observations of the Uranian moons detected carbon dioxide (CO₂) ice (Cartwright et al., 2015, 2022; Grundy et al., 2003, 2006) and possibly ammonia (NH₃) and ammonium (NH₄)‐bearing species (Bauer et al., 2002; Cartwright et al., 2018, 2020) on their surfaces.

The accretion of nonwater volatiles in the Uranian system is expected, based on cosmochemical models (Kargel, 1998). In solution CO₂, CO (carbon monoxide) and NH₄ should produce CO₃–NH₄ rich liquids (Castillo‐Rogez, Melwani Daswani, & Cockell, 2022). Cartwright et al. (2020) suggested the presence of NH₃ and NH₄–minerals on the surfaces of the Uranian moons. Because NH₃‐bearing species exposed on the surfaces of these moons may be efficiently decomposed over geologically short timescales by charged particles (e.g., Moore et al., 2007), this could point to a replenishment mechanism involving a deep ocean. On the other hand, the spectral signature of NH₃ could persist over longer timescales if irradiated fragments are able to recombine or if they form ammonium (NH₄ ⁺) cations that interact with surrounding molecules to make NH₄‐rich salts that could be more resistant to charged particle weathering (Cruikshank et al., 2019).

In the case of the Uranian moons, we lack spatially resolved reflectance spectra collected over different regions and geologic units. Hence, the origin of these compounds, whether from the deep interiors of the Uranian moons or whether they are the products of surface chemistry is not known. As a replenishment mechanism, subsurface NH₃ might readily diffuse through the H₂O ice shell to the surface (Livingston et al., 2002). The rate of diffusion could be enhanced by craters and other landforms that increase fracturing and porosity (see discussion in Cartwright et al., 2020). A limitation is that NH₃ diffusion rates at temperatures relevant to the Uranian moons are not well constrained.

3. Modeling Approach and Setup

Like previous studies (Bierson & Nimmo, 2022; Hussmann et al., 2006), our thermal modeling assumes conductive heat transfer. A major difference is the coupling between thermal and geochemical modeling, which has important implications. For example, many studies of icy moon evolution have assumed that accreted ammonia remains entirely available as antifreeze, when in practice ammonia turns partly into ammonium once in aqueous solution (e.g., Marion et al., 2012). On the other hand, other solutes such as chlorides can significantly decrease the eutectic temperature. Models have also assumed the occurrence of clathrate hydrates as possible insulating material but this prospect is highly dependent on environmental conditions (e.g., Castillo‐Rogez, Melwani Daswani, & Cockell, 2022; Sloan & Koh, 2008) and is not realized in the conditions considered in this study (see Appendix C for more information).

We assume the moons accreted in a circumplanetary disk (CPD), which determines a range of compositions for the material accreted in the moons. Alternative formation scenarios and their implications for thermal evolution are addressed in Section 5.1. After a general description of the thermal modeling approach, we describe the input parameters specific to these various features.

3.1. Thermal Modeling Approach

Our internal evolution modeling assumes differentiation of a mostly lithified rocky core and hydrosphere (ocean and ice‐rich shell) (e.g., Hussmann et al., 2006). We use the one‐dimensional thermal conduction model described in Castillo‐Rogez et al. (2019, 2007) (see Appendix D for more details). Hussmann et al. (2006) suggested that objects in the size range and surface temperature of the Uranian moons are either not likely to convect or that convection played a minor role in their evolution. King et al. (2022) predict that convection was possible in these bodies, assuming a pure water ice composition. On the other hand, rock grain impurities could likely increase the effective viscosity of the crust and impede the onset of convection (e.g., Qi et al., 2018). Also, porosity can counteract the buoyancy of deeper layers by creating a negative density gradient with decreasing depth. Here, we assume that the shells are not convecting, which leads to optimistic evolution outcomes in terms of liquid preservation.

The extent of early differentiation is primarily driven by the time of formation with respect to calcium aluminum‐rich inclusions (CAIs), which determines the amount of accreted short‐lived radioisotopes, in particular ²⁶Al. Accretional heating represents a minor contribution to the heat budget in objects less than 1,000 km in diameter (e.g., Matson et al., 2008) but it can help decrease the primordial microporosity. Long‐term internal evolution is driven by the heat from long‐lived radioisotope decay and potentially tidal heating. At present, tidal heating does not represent a significant heat source but it could have been important during periods of resonances (see Section 2).

3.2. Reference Rock and Volatile Compositions

Formation in the CPD reflects the solar nebula composition with potential addition of pebbles from farther out in the disk (e.g., Mousis et al., 2020). Although it has been suggested that Uranus migrated significantly during its growth, starting potentially at 7–10 AU or 9–15 AU in the protoplanetary disk (Helled & Bodenheimer, 2014; Nesvorný & Morbidelli, 2012; Thommes et al., 1999), the moons could have formed by the time the planet reached its current location (Szulágyi et al., 2018).

We assume a CI carbonaceous chondrite composition (Appendix A) with the addition of volatiles (Appendix A), which is likely appropriate for bodies formed at 10–19 AU (e.g., Desch et al., 2018; see Melwani Daswani & Castillo‐Rogez, 2022 for more detail). We explore two reference fractions of accreted NH₃ of 0.3 and 1 wt.% and initial abundances of CO₂ at 1 and 5 wt.%. Alternative moon origin scenarios, including the accretion of pebbles formed beyond 20 AU (e.g., Mousis et al., 2020) and their implications for the moons evolution, are discussed in Section 5.1. The material thermophysical properties used in the modeling are described in Section 3.3 for the rock phase and in Appendix D for the hydrosphere.

3.3. Thermophysical Properties of the Rock Phase

Previous studies have assumed a rock density of 3,500 kg/m³ (Bierson & Nimmo, 2022) for the Uranian moons, but this assumption is not consistent with the expected state of the core following differentiation as rock hydration is a relatively fast process (<<1 My, e.g., Martin & Fyfe, 1970; Zandanel et al., 2022). As the prospect of preserving a deep ocean depends in part on the thickness of the overlaying shell, it is important to track the rock density evolution with temperature. Based on recent experimental observations, we assume that during and following differentiation, the rock phase could become fully hydrated. Indeed, recent work by Zandanel et al. (2022) showed that aqueous alteration of rock in icy bodies proceeds on geologically fast timescales (a few My to tens My), even at low temperatures (at least as low as 250 K). Besides affecting the ratio of the ice shell to rocky mantle thicknesses (by up to 100 km), aqueously altered rock has thermomechanical properties drastically different from anhydrous rock. For example, the thermal conductivity of heavily altered carbonaceous chondrite may be 1/10th to 1/3rd of the thermal conductivity of anhydrous rock (see Opeil et al., 2010, 2020) depending on temperature. The rock thermal conductivity determines not just the thermal evolution of the mantle but also the heat input to the base of the hydrosphere, which plays a role in the maintenance of a deep ocean. See Appendix D for more detail.

The starting density of hydrated CI chondrite refractory material prior to thermal metamorphism is about 3,060 kg/m³ (at 273 K and 1 bar). This number results from thermodynamic equilibrium of all the phases in CI chondrites. The evolution of the rock density as a function of pressure and temperatures is mapped over the range of conditions relevant to the Uranian moons (Figure 3). This density is calculated with the Gibbs energy minimization program Perple_X (Connolly, 2005, 2009) which computes the thermodynamically stable phase assemblage, including fluid composition (Connolly & Galvez, 2018; Galvez et al., 2015). In the case of a 100% CI chondrite composition, the representative phase assemblage consists of talc + antigorite + siderite + H₂O + pyrite or troilite + chlorite + ankerite + graphite ± magnetite ± dolomite at low temperature (region A in Figure 3). At moderately high temperatures (B), carbonates and antigorite are destabilized, yielding olivine + H₂O + amphibole + troilite + CO₂ + chlorite + graphite. Finally, amphiboles are dehydrated at high temperatures (C), yielding olivine + H₂O + troilite + orthopyroxene + CO₂ + anorthite + clinopyroxene + graphite.

Figure 3.

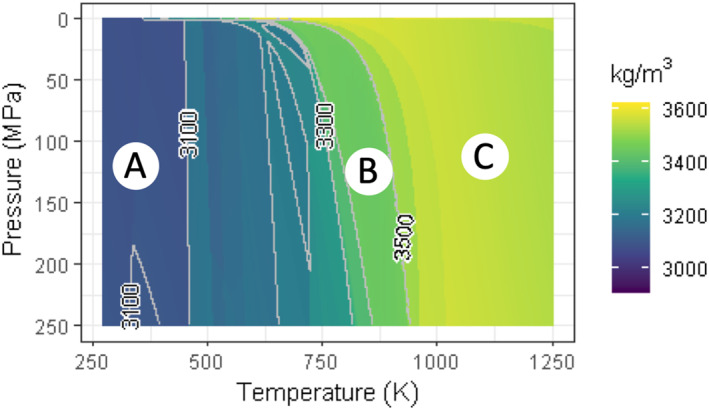
Density of the rock phase as a function of temperature and pressure for a CI chondrite composition (based on Palme et al. (2014)). See Table A1 for further details about the reference elemental composition. This chart covers the pressure and temperature domains relevant to the moons' rocky cores.

In the pressure‐temperature conditions expected in <1,000 km radius icy moons, insoluble organic matter (OM) is degraded into graphite at low temperature (<300 K, Melwani Daswani & Castillo‐Rogez, 2022). The fate of graphite is not well understood. It could potentially migrate from the rock with fluids also released from thermal metamorphism or it could remain trapped in the rocky cores. In the latter case, graphite's high thermal conductivity, 10–20 times that of rock (e.g., Pavlov et al., 2017), could accelerate the cooling of the core. Soluble OM that sunk with rock during differentiation would also degrade under low‐grade metamorphic conditions and release small‐chain molecules to the ocean (Melwani Daswani & Castillo‐Rogez, 2022). The fraction of OM that would eventually remain in the core has not been modeled in detail but should be considered in future work. In the case of Ceres, Melwani Daswani and Castillo‐Rogez (2022) found that the rocky interior would contain 1–3 wt.% of carbon at the end of metamorphism, if Ceres has a carbonaceous chondrite composition.

3.4. Heating From Tidal Dissipation Postrresonance

The tidal heating rate depends on a moon's orbital properties as well as its internal properties expressed in the form of the tidal Love number, k ₂, and dissipation factor, Q. Both parameters are dependent on the tidal forcing frequency, n = 2π/P, where P is the orbital period. The heating rate, time‐averaged over the spin‐synchronous body's orbit and averaged over its interior under the assumption of a small eccentricity and zero obliquity, can be estimated as W ≈ k ₂/Q 7e ² (3/2 G M _U ² n R ⁵/D ⁶) (e.g., Renaud et al., 2021), where G is the gravitational constant, M _U is the mass of Uranus, and other parameters are given in Table 1. It is important to note that all other things being equal, tidal heat production in the Uranian moons would be ∼50 times less than in the Saturnian moons due to Uranus' lower mass.

Because of the moons' limited long‐lived radioisotope budget, dramatic geological events may reflect increased tidal heating via resonance crossings. As discussed in Section 2.2, the most recent one is thought to be the Ariel:Umbriel 5:3 MMR, which Ćuk et al. (2020) have shown to influence the moon system on a global scale.Ćuk et al. (2020) modeled the evolution of the moons' orbital properties since they broke from their latest resonances (Table 1). We are not considering these events as part of our thermal evolution modeling because they require combining dynamical and thermal evolution, which is beyond the scope of this work. Outside dynamical resonances, the heating rate from the dissipation of solid tides is several orders of magnitude lower than that from radioisotope decay, depending on the moon (see also Chen et al., 2014).

We added to Table 1 the estimated power generated from obliquity‐driven tides in the moon oceans (assuming they hold large oceans at present) following Chen et al. (2014). This power source contributes at most a few MW in the case of Miranda and Oberon. Altogether, the combined energy produced by present‐day tidal dissipation is several orders of magnitude less than the integrated energy lost via conduction through the ice shell in the case of Miranda (∼0.002 GJ/s produced vs. 0.3 GJ/s lost for an average crustal Tc of 1 W/m/K).

We compute the tidal Love number and dissipation factor in order to compare the current state derived from our thermal models to the Ćuk et al. (2020) estimates. These parameters are computed for multilayered interior models for the moons derived from the thermal evolution models. We use the modeling approach described in Castillo‐Rogez et al. (2010) in which the material response to tidal forcing accounts for anelasticity via the Andrade rheology model (Andrade, 1910) fit by laboratory measurements. The Andrade model includes an anelastic component represented by an infinite number of dashpots in series in parallel with an infinite number of springs and represents a continuous distribution of compliances and thus relaxation times.

Because of the many uncertainties in the description of water ice's viscoelastic behavior, we do not explicitly vary temperatures and grain size but instead consider a range of relevant viscosities between ∼10¹⁴ Pa s (relevant for the water melting point) and ∼10²⁷ Pa s (relevant for <120 K). Hence, the viscosities derived from the inversion of available Q/k ₂ estimates do not provide direct constraints on the shell composition. Results are presented in Sections 5.2 and 5.3.

3.5. Ocean Composition

We model the composition of the ocean as a consequence of freezing using FREZCHEM (Marion et al., 2010) based on earlier work (Castillo‐Rogez et al., 2018). FREZCHEM produces the composition of precipitated solids (e.g., ice, gas hydrates, and salts) and residual liquid as a function of temperature and pressure. Liquid can remain at low temperature due to the presence of ammonia (peritectic at ∼176 K) and chlorides (eutectic at ∼220 K) in particular.

We start with the solution compositions investigated in Castillo‐Rogez, Melwani Daswani, Glein, et al. (2022) (hereafter referred to as CR22). The assumed fractions of [CO₂] = 1 to 5 wt.% and [NH₃] = 0.3 to 1 wt. are on the low end of abundances predicted in the literature and thus provides a lower bound on the influence of that compound on the persistence of liquid in the large Uranian moons. CR22 also show that the prospect for CO₂ to preferentially form carbonates is in part determined by the effective water‐to‐rock ratio, W/R (i.e., the mass of water that a unit mass of rock is exposed to during aqueous alteration). This parameter is not well constrained but the literature on icy moons and carbonaceous chondrite parent bodies has reported W/R values of the order of 0.5–4 (see CR22 for a review). Hence, we assume W/R = 1 as a reference for this study. A higher W/R in the aforementioned range would lead to an increase in salinity by up to a factor two (CR22, Figure 1). This would impact the evolution of ocean composition, in particular the ocean thickness for which certain species would reach saturation and precipitate, but not the overall results from this study. A more extensive analysis of the parameter space that covers alternative origins for Uranus and its moons is left for future work.

3.6. Electrical Conductivity

Our geochemical modeling approach uses the EC estimates from CR22 following the general empirical model embedded in the Geochemist's Workbench software (McCleskey et al., 2012). However, the applicability of that model is limited to dilute solutions (<1 mol/[kg H₂O]), and experimental data for more concentrated solutions are missing. CR22 show that [CO₂] ∼ 4 wt.% and [NH₃] ∼ 0.3 wt.% leads to a salinity >1 wt.% prior to any freezing. For a solution dominated by Na⁺, HCO₃ ⁻, NH₄ ⁺, Cl⁻, and CO₃ ²⁻, this corresponds to an EC of about 1.5 S/m at 0°C and 1 bar (McCleskey et al., 2012).

As shown below, our thermal models yield thin oceans with high salt concentrations. For example, in a residual layer about 30 km thick, we find that the solution has a Na⁺ and Cl⁻ salinity of 150 g/kg of water (∼2.5 mol/kg) for a starting salinity (i.e., prior to concentration) of 1.5 wt.%. There is no general formalism for describing the EC of hypersaline solutions. For high ionic strength (above 1 mol/kg), the McCleskey et al. method is not applicable. Instead, we rely on analogs and laboratory studies to constrain the EC of hypersaline solutions. Direct measurements of NaCl brine at 273 K for a concentration of 149 g/kg yield an EC of 10 S/m (Oldenborger, 2021). NaCl reaches saturation at about 357 g/kg (or ∼6 mol/kg) at 0°C. Extrapolation of the temperature dependence of NaCl solubility suggests only a slight increase of this value at subzero temperatures (e.g., about 10% increase from 273 to 233 K; Cong et al., 2019). Brines saturated in sodium chloride are common on Earth and have conductivities of about 23 S/m for a reference temperature of 298 K (e.g., Rebello et al., 2020).

However, aqueous solution ECs show a positive dependence on temperature (e.g., Pan et al., 2021; Smith, 1962). Hence, we use a temperature correction factor f _c (e.g., Smith, 1962) to derive the EC at a targeted temperature T ₀, σ _T0, from the EC measured at a reference temperature T _ref, σ _ref:

$${\sigma }_{T0}={\sigma }_{\mathrm{r}\mathrm{e}\mathrm{f}}\left[1+f_{\mathrm{c}}\left(T_0-T_{\mathrm{r}\mathrm{e}\mathrm{f}}\right)\right]$$ (1)

Correction factors found in the literature are largely consistent with each other and are of the order of 0.02/K (Oldenborger, 2021; Smith, 1962), independent of the composition. Hence, an EC of 23 S/m at 298 K scales down to an EC of ∼12 S/m at 273 K. Although in reality, the correction factor depends on concentration and varies with respect to temperature and concentration (e.g., Oldenborger, 2021), considering the many uncertainties in the composition of the ocean, we consider it a constant here (f _c = −0.02/K).

3.6.1. Brine‐Filled Porous Core Models

In the case of porosity in the rocky mantle (e.g., like in the case of Enceladus), the brine temperature may be above 373 K. Then, the EC of a chloride‐rich brine may be at least 50 S/m and potentially greater than 100 S/m (Ucok et al., 1980; Ussher et al., 2000). The EC of a mixture of this brine and the surrounding rock is computed with Archie's law. It defines the resistivity formation factor as follows:

$$F={\rho }_0/{\rho }_w$$ (2)

where ρ ₀ is the macroscopic resistivity (porous rock and brines) and ρ _w the resistivity of the pore fluid. The resistivity is the inverse of the conductivity. Hence, combined with Equation 1, the EC of a porous core filled with brine is as follows:

$${\sigma }_{T0}=1/{\rho }_0\left[1+f_{\mathrm{c}}\left(T_0-T_{\mathrm{r}\mathrm{e}\mathrm{f}}\right)\right]=F{\rho }_w\left[1+f_{\mathrm{c}}\left(T_0-T_{\mathrm{r}\mathrm{e}\mathrm{f}}\right)\right]$$ (3)

Experimental work by Archie (1942) led to the inference that F is proportional to the porosity Φ to an exponent m called the cementation index: F = Φ ^−m . The value of the cementation index depends on permeability and is a function of pore shape and tortuosity (e.g., Saner & Kissami, 2003). In an ideal situation where the flow of brines in the rock is unhindered, m tends toward 1. Values are generally found between 1.5 and 2.5 (Glover et al., 1997; Revil et al., 1998) and are about 2 for porous clays (Revil et al., 1998). The uncertainty in this parameter m results in a factor 5 uncertainty in the resistivity formation factor F for a porosity of 0.2 and a factor 3 uncertainty for a porosity of 0.4. Assuming ρ _w  = 1/50 Ω⋅m for a brine temperature of 373 K and Φ = 0.2, the conductivity of the brine rock mixture may range between 0.9 and 4 S/m. In the calculations, we assume the average value m = 2, which yields an EC of about 2 S/m. Considering these uncertainties (including also in Φ), these estimates are intended to support working models for the formulation of future investigations and should be refined with dedicated laboratory work.

3.6.2. Effect of Pressure

Pressure tends to increase EC by up to ∼10% at the pressures of tens of MPa that are relevant to the residual oceans considered in the Uranian moons (Bradshaw & Schleicher, 1980; Horne & Frysinger, 1963; Pan et al., 2021; Schmidt & Manning, 2017). However, we lack measurements specific to the carbonate‐rich compositions considered here. Overall, this effect is small because the pressures at the base of the moon shells are of the order of 40–70 MPa.

3.6.3. Effect of Organics

Some soluble organics can be charged and contribute to the EC, like for example, carboxylic acids (CR22). However, the abundance of these organics in solution is unknown. A 0.5 wt.% concentration of the carboxylic acid CH₃COOH yields an EC of 0.03 S/m while the acetate form Na⁺CH₃COO⁻ expressed in alkaline conditions is 0.39 S/m (at 25°C). This could prove important for bodies whose residual oceans concentrate organic compounds (e.g., Ceres; Melwani Daswani & Castillo‐Rogez, 2022).

4. Results of Thermal Modeling

We describe the results obtained for the moons' current thermal state (Section 4.1) and prospect for the preservation of liquid at present (Section 4.2). Examples of thermal evolution results are presented for Miranda, Ariel (which is also representative for Umbriel because the two bodies share similar physical properties), and Titania (which is also representative of Oberon) in Figures 4 and 5. First, we describe the findings of the thermal model. Then, we assess the properties of the oceans that may be present in some of the moons at present. Possible evolutionary pathways are summarized in Section 4.4. As an important note of caution, many uncertainties in the history of these bodies and material properties allow only bounds on possible outcomes.

Figure 4.

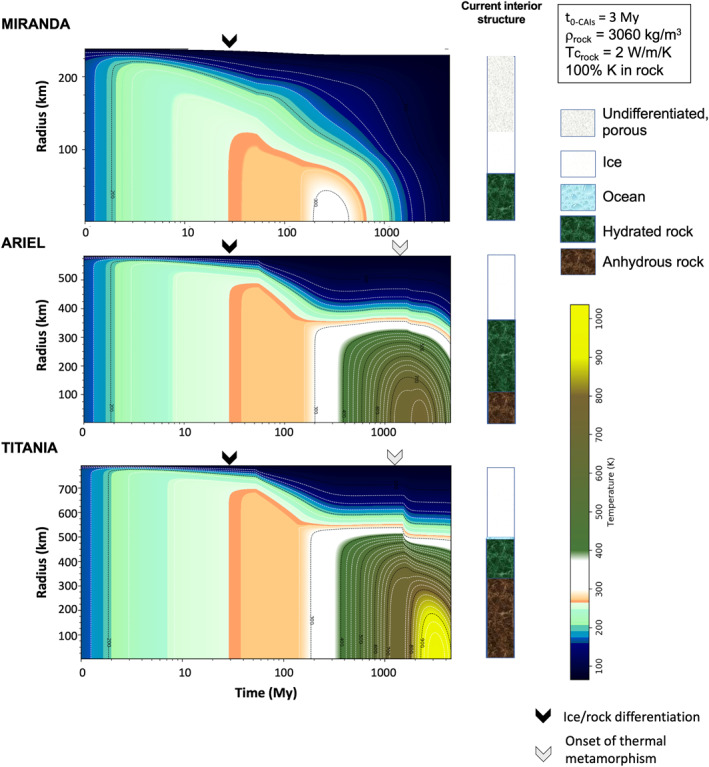
Examples of thermal evolution models for Miranda, Ariel, and Titania. Models assume a CI composition, a time of formation of 3 My after calcium aluminum‐rich inclusions, and a starting porosity of 40%. Miranda's interior mostly compacts but partially melts and differentiates. On the other hand, Ariel and Titania undergo near global melting of their volatile phase (assuming foundering of a thin undifferentiated shell) and differentiate a rocky core. The rocky core may undergo further differentiation as a consequence of thermal metamorphism in the case of Titania. The final interior structures outlined on the right assume current residual liquid is at the water freezing point. The Ariel and Titania thermal models are also representative of Umbriel and Oberon, respectively.

Figure 5.

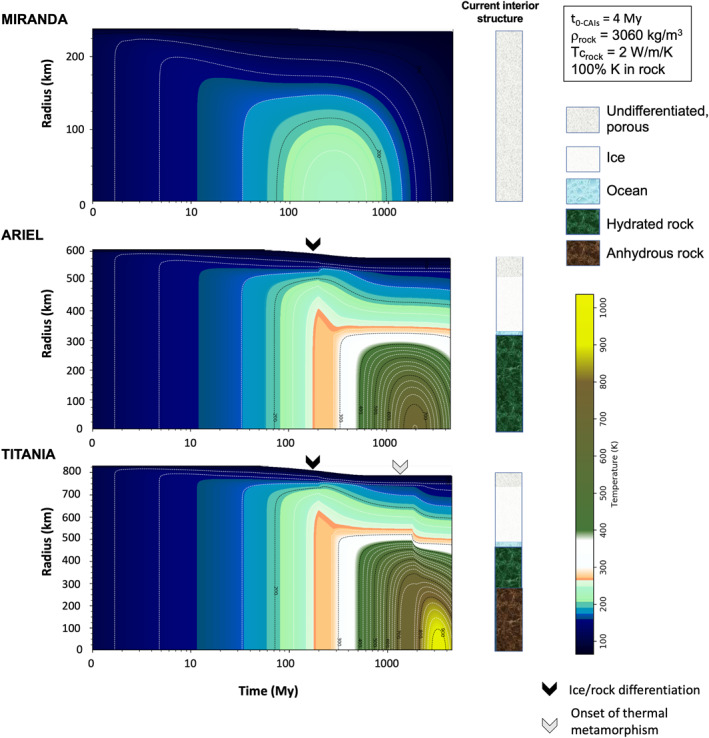
Same as Figure 4 for a time of formation of 4 My after calcium aluminum‐rich inclusions. Miranda's interior could not get warm enough for its interior to evolve, whereas Ariel's and Titania's ice could partially melt, leading to partial differentiation. The preservation of a porous lid on the latter moons enables the preservation of a ∼10–20 km liquid layer until present. Here, we represented the final interior structure assuming the water freezing temperature.

4.1. Extent of Internal Evolution

For bodies accreted in the CPD, presumably as a mixture of ices and rock, with some porosity, differentiation of an ice‐dominated shell and rocky core is not expected for all models. This end state requires sufficient heating to melt the ice phase on a global scale. This is realized for times of formation t _0‐CAIs < 4 My after CAIs for most of the moons (Figure 4). For t _0‐CAIs > 4 Ma, melting is partial and a thick porous, undifferentiated crust may overlay a solid icy mantle until present, of the order of 60 km in the case of Ariel and ∼80 km for Titania (Figure 5). With a density of about 1,000–1,050 kg/m³, these crusts are unlikely to founder, consistent with the Neumann et al. (2020) study of Kuiper belt objects.

Due to its lesser rock content, Miranda would have to form <3 My after CAIs, in order to differentiate a rocky core early on, which may not be consistent with the formation timeframe for the Uranian regular moon system. For later t _0‐CAIs, our models indicate partial or no melting of Miranda's ice and preservation of a large porosity fraction. If Miranda has differentiated a rocky core, as suggested by observations reported in Section 2, then it is likely the result of tidal heating, potentially during the event that formed Arden Corona (Beddingfield et al., 2015) and the thin lithosphere in that location (Pappalardo et al., 1997).

An additional event of differentiation may occur in some of the moons as a consequence of thermal metamorphism. In Titania and Oberon, part of the rocky core could reach the dehydration temperature of serpentine, at about 725 K, if the moons formed less than 5 My after CAIs and no K was leached from the rock early on. This would increase the density of the rock to above 3,100 kg/m³ and lead to a late release of liquid to the hydrosphere (see Section 4.2). In the case of Titania, Figure D3 shows the possible range of timing for metamorphism onset and fraction of impacted core as a function of the time of formation and other parameters. In the most favorable conditions (time of formation of 3 My after CAIs and no loss of K to the liquid phase during differentiation), up to 50 vol.% of Titania's core could be dehydrated in the first 2 Gy after formation. A late (>4 Gy) stage of rock dehydration is possible but would affect only the central 10 vol.% of the core. Whether that liquid could reach the base of the hydrosphere or would react again (e.g., rehydration) with the ambient material is uncertain. Some thermal metamorphism is also predicted in Ariel and Umbriel if their core conductivity is lower than 2 W/m/K, but that process is limited to a radius <150 km and thus the late release of liquid is minimal, assuming it could even upwell to the base of the hydrosphere.

Lastly, we find that the pressure and temperature conditions for differentiation of a metallic core are not met for any of the conditions explored in this study, which supports the assumption made by Hussmann et al. (2006).

The range of hydrosphere thicknesses over the space of possible rocky core densities is represented in Figure 6 for all the moons, assuming the mean values for the radii and densities in Table 1. The hydrosphere thicknesses are ∼200–220 km in the case of Ariel and Umbriel and ∼240 to ∼270 km in the case of Titania and Oberon.

Figure 6.

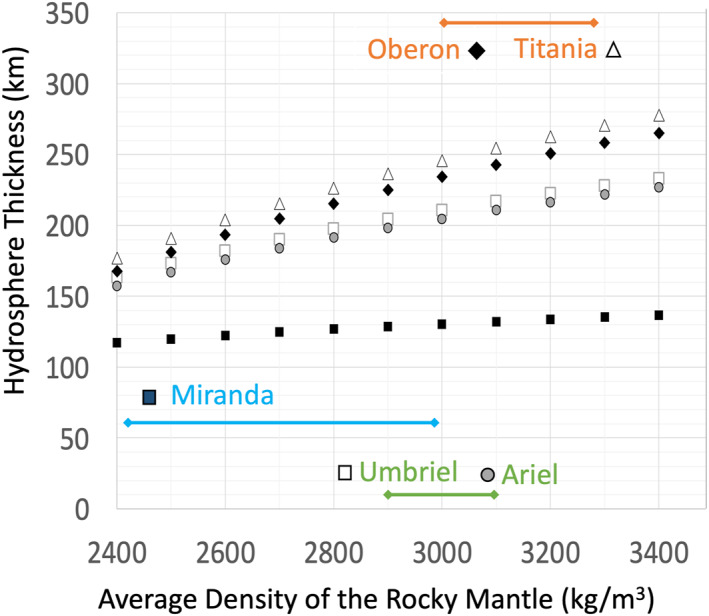
Interior structures of the large Uranian moons. Models assume a two‐layer interior, the mean bulk density values available in NASA's Solar System Dynamics website and a mean hydrosphere density of 1,000 kg/m³. The colored bars indicate the expected average densities for the rocky core based on thermal evolution modeling and the prospect for partial thermal metamorphism. A rock density greater than 3,400 kg/m³ is not expected in any of the moons.

The bars map the more likely rock densities based on thermal modeling (the higher the peak temperature reached, the more devolatilized the rock and the higher its density; see Figure 2). We note that the core temperature expected for Titania and Oberon corresponds to core densities of less than 3,200 kg/m³. This result differs from Bierson and Nimmo (2022) who assumed a rock density of 3,500 kg/m³, a dry rock value (similar to Io's mean value) that does not appear consistent with the origin and evolution of the moons' material.

Considering Miranda's small size, it is possible that the rock particles did not settle and form a compact core. Instead, the core could preserve Φ _p = 20%–30% as modeled in the case of carbonaceous chondrite parent bodies in the same size range (Bland & Travis, 2017) and per analogy with Enceladus (Neveu & Rhoden, 2019). Neumann and Kruse. (2019) and references therein show that Enceladus' core is likely stratified as a result of this compaction‐diagenesis‐heating process, with a porous outer layer less than 10 km thick over a compacted inner core.

However, a high porosity core is unlikely in the larger moons. The overburden pressure at the center of Titania (∼240 MPa) is one order of magnitude higher than at Enceladus. Compaction observations in pelagic environments show a drop in porosity from Φ _p ∼50% to <20% when the overburden pressure increases to 25 MPa. The porosity tends toward Φ _p ∼ 10% at pressures >150 MPa (e.g., Allen & Allen, 2005; Kim et al., 2018). At these porosities, permeability is very low, of the order of 10⁻²⁰ m² (e.g., Daigle & Screaton, 2015). This is at least five orders of magnitude less than the permeabilities considered by Choblet et al. (2017) in their modeling of hydrothermal circulation in Enceladus' core. In pelagic sediments, lithification starts at a lithostatic pressure of about 40 MPa, helped by cementation due to salt precipitation (e.g., Neveu et al., 2015; Obradors‐Prats et al., 2019). The pressure at the base of Titania's ice‐rich shell is at least 65 MPa. Hence, it is very unlikely that the core of Titania would contain significant porosity. Following compaction and cementation, hydrothermal circulation that could control the temperature in the core (e.g., Choblet et al., 2017) shuts down and conductive heat transfer takes over, driving compaction creep (Neumann and Kruse. 2019). A similar assessment applies to Ariel (∼45 MPa at the base of the shell).

In the case of Ceres, a bigger and denser body, Melwani Daswani and Castillo‐Rogez (2022) showed that Ceres' low core density could be attributed to porosity introduced as a consequence of the release of brines following dehydration. A similar situation could happen in Titania and Oberon, but the modeling of this process is left for future work.

4.2. Long‐Term Preservation of a Deep Ocean

For a time of formation about 3 My after that of CAIs (t _0‐CAIs), short‐lived radiogenic heating is high enough for Miranda's internal temperatures to reach the water melting point and for some ice‐rock differentiation to occur. However, the modeled interior entirely freezes by about 1 Gy after formation. Miranda is so small that outside of tidal resonances, it takes just a few tens of My for an ocean to freeze. The rest of this section focuses on the larger moons.

The shell thermal conductivity is the primary property determining the long‐term preservation of a deep ocean. Melting on a global scale leads to internal differentiation but also alters the properties of the shell via removal of porosity and second‐phase impurities, such as ammonia hydrates, that would otherwise act in decreasing the shell thermal conductivity. As noted above and in Appendix C, the formation of clathrate is not favored as CO₂ preferentially forms carbonates in the high‐pH (>9) environment fostered by the presence of NH₃. Hence, the models presented in Figures 4 and 5 assume pure water as an end‐member composition for the refrozen shell. A remnant outer layer of undifferentiated and porous material may be present depending on the extent of melting.

Liquid above the water freezing point can remain if the averaged shell thermal conductivity is less than 3 W/m/K (averaged). This is about a factor 2.5 lower than the value expected for a shell made of pure solid (nonporous) ice. This low T _c can be realized for a time of formation t _0‐CAIs > 4 My, leading to the retention of a thick porous layer on all the moons characterized (see Section 3). The second key parameter driving long‐term liquid preservation is the amount of heat coming out of the rocky mantle, which is a combination of the rock thermal conductivity, ≤2 W/m/K, and the amount of potassium removed from the rock as a consequence of leaching.

Figures 4 and 5 show that Ariel (Umbriel) cannot preserve a deep ocean until present, unless porosity slows down heat loss. On the other hand, Titania (Oberon) can preserve a few tens km thick ocean whether or not the crust contains a large fraction of porosity.

Below, we discuss additional factors that can help increase the amount of liquid preserved until present.

4.2.1. Additional Physical Processes Not Modeled

Two events can favor the prospect of a deep ocean at present: enhanced tidal heating through resonance crossing and a late phase of thermal metamorphism. Large‐scale ice melting due to tidal heating would result in removing porosity. In these conditions, a transient ocean in Ariel formed 1 Gy ago may cool to below the water eutectic in a few tens of My and below 250 K in ∼220 My. In the case of Titania, a tidally generated ocean would cool below the water eutectic in about 250 My and contribute little to increasing the fraction of liquid preserved at present. An important implication of this short freezing timescale is that the present occurrence of brines is disconnected from occurrence of tidal heating events in the past. The four large moons may end up with similar thin residual oceans at present even if Ariel and Umbriel were subject to strong tidal heating in the past.

The release of fluids from the rocky core as a result of thermal metamorphism (see Appendix D and Figure D3) could theoretically supply additional amount of liquid equivalent to a 10 km thick layer in the case of Titania and Oberon and 2–3 km in the case of Ariel and Umbriel but the transfer of that liquid from the core to the hydrosphere needs to be accurately modeled in future work.

4.2.2. Role of Composition

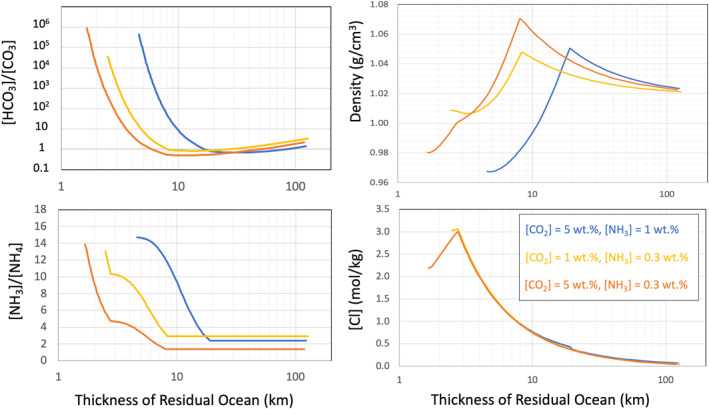
The concentrations of key ocean compounds as a function of ocean thickness are presented in Figure 7 for three examples of nonwater ice compositions. The three cases display the same evolution of the liquid composition: a relative increase in [NH₃] in residual liquid layers less than 20 km thick, whereas NH₃ and NH₄ ⁺ have about the same concentrations for thicker layers. Similarly, the concentration in HCO₃ ⁻ dominates over CO₃ ²⁻ in liquid layers a few tens of kilometers thick.

Figure 7.

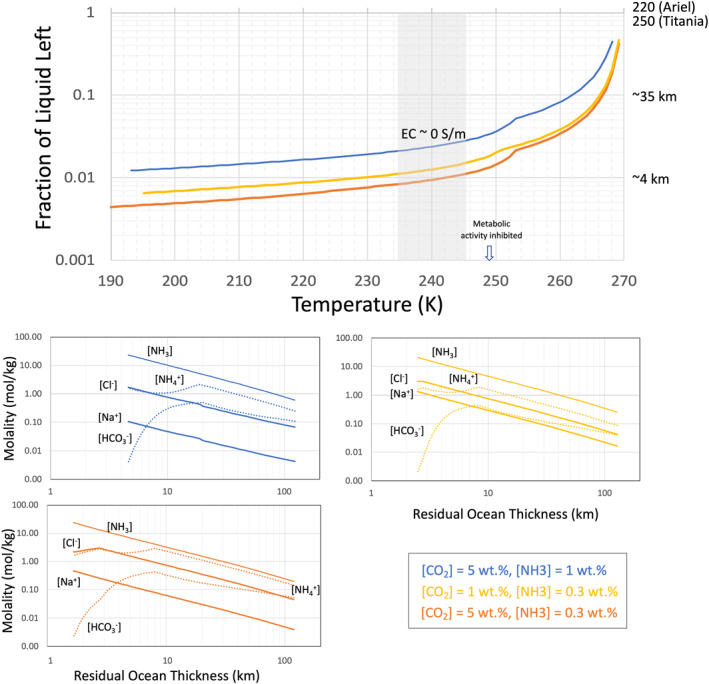
(Top) fraction of liquid left as a function of temperature for three different mixtures of water, ice, [CO₂], and [NH₃], and in presence of a CI chondrite rock composition. This chart highlights a temperature region for which the liquid electrical conductivity will be close to zero, making it potentially undetectable to a magnetometer and the temperature below which metabolic activity (for life as we know it) becomes inhibited. These aspects will be addressed in more detail in Section 6. (Bottom charts) Key species concentrating in residual oceans evolved from the featured volatile mixtures. The ocean thickness is computed for Ariel assuming a 220 km initial ocean layer and the W/R is assumed equal to 1. A W/R of 4 (see text) would result in shifting these curves by a few kilometers. The results are scalable to Titania and Oberon.

For the fractions of 0.3–1 wt.% of NH₃ accreted in our models, the residual ocean thickness at 180 K found in our model of Ariel (Figure 4) may be between 1 and 5 km for a reference hydrosphere thickness of 220 km (see Figure 6).

An ocean thickness of up to 80 km has been suggested for Titania assuming accretion of 3 wt.% NH₃ (Bierson & Nimmo, 2022). Although this concentration is theoretically possible (e.g., Mousis et al., 2002), NH₃ speciates into NH₄ ⁺, which is then removed from the system in the form of precipitated salts (NH₄Cl and NH₄HCO₃) at temperatures below ∼250 K. Depending on the ocean conditions, the residual fraction of NH₃ may be only ∼10%–50% of the accreted amount.

Chlorides can also play an antifreeze role and preserve residual liquid layers above 245 K. The thickness of these layers is still just a few to ∼10 km.

4.3. Summary

The possible evolution outcomes for the five moons derived from our models are presented in Figure 8. As these models assume radioisotope decay as the only heat source, they offer a baseline for formulating hypothesis about the moon internal properties that future missions can test. A departure from that basic heat source assumption can already be inferred from geological observations at Miranda and Ariel as discussed below.

Figure 8.

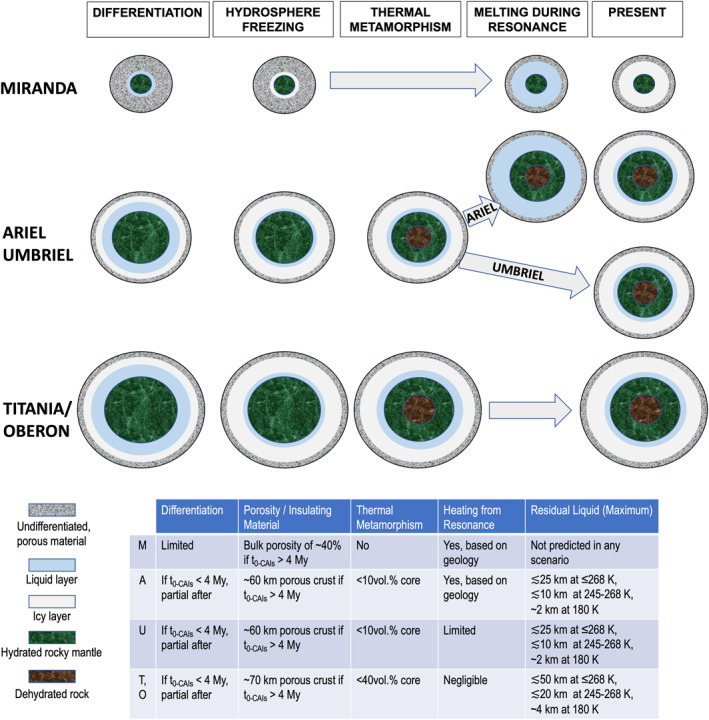
Stages of evolution and projected outcomes for the Uranian moons and prospects for liquid preservation in these bodies. Significant porosity may remain if the bodies formed later than 4 My after calcium aluminum‐rich inclusions and act as insulator. For Miranda and Ariel, porosity would likely be removed during intense heating generated during resonance crossing. We distinguish (1) residual oceans at a temperature greater than the water freezing point (268 K when accounting for pressure); (2) residual liquid at a temperature of 245 K where the electrical conductivity is significant; and (3) colder oceans kept liquid due to the presence of ammonia but which have near‐zero conductivity.

4.3.1. Miranda

Early differentiation in Miranda is unlikely if radioisotope decay is the only source acting in Miranda. As noted above, high heat flux estimated from geological observations indicates that significant tidal heating which was at play during resonance crossing could have triggered extensive melting and late differentiation of a rocky core. The prospect for liquid to remain at present depends on the timing of that resonance event. The error bar on the age of the youngest feature (0.1 (−0.1/+0.4) Ga, Kirchoff et al., 2022) allows for this possibility but needs to be refined by a future mission.

4.3.2. Ariel

The thermal evolution of Ariel is in large part determined by its time of formation. For t _0‐CAIs < 4 My, ²⁶Al decay heating was sufficient to trigger global melting, differentiation of a hydrated rocky core, and porosity closure. A later time of formation leads to partial interior melting and differentiation and the preservation of an undifferentiated porous crust tens of kilometers thick. In both cases, intense tidal heating during resonance crossing could result in at least partial melting of the volatile phase. Resurfacing observed on a near global scale might be evidence of such an event and likely involved the closure of crustal porosity, as suggested by the high heat flow recorded in the geology. As a result, resonance crossing could “reset” the structure of the hydrosphere. After breaking from resonance, crustal insulation would have been limited so that the preservation of liquid above the water freezing point primarily depends on the timing of the resonance. If the 5:3 Ariel‐Umbriel resonance happened about 1 Gy ago, as suggested by recent tidal evolution models (Stixrude et al., 2021), then it is unlikely that residual from that event still influences Ariel's state. The surface ages derived by Kirchoff et al. (2022) are around 1 Gy but with large error bars, so it is not possible to elaborate further. A late release of fluids as a consequence of thermal metamorphism is possible but limited in extent.

4.3.3. Umbriel

Umbriel's evolution is similar to Ariel, except for more limited tidal heating and no significant implications from resonance crossings, as also suggested by its older surface. As a result, the long‐term retention of porosity could help preserve ∼10–15 km of liquid until present.

4.3.4. Titania and Oberon

Like Ariel and Umbriel, formation in <4 My after CAIs would lead to global melting and differentiation of a rocky core. About 10 km of liquid above the water freezing point could remain at present. For a later time of formation, up to 80 km of undifferentiated, porous crust could be retained, helping preserve up to 30 km of liquid. A potential late contribution of fluids evolved from core metamorphism could add up to 10 km of liquid to the residual ocean.

5. Discussion

5.1. Assumptions on Origin and Composition

There are three formation models for the satellites presented in the literature: formation in the CPD, formation from a ring of ejecta from the giant planets, and late formation within a ring‐moon system.

A formation in the CPD is most likely to involve accretion of carbon‐based ices (Mousis et al., 2020). The most recent CPD model suggests that the moons formed toward the end of the CPD lifetime (Szulágyi et al., 2018). Except in the case of Miranda, if the moons formed less than about 3.5 My after CAIs, then they would be able to fully differentiate an ice‐enriched shell from a rocky interior. For longer times of formation, Titania and Oberon would keep a thick porous and undifferentiated crust that would help preserve deep liquid until present. This reinforces the prospect that Titania and Oberon are likely to host deep oceans at present.

Pebbles of cometary origin might enrich the volatile budget of the moons (Helled et al., 2020; Lambrechts et al., 2014). The addition of pebble material of cometary composition decreases the bulk content in radioisotopes. In particular, elemental measurements at 67P by the Rosetta mission (Table A1) report a factor five depletion in aluminum and factor three depletion in iron with respect to a CI composition (see references in Appendix A). Potassium appears to be depleted by a factor 2. Data for U and Th are missing but the abundances of these refractory elements are also expected to be lower than in CI material. On the other hand, a cometary component increases the carbon and nitrogen fraction of the mixture in the form of additional OM and volatiles such as CO₂ and NH₃. It was recently proposed that a large fraction of organics matter, up to 40 wt.%, could be responsible for the relatively low rocky mantle densities inferred for Titan and Ganymede (Néri et al., 2020). However, these models have not accounted for the thermal implications of OM's low thermal conductivity, up to one order of magnitude lower than rock's thermal conductivity (e.g., He et al., 2021; Zhu et al., 2019). As noted in Section 3.3, OM is likely to be converted to thermally conductive graphite at low temperature (<400 K) and/or break down into smaller molecules at higher temperatures (∼550 K) (see Melwani Daswani & Castillo‐Rogez, 2022, Figure 5). These temperatures are expected in Ariel, Umbriel, Titania, and Oberon (see Figures 4 and 5). Hence, the viability of models with large fractions of OM trapped in the mantle remains to be demonstrated.

Another formation model for Uranus' regular moons is their accretion from ejecta after Uranus encountered a large impactor that could also be responsible for its obliquity (Morbidelli et al., 2012; Salmon & Canup, 2022). Two important implications of this model are that (a) the moon material could contain a significant fraction of impactor material (Kegerreis et al., 2018); (b) also, Ida et al. (2020) predict that the temperature in the disk formed from ejecta could be >1,000 K and lead to a significant loss of water. We infer that more volatile species, like NH₃ and CO₂, could also be lost in the process, although this needs to be considered in greater detail. In these conditions, the moons' nonice volatiles might be depleted in comparison to a formation in the CPD.

Lastly, a ring origin for the moons suggested by Crida and Charnoz (2012) based on a similar scenario proposed for Saturn's moons (Charnoz et al., 2010) may have different long‐term outcomes depending on the composition of the rings. In this model, the moons would form from the accretion of ring ice on rock shards (i.e., already differentiated) and exit the rings with possibly high eccentricities and obliquities (Charnoz et al., 2010). These conditions could lead to significant tidal heating. This formation model might be particularly relevant to Miranda: it could explain the moon's low density compared to the other large moons and would produce an internal structure layered in a rocky mantle and an ice‐rich shell.

These scenarios are summarized in Table 2 with a qualitative assessment of their implications for various aspects of the moons' compositions and heat budgets. Some of these models are notional at this stage and end‐to‐end modeling from formation to the present remains to be performed. In particular, the early internal evolution of ring‐sourced moons exiting the rings has not been investigated.

Table 2.

Summary of Heat Sources and Insulating Material Available to the Large Uranian Moons Based on Their Origin

Origin	26Al decay heat	Carbon ices and ammonia	Clathrate formation	Tidal heating	Porosity
CPD at ∼19 AU				Depends on formation distance
Impact Ejecta				Depends on formation distance
Rings		Depends on ring progenitor	Depends on ring progenitor
Key	None/Unlikely	Some	Likely important	Major Source

Note. Objects accreted in the rings would form late but benefit from significant tidal heating in their early history whereas objects formed in the circumplanetary disk (CPD) might accrete early enough to benefit from short‐lived radioisotope decay. Nonwater ices such as CO₂ and NH₃ contribute to the formation of brines and can decrease the ocean freezing point. A formation from Uranus ejecta leads to a limited heat budget overall.

5.2. Constraints on the Past Tidal Heat Flows of Ariel and Miranda

We reexamine the heat flow of Ariel derived from flexure analysis in the context of our models. We compute the complex tidal Love number k ₂ for undifferentiated and differentiated interiors (see Section 3.5) with and without a deep ocean at present. We range the crustal thickness as well as the viscosity for the lower part of the crust below a 10‐km thick conductive shell. The dependence of Q/k ₂ on shell thickness and viscosity is presented in Figure 9. The k ₂ for oceanless interiors ranges from 3.8 × 10⁻³ (frozen) to 4.7 × 10⁻³ (warm). The upper bound matches the results from Hussmann et al. (2006). Values for k ₂ are found to be between 1.6 and 16.4 × 10⁻² when an ocean is present. The Q values range from 20 to 1,500 over the set of models. Figure 9 shows that the range of heat flow derived from geological analysis can be explained if a deep ocean is present and the shell viscosity was of the order of 10¹⁴ Pa s. This implies that the moon held an ocean at the time of a recent MMR, potentially the 5:3 MMR with Umbriel (Ćuk et al., 2020), or that enhanced tidal heating resulting from the increased eccentricity triggered melting and internal differentiation.

Figure 9.

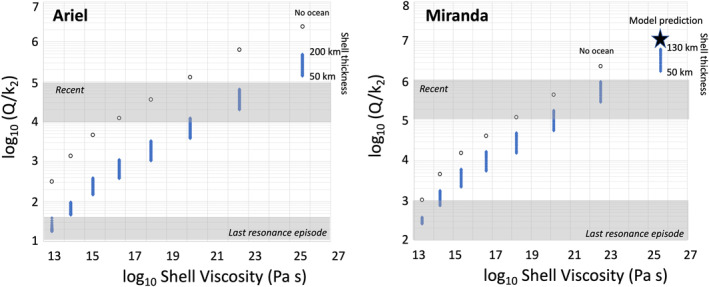
Q/k ₂ for three‐layer models of Ariel and Miranda (rocky core at 3,060 kg/m³, ocean, ice shell, and closed circles) and ocean‐less models (open circles) as a function of shell viscosity and thicknesses. The Q/k ₂ ranges estimated in the literature are presented in gray boxes; Ariel: Ćuk et al. (2020) for recent Q/k ₂; Peterson et al. (2015) for geology‐derived Q/k ₂; Miranda: Ćuk et al. (2020) for recent Q/k ₂ and Beddingfield et al. (2015) for geology‐derived Q/k ₂.

A similar analysis carried out for Miranda shows that the Q/k ₂ ∼10²–10³ suggested by Ćuk et al. (2020) at the time of the Ariel‐Umbriel 5:3 MMR also requires the presence of a deep ocean and warm shell (viscosity ∼10¹⁴ Pa s). This supports the Ćuk et al. (2020) suggestion that Miranda's ice melted during that phase and explains the high heat flow inferred by Beddingfield et al. (2015) from their investigation of Arden Corona.

5.3. Constraints on Interior Structures From Tidal Evolution Since Resonance

We assess whether our interior predictions could be consistent with the Q/k ₂ ranges estimated for each moon by Ćuk et al. (2020) (Table 1). These estimates are based on the extent of eccentricity decay since the moons evolved out of MMRs supposedly about 1 Ga based on the age inferred for Miranda's coronae and Ariel's surface (Kirchoff et al., 2022; Zahnle et al., 2003). As pointed out by Ćuk et al. (2020), resonance timing is highly dependent on Uranus' Q/k ₂, which may be frequency dependent (Fuller et al., 2016). Also, Q/k ₂ is averaged over the period of time since the moons broke out of their respective resonances. Hence, that parameter could have been smaller in the past and is higher at present. In practice, shortly after the moons left resonances, their eccentricities are expected to damp over <100 My (Ćuk et al., 2020), yielding a drop in tidal heating and leading to internal freezing until eccentricity decay became very slow. Hence, the Q/k ₂ inferred by Ćuk et al. (2020) for an evolution timescale of 1 Gy are representative of the moons' current states. Since the moon's geological activity is likely triggered by enhanced tidal heating, refined constraints on resonance timing may be obtained through future geological observations (e.g., crater‐based dating) using the most recent impact flux models.

Q/k ₂ are presented for three‐layer models (rocky core, ocean, and ice shell) as a function of ice shell thickness and ice shell viscosity. The shell thickness determines the volume of material that may be dissipating, depending on viscosity. Thin shells are prone to high deformation as a consequence of tidal forcing but may host little tidal dissipation. Thicker shells may deform less but offer a greater dissipative volume depending on viscosity. As a result, all results show that for three‐layer models, Q/k ₂ varies by only one order of magnitude over the range of shell thicknesses determined for each moon. We also show results for models without a liquid layer. The latter results were vetted against the results from Hussmann et al. (2006).

The Ćuk et al. study is not exhaustive and other interpretations for Q/k ₂ are possible. For example, simulations of coupled thermal‐orbital evolution with the model of Neveu and Rhoden (2019) yield present‐day values of Q/k ₂ of order 10³ for Titania and Oberon with an ice shell surrounding a rocky core with 25 vol.% warm ice (175–270 K) and 10³–10⁵ for Ariel and Umbriel in which part of the water in the core is liquid. These values are similar to the estimates of Ćuk et al. (2020). For both those models and for the Q/k ₂ estimates presented in this section, obliquity‐driven tides are not accounted for.

5.3.1. Miranda

Ćuk et al. (2020) find a Q/k ₂ between 10⁵ and 10⁶ for Miranda. As shown in Figure 9, a deep ocean cannot be ruled out but the shell viscosity has to be greater than 10²¹ Pa s. In the absence of an ocean, k ₂ ∼ 1.9 × 10⁻³ and therefore the dissipation factor is between 50 and 500, which allows for a warmer shell of up to ∼210 K. We plotted (star) the Q/k ₂ corresponding to the current state predicted by our models (see Figures 4 and 5). It is greater than the Ćuk et al. estimate by one order of magnitude. This could imply that Miranda is warmer than predicted by our models or could reflect the various uncertainties in this study (tidal heating not accounted for) and the Ćuk et al. analysis (e.g., constant k ₂/Q for Uranus).

5.3.2. Ariel and Umbriel

For Ariel, Ćuk et al. (2020) infer Q/k ₂ between 10⁴ and 10⁵, assuming the moon broke from resonance with Umbriel about 1 Gya. Figure 9 shows that this range can be explained by a high‐viscosity shell (>3 × 10²² Pa s) corresponding to a temperature <150 K. The presence of an ocean a few tens of kilometers thick is consistent with these estimated values of Q/k ₂. An alternative interpretation has no ocean but a warm shell (Q of ∼20–200 corresponding to a viscosity <2 × 10¹⁵ Pa s). For this kind of viscosity, an ice shell would be convecting and could lead to rapid freezing, hence this kind of model may not be sustainable over long timescales.

The same reasoning applies to Umbriel (same Q/k ₂ derived by Ćuk et al. as for Ariel). The moon's large eccentricity (three times that of Ariel) indicates low tidal heating and is commensurate with Umbriel's greater orbital distance with respect to Ariel.

5.3.3. Titania

Ćuk et al. (2020) pointed out that the constraint of Q/k ₂ < 10³ inferred from its dynamical evolution to explain Titania's current eccentricity suggests the presence of a deep ocean (Figure 10). In absence of a deep ocean, Titania's k ₂ is ∼0.004, leading to Q < 4. This would correspond to a shell viscosity of 3 × 10¹³ Pa s that is difficult to reconcile with thermal evolution models, Titania's tidal dissipation state, and its surface geology. On the other hand, the presence of a deep ocean increases k ₂ by one order of magnitude with respect to an ocean‐less model while yielding Q values that are more consistent with the thermal evolution models reported in this study. For example, the model of Titania presented in Figure 4 has a k ₂ ∼ 0.24 and Q ∼ 140 or Q/k ₂ ∼ 600.

Figure 10.

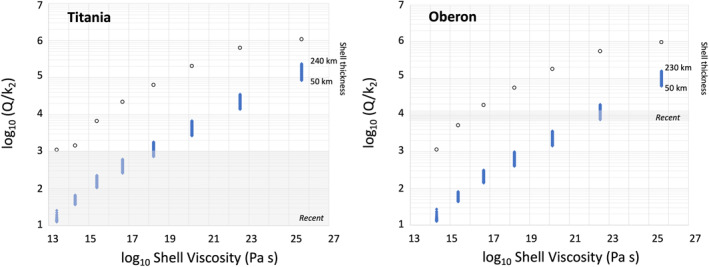
Same as Figure 9 but for Titania and Oberon. In the case of Titania, the low Q/k ₂ derived by Ćuk et al. (2020) strongly suggests the presence of a deep ocean.

5.3.4. Oberon

Similar reasoning applies to Oberon, for Q/k ₂ ∼ 10⁴ inferred by Ćuk et al. (2020). A residual ocean in Oberon is as likely as in Titania considering their shared physical properties. However, a difference of one order of magnitude between the Q/k ₂ values for Oberon and Titania translates into a greater viscosity (order 10²¹–10²² Pa s). Ocean‐less models of Oberon's interior can match Q/k ₂ ∼ 10⁴ if the average shell viscosity is about 5 × 10¹⁵–5 × 10¹⁶ Pa s. A warm shell at present is unlikely due to the limited heat production from long‐lived radioisotopes and tidal heating corresponding to Q/k ₂ ∼ 10⁴ is <<1 MW.

6. Observables for Future Mission

We discuss observations that may be carried out by a future spacecraft mission to investigate the extent of differentiation of the Uranian moons and search for deep oceans in these bodies. We focus on geophysical observations but also discuss possible compositional observations.

6.1. Interior Structure From Gravity and Shape Observations

The extent of differentiation can be inferred from the polar moment of inertia, C, via measurements of the triaxial shape and degree‐two gravity coefficients under the assumption of hydrostatic equilibrium. It is important to note that the current uncertainties on the GM and mean radii for all the moons are large. The results presented below assume mean values for these parameters. Refining them should be a top priority of a future mission, as recommended by the UOP mission (NASEM, 2022).

To estimate degree‐2 gravity and shape parameters, we assume the bodies are relaxed to hydrostatic equilibrium. This allows the use of the Radau‐Darwin approximation (e.g., Zharkov et al., 1985). Under this assumption, gravity and shape are determined by the rotation parameter (q = ω ² R ³/GM) and orbital properties. Then, the three shape radii are computed with

$$\begin{array}{c}a=R(1+7/6q)\left(k_{\mathrm{s}}+1\right)\\ b=R(1-1/3q)\left(k_{\mathrm{s}}+1\right)\\ c=R(1-5/6q)\left(k_{\mathrm{s}}+1\right)\end{array}$$ (4)

and

$$\begin{array}{c}{J}_2=5/6q{k}_{\mathrm{s}}\\ C_{22}=1/4q{k}_{\mathrm{s}}\end{array}$$ (5)

where k _s is the secular tidal Love number related to the normalized moment of inertia via

$$k_{\mathrm{s}}=(4-X)/(1+X)$$ (6)

$$\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}X={\left[-5/2\left(3/2\times C/M{R}^2-1\right)\right]}^2$$ (7)

We use the normalized moment of inertia C/MR ² where M is the mass of the moon. The relationship between C/MR ² and interior structure properties are presented in Figure 11 for two‐layer models with a rocky core and hydrosphere (which encompasses an ocean if present and icy shell). Due to limited constraints on layer properties, a single value of C/MR ² corresponds to a broad range of interior structures. In particular, the unknown shell density, which is determined by the relative fractions of porous undifferentiated material and water ice, introduces degeneracies when interpreting C/MR ² in terms of interior structure. Hence, a precision of ±0.005 on C/MR ² leads to a precision on the hydrosphere thickness no better than ±50 km for all the moons but Miranda. In the latter case, a precision of ±0.005 on C/MR ² narrows the uncertainties on the hydrosphere density to <50 kg/m³ and thickness to ±15 km.

Figure 11.

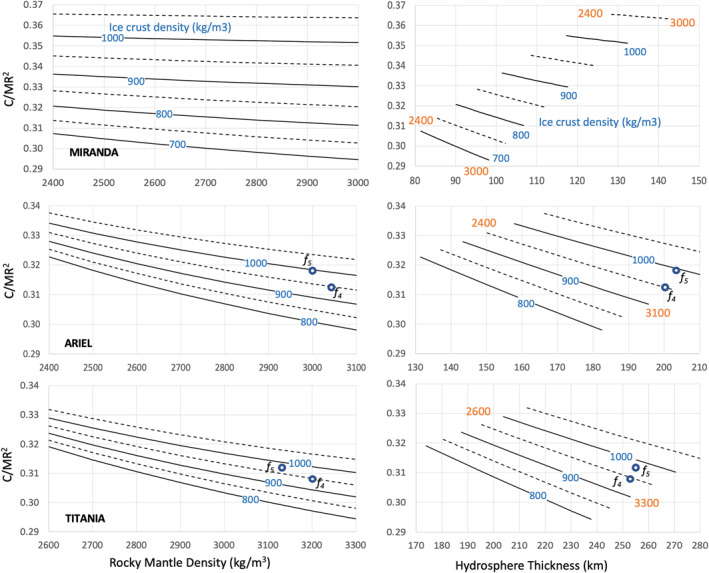
Estimates of the normalized polar moment of inertia C/MR ² as a function of the rocky core density, hydrosphere thickness, and hydrosphere density for two‐layer model of Miranda, Ariel (also a proxy for Umbriel), and Titania (proxy for Oberon). Due to Miranda's low bulk density, the C/MR ² is primarily influenced by the hydrosphere density, while that parameter is primarily driven by core properties in the other cases. The circle points to specific examples represented in Figures 4 (f ₄) and 5 (f ₅). This figure covers a wide range of crust density, including highly porous and undifferentiated material (<900 kg/m³) like in the case of Miranda (Figure 5).

The dependence of the degree‐two longitudinal gravity coefficient, C ₂₂, and the difference between equatorial and polar radii (a–c) on rock density and mean density are presented in Figure 12 for all the moons and the parametric space covered in Figure 11. J ₂ can be inferred from C ₂₂ under the assumption of hydrostatic equilibrium, J ₂ = 10/3 C ₂₂. These parameters are also estimated for uniform interiors (circles on right axes). Testing if the moons are differentiated or undifferentiated using shape data requires measuring (a–c) with a precision better than 1.15 km in the case of Miranda and Ariel, 0.44 km for Umbriel, 0.13 km for Titania, and 0.05 km for Oberon. The latter case corresponds to measurement requirements on each shape axes of better than 20 m.

Figure 12.

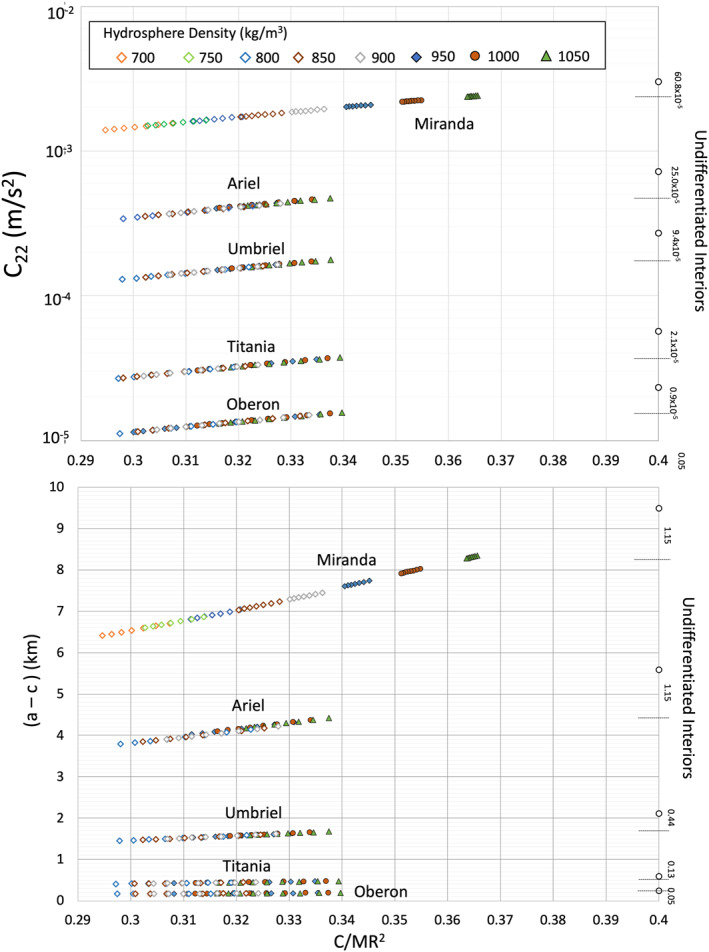
Estimates of the moon's (a–c) and degree‐two gravity coefficient C ₂₂ under assumption of hydrostatic equilibrium for the two‐layer models presented in Figure 11 and for uniform interiors (open circles on right). Numbers on the right‐hand side represent the separation between uniform models and differentiated models in m/s² for C ₂₂ and km for (a–c).

Seeking information on the extent of differentiation sets even tighter constraints. A ±0.005 requirement on the determination C/MR ² translates into a measurement requirement on (a–c) of about ±0.060 m. Achieving this level of accuracy from imaging would levy stringent requirements on the camera performance and flyby parameters (e.g., distance) for a future Uranus tour concept to consider.

Additional constraint on internal structure can also be sought in the degree‐two gravity harmonics. Figure 12 shows that distinguishing between a differentiated and undifferentiated interior requires a precision on C ₂₂ better than 6 × 10⁻⁴ m/s² at Miranda and 9 × 10⁻⁶ m/s² at Oberon (or 60 and 0.7 mgal, respectively).

We note that the tidal responses of the moons have low amplitudes. The tidal deformation of Ariel has a maximum amplitude of ∼0.3 m (equator) if the moon hosts a deep ocean (see Section 5). It is of the order of 0.02 m at Miranda and ∼0.1 m at the other moons. The values of the periodic component of C ₂₂ due to tides are 4–5 orders of magnitude smaller than the static values reported in this study. These measurements would be challenging for a multi‐flyby missions, so we do not provide a detailed analysis of periodic amplitudes as a function of interior structure.

Acquiring shape data and degree‐two gravity harmonics can lead to independent estimations of C/MR ² and to detection and quantification of nonhydrostatic anomalies. Departure from hydrostatic equilibrium has been frequently found at bodies in the <1,500 km size class. Nonhydrostatic anomalies can take the form of a frozen, fossil shape (e.g., Iapetus (Castillo‐Rogez et al., 2007)) or a core shape anomaly (as found at Enceladus (McKinnon, 2013)); sometimes, no explanation can be found (e.g., Ceres (Park et al., 2016) or Rhea (Tortora et al., 2016 and references therein)). Dynamic equilibrium can also create departures from hydrostaticity (e.g., for Enceladus, Čadek et al., 2019). Hence, gathering both gravity and shape information on the global properties of the moons can increase the level of confidence in the determination of their internal structures.

6.2. Detectability of Liquid Layers by Magnetic Induction

6.2.1. Ocean Electrical Conductivity

We distinguish the cases when the ocean temperature is at the water freezing temperature (hereafter referred to as “warm” ocean) and colder oceans sustained by the eutectic/peritectic of antifreeze solutes, in particular NH₃ and chlorides.

For the “warm” ocean cases, the residual ocean is dominated by NH₄ ⁺, Cl⁻, CO₃ ²⁻, HCO₃ ⁻, as well as other cations (in particular Na⁺ and K⁺) (Figure 13). The presence of bi/carbonates and ammonium ions increases EC beyond the contribution of major elements leached from rock (CR22). The ionic strengths of the solutions are between 0.8 and 1.5 mol/kg, hence approaching or exceeding the applicability limit of the McCleskey et al. (2012) model. Analog solutions observed at a soda lake such as Mono Lake (Jellison et al., 1999) indicate an EC of the order of 8 S/m at 298 K or ∼4.5 S/m at 273 K. This is only a rough estimate and experimental measurements of relevant solutions are needed in order to provide support to future missions.

Figure 13.

(Relative) concentrations of key species driving the electrical conductivity of residual oceans in Uranus' large moons (see also Figure 7). Besides NH₃, residual oceans are dominated by sodium chloride and sodium bicarbonate. The corresponding range of density is presented in the upper right panel. The W/R is assumed equal to 1. A W/R of 4 (see text) would result in shifting these curves by a few kilometers.

Oceans at a temperature greater than 245 K are of greater interest in this study because there is a concern that the ocean EC could tend toward zero at cold temperatures (see above). Also the habitability potential of these oceans is of interest at these warmer temperatures (e.g., Clarke, 2014).

The concentration of Cl⁻ steadily increases in a thinning ocean. As a result, the ocean density increases with its decreasing thickness up to 1,040–1,060 kg/m³, then decreases as ammonium bicarbonate (NH₄HCO₃) precipitates; this leads to residual liquid enriched in ammonia, whose density tends toward 0.980 kg/m³. Sulfates are not produced in these conditions as sulfur is preferentially reduced (i.e., in the form of sulfides) (see CR22 and Melwani Daswani & Castillo‐Rogez, 2022).

For residual layers below the water freezing temperature, the temperature could be theoretically as low as 176 K, the water‐ammonia peritectic (our FREZCHEM simulations stop converging at about 185 K). At that point, the residual layer thickness is between 1 and 3 km. EC data are lacking for cold‐temperature brines. Assuming that the temperature correction coefficient of ∼−0.02/K is applicable at temperatures below 255 K (see Section 3.7), the EC of chloride‐rich solution would tend toward 0 S/m around 245 K or a thickness between 3 and 10 km. Below ∼245 K, a brine layer may be present without exhibiting an induced field signature. Other solutes could contribute to increasing the conductivity but low‐temperature EC measurements are missing for compositions with a large fraction of HCO₃ ⁻ and Na⁺. We use EC estimates introduced in Section 3.6.

6.2.2. Detection of Induced Field

The presence of salty bodies of liquid water on the major moons can be inferred from measurements of its inductive response to the time‐varying Uranian magnetospheric field (Arridge & Eggington, 2021; Cochrane et al., 2021; Weiss et al., 2021). In particular, it has been found that the synodic frequency of the Uranian field at each of the major moons (as well as the second and third harmonics at Miranda and second harmonic at Ariel) would generate time‐varying electrical currents whose maximum induced surface magnetic field amplitude should exceed the sensitivity of typical spacecraft fluxgate magnetometers (∼1 nT) assuming that the moons are perfect conductors.

More generally, here we consider 2‐ and 3‐layer models like those in Section 3 in which either a porous conducting core is overlain by a nonconducting ice shell or a nonconducting core is overlain by a conducting relict ocean in turn overlain by a nonconducting ice shell. In particular, it has been previously shown that if Ariel contains either a 30‐km‐thick relict ocean with conductivity of 15 S m⁻¹ or a porous, briny core with conductivity of 2 S m⁻¹, it should generate a detectable induced surface field (Weiss et al., 2021).

We expand the analysis of Weiss et al. (2021) by calculating the induction field for relict ocean and porous core models for all five major moons (Table 3). Following their approach, we calculate the time‐varying field at each moon using the AH5 internal hexadecapole field model for Uranus in 1987 (Herbert, 2009). This provides a good approximation for the actual field experienced by the innermost three moons (Miranda, Ariel, and Umbriel) but only a first‐order estimate of the field experienced by the outer moons Titania and Oberon, which are likely more affected by diurnal and seasonal effects associated with the interaction of the solar wind with the Uranian magnetosphere. For a more detailed study of the induction responses of the latter moons, we refer the reader to Arridge and Eggington (2021). Additionally we adopt more realistic assumptions for the briny core scenario. We reduce the conductivity to 1 S m⁻¹ and limit the porous, conducting region of the core to an outer layer for all the moons apart from Miranda (see discussion in Section 4.1).

Table 3.

Reference Interior Structures Used for the Induced Field Models Presented in Figure 14

Moon	#1—Relict ocean model Assumes solid rocky mantle Ocean conductivity, EC = 15 S m−1		#2—Briny core model Assumes no ocean but pore liquid in the rocky mantle Briny rock conductivity, EC = 1 S m−1		#3—Core model with porous layer Assumes no ocean but pore liquid in the upper part of the rocky mantle Briny rock conductivity, EC = 1 S m−1
	Ice thickness, d (km)	Ocean thickness, h (km)	Ice thickness, d (km)	Porous rock thickness, h (km)	Ice thickness, d (km)	Thickness of porous rock layer on top of solid rock, h (km)
Miranda	121	20	126	110	126	110
Ariel	184	30	150	429	174	50
Umbriel	201	20	156	429	200	50
Titania	222	30	169	619	254	30
Oberon	209	30	160	601	241	30

Note. Note that for Miranda, the reference interior model is not an outcome from the modeling presented in Section 4. It assumes that Miranda differentiated, possibly due to a recent phase of intense tidal heating, and it still contains liquid at present.

We find that the maximum induced field amplitude for the thickest relict oceans (e.g., 20–30 km) as well as the porous core structures should be detectable (≳1 nT) during a nominal 100‐km altitude spacecraft flyby with two exceptions. In the briny core scenario, the induced fields 100 km from Miranda and Oberon are <1 nT, owing to Miranda's small size and the weak driving field at Oberon. Signals from the porous cores are weaker than those of the relict oceans due to the cores' 15 times lower EC. This effect overwhelms the positive contribution from the 1.7–5 times larger conducting layer thickness h at Miranda, Ariel, and Umbriel. This tradeoff between ocean conductivity and thickness illustrates the nonunique nature of the induction response. Each contour in Figure 14 represents a family of internal structures, with different ocean thicknesses and conductivities, producing the same induction amplitude or phase. When the driving magnetic field has oscillations at multiple frequencies, measuring the induced response at each frequency may break this degeneracy. This may be possible at Miranda and Ariel, where the magnetic oscillation at the second harmonic of the synodic frequency is significant. Additionally, measuring the phase delay of the induced response with respect to the driving field can aid characterization, including at the outer moons where only one frequency is available for magnetic sounding. In conjunction with restrictions on the range of plausible interiors from gravity, shape, and compositional measurements it may be possible to broadly characterize a subsurface ocean with a limited number of flybys (e.g., Weiss et al., 2021).

Figure 14.

Induced fields at the synodic frequencies of the major moons. (a, c, e, g, and i) Amplitude and (b, d, f, h, and j) phase for various frequencies of the induced field at the surface induction pole for each moon. The ocean thickness represented on the y‐axis refers to ocean layers (models #1) or brine‐filled rock (models #2 and 3). Solid and dashed curves denote models with two different ice shell thicknesses that span the full range sampled by the relict ocean, briny core, and core with porous layer models (#1, #2, and #3 in Table 3). Shown are the inductive responses to the first (red), second (blue) and third (green) harmonics of the synodic frequency. Numerical values of contours correspond to labeled values on colorbars. The contours are 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90%, and 95% of the response of a perfect conductor the size of each moon. Three icons denote briny core, relict ocean, and core with porous layer as shown in legend and Table 3. (a, b) Miranda, (c, d) Ariel, (e, f) Umbriel, (g, h) Titania, and (i, j) Oberon. Calculated using Uranus AH5 internal magnetic field model of Herbert (2009) for the year 1986. The actual inductive responses of Oberon and Titania may differ from what is calculated here due to the effects of the solar wind and its dependence on diurnal and seasonal variations.

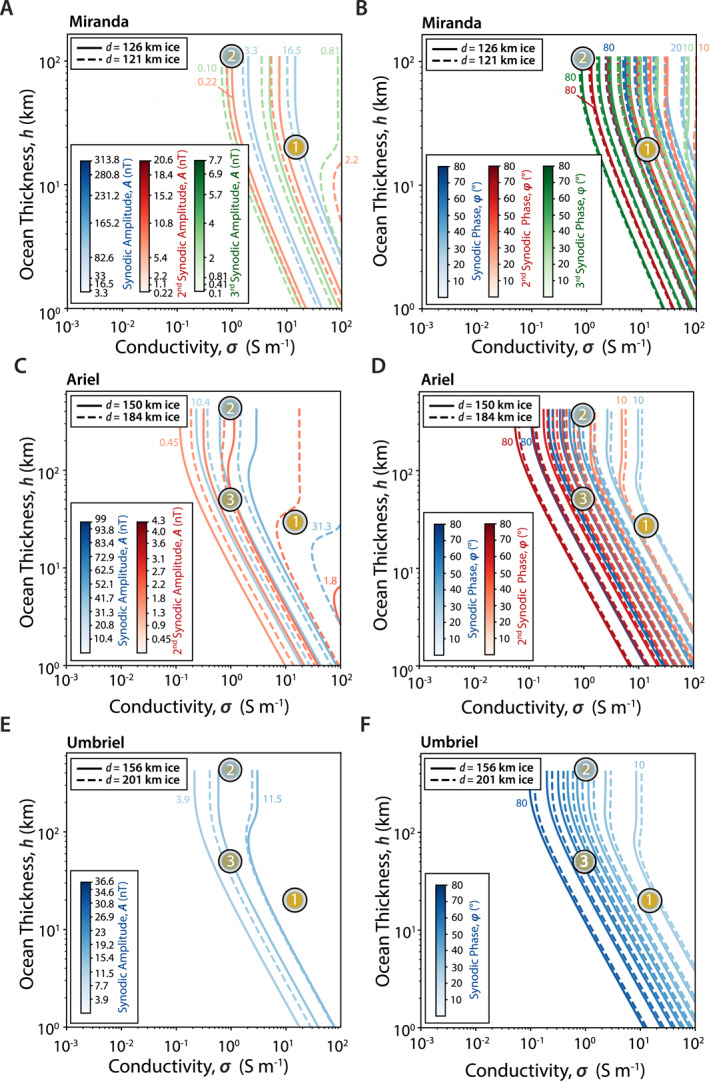
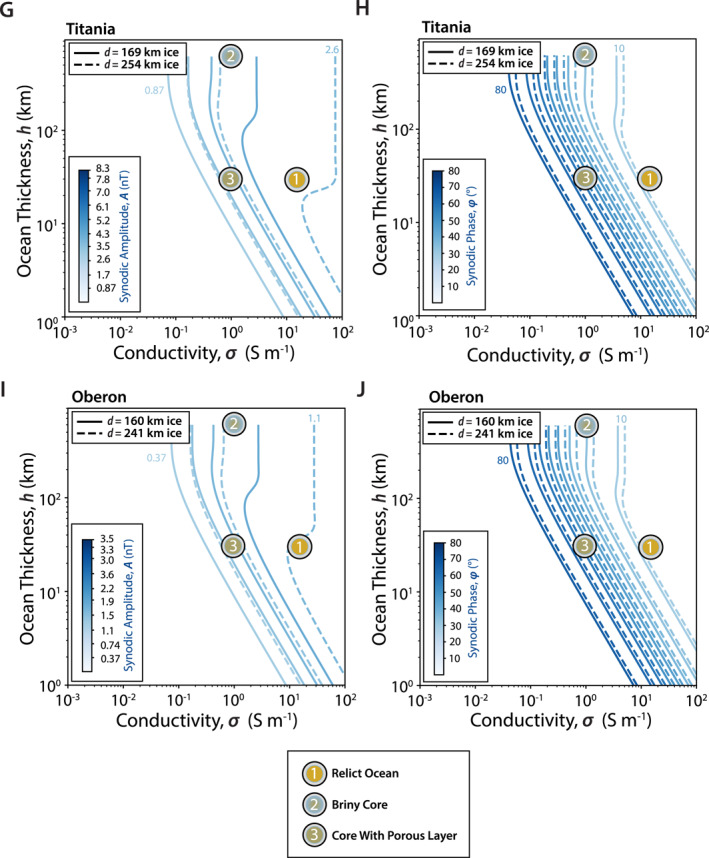
The nondetection of an induced field at a moon would not necessarily exclude the presence of liquid. The conducting layer in either the relict ocean or porous core scenarios could be thinner than what is assumed here, reducing the induction response (Figure 15). Additionally, the liquid temperature could also be significantly below the water freezing temperature, such that the EC would be much lower than the assumptions used here, to the point that a deep ocean might not be detectable at all.

Figure 15.

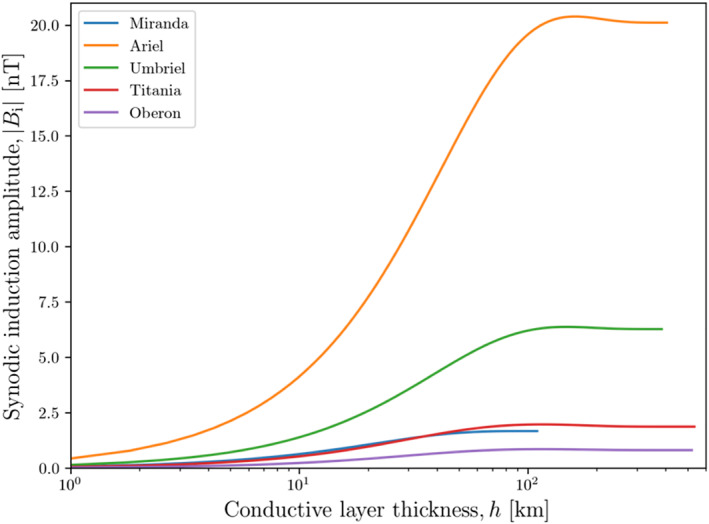
Maximum amplitude of the induced response to the synodic driving field at the surfaces of the major moons as function of the thickness of the porous, conducting layer in the moon's core. Each moon has a nonconducting ice shell with thickness defined for model #3 in Table 3.

6.3. Exposure of Deep Interior Material

If deep oceans are present in the large Uranian moons at present, then they are likely thin (tens of kilometers) layers below a thick shell (>100 km in Miranda and >200 km in the other moons). As noted in the introduction, the reports of NH₃‐ or NH₄ ⁺‐rich deposits found at Miranda and Ariel may imply recent exposure. Per the ocean composition models presented in Section 4.3, a few to tens of km thick liquid layers may be enriched in NH₃ and thus relatively buoyant with respect to an icy crust (Figure 7), especially if they contain dissolved gas. This system may be under pressure as a consequence of advanced freezing of the hydrosphere, as suggested for Ceres (Neveu & Desch, 2015). In these conditions, NH₃‐based cryovolcanism is a possibility, as suggested earlier by Kargel (1991), although the actual mechanism for establishing communication between the surface and liquid at >150 km depth remains to be investigated. The current basal heat flow at Ariel's crust is of the order of 1 mW/m² and might be too low to drive convection. Furthermore, if Ariel's crust is convecting, then it is most likely in the stagnant lid regime (Stern et al., 2018). This applies to the other Uranian moons as well.

Transfer of deep ocean material via fractures (e.g., induced by impacts) or tectonic activity (e.g., extensional faulting) is another possibility, although porosity would close as a result of compaction creep at temperatures above ∼170 K, several tens of kilometers above the interface between the ice shell and the deep ocean. Alternative emplacement mechanisms may include impacts (excavation and ejecta) or mass wasting of oceanic material captured in the crust upon freezing. Heating produced by large impacts could drive the formation of shallow melt ponds that froze on a ∼1 My timescale (e.g., Bowling et al., 2019) and create localized concentration of salts trapped in the shell. Lastly, the features observed by Cartwright et al. (2020) in the 2.18 and 2.24 micron range could also result from the irradiation of NH₃/CO₂/H₂O/etc. substrates.

Spatially resolved reflectance spectra collected over Ariel could look for spatial associations between NH₃/NH₄ and specific geologic features. Exposure via impacts would imply higher concentration of that material in fresher craters, similar to Charon (e.g., Grundy et al., 2016). Deeper sourcing from a residual ocean via fractures would lead to an association of these compounds with chasmata and double ridges. Upcoming observations with the NIRSpec spectrograph on the James Webb Space Telescope (program 1,786, spanning 2.9–5 μm) will improve our understanding of the Uranian moons' surface compositions but will not provide spatial context. Hence, both high‐resolution imaging and infrared spectroscopy by a future spacecraft mission would confirm the nature of the material and test its association with craters, mass wasting features (e.g., landslides), or faults.

6.4. Constraints on the Moons' Habitability Potential

Assessing the habitability potential of the large Uranian moons is an important goal stated by the Roadmap to Ocean Worlds (Hendrix et al., 2019) and UOP study (NASEM, 2022). This knowledge would add to our understanding of the processes that drive the evolution of icy bodies in the 1,000‐km size range. A major question raised in these two references is about the nature of heat sources that keep oceans worlds going. This question should be expanded to encompass the mechanisms that preserve internal heat by decreasing heat loss. Clathrate hydrates have been suggested as insulating material and inhibitor of convection (e.g., Castillo‐Rogez et al., 2019; Kamata et al., 2019) but chemical modeling suggests these compounds may not be favored in the environments hosted by the Uranian moons. If present, they would increase the shell densities to >1,000 kg/m³; however, their signature in the gravity (Figures 11 and 12) is likely to be overwhelmed by the contributions of other interior properties (or at least the gravity inversion will not be unique).

Porosity provides another means to decrease heat loss and could exhibit some signature in the geology. For example, Bland et al. (2022) point out that the relaxed morphology of Yangoor crater on Ariel cannot be explained by the radiogenic heat flow. Instead >60 times higher heat flow sustained for hundreds of My or weaker thermomechanical properties of Ariel's crust may be required. Bland et al. suggest a thick porous layer could insulate heat loss and increase the temperature of the lithosphere, a hypothesis that our modeling supports with the caveat that an episode of intense tidal heating could have led to significant creep‐driven compaction. A future mission should aim at characterizing crater morphologies for a wide range of crater sizes in order to inform the thermophysical properties of the moons' upper crusts.

Similarly, the large fraction of porosity that may remain in Miranda's shallow subsurface, based on our modeling and assuming that tidal heating did not drive compaction or melting on a global scale, can affect the interpretation of geological features in terms of heat flow (Beddingfield, Leonard, et al., 2022). These authors point out evidence of high‐porosity material at least regionally, the radial extent of which may be determined by a future mission.

If the occurrence of NH₃ and NH₄ compounds associated with recent geological features is confirmed at Ariel, then their relative concentrations could provide a rough estimate of the temperature regime of the ocean (Figures 7 and 13). This could prove a critical source of information if the ocean temperature is below ∼245 K and does not exhibit an induced magnetic field detectable by spacecraft. Incidentally, that temperature is close to the lower limit for metabolic activity and reproduction of terrestrial microbes, based on the current state of knowledge (see Clarke, 2014; Cockell et al., 2016 and references therein). Hence, this kind of ocean may not be of great interest for astrobiology, although one cannot rule out that certain life‐forms may be able to thrive in this environment. In any case, the EC of ammonium, carbonate, and chloride mixtures should be measured over a wide range of temperatures, down to ∼240 K in order to narrow down conditions under which liquid may be present but not carry a detectable magnetic field.

The relict oceans would be highly concentrated solutions because the starting composition of these bodies, if they formed in the Uranian CPD, was likely rich in CO and CO₂ ices and NH₃, leading to CO₃–NH₄‐rich compositions. Alternative formation models (i.e., Uranian ring origin) could lead to a feedstock depleted in volatiles but still involve chloride brines. The habitability potential of such briny environments with compositions not encountered naturally on Earth (e.g., high NH₃ abundance) needs to be addressed in greater detail. In particular, this potential depends in part on the preservation of chemical gradients. The thick ice shells (>100 km) limit the flux of surface oxidants and therefore the flux of surface chemical energy available to any life (e.g., Hand et al., 2007) over the long term. On the other hand, radiolysis of water has been suggested as a possible mechanism for creating chemical gradients in porous rocky layers (Altair et al., 2018; Bouquet et al., 2017). In Titania and Oberon, the warmest models include a late phase of silicate dehydration that could replenish the residual ocean in oxidants, as simulated by Melwani Daswani and Castillo‐Rogez (2022) in the case of Ceres. However, remote sensing techniques are limited in the number of minerals and ices they can tease out from the surface. Future near infrared (NIR) observations intended to address moon habitability should aim for both high spectral (<20 nm) and spatial (∼km scale) resolution in order to assay compounds that may be associated with recent geological features.

7. Summary

This study considered three sources of information for assessing the prospect that the Uranian moons currently host liquid water in their interiors: observational constraints about their internal and geological evolution, the current level of tidal heating, and thermal models. Based on the results presented in this study, we predict that Ariel, Umbriel, Titania, and Oberon could have preserved deep liquid until present, sustained by radioisotope decay heat combined with a decreased thermal conductivity of the outer shell that may be due to porosity (e.g., Bierson & Nimmo, 2022; Neumann et al., 2020). Even then, the oceans predicted at present would likely be thinner than ∼50 km or confined to porosity in the upper part of the rocky core. However, these residual oceans could still be detectable by in situ magnetic probing, provided that their temperatures do not fall too much below the water freezing point (≲245 K). Our models assumed conductive ice shells and thus represent a favorable outcome in terms of heat transfer. One cannot rule out convection onset in these moons, at least for some periods in their evolution (see King et al., 2022), which could accelerate freezing.

A notable exception is Miranda. Despite its intriguing geology and candidate ocean world categorization by Hendrix et al. (2019), this study could not find scenarios that would preserve a deep ocean in that moon until present. The shape data returned by Voyager 2 suggests that Miranda could be partially differentiated. However, differentiation cannot be explained by the scenarios simulated with the thermal evolution models presented here (CPD accretion >3 Myr after CAIs, no tidal heating). If confirmed, differentiation was likely triggered by an episode of intense tidal heating consistent with high heat flow signatures associated with some of the coronae (Beddingfield et al., 2015). Furthermore, the potential role of obliquity‐driven tides, dynamic fluid tides, and MMRs (Chen et al., 2014; Ćuk et al., 2020; Tyler, 2014) in heating Miranda should be explored in combination with its thermal evolution. Miranda could also have formed in conditions or circumstances different from those explored in this study, for example, within the Uranian rings (Crida & Charnoz, 2012; Hesselbrock & Minton, 2019).

Ariel is particularly interesting as a future mission target because of the potential detection of NH₃‐bearing species on its surface (Cartwright et al., 2021) that could be evidence of recent cryovolcanic activity, considering these species should degrade on a geologically short timescale. Geologic features, visible in Voyager 2 Imaging Science Subsystem images of Ariel, show some evidence for cryovolcanism in the form of double ridges and lobate features that may represent emplaced cryolava (Beddingfield & Cartwright, 2021). A future mission aimed at confirming the state of differentiation and presence of a deep ocean in Ariel would help put these surface observations in context. The largest moons, Titania and Oberon, are also expected to preserve a deep ocean with thicknesses of a few tens of kilometers. The presence of deep oceans is consistent with constraints on Q/k ₂ inferred from dynamical models (Ćuk et al., 2020), as a possible but not unique interpretation. A stronger case can be made for Titania, whose low Q/k ₂ appears to require both a low Q and high k ₂ (i.e., a thick shell decoupled from the rocky core by a deep ocean), at least within the assumptions of the Ćuk et al. study (e.g., assumed Q/k ₂ for Uranus).

Based on current understanding, we conclude that the Uranian moons are more likely to host residual or “relict” oceans than thick oceans. As such, they may be representative of many icy bodies, including Ceres, Callisto, Pluto, and Charon (De Sanctis et al., 2020). The detection and characterization (depth and thickness) of deep oceans inside the Uranian moons, Miranda and Ariel in particular, and refined constrain on surface ages would help assess whether these bodies still hold residual heat from a recent resonance crossing event and/or are undergoing tidal heating due to dynamical circumstances that are currently unknown (as was the case at Enceladus before the Cassini mission). Future work should aim to model the implications of increased tidal heating due to resonance crossing on the global evolution of the moons.

On the other hand, if freezing is more advanced than envisioned in this study, a residual ocean temperature may fall below ∼245 K and may not exhibit an induced magnetic field detectable by spacecraft. In this case, evidence and nature of a deep ocean may be found in the exposure of deep ocean material, as suggested for Ariel, and may be Miranda. In any case, the EC of ammonium, carbonate, and chloride mixtures should be measured over a wide range of temperatures, down to ∼240 K in order to narrow down conditions under which liquid may be present but not carry a detectable magnetic field.

Testing for the presence of deep oceans in the Uranian moons and their communication with the surface would increase our understanding of the processes preserving liquid reservoirs in icy moons <1,000 km in diameter, and address the prospect for the existence of habitable environments across the outer solar system.

Erratum

In the originally published version of this article, figure 14 incorrectly omitted parts G, H, I, and J. The figure has been corrected, and this updated version may be considered the authoritative version of record.

Appendix A. Perple_X Model Input

See Table A1.

Table A1.

Bulk Compositions Used in Perple_X Models

Element	Comet 67P/C‐G	CI chondrite
	wt.%	wt.%
H	11.4	2.02
C	27.08	3.56
N	1.03	0.30
O	41.06	45.96
K	0.03	0.06
Mg	0.99	9.80
Al	0.18	0.87
Si	10.54	10.95
S	1.81	5.47
Ca	0.08	0.94
Fe	6.10	18.93

Note. The composition of Comet 67P/Churyumov‐Gerasimenko is a synthesis from Pätzold et al. (2016), Dhooghe et al. (2017), Le Roy et al. (2015), and Bardyn et al. (2017), and using a dust‐to‐ice mass ratio of 4:1, as inferred by Pätzold et al. (2016). The CI chondrite composition was obtained from the compilation by Palme et al. (2014).

Appendix B. Radioisotope Decay Parameters

We include heat produced from the decay of short‐ (aluminum: ²⁶Al) and long‐lived (uranium: ²³⁵U, ²³⁸U; thorium: ²³²Th; and potassium: ⁴⁰K) radioisotopes. For an origin in Uranus’ circumplanetary disk (CPD), we assume a time of formation between 3 and 4.5 million years (Ma) after calcium aluminum‐rich inclusion (CAI)‐formation, consistent with aforementioned references (Section 3.2). We use the CI composition for K, U, and Th abundances (e.g., Lodders, 2021) (see Appendix A).

The present‐day (t = 4.56 Gy after CAI‐formation) long‐lived radiogenic heating rate per unit mass of rock is the sum Σ (X _i H _oi ln(2)/t _1/2 exp[–ln(2) t/t _1/2]) with H ₀ representing decay energy, t _1/2 half‐life, and X _i abundances per kg of rock for each isotope i. Parameter values are provided in Table B1.

Table B1.

Isotope Concentrations and Decay Parameters Used in This Study

Species i	Isotope fraction (wt.%) of element at present	Decay heat production H 0 (W/kg)	Half‐life t 1/2 (year)
26Al/27Al	5 × 10−5	3.57 × 10−1	7.16 × 105
40K/39K	0.0119	29.17 × 10−6	1.277 × 109
238U/U	99.28	94.65 × 10−6	4.47 × 109
235U/U	0.71	568.7 × 10−6	7.0381 × 108
232Th/Th	100.00	26.38 × 10−6	14.01 × 109

Note. Isotope parameters are from Van Schmus (1995) for the long‐lived radioisotopes and Castillo‐Rogez et al. (2009) for ²⁶Al. Elemental abundances for a CI chondrite compositions are [U] = 0.00816 ppm, [Th] = 0.0298 ppm, [K] = 539 ppm, and [Al] = 8,370 ppm (Lodders, 2021).

The potential extraction of K as a consequence of rock‐leaching during a phase of aqueous alteration and the potential exchange of NH₄ ⁺ with K⁺ (Engel et al., 1994; Neveu et al., 2017; Zolotov & Shock, 2001) are possibilities depending on the moon and its aqueous environment. From modeling the dependence of ocean composition on various parameters, in particular the effective W/R, Castillo‐Rogez, Melwani Daswani, Glein et al. (2022) (hereafter referred to as CR22) found that the fraction of K leached from the rock may range from 10% to 30% of the accreted K abundance. For the W/R ∼ 1 assumed for the small moons considered in this study, K leaching is limited (about 10%). Melwani Daswani and Castillo‐Rogez (2022) find that up to 50% of the K may be redistributed from the processed rock to the liquid phase as a consequence of thermal metamorphism. This displacement of a major heat source could contribute to heating the base of the hydrosphere (see Castillo‐Rogez et al., 2019), However, thermal metamorphism was generally limited in extent in the Uranian moons, except may be for Titania and Oberon, as shown in the text.

Appendix C. Conditions for Clathrate Formation

Depending on the composition of accreted volatiles and internal evolution, clathrate hydrate formation may be possible (see Castillo‐Rogez, Melwani Daswani, Glein, et al., 2022; Castillo‐Rogez et al., 2010). It depends primarily on the fate of accreted carbon ices, in particular how much CO₂ is dissolved into the ocean (which occurs when pH << 7) and how much is turned into carbonates (which occurs when pH >> 7) (see CR22). CR22 show that the fate of the CO₂ is in part determined by the effective water‐to‐rock ratio, W/R (i.e., the mass of water that a unit mass of rock is exposed to during aqueous alteration). This parameter is not well constrained but the literature on icy moons and carbonaceous chondrite parent bodies has reported W/R values of the order of 0.5–4 (see CR22 for a review). For the several wt.% of CO₂ and ∼1 wt.% NH₃ expected in the Uranian moons (e.g., Mousis et al., 2020), and a W/R < 4, the oceanic environment is more likely to be favorable to the formation of carbonates, resulting in a high fraction of bi/carbonate ions in solution (CR22) with little CO₂ left in solution.

We examined the freezing of the only scenario in CR22 that could lead to a pH < 7 and the concentration of CO₂, which occurs when the accreted [CO₂] = 5 wt.% and [NH₃] = 0.3 wt.% and a water to rock ratio of 10 (we refer the reader to that paper for more context). The molality of CO₂ at equilibrium is 0.3 mol/kg. FREZCHEM modeling shows that water is still primarily used for ice formation and only 1.5 mol.% of water is used for the formation of clathrates, leading to the production of a marginal amount of that material. Clathrate formation consumes residual liquid until full freezing at about 250 K. The thickness of a global layer of CO₂ clathrates formed in this example is 7 km and lies below a ∼220 km thick ice shell. The production of clathrates could be inhibited by the presence of salts (e.g., Sloan & Koh, 2008), although this inhibition might be counteracted by a self‐preservation mechanism for low salt concentrations (<0.2 mol; see Boström et al., 2021). For a high salt concentration in a residual ocean, clathrates are likely to become unstable, resulting in erosion of clathrate accreted in the shell and the release of CO₂ in the residual ocean. Altogether, it appears that the occurrence of a thick layer of CO₂ clathrates is unlikely in the Uranian moons. Methane clathrates are not expected either because there is little methane in the system. Kamata et al. (2019) and Carnahan et al. (2022) have suggested methane clathrates to be abundant in large icy bodies due to the breakdown of abundant OM mixed with rock in the core of these bodies. In the case of Ceres, a relevant analog to the Uranian moons in terms of size (central pressure ∼150 MPa), radioisotope heat budget, and composition, Melwani Daswani and Castillo‐Rogez (2022) shows that the output of methane from thermal metamorphism of the core is negligible (<10⁻⁴ mol/kg).

Appendix D. Interior Evolution Modeling

The model used in this study combines modules that compute thermal and chemical evolution (Figure D1). All the software pieces have been demonstrated in previous studies (e.g., Thermal code with crust compaction module, Castillo‐Rogez et al., 2007; GWB: Geochemist's Workbench, Castillo‐Rogez et al., 2018, 2022; FREZCHEM, Marion et al., 2010; Castillo‐Rogez et al., 2018). We pursue two kinds of simulations: evolution of the ocean composition and physical evolution of the interior. The two aspects are not coupled at present, the main implication being that we obtain bounds on possible evolution outcomes. Future work funded to couple the two aspects (Castillo‐Rogez, Melwani Daswani, & Cockell, 2022) will be able to estimate the likelihood of particular outcome for a set of starting assumptions.

Figure D1.

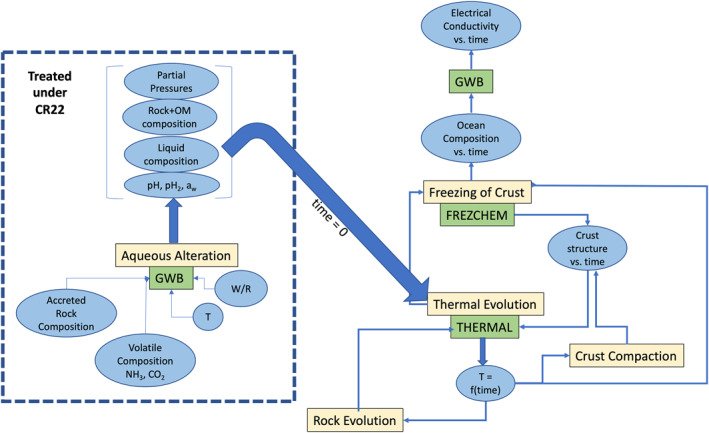
Modeling scheme used in this study. The initial compositions used for the ocean evolution modeling via FREZCHEM are inherited from the CR22 study. See text for additional information.

Heat transfer is computed by conduction

$$\frac{\partial \left(kT\right)\partial T\left(r\right)/\mathrm{d}r}{\partial r}+\frac{2}{r}\left(k\left(T\right)\frac{\partial T\left(r\right)}{\partial r}\right)=\rho \left(r\right)C_{\mathrm{p}}\left(T\right)\left(\frac{\mathrm{d}T\left(r\right)}{\mathrm{d}t}\right)-H\left(r\right)$$ (D1)

where T is temperature (in Kelvin), r local radius (in meters), k thermal conductivity, r material density, C _p specific heat, time, and H internal heating (radiogenic, tidal dissipation).

This is a one‐dimensional thermal model. Equation (D1) is integrated through a series of layers of varying composition using the Crank‐Nicolson scheme (e.g., Parker & Crank, 1964). The radial step is 2 km and the time step is 10⁴ yr for all the models.

The thermophysical properties of the materials are recomputed at each time step (see details below). Latent heat is accounted for both in the freezing of the ice shell and the hydration and then dehydration of the rock.

It is assumed that early on, ice melt occurs as a consequence of radioisotope decay heat, that is, convection onset does not prevent ice melting. The latter situation would limit the prospect of internal differentiation. This assumption is motivated by observational constraints indicating objects in the same size range are differentiated in a high‐density, rocky mantle, and a rich‐rich shell (e.g., Ceres, Park et al., 2016; Dione, Beuthe et al., 2016). Convection in the ocean is not modeled but thermal equilibrium is assumed between the base and top of the ocean. That is, the ocean temperature remains slightly above the water ice melting point. The latter assumption may not apply in the case of residual oceans at the base of which kilometers‐thick salt layers could accumulate (see Melwani Daswani et al., 2021 who suggest that kilometers of gypsum could sediment at the base of Europa's ocean.) More accurate modeling of heat transfer in a thin ocean with a high concentration of salts is left for future work.

Lastly, the thermal code handles rock dehydration at ∼725 K, accounting for latent heat. As an example, Figure D3 summarizes the outcomes of Titania's rocky core thermal evolution. Titania is taken as an example because of the high likelihood that its core underwent some thermal metamorphism. However, the broad input parametric space leads to a wide range of outcomes.

D1. Porosity Evolution

Porosity compaction proceeds via two mechanisms: pore crushing when the burden pressure exceeds the ice strength. The maximum initial porosity (before compaction) is taken as 0.5, an upper bound generally assumed in the literature (e.g., Durham et al., 2005; Kossacki & Leliwa‐Kopystyński, 1993; Yasui & Arakawa, 2009). We use the experimental work by Durham et al. (2005) to describe the initial porosity profile in the crust. The lowest temperature tested in that paper (77 K) is close to the surface temperature of the moons (Table 1). The residual porosity at 150 MPa is ∼0.15. Experimental work by Yasui and Arakawa (2009) shows that the effect of rock on the evolution of the bulk porosity is negligible for the rock volume fractions relevant to the Uranian moons (∼12 vol.% for Miranda; ∼28 vol.% for Ariel and Umbriel; ∼34 vol.% for Titania and Oberon). These authors find that porosity may be up to 0.3 at 10 MPa and 0.2 at 20 MPa, which corresponds to a depth of about 80 km in Titania (see Figure D2).

Figure D2.

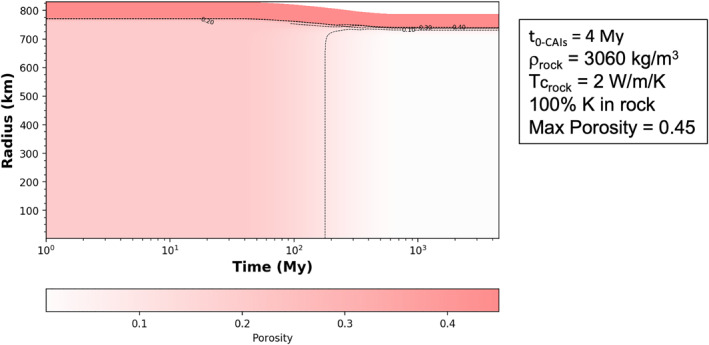
Porosity evolution for the model of Titania presented in Figure 5.

As temperature increases, compaction is driven by viscous flow following the description in Nimmo et al. (2003), based after Fowler (1985). The rate of removal is as follows:

$$\mathrm{d}\varphi /\mathrm{d}t=-\varphi P/\eta$$ (D2)

with P the lithostatic pressure and η the viscosity of the ice‐rock mixture (assumed to be Newtonian, i.e., only a function of stress). Then, the porosity decrease with depth is computed after

$$\varphi (z,t)={\varphi }_0\left(z\right)\exp (-t/\tau )$$ (D3)

where ϕ ₀ (z) is the initial porosity profile (as a function of depth z) and τ is a function of the material porosity as τ (z) = η(z)/P(z). We adopt the ice flow law from Durham and Stern. (2001) based on observation that the low rock volume fractions have little bearing on the overall material behavior (e.g., Durham et al., 2009).

Figure D3.

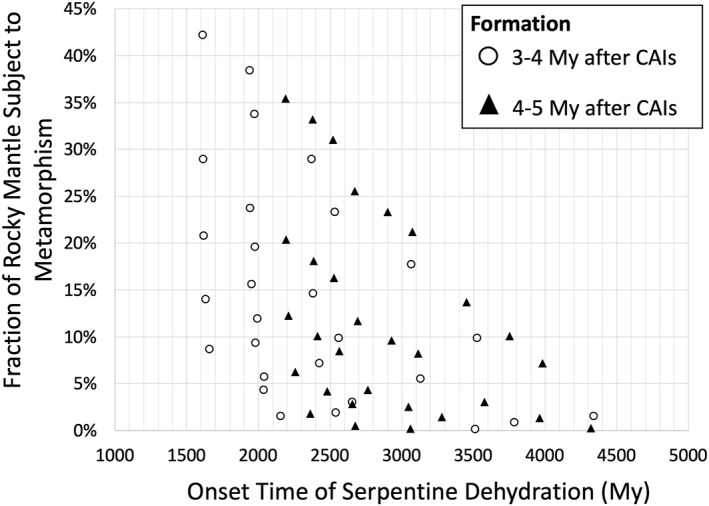
Onset time and extent of thermal metamorphism (dehydration of serpentine) in Titania's rocky core, assuming the moon accreted from chondritic material for various conditions (time of formation with respect to calcium aluminum‐rich inclusions, rocky core thermal conductivity).

Porosity could be preserved in the crust, depending on its composition and thermal evolution. Bierson and Nimmo (2022) assume the preservation of porosity in a pure ice shell, assuming the body is already differentiated. However, Neumann et al. (2020) showed that bodies with a cold crust, such as Kuiper belt objects, may preserve a thick and undifferentiated crust. That is, a porous crust would also entail the presence of silicate and other compounds, such as nonwater ices (e.g., NH₃ hydrates and CO₂).

D2. Material Thermal Properties

Rock thermal conductivity (T _c) shows little dependence on temperature above 300 K (e.g., Opeil et al., 2010, 2020). However, the T _c of dry rock can decrease to 1 W/m/K at 70 K. Opeil et al. (2020, 2010) showed that the T _c of CM chondrites is <1 W/m/K between 70 and 300 K. The T _c of ordinary chondrites (H and L) is ∼1.5–2 W/m/K at and above 100 K. We also use specific heat capacities for carbonaceous materials reported in Opeil et al. (2020, Table 3).

Ice thermal conductivity strongly depends on temperature T after the relationship: 0.4685 + 488.12/T (Slack, 1980). The T _c of H₂O ice at the effective surface temperature at 19 AU (∼70 K) is about 7.5 W/m/K. At 273 K, the water ice T _c is 2.3 W/m/K. Hence, the prospect for the Uranian moons to preserve a deep ocean despite their cold environment depends in part on the presence of porosity or of materials that act as insulators.

Previous studies have assumed that the microporosity of freshly accreted material may be up to 50% (e.g., Eluszkiewicz & Leliwa‐Kopystyński, 1989). To account for the effect of porosity on thermal conductivity, we use the relationship derived by Bierson et al. (2018) based on the Shoshany et al. (2002) empirical results 5:

$$K\left(\mathrm{\Phi }\right)=k_{\mathrm{i}\mathrm{c}\mathrm{e}}\left(T\right){\left(1–\mathrm{\Phi }/{\mathrm{\Phi }}_{\mathrm{p}}\right)}^{(a\mathrm{\Phi }+b)}$$ (D4)

with Φ the porosity, T the temperature (K), k _ice the thermal conductivity of the ice and a, b, and Φ _p are empirical constants: a = 4.1, b = 0.22, and Φ _p = 0.7.

This equation is valid for a porous mixture if the fraction of porosity Φ _p is lower than 20%. For higher fractions the effect becomes more complex as grains may become loosely connected (e.g., Shoshany et al., 2002).

The effective thermal conductivity of a mixture of materials is the sum of the volume fractions f _i of each material I, after

$$k_{\mathrm{m}\mathrm{i}\mathrm{x}}={\sum }_i{f}_i{k}_i$$ (D5)

For a temperature of 70 K, a mixture of ∼70 vol.% ice (∼7.5 W/m/K) and 30 vol.% rock (∼1 W/m/K) is about 5.5 W/m/K. For Φ _p = 15%, T _c becomes ∼4.5 W/m/K; Φ _p = 40% decreases this value to ∼1.1 W/m/K; and Φ _p = 50% to ∼0.3 W/m/K.

At 150 K, the T _c of the solid ice‐rock mixture is ∼2.9 W/m/K. If Φ _p = 15% remains at the corresponding pressure, then T _c may be ∼2.4 W/m/K.

Our thermal modeling tracks the evolution of T _c with compaction, composition (porous mixture vs. ice and rock layers), and temperature. Lastly, the core size is adjusted based on the amount of rock trapped in the undifferentiated crust and the grain density is slightly updated to account for the effect of porosity in decreasing the overall density. This is particularly important for Miranda whose residual porosity may be up to 20% (Figure 5), which implies a grain density of about 1,450 kg/m³.

An example of porosity evolution model (Titania) is presented in Figure D2. The difference in evolution between the assumed Φ _p = 45% and maximum porosities of 0.4 and 0.5 is negligible, in part because the ice high thermal conductivity in the shallow subsurface conditions leads to a similar bulk thermal conductivity in all cases.

Castillo‐Rogez, J. , Weiss, B. , Beddingfield, C. , Biersteker, J. , Cartwright, R. , Goode, A. , et al. (2023). Compositions and interior structures of the large moons of Uranus and implications for future spacecraft observations. Journal of Geophysical Research: Planets, 128, e2022JE007432. 10.1029/2022JE007432

Data Availability Statement

This work uses physical and dynamical properties for the Uranian moons from NASA's Solar System Dynamics websites: https://ssd.jpl.nasa.gov/sats/phys_par/ and https://ssd.jpl.nasa.gov/sats/ephem/. The physical properties (shape radii and GM) are the values adopted by the International Astronomical Union (Archinal et al., 2018). The density and thermophysical parameters used for the models are available in Castillo‐Rogez et al. (2019) and in Appendix D. The files used to build Figures 3, 4, 5, 7, 9, 10, and 13 are available in Castillo‐Rogez, Weiss, et al. (2022). Figure 1 is based on Hussmann et al. (2006) updated with the latest radii and density estimates in https://ssd.jpl.nasa.gov/sats/phys_par/. Figure 2 is based on equations provided by Zharkov et al. (1985). Figure 6 is a simple mass balance calculation. Figures 11 and 12 are based on Equations (4), (5), (6), (7) provided in the text. Figures 14 and 15 are based on equations provided in Weiss et al. (2021).